1 Introduction

The collision-less cold dark matter (CDM), along with the cosmological constant (\(\varLambda \)CDM model of cosmology) explains the large scale structure (greater than the \({\mathcal {O}}\) (100 Mpc) scale) of the Universe. But on the small scales, it faces major issues such as the core cusp problem, missing satellites problem, too big to fail problem etc. For more detail on the small scale issues, see reviews [1, 2]. It has been proposed that instead of the DM to be collision-less, if the DM particles interact with each other via elastic scattering over the scale where the problem is severe, then it can address the above mentioned problems [3,4,5,6,7]. The success of the SIDM lies in the fact that at the small scale due to large density, the SIDM behaves like a collisional dark matter, but on a large scale due to small density, it behaves like the collision-less DM. Thus the SIDM can explain both the small and large scale observations very well.

It is pointed out that the collisional nature of SIDM on the small scales can lead to viscosity. The SIDM fluid having viscosity is defined as viscous self-interacting dark matter (VSIDM) fluid. In Ref. [8], using the kinetic theory formalism, we have calculated the viscous coefficients of the VSIDM fluid. There we show that the viscous dissipation of the VSIDM becomes prominent at present, and consequently, it can explain the present observed accelerated expansion of the Universe. Therefore, the VSIDM fluid model can unify both the dark sectors, i.e., dark matter and dark energy, of the Universe. Furthermore, in Refs. [9, 10], using this framework, we study the cosmic evolution at the small redshifts, and report that the decreasing fluid velocity gradients on earlier time can explain the late time cosmological observations.

The inclusion of viscosity in the cosmic fluid has richer dynamical consequences in comparison with the ideal cosmic fluid. In literature, the effect of cosmic viscosity, especially bulk viscosity (unlikely shear viscosity, it is consistent with the homogeneity and isotropy on the large scale structure), has been explored in the different epochs of cosmic evolution. For a homogeneous and isotropic expansion (Friedmann–Lamaitre–Robertson–Walker space time metric) of Universe, the presence of the bulk viscosity contribute the negative pressure, so the total cosmic fluid pressure (\(P_{T}\)) becomes, \( P_{T} = P -3\zeta H \), where P is kinetic pressure and H is Hubble expansion rate. In case of sufficiently large cosmic viscosity, the total fluid pressure may be negative and leads to accelerated expansion of the Universe. Therefore, the viscous cosmic fluid may explain the early time acceleration (cosmic inflation) [11,12,13,14], and also the late-time cosmic acceleration [15,16,17,18,19,20,21,22,23,24,25,26]. In recent work, Floerchinger et al. [27], argued that at late time of the cosmic evolution when the structure formation takes place then due to large velocity gradients, the shear viscosity may also become important and play significant role in cosmic dissipation. If the shear viscosity is large enough, it can also leads to accelerated expansion. However, it remains unclear which kind of particles in the Universe can produce such a large viscosity. Later, in Ref. [8], we proposed that the VSIDM could provide a possible source to create such a large viscosity. Further, in Ref. [28], authors have found that the viscous dark matter can reduce the tension between the Planck and local measurements of the Hubble expansion rate. In other works [29, 30], we show that the dark matter viscous energy dissipation can increase its temperature, and also lead to visible photon production [30, 31]. These generated photons may increase the number density of photons in the Rayleigh–Jeans limit of the Cosmic Microwave Background (CMB) radiation, and can explain the 21-cm anomaly reported by EDGES collaboration [30].

Furthermore, the presence of the cosmic viscosity may cause to alter the standard cosmic evolution history and the large scale structure formation. A large DM viscosity can increase the DM temperature [29], decay of gravitational potential fluctuations [24], reduces the growth of the density perturbation [32, 33] and damping of the gravitational waves [34,35,36]. Therefore, the DM viscosity is severely constrained from the different astrophysical and cosmological observations. For recent work on cosmic viscosity, see Refs. [37,38,39,40,41], and also, to study the effect of cosmic viscosity on early and late time of evolution of the Universe, see review [42].

In this work, we estimate the bulk and shear viscosity of SIDM in the kinetic theory framework and study its evolution at late time of the cosmic evolution. We check the dependency of bulk viscosity onto the sound speed and find that for a large sound speed \( C_{n}>0.0027 \), \( \zeta \) becomes large in comparison with the \( C_{n}=0 \) case. Further, considering the astrophysical limit on \( \sigma /m \), we show that the VSIDM violates the lower bound on \(\eta /\mathfrak {s}\), given by \( \eta /\mathfrak {s}= \frac{1}{4\pi }\) [43], Then in the assumption that the conjectured KSS bound is universal, we derive a constraint on ratio of velocity average self-interacting scattering cross-section to its mass. Later, we also explore the parameter space for SIDM mass and report that the SIDM particle mass should be sub-GeV scale.

Here, we also explore the evolution of SIDM viscosities (both shear and bulk viscosity) in light of the low redshift observations. For this purpose, we assume that during the small redshift \( 0 < z \le 2.5 \), the cluster scale may not be completely virialized, but gravitationally bound, and the DM fluid velocity gradient is constant on a scale \(\sim 3- 20 \) Mpc. In this case, the viscous coefficients of SIDM fluid may vary with the redshift. Further, in order to study the viscous evolution, we consider the power-law form for bulk \(\zeta (a)= \zeta _{0} \left( a/a_{0}\right) ^{\alpha }\), and shear viscosity, \(\eta (a)= \zeta _{0} \left( a/a_{0}\right) ^{\alpha }\) for \( C_{n}=0 \) case, where a and \( a_{0} \) represents the scale factor at any epoch and its present value, respectively. We then use Einstein’s equation and energy–momentum conservation equations and calculate the background quantities such as the Hubble expansion rate, H(z) and deceleration parameter, q(z) for small redshift.

Then, assuming the length scale of spatial average as \( \sim 20 \) Mpc [9], which is much larger than the cluster scale, we estimate the best fit value of the model parameter, \(\alpha \) which explain the cosmic chronometer data and also obtained the correct value of deceleration parameter in the matter-dominated era. The best fit value of the model parameter suggests the decreasing DM viscosity on the earlier times (large redshift) and also explains the low redshift observations. In the VSIDM fluid model, we also calculate the age of the Universe and find that it is smaller than the age inferred from the CMB anisotropy data [44] but larger than the globular cluster age [45].

The arrangement of our work is as follows: in Sect. 2, we briefly discuss the motivation of viscous self-interacting dark matter and estimate the mean free path and the length scale over which the SIDM viscosity and spatial averages should be estimated. Then we calculate the bulk and shear viscosity of SIDM from the kinetic theory in relaxation time approximation. In Sect. 3, we study the KSS bound violation in the presence of VSDIM fluid. Later, in the assumption that KSS lower bound is universal, we derive a theoretical upper limit on \( \langle \sigma v \rangle /m \) and also estimate the constraint on SIDM mass. In Sect. 4, using the Einstein field equations and energy–momentum conservation equations, we derive the dependency of the deceleration parameter on the SIDM viscosity. Further, we set up the coupled differential equations for the Hubble rate and deceleration parameter at low redshifts. In Sect. 5, we estimate the best-fit values of the model parameter and discuss our results. In the last Sect. 6, we conclude our work.

2 Viscous self-interacting dark matter (VSIDM)

SIDM is a lucrative alternative candidate to address the small scale problems faced by the collisionless dark matter, due to large DM self-interactions at those relevant scales, see a review [2]. On the small scales, the DM density is large; hence the collisions are efficient, whereas, on the large scales due to small density, DM behaves as collisionless. Therefore, the SIDM can explain both the small and large scale structure data. Unlike the CDM, where only the gravitational interaction is important, in case the SIDM halo, the collisions between the DM particles also participate into the halo formation. A large DM self-interaction cross-section causes the heat transfer between the outer and inner layer of the DM halo, and leads to the core profile towards the central region of the DM halo which matches with the astrophysical observations [46,47,48].

Since the small scales demands the non zero self-interaction between the DM particles, hence it is interesting to explore the viscous effect contributed via this interaction. But before this, we estimate the scale over which the SIDM viscosity needs to be calculated.

2.1 Scale of the SIDM viscosity and spatial averages

The minimum scale on which the viscosity coefficients of VSIDM fluid should be calculated will depend on the length scale over which the fluid description of the SIDM particle is valid. The hydrodynamic description of the SIDM particles will be valid when the mean free path of the dark matter particle, \(\lambda _{\textrm{SIDM}}\) is less than the length scale, L under consideration, i.e. \(\lambda _{\textrm{SIDM}} < L\) (also see Section 4). In the dilute gas approximation, the mean free path of SIDM particle is given by \( \lambda _{\textrm{SIDM}}= \frac{1}{\sqrt{2}}\left( \frac{1}{n\sigma }\right) \) [49]. In a simplified manner, the expression can be re-written as

$$\begin{aligned} \lambda _{\textrm{SIDM}}\sim 3\times 10^{9} \left( \frac{m/\sigma }{\mathrm {gm/cm}^{2}} \right) \left( \frac{ \textrm{M}_{\odot }\textrm{kpc}^{-3}}{\rho } \right) \textrm{kpc}~, \end{aligned}$$
(1)

where, \(m/\sigma \) and \( \rho \) should be taken in units of \( \mathrm {gm/cm}^{2} \) and \( \textrm{M}_{\odot }\textrm{kpc}^{-3} \), respectively. Using the isothermal profile for the SIDM particles (which happens due to at least one scattering between the DM particles) for cluster scale and \( \rho \sim 2\times 10^{7}~\textrm{M}_{\odot }\textrm{kpc}^{-3}\), \(\sigma /m = 0.1\) cm\(^2/\)g as obtained from Ref. [50], we get \( \lambda _{\textrm{SIDM}}=150\) kpc, which is smaller than the cluster size DM halo (\(\sim \) Mpc). Thus we assume that the length scale, where viscosity estimation has to be done, should be at least cluster or larger scales (i.e. supercluster scale), see also Refs. [8, 9].

In this study, we are interested to calculate the viscous coefficients of SIDM fluid at a late time, when the DM halo has been gravitationally bound and more or less virialized (so that the fluid description is valid). In order to estimate the viscous coefficients of the SIDM, we apply the kinetic theory in the relaxation time approximation. Using the kinetic theory and hydrodynamics, one can derive the expression for bulk \(\zeta \) and shear viscosity \(\eta \) as [51,52,53]

$$\begin{aligned} \zeta= & {} \frac{1}{T}\int \frac{d^3p}{(2\pi )^3}~\tau (E_{p})~\left[ E_{p}C_{n}^2 - \frac{p^2}{3E_{p}}\right] ^2 f_{p}^{0}~~, \end{aligned}$$
(2)
$$\begin{aligned} \eta= & {} \frac{1}{15T}\int \frac{d^{3}p}{(2\pi )^{3}}~\tau (E_{p})~\frac{p^{4}}{E_{p}^{2}}~f_{p}^{0}~~, \end{aligned}$$
(3)

where \( \tau (E_{p})\), T and \( f_{p}^{0} \) represent the relaxation time, temperature and the equilibrium distribution function of the SIDM, respectively. Here \(C_{n} = \left. \frac{\partial P}{\partial \epsilon }\right| _{n}\) is the speed of sound at constant number density and \( E_{p}=(p^{2}+m^{2})^{\frac{1}{2}} \) is the total energy of a SIDM particle. Further, one can also obtain the entropy density, \( \mathfrak {s} \) of the viscous SIDM medium as

$$\begin{aligned} \mathfrak {s} =\frac{1}{T} \int \frac{d^{3}p}{(2\pi )^{3}}~\left[ E_{p}+ \frac{p^{2}}{E_{p}}\right] ~f_{p}^{0}~~. \end{aligned}$$
(4)

In the relaxation time approximation, one assumes that collisions between the particles are sufficient enough to take system close to the local thermodynamic equilibrium in relaxation time. In this work, we approximate the relaxation time to the thermal average relaxation time, \( \tilde{\tau } \). For the scattering process \( a (p_{a})+b(p_{b})\leftrightarrow c (p_{c})+d(p_{d}) \), \( \tilde{\tau }_{a} \) is defined as

$$\begin{aligned} \tilde{\tau }_{a}^{-1} =\sum _{b}^{} n_{b} \langle \sigma _{ab} v_{ab}\rangle , \end{aligned}$$
(5)

Here, \( \langle \sigma _{ab} v_{ab}\rangle \) is the average velocity weighted cross-section, defined as

$$\begin{aligned} \langle \sigma _{ab} v_{ab}\rangle =\frac{\int d^{3}p_{a}d^{3}p_{b}~\sigma _{ab}~v_{ab}~\exp \left( \frac{-E_{a}}{T}\right) \exp \left( \frac{-E_{b}}{T}\right) }{\int d^{3}p_{a}d^{3}p_{b}~\exp \left( \frac{-E_{a}}{T}\right) \exp \left( \frac{-E_{b}}{T}\right) }~. \end{aligned}$$
(6)

where, \(\sigma _{ab}\) is the scattering cross-section and \(v_{ab}\) is the relative velocity between a and b interacting particle. Further, \(n_{b}\) represents the number density of particle b, given by

$$\begin{aligned} n_{b} = \int _{0}^{\infty }\frac{d^{3}p_{b}}{(2\pi )^{3}}~f_{p_{b}}^{0}~~. \end{aligned}$$
(7)

From Eq. (5), we see that the value of \( \tilde{\tau }_{a}\) depends on the particle physics motivated model. Here we assume that the DM particles are colliding with themselves elastically and take \( n_{a}=n \) and \( \langle \sigma _{ab} v_{ab}\rangle =\langle \sigma v\rangle \). We emphasize the assumption that the relaxation time approximation holds, when the dark matter particle scatters with each other at least one time in the DM halo formation time \( t_{\textrm{halo}} \), i.e. \( t_{\textrm{halo}}/\tilde{\tau }_{a}\approx 1 \). In Ref. [8], it has been shown that for the SIDM, the relaxation time approximation is valid at galactic and cluster scale and hence can be applied for its viscosity estimation on these scales.

In order to calculate the SIDM viscosity, we assume that the DM is non-relativistic, and follow the Maxwell-Boltzmann distribution. This implies that \( E_{p}\sim m+\frac{p^{2}}{2m} \) and \( f_{p}^{0}=\exp \left( -\frac{p^{\mu }u_{\mu }}{T} \right) \), where \( p^{\mu }\) and \(u_{\mu } \) represents the four momentum and four velocity of the SIDM particle, respectively. In the rest frame of DM fluid, i.e., \(u^{\mu } =(1,0,0,0)\) and constant sound speed, integration of Eq. (2) provides us an expression for the SIDM bulk viscosity as (keeping terms upto \((T/m)^{3}\) and neglecting higher orders)

$$\begin{aligned} \zeta&= \frac{m}{12\langle \sigma v\rangle } \left[ 12C^{4}_{n}\left( \frac{m}{T} \right) + 5(4+9C^{4}_{n})\left( \frac{T}{m} \right) \right. \nonumber \\&\quad \left. + ~ (-2+3C^{2}_{n})\left\{ 12C^{2}_{n} + 70\left( \frac{T}{m} \right) ^{2}\right\} + 315\left( \frac{T}{m} \right) ^{3}\right] \end{aligned}$$
(8)

Using the same assumptions as above, we can also estimate the shear viscosity from Eq. (3) as

$$\begin{aligned} \eta = \frac{m}{\langle \sigma v\rangle }\left( \frac{T}{m} \right) \bigg [1-7\left( \frac{T}{m} \right) + \frac{63}{4}\left( \frac{T}{m} \right) ^{2}\bigg ]~. \end{aligned}$$
(9)

Further, from Eq. (4) the expression for entropy density is obtained as

$$\begin{aligned} \mathfrak {s}=\left( \frac{m^{2}}{2\pi }\right) ^{\frac{3}{2}}\left( \frac{T}{m} \right) ^{\frac{1}{2}} \left[ 2+5\left( \frac{T}{m} \right) -15\left( \frac{T}{m} \right) ^{2} \right] \end{aligned}$$
(10)

From above Eqs.  (8), (9) and (4), we see that the viscous coefficients (\( \eta , \zeta \)) and entropy density depends on the ratio of SIDM temperature to its mass (T/m) and its higher orders \( {\mathcal {O}} \left[ (T/m)^{2}, ...\right] \). We assume that the VSIDM behaves like cold dark matter, hence \(T/m \sim v^{2}_{\textrm{vd}}\ll 1 \), where \( v_{\textrm{vd}} \) is the DM velocity dispersion on the scale of our interest. The VSIDM model respect the DM coldness criteria since from cluster to supercluster scale T/m varies from \( 10^{-5} \) to \( 10^{-4} \). Thus, for a good approximation it is sufficient to put the linear term in T/m and neglect the higher order term in the expressions of Eqs. (8), (9) and (4). Therefore the simplified form of the bulk and shear viscosity is written as

$$\begin{aligned} \zeta =&\frac{m}{\langle \sigma v\rangle }\left( \frac{T}{m} \right) \left[ \frac{5}{3}\bigg ( 1+\frac{9}{4}C^{4}_{n}\bigg ) -2C^{2}_{n}\bigg (1-\frac{3}{2}C^{2}_{n}\bigg )\left( \frac{m}{T} \right) \right. \nonumber \\&\left. + ~ C^{4}_{n}\left( \frac{m}{T} \right) ^{2} \right] , \end{aligned}$$
(11)
$$\begin{aligned} \eta =&\frac{m}{\langle \sigma v\rangle }\left( \frac{T}{m} \right) . \end{aligned}$$
(12)

Here we find that the shear and bulk viscosities depend on mass (m), temperature T, velocity average scattering cross-section (\( \langle \sigma v\rangle \)) of the SIDM particles. We emphasize that the expression for shear and bulk viscosity is quite general and can be applied to the non-relativistic fluid follow the Maxwellian distribution with constant sound speed, and validates the relaxation time approximation.

Further, using the argument of equi-partition of energy \(\frac{1}{2}m\langle v^{2} \rangle = \frac{3}{2}T\) and relation between the root-mean square and average velocity relation, \(\sqrt{\langle v^{2} \rangle }=1.085 \langle v \rangle \), we get the simplified form of the SIDM bulk and shear viscosity from Eqs. (11) and (12) as

$$\begin{aligned} \zeta&= \frac{1.18}{3} \frac{m\langle v \rangle ^{2}}{\langle \sigma v\rangle }\left[ \frac{5}{3}\bigg ( 1+\frac{9C^{4}_{n}}{4}\bigg ) -5.1\frac{C^{2}_{n}}{\langle v\rangle ^{2}} \bigg (1-\frac{3}{2}C^{2}_{n}\bigg )\right. \nonumber \\&\quad \left. + ~ 6.5 \left( \frac{C_{n}}{\langle v\rangle } \right) ^{4} \right] , \end{aligned}$$
(13)
$$\begin{aligned} \eta&= \frac{1.18}{3} \left( \frac{m}{\langle \sigma v\rangle }\right) \langle v\rangle ^{2}~ \end{aligned}$$
(14)

We point out that for vanishing sound speed case, i.e., \(C_{n} = 0 \), we get the expressions of SIDM viscosity as same as reported in Ref. [8].

3 Fundamental properties of SIDM from \( \eta /\mathfrak {s} \) bound

In the previous section, we have calculated the SIDM viscosity. Here, we study the SIDM properties in the light of \(\eta /\mathfrak {s}\) bound. In Ref. [43], Kovtun, Son and Starinets (KSS) have conjectured a bound on the ratio between the shear viscosity to entropy density \( \eta /\mathfrak {s} \) (also known as KSS bound), given by

$$\begin{aligned} \frac{\eta }{\mathfrak {s}}\ge \frac{1}{4\pi }. \end{aligned}$$
(15)

There it has been argued that the lower bound on \( \eta /\mathfrak {s} \), i.e. \(\frac{\eta }{\mathfrak {s}}= \frac{1}{4\pi } \) is universal and can be applied for various classes of quantum field theories. The success of the viscosity bound lies in the fact that no experiment has yet confirmed the violation of the lower bound given in Eq. (15). However, there are some theoretical studies where the violation from the KSS bound has been reported, see Refs. [54,55,56,57]. For a status report on this topic, we refer [58].

In our VSIDM model, the ratio of shear viscosity to entropy density, \( \eta /\mathfrak {s}\) is obtained by using Eqs. (9) and (10), which gives us

$$\begin{aligned} \frac{\eta }{\mathfrak {s}}=\frac{1}{2}\left( \frac{2\pi }{m^{2}} \right) ^{\frac{3}{2}} \left( \frac{m}{\langle \sigma v \rangle }\right) \left( \frac{T}{m}\right) ^{\frac{1}{2}}. \end{aligned}$$
(16)

From the above equation, we see that \( \eta /\mathfrak {s}\) depends on the velocity average cross section \( \langle \sigma v \rangle \), temperature, T and mass of SIDM particle. Using \(\langle \sigma v \rangle \sim \sigma \langle v \rangle \) in Eq. (16), we see that \( \eta /\mathfrak {s} \) only depends on m and \( \sigma /m \). Thus to study the \( \eta /\mathfrak {s} \) as a function of DM mass, m we need to provide the \( \sigma /m \) values on cluster scales.

As discussed in Sect. 2, the constraint on \( \sigma /m \) are obtained from the small scale observations, which explanation requires the self-interactions between the DM particles. A strong upper limit on the \( \sigma /m \) comes from the merging cluster IE 0657-56, which require \( \sigma /m< 1.25~ \textrm{cm}^2/\textrm{gm}~ \) [5]. However, a velocity dependent scattering cross-section, which explain the galactic to cluster scale issues requires slightly smaller value of \(\sigma /m\). On cluster scale, the velocity dependent \(\sigma \) demands \( \sigma /m \approx 0.1\) cm\(^{2}/\)gm [50].

Fig. 1
figure 1

The ratio of shear viscosity to entropy density, \( \eta /\mathfrak {s}\) is plotted as a function of DM mass. The red line corresponds for KSS lower bound, \(\frac{\eta }{\mathfrak {s}} = \frac{1}{4\pi }\) [43]

Full size image

In Fig. 1, using Eq. (16), we plot \( \eta /\mathfrak {s} \) on the cluster scale as a function of DM mass for the different values of \( \sigma /m \) at present \( z=0 \). Here solid blue and solid black line corresponds for \(\sigma /m =1.25\)cm\(^{2}/\)gm and \(\sigma /m =0.1 \)cm\(^{2}/\)gm, respectively. The red solid line corresponds for the lower KSS bound, i.e. \( \eta /\mathfrak {s} = 1/4\pi \). Since \(\eta /\mathfrak {s}\propto m^{-3}\), so it decreases for large DM mass, therefore it is possible that for some large DM mass, \( \eta /\mathfrak {s}\) may be smaller than its lower limit inferred from KSS bound (solid red line). From Fig. 1, it is clear that larger is the \(\sigma /m \), smaller is the DM mass on which the \(\eta /\mathfrak {s}\) comes below the KSS lower bound. For example, for \(\sigma /m =1.25\) cm\(^{2}/\)gm , \(m = 0.21 \) GeV and for \(\sigma /m =0.1\)cm\(^{2}/\)gm, \(m = 0.5\) GeV.

In the above discussion, it becomes clear that in the VSIDM model, the KSS bound is violated or not depends on the DM mass. We will explain both the possibility in upcoming subsections.

3.1 KSS lower bound violation in VSIDM fluid

In Fig. 1, since the \( \eta /\mathfrak {s}\) comes below the KSS lower bound, thus we may assume that the VSIDM fluid can violate the \( \eta /\mathfrak {s}=\frac{1}{4\pi }\) bound. The DM mass over which the DM does not respect the KSS bound depends crucially on the \(\sigma /m\) value. The violation of \( \eta /\mathfrak {s}\) bound can be confirmed when the future DM detection experiment will detect the larger mass of DM particle inferred from the KSS lower bound.

3.2 Constraint on SIDM properties from KSS bound

In this case, we assume that the KSS lower bound is universal; thus, it allows us to study the SIDM microphysics such as scattering cross-section \(\sigma \) and it’s mass. This assumption is based on the fact that no experiment has reported the violation of KSS bound in any fluid, viz superfluid Fermi gas [59], Quark–Gluon liquid [60]; therefore, this bound is well established by the experiment up to their current precision. Furthermore, considering the KSS bound as universal, the properties of dark sectors, viz dark matter [61] and dark energy [57] has also been investigated in the literature.

The constraint on \(\langle \sigma v \rangle /m\) can be obtained by using Eqs. (16) and (15), which provides us

$$\begin{aligned} \frac{\langle \sigma v \rangle }{m}\le (2\pi )^{\frac{5}{2}}\left( \frac{1}{m}\right) ^{3} \left( \frac{T}{m}\right) ^{\frac{1}{2}}~. \end{aligned}$$
(17)

This represents a theoretical constraint on the ratio of velocity average DM self-interaction cross-section to its mass using the KSS bound. We see that the bound on \(\langle \sigma v \rangle /m\) depends on the mass and the temperature of the SIDM particles. We emphasize that this limit is general and can be used to estimate the model parameters for the various particle physics model of SIDM. In the approximation \(\langle \sigma v \rangle \sim \sigma \langle v \rangle \) and \(\langle v \rangle \sim \left( \frac{3T}{m}\right) ^{\frac{1}{2}}\), the above inequality can be manifest in term of \(\sigma /m\) as

$$\begin{aligned} \frac{\sigma }{m}\le 1.2\times 10^{-2}\left( \frac{\textrm{GeV}}{m}\right) ^{3}~ \left[ \frac{\textrm{cm}^{2}}{\textrm{gm}}\right] . \end{aligned}$$
(18)

We see that the constraint on \(\sigma /m\) depends on the SIDM mass and not on its temperature.

Furthermore we point out that the small scale observations provides a constraint on \( \sigma /m \) value, which have discussed above. Therefore, now our interest is to derive a constraint on the DM mass. For this purpose, we use Eq. (18), and obtained as

$$\begin{aligned} m\le 0.23 \left( \frac{m/\sigma }{\textrm{gm}/\textrm{cm}^{2}} \right) ^{\frac{1}{3}} ~\textrm{GeV}. \end{aligned}$$
(19)

The implies that the DM mass allowed from KSS bound depends only on \( \sigma /m \) value. It is also clear that the larger \(\sigma /m\), the smaller the DM mass allowed. For \(\sigma /m =1.25\)cm\(^{2}/\)gm (upper limit from the cluster merger) , \(m\le 0.21 \) GeV and for \(\sigma /m =0.1\)cm\(^{2}/\)gm (required to explain the cluster scale issues for velocity dependent \(\sigma \)), we get slightly larger DM mass, \(m\le 0.5\) GeV.

Here, we mainly focus on the second possibility, which assumes that the VSIDM respects the KSS bound. Thus, based on the above discussion, we conclude that the KSS lower bound impose restrictions on DM mass and allowed only sub-GeV SIDM mass. Since bound on the DM mass only depends on \( \sigma /m \) value; therefore, the constraint on the DM mass will be improved further for more precise numerical simulations and astrophysical observations on \(\sigma /m\) in future.

Recent direct detection experiments for the DM searches have almost failed to detect the particle dark matter candidate of the mass range varies from few GeV to TeV scale (Weakly-interacting massive particles (WIMP) like DM particles). Therefore, our result provides a new window of the DM mass range, which is crucial for the future dark matter search experiments. We refer Ref. [62] for details of the experiment, which will probe the sub-GeV DM mass range.

4 Viscous self interaction dark matter cosmology

In this Section, we investigate the effects of VSIDM fluid on the cosmic evolution history of the Universe through Einstein’s equation and energy–momentum conservation equations following the formalism discussed in Refs. [8, 27].

In the VSIDM model, we assume that the Universe is mainly dominated by the dark matter with no dark energy component. In the Landau frame with first-order gradient expansion, the energy momentum tensor of the VSIDM can be written in terms of the ideal and the viscous contributions as

$$\begin{aligned} T^{\mu \nu } = T^{\mu \nu }_{\textrm{ideal}} + T^{\mu \nu }_{\textrm{visc}} \end{aligned}$$
(20)

where, the ideal and viscous terms are given by

$$\begin{aligned} T^{\mu \nu }_{\textrm{ideal}}= & {} \epsilon u^{\mu } u^{\nu } + P \varDelta ^{\mu \nu }~~,\nonumber \\ T^{\mu \nu }_{\textrm{visc}}= & {} \varPi _{B} \varDelta ^{\mu \nu } + \varPi ^{\mu \nu }~, \end{aligned}$$
(21)

where, \(\epsilon \), \( u^{\mu } \) and P represents the energy density, four velocity and kinetic pressure of the dark matter fluid. In Eq. (21), \( \varDelta ^{\mu \nu } = u^{\mu } u^{\nu } + g^{\mu \nu }\) is defined as the projection operator, which is orthogonal to the four velocity vector, i.e. \( u_{\mu }\varDelta ^{\mu \nu }=0\). Here, \(\varPi _{B}\) and \(\varPi ^{\mu \nu }\) represents bulk and shear stress, which forms are given as

$$\begin{aligned} \varPi _{B}= & {} - \zeta \nabla _{\mu } u^{\mu } \end{aligned}$$
(22)
$$\begin{aligned} \varPi ^{\mu \nu }= & {} - \eta \left[ \varDelta ^{\mu \alpha }\varDelta ^{\nu \beta } + \varDelta ^{\mu \beta }\varDelta ^{\nu \alpha } - \frac{2}{3}\varDelta ^{\mu \nu }\varDelta ^{\alpha \beta }\right] \nabla _{\alpha }u_{\beta }.\nonumber \\ \end{aligned}$$
(23)

The important property of shear stress is that it is orthogonal to the four velocity vector, \(u_{\mu } \varPi ^{\mu \nu } = 0\) and also traceless, \( \varPi _{\mu }^{\mu } = 0\).

To study the cosmic evolution in the VSIDM model, we apply the Einstein equations, and energy momentum conservation equations, given as

$$\begin{aligned} G_{\mu \nu } =-8\pi G T_{\mu \nu }~~\textrm{and} ~~\nabla _{\mu } T^{\mu \nu } = 0. \end{aligned}$$
(24)

Further, we assume the scalar metric perturbation of the form

$$\begin{aligned} ds^{2} = a^{2}(\tau )\left[ -\big ( 1+2\psi (\tau ,\textbf{x})\big ) d\tau ^{2} + \big ( 1-2\phi (\tau ,\textbf{x})\big )\textbf{dx}^{2} \right] \end{aligned}$$
(25)

and neglect the vector and tensor perturbations in metric. In the above Eq. \( a(\tau ) \) is scale factor and \( \psi , \phi \) are the potentials, respectively. At the late time, we assume \( \psi , \phi \ll 1\) (see Ref. [27] and references therein) and fluid velocity is small, i.e. \({\textbf{v}}^{2}\ll 1\). Then, using the average energy density equation and the average trace of Einstein’s equation, one can get the evolution equation of deceleration parameter q as [27]

$$\begin{aligned} \frac{dq}{dz} + \left( \frac{q-1}{1+z}\right) \bigg [2q-(1+ 3 \hat{w}_{\textrm{eff}})\bigg ] = \frac{4\pi G D(1 - 3 \hat{w}_{\textrm{eff}})}{3(1+z) H^{3}} \end{aligned}$$
(26)

where, the D term is defined by

$$\begin{aligned} D&= (1+z)^{2}\left<\eta \left[ \partial _{i}v_{j} \partial _{i}v_{j}+\partial _{i}v_{j}\partial _{j}v_{i} - \frac{2}{3}\partial _{i}v_{i}\partial _{j}v_{j} \right] \right>_{s} \nonumber \\&\quad + (1+z)^{2}\left<\zeta [\mathbf {\nabla }\cdot \textbf{v}]^2\right>_{s} + (1+z)\left<{\textbf{v}}\cdot \mathbf {\nabla }(P-6\zeta H)\right>_{s}. \end{aligned}$$
(27)

Where \(\langle A \rangle _{s}\) represents the spatial average of A. Here v is the peculiar velocity, and spatial derivative represents the derivative w.r.t. comoving coordinate. The effective Equation of State (EoS) is given by \( \hat{w}_{\textrm{eff}}=\frac{\langle P\rangle _{\textrm{eff}}}{\langle \epsilon \rangle _{s}}~\), where \( \langle P\rangle _{\textrm{eff}} \) is effective pressure, which is the sum of the kinetic and the bulk viscous pressure of SIDM, i.e. \(\langle P\rangle _{\textrm{eff}} = \langle P\rangle _{s} +\langle \varPi _{B}\rangle _{s} \) . We also define the EoS corresponding to the bulk viscous pressure of the VSIDM as \( \hat{w}_{B} =\frac{\langle \varPi _{B}\rangle _{s}}{\langle \epsilon \rangle _{s}}\) . From Eq. (26) it is clear that the dynamics of the Universe depends on the dark matter effective EoS, \( \hat{w}_{\textrm{eff}} \) and D term.

Further, from Eq. (26) it is manifest that the Universe will be in accelerated phase if [27]

$$\begin{aligned} \frac{4\pi G D}{3 H^{3}} > \frac{1+3\hat{w}_{\textrm{eff}} }{1-\hat{w}_{\textrm{eff}}}~. \end{aligned}$$
(28)

provided that \( \hat{w}_{\textrm{eff}}\ne 1 \). The above condition suggests that for accelerated expansion, the dissipational effects of the DM should be sufficiently large. For example, for the present observed cosmic acceleration, \( \frac{4\pi G D}{3 H^{3}}|_{z=0} = 4.13 \) [9]. Thus, in order to study the strength of viscous dissipation and its effect on the cosmic evolution at small redshift, we need to calculate the D term given in Eq. (27), which will be done in the next Section.

4.1 Calculation of D term

From Eq. (27), we see that the term D crucially depends on the spatial average of the velocity gradient and viscosities. Thus its calculation demands the explicit estimation of the spatial averages. In this work, without going into the detail calculation of the spatial averages, we will approximate the dissipation term D using the following assumptions:

(i) We focus our analysis only on small redshift intervals. In this study, this interval can be typically estimated using the hydrodynamical validation of the SIDM model. For SIDM particles, the fluid description is applicable when the relaxation time or mean free time, \(\tau \) of SIDM is less than the Hubble time, i.e., \(\tau H <1\), where \(\tau =(\frac{\rho \sigma v}{m})^{-1} \) [27]. In order to estimate the relaxation time, we focus on massive clusters that were formed at an earlier time, \(z\sim 2.5\) [63, 64]. Further, we also consider that the density profile of the cluster and the velocity dispersion of the DM do not change substantially, although this is not always the case [64]. For simplicity, we take \( \rho \sim 2\times 10^{7}~\textrm{M}_{\odot }\textrm{kpc}^{-3}\), \(\sigma /m = 0.1\) cm\(^2/\)g and \( v \sim 1000\) km/sec [50]. The Hubble expansion rate is given by \( H(z) \approx H_{0}\left[ \varOmega _{M0}\left( 1+z \right) ^{3}+ \varOmega _{\varLambda }\right] ^{1/2}\), where \( \varOmega _{M0} \), \(\varOmega _{\varLambda }\) and \( H_{0} \) correspond to the present values of matter density (DM and baryon), dark energy, and the Hubble expansion rate, respectively. Their values are taken from the Planck 2018 data [65]. Then, using the above-mentioned values we find that on large redshifts, the \(\tau H \) value increases and on \(z=2.5\), \(\tau H (z=2.5)\sim 0.64 < 1~.\) So, using the above-simplified assumptions, we find that the fluid dynamics is valid for \( 0\le z \le 2.5\). However, at a comparably larger redshift, \( z>2.5 \), the clusters have not been observed except their progenitors, i.e., protoclusters [64, 66] and thus limit out analysis. In the future, information about a more precise cluster formation history will constrain our analysis further. Therefore, in light of the above, we focus our study on a small redshift, \( 0\le z \le 2.5\).

(ii) To estimate the spatial avarges, we assumed the lower limit of the spatial average as a fluid scale (from which the fluid description of the DM starts, i.e., cluster size scale, \(\sim 3\) Mpc) and an upper limit as a homogeneity scale of Universe, i.e., \(\sim 100\) Mpc. It is because our interest is to estimate the effect of the local inhomogeneities on the background quantities such as Hubble expansion rate and deceleration parameter, which is defined on the homogeneity scale. Furthermore, we argue that the small length scale physics is contributing significantly to the viscosity contribution; therefore, spatial averages should be estimated on small scales. This can be understood using the Navier–Stokes equation, given by [67]

$$\begin{aligned}&\rho \left( \partial _t u^i+ u^j\cdot \nabla _j u^i\right) = -\frac{\partial P}{\partial x^{i}} \nonumber \\&\quad +\frac{\partial }{\partial x^j}\left[ \eta \left( \frac{\partial u^i}{\partial x^j}+\frac{\partial u^j}{\partial x^i} -\frac{2}{3}\frac{\partial u^k}{\partial x^k}\delta ^{ij}\right) +\zeta \frac{\partial u^k}{\partial x^k}\delta ^{ij}\right] ~. \end{aligned}$$
(29)

Now since the viscous coefficient is proportional to the mean free path, \(\eta \sim \rho v\lambda _{\textrm{mfp}}/3\) (where v and \(\lambda _{\textrm{mfp}}\) represents the average velocity, and mean free path, respectively), therefore if we compare the second or third term on the right-hand side with the last term on the left-hand side, we find that as the length scale increases the viscous contribution decreases and hence on the large scale, the effect of the viscosity can be ignored. Thus we may conclude that the major contribution from the viscous term comes from the smaller length scales, i.e., cluster scales. Our argument also supports the conclusion as suggested in Ref. [68] that the viscosity effect plays an important role on the length scale less than the Hubble scale.

(iii) Further we assume that on the redshift of our interest \( 0\le z \le 2.5\), the length scale equal to or larger than the cluster scale (between the fluid element scale to homogeneity scale, viz \(3~\textrm{Mpc}~ \le L\le 100\) Mpc.), the spatial average peculiar velocity gradient \(\langle \partial v \rangle _{s} \) is constant, i.e. \(\langle \partial v \rangle _{s} \sim constant\). Then we can approximate

$$\begin{aligned} \langle \partial v \rangle _{s} \sim v_{0}/L~~, \end{aligned}$$
(30)

where \(v_{0}\) and L represents the peculiar velocity and comoving length scale. In particular, our assumption implies that the peculiar velocity and comoving length scale varies in such a way that so that the ratio of these two becomes constant for the low redshift. To check the validity of the above assumption at present, we calculate the \( v_{0}/L \) on a typical cluster and larger scale. For typical cluster scale \(L \sim 3 \) Mpc, DM velocity \( v_{0} \sim 1000\) km/s, so \( v_{0}/L \sim 10^{-17}\) sec\(^{-1}\) and for typical larger scale \(L \sim 20\) Mpc and \(v_{0}\sim 6000\) km/s so \( v_{0}/L\sim 9\times 10^{-18}\) s\(^{-1}\). This suggests that the velocity gradient decreases but in a first approximation, we treat the velocity gradient as a constant on these scales, and hence validates our assumption. However, as the scales become large and approach towards homogeneity viz \(20~\textrm{Mpc} < L\le 100\) Mpc, the fluid velocity gradient decreases significantly and they does not contribute much in dissipation. Therefore, we neglect the contribution of velocity gradient on the large scale, \(L>20\) Mpc in the calculation of dissipation.

(iv) The variation of viscosity coefficients \(\zeta ,\eta \) are independent with space since they depend on the thermal distribution of the dark matter [9]. Here we assume that the dark matter viscosity may vary within the low redshift interval, \( 0 < z \le 2.5\). In order to study the variation in \(\zeta \) and \(\eta \) from Eqs. (13) and (14), we need to understand the evolution of the \( m/\langle \sigma v\rangle \), \(C_{n} = 0\) and \( \langle v\rangle \) with redshift individually, that depends on the particle physics model of the SIDM. In this study, assigning the redshift dependence information in the power-law form, we consider the bulk and shear viscosities of the SIDM fluid as

$$\begin{aligned} \zeta (z)= & {} \zeta _{0} \left( \frac{a}{a_{0}}\right) ^{\alpha }= \zeta _{0}\left( \frac{1}{1+z}\right) ^{\alpha } , \end{aligned}$$
(31)
$$\begin{aligned} \eta (z)= & {} \eta _{0} \left( \frac{a}{a_{0}}\right) ^{\alpha }= \eta _{0}\left( \frac{1}{1+z}\right) ^{\alpha } , \end{aligned}$$
(32)

where, \(\alpha \) is the viscosity parameter whose sign decides how the SIDM viscosities are evolving with the redshift. Here, \( \frac{a}{a_{0}} =\frac{1}{1+z}\), where \( a_{0}=1 \) is the present value of the scale factor. Furthermore, \( \zeta _{0}=\zeta (z=0) \) and \( \eta _{0}=\eta (z=0) \) represents the present values of bulk and shear viscosity, respectively. Their values can be estimated from the Eqs. (13) and (14) using the cluster scale constraint at present.

Thus, utilizing the above approximations, we may evaluate the D term given in Eq. (27) as

$$\begin{aligned} D \sim \left( \frac{4}{3}{\eta _{0}} + 2\zeta _{0} \right) \left( \frac{v_{0}}{L}\right) ^2\big (1+z\big ) ^{2-\alpha }~. \end{aligned}$$
(33)

From the above equation, it is clear that for very large averaging length scale (\( L \rightarrow \infty \)) or vanishing viscosity coefficients (\( \eta =0, \zeta =0 \)), D term becomes zero and the VSIDM fluid behaves like a dissipationless fluid. We also see that for \(\alpha =2\), the dissipation will constant with the redshift. In the assumption \( v_{0}/L \) is constant, \(\eta _{0}\) and \(\zeta _{0}\) is fixed at \(z=0\), therefore, D terms will depend only on \(\alpha \) parameter.

4.2 Background cosmology in VSIDM model

Furthermore, equipped with the simplified form of D, now we will set up the evolution equations for the Hubble expansion rate and deceleration parameter. Assuming the cold VSIDM fluid, i.e. \( \hat{w}_{\textrm{eff}} \approx 0 \) and using Eq. (33), Eq. (26) simplifies as

$$\begin{aligned} \frac{dq}{dz} + \frac{(q-1) \left( 2q- 1\right) }{(1+z)} = \beta \left( \frac{1+z }{\bar{H}^{3}}\right) . \end{aligned}$$
(34)

Here \( \beta \) is the dissipation parameter, which is given as

$$\begin{aligned} \beta = \frac{4\pi G }{3H^{3}_{0}}\left( \frac{4}{3}{\eta _{0}} + 2\zeta _{0} \right) \left( \frac{v_{0}}{L}\right) ^2\big (1+z\big ) ^{-\alpha }~. \end{aligned}$$
(35)

where \(\bar{H} = H/H_{0}\) is dimension-less Hubble expansion rate and \(H_{0}=H(z=0)\) is the value of the present Hubble expansion rate. The dissipation term, \(\beta \) depends on exponent power, \(\alpha \) and averaging length scale, L.

In order to solve the Eq. (34), we need to provide the expression for the Hubble expansion rate. For this purpose, we use the definition of deceleration parameter \(q(z) = -1 + (1+z)~\frac{H'}{H} \), and obtain the evolution equation for \( \bar{H} \) as

$$\begin{aligned} \frac{d\bar{H}}{dz} = \left( \frac{q+1}{1+z}\right) \bar{H}~. \end{aligned}$$
(36)

Thus, we have obtained the coupled differential equations in q(z) and \( \bar{H}(z)\) given by Eqs. (34) and (36). These equations can be solved numerically by using the initial conditions at present, i.e. \(\bar{H}(z=0) = 1\) and \(q(z=0) = -0.60\) [69]. The solution of q(z) and \( \bar{H}(z)\) effectively depends on two free parameters \( \alpha \) and L, i.e. \( q(z,\alpha ,L) \) and \( \bar{H}(z,\alpha ,L) \). In this work, we will not calculate the averaging length scale, L but for the rest of our analysis we consider \(L\sim 20\) Mpc which is estimated in Ref. [9]. So the solutions for q and \( \bar{H}\) depend on only one free parameter, \( \alpha \), which will be estimated in next Section.

5 Analysis and results

In this section, we will first estimate the value of the free parameter, \(\alpha \) using the low redshift observations, and the standard \(\varLambda \)CDM model prediction. Then, using the best fit value of \(\alpha \), we will see the evolution of viscosity and bulk viscous EoS of the VSIDM fluid.

Fig. 2
figure 2

The Hubble expansion rate, H(z) obtained from our VSIDM model have been plotted with cosmic chronometer data and \(\varLambda \)CDM prediction as a function of redshift. A model with \(\alpha =1.22\) fit the cosmic chronometer data and matches with the \(\varLambda \)CDM prediction

Full size image

5.1 Hubble expansion rate

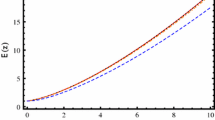
In Fig. 2, we have plotted the Hubble expansion rate, H(z) as a function of redshift for different values of \(\alpha \) with the cosmic chronometer data obtained from the Ref. [70]. The black, red and blue solid lines corresponds for \( \alpha =1.11, ~ \alpha =1.22 \) and \( \alpha =1.33 \), respectively.

To compare our viscous model with the standard cosmology, we have also plotted the Hubble expansion rate derived from the standard \(\varLambda \)CDM model (purple dashed line) in the Fig. 2. Here we see that the Hubble expansion depends on the dissipative strength of the dark matter, high is dissipation, large will be the H(z) . Although on small redshift, all models contribute equally to the Hubble rate, while on the large redshift due to difference in the dissipation term, all models contribute unequally in the H(z) and start deviating with each other.

We find that for \(\alpha =1.11\) case, the H(z) increases quickly and becomes very large at earlier times and does not fit the Hubble data at large redshift. Further, \( \alpha =1.33\) case the H(z) increases slowly in comparison with the \(\alpha =1.11\) case and does not fit the high redshift Hubble data. But for \( \alpha =1.22\) case, the H(z) explain the cosmic chronometer data and matches with the standard cosmological prediction.

Fig. 3
figure 3

The Distance modulus, \(\mu (z)\) obtained from the VSIDM model, have been plotted with the Union 2.1 SNe Ia data for different values of viscosity parameter, \(\alpha \). The plot suggests that the VSIDM model fits the SNe Ia data very well

Full size image

5.2 Fitting of Supernovae data

To fit the supernovae data from the VSIDM model, we calculate the measurable quantity distance modulus \(\mu \). It is defined as \(\mu \equiv m-M\), where m and M represents the apparent and absolute magnitude of Type Ia supernovae (SNe Ia). In terms of the luminosity distance \( d_{\textrm{L}} \), the distance modulus, \(\mu \) is defined as

$$\begin{aligned} \mu (z,\alpha )= 5\log _{10}{\left( \frac{\bar{d}_{\textrm{L}}(z,\alpha )}{\textrm{Mpc}} \right) } + 25, \end{aligned}$$
(37)

where, \( \bar{d}_{L}(z,\alpha )\) is a dimensionless luminosity distance, defined as \( \bar{d_{\textrm{L}}}(z,\alpha ) = H_{0}~d_{\textrm{L}} (z,\alpha )\). The luminosity distance is given as

$$\begin{aligned} d_{\textrm{L}}(z,\alpha ) =\frac{ (1+z)}{H_{0}}\int _{0}^{z}\frac{dz}{\bar{H}(z,\alpha )}. \end{aligned}$$
(38)

Further, using Eq. (37), we plot the distance modulus as a function of redshift for different values of \(\alpha \) along with the SNe Ia data in Fig. 3. We take Union 2.1 compilation SNe Ia data from the Refs. [71, 72], which consists of 580 SNe data. It can be clearly seen that the values of \(\alpha \) considered here, i.e., \(\alpha =1.11, 1.22\), and \(\alpha =1.33\), fit the SNe Ia data equally well. It implies that the fitting of SNe Ia data cannot suggest the correct evolution of the SIDM viscosity.

Fig. 4
figure 4

The deceleration parameter, q(z) obtained from the VSIDM model parameters, have been plotted with the \(\varLambda \)CDM model prediction

Full size image

5.3 Deceleration parameter, q

The deceleration parameter (q) defined in the Eq. (34) provides the information, whether the Universe is in the accelerating (for \(q>0\)) or the decelerating phase (for \(q<0\)). In order to see the epoch of decelerated to accelerated phase transition \(z_{\textrm{tr}}\) (i.e. epoch of \(q>0\) to \(q<0\)) in our VSIDM model, we plot the q(z) for different values of \(\alpha \), as a function of redshift in Fig. 4. The black, red and purple solid lines corresponds for \( \alpha =1.11, \alpha =1.22 \) and \( \alpha =1.33\), respectively. The purple dashed line corresponds for \(\varLambda \)CDM prediction. We can see that for large \(\alpha \), the transition point is earlier (on large redshift). For \(\alpha =1.11, ~1.22\) and \(\alpha =1.33\), the transition points are \(z_{\textrm{tr}}=0.58, ~ z_{\textrm{tr}}=0.66\) and \(z_{\textrm{tr}}= 0.81\), respectively. The transition point corresponding to \(\alpha = 1.22\) matches with the \(\varLambda \)CDM model prediction.

We point out from Fig. 4 that for \(\alpha =1.11\) case, the deceleration parameter increases and settles around \(q\sim 0.7\) for large redshift. It is quite in contrast with our expectation that q should approach 0.5 in the matter-dominated era. Also, it does not explain the large redshift Hubble data correctly, see Sect. 5.1. For \(\alpha =1.33\) case, at higher redshift, q is decreasing and approaching towards \(q\sim 0.16\), which is below the expected value of \(q=0.5\) in matter-dominated era. We may thus safely conclude that the case for \(\alpha =1.11\) or \(\alpha =1.33\) is surely not the case to describe the cosmic evolution appropriately.

Furthermore, from Fig. 4 we can see that for \(\alpha =1.22\) case, the deceleration parameter saturates around \(q\sim 0.49\), which is very close to our expectation and slightly different from the \(\varLambda \)CDM model q prediction. The important feature of this model is that the H(z) obtained from this model overlaps with the \(\varLambda \)CDM expectation of the Hubble parameter and describes the cosmic chronometer data correctly. Hence assuming \( C_{n} =0 \), \(\alpha =1.22\) is the most intriguing possibility to explain the Hubble data and q value and matches with some of the \(\varLambda \)CDM prediction.

Fig. 5
figure 5

The Statefinder pair \((r,\textrm{s}) \) evolution for the best fit model parameter \(\alpha =1.22\) in the VSIDM model of the Universe

Full size image

5.4 Statefinder technique

As we have seen in the previous subsection that the best fit value of the model parameter for VSIDM, \(\alpha =1.22\) matches with the \(\varLambda \)CDM model prediction. To see the deviation of the VSIDM model with the \(\varLambda \)CDM model, we adopt a geometric diagnostic approach, as discussed in Ref. [73], which was introduced to differentiate between the different dark energy models.

In this approach, one calculates a Statefinder parameter pair \( \left\{ r, \textrm{s} \right\} \), which is related to the higher-order derivative of the Hubble expansion rate. In terms of the redshift, the Statefinder parameters are defined as

$$\begin{aligned} r(z)= & {} 1 - 2(1+z)\left( \frac{H'}{H} \right) +(1+z)^{2}\left[ \left( \frac{H'}{H}\right) ^{2}+\frac{H''}{H} \right] \end{aligned}$$
(39)
$$\begin{aligned} \textrm{s}(z)= & {} \frac{1}{3}\left( \frac{r(z)-1}{q(z)-\frac{1}{2}}\right) \end{aligned}$$
(40)

The idea lies in the fact that \( \left\{ r, s \right\} \) pair is a fixed point given by \( \left\{ 1, 0 \right\} \) for \(\varLambda \)CDM model , and may varies for the other models. In Fig. 5, we plot the evolution of \(r - \textrm{s}\) plane for the best fit value of the parameter \(\alpha \). We find that for our VSIDM model the pair lies on the second quadrant of \(r - \textrm{s}\) plane in the past and evolve towards the first quadrant. The present value of pair in VSIDM model \( \left\{ r, \textrm{s} \right\} \) is \( \left\{ 0.87,0.03 \right\} \) which clearly implies that the VSIDM model is different from the \(\varLambda \)CDM model.

Fig. 6
figure 6

The bulk viscosity (\(\zeta \)) and shear viscosity (\(\eta \)) of VSIDM have been plotted as a function of redshift for the best fit model parameter, \(\alpha =1.22\). The blue line corresponds for shear viscosity, and the rest of the lines corresponds for bulk viscosity at different sound speeds

Full size image

5.5 Evolution of VSIDM viscosity on small redshift

In this subsection, we study the evolution of the bulk and shear viscosity of the VSIDM fluid with the redshift. In Fig. 6, using Eqs. (31) and (32), we plot, \( \eta (z) \) and \( \zeta (z)\) as a function of redshift for the best fit values of the viscosity parameter, i.e. \(\alpha =1.22\). The blue line refer for the shear viscosity and the rest of the other lines corresponds for the bulk viscosity for different values of sound speed. We see that the \(\zeta \) and \(\eta \) are large at present, \( z=0 \) and decreases on the larger redshift \( z>0 \). We also find that for small sound speed, \( C_{n} <0.027\), negative term in Eq. (11) becomes large and decreases \(\zeta \) in comparison with the \( C_{n} =0\) counterpart. But for large sound speed, \( C_{n} >0.027\), the positive term in Eq. (11) becomes large and increases \(\zeta \).

Further, we emphasize that the value of the VSIDM viscosity obtained here can only be possible at the late times when the non-linear structure formation takes place, and collapse objects are formed. Otherwise, as shown in Refs. [32, 33], for a sufficiently large DM viscosity at earlier times, the DM density perturbation may washout, and non-linear structure formation will not be possible.

As we have discussed above, at present (\(z=0\)), the viscous contribution from the bulk as well as shear DM viscosity increases on low redshift; thus, we may expect some consequences. In the Ref. [8], we have shown that at present, \( z=0 \), the viscous effects of VSIDM are significant and can explain the present observed acceleration of the Universe. Further, these results also provide us the physical basis of the cosmic acceleration and also why it starts at a late (low redshift), not at an early (large redshift).

5.6 EoS for VSIDM bulk viscosity

In this subsection, we study the evolution of EoS of VSIDM fluid on small redshift. In Fig. 7, we plot the equation of state corresponding the SIDM bulk viscosity, \( \hat{w}_{B}\) as a function of the redshift for the best fit value of viscosity parameter, i.e. \( \alpha = 1.22\). We see that on the small redshift \( \hat{w}_{B}\) subsequently becomes more negative and at present, \( \hat{w}_{B}(z=0)=-1.2\) and on large redshift, \( \hat{w}_{B}\) increases and approaches towards \( \hat{w}_{B}\sim 0\).

Fig. 7
figure 7

The equation of state, \( \hat{w}_{B}\) of VSIDM model as a function of redshift for best fit model parameter

Full size image

5.7 Age of universe

Further, using the VSIDM model, we calculate the Universe age, which is required for a model to describe the cosmic evolution correctly. The age of Universe at any redshift, \( t_{\textrm{U}}(z) \) is obtained from the Hubble expansion rate as

$$\begin{aligned} t_{\textrm{U}}(z)=\int _{z}^{\infty }~\frac{dz}{(1+z)H(z)} \end{aligned}$$
(41)

In this work, we have assumed that the SIDM viscosity becomes effective only at late time \( z\le 2.5 \), and consequently, the viscous effect modifies the evolution of the Universe only at a late time. At the early time \( z>2.5 \), the evolution of the Universe is governed through standard cosmology. Thus we consider

$$\begin{aligned} H(z) = \left\{ \, \begin{array}{ll} H_{\textrm{visc}} &{} \text {if} z\le 2.5 , \\ H_{\mathrm {\varLambda CDM}} &{} \text {if} z>2.5,\\ \end{array} \right. \end{aligned}$$
(42)

where \( H_{\textrm{visc}} \) is obtained from the Eqs. (34) and (36) and \( H_{\mathrm {\varLambda CDM}}\approx H_{0}\big [ \varOmega _{B}(z) + \varOmega _{\chi }(z) \big ]^{1/2}\). Thus, using the best fit value of \( \alpha \), we get

$$\begin{aligned} t_{\textrm{U}}\sim \frac{ 0.974}{H_{0}}. \end{aligned}$$
(43)
Fig. 8
figure 8

The age of the Universe is plotted as a function of the Hubble expansion rate. The red point corresponds for \( t_{\textrm{U}}=13 \) Gyr and \( H_{0} =71.5\) Km sec\(^{-1}\)Mpc\(^{-1}\) obtained from the best fit model parameter

Full size image

In Fig. 8, we plot the age of the Univere, \( t_{\textrm{U}} \) in the VSIDM model as a function of the Hubble expansion rate. We see that as the \( H_{0} \) increases, \( t_{\textrm{U}} \) decreases. In VSIDM model, using the best fit value of model parameter, \( \alpha =1.22 \), \(t_{\textrm{U}}=13 \) Gyr. Our estimation of \(t_{\textrm{U}}\) is slightly small in comparison with the age of the Univere (13.76 Gyr) obtained in the CMB anisotropy data [44] and larger than the age of globular cluster (12.9 Gyr) [45].

6 Conclusion

The self-interacting dark matter may solve the small scale puzzles of collision-less cold dark matter. In the case, if SIDM fluid is viscous, it may affect the cosmic evolution history and explain the present observed accelerated expansion of the Universe. In this work, we study the evolution of the viscous effect of SIDM from the low redshift observational data.

We calculate the bulk viscosity of VSIDM using the kinetic theory and relaxation time approximation. The VSIDM viscosities are calculated in the non-linear regime, assuming that the DM halos are gravitationally bound and may not completely virialize in \( 0 < z \le 2.5\). We check the dependency of bulk viscosity on sound speed and find that for low sound speed, \( C_{n}<0.0027 \), \( \zeta \) is small but for a high sound speed \( C_{n}>0.0027 \), \( \zeta \) becomes large in contrast with the \( C_{n}=0 \) case.

Furthermore, using the astrophysical constraints on the cluster scale, we find that the VSIDM fluid violates the KSS lower bound, i.e., \(\eta /\mathfrak {s}= \frac{1}{4\pi }\). Later assuming the KSS bound as Universal, we derive a constraint on velocity average self-interacting scattering cross-section to its mass and explore the SIDM mass for the values of \( \sigma /m \) from the observations. We show that the KSS bound constraint the DM mass range severely and allowed only a sub-GeV (\( {\mathcal {O}} (0.1)\) GeV) mass of the SIDM particle. In the future, this limit will be improved for a more precise estimation of \(\sigma /m \).

In this work, we also explore the SIDM viscosity evolution in the light of low redshift observations. For this purpose, we assume the power law form of bulk \( \zeta (z) =\zeta _{0}\left( a/a_{0}\right) ^{\alpha } \) and shear viscosity \( \eta (z) =\eta _{0}\left( a/a_{0}\right) ^{\alpha } \) of SIDM at the redshift of our interest. Then inspired from the observational evidence that velocity gradient is constant on typical cluster and supercluster scale at the present, we assume it to be constant on the low redshift interval \( 0 \le z \le 2.5 \).

Later, we calculate the Hubble expansion rate and deceleration parameter and find that it depends on the viscosity parameter, \(\alpha \), and fluid length scale, L. We assume the \(L=20\) Mpc, which is larger than the typical cluster size DM halo. Further, using the cosmic chronometer data points and the correct value of the deceleration parameter at the matter-dominated era, we obtain \( \alpha = 1.22\). The best fit values of model parameter shows that the viscous coefficients, \( \eta \) and \( \zeta \) are large at present, \( z=0 \) and decrease at earlier time \( z>0 \). The deceleration to an acceleration transition point in this model is \(z_{\textrm{tr}}= 0.66\) We also find that the VSIDM model fits with the supernovae data very well. Although our VSIDM model matches the \( \varLambda \)CDM prediction but using the Statefinder technique, we find that our model is different from the \( \varLambda \)CDM model. In VSIDM model, the age of the Universe is 13 Gyr, which is smaller than the age inferred from the CMB anisotropy data but larger than the globular cluster age.

Thus we conclude the VSIDM model can unify the dark sectors (DM and dark energy) and maybe a possible alternative theory of the standard model of cosmology at a small redshift. In case the KSS bound is Universal, our result provides a new DM mass window (sub-GeV scale), which will be crucial for future particle dark matter searches. We also point out that if the future DM detectors confirm a larger DM mass particles inferred from our bound, then KSS bound may not be Universal. Our results are independent of the SIDM particle physics model.