1 Introduction

The CERN Large Hadron Collider (LHC) has been operating since 2009 and has accumulated lots of data, in particular in the production of W and Z electroweak (EW) gauge bosons. The detailed study of their properties allows theorists and experimentalists for probing deeply the Standard Model (SM) and in particular the EW symmetries, as well as for searching for potential new-physics effects signaled by deviations from SM expected shapes in various observables. With 13 TeV data as well as with new data coming from run 3 and beyond in the next years, it is possible to study non-trivial observables such as the polarization of the gauge bosons, in particular in the four-lepton channel via ZZ production and in the three-lepton channel via WZ production. The latest measurements from ATLAS and CMS collaborations in the three-lepton channel can be found in Refs. [1, 2], respectively.

Higher order QCD and EW corrections to three-lepton production in the WZ channel have reached a high precision. The next-to-leading order (NLO) QCD corrections were calculated in Refs. [3, 4] for on-shell production and in Refs. [5, 6] for off-shell production. The NLO EW corrections were presented in Refs. [7,8,9,10], showing in particular the importance of the quark-photon induced correction. The full NLO QCD predictions including full off-shell and spin-correlation effects for leptonic final states can be numerically calculated with the help of public computer programs such as MCFM [11, 12] or VBFNLO [13, 14]. In 2018 these calculations have been extended to include anomalous couplings effects at the NLO QCD + EW accuracy as well [15]. QCD precision has reached the next-to-next-to-leading order (NNLO) accuracy [16,17,18] and a combination of NLO EW and NNLO QCD corrections has been performed in Ref. [19]. Parton shower effects have also been calculated at NLO QCD [20, 21], later extended to include SM effective field theory effects in Refs. [22, 23], while the consistent matching of NLO QCD + EW corrections has been performed in Ref. [24].

As more data is available, there is a growing interest in the study of the polarization of the gauge bosons in the three-lepton channel.Footnote 1 Notably, ATLAS presented in 2019 results for angular observables with 13 TeV data in the WZ channel [26]. On the theory side, the study of gauge boson polarizations effects started in the eighties [27, 28] and the NLO QCD corrections were included in Ref. [29]. The EW corrections have been calculated in detail in Refs. [30, 31]. The latter studies have introduced in particular the concept of fiducial polarization observables constructed out of the final-state angular observables in the fiducial volume, including the experimental cuts, but they have not investigated the separation of polarization states at the amplitude level. In order to do it is necessary to study three-lepton production in the double-pole approximation (DPA) where the production and decay amplitudes are calculated in the on-shell approximations, and then combined using a sum over all polarizations retaining the full phase-space in the gauge boson propagators. This study has been performed at NLO QCD in Ref. [32], but is still lacking the NLO EW corrections, contrary to the four-lepton channel [33]. Our study closes the gap by including the NLO QCD and EW corrections in the DPA for the three-lepton channels, separating the polarization states at the amplitude level. In this letter, we provide results for the \(W^+ Z\) channel using the same fiducial cuts and reference frame as ATLAS [26].

The paper is organized as follows. The definition of polarizations and a sketch of our calculation framework are given in Sect. 2. Numerical results at the 13 TeV LHC are presented in Sect. 3, starting with the integrated polarized cross sections in Sect. 3.1 before describing kinematical distributions in Sect. 3.2. Conclusions are provided in Sect. 4.

2 Calculation of polarized cross sections

The process considered in this paper reads

$$\begin{aligned}&p + p \rightarrow V_1(q_1) + V_2(q_2) \rightarrow \ell _1(k_1) \nonumber \\&\quad + \ell _2(k_2) + \ell _3 (k_3) + \ell _4(k_4) + X, \end{aligned}$$
(2.1)

where the final-state leptons can be either \(e^+\nu _e\mu ^+\mu ^-\) or \(e^-\bar{\nu }_e\mu ^+\mu ^-\) and the intermediate gauge bosons are \(V_1=W^\pm \), \(V_2=Z\).

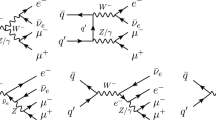
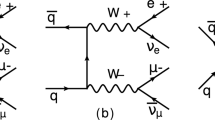
The polarization signals are defined using the double-pole approximation. In this framework, the final state leptons are created from intermediate states of an on-shell diboson system as can be seen from Fig. 1. Non-double-pole contributions such as \(W \rightarrow 4l\) or \(W\gamma \rightarrow 4l\) shown in Fig. 2 are excluded.

Fig. 1
figure 1

Doubly resonant diagrams at leading order

Full size image
Fig. 2
figure 2

Non-doubly resonant diagrams at leading order

Full size image

Each massive gauge boson has three polarization states, two transverse (T) and one longitudinal (L). The diboson system has therefore nine polarization states. One can thus imagine the process Eq. (2.1) occurs in a way similar to a 9-slit experiment, each slit corresponds to a polarization state of the WZ system. It is therefore natural to expect that there must be interferences between waves passing through the different slits.

Quantitatively, the contributions of those nine polarization states can be calculated as follows. At LO, the amplitude in the DPA is defined as (see e.g. Ref. [34])

$$\begin{aligned} \mathcal {A}_\text {LO,DPA}^{\bar{q}q'\rightarrow V_1V_2\rightarrow 4l} = \frac{1}{Q_1Q_2} \sum _{\lambda _1,\lambda _2=1}^{3} \mathcal {A}_\text {LO}^{\bar{q}q'\rightarrow V_1V_2}\mathcal {A}_\text {LO}^{V_1\rightarrow \ell _1\ell _2}\mathcal {A}_\text {LO}^{V_2\rightarrow \ell _3\ell _4} ,\nonumber \\ \end{aligned}$$
(2.2)

with

$$\begin{aligned} Q_j = q_j^2 - M_{V_j}^2 + iM_{V_j}\Gamma _{V_j}, \end{aligned}$$
(2.3)

where \(q_1 = k_1+k_2\), \(q_2 = k_3 + k_4\), \(M_V\) and \(\Gamma _V\) are the physical mass and width of the gauge bosons. We note that all helicity amplitudes in the numerator must be calculated using on-shell momenta. This is important to make sure that the amplitudes are gauge invariant. The OS momenta can be calculated from the original momenta \(k_i\) by means of an OS mapping. This mapping is not unique. However, it has been pointed out in Ref. [34] that different mappings lead to small differences of the order of \(\alpha \Gamma _V/(\pi M_V)\).

From Eq. (2.2) we can define the nine polarization contributions and their interferences. For example, the longitudinal–longitudinal (LL) contribution is calculated by selecting the \(\lambda _1=\lambda _2=2\) term in the r.h.s. Similarly, the transverse-transverse (TT) polarization is obtained by adding the (1, 1), (1, 3), (3, 1), (3, 3) amplitudes. Interferences between these polarization states are therefore included in the TT contribution after squaring the amplitude. The TL amplitude is the sum of the (1, 2) and (3, 2) amplitudes, therefore the TL cross section includes the interference between the (1, 2) and (3, 2) polarization modes. In the following, we will classify all polarization states into four groups LL, LT, TL, TT. The unpolarized result, calculated from Eq. (2.2), is thus the sum of these contributions and their interferences. While the unpolarized cross section is Lorentz invariant, individual polarized cross sections are not, hence dependent on a chosen reference frame. In this paper, we provide results in the WZ center-of-mass system (c.m.s.), which was recently used by ATLAS in Ref. [26].

NLO QCD and EW corrections are also calculated in the DPA. The NLO QCD calculation has been done in [32], which is the same as for the WW [35] and ZZ [33] production. NLO EW corrections for the ZZ case has been very recently calculated in [33]. For the present process of WZ, the NLO EW corrections are more complicated because the photon can be radiated off the W boson, which is treated as on-shell. Technical details of this calculation are provided in a separate longer publication [36]. Concerning the OS mappings, the mappings \(\text {DPA}^{(2,2)}\) and \(\text {DPA}^{(3,2)}\) given in [33] for \(1\rightarrow 2\) and \(1\rightarrow 3\) decays of the massive gauge bosons, repectively, are used for both gauge bosons, see Ref. [36] for the details.

3 Numerical results

The input parameters are the same as in Ref. [30]. We re-provide them here for the sake of completeness.

$$\begin{aligned} G_{\mu }= & {} 1.16637\times 10^{-5} {\,\text {GeV}}^{-2}, \,\nonumber \\ M_W= & {} 80.385 {\,\text {GeV}}, \quad M_Z = 91.1876 {\,\text {GeV}}, \nonumber \\ \Gamma _W= & {} 2.085{\,\text {GeV}}, \quad \Gamma _Z = 2.4952{\,\text {GeV}}, \nonumber \\ M_t= & {} 173 {\,\text {GeV}}, \quad M_H=125{\,\text {GeV}}. \end{aligned}$$
(3.1)

The masses of the leptons and the light quarks, i.e. all but the top mass, are neglected. The electromagnetic coupling is calculated as \(\alpha _{G_\mu }=\sqrt{2}G_\mu M_W^2(1-M_W^2/M_Z^2)/\pi \). For the factorization and renormalization scales, we use \(\mu _F = \mu _R = (M_W + M_Z)/2\). Moreover, the parton distribution functions (PDF) are calculated using the Hessian set LUXqed17_plus_PDF4LHC15_nnlo_30  [37,38,39,40,41,42,43,44,45,46] via the library LHAPDF6  [47].

We will present results for the LHC at a center-of-mass energy\(\sqrt{s} = 13\,{\,\text {TeV}}\). The extra parton radiation occurring in the NLO QCD corrections is treated inclusively and no jet cuts are applied. Lepton–photon recombination is implemented, where the momentum of a given charged lepton \(\ell \) is redefined as \(p'_\ell = p_\ell + p_\gamma \) if \(\Delta R(\ell ,\gamma ) \equiv \sqrt{(\Delta \eta )^2+(\Delta \phi )^2}< 0.1\). The letter \(\ell \) denotes either e or \(\mu \). After the possible lepton–photon recombination we then apply the following phase-space cut:

$$\begin{aligned}&p_{T,\mu }> 15{\,\text {GeV}}, \quad p_{T,e}> 20{\,\text {GeV}}, \quad |\eta _\ell |<2.5,\nonumber \\&\Delta R\left( e,\mu ^\pm \right)> 0.3, \quad \Delta R\left( \mu ^+,\mu ^-\right)> 0.2,\nonumber \\&\left| m_{\mu ^+\mu ^-} - M_Z\right| < 10{\,\text {GeV}}, \quad m_{T,W} > 30{\,\text {GeV}}, \end{aligned}$$
(3.2)

where \(m_{T,W} = \sqrt{2p_{T,\nu } p_{T,e} [1-\cos \Delta \phi (e,\nu )]}\) with \(\Delta \phi (e,\nu )\) being the angle between the electron and the neutrino in the transverse plane. This setup is used by ATLAS in Refs. [26, 48] to define the fiducial phase space.

3.1 Integrated polarized cross sections

We first present results for the doubly polarized integrated cross sections in Table 1. The unpolarized value is also provided. The interference shown in the last row is calculated by subtracting the sum of the LL, LT, TL, and TT cross sections from the unpolarized one. The polarization fractions, f, are the ratios of the polarized cross sections to the corresponding unpolarized one.

For the unpolarized cross section, the NLO QCD correction is rather large, of the order of + 80%, while the NLO EW correction relative to the LO result (usually denoted by \(\delta _{\text {EW}}\) in the literature) is negative and amounts to \(-\,4.2\%\). We define a correction factor \(\bar{\delta }_{\text {EW}}\) which gives the amount of NLO EW corrections with respect to the NLO QCD cross section, so that we can assess the importance of the EW corrections with respect to the QCD-corrected cross sections. This quantity is also shown in Table 1 (last column). For the unpolarized cross section we get \(\bar{\delta }_{\text {EW}}=-\,2.3\%\). We also provide the seven-point scale uncertainties. The scale uncertainties are calculated by varying independently the two scales \(\mu _F\) and \(\mu _R\) as \(n\mu _0/2\) with \(n=1,2,4\) and \(\mu _0 = (M_W + M_Z)/2\) being the central scale. Additional constraint \(1/2 \le \mu _R/\mu _F \le 2\) is used to limit the number of scale choices to seven at NLO QCD. The cases \(\mu _R/\mu _F = 1/4\) or 4 are excluded, being considered too extreme. Since \(\mu _R\) does not appear at LO and NLO EW, there are only three possibilities for choosing \(\mu _F\) at these levels. The LO (and NLO EW) scale uncertainty of the unpolarized cross section is quite small, \(\sim +\,5\%/-\,6\%\), while the NLO QCD (and NLO QCD + EW, written also as NLO QCDEW) scale uncertainty is approximately the same, \(\sim +\,5.5\%/-\,4.5\%\).

We have computed the polarized cross sections for the four polarization combinations: the doubly longitudinal polarization \(W_L^{}Z_L^{}\), the doubly transverse polarization \(W_T^{}Z_T^{}\), as well as the mixed polarizations \(W_L^{}Z_T^{}\) and \(W_T^{}Z_L^{}\). We also provide numbers for the interference term, that when summed with the four polarized cross sections helps to recover the unpolarized cross section. Both at LO and at NLO the doubly transverse polarization cross section has the highest fraction, around 70.5% at LO and 63% at NLO QCDEW. The NLO EW corrections are quite small and negative, as in the unpolarized case, and of the order of − 5% while \(\bar{\delta }_{\text {EW}}=-\,3\%\). The scale uncertainty for the doubly transverse cross section is + 4.7%/− 3.8% at NLO QCDEW.

The doubly longitudinal polarization contributes to 8% to the unpolarized cross section at LO and to 5.6% at NLO QCDEW. The NLO QCD corrections are much smaller than those of the unpolarized and doubly transverse polarization cross sections, of the order of + 30%, while the NLO EW corrections and \(\bar{\delta }_{\text {EW}}\) are quite similar, − 4.3% and − 3.3% respectively. There is a strong reduction of the scale uncertainty from LO to NLO QCDEW, with + 5.1%/− 6.3% at LO down to + 2.8%/− 2.3% at NLO QCDEW.

Table 1 Unpolarized and doubly polarized cross sections in fb together with polarization fractions calculated at LO, NLO EW, NLO QCD, and NLO QCD + EW, all in the DPA, in the WZ center-of-mass system for the process \(p p \rightarrow W^+ Z\rightarrow e^+ \nu _e \mu ^+\mu ^-\). The statistical uncertainties (in parenthesis) are given on the last digits of the central prediction when significant. Seven-point scale uncertainty is also provided for the cross sections as sub- and superscripts in percent. In the last column the EW correction relative to the NLO QCD prediction is provided
Full size table

The mixed polarizations contribute to around 10% each to the unpolarized cross section at LO and to around 15% each at NLO QCDEW. The NLO QCD corrections are much bigger than in the other polarizations: the ratio NLO QCD/LO amounts to around 2.6. The NLO EW corrections are very small in comparison as we get \(\bar{\delta }_{\text {EW}}=-\,1.3\%\) for the \(W_L^{}Z_T^{}\) cross section and \(\bar{\delta }_{\text {EW}}=-\,0.2\%\) for the \(W_T^{}Z_L^{}\) cross section. The scale uncertainty is quite similar at LO and NLO QCDEW.

The last row of Table 1 gives the results for the interference term. It is one to two orders of magnitude smaller than the doubly polarized cross sections and contributes to only 1% to the unpolarized cross section at LO and to 0.6% at NLO QCDEW, indicating that the interference effects are subdominant. The scale uncertainty at NLO EW is slightly bigger than at LO, but given that the cross section is so small this may be attributed to numerical effects: we calculate the interference cross section as the difference between the unpolarized cross section and the sum of the doubly-polarized cross sections, so that the scale variation is very sensitive to the numerical error on the cross sections. This effect is mitigated when comparing the NLO QCD and NLO QCDEW results.

Fig. 3
figure 3

Distributions in \(\cos \theta ^{WZ}_{e^+}\) (left) and \(\cos \theta ^{WZ}_{\mu ^-}\) (right). These angles are calculated in the WZ center-of-mass system (more details are provided in the text), hence denoted with the WZ superscript. The big panel shows the absolute values of the cross sections at NLO QCD + EW. The middle-up panel displays the ratio of the NLO QCD cross sections to the corresponding LO ones. The middle-down panel shows \(\bar{\delta }_{\text {EW}}\), the EW corrections relative to the NLO QCD cross sections, in percent. In the bottom panel, the normalized shapes of the distributions are plotted to highlight differences in shape

Full size image

It is interesting to compare the EW corrections to the ones of the ZZ process published in [33]. For this comparison, the EW correction is calculated with respect to the LO result. The \(W^+ Z\) results read \(-\,4.2\%\), \(-\,4.3\%\), \(-\,3.3\%\), \(-\,0.5\%\), and \(-\,4.8\%\) for the unpolarized, \(W_L Z_L\), \(W_L Z_T\), \(W_T Z_L\), \(W_T Z_T\) cross sections, respectively. The ZZ EW corrections, for the unpolarized and fully polarized cross sections, are about \(-\,10\%\) for both inclusive and fiducial cuts [33]. We see that the EW corrections are significantly smaller in the \(W^+ Z\) process than in the ZZ process. This can be explained as follows. For on-shell production, the photon-quark induced correction, which is positive, is larger in the \(W^+ Z\) process [9]. This leads to smaller total EW corrections in the \(W^+ Z\) channel because of a stronger cancellation between the photon-quark induced correction and the negative virtual one. When leptonic decays are turned on, the dimuon invariant mass distribution in [49] shows that using a looser invariant mass cut reduces the impact of the EW correction. In the ZZ case, the cut\(|m_{\ell ^+\ell ^-} - M_Z| < 10{\,\text {GeV}}\) is applied for both gauge bosons, while it is used only for the Z boson in the WZ process. The W boson is constrained by a much milder cut of\(m_{T,W} > 30{\,\text {GeV}}\). These arguments explain why the EW corrections are much smaller in the \(W^+ Z\) process.

Finally, we comment on the comparison with Ref. [32] for the NLO QCD results. Using the same PDF sets and same kinematic cuts as in Ref. [32], we found that the differences between our results and theirs are within \(0.6\%\) for all polarized cross sections at LO. The differences are within \(0.5\%\) at NLO QCD. The difference for the unpolarized DPA cross section is \(0.5\%\) at LO and \(0.4\%\) at NLO QCD. For this comparison, the on-shell mapping is not the \(\text {DPA}^{(2,2)}\) mapping but the one defined in Ref. [34] (for the \(W^+W^-\) process, see the Appendix A of Ref. [30] for similar results for the WZ case), because from Ref. [32] we conclude that the authors used this on-shell mapping (of Ref. [34]) for their calculation. Note that Ref. [32] uses the complex mass scheme while we use the real pole masses for the gauge bosons, which amounts to \(0.3\%\) difference in the integrated cross sections. The remaining 0.1–0.3% differences may be due to differences in the LHAPDF version (for PDFs), or exact values of the input parameters, or details of the DPA, \(\cdots \). We note that the statistical errors are at the level of \(0.05\%\). These effects are completely negligible compared to the scale uncertainties and we conclude that the level of agreement between our results and that of Ref. [32] is satisfactory.

Fig. 4
figure 4

Same as Fig. 3 but for the azimuthal angles between the momenta of the electron and the muons, \(\Delta \phi (e^+,\mu ^-)\) (left) and \(\Delta \phi (e^+,\mu ^+)\) (right)

Full size image

3.2 Kinematic distributions

We now present results for differential cross sections. The most important distribution in the analysis of W/Z boson polarizations is the angular distribution of the decay lepton. In this paper, the polarizations are calculated in the WZ center-of-mass system. The charged lepton angle \(\theta ^{WZ}_{\ell }\) is therefore defined as the angle between the momentum of the parent gauge boson calculated in the WZ c.m.s. (\(\vec {p}^\text {WZ-cms}_V\)) and the momentum of the lepton calculated in the gauge boson rest frame (\(\vec {p}^\text {V-rest}_{\ell }\)). From this distribution, the polarization fractions of the gauge boson can be directly extracted (see e.g. Refs. [30, 50]). It is therefore important to see the various sub-contributions to this distribution from the individual polarizations of the WZ system. This information is shown in Fig. 3 for the cases of \(e^+\) (coming from the decay of the \(W^+\) boson) and \(\mu ^-\) (coming from the decay of the Z boson). The NLO QCD results have been recently presented in [32], which agree very well with our results (see the middle-up panels). The new results of this work are the EW corrections, shown in the middle-down panel. We remind that the EW corrections are defined with respect to the NLO QCD results. We see that the EW corrections are ranging from \(-\,4.5\) to \(+\,0.5\)% for both cases and for all individual double polarizations. The interference effects can be seen from the difference between the unpolarized cross section and the sum of the \(W_T^{}Z_T^{}\), \(W_T^{}Z_L^{}\), \(W_L^{}Z_T^{}\), and \(W_L^{}Z_L^{}\) ones. We observe that this effect is uniformly very small here. In the bottom panel, we highlight the shape differences by showing the normalized distributions, i.e. the distributions in the big panels are normalized by the corresponding integrated cross sections. Looking at these normalized shapes, we see that, as expected, the electron-angle distribution is insensitive to the polarizations of the Z boson, while it is highly sensitive to the polarizations of the W boson. The unpolarized shape is mostly defined by the W’s transverse polarization. The same things can be said for the muon case. However, the unpolarized shape is more affected by the Z’s longitudial polarization. We observe also that the shapes of \(W_T^{}Z_T^{}\) (blue) and \(W_L^{}Z_T^{}\) (orange) are more identical than the electron plot (see the \(W_T^{}Z_T^{}\) and \(W_T^{}Z_L^{}\)). In other words, the \(Z_L\) and \(Z_T\) are affecting the electron angle in a significantly different way when \(|\cos \theta ^{WZ}_{e^+}|\approx 1\), while the \(W_L\) and \(W_T\) are affecting the muon angle in the same manner. The results at NLO QCD only, as presented in [32], display the same behavior. Naively it would have been expected to see the same pattern for the W boson and for the Z boson, but the cuts that have been applied are not inclusive. As stated in [32] the differences we observe are due to the differences in the kinematic cuts applied on the Z and W decay leptons.

We next move to distributions in azimuthal angles, namely the angles between the momenta of the electron and the muons, \(\Delta \phi (e^+,\mu ^-)\) and \(\Delta \phi (e^+,\mu ^+)\). We obviously expect that different polarizations contribute differently to these observables. The results are provided in Fig. 4, presented in the same format as the previous distributions. The first interesting thing to notice is that the \(W_T^{}Z_L^{}\) and \(W_L^{}Z_T^{}\) are the same in magnitude and in shape. They are only different in the EW corrections (middle-down panels), but these effects are too small to be visible in actual measurements. The shape of the \(W_L^{}Z_L^{}\) is distinctly different from the other ones, hence this can be used as a discriminator to measure the \(W_L^{}Z_L^{}\) component. The EW corrections are small, being from \(-5\) to \(+1\)% for all polarizations and for both distributions.

Fig. 5
figure 5

Same as Fig. 3 but for the transverse momentum of the electron (left) and the Z boson (right). In the middle-down panel, the grey line is the Sudakov fit (see text) of the \(W_L^{}Z_L^{}\) EW correction

Full size image

Finally, the transverse momentum distributions for the electron and the Z boson are shown in Fig. 5. Very unexpectedly, as opposed to the above angular distributions, the \(W_L^{}Z_L^{}\) contributions are not smallest in both plots at large \(p_T\). For the electron case, at large \(p_{T,e}\), the \(W_L^{}Z_L^{}\) and \(W_L^{}Z_T^{}\) components fall fastest and become very small. They must vanish in the large \(p_{T,e}\) limit, being equal to the Goldstone contribution, according to the equivalence theorem [28]. At small \(p_{T,e}\), the \(W_L^{}Z_L^{}\) is smallest. With increasing \(p_T\), the \(W_L^{}Z_T^{}\) drops faster and becomes smallest at around 150 GeV. Similar phenomenon happens for the \(p_{T,Z}\) case: the \(W_T^{}Z_L^{}\) becomes smaller than the \(W_L^{}Z_L^{}\) at around 200 GeV. Same kind of behavior was obtained in [33] (see Figs. 8 and 9 there) for the ZZ process. To understand why the \(W_L^{}Z_T^{}\) and \(W_T^{}Z_L^{}\) contributions can be so small, it is interesting to look at the LO results (the reader can also see this from the big panels by removing the QCD corrections using the information in the NLO QCD/LO panels. The EW corrections are small and irrelevant here.). The picture at LO (not shown here) for the \(p_{T,e}\) distribution reads: at small \(p_{T,e}\) the \(W_T^{}Z_L^{}\), \(W_L^{}Z_T^{}\), \(W_L^{}Z_L^{}\) are at the same order of magnitude; then with increasing momentum the \(W_T^{}Z_L^{}\) and \(W_L^{}Z_T^{}\) drop much faster and become much smaller than the \(W_L^{}Z_L^{}\). We now take into account the QCD corrections. Fig. 5 (left) shows that the \(W_T^{}Z_L^{}\) gets a huge correction, the \(W_L^{}Z_T^{}\) a large correction, and the \(W_L^{}Z_L^{}\) a small correction. This changes the hierarchy, making the \(W_T^{}Z_L^{}\) largest and \(W_L^{}Z_T^{}\) smallest at NLO QCD. Similar things happen in the \(p_{T,Z}\) distribution with the \(W_T^{}Z_L^{}\) and \(W_L^{}Z_T^{}\) interchanged.

The other important result is the magnitude of the EW corrections, which can be important for the interesting case of doubly longitudinal cross section. EW correction is about \(-20\)% at \(p_{T,e}\approx 450\) GeV, and is about \(-10\)% at \(p_{T,e}\approx 200\) GeV which is currently accessible at the LHC (see Refs. [2, 26]). For the \(p_{T,Z}\) distribution, the corrections are significantly smaller. This correction originates from the negative Sudakov corrections in the virtual contribution. It can therefore be fitted using the single and double Sudakov logarithms. Our fit yields

$$\begin{aligned} \bar{\delta }^\text {fit,e}_{\text {EW}}&=-0.034 \left[ 1 + 0.7 \log \left( \frac{p_{T,e}}{M_W}\right) + 1.3 \log ^2\left( \frac{p_{T,e}}{M_W}\right) \right] , \end{aligned}$$
(3.3)
$$\begin{aligned} \bar{\delta }^\text {fit,Z}_{\text {EW}}&=-0.015 \left[ 1 + \log \left( \frac{p_{T,Z}}{M_Z}\right) + 2.8 \log ^2\left( \frac{p_{T,Z}}{M_Z}\right) \right] , \end{aligned}$$
(3.4)

where a constant term has been added in the fit to account for the low energy regime. These fits are shown in the plots (grey line), showing excellent agreement with the exact values. For the other polarizations, EW corrections are smaller than 5%, hence can be neglected.

4 Conclusions

We have presented, for the first time, the NLO EW corrections to the doubly-polarized cross sections of the process \(pp \rightarrow W^+ Z \rightarrow e^+ \nu _e \mu ^+ \mu ^- + X\) at the LHC. The results are of direct consequences to the measurements of double-polarization signals in the WZ production channel at the LHC. To be as close as possible to the current experimental setup, the ATLAS fiducial cuts have been used and the polarization signals are defined in the WZ c.m.s as implemented in the latest polarization measurement by ATLAS [26].

For completeness and putting everyone in the same footing, we have re-calculated the known NLO QCD corrections and obtained good agreement with the results of Denner and Pelliccioli [32]. The QCD corrections are then combined with the EW ones to obtain the full NLO QCD + EW results.

We found that the impact of EW corrections on the integrated polarized cross sections is negligible, being smaller than 3% (relative to the NLO QCD results) for all polarizations. For angular distributions (\(\cos \theta ^{WZ}_{e^+}\), \(\cos \theta ^{WZ}_{\mu ^-}\), \(\Delta \phi (e^+,\mu ^-)\), and \(\Delta \phi (e^+,\mu ^+)\)), the EW corrections are also very small, being smaller than 5% across the full ranges. For transverse momentum distributions (\(p_{T,e}\) and \(p_{T,Z}\)), the EW corrections are found to be sizable only in the doubly longitudinal cross section. At the current LHC accessible range of \(p_{T,e}\approx 200\) GeV, the correction is about \(-\,10\)%. The magnitude of the correction increases rapidly with \(p_{T}\). The shape of this correction can be excellently fitted using the single and double Sudakov logarithms.