Superintegrability for ($\beta$-deformed) partition function hierarchies with W-representations

Abstract

We construct the ($\beta$-deformed) partition function hierarchies with W-representations. Based on the W-representations, we analyze the superintegrability property and derive their character expansions with respect to the Schur functions and Jack polynomials, respectively. Some well known superintegrable matrix models such as the Gaussian hermitian one-matrix model (in the external field), $N\times N$ complex matrix model, $\beta$-deformed Gaussian hermitian and rectangular complex matrix models are contained in the constructed hierarchies.

1 Introduction

Recently there has been increasing interest in the superintegrability for matrix models [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. The superintegrability means that for the character expansions of the matrix models, the average of a properly chosen symmetric function is proportional to ratios of symmetric functions on a proper locus, i.e., $< character > \sim character$. A wide range of matrix models are known to be superintegrable, such as the (deformed) Gaussian hermitian and complex matrix models [1,2,3,4], (Hurwitz-)Kontsevich matrix models [5, 6], unitary matrix models [7], fermionic matrix models [8, 9], and even some non-Gaussian matrix models [10, 11]. The constraints for matrix models are useful to analyze the structures of matrix models. For the Gaussian hermitian one-matrix model, its character expansion with respect to the Schur functions can be derived recursively from a single w-constraint [13]. There are the Virasoro constraints (with higher algebraic structures) for matrix models. They can be applied to analyze the character expansions of the matrix models as well, such as the Gaussian hermitian one-matrix, complex matrix and fermionic matrix models [8, 14].

W-representations of matrix models give the dual expressions for the partition functions through differentiation rather than integration [5]. More precisely, the partition functions are realized by acting on elementary functions with exponents of the given W-operators. For the Gaussian tensor model [19] and (fermionic) rainbow tensor models [8, 20], they can still be expressed as the W-representations. Recently it was shown that the superintegrability for ($\beta$-deformed) matrix models can be analyzed from their W-representations [15, 16]. In this paper, we will construct the partition function hierarchies with W-representations and analyze the superintegrability property.

2 Partition function hierarchies with W-representations

The Hurwitz–Kontsevich matrix model is a deformation of the Kontsevich model, which can be used to describe the Hurwitz numbers and Hodge integrals over the moduli space of complex curves [5, 21, 22]. It is the special case of the more general Hurwitz partition functions [23,24,25]. The Hurwitz–Kontsevich model is generated by the exponent of the Hurwitz operator $W_0$ acting on the function $e^{p_1/e^{tN}}$,

$$\begin{aligned} Z_{0}\{p\}= & {} e^{tW_0}\cdot e^{p_1/e^{tN}}\nonumber \\= & {} \sum _{\lambda }e^{tc_{\lambda }}S_\lambda \left\{ p_k=e^{-tN}\delta _{k,1}\right\} S_{\lambda }\{p\}, \end{aligned}$$

(1)

where t is a deformation parameter, the Hurwitz operator $W_0$ is given by

$$\begin{aligned} W_0= & {} \frac{1}{2}\sum _{k,l=1}^{\infty }\bigg ((k+l)p_{k}p_l \frac{\partial }{\partial p_{k+l}}+klp_{k+l}\frac{\partial }{\partial p_k}\frac{\partial }{\partial p_l}\bigg )\nonumber \\&+N\sum _{k=1}^{\infty }kp_{k}\frac{\partial }{\partial p_{k}}, \end{aligned}$$

(2)

and $c_{\lambda }=\sum _{(i,j)\in \lambda }(N-i+j)$.

The partition function (1) possesses the matrix model representation [5]

$$\begin{aligned} Z_{0}\{p\}= & {} \int _{N\times N} \sqrt{\mathrm{det}\left( \frac{\mathrm{sinh}(\frac{\phi \otimes I-I\otimes \phi }{2})}{\frac{\phi \otimes I-I\otimes \phi }{2}} \right) }\nonumber \\&\times d\phi e^{-\frac{1}{2t}\mathrm{Tr}\phi ^2 -\frac{N}{2}\mathrm{Tr}\phi -\frac{1}{6}tN^3+\frac{1}{24}tN+\mathrm{Tr}(e^{\phi }\psi )}, \end{aligned}$$

(3)

where $\psi$ is an $N\times N$ matrix and the time variables $p_k=\mathrm{Tr}\psi ^k$.

Let us define the operator

$$\begin{aligned} E_{1}=[W_0, p_1] =\sum _{n=1}^{\infty }np_{n+1}\frac{\partial }{\partial p_{n}}+ Np_1. \end{aligned}$$

(4)

Using the actions

$$\begin{aligned} W_0 S_{\lambda }=c_{\lambda }S_{\lambda }, \end{aligned}$$

(5)

and

$$\begin{aligned} p_1S_{\lambda }=\sum _{\lambda +\square }S_{\lambda +\square }, \end{aligned}$$

(6)

we have

$$\begin{aligned} E_{1}S_{\lambda }=\sum _{\lambda +\square }(j_\square -i_\square +N) S_{\lambda +\square }, \end{aligned}$$

(7)

where $\lambda +\square$ are the Young diagrams obtained by adding one square $\square =(i_\square , j_\square )$ to $\lambda$.

Let us set

$$\begin{aligned} W_{-1}=[W_0, E_{1}]. \end{aligned}$$

(8)

The action of $W_{-1}$ on the Schur functions is

$$\begin{aligned} W_{-1}S_{\lambda }=\sum _{\lambda +\square }(j_\square -i_\square +N)^2 S_{\lambda +\square }. \end{aligned}$$

(9)

In terms of $W_{-1}$ and $E_{1}$, we introduce a series of operators

$$\begin{aligned} W_{-n}=\frac{1}{(n-1)!}\underbrace{[W_{-1}, [W_{-1}, \ldots [W_{-1} }_{n-1}, E_{1}]\ldots ]],\ \ n\ge 2. \nonumber \\ \end{aligned}$$

(10)

The actions of $W_{-n}$ with $n\ge 1$ on the Schur functions are given by

$$\begin{aligned} W_{-n}S_{\lambda }= & {} \sum _{\lambda +\square _1+\cdots +\square _n} \prod _{k=1}^{n}(j_{\square _k}-i_{\square _k}+N)^{\alpha }\nonumber \\&A_{\lambda } ^{\lambda +\square _1+\cdots +\square _n}S_{\lambda +\square _1+\cdots +\square _n}, \end{aligned}$$

(11)

where we denote $\alpha =1+\delta _{n,1}$ in this paper for later convenience, $\lambda +\square _1+\cdots +\square _n$ are the Young diagrams obtained by adding n squares to $\lambda$, $A_{\lambda }^{\lambda +\square _1+\cdots +\square _n}$ are the coefficients in the actions

$$\begin{aligned} p_nS_{\lambda }=\sum _{\lambda +\square _1+\cdots +\square _n} A_{\lambda }^{\lambda +\square _1+\cdots +\square _n} S_{\lambda +\square _1+\cdots +\square _n}. \end{aligned}$$

(12)

It is known that $A_{\lambda }^{\lambda +\square _1+\cdots +\square _n}=\sum _{k=1}^n (-1)^{k}a^{\lambda +\square _1+\cdots +\square _n}_{\lambda ,(k,1^{n-k})}$, with the Littlewood-Richardson coefficients $a^{\lambda }_{\mu ,\nu }$ defined by $S_{\mu }S_{\nu }=\sum _{\lambda }a^{\lambda }_{\mu ,\nu }S_{\lambda }$ [26]. The actions (11) can be proved inductively by using the relations $p_n=\frac{1}{n-1}[E_{1},p_{n-1}],\ \ n\ge 2$.

Let us introduce the partition function hierarchy with W-representations

$$\begin{aligned} Z_{-n}\{p\}=e^{{W}_{-n}/n}\cdot 1, \ \ n\ge 1. \end{aligned}$$

(13)

It is straightforward to calculate the powers of $W_{-n}$ acting on $S_{\lambda }$ with $\lambda =\varnothing$, leading to the explicit results

$$\begin{aligned} \frac{1}{n^mm!}{W}^m_{-n}\cdot 1= \sum _{\lambda \mapsto nm} \left( \frac{S_{\lambda }\{p_k=N\}}{S_{\lambda }\{p_k=\delta _{k,1}\}}\right) ^{\alpha } S_{\lambda }\{p_k=\delta _{k,n}\} S_{\lambda },\nonumber \\ \end{aligned}$$

(14)

where we have used the hook length formula $\frac{S_{\lambda }\{p_k=N\}}{S_{\lambda }\{p_k=\delta _{k,1}\}}=\prod _{(i,j)\in \lambda } (j-i+N)$.

Then we have

$$\begin{aligned} Z_{-n}\{p\}=e^{{W}_{-n}/n}\cdot 1= & {} \sum _{\lambda } \left( \frac{S_{\lambda }\{p_k=N\}}{S_{\lambda }\{p_k=\delta _{k,1}\}}\right) ^{\alpha }\nonumber \\&\quad S_{\lambda }\{p_k=\delta _{k,n}\} S_{\lambda }\{p\}. \end{aligned}$$

(15)

We see that $Z_{-1}\{p\}$ and $Z_{-2}\{p\}$ are the $N\times N$ complex matrix model [1, 27] and Gaussian hermitian one-matrix model [1, 5], respectively,

$$\begin{aligned} Z_{-1}\{p\}= & {} \frac{\int _{N\times N} d^2M e^{-\mathrm{Tr}MM^{\dagger }+\sum _{k=1}^{\infty }\frac{p_k}{k}\mathrm{Tr}(MM^{\dagger })^k}}{\int _{N\times N} d^2M e^{-\mathrm{Tr}MM^{\dagger }}}\nonumber \\= & {} \sum _{\lambda }\frac{S_{\lambda }\{p_k=N\}^2}{S_{\lambda }\{p_k=\delta _{k,1}\}}S_{\lambda }\{p\},\nonumber \\ Z_{-2}\{p\}= & {} 2^{-\frac{N}{2}}\pi ^{-\frac{N^2}{2}}\int _{N\times N} dM e^{-\frac{1}{2}\mathrm{Tr}M^{2}+\sum _{k=1}^{\infty } \frac{p_k}{k}\mathrm{Tr}M^k}\nonumber \\= & {} \sum _{\lambda }\frac{S_{\lambda }\{p_k=N\}}{S_{\lambda }\{p_k=\delta _{k,1}\}} S_{\lambda }\{p_k=\delta _{k,2}\} S_{\lambda }\{p\}. \end{aligned}$$

(16)

Note that for any partition function of the form [25]

$$\begin{aligned} {\bar{Z}}=\sum _{\lambda }\prod _{(i,j)\in {\lambda }}f(i-j)S_{\lambda }\{\bar{p}_k\}S_{\lambda }\{p_k\} \end{aligned}$$

(17)

with the arbitrary function f and parameters $\bar{p}_k$, it is a $\tau$-function of the KP hierarchy. It is clear that the partition function hierarchy (15) gives the $\tau$-functions of the KP hierarchy.

Similarly, we define the operator

$$\begin{aligned} E_{-1}=\left[ W_0, \frac{\partial }{\partial {p_{1}}}\right] =-\sum _{n=1}^{\infty }(n+1)p_{n}\frac{\partial }{\partial p_{n+1}}- N\frac{\partial }{\partial p_1}, \nonumber \\ \end{aligned}$$

(18)

and

$$\begin{aligned} E_{-1}S_{\lambda }=-\sum _{\lambda -\square }\left( j_\square -i_\square +N \right) S_{\lambda -\square }, \end{aligned}$$

(19)

where $\lambda -\square$ are the Young diagrams obtained by removing one square $\square =(i_\square , j_\square )$ from $\lambda$.

We set

$$\begin{aligned} W_{1}=[W_0, E_{-1}]. \end{aligned}$$

(20)

There is the action

$$\begin{aligned} W_{1}S_{\lambda }=\sum _{\lambda -\square }(j_\square -i_\square +N)^2 S_{\lambda -\square }. \end{aligned}$$

(21)

In terms of $W_{1}$ and $E_{-1}$, we introduce a series of operators

$$\begin{aligned} W_{n}=\frac{(-1)^n}{(n-1)!}\underbrace{[W_{1}, [W_{1}, \ldots [W_{1}}_{n-1}, E_{-1}]\ldots ]],\ \ n\ge 2. \nonumber \\ \end{aligned}$$

(22)

The actions of $W_{n}$ on the Schur functions are given by

$$\begin{aligned} W_{n}S_{\lambda }= & {} \sum _{\lambda -\square _1-\cdots -\square _n} \prod _{k=1}^{n} (j_{\square _k}-i_{\square _k}+N)^{\alpha }\nonumber \\&A_{\lambda } ^{\lambda -\square _1-\cdots -\square _n} S_{\lambda -\square _1-\cdots -\square _n},\ \ n\ge 1, \end{aligned}$$

(23)

where $\lambda -\square _1-\cdots -\square _n$ are the Young diagrams obtained by removing n squares from $\lambda$, $A_{\lambda }^{\lambda -\square _1-\cdots -\square _n}=\sum _{k=1}^{n} (-1)^{k}a^{\lambda }_{\lambda -\square _1-\cdots -\square _n,(k,1^{n-k})}$ are the coefficients in the actions

$$\begin{aligned} n\frac{\partial }{\partial p_n}S_{\lambda }=\sum _{\lambda -\square _1-\cdots -\square _n} A_{\lambda }^{\lambda -\square _1-\cdots -\square _n} S_{\lambda -\square _1-\cdots -\square _n}. \end{aligned}$$

(24)

The actions (23) can be proved inductively by using the relations $\frac{\partial }{\partial p_n}=\frac{1}{n}[E_{-1},\frac{\partial }{\partial p_{n-1}}],\ \ n\ge 2$. It is interesting to note that there are the same actions as (23) for the operators $W^-_n$ given by [18]

$$\begin{aligned} W^-_n=\mathrm{Tr}\frac{\partial ^n}{\partial H^n}, \ \ n\ge 2, \end{aligned}$$

(25)

where H is an $N\times N$ matrix.

Taking $p_k=\mathrm{Tr}H^k$, we can rewrite the operators (18), (20) and $W_2$ in (22) as

$$\begin{aligned} E_{-1}= & {} -W^-_1=-\mathrm{Tr}\frac{\partial }{\partial H},\nonumber \\ W_1= & {} \sum _{k,l=1}^{\infty }\left( (k+l+1)p_{k}p_l \frac{\partial }{\partial p_{k+l+1}}+klp_{k+l-1}\frac{\partial }{\partial p_k}\frac{\partial }{\partial p_l}\right) \nonumber \\&+2N\sum _{k=1}^{\infty }(k+1)p_{k} \frac{\partial }{\partial p_{k+1}} +N^2\frac{\partial }{\partial p_1}\nonumber \\= & {} \mathrm{Tr}\left( H^{T}\frac{\partial ^2}{\partial H^2}\right) ,\nonumber \\ W_{2}= & {} \sum _{k,l=1}^{\infty }\left( (k+l+2)p_{k}p_l \frac{\partial }{\partial p_{k+l+2}}+klp_{k+l-2}\frac{\partial }{\partial p_k}\frac{\partial }{\partial p_l}\right) \nonumber \\&+2N\sum _{k=1}^{\infty }(k+2)p_{k} \frac{\partial }{\partial p_{k+2}}+2N^2\frac{\partial }{\partial p_{2}}+N\frac{\partial ^2}{\partial p^2_{1}}\nonumber \\= & {} \mathrm{Tr}\frac{\partial ^2}{\partial H^2}, \end{aligned}$$

(26)

where $H^{T}$ is the transpose of the matrix H.

Since (22) can be expressed as $W_{n}=\frac{1}{n-1}\left[ W_{n-1},W_{1}\right] , \ n\ge 3,$ it is clear that the operators $W_n$ (22) and $W^-_n$ (25) are equivalent for $n\ge 2$.

Let us introduce the partition function hierarchy with W-representations

$$\begin{aligned} { Z}_n\{g|p\} =e^{W_{n}/n}e^{\sum _{k=1}^{\infty } \frac{p_kg_k}{k}},\ \ n\ge 1. \end{aligned}$$

(27)

Since there are the actions

$$\begin{aligned} \frac{1}{n^m m!}W_{n}^m S_{\lambda }= & {} \sum _{\mu \mapsto |\lambda |-nm} \left( \frac{S_{\lambda }\{p_k=N\}S_{\mu }\{p_k=\delta _{k,1}\}}{S_{\mu }\{p_k=N\}S_{\lambda }\{p_k=\delta _{k,1}\}}\right) ^{\alpha }\nonumber \\&\times S_{\lambda /\mu } \{p_k=\delta _{k,n}\} S_{\mu }, \end{aligned}$$

(28)

where $S_{\lambda /\mu }$ are the skew Schur functions, we obtain the character expansions for the partition function hierarchy (27)

$$\begin{aligned} {{ Z}}_n\{g|p\}= & {} \sum _{\lambda ,\mu } \left( \frac{S_{\lambda }\{p_k=N\}S_{\mu }\{p_k=\delta _{k,1}\}}{S_{\mu }\{p_k=N\}S_{\lambda }\{p_k=\delta _{k,1}\}}\right) ^{\alpha }\nonumber \\&\times S_{\lambda /\mu } \{p_k=\delta _{k,n}\} S_{\lambda }\{g\}S_{\mu }\{p\}. \end{aligned}$$

(29)

Here we have used the Cauchy formula $e^{\sum _{k=1}^{\infty }\frac{1}{k}p_k\bar{p}_k}=\sum _{\lambda }S_{\lambda }\{p\}S_{\lambda }\{\bar{p}\}$.

When particularized to the $n=2$ case in (29), it gives the character expansion [15] of Gaussian hermitian one-matrix model in the external field [5]

$$\begin{aligned} Z_{2}\{g|p\}= & {} \int dM_1 e^{-\mathrm{Tr}\frac{M_1^{2}}{2}+\sum _{k=1}^{\infty }\frac{g_k}{k}\mathrm{Tr}(M_1+M_2)^k}\nonumber \\= & {} \sum _{\lambda ,\mu }\frac{S_{\lambda }\{p_k=N\}S_{\mu }\{p_k=\delta _{k,1}\}}{S_{\mu }\{p_k=N\}S_{\lambda }\{p_k=\delta _{k,1}\}}\nonumber \\&\times S_{\lambda /\mu } \{p_k=\delta _{k,2}\}S_{\lambda }\{g\}S_{\mu }\{p\}, \end{aligned}$$

(30)

where $p_k=\mathrm{Tr}M_2^k$.

3 $\beta$-deformed partition function hierarchies with W-representations

Let us extend the Hurwitz–Kontsevich matrix model (1) to the $\beta$-deformed case,

$$\begin{aligned} {{\mathcal {Z}}}_{0}\{p\} =e^{t{\mathcal {W}}_0}\cdot e^{\beta p_1/e^{tN}}, \end{aligned}$$

(31)

where

$$\begin{aligned} {\mathcal {W}}_0= & {} \frac{1}{2}\sum _{k,l=1}^{\infty }\bigg (\beta (k+l)p_{k}p_l \frac{\partial }{\partial p_{k+l}}+klp_{k+l}\frac{\partial }{\partial p_k}\frac{\partial }{\partial p_l}\bigg )\nonumber \\&+\frac{1}{2}\sum _{k=1}^{\infty }\bigg ((1-\beta )(k-1)+2\beta N\bigg )kp_{k}\frac{\partial }{\partial p_k}. \end{aligned}$$

(32)

Taking $\bar{p}_k=e^{-tN}\delta _{k,1}$ in the Cauchy formula

$$\begin{aligned} e^{\beta \sum _{k=1}^{\infty }\frac{p_k\bar{p}_k}{k}}=\sum _{\lambda }\frac{1}{\langle J_{\lambda }, J_{\lambda }\rangle _{\beta }}J_{\lambda }\{p_k\} J_{\lambda }\{\bar{p}_k\}, \end{aligned}$$

(33)

we have

$$\begin{aligned} e^{\beta p_1/e^{tN}}=\sum _{\lambda }\frac{1}{\langle J_{\lambda }, J_{\lambda }\rangle _{\beta }} J_{\lambda }\{p_k=e^{-tN}\delta _{k,1}\}J_{\lambda }\{p_k\}. \end{aligned}$$

(34)

Here $\langle J_{\lambda }, J_{\lambda }\rangle _{\beta }=\frac{h_{\lambda }}{h^{'}_{\lambda }}$, $h_{\lambda }=\prod _{(i,j)\in \lambda }(1+\lambda _i-j+\beta (\lambda _j^{'}-i))$ and $h^{'}_{\lambda }=\prod _{(i,j)\in \lambda }(\lambda _i-j+\beta (\lambda _j^{'}-i+1))$ are the deformed hook length, in which $\lambda ^{'}=(\lambda _1^{'},\lambda _2^{'},\ldots )$ is the conjugate partition of $\lambda$.

Using the expansion (34) and the action [28]

$$\begin{aligned} {\mathcal {W}}_0 J_{\lambda }=\bar{c}_{\lambda }J_{\lambda }, \end{aligned}$$

(35)

where $\bar{c}_{\lambda }=\sum _{(i,j)\in \lambda }c(i,j)$ and $c(i,j)=j-1+\beta (N-i+1)$, we then obtain

$$\begin{aligned} {\mathcal {Z}}_{0}\{p\} =\sum _{\lambda }\frac{e^{t\bar{c}_{\lambda }}}{\langle J_{\lambda }, J_{\lambda }\rangle _{\beta }} J_\lambda \{p_k=e^{-tN}\delta _{k,1}\} J_{\lambda }\{p\}. \end{aligned}$$

(36)

Let us define the operator

$$\begin{aligned} \bar{E}_{1}=[{\mathcal {W}}_0, p_1] =\sum _{n=1}^{\infty }np_{n+1}\frac{\partial }{\partial p_{n}}+ \beta Np_1. \end{aligned}$$

(37)

We have

$$\begin{aligned} \bar{E}_{1}J_{\lambda }=\sum _{\lambda +\square }c(i_\square ,j_\square ) B_{\lambda }^{\lambda +\square } J_{\lambda +\square }, \end{aligned}$$

(38)

where $B_{\lambda }^{\lambda +\square }$ are the coefficients in the action

$$\begin{aligned} p_1J_{\lambda }=\sum _{\lambda +\square }B_{\lambda } ^{\lambda +\square }J_{\lambda +\square }. \end{aligned}$$

(39)

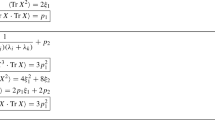
Since $p_2=[\bar{E}_1, p_1]$, from the actions (38) and (39), we obtain

$$\begin{aligned} p_2J_{\lambda }=\sum _{\lambda +\square _1+\square _2} B_{\lambda }^{\lambda +\square _1+\square _2} J_{\lambda +\square _1+\square _2}, \end{aligned}$$

(40)

where $B_{\lambda }^{\lambda +\square _1+\square _2}= (c(i_{\square _2},j_{\square _2})- c(i_{\square _1},j_{\square _1}))B_{\lambda }^{\lambda +\square _1} B_{\lambda +\square _1}^{\lambda +\square _1+\square _2}$.

For the operator

$$\begin{aligned} {{\mathcal {W}}}_{-1}=[{\mathcal {W}}_0, \bar{E}_{1}], \end{aligned}$$

(41)

we have

$$\begin{aligned} \mathcal W_{-1}J_{\lambda }=\sum _{\lambda +\square }c^2(i_\square ,j_\square ) B_{\lambda }^{\lambda +\square } J_{\lambda +\square }. \end{aligned}$$

(42)

Note that the combination of ${\mathcal {W}}_{-1}$ and $\bar{E}_{1}$, i.e., ${{\mathcal {W}}}_{-1}+(1-\beta )\bar{E}_{1}$, gives the W-representation of the $\beta$-deformed $N\times N$ complex matrix model [4, 29].

For the operator

$$\begin{aligned} {{\mathcal {W}}}_{-2}=[{\mathcal {W}}_{-1}, \bar{E}_{1}], \end{aligned}$$

(43)

it gives the W-operator in the W-representations of $\beta$-deformed Gaussian hermitian matrix model [3]. By the actions (38) and (42), we have

$$\begin{aligned} {\mathcal {W}}_{-2}J_{\lambda }= & {} \sum _{\lambda +\square _1+\square _2} c(i_{\square _1},j_{\square _1}) c(i_{\square _2},j_{\square _2}) B_{\lambda }^{\lambda +\square _1+\square _2}\nonumber \\&J_{\lambda +\square _1+\square _2}, \end{aligned}$$

(44)

where $B_{\lambda }^{\lambda +\square _1+\square _2}$ are the coefficients in (40).

Let us introduce a series of operators

$$\begin{aligned} {\mathcal {W}}_{-n}=\frac{1}{(n-1)!}\underbrace{[{\mathcal {W}}_{-1}, [{\mathcal {W}}_{-1}, \ldots [{\mathcal {W}}_{-1} }_{n-1}, \bar{E}_{1}]\ldots ]],\ \ n\ge 2. \nonumber \\ \end{aligned}$$

(45)

There are the actions

$$\begin{aligned} {\mathcal {W}}_{-n}J_\lambda= & {} \sum _{\lambda +\square _1+\cdots +\square _n} \prod _{k=1}^{n}c(i_{\square _k},j_{\square _k})^\alpha B_{\lambda } ^{\lambda +\square _1+\cdots +\square _n}\nonumber \\&J_{\lambda +\square _1+\cdots +\square _n}, n\ge 1, \end{aligned}$$

(46)

where $B_{\lambda } ^{\lambda +\square _1+\cdots +\square _n}$ are the coefficients in

$$\begin{aligned} p_nJ_{\lambda }=\sum _{\lambda +\square _1+\cdots +\square _n}B_{\lambda } ^{\lambda +\square _1+\cdots +\square _n} J_{\lambda +\square _1+\cdots +\square _n}. \end{aligned}$$

(47)

The actions (46) can be proved inductively by using the relations $p_n=\frac{1}{n-1}[\bar{E}_{1},p_{n-1}],\ \ n\ge 2$.

Let us introduce the partition function hierarchy with W-representations

$$\begin{aligned} {{\mathcal {Z}}}_{-n}\{p\}= e^{{\mathcal {W}}_{-n}/n}\cdot 1, \ \ n\ge 1. \end{aligned}$$

(48)

It is straightforward to calculate the power of ${\mathcal {W}}_{-n}$ acting on $J_{\lambda }$ with $\lambda =\varnothing$, leading to the explicit result

$$\begin{aligned} {\mathcal {W}}^m_{-n}\cdot 1=\sum _{\lambda \mapsto nm}\prod _{(i,j)\in \lambda } c(i,j)^{\alpha }b(\lambda ) J_{\lambda }, \ \ n\ge 1, \end{aligned}$$

(49)

where

$$\begin{aligned} b(\lambda )=\frac{\langle p_n^m,J_{\lambda }\rangle _{\beta }}{\langle J_{\lambda }, J_{\lambda }\rangle _{\beta }} =m!n^m\beta ^{-m}\frac{J_{\lambda }\{p_k=\delta _{k,n}\}}{\langle J_{\lambda }, J_{\lambda }\rangle _{\beta }}. \end{aligned}$$

(50)

Using the hook length formula

$$\begin{aligned} \frac{J_{\lambda }\{p_k=N\}}{J_{\lambda }\{p_k=\delta _{k,1}\}}=\beta ^{-|\lambda |} \prod _{(i,j)\in \lambda }c(i,j), \end{aligned}$$

(51)

we further obtain

$$\begin{aligned} {{\mathcal {Z}}}_{-n}\{p\}= & {} \sum _{\lambda }\beta ^{|\lambda |(n\alpha -1)/n}\nonumber \\&\times \left( \frac{J_{\lambda }\{p_k=N\}}{J_{\lambda }\{p_k=\delta _{k,1}\}}\right) ^{\alpha } \frac{J_{\lambda }\{p_k=\delta _{k,n}\}}{\langle J_{\lambda }, J_{\lambda }\rangle _{\beta }} J_{\lambda }\{p\}. \end{aligned}$$

(52)

When particularized to the $n=1, 2$ cases in (52), it gives the $\beta$-deformed rectangular complex (with $N_1=N_2$) and Gaussian hermitian matrix models [3], respectively,

$$\begin{aligned} {{\mathcal {Z}}}_{-1}\{p\}= & {} \sum _{\lambda }\beta ^{|\lambda |} \frac{J_{\lambda }\{p_k=N\}^2}{J_{\lambda }\{p_k=\delta _{k,1}\}\langle J_{\lambda }, J_{\lambda }\rangle _{\beta }} J_{\lambda }\{p\},\nonumber \\ {{\mathcal {Z}}}_{-2}\{p\}= & {} \prod _{i=1}^N\int _{-\infty }^{+\infty } dz_i\Delta (z)^{2\beta } e^{\sum _{i=1}^{N}\sum _{k=1}^{\infty }\beta \frac{ p_k}{k}z_i^k- \frac{1}{2}\sum _{i=1}^Nz_i^2}\nonumber \\= & {} \sum _{\lambda }\beta ^{|\lambda |/2} \frac{J_{\lambda }\{p_k=N\}J_{\lambda }\{p_k=\delta _{k,2}\}}{J_{\lambda }\{p_k=\delta _{k,1}\} \langle J_{\lambda }, J_{\lambda }\rangle _{\beta }} J_{\lambda }\{p\}. \end{aligned}$$

(53)

Let us turn to construct the operator

$$\begin{aligned} {\mathcal {W}}_{1}=[{\mathcal {W}}_{0},{\bar{E}}_{-1}], \end{aligned}$$

(54)

where the operator $\bar{E}_{-1}$ is given by

$$\begin{aligned} \bar{E}_{-1}= & {} \beta ^{-1}\left[ {\mathcal {W}}_0, \frac{\partial }{\partial p_1}\right] \nonumber \\= & {} -\sum _{n=1}^{\infty }(n+1)p_{n}\frac{\partial }{\partial {p_{n+1}}} -N\frac{\partial }{\partial {p_{1}}}. \end{aligned}$$

(55)

We have the action

$$\begin{aligned} {\mathcal {W}}_{1}J_{\lambda }=\sum _{\lambda -\square } c^{2}(i_\square ,j_\square )B_\lambda ^{\lambda -\square }J_{\lambda -\square }, \end{aligned}$$

(56)

where $B_\lambda ^{\lambda -\square }$ are the coefficients in

$$\begin{aligned} \beta ^{-1} \frac{\partial }{\partial p_1}J_{\lambda }=\sum _{\lambda -\square } B_{\lambda }^{\lambda -\square } J_{\lambda -\square }. \end{aligned}$$

(57)

Let us introduce the operators

$$\begin{aligned} {\mathcal {W}}_{n}=\frac{(-1)^n}{(n-1)!}\underbrace{[{\mathcal {W}}_{1}, [{\mathcal {W}}_{1}, \ldots [{\mathcal {W}}_{1} }_{n-1}, \bar{E}_{-1}]\ldots ]],\ \ n\ge 2. \nonumber \\ \end{aligned}$$

(58)

We have the actions

$$\begin{aligned} {\mathcal {W}}_{n}J_{\lambda }= & {} \sum _{\lambda -\square _1-\cdots -\square _n} \prod _{k=1}^{n} c(i_{\square _k},j_{\square _k})^\alpha \nonumber \\&B_{\lambda }^{\lambda -\square _1-\cdots -\square _n} J_{\lambda -\square _1-\cdots -\square _n}, \ \ n\ge 1, \end{aligned}$$

(59)

where $B_{\lambda }^{\lambda -\square _1-\cdots -\square _n}$ are the coefficients in

$$\begin{aligned} \beta ^{-1} n\frac{\partial }{\partial p_n}J_{\lambda }=\sum _{\lambda -\square _1-\cdots -\square _n} B_{\lambda }^{\lambda -\square _1-\cdots -\square _n} J_{\lambda -\square _1-\cdots -\square _n}. \nonumber \\ \end{aligned}$$

(60)

We introduce the partition function hierarchy with W-representations

$$\begin{aligned} {{\mathcal {Z}}}_n\{g|p\}=e^{\mathcal W_{n}/n}e^{\beta \sum _{k=1}^{\infty } \frac{p_kg_k}{k}},\ \ n\ge 1. \end{aligned}$$

(61)

Due to

$$\begin{aligned} \frac{1}{n^m m!}{\mathcal {W}}_{n}^m J_\lambda= & {} \sum _{\mu \mapsto |\lambda |-nm}\beta ^{m(n\alpha -1)}\nonumber \\&\times \left( \frac{J_{\lambda }\{p_k=N\}J_{\mu }\{p_k=\delta _{k,1}\}}{J_{\mu }\{p_k=N\}J_{\lambda }\{p_k=\delta _{k,1}\}}\right) ^{\alpha }\nonumber \\&\times \frac{J_{\lambda /\mu }\{p_k=\delta _{k,n}\}}{\langle J_{\mu }, J_{\mu }\rangle _{\beta }}J_{\mu }, \end{aligned}$$

(62)

and the Cauchy formula (33), there are the character expansions for the partition function hierarchy (61)

$$\begin{aligned} {\mathcal Z}_n\{g|p\}= & {} \sum _{\lambda ,\mu }\beta ^{|\lambda /\mu |(n\alpha -1)/n} \left( \frac{J_{\lambda }\{p_k=N\}J_{\mu }\{p_k=\delta _{k,1}\}}{J_{\mu }\{p_k=N\}J_{\lambda }\{p_k=\delta _{k,1}\}}\right) ^{\alpha }\nonumber \\&\times \frac{J_{\lambda /\mu } \{p_k=\delta _{k,n}\}}{\langle J_{\lambda }, J_{\lambda }\rangle _{\beta }\langle J_{\mu }, J_{\mu }\rangle _{\beta }} J_{\lambda }\{g\}J_{\mu }\{p\}. \end{aligned}$$

(63)

4 Summary

It was known that the Hurwitz–Kontsevich matrix model (1) can be expressed as the exponent of the Hurwitz operator $W_0$ acting on the function $e^{p_1/e^{tN}}$. In terms of the Hurwitz operator $W_0$, $p_1$ and $\frac{\partial }{\partial p_1}$, we have constructed the partition function hierarchies with W-representations. Based on the W-representations, we showed that these partition functions can be expressed as the character expansions with respect to the Schur functions. It was noted that the character expansions of hierarchy (15) give the $\tau$-functions of the KP hierarchy, and the $N\times N$ complex matrix and Gaussian hermitian one-matrix models are contained in the hierarchy (15). For the constructed partition function hierarchy (29), it contains the Gaussian hermitian one-matrix model in the external field. We have also extended the Hurwitz–Kontsevich matrix model (1) to the $\beta$-deformed case. Similarly, the $\beta$-deformed partition function hierarchies with W-representations were constructed and their character expansions with respect to the Jack polynomials were presented as well. The $\beta$-deformed rectangular complex and Gaussian hermitian matrix models are contained in the hierarchy (52). Searching for the matrix model representations of the partition functions in the hierarchies presented in this paper would merit further investigations. Furthermore, it would be interesting to construct q, t-deformed partition function hierarchies with W-representations and study their character expansions with respect to the Macdonald polynomials.