Abstract
We study the influence of parameter \(\alpha \) on the optical features of Schwarzschild-MOG black holes with different thin accretions in scalar-tensor-vector gravity. As \(\alpha \) increases from 0, the radii of the event horizon, photon sphere, and observed shadow increase in comparison with the Schwarzschild black hole. We constrain the parameter \(\alpha \) with the experimental data reported by the Event Horizon Telescope Collaboration for M87\(^{*}\) and Sagittarius A\(^{*}\). In the situation of spherical accretions, we unveil that the parameter \(\alpha \) has a positive effect on the shadow size but a negative effect on the observed specific intensities. Considering that the Schwarzschild-MOG black hole is surrounded by an optical and geometrically thin accretion disk, we find that the total observed specific intensities are mainly contributed by the direct emissions, while the photon rings and lensed rings provide small contributions. It is also found that with the increase of \(\alpha \), the black hole shadow expands, the photon rings and lensed rings become larger and thicker. Besides, we emphasize that the boundary of the observed shadow cast by the aim black hole in the disk accretion scenario is determined by the direct emissions rather than the photon ring emissions. Consequently, we unveil that there is a linear relationship involving the critical impact parameter and the starting point of the direct emissions. This finding helps to use the experimental results of the Event Horizon Telescope to infer the critical impact parameter and to test General Relativity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Black holes are extremely compact celestial bodies predicted by General Relativity, and they have attracted much attention since the first black hole solution was obtained by Karl \(\cdot \) Schwarzschild in 1916 [1]. In recent years, the successful detection of the gravitational-wave signals radiated from binary black hole mergers with Laser-Interferometer Gravitational Wave-Observatory (LIGO) experiments and a wide star-black-hole binary system discovered by radial-velocity measurements strongly confirm the existence of black holes in our universe [2,3,4,5]. While, more intuitive evidences of the existence of black holes are the ultra-high angular resolution images of M87\(^{*}\) and Sagittarius A\(^{*}\), which were announced by the Event Horizon Telescope Collaboration (EHT) [6,7,8,9,10,11,12,13,14,15,16,17]. There is a faint region in the center of these images, called the black hole shadow. It is well known that the light ray will deflect in the vicinity of a black hole due to the lensing effect [18,19,20,21], resulting in a deficit of the observed specific intensity inside the sharp-edged boundary, thus a region of brightness depression can be observed on the distant image plane. The black hole shadow is closely related to spacetime geometry. Consequently, it is a robust tool for estimating black hole parameters [22,23,24,25] and testing General Relativity or its alternatives [26,27,28,29,30,31,32].
It is generally believed that the astrophysical black holes in the universe are rotating black holes. This is because black holes are the final stages of the collapse of a massive star and obtain most of the progenitor’s angular momentum. Bardeen first analytically solved the shadow of the Kerr black hole and pointed out that the shape of the shadow is deformed into a figure “D” due to the drag effect [33]. This triggered a series of works investigating the shadows of rotating black holes and the relationship involving shadow shapes, spin parameters, and observational angles [34,35,36,37,38,39,40,41,42,43]. Considering that a rotating black hole is surrounded by superfluid dark matter and baryonic matter, the authors of [44] studied the effects of surrounding matter on the black hole shadow. The results show that the shadow size increases with the increase of baryonic mass. One can see [45,46,47] for a comprehensive study. In addition, the shadow of rotating black holes in modified gravity also attracts public attentions. In the four-dimensional Einstein-Gauss-Bonnet gravity, the authors of [48] investigated the horizon properties and shadows of the rotating black holes. They unveiled that the Gauss-Bonnet coupling parameter exerts a non-neglect influence on the shadow profiles. The shadow cast by the rotating black hole in the asymptotically safe gravity (ASG) was presented in [49], and the relationship between the shadow and the ASG parameter was discussed in detail. In Rastall gravity, the field structure parameter and the Rastall parameter exert significant influence on the apparent size of the shadow cast by a rotating black hole surrounded by anisotropic fluid, which has been studied by the authors of [50]. It is interesting to note that the rotational energy of a spinning black hole can be extracted from the ergosphere via the Penrose superradiance process [51] or the Blandford and Znajek mechanism [52], resulting in a rotating black hole degenerating into a non-rotating one. Therefore, we cannot exclude the possibility that static black holes exist in the universe. The shadows and optical images of such black holes also need to be investigated in detail for the purpose of exploring the nature of the black holes.
Taking an optical thin spherical accretion flow as the light source, Bambi investigated apparent images of the Schwarzschild black hole and the static wormhole. He pointed out that it is relatively easy to distinguish the former from the latter according to shadow images [53]. The difference in the shadows between non-rotating black holes and wormholes in the condition of spherical accretion was also presented in [54]. Narayan et al. studied the observed shadow of a spherically accreting Schwarzschild black hole and argued that the shadow profile is insensitive to spherical accretion details [55]. Zeng et al. investigated the shadow and photon rings of the four-dimensional Gauss-Bonnet black hole and proposed that the variations of the profile of the specific emissivity of spherical accretion introduce no changes in the shadow size, but can significantly affect the shadow luminosity [56]. Gan et al. focused on the features of the shadow cast by a hairy black hole with spherical accretion. They found two photon rings appeared in the vicinity of this black hole, where the smaller one serves as the boundary of the shadow [57]. By investigating the shadow and photon sphere of a charged black hole in Rastall gravity, Guo et al. claimed that the luminosity of the photon sphere is affected by spherical accretion materials and the property of spacetime geometry [58]. The authors of [59] studied the shadow of the black hole with the dark matter halo in Verlinde’s emergent gravity and unveiled that the observed intensity is depending on the surrounding mass. The influence of the perfect fluid dark matter on the black hole shadows was well studied by the authors of [60]. They also found that the distribution of dark matter around the black hole plays a key role in the shadow radius and the intensity of the electromagnetic flux radiation. In [61], the shadow and photon sphere of the uncharged static black bole in clouds of strings and quintessence with spherical accretions were investigated. It is worth mentioning that the non-monochromatic light sources that follow a normal distribution are considered in the investigation. In short, these studies help us understand the effect of spherical accretion flow on the characteristics of black hole shadows.
Spherical accretion is a quietly ideal description of the accretion mechanism in the vicinity of the astrophysical black holes. In fact, the materials in the universe, such as plasma, gas, and dust, will be trapped by a black hole due to the strong gravity and formed a giant disk-shaped accretion flow surrounding the black hole. For a remote observer, the lights emitting from this disk are the main source that illuminates the black hole. Gralla et al. first investigated the shadow cast by a Schwarzschild black hole with an optically and geometrically thin accretion disk, claiming that the features of the black hole shadow are not only photon rings but also lensed rings [62]. However, these two rings are barely visible in the condition of the particular emission profile of the accretion disk because of the deficiency of the angular resolution of the EHT. This elaborate investigation triggers a new era of studying the influence of the thin accretion disk on the observed black hole shadow. By considering a non-rotating black hole in the background of the quintessence dark energy, the authors of [63] studied the effect of the quintessence on the shadow of the black hole with a thin accretion disk and pointed out that the cosmological horizon plays an important role in the shadow images. Peng et al. investigated the optical appearance of the Schwarzschild black hole surrounded by a thin disk accretion with the quantum modification of Einstein gravity and the influence of the quantum corrections on black hole shadows [64]. The effects of a thin accretion disk with different emission profiles on the observed features of shadows cast by the power-Yang-Mills black hole were presented in [65], and the relationship between the power parameter and the shadow size was also studied in this literature. Guo et al. focused on the effect of the magnetic charge on observed shadows of the Hayward black hole with different accretion flows and argued that the luminosities of shadows are affected by the accretion properties and the magnetic charge [66]. In addition, many other studies have focused on the influence of the thin accretion disk on the black hole shadows [67,68,69,70,71,72], and the effect of the thin accretion disk on the optical appearance of wormholes [73, 74] and other compact objects [75] has also received enough interests.
The Schwarzschild-MOG black hole is a static spherically symmetric vacuum solution derived from scalar-tensor-vector gravity (STVG) based on the Einstein-Hilbert action combined with massive vector field and matter action [76,77,78]. The investigation of such black holes is necessary and has profound implications for our understanding of the universe, as STVG not only successfully explains some phenomena in the solar system observation, the dynamics of galactic clusters, and the rotation curves of galaxies [79,80,81,82], but also fits the lensing and Einstein ring in Abell 3827 [83], and the signal of GW150914 [84]. In [85], the author introduced the Hamiltonian formalism for the dynamics of the massive and massless particles in STVG, as well as the post-Newtonian approximation of the equations of motion. The circular motions of neutral test particles on the equatorial plane of a Schwarzschild-MOG black hole were reported in [86], while the dynamics of massive charged particles around this black hole with an external magnetic field were investigated in [87]. In addition, the light deflections and lensing effects in this gravitational field were solved in [88,89,90]. The shadow, which is the fingerprint of the black holes, was first investigated by Moffat [91], and late studied by the authors of [92]. However, these studies only focus on the size and silhouette of the Schwarzschild-MOG black hole shadow, while the influences of the accretion flow on the shadow of this object are still unclear. Since the accretion flow plays a pivotal role in black hole shadow observations, here we concentrate on the brightness depression and optical images of this black hole illuminated by different accretions, which is the main purpose of this paper.
The remainder of this paper is organized as follows. In Sect. 2, we study the photon deflections and shadow radii of Schwarzschild-MOG black holes with the help of Lagrangian formalism. The constraints of the parameter \(\alpha \) with the EHT data are also presented. In Sect. 3, we investigate the specific intensities and optical appearances of Schwarzschild-MOG black holes with static and infalling spherical accretion. The effects of an optically and geometrically thin accretion disk on the observed features of this black hole are investigated in Sect. 4. Finally, the conclusions and discussions are concluded in Sect. 5.
2 The photon deflections and shadow radii of the Schwarzschild-MOG black holes
In Boyer–Lindquist coordinates \(x^{\alpha } = (t,r,\theta ,\varphi )\), the static spherically symmetric Schwarzschild-MOG black hole obtained from the modified gravitational field equations is given by [77, 78]
where \(\text {d}\varOmega ^{2}=\text {d}\theta ^{2}+\text {sin}^{2}\theta \text {d}\varphi ^{2}\) is the surface-element of the two-spheres and f(r) denotes the metric potential,
M stands for the black hole mass and \(\alpha \) is a dimensionless parameter defined by \(G=G_{N}(1+\alpha )\), where G and \(G_{N}\) is enhanced gravitational constant and Newton’s constant, respectively. When \(\alpha =0\), the Schwarzschild-MOG black hole reduces to the Schwarzschild black hole. When \(\alpha > 0\), there are two positive real roots satisfied the condition of \(f(r)=0\), and the larger root \(r_{e}\) corresponds to the event horizon, whereas the smaller one \(r_{c}\) is called the Cauchy horizon,
In addition, \(\alpha \) determines the strength of the gravitational field around the black hole. The larger the \(\alpha \), the stronger the gravitational field strength. To simplify our problem, the dimensionless operations and geometric units are adopted, which are \(r\rightarrow rM, t\rightarrow tM\) and \(G=c=1\). As a result, the black hole mass M becomes 1. And we only consider the situation of \(0\le \alpha \le 1\) in this paper.
The motions of photon in the vicinity of a Schwarzschild-MOG black hole are described by a Lagrangian formulism,
where \({\dot{x}}^{\mu }\) represents the four-velocity of photon, which is a derivative of the general coordinate with respect to an affine parameter \(\lambda \). Apparently, there are two conserved quantities along with the motion of photon, one is the energy E, another is the angular momentum L,
With the help of static spherically symmetric of spacetime, we confined the photon motions on the equatorial plane without loss of generality. Therefore, the \(\theta \) and \({\dot{\theta }}\) are fixed at \(\pi /2\) and 0. The photon travels along the null geodesics, which means Eq. (5) satisfied \({\mathscr {L}}=0\). Consequently, we obtained the equations of photon motions around a Schwarzschild-MOG black hole according to the Euler-Lagrange equations,
The direction of photon motion is determined by the L in Eq. (10), when \(L<0\), the photon travels in a clockwise direction, or in a counterclockwise direction when \(L>0\). By defining an impact parameter \(b=L/E\), we derive the effective potential \(V_{\text {eff}}\) from Eq. (9) with \({\dot{r}}=0\), which read as
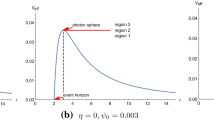
Here, b is given the scale transformation \(b \rightarrow bM\). We plot effective potential as a function of radius r with three values of the parameter \(\alpha \), as shown in Fig. 1. The effective potential starts from 0 at the event horizon and immediately increases to a maximum value as r increases, then shows a moderate attenuation trend with the increase of r. The parameter \(\alpha \) has a negative effect on the effective potential. Besides, the \(r_{p}\), which corresponds to the local maximum of the effective potential, increases as the increase of \(\alpha \).
In fact, \(r_{p}\) is the radius of the photon sphere, it can be deduced by solving the following equation,
It is not difficult to find an explicit expression between \(r_{p}\) and \(\alpha \) according to above equation,
We substitute \(r_{p}\) into Eq. (11), then the explicit expression involving the critical impact parameter \(b_{p}\) for the photon sphere is written as
It is worth mentioning that the value of the impact parameter b corresponds to the vertical distance between the null geodesic line and the parallel line passing through the singularity of the black hole in Boyer–Lindquist coordinates, which means the \(b_{p}\) is the radius of the black hole shadow observed by a distant observer [69]. We obtain the event horizon \(r_{e}\), photon sphere \(r_{p}\), and observed shadow \(b_{p}\) of Schwarzschild-MOG black holes with different values of \(\alpha \) by solving Eqs. (3), (13) and (14), as listed in Table 1. The results show that \(\alpha \) has a positive influence on the radius of the event horizon, the photon sphere, and the black hole shadow. This is because as \(\alpha \) increases, the strength of the gravitational field around the black hole increases, so the black hole has a stronger ability to capture light rays, resulting in the expansion of the photon spheres and black hole shadows. In addition, when \(0<\alpha \le 1\), both \(r_{e}\), \(r_{p}\) and \(b_{p}\) are bigger than that of Schwarzschild case.
Next, we focus on the photon trajectories in the vicinity of Schwarzschild-MOG black holes with different values of the parameter \(\alpha \). Combing Eqs. (9) and (10), we easily obtain the relation between the photon coordinate r and azimuthal angle \(\varphi \),
the direction of photon motion is determined by the sign of L/|L|, which has discussed before. By introducing a new parameter \(u=1/r\), we arrange Eq. (15) as
It is worth mentioning that for the light rays with \(b>b_{p}\), the turn point \(u_{t}\) on their traveling paths needs to be carefully handled, and it can be derived from
With the help of compound Simpson integral formula, we plot photon trajectories in the vicinity of Schwarzschild-MOG black holes with different \(\alpha \), as shown in Fig. 2. One can find that every panel consists of red lines and green lines, which correspond to the light rays of \(b<b_{p}\), \(b>b_{p}\), respectively. The blue dashed line is the photon sphere (\(b=b_{p}\)), and the projection of the event horizon surface is represented as a black disk. These photon trajectories with different colors represent three kinds of photon propagation in the Schwarzschild-MOG spacetime. The light rays with \(b=b_{p}\) will asymptotically approach the photon sphere and will orbit the black hole along the unstable circular orbit infinite times without perturbations; the light rays with \(b>b_{p}\) will encounter the potential barrier and then be scattered to infinite after passing through the turn point. The light rays with \(b<b_{p}\) move in the inward direction and are absorbed by the black hole eventually. This kind of light rays cannot be received by the distant observer, so a shadow forms in the observational sky. In addition, it is clear that as \(\alpha \) increases, more light rays are absorbed by the black hole, implying that the shadow expanded accordingly.
Trajectories of light rays in the vicinity of Schwarzschild-MOG black holes of different \(\alpha \) in the polar coordinates (\(r,\varphi \)). The \(\alpha \) from panel a–d is 0.2, 0.4, 0.6, and 0.8, respectively. In each panel, the red lines, green lines, and blue dashed lines represent the light rays of \(b < b_{p}\), \(b > b_{p}\), and \(b = b_{p}\), respectively. The event horizon is represented by a black disk
The shadow is the fingerprint of the spacetime geometry, and the parameter \(\alpha \) of the Schwarzschild-MOG black hole can be inferred by the observed shadow. For a distant observer, the black hole shadow is always measured by angular diameter \(\varOmega \) [30]
where D is the distance between the black hole and observer. The above equation can be rewritten as
in which \(\gamma \) is the mass ratio of the black hole to the Sun, and \(b_{p}\) is obtained from the Eq. (14).
By solving Eqs. (14) and (19), we study the dependence of angular diameter \(\varOmega \) of the black hole shadow on different values of the parameter \(\alpha \), as shown in Fig. 3. Here we have \(\gamma =4.14 \times 10^{6}\) and distance \(D=8.127\) kpc for the red line, \(\gamma =6.2 \times 10^{9}\) and distance \(D=16.8\) Mpc for the black line. It is found that \(\varOmega \) grows linearly with \(\alpha \) in the range of \(0\le \alpha \le 1\). The green and blue regions are the shadow diameters of M87\(^{*}\) (\(42\pm 3\) \(\mu \)as) and Sagittarius A\(^{*}\) (\(51.8\pm 2.3\) \(\mu \)as) estimated with the EHT observations [6, 12]. Consequently, we constrain the parameter \(\alpha \) of the Schwarzschild-MOG black hole as \(0.040<\alpha < 0.232\) for M87\(^{*}\), and \(0<\alpha < 0.044\) for Sagittarius A\(^{*}\). It hints that such black holes satisfies the EHT constraints, and it is possible to detect the Schwarzschild-MOG black hole in the future.
3 Shadows and rings of the Schwarzschild-MOG black holes with different spherical accretions
There is an ocean of free-moving matter in the universe that can be accreted by a black hole. The light rays radiated by these substances are the light source that illuminates the black hole. In this section, we investigate the shadows and photon rings of Schwarzschild-MOG black holes with static and infalling spherical accretions.
3.1 Shadows and photon rings with static spherical accretion
We consider an optically and geometrically thin accretion flow which static spherically symmetric distributed outside the event horizon of a Schwarzschild-MOG black hole. The specific intensity \(I(v_{\text {o}})\) (measured in erg s\(^{-1}\) cm\(^{-2}\) str\(^{-1}\) Hz\(^{-1}\)) radiated by the accretion flow can be obtained by integrating the specific emissivity along the photon path [56, 58],
where \(v_{\text {o}}\), \(v_{\text {e}}\) are observed photon frequency and emit photon frequency, while their ratio is called the redshift factor, which is \(g=v_{\text {o}}/v_{\text {e}}\); \(j(v_{\text {e}})\) is emissivity per unit volume measured in the static frame, and we choose \(j(v_{\text {e}})\) \(\propto \) \(1/r^{2}\) for monochromatic emission with rest-frame frequency \(v_{\text {e}}\); \(\text {d}l_{\text {prop}}\) is the infinitesimal proper length. In the Schwarzschild-MOG spacetime, the redshift factor g and the infinitesimal proper length \(\text {d}l_{\text {prop}}\) are expressed as follows
where \(\text {d}\varphi /\text {d}r\) is given by Eq. (15). Therefore, the specific intensity observed by a distant observer is governed by
The relationship between the angular diameter \(\varOmega \) of the observed shadow and the parameter \(\alpha \). The green and blue regions are the experimental data of M87\(^{*}\) (\(42\pm 3\) \(\mu \)as) and Sagittarius A\(^{*}\) (\(51.8\pm 2.3\) \(\mu \)as) reported by the EHT, respectively. Thus, the parameter \(\alpha \) can be constrained as \(0.040<\alpha <0.232\) for M87\(^{*}\), and \(0<\alpha < 0.044\) for Sagittarius A\(^{*}\)
The observed specific intensity \(I_{\text {obs}}\) is not only a function of impact parameter b but also affected by the parameter \(\alpha \). Figure 4 depicts the \(I_{\text {obs}}\) radiated by a static spherical accretion flow surrounding Schwarzschild-MOG black holes, while \(I_{\text {obs}}\) corresponding to negative b is obtained by the symmetry of spacetime. In the region of positive b, we find that no matter \(\alpha \) takes, the specific intensity \(I_{\text {obs}}\) increases with the increase of b and reaches a peak quickly, then drops asymptotically to a small value with increasing b. However, the parameter \(\alpha \) significantly harm the specific intensity, which means that the brightness around the Schwarzschild-MOG black hole is lower than that of the Schwarzschild case, and this evidence allows us to distinguish the former from the latter. Besides, the impact parameter corresponding to the maximum specific intensity is the critical impact parameter \(b_{p}\), which is the radius of the black hole shadow. Clearly, larger \(\alpha \) correspond to a larger shadow diameter.
Dependence of observed specific intensity \(I_{\text {obs}}\) on the impact parameter b for several values of \(\alpha \) in the case of the static spherical accretion, where the curves for \(b < 0\) are obtained by symmetry. It is shown that \(\alpha \) has a negative effect on the observed specific intensity in comparison with the Schwarzschild case (\(\alpha =0\))
Using the condition of \(b^{2}=x^{2}+y^{2}\), we perform the distribution of specific intensity \(I_{\text {obs}}\) on the observational plane (x, y), as shown in Fig. 5. The disc region with a faint luminosity in the center of each panel is the black hole shadow, while the brightest ring surrounding the shadow represents the photon ring. With the increase of the parameter \(\alpha \), the radius of the shadow expands with a larger photon ring. This result is consistent with that of Table 1 and Fig. 4. Moreover, the specific intensity decreases with the increase of \(\alpha \). The reason for this is that as the parameter \(\alpha \) increases, the strength of the gravitational field of the black hole also increases (we have mentioned this before), resulting in more light rays being trapped by the black hole and a lower luminosity of shadow and photon ring being observed.
3.2 Shadows and photon rings with infalling spherical accretion
Static spherical accretion is an ideal description of the accretion process around the black holes. Actually, the matter, such as plasma, is free-moving in the universe and can be trapped by the black hole with its initial velocity. In this case, the infalling spherical accretion should be considered. The specific intensity of this scenario can still be calculated by Eq. (20), but the redshift factor g needs to be rewritten as [53]
where \(u_{\text {o}}^{\mu }\), \(u_{\text {e}}^{\nu }\) are four-velocity of the distant observer and accretion matters. For simplicity, we assume that the distant observer is stationary with \(u_{\text {o}}^{\mu }=(1,0,0,0)\). In the Schwarzschild-MOG spacetime, the \(u_{\text {e}}^{\nu }\) is given as
The \(k_{\mu }\) of Eq. (24) is the four-momentum of the photon radiated from accretion matters, which can be obtained with the help of \(k_{\mu }=\partial {\mathscr {L}}/\partial {\dot{x}}^{\mu }\). Note that both \(u_{\text {o}}^{\mu }\) and \(u_{\text {e}}^{\nu }\) only contain components in the t or r direction, thus it is reasonable to only calculate the relationship between \(k_{r}\) and \(k_{t}\),which is [53]
where the symbol \(+\) (−) corresponds to the motion that the photon approaches (goes away from) the black hole. Based on Eqs. (24)–(28), we have the redshift factor g as
and the infinitesimal proper length is
Hence, we have the observed specific intensity for the scenario of the infalling spherical accretion (the emission profile \(j(v_{\text {e}})\) is the same as that of static accretion),
Figure 6 shows the influence of the parameter \(\alpha \) on the specific intensity \(I_{\text {obs}}\) of the Schwarzschild-MOG black hole with an infalling accretion. The trends of \(I_{\text {obs}}\) with different \(\alpha \) are similar to those in Fig. 4, where the peak of each curve appears at \(b=b_{p}\). The maximum value of \(I_{\text {obs}}\) comes from the contribution of the light rays that are marginally escaped from the black hole and decreases moderately with the increase of \(\alpha \). By the way, the width between the two maximums of each curve, which increases with the increase of \(\alpha \) is \(2b_{p}\), indicating that \(\alpha \) has a positive effect on the diameter of the observed shadow.
Similar to Fig. 4 but an infalling spherical accretion is used instead of the static spherical accretion
The specific intensity maps with different values of \(\alpha \) are demonstrated in Fig. 7. Obviously, the center of the intensity map is the black hole shadow with very low luminosity and encircled by the brightest photon ring. The shadow and photon ring expand with the increase of \(\alpha \), while their luminosity reduce accordingly. Comparing the results of Figs. 4 and 6, we find that the specific intensity of static accretion is significantly higher than that of infalling accretion for the same parameter \(\alpha \), resulting in the shadow with infalling accretion being darker than that of static accretion. This is due to the Doppler effect caused by the initial velocity of the matter in the case of infalling accretion. In addition, the shadow radius measured by the intensity map is strictly equal to \(b_{p}\) for different \(\alpha \), which means the observed shadow size has nothing to do with spherical accretion flow.
4 Shadows and rings of the Schwarzschild-MOG black holes with thin disk accretions
In this section, we consider an optically and geometrically thin accretion disk located on the equatorial plane and study the features of the optical appearance of Schwarzschild-MOG black holes. We also focus on the relationship between the critical impact parameter (observed shadow radius from the theoretical viewpoint) and the shadow boundary observed by the EHT with its current angular resolution. We assume that the emission from the accretion disk is isotropic and the distant static observer is in the north pole direction.
4.1 Thin disk emission viewed from a face-on orientation
4.1.1 Direct emissions, lensed ring emissions and photon ring emissions
As shown in Fig. 8, the light rays emitted from a disk-shaped accretion flow transmit their luminosities to the remote observer in the z direction. Clearly, the light will intersect the accretion disk several times before reaching the screen of the observer. The deflection angle of the light for qth intersection is \(\varphi =\pi /2+(q-1)\pi \). Hence, we have the total number of photon orbits n
According to the criterion firstly proposed by the authors of [62], the light around the black hole can be divided into three types based on the value of the total number of photon orbits n. More specifically, the light rays hit the accretion disk only once when \(0.25<n<0.75\), and they correspond to the direct emission; when \(0.75<n<1.25\), the light rays intersect the accretion disk twice and correspond to the lensed ring emissions; the photon ring emissions are determined by the light rays that crossing the accretion disk at least three times, where \(n>1.25\) in this situation. The light rays of the direct emissions, lensed ring emissions, and photon ring emissions are represented by red, green, and blue lines in Fig. 8, respectively.
Similar to Fig. 5 but an infalling spherical accretion is used instead of the static spherical accretion
Different trajectories of light rays emit from the accretion disk. The accretion disk (blue solid disk) is located on the equatorial plane of the black hole, and the observer is in the north pole direction (z direction). Apparently, the light will intersect the accretion disk many times before being seen by the distant observer
The relations between the total number of photon orbits n and the impact parameter b for different values of parameter \(\alpha \) are demonstrated in Fig. 9. The Red lines, Green lines, and Blue lines in each panel correspond to the direct emissions, lensed ring emissions, and photon ring emissions, respectively. The b corresponds to the peak of n is the critical impact parameter \(b_{p}\) because a photon can orbit around the black hole many times in this situation. As b increases, the total number of orbits n gets larger for \(b<b_{p}\), while asymptotically decrease to a certain value in the condition of \(b>b_{p}\). It is found that both the width of the lensed ring emissions and photon ring emissions are slightly expanded with the increase of parameter \(\alpha \). This phenomenon can be revealed by recording the range of b for the direct emissions, lensed ring emissions and photon ring emissions, as listed in Table 2. Clearly, with the increase of \(\alpha \), the ranges of b for lensed ring emissions and photon ring emissions get larger, while that for the direct emissions shrinks. We plot the photon trajectories for different \(\alpha \) in polar coordinates, as demonstrated in Fig. 10. The results shows that the thicknesses of the lensed rings and photon rings are getting thicker for the increase of \(\alpha \).
4.1.2 Observed intensities and transfer functions
We assume that the specific intensity and frequency of the emitted light are \(I_{\text {e}}(r)\) and \(\nu _{\text {e}}\). According to the Liouville’s theorem, the value of \(I_{\text {e}}(r)/ \nu _{\text {e}}^{3}\) is an invariant along the entire path of the photon propagation, and satisfied the equation of \(I_{\text {e}}(r)/ \nu _{\text {e}}^{3}=I_{\text {ray}}(r)/ \nu _{\text {o}}^{3}\), where \(I_{\text {ray}}(r)\) and \(\nu _{\text {o}}\) are the specific intensity and frequency of the observed light [93]. Hence, we have the relation
By integrating over the whole range of the observed photon frequencies \(v_{\text {o}}\), we have the total observed specific intensity
where \(I_{\text {emit}}(r)\) is the total emission intensity of the accretion disk, which is defined as \(I_{\text {emit}}(r)=\int I_{\text {e}}(r)\text {d}v_{\text {e}}\). Considering the fact that the light can pick up an additional brightness for each intersection between the light and the accretion disk, thus, the total observed intensities of the direct emissions, lensed ring emissions, and the photon ring emissions are the sum of the extra intensity the light ray obtains each time it passes through the accretion disk. Consequently, the total observed specific intensity \(I_{\text {obs}}\) should be rewritten as
where \(r_{q}(b)\) is the transfer function [62], which is the correlation between the impact parameter of the photon in the distant observational sky and the radial coordinate of the qth intersections of the light ray and the accretion disk. Moreover, the slope of the transfer function, \(\text {d}r/\text {d}b=\varGamma \), is defined as a (de)magnification factor, which reveals the (de)magnification scale of the image.
Panel a–c: The total number of photon orbits n as a function of the impact parameter b for Schwarzschild-MOG black holes with different values of \(\alpha \). The red lines, green lines, and blue lines correspond to the direct emissions, lensed ring emissions, and photon ring emissions, respectively. Panel d–f: The behavior of photon rays according to the direct emissions (red), lensed ring emissions (green), and photon ring emissions (blue). The yellow dashed lines and black disks denote the photon ring and event horizon. The gray dashed line indicates the plane of the accretion disk. As the parameter \(\alpha \) increases, the lensed rings and photon rings thickens
We show the first three transfer functions \(r_{q}(b)\) for different parameter \(\alpha \) in Fig. 11. The red dashed line in each panel is the first transfer function with \(q=1\), corresponding to the direct emission of the accretion disk. The first transfer function is in direct proportion to the impact parameter b with a slope of nearly 1 no matter \(\alpha \) takes, so the direct image profile is the gravitational redshifted source profile. We can infer that the direct emissions contribute to a dominant part of the total observed intensity. The green dashed line represents the second transfer function with \(q=2\), which corresponds to the lensed ring emissions. One can find that the slopes of the second transfer function is sufficiently large, which are \(\varGamma =16.7\) in panel (a), \(\varGamma =13.6\) in panel (b), and \(\varGamma =11.4\) in panel (c). This shows that the lensed images are highly demagnified and the intensity of the lensed ring is around \(1/\varGamma \) of the total observed intensity. Finally, the blue dashed line located around \(b=b_{p}\) is the third transfer function (\(q=3\)) and corresponds to the photon ring emissions. The slope of the third transfer function is nearly infinite, which means the photon ring image will be extremely demagnified. Hence, the observed intensity of the photon ring is negligible.
4.1.3 Observational signatures of the Schwarzschild-MOG black holes
The light rays emitted from a thin accretion disk are the dominant part of the light source that illuminate the black hole. The total emission intensity \(I_{\text {emit}}(r)\) depends on the emission position r on the accretion disk. In this subsection, we investigate the observed features of Schwarzschild-MOG black holes for three toy models of disk emission profiles.
In Model I, the emission of the accretion disk starts from the position of the radius of the innermost stable circular orbit \(r_{\text {ISCO}}\) of the massive particle, and the total emission specific intensity is a decay function of the power of second-order related to the radial coordinate,
where \(r_{\text {ISCO}}\) is obtain by [66]
in which \(f^{\prime }\), \(f^{\prime \prime }\) represent the first and second partial derivatives of metric potential to r, respectively. In Model II, we consider that the emission starts from the position of the radius of the photon sphere \(r_{p}\), and exhibits a cubic decay trend when \(r>r_{p}\), which is
Finally, we consider a model in which the emission intensity decays more moderate than in the first two models, while emission starts from the radius of event horizon \(r_{e}\),
We show the variations of the total emission intensities \(I_{\text {emit}}(r)\) with r in the left column in Fig. 11 for \(\alpha =0.3\) and Fig. 12 for \(\alpha =0.9\), where the first, second, and third of each column represent the emission profiles of Model I, II, and III, respectively. As we mentioned before, the starting position of emission is different from model to model. When the parameter \(\alpha \) is increased, the emission starting points \(r_{\text {ISCO}}\), \(r_{p}\), \(r_{e}\) of three emission profiles are increased because the strength of the gravitational field will be stronger when \(\alpha \) gets larger.
Total emission intensities \(I_{\text {emit}}\) of the optical and geometrically thin accretion disks as a function of radius r (left column), the total observed specific intensities as a function of the impact parameter b (middle column), optical appearances of Schwarzschild-MOG black holes with a thin accretion disk (right column). The emission profile from top to bottom in each row is Model I, II, and III, respectively. Here we have set \(\alpha =0.3\)
Similar to Fig. 11 but for \(\alpha =0.9\)
In what follows, with the help of the Eq. (35), \(I_{\text {emit}}(r)\) and the transfer function \(r_{q}(b)\), we study the features of the optical appearance of the Schwarzschild-MOG black hole with a thin accretion disk. Fig. 11d shows the total observed specific intensity \(I_{\text {obs}}\) as a function of the impact parameter b. One can find that there is a peak at \(b\simeq 6.51\) with a very low intensity of \(I_{\text {obs}}=0.018\), which is the contribution of the photon ring emissions. The peak contributed by the lensed ring emissions appears in the emission region of \(6.85\le b\le 7.53\). The value of this peak is about 20 times larger than the corresponding value of the photon ring emissions. The \(I_{\text {obs}}\) in the range of \(b\ge 8.52\) is contributed by the direct emission and shows a trend that decays with increasing b. These features can be seen more clearly in Fig. 11g. The brightest ring surrounding the black disk is the contributions of the direct emissions, which are the dominant part of the total emission. The distinct thin circle with the radius of about 6.85 inner of the black disk is the so-called lensed ring. The photon ring appears inside the lensed ring but it is almost invisible because of its negligible intensity and extremely narrow region.
When we consider Model II as the emission profile of the accretion disk, the total observed specific intensity \(I_{\text {obs}}\) as a function of b is displayed in Fig. 11e. There are two distinct peaks in the whole range of \(0<b\le 18\), where the first peak from the left is located at \(b\simeq 4.8\), which is defined as the contribution of the direct emission. The lensed ring and photon ring almost overlap, and their combined contributions to the total observed intensity form a second peak with a large intensity of \(I_{\text {obs}}=0.11\). This peak is limited in a narrow interval of \(6.47<b<6.86\). Figure 11h demonstrated the distribution of the observed intensities in celestial coordinates (x, y). There is a black disk with the radius of 4.8 in the center of the image and surrounded by a bright ring that contributed by the direct emission. Both the photon ring and the lensed ring lie on a circle of radius about 6.48, making it difficult to spot one from another. Obviously, the shadow size of this scenario is smaller than that of Model I.
When emission of the accretion disk starts from the event horizon \(r_{e}\) of the black hole (Model III), the total observed specific intensity is shown in Fig. 11f. The specific intensity \(I_{\text {obs}}\) starts from \(b\simeq 3.49\) and grows fastly from 0, then reaches a peak at \(b\simeq 6.49\). This peak is located in the emission region of the photon ring. The peak due to the lensed ring emission emerges in the range of \(6.53<b<6.82\), which is much wider than that of the photon ring emissions. The optical appearance of the Schwarzschild-MOG black hole in this situation is displayed in Fig. 11i. As we can see, the radius of the shadow is about 3.5, which is slightly bigger than that of the event horizon. The brightness ring outside the shadow contains the photon ring and the lensed ring because they are very close together in panel (f). The region with moderate luminosity between the photon ring and the shadow is the contribution of the direct emission. This infers that the shadow boundary is contributed by direct emission in this case.
Figure 12 is similar to Fig. 11, except that the parameter \(\alpha \) is changed to 0.9. It is found that the emission region of the lensed ring and the photon ring becomes wider when increasing \(\alpha \). This is consistent with our results summarized in Table 2. In addition, by comparing the panels (g)–(i) of Figs. 11 and 12, we find that the black disks in the center of the intensity maps for \(\alpha =0.9\) are significantly larger than that for \(\alpha =0.3\), which means a larger \(\alpha \) leads to a bigger black hole shadow in thin disk accretions scenario.
We have emphasized in Sect. 3 that the shadow size has nothing to do with spherical accretion flow. However, a thin accretion disk can dramatically influence the size of the observed black hole shadow. We take Fig. 11g as a prominent example to interpret this issue. In order to simulate the angular resolution of the EHT, we applied a gaussian filter to Fig. 11g and obtained Fig. 13, see [62, 72] for more details about this operation. Apparently, the lensed ring and photon ring disappear after gaussian blurring, and the black hole shadow is measured to have a radius of 8.52, which is much larger than the theoretically predicted value (\(b_{p}=6.48\) for \(\alpha =0.3\)). This difference exists not only when \(\alpha \) is different, but also when the emission profile of disk is different. Therefore, it is convinced that the critical impact parameter \(b_{p}\) cannot be obtained through the black hole shadow directly. This makes it difficult to use the results of the EHT to test General Relativity [94].
Figure 11g after blurring with a gaussian filter (simulating the nominal resolution of the Event Horizon Telescope). The photon ring and lensed ring are washed out after gaussian blurring. Thus, the measured radius of the black hole shadow is 8.52, which is larger than the radius of the photon ring (\(b_{p}=6.48\)). Besides, the boundary of the shadow is contributed by the direct emissions
In fact, the observed shadow boundary of the black hole with the thin accretion flow is closely associated with the direct emissions. More specifically, the value of the starting point of direct emissions \(\delta \) can serve as the radius of the observed shadow, and this value can be obtained from the relationship between the observed specific intensity \(I_{\text {obs}}\) and the impact parameter b. Hence, we investigate the relationship between the parameter \(\alpha \) and the starting point of direct emissions for different emission profiles of the accretion disk, as shown in Fig. 14a. It is found that \(\delta \) increases linearly with respect to \(\alpha \) in the three models, which means that the parameter \(\alpha \) exerts a positive effect on the radius of the black hole shadow in the disk accretion scenario. We further studied the dependence of the starting point of direct emissions \(\delta \) on the critical impact parameter, as shown in panel (b) of Fig. 14. The results show that \(b_{p}\) and \(\delta \) are linearly related, meaning it is easy to obtain the critical impact parameter \(b_{p}\) for a given \(\delta \). It hints that there is the possibility of deriving the critical impact parameter from the EHT observational data and utilizing it to test General Relativity.
5 Conclusions
In this paper, we investigate the observed shadow and optical appearance of Schwarzschild-MOG black holes with spherical accretions and thin disk-shaped accretions. For \(0< \alpha \le 1\), the radii of the event horizon, photon sphere, and shadow of the aim black hole are increase with the increase of parameter \(\alpha \), and all larger than the corresponding values of the Schwarzschild case (\(\alpha =0\)). These results are due to the increase of the parameter \(\alpha \) strengthening the black hole’s gravitation effects. We also obtain the constraints of the parameter \(\alpha \) according to the observed shadow diameters estimated by the EHT, which are \(0.040<\alpha <0.232\) for M87\(^{*}\), and \(0<\alpha <0.044\) for Sagittarius A\(^{*}\). These results may helpful for the detection of Schwarzschild-MOG black holes in the future.
Then, in the scenarios of two toy models of spherical accretions, we study the observed specific intensities and their distribution in the observational sky. The results show that whether static spherical accretion or infalling spherical accretion is adopted, the luminosities of the shadows and photon rings of Schwarzschild-MOG black holes are decreased with the increase of \(\alpha \), and all lower than that of the Schwarzschild black hole. This finding can serve as an efficient feature to distinguish the former from the latter. We emphasize that the spherical accretion profiles hardly affect the shadow radius, while its influence on the observed intensity of shadow cannot be ignored based on the fact that the shadow observed in the infalling spherical accretion scenario is significantly darker than that of the static spherical accretion.
Finally, we assume that Schwarzschild-MOG black holes are surrounded by an optically and geometrically thin accretion disk with different emission profiles, hence the observational signatures of such black holes are investigated in detail. It is shown that there are not only narrow photon rings in the optical appearance of black holes but also lensed rings that appear outside the photon ring, and these two rings thicken as \(\alpha \) increases. On the other hand, the dominant part of the total observed specific intensity is contributed by the direct emissions, while the contributions of the photon rings and lensed rings are small. It is worth mentioning that in the disk accretion scenario, the boundary of the observed black hole shadow is neither a photon ring nor a lensed ring, but is determined by the direct emissions. The value of starting point of the direct emissions can serve as the radius of the observed shadow. Therefore, we further obtain a linear relationship involving the starting point of the direct emissions and the critical impact parameter. This correlation may help us to utilize the EHT observations to determine the critical impact parameter, and then to test General Relativity.
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: All the data are shown as the figures and formulae in this paper. No other associated movie or animation data.]
References
K. Schwarzschild, Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Math. Phys. Tech., pp. 189–196 (1916)
B.P. Abbott et al. [LIGO Scientific and Virgo Collaborations], Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016)
R. Abbott et al. [LIGO Scientific and Virgo Collaborations], GW190412: observation of a binary-black-hole coalescence with asymmetric masses. Phys. Rev. D 102, 043015 (2020)
R. Abbott et al. [LIGO Scientific and Virgo Collaborations], GW190521: a binary black hole merger with a total mass of 150 M\(_{\odot }\). Phys. Rev. Lett. 125, 101102 (2020)
J.-F. Liu et al., A wide star-black-hole binary system from radial-velocity measurements. Nature 575, 618–621 (2019)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First M87 Event Horizon Telescope results. I. The shadow of the supermassive black hole. Astrophys. J. Lett. 875, L1 (2019)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First M87 Event Horizon Telescope results. II. Array and instrumentation. Astrophys. J. Lett. 875, L2 (2019)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First M87 Event Horizon Telescope results. III. Data processing and calibration. Astrophys. J. Lett. 875, L3 (2019)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First M87 Event Horizon Telescope results. IV. Imaging the central supermassive black hole. Astrophys. J. Lett. 875, L4 (2019)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First M87 Event Horizon Telescope results. V. Physical origin of the asymmetric ring. Astrophys. J. Lett. 875, L5 (2019)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First M87 Event Horizon Telescope results. VI. The shadow and mass of the central black hole. Astrophys. J. Lett. 875, L6 (2019)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First Sagittarius A\(^*\) Event Horizon Telescope results. I. The shadow of the supermassive black hole in the center of the Milky Way. Astrophys. J. Lett. 930, L12 (2022)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First Sagittarius A\(^*\) Event Horizon Telescope results. II. EHT and multiwavelength observations, data processing, and calibration. Astrophys. J. Lett. 930, L13 (2022)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First Sagittarius A\(^*\) Event Horizon Telescope results. III. Imaging of the galactic center supermassive black hole. Astrophys. J. Lett. 930, L14 (2022)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First Sagittarius A\(^*\) Event Horizon Telescope results. IV. Variability, morphology, and black hole mass. Astrophys. J. Lett. 930, L15 (2022)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First Sagittarius A\(^*\) Event Horizon Telescope results. V. Testing astrophysical models of the galactic center black hole. Astrophys. J. Lett. 930, L16 (2022)
K. Akiyama et al. [Event Horizon Telescope Collaboration], First Sagittarius A\(^*\) Event Horizon Telescope results. VI. Testing the black hole metric. Astrophys. J. Lett. 930, L17 (2022)
A. Einstein, Lens-like action of a star by the deviation of light in the gravitational field. Science 84, 506–507 (1936)
K.S. Virbhadra, G.F.R. Ellis, Schwarzschild black hole lensing. Phys. Rev. D 62, 084003 (2000)
V. Perlick, Gravitational lensing from a spacetime perspective. Living Rev. Relativ. 7, 9 (2004)
P.V.P. Cunha, C.A.R. Herdeiro, Shadows and strong gravitational lensing: a brief review. Gen. Relativ. Gravit. 50, 42 (2018)
R. Kumar, S.G. Ghosh, Black hole parameter estimation from its shadow. Astrophys. J 892, 78 (2020)
S.G. Ghosh, R. Kumar, S. UI Islam, Parameters estimation and strong gravitational lensing of nonsingular Kerr–Sen black holes. J. Cosmol. Astropart. Phys. 03, 056 (2021)
M. Afrin, R. Kumar, S.G. Ghosh, Parameter estimation of hairy Kerr black holes from its shadow and constraints from M87\(^{*}\). Mon. Not. R. Astron. Soc. 504, 5927–5940 (2021)
S.G. Ghosh, M. Afrin, Constraining Kerr-like black holes from Event Horizon Telescope results of Sgr A\(^{*}\), e-Print. arXiv:2206.02488v1 [gr-qc] (2022)
Y. Mizuno, Z. Younsi, C.M. Fromm et al., The current ability to test theories of gravity with black hole shadows. Nat. Astron. 2, 585–590 (2018)
D. Psaltis, Testing general relativity with the Event Horizon Telescope. Gen. Relat. Gravit. 51, 137 (2019)
A. Stepanian, S. Khlghatyan, V.G. Gurzadyan, Black hole shadow to probe modified gravity. Eur. Phys. J. Plus 136, 127 (2021)
Z. Younsi, D. Psaltis, F. Özel, Black hole images as tests of general relativity: effects of spacetime geometry, e-Print. arXiv:2111.01752v1 [astro-ph.HE] (2021)
V. Perlick, O.Y. Tsupko, Calculating black hole shadows: review of analytical studies. Phys. Rep. 947, 1–39 (2022)
R.K. Walia, S.G. Ghosh, S.D. Maharaj, Testing rotating regular metrics with EHT results of Sgr A\(^{*}\), e-Print. arXiv:2207.00078v1 [gr-qc] (2022)
S. Vagnozzi, R. Roy, Y.-D. Tsai, L. Visinelli, M. Afrin, A. Allahyari, P. Bambhaniya, D. Dey, S.G. Ghosh, P.S. Joshi, K. Jusufi, M. Khodadi, R.K. Walia, A. Övgün, C. Bambi, Horizon-scale tests of gravity theories and fundamental physics from the Event Horizon Telescope image of Sagittarius A\(^{*}\), e-Print. arXiv: 2205.07787v2 [gr-qc] (2022)
J.M. Bardeen, Timelike and null geodesics in the Kerr metric, in Blcak holes. ed. by C. Dewitt (Gordon and Breach, New York, 1972), pp.229–236
R. Takahashi, Shapes and positions of black hole shadows in accretion disks and spin parameters of black holes. Astrophys. J. 611, 996–1004 (2004)
R. Takahashi, Black hole shadows of charged spinning black holes. Publ. Astron. Soc. Jpn. 57, 273–277 (2005)
K. Hioki, K. Maeda, Measurement of the Kerr spin parameter by observation of a compact object’s shadow. Phys. Rev. D 80, 024042 (2009)
Z.-L. Li, C. Bambi, Measuring the Kerr spin parameter of regular black holes from their shadow. J. Cosmol. Astropart. Phys. 01, 041 (2014)
P.V.P. Cunha, C.A.R. Herdeiro, E. Radu, H.F. Rúnarsson, Shadows of Kerr black holes with scalar hair. Phys. Rev. Lett. 115, 211102 (2015)
P.V.P. Cunha, C.A.R. Herdeiro, E. Radu, H.F. Rúnarsson, Shadows of Kerr black holes with and without scalar hair. Int. J. Mod. Phys. D 25, 1641021 (2016)
L.-Y. Yang, Z.-L. Li, Shadow of a dressed black hole and determination of spin and viewing angle. Int. J. Mod. Phys. D 25, 1650026 (2016)
O.Y. Tsupko, Analytical calculation of black hole spin using deformation of the shadow. Phys. Rev. D 95, 104058 (2017)
C. Bambi, K. Freese, S. Vagnozzi, L. Visinelli, Testing the rotational nature of the supermassive object M87\(^{*}\) from the circularity and size of its first image. Phys. Rev. D 100, 044057 (2019)
S.E. Gralla, A. Lupsasca, Lensing by Kerr black holes. Phys. Rev. D 101, 044031 (2020)
K. Jusufi, M. Jamil, T. Zhu, Shadows of Sgr A\(^{*}\) black hole surrounded by superfluid dark matter halo. Eur. Phys. J. C 80, 354 (2020)
K. Jusufi, M. Jamil, P. Salucci, T. Zhu, S. Haroon, Black hole surrounded by a dark matter halo in the M87 galactic center and its identification with shadow images. Phys. Rev. D 100, 044012 (2019)
K. Jusufi, Quasinormal modes of black holes surrounded by dark matter and their connection with the shadow radius. Phys. Rev. D 101, 084055 (2020)
F. Atamurotov, U. Papnoi, K. Jusufi, Shadow and deflection angle of charged rotating black hole surrounded by perfect fluid dark matter. Class. Quantum Gravity 39, 025014 (2022)
R. Kumar, G. Sushant Ghosh, Rotating black holes in 4D Einstein–Gauss–Bonnet gravity and its shadow. J. Cosmol. Astropart. Phys. 07, 053 (2020)
R. Kumar, B.P. Singh, Md. Sabir Ali, S.G. Ghosh, Shadow and deflection angle of rotating black hole in asymptotically safe gravity. Ann. Phys. N. Y. 420, 168252 (2020)
R. Kumar, B.P. Singh, Md. Sabir Ali, S.G. Ghosh, Shadows of black hole surrounded by anisotropic fluid in Rastall theory. Phys. Dark Universe 34, 100881 (2021)
R. Penrose, “Golden Oldie’’: gravitational collapse: the role of general relativity. Gen. Relataiv. Gravit. 34, 7 (2002)
R.D. Blandford, R.L. Znajek, Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 179, 433–456 (1977)
C. Bambi, Can the supermassive objects at the centers of galaxies be traversable wormholes ? The first test of strong gravity for mm/sub-mm very long baseline interferometry facilities. Phys. Rev. D 87, 107501 (2013)
X. Qin, S.-B. Chen, J.-L. Jing, Image of a regular phantom compact object and its luminosity under spherical accretions. Class. Quantum Gravity 38, 115008 (2021)
R. Narayan, M.D. Johnson, C.F. Gammie, The shadow of a spherically accreting black hole. Astrophys. J. Lett. 885, L33 (2019)
X.-X. Zeng, H.-Q. Zhang, H.-B. Zhang, Shadows and photon spheres with spherical accretions in the four-dimensional Gauss–Bonnet black hole. Eur. Phys. J. C 80, 872 (2020)
Q.-Y. Gan, P. Wang, H.-W. Wu, H.-T. Yang, Photon spheres and spherical accretion image of a hairy black hole. Phys. Rev. D 104, 024003 (2021)
S. Guo, K.-J. He, G.-R. Li, G.-P. Li, The shadow and photon sphere of the charged black hole in Rastall gravity. Class. Quantum Gravity 38, 165013 (2021)
K. Jusufi, Saurabh, Black hole shadows in Verlinde’s emergent gravity. Mon. Not. R. Astron. Soc. 503, 1310–1318 (2021)
K. Saurabh, K. Jusufi, Imprints of dark matter on black hole shadows using spherical accretions. Eur. Phys. J. C 81, 490 (2021)
A.-Y. He, J. Tao, Y.-D Xue, L.-K. Zhang, Shadow and photon sphere of black hole in clouds of strings and quintessence, e-Print. arXiv:2109.13807v3 [gr-qc] (2022)
S.E. Gralla, D.E. Holz, R.M. Wald, Black hole shadows, photon rings, and lensing rings. Phys. Rev. D 100, 024018 (2019)
X.-X. Zeng, H.-Q. Zhang, Influence of quintessence dark energy on the shadow of black hole. Eur. Phys. J. C 80, 1058 (2020)
J. Peng, M.-Y. Guo, X.-H. Feng, Influence of quantum correction on black hole shadows, photon rings, and lensing rings. Chin. Phys. C 45, 085103 (2021)
L. Chakhchi, H. El Moumni, K. Masmar, Shadows and optical appearance of a power-Yang–Mills black hole surrounded by different accretion disk profiles. Phys. Rev. D 105, 064031 (2022)
S. Guo, G.-R. Li, E.-W. Liang, Influence of accretion flow and magnetic charge on the observed shadows and rings of the Hayward black hole. Phys. Rev. D 105, 023024 (2022)
K.-J. He, S.-C. Tan, G.-P. Li, Influence of torsion charge on shadow and observation signature of black hole surrounded by various profiles of accretions. Eur. Phys. J. C 82, 81 (2022)
G.-P. Li, K.-J. He, Shadows and rings of the Kehagias–Sfetsos black hole surrounded by thin disk accretion. J. Cosmol. Astropart. Phys. 06, 037 (2021)
X.-X. Zeng, G.-P. Li, K.-J. He, The shadows and observational appearance of a noncommutative black hole surrounded by various profiles of accretions. Nucl. Phys. B 974, 115639 (2022)
X.-X. Zeng, K.-J. He, G.-P. Li, Influence of dark matter on shadows and rings of a brane-world black hole illuminated by various accretions, e-Print. arXiv:2111.05090v1 [gr-qc] (2021)
K.-J. He, S. Guo, S.-C. Tan, G.-P. Li, The feature of shadow images and observed luminosity of the Bardeen black hole surrounded by different accretions, e-Print. arXiv:2103.13664v2 [hep-th] (2022)
S. Guo, G.-R. Li, E.-W. Liang, Observable characteristics of the charged black hole surrounded by thin disk accretion in Rastall gravity. Class. Quantum Gravity 39, 135004 (2022)
M. Guerrero, G.J. Olmo, D. Rubiera-Garcia, D.S.-C. Gómez, Shadows and optical appearance of black bounces illuminated by a thin accretion disk. J. Cosmol. Astropart. Phys. 08, 036 (2021)
M. Guerrero, G.J. Olmo, D. Rubiera-Garcia, D.S.-C. Gómez, Light ring images of double photon spheres in black hole and wormhole space-times, e-Print. arXiv:2202.03809v1 [gr-qc] (2022)
J.L. Rosa, D. Rubiera-Garcia, Shadows of boson and Proca stars with thin accretion disks, e-Print. arXiv:2204.12949v1 [gr-qc] (2022)
J.W. Moffat, Scalar-tensor-vector gravity theory. J. Cosmol. Astropart. Phys. 03, 004 (2006)
J.W. Moffat, Black holes in modified gravity (MOG). Eur. Phys. J. C 75, 175 (2015)
J.W. Moffat, Modified gravity (MOG), cosmology and black holes. J. Cosmol. Astropart. Phys. 02, 017 (2021)
J.R. Brownstein, J.W. Moffat, The Bullet Cluster 1E0657-558 evidence shows modified gravity in the absence of dark matter. Mon. Not. R. Astron. Soc. 382, 29–47 (2007)
J.W. Moffat, S. Rahvar, The MOG weak field approximation and observational test of galaxy rotation curves. Mon. Not. R. Astron. Soc. 436, 1439–1451 (2013)
J.W. Moffat, S. Rahvar, The MOG weak field approximation—II. Observational test of Chandra X-ray clusters. Mon. Not. R. Astron. Soc. 441, 3724–3732 (2014)
J.W. Moffat, V.T. Toth, Rotational velocity curves in the Milky Way as a test of modified gravity. Phys. Rev. D 91, 043004 (2015)
J.W. Moffat, V.T. Toth, Applying modified gravity to the lensing and Einstein ring in Abell 3827. Phys. Rev. D 103, 044045 (2021)
J.W. Moffat, LIGO GW150914 and GW151226 gravitational wave detection and generalized gravitation theory (MOG). Phys. Lett. B 763, 427–433 (2016)
S. Rahvar, Hamiltonian formalism for dynamics of particles in MOG, e-Print. arXiv:2206.02453v1 [gr-qc] (2022)
M. Sharif, M. Shahzadi, Neutral particle motion around a Schwarzschild black hole in modified gravity. J. Exp. Theor. Phys. 127, 491–502 (2018)
D.-Q. Yang, W.-F. Cao, N.-Y. Zhou, H.-X. Zhang, W.-F. Liu, X. Wu, Chaos in a magnetized modified gravity Schwarzschild spacetime. Universe 8, 320 (2022)
J.W. Moffat, V.T. Toth, The bending of light and lensing in modified gravity. Mon. Not. R. Astron. Soc. 397, 1885–1892 (2009)
R.N. Izmailov, R.K. Karimov, E.R. Zhdanov, K.K. Nandi, Modified gravity black hole lensing observables in weak and strong field of gravity. Mon. Not. R. Astron. Soc. 483, 3754–3761 (2019)
F. Atamurotov, A. Abdujabbarov, J. Rayimbaev, Weak gravitational lensing Schwarzschild-MOG black hole in plasma. Eur. Phys. J. C 81, 118 (2021)
J.W. Moffat, Modified gravity black holes and their observable shadows. Eur. Phys. J. C 75, 130 (2015)
K. Haydarov, M. Boboqambarova, B. Turimov, A. Abdujabbarov, A. Akhmedov, Circular motion of particle around Schwarzschild-MOG black hole, e-Print. arXiv:2110.05764v1 [gr-qc] (2021)
B.C. Bromley, K. Chen, W.A. Miller, Line emission from an accretion disk around a rotating black hole: toward a measurement of frame dragging. Astrophys. J. 475, 57 (1997)
S.E. Gralla, Can the EHT M87 results be used to test general relativity? Phys. Rev. D 103, 024023 (2021)
Acknowledgements
The authors are very grateful to the referee for valuable comments and suggestions. This research has been supported by the National Natural Science Foundation of China [Grant Nos. 11973020, 11533004, and 12133003], the Special Funding for Guangxi Distinguished Professors (2017AD22006), and the National Natural Science Foundation of Guangxi (Nos. 2018GXNSFGA281007 and 2019JJD110006).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Hu, S., Deng, C., Li, D. et al. Observational signatures of Schwarzschild-MOG black holes in scalar-tensor-vector gravity: shadows and rings with different accretions. Eur. Phys. J. C 82, 885 (2022). https://doi.org/10.1140/epjc/s10052-022-10868-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10868-y