Observational signatures of Schwarzschild-MOG black holes in scalar–tensor–vector gravity: images of the accretion disk

Abstract

The present paper contains the investigations with respect to the optical appearance, redshift distribution, and observed energy flux of the thin accretion disk described by the Novikov-Thorne model in modified gravity (MOG) proposed by Moffat. The results show that the gravity coupling parameter $\alpha$ plays an indispensable role in the size of direct and secondary images of the accretion disk, while the image profile is mainly affected by the observational angles. In addition, an increase of the parameter $\alpha$ leads to that of the redshift factor, but a decrease in the radiation energy flux of the accretion disk. These results are due to the enhancement of the parameter $\alpha$ that strengthens the black hole’s gravitational effects. By comparing the accretion disk images of the Schwarzschild-MOG black hole, the Schwarzschild black hole, and the Reissner–Nordström black hole, we point out that the Schwarzschild-MOG black hole exhibits the largest inner shadow and the lowest luminosity. This finding provides a potential way to distinguish Schwarzschild-MOG black holes from their counterparts in General Relativity.

1 Introduction

Black holes (BHs) are predicted in General Relativity and are extremely mysterious compact objects in the Universe. However, the direct observation of BHs is a brutal challenge since they can absorb matter and even light rays in their vicinity. For decades, great efforts have been made both in theoretical analysis and astronomical observations for the purpose of exploring the existence of BHs and unveiling their haunting appearances. To date, the observed properties of High-Energy X-rays fluorescence radiated from Cygnus X-1 binary [1], the signals of the gravitational-wave emitted from binary BH mergers detected by the Laser-Interferometer Gravitational Wave Observatory (LIGO) [2, 3], and the discovery of a wide star-BH binary system with radial-velocity measurements [4] have strongly confirmed the existence of BHs. More exciting achievements are the successful capture of images of the supermassive BHs at the center of the M87 galaxy and Milky Way by the Event Horizon Telescope Collaboration (EHT) with very long baseline interferometry (VLBI) [5,6,7,8,9,10,11,12,13,14,15,16]. This milestone not only visually shows the appearance of BHs but also triggers a range of theoretical research on their shadows [17,18,19] and the use of images to test General Relativity [20,21,22,23,24].

In fact, the electromagnetic radiation that contributes to the BH’s images is mainly emitted from the accretion disk. This indicates that it is meaningful to study the accretion disk since the physical properties, such as mass, spin parameter, and spacetime configuration of the BH, can be inferred by its radiation. Several authors investigated the energy flux, emission spectrum, and the conversion efficiency of the accretion disk surrounding different BHs under the assumption that the radiation emitted from the disk surface can be regarded as a perfect black body radiation [25,26,27]. The thin accretion disk has significant influences on the observed shadows of BHs, which have been well discussed in numerous papers [17, 18, 28,29,30,31,32,33,34,35,36]. However, the most fascinating and intuitive research is the exploration of accretion disk images. Generally speaking, to obtain an ultra-realistic BH picture, one needs to explore the plasma motion in the accretion disk as well as the radiation by means of general relativistic magnetohydrodynamic simulation and then calculate the luminosities corresponding to each pixel in the observational plane by integrating the radiative transfer equation and geodesic equations [37,38,39,40]. These procedures are highly sophisticated and time-consuming. However, the calculation can be simplified when postulating that the radiation from the accretion disk is only related to the source radius. The BH images obtained following this approach can likewise provide qualitative and reliable observational features.

In 1979, Luminet solved photon trajectories by the first kind of elliptic integral and numerically obtained the first black-and-white photographic image of the accretion disk around a Schwarzschild BH in human history [41]. It is worth mentioning that, due to the lack of appropriate computer technology, this pioneering image was created by drawing a few thousand dots representing light rays on sketch paper with his hands, where the density of the dots corresponds to the intensity of the light. This work was the beginning of the investigation of accretion disk images, and similar studies became popular thereafter. Fukue and Yokoyama investigated the color photographs of an accretion disk surrounding a stellar-mass Schwarzschild BH, including the bolometric image, X-ray image in the 2–30 keV band, and the optical image in the 0.38–0.77 $\upmu$m obtained through a monochromatic filter [42]. They also carefully analyzed the reason for the asymmetry of the images in both horizontal and vertical directions. Marck developed a short-cut method to calculate the geodesic equations for Schwarzschild spacetime and consequently obtained a series of images of the BH with an accretion disk as seen by an observer at different locations [43]. The authors of [44] proposed a parametrized Schwarzschild BH and studied the accretion disk’s images with different viewing angles. Note that they took the projection effect into consideration since the light rays do not always escape vertically from the disk’s surface. Gyulchev et al. compared the images of accretion disks in Einstein–Gauss–Bonnet gravity with their counterpart in Schwarzschild spacetime and pointed out that the differences are pretty small [45]. Also, they unveiled an observational window for different-order images of the accretion disk based on the relationship between the impact parameters and photon deflections. Recently, the authors of [46] focused on the thin accretion disk around the Schwarzschild BH pierced by a cosmic string and studied its optical appearance. The influences of the cosmic string parameter on the accretion disk’s images are discussed in detail. In addition, one can see [47,48,49,50] for the investigations of the images of accretion disks around rotating BHs, and [51,52,53] for a comprehensive review with respect to the road towards imaging BHs.

In order to modify gravitational acceleration law that can fit galaxy rotation curves and cluster data without dark matter, Moffat proposed scalar–tensor–vector gravity (STVG) based on the combination of the Einstein–Hilbert action, massive vector field, and matter action in 2006 [54]. So far, STVG has successfully explained the solar system observation, the dynamics of galactic clusters, the rotation curves of galaxies [55,56,57,58,59], the galaxy clusters matter power spectrum [60], and the Einstein ring in Abell 3827 [62]. More recently, Davari and Rahvar investigated the STVG theory for the dynamics of the Universe with the currently available cosmological data and compared the results with that in the Lambda cold dark matter cosmology [63]. They claimed that the STVG model fits the observational data well, as does the Lambda cold dark matter model. In [61], Harikumar and Biesiada tested the STVG theory on the X-COP galaxy cluster background and found an interesting result that the STVG theory has the ability to explain the mass of galaxy clusters without assuming non-baryonic matter. Overall, the STVG theory has passed many tests in astrophysics and seems to be a promising alternative to General Relativity. Therefore, it is possible that the astrophysical BH can be described in terms of the BH metric derived from the STVG theory. Consequently, it is necessary to study the features of such objects, which might not only provide hints for distinguishing them from other compact objects but also help to improve our understanding of STVG theory. Lee and Han investigated the circular orbits of photons and massive particles around the Kerr-MOG BH [64], and showed the difference in particle trajectories between Kerr and Kerr-MOG spacetime. By employing the effective potential and Lyapunov exponent, Sharif and Shahzadi studied the stability of particle orbits in the vicinity of the Kerr-MOG BH immersed in a magnetic field [65]. The polarized images of Kerr-MOG BH were studied in [66], whereas the BH shadow and the constraint of the MOG parameter were well investigated by the authors of [67]. In [68], Haydarov et al. explored the motion of particles around the magnetized Schwarzschild-MOG BH. Interestingly, they found that the MOG parameter can mimic not only the magnetic coupling parameter but also the spin of Kerr BH. The authors of [69] numerically obtained the chaotic orbits of charged particles around the Schwarzschild-MOG BH in a uniform magnetic field. They also claimed that the MOG parameter exerts a positive effect on the chaotic strength of particle motion.

In our previous work [36], the shadows and rings cast by Schwarzschild-MOG BHs with spherical accretions and thin disk accretions are explored. The impacts of the gravity coupling parameter on the optical appearances of the BH as seen by a distant observer at a face-on orientation are also well studied. However, some physical quantities that play a critical role in the observation of Schwarzschild-MOG BHs, such as the isoradial curves and bolometric radiation of the accretion disk, are still unclear. Inspired by this, here we investigate the apparent images of the accretion disk around Schwarzschild-MOG BHs, and consequently reveal some qualitative observational signatures for this object. The remainder of this paper is organized as follows. In Sect. 2, we briefly review the Schwarzschild-MOG BH metric and discuss the geodesic equations for the time-like and light-like particles. In Sect. 3, we investigate the optical appearance of the BH surrounded by a geometrically thin accretion disk in the Novikov-Thorne model and probe the influences of parameter $\alpha$ on the geometric structure, redshift factor distributions, and radiation flux of the accretion disk as seen by a remote observer at different inclination angles. The results and discussions are concluded in Sect. 4.

2 Geodesics in Schwarzschild-MOG spacetime

The observational characteristics of the accretion disk can be inferred by the observable light rays emitted from massive particles that move in a range of stable circular orbits in the equatorial plane of the Schwarzschild-MOG BH. Therefore, the motions of massive particles and photons play a pivotal role in this context. In this section, we first review the line elements in the Schwarzschild-MOG spacetime. Then, the geodesic equations of time-like and null-like particles are introduced with the aid of Lagrangian formulism.

Fig. 1

The variation of radii of event horizon $r_{\text {e}}$ and Cauchy horizon $r_{\text {c}}$ with respect to the parameter $\alpha$. The green region satisfies $\alpha >0$, where both $r_{\text {e}}$ and $r_{\text {c}}$ are greater than 0

Fig. 2

The coordinate system for the description of photon trajectory (red line) that emits from the disk element $\text {P}_{\text {S}}$ and vertically intersects the observational plane (The area enclosed by the green dashed line) at point $\text {P}_{\text {O}}$. Here, the disk element is moving around Schwarzschild-MOG BH in a stable circular orbit (blue line) of radius $r_{\text {s}}$, point $\text {P}_{\text {O}}$ is marked by polar coordinates $(b,\eta )$. The photon deflection angle and viewing angle are represented by $\varphi$ and $\omega$, where $\omega$ satisfied the condition $0\le \omega <90^{\circ }$

Fig. 3

The variation relationship between the photon deflection angle $\varphi$ and polar coordinate $\eta$ when observational angle $\omega$ takes different values. Clearly, the deflection angle satisfied the condition of $\pi /2-\omega \le \varphi \le \pi /2+\omega$

2.1 Schwarzschild-MOG BH metric

In Schwarzschild coordinates $x^{\mu }=(t, r, \theta , \varphi )$, the static spherically symmetric Schwarzschild-MOG BH is read as [70,71,72]

$$\begin{aligned} \text {d}s^{2} = -f(r) \text {d}t^{2} + \frac{1}{f(r)} \text {d}r^{2} + r^{2} \text {d} \varOmega ^{2}, \end{aligned}$$

(1)

where $\text {d}\varOmega ^{2}$ and f(r) represent the surface-element of the two-spheres and metric potential,

$$\begin{aligned} \text {d}\varOmega ^{2}= & {} \text {d}\theta ^{2}+\text {sin}^{2}\theta \text {d}\varphi ^{2}, \end{aligned}$$

(2)

$$\begin{aligned} f(r)= & {} 1-\frac{2GM}{rc^{2}}+\frac{\alpha G_{N}GM^{2}}{r^{2}c^{4}}. \end{aligned}$$

(3)

Here, M stands for the BH mass and c represents the speed of light. Note that G denotes the enhanced gravitational constant, which is related to Newton’s constant $G_{N}$ by $G=G_{N}(1+\alpha )$, where $\alpha$ is a dimensionless gravity coupling parameter. This means that the strength of gravitational field and spacetime structure of the Schwarzschild-MOG BH are determined by the parameter $\alpha$. When $\alpha =0$, metric (1) reduces to the Schwarzschild solution. Note that the Schwarzschild-MOG metric can be rewritten in the same form as the Reissner–Nordström (RN) metric when an appropriate mathematical replacement is made to the parameter $\alpha$. For the sake of conciseness and coherence of the article, we would like to show this operation and discuss the difference between the Schwarzschild-MOG metric and the RN metric in Appendix.

Throughout this paper, the dimensionless operations and geometric units are taken to simplify our simulation, i.e., $r \rightarrow rM$, $G_{N}=c=1$. Hence, we reduce Eq. (3) as

$$\begin{aligned} f(r) = 1 - \frac{2(1+\alpha )}{r}+\frac{\alpha (1+\alpha )}{r^{2}}. \end{aligned}$$

(4)

It is easy to obtain two real roots satisfied the condition of $f(r)=0$ when $\alpha > -1$, in which

$$\begin{aligned} r_{\text {e}}= & {} 1+\alpha +\sqrt{1+\alpha }, \end{aligned}$$

(5)

$$\begin{aligned} r_{\text {c}}= & {} 1+\alpha -\sqrt{1+\alpha }. \end{aligned}$$

(6)

The relationship involving $r_{\text {e}}$, $r_{\text {c}}$, and $\alpha$ is displayed in Fig. 1. Clearly, both $r_{\text {e}}$ and $r_{\text {c}}$ are positive in the condition of $\alpha >0$ (green shade region), and they correspond to the radii of event horizon and Cauchy horizon of the Schwarzschild-MOG BH, respectively. Figure 1 also shows that the radius of the event horizon $r_{\text {e}}$ for positive $\alpha$ in the Schwarzschild-MOG background is always larger than the counterpart in the Schwarzschild case, which is sufficient to show that the Schwarzschild-MOG’s $r_{\text {e}}$ is likewise larger than that of the RN BH.

Fig. 4

Direct (black line) and secondary (red line) images of the thin accretion disk surrounding the Schwarzschild-MOG BH under different values of parameter $\alpha$ and inclination angles. From the center of each panel outward, the profiles correspond to the stable circular orbit with radii $r=r_{\text {ms}}$, 15, 20, 25, and 30 in sequence

Fig. 5

Continuous distributions of redshift z in the direct images cast by the accretion disk in Schwarzschild-MOG spacetime under different values of parameter $\alpha$ and inclination angles. The red corresponds to the maximum value of the redshift, while the minimum value is represented by blue. The black dashed line denotes the contour curve of $z=0$. Here, the inner and outer boundaries of the accretion disk are the stable circular orbits with radii $r=r_{\text {ms}}$ and $r=40$, respectively

2.2 Time-like geodesics of the equatorial plane

The motions of particles in Schwarzschild-MOG spacetime can be described by a Lagrangian formulism,

$$\begin{aligned} \mathscr {L}= & {} \frac{1}{2} g_{\mu \nu } \dot{x}^{\mu } \dot{x}^{\nu } \nonumber \\= & {} \frac{1}{2} \left[ -f(r) \dot{t}^{2} +\frac{1}{f(r)} \dot{r}^{2}+r^{2} \left( \dot{\theta }^{2}+\sin ^{2}{\theta }\dot{\varphi }^{2} \right) \right] , \end{aligned}$$

(7)

where $\dot{x}^{\mu }=(\dot{t},\dot{r},\dot{\theta },\dot{\varphi })$ are the four-velocity of particles. Note that $\mathscr {L}=-1/2$ for the massive particles while $\mathscr {L}=0$ corresponds to the massless particles, i.e., photons. We assume that the geometrically thin accretion flow moves along the Keplerian stable circular orbits in the equatorial plane of the Schwarzschild-MOG BH, which means that the coordinate $\theta$ and velocity $\dot{\theta }$ of the matter in the accretion disk are fixed to $\pi /2$ and 0, respectively. Therefore, we have the time-like geodesic equations with the help of the Euler–Lagrange equations,

$$\begin{aligned} \dot{t}= & {} \frac{\text {d}t}{\text {d}\lambda } = \frac{E}{f(r)}, \end{aligned}$$

(8)

$$\begin{aligned} \dot{r}= & {} \frac{\text {d}r}{\text {d}\lambda } = \sqrt{E^{2}-f(r)\left( 1+\frac{L^{2}}{r^{2}}\right) }, \end{aligned}$$

(9)

$$\begin{aligned} \dot{\varphi }= & {} \frac{\text {d}\varphi }{\text {d}\lambda } = \frac{L}{r^{2}}. \end{aligned}$$

(10)

Here $\lambda$ is an affine parameter, which is given the scale transformation $\lambda \rightarrow \lambda M$. E and L are the specific energy and specific angular momentum, which are the invariant quantities along with the particle’s motion.

According to Eq. (9), the effective potential $V_{\text {eff}}^{\text {T}}$ of massive particles moving in the equatorial plane can be expressed as

$$\begin{aligned} V_{\text {eff}}^{\text {T}} = \sqrt{f(r)\left( 1+\frac{L^{2}}{r^{2}}\right) }. \end{aligned}$$

(11)

Despite the simplicity of the above expression, the effective potential is crucial for particle radial motions. That is, the local minimal and maximal values of the effective potential correspond to stable and unstable circular orbits, respectively. More importantly, by taking into account the condition of $\partial V_{\text {eff}}^{\text {T}}/\partial r =$ $\partial ^{2} V_{\text {eff}}^{\text {T}}/\partial r^{2} =0$, it is possible to derive the innermost stable circular orbit (ISCO), which is not only the inner boundary but also the starting position of electromagnetic radiation of the accretion disk in the Novikov-Thorne model [73,74,75]. In the Schwarzschild-MOG spacetime, the radius of ISCO, $r_{\text {ms}}$, is obtained from [33]

$$\begin{aligned} r_{\text {ms}} = \frac{3f(r_{\text {ms}})f^{\prime }(r_{\text {ms}})}{2f^{\prime }(r_{\text {ms}})^{2}-f(r_{\text {ms}})f^{\prime \prime }(r_{\text {ms}})}, \end{aligned}$$

(12)

where $f^{\prime }$ and $f^{\prime \prime }$ denote the first and second order partial derivatives of Eq. (4) with respect to radius r, respectively.

Next, taking the conditions of $V_{\text {eff}}^{\text {T}}=E$ and $\partial V_{\text {eff}}^{\text {T}}/\partial r =0$ into consideration, we are able to explore the specific energy E, the specific angular momentum L, and the angular velocity $\varOmega$ for the stable circular orbits with radius $r_{\text {s}} \ge r_{\text {ms}}$ in the equatorial plane of the Schwarzschild-MOG BH. The general expressions of those quantities are given in [25,26,27] as

$$\begin{aligned} E= & {} \frac{f(r_{\text {s}})}{\sqrt{f(r_{\text {s}})-\frac{1}{2}r_{\text {s}}f^{\prime }(r_{\text {s}})}}, \end{aligned}$$

(13)

$$\begin{aligned} L= & {} \frac{r_{\text {s}}\sqrt{r_{\text {s}}f^{\prime }(r_{\text {s}})}}{\sqrt{2f(r_{\text {s}})-r_{\text {s}}f^{\prime }(r_{\text {s}})}}, \end{aligned}$$

(14)

$$\begin{aligned} \varOmega= & {} \frac{f^{\prime }(r_{\text {s}})}{\sqrt{2r_{\text {s}}f^{\prime }(r_{\text {s}})}}. \end{aligned}$$

(15)

One can see [76] for more specific expressions with respect to E, L, and $\varOmega$ in Schwarzschild-MOG spacetime.

2.3 Null geodesics

The light rays radiated from the accretion disk can be deflected by the BH, and their dynamics can be well described by Eq. (7) with $\mathscr {L}=0$. Since photons travel in static spherically symmetric spacetime, it is convenient to confine the photon motion to an arbitrary equatorial plane without losing generality. Hence, the null geodesic equations for photon propagation can be expressed as

$$\begin{aligned} \dot{t}= & {} \frac{\text {d}t}{\text {d}\lambda } = \frac{\mathscr {E}}{f(r)}, \end{aligned}$$

(16)

$$\begin{aligned} \dot{r}= & {} \frac{\text {d}r}{\text {d}\lambda } = \sqrt{\mathscr {E}^{2}-\frac{\mathscr {J}^{2}}{r^{2}}f(r)}, \end{aligned}$$

(17)

$$\begin{aligned} \dot{\varphi }= & {} \frac{\text {d}\varphi }{\text {d}\lambda } = \frac{\mathscr {J}}{r^{2}}, \end{aligned}$$

(18)

where $\mathscr {E}$ and $\mathscr {J}$ are the specific energy and the specific angular momentum of the photon. We define an impact parameter $b=\mathscr {J}/\mathscr {E}$ and derive the effective potential $V_{\text {eff}}^{\text {N}}$ of photon from Eq. (17) by setting $\dot{r}=0$,

$$\begin{aligned} V_{\text {eff}}^{\text {N}} = \frac{1}{b} = \frac{\sqrt{f(r)}}{r}. \end{aligned}$$

(19)

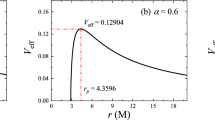
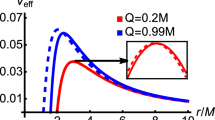
Unlike the effective potential of the time-like particle, the effective potential of the photon generally has only one local maximal value, which corresponds to the photon sphere. The radius $r_{\text {p}}$ and critical impact parameter $b_{\text {p}}$ of the photon sphere can be obtained by

$$\begin{aligned}{} & {} \frac{1}{b_{\text {p}}}=\frac{\sqrt{f(r_{\text {p}})}}{r_{\text {p}}}, \end{aligned}$$

(20)

$$\begin{aligned}{} & {} \frac{\partial V_{\text {eff}}^{\text {N}}(r_{p})}{\partial r_{\text {p}}} = 0. \end{aligned}$$

(21)

It is worth noticing that $b_{\text {p}}$ is the radius of the photon ring observed by a distant observer.

Next, we use the semi-analytical method to obtain the trajectories of the photon in the equatorial plane. By combining Eqs. (17) and (18), the relationship involving photon coordinate r and azimuthal angle $\varphi$ can be expressed as

$$\begin{aligned} \frac{\text {d}r}{\text {d}\varphi } = \frac{\mathscr {J}}{|\mathscr {J}|}r^{2}\sqrt{\frac{1}{b^{2}}-\frac{f(r)}{r^{2}}}, \end{aligned}$$

(22)

in which the sign of $\mathscr {J}/|\mathscr {J}|$ determines the direction of photon motion. By introducing a new parameter $u \equiv 1/r$, Eq. (22) can be arranged as

$$\begin{aligned} \frac{\text {d}u}{\text {d}\varphi } = \frac{\mathscr {J}}{|\mathscr {J}|}\sqrt{\frac{1}{b^{2}}-u^{2}f(u)}, \end{aligned}$$

(23)

more specific,

$$\begin{aligned} \varphi = \frac{\mathscr {J}}{|\mathscr {J}|}\int _{u_{\text {o}}}^{u_{\text {s}}}\frac{\text {d}u}{\sqrt{\frac{1}{b^{2}}-u^{2}f(u)}}, \end{aligned}$$

(24)

where $\varphi$ is the deflection angle of the light ray that traveled from the source, $u_{\text {s}}$, to the distant observer, $u_{\text {o}}$. Note that some light rays with $b>b_{\text {p}}$ possess a radial turn point $u_{\text {t}}$, then the photon deflections can be solved by

$$\begin{aligned} \varphi= & {} \frac{\mathscr {J}}{|\mathscr {J}|}\int _{u_{\text {o}}}^{u_{\text {t}}}\frac{\text {d}u}{\sqrt{\frac{1}{b^{2}}-u^{2}f(u)}} \nonumber \\{} & {} +\frac{\mathscr {J}}{|\mathscr {J}|}\int _{u_{\text {t}}}^{u_{\text {s}}}\frac{\text {d}u}{\sqrt{\frac{1}{b^{2}}-u^{2}f(u)}}, \end{aligned}$$

(25)

in which the turn point $u_{\text {t}}$ can be derived from

$$\begin{aligned} \frac{1}{b^{2}} = u_{\text {t}}^{2}f(u_{\text {t}}). \end{aligned}$$

(26)

Consequently, we are able to obtain all trajectories of observable light rays emanated from the accretion disk with the help of Eqs. (24)–(26), and appropriate numerical integration algorithms, such as the compound Simpson integral formula and the Runge-Kutta method.

3 Observational features of the accretion disk in Schwarzschild-MOG spacetime

In this section, we first introduce the coordinate system of the thin accretion disk and deduce the projections of a range of stable circular orbits on the observational plane. Then, by considering the Novikov-Thorne model, the redshift factor and the energy flux of the accretion disk surrounding the Schwarzschild-MOG BH, as well as the influences of the parameter $\alpha$ on these physical properties are explored. Finally, we compare the images of the Schwarzschild-MOG BH, the Schwarzschild BH, and the RN BH.

3.1 Projections of the accretion disk in the observational sky

The coordinate system used for the investigation of the trajectories of light rays that connect the disk element with the screen of the distant observer was presented earlier in [41] and recently discussed in detail by the authors of [44]. Here we briefly review this issue. As demonstrated in Fig. 2, the singularity of Schwarzschild-MOG BH, labeled by $o^{\prime }$ point, is the origin of cartesian coordinates ($x^{\prime }, y^{\prime }, z^{\prime }$), and the accretion disk is placed on the $\overline{x^{\prime }o^{\prime }y^{\prime }}$ plane. The disk element $\text {P}_{\text {S}}$ emits light rays (red line) through synchrotron or bremsstrahlung as it revolves around the BH in the stable circular orbit with a radius of $r_{\text {s}}\ge r_{\text {ms}}$. These lights traveling a long path and deflecting by a angle $\varphi$, may hit vertically the point $\text {P}_{\text {O}}$ on the distant observational plane $\overline{xoy}$, where $\text {P}_{\text {O}}$ is marked by $(b, \eta )$. Note that the line $\overline{o^{\prime }o}$ is perpendicular to the observational plane. Hence, b can be considered as the impact parameter of the photon, and $\omega$ can be defined as the inclination angle of the observer.

Fig. 6

Similar to Fig. 5, but for the secondary images

Based on the spherical triangle theory, the relationship involving the photon deflection angle $\varphi$, the polar coordinate $\eta$ on the observational screen, and the inclination angle $\omega$ is given in [45, 77,78,79] as

$$\begin{aligned} \cos {\varphi } = -\frac{\sin {\eta }\tan {\omega }}{\sqrt{\sin ^{2}{\eta }\tan ^{2}{\omega }+1}}. \end{aligned}$$

(27)

Here, $\eta$ is in the range of $[0,2\pi ]$. One can verify that the deflection angle $\varphi$ deduced by the above equation is satisfied the condition of $\pi /2-\omega \le \varphi \le \pi /2+\omega$ by examining the variation of $\varphi$ range with different values of the inclination angle in Fig. 3. However, this range of $\varphi$ is only suitable for the light rays that form the direct images of the accretion disk on the photographic plate. In fact, some light rays emitted from the disk element are deflected at larger angles or even revolve around the BH many times before reaching the distant observer, consequently forming a secondary or a higher-order image. Hence, it is necessary to modify Eq. (27) as

$$\begin{aligned} \varphi = k\pi -\arccos {\frac{\sin {\eta }\tan {\omega }}{\sqrt{\sin ^{2}{\eta }\tan ^{2}{\omega }+1}}}, \end{aligned}$$

(28)

where k is a positive integer and can be treated as the image order, i.e., $k=1$ corresponds to the direct (first-order) images while the secondary (second-order) images satisfied the $k=2$. Note that the k-order images with $k\ge 2$ are very close to the photon ring [45, 78, 79].

In order to obtain the projection of the accretion disk, we also need to determine the impact parameter b for the photon trajectory whose deflection angle is given by Eq. (28), and this problem can be solve by Eqs. (24) and (25). Therefore, we have the relation between the impact parameter b and the polar coordinate $\eta$ as¹

$$\begin{aligned}{} & {} \frac{\mathscr {J}}{|\mathscr {J}|}\int _{u_{\text {o}}}^{u_{\text {s}}}\frac{\text {d}u}{\sqrt{\frac{1}{b^{2}}-u^{2}f(u)}} \nonumber \\{} & {} \quad = k\pi -\arccos {\frac{\sin {\eta }\tan {\omega }}{\sqrt{\sin ^{2}{\eta }\tan ^{2}{\omega }+1}}}, \end{aligned}$$

(29)

where $u_{\text {s}}\equiv 1/r_{\text {s}}$ and $u_{\text {o}}=0$ denote the positions of the light source and distant observer, respectively. By scanning the polar coordinate $\eta$ in the range of $[0,2\pi ]$, the corresponding impact parameter b can be solved numerically based on the above equation, then the projections of disk elements at various stable circular orbits with radii of $r_{\text {s}}\ge r_{\text {ms}}$ are obtained.

Figure 4 presents the direct and secondary images of several representative stable circular orbits of Schwarzschild-MOG BHs with different values of parameter $\alpha$ observed by a remote observer at various inclination angles. The inclination angles in each column are $45^{\circ }$, $75^{\circ }$, and $85^{\circ }$ from top to bottom; the parameters $\alpha$ in each row are 0 (Schwarzschild case), 0.3, and 0.9 from left to right, respectively. In each panel, the direct and secondary images are depicted in black lines and red lines, respectively. From the inside to the outside, these images correspond to the stable circular orbits with radii of $r_{\text {s}}=r_{\text {ms}}$,² 15, 20, 25, and 30. We found that the direct and secondary images expand outward in horizontal and vertical directions as the parameter $\alpha$ increases. It is also found that the expansion is more significant in the vertical direction when the inclination angle takes a large value. These expansions are due to the fact that increasing the parameter $\alpha$ makes the Schwarzschild-MOG BH’s gravitational effect stronger, resulting in an increase in the deflection angle of the light. In other words, the Schwarzschild-MOG BH with a larger parameter $\alpha$ is capable of bending the light with a larger impact parameter and making it intersect the stable circular orbit we considered.

Figure 4 also shows that the observed direct and secondary images depend closely on the inclination angle. More specifically, the direct image is deformed into a hat-shaped when an observer views along the edge-on orientation. This is because the light rays emitted from the disk elements blocked by the BH can be scattered to the upper region of the BH by gravitational lensing. In addition, the range of the photon deflection angle is $5\pi /2-\omega \le \varphi \le 5\pi /2+\omega$ for $k=2$, which implies that when the observation angle $\omega$ takes a larger value, there exist some light rays with smaller deflection angles that can contribute to the secondary images with a deviation from circularity. This reveals why the deviations from the circularity of secondary images become significant as the inclination angle increases.

3.2 Redshift factor

The redshift factor g has an essential influence on the observed energy flux of the accretion disk, which can be expressed as

$$\begin{aligned} g=1+z=\frac{E_{\text {e}}}{E_{\text {o}}}, \end{aligned}$$

(30)

in which z denotes the redshift, $E_{\text {e}}$ and $E_{\text {o}}$ correspond to the projections of the photon’s four-momentum $k_{\mu }$ on the four-velocity of the disk elements $p_{\text {s}}^{\mu }$ and the distant observer $p_{\text {o}}^{\mu }$, respectively. In the rest frame of the emitting light source, $E_{\text {e}}$ is read as [41, 44,45,46]

$$\begin{aligned} E_{\text {e}} = k_{\mu }p^{\mu }_{\text {s}} = k_{t}p^{t}_{\text {s}}\left( 1+\varOmega \frac{k_{\varphi }}{k_{t}}\right) . \end{aligned}$$

(31)

Note that the ratio $k_{\varphi }/k_{t}$ is invariant along the photon path and it is related to the impact parameter b by $k_{\varphi }/k_{t}=b\sin {\omega }\cos {\eta }$ according to the geometry introduced in Fig. 2 [41, 44,45,46]. Hence, we have

$$\begin{aligned} E_{\text {e}} = k_{t}p^{t}_{\text {s}}\left( 1+\varOmega b\sin {\omega }\cos {\eta }\right) . \end{aligned}$$

(32)

Fig. 7

Linear velocity $v_{r}$ plotted versus radius r of the accretion flow for various values of $\alpha$

Fig. 8

The radiation flux $F_{\text {e}}$ from the thin accretion disk around Schwarzschild-MOG BHs under different $\alpha$ as a function of disk element’s radius $r_{\text {s}}$. Here, the BH mass and accretion rate are, respectively, $10^{6}M_{\odot }$ and $10^{-12}M_{\odot }/$year

Fig. 9

Continuous distributions of the observed energy flux in the direct images cast by the thin accretion disk around Schwarzschild-MOG BHs under different $\alpha$ and viewing angles. Here, the inner and outer boundaries of the accretion disk are stable circular orbits with radii $r=r_{\text {ms}}$ and $r=40$, respectively

Fig. 10

Similar to Fig. 9, but for RN BHs

Fig. 11

The distribution of observed flux along the x-axis of the observation screen for the three types of BHs. The black, green, and red lines correspond to the RN BH, Schwarzschild BH, and Schwarzschild-MOG BH, respectively

Fig. 12

The complete apparent images of the thin accretion disk for different values of parameter $\alpha$ and inclination $\omega$. Each panel is composed of the superposition of direct and secondary images

Fig. 13

The complete apparent images of the Schwarzschild BH with mass $1.732 \times 10^{6} M_{\odot }$ and the Schwarzschild-MOG BH with mass $10^{6} M_{\odot }$ and $\alpha =0.9$. Here, the observational angle and BH distance are $17^{\circ }$ and 5 kpc, respectively. Evidently, the Schwarzschild BH is capable of mimicking a Schwarzschild-MOG BH in this situation

For a static distant observer with the four-velocity $p_{\text {o}}^{\mu }=(1,0,0,0)$, the projection of the photon’s four-momentum on his four-velocity is

$$\begin{aligned} E_{\text {o}} = k_{\mu }p^{\mu }_{\text {o}}=k_{t}. \end{aligned}$$

(33)

By combining Eqs. (30), (32), and (33), we arrange the redshift factor as

$$\begin{aligned} g=1+z=\frac{1+b\varOmega \sin {\omega }\cos {\eta }}{f(r_{\text {s}})}E, \end{aligned}$$

(34)

where E and $\varOmega$ are obtained from Eqs. (13) and (15), respectively. Obviously, the redshift factor is closely related to the coordinate $r_{\text {s}}$ of the disk element and its projection $(b,\eta )$ on the observational plane, as well as the observational angle $\omega$.

We assume that the inner and outer boundaries of the accretion disk are, respectively, the stable circular orbits of $r=r_{\text {ms}}$ and $r=40$, and investigate the redshift distributions (contour map of redshift z) in the direct images for various inclination angles and parameter $\alpha$, as demonstrated in Fig. 5. In each panel, the black dashed line corresponds to the contour curve of $z=0$, which divides the direct image into two parts: the left side correspond to the blueshift with $z<0$, while the right side is the redshift. Intuitively, it is found that as the parameter $\alpha$ increases, the redshift in the image also increases, as does the blueshift (One can see the expansion of the contour curve corresponds to a larger blueshift when zooming in on the left part of the images). The dependency of the redshift on parameter $\alpha$ is also shown in the secondary images, which are plotted in Fig. 6.

As we know, the redshift is caused by the Doppler effect due to the motion of accretion flow and consequently depends mainly on the relative velocity of the disk elements with respect to the observer. Figure 7 presents the variation of the linear velocity $v_{r}=\varOmega r$ of the accretion flow at various radius for different values of parameter $\alpha$. It is clear that $v_{r}$ increases with the increase of $\alpha$ for a certain radius, which can explain the relationship between the redshift (blueshift) and the parameter $\alpha$ we discussed before.

3.3 The images of the accretion disk

In this section, the steady-state thin accretion disk is placed on the equatorial plane of the Schwarzschild-MOG BH, and the thickness of the disk is negligible compared to its radial dimension. Meanwhile, the accretion disk is considered to be stabilized at hydrodynamic equilibrium. Hence, by using the Novikov-Thorne model proposed in [73,74,75], the emitted energy flux $F_{\text {e}}$ of the disk can be expressed as

$$\begin{aligned} F_{\text {e}} = -\frac{\dot{M_{D}}}{4\pi \sqrt{-A}}\frac{\varOmega ^{\prime }}{\left( E-\varOmega L\right) ^{2}}\int ^{r_{\text {s}}}_{r_{\text {ms}}}\left( E-\varOmega L\right) L^{\prime }\text {d}r, \end{aligned}$$

(35)

where $F_{\text {e}}$ is given the scale transformation $F_{\text {e}} \rightarrow F_{\text {e}}/M^{2}$, $\dot{M_{D}}$ denotes the accretion rate of the BH, and A is the determinant of the induced metric in the equatorial plane. Clearly, the emitted energy flux $F_{\text {e}}$ is a function of the radius $r_{\text {s}}$ of the disk element since E, L, and $\varOmega$ are obtained with the aid of Eqs. (13)–(15).

Figure 8 presents the variation relationship between emitted energy flux and the disk element’s radius when the gravity coupling parameter takes different values. Here we have the Schwarzschild-MOG BH mass and accretion rate respectively as $10^{6}M_{\odot }$ and $10^{-12}M_{\odot }/$year, where $M_{\odot }$ denotes the mass of Sun. It is found that for arbitrary parameter $\alpha$, $F_{\text {e}}$ grows from 0 at $r_{\text {ms}}$ and reaches the peak rapidly, then exhibits a decaying behavior. One can also see that the maximum energy flux decreases with the increment of $\alpha$, i.e., the maximum energy flux corresponding to $\alpha =0.9$ is only $40\%$ of that corresponding to $\alpha =0$. This is because when the parameter $\alpha$ increases, the velocity of the accretion flow around the Schwarzschild-MOG BH becomes faster, causing the accretion disk to become hotter and its optical depth to become larger, which is not conducive to the escape of photons from the surface of the accretion disk.

As we mentioned before, the observed energy flux $F_{\text {o}}$ is significantly affected by the redshift factor and can be expressed as

$$\begin{aligned} F_{\text {o}} = \frac{F_{\text {e}}}{g^{4}}. \end{aligned}$$

(36)

We take the same Schwarzschild-MOG BH mass and accretion rate as in Fig. 8 and explore the observed energy flux in the direct images of the accretion disk for various parameter $\alpha$ and inclinations, as intuitively shown in Fig. 9. In each panel, the intensity of the energy flux is presented with a continuous color map, as white is associated with the maximal flux intensity, while dark red corresponds to the minimum value. Evidently, an accumulation of brightness occurs on the left side of the image, and it becomes significant when the inclination angle gets larger. This is caused by the Doppler effect due to the rotation of the accretion disk. We can confirm that this brightness accumulation will disappear when the distant observer is at a face-on orientation. It is also found that the intensity of the observed energy flux decays with increasing $\alpha$, i.e., the maximum values of $F_{\text {o}}$ are 5.39 $\times$ $10^{7}$ erg s$^{-1}$ cm$^{-2}$ in Panel (a), $3.78 \times 10^{7}$ erg s$^{-1}$ cm$^{-2}$ in Panel (b), and $2.18 \times 10^{7}$ erg s$^{-1}$ cm$^{-2}$ in Panel (c). There are two points that account for this attenuation trend: one is that the parameter $\alpha$ has a negative impact on the radiation energy flux $F_{\text {e}}$; another is that the gravitational effects of the Schwarzschild-MOG BH are enhanced for a larger $\alpha$, making it difficult for light rays to evade the absorption of the BH.

Figure 9 also presents the fact that for a positive parameter $\alpha$, the Schwarzschild-MOG BH appears darker than the Schwarzschild BH, but its inner shadow is visibly larger. In order to compare the images of Schwarzschild-MOG BHs with those of RN BHs, we simulated the optical appearance of the RN BH surrounded by a thin accretion disk and displayed the results in Fig. 10. It is shown that the inner shadow of RN BH shrinks as the charge Q increases, while the luminosity increases significantly. By combining the results of Figs. 9 and 10, we point out that for fixed observational angle, BH mass, and accretion rate, the Schwarzschild-MOG BH exhibits the largest inner shadow and the lowest brightness, whereas the RN BH shows the smallest inner shadow and the largest luminosity. In comparison, the size and luminosity of the Schwarzschild BH fall in between those of the other two BHs. Figure 11 demonstrates the distribution of observed flux along the x-axis of the observation screen for the Schwarzschild-MOG BH (red line), Schwarzschild BH (green line), and the RN BH (black line). These results not only further confirm the above statement, but also provide a robust criterion for distinguishing between the three types of BHs.

Next, we investigate the complete observable images with respect to the energy flux of the accretion disk under different parameter $\alpha$ and inclination $\omega$, as demonstrated in Fig. 12. These images are composed of the superposition of direct and secondary images. It is found that the apparent energy flux $F_{\text {o}}$ both in the direct and secondary image decreases with the increases of $\alpha$. Another signature of the complete images is the ring structure shown in the center of the photo, which is contributed by the secondary image and expands as $\alpha$ increases. These rings are closely related to the photon ring and can serve as the fingerprint of spacetime geometry. Therefore, one can use this critical ring to identify the Schwarzschild-MOG BHs and constrain the gravitational coupling parameter $\alpha$.

Fig. 14

The critical ring diameter $S_{\text {d}}$ of Schwarzschild-MOG BHs in the two-dimensional space of parameter $\alpha$ and mass M. Here the observational angle and BH distance are fixed at $0^{\circ }$ and 16.8 Mpc, respectively. It is clear that for a given BH mass and ring diameter, the gravitational coupling parameter $\alpha$ of the Schwarzschild-MOG BH can be uniquely determined

Fig. 15

Images from Fig. 12 before (first and third row) and after (second and fourth row) blurring with a Gaussian filter in order to simulate the nominal resolution of the EHT. Evidently, the ring structures in the center of images are washed out after blurring

Well, it is rational to question whether it is possible to adjust the mass of a Schwarzschild BH to mimic a Schwarzschild-MOG BH. To address this inquiry, we simulate the apparent images of the Schwarzschild BH with mass $1.732 \times 10^{6} M_{\odot }$, and the Schwarzschild-MOG BH with mass $10^{6} M_{\odot }$, as depicted in Fig. 13. Here, the celestial coordinates $\delta (\xi )$ is obtained from x(y) by [36]

$$\begin{aligned} \frac{\delta }{\mu \text {as}} = \left( \frac{6.191165 \times 10^{-8}}{2\pi } \frac{\sigma }{D/\text {Mpc}} \right) \left( \frac{x}{M}\right) , \end{aligned}$$

(37)

where $\delta$ is the mass ratio of the BH to the Sun, D represents distance and is fixed at 5 kpc. Apparently, the critical rings of the Schwarzschild BH and the Schwarzschild-MOG BH are similar in structure and resemble circles of diameter about 40 $\upmu \text {as}$. Meanwhile, the difference in brightness between the two BHs is relatively small since the maximum luminosities of the rings are 7.02 $\times$ $10^{6}$ erg s$^{-1}$ cm$^{-2}$ in Panel (a) and $8.27 \times 10^{6}$ erg s$^{-1}$ cm$^{-2}$ in Panel (b). Hence, identifying a Schwarzschild-MOG BH in this situation seems to be a Herculean task due to the degeneracy that makes it difficult to differentiate between the image cast by a Schwarzschild-MOG BH and a more massive Schwarzschild BH. Fortunately, this degeneracy can be eliminated by measuring the mass of the BH with other astronomical observations. As displayed in Fig. 14, when a BH is observed to have a critical ring diameter of 42 $\upmu$as, we cannot directly determine whether it is a Schwarzschild BH $(\alpha =0)$ with mass $6.89 \times 10^{9} M_{\odot }$ or a Schwarzschild-MOG BH with mass $3.79 \times 10^{9} M_{\odot }$ and parameter $\alpha =1$. However, when the BH mass is estimated as $4.94 \times 10^{9} M_{\odot }$ using other astronomical measurements, $\alpha =0.5$ can be uniquely determined.

Fig. 16

Gravitational force $\varPsi$ plotted versus radius r for Schwarzschild-MOG BHs (solid line) and RN BHs (dashed line). Here we take $G_{\text {N}}=M=c=1$

It is worth noting that the radio signals of the extremely narrow ring cannot be captured by the Earth-extended EHT with its current angular resolution (about 20 $\upmu$as at 1.3 mm), which is limited by the Earth’s diameter. In order to simulate the nominal resolution of the EHT [17, 34], we blur Fig. 12 with a Gaussian filter with standard deviation equal to 1/12 the field of view and obtain the second and fourth rows of Fig. 15 (The first and third rows are the copy of Fig. 12). One can realize that not only is the luminosity of the image reduced, but more critically, the ring structure is washed out. Nevertheless, we still believe that our results are potentially valuable for identifying the Schwrzschild-MOG BHs and constraining the gravitational coupling parameter $\alpha$ when the high-resolution images of the BHs are obtained with Space-Earth VLBI of the observatory located around the Lagrangian L2 point of the Sun-Earth system [80, 81].

4 Conclusions and discussions

In our previous work, the observed shadows and rings cast by the Schwarzschild-MOG BHs with spherical and thin disk accretion were investigated in detail [36]. In this paper, we focus on the observed images of the geometrically thin accretion disk surrounding the Schwarzschild-MOG BH and explore its configurations, redshift distributions, and observed energy flux for different values of parameter $\alpha$ and inclination angles $\omega$ in the framework of the Novikov-Thorne model. These physical properties are further compared with those obtained in Schwarzschild and RN spacetime.

It is found that the gravity coupling parameter $\alpha$ indeed has an impact on the profiles of images cast by the thin accretion disk. The direct and secondary images expand outward in both horizontal and vertical directions with the increase of $\alpha$. The expansion of secondary images becomes significant as the viewing angle increases. It is interesting to note that for large viewing angles, the direct image is deformed into a hat shape due to the gravitational lensing effect. Overall, the image size depends on the values of parameter $\alpha$, while the inclination exerts an important influence on the image silhouette. On the other hand, the growth in $\alpha$ strengthens the gravitational effects of the Schwarzschild-MOG BH and, consequently, accelerates the linear velocity of the accretion flow. This leads to an enhanced Doppler effect between the light source and the distant observer, which accounts for the dependency of the redshift and blueshift distributions on the parameter $\alpha$. Meanwhile, the rapidly moving accretion flow around the central body causes the inner region of the disk to heat up because of the friction effect, resulting in the increment of the optical depth. This is not conducive to the escape of photons from the surface of the accretion disk, so the radiation flux $F_{\text {e}}$ decreases. This can self-consistent explain why the observed energy flux $F_{\text {o}}$ shows a downward trend with the enhancement of the parameter $\alpha$.

We also notice a kind of ring structure in the secondary images of the accretion disk, which is closely related to the photon ring and can serve as a fingerprint of the spacetime geometry. At present, the earth-extended VLBI with a maximum long baseline of 10,700 km, cannot provide sufficient angular resolution to capture this configuration. However, the Space-Earth VLBI of an observatory located in near-Earth orbit can provide a sufficient angular resolution of about 5 $\upmu$as to improve the quality of the image significantly [80, 81]. Even more excitingly, the Space-Earth VLBI has the possibility to observe the visibility function at a high-angular resolution up to 0.1 $\upmu$as [81]. This hints at the possibility of employing Space-Earth VLBI to study BH photon rings through the visibility function in the future [81,82,83].

Based on the comparison of accretion disk images of Schwarzschild-MOG BH, Schwarzschild BH, and RN BH, we find that for fixed observational angle, BH mass, and accretion rate, the Schwarzschild-MOG BH with an arbitrary positive $\alpha$ exhibits the largest inner shadow and the lowest brightness. In contrast, the RN BH shows the smallest inner shadow and the largest luminosity. The size and luminosity of the Schwarzschild BH are somewhere between the other two BHs. These apparent differences provide potentially, qualitatively observational features to distinguish Schwarzschild-MOG BH from the counterpart in standard General Relativity, as well as a window to probe scalar–tensor–vector modified gravity. In future work, we will study the emission spectrum of the thin accretion disk surrounding the Schwarzschild-MOG BH and its observed luminosity in different bands.

Appendix: The difference between the Schwarzschild-MOG metric and the Reissner–Nordström metric

According to the literature [71], we assume that the BH charge Q is proportional to the BH mass in the form $Q=\sqrt{\alpha G_{\text {N}}} M$. The Schwarzschild-MOG metric potential Eq.(3) is therefore rewritten as

$$\begin{aligned} f(r)=1-\frac{2GM}{rc^{2}}+\frac{GQ^{2}}{r^{2}c^{4}}, \end{aligned}$$

(38)

and we obtain a line element

$$\begin{aligned} \text {d}s^{2}= & {} -\left( 1-\frac{2GM}{rc^{2}}+\frac{GQ^{2}}{r^{2}c^{4}}\right) \text {d}t^{2} \nonumber \\{} & {} +\frac{\text {d}r^{2}}{1-\frac{2GM}{rc^{2}}+\frac{GQ^{2}}{r^{2}c^{4}}}+r^{2}\text {d}\varOmega ^{2}. \end{aligned}$$

(39)

Evidently, the above metric has a similar form to that of the RN solution [84],

$$\begin{aligned} \text {d}s^{2}= & {} -\left( 1-\frac{2G_{\text {N}}M}{rc^{2}}+\frac{G_{\text {N}}Q^{2}}{r^{2}c^{4}}\right) \text {d}t^{2} \nonumber \\{} & {} +\frac{\text {d}r^{2}}{1-\frac{2G_{\text {N}}M}{rc^{2}}+\frac{G_{\text {N}}Q^{2}}{r^{2}c^{4}}}+r^{2}\text {d}\varOmega ^{2}. \end{aligned}$$

(40)

However, it’s important to note that the gravitational constant in metric (39) is an enhanced one, $G=(1+\alpha )G_{\text {N}}$, rather than Newton’s constant $G_{\text {N}}$ in Eq. (40). Therefore, the Schwarzschild-MOG solution and RN solution are substantially different, although some mathematical operations can transform the former into a form similar to that of the latter.

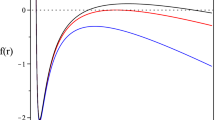
By analyzing the strength of the gravitational field, we can further unveil the differences between the Schwarzschild-MOG BH and the RN BH. As we know, the gravitational force $\varPsi$ is the first-order partial derivative of $g_{tt}$ with respect to radius r, namely, $\varPsi =-\partial f(r)/\partial r$. Figure 16 shows the variation relationship between the gravitational force $\varPsi$ and radius r for the Schwarzschild-MOG BHs (solid line) and the RN BHs (dashed line). We find that an increase in gravity coupling parameter $\alpha$ significantly enhances the attractive force of the Schwarzschild-MOG BH to matter, while the charge Q has a negative effect on the gravitational field of the RN BH. It is also found that the gravitational strength of Schwarzschild-MOG BHs is always greater than that of RN BHs when $\alpha > 0$. This implies that they differ in their optical appearance and can be distinguished by their images. We focus on this issue in the main text.