1 Introduction

In recent years, quantum information science has been widely combined with many other theories and has served as a foundation for the quantum world. The development of quantum information science has yielded useful concepts that have been used to interpret several puzzles in relativity theory, including the black hole information-loss paradox. Meanwhile, because the world is non-inertial in nature, comprehending quantum information science within the framework of relativity leads to a better understanding of quantum mechanics [1,2,3,4,5,6,7,8]. For examples, Fuentes et al. [1] investigated that entanglement in noninertial frames is characterized by the observer-dependent property. Friis [2] showed that any quantum information theory based on anticommuting operators ought to be supplemented by a superselection rule deeply rooted in relativity, to form the so-called entanglement. Martín-Martínez et al. [3] studied entanglement degradation affected by the Hawking effect of Schwarzschild black hole. Mann et al. [4] pointed out that incorporating concepts from quantum theory into relativity can yield novel and interesting effects.

Quantum coherence [9] is a fundamental concept that can be rigorously characterised in the context of quantum resource theory. Quantum coherence is regarded as a key quantum resource that originates from the principle of superposition of states and can be widely used to implement various quantum tasks. Several methods are available for quantifying coherence [10, 11]. Among these, \(l_1\)-norm of coherence is valid and widely used in quantum physics, and is expressed as follows:

$$\begin{aligned} C(\rho ) =\sum \limits _{i \ne j} {\left| {{\rho _{i,j}}} \right| }. \end{aligned}$$
(1)

As can be seen from the above equation, the value of \(l_1\)-norm coherence is equal to the sum of the absolute values of all off-diagonal elements under the chosen basis.

In addition, according to Bell’s theorem [12], the correlation between the results of local observables may be nonlocal for some quantum states. Bell nonlocality [13, 14] is a property of quantum correlations, and this nonlocal property of quantum states can be revealed by exploiting corresponding Bell-type inequalities [14,15,16,17]. With regard to tripartite states, the Svetlichny inequality can be employed to detect genuine nonlocality. Initially, the Svetlichny inequality was proposed in [18] in 1987, and its form for the three-qubit state \(\rho _{ABE} \) can be expressed as follows:

$$\begin{aligned} \mathrm {Tr}(S' \cdot \rho ) \le 4 \end{aligned}$$
(2)

with

$$\begin{aligned} \mathrm {S'}&= ABE + A'BE + AB'E + ABE' \nonumber \\&\quad - A'BE' - A'B'E - AB'E'- A'B'E' \end{aligned}$$
(3)

where X and \(X'\) denote the measurement operators that are used to perform measurements on the corresponding qubit X (\(X=A, B, E\)). Mathematically, the measurement form is can be expressed as follows:

$$\begin{aligned} A&= \vec a \cdot \vec \sigma \nonumber \\ A'&= \vec a' \cdot \vec \sigma , \end{aligned}$$
(4)

where \(\vec \sigma = ({\hat{\sigma } _1},{\hat{\sigma } _2},{\hat{\sigma } _3})\) is a vector composed of Pauli matrices and \(\vec a = ({a_1},{a_2},{a_3})\) and \(\vec a' = (a{'_1},a{'_2},a{'_3})\) are unit vectors in three dimensions. The other four measurements of the corresponding qubits B and E are similar to those of A.

The uncertainty principle proposed by Heisenberg, which is one of the most well-known principles of quantum mechanics, [19] states that the position and momentum of a moving particle cannot be determined simultaneously. Later, Kennard [20] and Robertson [21] generalised it in terms of the standard deviation, where \(\Delta \hat{R} \cdot \Delta \hat{S} \ge \frac{1}{2}| {\langle {[ {\hat{R}\mathrm{{ }},\mathrm{{ }}\hat{S}}]} \rangle }|\), \(\hat{R}\) and \(\hat{S}\) are two arbitrary non-commuting observables and \([ {\hat{R}\mathrm{{ }},\mathrm{{ }}\hat{S}} ]\) represents the commutator. It can be seen that the lower bound yields trivial measurement results once the state is prepared in one of the eigenstates of \(\hat{R}\) or \(\hat{S}\). Everett [22] and Hirschman [23] were the first to use entropy to describe the principle of uncertainty. Deutsch then developed the entropy-based uncertainty relation to address the flaw of state dependency [24]. Thereafter, Kraus [25] and Maassen and Uffink [26] improved it as follows:

$$\begin{aligned} H ( \hat{R} ) + H( \hat{S} ) \ge {\log _2}\frac{1}{c}=:{q_{MU}}, \end{aligned}$$
(5)

where the Shannon entropy \(H( \hat{R} ) = - \sum \nolimits _i^{} {{p_i}{{\log }_2}{p_i}}\), \({p_i} = \left\langle {{\mu _i}} \right| \mathrm{{ }}{\hat{{\rho }}} \mathrm{{ }}\left| {{\mu _i}} \right\rangle \), \(c = \mathop {\max }\nolimits _{i\mathrm{{ }}j} {\left| {\left\langle {{{\mu _i}\mathrm{{ }}}}/{{{\vartheta _j}}} \right\rangle } \right| ^2}\) refers to the maximal overlap of \(\hat{R}\) and \(\hat{S}\), \(\left| {{\mu _i}} \right\rangle \) (or \(\left| {{\vartheta _j}} \right\rangle \) ) is the eigenstate of \(\hat{R}\) (or \(\hat{S}\)). In sharp contrast to Kennard’s inequality, the bound of Eq. (5) is state independent.

Thus, the uncertainty relations are limited to single-particle system scenarios. Thus, a logical issue arises: how can uncertainty be expressed when the measured subsystems are correlated to each other? In this regard, Renes and Boileau [27] originally proposed a brand-new uncertainty relation for bipartite and tripartite systems, that is, quantum-memory-assisted entropic uncertainty relations (QMA-EUR) [28]. Specifically, the tripartite QMA-EUR can be expressed as follows:

$$\begin{aligned} S(\hat{X}|B) + S(\hat{Z}|E) \ge q_{MU}. \end{aligned}$$
(6)

where \(S(\hat{X}|B) = S({\rho _{\hat{X}B}}) - S({\rho _B})\) [29] represents the conditional entropy of state \({\rho _{\hat{X}B}}\). The measured state can be expressed as \({\rho _{\hat{X}B}} = \sum \nolimits _i {(\Pi _i^{\hat{X}} \otimes {\mathbb {I}_B}){\rho _{AB}}(\Pi _i^{\hat{X}} \otimes {\mathbb {I}_B})}\), \(\Pi _i^{\hat{X}}= | {\psi _i^{\hat{X}}} \rangle \langle {\psi _i^{\hat{X}}} |\) is the measurement operator acting on the subsystem A, \(| {\psi _i^{\hat{X}} } \rangle \) is the eigenvector of observable \(\hat{X}\). \(S(\hat{X}|B)\) is used to measure Bob’s uncertainty regarding Alice’s measurement result for the observable \(\hat{X}\). Essentially, this inequality can be explained by a monogamy game, assuming that the source outputs the tripartite state \({\rho _{ABE}}\) and the subsystems A, B and E are sent to Alice, Bob, and Eric, respectively. Alice selects measurement \(\hat{X}\) or \(\hat{Z}\) on system A and obtains results \(\mathcal K\) before informing Bob and Eric about her measurement selection. Bob and Eric win this game only if they both guess the result \(\mathcal K\) correctly. In fact, QMA-EUR [30, 31] gives rise to a variety of potential applications in quantum information theory, including entanglement witness [32, 33], quantum key distribution [34,35,36], and EPR steering [37, 38]. Additionally, it also plays an important role in probing the quantumness of many different systems [39, 40], such as neutrino systems [41,42,43] and the Heisenberg spin-chain model [44,45,46]. To date, much effort has been made to improve bipartite [47,48,49,50,51,52,53,54,55,56] and tripartite [57, 58] QMA-EUR.

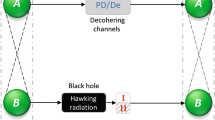
Black holes have garnered a lot of attention. Many investigations have been conducted on the dynamics of QMA-EUR [59,60,61] and the quantum properties [62] of Schwarzschild black holes. More recently, several promising studies have been conducted on the quantumness of Garfinkle–Horowitz–Strominger dilation (GHS-dilation) black holes [63,64,65]. There have been few investigations concerning the tripartite quantum correlation and QMA-EUR of Dirac fields in the background of GHS-dilation black holes, which is a fundamental requirement for understanding the quantumness of black holes. This prompted us to conduct research on the issue. The remainder of this paper is organised as follows: Sect. 2 briefly describes the vacuum structure for Dirac fields in the GHS-dilation black hole. Sections 3 and 4 investigate the dynamics of the tripartite quantum correlation and QMA-EUR against the backdrop of GHS-dilation space-time, respectively. Therefore, the intrinsic relationship between quantum correlation and QMA-EUR was revealed. Section 5 concludes with concise discussions and summaries.

2 Vacuum states in GHS-dilation space-time

First, according to the definition of vacuum states in a curved space, the GHS-dilated black hole [66,67,68] can be written as follows:

$$\begin{aligned} d{s^2}&= - \left( {\frac{{r - 2M}}{{r - 2D}}} \right) d{t^2} + {\left( {\frac{{r - 2M}}{{r - 2D}}} \right) ^{ - 1}}d{r^2} \nonumber \\&\quad + r(r - 2D)(d{\theta ^2} + \sin ^2\theta d{\phi ^2}), \end{aligned}$$
(7)

where M is related to the mass of the black hole, and D denotes the parameter of the dilation field. The Hawking temperature can be expressed as \(T = \frac{1}{{8\pi (M - D)}}\), and the thermal Fermi-Dirac distribution of particles with T was observed in Refs. [69,70,71]. For simplicity, we treat G, c,  \(\hbar \), \({\kappa _B}\) as unity, and M, D and the charge Q satisfy \(D = {Q^2}/2M\).

For GHS-dilation space-time, the Dirac equation can be written as follows:

$$\begin{aligned}{}[ {{\gamma ^a}e_a^\mu ({\partial _\mu } + {\Gamma _\mu })} ]\psi = 0, \end{aligned}$$
(8)

where \(\gamma ^a\) is the Dirac matrix, and \(\partial _\mu \) stands for the spin connection coefficient, \(e_a^\mu \) represents the inverse of the tetrad \(e_\mu ^a\). By solving the Dirac equation under the GHS-dilation space-time, one can obtain the positive frequency outgoing solutions in the inside (I) and outside (II) regions of the event horizon as [67]

$$\begin{aligned}&\psi _k^{\mathrm{I} + }= \xi {e^{ - i\omega u}};\nonumber \\&\psi _k^{\mathrm{I}\mathrm{I} + }= \xi {e^{i\omega u}}, \end{aligned}$$
(9)

where k represents the field mode, \(\xi \) is the 4-component Dirac spinor, and \(\omega \) is the monochromatic frequency of the Dirac field. The retarded time u is expressed as:

$$\begin{aligned} u = t - {r_ * }, \end{aligned}$$
(10)

where the tortoise coordinates are \({r_ *} =2(M - D)\ln [\frac{{r - 2M}}{{2(M - D)}}] + r\). \(\psi _k^{\mathrm{I} + }\) and \(\psi _k^{\mathrm{I}\mathrm{I} + }\) constitute a set of complete orthogonal bases, and the Dirac field can be written as follows:

$$\begin{aligned} {\psi _{out}} = \sum \limits _{\nu = \mathrm{I,II}} {\int {dk} } (a_k^\nu \psi _k^{\nu + })(b_k^{\nu * }\psi _k^{\nu - }), \end{aligned}$$
(11)

where \(a_k^\nu \) and \(b_k^{\nu * }\) are the fermion annihilation and anti-fermion creation operators, respectively. Then, for the positive energy mode, using the generalised Kruskal coordinates, the new orthogonal basis can be obtained by

$$\begin{aligned} \chi _k^{\mathrm{I} + }&= {e^{2(M - D)\pi \omega }}\psi _k^{\mathrm{I} + } + {e^{ - 2(M - D)\pi \omega }}\psi _{ - k}^{\mathrm{II} - }, \nonumber \\ \chi _k^{\mathrm{II} + }&= {e^{ - 2(M - D)\pi \omega }}\psi _{ - k}^{\mathrm{I} - } + {e^{2(M - D)\pi \omega }}\psi _k^{\mathrm{II} + }. \end{aligned}$$
(12)

Next, to depict the Dirac field, these new bases can be expressed as follows:

$$\begin{aligned}&{\psi _{out}} \nonumber \\&= \sum \limits _{\nu = \mathrm{I,II}} {\int {dk} \frac{1}{{\sqrt{2\cosh [4(M - D)\pi \omega ]} }}} (c_k^\nu \chi _k^{\nu +}+d_k^{\nu *} \chi _k^{\nu -}), \end{aligned}$$
(13)

where \(c_k^\nu \) and \(d_k^{\nu * }\) are the fermion annihilation and antifermion creation operators which act on the state of the exterior region (\(\nu =\mathrm{I}\)) and interior region (\(\nu =\mathrm{II}\)), respectively. Equations (11) and (13) correspond to the decomposition of the Dirac fields in GHS-dilation and Kruskal modes, respectively. The annihilation operator can then be obtained using the Bogoliubov transformation in the GHS-dilation and Kruskal modes. Taking into account the orthonormality of the modes, each annihilation operator \(c_k^\mathrm{I}\) can be attained by a union of dilation particle operators of only one frequency \(\omega _i\), described as follows:

$$\begin{aligned} c_k^\mathrm{I}&= \cos \beta \cdot a_k^\mathrm{I} -\sin \beta \cdot b_k^{\mathrm{II} * };\nonumber \\ \cos \beta&=\left( {e^{ - 8(M - D)\pi {\omega _i}}} + 1\right) ^{ - \frac{1}{2}};\nonumber \\ \sin \beta&=\left( {e^{ 8(M- D)\pi {\omega _i}}} + 1\right) ^{ - \frac{1}{2}}. \end{aligned}$$
(14)

Because the GHS-dilation space-time can be divided into physically inaccessible and accessible regions, the mode of the ground state in a GHS-dilation black hole coordinate corresponds to a two-mode squeezed state in the Kruskal coordinate. After properly normalising the state vector, the vacuum state of the Kruskal particle for mode can be expressed as follows:

$$\begin{aligned} \left| {{0_k}} \right\rangle _k^ +&= \cos \beta \cdot \left| {{0_k}} \right\rangle _\mathrm{I}^ + \left| {{0_{ - k}}} \right\rangle _{\mathrm{II}}^ - \nonumber \\&\quad + \sin \beta \cdot \left| {{1_k}} \right\rangle _\mathrm{I}^ + \left| {{1_{ - k}}} \right\rangle _{\mathrm{II}}^ -, \end{aligned}$$
(15)

where \(\left| n \right\rangle _\mathrm{I}\) and \(\left| n \right\rangle _{\mathrm{II}}\) correspond to the orthonormal bases for the outside and inside regions of the event horizon, respectively, the superscripts + and - indicate the particle and antiparticle, respectively. For simplicity, we assume \(\omega _i = \omega = 1\). Similarly, only the excited state can be expanded as follows:

$$\begin{aligned} \left| {{1_k}} \right\rangle _k^ + = \left| {{1_k}} \right\rangle _\mathrm{I}^ + \left| {{0_{ - k}}} \right\rangle _{\mathrm{II}}^ -. \end{aligned}$$
(16)

3 Evolution of the nonlocality and coherence in GHS-dilation black hole

Fig. 1
figure 1

Nonlocality and coherence for \(\rho _{AB_\mathrm{I}E_\mathrm{I}}\) in physical accessible regions. a Svetlichny value S versus the dilation parameter D with different state parameters \(\alpha \); b Svetlichny value S versus state parameters \(\alpha ^2\) the with different dilation parameter D; c Coherence C versus the dilation parameter D with different state parameters \(\alpha \); d Coherence C versus state parameters \(\alpha ^2\) with different dilation parameter D. (All plotted with \(M = 1\).)

Full size image

Here, we consider the Greenberger–Horne–Zeilinger-like (GHZ-like) state of the Dirac fields shared by Alice, Bob, and Eric.

$$\begin{aligned} {\left| \psi \right\rangle _{ABE}} = \alpha \left| {{0_A}{0_B}{0_E}} \right\rangle + \sqrt{1 - {\alpha ^2}} \left| {{1_A}{1_B}{1_E}} \right\rangle , \end{aligned}$$
(17)

where \(\alpha \in [0,1]\) denotes the state parameter. First, Alice, Bob, and Eric remain in an asymptotically flat region. Then, Alice was left in the asymptotically flat region, and Bob and Eric fell towards a GHS-dilation black hole freely and later hovered around the event horizon. According to the Kruskal modes above for Bob and Eric, the initial state can be rewritten as follows:

$$\begin{aligned}&{\left| \psi \right\rangle _{A{B_\mathrm{I}}{B_{\mathrm{II}}}{E_\mathrm{I}}{E_{\mathrm{II}}}}} \nonumber \\&\quad = \alpha {\cos ^2}\beta {\left| 0 \right\rangle _A}{\left| 1 \right\rangle _{{B_\mathrm{I}}}}{\left| 1 \right\rangle _{{B_{\mathrm{II}}}}}{\left| 1 \right\rangle _{{E_\mathrm{I}}}}{\left| 1 \right\rangle _{{E_{\mathrm{II}}}}} \nonumber \\&\qquad + \alpha {\sin ^2}\beta {\left| 0 \right\rangle _A}{\left| 0 \right\rangle _{{B_\mathrm{I}}}}{\left| 0 \right\rangle _{{B_{\mathrm{II}}}}}{\left| 0 \right\rangle _{{E_\mathrm{I}}}}{\left| 0 \right\rangle _{{E_{\mathrm{II}}}}}\nonumber \\&\qquad + \sqrt{1 - {\alpha ^2}}{\left| 1 \right\rangle _A}{\left| 1 \right\rangle _{{B_\mathrm{I}}}}{\left| 0 \right\rangle _{{B_{\mathrm{II}}}}}{\left| 1 \right\rangle _{{E_\mathrm{I}}}}{\left| 0 \right\rangle _{{E_{\mathrm{II}}}}}\nonumber \\&\qquad + \alpha \sin \beta \cos \beta ({\left| 0 \right\rangle _A}{\left| 0 \right\rangle _{{B_\mathrm{I}}}}{\left| 0 \right\rangle _{{B_{\mathrm{II}}}}}{\left| 1 \right\rangle _{{E_\mathrm{I}}}}{\left| 1 \right\rangle _{{E_{\mathrm{II}}}}} \nonumber \\&\qquad + {\left| 0 \right\rangle _A}{\left| 1 \right\rangle _{{B_\mathrm{I}}}}{\left| 1 \right\rangle _{{B_{\mathrm{II}}}}}{\left| 0 \right\rangle _{{E_\mathrm{I}}}}{\left| 0 \right\rangle _{{E_{\mathrm{II}}}}}). \end{aligned}$$
(18)

Because regions I and II are disconnected, and the modes inside the event horizon cannot be accessed by Bob and Eric, thus the modes \({B_{\mathrm{I}}}\) and \({E_{\mathrm{I}}}\) outside the event horizon are called physically accessible modes, \({B_{\mathrm{II}}}\) and \({E_{\mathrm{II}}}\) inside the event horizon are called inaccessible modes. Thereafter, the physically accessible part I state for the tripartite system may be determined by tracing across all degrees of freedom in region II, which decreases the density matrix \({\rho _{A{B_\mathrm{I}}{E_\mathrm{I}}}}\) and is expressed as follows:

$$\begin{aligned} {\rho _{A{B_\mathrm{I}}{E_\mathrm{I}}}} = \left( {\begin{array}{*{20}{c}} {{\rho _{11}}}&{}0&{}0&{}0&{}0&{}0&{}0&{}{{\rho _{18}}}\\ 0&{}{{\rho _{22}}}&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}{{\rho _{33}}}&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}{{\rho _{44}}}&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ {{\rho _{81}}}&{}0&{}0&{}0&{}0&{}0&{}0&{}{{\rho _{88}}} \end{array}} \right) \end{aligned}$$
(19)

with

$$\begin{aligned} {\rho _{11}}&= {\alpha ^2}{{\cos ^4}\beta };\nonumber \\ {\rho _{44}}&= {\alpha ^2}{{\sin ^4}\beta }; \quad {\rho _{88}}= 1 - \alpha ^2;\nonumber \\ {\rho _{18}}&= {\rho _{81}} = \alpha \sqrt{1 - {\alpha ^2}} {{\cos ^2}\beta };\nonumber \\ {\rho _{22}}&= {\rho _{33}} = \alpha ^2 \sin ^2\beta \cos ^2\beta . \end{aligned}$$
(20)

If a three-qubit state violates the Svetlichny inequality, then the state satisfies genuine tripartite nonlocality [72,73,74]. For the X state with the density operator

$$\begin{aligned} {\rho _X} = \left( {\begin{array}{*{20}{c}} {{\rho _{11}}}&{}0&{}0&{}0&{}0&{}0&{}0&{}{{\rho _{18}}}\\ 0&{}{{\rho _{22}}}&{}0&{}0&{}0&{}0&{}{{\rho _{27}}}&{}0\\ 0&{}0&{}{{\rho _{33}}}&{}0&{}0&{}{{\rho _{36}}}&{}0&{}0\\ 0&{}0&{}0&{}{{\rho _{44}}}&{}{{\rho _{45}}}&{}0&{}0&{}0\\ 0&{}0&{}0&{}{{\rho _{54}}}&{}{{\rho _{55}}}&{}0&{}0&{}0\\ 0&{}0&{}{{\rho _{63}}}&{}0&{}0&{}{{\rho _{66}}}&{}0&{}0\\ 0&{}{{\rho _{72}}}&{}0&{}0&{}0&{}0&{}{{\rho _{77}}}&{}0\\ {{\rho _{81}}}&{}0&{}0&{}0&{}0&{}0&{}0&{}{{\rho _{88}}} \end{array}} \right) , \end{aligned}$$
(21)

there is a more direct formula [65, 75] to detect the nonlocality, which can be expressed by the maximal violation of Svetlichny inequality as follows:

$$\begin{aligned} S =\max \mathrm {Tr}(S' \cdot \rho ). \end{aligned}$$
(22)

For any element \(\rho _{ij}\) in \(\rho _X\) with \(i + j = 9\), the Svetlichny value can be quantified as follows:

$$\begin{aligned} S({\rho _X}) = \max \{ 8\sqrt{2} \left| {{\rho _{ij}}} \right| ,4\left| T \right| \}, \end{aligned}$$
(23)

where \(T = {\rho _{11}} - {\rho _{22}} - {\rho _{33}} + {\rho _{44}} - {\rho _{55}} + {\rho _{66}} + {\rho _{77}} - {\rho _{88}}\). As a result, according to Eqs. (1) and (23), the Svetlichny value and coherence of \({\rho {A{B_\mathrm{I}}{E_\mathrm{I}}}}\) in physically accessible regions can be expressed as follows:

$$\begin{aligned}&{S_\mathrm{{I}}}= \max \left\{ 8\alpha \sqrt{2(1 - {\alpha ^2})} {\cos ^2}\beta ,\right. \nonumber \\&\quad \left. 4\left| {{\alpha ^2}{{\cos ^4}\beta }+{\alpha ^2}{\sin ^4}\beta - 2\alpha ^2 \sin ^2\beta \cos ^2\beta - (1 - {\alpha ^2})} \right| \right\} \end{aligned}$$
(24)

and

$$\begin{aligned} {C_\mathrm{I}}= 2\alpha \sqrt{1 - {\alpha ^2}} {\cos ^2}\beta . \end{aligned}$$
(25)
Fig. 2
figure 2

Nonlocality and coherence for \(\rho _{AB_{\mathrm{II}}E_{\mathrm{II}}}\). a Svetlichny value S versus the dilation parameter D with different state parameters \(\alpha \); b Svetlichny value S versus state parameters \(\alpha ^2\) with different dilation parameter D; c Coherence C versus the dilation parameter D with different state parameters \(\alpha \); d Coherence C versus state parameters \(\alpha ^2\) with different dilation parameter D. (All plotted with \(M = 1\).)

Full size image

Svetlichny value and coherence with respect to the variation in the dilation parameter D and state parameter \(\alpha ^2\) are plotted in Fig. 1 to explore the nonlocality and coherence of the proposed model. As previously mentioned, the dilation parameter D is correlated with the Hawking temperature T; that is, \(T\propto -1/D\). As displayed in Fig. 1a, the Svetlichny value keeps at a certain value when \(D < 0.8\), and its value begins to decrease when \(D >0.8\). It is discovered that the Svetlichny value S is greater than four in some cases, corresponding to a violation of the Svetlichny inequality in Eq. 2, indicating that the system has quantum nonlocality. Note that S eventually decreases to less than 4. In addition, there are cases where S is always less than four. As indicated by the purple line in Fig. 1a, S never exceeds 4 when \(\alpha =0.3\). This is because the thermal noise induced by Hawking radiation destroys the physically accessible nonlocality among Alice, Bob, and Eric in the situation. Furthermore, Fig. 1b indicates the nonlocality of the tripartite subsystem \(\rho _{A{B_\mathrm{I}}{E_\mathrm{I}}}\) with state’s parameter \(\alpha ^2 \in [0,1]\). As shown in the figure, S is symmetric around \({\alpha ^2} = 1/2\) and \(S(\rho _{A{B_\mathrm{I}}{E_\mathrm{I}}}) \ge 4\), implying that the state of the system is nonlocal. Furthermore, the Svetlichny value is the largest with respect to \(\alpha ^2=0.5\). It should be noted that S exhibits an inflection point for \(S<4\). This can be explained as follows. The first term in Eq. (24) dominates the Svetlichny value before and after the inflection point, whereas S is determined by the second term in Eq. (24). This also shows that the physically accessible nonlocality between Alice, Bob, and Eric is destroyed when \(\alpha \) approaches 0 or 1.

Fig. 3
figure 3

Coherence of physically accessible region I, physically inaccessible region II, and the summation of regions I and II. a Coherence C versus the dilation parameter D with \(\alpha =\sqrt{2} /2\); b Coherence C versus state parameters \(\alpha ^2\) with \(D=0.95\). (All plotted with \(M = 1\).)

Full size image

The system’s coherence (C) is plotted as a function of the dilation parameter D with different state parameters \(\alpha \) in Fig. 1c. The coherence is initially stable at a fixed value, and it gradually decreases but never disappears as D increases after approximately 0.8 . This indicates that the Hawking temperature T will induce a reduction in the coherence and never lead to the disappearance of quantum coherence. C is maximised when the initial state is a GHZ state with \(\alpha =\sqrt{2} /2\). Moreover, as \(\alpha ^2\) increases, the coherence first increases and then decreases, and its value is fully symmetric with \(\alpha ^2\), as shown in Fig. 1d. The figure also supports the idea that a larger D will result in a smaller coherence, which is essentially consistent with the conclusion made before.

To better understand the dynamics of quantum coherence and nonlocality in physically accessible modes, we consider the quantum correlation of \({\rho _{A{B_{\mathrm{II}}}{E_{\mathrm{II}}}}}\) in the physically inaccessible modes. First, we need to trace the modes \({B_{\mathrm{I}}}\) and \({E_{\mathrm{I}}}\) of \({\left| \psi \right\rangle _{A{B_\mathrm{I}}{B_{\mathrm{II}}}{E_\mathrm{I}}{E_{\mathrm{II}}}}} \) to obtain the reduced density operator \({\rho _{A{B_{\mathrm{II}}}{E_{\mathrm{II}}}}}\) as follows:

$$\begin{aligned} {\rho _{A{B_{\mathrm{II}}}{E_{\mathrm{II}}}}} = \left( {\begin{array}{*{20}{c}} {{\rho _{11}}}&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}{{\rho _{22}}}&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}{{\rho _{33}}}&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}{{\rho _{44}}}&{}{{\rho _{45}}}&{}0&{}0&{}0\\ 0&{}0&{}0&{}{{\rho _{54}}}&{}{{\rho _{55}}}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}0&{}0&{}0 \end{array}} \right) \end{aligned}$$
(26)

with

$$\begin{aligned} {\rho _{11}}&= {\alpha ^2}{\cos ^4}\beta ;\nonumber \\ {\rho _{44}}&= {\alpha ^2}{\sin ^4}\beta ; {\rho _{55}}=1 - {\alpha ^2};\nonumber \\ {\rho _{45}}&= {\rho _{54}} = \alpha \sqrt{1 - {\alpha ^2}} {\sin ^2}\beta ;\nonumber \\ {\rho _{22}}&= {\rho _{33}} = \alpha ^2 \sin ^2\beta \cos ^2\beta . \end{aligned}$$
(27)

According to Eqs. (1) and (23), the Svetlichny value and coherence of the physically inaccessible region can be written as follows:

$$\begin{aligned} {S_\mathrm{{II}}}&= \max \left\{ 8\alpha \sqrt{2(1 - {\alpha ^2})} {\sin ^2}\beta ,\right. 4\left| {{\alpha ^2}{\cos ^4}}\right. \nonumber \\&\left. \left. {\beta + {\alpha ^2}{\sin ^4}\beta - 2\alpha ^2 \sin ^2\beta \cos ^2\beta - (1 - {\alpha ^2})} \right| \right\} \end{aligned}$$
(28)
$$\begin{aligned} {C_\mathrm{{II}}}= 2\alpha \sqrt{1 - {\alpha ^2}} {\sin ^2}\beta . \end{aligned}$$
(29)
Fig. 4
figure 4

Uncertainty of \(\rho _{AB_\mathrm{I}E_\mathrm{I}}\) in physical accessible regions. a Uncertainty versus the dilation parameter D with different state parameters \(\alpha \); b Uncertainty versus state parameters \(\alpha \) with different dilation parameter D. (All plotted with \(M = 1\).)

Full size image

The same has been plotted in Fig. 2. Overall, Fig. 2a, b show that the Svetlichny is always less than 4, implying that the nonlocality is always absent in physically inaccessible region II. Coherence, on the other hand, still exists in region II, as shown in Fig. 2c, d. Quantum coherence first remains invariable and subsequently increases with increasing Hawking temperature T, the dynamics of which are obviously opposite to those shown in Fig. 1c in physically accessible regions.

To investigate the quantification relationship between the coherences of regions I and II, we can define the total coherence of the composite system as follows:

$$\begin{aligned} C_\mathrm{tot}&={C_\mathrm{I}} + {C_\mathrm{II}} \nonumber \\&= 2\alpha \sqrt{1 - {\alpha ^2}} {\cos ^2}\beta + 2\alpha \sqrt{1 - {\alpha ^2}} {\sin ^2}\beta \nonumber \\&\equiv 2\alpha \sqrt{1 - {\alpha ^2}}, \end{aligned}$$
(30)
Fig. 5
figure 5

Uncertainty of \(\rho _{AB_\mathrm{II}E_\mathrm{II}}\) in physical inaccessible regions. a Uncertainty U versus the dilation parameter D with different state parameters \(\alpha \); b Uncertainty versus state parameters \(\alpha ^2\) with different dilation parameter D; All plotted with \(M = 1\)

Full size image

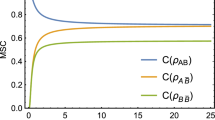
by employing Eqs. (25) and (29), respectively. The preceding equation shows that the total coherence \(C_\mathrm{tot}\) is determined only by state parameter \(\alpha \) and is independent of dilation parameter D (and T). Meanwhile, we draw \(C_\mathrm{tot}\), \(C_\mathrm{I}\) and \(C_\mathrm{II}\) as functions of D and \(\alpha ^2\) in Fig. 3. Figure 3a clearly shows the trade-off relationship between the coherence of regions I and II with \(\alpha =\sqrt{2}/2\). As the Hawking temperature T increases, \({C_\mathrm{I}}\) decreases and \({C_\mathrm{II}}\) simultaneously inflates. In principle, this phenomenon can be explained using information flow theory. Technically, a change in the Hawking temperature causes the flow of information. When T increases, the information in physically accessible region I flows into physically inaccessible region II, while the total coherence remains unchanged. Likewise, Fig. 3b supports our result obtained in Eq. (30). Considering all this, we conclude that total coherence \(C_\mathrm{tot}\) is fixed when the initial state is prepared. Thus, we argue that quantum coherence is a good candidate for illustrating the information-loss paradox.

4 QMA-EUR in GHS-dilation black hole

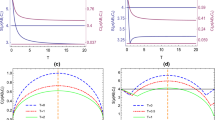
Uncertainty is considered one of the basic and nontrivial topics in quantum physics as it is an important feature of the quantum world. To observe the dynamic features of the measured uncertainty in the curved space-time, we choose \({\hat{\sigma } _x}\) and \({\hat{\sigma } _z}\) as two incompatible measurements so that the maximal overlap of measurement \(c({\hat{\sigma } _x},{\hat{\sigma } _z}) = \frac{1}{2}\). Then, according to Eq. (6), we obtain the post-measurement states, \({\rho _{{\hat{\sigma } _x}{B_I}}}\) and \({\rho _{{\hat{\sigma } _z}{C_I}}}\). Through calculation, we found that the uncertainty is not only related to the Hawking temperature but also to the coefficient of the state. We show the uncertainty versus dilation parameter D and the state parameter \(\alpha \) in Figs. 4 and 5, respectively, based on the left side of the inequality in Eq. (6). In addition, Figs. 4 and 5 correspond to the uncertainty in the physically accessible region I and inaccessible region II, respectively.

The entropic uncertainty is plotted in terms of the dilation parameter D for different values of \(\alpha \) for the physically accessible region I in Fig. 4a. As shown, when \(D\le 0.5\), the entropic uncertainty is small and remains at a stable value that is independent of \(\alpha \). For the region \(D>0.5\), the uncertainty starts to increase with an increase in D. That is to say that an increase in the Hawking temperature will cause an increase in uncertainty in these situations. Furthermore, Fig. 4b depicts the uncertainty versus \(\alpha ^2\) with different D. In general, a large D will lead to higher uncertainty, which supports the conclusions derived from Fig. 4a. By comparing Figs. 1c and 2c with Figs. 4a and 5a respectively, we find that the uncertainty is anti-correlated with quantum coherence.

Based on the above analysis, we can conclude that the uncertainty in physically accessible region I is sensitive to the Hawking temperature and the uncertainty in the physically inaccessible region II is sensitive to the chosen initial state parameter \(\alpha \) in the current architecture.

5 Conclusion

In conclusion, we investigated quantum coherence, nonlocality, and entropic uncertainty in Garfinkle–Horowitz–Strominger dilation black hole. It has been shown that the Hawking effect degrades both physically accessible nonlocality and physically accessible coherence. In particular, it was shown that the nonlocality can be destroyed by the Hawking temperature while the amount of coherence remains nonzero regardless of the Hawking temperature. In this regard, it was concluded that quantum coherence is more robust against the Hawking effect than nonlocality. Meanwhile, the coherence flows between regions I and II under the influence of Hawking radiation. More importantly, we observed an interesting phenomenon in which the total coherence is conserved for a given initial state. Specifically, the coherences of regions I and II exhibit a tradeoff relationship, and every coherence variation stems from information flows between the physically accessible and inaccessible regions. Regarding the measurement uncertainty, it has been found that the Hawking effect leads to an inflation of the measurement uncertainty in the physically accessible region. In addition, it is worth noting that uncertainty and coherence exhibit anti-correlation characteristics with increasing T. This is because coherence is essentially a sort of nonclassical correlation, and a stronger quantum correlation would lead to a smaller measurement uncertainty. Thus, we have greater coherence and lower uncertainty, and vice versa. In the end, we hope that our investigations could be helpful for simulating the development of relativistic quantum information science.