1 Introduction

Nowadays, cosmology is facing with the most challenging problems regarding accelerated expansion of the universe or dark energy as well as dark mater. The mysterious acceleration of the universe has been supported by the various cosmological observational data [1,2,3,4,5,6,7,8,9]. As these observations are not consistent with the predictions of the Einstein gravity, this theory has generally been amended/modified/generalized, in particular to explain dark energy and dark matter (see, e.g., Refs. [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35] and references therein). For dark energy, numerous attempts have been performed, which explain that the acceleration of the universe could have arisen either from a dark energy component or being due to departure of gravity from general relativity on cosmological scales. In the former approach, dark energy models can be classified in two main categories. The \(\Lambda \)CDM model (in which the universe contains a constant energy density, cold dark matter and ordinary matter) and the scalar field models with a dynamical equation of state, see, e.g., Refs. [36,37,38,39,40,41]. The first category models have some difficulties, such as the cosmological constant problem and the coincidence problem [42,43,44,45,46,47,48]. Some believe that the scalar field models are perhaps better alternatives to the Einstein gravitational theory [49,50,51]. In particular, quintessence is a more general dynamical model in which the energy source of the universe, unlike the cosmological constant, varies in space and time [52,53,54,55,56]. However, if one considers the scalar field coupled to the matter in such theories, then a fifth force and also large violation of the equivalence principle (EP) will arise, whereas these results have not been detected in the solar system tests of gravity. To solve such a problem, the chameleon model and its generalization have been proposed [57,58,59,60,61]. Nevertheless, it should be noted that a large class of scalar field theory dark energy models lower the Hubble constant \(H_{0}\) relative to the \(\Lambda \)CDM model [62, 63].

In the chameleon model, as a scalar-tensor theory model for dark energy, the scalar field couples minimally with geometry and non-minimally with the matter field. It also uses an environment-dependent screening mechanism that, although allows it to deviate from general relativity at large scales, keeps it consistent with the results of that at small scales. Indeed, the scalar field couples to matter with a gravitational strength to acquire a mass-dependent on the background matter density of the environment, which leads its interaction to be effectively short-ranged. Due to such a screening mechanism, the model remains consistent with the tests of gravity on the terrestrial and the solar system scales. The strength of force depends on the amount of matter in the environment [57,58,59, 64,65,66,67,68]. In dense environments, such as on the earth, the force gets weaker whose effects are barely detectable, and hence the theory will be consistent with the experimental and observational tests in the case of EP-violation and fifth force. On the other hand, as the amount of matter decreases, the force becomes stronger. Hence, at empty spaces, the force extends to a powerful range and one expects detecting a fifth force and also the EP-violation. However, despite some controversy, it is believed that the chameleon field may play the role of dark energy causing the cosmic late-time acceleration, see, e.g., Ref. [69] and references therein. In addition, the chameleon model during inflation has also been investigated, see, e.g., Refs. [69,70,71,72,73].

In the present work, we consider such a model and investigate the late-time accelerated expansion of the universe. By applying the typical potential usually used in the context of the chameleon theory in the literature, we set some constraints on the free parameters of the model such as the chameleon coupling constant and the slope of the potential. Moreover, we generalize the geodesic deviation equation (GDE) of the presented chameleon model to probe the acceleration of the universe more instructive and hopefully getting a better view of the cosmic acceleration phase. Practically, the GDE offers a subtle understanding of the structure of spacetime and characterizes the nature of gravitational forces in an invariant procedure. The equation of timelike geodesics in the Einstein frame receives a correction, which is interpreted as the effects of a fifth force and the violation of weak EP [50]. A physical definition of geodesic is expressed as a trajectory of a body that is solely under the influence of gravity, and mathematically, it is defined as a curve that parallel transports its tangent vector. Actually, the existence of a fifth force leads to modifications of the GDE. Indeed, the GDE is one of the most significant equation in gravitation that represents the effects of the curvature in the spacetime and relates the Riemann curvature tensor to the relative acceleration of two adjacent geodesics [74,75,76,77,78,79]. It has also been studied in the contest of modified theories of gravitation, see, e.g., Refs. [30, 80,81,82] and references therein.

The work is organized as follows. In the next section, we introduce the chameleon model and obtain the field equations of motion by taking the variation of the action. The cosmological equations of the chameleon scalar field model are investigated in Sect. 3, where matter-dominated phase and cosmic accelerated phase are studied. In Sect. 4, we investigate the GDE of this model for the timelike and null geodesics within the spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) background and then, attain the corresponding Raychaudhuri equation and the observer area-distance as a measurable physical quantity. At last, we conclude the work in Sect. 5 with the summary of the results.

2 Chameleon scalar field model

We start with the action of the chameleon scalar field model in four dimensions as

$$\begin{aligned} S={S}_\mathrm{EH}+{S}_\mathrm{\phi }+{S}_\mathrm{\phi -m}, \end{aligned}$$
(2.1)

where \({S}_\mathrm{EH}\) is the Einstein-Hilbert action, \({S}_{\phi }\) is the part of minimally coupled scalar field action and \({S}_\mathrm{\phi -m}\) is the action representing coupling between the matter field and the scalar field. More specifically, the action is

$$\begin{aligned} S= & {} \int \mathrm{d}^{4}x\sqrt{-g}\left( \frac{M^{2}_\mathrm{Pl}R}{2}\right) \nonumber \\&-\int \mathrm{d}^{4}x\sqrt{-g}\left[ \frac{1}{2}\partial _{\mu }\phi \, \partial ^{\mu }\phi +V(\phi )\right] \nonumber \\&+\sum _{i}\int \mathrm{d}^{4}x\sqrt{-{\tilde{g}}^{(i)}}{L^{(i)}_\mathrm{m}}\left( {\psi }^{(i)}_\mathrm{m},{\tilde{g}}^{(i)}_{\mu \nu }\right) , \end{aligned}$$
(2.2)

where g is the determinant of the metric, R is the Ricci scalar, \(M_\mathrm{Pl}\equiv (8\pi G)^{-1/2}\approx 10^{27}eV\) is the reduced Planck mass (in the natural units, \(\hbar =1=c\)) and the lower case Greek indices run from zero to three. Also, \(V(\phi )\) is a self-interacting potential, \(\psi ^{(i)}\)s are various matter fields, \({L_\mathrm{m}^{(i)}}\)s are Lagrangians of matter fields, \(\tilde{g}_{\mu \nu }^{(i)}\)s are the matter field metrics that are conformally related to the Einstein frame metric as

$$\begin{aligned} {\tilde{g}}^{(i)}_{\mu \nu }={e}^{ {2\frac{{\beta } _{i}\phi }{M_\mathrm{Pl}}}}{g}_{\mu \nu }, \end{aligned}$$
(2.3)

where \(\beta _{i}\)s are dimensionless constants, which represent different non-minimal couplings between the scalar field \( \phi \) and each matter species. However in this work, we just consider a single matter component, and hence we omit the index i. The scalar potential commonly used for the chameleon model in the literature is the well-known run-away potential

$$\begin{aligned} V\left( \phi \right) = \frac{{{M^{4 + n}}}}{{{\phi ^n}}}, \end{aligned}$$
(2.4)

with M as some mass scale and n as a positive or negative integer constant.

The variation of action (2.2) with respect to the metric tensor \(g_{\mu \nu }\) gives the field equations

$$\begin{aligned} {G_{\mu \nu }} = \frac{1}{M_\mathrm{Pl}^2}\left( T_{\mu \nu }^{(\phi )}+T_{\mu \nu }^{(m)}\right) = \frac{1}{M_\mathrm{Pl}^2}\left( T_{\mu \nu }^{(\phi )}+ {e}^{ {2\frac{{\beta }\phi }{M_\mathrm{Pl}}}}\tilde{T}_{\mu \nu }^{(m)}\right) , \end{aligned}$$
(2.5)

where \( T_{\mu \nu }^{(\phi )} \) is the energy–momentum tensor of the scalar field, namely

$$\begin{aligned} T_{\mu \nu }^{(\phi )} = - \frac{1}{2}{g_{\mu \nu }}{\partial ^\alpha }\phi \, {\partial _\alpha }\phi - {g_{\mu \nu }}V\left( \phi \right) + {\partial _\mu }\phi \, {\partial _\nu }\phi , \end{aligned}$$
(2.6)

and \(\tilde{T}_{\mu \nu }^{(m)}\) is the energy–momentum tensor of matter in the Jordan frame that is conserved within this frame, i.e. \(\widetilde{\nabla }^{\mu } {\tilde{T}{^{(m)}_{\mu \nu }}}=0\), and is defined as

$$\begin{aligned} \tilde{T}_{\mu \nu }^{(m)}=-\frac{2}{\sqrt{-\tilde{g}}}\frac{\left( \delta {\sqrt{-\tilde{g}}}{L_{m}}\right) }{\delta {\tilde{g}}^{\mu \nu }}. \end{aligned}$$
(2.7)

In addition, the variation of action (2.2) with respect to the scalar field gives

$$\begin{aligned} \Box \phi =\frac{{dV\left( \phi \right) }}{{d\phi }}-\frac{{\beta }}{M_\mathrm{Pl}}e^{4\frac{{\beta }\phi }{{M}_\mathrm{Pl}}}{\tilde{g}}^{\mu \nu }{\tilde{T}}_{\mu \nu }^{(m)}, \end{aligned}$$
(2.8)

where \(\Box \equiv \nabla ^{\alpha }\nabla _{\alpha }\) with respect to the metric \(g_{\mu \nu }\). Also, we assume the matter field as a perfect fluid with the same state parameter \(w^{(m)} \) in the both frames. Hence, the trace of the energy–momentum tensor of matter is

$$\begin{aligned} \tilde{T}^{(m)}={\tilde{g}}^{\mu \nu }\tilde{T}_{\mu \nu }^{(m)}=-\left( 1-3w^{(m)}\right) \tilde{\rho }^{(m)}, \end{aligned}$$
(2.9)

and the relation of the matter density in the Einstein frame with the one in the Jordan frame is

$$\begin{aligned} \rho ^{(m)}= e^{4\frac{{\beta }\phi }{M_\mathrm{Pl}}}\tilde{\rho }^{(m)}. \end{aligned}$$
(2.10)

Note that \(\left( 1-3w^{(m)}\right) \rho ^{(m)}=- {g^{\mu \nu }}T_{\mu \nu }^{\left( m \right) } \), where \( T_{\mu \nu }^{\left( m \right) }\) is the energy–momentum tensor of matter in the Einstein frame that is not covariantly conserved, i.e. \( {\nabla ^\mu }T_{\mu \nu }^{\left( m \right) } \ne 0 \). Moreover, for more mathematical facilities, we can define a matter density as a quantity independent of the chameleon scalar field \(\phi \), which is not a physical matter density but is a conserved quantity within the Einstein frame as [69]

$$\begin{aligned} \rho (t)\equiv e^{3\left( 1+w^{(m)}\right) \frac{{\beta }\phi }{M_\mathrm{Pl}}}\tilde{\rho }^{(m)}, \end{aligned}$$
(2.11)

and in turn obtain \( \rho ^{(m)}=\rho \, e^{\left( 1-3w^{(m)}\right) \frac{\beta \phi }{M_\mathrm{Pl}}} \). Furthermore, substituting relation (2.11) into Eq. (2.8) indicates that the scalar field is dynamically governed by an effective potential, i.e.

$$\begin{aligned} \Box \phi =\frac{{d{V_\mathrm{eff}}\left( \phi \right) }}{{d\phi }}, \end{aligned}$$
(2.12)

with

$$\begin{aligned} {V}_\mathrm{eff}(\phi )\equiv V(\phi )+\rho \, e^{\left( 1-3w^{(m)}\right) \frac{\beta \phi }{M_\mathrm{Pl}}}=V(\phi )+\rho ^{(m)} \end{aligned}$$
(2.13)

that depends on the background matter density \(\rho ^{(m)}\) of the environment.

3 Cosmological equations

In this section, we investigate the cosmological equations of the chameleon scalar field model by considering the spatially flat FLRW metric in the Einstein frame as

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}(t)\left( dx^{2}+dy^{2}+dz^{2}\right) , \end{aligned}$$
(3.1)

where t is the cosmic time, a(t) is the scale factor describing the cosmological expansion, and in turn \(\tilde{a}(t)=a(t)\exp (\beta \phi /M_\mathrm{Pl})\) is the corresponding one within the Jordan frame. Also, by accepting the homogeneity and isotropy, and the scalar field being just a function of the cosmic time, then by metric (3.1), the field equation (2.12) reads

$$\begin{aligned} \ddot{\phi }+3H\dot{\phi }+\frac{{d{V_\mathrm{eff}}\left( \phi \right) }}{{d\phi }} = 0, \end{aligned}$$
(3.2)

where \(H(t)\equiv \dot{a}/a\) is the Hubble parameter and dot denotes the derivative with respect to t. Moreover, by inserting metric (3.1) into Eq. (2.5), it yields the Friedmann-like equation as

$$\begin{aligned} {H^2} = \frac{1}{3{M_\mathrm{Pl}^2}}\left[ {\frac{1}{2}{{\dot{\phi }}^2} + V\left( \phi \right) + \rho \, {e^{\left( {1 - 3w^{(m)}} \right) \frac{{\beta \phi }}{{{M_\mathrm{Pl}}}}}}} \right] \end{aligned}$$
(3.3)

and the generalized Raychaudhuri equation as

$$\begin{aligned} \frac{{\ddot{a}}}{a}\! =\! - \frac{1}{{3M_\mathrm{Pl}^2}}\! \left[ \! {{{\dot{\phi }}^2}\! -\! V\left( \phi \right) \! +\! \left( \! {\frac{{1\! +\! 3w^{(m)}}}{2}}\! \right) \!\rho {e^{\left( {1 - 3w^{(m)}} \right) \frac{{\beta \phi }}{{{M_\mathrm{Pl}}}}}}}\! \right] \!. \end{aligned}$$
(3.4)

On the other hand, from relation (2.6), one obtains the energy density and the pressure density of the chameleon scalar field as

$$\begin{aligned} {\rho ^{\left( \phi \right) }} = \frac{1}{2}{\dot{\phi }^2} + V\left( \phi \right) \end{aligned}$$
(3.5)

and

$$\begin{aligned} {p^{\left( \phi \right) }} = \frac{1}{2}{\dot{\phi }^2} - V\left( \phi \right) . \end{aligned}$$
(3.6)

Then, using Eqs. (3.5) and (3.6), Eqs. (3.3) and (3.4) read as

$$\begin{aligned} {H^2} = \frac{1}{{3M_\mathrm{Pl}^2}}\left( {{\rho ^{\left( \phi \right) }} + {\rho ^{\left( m \right) }}} \right) = \frac{1}{{3M_\mathrm{Pl}^2}} {\rho ^{\left( \mathrm{tot} \right) }} \end{aligned}$$
(3.7)

and

$$\begin{aligned} \frac{{\ddot{a}}}{a}= & {} - \frac{1}{{6M_\mathrm{Pl}^2}}\Big [ {{\rho ^{\left( \phi \right) }} + {\rho ^{\left( m \right) }} + 3\left( {{p^{\left( \phi \right) }} + {p^{\left( m \right) }}} \right) } \Big ]\\= & {} - \frac{1}{{6M_\mathrm{Pl}^2}}\left( {{\rho ^{\left( \mathrm{tot} \right) }} + 3{p^{\left( \mathrm{tot} \right) }}} \right) , \end{aligned}$$
(3.8)

where \(\rho ^{(\mathrm tot)} \equiv \rho ^{(\phi )}+\rho ^{(m)}\) and \(p^{(\mathrm tot)} \equiv p^{(\phi )}+p^{(m)}\) are considered as the total energy density and total pressure density, respectively. Also, by employing Eqs. (3.2), (3.5) and (3.6), we obtain

$$\begin{aligned} \dot{\rho }^{(\phi )}+3H\left( \rho ^{(\phi )}+p^{(\phi )}\right) =-X, \end{aligned}$$
(3.9)

and by the continuity equation for \(\rho (t)\) in the Einstein frame, i.e. \(\dot{\rho }+3H\left( 1+w^{(m)}\right) \rho =0\), we get

$$\begin{aligned} \dot{\rho }^{(m)}+3H\left( \rho ^{(m)}+p^{(m)}\right) =X, \end{aligned}$$
(3.10)

and in turn

$$\begin{aligned} \dot{\rho }^{(\mathrm tot)}+3H\left( \rho ^{(\mathrm tot)}+p^{(\mathrm tot)}\right) =0, \end{aligned}$$
(3.11)

where

$$\begin{aligned} X\equiv \left( 1-3w^{(m)}\right) \frac{\beta \dot{\phi }}{M_\mathrm{Pl}}\rho e^{\left( 1-3w^{(m)}\right) \frac{\beta \phi }{M_\mathrm{Pl}}}. \end{aligned}$$
(3.12)

The X term acts as an interacting term among the scalar and matter fields, which manifests itself as a deviation term into the geodesic equation and is interpreted as some kind of internal force among those. That is, due to the coupling between the scalar and matter fields, the energy–momentum tensor of each one is not conserved. Nevertheless, the above relations indicate that, although the energy density is not separately conserved (and conservation equations of the internal parts are not independent), its total is conserved as expected.

In the analysis of this work, we investigate the chameleon scalar field during late-time of the universe. To proceed, we assume that the evaluation of the chameleon scalar field with respect to time being as the corresponding one considered in Ref. [71], namelyFootnote 1

$$\begin{aligned} \dot{\phi } = \frac{{3(1+w^{(m)}){M_\mathrm{Pl}}}}{\beta (1-3w^{(m)})}H. \end{aligned}$$
(3.13)

Also, we plausibly assume that the matter density is a non-relativistic perfect fluid, i.e. dust matter with \(w^{(m)}=0\), and hence, relation (3.13) reads

$$\begin{aligned} \dot{\phi } = \frac{{3{M_\mathrm{Pl}}}}{\beta }H. \end{aligned}$$
(3.14)

Furthermore, we prefer to obtain the behavior of the chameleon scalar field with respect to the redshift instead of time. For this purpose, with the relationFootnote 2\(1+z=a_0/a\), we use the simple differential operator

$$\begin{aligned} \frac{d}{{dt}} = \frac{{da}}{{dt}}\frac{{dz}}{{da}}\frac{d}{{dz}} = - \left( {1 + z} \right) H\frac{d}{{dz}}. \end{aligned}$$
(3.15)

Thus, while employing relation (3.15), relation (3.14) gives

$$\begin{aligned} \phi \left( z \right) = {\phi _0} - \frac{{3{M_\mathrm{Pl}}}}{\beta }\ln \left( {1 + z} \right) , \end{aligned}$$
(3.16)

where \( {\phi _0} \) is an integration constant that is equal to \( \phi \left( z \right) \) for \(z = 0\).

Now, to obtain the total (or, the effective) state parameter of this chameleon model, we start by the dimensionless density parameters defined as

$$\begin{aligned} {\Omega _{\dot{\phi }}}\equiv \frac{{{{\dot{\phi }}^2}}}{2{\rho _0^\mathrm{(crit)}}}, \quad \ \ {\Omega _{V}} \equiv \frac{V(\phi )}{{\rho _0^\mathrm{(crit)}}} \quad \ \mathrm{and} \quad \ {\Omega _m} \equiv \frac{\rho ^{(m)}}{{\rho _0^\mathrm{(crit)}}}, \end{aligned}$$
(3.17)

where \( \rho _0^\mathrm{(crit)} \equiv 3H_0^2M_\mathrm{Pl}^2 \) is the critical density of the universe at the present time. Hence, in general case, Eq. (3.7) can be rewritten as

$$\begin{aligned} {H^2} = H_0^2\left( {{\Omega _{\dot{\phi }}}+{\Omega _V }+{\Omega _m}} \right) , \end{aligned}$$
(3.18)

and the total state parameter of this model is

$$\begin{aligned} {w^{\left( \mathrm{tot} \right) }} \equiv \frac{{{p^{\left( \mathrm{tot} \right) }}}}{{{\rho ^{\left( \mathrm{tot} \right) }}}} = \frac{{{\Omega _{\dot{\phi }}} - {\Omega _V}}}{{{\Omega _{\dot{\phi }}} + {\Omega _V} + {\Omega _m}}}, \end{aligned}$$
(3.19)

and equivalently

$$\begin{aligned} {w^{\left( \mathrm{tot} \right) }} = \frac{{H_0^2}}{{{H^2}}} \left( {{\Omega _{\dot{\phi }}} - {\Omega _V}} \right) . \end{aligned}$$
(3.20)

Substituting relation (3.14), for the case of \(w^{(m)}=0\), into the first definition (3.17) leads to

$$\begin{aligned} {\Omega _{\dot{\phi }}} =\frac{3{H^2}}{2{\beta ^2}H_0^2} \end{aligned}$$
(3.21)

and then, inserting it into relation (3.20) yields

$$\begin{aligned} {w^{\left( \mathrm{tot} \right) }} = \frac{3}{{2{\beta ^2}}} - \frac{{H_0^2}}{{{H^2}}}{\Omega _V}. \end{aligned}$$
(3.22)

At this stage, we manage to get \( {\Omega _V} \) and \( H^{2} \) in terms of z. For this purpose, inserting function (3.16) into (2.4) gives

$$\begin{aligned} {\Omega _V} = {\Omega _{\left( 0 \right) V}}{\left( {\frac{{{\phi _0}}}{\phi }} \right) ^n} = {\Omega _{\left( 0 \right) V}}{\left[ {1 - \frac{{3{M_\mathrm{Pl}}}}{{\beta {\phi _0}}}\ln \left( {1 + z} \right) } \right] ^{ - n}}, \end{aligned}$$
(3.23)

where

$$\begin{aligned} {\Omega _{\left( 0 \right) V}} = \frac{{V\left( {{\phi _0}} \right) }}{{\rho _0^\mathrm{(crit)}}} = \frac{1}{{\rho _0^\mathrm{(crit)}}}\left( {\frac{{{M^{4 + n}}}}{{\phi _0^n}}} \right) . \end{aligned}$$
(3.24)

Also, for the conserved matter within the Jordan frameFootnote 3 with \(w^{(m)}=0\), we have \({\tilde{\rho }^{\left( m \right) }} = \tilde{\rho }_0^{\left( m \right) } {\left( {1 + z} \right) ^3} \), hence within the Einstein frame, considering function (3.16) while using (2.10), we obtain

$$\begin{aligned} {\Omega _m} = {\tilde{\Omega }_{\left( 0 \right) m}} \, {e^{4\frac{{\beta {\phi _0}}}{{{M_\mathrm{Pl}}}}}}{\left( {1 + z} \right) ^{ - 9}}, \end{aligned}$$
(3.25)

where \( {\tilde{\Omega }_{\left( 0 \right) m}}\equiv \tilde{\rho }_0^{\left( m \right) }/\rho _0^\mathrm{(crit)} \). Then, using relations (3.21), (3.23) and (3.25), Eq. (3.18) reads

$$\begin{aligned} H^2= & {} \frac{H_0^2}{1 - \frac{3}{2\beta ^2}} \Bigg \{ \Omega _{(0)V}\left[ 1 - \frac{3M_\mathrm{Pl}}{\beta \phi _0}\ln (1 + z) \right] ^{- n}\\&+ \tilde{\Omega }_{( 0 )m} \, e^{4\frac{\beta \phi _0}{M_\mathrm{Pl}}}( 1 + z)^{-9}\Bigg \}, \end{aligned}$$
(3.26)

for when \(\beta \ne \pm \sqrt{3/2}\). Finally, substituting relation (3.23) and Eq. (3.26) into relation (3.22) gives the total state parameter for non-relativistic perfect fluids, in the case of dust matters, in terms of the redshift as

$$\begin{aligned} {w^{\left( \mathrm{tot} \right) }}= & {} \frac{3}{{2{\beta ^2}}} - \left( {1 - \frac{3}{{2{\beta ^2}}}} \right) \Bigg \{ 1 + \frac{{{\tilde{\Omega }_{\left( 0 \right) m}} \, {e^{4\beta {\phi _0}/{M_\mathrm{Pl}}}} }}{{{\Omega _{\left( 0\right) V}} {\left( {1 + z} \right) ^{ 9}} }}\\&\times {{\left[ {1 - \frac{{3{M_\mathrm{Pl}}}}{{\beta {\phi _0}}}\ln \left( {1 + z} \right) } \right] }^n}\Bigg \}^{-1}. \end{aligned}$$
(3.27)

Meanwhile, let us also employ the deceleration parameter, which is a dimensionless measure of the cosmic acceleration of the expansion of the universe, defined as \( q \equiv - \ddot{a}a/{\dot{a}^2} = - \ddot{a}/(a{H^2}) \). In this regard, inserting Eqs. (3.7) and (3.8) into the definition of q and using the definition of the total state parameter, leads to

$$\begin{aligned} q = \frac{{1 + 3{w^{\left( \mathrm{tot} \right) }}}}{2}. \end{aligned}$$
(3.28)

Obviously, if \( q>0 \), then the expansion of the universe will be a decelerated one, and if \( q<0 \), then it will be an accelerated one. The transition point from the deceleration to the acceleration phase is when \( q=0 \), and in this case, relation (3.28) shows that it corresponds to \(w_\mathrm{trans.}^{\left( \mathrm{tot} \right) }=-1/3 \), as expected. Hence, in general case, using relation (3.20), it obviously gives \(\left[ \Omega _{\dot{\phi }}- \Omega _V=-H^2/(3H_0^2)\right] _\mathrm{trans.}\), and in turn, \(\left[ p^{(\phi )}=-H^2M^2_\mathrm{Pl}\right] _\mathrm{trans.}\). Also, for the case of dust matters with \(w^{(m)}=0\), using relation (3.22), it yields \(\left[ V=H^2M^2_\mathrm{Pl}(9+2\beta ^2)/(2\beta ^2)\right] _\mathrm{trans.}\). We pursue this issue to discuss about the transition redshift in the next section.

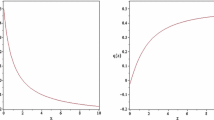
We have plotted relation (3.27) in Fig. 1 to obtain the allowed values of the n parameter in this model for \( \beta =3.7 \times {10^2} \) and \( \beta =1 \) with initial value \( {\phi _0} = {\beta ^{ - 1}} \) (regardless of units) as assumptions. Note that, the value \( \beta =3.7 \times {10^2} \) is an upper bound on this parameter in the chameleon model that is consistent with the experimental constrain obtained in Ref. [83].

Fig. 1
figure 1

The plot of the total state parameter with assumptions \( { \tilde{\Omega }}_{\left( 0 \right) m}/\Omega _{\left( 0 \right) V} \simeq 3/7\), \( {M_\mathrm{Pl}}=1 \) and, regardless of units, \({\phi _0} = {\beta ^{ - 1}} \). Besides, the top and bottom diagrams have been plotted with \( \beta =3.7 \times {10^2} \) and \( \beta = 1 \), respectively

Full size image

The top diagram in Fig. 1 indicates that, for the case \( \beta =3.7 \times {10^2} \) with \( n>0 \), the total state parameter in the present time, i.e. at \( z=0 \), starts to increase from the value less than \( -1/3 \) with increasing redshift, which is a suitable model for the evolution of the universe. In addition, the presence of constraint \(n>0\) is consistent with the inverse power-law potentials first considered in the original suggestion for the chameleon model [57]. Whereas, the bottom diagram in this figure, for \(-10<n<10\) and \(0<z<10\), shows unacceptable results for the case \( \beta = 1 \) because, at the present time, one expects the total state parameter to be less than \( -1/3\). However, with \( n<0 \), the top diagram in Fig. 1 also illustrates not a true model because by increasing redshift from \( z=0 \) up to \( z=10 \), the total state parameter does not increase.

3.1 Matter-dominated phase

In the matter-dominated phase of the universe, i.e. under assumption \({\rho ^{\left( m \right) }} \gg {\rho ^{\left( \phi \right) }} \) that corresponds to \( {\Omega _m} \gg {\Omega _{\dot{\phi }}}+{\Omega _V} \), Eq. (3.18) leads to

$$\begin{aligned} {H^2} \simeq H_0^2 \Omega {_m} \end{aligned}$$
(3.29)

and in turn, the state parameter from relation (3.20) gives

$$\begin{aligned} {w^{\left( \mathrm{tot} \right) }} \simeq \frac{{{\Omega _{\dot{\phi }}} - {\Omega _V}}}{{{\Omega _m}}}. \end{aligned}$$
(3.30)

In situations that stillFootnote 4\( {\Omega _m} \gg {\Omega _{\dot{\phi }}}-{\Omega _V} \), then \(w^{\left( \mathrm{tot} \right) }\simeq 0\), which is consistent with the expected value in the matter-dominated epoch of the universe.

3.2 Cosmic accelerated phase

Since the dust matter density decreases over the time, one can plausibly assume the chameleon scalar field-dominated phase, i.e. \( {\rho ^{\left( \phi \right) }} \gg {\rho ^{\left( m \right) }} \), at the late-time universe. Under such an assumption, Eq. (3.18) leads to

$$\begin{aligned} {H^2} \simeq H_0^2\left( {{\Omega _{\dot{\phi }}} + {\Omega _V}} \right) . \end{aligned}$$
(3.31)

Then, inserting Eq. (3.31) into relation (3.22) gives the state parameter at the late-time accelerating phase to be

$$\begin{aligned} {w^{\left( \mathrm{tot} \right) }} \simeq \frac{3}{{2{\beta ^2}}} - \frac{{{\Omega _V}}}{{{\Omega _{\dot{\phi }}} + {\Omega _V}}}. \end{aligned}$$
(3.32)

In this phase of the universe, if we consider \( \beta =1 \) while inserting Eq. (3.31) into relation (3.21) that yields \( {\Omega _{\dot{\phi }}} = -3{\Omega _V} \), then relation (3.32) will give \( {w^{\left( \mathrm{tot} \right) }}=2 \) that is inconsistent with the observations at the late-time universe. Whereas with the value \( \beta =3.7 \times {10^2} \), relation (3.21), while inserting Eq. (3.31) into it, renders \( {\Omega _{\dot{\phi }}} \simeq {10^{ - 5}}\,\Omega _V \), and in turn in this case for dust matters, relation (3.32) gives

$$\begin{aligned} {w^{\left( \mathrm{tot} \right) }} \simeq \frac{3}{{2{\beta ^2}}} - 1 \simeq {10^{ - 5}} - 1 \simeq - 1. \end{aligned}$$
(3.33)

Accordingly, the analysis shows that in order to have a viable chameleon model with \(w^{(m)}=0\) during the acceleration phase of the universe at the late-time universe, the coupling constant between the matter and scalar fields should be much greater than unity. In this respect, it is worth mentioning that, although Weltman and Khoury, in their original suggestion for the chameleon model, considered the possibility of coupling the scalar field to the matter field with the gravitational strength of the order of unity, Mota and Shaw showed that the scalar field theories with strongly coupling are viable due to the non-linearity effects of the theory [84, 85].

4 Geodesic deviation equation

The Einstein field equations specify how the curvature depends on the matter sources, where one can obtain the consequences of the spacetime curvature through the GDE. Formulating the cosmological equation in the GDE form would be a model independent way. Hence, in this section, in order to probe the acceleration of the universe at the late-time more instructive, we derive the GDE in the presented chameleon model. For this purpose, we start from the general expression for the GDE [86, 87]

$$\begin{aligned} \frac{{{D^2}{\eta ^\mu }}}{{D{\nu ^2}}} = R^\mu {}_{\nu \alpha \beta } {V^\nu }{V^\alpha }{\eta ^\beta } - \frac{\beta }{{{M_\mathrm{Pl}}}}{\eta ^\alpha }{\nabla _\alpha }\left( {{\partial ^\mu }\phi } \right) , \end{aligned}$$
(4.1)

with the parametric \(x^\mu (s,\nu )\), where s labels distinct geodesics, the parameter \( \nu \) is an affine parameter along the geodesic and \({\eta ^\mu } = \partial x^\mu /\partial s \) is the orthogonal deviation vector of two adjacent geodesics. Also, \( D/D\nu \) is the covariant derivative along the curve and the normalized vector field \( {V^\mu } = \partial {x^\mu }/\partial \nu \) is tangent to the geodesics. The second term, which appears in the right side of this equation, illustrates that, in general, there is a fifth force mediated by \( \phi \), which acts on any massive test particle. However, as we have assumed that the universe is isotropic and homogeneous, only the time derivatives of the scalar field do not vanish, and also in the comoving frame, one has \( \eta ^{0}=0 \), hence in this case, Eq. (4.1) reads [77, 82]

$$\begin{aligned} \frac{{{D^2}{\eta ^\mu }}}{{D{\nu ^2}}} = R^\mu {}_{\nu \alpha \beta } {V^\nu }{V^\alpha }{\eta ^\beta }. \end{aligned}$$
(4.2)

Now, to attain the relation between the geometrical properties of the spacetime with the field equations governed from the chameleon model, we use the expression of the Riemann tensor in 4-dimensions, namely

$$\begin{aligned} {R_{\mu \nu \alpha \beta }}= & {} {C_{\mu \nu \alpha \beta }} + \frac{1}{2} \Big ( {g_{\mu \alpha }}{R_{\nu \beta }} - {g_{\mu \beta }}{R_{\nu \alpha }} + {g_{\nu \beta }}{R_{\mu \alpha }}\\&-{g_{\nu \alpha }}{R_{\mu \beta }} \Big ) - \frac{1}{6}R\Big ( {{g_{\mu \alpha }}{g_{\nu \beta }} - {g_{\mu \beta }}{g_{\nu \alpha }}} \Big ), \end{aligned}$$
(4.3)

and note that, in the case of the FLRW metric, the corresponding Weyl tensor \( {C_{\mu \nu \alpha \beta }} \) is zero. In addition, for \(w^{(m)}=0\) with \( T_{\mu \nu }^{(m)} = {\rho ^{(m)}}{u_\mu }{u_\nu }=\left( \rho \, {e^{\beta \phi /{M_\mathrm{Pl}}}}\right) u_\mu {u_\nu } \), where \( {u^\mu } \) is the comoving unit velocity vector to the matter flow, one easily obtains the Ricci tensor from Eq. (2.5) as

$$\begin{aligned} {R_{\mu \nu }}= & {} \frac{1}{{M_\mathrm{Pl}^2}}\Big [ \frac{1}{2}{g_{\mu \nu }}{{\dot{\phi }}^2} - {g_{\mu \nu }} V(\phi ) + {\partial _\mu }\phi \, {\partial _\nu }\phi \\&+ \rho \, {e^{^{\beta \phi /{M_\mathrm{Pl}}}}}{u_\mu }{u_\nu }\Big ] + \frac{1}{2}{g_{\mu \nu }}R, \end{aligned}$$
(4.4)

and in turn with \( u_{\mu } u^{\mu }=-1 \), the Ricci scalar as

$$\begin{aligned} R = \frac{1}{{M_\mathrm{Pl}^2}}\left[ { - {{\dot{\phi }}^2} + 4V(\phi ) + \rho \, {e^{\beta \phi /{M_\mathrm{Pl}}}}} \right] . \end{aligned}$$
(4.5)

Inserting these relations into relation (4.3) gives

$$\begin{aligned} {R_{\mu \nu \alpha \beta }}= & {} \frac{1}{{2M_\mathrm{Pl}^2}} \Big ( {g_{\mu \alpha }}{\partial _\nu }\phi \, {\partial _\beta }\phi - {g_{\mu \beta }}{\partial _\nu }\phi \, {\partial _\alpha }\phi \nonumber \\&+ {g_{\nu \beta }} {\partial _\mu }\phi \, {\partial _\alpha }\phi - {g_{\nu \alpha }}{\partial _\mu }\phi \, {\partial _\beta }\phi \Big ) \nonumber \\&+ \frac{{ \rho \, {e^{\beta \phi /{M_\mathrm{Pl}}}}}}{{2M_\mathrm{Pl}^2}} \Big ( {g_{\mu \alpha }}{u_\nu }{u_\beta } - {g_{\mu \beta }}{u_\nu }{u_\alpha } \nonumber \\&+ {g_{\nu \beta }}{u_\mu }{u_\alpha } - {g_{\nu \alpha }}{u_\mu }{u_\beta } \Big ) \nonumber \\&+ \frac{1}{{3M_\mathrm{Pl}^2}}\Big [ {\frac{1}{2}{{\dot{\phi }}^2} + V \left( \phi \right) + \rho \, {e^{\beta \phi /{M_\mathrm{Pl}}}}}\Big ] \\&\times \Big ( {{g_{\mu \alpha }}{g_{\nu \beta }} - {g_{\mu \beta }}{g_{\nu \alpha }}} \Big ), \end{aligned}$$
(4.6)

and then, under conditions \( {\eta ^0 }=0 \) in the comoving frame and \({\eta _\mu }{u^\mu } = 0 = {\eta _\mu }{V^\mu } \), we obtain

$$\begin{aligned}&R{^\mu }_{\nu \alpha \beta } {V^\nu }{V^\alpha }{\eta ^\beta }\nonumber \\&\quad = -\frac{1}{{2M_\mathrm{Pl}^2}} \Big [ {{\left( {{V^\nu }{\partial _\nu }\phi } \right) }^2} + \rho \, {e^{\beta \phi /{M_\mathrm{Pl}}}}{{\left( {{u_\nu }{V^\nu }} \right) }^2}\Big ]{\eta ^\mu } \nonumber \\&\qquad -\frac{1}{3M_\mathrm{Pl}^2} \Big [ {\frac{1}{2}{{\dot{\phi }}^2} + V \left( \phi \right) + \rho \, {e^{\beta \phi /{M_\mathrm{Pl}}}}} \Big ] {V^\nu }{V_\nu } {\eta ^\mu }. \end{aligned}$$
(4.7)

Accordingly, by employing the total energy \( E=-u^{\mu }V_{\mu } \), \(\varepsilon \equiv {V^\mu }{V_\mu } \), relation (4.5) and the definitions \(\rho ^{(\mathrm tot)} \) and \( p^{(\mathrm tot)} \) for \(w^{(m)}=0\) into relation (4.7), Eq. (4.2) reads

$$\begin{aligned}&\frac{{{D^2}{\eta ^\mu }}}{{D{\nu ^2}}}+ \frac{1}{{2M_\mathrm{Pl}^2}} \Big [{\left( {\dot{\phi }{V^0}} \right) ^2} + {\rho ^{\left( m \right) }}{E^2} \nonumber \\&\quad \qquad + \frac{\varepsilon }{3}\Big ( {{\rho ^{\left( \mathrm{tot} \right) }} + 3{p^{\left( \mathrm{tot} \right) }} + M_\mathrm{Pl}^2R} \Big ) \Big ]{\eta ^\mu } = 0. \end{aligned}$$
(4.8)

The four-velocity of FLRW comoving observers is \( u^\mu =(1,0,0,0) \), hence \( E=V^0 \), and finally the GDE for the presented chameleon model for dust matters with \(w^{(m)}=0\) is

$$\begin{aligned}&\frac{{{D^2}{\eta ^\mu }}}{{D{\nu ^2}}} + \frac{1}{{2M_\mathrm{Pl}^2}}\Big [ {E^2} \left( {{\rho ^{\left( \mathrm{tot} \right) }} + {p^{\left( \mathrm{tot} \right) }}} \right) \nonumber \\&\qquad \quad + \frac{\varepsilon }{3}\left( {{\rho ^{\left( \mathrm{tot} \right) }} + 3{p^{\left( \mathrm{tot} \right) }} + M_\mathrm{Pl}^2R} \right) \Big ]{\eta ^\mu } = 0. \end{aligned}$$
(4.9)

4.1 GDE for timelike vector fields

For timelike vector fields corresponded to the comoving observers within the FLRW background, the affine parameter \( \nu \) is actually the proper time t. Hence in this case, \( \varepsilon =-1 \), \( E=1 \) and GDE (4.9) reads

$$\begin{aligned} \frac{{{D^2}{\eta ^\mu }}}{{D{t^2}}} + \frac{1}{{6M_\mathrm{Pl}^2}}\left( {2{\rho ^{\left( \mathrm{tot} \right) }} - M_\mathrm{Pl}^2R} \right) {\eta ^\mu } = 0, \end{aligned}$$
(4.10)

which in turn, by substituting \(\rho ^{\left( \mathrm{tot} \right) }\) and relation (4.5), in the case of dust matters, we obtain

$$\begin{aligned} \frac{{{D^2}{\eta ^\mu }}}{{D{t ^2}}} + \frac{1}{{6M_\mathrm{Pl}^2}}\left( {2{{\dot{\phi }}^2} - 2V\left( \phi \right) + \rho \, {e^{\beta \phi /{M_\mathrm{Pl}}}}} \right) {\eta ^\mu } = 0. \end{aligned}$$
(4.11)

On the other hand, with respect to the comoving tetrad frame, the deviation vector can be rewritten as \( {\eta ^\mu } = a\left( t \right) {e^\mu } \), and in addition, due to the isotropy of the spacetime, one has

$$\begin{aligned} \frac{{D{e^\mu }}}{{Dt}} = 0. \end{aligned}$$
(4.12)

Therefore, Eq. (4.11) becomes

$$\begin{aligned} \frac{{\ddot{a}}}{a} = - \frac{1}{{6M_\mathrm{Pl}^2}}\left( {2{{\dot{\phi }}^2} - 2V\left( \phi \right) + \rho \, {e^{\beta \phi /{M_\mathrm{Pl}}}}} \right) , \end{aligned}$$
(4.13)

which is a particular case of the Raychaudhuri dynamical Eq. (3.4) for \(w^{(m)}=0\), as expected to be true even for any value of it. Clearly, Eq. (4.11) illustrates that in order to have an accelerated expansion of the universe, two adjacent geodesics should recede from each other, i.e. \( {D^2 \eta ^\mu } / Dt^2 >0 \), that corresponds to \({\ddot{a}}>0 \) in Eq. (4.13).

In the following, we proceed to obtain the value of the transition redshift from the deceleration to the acceleration phase of the universe in the chameleon model for dust matters (i.e., \(w^{(m)}=0\)) with a strong coupling. For this purpose, as the transition point is when \( {\ddot{a}}=0 \), thus according to Eq. (4.13), it occurs when

$$\begin{aligned} \left[ {\Omega _{\dot{\phi }}} = \frac{\Omega _V}{2} - \frac{\Omega _m}{4}\right] _\mathrm{trans.}. \end{aligned}$$
(4.14)

By inserting relation (4.14) into Eq. (3.18), it gives

$$\begin{aligned} \left[ {H^2} = \frac{3}{2}H_0^2\left( {{\Omega _V} + \frac{{{\Omega _m}}}{2}} \right) \right] _\mathrm{trans.}, \end{aligned}$$
(4.15)

and in turn, relation (3.22) reads

$$\begin{aligned} \left[ {w^{\left( \mathrm{tot} \right) }} = \frac{3}{{2{\beta ^2}}} - \frac{4}{{6 + 3\Omega _m/\Omega _V}}\right] _\mathrm{trans.}. \end{aligned}$$
(4.16)

On the other hand, as at the transition point \(w_\mathrm{trans.}^{\left( \mathrm{tot} \right) }=-1/3\), hence with the strong coupling \( \beta =3.7 \times {10^2} \), one approximately obtainsFootnote 5\(\left[ \Omega _m/\Omega _V\right] _\mathrm{trans.}\simeq 2\). By substituting relations (3.23) and (3.25) into this result, we achieve the constraint

$$\begin{aligned} \frac{{\tilde{\Omega }}_{\left( 0 \right) m} \, e^{4\beta \phi _0/M_\mathrm{Pl}}}{{{\Omega _{\left( 0 \right) V}} \, {{\left( {1 + z_\mathrm{trans.}} \right) }^9}}} {\left[ {1 - \frac{{3{M_\mathrm{Pl}}}}{{\beta {\phi _0}}}\ln \left( {1 + z_\mathrm{trans.}} \right) } \right] ^n}\simeq 2. \end{aligned}$$
(4.17)

Now, with assumptions \( \beta =3.7 \times {10^2} \), \({ \tilde{\Omega }}_{\left( 0 \right) m}/\Omega _{\left( 0 \right) V} \simeq 3/7\), \({M_\mathrm{Pl}}=1 \) and (regardless of units) \({\phi _0} = {\beta ^{ - 1}} \), we can attain the transition redshift in the chameleon model. Indeed, Eq. (4.17) gives the value of the transition redshiftFootnote 6 to be \( z_\mathrm{trans.} \simeq 0.202\) with \( n=1 \), \( z_\mathrm{trans.} \simeq 0.157\) with \( n=2 \), \( z_\mathrm{trans.} \simeq 0.097\) with \( n=5 \), and \( z_\mathrm{trans.} \simeq 0.060\) with \( n=10 \). These obtained values are less than the corresponding value of the \( \Lambda \mathrm CDM \) model.Footnote 7 Also, in Ref. [30], the corresponding value obtained in the f(R, T) gravity model is \( z_\mathrm{trans.} =0.11 \). Hence, the obtained results indicate that the coupling between the matter field and the scalar field in the chameleon model (and also between the matter field and geometry in the f(R, T) gravity model) leads to have the matter-dominated phase ending later than a model without considering such coupling.

It is worth noting that the chameleon theory, due to the non-minimal coupling between the matter and scalar field, has led to an additional force. Indeed, the equation of timelike geodesics shows such a fifth force by receiving an amendment in the Einstein frame. In other words, the GDE shows that, although a freely falling particle appears to be at rest in a comoving frame falling with the particle, a pair of nearby freely falling particles indicates a relative motion that can reveal the presence of a gravitational field to an observer that falls with those.

4.2 GDE for null vector fields

In this subsection, we investigate the past-directed null vector fields. With the FLRW metric, for null vector fields, one has \( \varepsilon = 0 \). Also, by considering \({\eta ^\mu } = \eta \, {e^\mu } \) and using a parallelly propagated and aligned coordinate basis, we have \( D{e^\mu }/D\nu = {V^\alpha }{\nabla _\alpha }{e^\mu } = 0 \), and hence GDE (4.9) (for dust matters) reduces to

$$\begin{aligned} \frac{{{d^2}\eta }}{{d{\nu ^2}}} + \frac{1}{{2M_\mathrm{Pl}^2}}\left( {{\rho ^{\left( \mathrm{tot} \right) }} + {p^{\left( \mathrm{tot} \right) }}} \right) {E^2}\eta = 0, \end{aligned}$$
(4.18)

and actually, using definitions \(\rho ^{(\mathrm{tot})}\) and \(p^{(\mathrm{tot})}\) for \(w^{(m)}=0\), it reads

$$\begin{aligned} \frac{{{d^2}\eta }}{{d{\nu ^2}}} + \frac{1}{{2M_\mathrm{Pl}^2}}\left( {{{\dot{\phi }}^2} + \rho \, {e^{\frac{{\beta \phi }}{{{M_\mathrm{Pl}}}}}}} \right) {E^2}\eta = 0. \end{aligned}$$
(4.19)

Regarding the focusing condition mentioned in Refs. [78, 79], all the past-directed null geodesics from Eq. (4.18) will experience focusing if the condition \( {\rho ^{\left( \mathrm{tot} \right) }}+{p ^{\left( \mathrm{tot} \right) }}>0 \) is met. For the chameleon model in this case, this condition is actually

$$\begin{aligned} {{{\dot{\phi }}^2} + \rho {e^{\frac{{\beta \phi }}{{{M_\mathrm{Pl}}}}}}}>0, \end{aligned}$$
(4.20)

which, as the density of matter is always positive, is confirmed.

In continuation, it is more suitable to write the GDE for null vector fields as a function of the redshift to obtain the observer area-distance in the chameleon model. To perform this task, we start from the differential operator

$$\begin{aligned} \frac{d}{{d\nu }} = \frac{{dz}}{{d\nu }}\frac{d}{{dz}} \end{aligned}$$
(4.21)

that obviously yields

$$\begin{aligned} \frac{d^2}{d\nu ^2}= & {} \left( \frac{dz}{d\nu }\right) ^2\frac{d^2}{dz^2}+ \frac{d^2z}{d\nu ^2}\frac{d}{dz} \nonumber \\= & {} \left( \frac{d\nu }{dz}\right) ^{-2}\left[ \frac{d^2}{dz^2} - (\frac{d\nu }{dz})^{- 1}\frac{d^2\nu }{dz^2}\frac{d}{dz}\right] . \end{aligned}$$
(4.22)

Then, using the relation \((1+z) = a_0/a = E/E_0\) with assumption \( a_0=1 \) for the present-time, one obtains [79]

$$\begin{aligned} dz = - \left( {1 + z}\right) \frac{{\dot{a}}}{a}\frac{{dt}}{{d\nu }}d\nu = - \left( {1 + z} \right) HEd\nu , \end{aligned}$$
(4.23)

that can be rearranged into

$$\begin{aligned} \frac{{d\nu }}{{dz}} = - \frac{1}{{{E_0}H{{\left( {1 + z} \right) }^2}}}, \end{aligned}$$
(4.24)

and in turn, get

$$\begin{aligned} \frac{{{d^2}\nu }}{{d{z^2}}} = \frac{1}{{{E_0}H{{\left( {1 + z} \right) }^3}}}\left[ 2 + \frac{{\left( {1 + z} \right) }}{H}\left( {\frac{dH}{dz}} \right) \right] . \end{aligned}$$
(4.25)

By inserting the relation

$$\begin{aligned} \frac{dH}{dz} = \frac{d\nu }{dz}\frac{{dt}}{d\nu }\frac{dH}{dt}= - \frac{\dot{H}}{H\left( {1 + z}\right) } \end{aligned}$$
(4.26)

into relation (4.25), it reads

$$\begin{aligned} \frac{{{d^2}\nu }}{{d{z^2}}} = \frac{1}{{{E_0}H{{\left( {1 + z}\right) }^3}}}\left( {2 - \frac{{\dot{H}}}{{{H^2}}}} \right) . \end{aligned}$$
(4.27)

By substituting \(\dot{H} ={\ddot{a}}/a - {H^2}\) into relation (4.27) while using Eq. (3.8), one obtains

$$\begin{aligned} \frac{{{d^2}\nu }}{{d{z^2}}} = \frac{1}{{{E_0}H{{\left( {1 + z}\right) }^3}}}\left( {3 + \frac{{ {{\rho ^{\left( \mathrm{tot} \right) }} + 3{p^{\left( \mathrm{tot} \right) }}}}}{{6{M^{2}_\mathrm{Pl}}{H^2}}}} \right) , \end{aligned}$$
(4.28)

and in turn, by substituting Eq. (4.28) and relation (4.24) into relation (4.22), we get

$$\begin{aligned} \frac{{{d^2}\eta }}{{d{\nu ^2}}}= & {} E_0^2{H^2}{\left( {1 + z}\right) ^4}\Bigg [ \frac{{{d^2}\eta }}{{d{z^2}}} +\frac{1}{{\left( {1 + z} \right) }} \nonumber \\&\times \left( {3 + \frac{{ {{\rho ^{\left( \mathrm{tot} \right) }} + 3{p^{\left( \mathrm{tot} \right) }}} }}{{6{M^{2}_\mathrm{Pl}}{H^2}}}} \right) \frac{{d\eta }}{{dz}} \Bigg ]. \end{aligned}$$
(4.29)

Finally, by inserting Eq. (4.18) into Eq. (4.29), the null GDE corresponding to the chameleon scalar field model for dust matters is obtained as

$$\begin{aligned}&\frac{{{d^2}\eta }}{{d{z^2}}}+ \frac{3}{{1 + z}}\left( 1 + \frac{ \rho ^{\left( \mathrm{tot} \right) } + 3p^{\left( \mathrm{tot} \right) }}{{18M_\mathrm{Pl}^2{H^2}}} \right) \frac{{d\eta }}{{dz}} \\&\qquad \quad +\frac{{\left( {{\rho ^{\left( \mathrm{tot} \right) }} + {p^{\left( \mathrm{tot} \right) }}} \right) }}{{2{{\left( {1 + z} \right) }^2}M_\mathrm{Pl}^2{H^2}}}\eta = 0. \end{aligned}$$
(4.30)

However, using relations (3.7) and (3.19), Eq. (4.30) reads

$$\begin{aligned} \frac{{{d^2}\eta }}{{d{z^2}}} + \frac{{\left( {7 + 3{w^{(\mathrm tot)}}}\right) }}{{2\left( {1 + z} \right) }}\frac{{d\eta }}{{dz}} + \frac{{3\left( {1 + {w^{(\mathrm tot)}}} \right) }}{{2{{\left( {1 + z} \right) }^2}}}\eta = 0. \end{aligned}$$
(4.31)

An analytical solution of Eq. (4.31), as a linear homogeneous second-order ordinary differential equation, is

$$\begin{aligned} \eta \left( z \right)= & {} {C_1}{\left( {1 + z} \right) ^{\frac{1}{4}\left( { - 5 - 3{w^{\left( \mathrm{tot} \right) }} - \left| {1 + 3{w^{\left( \mathrm{tot} \right) }}} \right| } \right) }} \nonumber \\&+ {C_2}{\left( {1 + z} \right) ^{\frac{1}{4}\left( { - 5 - 3{w^{\left( \mathrm{tot} \right) }} + \left| {1 + 3{w^{\left( \mathrm{tot} \right) }}} \right| } \right) }}, \end{aligned}$$
(4.32)

where \( {C_1} \) and \( {C_2} \) are integration constants. Relation (4.32) is the obtained result for the null vector fields in the chameleon model that corresponds to the related one obtained in the Brans–Dicke theory [82]. With appropriate initial conditions \( \eta \left( 0 \right) = 0 \) and \({\left. {d\eta /dz} \right| _{z = 0}} = 1 \), solution (4.32) gives

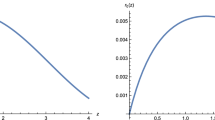
$$\begin{aligned} {C_1} = - {C_2} = \frac{{ - 2}}{{\left| {1 + 3{w^{\left( \mathrm{tot} \right) }}} \right| }}, \end{aligned}$$
(4.33)

where the derivative of the state parameter with respect to the redshift has been assumed to be zero at the present time. We have plotted the behavior of the deviation vector with respect to the redshift for some range of allowed values of the total state parameter in the top diagram of Fig. 2.

Fig. 2
figure 2

The behavior of the deviation vector (the top diagram) and the observer area-distance (the bottom diagram) are depicted with respect to the redshift for null vector fields with the initial conditions \(\eta (z)|_{z=0}=0\), \(d\eta (z)/dz|_{z=0}=1\) and the parametric values \(H_0\simeq 67.6\) (km/s)/Mpc

Full size image

Furthermore, we can indicate the observer area-distance \({r_0}\left( z \right) \) that is given by

$$\begin{aligned} {r_0}\left( z \right) := \sqrt{\left| {\frac{{d{A_0}\left( z \right) }}{{d\Omega }_0}}\right| } = \left| {\frac{{\eta \left( {z'} \right) \left| {_{z' = z}} \right. }}{{d\eta \left( {z'} \right) /dl\left| {_{z' = 0}} \right. }}} \right| , \end{aligned}$$
(4.34)

where \({A_0}\) is the area of the object and \(\Omega _0\) is the solid angle [78, 79]. In this respect, using the relation \(\left| {d/dl} \right| = E_0^{ - 1}{\left( {1 + z} \right) ^{ - 1}}d/d\nu =H\left( {1 + z} \right) d/dz \), wherein \( dl = a\left( t \right) dr \), while assuming that the deviation vector to be zero at \(z=0\), relation (4.34) yields

$$\begin{aligned} {r_0}\left( z \right) = \left| {\frac{{\eta \left( z \right) }}{H_0{d\eta \left( {z'} \right) /dz'\left| {_{z' = 0}} \right. }}} \right| . \end{aligned}$$
(4.35)

This relation represents the observed area-distance as a function of the redshift in units of the present-day Hubble radius [79]. By inserting solution (4.32) into relation (4.35), we attain the observed area-distance for the chameleon model with dust matters, which has been depicted in the bottom diagram of Fig. 2. The comparison of the diagrams in Fig. 2 with the corresponding ones in the \( \Lambda \mathrm CDM \) model [79], the f(R) theory [88], the Hu–Sawicki models [89], the f(R, T) theory [30], the Brans–Dicke theory [82] and the space-time-matter theory [33] indicates that the general behavior of the null geodesic deviation and the observer area-distance in the chameleon model are similar to these models. The similarity of our results to the corresponding ones in the \( \Lambda \mathrm CDM \) model reveals that the chameleon model remains phenomenologically viable and can be tested with the observational data [79].

5 Conclusions

We have considered the chameleon model as one of the scalar-tensor theories, in which the chameleon scalar field non-minimally interact with the baryonic matter field, within the homogeneous and isotropic spatially flat FLRW background. The scalar field in such theories (which usually plays the role of dark energy) have been introduced in the Einstein gravitational theory to explain the accelerated expansion of the universe. However, such a scalar field in the chameleon model (as a chameleon field) was introduced to remedy the problem of the EP-violation as well. On the other hand, it would be interesting to be able to describe the evolution of the universe with just one single scalar field from inflation till late-time. In this regard, we had investigated the chameleon model during inflation [69, 71], wherein it has been shown that, at the beginning of the inflation, the cosmological constant drives the inflation and then the chameleon scalar field plays the role of inflation [71]. Now, in this work, the role of the chameleon scalar field as dark energy has been studied.

It has been indicated that the chameleon model for dust matters with the strong coupling and positive values of the n parameter can explain the late-time accelerated expansion of the universe. Hence, such a model justifies dark energy with stronger confirmation. The results not only reveal that the strongly coupling chameleon scalar field is viable at the late-time, but also set some constraints on the potential of the model. Also, in this work, we have obtained the total state parameter and shown that the case of matter-dominated epoch causes a decelerated evolution, and the case of the chameleon scalar field-dominated epoch corresponds to an accelerated phase. Moreover, the analysis shows that the inverse power-law potential remains a model-consistent with the explanation of the universe at the late-time.

On the other side, in order to make the investigations more instructive, we have calculated the GDE in the chameleonic scalar field model for the timelike and null vector fields to study the relative acceleration of these geodesics as an effect of the curvature of the spacetime. The case of the timelike vector fields gives the generalized Raychaudhuri equation. The presence of the fifth force in the chameleon model leads to the appearance of some new terms in the GDE and the Raychaudhuri equation, which are a direct consequence of the coupling between the chameleon scalar field and matter field. Furthermore, we have obtained the value of the transition redshift from the matter-dominated phase to the late-time accelerated phase of the universe for the chameleon model. The obtained values indicate that the transition redshift in the chameleon model with dust matters is less than the corresponding value of the \(\Lambda \mathrm CDM \) model but is similar to the f(R, T) gravity model. Hence, we conclude that the coupling of the matter field with the scalar field or with the geometry leads to a longer matter-dominated epoch in the evolution of the universe.

Also, we have specified the observed area-distance of the model through the GDE of the null vector fields. Moreover, the results show that the general behaviors of the null deviation vector fields and the observer area-distance in the chameleon model for dust matters have an evolution almost similar to the other corresponding modified gravity models. In fact, the behavior of almost all models, for the deviation evolution, is similar to the \(\Lambda \mathrm CDM \) model for small values of z, as expected. That is, their results remain like a cosmological constant with small corrections to GR.

The relations of the area-distance (4.34) and (4.35) can be used for the angular size-redshift relation derived from the Sunyaev–Zel’dovich effect X-ray technique [90, 91], and also to compact the radio sources as cosmic rulers [92, 93]. Moreover, by considering the relation between the area- and the luminosity-distances (see, e.g. Ref. [94]), it is also possible to extend the investigations in the chameleon model with the data obtained from the observations of type Ia supernovae [95, 96]. In addition to the observed area-distance, the geodesic deviation equation can be used to study the effect of the generalized tidal forces, which could lead to the possibility of observationally testing the model through the observational effects of tides due to an extended mass distribution, for more details see Refs. [97, 98].