Superradiance scattering off Kerr-like black hole and its shadow in the bumblebee gravity with noncommutative spacetime

Abstract

We consider a bumblebee gravity-based Kerr-like black hole in a noncommutative (NC) background and study the superradiance effect and the shadow cast. We extensively study the different aspects of the black hole associated with a generalized Kerr-like spacetime metric endowed with the corrections jointly linked with Lorentz violation and NC spacetime effect. We examine the deviation of shape, and size of the ergosphere, energy emission rate, in this generalized situation. We also examine the influence of admissible values of Lorentz violating parameter $\ell$ and NC parameter b on the superradiance effect and shadow of the black hole. The admissible range has been determined from the observation of the Event Horizon Telescope (EHT) collaboration concerning $M87^{*}$ astronomical black hole. We observe that the superradiance phenomena has a crucial dependence on the parameter $\ell$ and b apart from its dependence on a or ${\hat{a}}= \sqrt{\ell +1}a$ which is linked with the spin of the black hole. We also observe that with the increase in Lorentz violating parameter $\ell$, the size of the black hole shadow increases, and with the increase in the NC parameter b the size of the black hole decreases. We have made an attempt to constrain the NC parameters b of this modified Kerr-like black hole by using the data available from the Event Horizon Telescope (EHT) collaboration. This study shows that black holes associated with NC Kerr-like spacetime may be a suitable candidate for the astrophysical black holes.

1 Introduction

Different exciting optical phenomena have been encountered when light approaches the vicinity of a black hole. Lensing (strong and weak), superradiance, and formation of the shadow of the black holes are essential in this context. From the time of Einstein, the study of the optical effect in the vicinity of a black hole was started and this field has been getting enriched through the investigation by different scientists. In the lensing effect, the black hole behaves as a natural celestial lens that makes a deviation in the path of the light. Here bending takes place due to the strong gravitational field of the black hole. Here, we concentrate on investigating the impact of quantum gravity effect on the superradiance phenomenon and the shadow of black holes.

In a gravitational system, the scattering of radiation off absorbing rotating objects produce waves with amplitude larger than incident one under certain conditions which is known as rotational superradiance [1, 2]. In 1971, Zel’dovich showed that scattering of radiation off rotating absorbing surfaces result in waves with a larger amplitude as $\omega < m\Omega$ where $\omega$ is the frequency of the incident monochromatic radiation with m, the azimuthal number with respect to the rotation axis and $\Omega$ is the angular velocity of the rotating gravitational system [1, 2]. The important contemporary contributions in the articles [3,4,5,6,7] related to superradiance made these astounding astronomical phenomena a tempting field of research. For review, we would like to mention the lecture notes [8], and the references therein. Rotational superradiance belongs to a wider class of classical problems displaying stimulated or spontaneous energy emission, such as the Vavilov-Cherenkov effect and the anomalous Doppler effect. When quantum effects were incorporated it was argued that rotational superradiance would become a spontaneous process and that rotating bodies including black holes would slow down by the spontaneous emission of photons. From the historical perspective, the discovery of black hole evaporation was well understood from the studies of black hole superradiance [9]. Interest in the study of black hole superradiance has recently been revived in different areas, including astrophysics and high-energy physics via the gauge/gravity duality along with fundamental issues in General Theory of Relativity (GTR). Superradiant instabilities can be used to constrain the mass of ultra-light degrees of freedom [10,11,12,13], with important applications to dark-matter searches. The black hole superradiance is also associated with the existence of new asymptotically flat hairy black-hole solutions [14] and with phase transitions between spinning or charged black objects and asymptotically anti-de Sitter (AdS) spacetime [15,16,17] or in higher dimensions [18]. Finally, the knowledge of superradiance is instrumental in describing the stability of black holes and determining the fate of the gravitational collapse in confining geometries [15]

Shadow is a two-dimensional dark area in the celestial sphere which is known as a black hole caused by the strong gravity of the black hole. It was first examined by Synge in 1966 for a Schwarzschild black hole [19], and the radius of the shadow was given by Luminet [20]. The shadow of a non-rotating black hole is a standard circle, while the shadow of a rotating black hole elongates in the direction of the rotating axis due to the dragging effects of spacetime [21, 22]. Hioki and Maeda [23] proposed two observables based on the feature that points at the boundary of the Kerr shadow to match the astronomical observations. One of which roughly describes the size of the shadow and the other describes the deformation of its shape from a reference circle. Also, using the method given in [24] one can find the deviation from circularity $\Delta C$. These various observables are very useful in testing and constraining the parameters involved in the modified theories of gravity.

The black hole itself is one of the important predictions of the GTR. Just after the announcement of capturing of the shadow of the supermassive black hole $M87^*$ at the center of the nearby galaxy Messier 87 by the EHT collaboration [25,26,27,28,29,30], the study of optical phenomena in the vicinity of black holes has gained renewed impetus [31,32,33,34,35,36]. Various types of modified gravity along with the standard one were developed from time to time to resolve ambiguities in different physical observables. These modified theories have also provided precise explanations for observations made possible by the use of modern sophisticated instruments. In this regard, a potential direction of improvement over the conventional theory of gravity is to give the theory of gravity a quantum correction. It is of great importance since quantization of gravity is still not available in a mature form. Therefore the correction that comes to incorporate the effect of the Planck scale is highly appreciated in recent times. Two such ideas of taking into the effect of the Planck scale are considered with significance in the recent time literature: one is the Lorentz violation effect and another is the impact of the NC spacetime. Both effects have been studied earlier separably in the different physical systems, however, the framework of having the combined effect treating these two on the same footing effect is still lacking to the best of our knowledge.

The formulation of the Standard Model of physics and the GTR entirely depends on the principle of Lorentz invariance. The GTR does not take into account the quantum properties of particles, and Standard Model (SM), on the other hand, neglects all gravitational effects of particles. At the Planck scale, one cannot neglect gravitational interactions between particles, and hence merger of SM with GTR in a single theory becomes essential. It is indeed available from the quantum gravity concept. At this scale, it is expected to face a violation of Lorentz symmetry [42]. Several studies related to Lorentz violation in different aspects have come in the literature [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68]. The standard model extension (SME) is an effective field theory that couples SM to GTR [69,70,71,72] where Lorentz violation has been introduced. One of the theories that belong to this class is the bumblebee model, where the Lorentz violation is introduced through an axial-vector field $B_{\mu }$ which is known as the bumblebee field. Recently, in [73, 74], a Kerr-like solution was obtained from the Einstein-bumblebee theory. In [75], it has been found that a Kerr-Sen-like solution is also possible from the Einstein-bumblebee theory.

NC spacetime has been extensively studied in recent years [76,77,78,79,80,81]. The impact of NC spacetime has been studied in various fields. A fertile field for studying the impact of NC spacetime is black hole physics. Several ways are available in the literature to implement NC spacetime in theories of gravity [82,83,84,85,86]. Through a modification of the matter source by a Gaussian mass distribution NC spacetime has been brought into the black hole physics in the paper [87] and through Lorentzian mass distribution NC spaspetime has been introduced in the paper [88]. An interesting extension concerning the thermodynamic similarity between Reissner-Nordstr$\ddot{o}$m black hole and the NC Schwarzschild black hole has been made in the paper [89]. The thermodynamical aspects of NC black holes have been investigated by taking on the tunnelling formalism in the papers [90,91,92,93,94,95,96,97]. The impact of NC spacetime in cosmology has been studied extensively in the papers [98,99,100,101,102]. In [103], by taking the mass density to be a Lorentzian smeared mass distribution the thermodynamic properties of NC BTZ black holes have been studied. So far we have found NC spacetime can be implemented by modifying the point-like source of matter designated by the Dirac delta function by replacing it with a distribution of matter. In the papers [87, 88] Gaussian and Lorentzian distributions are used to incorporate the idea of NC spacetime. In this manuscript, we have introduced NC spacetime into Kerr-like black hole [73] by considering Lorentzian distribution as it has been used in [88].

Correction due to quantum gravity is believed to be bestowed on the theory of gravity introducing Lorentz violation, and NC spacetime. In this paper, we develop a framework where we can study the impact of both the Lorentz violation and NC aspect of spacetime simultaneously on the same footing and consequently carry out an investigation through this generalized framework. Due to the presence of the real and anti-symmetric $\theta _{\mu \nu }$ within the basic formulation of implementation of the NC aspect of spacetime $[x_\mu , x_\nu ] = i\theta _{\mu \nu }$, violation of Lorentz symmetry is inherent to NC theories. However in the papers [104] Smailagic et al. and in [105] Nicolini et al. simulated NC spacetime in an intriguing manner by invoking the ingenious coordinate coherent state formalism that kept the Lorentz invariance preserved. Although the NC spacetime has been introduced here following article [88, 114], it is undoubtedly a precise continuation of the studies of Smailagic et al. and Nicolini et al. [104, 105]. In this extension, we tried to provide a faithful and decent framework that takes into account both NC spacetime and the Lorentz violation simultaneously. Therefore in this extended framework Lorentz violation is obvious, but the origin of the Lorentz violation lies in the bumblebee vector field. The way NC spacetime has been amended here has no direct connection to the Lorentz violation. This new framework will allow studying systematically the quantum correction on superradiance phenomena, the energy emission due to radiation, and the black hole shadow. What light the knowledge gathered from the $\mathrm {M}87^{*}$ data can shed on this updated framework that has been thoroughly investigated here. Constraining of the Lorentz violation parameter $(\ell )$ and the NC parameter (b) also has been executed from the data of EHT collaboration concerning the shadow of the $\mathrm {M}87^{*}$ black hole.

We, therefore, make an attempt to have the combined effect of these two corrections and study their effect on the superradiance and the shadow corresponding to this black hole. Although a general study of the superradiance phenomena will be provided here with the theories endowed with the quantum correction, we will be able to test this modified theory in light of the recently available data of the EHT collaboration. The important information about the shadow is that it is found to have an angular diameter $42\pm 3\mu$ with the deviation from circularity $\Delta C= 0.1$ and axial ratio $\approx \frac{4}{3}$. It helps us to constrain the free parameter involved in this modified theory of gravity.

The manuscript is organized as follows. In Sect. 2, we briefly describe how the Kerr-like black hole metric is endowed with Lorentz-violation and NC spacetime. In Sect. 3, we study the geometrical aspects concerning the horizon and ergosphere of this modifies metric. Section 4 is devoted to superradiance scattering off the black hole corresponding to this modified metric. In Sect. 5 we describe the photon orbit and shadow corresponding to this black hole. Section 6 contains the computation of energy emission rate. In Sect. 7 an attempt has been made to constrain the parameters from the observation of the EHT collaboration conserving the $\mathrm {M}87^{*}$ black hole Sect. 8 contains a brief summary and conclusion of the work

2 Modification of gravity containing Lorentz violation in a noncommutative spacetime

Let us first develop a framework where we can incorporate both the Lorentz violation and the NC spacetime on the same footing. To this end, we give a brief description of how the Lorentz violation effect was introduced.

2.1 Lorentz violation effect

Lorentz violation effect is believed to have the ability that it may lead to significant effects on the properties of the black holes anticipated beforehand. So it was attempted to introduce through Einstein-bumblebee theory. It is an effective field theory where the bumblebee field receives vacuum expectation through a spontaneous breaking of symmetry. The action of which is given by

$$\begin{aligned} {\mathcal {S}}= & {} \int d^{4} x \sqrt{-g}\Bigg [\frac{1}{16 \pi G_{N}}\left( {\mathcal {R}}+\varrho B^{\mu } B^{\nu } {\mathcal {R}}_{\mu \nu }\right) \nonumber \\&-\frac{1}{4} B^{\mu \nu } B_{\mu \nu }-V\left( B^{\mu }\right) \Bigg ]. \end{aligned}$$

(1)

where $\varrho ^{2}$ represents the real coupling constant that controls the non-minimal gravity interaction to bumblebee field $B_{\mu }$. Like electromagnetic field the dynamics of the bumblebee sector is described by the field strength tensor corresponding to the bumblebee field which is defined by

$$\begin{aligned} B_{\mu \nu }=\partial _{\mu } B_{\nu }-\partial _{\nu } B_{\mu }. \end{aligned}$$

(2)

The field $B_{\mu }$ receives a vacuum expectation value from a suitable potential through the spontaneous breaking of the symmetry of the theory. The potential $V\left( B^{\mu }\right)$ that induces Lorentz symmetry breaking is given by

$$\begin{aligned} V=V\left( B_{\mu } B^{\mu }\pm b^2)\right. \end{aligned}$$

(3)

Here $b^{2}$ is a real positive constant. It refers to a non-vanishing vacuum expectation value for the field $B_{\mu }$. It is assumed that the potential has a minimum described by the condition

$$\begin{aligned} B_{\mu }B^{\mu }\pm b^2=0. \end{aligned}$$

(4)

The Eq. (4) ensures that a non-vanishing vacuum expectation value

$$\begin{aligned} \left\langle B^{\mu }\right\rangle =b^{\mu } \end{aligned}$$

(5)

will be received by the field $B_{\mu }$ from the potential V. The field $b^{\mu }$ indeed is a function of the spacetime coordinates which have a constant magnitude $b_{\mu } b^{\mu }=\mp b^{2}$ which may have a time-like as well as space-like nature depending upon the choice of sign in front of $b^{2}$. The gravitational field equation in a vacuum that follows from the action (1) reads

$$\begin{aligned} {\mathcal {R}}_{\mu \nu }-\frac{1}{2} g_{\mu \nu } {\mathcal {R}}=\kappa T_{\mu \nu }^{B}. \end{aligned}$$

(6)

where $\kappa =8 \pi G_{N}$ is the gravitational coupling and the bumblebee energy–momentum tensor $T_{\mu \nu }^{B}$ has the following expression.

$$\begin{aligned} T_{\mu \nu }^{B}&=B_{\mu \alpha } B_{\nu }^{\alpha }-\frac{1}{4} g_{\mu \nu } B^{\alpha \beta } B_{\alpha \beta }-g_{\mu \nu } V+2 B_{\mu } B_{\nu } V^{\prime } \nonumber \\&\quad +\frac{\varrho }{\kappa }\Bigg [\frac{1}{2} g_{\mu \nu } B^{\alpha } B^{\beta } R_{\alpha \beta } -B_{\mu } B^{\alpha } R_{\alpha \nu }-B_{\nu } B^{\alpha } R_{\alpha \mu }\nonumber \\&\quad +\frac{1}{2} \nabla _{\alpha } \nabla _{\mu }\left( B^{\alpha } B_{\nu }\right) +\frac{1}{2} \nabla _{\alpha } \nabla _{\nu }\left( B^{\alpha } B_{\mu }\right) \nonumber \\&\quad -\frac{1}{2} \nabla ^{2}\left( B^{\mu } B_{\nu }\right) -\frac{1}{2} g_{\mu \nu } \nabla _{\alpha } \nabla _{\beta } \left( B^{\alpha } B^{\beta }\right) \Bigg ]. \end{aligned}$$

(7)

Here prime(’) denotes differentiation with respect to the argument.

$$\begin{aligned} V^{\prime }=\left. \frac{\partial V(x)}{\partial x}\right| _{x=B^{\mu } B_{\mu } \pm b^{2}} \end{aligned}$$

(8)

Now following the road map of Casana et al. [106], Ding et al. obtained a Kerr-like solution [73] keeping in view of the development of Koltz to reproduce the Kerr solution [107]. According to the development of Koltz the generalized form of radiating stationery axially symmetric black hole metric can be written down as [73, 107]

$$\begin{aligned} d s^{2}= & {} -\gamma (\zeta , \theta ) d \tau ^{2}+a[p(\zeta )-q(\theta )]\nonumber \\&\times \left( d \zeta ^{2}+d \theta ^{2}+\frac{q}{a} d \phi ^{2}\right) -2q(\theta )d\tau d\phi . \end{aligned}$$

(9)

where a is a dimensional constant which is introduced matching the dimension. The time t and $\tau$ has the relation

$$\begin{aligned} d \tau =d t-q d \phi . \end{aligned}$$

(10)

In terms of t Eq. (9) turns into

$$\begin{aligned} d s^{2}= & {} -\gamma (\zeta , \theta ) d t^{2}+a[p(\zeta ) -q(\theta )]\left( d \zeta ^{2}+d \theta ^{2}\right) \nonumber \\&+\left\{ [1-\gamma (\zeta , \theta )] q^{2}(\theta )+p(\zeta ) q(\theta )\right\} d \phi ^{2}\nonumber \\&-2 q(\theta )[1-\gamma (\zeta , \theta )] d t d \phi . \end{aligned}$$

(11)

The metric ansatz (11) is then used to compute the gravitational field equations considering bumblebee space-like nature of the field $b_{\mu }$:

$$\begin{aligned} b_{\mu }=(0, b(\zeta , \theta ), 0,0). \end{aligned}$$

(12)

The space-like nature of the bumblebee field was chosen in this situation since spacetime curvature showed up great radial variation compared to its temporal variation. The condition

$$\begin{aligned} b_{\mu } b^{\mu }=b_{0}^{2}, \end{aligned}$$

(13)

where $b_{0}$ is a constant led us to find out $b_{\mu }$ in the form

$$\begin{aligned} b_{\mu }=\left( 0, b_{0} \sqrt{a(p-q)}, 0,0\right) . \end{aligned}$$

(14)

in a straightforward manner. With this set up they established that Einstein-bumblebee modified theory permitted to write the bumblebee field as $b_{\mu }=\left( 0, b_{0}\ell , 0,0\right)$. Note that it contained the Lorentz violation parameter $\ell$ and landed onto a Kerr-like metric. In the Boyer–Lindquist coordinate it reads

$$\begin{aligned} d s^{2}= & {} -\left( 1-\frac{2 M r}{\rho ^{2}}\right) d t^{2}-\frac{4 M r a \sqrt{1+\ell } \sin ^{2} \theta }{\rho ^{2}} d t d \varphi \nonumber \\&+\frac{\rho ^{2}}{\Delta } d r^{2}+\rho ^{2} d \theta ^{2}+\frac{A \sin ^{2} \theta }{\rho ^{2}} d \varphi ^{2}. \end{aligned}$$

(15)

where

$$\begin{aligned} \Delta= & {} \frac{r^2-2 M r}{1+\ell }+a^{2}, A=\left[ r^2+(1+\ell ) a^{2}\right] ^{2}\nonumber \\&-\Delta (1+\ell )^{2} a^{2} \sin ^{2} \theta . \end{aligned}$$

(16)

In the slow rotating [123] case, i.e. for $a^2\rightarrow 0$ the metric has the form

$$\begin{aligned} d s^{2}\approx & {} -\left( 1-\frac{2 M}{r}\right) d t^{2}-\frac{Ma(1+\ell )sin^2\theta }{r}d\theta d\varphi \nonumber \\&+\frac{1+\ell }{1-2 M / r} d r^{2}+r^{2}(d \theta ^{2}+ \sin ^{2} \theta )d \varphi ^{2}, \end{aligned}$$

(17)

If $\ell \rightarrow 0$ it recovers the usual Kerr metric and for $a \rightarrow 0$ it becomes

$$\begin{aligned} d s^{2}= & {} -\left( 1-\frac{2 M}{r}\right) d t^{2}+\frac{1+\ell }{1-2 M / r} d r^{2}+r^{2} (d \theta ^{2}\nonumber \\&+ \sin ^{2} \theta ) d \varphi ^{2}, \end{aligned}$$

(18)

which is Schwarzschild metric with the Lorentz violation parameter $\ell$.

2.2 Noncommutative Kerr-like black hole

Let us now describe in brief the incorporation of the NC spacetime in the known commutating setup. Like the Lorentz violation effect, the NC spacetime also believed to have the potential that leads to significant effects on the properties of the black holes. Therefore the implementation of NC spacetime in the standard commutative theories of gravity have been the subject of several interests [108, 109]. Although an ideal NC extension of the standard theory has not yet been available, it necessitates receiving the impact of NC spacetime in the frame of the commutative theory of standard GTR. In recent times, the authors in the papers [105, 108,109,110,111] made physically inspired, decent as well as obedient NC amendments to Schwarzschild black hole solutions. In particular, the study considering the effects of NC spacetime on black hole physics has been an area of huge interest. The generalization of quantum field theory of NC spacetime based on coordinate coherent state formalism is of interest in this respect which cures the short distance behavior of point-like structures [105, 110,111,112]. It also protect Lorentz symmetry. In this approach, the point mass M is considered to be distributed throughout a region of linear size instead of being localized at a point. Therefore, NC spacetime has been introduced by modifying the mass density. In this respect, the Dirac delta function is replaced by a Gaussian distribution [105] or alternatively by a Lorentzian distribution [112]. The implementation of these argument leads to the replacement of the position Dirac-delta function that describes a point-like structure, with suitable a function capable of describing smeared structure. Gaussian distribution function as well as Lorentzian distribution serve this purpose in a significant ad well behaved manner. In a real sense, the description of matter would not be a point like Dirac-delta distribution. It will be better described by the distribution function that provides smeared structure like Gaussian distribution or some other type of distribution such that it turns into a Dirac-delta function when the width of the distribution approaches to zero.

To incorporate the impact of NC spacetime we consider that the mass density of the black hole has a Lorentzian distribution as it was found in paper [88, 114]

$$\begin{aligned} \rho _{b}=\frac{\sqrt{b} M}{\pi ^{3 / 2}\left( \pi b+r^{2}\right) ^{2}}. \end{aligned}$$

(19)

Here b is the strength of NC aspect of the spacetime manifold and M is the total mass distributed throughout a region with a linear size $\sqrt{b}$. For the smeared matter distribution, it can be shown that [114]

$$\begin{aligned} {\mathcal {M}}_{b}= & {} \int _{0}^{r} \rho _{b}(r) 4 \pi r^{2} d r\nonumber \\= & {} \frac{2 M}{\pi }\left( \tan ^{-1}\left( \frac{r}{\sqrt{\pi b}}\right) -\frac{\sqrt{\pi b} r}{\pi b+r^{2}}\right) \nonumber \\\approx & {} -\frac{4 \sqrt{b} M}{\sqrt{\pi } r}+M+{\mathcal {O}}\left( b^{3 / 2}\right) . \end{aligned}$$

(20)

It indicates that the mass is point-like when the spread of the distribution approaches towards a vanishing value since $\lim _{b \rightarrow 0 }M_b = M$.

To combine these two effects we need a suitable framework where these two can fit suitably. Now, these two can be amalgamated if we replace M by $M_b$ in the expression of the spacetime metric given in Eq. (15), which is already endowed with the Lorentz violation effect. Therefore the generalized spacetime metric where both the Lorentz violation and NC spacetime effects are bestowed simultaneously takes the form

$$\begin{aligned} d s^{2}= & {} -\left( 1-\frac{2 M_{b} r}{\rho ^{2}}\right) d t^{2}-\frac{4 M_{b} r a \sqrt{1+\ell } \sin ^{2} \theta }{\rho ^{2}} d t d \varphi \nonumber \\&+\frac{\rho ^{2}}{{\hat{\Delta }}} d r^{2}+\rho ^{2} d \theta ^{2}+\frac{A \sin ^{2} \theta }{\rho ^{2}} d \varphi ^{2}, \end{aligned}$$

(21)

where

$$\begin{aligned} \rho ^{2}= & {} r^{2}+(1+\ell ) a^{2} \cos ^{2} \theta ,{\hat{\Delta }}=\frac{r^{2} -2 M_{b} r}{1+\ell }+a^{2}, \nonumber \\ A= & {} \left[ r^{2}+(1+\ell ) a^{2}\right] ^{2}-{\hat{\Delta }}(1+\ell )^{2} a^{2} \sin ^{2} \theta . \end{aligned}$$

(22)

The metric (21) carries the information of two significant effects which have already been found needful to take taken into account the quantum gravity correction to the black hole physics. Although these two are supposed to show a prominent role in the vicinity of Planck scale it is believed that these two have the ability to lead to significant effects on the properties of the black holes at an observable scale. The parameter b is connected with the amended NC property of the spacetime and the parameter $\ell$ is associated with the Lorentz violation scenario. If the Lorentz violation effect is switched off by setting $\ell = 0$ it will render only the NC effect and the reverse will be the case if the NC effect be switched off by setting $b = 0$. If both the effects are made off by setting $\ell \rightarrow 0$ along with $b \rightarrow 0$, it recovers the usual Kerr metric having no quantum correction.

3 Geometry concerning horizon and ergosphere

Let us now focus on to our investigation with the metric developed in Eq. (15). We get the expressions for the event horizon and Cauchy horizon setting ${\hat{\Delta }}=0$, which are given by

$$\begin{aligned} r_{\pm }=M\pm \frac{\sqrt{-\pi \ell a^2-\pi a^2+\pi M^2-8 \sqrt{\pi } M \sqrt{b}}}{\sqrt{\pi }}, \end{aligned}$$

(23)

where ± signs correspond to the event horizon and Cauchy horizon respectively. The event horizon and Cauchy horizon are labelled by $r_{eh}$ and $r_{ch}$ respectively. What follows next is the sketch of ${\hat{\Delta }}$ for different values of b and $\ell$ (Figs. 1, 2).

Fig. 1

The left one gives variation of ${\hat{\Delta }}$ for various values of ${\hat{a}}$ with $b=0.02M^{2}$ and $\ell =0.3$, and the right one gives variation for various values of b with ${\hat{a}}=0.5M$ and $\ell =0.3$

Fig. 2

It gives variation of ${\hat{\Delta }}$for various values of $\ell$ with $b=0.01M^{2}$ and ${\hat{a}}=0.6$

From the above plots we see that there exist critical values of a, for fixed values of b and $\ell$. Similarly we have critical values of b for fixed values of a, l, and consequently, critical values of $\ell$ for fixed values of b, a. The critical value of a, b and $\ell$ are designated by $a_c, b_c$ and $\ell _c$ respectively. In these cases ${\hat{\Delta }}=0$ has only one root. For $a < a_{c}$ we have black hole and for $a > a_{c}$ we have naked singularity. Similarly for $b < b_{c}$ we have black hole, but for $b > b_{c}$ we have naked singularity. The condition $\ell < l_{c}$ signifies the black hole, however $\ell > l_{c}$ represents the naked singularity. Numerical computation shows that we have ${\hat{a}}_{c}=0.52747M$ for $b=0.02M^{2}$ and $\ell =0.3$. Similarly for $a=0.5M$ and $\ell =0.3$ we have $b_{c}=0.0223654M^{2}$, and also for $a=0.6M$ and $b=0.01M^{2}$ we find $\ell _{c}=0.524023$.

There exists a black hole when the following inequality is maintained

$$\begin{aligned} -\pi \ell a^2-\pi a^2+\pi M^2-8 \sqrt{\pi } M \sqrt{b} \ge 0, \end{aligned}$$

(24)

Note that when in the Eq. (24) equality is maintained it corresponds to extremal black holes. However if the equation (24) strictly maintains the condition greater than 0 we have non-extremal black holes which have both the Cauchy and Event horizons (Fig. 3).

Fig. 3

It is the parameter space $({\hat{a}}/M-b/M^{2})$. The colored regions correspond to parameter space for which we have a black hole

Let us now focus on to the static limit surface (SLS). At the SLS, the asymptotic time-translational Killing vector becomes null which is mathematically given by

$$\begin{aligned} g_{tt}=\rho ^{2}-2M_{b}r=0. \end{aligned}$$

(25)

The real positive solutions of the above equation give radial coordinates of the ergosphere:

$$\begin{aligned} r^{ergo}_{\pm } =\frac{2 \sqrt{\pi } M\pm \sqrt{-4 \pi a^2 \cos ^2(\theta ) -4 \pi a^2 \ell \cos ^2(\theta )+4 \pi M^2-32 \sqrt{\pi } M \sqrt{b}}}{2 \sqrt{\pi }}. \end{aligned}$$

(26)

Fig. 4

The cross-section of the event horizon (outer red line), SLS (outer blue dotted line), and ergoregion of NC Kerr-like black holes

The ergosphere, which lies between SLS and the event horizon, is depicted above. Energy can be extracted from the ergosphere [115]. From the above Fig. 4 we can conclude that the shape and size of the ergosphere depend on rotational parameter ${\hat{a}}$ and NC parameter b. The size of the ergosphere increases with the increase of the value of b and ${\hat{a}}$. This completes our discussion concerning the geometrical structure of this modified spacetime metric. Let us now turn toward our main part of the investigation which is connected to the optical properties in the viscidity of this black hole. To this end let us first consider the superradiance phenomena.

4 Superradiance scattering of the scalar field off noncommutative Kerr-like black hole

We bring the Klein–Gordon equation for the curved spacetime into action to study the superradiance scattering of a scalar field $\Phi$.

$$\begin{aligned}&\left( \bigtriangledown _{\alpha }\bigtriangledown ^{\alpha }+\mu ^{2}\right) \Phi (t,r,\theta ,\phi )\nonumber \\&\quad = \left[ \frac{-1}{\sqrt{-g}}\partial _{\sigma }\left( g^{\sigma \tau }\sqrt{-g}\partial _{\tau }\right) +\mu ^{2}\right] \Phi (t,r,\theta ,\phi )=0. \qquad \end{aligned}$$

(27)

Here $\mu$ represents the mass of the scalar field $\Phi$. We now adopt the standard separation of variables method to the equation Eq. (27) in order to separate it into radial and angular part using the following ansatz. With the standard Boyer-Lindquist coordinates $(t, r, \theta , \phi )$ we can write

$$\begin{aligned}&\Phi (t, r, \theta , \phi )=R_{\omega j m}(r) \Theta (\theta ) e^{-i \omega t} e^{i m \phi },\nonumber \\&j \ge 0, \quad -j \le m \le j, \quad \omega >0, \end{aligned}$$

(28)

where $R_{\omega j m}(r)$ represents the radial function and $\Theta (\theta )$ refers to the oblate spheroidal wave function. The symbols j, m, and $\omega$ respectively stand for the angular eigenfunction, angular quantum number, and the positive frequency of the field under investigation as viewed by a far away observer. Using the ansatz (28), the differential Eq. (27) is found to get separated into the following two ordinary differential equations. For radial part the equation reads

$$\begin{aligned}&\frac{d}{d r}\left( {\hat{\Delta }} \frac{d R_{\omega j m}(r)}{d r}\right) \nonumber \\&\quad +\left( \frac{((r^2+a^{2}(1+\ell )) \omega -am\sqrt{1+\ell } )^{2}}{{\hat{\Delta }}(1+\ell )}\right) R_{\omega l m}(r) \nonumber \\&\quad -(\mu ^{2} r^2+j(j+1)+a^{2}(1+\ell ) \omega ^{2}\nonumber \\&\quad -2 m \omega a\sqrt{1+\ell }) R_{\omega l m}(r)=0, \end{aligned}$$

(29)

and the angular part of it is

$$\begin{aligned}&\sin \theta \frac{d}{d \theta }\left( \sin \theta \frac{d \Theta _{\omega j m}(\theta )}{d \theta }\right) +\left( j(j+1) \sin ^{2} \theta \right. \nonumber \\&\quad \left. -\left( \left( a\sqrt{1+\ell } \omega \sin ^{2} \theta -m\right) ^{2}\right) \right) \Theta _{\omega j m}(\theta )\nonumber \\&\quad + a^{2}(1+\ell ) \mu ^{2} \sin ^{2} \theta \cos ^{2} \theta ~ \Theta _{\omega j m}(\theta )=0. \end{aligned}$$

(30)

Following the earlier investigation [130, 131] we may have a general solution of the radial Eq. (29). However, we are intended to study the scattering of the field $\Phi$. So in this situation, we have used the asymptotic matching procedure used in [4, 5, 7, 125, 126]. The road map of the important contributions [4, 5, 7, 125, 126, 128] and the recent studies [127,128,129] led us to reach to the required result without using the general solution. First of all we consider the radial part of the Eq. (29) to find an asymptotic solution. Use of Regge–Wheeler-like coordinate $r_{*}$ is helpful in this situation in order to deal with the radial equation as per our requirement, which is given by

$$\begin{aligned} r_{*}\equiv & {} \int d r \frac{r^2+a^{2}(1+\ell )}{{\hat{\Delta }}},\nonumber \\&\left( r_{*} \rightarrow -\infty \quad \text {at event horizon}, r_{*} \rightarrow \infty \quad \text {at infinity}\right) .\nonumber \\ \end{aligned}$$

(31)

To have the equation into the desired shape, we take on a new radial function ${\mathcal {R}}_{\omega j m}\left( r_{*}\right) =\sqrt{r^2+a^{2}(1+\ell )} R_{\omega j m}(r)$. A few steps of algebra, lead us to obtain the radial equation with our desired form.

$$\begin{aligned} \frac{d^{2} {\mathcal {R}}_{\omega l m}\left( r_{*}\right) }{d r_{*}^{2}}+V_{\omega j m}(r) {\mathcal {R}}_{\omega j m}\left( r_{*}\right) =0. \end{aligned}$$

(32)

An effective potential takes entry into the picture now and that has a crucial role in the scattering. It reads

$$\begin{aligned} V_{\omega j m}(r)= & {} \frac{1}{1+\ell }\left( \omega -\frac{m {\hat{a}}}{r^2+{\hat{a}}^{2}}\right) ^{2}\nonumber \\&-\frac{{\hat{\Delta }}}{\left( r^2 +{\hat{a}}^{2}\right) ^{2}}\left[ j(j+1)+{\hat{a}}^{2} \omega ^{2}-2 m {\hat{a}} \omega \right. \nonumber \\&\left. +\mu ^{2} r^2+\sqrt{r^2+{\hat{a}}^{2}}\frac{d}{dr}\left( \frac{r{\hat{\Delta }} }{\left( r^2+{\hat{a}}^{2}\right) ^{\frac{3}{2}}}\right) \right] , \end{aligned}$$

(33)

where ${\hat{a}}=a(1+\ell )^{\frac{1}{2}}$. So it appears that it is equivalent to the study of the scattering of the scalar field $\Phi$ under this effective potential (33). It is beneficial in this regard to study the asymptotic behavior of the scattering potential at the event horizon and at spatial infinity potential. The potential at the event horizon in the asymptotic limit simplifies into

$$\begin{aligned} \lim _{r \rightarrow r_{eh}} V_{\omega j m}(r)=\frac{1}{1+\ell }\left( \omega -m {\hat{\Omega }}_{h}\right) ^{2} \equiv k_{e h}^{2}. \end{aligned}$$

(34)

and the same at spatial infinity turns into the following after a few step of algebra

$$\begin{aligned}&\lim _{r \rightarrow \infty } V_{\omega j m}(r)=\frac{\omega ^{2}}{1+\ell }-\lim _{r \rightarrow \infty } \frac{\mu ^{2} r^2 {\hat{\Delta }}}{\left( r^2+{\tilde{a}}^{2}\right) ^{2}}\nonumber \\&\quad =\frac{\omega ^{2}}{1+\ell } -{\hat{\mu }}^{2}\equiv k_{\infty }^{2}, ~~~ {\hat{\mu }}=\frac{\mu }{\sqrt{\ell +1}}. \end{aligned}$$

(35)

Note that the potential shows constant behavior at the two extremal points namely at event horizon and at spatial infinity. The numerical values of the constants however are different indeed at the two extremal points.

Since the behavior of the potential at the two extremal points are known, we now move on to observe the asymptotic behavior of the radial solution. A little algebra shows that the radial equation (32) has the following solution

$$\begin{aligned} R_{\omega j m}(r) \rightarrow \left\{ \begin{array}{cl} \frac{{\mathcal {D}}_{i n}^{eh} e^{-i k_{eh} r_{*}}}{\sqrt{r_{e h}^2 +{\hat{a}}^{2}}} &{} \text{ for } r \rightarrow r_{e h} \\ {\mathcal {D}}_{i n}^{\infty } \frac{e^{-i k_{\infty } r_{*}}}{r}+{\mathcal {D}}_{r e f}^{\infty } \frac{e^{i k_{\infty } r_{*}}}{r} &{} \text{ for } r \rightarrow \infty \end{array}\right\} \end{aligned}$$

(36)

in the asymptotic limit. Here ${\mathcal {D}}_{in}^{eh}$ be the amplitude of the incoming scalar wave at event horizon($r_{eh}$), and ${\mathcal {D}}_{in}^{\infty }$ is the corresponding quantity of the incoming scalar wave at infinity $(\infty )$. The amplitude of the reflected part of scalar wave at infinity $(\infty )$ is designated by ${\mathcal {D}}_{ref}^{\infty }$. So the stage is set to compute the Wronskian for the region adjacent to the event horizon and at infinity. The Wronskian for the event horizon is found out to be

$$\begin{aligned} W_{eh}=\left( R_{\omega j m}^{e h} \frac{d R_{\omega j m}^{* e h}}{d r_{*}}-R_{\omega j m}^{* eh} \frac{d R_{\omega j m}^{eh}}{d r_{*}}\right) , \end{aligned}$$

(37)

and the Wronskian at infinity results out to

$$\begin{aligned} W_{\infty }=\left( R_{\omega j m}^{\infty } \frac{d R_{\omega j m}^{* \infty }}{d r_{*}}-R_{\omega j m}^{* \infty } \frac{d R_{\omega j m}^{\infty }}{d r_{*}}\right) . \end{aligned}$$

(38)

The knowledge of standard theory of ordinary differential equation provides the information that the Wronskian corresponding to the solutions will be independent of $r^*$ since the solution are linearly independent. Thus, the Wronskian evaluated at the horizon is compatible to equate with the Wronskian evaluated at infinity. In fact, in the physical sense, it is associated with the flux conservation of the process [8]. From the matching condition an important relation between the amplitudes of incoming and reflected waves at different regions of interest results.

$$\begin{aligned} \left| {\mathcal {D}}_{r e f}^{\infty }\right| ^{2}=\left| {\mathcal {D}}_{i n}^{\infty }\right| ^{2}-\frac{k_{e h}}{k_{\infty }}\left| {\mathcal {D}}_{i n}^{e h}\right| ^{2}. \end{aligned}$$

(39)

A careful look reveals that if $\frac{k_{e h}}{k_{\infty }} <0$ i.e., $\omega <m {\hat{\Omega }}_{e h}$, the scalar wave will be superradiantly amplified, since the relation $\left| {\mathcal {D}}_{r e f}^{\infty }\right| ^{2}>\left| {\mathcal {D}}_{i n}^{\infty }\right| ^{2}$ holds explicitly in this situation.

4.1 Amplification factor $Z_{jm}$ for superradiance

It is straightforward to express the radial equation (29) in the following form

$$\begin{aligned}&{\hat{\Delta }}^{2} \frac{d^{2} R_{\omega j m}(r)}{d r^{2}}+{\hat{\Delta }} \frac{d {\hat{\Delta }}}{d r} \cdot \frac{d R_{\omega j m}(r)}{d r}\nonumber \\&\quad +\Bigg (\frac{\left( \left( r^2+{\hat{a}}^{2}\right) \omega -{\hat{a}} m\right) ^{2}}{1+\ell }-{\hat{\Delta }}\left( \mu ^{2} r^2+j(j+1)\right. \nonumber \\&\quad \times \left. {\hat{a}}^{2} \omega ^{2}-2 m {\hat{a}} \omega \right) \Bigg ) R_{\omega j m}(r)=0. \end{aligned}$$

(40)

We now proceed to derive the solution for the near and the far region and try to find out a single solution by matching the solution for near-region at infinitely with solution for the far-region at its initial point such that this specific single solution be useful in the vicinity of the cardinal region. It is beneficial at this stage to introduce a new variable y which is defined by $y=\frac{r-r_{eh}}{r_{eh}-r_{ch}}$. In terms of y the equation (40) turns into

$$\begin{aligned}&\frac{y^{2}(y+1)^{2}}{(\ell +1)^{2}} \frac{\mathrm {d}^{2} R_{\omega j m}(y)}{\mathrm {d} y^{2}}+\frac{y(y+1)(2 y+1)}{(\ell +1)^{2}} \frac{\mathrm {d} R_{\omega j m}(y)}{\mathrm {d} y} \nonumber \\&\quad +\left( \frac{{\mathcal {Q}}^2 y^{4}}{1+\ell }+\frac{B^{2}}{1+\ell }-\frac{j(j+1)}{\ell +1} y(y+1)\right. \nonumber \\&\quad \left. -\frac{{\hat{\mu }}^{2} {\mathcal {Q}}^{2}}{\omega ^{2}} y^{3}(y+1)-{\hat{\mu }}^{2} r_{e h}^{2} y(y+1)\right. \nonumber \\&\quad \left. -\frac{2 {\hat{\mu }}^{2} r_{e h} {\mathcal {Q}}}{\omega } y^{2}(y+1) \right) R_{\omega j m}(y)=0, \end{aligned}$$

(41)

Under the approximation ${\hat{a}} \omega \ll 1$, where ${\mathcal {Q}}=\left( r_{e h}-r_{c h}\right) \omega$ and $B=\frac{(\omega -m {\hat{\Omega }})}{r_{e h}-r_{c h}} r_{e h}^{2}$. For the near-region, we have $P y \ll 1$ and ${\hat{\mu }}^{2} r_{e h}^{2} \ll 1$. The above equation is simplified to

$$\begin{aligned}&y^{2}(y+1)^{2} \frac{\mathrm {d}^{2} R_{\omega j m}(y)}{\mathrm {d} y^{2}}+y(y+1)(2 y+1) \frac{\mathrm {d} R_{\omega j m}(y)}{\mathrm {d} y}\nonumber \\&\quad +\left( (\ell +1)B^{2}-j(j+1)(\ell +1) y(y+1)\right) R_{\omega j m}(r) =0.\nonumber \\ \end{aligned}$$

(42)

Since the Compton wavelength of the boson participating in the scattering process is much smaller than the size of the black hole the approximation $\left( {\hat{\mu }}^{2} r_{e h}^{2} \ll 1\right)$ holds good. The general solution of the above equation in terms of associated Legendre function of the first kind $P_{\lambda }^{\nu }(y)$ can be written down as

$$\begin{aligned} R_{\omega j m}(y)=d P^{2i\sqrt{1+\ell }B}_{\frac{\sqrt{1+4j(j+1) (\ell +1)}-1}{2}}(1+2y). \end{aligned}$$

(43)

If we now use the relation

$$\begin{aligned} P_{\lambda }^{\nu }(z)= & {} \frac{1}{\Gamma (1-\nu )}\left( \frac{1+z}{1-z}\right) ^{\nu / 2}\nonumber \\&\times { }_{2} F_{1}\left( -\lambda , \lambda +1 ; 1-\nu ; \frac{1-z}{2}\right) , \end{aligned}$$

(44)

it enables us to express $R_{\omega j m}(y)$ in terms of the ordinary hypergeometric functions ${ }_{2} F_{1}(a, b ; c ; z)$ :

$$\begin{aligned}&R_{\omega j m}(y)\nonumber \\&\quad =d\left( \frac{y}{y+1}\right) ^{-i\sqrt{\ell +1} B}{ }_{2} F_{1}\left( \frac{1-\sqrt{1+4(\ell +1) j(j+1)}}{2},\right. \nonumber \\&\qquad \left. \frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2} ; 1-2 i\sqrt{\ell +1} B ;-y\right) .\nonumber \\ \end{aligned}$$

(45)

We are intended to find out a single solution using the matching condition at the desired position where the two solutions mingle with each other. In this respect, we need to observe the large y behavior of the above expression. The Eq. (45) for large y, i.e., $(y \rightarrow \infty$ reduces to

$$\begin{aligned}&R_{\text{ near-large } y} \nonumber \\&\quad \sim d \left( \frac{\Gamma (\sqrt{1+4(\ell +1) j(j+1)}) \Gamma (1-2 i\sqrt{\ell +1} B)}{\Gamma \left( \frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2} -2 i\sqrt{\ell +1} B\right) \Gamma \left( \frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}\right) }\right. \nonumber \\&\qquad \times \left. y^{\frac{\sqrt{1+4(\ell +1) j(j+1)}-1}{2}}+\right. \end{aligned}$$

(46)

$$\begin{aligned}&\frac{\Gamma (-\sqrt{1+4(\ell +1) j(j+1)}) \Gamma (1-2 i\sqrt{\ell +1} B)}{\Gamma \left( \frac{1-\sqrt{1+4(\ell +1) j(j+1)}}{2}\right) \Gamma \left( \frac{1-\sqrt{1+4(\ell +1) j(j+1)}}{2}-2 i\sqrt{\ell +1} B\right) }\nonumber \\&\quad \times y^{\left. -\frac{\sqrt{1+4(\ell +1) j(j+1)}+1}{2}\right) } . \end{aligned}$$

(47)

For the far-region, we can use the approximations $y+1 \approx y$ and ${\hat{\mu }}^{2} r_{e h}^{2} \ll 1$. We may drop all the terms except those which describe the free motion with momentum j and that reduces equation (40) to

$$\begin{aligned}&\frac{\mathrm {d}^{2} R_{\omega j m}(y)}{\mathrm {d} y^{2}}+\frac{2}{y} \frac{\mathrm {d} R_{\omega j m}(y)}{\mathrm {d} y}\nonumber \\&\quad +\left( k_{\ell }^{2}-\frac{j(j+1)(\ell +1)}{y^{2}}\right) R_{\omega j m}(y)=0, \end{aligned}$$

(48)

where $k_{\ell } \equiv \frac{P\sqrt{1+\ell }}{\omega } \sqrt{\omega ^{2}-\mu ^{2}}$. Equation (48) has the general solution

$$\begin{aligned} R_{\omega j m, \text{ far } }= & {} e^{-i k y}\Bigg (c_{1} y^{\frac{\sqrt{1+4(\ell +1) j(j+1)}-1}{2}} \nonumber \\&\times M\Bigg (\frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2},\nonumber \\&1+\sqrt{1+4(\ell +1) j(j+1)}, 2 i k_{\ell } y\Bigg )\nonumber \\&+c_{2} y^{-\frac{\sqrt{1+4(\ell +1) j(j+1)}+1}{2}}\nonumber \\&\times M\Bigg (\frac{1-\sqrt{1+4(\ell +1) j(j+1)}}{2},\nonumber \\&1-\sqrt{1+4(\ell +1) j(j+1)}, 2 i k_{\ell } y)\Bigg ). \end{aligned}$$

(49)

Here M(a; b; y) stands for the confluent hypergeometric Kummer function of the first kind. In order to match the solution with (47), we look for the small y behavior of the solution (49). The solutions (47) and (51) are susceptible for matching, since these two have common region of interest. The matching of the asymptotic solutions (47) and (51) enables us to compute the scalar wave flux at infinity that results in

$$\begin{aligned} c_{1}=&d \frac{\Gamma (\sqrt{1+4(\ell +1) j(j+1)}) \Gamma (1-2 i\sqrt{\ell +1} B)}{\Gamma \left( \frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2} -2 i\sqrt{\ell +1} B\right) \Gamma \left( \frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}\right) }, \nonumber \\ c_{2}=&d \frac{\Gamma (-\sqrt{1+4(\ell +1) j(j+1)}) \Gamma (1-2 i\sqrt{\ell +1} B)}{\Gamma \left( \frac{1-\sqrt{1+4(\ell +1) j(j+1)}}{2}-2 i\sqrt{\ell +1} B\right) \Gamma \left( \frac{1-\sqrt{1+4(\ell +1) j(j+1)}}{2}\right) }. \end{aligned}$$

(50)

For small $y (y \rightarrow 0)$, the Eq. (49) turns into

$$\begin{aligned} R_{\omega j m, \text{ far-small } \mathrm {y}} \sim y^{-\frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}}. \end{aligned}$$

(51)

Since these two solutions (47) and (51) have a common region of interest, the solutions are susceptible for matching. We therefore compute the scalar wave flux at infinity resulted in by matching the asymptotic solutions (47) and (51) and we have

$$\begin{aligned} c_{1}=&d \frac{\Gamma (\sqrt{1+4(\ell +1) j(j+1)}) \Gamma (1-2 i\sqrt{\ell +1} B)}{\Gamma \left( \frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2} -2 i\sqrt{\ell +1} B\right) \Gamma \left( \frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}\right) }, \nonumber \\ c_{2}=&d \frac{\Gamma (-\sqrt{1+4(\ell +1) j(j+1)}) \Gamma (1-2 i\sqrt{\ell +1} B)}{\Gamma \left( \frac{1-\sqrt{1+4(\ell +1) j(j+1)}}{2}-2 i\sqrt{\ell +1} B\right) \Gamma \left( \frac{1-\sqrt{1+4(\ell +1) j(j+1)}}{2}\right) }. \end{aligned}$$

(52)

We expand Eq. (49) around infinity which after expansion turns into

$$\begin{aligned}&c_{1} \frac{\Gamma (1+\sqrt{1+4(\ell +1) j(j+1)})}{\Gamma \left( \frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}\right) } k_{\ell }^{-\frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}}\nonumber \\&\quad \times \left( (-2 i)^{-\frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}} \frac{e^{-i k_{\ell } y}}{y}\right. \nonumber \\&\quad \left. +(2 i)^{-\frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}} \frac{e^{i k_{\ell } y}}{y}\right) \nonumber \\&\quad +c_{2} \frac{\Gamma (1-\sqrt{1+4(\ell +1) j(j+1)})}{\Gamma \left( \frac{1-\sqrt{1+4(\ell +1) j(j+1)}}{2}\right) } k_{\ell }^{\frac{\sqrt{1+4(\ell +1) j(j+1)}-1}{2}}\nonumber \\&\quad \times \left( (-2 i)^{\frac{\sqrt{1+4(\ell +1) j(j+1)}-1}{2}} \frac{e^{-i k_{\ell } y}}{y}\right. \nonumber \\&\quad \left. +(2 i)^{\frac{\sqrt{1+4(\ell +1) j(j+1)}-1}{2}} \frac{e^{i k_{\ell } y}}{y}\right) . \end{aligned}$$

(53)

With the approximations $\frac{1}{y} \sim \frac{{\mathcal {Q}}}{\omega } \cdot \frac{1}{r}, \quad e^{\pm i k_{\ell } y} \sim e^{\pm i \sqrt{(1+\ell )(\omega ^{2}-\mu ^{2})} r}$, if we match the above solution with the radial solution (36)

$$\begin{aligned}&R_{\infty }(r) \sim {\mathcal {D}}_{i n}^{\infty } \frac{e^{-i \sqrt{\frac{\omega ^{2}}{1+\ell }-{\hat{\mu }}^{2}} r^{*}}}{r}+{\mathcal {D}}_{r e f}^{\infty } \frac{e^{i \sqrt{\frac{\omega ^{2}}{1+\ell }-{\hat{\mu }}^{2}} r^{*}}}{r}, \quad \text{ for } \quad \\&r \rightarrow \infty \end{aligned}$$

we get

$$\begin{aligned} \begin{array}{l} {\mathcal {D}}_{i n}^{\infty }=\frac{{\mathcal {Q}}}{\omega }\left( c_{1}(-2 i)^{-\frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}} \frac{\Gamma (1+\sqrt{1+4(\ell +1)j(j+1)})}{\Gamma \left( \frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}\right) } k_{\ell }^{-\frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}}\right. \\ \qquad \qquad \left. + c_{2}(-2 i)^{\frac{\sqrt{1+4(\ell +1)j(j+1)}-1}{2}} \frac{\Gamma (1-\sqrt{1+4(\ell +1)j(j+1)})}{\Gamma \left( \frac{1-\sqrt{1+4(\ell +1)j(j+1)}}{2}\right) } k_{\ell }^{\frac{\sqrt{1+4(\ell +1)j(j+1)}-1}{2}}\right) , \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{l} {\mathcal {D}}_{r e f}^{\infty }=\frac{{\mathcal {Q}}}{\omega }\left( c_{1}(2 i)^{-\frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}} \frac{\Gamma (1+\sqrt{1+4(\ell +1)j(j+1)})}{\Gamma \left( \frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}\right) } k_{\ell }^{-\frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}}\right. \\ \qquad \qquad \left. +c_{2}(2 i) \frac{\sqrt{1+4(\ell +1)j(j+1)}-1}{2} \frac{\Gamma (1-\sqrt{1+4(\ell +1)j(j+1)})}{\Gamma \left( \frac{1-\sqrt{1+4(\ell +1)j(j+1)}}{2}\right) } k_{\ell }^{\frac{\sqrt{1+4(\ell +1)j(j+1)}-1}{2}}\right) . \end{array} \end{aligned}$$

Fig. 5

Variation of amplification factors with $\ell$ for non-superradiant multipoles with ${\hat{\mu }}=0.1, b=0.01M^2$, and ${\hat{a}}=0.3 M$

Fig. 6

Variation of amplification factors with $\ell$ for various multipoles with ${\hat{\mu }}=0.1, b=0.02M^2$, and ${\hat{a}}=0.55 M$

Substituting the expressions of $c_{1}$ and $c_{2}$ from Eq. (50) into the above expressions we have

$$\begin{aligned} {\mathcal {D}}_{in}^{\infty }= & {} \frac{d(-2 i)^{-\frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}}}{\sqrt{(1+\ell )(\omega ^{2}-\mu ^{2})}} \nonumber \\&\cdot \frac{\Gamma (\sqrt{1+4(\ell +1) j(j+1)}) \Gamma (1+\sqrt{1+4(\ell +1) j(j+1)})}{\Gamma \left( \frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}-2 i\sqrt{\ell +1} B\right) \left( \Gamma \left( \frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}\right) \right) ^{2}} \nonumber \\&\times \Gamma (1-2 i\sqrt{\ell +1} B) k_{\ell }^{\frac{1-\sqrt{1+4(\ell +1)j(j+1)}}{2}}\nonumber \\&+\frac{d(-2 i)^{\frac{\sqrt{1+4(\ell +1)j(j+1)}-1}{2}}}{\sqrt{(1+\ell )(\omega ^{2}-{\hat{\mu }}^{2})}} \nonumber \\&\times \frac{\Gamma (1-\sqrt{1+4(\ell +1)j(j+1)}) \Gamma (-\sqrt{1+4(\ell +1)j(j+1)})}{\left( \Gamma \left( \frac{1-\sqrt{1+4(\ell +1)j(j+1)}}{2}\right) \right) ^{2} \Gamma \left( \frac{1-\sqrt{1+4(\ell +1)j(j+1)}}{2}-2 i\sqrt{\ell +1} B\right) } \nonumber \\&\times \Gamma (1-2 i\sqrt{\ell +1} B) k_{\ell }^{\frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}}, \end{aligned}$$

(54)

and

$$\begin{aligned} {\mathcal {D}}_{ref}^{\infty }= & {} \frac{d(2 i)^{-\frac{1+\sqrt{1+4(\ell +1) j(j+1)}}{2}}}{\sqrt{(1+\ell )(\omega ^{2}-\mu ^{2})}} \nonumber \\&\cdot \frac{\Gamma (\sqrt{1+4(\ell +1) j(j+1)}) \Gamma (1+\sqrt{1+4(\ell +1) j(j+1)})}{\Gamma \left( \frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}-2 i\sqrt{\ell +1} B\right) \left( \Gamma \left( \frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}\right) \right) ^{2}}\nonumber \\&\times \Gamma (1-2 i\sqrt{\ell +1} B) k_{\ell }^{\frac{1-\sqrt{1+4(\ell +1)j(j+1)}}{2}}+\frac{d(2 i)^{\frac{\sqrt{1+4(\ell +1)j(j+1)}-1}{2}}}{\sqrt{(1+\ell )(\omega ^{2}-{\hat{\mu }}^{2})}} \nonumber \\&\times \frac{\Gamma (1-\sqrt{1+4(\ell +1)j(j+1)}) \Gamma (-\sqrt{1+4(\ell +1)j(j+1)})}{\left( \Gamma \left( \frac{1-\sqrt{1+4(\ell +1)j(j+1)}}{2}\right) \right) ^{2} \Gamma \left( \frac{1-\sqrt{1+4(\ell +1)j(j+1)}}{2}-2 i\sqrt{\ell +1} B\right) } \nonumber \\&\times \Gamma (1-2 i\sqrt{\ell +1} B) k_{\ell }^{\frac{1+\sqrt{1+4(\ell +1)j(j+1)}}{2}}. \end{aligned}$$

(55)

The amplification factor ultimately results out to be

$$\begin{aligned} Z_{j m} \equiv \frac{\left| {\mathcal {D}}_{r e f}^{\infty }\right| ^{2}}{\left| {\mathcal {D}}_{i n}^{\infty }\right| ^{2}}-1. \end{aligned}$$

(56)

Equation (56) is a general expression of the amplification factor obtained by making use of the asymptotic matching method. When $\frac{\left| {\mathcal {D}}_{ref}^{\infty }\right| ^{2}}{\left| {\mathcal {D}}_{i n}^{\infty }\right| ^{2}}$ acquires a value greater than unity there will be a gain in amplification factor that corresponds to superradiance phenomena. However, a negative value of the amplification factor indicates a loss in amplification that corresponds to the non-appearance of superradiance. To study the effect of Lorentz violation on the superradiance phenomena, it will be useful to plot $Z_{j m}$ versus $M\omega$ for different values of the the Lorentz violation parameters. In Fig. 6, we present the variation of $Z_{j m}$ versus $M\omega$ for the leading multipoles $j= 1$ and 2 taking different values (both negative and positive) of the Lorentz violation parameter $\ell$. From the Fig. 5 along with Fig. 6, it is evident that superradiance for a particular j occurs when the allowed values of m are restricted to $m > 0$.

For negative m, amplification factor takes negative value which refers to the nonoccurrence of superradiance. The plots also show transparently that with the decrease in the value of the Lorentz violation parameters $\ell$ the superradiance process enhances. The reverse is the case of course when the value of the Lorentz violation parameter decreases. In Fig. 8 we have also studied the effect of the parameter b on the superradiance scenario. It shows that the superradiance scenario gets diminished with the increase in the value of the parameter b. In [75] we have noticed that the size of the shadow decreases with the increase in the value of both the parameters $\ell$ and b. The only difference is that $\ell$ can take both positive and negative values, however, b as per definition can not be negative. However, with the increase in ${\hat{a}}$ the superradiance effect increases as is found from Fig. 7. Therefore, an indirect relation of superradiance with the size of the shadow is being revealed through this analysis. A decrease in the value of b and $\ell$ indicate the increase in the size of the shadow (Fig. 8).

Fig. 7

Variation of amplification factors with ${\hat{a}}$ for various multipoles with ${\hat{\mu }}=0.1$ and $b=0.02 M^2$. For left ones $\ell =-0.5$ and for right ones $\ell =0.5$

Fig. 8

Variation of amplification factors with b for various multipoles with ${\hat{\mu }}=0.1$ and ${\hat{a}}=0.55 M$. For left ones $\ell =-0.5$ and for right ones $\ell =0.5$

Fig. 9

Parameter space($m\Omega$-$\mu$) for massive scalar field where colored area represents region with stable dynamics and non-colored area represents region with unstable dynamics. Here ${\hat{a}}=0.51\, {\text {M}} \text { and } b=0.01 M^{2}$

Fig. 10

Parameter space($m\Omega$-$\mu$) for massive scalar field where colored area represents region with stable dynamics and non-colored area represents region with unstable dynamics. Here ${\hat{a}}=0.51\, {\text {M}} \text { and } l=0.5$

4.2 Superradiant instability for Lorentz violating and NC Kerr-like black hole

From Eq. (29) we have

$$\begin{aligned} {\hat{\Delta }} \frac{d}{d r}\left( {\hat{\Delta }} \frac{d R_{\omega j m}}{d r}\right) +{\mathcal {F}} R_{\omega j m}=0, \end{aligned}$$

(57)

where for a slowly rotating black hole $({\hat{a}} \omega \ll 1)$

$$\begin{aligned} {\mathcal {F}}\equiv & {} \frac{\left( \left( r^2+{\hat{a}}^{2}\right) \omega -m {\hat{a}}\right) ^{2}}{1+\ell }\\&+{\hat{\Delta }}\left( 2 m {\hat{a}} \omega -j(j+1)-\mu ^{2}r^2\right) . \end{aligned}$$

If we now look for the black hole bomb mechanism, we would have the following solutions for the radial Eq. (57)

$$\begin{aligned} R_{\omega j m} \sim \left\{ \begin{array}{ll} e^{-i(\omega -m {\hat{\Omega }}) r_{*}} &{} \text{ as } r \rightarrow r_{e h} \left( r_{*} \rightarrow -\infty \right) \\ \frac{e^{-\sqrt{\mu ^{2}-\omega ^{2} r_{*}}}}{r} &{} \text{ as } r \rightarrow \infty \left( r_{*} \rightarrow \infty \right) \end{array}\right. \end{aligned}$$

The above solution represents the physical boundary condition that the scalar wave at the black hole horizon is purely in-going while at spatial infinity it is decaying exponentially (bounded) solution, provided that $\omega ^{2}<\mu ^{2}$ (Figs. 9, 10). With the new radial function

$$\begin{aligned} \psi _{\omega j m} \equiv \sqrt{{\hat{\Delta }}} R_{\omega j m}, \end{aligned}$$

the radial Eq. (57) turns into

$$\begin{aligned} \left( \frac{d^{2}}{d r^{2}}+\omega ^{2}-V\right) \psi _{\omega j m}=0. \end{aligned}$$

with

$$\begin{aligned} \omega ^{2}-V=\frac{{\mathcal {F}}+\frac{M \left( M-\frac{8 \sqrt{t}}{\sqrt{\pi }}\right) -a^2 (\ell +1)}{(\ell +1)^2}}{{\hat{\Delta }}^{2}}, \end{aligned}$$

which is the Regge-Wheel equation. By discarding the terms ${\mathcal {O}}\left( 1 / r^{2}\right)$ the asymptotic form of the effective potential V(r) looks

$$\begin{aligned} V(r)=\mu ^{2}\left( 1+\ell \right) -\left( 1+\ell \right) \frac{4 M \omega ^{2}}{r}+(\ell +1) \frac{2 M \mu ^{2}}{r}. \end{aligned}$$

To realize the trapping meaningfully by the above effective potential it is necessary that its asymptotic derivative will be positive i.e. $V^{\prime } \rightarrow 0^{+}$ as $r \rightarrow \infty$ [124]. This along with the fact that superradiant amplification of scattered waves occurs when $\omega < m {\hat{\Omega }}$ we get the regime

$$\begin{aligned} \frac{\mu }{\sqrt{2}}<\omega ^{2}<m {\hat{\Omega }}, \end{aligned}$$

in which the integrated system of NC Kerr-like bumblebee black hole and massive scalar field may experience a superradiant instability which known as the black hole bomb. The dynamics of the massive scalar field in NC Kerr like black hole will remain stable when $\mu \ge \sqrt{2}m{\hat{\Omega }}$.

5 Photon orbit and black hole shadow

In this section, we study the black hole shadow related to this modified theory. There are several studies related to the black hole shadow from which we will get the necessary inputs for the study [37,38,39,40]. In order to study the shadow, we introduce two conserved parameters $\xi$ and $\eta$ as usual which are defined by

$$\begin{aligned} \xi =\frac{L_{z}}{E} \quad \text {and} \quad \eta =\frac{{\mathcal {Q}}}{E^{2}}, \end{aligned}$$

(58)

where $E, L_{z}$, and ${\mathcal {Q}}$ are the energy, the axial component of the angular momentum, and the Carter constant respectively. Then the null geodesics in the bumblebee rotating black hole spacetime in terms of $\xi$ are given by

$$\begin{aligned} \rho ^{2} \frac{d r}{d \lambda }&=\pm \sqrt{R}, \quad \rho ^{2} \frac{d \theta }{d \lambda }=\pm \sqrt{\Theta }, \nonumber \\ (1+\ell ) {\hat{\Delta }} \rho ^{2} \frac{d t}{d \lambda }&=A-2 \sqrt{1+\ell } {\text {Mra}}\xi ,\nonumber \\ (1+\ell ) {\hat{\Delta }} \rho ^{2} \frac{d \phi }{d \lambda }&=2 \sqrt{1+\ell } M r a+\frac{\xi }{\sin ^{2} \theta }\left( \rho ^{2}-2 M r\right) ,\nonumber \\ \end{aligned}$$

(59)

where $\lambda$ is the affine parameter and

$$\begin{aligned} R(r)= & {} \left[ \frac{r^{2}+(1+\ell ) a^{2}}{\sqrt{1+\ell }}-a \xi \right] ^{2}\nonumber \\&-{\hat{\Delta }}\left[ \eta +(\xi -a\sqrt{1+\ell })^{2}\right] ,\quad \nonumber \\ \Theta (\theta )= & {} \eta +(1+\ell ) a^{2} \cos ^{2} \theta -\xi ^{2} \cot ^{2} \theta . \end{aligned}$$

(60)

The radial equation of motion can be written down in the familiar form

$$\begin{aligned} \left( \rho ^{2} \frac{d r}{d \lambda }\right) ^{2}+V_{e f f}=0. \end{aligned}$$

(61)

The effective potential $V_{e f f}$ then reads

$$\begin{aligned} V_{e f f}&=-\left[ \frac{r^{2}+(1+\ell ) a^{2}}{\sqrt{1+\ell }}-a \xi \right] ^{2}\nonumber \\&\quad +{\hat{\Delta }}\left[ \eta +(\xi -a\sqrt{1+\ell })^{2}\right] . \end{aligned}$$

(62)

The following equations describe the unstable spherical orbit on the equatorial plane, $\theta =\frac{\pi }{2}$.

$$\begin{aligned}&\theta =\frac{\pi }{2},\quad R(r)=0,\quad \frac{d R}{d r}=0,\quad \nonumber \\&\frac{d^{2} R}{d r^{2}}<0,\quad \text {and} \quad \eta =0. \end{aligned}$$

(63)

We plot the potential $V_{e f f}$ versus r/M with $\xi =\xi _{c}+0.2$, where $\xi _{c}$ is the value of $\xi$ for equatorial spherical unstable orbit (Figs. 11, 12, 13).

Fig. 11

The left and the right panels describe the effective potential for prograde orbits and the retrograde orbits respectively for various values of ${\hat{a}}$ with $b=0.01 M^{2}$ and $\ell =0.1$

Fig. 12

The left and the right panels describe the effective potential for prograde orbits and the retrograde orbits respectively for various values of b with ${\hat{a}}=0.1 M$ and $\ell =0.1$

Fig. 13

The left panel describes the effective potential for prograde orbits and right panel describes the retrograde orbits for various values of $\ell$ with ${\hat{a}}=0.1 M$ and $b=0.03 M^{2}$

The plots depicted above show that the turning points for prograde orbits shift towards the left when a or b increases. We also plot critical radii of prograde and retrograde orbits for the different scenarios in the Fig. 14 furnished below.

Fig. 14

The left panel shows the variation of critical radius for prograde orbits and the right panel shows the variation of critical radius for retrograde orbits for various values of b with $\ell =0.3$

It can be concluded from the above plots that critical radii, both for the prograde and retrograde orbits, decrease with the increase in the NC parameter b. For more generic orbits $\theta \ne \pi / 2$ and $\eta \ne 0,$ the solution of Eq. (63) $r=r_{s}$, gives the r-constant orbit, which is also called spherical orbit and the conserved parameters of the spherical orbits are given by

$$\begin{aligned}&\xi _{s}=\frac{\left( a^{2}\left( 1+\ell \right) +r^{2}\right) {\hat{\Delta }}^{'}(r) -4r{\hat{\Delta }}(r)}{a\sqrt{1+\ell }{\hat{\Delta }}^{'}(r)},\nonumber \\&\eta _{s}= \frac{r^{2}\left( 8{\hat{\Delta }}(r)\left( 2a^{2}\left( 1+\ell \right) +r{\hat{\Delta }}^{'}(r)\right) -r^{2}{\hat{\Delta }}^{'}(r)^{2} -16{\hat{\Delta }}^{'}(r)^{2}\right) }{a^{2}\left( 1+l\right) {\hat{\Delta }}^{'}(r)^{2}},\nonumber \\ \end{aligned}$$

(64)

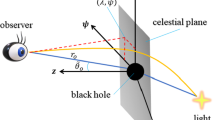
where $'$ stands for differentiation with respect to radial coordinate. The above expressions in the limit $\ell \rightarrow 0$ and $b \rightarrow 0$ reduce to those for Kerr black hole. It would be useful at this point to introduce two celestial coordinates for a better study of the shadow. The two celestial coordinates, which are used to describe the shape of the shadow that an observer sees in the sky, can be given by

$$\begin{aligned} \alpha (\xi , \eta ; \theta )= & {} \lim _{r \rightarrow \infty } \frac{-r p^{(\varphi )}}{p^{(t)}} = -\xi _{s} \csc \theta ,\nonumber \\ \beta (\xi , \eta ; \theta )= & {} \lim _{r \rightarrow \infty } \frac{r p^{(\theta )}}{p^{(t)}} =\sqrt{\left( \eta _{s}+a^{2} \cos ^{2} \theta -\xi _{s}^{2} \cot ^{2} \theta \right) },\nonumber \\ \end{aligned}$$

(65)

where $\left( p^{(t)}, p^{(r)}, p^{(\theta )}, p^{(\phi )}\right)$ are the tetrad components of the photon momentum with respect to locally non-rotating reference frames [21].

With these inputs, we now plot black hole shadows for various cases which are depicted in the Figs. 15 and 16.

Fig. 15

The left panel gives shapes of the shadow for various values of ${\hat{a}}$ with $b=0.01 M^{2}$, $\ell =0.1$ and $\theta =\pi /2$. The right panel gives shapes of the shadow for various values of b with $a=0.1 M$, $\ell =0.1$, and $\theta =\pi /2$

From the above plots, we observe that the size of the shadow increases with the increase in ${\hat{a}}$, whereas it decreases with the increase in b. Using the parameters which are introduced by Hioki and Maeda [23], we analyze the deviation from the circularity $\left( {\hat{\Delta }}_{s}\right)$ and the size $\left( R_{s}\right)$ of the shadow cast by the black hole.

Fig. 16

The black hole shadow and reference circle. ds is the distance between the left points of the shadow and the reference circle

For calculating these parameters, we consider five points $\left( \alpha _{t}, \beta _{t}\right) ,\left( \alpha _{b}, \beta _{b}\right) ,\left( \alpha _{r}, 0\right)$ $\left( \alpha _{p}, 0\right)$ and $\left( {\bar{\alpha }}_{p}, 0\right)$ which represent top, bottom, rightmost, and leftmost point of the shadow and leftmost point of the reference circle respectively. So, we have

$$\begin{aligned} R_{s}=\frac{\left( \alpha _{t}-\alpha _{r}\right) ^{2}+\beta _{t}^{2}}{2\left| \alpha _{t}-\alpha _{r}\right| } \end{aligned}$$

and

$$\begin{aligned} \delta _{s}=\frac{\left| {\bar{\alpha }}_{p}-\alpha _{p}\right| }{R_{s}}. \end{aligned}$$

In the following Fig. 17, we plot $R_{s}$ and $\delta _{s}$ for various scenarios to study how $R_{s}$ and $\delta _{s}$ vary with parameters of the modified theory of gravity.

Fig. 17

The left one shows variation of $R_{s}$ for various values of ${\hat{a}}$ with $\ell =-0.2$ and $\theta =\pi /2$. The right one shows variation of $\delta _{s}$ for various values of ${\hat{a}}$ with $\ell =-0.2$ and $\theta =\pi /2$

From the above plots we observe that $R_{s }$ decreases with an increase in b for fixed values of ${\hat{a}}$, whereas for fixed values of b, it increases with the increase in ${\hat{a}}$. On the other hand, $\delta _{s}$ increases with the increase in ${\hat{a}}$ for fixed value of b as well as with the increase in b for fixed values of ${\hat{a}}$.

6 Computation of energy emission rate

In this section, we study the possible visibility of the NC Kerr-like black hole through the shadow cast. In the vicinity of limiting constant value, the cross-section of the black hole’s absorption moderates lightly at high energy. We know that a rotating black hole can absorb electromagnetic waves. So the absorbing cross-section for a spherically symmetric black hole is given by [116]

$$\begin{aligned} \sigma _{l i m}=\pi R_{s}^{2}. \end{aligned}$$

(66)

Using the above equation the energy emission rate is obtained [117]:

$$\begin{aligned} \frac{d^{2} E}{d \omega d t}=\frac{2 \pi ^{3} R_{s}^{2}}{e^{\left( \frac{\omega }{T}\right) }-1} \omega ^{3}, \end{aligned}$$

(67)

where $T=\frac{\sqrt{1+\ell } {\hat{\Delta }}^{\prime }\left( r_{+}\right) }{4 \pi \left[ r_{+}^{2} +(1+\ell ) a^{2}\right] }$ is the Hawking temperature and $\omega$ the frequency of radiation.

Fig. 18

The left panel gives variation of emission rate against $\omega$ for various values of ${\hat{a}}$ with $b=0.01 M^{2}$ and $\ell =0.3$. The right panel gives variation of emission rate against $\omega$ for various values of b with $a=0.1 M$ and $\ell =0.3$

Fig. 19

It gives variation of emission rate against $\omega$ for various values of $\ell$ with $b=0.02 M^{2}$ and ${\hat{a}}=0.1 M$

In Figs. 18 and 19, we have shown the plots of energy emission rate versus $\omega$ for various cases. It is clear from the plots that the emission rate decreases with the increase in the value of b for any set of fixed values of ${\hat{a}}$ and $\ell$. It also decreases with an increase in $\ell$, for ${\hat{a}}$ and b being fixed, and with an increase in ${\hat{a}}$, when $\ell$ and b remain fixed.

7 Constraining from the observed data for $\mathrm {M}87^{*}$

This section is devoted to the constraining of the parameters involved in this extended theory. We compare the shadows generated from the numerical calculation for NC Kerr-like black holes with the observed shadow for the $\mathrm {M}87^{*}$ black hole. For comparison, we consider the experimentally obtained astronomical data corresponding to the deviation from circularity $\Delta C \le 0.10$ and angular diameter $\theta _{d}=42\pm 3 \mu as$. The boundary of the shadow is described by the polar coordinate $(R(\phi ),\phi )$ with the origin at the center of the shadow $(\alpha _{C}, \beta _{C})$ where $\alpha _{C}=\frac{|\alpha _{max}+\alpha _{min}|}{2}$, and $\beta _{C}=0$.

Fig. 20

For the left panel the inclination angle is $90^{\circ }$ and for the right panel the inclination angle is $17^{\circ }$. The black solid lines correspond to $\Delta C=0.1$

Fig. 21

For the left panel the inclination angle is $90^{\circ }$ and for the right panel the inclination angle is $17^{\circ }$. The black solid lines correspond to $\theta _{d}=39 \mu as$

If a point $(\alpha , \beta )$ over the boundary of the image subtends an angle $\phi$ on the $\alpha$ axis at the geometric center, $\left( \alpha _{C}, 0\right)$. If $R(\phi )$ be the distance between the point $(\alpha , \beta )$ and $\left( \alpha _{C}, 0\right)$, then the average radius $R_{\text {avg}}$ of the image is given by [120]

$$\begin{aligned} R_{\text{ avg }}^{2} \equiv \frac{1}{2 \pi } \int _{0}^{2 \pi } d \phi R^{2}(\phi ), \end{aligned}$$

(68)

where $R(\phi ) \equiv \sqrt{\left( \alpha (\phi )-\alpha _{C}\right) ^{2}+\beta (\phi )^{2}}$, and $\phi = tan^{-1}\frac{\beta (\phi )}{\alpha (\phi )-\alpha _{C}}$.

With the above inputs, the circularity deviation $\Delta C$ is defined by [24]

$$\begin{aligned} \Delta C \equiv 2\sqrt{\frac{1}{2 \pi } \int _{0}^{2 \pi } d \phi \left( R(\phi )-R_{\text{ avg } }\right) ^{2}}. \end{aligned}$$

(69)

We also consider the angular diameter of the shadow which is define by

$$\begin{aligned} \theta _{d}=\frac{2}{d}\sqrt{\frac{A}{\pi }}, \end{aligned}$$

(70)

where $A=2\int _{r_{-}}^{r_{+}} \beta d\alpha$ is the area of the shadow and $d=16.8 Mpc$ is the distance of $M87^{*}$ from the Earth. These relations will enable us to accomplish a comparison between the theoretical predictions for NC Kerr-like black-hole shadows and the experimental findings of the EHT collaboration. In the Figs. 20 and 21, the deviation from circularity, $\Delta C$ is shown for NC Kerr-like black holes for inclination angles $\theta =90^{\circ }$ and $\theta =17^{\circ }$ respectively.

From the above plots, we can conclude that the constraint $\Delta C\le 0.1$ is satisfied for finite parameter space when the inclination angle is $90^{\circ }$, whereas, when the inclination angle is $17^{\circ }$, the constraint is satisfied for the entire parameter space. For inclination angles $\theta =90^{\circ }$ and $\theta =17^{\circ }$, the constraint $\theta _{d}=42\pm 3\mu$ within $1\sigma$ region is satisfied for finite parameter space. The circular asymmetry in the $M87^{*}$ shadow can also be defined in terms of the axial ratio $D_{X}$ which is the ratio of the major to the minor diameter of the shadow [25]. It is defined by [121]

$$\begin{aligned} D_{X}=\frac{{\hat{\Delta }} Y}{{\hat{\Delta }} X}=\frac{\beta _{t}-\beta _{b}}{\alpha _{r}-\alpha _{p}}. \end{aligned}$$

(71)

We should have $1 < D_{X}\lesssim 4/3$ in accordance with the EHT observations concerning $M87^{*}$ black hole [25]. Note that $D_{X}$ is another way of defining $\Delta C$. The observed axial ratio 4 : 3 indeed corresponds to $\Delta C \le 0.1$ [25]. In the Fig. 22, axial ratio, $D_{X}$ is shown for NC Kerr-like black holes for inclination angles $\theta =90^{\circ }$ and $\theta =17^{\circ }$ respectively.

Fig. 22

For the left panel the inclination angle is $90^{\circ }$ and for the right panel the inclination angle is $17^{\circ }$

From the plots above we have seen that the condition $1 <D_{X} \lesssim 4/3$ is satisfied for the entire parameter space of NC Kerr-like black holes. Thus NC Kerr-like black holes are remarkably consistent with EHT observed images of $M87^{*}$ black hole. Therefore, we can not rule out NC Kerr-like black holes from the observational data of $M87^{*}$ astronomical black hole shadow.

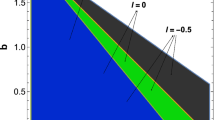
We can have the bound of the parameter b associated with the NC spacetime in a similar way we determined the bound of the parameter $\ell$ in [118]. By modelling M$87^{*}$ black hole as Kerr black hole, the author of the paper [122] obtained a lower limit of a for the M$87^{*}$ black hole. Bringing this result under consideration in [118] we put the interval of interest for a as [0.50M, 0.99M], and using the experimental constraints $\Delta C \le 0.10$ and $\theta _{d}=42\pm 3 \mu as$ with the information $a\in [0.50M,0.99M]$, we observed that $\ell \in (-1,0.621031]$. In a similar way taking into account the bounds $a\in [0.50M,0.99M]$ and $\ell \in (-1,0.621031]$ and the experimental constraints $\Delta C\le 0.1$ and $\theta _{d}=39\pm 3\mu as$, we get a bound on the parameter b which is linked with the NC spacetime. We find that the parameter $b\in [0,0.000505973M^{2}]$. It is intriguing to have an upper bound of b which is found out to be $0.000505973M^{2}$. Note that in [122] lower limit of is available for a. During the calculation the conversion between a and ${\hat{a}}$ is to be considered carefully. To the best of our knowledge, the bound of the parameter b from the shadow of the astronomical black hole has not yet been reported so far.

8 Summary and conclusion

In this work, we have developed a useful and decent framework where quantum correction because of the Lorentz violation and NC spacetime have been taken under consideration at the identical footing. The Lorentz violation is evident in this extended formalism due to the presence of bumblebee field. There is no direct connection to the Lorentz violation between the way NC spacetime is introduced [104, 105]. The bumblebee field serves as the sole source of the Lorentz violation in this formulation. The spacetime background in this extended formulation renders a NC Kerr-like Lorentz symmetry violating black hole. We have extensively studied different aspects of superradiance and shadow cast by the Kerr-like quantum corrected black hole. The spin, mass, Lorentz violation parameter, and the NC parameter involved in it determine the gravitational field of this black hole. First of all, we study geometry in detail concerning its horizon structure and ergosphere. Then we proceed on to study the two important optical phenomena in the vicinity of this black hole which was our main objective in this paper. We have found that superradiance process crucially depends on the parameter $\ell$ and b apart from its dependence on a or ${\hat{a}}$ which is linked with the spin of the black hole. The superradiance process enhances with the drop of the value of the Lorentz violation parameters and it diminishes when the increase in value of the Lorentz violation parameter $\ell$. We also observe that with the increase in the value of the parameter b the superradiance process gets diminished. However, with the increase in the value of ${\hat{a}}$ the superradiance process increases.

Next, we have brought into our investigation the effect of Lorentz violating parameter $\ell$ and NC parameter b on the size of the black hole shadow. We have observed that the size of the black hole shadow increases with an increase in the value of the parameter $\ell$, and it decreases with an increase in the value of the parameter b. Thus, it can be safely concluded that like the superradiance phenomena both the Lorentz violation and the NC spacetime have significant impacts on the shadow of the black hole.

We have also studied energy emission rates. These results have clearly established the influence of the Lorentz violation parameter and NC parameter on emission rate. We observe that energy emission rate decreases with an increase in the value of b for any set of fixed values of ${\hat{a}}$ and $\ell$. It also decreases with an increase in the value of $\ell$, when ${\hat{a}}$ and b are held fixed, and with an increase in the value of ${\hat{a}}$, when $\ell$ and b are kept fixed.

We have made an attempt to constrain parameters in our modified theories using the observations of EHT collaboration. For inclination angle $\theta =90^{\circ }$, the deviation from circularity $\Delta C\le 0.1$ and angular diameter $\theta _{d}=42\pm 3\mu$as within $1\sigma$ region are satisfied for finite parameter space $(\frac{b}{M^{2}} - \frac{{\hat{a}}}{M})$. For inclination angle $\theta =17^{\circ }$, the circularity deviation $\Delta C\le 0.1$ is satisfied for entire parameter space $(\frac{b}{M^{2}} - \frac{{\hat{a}}}{M})$. The angular diameter $\theta _{d}=42\pm 3\mu$ as within $1\sigma$ is satisfied for finite parameter space $(\frac{b}{M^{2}}-\frac{{\hat{a}}}{M})$. The axis ratio $D_{X}$ satisfies the constraint $1<D_{X}\lesssim 4/3$ for the entire parameter space at both the inclination angles $\theta =90^{\circ }$ as well as $\theta =17^{\circ }$. Therefore our study enables us to establish the fact that NC Kerr-like black holes are remarkably consistent with EHT images of $M87^{*}$. It demands that ruling NC Kerr-like black holes from the observational data of black hole shadow would be illogical. Thus NC Kerr-like black hole may be considered as a suitable candidate for the astrophysical black hole. It has also been shown that the possible upper bound of b which is associated with the NC spacetime is $0.000505973M^{2}$. It is intriguing and indeed a novel way to constrain the parameter associated with the NC spacetime from the shadow of an astronomical black hole.

Till now we do not have any available data to constrain the parameter $\ell$ and b from the superradiance effect and from the energy emission process. So the parameter con not be constrained from the knowledge of the superradiance phenomena and the energy emission process. We have made all the plots for the superradiance and the energy emission process maintaining the constraint obtained from the EHT data concerning the shadow of the $M87^*$ black hole.