1 Introduction

Various kinds of astronomical observations strongly confirm the existence of the black-hole in the Universe. The recent message of the detection of gravitational waves (GWs) [1] by the LIGO and VIRGO observatories, and the captured image of the black hole shadow of a super-massive \(M87^*\) black hole by the Event Horizon Telescope based on the very long baseline interferometry [2, 3] provides substantial evidence in support of the existence of black-hole. The perception of the fundamental nature of spacetime would also likely be enriched with the information accessible from these recent astronomical observations. So physics of black-hole acquire renewed interest.

General relativity and the standard model of particle physics are two very successful field theoretical models that assist us to describe our Universe. The formulation of both these theories is based on the well celebrated Lorentz symmetry. However, the regime of applicability and the nature of service towards describing the Universe by these two theories are profoundly different. The general relativity describes the gravitational interaction and it is a classical field theory in the curved spacetime and there is no direct way to include the quantum effect. On the contrary, the standard model describes the other fundamental interactions and it is the quantum field theory in the flat spacetime that neglects all gravitational effects, but to study the physical system in the vicinity of the Plank scale \((10^{-19} \ \mathrm{{GeV}})\), the effect due to gravity cannot be ignored, since the gravitational interaction is strong enough in that energy scale. Therefore, the study of physics in the vicinity of the Planck scale necessarily entails the unification of general relativity and standard model particle physics. Unfortunately, it is not yet developed with its full wings because there is no straightforward way to quantize the gravity. Moreover, Lorentz invariance is not tenable in the regime where spacetime is discrete in nature. So in the vicinity of the Planck scale, it would not be unreasonable to discard Lorentz invariance. On the other hand, Lorentz symmetry breaking in nature is considered as an interesting and useful idea because it arises as a possibility in the context of string theory [4,5,6,7], noncommutative field theories [8] or loop quantum gravity theory [9, 10]. As a consequence, nowadays Lorentz violation is considered as relevant as well as a beneficial tool to probe the foundations of modern physics. This fact suggests that signals associated with LV are a promising way to investigate quantum gravity at the Planck scale. The LV in the neutrino sector [11], the extended standard model (ESM) [12], and the LV effect on the formation of atmospheric shower [13] are some important studies involving LV in this regard.

The theory that would be compatible should contain the LV sector. The Standard model Extension (SME) is an effective field theory which is worth mentioning that describes the general relativity and the standard model at low energies, that includes additional terms containing information about the LV occurring at the Planck scale [12]. The electromagnetic sector of the SME has been extensively studied in the literatures [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. The electro-weak sector of it is described the articles [30, 31]. Furthermore, some effects of LV in the gravitational sector have been studied in [32,33,34,35,36], specifically the case of the gravitational waves were analyzed in the article [37, 38].

For any theory of gravity looking for a black-hole solution is a significantly important extension since black holes provide into the quantum gravity realm. In this respect, rotating black hole solutions are the most relevant subjects for astrophysics. It is known that the LV effect can be introduced in the gravitational sector inviting the bumblebee field into the service. In [39], an attempt has been made to find out an exact Kerr-like solution through solving Einstein-bumblebee equations. In earlier work, Casana et al. found an exact Schwarzschild-like solution in this bumblebee gravity model and investigated its some classical tests [40]. Then Rong-Jia Yang et al. study the accretion onto this black hole [41] and find the LV parameter \(\ell \) will slow down the mass accretion rate. Sequential development entails that the Kerr–Sen-like solution from Einstein-bumblebee would also be of worth investigation. It would be useful when the black hole contains both charge and angular momentum. We, therefore make an attempt to seek Kerr–Sen-like the solution from Einstein-bumblebee equations of motion.

2 Einstein-bumblebee theory

Bumblebee theory is an effective field theory where a vector field receives vacuum expectation through a spontaneously breaking of Lorentz symmetry the action of which is given by

$$\begin{aligned} \mathcal {S}= & {} \int d^{4} x \sqrt{-g}\left[ \frac{1}{16 \pi G_{N}}\left( \mathcal {R}+\varrho B^{\mu } B^{\nu } \mathcal {R}_{\mu \nu }\right) \right. \nonumber \\&\left. -\frac{1}{4} B^{\mu \nu } B_{\mu \nu }-V\left( B^{\mu }\right) \right] . \end{aligned}$$
(1)

where \(\varrho ^{2}\) is a real coupling constant (with mass dimension \(-1\)) which controls the non-minimal gravity interaction to bumblebee field \(B_{\mu }\) (with the mass dimension 1). The field strength tensor corresponding to the bumblebee field reads

$$\begin{aligned} B_{\mu \nu }=\partial _{\mu } B_{\nu }-\partial _{\nu } B_{\mu }. \end{aligned}$$
(2)

A suitable potential gives rise to a spontaneous Lorentz symmetry rendering a vacuum expectation value to the field \(B_{\mu }\). The conventional functional form of the potential \(V\left( B^{\mu }\right) \) that induces Lorentz symmetry breaking is

$$\begin{aligned} V=V\left( B_{\mu } B^{\mu }\pm b^2)\right. \end{aligned}$$
(3)

\(\mathrm {in}\) which \(b^{2}\) is a real positive constant. It donates a non-vanishing vacuum expectation value (VEV) for the field \(B_{\mu }\). This potential is assumed to have a minimum through the condition

$$\begin{aligned} B_{\mu }B^{\mu }\pm b^2=0. \end{aligned}$$
(4)

The Eq. (4) ensures that a nonzero VEV,

$$\begin{aligned} \left<B^{\mu }\right>=b^{\mu } \end{aligned}$$
(5)

will be supplied to the field \(B_{\mu }\) by the potential V. The vector \(b^{\mu }\) is a function of the spacetime coordinates having constant magnitude \(b_{\mu } b^{\mu }=\mp b^{2}\). Here ± signs indicates that \(b^{\mu }\) may have time-like as well as space-like nature depending upon the choice of sign. The gravitational field equation in vacuum that follows from the action (1) reads

$$\begin{aligned} \mathcal {R}_{\mu \nu }-\frac{1}{2} g_{\mu \nu } \mathcal {R}=\kappa T_{\mu \nu }^{B}. \end{aligned}$$
(6)

where \(\kappa =8 \pi G_{N}\) is the gravitational coupling and the bumblebee energy momentum tensor \(T_{\mu \nu }^{B}\) has the following expression

$$\begin{aligned} T_{\mu \nu }^{B}= & {} B_{\mu \alpha } B_{\nu }^{\alpha }-\frac{1}{4} g_{\mu \nu } B^{\alpha \beta } B_{\alpha \beta }-g_{\mu \nu } V+2 B_{\mu } B_{\nu } V^{\prime } \nonumber \\&+\frac{\varrho }{\kappa }\bigg [\frac{1}{2} g_{\mu \nu } B^{\alpha } B^{\beta } R_{\alpha \beta } -B_{\mu } B^{\alpha } R_{\alpha \nu }-B_{\nu } B^{\alpha } R_{\alpha \mu } \nonumber \\&+\frac{1}{2} \nabla _{\alpha } \nabla _{\mu }\left( B^{\alpha } B_{\nu }\right) +\frac{1}{2} \nabla _{\alpha } \nabla _{\nu }\left( B^{\alpha } B_{\mu }\right) -\frac{1}{2} \nabla ^{2}\left( B^{\mu } B_{\nu }\right) \nonumber \\&-\frac{1}{2} g_{\mu \nu } \nabla _{\alpha } \nabla _{\beta } \left( B^{\alpha } B^{\beta }\right) \bigg ]. \end{aligned}$$
(7)

Here prime(’) denotes differentiation with respect to the argument,

$$\begin{aligned} V^{\prime }=\left. \frac{\partial V(x)}{\partial x}\right| _{x=B^{\mu } B_{\mu } \pm b^{2}} \end{aligned}$$
(8)

Using the trace of Eq. (6) we obtain the trace-reversed version

$$\begin{aligned} \mathcal {R}_{\mu \nu }= & {} \kappa T_{\mu \nu }^{B}+2 \kappa g_{\mu \nu } V-\kappa g_{\mu \nu } B^{\alpha } B_{\alpha } V^{\prime }\nonumber \\&+\frac{\varrho }{4} g_{\mu \nu } \nabla ^{2}\left( B^{\alpha } B_{\alpha }\right) +\frac{\varrho }{2} g_{\mu \nu } \nabla _{\alpha } \nabla _{\beta }\left( B^{\alpha } B^{\beta }\right) \end{aligned}$$
(9)

One can immediately see that when the bumblebee field \(B_{\mu }\) vanishes, we recover the ordinary Einstein equations.The equation of motion for the bumblebee field is

$$\begin{aligned} \nabla ^{\mu } B_{\mu \nu }=2 V^{\prime } B_{\nu }-\frac{\varrho }{\kappa } B^{\mu } R_{\mu \nu } \end{aligned}$$
(10)

When the bumblebee field remains frozen in its vacuum expectation value (VEV) we are allowed to write

$$\begin{aligned} B_{\mu }= & {} b_{\mu } \nonumber \\ b_{\mu \nu }= & {} \partial _{\mu } b_{\nu }-\partial _{\nu } b_{\mu } \end{aligned}$$
(11)

Under this condition form of the potential is irrelevant. We have

$$\begin{aligned} V=0, \quad V^{\prime }=0 . \end{aligned}$$
(12)

In this situation, Einstein equations acquires a generalized form:

$$\begin{aligned}&\mathcal {R}_{\mu \nu }-\kappa b_{\mu \alpha } b_{\nu }^{\alpha }+\frac{\kappa }{4} g_{\mu \nu } b^{\alpha \beta } b_{\alpha \beta }+\varrho b_{\mu } b^{\alpha } \mathcal {R}_{\alpha \nu }+\varrho b_{\nu } b^{\alpha } \mathcal {R}_{\alpha \mu } \nonumber \\&-\frac{\varrho }{2} g_{\mu \nu } b^{\alpha } b^{\beta } \mathcal {R}_{\alpha \beta } -\frac{\varrho }{2}\left[ \nabla _{\alpha } \nabla _{\mu }\left( b^{\alpha } b_{\nu }\right) \right. \nonumber \\&\left. +\nabla _{\alpha } \nabla _{\nu }\left( b^{\alpha } b_{\mu }\right) -\nabla ^{2}\left( b_{\mu } b_{\nu }\right) \right] =0 \nonumber \\&\Rightarrow \bar{R}_{\mu \nu }=0 \end{aligned}$$
(13)

with

$$\begin{aligned} \bar{R}_{\mu \nu }= & {} \mathcal {R}_{\mu \nu }-\kappa b_{\mu \alpha } b_{\nu }^{\alpha } +\frac{\kappa }{4} g_{\mu \nu } b^{\alpha \beta } b_{\alpha \beta } +\varrho b_{\mu } b^{\alpha } \mathcal {R}_{\alpha \nu } \nonumber \\&+\varrho b_{\nu } b^{\alpha } \mathcal {R}_{\alpha \mu } -\frac{\varrho }{2} g_{\mu \nu } b^{\alpha } b^{\beta } \mathcal {R}_{\alpha \beta } +\bar{B}_{\mu \nu } \nonumber \\ \bar{B}_{\mu \nu }= & {} -\frac{\varrho }{2}\left[ \nabla _{\alpha } \nabla _{\mu }\left( b^{\alpha } b_{\nu }\right) +\nabla _{\alpha } \nabla _{\nu }\left( b^{\alpha } b_{\mu }\right) -\nabla ^{2}\left( b_{\mu } b_{\nu }\right) \right] \nonumber \\ \end{aligned}$$
(14)

3 Exact Kerr Sen-like solution in Einstein-bumblebee model

We are now intended to find out the exact Kerr–Sen-like solution from Einstein-bumblebee equation in a similar way the Ding et al. offered the exact Kerr-like solution [39] following the development of Koltz to reproduce the Kerr solution [42, 43]. According to the development of Koltz the generalized form of a radiating stationary axially symmetric black hole metric can be written down as [39, 42, 43]

$$\begin{aligned} d s^{2}= & {} -\gamma (\zeta , \theta ) d \tau ^{2}+a[p(\zeta )-q(\theta )]\left( d \zeta ^{2}+d \theta ^{2}+\frac{q}{a} d \phi ^{2}\right) \nonumber \\&-2q(\theta )d\tau d\phi . \end{aligned}$$
(15)

where a is a dimensional constant which is introduced matching the dimension. The time t and \(\tau \) has the relation

$$\begin{aligned} d \tau =d t-q d \phi . \end{aligned}$$
(16)

In terms of t Eq. (15) turns into

$$\begin{aligned} d s^{2}= & {} -\gamma (\zeta , \theta ) d t^{2}+a[p(\zeta ) -q(\theta )]\left( d \zeta ^{2}+d \theta ^{2}\right) \nonumber \\&+\left\{ [1-\gamma (\zeta , \theta )] q^{2}(\theta )+p(\zeta ) q(\theta )\right\} d \phi ^{2}\nonumber \\&-2 q(\theta )[1-\gamma (\zeta , \theta )] d t d \phi . \end{aligned}$$
(17)

We now use this metric ansatz (17) to compute the gravitational field equations. If we consider that bumblebee field is space-like it can be written down as

$$\begin{aligned} b_{\mu }=(0, b(\zeta , \theta ), 0,0). \end{aligned}$$
(18)

Our focus will be on the bumblebee field acquiring the pure radial vacuum energy expectation value. It is reasonable to consider the space-like nature of the bumblebee field since in this situation spacetime curvature has great radial variation compared to its temporal variation. Now we have

$$\begin{aligned}&b_{\mu } b^{\mu }=b_{0}^{2} \nonumber \\&\quad \Rightarrow g^{\mu \nu } b_{\mu } b_{\nu }=b_{0}^{2} \nonumber \\&\quad \Rightarrow \frac{b^{2}}{a\left( p-q\right) }=b_{0}^{2}\nonumber \\&\quad \Rightarrow b=b_{0} \sqrt{a\left( p-q\right) }. \end{aligned}$$
(19)

where \(b_{0}\) is a constant. Hence the explicit form of \(b_{\mu }\) comes out as

$$\begin{aligned} b_{\mu }=\left( 0, b_{0} \sqrt{a(p-q)}, 0,0\right) . \end{aligned}$$
(20)

in a straightforward manner. Therefore, the non-vanishing components of the bumblebee field are

$$\begin{aligned} b_{\zeta \theta }= & {} -b_{\theta \zeta } \nonumber \\= & {} \partial _{\zeta }b_{\theta }-\partial _{\theta }b_{\zeta }\nonumber \\= & {} -\frac{\partial }{\partial \theta }b\left( \zeta ,\theta \right) = -\frac{\partial }{\partial \theta }b_{0}\sqrt{a\left( p-q\right) }\nonumber \\= & {} \frac{a b_{0} q^{\prime }}{ 2 \sqrt{a(p-q)}}. \end{aligned}$$
(21)

where the prime is used to indicate a derivative with respect to its argument. In addition the quantity \(b_{\mu }^{\alpha } b_{\nu \alpha }\) has the following non-vanishing components:

$$\begin{aligned} b_{\zeta }^{\alpha } b_{\zeta \alpha }= & {} b_{\theta }^{\alpha } b_{\theta \alpha } \nonumber \\= & {} g^{\alpha \beta }b_{\theta \beta }b_{\theta \alpha } =g^{\zeta \zeta }b_{\theta \zeta }b_{\theta \zeta }\nonumber \\= & {} \frac{b_{0}^{2} q^{\prime 2}}{4(p-q)^{2}}, \end{aligned}$$
(22)

and the quantity \(b^{\alpha \beta } b_{\alpha \beta }\) has a non-vanishing contribution

$$\begin{aligned} b^{\alpha \beta } b_{\alpha \beta }= & {} g^{\mu \alpha }g^{\nu \beta }b_{\mu \nu }b_{\alpha \beta }\nonumber \\= & {} g^{\mu \zeta }g^{\nu \theta }b_{\mu \nu }b_{\zeta \theta } +g^{\mu \theta }g^{\nu \zeta }b_{\mu \nu }b_{\theta \zeta }\nonumber \\= & {} \frac{b_{0}^{2} q^{\prime 2}}{2 a(p-q)^{3}}. \end{aligned}$$
(23)

For the metric (17) the nonzero components of Ricci tensor are \(\mathcal {R}_{t t}, \mathcal {R}_{t \phi }, \mathcal {R}_{\zeta \zeta }, \mathcal {R}_{\zeta \theta }, \mathcal {R}_{\theta \theta }, \mathcal {R}_{\phi \phi }\). It is straightforward to see that \(\bar{B}_{\zeta \theta }=0\). The gravitational field equations which are needed for our purpose are

$$\begin{aligned} \bar{R}_{\zeta \theta }= & {} \mathcal {R}_{\zeta \theta }-\kappa b_{\zeta \alpha }b^{\alpha }_{\theta }+\varrho b_{\zeta }b^{\alpha }\mathcal {R}_{\alpha \theta }+\varrho b_{\theta }b^{\alpha }\mathcal {R}_{\alpha \mu }\nonumber \\= & {} \mathcal {R}_{\zeta \theta }-\kappa b_{\zeta \alpha }b^{\alpha }_{\theta }+\varrho b^{2}_{0}\mathcal {R}_{\zeta \theta }\nonumber \\= & {} (1+\ell ) \mathcal {R}_{\zeta \theta } \nonumber \\ \bar{R}_{t t}= & {} \mathcal {R}_{t t}+g_{t t}\left( \frac{\kappa }{4} b^{\alpha \beta } b_{\alpha \beta } -\frac{\varrho }{2} b^{\zeta } b^{\zeta } \mathcal {R}_{\zeta \zeta }\right) +\bar{B}_{t t} \nonumber \\ \bar{R}_{t \phi }= & {} \mathcal {R}_{t \phi }+g_{t \phi }\left( \frac{\kappa }{4} b^{\alpha \beta } b_{\alpha \beta }-\frac{\varrho }{2} b^{\zeta } b^{\zeta } \mathcal {R}_{\zeta \zeta }\right) +\bar{B}_{t \phi } \end{aligned}$$
(24)

where \(\ell =\varrho b_{0}^{2}\). The quantities \(\mathcal {R}_{\zeta \theta }, \bar{B}_{t t}, \bar{B}_{t \phi }\) are as

$$\begin{aligned} \mathcal {R}_{\zeta \theta }= & {} -\frac{{\bar{\Delta }}_{12}}{2 {\bar{\Delta }}}+\frac{\Delta _{2}\left[ (p-q) {\bar{\Delta }}_{1}+2 {\bar{\Delta }} p_{1}\right] }{4(p-q) {\bar{\Delta }}^{2}} \nonumber \\ \bar{B}_{t t}= & {} \ell \left[ \frac{\gamma _{11}}{2 a(p-q)} +\frac{\gamma }{4 a(p-q) {\bar{\Delta }}} p_{1} \gamma _{1} -\frac{1}{4 a {\bar{\Delta }}} \gamma _{1}^{2}\right] \nonumber \\ \bar{B}_{t \phi }= & {} \ell \left[ -\frac{q \gamma _{11}}{2 a(p-q)}+\frac{q(2-\gamma )}{4 a(p-q) \Delta } p_{1} \gamma _{1}+\frac{q}{4 a {\bar{\Delta }}} \gamma _{1}^{2}\right] .\nonumber \\ \end{aligned}$$
(25)

where \({\bar{\Delta }}=q+\gamma (p-q)\). The differentiation with respect to the variable \(\zeta \) and \(\theta \) are denoted by the suffixes 1 and 2 respectively in the Eq. (25). Note that \(\bar{R}_{\zeta \theta }=0\) implies that \(\mathcal {R}_{\zeta \theta }\) vanishes. This helps us to set \({\bar{\Delta }}_{2}=0\) which in turn yields to

$$\begin{aligned}&\gamma _{2}p+\left( 1-\gamma \right) q_{2}-\gamma _{2}q=0\nonumber \\&\Rightarrow \gamma _{2}=-\frac{(1-\gamma ) q_{2}}{p-q}. \end{aligned}$$
(26)

A few steps of algebra gives the expression \(\gamma \):

$$\begin{aligned} \gamma =1-\frac{2 h(\zeta )}{p(\zeta )-q(\theta )} \end{aligned}$$
(27)

We are allowed to introduce new independent variable \(\sigma \) exploiting the condition \({\bar{\Delta }}_{2}=0\).

$$\begin{aligned} \sigma =\int \sqrt{{\bar{\Delta }}} d \zeta . \end{aligned}$$
(28)

where \({\bar{\Delta }}=p-2 h\). Now taking the derivatives f p with respect to \(\zeta \) we have

$$\begin{aligned} p_{1}= & {} \frac{d p}{d \zeta }=\frac{d \sigma }{d \zeta } \frac{d p}{d \sigma }=\sqrt{\bar{\Delta }} \frac{d p}{d \sigma } \nonumber \\ p_{11}= & {} \frac{d^{2} p}{d \zeta ^{2}}=\frac{d}{d \zeta }\left( \sqrt{\bar{\Delta }}\frac{dp}{d \sigma }\right) \nonumber \\= & {} \sqrt{\bar{\Delta }}\frac{d^{2}p}{d \sigma ^{2}}\frac{d \sigma }{d \zeta }+\frac{dp}{d \sigma }\frac{d}{d \zeta }\left( \sqrt{\bar{\Delta }}\right) \nonumber \\= & {} \bar{\Delta } \frac{d^{2} p}{d \sigma ^{2}}+\frac{1}{2}\left( \frac{d p}{d \sigma }\right) ^{2}-\frac{d h}{d \sigma } \frac{d p}{d \sigma } \end{aligned}$$
(29)

A careful look on the Eqs. (13) and (24), reveals that the following equation holds.

$$\begin{aligned} g_{t \phi } \bar{R}_{t t}-g_{t t} \bar{R}_{t \phi }=0. \end{aligned}$$
(30)

After inserting the expressions of \(g_{t \phi }\), \(\bar{R}_{t t}\),\(g_{t t}\) and \(\bar{R}_{t \phi }\) in (30), we find

$$\begin{aligned}&p\left[ 4(1+\ell ) \frac{\dot{h} \dot{p}}{h} q^{2}-2 q q_{22}+q_{2}^{2}+2(1+\ell ) \ddot{p} q^{2}\right] \nonumber \\&\quad -4(1+\ell ) \dot{p}^{2} q^{2}-2(p-q)^{2} q^{2} \ddot{h}\left( 1+\frac{\ell }{h}\right) \nonumber \\&\quad -q\left[ 4(1+\ell ) \frac{\dot{h} \dot{p}}{h} q^{2}-2 q q_{22}+5 q_{2}^{2}+2(1+\ell ) \ddot{p} q^{2}\right] =0, \nonumber \\ \end{aligned}$$
(31)

where dot denotes derivative with respect to \(\sigma \). Here p and h are functions of \(\sigma \), and q is a function of \(\theta \). We, therefore, can write the following

$$\begin{aligned} \frac{\dot{h} \dot{p}}{h}=k, \dot{p}^{2}=c p+n, \ddot{h}=0, \end{aligned}$$
(32)

without any loss of generality. Note that k, c, n are some constants. We find that \(\ddot{p}=k=c / 2\) and Eq. (31) can be reduced to

$$\begin{aligned}&4(1+\ell )(k-c) q^{2}-2 q q_{22}+q_{2}^{2}+(1+\ell ) c q^{2}=0 \nonumber \\&4k(1+\ell ) q^{2}-2 q q_{22}+5 q_{2}^{2}+(1+\ell ) c q^{2}\nonumber \\&\quad +4(1+\ell ) n q=0. \end{aligned}$$
(33)

They both give

$$\begin{aligned} q_{2}^{2}=-(1+\ell )\left( c q^{2}+n q\right) . \end{aligned}$$
(34)

which gives the following

$$\begin{aligned} q=-\frac{n}{c} \sin ^{2}[\sqrt{(1+\ell ) c} \theta / 2]. \end{aligned}$$
(35)

By setting the constants \(c=4 /(1+\ell )\) and \(n=-4a\) it becomes

$$\begin{aligned} q=(1+\ell ) a \sin ^{2} \theta \end{aligned}$$
(36)

From the conditions (32), we find that

$$\begin{aligned} p= & {} \frac{\sigma ^{2}}{1+\ell }+a(1+\ell ), h=c^{\prime } \sigma , \gamma =1\nonumber \\&-\frac{2(1+\ell ) c^{\prime } \sigma }{\sigma ^{2}+a\left( 1+\ell \right) ^{2} \cos ^{2} \theta }, \end{aligned}$$
(37)

where \(c^{\prime }\) is a constant. After choosing \(\sigma =\sqrt{\frac{\ell +1}{a}\frac{r+b}{r}} r, c^{\prime }=M / \sqrt{(\ell +1) a\frac{r+b}{r}}\) and \(\phi =\varphi / \sqrt{1+\ell }\) for Boyer–Lindquist coordinates, we arrive at

$$\begin{aligned} p=\frac{r(r+b)}{a}+a(\ell +1), h=\frac{M r}{a}, \gamma =1-\frac{2 M r}{\rho ^{2}}, \end{aligned}$$
(38)

where \(\rho ^{2}=r(r+b)+(1+\ell ) a^{2} \cos ^{2} \theta \). Finally, substituting these quantities into Eqs. (17) and (20), we obtain the bumblebee field \(b_{\mu }=\left( 0, b_{0} \rho , 0,0\right) \) and the rotating metric in the bumblebee gravity

$$\begin{aligned} d s^{2}= & {} -\left( 1-\frac{2 M r}{\rho ^{2}}\right) d t^{2}-\frac{4 M r a \sqrt{1+\ell } \sin ^{2} \theta }{\rho ^{2}} d t d \varphi +\frac{\rho ^{2}}{\Delta } d r^{2}\nonumber \\&+\rho ^{2} d \theta ^{2}+\frac{A \sin ^{2} \theta }{\rho ^{2}} d \varphi ^{2}. \end{aligned}$$
(39)

where

$$\begin{aligned} \Delta= & {} \frac{r(r+b)-2 M r}{1+\ell }+a^{2}, A=\left[ r(r+b)+(1+\ell ) a^{2}\right] ^{2}\nonumber \\&-\Delta (1+\ell )^{2} a^{2} \sin ^{2} \theta . \end{aligned}$$
(40)

If \(\ell \rightarrow 0 \) it recovers the usual Kerr–Sen metric and for \(a \rightarrow 0,\) and \(b \rightarrow 0,\) it becomes

$$\begin{aligned} d s^{2}= & {} -\left( 1-\frac{2 M}{r}\right) d t^{2}+\frac{1+\ell }{1-2 M / r} d r^{2}\nonumber \\&+r^{2} d \theta ^{2}+r^{2} \sin ^{2} \theta d \varphi ^{2}, \end{aligned}$$
(41)

which is the same as that of the article [40]. The metric (39), represents a purely radial Lorentz-violating black hole solution with rotating angular momentum a and charge \(\sqrt{bM}\). It is singular at \(\rho ^{2}=0\) and at \(\Delta =0\). Its event horizons and ergosphere are located at

$$\begin{aligned} r_{\pm }= & {} M-\frac{b}{2} \pm \frac{ \sqrt{(b-2M)^{2}-4a^{2}(1+\ell )}}{2}, \nonumber \\ r_{\pm }^{e r g o}= & {} M -\frac{b}{2}\pm \frac{\sqrt{(b-2M)^{2}-4a^{2}(1+\ell ) \cos ^{2} \theta }}{2}, \end{aligned}$$
(42)

where ± signs correspond to outer and inner horizon/ergosphere respectively. So there exists a black hole if and only if

$$\begin{aligned} |b-2M| \ge 2|a|\sqrt{1+\ell }. \end{aligned}$$
(43)

Let us now calculate the Hawking temperature corresponding to this black-hole which we obtained from its surface gravity [44] as follows

$$\begin{aligned} T=\frac{\kappa }{2 \pi }, \kappa =-\frac{1}{2} \lim _{r \rightarrow r_{+}} \sqrt{\frac{-1}{X}} \frac{d X}{d r}, X \equiv g_{t t}-\frac{g_{t \varphi }^{2}}{g_{\varphi \varphi }}. \end{aligned}$$
(44)

Inserting corresponding metric components in Eq. (39), we get

$$\begin{aligned} T=\frac{\sqrt{\left( 2M-b\right) ^2-4a^2\left( 1+l\right) }}{4\pi M \sqrt{1+l}\left( 2M-b+\sqrt{\left( 2M-b\right) ^2 -4a^2\left( 1+l\right) }\right) }.\nonumber \\ \end{aligned}$$
(45)

4 Photon orbit and black-hole shadow

A black hole shadow is the optical appearance that occurs when there is a bright distant light source behind the black hole. To determine the nature of the black hole, probably the shadow of the black will provides much insight. It looks like a two dimensional dark zone for a distant observer. This shadow shows a tentative way of finding out the parameters of the black hole. Synge [45] studied the shadow of the Schwarzschild black hole. He pointed out that the edge of the shadow is rounded. Bardeen in the article [46] studied the shadow of the Kerr black hole and argued that the this shadow is no longer circular. The articles [47,48,49,50,51,52,53] contain more recent research on this issue. We are intended to study the Lorentz violating effect on the black hole shadow. In this contest we have considered the Kerr–Sen Black hole with a bumblebee background and study how the shadow of this black-hole gets affected by the Lorentz-violating parameter associated with the bumblebee field.

In order to study black hole shadow we introduce two conserved parameters \(\xi \) and \(\eta \) which are defined by

$$\begin{aligned} \xi =\frac{L_{z}}{E}, \eta =\frac{\mathcal {Q}}{E^{2}}, \end{aligned}$$
(46)

respectively, where \(E, L_{z}\), and \(\mathcal {Q}\) are the energy, the axial component of the angular momentum and Carter constant, respectively. Then the null geodesics in the bumblebee rotating black hole spacetime in terms of \(\xi \) are given by

$$\begin{aligned} \rho ^{2} \frac{d r}{d \lambda }= & {} \pm \sqrt{R}, \rho ^{2} \frac{d \theta }{d \lambda }=\pm \sqrt{\Theta } \nonumber \\ (1+\ell ) \Delta \rho ^{2} \frac{d t}{d \lambda }= & {} A-2 \sqrt{1+\ell } {\text {Mra}}\xi \nonumber \\ (1+\ell ) \Delta \rho ^{2} \frac{d \phi }{d \lambda }= & {} 2 \sqrt{1+\ell } M r a+\frac{\xi }{\sin ^{2} \theta }\left( \rho ^{2}-2 M r\right) ,\nonumber \\ \end{aligned}$$
(47)

where \(\lambda \) is the affine parameter, and

$$\begin{aligned} R(r)= & {} \left[ \frac{r(r+b)+(1+\ell ) a^{2}}{\sqrt{1+\ell }}-a \xi \right] ^{2}\nonumber \\&-\Delta \left[ \eta +(\xi -\sqrt{1+\ell }a)^{2}\right] , \Theta (\theta )=\eta \nonumber \\&+(1+\ell ) a^{2} \cos ^{2} \theta -\xi ^{2} \cot ^{2} \theta . \end{aligned}$$
(48)
Fig. 1
figure 1

The left panel describes the effective potential for various values of l with \(b/M=.36,a/M=.5\) and right panel describes critical radius for various values of l with \(b=.36\) in case of prograde orbits

Full size image
Fig. 2
figure 2

The left panel describes effective potential for various values of b with \(a=.5,l=-.1\) and right panel describes effective potential for various values of b with \(a=.5,l=.6\) in case of prograde orbits

Full size image
Fig. 3
figure 3

The left panel describes critical radius for various values of b with \(l=-.1\) and right panel describes critical radius for various values of b with \(l=.6\) in case of prograde orbits

Full size image
Fig. 4
figure 4

The left panel describes the effective potential for various values of l with \(b/M=.36,a/M=.5\) and right panel describes critical radius for various values of l with \(b=.36\) for retrograde orbits

Full size image
Fig. 5
figure 5

The left panel describes effective potential for various values of b with \(a=.5,l=-.1\) and right panel describes effective potential for various values of b with \(a=.5,l=.6\) in case of retrograde orbits

Full size image
Fig. 6
figure 6

The left panel describes critical radius for various values of b with \(l=-.1\) and right panel describes critical radius for various values of b with \(l=.6\) in case of retrograde orbits

Full size image

The radial equation of motion can be written down in the form

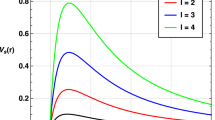
$$\begin{aligned} \left( \rho ^{2} \frac{d r}{d \lambda }\right) ^{2}+V_{e f f}=0. \end{aligned}$$
(49)

The effective potential \(V_{e f f}\) reads

$$\begin{aligned} V_{e f f}= & {} -\left[ \frac{r(r+b)+(1+\ell ) a^{2}}{\sqrt{1+\ell }}-a \xi \right] ^{2}\nonumber \\&+\Delta \left[ \eta +(\xi -\sqrt{1+\ell }a)^{2}\right] . \end{aligned}$$
(50)

Note that \(V_{e f f}(0)=0\), and \(\quad V_{e f f}(r \rightarrow \infty ) \rightarrow \infty \).

The unstable spherical orbit on the equatorial plane is given by the following equations

$$\begin{aligned} \theta =\frac{\pi }{2}, R(r)=0, \frac{d R}{d r}=0, \frac{d^{2} R}{d r^{2}}<0, \eta =0. \end{aligned}$$
(51)

We plot the \(V_{e f f}\) against r/M with \(\xi =\xi _{c}+0.2\) where \(\xi _{c}\) is the value of \(\xi \) for equatorial spherical unstable direct orbit. Plots show that the photon starting from infinity will meet a turning point, and then turns back to infinity. When \(\xi =\xi _{c},\) this turning point is an unstable spherical orbit which gives the boundary of the shadow [54]. It also shows that the deviation from GR (Kerr–Sen): when \(\mathrm {LV}\) constant \(\ell > 0\), the turning point shifts to the left however when \(\ell < 0\) it shifts to the right. These shifts are similar to those of the Einstein-aether black hole [55], which is also a LV black hole. The same type of shifting was reported in [39] for Kerr-like black-hole. Let us look towards the \(r_c\). In [56, 57], an elaborate discussion related to different roots and different spacetime region corresponding to that are made. However, the two real roots are of particular interest. One corresponds to direct (prograde) orbit and the other corresponds to retrograde orbit. We have a plotted radius \(r_{c}\) of unstable equatorial spherical direct (prograde) as well as retrograde orbit against a/M for various scenarios. It shows that the \(r_{c}\) decreases with \(\ell >0\), for direct orbit, however it increases when \(\ell <0\), which are similar to those of the noncommutative black hole [54]. This is also similar to the observation of the article [39]. The \(r_{c}\) decreases with b for a particular \(\ell \) irrespective of its sign. For retrograde orbit the slope of the \(r_c versus a/M\) increases with the increase of values of \(\ell \) when \(\ell <0\) and opposite the case when \(\ell >0\) and for retrograde orbit \(r_c\) increases with b for any particular \(\ell \) irrespective of its sign.

For more generic orbits \(\theta \ne \pi / 2\) and \(\eta \ne 0,\) the solution of Eq. (51) \( r=r_{s}\) gives the \(r-\) constant orbit, which is also called spherical orbit and the conserved parameters of the spherical orbits are given by

$$\begin{aligned} \begin{aligned} \xi _{s}&=\frac{a^{2}\left( 1+\mathrm {l}\right) \left( 2 M+2 r_{\mathrm {s}} +b\right) +r_{\mathrm {s}}\left( 2 r_{\mathrm {s}}^{2} +3 b r_{\mathrm {s}}+b^{2}-2 M\left( 3 r_{\mathrm {s}} +b\right) \right) }{a\sqrt{1+\mathrm {l}}\left( 2 M-2 r_{\mathrm {s}}-b\right) } \\ \eta _{s}&=-\frac{r_{\mathrm {s}}^{2}\left( -8 a^{2}\left( 1+\mathrm {l}\right) M\left( 2 r_{\mathrm {s}}+b\right) +\left( 2 r_{\mathrm {s}}^{2}+3b r_{\mathrm {s}} +b^{2} -2 M\left( 3 r_{\mathrm {s}}+b\right) \right) ^{2}\right) }{a^{2}\left( 1+\mathrm {l}\right) \left( 2 M-2 r_{\mathrm {s}}-b\right) ^{2}} . \end{aligned} \end{aligned}$$
(52)

The two celestial coordinates, which are used to describe the shape of the shadow that an observers see in the sky, can be given by

$$\begin{aligned} \alpha (\xi , \eta ; \theta )= & {} \lim _{r \rightarrow \infty } \frac{-r p^{(\varphi )}}{p^{(t)}} = -\xi _{s} \csc \theta \nonumber \\ \beta (\xi , \eta ; \theta )= & {} \lim _{r \rightarrow \infty } \frac{r p^{(\theta )}}{p^{(t)}} =\sqrt{\left( \eta _{s}+a^{2} \cos ^{2} \theta -\xi _{s}^{2} \cot ^{2} \theta \right) }\nonumber \\ \end{aligned}$$
(53)

where \(\left( p^{(t)}, p^{(r)}, p^{(\theta )}, p^{(\phi )}\right) \) are the tetrad components of the photon momentum with respect to locally non-rotating reference frames [46].

The shadow of the collapsed object is defined as follows: Suppose some light rays are emitted at infinity (\(r = +\infty \)) and propagate near the collapsed object. If they can reach the observer at infinity after scattering, then its direction is not dark. On the other hand, when they fall into the event horizon of a black hole, the observer will never see such light rays. Such a direction becomes dark. It makes a shadow. We define the apparent shape of a black hole by the boundary of the shadow [58]. We show the shapes of the shadow. With the increase of the \(\mathrm {LV}\) parameter \(\ell ,\) its left endpoint moves to the right and then the right endpoint moves to the right slightly.

Fig. 7
figure 7

The left one gives shapes of the shadow for various values of l with \(a/M=0.5\), \(b=0.76\) and \(\theta =\pi /2\) and the right one gives shapes of the shadow for various values of b with \(a/M=0.7\) , \(l=-.1\) and \(\theta =\pi /2\)

Full size image
Fig. 8
figure 8

The shapes of the shadow for various values of b with \(a/M=0.7\), \(l=0.3\) and \(\theta =\pi /2\)

Full size image

The Fig. 1b shows that the left end of the shadow shifts towards right for positive values of \(\ell \) for a particular b and reverse is the case when \(\ell \) is negative. However irrespective of the sign of ell the shifting of the left end of the shadow is towards right for increasing b. Using the parameters which are introduced by Hioki and Maeda [47] we analyze deviation from circular form \(\left( \delta _{s}\right) \) and the size \(\left( R_{s}\right) \) of the shadow image of the black hole (Figs. 2, 3, 4, 5, 6).

For calculating these parameters, we consider five points \(\left( \alpha _{t}, \beta _{t}\right) ,\left( \alpha _{b}, \beta _{b}\right) ,\left( \alpha _{r}, 0\right) \) \(\left( \alpha _{p}, 0\right) \) and \(\left( \bar{\alpha }_{p}, 0\right) \) which are top, bottom, rightmost, leftmost of the shadow and leftmost of the reference circle respectively, so we have

$$\begin{aligned} R_{s}=\frac{\left( \alpha _{t}-\alpha _{r}\right) ^{2}+\beta _{t}^{2}}{2\left( \alpha _{t}-\alpha _{r}\right) } \end{aligned}$$

and

$$\begin{aligned} \delta _{s}=\frac{\left( \bar{\alpha }_{p}-\alpha _{p}\right) }{R_{s}} \end{aligned}$$
Fig. 9
figure 9

The black hole shadow and reference circle. \(d_s\) is the distance between the left point of the shadow and the reference [59]

Full size image

From the plots we see that as we increase b for a fixed value l and a , \(R_{s}\) decreases and \(\delta _{s}\) increases. For fixed values of b and a both \(R_{s}\) and \(\delta _{s}\) increases but the nature of variation differ for different values of a. Thus the Lorentz Violating term has a significant impact on the size of the shadow and its deviation from the circular form. For all plots, we have taken \(M=1\). Note that in Fig. 7, when the negative value of \(\ell \) is taken the left end of the shadow came left to the shadow corresponding to \(\ell =0\). Mathematically, there is no problem since as we increase the value of \(\ell \) the shifting takes place towards the right and that chronology is maintained. However, physical what does actually happen is beyond the scope of our study. It may need more involved investigation. However, it can be seen from the plot that when \(\ell > 0\) the turning point of the effective potential shift towards the left and, it shifts to the right when \(\ell <0\). So for \(\ell >0\) equatorial circular orbit decreases whereas for \(\ell <0\) the equatorial circular orbit increases (Figs. 8, 9, 10, 11, 12, 13).

5 Energy emission rate

Scattering of electromagnetic and gravitational from rotating black hole whose gravitational field is described by the Kerr metric is calculated in [60] and insight for absorption phenomena is well understood from there. Here we study the possible visibility of the Kerr–Sen-like black hole through the shadow. In the vicinity of limiting constant value, the cross-section of the black hole’s absorption moderates lightly at high energy. We know that a rotating black hole can absorb electromagnetic waves, so the absorbing cross-section for a spherically symmetric black hole is [61]

$$\begin{aligned} \sigma _{l i m}=\pi R_{s}^{2} \end{aligned}$$
(54)

using above equation the energy emission rate is [62]

$$\begin{aligned} \frac{d^{2} E}{d \omega d t}=\frac{2 \pi ^{3} R_{s}^{2}}{e^{\left( \frac{\omega }{T}\right) }-1} \omega ^{3} \end{aligned}$$
(55)

where T is the Hawking temperature and \(\omega \) the frequency of the electromagnetic radiation.

Fig. 10
figure 10

The left one gives variation of \(R_{s}\) for various values of l with \(a=.2\) and \(\theta =\pi /2\) and the right one gives variation of \(R_{s}\) against l for various values of a with \(b=0.16\) and \(\theta =\pi /2\)

Full size image
Fig. 11
figure 11

The left one gives variation of \(\delta _{s}\) for various values of a with \(l=0\) and \(\theta =\pi /2\) and the right one gives variation of \(\delta _{s}\) for various values of l with \(a=0.2\) and \(\theta =\pi /2\)

Full size image

If we take into account the angular velocity of black hole then from the information available from the article [63] the above equation gets modified into

$$\begin{aligned} \frac{d^{2} E}{d \omega d t}=\frac{2 \pi ^{3} R_{s}^{2}}{e^{\left( \frac{\omega -\omega _{H}}{T}\right) }-1} \omega ^{3} \end{aligned}$$
(56)

where \(\omega _{H}=\frac{a\sqrt{1+l}}{r_{+}\left( r_{+}+b\right) +\left( 1+l\right) a^{2}}\) with \(r_{+}=M-\frac{b}{2}+\frac{ \sqrt{(b-2M)^{2}-4a^{2}(1+\ell )}}{2}\) is the angular velocity of the black hole. Let us first give the different plots without considering the black hole frequency in Figs. 14, 15 and 16. After that in Fig. 17, we have given the sketch considering the black hole frequency considering both the cases \(omega >\omega _H\) as well as s \(\omega < \omega _H\) . The figure indicates that depending on the value of electromagnetic frequency both absorption and emission may happen. Because for \(\omega _H > \omega \) the nature of the plot takes reverse shave (Figs. 18, 19).

We have plotted the energy emission rate for versus \(\omega \) for various cases. It is clear from the graphs that the emission rate decreases with the increase in b for any set of fixed values of a and \(\ell \). It also decreases when \(\ell \) increases for any set of fixed values of a and b. However, there is a crucial difference in the situation when \(\ell \) increases. It is true that the emission rate decreases with the increase in \(\ell \) like the case when b increases but unlike the situation when b increases the pick of the curve gets shifted when \(\ell \) increases. From the plot, we see there is a discontinuity at \(\omega =\omega _{H}\) and the graphs shift to the right as we increase the value of \(\ell \).

6 Comparison between Schwarzschild-like, Kerr-like and Kerr–Sen like black holes

It would be beneficial if a comparison for the shift of the shadows corresponding to the Schwarzschild-like, Kerr-like and Kerr–Sen like Black holes is made. In this contest, we have included the sketch of the shadows for these three black holes for the different values of \(\ell = 0, .2, -.2\) keeping the values of \(a/M=.5\) and \(b=.4\) fixed in all the cases.

Fig. 12
figure 12

The variation of \(\delta _{s}\) against l for various values of a with \(b=1\) and \(\theta =\pi /2\)

Full size image

The plots show that the size of the shadow of Schwarzschild-like Black hole does not depend on the Lorentz-violation parameter \(\ell \).The shadows of Kerr-like BH and Kerr–Sen like BH shift to the right of the shadow of Schwarzschild-like BH. It is also clear from the plots that the size of the shadow of Kerr-like BH is bigger than that of Kerr–Sen like BH. Deviations of Kerr-like BH and Kerr–Sen like BH from Schwarzschild-like BH is given in the table below (Table 1).

Fig. 13
figure 13

The left one gives variation of emission rate against \(\omega \) for various values of b with \(a=0\) and \(l=0\) and the right one gives variation of emission rate against \(\omega \) for various values of b with \(a=0.2\) and \(l=0\)

Full size image
Fig. 14
figure 14

The left one gives variation of emission rate against \(\omega \) for various values of b with \(a=0.5\) and \(l=0\) and the right one gives variation of emission rate against \(\omega \) for various values of b with \(a=0.7\) and \(l=0\)

Full size image
Fig. 15
figure 15

The left one gives variation of emission rate against \(\omega \) for various values of l with \(a=0\) and \(b=1\) and the right one gives variation of emission rate against \(\omega \) for various values of l with \(a=0.2\) and \(b=1\)

Full size image
Fig. 16
figure 16

The left one gives variation of emission rate against \(\omega \) for various values of l with \(a=0.5\) and \(b=.16\) and the right gives variation of emission rate against \(\omega \) for various values of l with \(a=0.7\) and \(b=.04\)

Full size image

It is evident from the table that as value of l is increased deviation is increasing for both Kerr-like and Kerr–Sen like BHs.

7 Bending of light

Let us study the bending of light which may be considered as an observable on the angular plane. With the change of variable as \(r+b=1 / v\), following the same procedure as adopted in [56] the orbit equation on an angular plane for massless test particles (i.e. \(\theta =\pi / 2\)) can be written down as

$$\begin{aligned} \left( \frac{d v}{d \phi }\right) ^{2}= & {} \frac{\left[ j^{2}\left( (1-b v)^{2}+(1-b v) a^{2}\left( 1+l\right) v^{2}+2 M a^{2}\left( 1+l\right) v^{3}\right) -4 j M a\sqrt{\left( 1+l\right) } v^{3}-B(v) v^{2}\right] }{\mathcal {B}^{2}(v)}\nonumber \\&\times \left( \mathcal {B}(v)+2 M b v^{2}+a^{2}\left( 1+l\right) v^{2}\right) \left( \mathcal {B}(v)+a^{2}\left( 1+l\right) v^{2}\right) , \end{aligned}$$
(57)

where, \(j=a\sqrt{\left( 1+l\right) } / M, b=Q^{2} / M\) and \(\mathcal {B}(u)=1-(b+2 M) v\). Expanding the right hand side of the above equation and retaining the terms up to cubic power in v we obtain

$$\begin{aligned} \frac{d \phi }{d v}= & {} \frac{1}{\sqrt{j^{2}+\mathcal {G} v+\mathcal {H} v^{2}+\mathcal {I} v^{3}}} \Rightarrow \phi -\phi _{0}\nonumber \\= & {} \int _{v_{0}}^{v} \frac{d v}{\sqrt{j^{2}+\mathcal {G} v+\mathcal {H} v^{2}+\mathcal {I} v^{3}}}. \end{aligned}$$
(58)

Here \(\mathcal {G}=-2 j^{2} b, \mathcal {H}=j^{2}\left( b^{2}+2 M b+3 a^{2}\left( 1+l\right) \right) -1\) and \(\mathcal {I}=j^{2}\left[ a^{2}\left( 1+l\right) (2 M-5)-4 M b^{2}\right] -4 a^{2}\left( 1+l\right) +\) \(y\left[ 1-2\left( a^{2}\left( 1+l\right) +M b\right) \right] \). Solving the first order differential equation we have

$$\begin{aligned} \Delta \phi =\frac{C}{\mathcal {N}} \arctan \left[ \frac{\mathcal {N} v+j^{2} b}{\mathcal {N} \sqrt{j^{2}-2 j^{2} b v-\mathcal {N} v^{2}}}\right] , \end{aligned}$$
(59)

with \(r+b=1/v\),\(j=\frac{a\sqrt{1+l}}{M}\) and \(\mathcal {N}=\left[ 1-j^{2}\left( 2bM+3 a^{2}\right. \right. \left. \left. \left( 1+l\right) \right) -j^{2} b^{2}\right] ^{1 / 2}\). The corresponding equation for Kerr-like Black holes is obtained if we set \(b=0\) and the expression for \(\Delta \phi \) turns into

$$\begin{aligned} \Delta \phi =\frac{C}{\mathcal {P}} \arctan \left[ \frac{\mathcal {P} v}{\mathcal {P} \sqrt{j^{2}-\mathcal {P} v^{2}}}\right] , \end{aligned}$$
(60)

with \(r=1/v\), \(j=\frac{a\sqrt{1+l}}{M}\) and \(\mathcal {P}=\left[ 1-3j^{2} a^{2}\left( 1+l\right) \right] ^{1 / 2}\).

Fig. 17
figure 17

It gives emission rate for various values of l with \(b=.16\) and \(a=.5\) taking angular velocity of BH into consideration

Full size image
Fig. 18
figure 18

The left one gives shapes of the shadow for various Black holes with \(l=-.2,a/M=0.5\), \(b=0.4\) and \(\theta =\pi /2\) and the right one gives shapes of the shadow for various Black holes with \(l=.2,a/M=0.5\) , \(b=.4\) and \(\theta =\pi /2\)

Full size image

8 Summary and discussion

Fig. 19
figure 19

This one gives shapes of the shadow for various Black holes with \(l=0,a/M=0.5\), \(b=0.4\)

Full size image
Table 1 Deviations of Kerr-like BH and Kerr–Sen like BH from Schwarzschild-like BH
Full size table

We have considered the Einstein-bumblebee gravity model where LV scenario gets involved through a bumblebee field vector field \(B_\mu \). A spontaneous symmetry breaking allows the field to acquires a vacuum expectation value that generates LV into the system. A Kerr–Sen-like solution has been found out starting from the generalized form of a radiating stationery axially symmetric black hole metric. For the parameter \(b=0\) the matric turns into Kerr-like metric and for both \(b=0\) and \(a=0\) the metric lands onto Schwarzschild-like metric. The effective potential that results from the null geodesics in the bumblebee rotating black hole spacetime is computed that in turn helps to get the tentative nature of the motion of photon is predicted for different choices of the parameters a, b and \(\ell \). The nature of shadow is studied and how does the shadow gets deformed that has also been studied for different variations of a, b, and \(\ell \). We observe that shadow gets shifted towards the right for positive ell and shifted towards left for negative \(\ell \) when a and b remains fixed. However, shifting is always towards the right when bl increases whatever the set of values of ell and a are taken. We have also studied the rate of emission of energy for this type of black-hole. The emission rate decreases when b increases for any set of fixed values of a and \(\ell \). It also decreases when \(\ell \) increases for an arbitrary set of fixed values of a and b. A crucial difference however in the situation is noticed when \(\ell \) increases. The emission rate although decrease with the increase of \(\ell \) like the case when b increases, the pick of the curve gets shifted towards lower \(\omega \) in the situation when \(\ell \) increases. The deformation of the shadow for Kerr–Sen-like black-hole in the Einstein-bumblebee gravity model with the variation of \(\ell \) observed here is a theoretical prediction. It shows that it enhances the distortion of shadow, and it would be detected by the new generation gravitational antennas.