The exclusive vision of rare K and B decays and of the quark mixing in the standard model

Abstract

The most common predictions for rare K and B decay branching ratios in the Standard Model in the literature are based on the CKM elements $|V_{cb}|$ and $|V_{ub}|$ resulting from global fits, that are in the ballpark of their inclusive and exclusive determinations, respectively. In the present paper we follow another route, which to our knowledge has not been explored for $\Delta M_{s,d}$ and rare K and B decays by anybody to date. We assume, in contrast to the prevailing inclusive expectations for $|V_{cb}|$, that the future true values of $|V_{cb}|$ and $|V_{ub}|$ will be both from exclusive determinations; in practice we use the most recent averages from FLAG. With the precisely known $|V_{us}|$ the resulting rare decay branching ratios, $\varepsilon _K$, $\Delta M_d$, $\Delta M_s$ and $S_{\psi K_S}$ depend then only on the angles $\beta$ and $\gamma$ in the unitarity triangle that moreover are correlated through the CKM unitarity. An unusual pattern of SM predictions results from this study with some existing tensions being dwarfed and new tensions being born. In particular using HPQCD $B^0_{s,d}-{{\bar{B}}}^0_{s,d}$ hadronic matrix elements a $3.1\sigma$ tension in $\Delta M_s$ independently of $\gamma$ is found. For $60^\circ \le \gamma \le 75^\circ$ the tension in $\Delta M_d$ between $4.0\sigma$ and $1.1\sigma$ is found and in the case of $\varepsilon _K$ between $5.2\sigma$ and $2.1\sigma$. Moreover, the room for new physics in $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$, $K_L\rightarrow \pi ^0\nu {\bar{\nu }}$ and $B\rightarrow K(K^*)\nu {\bar{\nu }}$ decays is significantly increased. We compare the results in this EXCLUSIVE scenario with the HYBRID one in which $|V_{cb}|$ in the former scenario is replaced by the most recent inclusive $|V_{cb}|$ and present the dependence of all observables considered by us in both scenarios as functions of $\gamma$. As a byproduct we compare the determination of $|V_{cb}|$ from $\Delta M_s$, $\Delta M_d$, $\varepsilon _K$ and $S_{\psi K_S}$ using $B^0_{s,d}-{{\bar{B}}}^0_{s,d}$ hadronic matrix elements from LQCD with $2+1+1$ flavours, $2+1$ flavours and their average. Only for the $2+1+1$ case values for $\beta$ and $\gamma$ exist for which the same value of $|V_{cb}|$ is found: $|V_{cb}|=42.6(4)\times 10^{-3}$, $\gamma =64.6(16)^\circ$ and $\beta =22.2(7)^\circ$. This in turn implies a $2.7\sigma$ anomaly in $B_s\rightarrow \mu ^+\mu ^-$.

1 Introduction

The rare K and B decays and the quark mixing being GIM [1] suppressed in the Standard Model (SM) and simultaneously being often theoretically clean are very powerful tools for the search of New Physics (NP) [2]. Unfortunately the persistent tension between inclusive and exclusive determinations of $|V_{cb}|$ (see e.g. [3,4,5,6]) weakens this power significantly. As recently reemphasized by us [7] this is in particular the case of the branching ratios for rare K-meson decays and the parameter $\varepsilon _K$ that exhibit stronger $|V_{cb}|$ dependences than rare B decay branching ratios and the $\Delta M_{s,d}$ mass differences. Also similar tensions in the determination of $|V_{ub}|$ [8] matter.

One possible solution to cope with this difficulty is to consider within the SM suitable ratios of two properly chosen observables so that the dependences on $|V_{cb}|$ and $|V_{ub}|$ are eliminated [7, 9, 10]. While in [9, 10] B physics observables were considered, the analysis in [7] was dominated by the K system and its correlation with rare B decays and $B_{s,d}^0-{{\bar{B}}}_{s,d}^0$ mixing. In this manner we could construct 16 $|V_{cb}|$-independent ratios that were either independent of the CKM parameters or only dependent on the angles $\beta$ and $\gamma$, that can be determined in tree-level processes. Having one day precise experimental values for the ratios in question and also precise values on $\beta$ and $\gamma$ will hopefully allow one to identify particular pattern of deviations from SM expectations independently of $|V_{cb}|$ pointing towards a particular extension of the SM.

But these ratios, even if useful in the context of the tensions in question, are not as interesting as the observables themselves. Therefore, assuming in addition no NP in $\varepsilon _K$, $\Delta M_d$ and $\Delta M_s$ and in the mixing induced CP-asymmetry $S_{\psi K_S}$, these ratios allowed to obtain $|V_{cb}|$-independent SM predictions for a number of branching ratios [7]. As these four quark mixing observables are very precisely measured and theoretically rather clean, the resulting SM predictions obtained in this manner turned out to be the most precise to date. A brief summary of the results of this analysis just appeared [11].

Another insight in this problematic has been provided recently by the authors of [12] who made a determination of $|V_{cb}|$ and $|V_{ub}|$ from loop processes, rare decays and quark mixing, by assuming no NP contributions to these observables. To this end they could use only well measured observables in the B system and $\varepsilon _K$. This strategy has already been explored in [13] but there only $\varepsilon _K$, $\Delta M_d$ and $\Delta M_s$ and $S_{\psi K_S}$ have been considered.

There is no question about that the analyses in [7, 9, 10] will help us to identify possible departures from SM predictions for the $|V_{cb}|$-independent ratios and possible pattern of $|V_{cb}|$ determinations from various loop processes as analysed in [12, 13], but also to some extent in [7]. See in particular Figs. 12 and 14 of the latter paper. Yet, eventually the most obvious procedure to look for NP is to determine all CKM parameters in tree-level processes under the assumption that NP contributions to these decays are negligible. This assumption is more likely to be correct than assuming no NP contributions in loop induced decays. Subsequently the resulting values of the CKM parameters inserted into SM amplitudes for loop induced processes would allow for definite predictions for GIM suppressed observables.

In this spirit in the present paper we follow a more direct but a novel route, which to our knowledge has not been explored by anybody to date, at least as far as SM predictions for theoretically clean observables like rare K and B decays, $\Delta M_{s,d}$ and the mixing induced CP asymmetry $S_{\psi K_S}$ are concerned. Instead of using the values of $|V_{cb}|$ and $|V_{ub}|$ resulting from the global fits of the CKM matrix [14, 15], we assume, in contrast to the prevailing inclusive expectations in the case of $|V_{cb}|$, that the future values of both $|V_{cb}|$ and $|V_{ub}|$ will be determined from exclusive tree-level decays. Therefore we use FLAG [6] averages,¹ which are based on a number of LQCD calculations that are listed after (2). With the precisely known $|V_{us}|$ the resulting rare decay branching ratios, $\varepsilon _K$, $\Delta M_d$, $\Delta M_s$ and $S_{\psi K_S}$ depend than only on the angles $\beta$ and $\gamma$ in the unitarity triangle that are moreover correlated through the CKM unitarity. An unusual pattern of SM predictions results from this study. Some present tensions are dwarfed and new tensions are born. In some cases their sizes depend sensitively on the value of $\gamma$ which enhances the importance of precise measurements of this parameter, stressed in particular in [7, 16].

The view that exclusive decays will eventually lead to the best determination of $|V_{cb}|$ is rather unusual but has been already expressed by the first author in the past [2]. The point is that precise measurements of formfactors by Lattice QCD (LQCD) accompanied by improved measurements of the relevant branching ratios should allow eventually a better control over theoretical uncertainties than it is possible in inclusive decays and consequently determinations of $|V_{cb}|$ and $|V_{ub}|$ that do not rely on quark-hadron duality. Yet, to be on the safe side, in view of the important progress in the inclusive determination of $|V_{cb}|$ [3,4,5,6], we compare at all stages the results in this EXCLUSIVE scenario with the HYBRID one in which $|V_{cb}|$ in the former scenario is replaced by the most recent inclusive $|V_{cb}|$ from [4].

To our knowledge in the literature only the authors of [17] performed a similar study, but only for $\varepsilon _K$, finding, similar to us, a significant deviation of the SM prediction from the data. However, their analysis differs from ours in that for the CKM parameters they used the values obtained from global fits of the UT which can be questioned because in fact these SM global analyses used already $\varepsilon _K$ in their fits. Moreover, until now they did not incorporate the theoretical advances in $\varepsilon _K$ from [18] which have been taken by us into account in [7] and also in the present analysis.

The outline of our paper is as follows. In Sect. 2 we set up our strategy as far as CKM parameters are concerned. We also list the input parameters used in our numerical analysis. However, we refrain from the expressions for the observables which have been studied already by us in [7] and are collected there and in [2]. The numerical analysis is presented in Sect. 3 with the SM predictions for many observables resulting from the EXCLUSIVE LQCD scenario and from the HYBRID scenario. In Sect. 4 we calculate the impact of the hadronic matrix elements with $2+1+1$ flavours from the HPQCD collaboration [19] on our results for rare B decays in [7], where the averages of HPQCD results and $2+1$ results from Fermilab Lattice and MILC Collaborations (FNAL/MILC) [20] calculated in [10] have been used. We also illustrate how the determination of $|V_{cb}|$ from $\Delta M_s$, $\Delta M_d$ and $\varepsilon _K$ depends on the number of flavours used in LQCD calculations of the relevant hadronic matrix elements. We conclude in Sect. 5. Two short appendices list LQCD results for $F_{B_q}$ and $F_{B_q}\sqrt{{\hat{B}}_{B_q}}$ for $N_f=2+1$ and $N_f=2+1+1$.

2 Strategy

The CKM parameters entering our analysis will be

$$\begin{aligned} \boxed {\lambda =|V_{us}|,\quad |V_{cb}|, \quad |V_{ub}|,\quad \gamma } \end{aligned}$$

(1)

with $\gamma$ one of the angles in the UT, shown in Fig. 1. It is equal, within an excellent accuracy, to the single phase in the standard parametrization of the CKM matrix [21, 22].

As the input parameters we will use $\lambda =0.225$ and the FLAG values for $|V_{cb}|$ and $|V_{ub}|$ extracted from tree-level decays. Now these values, as given in the latest FLAG’s report, read [6]

$$\begin{aligned}&|V_{cb}|=39.48(68)\times 10^{-3},\quad |V_{ub}|=3.63(14)\times 10^{-3}, \nonumber \\&\quad {(\mathrm FLAG-2021)}. \end{aligned}$$

(2)

These results are based on a number of different LQCD analyses as summarized in Fig. 38 of [6]. These are from FNAL/MILC [23,24,25,26], HPQCD [27,28,29] and RBC/UKQCD [30] with further details given in the original papers and [6].

However, the value for $|V_{cb}|$ in (2) does not include the most recent one from Fermilab/MILC [31] that is significantly lower $38.40(74)\times 10^{-3}$. Fortunately, we were able to obtain from FLAG a preliminary result for $|V_{cb}|$² that includes the latter result. Our basic values for $|V_{cb}|$ and $|V_{ub}|$ obtained from the overall 2022 FLAG’s ($|V_{cb}|$,$|V_{ub}|$) fit will be then as follows³

$$\begin{aligned} \boxed {|V_{cb}|=39.21(62)\times 10^{-3},|V_{ub}|=3.61(13)\times 10^{-3}, {(\mathrm FLAG-2022)},}\nonumber \\ \end{aligned}$$

(3)

with $|V_{ub}|$ practically unchanged. Larger values for $|V_{cb}|$ from exclusive decays using LQCD, in the ballpark of $41.0\times 10^{-3}$, have been reported in [32,33,34,35] and we are looking forward to the 2023 FLAG report incorporating these results.

We will also compare our EXCLUSIVE scenario with the HYBRID one in which the value for $|V_{cb}|$ is the inclusive one from [4] and the exclusive one for $|V_{ub}|$ as above:

$$\begin{aligned} \boxed {|V_{cb}|=42.16(50)\times 10^{-3},|V_{ub}|=3.61(13)\times 10^{-3}, {(\mathrm HYBRID)}.}\nonumber \\ \end{aligned}$$

(4)

For $\gamma$ we will use a broad range $60^\circ \le \gamma \le 75^\circ$. Using CKM unitarity the angle $\beta$ in the UT can then be determined through the correlation of $\beta$ and $\gamma$

$$\begin{aligned} \boxed {\cot \beta =\frac{1-R_b\cos \gamma }{R_b\sin \gamma }, \quad R_b=(1-\frac{\lambda ^2}{2})\frac{1}{\lambda } \left| \frac{V_{ub}}{V_{cb}} \right| .} \end{aligned}$$

(5)

On the other hand the sides of the UT, $R_t$ and $R_b$, can be solely expressed in terms of the angles $\beta$ and $\gamma$, as follows [36]

$$\begin{aligned} R_t=\frac{\sin \gamma }{\sin (\beta +\gamma )}\approx \sin \gamma , \quad R_b=\frac{\sin \beta }{\sin (\beta +\gamma )}\approx \sin \beta . \end{aligned}$$

(6)

We observe that $R_t$ depends dominantly on $\gamma$, while $R_b$ on $\beta$. These approximations follow from the experimental fact that $\beta +\gamma \approx 90^\circ$ and it is an excellent approximation to set $\sin (\beta +\gamma )=1$ in the formulae below although we will not do it in the numerical evaluations.

The values of $|V_{cb}|$ and $|V_{ub}|$ in (3) imply then

$$\begin{aligned} \frac{|V_{ub}|}{|V_{cb}|}= & {} 0.0921\pm 0.0036, \nonumber \\ R_b= & {} 0.399\pm 0.016 ,\quad (\text {EXCLUSIVE}) \end{aligned}$$

(7)

and using [37]

$$\begin{aligned}&\gamma = (65.4^{+3.8}_{-4.2})^\circ . \end{aligned}$$

(8)

$$\begin{aligned}&\beta = (23.50\pm 0.93)^\circ , S_{\psi K_S}=\sin (2\beta )=0.731\pm 0.024,\nonumber \\&\quad (\text {EXCLUSIVE}) \end{aligned}$$

(9)

that both differ mildly from the measured values [22]

$$\begin{aligned}&\beta =(22.2\pm 0.7)^\circ , \quad S_{\psi K_S}=0.699(17), \quad (\text {PDG}). \end{aligned}$$

(10)

On the other hand in the HYBRID scenario we find

$$\begin{aligned} \frac{|V_{ub}|}{|V_{cb}|}=0.0856\pm 0.0032,&\quad R_b= 0.371\pm 0.014,\nonumber \\&\quad (\text {HYBRID}) \end{aligned}$$

(11)

and

$$\begin{aligned} \beta= & {} (21.74\pm 0.84)^\circ ,\nonumber \\ S_{\psi K_S}= & {} \sin (2\beta )=0.688\pm 0.022, \quad (\text {HYBRID}) \end{aligned}$$

(12)

in perfect agreement with the experimental measurements in (10).

Fig. 1

The unitarity triangle

This brief exercise is an overture to the new tensions emerging from the exclusive strategy. In Fig. 2 we show $\beta$ as a function of $\gamma$ for the values of $|V_{ub}|/|V_{cb}|$ in two scenarios in question and compare them to the one-sigma range for $\beta$ in (10). We observe that in the case of the EXCLUSIVE strategy there is indeed a mild tension. To remove this tension a negative NP phase has to be added to $\beta$ in the formula for $S_{\psi K_S}$ in (9). See (23). This negative phase originates in a NP phase in $B_d^0-{{\bar{B}}}_d^0$ mixing. Significantly larger tensions will be found in most observables analyzed by us.

Fig. 2

The UT angle $\beta$ as functions of $\gamma$, in the EXCLUSIVE and HYBRID scenarios. The bands represent the uncertainties related to $|V_{cb}|$, $|V_{ub}|$ and $|V_{us}|$. The one-sigma range for $\beta$ in (10) is shown as a red band

In this context we would like to mention the analysis in [38] in which the ratio $|V_{ub}|/|V_{cb}|$ was proposed as a useful test of the SM because of reduced hadronic uncertainties combined with the fact that this ratio is almost the same for the exclusive and inclusive determinations of $|V_{cb}|$ and $|V_{ub}|$.

Finally, useful are also the following expressions ($\lambda _t=V_{td}V^*_{ts}$)

$$\begin{aligned}&|V_{td}|=\lambda |V_{cb}|\sin \gamma =(8.82\pm 0.14)\,\sin \gamma \times 10^{-3},\nonumber \\&\quad (\text {EXCLUSIVE}), \end{aligned}$$

(13)

$$\begin{aligned}&\mathrm{{Im}}\lambda _t=|V_{ub}||V_{cb}|\sin \gamma =(1.42\pm 0.06)\,\sin \gamma \times 10^{-4},\nonumber \\&\quad (\text {EXCLUSIVE}), \end{aligned}$$

(14)

where the values in (3) have been used. For the HYBRID scenario we have

$$\begin{aligned}&|V_{td}|=\lambda |V_{cb}|\sin \gamma =(9.49\pm 0.12)\,\sin \gamma \times 10^{-3},\nonumber \\&\quad (\text {HYBRID}), \end{aligned}$$

(15)

$$\begin{aligned}&\mathrm{{Im}}\lambda _t=|V_{ub}||V_{cb}|\sin \gamma =(1.52\pm 0.06)\,\sin \gamma \times 10^{-4},\nonumber \\&\quad (\text {HYBRID}) . \end{aligned}$$

(16)

Moreover

$$\begin{aligned}&|V_{ts}|=[1 \!+\!\frac{\lambda ^2}{2}(1\!-\!2 \sin \gamma \cos \beta )] |V_{cb}|\approx 0.983|V_{cb}|.\nonumber \\ \end{aligned}$$

(17)

As $|V_{td}|$ and $\mathrm{{Im}}\lambda _t$ play an important role in rare K and B decays we show in Fig. 3 their dependence on $\gamma$ in both scenarios.

A recent review of tree-level determinations of $\beta$ and $\gamma$ can be found in Chapter 8 of [2]. See also [39, 40]. But here we will use $\gamma$ as a free parameter and $\beta$ as an output by means of (5).

Fig. 3

$|V_{td}|$ and $\mathrm{{Im}}\lambda _t$ as functions of $\gamma$ in the EXCLUSIVE and HYBRID scenarios

3 Numerical analysis

Our numerical analysis uses the formulae for various branching ratios that we have collected in [7]. The parameters, other than the CKM ones, entering the formulae in [2, 7] are collected in the Table 1. Except for the values of $F_{B_s} \sqrt{{{\hat{B}}}_s}$ and $F_{B_d} \sqrt{{{\hat{B}}}_d}$ that are taken this time from the HPQCD collaboration [19],⁴ other parameters are unchanged. These two inputs from $N_f=2+1+1$ LQCD calculations are only slightly lower than the ones used in [2, 7] but are significantly lower than the ones from $N_f=2+1$ LQCD average given by FLAG in [6]. These differences are summarized in Appendix B. Their impact on the determination of $|V_{cb}|$ from $\Delta M_s$ and $\Delta M_d$ will be analysed in Sect. 4.

Table 1 Values of the experimental and theoretical quantities used as input parameters. For future updates see FLAG [6], PDG [22] and HFLAV [42]

Here we only recall that the dependence of the observables considered by us on $|V_{us}|$ is negligible. As far as $\beta$ and $\gamma$ are concerned, the angle $\beta$ is already known from the mixing induced CP-asymmetry $S_{\psi K_S}$ with respectable precision as given in (10) and there is a significant progress by the LHCb collaboration on the determination of $\gamma$ from tree-level strategies [37] so that we have presently from tree-level decays the value given in (8). Moreover, in the coming years the determination of $\gamma$ by the LHCb and Belle II collaborations should be significantly improved so that precision tests of the SM using the strategy in [7] and the one presented here will be possible.

However we emphasize that we do not use the value of $\gamma$ above as an input parameter. Our strategy will be to treat $\gamma$ as a free parameter in the rather broad range $60^\circ \le \gamma \le 75^\circ$ and in view of the future measurements of $\gamma$ by LHCb and Belle II to exhibit the $\gamma$ dependence of the observables considered by us. We recall that the angle $\beta$ is the output by means of the unitarity relation (5) as given in Fig. 2.

In Table 2 we show SM predictions for a number of rare K and B branching ratios and $\Delta F=2$ observables resulting from the EXCLUSIVE input in (3) setting $\gamma =65.4^\circ$, the central LHCb value. The uncertainties appearing therein, thus, do not include any error on the $\gamma$ determination. We also show our results in the HYBRID scenario defined in (4). The latter are not far from the ones obtained in [7] where the absence of NP contributions to $\Delta F=2$ observables was assumed. We do not consider the decays like $B\rightarrow K(K^*)\ell ^+\ell ^-$ that have larger theoretical uncertainties than the observables considered by us. Their $|V_{cb}|$ dependence has been investigated recently in [12].

The decay $B_s\rightarrow X_s\gamma$ was not considered in [7]. The result for $B_s\rightarrow X_s\gamma$ in both scenarios is obtained here from [48] that effectively corresponds to the inclusive $|V_{cb}|=42.0\times 10^{-3}$. We just rescaled it using the exclusive and inclusive values of $|V_{cb}|$ for EXCLUSIVE and HYBRID scenarios, respectively.

Table 2 Predictions (second column) for various observables within the SM using the EXCLUSIVE strategy for $|V_{cb}|$ and $|V_{ub}|$ and $\gamma =65.4^\circ$. In the third column we show the results for the HYBRID choice of $|V_{cb}|$ and $|V_{ub}|$ as given in (4) and in the fourth the experimental data

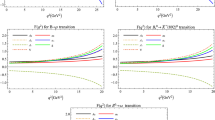
In Figs. 4, 5 and 6 we show the $\gamma$ dependence of the following observables

$$\begin{aligned}&\mathcal {B}(K^+\rightarrow \pi ^+\nu {\bar{\nu }}),\quad \mathcal {B}(K_{L}\rightarrow \pi ^0\nu {\bar{\nu }}),\quad \Delta M_d, \nonumber \\&\quad \mathcal {B}(B_d\rightarrow \mu ^+\mu ^-),\quad \varepsilon _K,\quad S_{\psi K_S} \end{aligned}$$

(18)

in both scenarios for $|V_{cb}|$ and $|V_{ub}|$. $\mathcal {B}(K_S\rightarrow \mu ^+\mu ^-)$ has the same $\gamma$ dependence as $\mathcal {B}(K_{L}\rightarrow \pi ^0\nu {\bar{\nu }})$ and the remaining observables do not depend or only weakly depend on $\gamma$.

Fig. 4

The branching ratios $\mathcal {B}(K^+\rightarrow \pi ^+\nu {\bar{\nu }})$ and $\mathcal {B}(K_{L}\rightarrow \pi ^0\nu {\bar{\nu }})$ as functions of $\gamma$, in the EXCLUSIVE and HYBRID scenarios. The bands represent the uncertainties related to $|V_{cb}|$, $|V_{ub}|$, $|V_{us}|$ and to the non-CKM parameters

Fig. 5

$\Delta M_d$ and the branching ratio $\mathcal {B}(B_d\rightarrow \mu ^+\mu ^-)$ as functions of $\gamma$, in the EXCLUSIVE and HYBRID scenarios. The bands represent the uncertainties related to $|V_{cb}|$, $|V_{ub}|$, $|V_{us}|$ and to the non-CKM parameters. The red band in the upper panel represents the experimental value for $\Delta M_d$, with its $1\sigma$ uncertainty

Fig. 6

$\varepsilon _K$ and the CP asymmetry $S_{\psi K_S}$ as functions of $\gamma$, in the EXCLUSIVE and HYBRID scenarios. The bands represent the uncertainties related to $|V_{cb}|$, $|V_{ub}|$, $|V_{us}|$ and to the non-CKM parameters. The red band in the upper panel represents the experimental value for $\varepsilon _K$, with its $1\sigma$ uncertainty. The same for $S_{\psi K_S}$

Concentrating first on the EXCLUSIVE scenario we observe:

• As seen in Table 2 for $\gamma =65.4^\circ$, the largest tensions are found for $\varepsilon _K$ ($4.1\sigma$), $\Delta M_s$ ($3.1\sigma$) and $\Delta M_d$ ($2.6 \sigma$).

• As $\Delta M_s$ is practically independent of $\gamma$ this tension remains for other values of $\gamma$.

• As seen in Fig. 4, the branching ratios for $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$ and $K_{L}\rightarrow \pi ^0\nu {\bar{\nu }}$ are significantly suppressed below the values found in the literature that are in the ballpark of $8.5\times 10^{-11}$ and $3.0\times 10^{-11}$, respectively [7]. But this suppression decreases with increasing $\gamma$.

• As seen in Fig. 5, the tension in $\Delta M_d$ decreases to ${0.6}\,\sigma$ for $\gamma =75^\circ$ but is as large as $4\sigma$ for $\gamma =60^\circ$. The branching ratio for $B_d\rightarrow \mu ^+\mu ^-$ shows a similar behaviour because its ratio to $\Delta M_d$ is CKM parameters independent. The uncertainty in $\Delta M_d$ is a bit larger because of the additional hadronic uncertainty in the parameter ${{\hat{B}}}_d$. The red band in the upper panel represents the experimental value for $\Delta M_d$, with its $1\sigma$ uncertainty.

• As seen in Fig. 6, the tension for $\varepsilon _K$ (with the experimental measurement shown in red) is practically linear in $\gamma$ and in the range of $\gamma$ considered varies from ${2.0}\sigma$ for $\gamma =75^\circ$ to $5.2\sigma$ for $\gamma =60^\circ$. While significant tension in $\varepsilon _K$ in the EXCLUSIVE scenario has been already identified in [17], our analysis differs in several respects from that paper as we already stated at the beginning of this writing. On the other hand the tension for $S_{\psi K_S}$ is practically independent of $\gamma$ and in the ballpark of $1.0\sigma$ so that in this case one really cannot talk about an anomaly.

• The tension in $B_s\rightarrow \mu ^+\mu ^-$ basically disappears.

On the other hand in the HYBRID scenario all these tensions disappear but the one in $B_s\rightarrow \mu ^+\mu ^-$ is independently of $\gamma$ in the ballpark of $2.1 \sigma$ [10].

4 The impact of the HPQCD results

It is of interest to see how the use of $2+1+1$ hadronic matrix elements from the HPQCD collaboration [19] used in the present paper, instead of the ones used in [7] (the average of 2 + 1 and 2 + 1 + 1 results), would modify our results for rare B decays of the latter paper in which no NP in $\Delta M_s$ and $\Delta M_d$ has been assumed. We make this comparison in Table 3. For completeness we list there also results for rare K decays which remain unchanged. This also allows the comparison with the results obtained in EXCLUSIVE and HYBRID scenarios in Table 2.

We observe that all B decays branching ratios in Table 3 are larger than our results obtained in [7] that were rather close to the ones in the HYBRID scenario. In view of still sizable experimental errors this impact of the HPQCD results cannot be fully appreciated with the exception of $B_s\rightarrow \mu ^+\mu ^-$. With the branching ratio for this decay in Table 3 and the experimental data in Table 2, assuming no NP in $\Delta M_s$, the anomaly in $B_s\rightarrow \mu ^+\mu ^-$ of $2.1\sigma$ found in [10] is raised to $2.7\sigma$.

It should be emphasized at this point that all the correlations found in [7] that do not involve $\Delta M_s$ and $\Delta M_d$ remain unchanged but the predictions for B decay branching ratios change as we have just seen. This then implies a different SM region in the correlation between $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$ and $B_s\rightarrow \mu ^+\mu ^-$ that we illustrate in Fig. 7. There the result using HPQCD $2+1+1$ input (left panel) is compared with the one of [7] (right panel) where the average of $2+1+1$ and $2+1$ matrix elements from [10] has been used. This difference shows the importance of charm contribution in LQCD calculations. Note that the result for $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$ did not change relative to [7].

Fig. 7

The correlation of $\mathcal {B}(K^+\rightarrow \pi ^+\nu {\bar{\nu }})$ with $\overline{\mathcal {B}}(B_s\rightarrow \mu ^+\mu ^-)^{1.4}$of [7] for different values of $\gamma$ within the SM. The SM area corresponds to the HPQCD $2+1+1$ input (left panel) and to the $2+1+1$ and $2+1$ average (right panel) used in [7]. The green area represents the EXCLUSIVE scenario and the gray area the present experimental situation

In fact our results for $B_{s,d}\rightarrow \mu ^+\mu ^-$ are rather consistent with the ones obtained by the HPQCD collaboration [19] in 2019. But since then the experimental accuracy of $B_{s,d}\rightarrow \mu ^+\mu ^-$ significantly increased [52,53,54] allowing a better estimate of the anomaly in question.

Finally, we would like to address another important issue. In [7], using the averages of $B^0_{s,d}-{{\bar{B}}}^0_{s,d}$ hadronic matrix elements from LQCD calculations with $2+1$ and $2+1+1$ flavours, as given in (32), we found that there are no values of $\beta$ and $\gamma$ for which the same value for $|V_{cb}|$ can be obtained from $\varepsilon _K$, $\Delta M_d$ and $\Delta M_s$ when imposing the experimental constraint from $S_{\psi K_S}$. It is then of interest to investigate what happens when this analysis is repeated separately for the $2+1$ and $2+1+1$ matrix elements as given in (26) and (29), respectively.

The result of this exercise is shown in Fig. 8. We observe that only in the case of $2+1+1$ flavours consistent result for $|V_{cb}|$ from all observables considered by us is obtained which in turn provides unique values of $|V_{cb}|$ and $\gamma$. The determination of $\gamma$ and $|V_{cb}|$ can be further improved by considering first the $|V_{cb}|$-independent ratio $\Delta M_d/\Delta M_s$ from which one derives an accurate formula for $\sin \gamma$

$$\begin{aligned} \sin \gamma= & {} \frac{0.983(1)}{\lambda }\sqrt{\frac{m_{B_s}}{m_{B_d}}}\xi \sqrt{\frac{\Delta M_d}{\Delta M_s}} , \nonumber \\ \xi= & {} \frac{F_{B_s}\sqrt{{\hat{B}}_{B_s}}}{F_{B_d}\sqrt{{\hat{B}}_{B_d}}}=1.216(16), \end{aligned}$$

(19)

with the value for $\xi$ from HPQCD [19] and where (17) has been used.. The advantage of using this ratio for the determination of $\gamma$ over studying $\Delta M_s$ and $\Delta M_d$ separately is the reduced error on $\xi$ from LQCD relative to the individual errors of hadronic parameters in $\Delta M_s$ and $\Delta M_d$. See Appendix B.

Combining then $\varepsilon _K$, $\Delta M_d$, $\Delta M_s$, $S_{\psi K_S}$ and using (19) we obtain finally the following values of the CKM parameters

$$\begin{aligned} \boxed {|V_{cb}|=42.6(4)\times 10^{-3},\quad \gamma =64.6(16)^\circ ,\quad \beta =22.2(7)^\circ .}\nonumber \\ \end{aligned}$$

(20)

The value of $|V_{cb}|$ is somewhat larger than in the HYBRID scenario in (4) but consistent with it. It should be noted that the determination of $\gamma$ in this manner is more accurate than its present determination from tree-level decays in (8). The corresponding value of $|V_{ub}|$ is

$$\begin{aligned} \boxed {|V_{ub}|=3.72(11)\times 10^{-3},} \end{aligned}$$

(21)

which is slightly larger than the FLAG determination but consistent with it. We observe that $\varepsilon _K$ dominates this determination of $|V_{cb}|$. This can be traced back to its larger senitivity to $|V_{cb}|$ than it is the case for $\Delta M_{s,d}$. While $\Delta M_{s,d}$ are proportional to $|V_{cb}|^2$, $|\varepsilon _K|$ exhibits approximately $|V_{cb}|^{3.4}$ dependence [7]. Reducing the error on $\beta$, represented by the green band, and decreasing the error on $\gamma$ from its tree-level measurements will provide a determination of $|V_{cb}|$ with an error below $1\%$.

The $2+1$ case demonstrates significant inconsistencies between $|V_{cb}|$ values from $\Delta M_{d,s}$ and $\varepsilon _K$. The average in (32) considered by us in [7] is in a better shape but also various tensions are identified that we discussed in detail in the latter paper. The message from this exercise is clear. The inclusion of charm in the evaluation of $B^0_{s,d}-{{\bar{B}}}^0_{s,d}$ hadronic matrix elements by LQCD is mandatory and it is important that in addition to HPQCD [19] a second LQCD collaboration includes charm in the evaluation of these matrix elements.

Assuming that the HPQCD values will be confirmed by another LQCD group, the SM predictions in the left panel of Fig. 7 will be favoured implying

$$\begin{aligned} \overline{\mathcal {B}}(B_s\rightarrow \mu ^+\mu ^-)= & {} {(3.78^{+ 0.15}_{-0.10})}\times 10^{-9}, \nonumber \\ \mathcal {B}(K^+\rightarrow \pi ^+\nu {\bar{\nu }})= & {} (8.60\pm 0.42)\times 10^{-11}. \end{aligned}$$

(22)

But it should be remembered that in contrast to the EXCLUSIVE scenario discussed in previous sections these results assume that the SM predictions for $\Delta M_s$ and $\varepsilon _K$ agree with the data. If the EXCLUSIVE scenario will turn out to be true, the predictions above will be invalid and will be replaced by the ones in Table 2 and the green area in Fig. 7.

Fig. 8

The values of $|V_{cb}|$ extracted from $\varepsilon _K$, $\Delta M_d$ and $\Delta M_s$ as functions of $\gamma$. $2+1+1$ flavours (top), $2+1$ flavours (middle), average of $2+1+1$ and $2+1$ cases (bottom). The green band represents experimental $S_{\psi K_S}$ constraint on $\beta$

Table 3 Results for the rare B decay branching ratios using the strategy of [7] with the $2+1+1$ LQCD hadronic matrix elements of [19] (second column) compared with the ones obtained in [7] using the average of $2+1+1$ and $2+1$ LQCD data from [10] (third column). Results for rare K decays remain unchanged

5 Conclusions

The EXCLUSIVE vision of rare decays and quark mixing is still not excluded and could become reality in the coming years. The present paper shows, similarly to our analysis in [7], how important is the determination of $|V_{cb}|$ for rare decays, in particular for rare Kaon decays. A precise determination of the $\gamma$ in tree-level decays in the coming years will shed additional light on the tensions identified by us.

As we have seen, an unusual pattern of SM predictions results from this study with some existing tensions disappearing or being dwarfed and new ones being born. In particular the $B_s\rightarrow \mu ^+\mu ^-$ tension disappears and instead the anomalies at the level of $(2-5)\sigma$ are present in $\Delta M_s$, $\Delta M_d$ and in particular in $\varepsilon _K$. While the $3.1\sigma$ tension in $\Delta M_s$ is practically independent of $\gamma$, the one in $\Delta M_d$ increases from $0.6\,\sigma$ to $4\sigma$ when $\gamma$ is decreased from $75^\circ$ to $60^\circ$. In the case of $\varepsilon _K$ the corresponding variation is from $2.0\sigma$ to $5.2\sigma$.

Moreover, the room left for NP in $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$, $K_{L}\rightarrow \pi ^0\nu {\bar{\nu }}$ and $B\rightarrow K(K^*)\nu {\bar{\nu }}$ is significantly increased but as seen in Figs. 4 and 5 it depends sensitively on $\gamma$. The tension in $B\rightarrow X_s\gamma$ is also interesting.

It should be recalled that in 2018 with the values of $\gamma \approx 74^\circ$ from the LHCb, with the inclusive $|V_{cb}|$ and the $N_f=2+1$ hadronic $B^0_{s,d}-{{\bar{B}}}^0_{s,d}$ matrix elements, $\Delta M_d$ in the SM was found significantly above the data with a smaller enhancement in $\Delta M_s$ [16]. In 2022 with lower values for $\gamma \approx 65^\circ$ from the LHCb [37] and $N_f=2+1+1$ hadronic $B^0_{s,d}-{{\bar{B}}}^0_{s,d}$ matrix elements from HPQCD [19] the inclusive values of $|V_{cb}|$ imply good agreement of the SM with the data on $\Delta M_{s,d}$. But for the exclusive values of $|V_{cb}|$ used in the present paper $\Delta M_{s}$ is significantly below the experimental data. This also applies to $\Delta M_{d}$ unless $\gamma$ is chosen above $70^\circ$ that is not yet excluded by experiments.

In this context we should emphasize that the R(K) and $R(K^*)$ anomalies being independent of $|V_{cb}|$ remain. On the other hand, as analysed in [12], lowering the value of $|V_{cb}|$ decreases the anomalies in $B\rightarrow K\mu ^+\mu ^-$, $B\rightarrow K^*\mu ^+\mu ^-$ and $B_s\rightarrow \phi \mu ^+\mu ^-$ decay branching ratios but to remove them completely values of $|V_{cb}|$ significantly lower than the exclusive ones are required.

It is premature to make a detailed analysis of possible BSM scenarios that could remove the anomalies in the EXCLUSIVE scenario considered by us. Despite of this let us close our paper with a few observations.

As in the EXCLUSIVE scenario NP is required to enhance $\Delta M_s$, $\Delta M_d$ and $\varepsilon _K$, a natural scenario would be at first sight the constrained Minimal Flavour Violation scenario [57] because, as pointed out in [58], in this scenario the $\Delta F=2$ observables can only be enhanced. However, the fact that a new phase $\varphi _\mathrm{new}\approx -1.3^\circ$ is required to fit the data for $S_{\psi K_S}$, a more appropriate here would be the $\text {U(2)}^3$ scenario [59,60,61]. As pointed out in [62], in the $\text {U(2)}^3$ scenario the CP-asymmetry $S_{\psi K_S}$ is anti-correlated with the CP-asymmetry $S_{\psi \phi }$

$$\begin{aligned}&S_{\psi K_S} = \sin (2\beta +2\varphi _\mathrm{new}) , \quad S_{\psi \phi } = \sin (2|\beta _s|-2\varphi _\mathrm{new}) ,\nonumber \\&\quad (\mathrm{U(2)^3}), \end{aligned}$$

(23)

so that with $|\beta _s|\approx 1^\circ$ an enhancement of the latter asymmetry from the SM prediction $0.0363\pm 0.0013$ to $0.080\pm 0.020$ would follow. Somewhat above the present data $0.054\pm 0.020$ [22] but consistent with it.

As a byproduct we have investigated in Sect. 4 the impact of the hadronic matrix elements from the HPQCD collaboration [19] on our results for rare B decays in [7]. The most interesting result is the increase of the $B_s\rightarrow \mu ^+\mu ^-$ anomaly from $2.1\sigma$ to $2.7\sigma$. Moreover we compared the determination of $|V_{cb}|$ from $\Delta M_s$, $\Delta M_d$, $\varepsilon _K$ and $S_{\psi K_S}$ using $B^0_{s,d}-{{\bar{B}}}^0_{s,d}$ hadronic matrix elements from LQCD with $2+1+1$ flavours, $2+1$ flavours and their average. As seen in Fig. 8 only for the $2+1+1$ case values for $\beta$ and $\gamma$ can be found for which the same value of $|V_{cb}|$ is found. The resulting $|V_{cb}|$, $\gamma$ and $\beta$ are given in (20) and $|V_{ub}|$ in (21).

In any case the coming years will hopefully reveal for us which scenario for $|V_{cb}|$ and $|V_{ub}|$ has been chosen by nature. The measurement of $\gamma$ combined with the 16 $|V_{cb}|$-independent ratios constructed in [7] and with $\gamma$-dependence of various observables presented here will also play an important role in the search for NP. The importance of rare K decays in the search for NP has been recently summarized in [63] and the prospects for reducing hadronic uncertainties in K decays through intensive LQCD computations in the coming years are very good [64].

The EXCLUSIVE scenario appears to us to be more interesting than the HYBRID one because it implies more tensions between the SM predictions and the data. On the other the proponents of the inclusive determinations of $|V_{cb}|$ could consider the tensions found by us as an argument against exclusive determinations of $|V_{cb}|$.

Appendices

Appendix A: Weak decay constants from LQCD

For $N_f=2+1$ FLAG averages based on [65,66,67,68,69,70] read [6]

$$\begin{aligned} F_{B_d}= & {} 192.0(4.3) \;\mathrm{MeV},\quad F_{B_{s}} = 228.4(3.7) \; \mathrm{MeV}, \nonumber \\ \frac{F_{B_{s}}}{F_{B_d}}= & {} 1.201(16) , \end{aligned}$$

(24)

while for $N_f=2+1+1$ FLAG averages based on [71,72,73,74] are [6]

$$\begin{aligned} F_{B_d}= & {} 190.0(1.3) \;\mathrm{MeV},\quad F_{B_{s}} =230.3(1.3) \; \mathrm{MeV}, \nonumber \\ \frac{F_{B_{s}}}{F_{B_d}}= & {} 1.209(5) . \end{aligned}$$

(25)

While the central values in (24) and (25) are close to each other, the latter ones are much more accurate and we use them in our analysis.

Appendix B: Hadronic matrix elements from LQCD

For $N_f=2+1$ the FLAG averages dominated by FNAL/MILC results [20] and including [68, 75] are [6]

$$\begin{aligned}&F_{B_d}\sqrt{{\hat{B}}_{B_d}} = 225(9) \, \mathrm{MeV} F_{B_s}\quad \sqrt{{\hat{B}}_{B_s}} = 274(8) \, \mathrm{MeV} \end{aligned}$$

(26)

$$\begin{aligned}&{\hat{B}}_{B_d} = 1.30(10) \quad {\hat{B}}_{B_s} = 1.35(6) \end{aligned}$$

(27)

$$\begin{aligned}&\xi = 1.206(17) \quad {\hat{B}}_{B_s}/{\hat{B}}_{B_d} = 1.032(38) . \end{aligned}$$

(28)

For $N_f=2+1+1$ one finds [19]

$$\begin{aligned}&F_{B_d}\sqrt{{\hat{B}}_{B_d}}= 210.6(5.5) \;\mathrm{MeV}\;\; F_{B_s}\sqrt{{\hat{B}}_{B_s}}= 256.1(5.7)\; \mathrm{MeV} \end{aligned}$$

(29)

$$\begin{aligned}&{\hat{B}}_{B_d}= 1.222(61) \quad {\hat{B}}_{B_s}= 1.232(53) , \end{aligned}$$

(30)

$$\begin{aligned}&\xi = 1.216(16) \quad {\hat{B}}_{B_s}/{\hat{B}}_{B_d} = 1.008(25)\, . \end{aligned}$$

(31)

In this case there are significant differences between the $N_f=2+1$ and $N_f=2+1+1$ results. Moreover, the latter ones are more accurate and we use them in the present paper. In [7] we have used the averages of both results given by [10]

$$\begin{aligned} F_{B_d}\sqrt{{\hat{B}}_{B_d}}= & {} 214.0(39)\,\mathrm{MeV},\nonumber \\ F_{B_s}\sqrt{{\hat{B}}_{B_s}}= & {} 261.7(38)\,\mathrm{MeV} . \end{aligned}$$

(32)

These are consistent with the ones from [19] alone but higher. However FLAG-2021 advices not to make such averages so that this time we use the $N_f=2+1+1$ values.