1 Introduction

The current accelerated phase of expansion of the universe has been predicted by the Supernova observations almost three decades ago [1, 2]. It has been a constant motivation for the scientific community ever since to understand the fundamentals behind the present cosmic acceleration. There were attempts in the standard model of cosmology to explain the accelerated phase of expansion assuming a small cosmological constant \(\Lambda \) [3,4,5,6]. However, such a model of the universe suffers from the serious issue of fine tuning [7]. Thereafter, it was found that the accelerating expansion of the universe can be realized assuming the dynamics of the universe to be governed by a new type of fluid called dark energy (DE) which is dominating the present universe. It is predicted from observations that the DE constitutes around \(70\%\) of the total energy density of the universe, which has negative pressure and violates the strong energy condition [8,9,10]. In the literature several dark energy models are considered to solve the existing problems in cosmology. In the literature it is shown that the dynamical dark energy model is a candidate to get rid of the cosmological constant problem which further accommodates satisfactorily the present cosmic acceleration [11,12,13,14,15,16,17,18]. In this context there are various models of dynamical DE namely, quintessence \((-1<\omega <-\frac{1}{3})\) [19,20,21], phantom \((\omega <-1)\) [22], quintom [23] etc. which were introduced to understand the evolution of the late universe. In the case of dynamical DE, the equation of state (EoS) is a function of the redshift parameter or the scale factor of the universe [24, 25].

Alternatively, a modification of the gravitational sector of the Einstein’s general theory of relativity (GTR) is found to play an important role for a successful explanation of the DE era including accommodation of the early inflationary era for different coupling parameters [26,27,28,29,30,31]. As the GTR is not enough to describe various phases of the universe, there were attempts to consider gravitational action f(R) which is a non-linear function of the curvature scalar R [32]. In the literature a number of modified gravity theories namely, torsion based \(f({\mathcal {T}})\) [33, 34] theory where \({\mathcal {T}}\) is the torsion scalar, the f(R, T) theory of gravity with T being the trace of the energy momentum tensor [35], Gauss–Bonnet gravity [36] etc. are also taken up. It is also known that an alternative representation of GR can be constructed on a flat spacetime without the torsion. In this case the gravity is described by non-metricity (Q). The f(Q) gravity model is recently considered to investigate many interesting features of cosmology [37,38,39,40,41,42,43,44]. The gravitational theories based on f(Q) and \(f({\mathcal {T}})\) are found to have indistinguishable nature. The major differences between them arises in the cosmological perturbations. Recently, f(Q) gravity was employed to study the observational constraints [45,46,47,48,49], the theory is quite successful in describing the late time accelerating phase of the universe. The f(Q) gravity is also developed to study astrophysical objects namely, wormholes [50,51,52], spherically symmetric configuration [53], anisotropic stars [54]. The success of the theory motivate us to probe the astrophysical objects namely, primordial black holes and its evolution.

It is known that black holes are the final stage of evolution of a collapsing massive star whose mass exceeds twice the solar mass. There is another kind of black hole which is formed in the early universe due to the initial inhomogeneities in the scalar field [55, 56], phase transitions [57,58,59,60,61,62], bubble collision [63] or the decay of cosmic loops [64, 65]. These topological black holes are formed due to quantum fluctuations of the matter distribution of the early universe and are important in understanding the observed universe. The mass of such black holes are much smaller than the black holes formed due to the collapse of massive stars and they are known as primordial black holes (PBH).

The issues of the creation and subsequent evolution of PBHs in the early universe have become a topic of great interest as these may turn out to be interesting and promising candidates for dark matter. The discovery of Hawking radiation in 1975 started a new era in the study of black hole physics [66]. Hawking showed that the black holes emit thermal radiation when studied in the framework of relativistic quantum effects which leads to black hole evaporation. The black holes formed due to the gravitational collapse of massive stars are short lived but the lifetime of PBHs are comparatively long owing to their small masses, and is comparable to the age of the universe. Thus possibility of detecting Hawking radiation arises from PBHs because they are hotter compared to the surrounding temperature. In the case of interaction of dark matter with the Standard model field only gravitationally, the abundance of PBH in the universe may be shown due to evaporation by Hawking radiation [67]. Consequently, evaporating PBHs might have contributed for baryongenesis [68,69,70] whereas the black holes with larger masses could act as the seed for the structure formation or the generation of super-massive black holes [71, 72]. The accretion of matter from the surrounding medium by the PBHs may increase the lifetime of these black holes. Such long surviving PBHs may constitute a major portion of dark matter [73,74,75] contributing to the total energy density of the universe.

Recently, the accretion of phantom energy onto PBHs has been studied [76] and it was shown that mass of PBH gradually decreases due to the negative pressure of the phantom fluid. The evaporation time scale of PBHs increases when accretion of radiation is considered for different accretion efficiency [77]. Accretion of matter, radiation and dark energy (phantom as well as quintessence type) onto PBHs was probed in a modified \(f({\mathcal {T}})\) gravity [78]. The accretion of modified Chaplygin gas (MCG) onto PBHs has been studied in the framework of \(f({\mathcal {T}})\) gravity by Debnath and Paul [79] and they found that the mass accretion depends on the model parameters. The success of modified f(Q) gravity in cosmology motivate us to explore the PBHs in the framework of the modified gravity with a cosmic fluid described by a non-linear equation of state as it is a novel approach. We consider two branches of nonlinear EOS given by \(p=\omega \rho -B \rho ^{\alpha }\) as (i) \(\alpha <0\) representing modified Chaplygin gas (MCG) [80, 81] and (ii) \(\alpha >0\) representing the EoS of a cosmic fluid having dissipative effects. For \(\alpha =\frac{1}{2}\) the EoS corresponds to emergent universe [82, 85]. In the later case the important features of the nonlinear EOS are that it permit a singularity free emergent universe and the non-linear part of the EOS is analogous to the viscous fluid. The dissipative effects may arise due to a number of processes namely, decoupling of neutrinos from the radiation era, particle collisions involving gravitons and cosmological quantum particle creation processes in the early universe which are taken up in obtaining cosmological evolution [84]. It is also important to consider effects of viscosity which is quite natural around a black hole.

The plan of the paper is as follows: In Sect. 2, the basics of f(Q) gravity are presented with the field equations. In Sect. 3, the evolution of PBH is probed in f(Q) gravity in the presence of non-linear EoS. We consider two branches of non-linear EoS, (i) represents the MCG background and (ii) represents the EoS required for the EU. Finally in Sect. 4, we summarize the results obtained.

2 Gravitational action in f(Q) gravity and field equations

We consider the Palatini formalism where the metric and the connection are treated on equal footing although they are independent objects having a relation only through the field equations [86]. In this framework, the spacetime manifold is endowed with a metric structure determined by \(g_{\mu \nu }\), while the affine connection \(\Gamma ^{\alpha }_{\mu \nu }\) provides the affine structure that determines how the tensors are transported making use of the covariant derivative. The fundamental object in the theory is the non-metricity tensor which is defined as \(Q_{\alpha \mu \nu }=\nabla _{\alpha }g_{\mu \nu }\). Using the non-metricity tensor \(Q_{\alpha \mu \nu }\), one derives the disformation as

$$\begin{aligned} L^{\alpha }_{\mu \nu }=\frac{1}{2}Q^{\alpha }_{\mu \nu }-Q_{(\mu \nu )}^{\alpha } \end{aligned}$$
(1)

which determines deviation of the symmetric part of the full connection from the Levi-Civita connection. The non-metricity conjugate is defined as,

$$\begin{aligned} P^{\alpha }_{\mu \nu }=-\frac{1}{2}L^{\alpha }_{\mu \nu }+\frac{1}{4}(Q^{\alpha }-\tilde{Q^{\alpha }})g_{\mu \nu }-\frac{1}{4}\delta ^{\alpha }_{\mu }Q_{\nu }, \end{aligned}$$
(2)

which is related to the two independent traces \(Q_{\alpha }=g^{\mu \nu }Q_{\alpha \mu \nu }\) and \(\tilde{Q_{\alpha }}=g^{\mu \nu }Q_{\mu \alpha \nu }\) of the non-metricity tensor. In this case the non-metricity scalar is given by:

$$\begin{aligned} Q=-Q_{\alpha \mu \nu }P^{\alpha \mu \nu }. \end{aligned}$$
(3)

The non-metricity conjugate \(P^{\alpha \mu \nu }\) satisfies the relation

$$\begin{aligned} P^{\alpha \mu \nu }=-\frac{1}{2}\frac{\partial Q}{\partial Q_{\alpha \mu \nu }}. \end{aligned}$$
(4)

The non-metricity scalar can be used to write the action for the f(Q) modified theory which is given by,

$$\begin{aligned} {\mathcal {S}}=\int d^{4}x\sqrt{-g} \; \left( -\frac{1}{2} f(Q)+{{\mathcal {L}}}_{M} \right) \end{aligned}$$
(5)

where, \({\mathcal {L}}_{M}\) denotes the matter Lagrangian. The above non-metricity scalar and the action described by \(f(Q)=\frac{Q}{8\pi G}\) (where G is the Gravitational constant) reproduces GR classically up to boundary term [87]. It is important to mention here that the particular choice mentioned above recovers the Symmetric Teleparallel Equivalent of GR (STEGR).

In a flat and torsion free connection geometry it corresponds to a pure coordinate transformation obtained from the trivial connection. The connection can be parametrized with a set of functions \(\xi ^{\alpha }\) and is given by,

$$\begin{aligned} \Gamma ^{\alpha }_{\mu \beta }=\frac{\partial x^{\alpha }}{\partial \xi ^{\rho }}\partial _{\mu }\partial _{\beta }\xi ^{\rho }. \end{aligned}$$
(6)

The metric field equation in this case can be written as,

$$\begin{aligned}&\frac{2}{\sqrt{-g}}\nabla _{\alpha }(\sqrt{-g}f_{Q}P^{\alpha }_{\mu \nu })\nonumber \\&\quad +\frac{1}{2}g_{\mu \nu }f+f_{Q}(P_{\mu \alpha \beta }Q_{\nu }^{\alpha \beta }-2Q_{\alpha \beta \mu }P^{\alpha \beta }_{\nu })=T_{\mu \nu }, \end{aligned}$$
(7)

where, \(f_{Q}=\frac{\partial f}{\partial Q}\). By raising one index this adopts an even slightly more compact form,

$$\begin{aligned} \frac{2}{\sqrt{-g}}\nabla _{\alpha }(\sqrt{-g}f_{Q}P^{\alpha \mu }_{\nu }+\frac{1}{2}\delta ^{\mu }_{\nu }f+f_{Q}P^{\mu \alpha \beta }Q_{\nu \alpha \beta }=T^{\mu }_{\nu }. \end{aligned}$$
(8)

The cosmological models based on Eq. (5) does not differ from that of the \(f({\mathcal {T}})\) gravitational theory. However, a crucial difference arises at the level of cosmological perturbations. We consider a homogeneous flat Robertson–Walker metric which is given by,

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}(t)(dr^{2}+r^{2}(d\theta ^{2}+sin^{2}\theta d\phi ^{2})) \end{aligned}$$
(9)

where, a(t) represents the scale factor. The field equations corresponding to the action (5) are given by,

$$\begin{aligned}&6f_{Q}H^{2}-\frac{1}{2}f=\rho , \end{aligned}$$
(10)
$$\begin{aligned}&(12H^{2}f_{QQ}+f_{Q})\dot{H}=-\frac{1}{2}(\rho +p). \end{aligned}$$
(11)

where, \(f_{Q}=\frac{\partial {f}}{\partial Q}\) and \(f_{QQ}=\frac{\partial ^{2}f}{\partial Q^{2}}\) and \(H=\frac{\dot{a}}{a}\) represents the Hubble parameter. The non-metricity scalar in this case is given by \(Q=6H^{2}\) and \(\kappa ^{2}=8\pi G\). The energy density of the cosmic fluid is given by \(\rho \) and the total pressure of the cosmic background fluid is p.

We consider here a functional form of f(Q), which is STEGR supplemented with a general power-law term [86], i.e.,

$$\begin{aligned} f=\frac{1}{8\pi G}\Big [Q-6\lambda \tilde{m}^{2}\Big (\frac{Q}{6\tilde{m}^{2}}\Big )^{\xi }\Big ] \end{aligned}$$
(12)

where, \(\lambda \) and \(\xi \) are dimensionless parameters which give rise to branches of solutions permissible for the early universe cosmology or the late era accommodating dark energy depending on the values of \(\xi \) and a mass scale parameter \(\tilde{m}\). The field Eqs. (10) and (11) in this case are modified and are given by,

$$\begin{aligned}&H^{2}\Big [1+(1-2\xi )\lambda \Big (\frac{H^{2}}{\tilde{m}^{2}}\Big )^{\xi -1}\Big ]=\frac{8\pi G}{3}\rho , \end{aligned}$$
(13)
$$\begin{aligned}&2\xi (\xi -1)\lambda \frac{H^{2}}{\tilde{m}^{2}}\Big (\frac{Q}{6\tilde{m}^{2}}\Big )^{\xi -2}-\dot{H}\nonumber \\&\quad +\xi \lambda \dot{H}\Big (\frac{Q}{6\tilde{m}^{2}}\Big )^{\xi -1}=\frac{1}{2}(\rho +p). \end{aligned}$$
(14)

The special values of the parameter namely, \(\xi =\frac{1}{2}\) corresponds to GR, \(\xi =1\) corresponds to the STEGR and the additional terms can be absorbed into the gravitational constant G. Recently f(Q)-gravity with quintessence was used to study anisotropic compact object with an exponential form of f(Q) gravity [54]. For simplicity we consider \(\xi =2\) to probe the evolution of the PBH in the f(Q)-gravity. The field equations are highly non-linear, therefore, for \(\xi =2\), an analytic solution for H is obtained from Eq. (13) which is given by,

$$\begin{aligned} H=\Big (\frac{\tilde{m}^{2}+\tilde{m}\sqrt{\tilde{m}^{2}-4\lambda \rho }}{6\lambda }\Big )^{\frac{1}{2}}. \end{aligned}$$
(15)

It is evident from Eq. (15) that the Hubble parameter depends explicitly on both the model parameters: \(\lambda \) and \(\tilde{m}\).

In f(Q) gravity the standard matter fields satisfy the continuity equation

$$\begin{aligned} \dot{\rho }+3H(\rho +p)=0 \end{aligned}$$
(16)

which is consistent in accordance with the field equations. We now consider the EoS of the cosmic fluid be of the polynomial form,

$$\begin{aligned} p=f(\rho ),\ \text {with},\ f(\rho )=\omega \rho -{B}\rho ^{\alpha }\quad \omega>0,\ B>0. \end{aligned}$$
(17)

The above EoS corresponds to two different class of fluids depending on the value of \(\alpha \). For \(-1\le \alpha \le 0\) the EoS corresponds to the modified Chaplygin gas (MCG) which is widely used in cosmology to explain the late accelerating universe. The MCG is a promising candidate for describing the dark energy content of the universe. In the literature the role of MCG in different cosmological as well as astrophysical phenomena are studied including estimation of the observational bounds on the EoS parameters [88,89,90,91]. The evolution of PBH in the presence of MCG has been studied in the framework of \(f({\mathcal {T}})\) modified gravity and it is found that the parameters \(\omega \) and B played crucial role in obtaining the evolutionary scenario of PBH [79].

The positive magnitude of \(\alpha \) in the non linear EoS behaves as a perfect fluid with viscosity. For a special value of \(\alpha =\frac{1}{2}\), the EoS \(p=\omega \rho -B\rho ^{\frac{1}{2}}\) was employed to construct emergent universe (EU) model in GTR [85, 92, 93]. The EoS was used to construct cosmological models in \(D\ge 4\) [83]. In case of EU, the present universe emerged from a static de Sitter phase in the infinite past which was identified with the neck of the wormhole and as it evolves the universe encompass the present accelerating universe. Thus it is interesting to study the evolution of PBH in an ever-existing universe without the presence of exotic matter in the framework of f(Q) gravity, which eventually entered into the standard Big-Bang epoch at some stage and is consistent with the observational features known to us.

Using Eqs. (16) and (17) the energy density of the universe can be determined as,

$$\begin{aligned} \rho =\Big [\frac{B}{1+\omega }+Ca^{-3(1-\alpha )(1+\omega )}\Big ]^{\frac{1}{1-\alpha }}. \end{aligned}$$
(18)

The energy density can be expressed in terms of the redshift parameter z as,

$$\begin{aligned} \rho =\Big [\frac{B}{1+\omega }+C(1+z)^{3(1-\alpha )(1+\omega )}\Big ]^{\frac{1}{1-\alpha }}, \end{aligned}$$
(19)

where the scale factor and the redshift parameter z are related as \(a=\frac{1}{1+z}\) taking present size \(a(t_o)=1\).

3 Evolution of primordial black holes in the f(Q) gravity with non-linear EoS

The rate of loss of mass from PBH by Hawking radiation process is given by,

$$\begin{aligned} \dot{M(t)}_{{eva}}=-\frac{a_{H}}{256\pi ^{3}}\frac{1}{G^{2}M(t)^{2}} \end{aligned}$$
(20)

where, \(a_{H}\) represents the black body constant and the overdot \(\dot{( })\) denotes the derivative with respect to time. The evaporation of the primordial black holes will be delayed due to accretion of cosmic fluid surrounding the black hole. The mass of a PBH will increase due to the accretion of cosmic fluid. The mass accretion rate is given by,

$$\begin{aligned} \dot{M(t)}_{{accr}}=4\pi A M(t)^{2} (\rho +p) \end{aligned}$$
(21)

where, A denotes the accretion efficiency. We consider a non-linear EoS of the form of Eq. (17) in two different cases determined by the parameter \(\alpha \).

Fig. 1
figure 1

Evolution of PBH mass M(z) with redshift z for different \(\omega \) and \(\lambda =0.00007\). Here \(\omega =0.5\) (red), \(\omega =0.1\) (blue) and \(\omega =0\) (green) respectively

Full size image
Fig. 2
figure 2

Evolution of PBH mass M(z) with redshift z for different \(\lambda \) and \(\omega =0.5\). Here \(\lambda =0.00007\) (red), \(\lambda =0.00008\) (blue) and \(\lambda =0.00009\) (green) respectively

Full size image

3.1 Case I; evolution of PBH when \(-1\le \alpha \le 0\)

For \(-1\le \alpha \le 0\), Eq. (17) leads to the EoS of MCG. We consider the growth or decay of the mass of a PBH in the cosmological background of f(Q) gravity in presence of MCG as the cosmic fluid. The PBH density is assumed to be low enough to ensure radiation domination to begin with. We can now rewrite the mass evolution equation in terms of the redshift parameter z as,

$$\begin{aligned} \frac{dM}{dz}=-\frac{1}{H(1+z)}\Big [-\frac{a_{H}}{256\pi ^{3}G^{2}M^{2}}+4\pi A M^{2}(\rho +p)\Big ] \end{aligned}$$
(22)

where, the Hubble parameter is given by Eq. (15). The above equation can be rewritten by inserting the values of \(\rho \) and H as,

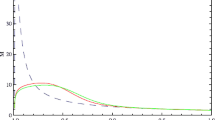
$$\begin{aligned} \frac{dM}{dz}=-\frac{1}{1+z}Y\Big (\frac{\tilde{m}^{2}+\tilde{m}\sqrt{\tilde{m}^{2}-4\lambda \rho }}{6\lambda }\Big )^{-\frac{1}{2}}. \end{aligned}$$
(23)

where, \(Y=\Big (-\frac{a_{H}}{256\pi ^{3}G^{2}M^{2}}+4\pi AM^{2} (1+\omega ) \eta (B,C)^{\frac{1}{1+\alpha }}-4\pi A B M^{2}\eta ^{-\frac{\alpha }{1+\alpha }}\Big )\) and \(\eta (B,C)=\Big [\frac{B}{1+\omega }+\frac{C}{a^{3(1+\alpha )(1+\omega )}}\Big ]\). The above equation will be used to study the evolution of PBH in the present era which corresponds to low z values. The first order differential equation describing the mass evolution is highly non-linear and cannot be solved analytically. So, a numerical technique is applied to determine the rate of change of the mass of the PBH with redshift parameter z. We note that the parameters \(\lambda \), \(\tilde{m}\), \(\omega \), B and \(\alpha \) act as free parameters in this case. We plot the variations of the mass of PBH with redshift parameter z for different values of the EoS parameter \(\omega \) in Fig. 1 and the coupling parameter \(\lambda \) in Fig. 2. In Fig. 1 the evolution of mass of PBH is plotted for different \(\omega =0, 0.1\) and 0.5 taking a given coupling parameter \(\lambda \). The accretion efficiency in all the cases is considered same. We note that the mass accretion rate for PBHs with same initial mass in the past depends on \(\omega \). The mass accretion rate increases with increase in \(\omega \) and we note that the model permits maximum value \(\omega =0.5\). It is also noted that the PBH mass increases and thereafter attains a saturation reaching a fixed mass. The accretion rate is found lowest when \(\omega =0\), this indicates that the accretion is low if one considers the Generalized Chaplygin gas (GCG). Considering the evolution of PBH mass determined by the joint interaction of Hawking radiation and the accretion of cosmic fluid surrounding the PBH given by Eq. (22), we found that the mass accretion dominates over the evaporation process and finally lead to an equilibrium which will attain a saturation in the future.

Figure 2 shows the variation of the mass of the PBH with redshift z for different \(\lambda \) keeping the other parameters fixed. We note that as \(\lambda \) increases the mass accretion rate increases and the PBH mass will attain a fixed value in the future. The mass evolution of PBHs having same mass to begin with depends on the model parameter \(\lambda \) when the other parameters are kept fixed. However, if \(\lambda \) is increased beyond a certain limiting value we do not find a realistic solution that admits PBH.

Fig. 3
figure 3

Evolution of PBH mass M(z) vs. redshift z for different A and \(\lambda =0.00007\). With \(A=0.3\) (red), \(A=0.5\) (blue) and \(A=0.7\) (green) respectively

Full size image
Fig. 4
figure 4

Evolution of PBH mass M(z) with redshift z for different B and \(\lambda =0.00007\). With \(B=0.3\) (red), \(B=0.5\) (blue) and \(B=0.7\) (green) respectively

Full size image

The evolution of PBH mass with redshift parameter z for different accretion efficiency A and EoS parameter B is plotted in Figs. 3 and 4 respectively. It is evident that as the accretion efficiency increases the growth rate of PBH mass also increases. PBHs that begin to evolve from a given mass grows in the framework of MCG around the black hole and the mass increment stops after some time leading to PBHs with no change in mass at the later epoch. In Fig. 4 evolution of PBH mass with z is plotted for different B values of MCG. In this case the growth rate is same in the beginning and after a certain redshift (\(z\sim 0.5\)), PBHs surrounded by MCG having smaller B values accumulate more mass, finally it reaches to a constant mass in the future. The variation of PBH mass with z having different initial masses is shown in Fig. 5. We note that the growth of mass depends on the accretion efficiency A and the PBH having the lowest mass to begin with and highest accretion efficiency accumulates maximum mass. However, for identical accretion efficiency A, PBH having higher initial mass accumulates more mass at a faster rate before it reaches saturation.

3.2 Evolution of PBH for \(\alpha >0\)

In this section we consider the evolution of PBHs surrounded by a cosmic fluid having non-linear EoS described by Eq. (17) in f(Q) gravity. Here, positive \(\alpha \) corresponds to the generalised EoS of a cosmic fluid with dissipative effects. It is important to mention that, for \(\alpha =\frac{1}{2}\), the EoS reduces to that of an EU as proposed by Mukherjee et al. [85] and can be expressed as:

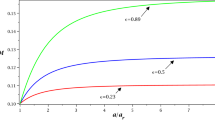
$$\begin{aligned} p=w\rho -B\rho ^{\frac{1}{2}} \end{aligned}$$
(24)

where, \(\omega \) and B are unknown parameters. In Fig. 6 we plot the variation of mass of the PBH with redshift parameter z considering different \(\alpha \) values. We note that for the EU scenario (\(\alpha =\frac{1}{2}\)), the mass accretion rate is maximum, however for PBHs surrounded by fluids with dissipative effects the mass accretion rate is slow compared to the EoS required for the EU scenario.

Fig. 5
figure 5

Evolution of PBH mass M(z) with redshift z for different A and \(\lambda =0.00007\). With \(A=0.5\) (red), \(A=0.3\) (blue) and \(A=0.1\) (green) respectively

Full size image
Fig. 6
figure 6

Evolution of PBH mass M(z) with redshift z for different \(\alpha \) having same initial mass. Here \(\alpha =\frac{1}{2}\) (EU, red), \(\alpha =\frac{2}{3}\) (blue) and \(\alpha =0.7\) (green) respectively

Full size image
Fig. 7
figure 7

Evolution of PBH mass M(z) with redshift z for different \(\lambda \) in case of an Emergent Universe. Here \(\lambda =0.0005\) (red), \(\lambda =0.001\) (blue) and \(\lambda =0.002\) (green) respectively

Full size image
Fig. 8
figure 8

Evolution of PBH mass M(z) with redshift z for different \(\omega \) in case of an Emergent Universe. Here \(\omega =\frac{1}{3}\) (red), \(\omega =-\frac{1}{3}\) (blue), \(\omega =1\) (green) and \(\omega =0\) (black) respectively

Full size image
Fig. 9
figure 9

Evolution of PBH mass M(z) with redshift z for different A in case of an Emergent Universe considering different initial mass. Here \(A=0.5\) (red), \(A=0.3\) (blue) and \(A=0.1\) (green) respectively

Full size image

We now consider \(\alpha =\frac{1}{2}\), i.e. the EU model, with different \(\omega \) which corresponds to different compositions of matter to study the accretion. In this case the mass evolution equation remains the same as given by Eq. (22), where the pressure of the cosmic fluid is expressed by Eq. (24). We plot the variations of the PBH mass with z in Fig. 7 considering different \(\lambda \) values keeping the other parameters fixed. For \(\omega =1\), which corresponds to the matter composition of dark energy, dust and stiff matter we note that for PBHs having the same mass to begin with the mass accretion rate is found to increase with the increase in \(\lambda \). For higher \(\lambda \), PBHs accumulate more mass as it evolves, eventually reaching a saturation. This behaviour is found analogous to the case when MCG is present around the PBH, but we note that the mass accumulation process around PBH in EU continues for a prolong time as \(\lambda \) increases.

The variation of the mass of the PBH with z is plotted in Fig. 8 taking \(\lambda =0.001\) and four different \(\omega \) values which corresponds to a set of composition of three different cosmic fluids as obtained in Ref. [85]. It is evident from the figure that the mass accretion rate for same initial mass PBHs depends on the matter combination of the cosmic fluid surrounding the black hole. It is found that the accretion rate is maximum for \(\omega =1\) and the PBH attains maximum mass but the mass accretion rate becomes minimum for \(\omega =-\frac{1}{3}\). Thus, PBHs with same initial mass to begin with will grow in mass depending on the matter composition of the cosmic fluids surrounding them. In Fig. 9 we plot the variation of the mass of PBH with z considering different accretion efficiency A taking \(\omega =1\), and different initial masses of the PBHs. It is evident from the plot that for a given A, PBHs with different mass to begin with, will follow the same accretion pattern. A PBH with lower initial mass will become more massive than a PBH with higher initial mass if accretion efficiency A is increased and vice-versa. Thus the mass accretion rate determines the final mass of the PBH when the other model parameters are kept fixed.

Fig. 10
figure 10

Evolution of PBH mass M(z) with redshift z for MCG (red, solid) and in case of an Emergent Universe considering different \(\omega \) (dashed). The solid Red curve corresponds to MCG with \(\omega =0.5\), the blue and green dashed curves correspond to EU with \(\omega =1\) and \(\omega =\frac{1}{3}\) respectively

Full size image

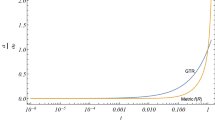
In Fig. 10 we compare the PBH mass accretion in both the cases, i.e., PBHs with a MCG background and PBHs surrounded by cosmic fluids having dissipative effects as well as for an EoS that is required for an EU. Considering \(\lambda =0.0001\) and \(A=0.5\), mass accretion rate of PBHs having same initial mass are plotted based on the surrounding matter composition. From Fig. 10 it is evident that for a PBH which is surrounded by MCG the mass accretion rate is much higher compared to a PBH in an EU environment. The PBH accumulates mass at a much higher rate initially, finally attaining a constant mass in the future. However, in the EU scenario the mass accumulation is much slower and in both the cases (\(\omega =1\) and \(\omega =\frac{1}{3}\)) the PBH attains a saturated mass much faster compared to that of MCG.

4 Discussion

In the paper we investigate the evolution of the primordial black holes surrounded by cosmic fluids having a non-linear EoS in f(Q) gravity. Two different types of non-linear EoS are considered. In the first case PBHs is surrounded by MCG (\(-1\le \alpha \le 0\)) and in the second case PBH is surrounded by a cosmic fluid having dissipative effects (\(\alpha >0\)). We have also probed \(\alpha =\frac{1}{2}\) which corresponds to EU scenario. As the mass evolution equations are highly non-linear we adopt numerical analysis here to study the evolution of PBH for different model parameters. We note the following:

  • The variation of the mass of PBH with z is plotted in Fig. 1 considering different values of the EoS parameter \(\omega \). The model parameters \(\tilde{m}\) and B are fixed to obtain realistic cosmological scenario. For \(\lambda =0.0001\) and \(\alpha =0.5\) it is seen that for PBHs with same initial mass to begin with, the mass accretion rate increases with the increase in \(\omega \). The generalized Chaplygin Gas corresponds to \(\omega =0\), in this case the mass accretion rate is found to be lowest. In this case PBH mass increases to begin with accretion and then attains a saturated value in the near future. The mass accretion from the surrounding medium is found to increase both the mass of the PBHs and the lifetime. This is quite different from the results followed from \(f({\mathcal {T}})\) gravity. In \(f({\mathcal {T}})\) modified gravity and MCG, the PBH mass initially increases which attains a maximum and then the PBH gradually losses mass due to radiation [79]. However, in f(Q) gravity the mass accretion initially dominates the radiation process by increasing the mass of PBH, finally it attains a saturated higher mass. In Fig. 2 the mass of the PBH is plotted against z for different \(\lambda \) values, which show that the mass accretion pattern remains the same but PBHs accumulates more mass for higher \(\lambda \) values. The numerical solution for mass accretion becomes singular at a large \(\lambda \).

  • In Fig. 3 it is evident that PBHs having same mass initially accumulates more mass for higher A. The mass accumulation is found to stop after a certain time and the saturated mass of PBH is attained in future. For different B values similar behaviour is found in Fig. 4. However, PBHs with low B values accumulate more mass.

  • For PBHs having different initial mass to begin with, the accretion efficiency determine the growth of mass which is shown in Fig. 5. The PBH having the lowest initial mass but highest A accumulate more mass and vice versa.

  • Considering positive values of \(\alpha \) in Eq. (17) we plot the mass evolution of PBHs with redshift z. In Fig. 6 we have considered three different \(\alpha \) values namely, \(\alpha =\frac{1}{2}\) which corresponds to EU and two other \(\alpha =\frac{2}{3}\) and \(\alpha =0.7\) to study the variation of the mass of the PBH with the redshift z. It is interesting to note that the mass accumulation is maximum in the first case which is needed for EU scenario.

  • In case of EU scenario, the type of cosmic fluid surrounding the PBH is determined by the EoS parameters \(\omega \) and B. We consider different \(\omega \) values as obtained in Ref. [85] to study the evolution of PBHs. In Fig. 7 the mass of the PBH is plotted against z for different \(\lambda \) values with \(\omega =1\). It is evident that for large \(\lambda \) values PBH accumulates more mass which is analogous to the MCG case. However, in the case of EU for higher \(\lambda \) the growth of mass of PBH continues for a longer time before reaching the saturation.

  • The dependence of \(\omega \) on the evolution of PBHs in EU scenario plotted in Fig. 8 show that for \(\omega =1\) the accretion rate becomes maximum and it attains maximum mass. For \(\omega =-\frac{1}{3}\) the mass accretion is minimum and the PBH attains much less mass compared to other cases. Thus, for a given initial mass and A, the matter combination of the cosmic fluid surrounding the PBH plays an important role in the increase in both mass and lifetime. For PBHs having different initial mass, the accretion efficiency A determines the growth of the black hole which is evident from Fig. 9.

  • The evolution of PBH is compared with MCG and non-linear EoS of the EU model in Fig. 10. It is evident that for similar set of model parameters, the mass accretion with MCG background is much more dominant than PBHs in EU scenario. The rate of mass accretion with MCG is much higher initially and finally the PBH attains a saturated mass. To conclude, employing f(Q) gravity to probe evolution of the PBHs in the presence of MCG and non-linear EoS, the PBH gains mass as time elapses finally attaining a saturated mass. The mass accretion process initially dominates over the Hawking evaporation and in the late time we note that the evaporation of PBH is not dominating. In the \(f({\mathcal {T}})\) gravity with MCG the mass of PBH increases initially attaining a maximum then finally decays [79]. The scenario in f(Q)-gravity is new where mass of PBH increases and then finally attains a saturated value indicating a new class of PBH which are long lived. The result obtained here is also different from that of the PBHs surrounded by phantom in GR background where the PBHs lose their mass throughout the evolution [78].