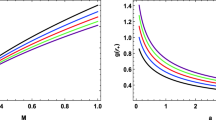
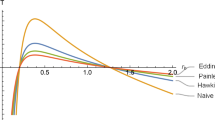
Abstract
In Vaidya–Bonner de Sitter black hole space-time, the tunneling radiation characteristics of fermions and bosons are corrected by taking Lorentz symmetry breaking theory into account. The corresponding gamma matrices and aether-like field vectors of the black hole are constructed, then the new modified form of Dirac equation for the fermion with spin 1/2 and the new modified form of Klein–Gordon equation for boson in the curved space-time of the black hole are obtained. Through solving the two equations, new and corrected expressions of surface gravity, Hawking temperature and tunneling rate of the black hole are obtained, and the results obtained are also discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, a series of significant studies have been conducted on quantum tunneling radiation and related contents of various static, stationary and non-stationary black holes [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. These studies have involved the tunneling radiation characteristics of fermions and bosons. Notably, the Lorentz dispersion relation has long been considered fundamental to modern physics, and both the theories of general relativity and quantum field seem to be based on this relation. However, the study on the theory of quantum gravity shows that the Lorentz dispersion relation may need to be modified in the high energy case, which must lead to the correction of the dynamical equations for bosons and fermions. Although a set of theories of dispersion relation in the high energy field has not been effectively established, it is certain that the order of magnitude of this correction term should be at Planck scale [19,20,21,22,23,24,25]. Considering the role of the Lorentz breaking in curved space-time, necessary corrections have been made to the tunneling radiation of bosons and fermions in static and stationary curved space-times, and some meaningful conclusions have been obtained [26,27,28,29]. However, for the case of non-stationary black holes, the problem of tunneling radiation correction to bosons and fermions in whose non-stationary curved space-time has not been investigated deeply, therefore, in this paper the characteristics of fermion’s and boson’s tunneling radiation from Vaidya–Bonner de Sitter black hole will be studied in detail. By constructing the gamma matrices and the aether-like field vectors in the curved space-time of the black hole, the modified Dirac equation and Klein–Gordon equation in the curved space-time of the black hole will be obtained, and the results obtained through solving the two modified equations will be discussed in depth.
The second section below will focus on constructing the gamma matrices of the black hole and obtaining the dynamical equation of Dirac particles. In the third section, the aether-like vectors associated with the black hole will be constructed and the characteristics of the tunneling radiation of the Dirac particle from the black hole will be studied. In the forth section, the Klein–Gordon equation will be reconstructed using aether-like vectors according to Lorentz breaking theory, and the properties of the tunneling radiation of the boson from the black hole will be studied. The last section will summarize the conclusions obtained above and will have a further discussion about black hole physics.
2 Gamma matrices in Vaidya–Bonner de Sitter black hole space-time and modified Dirac dynamical equation
Fermions with spin 1/2 are Dirac particles. After adding Lorentz symmetry violating term to the action of Dirac particles in flat space-time, the Dirac equation of Lorentz symmetry breaking in flat space-time can be derived by using Hamilton principle. To generalize the modified Dirac equation from flat space-time to the Vaidya–Bonner de Sitter curved space-time [30], we need to determine the corresponding gamma matrices \(\gamma ^{\mu }\) of the space-time of the black hole, and to extend the ordinary derivative to the covariant derivative. Taking into account the effect of Lorentz symmetry violating, the dynamical equation of the Fermion with spin 1/2 in the Vaidya–Bonner de Sitter black hole space-time is [31, 32]
where \(u^{\mu }\) are the aether-like field vectors, a, b, and c are all small quantities and \(\frac{a}{m}\), \(\frac{b}{m}\) and \(\frac{c}{m}\) are constants far less than 1, and \(\hbar \) is the Planck constant.
The space-time line element of the Vaidya–Bonner de Sitter black hole is [30]
from which the non-zero components of the contravariant metric tensor \(g^{\mu \nu }\) are respectively
In Eqs. (2) and (3), \(M=M(v)\), \(Q=Q(v)\), where v is the advanced Eddington coordinate, \(\chi \) is the parameter related to de Sitter space. According to Eqs. (2) and (3), the constructed gamma matrices \(\gamma ^{\mu }\) in Eq. (1) are
where I is a unit matrix, and \(\sigma ^{1}\), \(\sigma ^{2}\), \(\sigma ^{3}\) are Pauli matrices. Obviously, the constructed gamma matrices in Eq. (4) satisfy the following relations
In Eq. (1), the following relationship exists
where, \(\varGamma ^{\alpha \beta }_{\mu }\) is the spin connection, \(\frac{\text {i}}{2}\varGamma ^{\alpha \beta }_{\mu }\varPi _{\alpha \beta }\) is the rotational contact term, which can be ignored in semi-classical theory, and \(\varPi _{\alpha \beta }\) is the Lorentz spinor generator. In Eq. (1), there is the following relationship between \(\gamma ^{\mu }\) or \(\gamma ^{\nu }\) and \(\gamma ^{5}\)
According to Eqs. (4) and (7), the expression of \(\gamma ^{5}\) is constructed as following
According to semi-classical theory, for fermion with spin 1/2, the wave function in Eq. (1) can be expressed as
where S is the action of Dirac particles. Substituting Eq. (9) into Eq. (1), we get
For this black hole, the four-dimensional electromagnetic potential vector \(A_{\mu }=(A_{v},0,0,0)\), and
Multiply both sides of Eq. (10) by
\(\text {i}\gamma ^{\nu }\left( \partial _{\nu }S+qA_{\nu }\right) \left[ 1-\frac{a}{m^{2}}\gamma ^{\nu }\gamma ^{\mu } \left( \partial _{\nu }S+qA_{\nu }\right) \left( \partial _{\mu }S+qA_{\mu }\right) \right] \) and ignore small amount \(\frac{b}{m}\) and use Eq. (7) to obtain
which is the dynamical equation for a Dirac particle with spin 1/2, mass m and charge q, and which is derived from Eq. (1) by taking into account the prerequisites of Lorentz breaking. Eq. (12) and Eq. (1) are two equivalent equations. We only need to find the particle’s action S from Eq. (12), then according to the semi-classical theory and the WKB approximation theory, we can work out the new and corrected quantum tunneling rate and other important physical quantities that describe the black hole.
3 Correction to the characteristics of fermion’s tunneling radiation from Vaidya–Bonner de Sitter black hole
In order to solve Eq. (12), the correct aether-like field vectors \(u^{\mu }\) must be constructed according to Eqs. (2), (3) and (4). As is known to all, in the flat space-time of the canonical coordinate system, the aether-like field vectors \(u^{\mu }\) are constant vectors and satisfy the condition of \(u^{\mu }u_{\mu }=const\) , but in the curved space-time of the black hole, \(u^{\mu }\) are not constant vectors, but nevertheless, we still request
only according to which and Eqs. (2) and (3), the constructed \(u^{\mu }\) or \(u^{\nu }\) are correct. Based on Eqs. (2), (3) and (13), the aether-like field vectors can be constructed as
Obviously, Eq. (14) completely satisfy Eq. (13). In Eq. (14), \(c_{v}\), \(c_{r}\), \(c_{\theta }\) and \(c_{\phi }\) are real constants. Substituting Eqs. (3) and (14) into Eq. (12), we can obtain
where \(s_{0}\) is the constant related to \(\theta \) and \(\phi \) that appears in the process of separating variables.
To solve Eq. (15), the general tortoise coordinate transformation must be done, i.e.
From this transformation we can get
in which, \(\dot{r}_{H}=\frac{\text {d}r_{H}(v)}{\text {d}v}\). Since this black hole is spherically symmetric, the variables of the particle’s action S can be separated as
Let
where \(\omega \) is the energy of the particle. Now substitute Eqs. (16), (17), (18) and (19) into Eq. (15), and at \(r\rightarrow r_{H}\), \(v\rightarrow v_{0}\) to simplify the obtained equation preliminarily, we get
Now consider the zero hypersurface equation of the black hole, i.e.
Substituting Eq. (3) into Eq. (21), the equation of the horizon of the Vaidya–Bonner de Sitter black hole is obtained
At the event horizon, Eq. (22) can be expressed as
For the cosmic horizon, we have
To solve Eq. (20), the horizons of the black hole must be considered. Only in this way can we study the characteristics of fermion tunneling radiation at the horizons of the black hole and its related physical significance. Therefore, continue considering the case of \(r\rightarrow r_{H}\), \(v\rightarrow v_{0}\), and simplifying the form of the Eq. (20), we can get
where
Substituting the expressions of \(g_{00}\) and \(g_{01}\) in Eq. (2) and the expression of \(g^{11}\) in Eq. (3) into Eq. (27), and using Eq. (23), we get
Ignoring small quantities of the second order \((c_{v}^{2}+4c_{r}^{2}+4c_{v}c_{r})\) in Eq. (28), then when \(r \rightarrow r_{H}\), \(v \rightarrow v_{0}\) both the numerator and the denominator of Eq. (28) approach 0, let
Using L ’Hopital’s rule, then we get
where
It can be seen from Eqs. (30) and (31) that the surface gravity \(\kappa \) is related to c, a, \(c_{v}\), and \(c_{r}\), and that the introduced aether-like field vectors and the correction terms of gamma matrices considering Lorentz breaking are equivalent to the change of the mass of the particle, which also demonstrates the correlation of mass and space-time. Substituting Eq. (29) into Eq. (25), we get
According to Eq. (17), it can be obtained that
using residue theorem, which can be solved that
According to the quantum tunneling radiation theory and the semi-classical theory, the tunneling rate of fermion with spin 1/2 at the event horizon of the Vaidya–Bonner de Sitter black hole can be expressed as
where
where
Here \(T_{0}\) is the Hawking temperature at the event horizon of the black hole before correction, while \(T_{H}\) is the Hawking temperature at the event horizon of the black hole after correction, which is obtained by considering Lorentz breaking and aether-like field vectors introduced. It can be seen that Lorentz-breaking Dirac field affects the Hawking temperature, the surface gravity and the tunneling rate of the Dirac particle at the black hole event horizon. Equations (30), (35) and (36) are new and corrected expressions.
This black hole also has a cosmic horizon \(r_{c}\). Using the same research method above, we can get the surface gravity
the tunneling rate of the spin 1/2 fermion at the cosmic horizon of this black hole,
where \(T_{c}\) is the Hawking temperature at the cosmic event horizon of the black hole,
where
\(\omega _{0}^{c}\) in Eq. (39) is
It can be seen that the coefficient a corresponding to gamma matrices \(\gamma ^{\mu }\) and the coefficient c corresponding to the aether-like field vectors term both have influences on the tunneling rate and Hawking temperature at the event and cosmic horizons of the black hole, so, which is an important topic that must be paid attention to in the current research on the thermodynamic evolution of black holes.
For the fermion with spin 1/2 in the space-time of Vaidya–Banner de Sitter black hole, we can add the coupling term of Lorentz symmetry violating into the action of Dirac particle, based on which to study the characteristics of the Dirac particle’s radiation from this black hole, while for fermions with spin 3/2 and so on, we can study them in the same way, and correct the physical quantities such as the tunneling radiation rate and Hawking temperature etc., starting from the Rarita–Schwinger equation.
4 Correction to the characteristics of boson’s tunneling radiation from Vaidya–Bonner de Sitter black hole
For the bosons, we can rewrite the action of the scalar field in this black hole space-time, still considering the coupling term of Lorentz breaking. The action of the boson with mass m is [33, 34]
where \(\lambda \) is the coefficient of the correction term, and is a small constant. \(u^{\mu }\) are aether-like field vectors, just as shown in Eq. (14). Here, it still must be required to satisfy Eq. (13).
The dynamical equation of bosons is determined by the following equation
and noticing that
therefore, the dynamical equation of the boson with mass m in the space-time of this black hole is
This equation is actually the modified Klein–Gordon equation that takes the Lorentz breaking into account. By the same theoretical method, for the boson with mass m and charge e, the dynamical equation in the space-time of the black hole is
Here \(\varPhi \) is the boson’s wave function, \(A_{\mu }\) is the electromagnetic potential vectors. The relation between \(\varPhi \) and particle’s action \(S'\) is expressed as
Substituting Eq. (50) into Eq. (49), the dynamical equation of the boson with charge e and mass m is obtained
Substituting Eqs. (3), (11) and (14) into Eq. (51) and separating variables, the dynamical equation of the boson with mass m and charge e in the Vaidya–Banner de Sitter curved space-time is simplified as
where \(\eta _{0}\) is the constant introduced in the process of separating variables. Next we solve the Eq. (52) applying the general tortoise coordinate transformation just like we did above, we can get the boson’s surface gravity
the tunneling rate at the event horizon of the black hole
where
and the Hawking temperature
Obviously, considering the influence of Lorentz symmetry breaking, the boson’s tunneling rate and Hawking temperature at the event horizon of the black hole must be properly corrected, only that the Hawking temperature and other physical parameters obtained can be correct. It should be noted that the physical quantities such as the tunneling rate of bosons and the Hawking temperature at the cosmic horizon \(r_{c}\) of the black hole should also be properly corrected. Using the same method above, we can obtain the boson’s tunneling rate and the Hawking temperature at the cosmic horizon of the black hole. The results are simply to replace the \(r_{H}\) in Eqs. (54) and (57) with \(r_{c}\).
5 Conclusions and discussions
Lorentz symmetry breaking is an important subject worthy of further study, searching for which is one of the most sensitive ways of looking for new physics, either new interactions or modifications of known ones [35]. In this paper, we studied and corrected the quantum tunneling radiation properties of fermion and boson at the horizons of Vaidya–Bonner de Sitter black hole based on the Lorentz breaking theory. First, we constructed the gamma matrices [Eqs. (4) and (7)] and the aether-like field vectors [Eq. (14)] of the black hole, which is the key point to study this topic in our method, and then the new and modified form of Dirac equation was obtained. By solving the modified Dirac equation, the surface gravity [Eqs. (30) and (38)], the Hawking temperature [Eqs. (36) and (40)] and the tunneling rate [Eqs. (35) and (39)] of the fermion with spin 1/2 at the event horizon and the cosmic horizon were obtained. For the fermion with spin 3/2 and so on, it can be studied in the same way only need starting from the Rarita–Schwinger equation. For the boson, we got the new form of the Klein–Gordon equation by the constructed aether-like field vectors (Eq. (14)), by solving which we obtained the tunneling radiation properties [Eqs. (53), (54) and (57)] of the boson at the event horizon and the cosmic horizon of the black hole. Eqs. (30), (36), (35) and Eqs. (53), (54) and (57) are new and corrected expressions of the tunneling radiation properties of this black hole. We can see that the tunneling radiation properties of fermions are different from those of bosons. Meanwhile, if the correction terms in the expressions obtained above about the characteristics of the tunneling radiation of the black hole are got rid of, the results will be completely consistent with the original results, which also proves that the obtained results of the tunneling radiation characteristics of fermions and bosons in curved space-time of the Vaidya–Bonner de Sitter black hole are correct.
Another important physical concept of black hole physics is entropy \(S_{BH}\) of the black hole. From the expressions above about the tunneling rate of fermions and bosons and the Hawking temperature at the black hole horizons, we can know that Lorentz symmetry breaking has a certain effect on them, which will inevitably lead to the change of the black hole entropy. Here \(\Delta S_{BH}\) is employed to express the change of Bekenstein–Hawking entropy \(S_{BH}\), so the tunneling rate can be expressed as \(\varGamma \sim \exp (\Delta S_{BH})\). Black hole entropy is also a kind of subject worthy of study, which can help us to understand the thermodynamic evolution of black holes and related problems deeply.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study and no experimental data has been listed.]
References
P. Kraus, F. Wilczek, Self-interaction correction to black hole radiance. Nucl. Phys. 433(2), 403–420 (1995)
M.K. Parikh, F. Wiltzek, Hawking radiation as tunneling. Phys. Rev. Lett. 85(4), 5042–5049 (2000)
J.Y. Zhang, Z. Zhao, Massive particles’ black hole tunneling and de Sitter tunneling. Nucl. Phys. B 725(1–2), 173–180 (2005)
J.Y. Zhang, Z. Zhao, Massive particles’ Hawking radiation via tunneling. Acta Phys. Sin. 55, 3796 (2006). ((in Chines))
R. Kenner, R.B. Mann, Fermions tunnelling from black holes. Class. Quantum Gravity 25(9), 095014 (2008)
R. Kenner, R.B. Mann, Charged fermions tunnelling from Kerr–Newman black holes. Phys. Lett. B 665(4), 277–283 (2008)
Q.Q. Jiang, Dirac particle tunneling from black rings. Phys. Rev. D 78, 044009 (2008)
D.Y. Chen, Q.Q. Jiang, X.T. Zu, Fermions tunnelling from the charged dilatonic black holes. Class. Quantum Gravity 25, 205022 (2008)
K. Lin, S.Z. Yang, Fermion tunneling from higher-dimensional black holes. Phys. Rev. D 79(6), 064035 (2009)
K. Lin, S.Z. Yang, Fermions tunneling of higher-dimensional Kerr-anti-de Sitter black hole with one rotational parameter. Phys. Lett. B 674(2), 127–130 (2009)
Q.Q. Jiang, Y. Han, X. Cai, Quantum corrections and black hole spectroscopy. J. High Energy Phys. 2010(08), 049 (2010) (Erratum ibid 2012(06), 120 (2012))
S.Z. Yang, K. Lin, Hamilton–Jacobi equation and tunneling radiation from Kerr-TAUB-NUT black holes. Sci. Sin. Phys. Mech. Astron. 40(4), 507–512 (2010). (In Chinese)
M. Raman, Horizon tunneling revisited: the case of higher dimensional black holes. J. High Energy Phys. 2017, 144 (2017)
G.-P. Li, J. Pu, Q.-Q. Jiang et al., An application of Lorentz-invariance violation in black hole thermodynamics. Eur. Phys. J. C 77, 666 (2017)
T. Kanazawa, G. Lambiase, G. Vilasi, A. Yoshioka, Noncommutative Schwarzschild geometry and generalized uncertainty principle. Eur. Phys. J. C 79, 95 (2019)
L.A. Lessa, J.E.G. Silva, R.V. Maluf, C.A.S. Almeida, Modified black hole solution with a background KalbCRamond field. Eur. Phys. J. C 80, 335 (2020)
B. Sha, Z.E. Liu, Y.Z. Liu et al., Accurate correction of arbitrary spin fermions’ quantum tunneling from non-stationary Kerr-de Sitter black hole based on corrected Lorentz dispersion relation. Chin. Phys. C 44(12), 125104 (2020)
K. Saraswat, N. Afshordi, Extracting Hawking radiation near the horizon of AdS black holes. J. High Energy Phys. 2021(02), 77 (2021)
S.I. Kruglov, Modified Dirac equation with Lorentz invariance violation and its solutions for particles in an external magnetic field. Phys. Lett. B 718(1), 228–231 (2012)
T. Jacobson, S. Liberati, D. Mattingly, A strong astrophysical constraint on the violation of special relativity by quantum gravity. Nature 424(6952), 1019–1021 (2003)
S.I. Kruglov, Modified wave equation for spinless particles and its solutions in an external magnetic field. Mod. Phys. Lett. A 28(6), 1350014 (2013). arXiv:1207.6573
J.R. Ellis, N.E. Mavomatos, A.S. Sakharov, Synchrotron radiation from the Crab Nebula discriminates between models of space-time foam. Astropart. Phys. 20(6), 669–682 (2004)
J. Magueijo, L. Smolin, Generalized Lorentz invariance with an invariant energy scale. Phys. Rev. D 67(4), 044017 (2003)
J. Magueijo, L. Smolin, Lorentz invariance with an invariant energy scale. Phys. Rev. Lett. 88(19), 0112090 (2002)
G. Amelino-Camelia, Phenomenology of Plank-scale Lorentz-symmetry test theories. New J. Phys. 6, 188 (2004)
Z.E. Liu, Y.Z. Liu, X. Tan et al., Lorentz symmetry violation and accurate correction of bosons Hawking tunneling radiation for a stationary axisymmetric black hole. EPL 134(1), 50008 (2021)
S.Z. Yang, K. Lin, J. Li et al., Lorentz invariance violation and modified Hawking fermions tunneling radiation. Adv. High Energy Phys. 2016(1), 7058764 (2016)
B. Sha, Z.E. Liu, X. Tan et al., The accurate modification of tunneling radiation of fermions with arbitrary spin in Kerr-de Sitter black hole space-time. Adv. High Energy Phys. 2020, 3238401 (2020)
Z.E. Liu, X. Tan, B. Sha et al., Correction to the tunneling radiation of arbitrary spin fermions in Kerr Anti-de Sitter black hole. Mod. Phys. Lett. A 35(9), 2050055 (2020)
W.B. Bonner, P.C. Vaidya, Spherically symmetric radiation of charge in Einstein–Maxwell theory. Gen. Relativ. Gravit. 1, 127 (1970)
J.R. Nascimento, A.Y. Petrov, C.M. Reyes, Lorentz-breaking theory with higher derivatives in spinor sector. Phys. Rev. D 92(4), 045030 (2015)
J. Pu, S.Z. Yang, K. Lin, Lorentz-violating theory and tunneling radiation characteristics of Dirac particles in curved spacetime of Vaidya black hole. Acta Phys. Sin. 68, 190401 (2019)
M. Gomes, J.R. Nascimento, A.Y. Petrov, A.J. da Silva, Aetherlike Lorentz-breaking actions. Phys. Rev. D 81, 045018 (2010)
M.B. Cruz, E.R. Bezerra de Mello, A.Y. Petrov, Thermal corrections to the Casimir energy in a Lorentz-breaking scalar field theory. Mod. Phys. Lett. A 33(20), 1850115 (2018). arXiv:1803.07446v2 [hep-th]
E. Kiritsis, Lorentz violation, gravity, dissipation and holography. J. High Energy Phys. 2013, 30 (2013)
Acknowledgements
During the research of this topic, Professor Shu-Zheng Yang had a very useful discussion with us, and we would like to express our great thanks.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is supported by the National Natural Science Foundation of China (Grant no. U2031121) and Shandong Provincial Natural Science Foundation, China (Grant no. ZR2019MA059)
Appendix A: Derivation of Equation (1)
Appendix A: Derivation of Equation (1)
According to the Ref. [31] in this paper, in flat space-time, higher-derivative extension of the spinor QED in 4D is

where  are all the coefficients of the small correction terms, \(\overline{\varPsi }=\varPsi ^{\dagger }\bar{\gamma }^{0}\),
are all the coefficients of the small correction terms, \(\overline{\varPsi }=\varPsi ^{\dagger }\bar{\gamma }^{0}\),  , and \(\bar{D}_{\mu }=\partial _{\mu }-\text {i}eA_{\mu }\), which is an usual gauge covariant derivative. So, the usual Lorentz-breaking extension of the QED is modified by the higher derivatives. \(\bar{\gamma }^{5}\) and \(\bar{\gamma }^{\mu }\) satisfy the following relation
, and \(\bar{D}_{\mu }=\partial _{\mu }-\text {i}eA_{\mu }\), which is an usual gauge covariant derivative. So, the usual Lorentz-breaking extension of the QED is modified by the higher derivatives. \(\bar{\gamma }^{5}\) and \(\bar{\gamma }^{\mu }\) satisfy the following relation
where I is the identity matrix. Gamma matrices \(\bar{\gamma }^{\mu }\) and \(\bar{\gamma }^{5}\) need to be determined according to the characteristics of the space-time, the selection of coordinate system and the signature of the space-time line element. It should be noted that the wave functions in Eq. (A.1) is related to the spin of Fermions. For Fermions with spin 1/2, Eq. (A.1) is the modified action of Dirac particles in flat space-time.
In curved space-time, considering the Lorentz breaking effect, the expression of Fermions’ action is much more complex than that in flat space-time. The real action should be the integral of Lagrange density multiplied by four-dimensional volume element. The four-dimensional volume element in curved space-time is \(\sqrt{-g}\text {d}^{4}x\), Lagrange density should include Carroll–Field–Jackiw (CFJ) term, chirl term and aether-like term when considering Lorentz breaking, and noticing that in curved space-time \(\overline{\varPsi }=\varPsi ^{\dagger }\gamma ^{0}\), therefore according to the characteristics of Fermions’ action and Lagrange density, the Fermions’ action in general curved space-time should be correctly constructed as
where
The term containing a, b or c is the correction term corresponding to CFJ term, chirl term and aether-like term respectively, and a, b and c are all very small real numbers. \(\gamma ^{\mu }\) are the gamma matrices in curved space-time, \(\gamma ^{5}\) is the gamma matrix related to the characteristics of the space-time, \(u^{\mu }\) is aether-like factor. \(\gamma ^{\mu }\), \(\gamma ^{5}\) and \(u^{\mu }\) are all need to be determined by the specific curved space-time. \(\gamma ^{\mu }\) and \(\gamma ^{5}\) satisfy the following expression,
According to the variational principle and Eq. (A.3), we have
where
According to Hamilton principle \(\delta S=0\), the dynamics equation of the system is determined by the following equation
Therefore, according to Eqs. (A.7) and (A.8), we get
which is just the Eq. (1) in this paper.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3. SCOAP3 supports the goals of the International Year of Basic Sciences for Sustainable Development.
About this article
Cite this article
Sha, B., Liu, ZE. Lorentz-breaking theory and tunneling radiation correction to Vaidya–Bonner de Sitter Black Hole. Eur. Phys. J. C 82, 648 (2022). https://doi.org/10.1140/epjc/s10052-022-10577-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10577-6