1 Introduction

In 1974, Hawking [1] revealed that due to quantum mechanical effects, black holes (BHs) release radiations, which are known as Hawking radiations. Hawking radiation is a linkage between quantum physics and gravity which helps us to explain quantum gravity. The BH continuously loses mass and thermal entropy due to emission of radiations, which leads to the problematic information loss paradox [2]. We can predict BH’s lifetime and the particles emitting power with the help of spectrum of Hawking radiation. Stefan-Boltzmann law [3] was found a very helpful tool for the evaluation of Hawking emission rate of the BH. In Einstein gravity, the lifetime of a static BH follows \(t\sim M^{3}_{o}\), which is related to the initial mass \(M_{o}\) of the BH [4]. According to this relation if the BH has infinite initial mass, the lifetime of the BH become divergent.

In AdS spacetimes, the evaporation of BHs was largely ignored due to the asymptotical behavior of the AdS spacetime. The AdS/CFT connection [5] has drawn a lot of interest to BHs, particularly the thermodynamics of AdS BH and the evaluation process of AdS BHs in recent years [6]. Page [7] computed the lifetime of a static BH in Einstein gravity by implementing boundary conditions, and remarkably, for the extremely large initial mass, the lifetime of the BH was convergent. This is because although, the BH may have infinite initial mass, the temperature and emission power of the particles are also divergent, thus the infinite amount of mass can be evaporated in a finite time. Many gravity models including conformal [8], Lovelock [9], Horava-Lifshitz [10] and dRGT massive gravity [11], have been used to examine BH evaporation.

In 1915, Einstein claimed that gravitational lens can deflect light from its source as it approaches to the observer, this phenomenon is called gravitational lensing. The gravitational lens theory mainly deals with geometrical optics in vacuum and it utilizes the concept of deflection angle. According to general relativity, a light beam approaching to a circular body of mass M along a large impact parameter b can be deflected by a small angle, which is given by [12]

$$\begin{aligned} \vartheta =\frac{2R_{s}}{b}=\frac{4M}{b},~G=c=1, \end{aligned}$$

where \(R_{s} = 2M\) is the gravitating body’s Schwarzschild radius. Gravitational lensing is a useful astronomical and astrophysical instrument [13] in which a dark matter or a BH deviates light rays coming from different galaxies [14]. The detection of dark matter via weak deflection helps us in the study of the universe’s structure [15].

The shadows of static BHs have perfect circular geometries whose size depends on several quantities, including mass and charge. However the rotating BHs distort such a circular image, resulting in deformed D-shape structures [16]. In comparison to event horizon telescope collaborations, the shadows of Kerr solutions can yield significant results for appropriate values of the parameters [17]. The deflection angles have been investigated through various methodologies. Gibbons and Werner [18] proposed a direct technique to find such a quantity by applying the Guass Bonnet theorem (GBT) to a spacial background. The deflection angle has also been expressed using complete and incomplete elliptic functions [19, 20]. It has been shown that shadow behaviors can be used to approach BH thermodynamics [21]. It has been argued that such optics can be used to create a relationship between shadows and critical characteristics. A recent study revealed that the deflection angle may be influenced by thermodynamical parameters [22]. This observation came by comparing two RN-AdS BHs with different temperatures but equal impact factor. Belhaj et al. [23] studied thermodynamics of AdS BHs from deflection angle. They showed that the stable and the unstable phases can be derived from thermal variations of the deflection angle. They also analyzed that the large and small BH transition occurs at a specific value of the deflection angle.

Chaudhary et al. [24] studied the thermodynamic geometry and Joule–Thomson expansion of BHs in modified theories of gravity. Jawad et al. [25] discussed the logarithmic corrected phase transitions and shadows phenomenon of well-known classes of regular BHs. Jawad et al. [26] evaluated the influence of modified gravity BHs on the bounds of greybody factor. Jawad et al. [27] studied the impact of thermal fluctuations on logarithmic corrected massive gravity charged BHs. Shahid et al. [28] provided the extended GUP corrected thermodynamics, shadow radius and quasinormal modes of charged AdS BHs in Gauss–Bonnet gravity.

The goal of this study is to evaluate the evaporation rate and find out the influence of BH parameter on the evaporation process of AdS BHs with non linear electrodynamics (NED). We also investigate the shadow images obtain by radiating and infalling gas of the BH. We apply deflection angle formalism to this special type of exact BH with NED and find out how the extra term in the BH solution effects the thermodynamics as compared to literature work [23]. As the considered BH reduces to RN AdS for limiting case so we aslo compare the results for both the BHs.

This paper is outlined as follow: in Sect. 2, we study the evaporation of exact BH with NED field. In Sect. 3, we present the thermodynamic of exact BH through deflection angle. In Sect. 3.1, we investigate the stability of BH with NED via deflection angle. In Sect. 3.2, we discuss the phase transition of BH by using deflection angle. Finally in Sect. 4, we summarize our findings in conclusion.

2 Evaporation of exact black hole with NED field

Yu and Gao [29] provided the action of NED theory with minimal coupled to gravity, which is defined as

$$\begin{aligned} S=(16\pi )^{-1}\int (-g)^{\frac{1}{2}}[K(\psi )+R]d^{4}x, \end{aligned}$$
(1)

where R represents the Ricci scalar and K is a nonlinear function of \(\psi \) where \(\psi \) is defined in terms of electromagnetic field tensor as \(\psi =F_{\mu \nu }F^{\mu \nu }\). This electromagnetic field tensor depends on the partial derivatives of Maxwell field \(A_\mu \) whose expression is given by \(F_{\mu \nu }=\partial _{\mu } A_{\nu }-\partial _{\nu } A_{\mu }\). The field equations by the varying of action w.r.t., the metric turn out to be

$$\begin{aligned} G_{\mu \nu }=\frac{1}{2}g_{\mu \nu }K-2K_{,\psi }F_{\mu \lambda }F_{\nu }^{\lambda }, \end{aligned}$$
(2)

where \(K_{, \psi }\equiv \frac{dK}{d\psi }\). The generalized Maxwell equations by varying the action w.r.t \(A_{\mu }\) take the following form

$$\begin{aligned} \nabla _{\mu }(F^{\mu \nu }K_{, \psi })=0. \end{aligned}$$
(3)

The static and spherically symmetric metric is given by

$$\begin{aligned} ds^{2}=-U(r)dt^{2}+\frac{1}{U(r)}dr^{2}+f(r)^{2}d\Omega ^{2}_{2}, \end{aligned}$$
(4)

where \(d\Omega ^{2}_{2}=\sin ^{2}\theta d\phi ^{2}+d\theta ^{2}\). Due to the static spacetime, the non-vanishing Maxwell field \(A_{\mu }\) becomes \(A_{0}=\phi (r)\) which yields \(\psi =-2\phi ^{'2}\) by using a gauge transformation as \(A_{\mu }\rightarrow A_{\mu }+ \partial _{\mu }\chi \) where \(\chi \) is Euler characteristic number. Using Eq. (4) in (2) and (3), we obtain the Einstein and generalized Maxwell equations by considering \(G_{0}^{0}=\rho ,~G_{1}^{1}=p_{r}\) and \(G_{2}^{2}=p_{\theta }\) as [29]

$$\begin{aligned}&\frac{1}{f^{2}}-\frac{U'f'}{f}-\frac{Uf'^{2}}{f^{2}} -\frac{2Uf''}{f}=\frac{1}{2}K+2K_{,\psi }\phi '^{2},\end{aligned}$$
(5)
$$\begin{aligned}&\frac{1}{f^{2}}-\frac{U'f'}{f}-\frac{Uf'^{2}}{f^{2}} =\frac{1}{2}K+2K_{,\psi }\phi '^{2},\end{aligned}$$
(6)
$$\begin{aligned}&\frac{Uf''}{f}+\frac{U'f'}{f} +\frac{1}{2}U''=-\frac{1}{2}K,\end{aligned}$$
(7)
$$\begin{aligned}&\bigg (f^{2}K_{,\psi }\phi '\bigg )^{'}=0. \end{aligned}$$
(8)

Here \((')\) represents the derivative with respect to r. The last equation (8) represents the equation of motion related to the Maxwell field which indicates the electric charge contribution of BH by an integration constant. Integrating with respect to r, Eq. (8) yields

$$\begin{aligned} Q\equiv K_{, \psi }\phi 'f^{2}. \end{aligned}$$
(9)

In the field equations, we observe four unknowns which are \(K,~f,~\phi \) and U while three independent equations. So we have to choose one function initially and find rest of functions. We consider the following Lagrangian for K [29]

$$\begin{aligned} K=\psi +2\Lambda -2\sqrt{2}\zeta (-\psi )^{\frac{1}{2}}, \end{aligned}$$
(10)

where \(\zeta \) is coupling constant having dimension \((L_{a})^{-1}\). In order to find the value of f, we consider the difference of Eqs. (5) and (6) which gives \(f''=0\). The solution of this equation represents the physical solution as \(f=r\). Using Eq. (10) along with value of f, the static spherically symmetric BH solution takes the following form [29]

$$\begin{aligned} ds^{2}=-U(r)dt^{2}+\frac{dr^{2}}{U(r)}+r^{2}d\Omega _{2}^{2}. \end{aligned}$$
(11)

with metric function U(r) is

$$\begin{aligned} U(r)=1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}-\frac{1}{3}r^{2}\Lambda -\frac{r^{2}\zeta ^{2}}{3}+2Q\zeta , \end{aligned}$$
(12)

while Eq. (9) results the following expression of \(\phi \)

$$\begin{aligned} \phi =-r\zeta -\frac{Q}{r}. \end{aligned}$$
(13)

Here M is mass of the BH. The important aspect of this BH is that for \(\zeta =0\), it becomes the Reissner–Nordstrom-AdS BH. The spacetime becomes asymptotically de Sitter with \(r^{2} \zeta ^{2}\) provided \(\Lambda = 0\) and \(2Q\zeta \ll 1\). We can find the thermodynamical quantities of the BH by using the largest real root (which is known as event horizon \(r_{+}\)) of the metric function U. The relations for mass by solving \(U(r)=0\) for M, temperature by using \(T=\frac{U'(r)}{4\pi }\) and entropy of the BH turns out to be

$$\begin{aligned} M= & {} \frac{-\zeta ^2 l^2 r_{+}^4+6 \zeta l^2 Q r_{+}^2+3 l^2 Q^2+3 l^2 r_{+}^2+3 r_{+}^4}{6 l^2 r_{+}}, \end{aligned}$$
(14)
$$\begin{aligned} T= & {} \frac{\zeta ^2 (-r_{+})+\frac{2 \zeta Q}{r_{+}}+\frac{3 r_{+}}{l^2}-\frac{Q^2}{r_{+}^3}+\frac{1}{r_{+}}}{4 \pi }, \end{aligned}$$
(15)
$$\begin{aligned} S= & {} \pi r_{+}^{2}. \end{aligned}$$
(16)

After evaluating the important thermodynamical quantities, now we study the evaporation of BH with NED field. Due to the emission of Hawking radiations, the mass of BH decreases with time t. The geometrical optics have proved that the released particles traveled along null geodesics. The normalized affine parameter \(\lambda \) along orient angular coordinate provides the geodesic equation as follows [3]

$$\begin{aligned} \bigg (\frac{dr}{d\lambda }\bigg )^{2}=E^{2}-J^{2}\frac{U}{r^{2}}, \end{aligned}$$

where \(E = U\frac{dt}{d\lambda }\) and \(J = r^{2}\frac{d\theta }{d\lambda }\) are the energy and angular momentum respectively. If an emitted particle from the BH satisfies turning point condition \((\frac{dr}{d\lambda })^{2} = 0\), then it will move back towards the BH and thus cannot be seen by the observer on the AdS boundary. Now by defining the impact parameter as \(b \equiv \frac{J}{E}\), the emitted particle can reach infinity if

$$\begin{aligned} \frac{1}{b^{2}}>\frac{U}{r^{2}}, \end{aligned}$$

for all \(r >r_{+}\). The impact factor \(b_{c}\) can be obtained by using maximum value of \(U/r^{2}\). According to the Stefan-Boltzmann law, the Hawking emission rate by utilizing \(b_{c}\), can be defined as [3]

$$\begin{aligned} \frac{dM}{dt}=-\varsigma C b^{2}_{c} T^{4}, \end{aligned}$$
(17)

with the constant \(C=\frac{\pi ^{3}k^{4}}{15c^{3}h^{3}}\) where k,  c,  h are some constants and \(\varsigma \) denotes the grey-body factor. As we are concerned about the qualitative aspects of the evaporation of BH, we will absorb this constat into the grey-body factor \(\varsigma \) by setting \(\varsigma C = 1\) [30]. According to the Stefan-Boltzmann law, the emission power in 4-dimensional spacetime is proportional to the 2-dimensional cross section \(b^{2}_{c}\) and the photon energy density \(T^{4}\) in 3-dimensional space.

The behavior of the temperature T, particularly its asymptotic behavior has critical importance in BH evaporation because the \(T^{4}\) term is of a higher order. By scaling, we know \(M\sim l,~T \sim l^{-1}\) and \(b_{c}\sim l\), where l is some length. Taking the dimensionless variables \(x\equiv \frac{r_{+}}{l}, y\equiv \zeta l\) and \(Q^{*}=Q l\), we can express mass and temperature of BH in terms of dimensionless parameters as follow

$$\begin{aligned} M= & {} \bigg (\frac{3 Q^{*2} + 3 x^2 + 6y Q^{*} x^2 + 3 x^4 - y^2 x^4}{6x}\bigg )l, \\ T= & {} \frac{1}{4\pi l}\bigg (-\frac{Q^{*2}}{x^{3}} + \frac{1}{x} + \frac{2Q^{*}y}{x}- y^2 x +3x\bigg ). \end{aligned}$$

To find the impact factor \(b_{c} =\frac{r_{p}}{\sqrt{U(r_{p})}}\), we obtain two roots by solving the equation \(\frac{\partial }{\partial r}\big (\frac{U}{r^{2}}\big )=0\). The roots are given by

$$\begin{aligned} r_{p_{a}}= & {} \frac{3 M+\sqrt{-16 \zeta Q^3+9 M^2-8 Q^2}}{2 (2 \zeta Q+1)},\nonumber \\ r_{p_{b}}= & {} \frac{3 M-\sqrt{-16 \zeta Q^3+9 M^2-8 Q^2}}{2 (2 \zeta Q+1)}, \end{aligned}$$
(18)

where \(r_{p_{b}}<r_{p_{a}}\) and we use \(r_{p_{a}}\) in our work in order to make more comprehensive analysis. Using Eq. (12), along with positive largest photon orbit \(r_{p_{a}}\), we get \(b_{c}\) in terms of dimensionless parameters as follows

$$\begin{aligned} b_{c}= & {} (2 (2 \zeta Q^{*}+1) (-(\zeta ^2 ((-16 \zeta Q^{*3}\\&+\frac{(3Q^{*2}+6 Q^{*} x^2 y+x^4 (-y^2)+3 x^4+3 x^2)^2}{4x^2} -8 Q^{*2})^{\frac{1}{2}}\\&+\frac{(3 Q^{*2}+6 Q^{*} x^2 y+x^4 (-y^2)+3 x^4+3 x^2)}{2 x})^2)\\&(12 (2 \zeta Q^{*}+1)^2)^{-1}+(4 Q^{*2} (2 \zeta Q^{*}+1)^2)\times (((-16 \zeta Q^{*3}\\&+\frac{(3 Q^{*2}+6 Q^{*} x^2 y+x^4 (-y^2)+3 x^4+3 x^2)^2}{4 x^2}\\&-8Q^{*2})^{\frac{1}{2}}+((3 Q^{*2}+6 Q^{*} x^2 y +x^4(-y^2)\\&+3 x^4+3 x^2))(2 x)^{-1})^2)^{-1}\\&-(2 (2 \zeta Q^{*}+1)(3 Q^{*2}+6 Q^{*} x^2 y+x^4 (-y^2)+3 x^4\\&+3 x^2))(3 x((-16\zeta Q^{*3}\\&+\frac{(3 Q^{*2}+6 Q^{*} x^2 y+x^4(-y^2)+3 x^4+3 x^2)^2}{4 x^2}\\&-8 Q^{*2})^{\frac{1}{2}}+((3Q^{*2}\\&+6Q^{*} x^2 y+x^4(-y^2)+3 x^4+3 x^2))(2x)^{-1}))^{-1}\\&+(((-16\zeta Q^{*3}+( (3 Q^{*2}+6 Q^{*} x^2y+x^4\\&\times (-y^2)+3 x^4+3 x^2)^2)(4 x^2)^{-1}-8 Q^{*2})^{\frac{1}{2}}\\&+\frac{(3 Q^{*2}+6Q^{*} x^2 y+x^4(-y^2)+3 x^4+3 x^2)}{2 x})^2)\\&\times (4 (2\zeta Q^{*}+1)^2)^{-1}+2 \zeta Q^{*}+1)^{\frac{1}{2}})l. \end{aligned}$$

Inserting the relations T and \(b_{c}\) into Stefan-Boltzmann law, we get

$$\begin{aligned} dt=l^{3} H(x,y)dx, \end{aligned}$$
(19)

where H(x, y) represents a very lengthy expression (calculated through Mathematica software and we skip to write here). Fixing y and integrating the equation from \(\infty \) to \(x_{min} = 0\), we obtain that the BH lifetime is of order 3.

Fig. 1
figure 1

Plot of T versus \(r_+\) for charged BH with NED

Full size image
Fig. 2
figure 2

The numerical results of BH mass M w.r.t lifetime t by setting \(y > 0\) (corresponding to \(\zeta >0\)). We set \(y = 1\) with \(l= 1\), \(l= 1.5\) and \(l = 2\) from left to right

Full size image
Fig. 3
figure 3

The numerical results of BH mass M w.r.t lifetime t by setting \(y<0\) (corresponding to \(\zeta <0\)). We set \(y = -1\) with \(l= 1\), \(l= 1.5\) and \(l = 2\) from left to right

Full size image

We plot the expression of temperature which is given in Eq. (15) with respect to \(r_{+}\) for different cases of coupling constant \(\zeta =-1, 0, 1\) and \(Q=1,~l=1\) as shown in Fig. 1. One can observe that for all the cases, temperature starts from zero and goes to infinity for \(r_{+}\rightarrow \infty \). Figure shows that temperature is continuous and increasing function of \(r_{+}\) without any singularity. The temperature of BH plays a vital role in BH evaporation because it occupies the highest order. The value \(T=0\) provides critical radius which helps to find critical mass of the BH. Figures 2 and 3 demonstrate the numerical results of mass M of the BH as function of the lifetime t for \(y>0\) and \(y<0\), respectively (corresponding to \(\zeta =1\) and \(\zeta =-1\)) related to Eqs. (17) and (19). In each figure from left to right, the curves correspond to \(l = 1,~ l= 1.5\) and \(l = 2\) respectively. We find out that the BH lifetime is of the order \(l^{3}\) through H(x, y). For \(\zeta =1\), the temperature of BH becomes divergent for the extreme horizon radius, which leads to the singularity [31]. The \(r_{min}\) yields \(M_{min}\) = \(M(r_{min})\) and BH mass decreases to \(M_{min}\) in finite interval of time. For \(\zeta =-1\) the BH loses mass in short interval of time and then evaporation process becomes very slower for very small mass of the BH. As a result, the BH’s lifetime becomes infinite, satisfying the third law of BH thermodynamics. This means that the BH becomes a remnant, perhaps assisting us in resolving the information paradox [32]. We conclude that the lifetime of the BH evaporation for \(\zeta =-1\) is high as compared to \(\zeta =1\).

3 Thermodynamics of exact black hole with NED field through deflection angle

3.1 Deflection angle

In this section we are interested to explore the shadow images and the deflection angle to study the thermodynamics stability. Applying the variational principle to the metric (12) we find the Lagrangian

$$\begin{aligned} 2\,{\mathcal {L}}= & {} \left( 1-\frac{2M}{r(s)}+\frac{Q^{2}}{r(s)^{2}}-\frac{r(s)^{2}}{3}\Lambda -\frac{r(s)^{2}\zeta ^{2}}{3}+2Q\zeta \right) {\dot{t}}^2(s)\nonumber \\&\quad +\frac{{\dot{r}}^2(s)}{\left( 1-\frac{2M}{r(s)}+\frac{Q^{2}}{r(s)^{2}} -\frac{r(s)^{2}}{3}\Lambda -\frac{r(s)^{2}\zeta ^{2}}{3}+2Q\zeta \right) }\nonumber \\&\quad +r^2(s)\left( {\dot{\theta }}^2(s)+\sin ^2\theta {\dot{\phi }}^2 (s)\right) . \end{aligned}$$
(20)

It is worth noting that \({\mathcal {L}}\) is \(+1, 0,\) and \(-1\), for timelike, null, and spacelike geodesics, respectively. Taking the equatorial plane \(\theta =\pi /2\), the spacetime symmetries implies two constants of motion, namely J and \({\mathcal {E}}\), given as follows

$$\begin{aligned} r(s)^2 {\dot{\varphi }}= & {} J,\\ \left( 1-\frac{2M}{r(s)}+\frac{Q^{2}}{r(s)^{2}}-\frac{r(s)^{2}}{3}\Lambda -\frac{r(s)^{2}\zeta ^{2}}{3}+2Q\zeta \right) {\dot{t}}= & {} {\mathcal {E}}. \end{aligned}$$

To proceed further we need to introduce a new variable, say \(u(\varphi )\), which is can be given in terms of the radial coordinate as \(r=1/u(\varphi )\) which yields the identity

$$\begin{aligned} \frac{{\dot{r}}}{{\dot{\phi }}}= & {} \frac{\mathrm {d}r}{\mathrm {d}\phi }=-\frac{1}{u^2}\frac{\mathrm {d}u}{\mathrm {d}\phi }. \end{aligned}$$
(21)

We proceed by considering four special cases for different values of the parameter in the metric (12). After some algebraic manipulations one can show the following differential equation

$$\begin{aligned} \left( \frac{du}{d\varphi }\right) ^2\frac{1}{u^4 {\mathcal {K}}}+\frac{9 M}{u^7 b^2 {\mathcal {K}}^2}-\frac{9 Q^2}{2 u^6 b^2 {\mathcal {K}}^2}+\frac{3 \zeta ^2}{2 u^{10} b^2 {\mathcal {K}}^2}\nonumber \\ +\frac{3 \Lambda }{2 u^{10} b^2 {\mathcal {K}}^2}-\frac{9 \zeta Q }{u^8 b^2 {\mathcal {K}}^2}-\frac{9}{2 u^{8} b^2 {\mathcal {K}}^2}+\frac{1}{2 u^2}=0, \end{aligned}$$
(22)

where

$$\begin{aligned} {\mathcal {K}}=\zeta ^2/u^4+\Lambda /u^4-6Q\zeta /u^2+6M/u-3Q^2-3/u^2, \nonumber \\ \end{aligned}$$
(23)

and b is defined as

$$\begin{aligned} b=\frac{J}{{\mathcal {E}}}. \end{aligned}$$
(24)

We shall consider the affine parameter along the light rays to be \({\mathcal {E}}=1\), and we can evaluate the constant l in leading order terms \( b \simeq r_0\). From the above equation we find

$$\begin{aligned} \frac{du}{d\phi }=\pm \frac{\sqrt{-9Q^2b^2u^4+18Mb^2u^3+3b^2\zeta ^2+3\Lambda b^2+9-{\mathcal {A}}}}{3b}, \nonumber \\ \end{aligned}$$
(25)

where

$$\begin{aligned} {\mathcal {A}}= & {} 18 Q b^2 u^2\zeta +9b^2u^2, \end{aligned}$$
(26)

It is well known that the solution to the above equation in the weak limit can be written as follows

$$\begin{aligned} \vartheta =2 \int _{u=1/b}^{0}\bigg |\frac{d\phi }{du}\bigg |du-\pi , \end{aligned}$$
(27)

where \(\vartheta \) is the deflection angle which should be calculated. Finally, the deflection angle turns out to be approximated with

$$\begin{aligned} \vartheta\simeq & {} \frac{4M}{b}-\frac{3 \pi Q^2}{4 b^2}-\zeta Q \pi +\frac{2 b \Lambda M}{3}-\frac{\Lambda Q^2 \pi }{4}-\frac{16 \zeta Q M}{b}\nonumber \\&+ {\mathcal {O}}(Q^2 M/b^3)+{\mathcal {O}}(\Lambda M Q^2/b)+{\mathcal {O}}(\Lambda M Q \zeta b)\nonumber \\&+ {\mathcal {O}}(\Lambda b /u_{\Lambda })+ {\mathcal {O}}(\zeta ^2 b /u_{\Lambda })+... \end{aligned}$$
(28)

Notice that due to the presence of the cosmological constant, we have divergent term since \(u_{\Lambda } \rightarrow 0\), however one can simplify the work bu assuming that the observer is located at some large but finite distance from the black hole. In this way, for finite distance corrections, the divergent terms like \(\Lambda b r_{\Lambda }\) and \(\zeta ^2 b r_{\zeta }\) will be small since \(\Lambda<<1\), and \(\zeta<<1\) provided \(r_{\Lambda }\) and \(r_{\zeta }\) are some finite quantities.

Fig. 4
figure 4

Plot of deflection angle w.r.t impact parameter b for increasing values of the coupling constant \(\zeta \). We use \(Q=0.3,~M = 1,~~\Lambda =10^{-5} \)

Full size image

The examination of optical quantity \(\vartheta \) indicates that it is controlled by five factors (b, Q, l, \(\zeta \) and \(r_{+}\) or M) that constitute the BH moduli space.

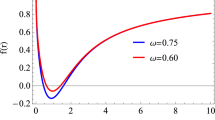
In Fig. 4 related to Eq. (28), we show the behavior deflection angle w.r.t impact parameter b for increasing values of coupling constant \(\zeta \). We obtain smaller values of deflection angle by increasing \(\zeta \). Fixing the values of M and \(\Lambda \), we observe that \(\vartheta \) decreases w.r.t b. As by setting \(\zeta =0\), our considered model of BH becomes RN-AdS BH. The range of the considered BH’s deflection angle is high as compared to RN-AdS BH and it decreases for increasing values of \(\zeta \). We can conclude that \(\vartheta \) as continuously decreasing function with respect to impact parameter b represents a stable BH.

Fig. 5
figure 5

The shadow images and the intensities for different values of Q. Note that the observer is located at distance \(r_0=30 M\) from the black hole

Full size image

3.2 Shadow images using infalling gas

There are different models to obtain the shadow images and the intensity, in the present work, we will use a simple accretion model which consists of an infalling and radiating gas onto a BH. This is a simplified model, in a more realistic setup the problem is more complicated, for example the model can depend not only on the size but also the shape of the accretion model or the distribution of different fields such as the magnetic fields around the BH. To do so, we need to solve numerically the equations of motion of light and we can start from the Hamilton-Jacobi which gives

$$\begin{aligned} \frac{1}{2}\left[ -\frac{p_{t}^{2}}{U(r)}+U(r)p_{r}^{2} +\frac{p_{\phi }^{2}}{r^{2}}\right] =0. \end{aligned}$$
(29)

From our metric we can see that due to the spacetime symmetries we have two constants of motion: \(p_{t}=-E\) and \(p_{\phi }=L\), that is the energy E and angular momentum L, respectively. Furthermore, if we now use the conditions for the unstable orbits given by

$$\begin{aligned} V_{\mathrm{eff}}(r)=\qquad \frac{\partial V_{\mathrm{eff}}(r)}{\partial r} \Big \vert _{r=r_{p}}=0, \end{aligned}$$
(30)

it is straightforward to obtain the equation of motion as follows

$$\begin{aligned} \frac{dr}{d\phi }=\pm r\sqrt{U(r)\left[ \frac{r^{2}U(R)}{R^{2}U(r)} -1\right] }. \end{aligned}$$
(31)

In the scenario in which light ray emits from the static observer which at the position \(r_{0} \) travels with an angle \(\varphi \), we have the relation [33]

$$\begin{aligned} \cot \varphi =\frac{\sqrt{g_{rr}}}{\sqrt{g_{\phi \phi }}}\frac{dr}{d\phi }\Big \vert _{r=r_{0}}. \end{aligned}$$
(32)

The shadow radius can be obtained from the following relation

$$\begin{aligned} R_{s}=r_{0}\sin \varphi = r\bigg ((U(r_{0})(f(r))^{-1}\bigg )^{\frac{1}{2}}\Bigg \vert _{r=r_{p}}, \end{aligned}$$
(33)

here \(r_{p}\) is the photon radius. One can calculate the intensity map and obtain the shadow images using the well known technique known as the Backward Raytracing (see, Refs. [34,35,36,37,38,39]). In particular the observed specific intensity \(I_{\nu 0}\) is given by [36]

$$\begin{aligned} I_{obs}({X,Y,\nu _{obs}}) = \int _{\gamma }\mathrm j(\nu _{e}){g}^3dl_\text {prop}, \end{aligned}$$
(34)

in the last equation we note that \(\mathrm {g}\) is the redshift function. In addition, the proper length is given by [34,35,36,37,38,39]

$$\begin{aligned} dl_{\text {prop}} = k_{\alpha }u^{\alpha }_{e}d\lambda = -\frac{k_t}{\mathrm {g}|k^r|}dr. \end{aligned}$$
(35)

Moreover, the relation between time and radial component of four velocity can be obtained as follow (see for details [34,35,36,37,38,39])

$$\begin{aligned} k^r(k^t)^{-1} = \pm U(r) \sqrt{\bigg (1-\frac{b^2U(r)}{r^2}\bigg )}. \end{aligned}$$
(36)

The physical meaning behind the sign +(−) is related to the fact that the photon approaches or goes away from the massive object. Let us also assume that the emission is monochromatic with emitter’s-rest frame frequency \(\nu _{\star }\), with a simple \(r^{-2}\) radial profile and then by integrating the intensity yields [34,35,36,37,38,39]

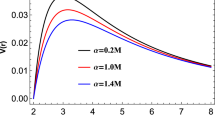
$$\begin{aligned} I_{obs}(X,Y) \propto -\int _{\gamma } \mathrm {g}^{3} k_{t} r^{-2}k^{-r} dr. \end{aligned}$$
(37)

In Fig. 5, we manifest result for the shadow using the black hole solution (11-12). We have found that increasing the value of charge Q the radius of the shadow decreases and the intensity of the electromagnetic waves detected at some finite distance \(r_0\) from the black hole increases. Also, it is important to note that the finite distance corrections play an important role and have a significant effect on the shadow images.

3.3 Stability of black hole with NED through deflection angle

Here we investigate the stability of BH through the deflection angle formalism. The heat capacity plays important role to make the relationship between the BH stability and optical quantity. In literature work [21], it has been shown that \(C=T(\frac{\partial S}{\partial T})>0\) represents the stable behavior while the unstable phase require \(C=T(\frac{\partial S}{\partial T})<0\). In order to study the stability of BH through new approach, the extended heat capacity is defined as

$$\begin{aligned} C=T\bigg (\frac{\partial S}{\partial r_{+}}\bigg )\bigg (\frac{\partial r_{+}}{\partial \vartheta }\bigg )\bigg (\frac{\partial \vartheta }{\partial T}\bigg ). \end{aligned}$$
(38)

Due to the constraint \(\bigg (\frac{\partial S}{\partial r_{+}}\bigg ) > 0\), the information related to stability can be uncovered by the sign of the product \(\bigg (\frac{\partial r_{+}}{\partial \vartheta }\bigg )\bigg (\frac{\partial \vartheta }{\partial T}\bigg )\). We first study the behavior of temperature in terms of \(r_{+}\) in various regions of the BH moduli space. This is required to check the phase structures [21]. The obtained data will be examined more precisely through the variation of deflection angle. Figure 6, demonstrates the behavior of temperature T of BH (given in Eq. (15)) versus horizon radius \(r_{+}\) for increasing values of coupling constant \(\zeta \). One can see that by fixing the value of AdS radius \(l^{2} = \frac{675}{4\pi }\), the range of temperature increases with increasing values of coupling constant \(\zeta \). The temperature first increases from zero and then it decreases after reaching maximum value.

Fig. 6
figure 6

Plot of the temperature w.r.t horizon radius \(r_{+}\) for \(l^{2}= \frac{675}{4\pi }\)

Full size image
Fig. 7
figure 7

Plot of deflection angle w.r.t \(r_{+}\) for increasing values of the coupling constant. We use \(Q=1\), \(b = 10\), \(l^{2} = \frac{675}{4\pi }\)

Full size image

It follows from Fig. 6 that BH remains stable in \(0.52\le r_{+}\le 0.83\) for all the trajectories while it becomes unstable for \(r_{+}> 0.83\). The range of temperature is low for \(\zeta =0\) (RN-AdS BH) as compared to increasing values of \(\zeta \). Thus, the phase structure of the BH can be examined from the quantity \(\frac{dT}{dr_{+}}\) by taking into account different values of model parameters.

In order to analyze the new technique for the phase structure, we plot \(\vartheta \) given in Eq. (28) with respect to \(r_{+}\) in Fig. 7. It is noted that initially the behavior of deflection angle curves decreases rapidly with the growth of \(r_{+}\), then gradually increases by increasing \(r_{+}\) without any critical value. In this way, the sign of the quantity \(\frac{dT}{d\vartheta }\) helps us to extract the information about the phase structures of BH. The increasing values of coupling constant \(\zeta \) lead to increasing range of deflection angles. More precisely, the stability and the instability require

$$\begin{aligned} \frac{dT}{d\vartheta }<0,\quad \frac{dT}{d\vartheta }>0. \end{aligned}$$

We depict parametric plots of the temperature of BH w.r.t deflection angle in Fig. 8 (related to Eqs. (15) and (28). We present stable (decreasing deflection angle w.r.t temperature) and unstable phases in this figure and observe that these results show consistency with Fig. 6 which show that the phase structure can be investigated through the deflection angle formalism. The sign changing heat capacity of BH can be discussed as temperature depending upon deflection angle. The deflection angle decreases with temperature which show the stable phase. These interesting results show that new approach for the study of phase transitions BHs is very much consistent.

Fig. 8
figure 8

Plot of the temperature w.r.t deflection angle for \(b = 10\) and \(l^{2}= \frac{675}{4\pi }\)

Full size image

3.4 Phase transition of black hole through deflection angle

We investigate the relationship of deflection angle and phase transition of BH in the presence of NED in this section. The Gibbs free energy is the key thermodynamical quantity for studying such a transition [6]. For BHs, the Gibbs free energy can be calculated as follows

$$\begin{aligned} G = M - T S -\Phi Q. \end{aligned}$$
(39)

where \(\Phi =\frac{Q}{r_{+}}\) is the electric potential. Using \(P = \frac{3}{8\pi l^{2}}\) and electric potential \(\Phi \), the relations for BH temperature and mass become

$$\begin{aligned} T= & {} \frac{-\zeta ^2 r_{+}^2+2 \zeta r_{+}\Phi +8 \pi Pr_{+}^2-\Phi ^2+1}{4 \pi r_{+}}, \nonumber \\ M= & {} \frac{1}{6} r \left( -\zeta ^2 r^2+6 \zeta r \Phi +8 \pi P r^2+3 \Phi ^2+3\right) . \end{aligned}$$
(40)

Substituting these relations in Eq. (39), the relation for Gibbs free energy takes the form

$$\begin{aligned} G=\frac{1}{12} r_{+} \left( \zeta ^2 r_{+}^2+6 \zeta r_{+} \Phi -8 \pi P r_{+}^2-3 \Phi ^2+3\right) . \end{aligned}$$
(41)
Fig. 9
figure 9

Plot of the event horizon radius \(r_{+}\) in terms of the temperature T

Full size image
Fig. 10
figure 10

Plot of the event horizon radius \(r_{+}\) in terms of the temperature T

Full size image
Fig. 11
figure 11

Variation of the Gibbs free energy G w.r.t temperature T for \(\Phi = 0.9\), \(\zeta = 0\) and \(P = 0.04\)

Full size image
Fig. 12
figure 12

Variation of the Gibbs free energy G w.r.t temperature T for \(\Phi = 0.9\), \(\zeta = 0.1\) and \(P = 0.04\)

Full size image

The analysis of temperature \(T = T(r_{+}, ~P,~\Phi ,~\zeta \)) reveals that it has two critical values for the charged-AdS BH with coupling constant. The first one is related to the critical value \(T_0=\frac{\sqrt{8 \pi P-\zeta ^2}-\Phi ^2\sqrt{8 \pi P-\zeta ^2}+\zeta \sqrt{1-\Phi ^2} \Phi }{2 \pi \sqrt{1-\Phi ^2}}\) which yields minimum function, below which no BH exists [40]. After calculating \(r_{+}\) in terms of T from Eq. (40), we obtain two event horizons \(r_{_{pos }}\) and \(r_{neg }\) which correspond to the large and small BHs respectively. In Figs. 9 and 10, we express \(r_{+}\) in terms of T for increasing values of charge Q and coupling constant \(\zeta \) for \(P = 0.04\). In both figures, the critical points are represents by intersections (LBH and SBH) of dashed and solid curves in Fig. 9. Similarly in Fig. 10, the intersection of solid and dashed curves show the critical points. The second critical value is \(T_{HP}=\frac{-\sqrt{8 \pi P-\zeta ^2}+\Phi ^2 \sqrt{8 \pi P-\zeta ^2}+\zeta \sqrt{1-\Phi ^2} \Phi }{2 \pi \sqrt{1-\Phi ^2}}\) for which BH and radiations have vanishing Gibbs energy G and the Hawking-Page transition occurs at this point. In order to understand more deeply, we use Eqs. (40) and (41) to demonstrate the graphical behavior of G w.r.t T in Figs. 11 and 12 respectively. In Fig. 13 we plot a 3-dimensional plot of the deflection angle \(\vartheta \) in terms of T and b. There exists temperature which is independent of b direction of the moduli space. We find out that for \(b > r_{+}^{0}\), where \(r_{+}^{0}\) is related to \(T_{0}\), the change in b does not alter the BH temperature.

Finally, in order to investigate the Hawking-Page transition of the charged BH through deflection angle, we depict the Gibbs free energy (using Eqs. (41)) w.r.t deflection angle (using Eqs. (28) in Figs. 14 and 15 for uncharged and charged cases respectively. We observe that \(G\rightarrow 0\) corresponding to \(\vartheta = \vartheta _{c}\), which show the Hawking-page transition where this critical value works similarly as \(r_{+} = r_{HP}\) for which \(T = T_{HP}\). We analyze that LBH appear when G is decreasing function of \(\vartheta \) while SBH appears when G increases with \(\vartheta \). Obviously, the intersection of SBH and LBH yields the minimum temperature occurs at a critical value \(\vartheta =\vartheta _{0}\). This result proved that the deflection angle can be considered as a relevant quantity to approach critical behaviors of charged AdS BHs.

Fig. 13
figure 13

Plot of deflection angle in terms of the temperature T and the impact parameter b for \(P = 0.04\) and \(\Phi = 0.9\)

Full size image
Fig. 14
figure 14

Plot of the Gibbs free energy G in term of \(\vartheta \) for \(P = 0.04,~\zeta =0\) and \(\Phi = 0.9\)

Full size image
Fig. 15
figure 15

Plot of the Gibbs free energy G in term of \(\vartheta \) for \(P = 0.04,~\zeta =0.1\) and \(\Phi = 0.9\)

Full size image
Fig. 16
figure 16

Plot of the heat capacity C w.r.t \(\vartheta \) for \(l^2 = \frac{675}{4\pi }\)

Full size image
Fig. 17
figure 17

Plot of the heat capacity C w.r.t \(\vartheta \) for \(Q = 0.5\)

Full size image

Figure 16 demonstrate the behavior of heat capacity given in Eq. (38) versus deflection angle for different values of coupling constant. For all the values of coupling constant, specific heat is continuous function of \(\vartheta \), which describes that BH is thermodynamically stable (Fig. 17).

4 Concluding remarks

In this work, we have discussed the evaporation process of the exact BH with NED. We have calculated the numerical results of mass M of BH as the function of the lifetime t for positive and negative coupling constant \(\zeta >0\) and \(\zeta <0\). We have analyzed that for \(\zeta =-1\), the BH loses mass in short interval of time and then the evaporation process becomes very slower for very small mass of the BH. As a result, the BH’s lifetime becomes infinite. However for \(\zeta =1\), the temperature of BH becomes divergent for the extreme horizon radius, which leads to the singularity and the BH mass decreases to \(M_{min}\) in a finite interval of time.

We have also investigated the shadow images obtained by radiating and infalling gas as well as the thermodynamics of exact BH through deflection angle formalism. For a fixed values of \(\zeta \) and \(\Lambda \) we found that the shadow radius decreases with the increase of the charge Q. We have shown that how different thermodynamical quantities can be expressed by the optical quantity. We evaluated deflection angle of the considered BH and studied the influence of impact parameter on the deflection angle. Then, we have established the relationship between stability/instability and phase transitions of the BH through deflection angle formalism. In our important findings, we have shown that the stable phase is linked with decreasing deflection angle, while unstable phase corresponds to increasing value of the angle. Moreover, we have also examined the transition of BH from Gibbs energy optical variation and observed that LBH/SBH transition exists at particular value of the deflection angle.

In comparison with the literature work [23], we observed that deflection angle w.r.t \(r_{+}\) is high for increasing values of the coupling constant. The coupling constant also influences the temperature and deflection angle w.r.t impact parameter plots. Moreover, the coupling constant effects the event horizon radii which leads to the change in phase transition points and the local and global stability of the black hole. The phase transition points and interval of stability and instability in our work changes significantly with coupling constant as compared to the published work.