Abstract
Proton–proton (pp) collision has been considered as a baseline to study the system produced in relativistic heavy-ion (AA) collisions with the basic assumption that no thermal medium is formed in pp collisions. This warrants a cautious analysis of the system produced in pp collisions at relativistic energies. In this work we investigate the charmonium suppression in pp collisions at \(\sqrt{s} = 5.02\), 7 and 13 TeV energies. Further, charmonium suppression has been studied for various event multiplicities and transverse momenta by including the mechanisms of color screening, gluonic dissociation, collisional damping along with regeneration due to correlated \(c{\bar{c}}\) pairs. Here we obtain a net suppression of charmonia at high-multiplicity events indicating the possibility of the formation of quark–gluon plasma in pp collisions.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The heavy-ion programs at the Relativistic Heavy Ion Collider (RHIC) and Large Hadron Collider (LHC) are dedicated to understanding the rich and complex nature of the phase transition at high temperature and/or density from hadrons to a deconfined state of thermal quarks and gluons. This new state of deconfined colored quarks and gluons is called quark–gluon plasma (QGP) [1,2,3]. The suppression of quarkonia [4] has been proposed as a signal of the formation of the transient phase of QGP. The production of heavy quark pairs (\(c\bar{c}\) or \(b\bar{b}\)) takes place at the initial stage of the collisions which can be treated perturbatively but the evolution of the quark pairs and the formation of their bound states (quarkonia) occur through non-perturbative processes [5]. A quarkonia state traversing through QGP gets dissociated to unbound quark anti-quark pair, which results in the reduction of quarkonia yields (which will otherwise remain as a bound state) referred as quarkonia suppression. The quarkonia production gets altered by the cold nuclear matter (CNM) effects (nuclear absorption and shadowing) [6]. The asymmetric pA collision can be used to disentangle the CNM effects from the QGP medium effects [7]. The pA collision has been used to serve as an important baseline for the understanding and interpretation of the heavy-ion (AA) collision data. As the CNM effects will be present both in pA and AA collisions, and also it is expected that QGP will be formed in AA but not in pA collisions, therefore, the data from pA may be used to distinguish the effects of QGP. In fact, the pA experimental data corresponding to quarkonia suppression have been explained by considering CNM effects only at various rapidities and collision centralities. For instance, the suppression pattern of \(J/\psi \) in d−Au collisions at RHIC is well explained by the CNM effects [8].
It is pertinent to mention here that the formation of hot QGP medium in AA collisions has been predicted by considering the ratio of hadronic spectra originating from AA to pp collisions. While calculating this ratio, the spectra from pp collisions required to be appropriately scaled up by the number of nucleon-nucleon collisions in AA interaction. The deviation of the ratio from unity has been treated as a signal of medium formation in AA interactions. The data from pp collision have been used in these studies as a benchmark. The formation of QGP and its collective nature has also been studied by evaluating various flow coefficients (like directed, elliptic, triangular, etc) [9, 10]. For example, the elliptic flow coefficient has been used to extract the ratio of shear viscosity (\(\eta \)) to entropy density (s) and the triangular flow coefficients have been used to understand the initial-state fluctuations.
It was expected that the elliptic flow for small systems formed in pp and pA collisions will be zero due to lack of thermalization in such systems. However, data from p−Pb collisions at \(\sqrt{s_{NN}}\; = \; 5.02,\; {\text {and}} \;8.16\) TeV and for pp collisions at \(\sqrt{s}\; = \; 7\; {\text {and}} \;13\) TeV at the LHC have provided hints towards the formation of a QGP medium [11,12,13,14,15,16,17]. The search for QGP in p−Pb collisions at \(\sqrt{s_{NN}}\; = \; 5.02\) TeV has been carried out by the theoretical model which will be called, “Unified Model of Quarkonia Suppression (UMQS)” henceforth. This model is based on the unification of the various suppression and regeneration mechanisms of quarkonia produced in ultra-relativistic collisions [18]. In the present work, UMQS model approach is employed to investigate the formation of QGP in pp collisions through charmonium suppression. The dissociation temperature (\(T_D\)) of charmonia states is much less than in bottomonia states. Therefore, in this work, we choose charmonia over bottomonia because the temperature of the system formed in pp collisions will not be high enough to dissociate bottomonia (\(T_D>650\) MeV). In previous works, it is found that bottomonia hardly gets suppressed even in p−Pb collisions at \(\sqrt{s_{NN}}\;=\; 5.02\) TeV [18]. Therefore, charmonia is a better choice to investigate QGP formation in small systems.
The dissociation of the quarkonia (\(J/\psi ,~\Upsilon \), etc.) occurs through various mechanisms [4, 19,20,21,22]. As mentioned, charmonium suppression in heavy-ion collisions can be caused by the cold nuclear matter (CNM) effects as well as by the Debye screening of color interaction, gluonic dissociation and collisional damping in hot QGP [4, 19, 23,24,25,26,27]. As the pp collisions lack the nuclear environment, i.e. the CNM effects, therefore, the hot QGP effects are considered to study the charmonia suppression in pp collision. Along with the suppression, there is a non-zero probability that a charmonia state can be regenerated in the medium at temperature (T), \(T<T_{D}\).
In the current study, we have used the UMQS model to predict the charmonia suppression in ultra-relativistic pp collisions. This model has been used to explain the bottomonia suppression in Pb−Pb and p−Pb collisions at LHC energies [18, 20, 28]. UMQS includes color screening, gluonic dissociation, collisional damping, and regeneration as the hot matter effects. Due to the absence of a nuclear environment in pp collisions, the cold nuclear matter effects like shadowing need not be considered here. We have used the second-order dissipative fluid dynamics [29,30,31,32] in (1+1) dimension with the assumption of boost invariance to study the propagation of the charmonia in the expanding QGP background.
The paper is organized as follows. The space-time evolution of QGP is discussed in Sect. 2. Section 3 is devoted for studying the charmonium kinematics and medium effects along with brief discussion of UMQS. The model prediction and comparison with experimental data are shown in Sect. 4. Finally, the summary and the outlook are presented in Sect. 5.
2 Space-time evolution of QGP
The QGP formed in pp and AA collisions with high internal pressure will expand in space with time. The evolution of QGP is governed by the hydrodynamics. Here we use the second order relativistic viscous hydrodynamics. For solving the hydrodynamical equations we need to specify the initial conditions and the equation of state (EoS). In absence of any method based on the first principle to estimate the initial temperature (\(T_0\)), the following relation [33] has been used in the present work to constrain \(T_0\) by data:
Although this equation is derived by assuming isentropic expansion, we have used it also for the present case. We feel that the uncertainties involved in this assumption at least for small viscosity, may not be large as compared to the uncertainties involved in the other quantities like transverse area of the system (\(A_T\)), statistical degeneracy (\(g_k\)) of the QGP phase and the thermalization time (\(\tau _0\)). In Eq. (1), \(C^{\prime } = \frac{2\pi ^{4}}{45\zeta (3)} \approx 3.6\). We have also taken, \(\frac{dN_{ch}}{dy} \cong \frac{dN_{ch}}{d\eta }\) which is exact in the massless limit.
Here the transverse overlap area \(A_{T} = \pi R_{T}^{2}\), is computed by using IP-Glasma model, where \(R_{T}\) is the transverse radius of the fireball [34]. This description of the transverse area is based on the impact parameter defined for pp collisions and combined with a description of the particle production based on the color glass condensate model. It is worthwhile to mention that initial thermalization time (\(\tau _{0}\)) plays a key role in estimating the \(T_0\). While, there is no way to estimate the \(\tau _{0}\) from first principle but it may be reasonable to assume that thermalization time will decrease with increasing center-of-mass collision energy, i.e. \(\tau _{0}\propto 1/\sqrt{s}\) [35, 36]. Here we consider \(\tau _{0} = 0.3,\; 0.2\; {\text {and}}\; 0.1\) fm respectively for \(\sqrt{s} = 5.02,\;7.0,\; {\text {and}} \; 13\) TeV for pp collisions. Corresponding to these values of \(\tau _0\), we obtain the values of \(T_0\) as a function of multiplicity. The results have been depicted in Fig. 1.
Figure 1, emphasizes the impact of the thermalization time (\(\tau _{0}\)) on the initial temperature (\(T_{0}\)). For \(\tau _{0} = 0.1\) to 0.3 fm, we get \(T_{0}\sim 200\) to 275 MeV at low multiplicities. At high multiplicity pp collision at \(\sqrt{s} = 13\) TeV, initial temperature reaches a value \(\sim 370\) MeV which is comparable to the initial temperature achieved in heavy-ion collisions. However, \(T_0\) obtained from Eq. (1), is a slowly varying function of the multiplicity (\(T_0\sim (dN/dy)^{1/3}\)). Therefore, we get \(T_{0} \simeq 200\) MeV at low multiplicity in pp collision at \(\sqrt{s} = 5.02\) TeV. However, we find that \(T_{0}>T_{c}\), suggesting that QGP-like medium may be produced even at low multiplicities in pp collisions at LHC energies, \(T_c \approx 155\) MeV is predicted in the Lattice QCD calculation [37]. It is expected that in such a hot medium formed at \(\sqrt{s}=13\) TeV, say, the \(J/\psi \) will be suppressed.
2.1 Variation of temperature (T) with proper time (\(\tau \))
The temperature of the system produced in ultra-relativistic heavy-ion collisions decrease with time. The rate of the decrease of temperature can be obtained by solving the second-order hydrodynamical equation [29]. These second order equations are derived from kinetic theory using Grad’s 14-moment approximation method within the framework of the Müller–Israel–Stewart equation [30,31,32, 38] which in (1+1) dimension with boost invariance reads:
and
The \(\phi \) in Eq. (3) measures the change in the shear viscosity (\(\eta \)) with time \(\tau \). In short, \(\phi \) indicates the characteristics of the medium formed under extreme conditions in ultra-relativistic collisions. For the first order solution of the Eq. (2), the \(\phi \) is defined as, \(\phi = 4\eta /3\tau \). The constants a and b are given by,
and
where \(N_{f} = 3\), is the number of flavors and \(\alpha _s\) is the strong coupling constant. We have taken \(\alpha _s=0.5\) here as in Ref. [29]. We have used an EoS with conformal symmetry (\(P=\epsilon /3\)). The bulk viscosity is zero for such EoS.
For an ideal system, the proper-time dependence of temperature is given by,
However, for a viscous system, the Eqs. (2) and (3) have been solved numerically. We have obtained the initial condition for \(\phi \) with the help of quasi-particle model equation of state (QPM EoS) where QGP is considered as viscous medium. In QPM EoS, entropy density, \(s = c + d T^{3}\) here \(c = 0.00482~GeV^{3}\) and \(d = 16.46\) are the fit parameters [18]. By taking the lower bound of \(\eta /s=1/(4\pi )\) from Ads/CFT, the value of \(\phi \) at \(\tau _{0}\) is obtained as: \(\phi _{0} = \frac{1}{3\pi }\frac{s_{0}}{\tau _{0}}\), here \(s_{0} = c + d T_{0}^{3}\). The variation of T with \(\tau \) is crucial to determine the lifetime of QGP and hence for the signal of QGP. This variation is sensitive to \(\phi _0\) as demonstrated in Ref. [39]. We have taken the low value of \(\eta /s\) to set the initial condition for \(\phi (\tau _0)=\phi _0\). The lower \(\eta /s\) will give faster cooling and hence a smaller lifetime of the thermal QGP system. Therefore, if the suppression is observed for such a conservative scenario (QGP with a small lifetime), then the realization of thermal system in pp collisions will be better assured.
In order to predict the transverse expansion effect on the medium evolution, transverse expansion is incorporated as a correction to the (1\(+\)1) dimension cooling rate. It is assumed that transverse expansion starts at a time (\(\tau _{tr}\)) as: \(\tau _{tr} = \tau + 0.2928 (r/{c_{s}})\) [18, 40, 41]. Here r is the transverse distance and \(c_s\) is the speed of sound in QCD medium. Expansion rate in transverse direction is estimated by replacing \(\tau _{tr}\) in coupled cooling rate Eqs. (2) and (3).
In Fig. 2, the variation of temperature with proper-time is displayed for viscous QGP (solid blue line), viscous QGP with the inclusion of transverse expansion (green dashed line) and ideal QGP (violet dashed line) for system produced in pp collisions at \(\sqrt{s}=13\) TeV. The generation of heat due to dissipation makes the cooling of viscous QGP slower. However, considering the transverse expansion correction to current formulation, marginally increases cooling rate compared to (1+1)-dimension expansion as the lifetime of the QGP in smaller system is shorter than bigger system produced in nuclear collisions. Transverse temperature cooling rate, \(T_{SO:Tr}\), mentioned in Fig. 2, uses initial transverse position \(r = 0.2\) fm (say) at \(\tau = \tau _{0}\). Change in the viscous cooling rate after including transverse correction is not much prominent. While cooling for ideal QGP medium is large throughout medium evolution as compare to both (with and without transverse correction) viscous cases. Solution of the second-order hydrodynamics excluding transverse expansion shows that the QGP lifetime will be enhanced (3.8 fm/c) compared to the ideal fluid (1.5 fm/c). Such an increase in lifetime will be crucially important for the signal of QGP.
2.2 Effective temperature
Charmonia being a massive object, does not become a part of the thermalized medium which induces a temperature gradient between the medium and charmonium. This can be measured by using the relativistic Doppler shift effect, which comes into the existence due to the velocity difference between medium particles and the charmonium. Therefore, relative velocity (\(v_{r}\)) between medium and charmonia is calculated to obtain an effective temperature felt by the charmonium. The velocities of the medium and charmonium are denoted by \(v_{m}\) and \(v_{J/\psi (nl)}\), respectively. This relativistic Doppler shift causes an angle dependent effective temperature (\(T_{eff}\)) expressed as (see Refs. [42, 43] for details):
where \(\theta \) is the angle between \(v_{r}\) and incoming light partons. To calculate the \(v_{r}\), we have taken medium velocity, \(v_{m} \sim 0.7c\), and charmonium velocity \(v_{J/\psi (nl)} = p_{T}/E_{T}\), where \(p_T\) is transverse momentum of charmonia and \(E_T=\sqrt{p_T^2 + M_{nl}^2}\) is its transverse energy, \(M_{nl}\) is the mass of the charmonium state. We have taken the average of Eq. (7) over the solid angle and obtained the average effective temperature as given by:
3 Modification in \(J/\psi \) and \(\psi (2S)\) yield in the QGP medium
The formulation of the current work is based on a model, UMQS recently proposed in [18]. The UMQS is described below briefly for the sake of completeness with particular emphasize on the modifications wherever required.
3.1 Charmonium kinematics in evolving QGP
The charmonia during their propagation through evolving medium get influenced by the medium in several ways. The kinematics of the charmonium (\(J/\psi (nl)\)) and \(c{\bar{c}}\) pairs formation and recombination with the evolution of the QGP medium, can be written by using the transport equation as:
The first term in the right hand side of Eq. (9), is a formation term and second one corresponds to the dissociation. \(\Gamma _{F,nl}\) and \(\Gamma _{D,nl}\) are the recombination and dissociation rates corresponding to the regeneration and dissociation of \(J/\psi (nl)\), respectively. \(V(\tau )\) is the volume of the medium. We assume that initially, the number of charm (\(N_{c}\)) and anti-charm quarks \((N_{\bar{c}})\) are produced in equal numbers, \(N_{c}\) = \(N_{\bar{c}}\) = \(N_{c\bar{c}}\). The Eq. (9) can be solved analytically under the assumption of \(N_{J/\psi }(nl) < N_{c\bar{c}}\) at \(\tau _{0}\) [44,45,46]:
Here \(N_{J/\psi (nl)} (\tau _{QGP},b,p_{T})\) is the net number of charmonium formed during the evolution of QGP, \(\tau _{QGP}\). The \(N_{J/\psi (nl)}(\tau _{0},b)\) is the number of initially produced charmonium at various centralities Footnote 1 at time \(\tau _0\). We have calculated the \(N_{J/\psi (nl)}(\tau _{0},b)\) corresponding to the centrality bins:
where, \(T_{pp}(b)\) is the overlap function for pp obtained by using the Glauber model as demonstrated in [47]. We have obtained the number of charm and anti-charm quarks given by, \(N_{c\bar{c}} = \sigma _{c\bar{c}}^{NN}\; T_{pp}(b)\). The values of \(\sigma _{J/\psi (nl)}^{NN}\) and \( \sigma _{c\bar{c}}^{NN}\), used in the calculation, are given in Table 1:
In Eq. (10), \(\epsilon _1(\tau _{QGP})\) and \(\epsilon _2(\tau )\) are the decay factors for the meson due to gluonic dissociation and collisional damping in QGP (of lifetime \(\tau _{QGP}\)) and \(\tau \) is the evolution time, respectively. These factors are obtained by using the following expressions:
and
Here, \(\Gamma _{D,nl}(\tau ,b,p_{T})\) is the sum of collisional damping and gluonic dissociation decay rates, discussed in the following sections. The lower limit of the above integral (\(\tau _{nl}^{'}= \gamma \tau _{nl}\), here \(\gamma \) is Lorentz factor) is taken as the charmonium dilated formation time where the dissociation due to color screening becomes negligible. In the equilibrated scenario of the QGP, these dissociation factors strongly depends on the evolution of the medium.
3.2 Suppression mechanisms
The charmonium floating in medium gets dissociated into its constitutions due to QGP medium effects and as a result the initial production of charmonia gets suppressed. The input parameters used in the model for calculating the charmonium suppression in the QGP medium are given in the Table 2.
In the following sections we describe the suppression mechanisms in brief along with the regeneration process which causes reduction in the suppression.
3.3 Color screening
The suppression mechanism due to color screening was first proposed by Matsui and Satz [4]. They proposed that like electric charge screening in QED plasma, the partons in the QGP medium screens the color charges. The screening prevents the formation of the \(c\bar{c}\) bound states [50]. The color screening of the real part of the quark–antiquark potential is an independent suppression mechanism that dominates in the initial phase of QGP where the medium temperature is very high. Original color screening mechanisms have gone through many refinements. In this work, the pressure is parameterized in the transverse plane instead of energy density [51,52,53]. In this model it is assumed that pressure vanishes at the phase boundary, i.e. at \(r = R_{T}\), where \(R_{T}\) is the transverse radius of cylindrical QGP.
where,
The factor \(p(\tau _{0},0)\) is obtained in the refs. [52, 53]. h(r) is the radial distribution function in transverse direction and \(\theta \) is the unit step function. The exponent \(\beta \) in the above equation depends on the energy deposition mechanism whose dependence on pressure is shown in Ref. [18].
The variation of pressure as the function of \(\tau \) is given by:
where A = -\(c_1\), B = \(c_2c_s^2\), C = \(\frac{4\eta q}{3(c_s^2 - 1)}\) and \(D = c_3\), here \(c_1\), \(c_2\), \(c_3\) are constants and have been calculated using different boundary conditions on energy density and pressure. Other parameters appeared above are: \(c_{s}\) is speed of sound in QGP medium, \(\eta \) is shear viscosity of the medium and \(q = c^{2}_{s} + 1\). Determining the pressure profile at initial time \(\tau = \tau _{0}\) and at screening time \(\tau = \tau _{s}\), we get:
where \(p_{QGP}\) is the pressure of the QGP phase. Putting variation of T and P with \(\tau \) we have determined the radius of the screening region, \(r_{s}\). The screening radius defines a region where effective medium temperature of a particle is larger than the dissociation temperature (i.e. \(T_{eff} \ge T_{D}\)). If \(T_{eff} < T_{D}\), then \(r_{s} \rightarrow 0\) which suggests that melting of the quarkonia due to color screening would be negligible in such a situation.
The \(c{\bar{c}}\) pairs formed inside the screening region at a point \({\vec r}_{J/\psi }\), may escape the region, if \(|\vec {r_{J/\psi }}\; +\; \vec {v_{J/\psi }}t_{f} |\; > \;r_{s}\). Here \(v_{J/\psi } = p_{T} / E_{T}\), is charmonium velocity. The condition for escape of \(c{\bar{c}}\) pair is expressed as:
where, \(\phi \) is the angle between the velocity (\(\vec {v_{J/\psi }}\)) and position vector (\(\vec {r_{J/\psi }}\)), and m is mass of a particular charmonium state.
Based on Eq. (19), the allowed values of the azimuthal angle, \(\phi _{max}(r)\) for survival of charmonium is expressed as:
Here r is the the radial separation between \(\bar{c}\) and c in the QGP medium.
The integration over \(\phi _{max}\) along with radial separation r gives the escape probability of \(c{\bar{c}}\) pair from the screening region, which is defined as the survival probability. The survival probability, \(S_{c}^{J/\psi }\), for a charmonium state is expressed as:
where \(\alpha _s=0.5\) [50, 51]. The \(R_{T}\) depends on the impact parameter (b). We have calculated it by using the transverse overlap area \(A_T\) as; \(R_{T}(b) = \sqrt{A_{T}/\pi }\). The value of \(\alpha _s\) is chosen in such a way that beyond the chosen value, color screening mechanism becomes almost independent with respect to change in its values.
3.4 Collisional damping
Collisional damping arises due to the inherent nature of the complex potential between (\(c{\bar{c}}\)) located inside the QCD medium. The imaginary part of the potential in the limit of \(t\rightarrow \infty \), represents the thermal decay width induced due to the low frequency gauge fields that mediate interaction between two heavy quarks [54].
The charmonium dissociation due to collisional damping is obtained by using the effective potential models. In the model under consideration, the singlet potential for \(c{\bar{c}}\) bound state in the QGP medium is given by [19, 54, 55]:
In Eq. (21) the first and second term in the right hand side are the string and the Coulombic terms, respectively. The third term is the imaginary part of the heavy-quark potential responsible for the collisional damping. Here \(\sigma \) is the string constant for \(c\bar{c}\) bound state, given as \(\sigma = 0.192\) GeV\(^2\) and \(m_{D}\) is the Debye mass, \(m_D = T_{eff} \sqrt{4\pi \alpha _s^T \left( \frac{N_c}{3} + \frac{N_f}{6} \right) }\). Here \(N_{c} = 3\), \(N_{f} = 3\). The \(\alpha _{s}^{T}\) is coupling constant at hard scale, as it should be \(\alpha _{s}^{T} = \alpha _{s}(2\pi T)\le 0.50\). We have taken \(\alpha _s^T \simeq 0.4430\) which is scaled at HTL energy \(\sim 2\pi T\). The effective coupling constant, \(\alpha _{eff}\) is defined at soft scale \(\alpha _{s}^{s} = \alpha _{s} (m_{c} \alpha _{s}/2) \simeq 0.48\), given as \(\alpha _{eff} = \frac{4}{3}\alpha _{s}^{s}\).
The collisional damping, \(\Gamma _{damp,nl}\) defines the charmonium decay induced due to the imaginary part of the complex potential. It is calculated using the first-order perturbation, by folding of imaginary part of the potential with the radial wave function:
where \(g_{nl}(r)\) is the charmonia singlet wave function. Corresponding to different values of n and l (here n and l are the principal and the orbital quantum numbers), the wave functions can be obtained by solving the Schrödinger equation for \(J/\psi \), \(\chi _{c}\), \(\psi (2S)\).
3.5 Gluonic dissociation
The dissociation of \(J/\psi \) by gluons contributes to the reduced yields of \(J/\psi \) in heavy-ion collisions. The the cross-section for such dissociation process is given by [19]:
where \(J_{nl}^{ql^{'}}\) is the probability density obtained by using the singlet and octet wave functions as follows:
where \(m_c=1.5\) GeV, is the mass of the charm quark and \(\alpha _s^u \simeq 0.59\), is the coupling constant, scaled as \(\alpha _{s}^{u} = \alpha _{s}(\alpha _{s}m_{c}^{2}/2)\). The \(E_{nl}\) is the energy eigen values corresponding to the charmonium wave function, \(g_{nl}(r)\). The octet wave function \(h_{ql'}(r)\) has been obtained by solving the Schrödinger equation with the octet potential \(V_{8} = \alpha _{eff}/8r\). The value of q is determined by using the conservation of energy, \(q = \sqrt{m_{c}(E_{g}+E_{nl})}\).
The gluonic dissociation rate, \(\Gamma _{gd,nl}\) is obtained, by taking the thermal average of the dissociation cross-section [18],
where \(p_T\) is the transverse momentum of the charmonium and \(g_d = 16\) is the statistical degeneracy of the gluons. Now summing the decay rates corresponding to the collisional damping and the gluonic dissociation, we have calculated the combined effect in terms of total decay width denoted by, \(\Gamma _{D,nl}(\tau ,p_{T},b)\):
3.6 Regeneration factor
There are two processes by which charmonia can be reproduced in the QGP medium. The first one is through the uncorrelated \(c{\bar{c}}\) pairs present in the medium. They can recombine within the QGP medium at a later stage [44,45,46, 56,57,58,59,60,61,62] to form a charmonium state. This regeneration process is found to be significant for charmonia in heavy-ion collisions at LHC energies because \(c{\bar{c}}\) are produced abundantly in the hot QGP medium. As pp is a small system, the production of \(c{\bar{c}}\) will be small compared to the heavy-ion collisions, therefore, the probability of regeneration due to uncorrelated \(c{\bar{c}}\) is not considered in the present work. The regeneration due to correlated \(c{\bar{c}}\) pairs is the regeneration mechanism which is just the reverse of gluonic dissociation. In this process, \(c{\bar{c}}\) pairs may undergo a transition from color octet state to color singlet state in the due course of time in QGP medium. To account for the regeneration via correlated \(c{\bar{c}}\) pairs in our current UMQS model, we have considered the de-excitation of octet state to singlet state via a gluon emission. We have calculated this de-excitation in terms of recombination cross-section \(\sigma _{f,nl}\) for charmonium by using the detailed balance to the gluonic dissociation cross-section \(\sigma _{d,nl}\) [18]:
where s is the Mandelstam variable, related with the center-of-mass energy of \(c{\bar{c}}\) pair, given as; \(s = (p_c + p_{\bar{c}})^2\), where \( p_c\) and \( p_{\bar{c}}\) are four momenta of c and \(\bar{c}\), respectively.
Finally we have obtained the recombination factor, \(\Gamma _{F,nl}=<\sigma _{f,nl}\;v_{rel}>_{p_{c}}\) by taking the thermal average of the product of recombination cross-section and relative velocity \(v_{rel}\) between c and \(\bar{c}\) :
where, \({p_c}\) and \({p_{\bar{c}}}\) are the 3-momentum of charm and anti-charm quark, respectively. The \(f_{c,\bar{c}}\) is the modified Fermi-Dirac distribution function of charm, anti-charm quark and expressed as; \(f_{c,\bar{c}} = \lambda _{c,\bar{c}}/(e^{E_{c,\bar{c}}/T_{eff}} + 1)\). Here \(E_{c,\bar{c}} = \sqrt{p_{c,\bar{c}}^{2} + m_{c,\bar{c}}^{2}}\) is the energy of the quarks and \(\lambda _{c,\bar{c}}\) is their respective fugacity factors [63]. We have calculated the relative velocity of \(c{\bar{c}}\) pair in medium as follows:
Since the gluonic dissociation increases with the increase in temperature, it leads to the production of significant number of \(c{\bar{c}}\) octet states in central collision where temperature is found to be around 300 MeV. Such that the de-excitation of \(c{\bar{c}}\) octet states to \(J/\psi \) enhance the regeneration of \(J/\psi \) in central collisions as compared with the peripheral collisions.
3.7 Net yield
The survival probability of charmonium (\(S_{gc}^{J/\psi }\)) in pp collisions due to gluonic dissociation along with collisional damping is given by:
It is assumed here that at \(\tau =\tau _0\) the color screening is the most dominating mechanism and would not allow for the charmonium to be formed. However, as QGP cools down, its effect on quarkonia suppression becomes insignificant at the later stage of the evolution. The color screening is incorporated in the model as an independent mechanism with the other suppression mechanisms in QGP. The net yield in terms of survival probability, \(S_{P}(p_{T},b)\) is expressed as:
Normalized inclusive \(p_{T}\)-integrated \(J/\psi \) yield as a function of normalized charged-particle multiplicity at mid-rapidity compared with ALICE data corresponding to V0M selection in pp collisions at \(\sqrt{s}= 7\) TeV [64], prediction for \(\sqrt{s}= 5.02\) TeV (left panel) and \(\sqrt{s}= 13\) TeV [65] (right panel). PYTHIA 8.2 results from [65] are also included to contrast with the results of our model (right panel). The dashed line is a linear function with the slope of unity
The feed-down formulation of the excited states of the charmonia, \(\chi _{c}\) and \(\psi (2S)\) into \(J/\psi \) has been adopted from the Refs. [18,19,20]. To obtain the feed-down, here we have taken the ratio between the net numbers of the initial and final \(J/\psi \). The net initial number is obtained considering the feed-down of the higher resonances into \(J/\psi \) in the absence of the QGP medium. This is given as \(N_{J/\psi }^{in} = \sum _{J\ge I} C_{IJ} N(J)\), where \(C_{IJ}\) is the branching ratio of state J to decay into the state I. The net final number of \(J/\psi \) includes medium effects in terms of survival probability (\(S_{P}(p_{T},b)\)) along with feed-down: \(N_{J/\psi }^{fi} = \sum _{J\ge I} C_{IJ} N(J) S_{P}(J)\). The net generalized survival probability including feed-down correction can be written as;
It has been observed that only \(60\%\) of \(J/\psi \) originates from direct production whereas \(30\%\) and \(10\%\) from the decays of \(\chi _{c}\) and \(\psi (2S)\) respectively. The net survival probability of the \(J/\psi \) after considering feed-down correction is given by,
4 Results and discussions
The results obtained from the calculation mentioned above is contrasted with the data available in the form of the \(J/\psi \) yield corresponding to the normalized multiplicities, defined as;
where \(N^{J/\psi }_{m}\) and \(N^{ch}_{m}\) are normalized by the corresponding mean values in minimum bias pp collisions.
The normalized \(p_{T}\)-integrated \(J/\psi \) production as a function of normalized charged-particle multiplicity is contrasted with the data from ALICE at mid-rapidity (\(|y|< 0.9\)) in pp collisions to check the feasibility of the UMQS model. Left panel of Fig. 3 shows this comparison at \(\sqrt{s} = 7\) TeV (data from [64]). The results from the present work for \(\sqrt{s} = 5.02\) TeV is shown by blue line. Right panel of Fig. 3 shows the prediction of our model (red line) and PYTHIA 8.2 of ALICE data at \(\sqrt{s} = 13\) TeV [65]. PYTHIA 8.2 results are extracted from Ref. [65]. It is worth mentioning here that in Ref. [65], the case of prompt \(J/\psi \) production (predicted by PYTHIA 8.2) is also included to illustrate the effect of non-prompt \(J/\psi \) in the inclusive production. Clearly, both the results of PYTHIA 8.2 reproduce the experimental data reasonably well at low \(N_{ch}\) but fails at higher \(N_{ch}\) as shown in the right panel of Fig. 3.
It is interesting to observe that UMQS prediction explains the data within the uncertainties. From Fig. 3, it is further observed that at high multiplicity the production of \(J/\psi \) is larger than low multiplicity regime. In UMQS charmonium can be produced through hard scattering and recombination. The combined effect of both of these production mechanisms dominates at high multiplicities. We have found that the regeneration plays an important role at high multiplicities while its contribution at low multiplicity bins is found to be negligible. The agreement of results displayed in Fig. 3 gives confidence to proceed with further analysis of quarkonia production by using UMQS in pp collisions at the LHC energies.
Further, we have predicted the charmonium suppression in ultra-relativistic pp collisions at the LHC energies. The UMQS model is used to calculate the \(p_{T}\) and centrality dependent survival probability of charmonium states formed in pp collisions at LHC energies at the mid-rapidity. The relative suppression of \(\psi (2S)\) over \(J/\psi \) is measured in the form of double ratio or yield ratio, \(S^{\psi (2S)}_{P}/S^{J/\psi }_{P}\) which is plotted as a function of multiplicity (\(dN_{ch}/d\eta \)) and transverse momentum, (\(p_{T}\)). It is to be noted that the “S”, “R” and “F” stand for “suppression”, “regeneration” and “feed-down”, respectively. The results are shown with and without combining all the medium effects to demonstrate the significance of an individual mechanism.
4.1 Centrality dependent suppression
We have obtained the centrality dependent survival probability for \(J/\psi \) and \(\psi (2S)\) by averaging over \(p_{T}\) with the \(p_{T}\)-distribution function \(1/E_{T}^{4}\) [66]. The \(p_{T}\)-integrated centrality dependent survival probability is given by,
The initial temperature obtained for low multiplicity exceeds the value of the QCD transition temperature (\(T_c\)) obtained from lattice QCD calculation (see Fig. 1). A marginal suppression of \(J/\psi \) is obtained at low multiplicity too and it increases with the final state multiplicities. However, \(\psi (2S)\) is effectively more suppressed at low multiplicity as compared with \(J/\psi \). The effects of the individual mechanisms including feed-down are also shown in this section. The higher resonances of charmonium are more suppressed than \(J/\psi \) and therefore the feed-down of these states into \(J/\psi \) enhances its suppression. However, regeneration mechanism reduces the suppression depending upon the medium size and temperature. For a relatively small QGP lifetime \(\tau _{QGP}\) for 5.02 TeV, the regeneration significantly reduces the suppression.
In Fig. 4, charmonium suppression is shown as a function of the charged-particle multiplicity and the impacts of individual mechanisms are also presented. In this figure, the effective regeneration is visible at high multiplicity while at low multiplicity, the effect of regeneration is found to be very small. Here, it is also shown that feed-correction enhances the \(J/\psi \) suppression a bit. It is an indirect observation of the fact that higher resonances of charmonium are more suppressed than \(J/\psi \). However, at \(\sqrt{s} = 5.02\) TeV, we have observed an effective regeneration for \(\psi (2S)\) which reduces its suppression significantly at high multiplicities. Inclusion of the regeneration along with feed-down correction almost cancels out the feed-down effect and suggests the possibility of regeneration for the higher resonances at high multiplicities for \(\sqrt{s} = 5.02\) TeV.
Figure 5 depicts the relative suppression of \(\psi (2S)\) over \(J/\psi \) including all the proposed medium effects. It shows, that at mid multiplicity bins \(\psi (2S)\) is more suppressed as compared to \(J/\psi \) for \(\sqrt{s} = 5.02\). The coinciding point corresponding to “S\(+\)F” and “S\(+\)R” at the lowest multiplicity bin, suggests that the difference between \(\psi (2S)\) and \(J/\psi \) suppression is almost the same at \(\sqrt{s} = 5.02\) TeV, if on one hand suppression for \(J/\psi \) is increased by including feed-down correction and on other hand, suppression of \(\psi (2S)\) is decreased by including regeneration.
At \(\sqrt{s} = 7\) TeV, \(J/\psi \) and \(\psi (2S)\) are almost equally suppressed at the high multiplicity, as shown in Fig. 6. However, \(\psi (2S)\) is found to be more suppressed at low and mid multiplicities. Regeneration effect is also found to be negligible for \(J/\psi \) and \(\psi (2S)\) at \(\sqrt{s} = 7\) TeV. An infinitesimal regeneration at very high multiplicity can be observed for \(J/\psi \) and \(\psi (2S)\) in Fig. 6. As regeneration being insignificant at \(\sqrt{s} = 7\) TeV, feed-down correction is found to take over the regeneration. Therefore, suppression along with regeneration and feed-down correction (“S+R+F”) follows the foot-step of the combined effects of the suppression and feed-down (“S+F”). Non-vanishing effect of regeneration at highest multiplicity bin, reduces the suppression a bit for \(J/\psi \) and \(\psi (2S)\) and almost takes away the effect of feed-down for \(J/\psi \).
Similar result is displayed in Fig. 7, where at high multiplicity \(\psi (2S)\) to \(J/\psi \) yield ratio is approximately one, while at low multiplicities the ratio is less than one. This indicates that \(J/\psi \) is less suppressed than \(\psi (2S)\) at peripheral pp collisions, which correspond to lower final state event multiplicities. Results in Fig. 7 also suggest a higher regeneration of \(J/\psi \) than \(\psi (2S)\) at high multiplicity. The results for suppression and suppression along with feed-down, and regeneration are found to coincide at the high multiplicity domain.
It is expected that at \(\sqrt{s}=13\) TeV the energy deposition is large which provides substantial suppression of \(J/\psi \) and \(\psi (2S)\), comparable to the heavy-ion collisions (see Fig. 8). Results displayed in Fig. 8 show that the effect of regeneration is almost negligible at low multiplicity (as in Fig. 6) while at high multiplicities it slightly reduces the suppression for both the charmonium states. \(\psi (2S)\) is suppressed slightly more than \(J/\psi \) at high multiplicity contrary to the results shown in Fig. 6.
As a consequence, “S\(+\)F” increases the suppression at high multiplicity, however, an effective regeneration for high resonances neutralizes feed-down effect in “S\(+\)R\(+\)F” (Fig. 8). The suppression ratio plotted in Fig. 9 shows that \(\psi (2S)\) is less suppressed at low and high multiplicities as compared to the intermediate multiplicity bins. Because for higher multiplicities, the temperature is higher and the regeneration effect creates the difference, which reduces the suppression of \(\psi (2S)\) relative to \(J/\psi \). Results depicted in Fig. 9 also show that individual effect (S) predicts a slightly more suppression of \(\psi (2S)\) than the combined effects (S\(+\)R) at the highest multiplicity bins.
4.2 \(p_{T}\)-dependent suppression
Now we discuss the transverse momentum (\(p_T\)) dependence of charmonia production by considering the \(p_T\)-dependent survival probability, (\(S_P\)) for minimum bias (\(0-100\%\) centrality) case by taking the weighted average over all centrality bins. The weighted average for \(S_{P}\) is given by,
where \(i = 1, 2, 3, \ldots \), indicate various centrality bins corresponding to different multiplicity classes. The weight function \(W_{i}\) is given as \(W_{i} = \int _{b_{i\;min}}^{b_{i\;max}} N_{coll}(b)\pi \; b\; db\). The number of binary collision, \(N_{coll}\) is calculated by using a Glauber model for pp collisions. In the Glauber model for pp collisions, a azimuthally asymmetric and inhomogeneous density distribution of a proton is considered, which is motivated by the shape of the structure function obtained in deep inelastic scattering. Therefore, same density profile is used to obtained \(N_{coll}\) [47].
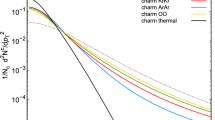
The \(p_T\)-dependent suppression of charmonium is shown in Fig. 10. It shows an increasing trend for regeneration of \(J/\psi \) for \(p_{T}<20\) GeV and then it slightly decreases with increasing \(p_T\). It seems that the thermodynamic conditions created at \(\sqrt{s} = 5.02\) TeV suits the regeneration of \(J/\psi \), as indicated by the results marked by S\(+\)R for \(12< p_T < 30\) GeV. While including the feed-down along with regeneration (S\(+\)R\(+\)F) predicts the suppression instead of enhancement for the mentioned \(p_{T}\)-range. However, for \(p_{T}<13\) GeV both the data sets predict a reduced suppression for \(J/\psi \). For \(p_{T}<3\) GeV, \(J/\psi \) and \(\psi (2S)\) are found to be less interactive with the medium, consequently we get a bit less suppression and regeneration at this \(p_{T}\)-range. All the medium effects predict a reduction in suppression with increasing \(p_T\). As shown in Fig. 10, a regeneration effect is observed for \(\psi (2S)\) for \(p_{T} > 6\) GeV. A relative suppression of \(\psi (2S)\) over \(J/\psi \) is plotted in Fig. 11, the double ratio shows that inclusion of regeneration (S\(+\)R) for \(\psi (2S)\) reduces its suppression for \(p_{T}<3\) GeV. While inclusion of feed-down and exclusion of regeneration effect (S\(+\)F) increases the \(J/\psi \) suppression relative to suppression (S) with increasing \(p_T\). A dip in double ratio at \(p_{T} = 6\) GeV, corresponds to the suppression of \(\psi (2S)\) when regeneration is almost insignificant while there is a regeneration for \(J/\psi \).
The charmonia suppression for \(\sqrt{s} = 7\) TeV is shown in Fig. 12 as a function of \(p_T\). We find less suppression at very low \(p_{T}\) range: \(1\le p_T \le 3\) GeV because the multiple scattering of the charmonium with medium constituents is less effective for very low \(p_T\). While for the intermediate \(p_T\) range: \(3\le p_{T} \le 6\) GeV, the scattering with medium will be at the peak, therefore \(J/\psi \) receives maximum suppression at the intermediate \(p_{T}\)-range. Further, suppression reduces with increase in \(p_T\), because the charmonia scattering with medium constituents will be comparably less for high-\(p_{T}\) particles as they quickly traverse through the medium and their abundances are low. The regeneration of charmonia increases up to a certain range of the \(p_{T}\) and at very high-\(p_{T}\) it gets saturated as the probability of the recombination of fast moving \(c{\bar{c}}\) reduces. The \(\psi (2S)\) feels maximum suppression for intermediate \(p_{T}\): \(2\le p_{T} \le 10\) GeV and gets a large suppression than \(J/\psi \) due to the low dissociation temperature (\(T_{D}\)) as compared to \(J/\psi \) (see Table 2).
The \(p_T\)-dependent suppression of \(\psi (2S)\) over \(J/\psi \) corresponding to minimum bias is plotted in Fig. 13. It shows that \(\psi (2S)\) is suppressed more over the entire \(p_T\)-range considered here. It depicts varying \(\psi (2S)\) suppression from intermediate to high-\(p_T\) as the difference in the suppression between \(J/\psi \) and \(\psi (2S)\) reduces at high-\(p_T\) regime. The results indicate that the higher resonances are more suppressed than the \(J/\psi \) and that is why the inclusion of feed-down correction (S\(+\)F) always predicts a higher suppression for \(J/\psi \).
The results displayed in Fig. 14 for \(\sqrt{s}=13\) TeV show that the charmonium states are largely suppressed at low-\(p_T\) and follows a trend similar to the results obtained for \(\sqrt{s} = 7\) TeV. But it shows a larger regeneration for \(J/\psi \) for \(p_{T}>5\). The regeneration effect gets saturated for \(p_T>20\) GeV. The regeneration of \(\psi (2S)\) is found to be negligible over the chosen \(p_{T}\)-range, however, its suppression reduces at higher transverse momenta: \(p_{T}>10\) GeV. Similar behavior for double ratio is also obtained in Fig. 15, where a large suppression for \(J/\psi \) reduces the relative suppression for \(\psi (2S)\), i.e. “S\(+\)F”. However, the relative suppression of \(\psi (2S)\) over \(J/\psi \) comes out to be approximately constant, a slightly reduced suppression may be observed at high-\(p_{T}\) regime (Fig. 15).
It is worthwhile to mention that in this work an interplay between regeneration and feed-down mechanisms for \(\sqrt{s} =\) 5.02 to 13 TeV has been demonstrated. In UMQS, not a single parameter is freely varied in order to explain the experimental data or predict the charmonium suppression.
5 Conclusions
The present analysis shows a QGP-like medium formation for all the multiplicity bins in ultra-relativistic pp collisions at LHC energies. We have observed that \(\psi (2S)\) is suppressed more and the effect of regeneration is also marginal for \(\psi (2S)\) as compared to \(J/\psi \). This makes \(\psi (2S)\) a relatively cleaner probe to investigate QGP-like medium in the small collision systems. As the cold nuclear environment is absent in the pp collision systems any modification in the charmonium yield can be considered as a pure effect of hot QCD medium. In contrast to this, the system formed in pA collision will show the combined effects of the hot and cold nuclear matter, therefore, pp collisions can be used as a scale to distinguish CNM effects. The pp collision results which are routinely used as a benchmark to understand the AA collision system is now become questionable because of the possibility of the creation of QGP-like medium in pp interactions. Thus, the formation of QGP in pp collisions will create a new puzzle and inevitably a new baseline will be required to analyze AA collisions.
Top panel shows the energy dependence of inclusive J/\(\psi \) (left) and \(c\bar{c}\) (right) production cross-section at mid-rapidity in pp collisions as fitted by a power-law function. The solid blue circles are ALICE data [68,69,70,71] and the black curve represents the power-law function. The quadratic sum of statistical and systematic uncertainties of ALICE data are presented in a single error bar. Bottom panels show the ratio between ALICE data and the fit. The dashed lines shows the value of \(\sigma _{J/\psi }^{pp}\) (top left) and \( \sigma _{c\bar{c}}^{pp}\) (top right) corresponding to \(\sqrt{s} = 13\) TeV
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The data that support the findings of the present work are available within the article.]
Notes
The impact parameter (b)-dependent centrality bins for pp collisions are obtained by using the formulation of Ref. [47].
References
J.C. Collins, M. Perry, Phys. Rev. Lett. 34, 1353 (1975)
E.V. Shuryak, Phys. Rep. 61, 71 (1980)
N. Brambilla et al., Eur. Phys. J. C 51, 1534 (2011)
T. Matsui, H. Satz, Phys. Lett. B 178, 416 (1986)
G.T. Bodwin, arXiv:1208.5506v3 [hep-ph]
R. Vogt, Phys. Rev. C 81, 044903 (2010)
A. Adare et al. [PHENIX Collaboration], Phys. Rev. Lett. 112, 252301 (2014)
A. Adare et al. [PHENIX Collaboration], Phys. Rev. C 77, 024912 (2008) [Erratum: Phys. Rev. C 79, 059901 (2009)]
A. Adare et al. [PHENIX Collaboration], Phys. Rev. Lett. 115, 142301 (2015)
D. Teaney, J. Lauret, E.V. Shuryak, Phys. Rev. Lett. 86, 4783 (2001)
J. Adam et al. [ALICE Collaboration], Phys. Rev. C 91, 064905 (2015)
B. Abelev et al. [ALICE Collaboration], Phys. Lett. B 740, 105 (2015)
Aamodt et al. [ALICE Collaboration], Phys. Rev. Lett. 105, 252302 (2010)
B. Abelev et al. [ALICE Collaboration], J. High Energy Phys. 2014, 73 (2014)
M. Aaboud et al. [ATLAS Collaboration], Eur. Phys. J. C 78, 171 (2018)
Q. Hu [ATLAS Collaboration], Nucl. Phys. A 982, 687 (2019)
A.M. Sirunyan et al. [CMS Collaboration], Phys. Rev. Lett. 120, 142301 (2018)
C.R. Singh, S. Ganesh, M. Mishra, Eur. Phys. J. C 79, 147 (2018)
F. Nendzig, G. Wolschin, Phys. Rev. C 87, 024911 (2013)
C.R. Singh, P.K. Srivastava, S. Ganesh, M. Mishra, Phys. Rev. C 92, 034916 (2015)
S. Ganesh, M. Mishra, Phys. Rev. C 88, 044908 (2013)
S. Ganesh, M. Mishra, Phys. Rev. C 91, 034901 (2015)
F. Brezinski, G. Wolschin, Phys. Lett. B 707, 534 (2012)
R. Sharma, I. Vitev, Phys. Rev. C 87, 044905 (2013)
N. Brambilla, J. Ghiglieri, A. Vairo, P. Petreczky, Phys. Rev. D 78, 014017 (2008)
M.E. Peskin, Nucl. Phys. B 156, 365 (1979)
G. Bhanot, M.E. Peskin, Nucl. Phys. B 156, 391 (1979)
N. Hatwar, C.R. Singh, S. Ganesh, M. Mishra, Phys. Rev. C 104, 034905 (2021)
A. Muronga, Phys. Rev. Lett. 88, 062302 (2002). [Erratum: A. Muronga, Phys. Rev. Lett. 89, 15 (2002)]
W. Israel, Ann. Phys. (N.Y.) 100, 310 (1976)
J.M. Stewart, Proc. R. Soc. Lond. A 357, 59 (1977)
W. Israel, J.M. Stewart, Ann. Phys. (N.Y.) 118, 341 (1979)
R.C. Hwa, K. Kajantie, Phys. Rev. D 32, 5 (1985)
L. McLerran, M. Praszalowicz, B. Schenke, Nucl. Phys. A 916, 210 (2013)
R.C. Hwa, Phys. Rev. D 10, 7 (1974)
R.C. Hwa, Phys. Rev. D 32, 3 (1985)
A. Bazavov et al., Phys. Rev. D 85, 054503 (2012)
H. Grad, Commun. Pure Appl. Math. 2, 331 (1949)
A. Muronga, Phys. Rev. C 69, 034903 (2004)
S. Kagiyama, A. Nakamura, A. Minaka, Prog. Theor. Phys. 76, 171 (1986)
I.P. Lokhtin, A.M. Snigirev, Phys. Lett. B 378, 247254 (1996)
F. Nendzig, G. Wolschin, J. Phys. G Nucl. Part. Phys. 41, 095003 (2014)
J. Hoelck, F. Nendzig, G. Wolschin, Phys. Rev. C 95, 024905 (2017)
R.L. Thews, M. Schroedter, J. Rafelski, Phys. Rev. C 63, 054905 (2001)
R.L. Thews, Eur. Phys. J. C 43, 97 (2005)
R.L. Thews, Nucl. Phys. A 702, 341 (2002)
S. Deb, G. Sarwar, D. Thakur, S. Pavish, R. Sahoo, Jan-e Alam, Phys. Rev. D 101, 014004 (2020)
A. Emerick, X. Zhao, R. Rapp, Eur. Phys. J. A 48, 72 (2012)
B. Chen, J. Zhao, Phys. Lett. B 772, 819 (2017)
M.-C. Chu, T. Matsui, Phys. Rev. D 37, 1851 (1988)
M. Mishra, C.P. Singh, V.J. Menon, R.K. Dubey, Phys. Lett. B 656, 45 (2007)
P.K. Srivastava, M. Mishra, C.P. Singh, Phys. Rev. C 87, 034903 (2013)
P.K. Srivastava, S.K. Tiwari, C.P. Singh, Phys. Rev. C 88, 044902 (2013)
M. Laine, O. Philipsen, P. Romatschke, M. Tassler, J. High Energy Phys. 03, 054 (2007)
A. Beraudo, J.P. Blaizot, C. Ratti, Nucl. Phys. A 806, 312 (2008)
P. Braun-Munzinger, J. Stachel, Phys. Lett. B 490, 196 (2000)
P. Braun-Munzinger, J. Stachel, Nucl. Phys. A 690, 119 (2001)
A. Andronic, P. Braun-Munzinger, K. Redlich, J. Stachel, Phys. Lett. B 571, 36 (2003)
A. Andronic, P. Braun-Munzinger, K. Redlich, J. Stachel, Phys. Lett. B 652, 259 (2007)
L. Grandchamp, R. Rapp, Nucl. Phys. A 709, 415 (2002)
L. Grandchamp, R. Rapp, G.E. Brown, Phys. Rev. Lett. 92, 212301 (2004)
R.L. Thews, M.L. Mangano, Phys. Rev. C 73, 014904 (2006)
D. Pal, A. Sen, M.G. Mustafa, D.K. Srivastava, Phys. Rev. C 65, 034901 (2002)
B. Abelev et al. [ALICE Collaboration], Phys. Lett. B 712, 165–175 (2012)
S. Acharya et al. [ALICE Collaboration], Phys. Lett. B 810, 135758 (2020)
B. Krouppa, A. Rothkopf, M. Strickland, Phys. Rev. D 97, 016017 (2018)
F. Bossu et. al., arXiv:1103.2394
S. Acharya et al. [ALICE Collaboration], arXiv:2105.06335 [nucl-ex]
B. Abelev et al. [ALICE Collaboration], Phys. Lett. B 718, 295 (2012)
S. Acharya et al. [ALICE Collaboration], JHEP 10, 084 (2019)
K. Aamodt et al. [ALICE Collaboration], Phys. Lett. B 704, 442 (2011)
S. Acharya et al. [ALICE Collaboration], arXiv:2108.01906 [nucl-ex]
Acknowledgements
This research work has been carried out under financial supports from DAE-BRNS, Government of India, Project No. 58/14/29/2019-BRNS of Raghunath Sahoo. CRS and RS acknowledge the financial support under the above BRNS project. Further R.S. acknowledges the financial supports under the CERN Scientific Associateship, CERN, Geneva, Switzerland. The authors would like to acknowledge interesting discussions with Dr. Sushanta Tripathy. The authors acknowledge the Tier-3 computing facility in the experimental high-energy physics laboratory of IIT Indore supported by the ALICE project.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
To extrapolate the energy dependence of inclusive J/\(\psi \) and \(c\bar{c}\) production cross-section at mid-rapidity in pp collisions, we have adopted the method of functional form fitting as discussed in Ref. [67]. In this method, the energy dependence of the inclusive J/\(\psi \) and \(c\bar{c}\) cross section are fitted with a power-law distribution of the form:
where A, \(s_0\) and b are free parameters. It is worth noting here that although it is not derived from a first principle, such a method of extrapolation reproduces the measured distribution very well. In Fig. 16 the solid blue circles are ALICE data and the black curves represent fitting function. The quadratic sum of statistical and systematic uncertainties of ALICE data are presented by a single error bar. The results obtained by extrapolation at \(\sqrt{s}\) = 13 TeV for inclusive J/\(\psi \) and \(c\bar{c}\) production cross-sections are reported in Table 1. Recent ALICE result [72] shows that the J/\(\psi \) production cross-section at mid-rapidity is \(\approx \) 16.15 ± 0.54 \(\mu \)b (quadratic sum of statistical and systematic uncertainties). This value is very close to our extrapolated result of 16.72 \(\mu \)b. This agreement provides a strong case for our extrapolated result of \(c\bar{c}\) production cross-section.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Singh, C.R., Deb, S., Sahoo, R. et al. Charmonium suppression in ultra-relativistic proton–proton collisions at LHC energies: a hint for QGP in small systems. Eur. Phys. J. C 82, 542 (2022). https://doi.org/10.1140/epjc/s10052-022-10500-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10500-z