Multi-charmed and singled charmed hadrons from coalescence: yields and ratios in different collision systems at LHC

Abstract

We study the production of charmed and multi-charmed hadrons in ultra-relativistic Heavy Ion Collisions coupling the transport approach for charm dynamics in the medium to an hybrid hadronization model of coalescence plus fragmentation. In this paper, we mainly discuss the particle yields for single charmed and multi-charmed baryons focusing mainly on the production of $\Xi _{cc}$ and $\Omega _{ccc}$. We provide first predictions for PbPb collision in $0 \! - \! 10\%\$centrality class and then we explore the system size dependence through KrKr , to ArAr and OO collisions, planned within the ALICE3 experiment. In these cases, a monotonic behavior for the yields emerges which can be tested in future experimental data. We found about three order of magnitude increase in the production of $\Omega _{ccc}$ in PbPb collisions compared with the yield in small collision systems like OO collisions. Furthermore, we investigate the effects on the $\Omega _{ccc}$ particle yield and spectra coming from the modification of the charm quark distribution due to the different size of the collision systems also comparing it to the case of thermalized charm distributions. These results suggest that observation on the $\Omega _{ccc}$ spectra and their evolution across system size can give novel information about the partial thermalization of the charm quark distribution as well as to its wave function width. Furthermore, we find that the $\Omega _{ccc}$ /$D^0$ ratio is an observable more sensitive with respect to $\Lambda _c$ /$D^0$ , this ratio is predicted to span over two order of magnitude from large to small systems.

1 Introduction

Many probes have been proposed to investigate the properties of the matter created in ultra-Relativistic Heavy Ion collisions (uRHICs). A preminent one is the heavy quark hadron production; all the observables related to them have been considered one of the most useful probes to characterize the quark-gluon plasma. Due to their large masses Heavy quarks, namely charm and bottom, are considered as a solid probe to characterize the QGP phase [1,2,3]. They are produced by pQCD processes with a formation time $\tau _{0}<0.08 fm/c\ll \tau _{QGP}$ that permits to probe also the strong electromagnetic and vortical fields expected in the initial stage of the collision [4,5,6]. On the other hand, the large mass implies a larger thermalization time w.r.t. light counterpart and appears currently to be comparable to the one of the QGP itself [1, 7] and HQs can probe the whole evolution of the plasma. Furthermore, they are expected to conserve memory of the history of the system evolution and the final hadrons can keep information about the out-of-equilibrium initial conditions. Two main observables have been studied in uRHICs for HF hadrons: the heavy mesons nuclear modification factor $R_{AA}(p_T)$ [8,9,10], and the elliptic flow, $v_2(p_T)$ [11, 12]. These observables have been studied in order to extract the heavy flavour transport coefficients and understand the HQs dynamics in QGP from a theoretical point of view [13,14,15,16,17,18,19,20,21,22,23]. Recently, further efforts have been done to extend the analysis to higher order anisotropic flows $v_n$ [24,25,26,27,28] that can provide more constraints on the extraction of the transport coefficients.

The coalescence mechanism is one of the possible description for the hadronization process present in the Quark-Gluon Plasma, it is able to explain the $p_T$ baryon to meson spectra and the splitting of elliptic flow of light mesons and baryons produced in heavy ion collisions at top RHIC energies [29,30,31,32,33] as well as at LHC [34]. In the last decades coalescence models were extended to include finite width to take into account for off-shell effects [35,36,37] which however preserve the main features of the initial modeling like the enhancement of baryon production and an approximate quark number scaling of the elliptic flow $v_2$. In particular, for open heavy flavor, the hadronization by coalescence play an important role to determine the $R_{AA}(p_T)$ and the elliptic flow $v_2(p_T)=\langle cos (2\phi ) \rangle$ of D meson affecting the evolution of $D_s$ [2, 7, 18, 20, 23, 38, 39]. Furthermore, coalescence approaches have predicted an unexpected large $\Lambda _c/D^0 \sim 0.5-1$ in AA collisions [40, 41], that has been recently observed at RHIC energies [42] and in pp, pA, AA collisions at LHC [43,44,45]. Such a large ratio appears to be a strong violation of the universality of the fragmentation function seen in elementary collision systems, where the observed $\Lambda _c/D^0$ is of $O(10^{-1})$ [46]. A large baryon over meson ratio in the charm sector, as observed in AA collision, is compatible with hadronization by coalescence [40, 47, 48]. Furthermore, very recently, the Catania coalescence model have correctly predicted the ratio of $\Lambda _c/D^0$, $\Xi _c/D^0$ and $\Omega _c/D^0$ even in pp collisions [49,50,51]. At the same time, in the heavy quark sector, theoretical studies [24, 52, 53] have shown that the investigation on the bottom quarks can provide further insight on the HQ thermalization looking at $R_{AA}$, anisotropic flows and hadronization mechanism of B mesons and $\Lambda _b$.

In this paper we are concentrating our focus on the production of the multi-charmed hadrons, which have two or three charm as constituent quarks. The study of these probes is, first of all, a natural extension of the investigation done for single-charmed hadrons, moreover it can provide further information about the hadronization mechanism, that should be much more sensitive to the charm quark features in the QGP medium. The production of multicharmed hadrons are part of the physical motivation of the ALICE3 proposal for HL-LHC [54]. First observations of multi-charmed baryons was reported in 2002 by SELEX collaboration at Fermilab for $\Xi _{cc}^+$ [55]. Recently, LHCb collaboration has observed $\Xi _{cc}^{++}$ in pp collisions at top LHC energies in two different decay channels [56, 57]. First theoretical studies on the multi-charmed production were made with statistical hadronization model in [58], and more recently an increasing interest has grown about the topic, with different calculations present in literature [59,60,61,62,63]. The multi-charmed hadrons, as well as the exotic states, e.g. $T_{cc}^+$, and pentaquarks, has been also indicated as interesting for future experimental developments and investigations [54].

The paper is organized in the following way: in Sect. 2, we describe our hybrid hadronization model by coalescence plus fragmentation. In Sect. 3, we discuss the collision systems characteristics and parton distribution setup for our calculations. In Sect. 4, we present our results for the single-charmed and multi-charmed yields in PbPb collision at LHC energies compared with Statistical Hadronization Model (SHM), and the effect on the production coming from microscopical details of our model. In Sect. 5, we study the multi-charm production varying the collision systems, i.e. PbPb , KrKr , ArAr and OO , and the role of non-equilibrium behaviour of charm quark distribution. Finally, in Sect.  6, we give our conclusions.

2 Hybrid hadronization by coalescence and fragmentation

Coalescence models have been widely applied as a mechanism of hadronization in HICs. These models were successful for the explanation of the constituent-quark number scaling of the elliptic flow $v_2(p_T)$ in AA collisions for light hadrons and the large baryon-to-meson ratios for light hadron production at “intermediate” $p_T$ [64]. In recent years, for the HF hadron chemistry in AA collisions, the charmed hadrons production has been investigated within these models predicting a large $\Lambda _c/D^0$ [40, 41, 65, 66]. This approach is also suitable to provide results in different collision systems, and it was proposed as an alternative approach of hadronization in very small collisions systems like pp collisions, assuming that also in this systems a small QGP droplet can be formed where the charm quarks, produced in perturbative processes, can hadronize via recombination with light thermal partons present in the medium [50]. It was shown that this hadronization mechanism can explain in a natural way the $p_T$ dependence of different charmed hadrons ratio like $\Lambda _c/D^0$, $\Xi _c/D^0$, $\Omega _c/D^0$ at top LHC energies.

In this section, we recall the basic elements of the coalescence model developed in [30,31,32, 38] and based on the Wigner formalism. The momentum spectrum of hadrons formed by coalescence of quarks can be written as:

$$\begin{aligned} \frac{dN_{H}}{dyd^{2}P_{T}}= & {} g_{H} \int \prod ^{N_{q}}_{i=1} \frac{d^{3}p_{i}}{(2\pi )^{3}E_{i}} p_{i} \cdot d\sigma _{i} \; f_{q_i}(x_{i}, p_{i}) \nonumber \\{} & {} \times C_{H}(x_{1}...x_{N_{q}}, p_{1}...p_{N_{q}})\, \delta ^{(2)} \left( P_{T}-\sum ^{n}_{i=1} p_{T,i} \right) \nonumber \\ \end{aligned}$$

(1)

with $g_{H}$ we indicate the statistical factor to form a colorless hadron from quarks and antiquarks with spin 1/2. For mesons with spin-0 the statistical factors $g=1/36$ gives the probability that two random quarks have the right colour, spin, isospin to match the quantum number of the considered mesons. For baryons with spin-1/2 the statistical factors is $g=1/108$. The $d\sigma _{i}$ denotes an element of a space-like hypersurface, while $f_{q_i}$ are the quark (anti-quark) phase-space distribution functions for i-th quark (anti-quark). $C_H(...)=\mathcal {N} f_H(...)$ with $\mathcal {N}$ a normalization factor; while $f_{H}(x_{1}...x_{N_{q}}, p_{1}...p_{N_{q}})$ is the Wigner function which describes the spatial and momentum distribution of quarks in a hadron.

Following the Refs. [38, 40, 41] we adopt for the Wigner distribution function a Gaussian shape in space and momentum,

$$\begin{aligned} f_H(...)=\prod ^{N_{q}-1}_{i=1} 8\exp {\Big (-\frac{x_{ri}^2}{\sigma _{ri}^2} - p_{ri}^2 \sigma _{ri}^2\Big )} \end{aligned}$$

(2)

where $N_{q}$ is the number of constituent quarks.

Notice that $\mathcal {N}$ has been fixed to guarantee that in the limit $p \rightarrow 0$ all the charm hadronize by coalescence in a heavy hadron. This is imposed by requiring that the total coalescence probability for charm quarks gives $\lim _{p \rightarrow 0} P^{tot}_{coal}=1$. It has been shown, by other studies, that the inclusion of missing charm-baryon states [66] or the variation of the width of the D meson wave function [48, 65], can permit that all the zero momentum charm quarks can be converted to charmed hadrons. The relative coordinate are evaluated going into the CM frame of the particles involved in the process and are defined as follows. For mesons the relative coordinates $(r_1, p_{r1})$ are given by,

$$\begin{aligned} r_1=|\vec {x}_1-\vec {x}_2|, ~ p_{r1}={|m_2\vec {p}_1-m_1\vec {p}_2|\over m_1+m_2}, \end{aligned}$$

(3)

while for baryons are defined as

$$\begin{aligned} r_{1}=\frac{|\vec {x}_1-\vec {x}_2|}{\sqrt{2}}, ~ p_{r1}=\sqrt{2} \; {|m_2\vec {p}_1-m_1\vec {p}_2|\over m_1+m_2}, \end{aligned}$$

(4)

and $r_{2}$, $p_{r2}$ are given by

$$\begin{aligned} r_{2}= & {} \sqrt{2 \over 3} \; \left| { {m_1\vec {x}_1+m_2\vec {x}_2\over m_1+m_2}}-\vec {x}_3 \right| , \nonumber \\ p_{r2}= & {} \sqrt{3 \over 2} \; {|m_3(\vec {p}_1+\vec {p}_2)-(m_1+m_2)\vec {p}_3|\over m_1+m_2+m_3}, \end{aligned}$$

(5)

The $\sigma _{ri}$ are the covariant widths, that can be related to the oscillator frequency $\omega$ by $\sigma _{ri}=1/\sqrt{\mu _i \omega }$ where $\mu _i$ are the reduced masses

$$\begin{aligned} \mu _1=\frac{m_1 m_2}{m_1+m_2},&\,&\mu _2= \frac{(m_1+ m_2)m_3}{m_1+m_2+m_3}. \end{aligned}$$

(6)

In our calculations the masses of light and heavy quarks have been fixed to $m_{u,d}\!=\!300$ MeV, $m_{s}\!=\!380$ MeV, $m_{c}\!=\!1.5$ GeV. The Wigner function for the heavy meson has only one parameter which is the width $\sigma _{r 1}$, while for baryons there are two parameters $\sigma _{r 1}$ and $\sigma _{r 2}$ that are related by the oscillatory frequency $\omega$ through the reduced masses by

$$\begin{aligned} \sigma _{p i}=\sigma _{ri}^{-1}=1/\sqrt{\mu _{i} \omega } \end{aligned}$$

(7)

The widths of the Wigner function $f_H$ are fixed by using the relation with the size of the hadron and in particular to the root-mean-square charge-radius of the hadron, $\langle r^2\rangle _{ch}= \sum _{i=1}^{N} Q_i\langle (x_i-X_{cm})^2\rangle$ with $N=2,3$ for mesons and baryons respectively; see Ref. [41, 50] for single-charmed mesons and baryons. The mean square charge radius of mesons and single charmed baryons used as reference come from quark model [67, 68]. The widths for heavy hadron used in this work are shown in Table 1. The corresponding mean square charge radii evaluated from these widths have values within the uncertainties coming from the quark models calculation mentioned above. In Table 2 we report the widths and radii for multi-charm hadrons. To fix the widths values of the Wigner function in the case of multi-charmed hadrons ($\Xi _{cc}^{++}$ and $\Omega _{ccc}$) we start from the frequency $\omega$ of the single charmed hadrons, $\Xi _{c}$ and $\Omega _c$ respectively; and then we calculate the widths with a scaling from the frequency and the new reduced masses according to Eq. (7).

Table 1 Mean square charge radius $\langle r^2\rangle _{ch}$ in $fm^2$ and the widths parameters $\sigma _{pi}$ in GeV. The mean square charge radius are taken quark model [67, 68]

Table 2 Multi-charmed widths parameters $\sigma _{pi}$ in GeV, mean radii $\langle r^2\rangle$ in $fm^2$ and frequencies compared with single-charmed baryons

As known from previous works on coalescence [19, 34, 40, 41, 69] the coalescence probability decreases at increasing $p_T$, this behaviour let the the standard independent fragmentation to be the dominant hadronization process for the production at high $p_T$. Hence, the inclusion of the hadronization by fragmentation is necessary to describe correctly the transition to the high momentum regime but does not affect significantly the yield. In our approach the smooth transition from low to high $p_T$ regime is given by introducing a fragmentation probability $P_{frag}(p_T)$. As done in Ref. [41, 50] we start from the probability that one charm quark can hadronize by coalescence and we assume that charm quarks that do not hadronize via coalescence are converted to hadrons by fragmentation. The fragmentation probability is given by $P_{frag}(p_T)=1- P^{tot}_{coal}(p_T)$, where $P^{tot}_{coal}$ is the total coalescence probability. Notice that with the same approach used in [41, 50] the coalescence probability for a charm quark to hadronize via coalescence is forced to be 1 at $p_T \approx 0$. The hadron momentum spectra from the charm parton fragmentation is given by:

$$\begin{aligned} \frac{dN_{had}}{d^{2}p_T\,dy}=\sum \int dz \frac{dN_{fragm}}{d^{2}p_T\, dy} \frac{D_{had/c}(z,Q^{2})}{z^{2}} \end{aligned}$$

(8)

$D_{had/c}(z,Q^{2})$ is the fragmentation function and $z=p_{had}/p_{c}$ is the momentum fraction of heavy quarks transferred to the final heavy hadron while $Q^2=(p_{had}/2z)^2$ is the momentum scale for the fragmentation process. In our calculations for charm quarks we have used the Peterson fragmentation function [70] $D_{had}(z) \propto 1/[ z [1-z^{-1}-\epsilon _c({1-z})^{-1}]^2 ]$ where $\epsilon _c$ is a free parameter that is determined assuring that the shape of the fragmentation function agrees with the experimental data on $p_T$ distributions for $D^0$ and $\Lambda _c$ at $p_T>10 \mathrm \; GeV$ The $\epsilon _c$ parameters used here are the same as in [41]. We notice that at high $p_T$ the fragmentation becomes to be the dominant charm hadronization mechanism and a quark will hadronize according to the different fragmentation fractions into specific final charmed hadron channels. The fragmentation fraction is evaluated according to PYTHIA8 ratios at high $p_T> 10 \mathrm \; GeV$ that are similar to the $e^++e^-$ [46] apart from an increase of the fraction for $\Lambda _c$ and moderate decrease of the fraction going to $D^0$ , as already done in [41, 50]. In our calculation the multi-dimensional integrals in the coalescence formula are evaluated by using a Monte-Carlo method, see [29, 41] for more details.

3 Fireball and parton distribution

In our calculation light quarks consist of a thermalized system of gluons and u, d, s quarks and anti-quarks. The partons are distributed uniformly in the transverse plane and in the rapidity range $|y_{z}|<0.5$. The longitudinal momentum distribution is assumed to be boost-invariant in the range $y\in (-0.5,+0.5)$, and is included a radial flow with the following radial profile $\beta _T(r_T)=\beta _{max}\frac{r_T}{R}$, where R is the transverse radius of the fireball. Partons at low transverse momentum, $p_T<2 \,\text{ GeV }$, are considered thermally distributed

$$\begin{aligned} \frac{dN_{q,\bar{q}}}{d^{2}r_{T}\,d^{2}p_{T}} = \frac{g_{q,\bar{q}} \tau m_{T}}{(2\pi )^{3}} \exp \left( -\frac{\gamma _{T}(m_{T}-p_{T}\cdot \beta _{T})}{T} \right) \end{aligned}$$

(9)

where $m_T=\sqrt{p_T^2+m_{q,\bar{q}}^2}$ is the transverse mass. The factors $g_{q}=g_{\bar{q}}=6$ are the spin-color degeneracy. The presence of gluons in the quark–gluon plasma is taken into account by converting them to quarks and anti-quark pairs according to the flavour compositions, as assumed in [31, 71].

The volume of the fireball in one unit of rapidity is given by $V = \pi R^2_\perp \tau$ where $R_\perp$ is the radius of the fireball taking into account the radial expansion. In PbPb collisions we fix the radial flow and the volume by imposing the total multiplicity dN/dy and the total transverse energy $dE_T /dy$ to be equal to the experimental data as done in [34, 41]. For the other collision systems we have extracted radial flow and fireball dimensions from the output of the solution of relativistic Boltzmann transport equation, developed for realistic heavy-ion collision simulation [72,73,74,75,76,77]. The volumes extracted from our simulations are similar to the active hadronization volume used by SHM in [60]. With the purpose of a more direct comparison we have modified our volume to the SHM one, which however correspond to an adjustment of about a 5%. The values for radial flow, radius and $\tau$ that we employed for the hadron spectra evaluation are shown in Table 3. Such values correspond in one unity of rapidity to fireball volume for PbPb, KrKr, ArAr and OO that are, respectively, $5000 \,\mathrm{{fm}}^3$, $2000 \,\mathrm{{fm}}^3$, $920\, \mathrm{{fm}}^3$ and $345\, \mathrm{{fm}}^3$. For the initial $p_T$ distribution of partons at high transverse momentum, $p_T > 2.5$ GeV, we have considered the mini-jets that have undergone the jet quenching mechanism. As done in Ref. [41], we have considered the initial $p_T$ distribution from pQCD calculation and the thickness function of the Glauber model to go from pp collisions to AA ones. The charm pair production is described by hard process and it is described by perturbative QCD (pQCD) at NNLO. Therefore, the starting point to compute the initial heavy quarks spectra at LHC collision energy of $\sqrt{s}=5.02$   TeV is by pQCD calculation. In our calculation the initial charm quark spectrum have been taken in accordance to the Fixed Order + Next-to-Leading Log (FONLL), as given in Refs. [78, 79]. The number of charm quarks has been chosen in accordance with a charm quark cross section of $d\sigma _{c\bar{c}}/dy \sim 0.500$ that scales from PbPb to ArAr, KrKr and OO with the mean nuclear thickness function $T_{AA}$ [80]. This cross section and $T_{AA}$ scaling gives, for these calculations, a number of charmed quarks that are $N_c^{PbPb}\!\sim \!15$, $N_c^{KrKr}\!\sim \!4.35$, $N_c^{ArAr}\!\sim \!1.5$ and $N_c^{OO}\!\sim \!0.4$.

Table 3 Fireball radii, lifetime, flow and volume considered in the different collision systems studied

Finally, the charm quark distribution evolution is obtained starting from the perturbative distribution (FONLL) and solving the relativistic Boltzmann transport equations for charm quarks scattering in a bulk medium of quarks and gluons. The scattering cross section giving a drag and diffusion corresponding to a space transport coefficient $D_s (p\rightarrow 0)$ in agreement to lQCD [1, 7, 53]. In PbPb such an approach is able to provide a good prediction for $R_{AA}(p_t)$,$v_2(p_t)$ and $v_3(p_t)$ [7, 20, 27, 28, 53].

In Fig. 1 are shown the final charm quark transverse momentum distribution obtained after the evolution in QGP, in different collision systems. The shown spectra are normalized to the same number of charm quarks in order to compare them as a function of $p_T$ . In particular we compare these spectra with the initial FONLL distribution, the fireball lifetime decreases with the system size, therefore in smaller systems charm quarks have a thermalization time that is larger w.r.t. the fireball lifetime, suggesting that the high $p_T$ distribution remains close to the non-equilibrium pQCD initial distribution. In fact, in Fig. 1, moving from larger systems, like PbPb (blue solid line), to small systems, i.e. OO (gold solid line), we observe a flattening of the charm quark spectra.

Furthermore, we have also explored the extreme scenario where the charm quark are fully thermalized as in Eq. (9) (black solid line in Fig. 1); from one hand this case allow us to have a more direct comparison with SHM model, and from the other hand it give us the opportunity to explore the sensitivity to the charm distribution function on the multi-charmed hadrons production.

Fig. 1

Normalized charm distributions: from FONLL (black dashed line) before evolution, after evolution in PbPb (blue solid line), KrKr (red solid line), ArAr (green solid line), OO (gold solid line) collisions and the thermal production (black solid line)

4 Production in Pb–Pb collisions

In this section, we discuss the results for the total yields of charmed and multi-charmed hadrons using the model described in the previous section in the case of PbPb collisions at $\sqrt{s}\!=\!5.02 \mathrm \; TeV$.

The presence of the resonances has a relevant impact because it supply a substantial contribution in addition to the ground state production. In this work we include multiple states for the different species, the complete set of considered states is listed in Table 4 for single charmed hadrons and in Table 5 for multi-charmed hadrons. The single-charmed resonances considered are the ones present and confirmed, at the moment, by the Particle Data Group [83]. Following the same approach used in [41] we consider a statistical factor given by $[m_{H^*}/m_H]^{3/2} \times \exp {\left( -\Delta m /T\right) }$ with $\Delta m=m_{H^*}-m_H$, where $m_{H^*}$ is the mass of the resonance. This statistical factor is given by the Boltzmann probability to populate an excited state of mass $m+\Delta m$, at a temperature T.

Table 4 Ground states of charmed mesons and baryons as well as their first excited states including their decay modes with their corresponding branching ratios as given in Particle Data Group [84, 85]

Table 5 Ground states and first excited states for multi-charmed baryons

Fig. 2

Single-charmed hadrons yields in PbPb collision at midrapidity in $0 \! - \! 10\%\$centrality class at $5.02 \mathrm \;TeV$. Our colescence plus fragmentation (red-yellow squares) results in comparison with SHM (blue open circles), SHM with enhanced set of baryons (green open diamonds) [60], and ALICE experimental data (black triangles) [43, 81, 82]

In Fig. 2 are shown the yields for single charmed hadrons in PbPb collisions for $0 \! - \! 10\%\$centrality at mid-rapidity obtained with our model of coalescence plus fragmentation (red-yellow square points). Our results are compared to ALICE experimental data shown by black triangles [43, 81, 82]. We recall that temperature and volume in our model have been set equal to SHM in order to have a more direct comparison with the particle production predicted by the Statistical Hadronization Model (blue open circle points), where the error bars refer to uncertainties from the model [60]. We can see a general very good agreement with the experimental data; only for $D^0$ and $D^{*+}$ mesons, the coalescence prediction is slightly below the data, giving a result which is around the lower part of the experimental error band; it can be considered a marginal discrepancy considering that we have employed particle mean square radius from quark model, and we have not performed any adjustment within the uncertainties of these values to fit the yield. The prediction for $\Xi ^0_c$ are quite larger than the one of SHM, however recent data on pp at $\sqrt{s}= 13 TeV$ from ALICE seem to be even larger than the $\Xi ^0_c/D^0$ similar to our model prediction in [50], hence suggesting a large $\Xi ^0_c$. In Fig. 2 are also shown the results for SHM considering an enhanced set of charmed baryons (green open diamond points) with respect to the ones listed by the PDG, as suggested in studies on charm hadron production with statistical models [66, 86]. This result seems in accord with former indication for the production of charmed baryons in pp and PbPb collisions; where our coalescence plus fragmentation model predicts a baryon enhancement with respect to SHM. Our results are in very good agreement with recent measurements in PbPb collisions at $5.02 \mathrm \;TeV$ with a $\Lambda _c$ production $dN^{\Lambda _c}/dy=3.28\pm 0.42(stat)\pm 0.44(syst)\pm 0.16(BR)$ [43]. In pp collisions the results of our coalescence plus fragmentation model are similar to the SHM ones, within the uncertainties, in the case of $D^0$, $D^+$, $D^*$, $D_s$, but exhibit a significant difference for $\Lambda _c$ and $\Xi _c$ considering statistical models with the same number of resonances [50, 86]; this behaviour seems to be also confirmed in PbPb collisions.

In Fig. 3 are shown the results for all charmed hadrons considered, adding with respect to Fig. 2 the $J/\psi$, the $\Omega _c$ and the multi-charmed baryons $\Xi _{cc}^{++}$ , $\Omega _{cc}$ and $\Omega _{ccc}$ . The $\Omega _c$ production in our model is about one order of magnitude smaller with respect to the $\Lambda _c$ yield, a results that is in line with what has been obtained in our previous work in pp collision [50], that turns out to be larger than the statistical yield of about a factor ten. The multi-charmed baryons that we consider, i.e. $\Xi _{cc}^{++}$ ,$\Omega _{cc}$ and $\Omega _{ccc}$ , have yields of about 3 and 5 order of magnitude smaller than the total charm quarks available in the system formed during the collision, i.e. the dN/dy for $\Xi _{cc}^{++}$ is about $(8\!\pm 2)\cdot \!10^{-3}$, for $\Omega _{cc}$ is about $(0.5\!\pm 0.02)\cdot \!10^{-3}$ and for $\Omega _{ccc}$ is between $1.2\!\cdot \!10^{-5}$ and $1.01\cdot \!10^{-4}$, see also Table 6.

For multi-charmed baryons we have found a quite large sensitivity to the underlying charm $p_T$ distribution function. If we assume a fully thermalized charm distribution we obtain an enhancement of the yields w.r.t. the realistic distribution shown in Fig. 1, this can be expected because when a thermal distribution is considered there is a large presence of charm quarks concentrated in a small momentum region at very low $p_T$ w.r.t. the realistic distributions. This feature, facilitates the recombination mechanism, because of the larger probability to find charm quarks close in phase space in the region where is present the peak of the charm distribution function. For the multi-charmed hadrons, this property results in an enhancement in the final total yields, that is more sensitive with respect to the single-charmed hadrons because of their quark content. In fact the range shown for this particles in the plot, corresponds to the yields obtained with realistic distribution for the lower limit and the one obtained with thermal distribution for the upper limit.

In Figs. 2 and 3 we compare our results for all the charmed hadrons with the production obtained with SHM (blue open circles) [60]. From the comparison we observe that our model gives an enhancement for the single-charmed baryons, i.e. $\Lambda _c$ , $\Xi _{c}$ and $\Omega _c$ of about a factor $\sim \!2\!-\!3$. However the baryons production becomes similar when in the SHM an enhanced set of baryon resonances is considered, as shown in figures by the green open triangles. For the multi-charmed hadrons production shown in Fig. 3, especially for $\Omega _{ccc}$ SHM predicts a larger production w.r.t. the coalescence results with realistic distribution (lower limit of the band), but a similar production is obtained when the thermal distribution is also used in the coalescence model. In Fig. 3 we have also reported the $J/\psi$ production in both dynamical and thermal charm cases, with a resulting yields that is in the range $(1\!-\!6) \cdot 10^{-2}$, about a factor 2 smaller than the SHM result and experimental measurements [87, 88]. However, with our modeling we are considering that the production for the $J/\psi$ happens at the freeze-out hypersurface with temperature $T_c$, while in dynamical dissociation and recombination approaches consider the survival probability of $J/\Psi$ above $T_c$ [89, 90] that we have not included in our modeling. Considering a recombination model based on a dynamical approach goes quite beyond the scope of this paper that is focused in providing first predictions and system size dependence of charmed baryons.

Fig. 3

Charmed hadrons yields in PbPb collision at midrapidity at $0 \! - \! 10\%\$centrality class at $5.02 \mathrm TeV$. Our coalescence plus fragmentation (red-yellow squares) results in Comparison with SHM (blue open circles) and SHM with enhanced set of baryons (green open triangles) [60]. The orange box represent the variation of the yield going from a thermal charm distribution (upper border) to the realistic charm distribution from transport simulation (lower border)

Fig. 4

$D^0$ (black open diamonds with line), $\Lambda _c$ (blue triangle with line) and $\Omega _{ccc}$ (orange circles with line) yield variation at variance of $\langle r_{ch}^2\rangle ^{1/2}$ variation normalized to the yield obtained with Wigner function widths present in Tables 1 and 2

4.1 Sensitivity to hadron size

In this section, we explore how the microscopic details of our hadronization model have a role on the $\Omega _{ccc}$ production. In fact while for D, $D_s$, $\Lambda _c$ and $\Xi _{c}$ we employ the results from the quarks model, for $\Omega _{ccc}$ the mean square radius and in general the wave function is quite unknown. As discussed in the previous section the Wigner function depends only on the widths, that are directly related to the mean charge radius. In order to obtain a quantitative estimate of the effect produced by the variation of the Wigner function widths we have performed a calculation in PbPb varying the widths in such a way to have a resulting variation in the square root of the charged squared radius in a range between -50% and 50% of the established value discussed in Sect. 2. It is also interesting to compare the effects on the $\Omega _{ccc}$ production with those for $D^0$ and $\Lambda _c$ . In Fig. 4 are shown the variation of the particle yield for $D^0$ (black open diamonds with line), $\Lambda _c$ (blue triangle with line) and $\Omega _{ccc}$ (orange circles with line) with respect to the yield obtained with the previous widths, used in this way as a baseline reference. This variation is shown as a function of the variation of $\langle r_{ch}^2\rangle ^{1/2}$. We notice that the $D^0$ (and so $D^+$, $D^*$,$D_s$) and $\Lambda _c$ yields are almost unchanged in the two extreme cases, this behaviour can be explained recalling that this two species provide the majority of the charm hadron production; an enlargement or a shrinking of the spatial widths would normally lead to a larger or a smaller production respectively, but the imposed charm quark conservation in conjunction with the constrained coalescence probability at zero momentum engender a compensation of the size change effect. The just mentioned concurrence of constraints has not a big effect on the $\Omega _{ccc}$ production; in particular because, in this case, the particle production is five orders of magnitude smaller than the two aforementioned particles. As a consequence, the production of this multi-charmed particle have an impact that is negligible on the condition about the charm quark conservation. In this way, the outcome of changing the hadron radius, in $\Omega _{ccc}$ case, is a larger variation of the total production w.r.t. $D^0$ and $\Lambda _c$ ; it can be quantitative described by an increase of about 60% when the radius is increased of the 50%, and a reduction of about 80% when the radius is decreased by 50%. Furthermore we have found for the $\Xi _{cc}^{++}$ a very similar behaviour like the one shown for the $\Omega _{ccc}$ , we don’t show it in Fig. 4.

Finally assuming that the $\Omega _{ccc}$ production via fragmentation is marginal, due to the very large mass of the baryons, this result suggests that the observations about this multi-charm particle production is very sensitive to the microscopic characteristics of the hadronization process and in particular to the wave function. This is particularly interesting because for charm quark it could be employed a potential model to compute the $\Omega _{ccc}$ wave function using the heavy quark free energy from the lQCD. This would be similar to the $J/\Psi$, but $\Omega _{ccc}$ production, having 3 charms, should be even more sensitive to the wave function. A seminal work in this direction can be found in [61]. Moreover the production of this multi-charmed hadrons can be a clearer probe with respect to other charmed hadrons production, because it is partially disentangled from the effects of charm number conservation constraint.

Fig. 5

$D^0$ (black circles with line), $\Lambda _c$ (blue circles with line), $\Xi _{cc}^{++}$ (green circles with line) and $\Omega _{ccc}$ (orange circles with line) yields from coalescence in central PbPb, KrKr, ArAr and OO collision at midrapidity, compared to SHM model (open squares) [60]

5 Production evolution with collision system: Pb–Pb, Kr–Kr, Ar–Ar, O–O

In this section, we want to examine the effect on the production caused by the specifics of parton distributions in different collision systems. We have employed the model set for PbPb collision system in some other collision system, in particular in KrKr , ArAr and OO . As discussed in Sect. 3 the fireball parameters are summarised in in Table 3 and the charm $dN_c/dy$ scales with the $T_{AA}$ thickness function.

As in the case of PbPb collisions, we start from FONLL $p_T$ distribution that evolves in a QGP medium described by a relativistic Boltzmann approach. The differences in the final $p_T$ distribution are shown in Fig. 1. As expected, in smaller systems, the final transverse momentum charm quark distributions are flatter. The dN/dy obtained by coalescence plus fragmentation for each species, as a function of $A^{1/3}$, are shown in Fig. 5 in comparison with SHM results and summarized in Table 6. As shown, our productions scales accordingly to SHM for the single charmed particle, albeit an overall larger production of $\Lambda _c$ (blue circles with line) as already shown in Fig. 2.

For $\Omega _{ccc}$ (orange circles with line) and $\Xi _{cc}^{++}$ (green circles with line), we evaluate the yields scaling the Wigner function widths assuming the same oscillator frequency of $\Xi _{c}$ and $\Omega _c$ as discussed in Sect. 2 (see Eq. (7)). We observe that our model predictions for the particle yields, have a similar but still different scaling with the decrease of the system size in comparison with SHM.

Notice that for the absolute yields we show a band where the upper limit comes from the assumption of fully thermalized charm quarks while the lower limit comes from the realistic simulation of partial thermalization evaluated through the Boltzmann transport approach. In the realistic case, the $\Xi _{cc}^{++}$ absolute production shown in Fig. 5 is close to SHM values (full square) for all the systems. Instead for the $\Omega _{ccc}$ absolute production we observe a reduction for the realistic case in all systems compared to SHM results; for the fully thermalized case there is an agreement in PbPb , as discussed before and showed in Fig. 3, and an enhancement w.r.t. SHM in smaller systems.

Table 6 $D^0$ , $\Lambda _c$ , $\Xi _{cc}^{++}$ and $\Omega _{ccc}$ hadron dN/dy in OO, ArAr, KrKr and PbPb. Upper values corresponds to thermal charm $p_T$ distribution, lower cases to realistic ones. See text for details

Moreover, going back to the $\Omega _{ccc}$ yield, its absolute value also depends on the assumption for the wave function width (as discussed in Sect. 4, see Fig. 4). An increase of 50% of the $\Omega _{ccc}$ charged radius $\langle r^2\rangle ^{1/2}_{ch}$ can give an increment of about a 60% for the lower limit of the band in Fig. 5. As already mentioned a study of $\Omega _{ccc}$ from lQCD potential can asses this aspect in a quite solid way. However, in Fig. 5 it is clear that the degree of charm thermalization play a major role. We discuss here the full thermal case for the sake of a more direct comparison to SHM. Upcoming data on $p_T$ distribution of $D^0$ , $D^+$ should put more stringent constraints on the $p_T$ distribution, but we see from Fig. 5 that $\Omega _{ccc}$ will be quite sensitive to the degree of charm thermalization. Furthermore, as we will discuss later in this Section, the $\Omega _{ccc}$ momentum spectra will be a strong meter of the charm thermalization.

In general the charmed hadrons production depends on the charm quark number ($N_c$) and the system size at the freeze-out, i.e. fireball volume (V). In order to understand how the production of multi-charmed hadrons changes with the system size, we can relate $N_c$ and V to the mass number A. In first approximation, neglecting the difference in the radial flow effect that are not so different from one system to another, the volume is proportional to the mass number $V\propto A$. The charm quark number comes from the perturbative hard processes in the initial stage of the collision, so the scaling of this quantity is expected to be proportional to $N_{coll}$. From Glauber model, in a central collision of two identical nuclei AA, the mean number of collisions scales as $N_{coll} \propto A^{4/3}$, then charm quark number should scales as $N_c\propto A^{4/3}$. From naive considerations, the coalescence mechanism has a production that is proportional to the product of the volume and the densities of the constituent quarks involved in the hadron formation. Therefore for a charmed hadron, this scaling can be expressed as $V\left( \frac{N_c}{V}\right) ^C=N_c\left( \frac{N_c}{V}\right) ^{C-1}$ where C is the number of charm quarks contained by the hadron. Finally, considering the above relation between these quantities and the mass number, the hadron production scaling roughly results in $N_H\propto A^{\frac{C+3}{3}}$. Such a scaling is also the one expected in SHM if canonical suppression is discarded. We now concentrate our focus on the yield dependence as a function of A in the $\Omega _{ccc}$ case, which is particularly sensitive to this scaling because of the presence of three charm quarks. In order to disentangle the effects coming from the distribution function and the ones coming from the system size change, we have performed calculation where we consider fireball size and parameters as in Table 3, but employing a charm momentum distribution with the same $p_T$ dependence of PbPb even in KrKr , ArAr and OO .

In Fig. 6 the $\Omega _{ccc}$ productions are shown, and for clarity’s sake we have scaled all the curves in such a way to obtain that different cases has the same yields when PbPb collisions are considered. In the above figure different cases are shown: the yields obtained with our model in the case of realistic distribution (red-yellow square with line), the expected scaling with A (black dashed line), the SHM production (blue circles with line), and finally what we obtain considering for KrKr , ArAr and OO the charm distribution used in PbPb in a fireball consistent with the reduced dimension, as said before (green open squares with line). The last case has been realized aiming to see an hypothetical effect of the increasingly non-equilibrium of the charm quark distribution with the decreasing of the system size. In the inset of Fig. 6 we show the cube of the normalized charm distribution in all the systems. One can easily realize that the integration in $p_T$ of this quantity provides a rough estimate of the effect to the $\Omega _{ccc}$ yield due to the difference in momentum dependence. For example going from PbPb to ArAr there is a reduction of the production by a factor $\sim 1.7$. Hence, in a coalescence approach, one should see a similar reduction of the $\Omega _{ccc}$ yield due only to the change of the $p_T$ charm distribution function between PbPb and other collision systems.

Therefore the results shown in Fig. 6 give the indication that the simple scaling $\propto A^{\frac{C+3}{3}}$ lacked information about the $p_T$ distribution impact on the final total production. On the other hand, this scaling is compatible with the production obtained when the charm distribution is maintained fixed, has can be seen comparing black dotted line and green solid line.

Fig. 6

$\Omega _{ccc}$ production in different collision systems considering: coalescence with realistic charm distributions (red-yellow squares), coalescence with fixed charm quark distributions (green open squares), the expected scaling with $N_c$ and V (blasck dashed line) compared with SHM model results (blue open circle) [60]. [inset] Cube of charm quark distribution in different collision systems PbPb (blue solid line), KrKr (red solid line), ArAr (green solid line) and OO (gold solid line)

It is relevant to underline that the SHM model uses a factor that consider the canonical suppression, this factor is close to the unity for single charmed hadrons in PbPb and has a decreasing behaviour going to systems with smaller A, and it becomes larger increasing the charm quark content C of the hadron [60]. In our model this suppression factor is not present; the impact of taking into account this factor in the multi-charmed hadrons yield turn out to be an underestimation when the system size decreases.

Fig. 7

$\Omega _{ccc}$ spectra showed in different collision system, PbPb (blue lines), KrKr (red lines), ArAr (green lines) and OO (yellow lines). Two cases are shown, results with realistic distributions (solid lines) and thermal distributions (dashed lines)

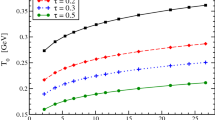
In Fig. 7 the $\Omega _{ccc}$ momentum distribution are shown in different collision systems in both realistic (solid lines) and thermal (dashed lines) cases. In Sect. 4 was pointed out that the shape of thermal distribution falls down quickly w.r.t. the realistic distributions, as one should expect such a behaviour is also reflected in the $\Omega _{ccc}$ spectra. Moreover, as shown for the $\Omega _{ccc}$ yield in PbPb collisions in Fig. 3, the production results enhanced in the thermal case. This behaviour should be expected looking at the parton distribution in Fig. 1, considering that the hadron $p_T$ is the sum of quark momenta and the fact that thermal distribution is higher than the dynamical one below to $\sim 2 \;\mathrm GeV$. Hence at $p_T$ above 6 GeV the slope of the $\Omega _{ccc}$ spectra are very different and at high momentum the tail of realistic distributions result in a $p_T$ spectrum various order of magnitude larger w.r.t. the thermal case.

Fig. 8

Ratios of $\Omega _{ccc}$ production normalized with a factor $N_c\left( N_c/V\right) ^{2}$, showed in different collision system, PbPb, KrKr, ArAr and OO. [inset] Ratio of normalized charm quark distribution in different collision systems

Finally, in Fig. 8 the ratios between the $\Omega _{ccc}$ transverse momentum spectra are shown in different collision systems. Each spectrum is normalized with a factor $N_c\!\left( N_c/V\right) ^{2}$ in order to have ratios that are comparable along the different system size and quantify the variation of our approach w.r.t. the standard scaling expected in a SHM approach, or in a naive coalescence approach based on fully thermalized charm distribution function. The low-$p_T$ part, up to $4 \text{ GeV }$, of the PbPb ratios shows an increasing trend that reflects the presence of a stronger flow with respect to KrKr , ArAr and OO ; on the other hand the decreasing ratio at high $p_T$ is determined by the large non-thermalization in KrKr, ArAr and OO distributions. Notice that the PbPb /OO ratio (orange line) with the normalization $N_c\!\left( N_c/V\right) ^{2}$ has a value that is approximately 2 at low $p_T$. This effect is related to the non-thermalization in OO , as pointed out in the discussion about Fig. 6, where the yields obtained in smaller systems with realistic distributions manifest a reduction with respect to the $A^{(C+3)/3}$ scaling. In the inset of Fig. 8, we show the corresponding ratios of charm distribution normalized to $N_c$ in various systems, with the same colours as for the $\Omega _{ccc}$ ratios. We can observe that the $\Omega _{ccc}$ ratios reflect the charm ratios; the role of the hadronization is to stretch in momentum the ratio obtained at the charm quark level, so that the behaviour at charm very low $p_T$ ($\sim \!1\mathrm GeV$) is transposed to the $\Omega _{ccc}$ intermediate momentum region, i.e. 4–5 GeV. The ratios at charm quark level reflect the non-equilibrium effect in the evolution through the QGP as discussed for Fig. 1. This behaviour, given the particularity of the $\Omega _{ccc}$, is much evident and sensitive with respect to similar ratios evaluated for $D^0$ and $\Lambda _c$, as shown in Fig. 9 where the PbPb and OO collision systems are considered.

For $\Omega _{ccc}$, we can see that, even rescaling the ratio for the natural factor $N_c(N_c/V)^{2}$ expected in the case of full thermalization, the ratio is much larger than unity mainly due to the higher degree of thermalization in PbPb w.r.t. OO; while $\Lambda _c$ shows deviations of only $\pm 20\%$ around one. Furthermore in the $D^0$ and $\Lambda _c$ ratio considered there is a contamination due to the light quarks presence, and also a strong effect coming from the fragmentation contribution. Hence the $\Omega _{ccc}$ momentum distributions should unveil direct information about the charm quark distribution with a larger sensitivity w.r.t. $D^0$ or $\Lambda _c$ .

Fig. 9

Ratios of $\Omega _{ccc}$, $D^0$ , $\Lambda _c$ and charm quarks production, normalized with $N_c(N_c/V)^{C-1}$ (C= charm number of the hadron) and V factors, showed in different collision system PbPb and OO

Summarizing, the consequence of the spectrum flattening going from larger to smaller systems (i.e. toward charm in non-equilibrium) is observed as a reduction of the $\Omega _{ccc}$ ratio at higher transverse momentum changing the collision system, as shown in Fig. 8; producing, on the other hand, an enhancement in the very low momentum region. This result suggests that a systematic study of the multi-charm production can provide information about the charm distribution in momentum region hardly accessible trough observables derived from other charmed hadrons, i.e. $D^0$ and $\Lambda _c$ ; providing in this way a further observable able to infer charm quark interaction in the hot QCD matter.

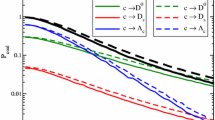
Finally to further point out the much larger sensitivity of the $\Omega _{ccc}$ production on the system size of the collision and its large sensitivity on the $p_T$ charm distribution, we show in Fig. 10 the comparison between $\Lambda _c/D^0$ (left panel) and $\Omega _{ccc}/D^0$ (right panel) ratios as a function of transverse momentum, for central collision at midrapidity. Notice that in the right panel the ratios, shown by solid lines, have been multiplied for a factor $10^5$ just to set the same scale of the left panel. Different symbols refer to different collision systems: PbPb (blue square), KrKr (red circles), ArAr (green triangles) and OO (yellow pentagon). We observe that the $\Omega _{ccc}/D^0$ ratio is an observable much more sensitive to the system size w.r.t. the single charmed ratio, spanning over about two order of magnitude going from PbPb to OO . This very large difference comes from two contributions. One is, as described in Sect. 5, the natural scaling of $\Omega _{ccc}$ with charm number and density that in case of full-equilibrium would follow $N_c^3/V^2$ scaling, while $D^0$ scales with $N_c$. However, this would give only about one order of magnitude difference between PbPb and OO . The remaining difference is yet about an order of magnitude. In fact, the grey lines in Fig. 10 are the results for the $\Omega _{ccc}/D^0$ after the $\Omega _{ccc}$ has been rescaled by $N_c(N_c/V)^2$ and $D^0$ by $N_c$. It is evident that the $\Omega _{ccc}/D^0$ is still quite different Therefore the $\Omega _{ccc}/D^0$ ratio across the different size system allows to explore hadronization under quite different conditions that in a realistic coalescence model are expected to induce very different values of $\Omega _{ccc}/D^0$ vs $p_T$, as we can see in Fig. 10. This evolution is really enhanced w.r.t. that in $\Lambda _c/D^0$ shown in the left panel. In particular, steeper charm distribution (closer to equilibrium w.r.t. bulk matter), present in larger system like PbPb produce a $\Omega _{ccc}/D^0$ ratio that has a quite more evident peak w.r.t. OO .

Fig. 10

$\Lambda _c$ /$D^0$ (left) and $\Omega _{ccc}$/$D^0$ (right) ratios as a function of $p_T$ , at midrapidity for central collision, showed in different collision system PbPb, KrKr, ArAr and OO. In the right panel the coloured solid line are $\Omega _{ccc}$/$D^0$ ratio multiplied by a factor $10^5$ for a more clear comparison. The grey lines are the $\Omega _{ccc}$/$D^0$ ratio multiplied only by the re-scaling factor $N_c(N_c/V)^2/N_c$

6 Conclusions

In this paper, we have studied the single-charmed and multi-charmed hadron production by using an hadronization model by coalescence manly focusing on $\Xi _{cc}^{++}$ and $\Omega _{ccc}$ that are new heavy baryons likely to be detected in the next ALICE3 experiment at LHC. In particular, we have discussed the HF production in different collision systems, PbPb, KrKr, ArAr and OO. We have considered in our study both realistic (”dynamical”) charm distribution function coming from the evolution in QGP described by Boltzmann Transport Equation and thermal distribution with flow coming from the assumption of a thermalized source for charm quarks in order to have a better comparison to SHM. For $D^0$ , $D^+$, $D^*$ and $\Lambda _c$ we have found a scaling with A of the colliding system that is quite similar to SHM, but with absolute yield of $\Lambda _c$ , $\Xi _{c}$ and $\Omega _c$ that are quite larger for the coalescence model. A result for PbPb that is in line with what found in pp collisions [50]. We have found that the charmed hadron yields in PbPb show a mass ordering with an enhancement for single-charmed baryons. For D mesons and $\Lambda _c$ our model has compatible results with SHM in the case where the latter includes an enhanced set for baryons resonances. We predict yields for multi-charmed hadrons that is of the order of $10^{-2}\!-\!10^{-3}$ for doubled charmed hadrons, while is nearly two order of magnitude smaller in the case of $\Omega _{ccc}$ . When we consider thermal distribution form charm quark we obtain a production that is comparable with the one from SHM. Moreover, we have studied the production of all hadrons changing the system size. Going from large to smaller collision systems we obtain roughly a decrease of the production of single-charmed and multi-charmed hadrons scaling with volume and number of charm as $N_c(N_c/V)^{C-1}$. But, focusing on the $\Omega _{ccc}$ , this study shows a breaking of this simple scaling due to the change in shape of the charm quark distribution when a realistic simulation of the QGP medium is performed; suggesting that, looking at the yields, the $\Omega _{ccc}$ production is an observable sensitive to the non-equilibrium features of charm quarks. We have seen that the ratio of $\Omega _{ccc}$ $p_T$ -spectra between different system size, in particular, can provide a solid signature of a lack of thermalization when going to smaller system like O–O. Furthermore, in PbPb we have seen a strong sensitivity of $\Omega _{ccc}$ yield to its mean square radius, at variance with D mesons and $\Lambda _c$ whose yields are mainly constrained by charm conservation. This means that the production of $\Omega _{ccc}$ can supply a tool to infer its wave function.