Production of $Z_{cs}$ in B and $B_s$ decays

Abstract

In the present work, we investigate the productions of $Z_{cs}^+$ in $B^+$ and $B_s^0$ decays, where $Z_{cs}^+$ is assigned as a $D_s^{+} {\bar{D}}^{*0} + D_s^{*+}{\bar{D}}^0$ molecular state. By using an effective Lagrangian approach, we evaluate the branching fractions of $B^0_s\rightarrow K^- Z^+_{cs}$ and $B^+\rightarrow \phi Z^{+}_{cs}$ via the triangle loop mechanism. The estimated branching fractions of $B^0_s\rightarrow K^- Z^+_{cs}$ and $B^+\rightarrow \phi Z^{+}_{cs}$ are of the order of $10^{-4}$ and $10^{-5}$, respectively. The ratio of these two branching fractions is estimated to be about 4, which indicate that the $B_s^0 \rightarrow K^\pm Z^\mp _{cs} \rightarrow K^+ K^- J/\psi$ may be a better process of searching $Z_{cs}$ and accessible for further experimental measurements of the Belle II and LHCb Collaborations.

1 Introduction

The conventional quark model classified the simplest hadrons as the mesons ($q{\bar{q}}$) and baryons (qqq), which has achieved great success in the past forty years. However, in recent two decades, a large number of new hadron states beyond the conventional quark model have been observed with the development of experimental techniques and the accumulations of the data samples, which becomes a great challenge to the conventional quark model (see Refs. [1,2,3,4,5,6,7,8,9,10,11] for recent reviews). Among the new hadron states, the charmoniumlike states have been developed into a large family since the observation of X(3872) in 2003 [12].

It is interesting to notice that there is a kind of charmoniumlike states which are close to the thresholds of a pair of charmed mesons. Such a particular phenomenon has attracted theorists great interests. The typical examples of such kind of charmonium-like states are X(3872)/$Z_c (3900)$ and $Z_c (4020)$, which are near the thresholds of $D{\bar{D}}^*$ and $D^* {\bar{D}}^*$, respectively. Thus, these states have been interpreted as molecular states composed of $D^*{\bar{D}}+c.c$ [13,14,15,16,17,18,19,20,21,22,23,24,25], $D^*{\bar{D}}^*$ [18, 24,25,26,27], respectively. By using the one-boson-exchange model (OBE), the authors in Refs. [14, 19] considered that X(3872) could be accommodated as a molecular state of $D {\bar{D}}^*+ c.c$ with isospin zero, while $Z_c (3900)$ and $Z_c (4020)$ were regarded as $D{\bar{D}}^*+c.c$ and $D^* {\bar{D}}^*$ molecular states with isospin one [18, 26], respectively. The calculations from QCD sum rule (QCDSR) by utilizing a $D^*{\bar{D}}^*$ current also support the $D^*{\bar{D}}^*$ molecular picture for $Z_c (4020)$ [27]. The production and decay properties of X(3872) and $Z_c (3900)$/$Z_c (4020)$ were investigated by using an effective Lagrangian approach and the results supported the molecular interpretations [22,23,24,25]. Moreover, considering the masses and decay properties of these charmoniumlike states, one can find the most likely quark components of these states are $c{\bar{c}}q{\bar{q}}$, which indicates that all these charmoniumlike states could be regarded as tetraquark candidates [28,29,30,31,32,33,34]. Besides the QCD exotic interpretations, the structures corresponding to $Z_c (3900)$ and $Z_c(4020)$ could be reproduced through initial-single-pion-emission mechanism (ISPE) [35,36,37,38,39,40].

After the observations of $Z_c$ states, the existence of their SU(3) flavor partner, $Z_{cs}$, has been investigated from both theoretical and experimental sides. In Refs. [41, 42], some compact tetraquark states with hidden charm and open strange were predicted, and the lowest one with $J^P=1^+$ was predicted to be around 4 GeV. Similarly, such a state was also predicted in molecular scenario [43, 44] and by ISPE mechanism [45]. On the experimental side, the Belle [46, 47] and BESIII [48] Collaborations attempted to search $Z_{cs}$ states in the process $e^+e^- \rightarrow K^+ K^- J/\psi$ successively. Unfortunately, no obvious structures were observed in the $KJ/\psi$ invariant mass distributions due to the low statistics of the data sample.

Table 1 The resonance parameters of the newly reported $Z_{cs}$ states from different collaborations [49, 50]

Recently, the experimental breakthrough of observing hidden charm and open strange states was made by the BESIII and LHCb Collaborations [49, 50]. The BESIII Collaboration reported a structure in the $K^+$ recoil-mass spectrum of the process $e^+ e^-\rightarrow K^+ (D^-_s D^{*0}+D^{*-}_s D^0)$ [49], which is named $Z^-_{cs}(3985)$. Later, the LHCb Collaboration observed $Z^+_{cs}(4000)$ in the $J/\psi K$ invariant mass spectrum of the process $B^+\rightarrow J/\psi \phi K^+$ and the $J^P$ quantum numbers were determined to be $1^+$ [50]. The observed resonance parameters from different collaborations are listed in Table 1. One can find the observed masses from two collaborations are very close, but the widths are different. In Ref. [51], the authors assigned $Z_{cs}(3985)$ and $Z_{cs}(4000)$ as ${\bar{D}}_s D^*/{\bar{D}}^*_s D$ molecular states with $J^P=1^-$ and $1^+$, respectively. However, It should be noticed that if one consider $Z_{cs}(3985)$ as the SU(3) flavor partner of $Z_c(3900)$, there should be another state corresponding to $Z_c(4020)$, which is around 4.1 GeV. Similar to the open charm observations of $Z_c(3900)$ and $Z_c(4020)$, only $Z_{cs}(3985)$ is expected to appear in the process $e^+ e^-\rightarrow K^+ (D^-_s D^{*0}+D^{*-}_s D^0)$, which is consistent with the BES III measurements [49]. However, in the process $B^+\rightarrow J/\psi \phi K^+$, the LHCb Collaboration reported another broad structure $Z_{cs}(4220)$, which is different from the expected one near 4.1 GeV. Furthermore, it is worthwhile to mention that the measured $J/\psi K$ invariant mass distributions near 4.1 GeV can not be well described with the broad $Z_{cs}(4000)$ and $Z_{cs}(4220)$. Further experimental analysis of the LHCb data with $Z_{cs}(3985)$ and a state near 4.1 GeV may reduce the discrepancy of width from BESIII and LHCb Collaboration. Such possibility has also been proposed in Ref. [53]. In the present work, we assume that $Z_{cs}(4000)$ observed by LHCb Collaboration should be the same states as $Z_{cs}(3985)$, and hereafter we use $Z_{cs}$ refer to this charmoniumlike state with strangeness.

Similar to $Z_c (3900)/Z_c (4020)$, the observations of $Z_{cs}$ state has been stimulated theorists to propose various pictures and explanations to interpret its properties. Similar to $Z_c (3900)/Z_c (4020)$ close to $D^{(*)}{\bar{D}}^{*}$, the observed mass of $Z_{cs}$ also locates near the threshold of ${\bar{D}}_s D^*/{\bar{D}}^*_s D$, thus, it is natural to investigate $Z_{cs}$ in the ${\bar{D}}_s D^*/{\bar{D}}^*_s D$ molecular frame [52,53,54,55,56,57,58,59,60,61,62,63]. However, the authors in Ref. [62] found that $Z_{cs}$ was not a pure ${\bar{D}}_s D^*/{\bar{D}}^*_s D$ molecular state and the ${\bar{D}}_s D^*/{\bar{D}}^*_s D$ resonance assignment was also excluded in Ref. [63] by using the OBE model. In the tetraquark scenario, the estimation from QCDSR [61, 64, 65] and quark model [66,67,68] supported $Z_{cs}$ as a $c{\bar{c}} s{\bar{u}}$ tetraquark state with $J^P=1^+$. In addition to molecular and tetraquark interpretations, reflection mechanism [69] and threshold effect [70] were also proposed to depict the structure corresponding to $Z_{cs}$. In Refs. [60, 71], we investigated the productions and hidden charm decays of $Z_{cs}$ with an effective Lagrangian approach. By studying the production of $Z_{cs}$ in kaon induced reactions [71], we find the cross section for $Kp\rightarrow Z_{cs}P_c$ could reach up to 10 nb. In the ${\bar{D}}_s D^*/{\bar{D}}^*_s D$ molecular frame, the dominating decay mode of $Z_{cs}$ is found to be the open charm channel [60]. Under the heavy quark spin symmetry, another higher $Z^\prime _{cs}$ state coupling to $D^{*-}_s D^{*0}+c.c.$ should exist [72, 73]. The authors in Ref. [72] suggest to search the $Z^\prime _{cs}$ in ${\bar{B}}^0_s\rightarrow J/\psi K^+ K^-$ at LHCb and in $e^+ e^-$ collision with the center of mass energy of 4.648 GeV.

Besides the resonance parameters, the LHCb Collaboration also reported the fit fraction of $Z_{cs}$ in the process $B^+\rightarrow J/\psi \phi K^+$ [50], which is,

$$\begin{aligned} \frac{{\mathcal {B}}[B^+\rightarrow Z^{+}_{cs}\phi \rightarrow J/\psi \phi K^+]}{{\mathcal {B}}[B^+\rightarrow J/\psi \phi K^+]} =(9.4\pm 2.1 \pm 3.4)\%. \end{aligned}$$

(1)

Considering the PDG average of the branching ratio of $B^+ \rightarrow J/\psi \phi K^+$ to be $(5.0 \pm 0.4) \times 10^{-5}$, one can conclude that the branching ratio of the cascade process is,

$$\begin{aligned} {\mathcal {B}}[B^+ \rightarrow \phi Z_{cs}^+ \rightarrow \phi (J/\psi K^+)]=(4.6\pm 2.0)\times 10^{-6}. \end{aligned}$$

(2)

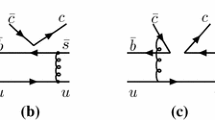
How to understand the branching ratio of the cascade decay process is crucial to reveal the nature of $Z_{cs}$ state. For the first step, we can analyze the production process in the quark level. As shown in Fig. 1, the ${\bar{b}}$ quark in the $B^+$ meson decays into ${\bar{c}}$ quark by emitting a $W^+$ boson and then the $W^+$ boson decays into a $c{\bar{s}}$ pair, i.e, the subprocess of the weak decay is ${\bar{b}} \rightarrow {\bar{c}} c{\bar{s}}$. These quarks, together with the u quark in the B meson, transit into $\phi$ meson and $Z_{cs}$ molecular state by creating a $s{\bar{s}}$ pair from the vacuum. Here, we use $H_W$ and $H_T$ to denote the weak interaction and transition processes, respectively, then the production of $Z_{cs}$ from $B^+$ decay can be expressed as,

$$\begin{aligned} \langle Z_{cs}^+ \phi \left| H \right| B^+\rangle = \sum _{B_1B_2} \langle Z_{cs}^+ \phi |H_T| B_1 B_2 \rangle \langle B_1 B_2 |H_W | B^+\rangle . \nonumber \\ \end{aligned}$$

(3)

In principle, one should consider all the possible loops which can connect the initial $B^+$ and final $Z_{cs}^+ \phi$. By checking the decay processes of $B^+$, we notice that the branching ratio of $B^+\rightarrow D^{(*)+}_s {\bar{D}}^{(*)0}$ are of the order of $10^{-3}$ [74]. In particular, the branching ratios are $(9.0\pm 0.9)\times 10^{-3}$, $(7.6\pm 1.6)\times 10^{-3}$, $(8.2\pm 1.7)\times 10^{-3}$, and $(1.71\pm 0.24)\%$ for $D^{+}_s {\bar{D}}^0$, $D^{*+}_s {\bar{D}}^0$, $D^{+}_s {\bar{D}}^{*0}$, and $D_s^{*+} {\bar{D}}^{*0}$ channels, respectively [74]. The charmed meson and charmed strange meson can transit into $\phi Z_{cs}^+$ by exchanging a proper charmed strange meson. Such a production mechanism will be checked in the present work. Moreover, it is worth mentioning that the branching ratio of $B_s^0\rightarrow D_{s}^{(*) +} {D}_s^{(*)-}$ are also sizable, the charmed strange meson pair can transit into $Z_{cs}^+ K^-$ by exchanging a proper charmed meson. Then the production of $Z_{cs}^+$ from $B_s^0$ decay will also be considered in the present work.

This work is organized as follows. After introduction, we present the model used in the present estimations of the $Z_{cs}$ productions. The numerical results and discussions are presented in Sects. 3, and 4 is devoted to a short summary.

Fig. 1

The production mechanism of $Z_{cs}$ in the B meson decay

Fig. 2

Diagrams contributing to $B^+\rightarrow \phi Z^{+}_{cs}$

Fig. 3

Diagrams contributing to $B^0_s\rightarrow K^- Z^+_{cs}$

2 Theoretical framework

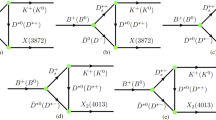
In the $D_s^+ {\bar{D}}^{*0} + D_s^{*+} {\bar{D}}^0$ molecular scenario, $Z_{cs}^+$ can produced from $B^+$ decay via the following way. The initial $B^+$ meson couples to a charmed and a charm-strange mesons, by exchanging a proper charm-strange meson, such as $D_s^+$ or $D_s^{*+}$, the charmed and charm-strange mesons transit into $\phi Z_{cs}^+$ in the final state. All the possible diagrams considered in the present work are listed in Fig. 2. Similarly, the $B_s^0$ meson can couple to $Z_{cs}^+ K^-$ in the final states by the meson loops as shown in Fig. 3.

2.1 Effective Lagrangian

In the present work, the diagrams in Figs.  2 and 3 are evaluated at the hadronic level, where the interactions between hadrons are described by effective Lagrangians. Here, the $Z_{cs}^+$ is assumed to be a S-wave shallow bound state of $D_s^+ {\bar{D}}^{*0} + D_s^{*+} {\bar{D}}^0$ with $I(J^P)=\frac{1}{2}(1^+)$, which is,

$$\begin{aligned} |Z^+_{cs}\rangle= & {} \frac{1}{\sqrt{2}} \left( |D^{*+}_s {\bar{D}}^0\rangle +|D^+_s {\bar{D}}^{*0}\rangle \right) . \end{aligned}$$

(4)

Notice that different from Ref. [51], we considered $Z_{cs}(3985)$ and $Z_{cs}(4000)$ as the same state, which is the partner of $Z_c(3900)$ and corresponding to $|{\bar{D}}_s^*D/{\bar{D}}_sD^*, +\rangle$ in Ref. [51].

The effective coupling of $Z^+_{cs}$ to its components can be written in terms of the following effective Lagrangian,

$$\begin{aligned} {{{\mathcal {L}}}}_{Z_{cs}}= & {} \frac{g_{Z_{cs}}}{\sqrt{2}}Z^{\dagger \mu }_{cs}\left( D^{*}_{s\mu } {\bar{D}}+ D_s {\bar{D}}^{*}_\mu \right) , \end{aligned}$$

(5)

where $g_{Z_{cs}}$ is the effective coupling constant.

As for the $BD^{(*)}_s D^{(*)}$ and $B_{s}D^{(*)}_s D^{(*)}_s$ couplings, they could be estimated by the naive factorization approach. The parametrized hadronic matrix elements can be obtained by applying the effective Hamiltonian at the quark level to the hadron states, which are [75, 76],

$$\begin{aligned}&\langle 0|J_\mu |P(p_1)\rangle = -if_p p_{1\mu },\nonumber \\&\langle 0|J_\mu |V(p_1,\epsilon )\rangle =f_V \epsilon _\mu m_V,\nonumber \\&\langle P(p_2)|J_\mu |B_{(s)}(p)\rangle \nonumber \\&\quad =\Big [P_\mu -\frac{m^2_{B_{(s)}}-m^2_P}{q^2}q_\mu \Big ]F_1(q^2)\nonumber \\&\qquad +\frac{m^2_{B_{(s)}}-m^2_P}{q^2}q_\mu F_0(q^2),\nonumber \\&\langle V(p_2,\epsilon )|J_\mu |B_{(s)}(p)\rangle \nonumber \\&\quad =\frac{i\epsilon ^\nu }{m_{B_{(s)}}+m_V}\Big \{i\varepsilon _{\mu \nu \alpha \beta }P^\alpha q^\beta A_V(q^2)\nonumber \\&\qquad +(m_{B_{(s)}}+m_V)^2 g_{\mu \nu }A_1(q^2) -P_\mu P_\nu A_2(q^2)\nonumber \\&\qquad -2m_V(m_{B_{(s)}}+m_V)\frac{P_\nu q_\mu }{q^2}[A_3(q^2)-A_0(q^2)]\Big \}, \end{aligned}$$

(6)

where P and V refer to the pseudoscalar and vector charmed and charm-strange mesons, respectively. p is the momentum of the initial $B_{(s)}$ meson, while $p_1$ and $p_2$ are the momenta of the relevant charmed and charmed strange mesons. The momenta P and q are the combinations of p and $p_2$, which are $P_\mu =(p+p_2)_\mu$ and $q_\mu =(p-p_2)_\mu$, while the current $J_\mu$ is defined as $J_\mu ={\bar{q}}_1 \gamma _\mu (1-\gamma _5)q_2$. The form factor $A_3(q^2)$ is the linear combination of $A_1(q^2)$ and $A_2(q^2)$, which is [75],

$$\begin{aligned} A_3(q^2)=\frac{m_{B_{(s)}}+m_V}{2m_V}A_1(q^2)-\frac{m_{B_{(s)}}-m_V}{2m_V}A_2(q^2). \end{aligned}$$

(7)

With Eq. (6), the amplitudes of $B^0_s\rightarrow D^{(*)+}_s D^{(*)-}_s$ and $B^+ \rightarrow D^{(*)+}_s {\bar{D}}^{(*)0}$ can be constructed as

$$\begin{aligned} {\mathcal {M}}(B^0_s\rightarrow D^{-}_s D^{+}_s)\equiv & {} {\mathcal {A}}^{B_s\rightarrow {\bar{D}}_s D_s}(p_1,p_2),\nonumber \\ {\mathcal {M}}(B^0_s\rightarrow D^{*-}_s D^{+}_s)\equiv & {} {\mathcal {A}}^{B_s\rightarrow {\bar{D}}^*_s D_s}_\nu (p_1,p_2)\epsilon ^\nu (p_1),\nonumber \\ {\mathcal {M}}(B^0_s\rightarrow D^{*-}_s D^{*+}_s)\equiv & {} {\mathcal {A}}^{B_s\rightarrow {\bar{D}}^*_s D^*_s}_{\mu \nu }(p_1,p_2)\epsilon ^\mu (p_1)\epsilon ^\nu (p_2),\nonumber \\ {\mathcal {M}}(B^+ \rightarrow D^{+}_s {\bar{D}}^0)\equiv & {} {\mathcal {A}}^{B\rightarrow D_s {\bar{D}}}(p_1,p_2),\nonumber \\ {\mathcal {M}}(B^+\rightarrow D^{*+}_s {\bar{D}}^0)\equiv & {} {\mathcal {A}}^{B\rightarrow D^*_s {\bar{D}}}_\mu (p_1,p_2)\epsilon ^\mu (p_1),\nonumber \\ {\mathcal {M}}(B^+\rightarrow D^{+}_s {\bar{D}}^{*0})\equiv & {} {\mathcal {A}}^{B\rightarrow D_s {\bar{D}}^*}_\nu (p_1,p_2)\epsilon ^\nu (p_2),\nonumber \\ {\mathcal {M}}(B^+\rightarrow D^{*+}_s {\bar{D}}^{*0})\equiv & {} {\mathcal {A}}^{B\rightarrow D^*_s {\bar{D}}^*}_{\mu \nu }(p_1,p_2)\epsilon ^\mu (p_1)\epsilon ^\nu (p_2),\qquad \end{aligned}$$

(8)

where the expressions of ${\mathcal {A}}(p_1,p_2)$, ${\mathcal {A}}_\nu (p_1,p_2)$ and ${\mathcal {A}}_{\mu \nu }(p_1,p_2)$ are collected in Appendix. A for brevity.

The effective Lagrangians relevant to the light vector and pseudoscalar mesons can be constructed based on the heavy quark limit and chiral symmetry [77,78,79], which are used to describe the interactions of $D^{(*)}_s D^{(*)}K$ and $D^{(*)}_s D^{(*)}_s \phi$ in the present work, which are,

$$\begin{aligned} {{{\mathcal {L}}}}= & {} -ig_{D^{*}D {\mathcal P}}\left( D^{\dag }_i \partial _\mu {\mathcal P}_{ij} D_j^{*\mu }-D_i^{*\mu \dagger } \partial _\mu {\mathcal P}_{ij} D_j\right) \nonumber \\&+\frac{1}{2}g_{D^*D^*{\mathcal P}}\varepsilon _{\mu \nu \alpha \beta }D_i^{*\mu \dag }\partial ^\nu {\mathcal P}_{ij} {\overset{ \leftrightarrow }{\partial }}{\!^{\alpha }} D_j^{*\beta } \nonumber \\&- ig_{{D}{D}{\mathcal {V}}} {D}_i^\dagger {{\mathop {\partial }\limits ^{\leftrightarrow }}}{\!_\mu } {D}^j({\mathcal {V}}^\mu )^i_j \nonumber \\&-2f_{{D}^*{D}{\mathcal {V}}} \epsilon _{\mu \nu \alpha \beta } (\partial ^\mu {\mathcal {V}}^\nu )^i_j ({D}_i^\dagger {{\mathop {\partial }\limits ^{\leftrightarrow }}}{\!^\alpha } {D}^{*\beta j}-{D}_i^{*\beta \dagger }{{\mathop {\partial }\limits ^{\leftrightarrow }}}{\!^\alpha } {D}^j) \nonumber \\&+ ig_{{D}^*{D}^*{\mathcal {V}}} {D}^{*\nu \dagger }_i {{\mathop {\partial }\limits ^{\leftrightarrow }}}{\!_\mu } {D}^{*j}_\nu ({\mathcal {V}}^\mu )^i_j \nonumber \\&+4if_{{D}^*{D}^*{\mathcal {V}}} {D}^{*\dagger }_{i\mu }(\partial ^\mu {\mathcal {V}}^\nu -\partial ^\nu {\mathcal {V}}^\mu )^i_j {D}^{*j}_\nu +\mathrm{H.c.} , \end{aligned}$$

(9)

where the ${D}^{(*)\dagger }=({\bar{D}}^{(*)0},D^{(*)-},D^{(*)-}_s)$ is the charmed meson triplet, while $\mathcal P$ and ${\mathcal V}$ refer to the pseudoscalar and vector meson nonets, respectively, and their concrete forms are,

$$\begin{aligned} {\mathcal {P}}= & {} \left( \begin{array}{ccc} \frac{\pi ^{0}}{\sqrt{2}}+\alpha \eta +\beta \eta ^\prime &{}\pi ^{+} &{}K^{+}\\ \pi ^{-} &{}-\frac{\pi ^{0}}{\sqrt{2}}+\alpha \eta +\beta \eta ^\prime &{}K^{0}\\ K^{-} &{}{{\bar{K}}}^{0} &{}\gamma \eta +\delta \eta ^\prime \end{array}\right) ,\nonumber \\ {\mathcal {V}}= & {} \left( \begin{array}{ccc}\frac{\rho ^0}{\sqrt{2}}+\frac{\omega }{\sqrt{2}}&{}\rho ^+ &{} K^{*+} \\ \rho ^- &{} -\frac{\rho ^0}{\sqrt{2}} + \frac{\omega }{\sqrt{2}} &{} K^{*0} \\ K^{*-}&{} {{{\bar{K}}}}^{*0} &{} \phi \\ \end{array}\right) , \end{aligned}$$

(10)

where the parameters related to the mixing angle are defined as

$$\begin{aligned} \alpha= & {} \frac{\cos \theta -\sqrt{2}\sin \theta }{\sqrt{6}},\quad \beta =\frac{\sin \theta +\sqrt{2}\cos \theta }{\sqrt{6}}, \nonumber \\ \gamma= & {} \frac{-2\cos \theta -\sqrt{2}\sin \theta }{\sqrt{6}},\quad \delta =\frac{-2\sin \theta +\sqrt{2}\cos \theta }{\sqrt{6}}, \end{aligned}$$

(11)

with $\alpha$ and $\beta$ are parameters related to the mixing angle $\theta$, which are $-19.1^\circ$ in Refs. [80, 81]. It is worthwhile to mention that in Ref. [82], the authors fit the experimental data by including the gluonium component in $\eta ^\prime$ and the corresponding mixing angle for $\eta$ meson is $14.34^\circ$.¹

2.2 Decay amplitude

With the above effective Lagrangians, we can obtain the amplitudes for $B^+\rightarrow \phi Z^{+}_{cs}$ corresponding to the diagrams in Fig. 2, which are,

$$\begin{aligned} {\mathcal {M}}_{a}= & {} i^3 \int \frac{d^4 q}{(2\pi )^4}{\mathcal {A}}^{B\rightarrow D_s {\bar{D}}}\Big (p_1,p_2\Big )\nonumber \\&\times \Big (-2f_{D_s D^*_s \phi }\varepsilon _{\mu \nu \alpha \beta }ip^\mu _3 \epsilon ^\nu _{\phi }(-) (-i)(p_1+q)^\alpha \Big )\nonumber \\&\times \Big (\frac{g_{Z_{cs}}}{\sqrt{2}}\epsilon ^{Z_{cs}}_\sigma \Big ) \frac{-g^{\beta \sigma }+q^{\beta } q^{\sigma } /m^2_q}{q^2-m^2_q}{\mathcal {F}}(q^2,m_q^2),\nonumber \\ {\mathcal {M}}_{b}= & {} i^3 \int \frac{d^4 q}{(2\pi )^4}{\mathcal {A}}_\mu ^{B\rightarrow D^*_s {\bar{D}}}\Big (p_1,p_2\Big )\nonumber \\&\times \Big (ig_{D^*_s D^*_s \phi }g^\nu _\tau g_{\theta \nu }(-ip_{1\kappa } -iq_{\kappa })\epsilon ^\kappa _{\phi }\nonumber \\&+4if_{D^*_s D^*_s \phi }g_{\tau \kappa }g_{\theta \nu }i(p^\kappa _3 \epsilon ^\nu _{\phi }-p^\nu _3 \epsilon ^\kappa _{\phi })\Big )\Big (\frac{g_{Z_{cs}}}{\sqrt{2}}\epsilon ^{Z_{cs}}_\sigma \Big )\nonumber \\&\frac{-g^{\mu \tau }+p^{\mu }_1 p^{\tau }_1 /m^2_1}{p^2_1-m^2_1}\frac{-g^{\theta \sigma }+q^{\theta } q^{\sigma } /m^2_q}{q^2-m^2_q}{\mathcal {F}}(q^2,m_q^2),\nonumber \\ {\mathcal {M}}_{c}= & {} i^3 \int \frac{d^4 q}{(2\pi )^4}{\mathcal {A}}_\nu ^{B\rightarrow D_s {\bar{D}}^*}\Big (p_1,p_2\Big )\Big (-ig_{D_s D_s \phi }(-ip_{1\rho }\nonumber \\&-iq_\rho )\epsilon ^\rho _{\phi }\Big )\Big (\frac{g_{Z_{cs}}}{\sqrt{2}}\epsilon ^{Z_{cs}}_\sigma \Big )\frac{-g^{\nu \sigma }+p^{\nu }_2 p^{\sigma }_2 /m^2_2}{p^2_2-m^2_2}{\mathcal {F}}(q^2,m_q^2),\nonumber \\ {\mathcal {M}}_{d}= & {} i^3 \int \frac{d^4 q}{(2\pi )^4}{\mathcal {A}}_{\mu \nu }^{B\rightarrow D^*_s {\bar{D}}^*}\Big (p_1,p_2\Big )\nonumber \\&\times \Big (-2f_{D_s D^*_s \phi }\varepsilon _{\rho \tau \delta \xi }ip^\rho _3 \epsilon ^\tau _{\phi } (-ip^\delta _1-iq^\delta )\Big )\nonumber \\&\times \Big (\frac{g_{Z_{cs}}}{\sqrt{2}}\epsilon ^{Z_{cs}}_\sigma \Big )\frac{-g^{\mu \xi }+p^{\mu }_1 p^{\xi }_1 /m^2_1}{p^2_1-m^2_1}\nonumber \\&\times \frac{-g^{\nu \sigma }+p^{\nu }_2 p^{\sigma }_2 /m^2_2}{p^2_2-m^2_2}{\mathcal {F}}(q^2,m_q^2), \end{aligned}$$

(12)

Similarly, the amplitudes for $B^0_s\rightarrow K^- Z^+_{cs}$ corresponding to diagrams in Fig. 3 are,

$$\begin{aligned} {\mathcal {M}}_{e}= & {} i^3 \int \frac{d^4 q}{(2\pi )^4}{\mathcal {A}}^{B_s\rightarrow D_s {\bar{D}}_s}\Big (p_1,p_2\Big )\Big (-ig_{D_s D^*K}(-)ip_{3\mu }\Big )\nonumber \\&\Big (\frac{g_{Z_{cs}}}{\sqrt{2}}\epsilon ^{Z_{cs}}_\sigma \Big )\frac{-g^{\mu \sigma }+q^{\mu } q^{\sigma } /m^2_q}{q^2-m^2_q}{\mathcal {F}}(q^2,m_q^2),\nonumber \\ {\mathcal {M}}_{f}= & {} i^3 \int \frac{d^4 q}{(2\pi )^4}{\mathcal {A}}^{B_s\rightarrow D^*_s {\bar{D}}_s}_\nu \Big (p_1,p_2\Big )\nonumber \\&\Big (\frac{1}{2}g_{D^*_s D^*K}\varepsilon _{\rho \tau \kappa \xi }ip^\tau _3 (-i) (p_1+q)^\kappa \Big )\nonumber \\&\Big (\frac{g_{Z_{cs}}}{\sqrt{2}}\epsilon ^{Z_{cs}}_\sigma \Big )\frac{-g^{\nu \xi }+p^{\nu }_1 p^{\xi }_1 /m^2_1}{p_1^2-m^2_1}\frac{-g^{\rho \sigma }+q^{\rho } q^{\sigma } /m^2_q}{q^2-m^2_q} {\mathcal {F}}(q^2,m_q^2),\nonumber \\ {\mathcal {M}}_{g}= & {} i^3 \int \frac{d^4 q}{(2\pi )^4}{\mathcal {A}}^{B_s\rightarrow D^*_s {\bar{D}}^*_s}_{\mu \nu }\Big (p_1,p_2\Big )\nonumber \\&\Big (-ig_{D^*_s D K}ip_{3\rho }\Big )\Big (\frac{g_{Z_{cs}}}{\sqrt{2}}\epsilon ^{Z_{cs}}_\sigma \Big )\nonumber \\&\frac{-g^{\mu \rho }+p^{\mu }_1 p^{\rho }_1 /m^2_1}{p_1^2-m^2_1}\frac{-g^{\nu \sigma }+p^{\nu }_2 p^{\sigma }_2 /m^2_2}{p_2^2-m^2_2}{\mathcal {F}}(q^2,m_q^2). \end{aligned}$$

(13)

In the above amplitudes, a form factor in monopole form is usually introduced to represent the off-shell effect of the exchanging charmed or charm-strange mesons, and the form factor also plays the role of avoiding ultraviolet divergences in the integrals. The concrete form of the form factor is [17, 79, 83,84,85] ,

$$\begin{aligned} {\mathcal {F}}(q^2,m^2) =\frac{m^2 -\Lambda ^2}{q^2-\Lambda ^2}, \end{aligned}$$

(14)

where $\Lambda =m+\alpha \Lambda _{QCD}$ with $\Lambda _{QCD}=220$ MeV. Empirically, the model parameter $\alpha$ should be of the order of unity, but its concrete value can not be determined by the first principle methods. In practice, we usually check the rationality of the model parameter by comparing our estimations with the corresponding experimental measurements. It is worthwhile to mention that there are different choices of the form factor with different model parameters. The form factor in the present scheme normalizes to one when $q^2=m^2$, which has been been proved to be effective in various decays processes [17, 60, 79, 83, 84].

3 Numerical results and discussions

3.1 Coupling constants

Considering heavy quark limit and chiral symmetry, the coupling constants relevant to the light vector and pseudoscalar mesons are [77, 79],

$$\begin{aligned} g_{{ D}{ D}V}= & {} g_{{ D}^*{ D}^*V}=\frac{\beta g_V}{\sqrt{2}} , \quad f_{{ D}^*{ D}V}=\frac{ f_{{ D}^*{ D}^*V}}{m_{{ D}^*}}=\frac{\lambda g_V}{\sqrt{2}} , \nonumber \\ g_{{D}^{*} {D} P}= & {} \frac{2 g}{f_{\pi }} \sqrt{m_{{D}} m_{{D}^{*}}}, \quad g_{{D}^{*} {D}^{*} {P}}=\frac{g_{{ D}^{*} { D} { P}}}{\sqrt{m_{{D}} m_{{D}^{*}}}}, \end{aligned}$$

(15)

where the parameter $\beta =0.9$, $g_V = {m_\rho /f_\pi }$ with $f_\pi = 132$ MeV to be the decay constant of pion [77]. P and V denote pseudoscalar and vector mesons, respectively. By matching the form factor obtained from the light cone sum rule and that calculated from lattice QCD, one can obtain the parameter $\lambda = 0.56 \, \mathrm{GeV}^{-1}$ and $g=0.59$ [86].

In general, the form factors in Eq. (6) can be usually estimated in the quark model and known only in spacelike region [75]. To cover the timelike region where the physical decay processes are relevant, some methods are needed, such as the analysis continues. In Refs. [75, 76], the form factors for $B_{(s)} \rightarrow D^{(*)}_{(s)}$ are parametrized in the form,

$$\begin{aligned} F(Q^2)=\frac{F(0)}{1-a\zeta +b\zeta ^2}, \end{aligned}$$

(16)

with $\zeta =Q^2/m^2_{B_s}$, while F(0), a and b are parameters which are collected in Table 2².

Table 2 The values of the parameters F(0), a and b in the form factors of $B\rightarrow D^{(*)}$ [75] and $B_s\rightarrow D^{(*)}_s$ [76]

Table 3 Values of the parameters $\Lambda _1$ and $\Lambda _2$ obtained by fitting the form factor

In order to avoid ultraviolet divergence in the loop integrals and evaluate the loop integrals with Feynman parameterization method, we further parameterize the form factors in the form

$$\begin{aligned} F(Q^2)=F(0)\frac{\Lambda ^2_1}{Q^2-\Lambda ^2_1}\frac{\Lambda ^2_2}{Q^2-\Lambda ^2_2}, \end{aligned}$$

(18)

where the values of $\Lambda _1$ and $\Lambda _2$ are obtained by fitting Eq. (14) with Eq. (18). The obtained values of $\Lambda _1$ and $\Lambda _2$ are listed in Table 3.

In Ref. [60], we investigated the decay properties of $Z^+_{cs}$ via triangle loop mechanism by using an effective Lagrangian approach, the coupling constant $g_{Z_{cs} D_s^*D}$ were determined to be 6.0–6.7, which is weakly dependent on the model parameter. In the following, we take $g_{Z_{cs} D_s^*D}=6.0$ to roughly estimate the branching ratios of $B^+\rightarrow \phi Z^{+}_{cs}$ and $B^0_s\rightarrow K^- Z^+_{cs}$.

Fig. 4

Branching ratios of $B^+\rightarrow \phi Z^{+}_{cs}$ and $B^0_s\rightarrow K^- Z^+_{cs}$ (left panel) and their ratio (right panel) depending on parameter $\alpha$

3.2 Branching ratios

The estimated branching ratio of $B^+ \rightarrow \phi Z_{cs}^+$ depending on the model parameter $\alpha$ are presented in the left panel of Fig. 4. As shown in the figure, the branching ratio of $B^+ \rightarrow \phi Z_{cs}^+$ is $(4.66^{+1.72}_{-1.38})\times 10^{-5}$, where the center value is estimated by taking $\alpha =2$ and the uncertainties result from variation of model parameter $\alpha$ from 1 to 3. In Ref. [60], our estimation indicated that the branching ratio of $Z_{cs}^+ \rightarrow J/\psi K^+$ was $(4.0^{+4.3}_{-2.7})\%$. Considering $Z_{cs}^+$ to be a narrow resonance, one can roughly estimate the branching ratio of the cascade process by the product of the branching ratios of $B^+ \rightarrow \phi Z_{cs}^+$ and $Z_{cs}^+ \rightarrow J/\psi K^+$, which is,

$$\begin{aligned}&{\mathcal {B}}[B^+ \rightarrow \phi Z_{cs}^+ \rightarrow \phi K^+ J/\psi ] =(1.86^{+2.12}_{-1.37})\times 10^{-6}. \end{aligned}$$

(19)

As mentioned in the introduction, the measured branching ratio of the cascade process is $(4.6 \pm 2.0)\times 10^{-6}$, and our estimation in the present work is comparable with the experimental measurement from the LHCb Collaboration [50]. However, it should be noticed that the measured branching ratio was obtained by fitting the experimental data with a broad $Z_{cs}$ state. A reanalysis of the data with a narrow $Z_{cs}$ and an additional new state near 4.1 GeV is expected and the new analysis may further test the present estimations.

Besides the observed channel, we also propose to search $Z_{cs}$ state in the process $B_s^0 \rightarrow J/\psi K^+ K^-$. In the process $B^+\rightarrow J/\psi \phi K^+$, the resonance contributions could come from $J/\psi \phi$, $J/\psi K$, and $\phi K$ invariant mass spectrum. However, in the process $B_s^0 \rightarrow J/\psi K^+ K^-$, the dominant contributions should come from the KK resonances and $J/\psi K$ resonances, i.e., the $Z_{cs}$ states. Thus, on the experimental side, the $B_s^0 \rightarrow J/\psi K^+ K^-$ may be a cleaner process of searching $Z_{cs}$ states. Our estimation of the branching ratio of $B^0_s\rightarrow K^- Z^+_{cs}$ depending on the model parameter is also presented in Fig. 4. The branching ratio is estimated to be $(2.07^{+0.47}_{-0.80})\times 10^{-4}$. Moreover, one can find the $\alpha$ dependences of the branching ratios of two processes are very similar, thus, we can evaluate the ratio of these two branching fractions as,

$$\begin{aligned} R_{B_s/B}= \frac{{\mathcal {B}}[B_s^0 \rightarrow K^- Z_{cs}^+]}{{\mathcal {B}}[B^+ \rightarrow \phi Z_{cs}^+]}=4.17\pm 0.28, \end{aligned}$$

(20)

where the lower and upper limits are corresponding the minimum and maximum values of the present estimations, while the center value is the average of the minimum and maximum values. Considering that the width of $Z_{cs}(3985)$ is very small, thus, one can roughly estimate the branching fractions of the cascade processes $B_{s}^0 \rightarrow K^\pm Z_{cs}^\mp \rightarrow J/\psi K^+ K^-$ and $B^+ \rightarrow \phi Z_{cs}^+ \rightarrow J/\psi K^+ \phi$ to be,

$$\begin{aligned}&{\mathcal {B}}[B_{s}^0 \rightarrow K^\pm Z_{cs}^\mp \rightarrow J/\psi K^+ K^-] \nonumber \\&\quad \simeq 2 {\mathcal {B}}[B_{s}^0 \rightarrow K^- Z_{cs}^+] {\mathcal {B}}[Z_{cs}^+ \rightarrow J/\psi K^+],\nonumber \\&{\mathcal {B}}[B^+ \rightarrow \phi Z_{cs}^+ \rightarrow J/\psi K^+ \phi ] \nonumber \\&\quad \simeq {\mathcal {B}}[B^+ \rightarrow \phi Z_{cs}^+] {\mathcal {B}}[Z_{cs}^+ \rightarrow J/\psi K^+], \end{aligned}$$

(21)

Then the ratio of the branching fractions of the above two processes is,

$$\begin{aligned} R_{B_s/B}^{\mathrm {Cascade}}= \frac{{\mathcal {B}}[B_s^0 \rightarrow K^\pm Z_{cs}^\mp \rightarrow J/\psi K^+ K^- ]}{{\mathcal {B}}[B^+ \rightarrow \phi Z_{cs}^+\rightarrow \phi J/\psi K^+] }\simeq 2 R_{B_s/B}.\nonumber \\ \end{aligned}$$

(22)

With the measured branching fraction of $B^+ \rightarrow \phi Z_{cs}^+ \rightarrow J/\psi K^+ \phi$ and the estimated $R_{B_s/B}$ in the present work, we obtain,

$$\begin{aligned} {\mathcal {B}}[B_s^0 \rightarrow K^\pm Z_{cs}^\mp \rightarrow J/\psi K^+ K^- ] = (3.83 \pm 1.69)\times 10^{-5}.\nonumber \\ \end{aligned}$$

(23)

Furthermore, the PDG average of the branching ratio of the process $B_s^0 \rightarrow J/\psi K^+ K^-$ is $(7.9\pm 0.7)\times 10^{-4}$ [74]. Then the production ratio of $Z_{cs}$ in $B^0_s\rightarrow J/\psi K^+ K^-$ is evaluated to be

$$\begin{aligned} \frac{{\mathcal {B}}[B^0_s\rightarrow Z^\pm _{cs}K^\mp \rightarrow J/\psi K^+ K^-]}{{\mathcal {B}}[B^0_s\rightarrow J/\psi K^+ K^-]} =(4.85\pm 2.17)\%,\nonumber \\ \end{aligned}$$

(24)

which can be tested by future experimental measurements.³

Here, we should mention that the starting-point of the above estimations is molecular structure of the $Z_{cs}(3985)$. However, it should be clarified that such a molecular assumption is not a groundless guess. Our investigations of the $Z_c(3900)$ decay properties indicated that $Z_c(3900)$ should be a $D^*{\bar{D}}+c.c$ molecular state [24], and as the strange partner of $Z_c(3900)$, our estimations in Ref. [60] showed the similarity between the decay properties of $Z_{cs}(3985)$ and $Z_c(3900)$, which indicate $Z_{cs}(3985)$ to be a $D_s^*{\bar{D}}$ molecule rather than a compact tetraquark. Moreover, the estimated branching ratio of the cascade process in Eq. (19) is comparable with the one reported by LHCb Collaboration, which in turn prove that our molecular assumption should be reasonable. Thus, the present estimations in the molecular scenario should be reliable.

4 Summary

Recently, the BESIII and LHCb Collaborations reported the observations of charmoniumlike state with strangeness, which is $Z_{cs}$. The mass of this newly observed charmoniumlike state is close to the threshold of $D_s^*D/D_s D^*$, which indicate that the $Z_{cs}$ could be a good candidates of molecular state composed of $D_s {\bar{D}}^*+D_s^*{\bar{D}}$. In the molecular scenario, the mass spectrum and decay properties have been investigated extensively. Besides the resonance parameters of $Z_{cs}$, the LHCb Collaboration also reported the branching ratio of the cascade decay process $B^+ \rightarrow \phi Z_{cs}^+ \rightarrow \phi K^+ J/\psi$, which is of the order of $10^{-6}$. How to understand the production properties of $Z_{cs}$ is important to reveal its inner structure. In the present work, we estimate the production of $Z_{cs}^+$ from $B^+$ decay by considering the triangle meson loop contributions. Our estimations indicate that the branching ratio of $B^+ \rightarrow \phi Z_{cs}^+$ is of the order of $10^{-5}$. Together with the decay properties of $Z_{cs}$ in our previous work, we find the estimated branching ratio of $B^+ \rightarrow \phi Z_{cs}^+ \rightarrow \phi K^+ J/\psi$ is of the order of $10^{-7}$–$10^{-6}$, which is comparable with the measurement from LHCb Collaboration.

Besides the process $B^+ \rightarrow \phi Z^+_{cs}$, our estimations indicate that the branching ratio of $B_{s}^0 \rightarrow K^- Z_{cs}^+$ is about 4 times of the one of $B^+ \rightarrow \phi Z_{cs}^+$, which indicate that the $B_s^0 \rightarrow K^\pm Z^\mp _{cs} \rightarrow K^+ K^- J/\psi$ may be a better process of searching $Z_{cs}$ and should be accessible for the experimental measurement of the Belle II and LHCb Collaborations.

Appendix A: The expressions of \({\mathcal {A}}(p_1,p_2)\), \({\mathcal {A}}_\nu (p_1,p_2)\) and \({\mathcal {A}}_{\mu \nu }(p_1,p_2)\)

Here we collect all the function used in Eq.  (8), which are,

$$\begin{aligned}&{\mathcal {A}}^{B_s\rightarrow D_s {\bar{D}}_s}(p_1,p_2)\\&\quad =-\frac{iG_F}{\sqrt{2}}V_{cb}V^*_{cs}a_1 f_{D_s}(m^2_{B_s}-m^2_{D_s})F_0^{B_s D_s}(p^2_1) \\&{\mathcal {A}}^{B_s\rightarrow D_s {\bar{D}}^*_s}_\nu (p_1,p_2)\\&\quad =\frac{G_F}{\sqrt{2}}V_{cb}V^*_{cs}a_1 f_{D_s}\frac{1}{m_{B_s}+m_{D^*_s}} \\&\qquad \times \Big \{(m_{B_s}+m_{D^*_s})^2 g_{\mu \nu }p^\mu _{1}A_1^{B_s D^*_s}(p^2_1) \\&\qquad -(p_1+2p_2)_\mu (p_1+2p_2)_\nu p^\mu _{1} A_2^{B_s D^*_s}(p^2_1) \\&\qquad -2m_{D^*_s}(m_{B_s}+m_{D^*_s})(p_1+2p_2)_\nu \\&\qquad \times [A_3^{B_s D^*_s}(p^2_1)-A_0^{B_s D^*_s}(p^2_1)]\Big \} \\&{\mathcal {A}}^{B_s\rightarrow D^*_s {\bar{D}}^*_s}_{\mu \nu }(p_1,p_2) \\&\quad =\frac{G_F}{\sqrt{2}}V_{cb}V^*_{cs}a_1 f_{D^*_s}m_{D^*_s}\frac{i}{m_{B_s}+m_{D^*_s}} \\&\qquad \times \Big \{i\varepsilon _{\mu \nu \alpha \beta }(p_1+2p_2)^\alpha p^\beta _1 A_V^{B_s D^*_s}(p^2_1) \\&\qquad +(m_{B_s}+m_{D^*_s})^2 g_{\mu \nu }A_1^{B_s D^*_s}(p^2_1) \\&\qquad -(p_1+2p_2)_\mu (p_1+2p_2)_\nu A_2^{B_s D^*_s}(p^2_1)\Big \} \\&{\mathcal {A}}^{B\rightarrow D_s {\bar{D}}}(p_1,p_2)\\&\quad =-\frac{iG_F}{\sqrt{2}}V_{cb}V^*_{cs}a_1 f_{D_s}(m^2_{B}-m^2_{D})F_0^{B D}(p^2_1) \\&{\mathcal {A}}_\mu ^{B\rightarrow D^*_s {\bar{D}}}(p_1,p_2)\\&\quad =\frac{2G_F}{\sqrt{2}}V_{cb}V^*_{cs}a_1 f_{D^*_s}m_{D^*_s} p_{2\mu } F_1^{B D}(p^2_1) \\&{\mathcal {A}}^{B\rightarrow D_s {\bar{D}}^*}_\nu (p_1,p_2)\\&\quad =\frac{G_F}{\sqrt{2}}V_{cb}V^*_{cs}a_1 f_{D_s}\frac{1}{m_{B}+m_{D^*}} \\&\qquad \times \Big \{(m_{B}+m_{D^*})^2 g_{\mu \nu }p^\mu _{1}A_1^{B D^*}(p^2_1) \\&\qquad -(p_1+2p_2)_\mu (p_1+2p_2)_\nu p^\mu _{1} A_2^{B D^*}(p^2_1) \\&\qquad -2m_{D^*}(m_{B}+m_{D^*})(p_1+2p_2)_\nu \\&\qquad \times [A_3^{B D^*}(p^2_1)-A_0^{B D^*}(p^2_1)]\Big \} \\&{\mathcal {A}}^{B\rightarrow D^*_s {\bar{D}}^*}_{\mu \nu }(p_1,p_2)\\&\quad =i\frac{G_F}{\sqrt{2}}V_{cb}V^*_{cs}a_1 f_{D^*_s}\frac{m_{D^*_s}}{m_{B_s}+m_{D^*}} \\&\qquad \times \Big \{i\varepsilon _{\mu \nu \alpha \beta }(p_1+2p_2)^\alpha p^\beta _1 A_V^{B D^*}(p^2_1) \\&\qquad +(m_{B}+m_{D^*})^2 g_{\mu \nu }A_1^{B D^*}(p^2_1) \\&\qquad -(p_1+2p_2)_\mu (p_1+2p_2)_\nu A_2^{B D^*}(p^2_1)\Big \} \end{aligned}$$