Abstract
Null energy condition (NEC) is revisited in the context of thin-shell wormholes (TSW). In a generic spherically symmetric configuration we introduce the condition upon which NEC is satisfied. Also, we present a general condition which specifies the stability of the generic spherically symmetric TSW against a radial linear perturbation. Furthermore, we introduce a specific bulk metric in the framework of gravity coupled minimally with nonlinear electrodynamics such that the corresponding TSW satisfies NEC, unconditionally. We study the mechanical stability of this TSW and show that, with a variable equation of state of the fluid present at the throat, this TSW remains stable irrespective of the value of the speed of sound.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Traversable wormholes satisfy the so-called flare-out conditions [1,2,3]. Applying these conditions reveals that the matter supporting a traversable wormhole doesn’t satisfy the minimum requirement for being a normal matter [1,2,3]. The minimum requirement is the Null Energy Condition (NEC). NEC states that for a physical or a normal matter with an energy–momentum tensor \(T_{\mu \nu },\) \(T_{\mu \nu }n^{\mu }n^{\nu }\ge 0\) where \(n^{\mu }\) is any null vector. Hence, in \({\mathcal {R}}\)-gravity it is a fact that traversable wormholes are supported by exotic matter, however, in modified theories of gravity the effective energy–momentum tensor ( including the matter plus the geometry) violates NEC but the actual matter respects it [4,5,6,7,8,9,10,11,12,13,14,15,16,17].
With thin-shell-wormholes (TSW) introduced by Visser [18, 19], it was realized that in certain conditions violation of NEC can be avoided [20]. Let’s add that, in a different approach [21, 22], Lobo considered a thin shell surrounding the traversable wormhole to reduce the amount of exotic matter (i.e., NEC-violating matter). Here in this paper, we look at the NEC in the context of generic spherically symmetric TSW. We provide a simple condition that should be satisfied by the metric tensor of the bulk spacetime in order to have the NEC satisfied at the throat of the TSW. In addition to the known TSWs, such as TSW in Schwarzschild and Reissner–Nordström (RN) spacetime (see the Appendix), we present a new TSW that gives additional freedoms to keep NEC satisfied. This TSW which satisfies the NEC, unconditionally, is constructed in a bulk spacetime supported by gravity coupled minimally with nonlinear electrodynamics. The bulk is purely supported by a magnetic monopole located at the origin which is, therefore, singular. It is better called a massless black point which asymptotically is an Anti-de Sitter spacetime.
One of the important physical arguments about a TSW is its mechanical stability against a radial linear perturbation [23]. In a spherical symmetric configuration, one has to assume an equilibrium radius where the radial velocity and acceleration of the throat before the perturbation are zero. Upon a radial perturbation, the throat is given an initial radial velocity. The motion of the throat after the perturbation yields whether the TSW is stable or not. We perform such stability analysis for the TSW constructed in this study.
2 The master conditions
Following the paper of Eiroa, [24] we consider a general static and spherically symmetric bulk spacetime with the line element given by
Applying the method of cut-and-paste we construct a TSW whose throat is the hypersurface \(\Sigma :=\left\{ x\backslash F\left( r\right) =r-a\left( \tau \right) =0\right\} \). All the details of making such a TSW are exactly the same as the one published in [24]. Therefore, we don’t repeat the formalism and instead, we use the results reported there. The line element of the bulk has to be continuous across the throat and consequently, the induced line element or the first fundamental form of the throat is continuous. Hence the induced line element on the throat is given by
in which \(\tau \) is the proper time on the shell. In accordance with [24], the energy–momentum tensor supporting the TSW is obtained to be \( S_{i}^{j}=diag\left[ -\sigma ,p,p\right] \) in which the surface energy density \(\sigma \) and the tangential pressure p are given by (\(G=1\))
and
Herein, a prime and a dot stand for the derivative with respect to r and \( \tau ,\) respectively, and all functions are evaluated at the throat i.e. \( r=a.\) In the static configuration, we set \(a=a_{0}\) such that \({\dot{a}}=\ddot{ a}=0\) and consequently
and
Applying the null energy condition to the matter present on the TSW yields
or explicitly
Having in mind that \(\sqrt{f\left( a_{0}\right) }>0\) the later equation simply reduces to
In a simple explanation, \(\frac{f\left( r\right) }{h\left( r\right) }\) should be an increasing function in the vicinity of the equilibrium radius \( r=a_{0}\). This should be noted that \(a=a_{0}\) is the equilibrium radius where \({\dot{a}}_{0}=\ddot{a}_{0}=0.\) Hence, a mechanical stability analysis is needed to make sure that such a TSW is stable at \(a=a_{0}.\) As we mentioned in the Introduction, in the mechanical stability analysis we perturb the throat radially by giving an small initial velocity to the throat at its equilibrium radius. From (2) we find
At \(a=a_{0}\) where \({\dot{a}}={\dot{a}}_{0}=0,\) (9) simply yields \(\sigma =\sigma _{0}\). By perturbing the wormhole, at \(a=a_{0},\) \({\dot{a}}_{0}\ne 0\) and therefore the dynamics of the perturbed system with initial speed \(\dot{a }_{0}\) can be described by
Furthermore, from the energy conservation law i.e., \(S_{;j}^{ij}=0\) one gets
Dividing both sides by \({\dot{a}}\) and using the chain rule yield
Equation (10) is a one-dimensional equation of motion for a particle of unit mass undergoing an effective potential
and total mechanical energy of \(\frac{1}{2}{\dot{a}}_{0}^{2}.\) Introducing a new variable \(x=a-a_{0}\) and using the Taylor expansion of the potential about \(a=a_{0}\) the one-dimensional equation of motion reduces to
Derivative of both sides of the latter equation with respect to \(\tau \) yields
which up to the first order reads as
This is the linearized equation of motion of the throat after the perturbation. To obtain the explicit forms of \(V^{\prime }\left( a_{0}\right) \) and \(V^{\prime \prime }\left( a_{0}\right) \) we assume a variable equation of state for the fluid present at the throat in the form \( p=\psi \left( a,\sigma \right) \) [28, 29], upon which (12) becomes
and
Considering (17) and (18), we obtain \(V^{\prime }\left( a_{0}\right) =0\) and
Herein a prime stands for the derivative with respect to a, \(\psi _{,\sigma }=\frac{\partial \psi }{\partial \sigma }\) and \(\psi _{,a}=\frac{ \partial \psi }{\partial a}.\) Finally the condition of having the TSW stable is \(V^{\prime \prime }\left( a_{0}\right) =\omega ^{2}>0\) such that (16) becomes
with a solution of the form \(x=\frac{{\dot{a}}_{0}}{\omega }\sin \omega \tau \) which indicates the throat oscillates about its equilibrium radius where \( x=0.\)
3 TSW in a massless asymptotically anti-de Sitter magnetic black point spacetime
In this section, we provide a massless asymptotically Anti-de Sitter magnetic black point bulk spacetime where the constructed TSW satisfies the NEC for all radii of the throat. In the theory of gravity coupled minimally to the nonlinear electrodynamics with a cosmological constant, the action is given by
in which \(\kappa ^{2}=8\pi G,\) \({\mathcal {R}}\) is the Ricci scalar, \(\Lambda \) is the cosmological constant, \(\alpha \) is a coupling constant, and \( {\mathcal {F}}=\frac{1}{4}F_{\alpha \beta }F^{\alpha \beta }\) is Maxwell’s invariant. Variation of the action with respect to \(g_{\mu \nu }\) yields Einstein’s field equations given by
where \(G_{\mu }^{\nu }=R_{\mu }^{\nu }-\delta _{\mu }^{\nu }{\mathcal {R}}\) is the mixed Einstein’s tensor and
is the energy–momentum tensor with the Maxwell nonlinear action \({\mathcal {L}} =-\frac{\alpha \sqrt{{\mathcal {F}}}}{4\pi }\) and \({\mathcal {L}}_{{\mathcal {F}}}= \frac{\partial {\mathcal {L}}}{\partial {\mathcal {F}}}.\) On the other hand, variation of the action with respect to the gauge potential \(A_{\mu }\) gives the nonlinear Maxwell equations given by
We choose the line-element of the form given in Eq. (1) with \(h\left( r\right) =r^{2}\) and the gauge field to be pure magnetic from a magnetic monopole located at the origin with
in which \(B_{r}\) is the radial component of the magnetic field. Applying the Bianchi identity
with \({\tilde{F}}^{\mu \nu }\) the dual electromagnetic field, we get
in which P is an integration constant representing the magnetic monopole. Furthermore, solving Einstein’s field equations gives the metric function (\( G=1\))
in which M is an integration constant representing the ADM mass of the solution [25]. Having considered \(-\frac{\Lambda }{3}=\frac{1}{\ell ^{2}}>0,\) the solution (28) becomes an asymptotically Anti de-Sitter black hole, however, setting \(M=0\) as well as \(1-\frac{\alpha \kappa ^{2}P}{ \sqrt{2}}=0,\) the solution becomes a massless black point with the line-element
We add that the energy–momentum tensor of the nonlinear electromagnetic Lagrangian is given by
where the energy density, the radial pressure, and the angular pressures are given by \(\rho =\frac{\alpha \sqrt{{\mathcal {F}}}}{4\pi },\) \(p_{r}=-\frac{ \alpha \sqrt{{\mathcal {F}}}}{4\pi }\) and \(p_{\theta }=p_{\varphi }=0,\) respectively. Therefore, in order to have at least the NEC satisfied i.e., \( \rho +p_{i}\ge 0,\) one has to impose \(\alpha >0.\) Having \(\alpha >0\) one also finds that all energy conditions are satisfied including Weak (\(\rho \ge 0,\rho +p_{i}\ge 0\)), Strong (\(\rho +\sum _{i=1}^{3}p_{i}\ge 0\)) and Dominant (\(\rho -\left| p_{i}\right| \ge 0\)).
Furthermore, applying the coordinate transformation given by \(r=\frac{1}{R}\) and \(t=\ell ^{2}T\), transforms (29) to
which is conformal to the Bertotti–Robinson spacetime [26, 27].
Constructing TSW in this bulk spacetime with the line element given in (29) one obtains (see Eqs. (4) and (5))
and
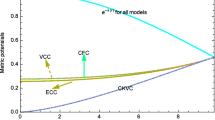
It is easy to observe that \(\sigma _{0}+p_{0}=0\) and consequently the NEC is satisfied, unconditionally. This is unlike the other known TSWs which we provide two of them in the Appendix. Finally, we comment that in addition to the NEC the strong energy condition (SEC) (i.e., \(\sigma +\sum _{i=1}^{2}p_{i}\ge 0\)) is also satisfied on the shell.
Finally, to investigate the mechanical stability of the TSW we apply the radial linear perturbation introduced in the previous section. All we should do is to set \(f\left( a\right) =\frac{a^{2}}{\ell ^{2}}\) and \(h\left( a\right) =a^{2}\) in (19) which yields
Hence, with \(\left( \frac{\partial \psi }{\partial a}\right) _{a=a_{0}}<0\) we find \(V^{\prime \prime }\left( a_{0}\right) >0\) and therefore the motion of the throat becomes oscillatory and consequently the TSW is stable against the linear radial perturbation. Physically, \(\left( \frac{\partial \psi }{ \partial a}\right) _{a=a_{0}}<0\) means that the angular pressure (or negative surface tension) should be a decreasing function of a. A typical example of such an EOS is
in which \(\zeta >0\) is a dimensionful constant.
4 Conclusion
We revisited the violation of NEC by TSW constructed in generic static spherically symmetric bulk spacetime. We obtained a condition, namely Eq. (8), in which upon being satisfied by the bulk metric tensor, the surface matter at the throat of TSW satisfies the NEC. In addition to that within a general formalism, we obtained another condition namely Eq. (19) which should be satisfied in order to have the TSW stable against a linear radial perturbation. Furthermore, we introduced the black-point bulk in the context of nonlinear electrodynamics minimally coupled with Einstein’s \({\mathcal {R}}\)-gravity, such that the constructed TSW in the resulting bulk spacetime satisfies the NEC and SEC, unconditionally. We also examined the stability of the TSW against a linear radial perturbation with a variable equation of state for the fluid present at the throat. It was shown that, irrespective of the value of the speed of sound i.e., \(\left( \frac{\partial \psi \left( a,\sigma \right) }{\partial \sigma }\right) _{a=a_{0}},\) the TSW is stable provided \(\left( \frac{\partial \psi \left( a,\sigma \right) }{\partial a}\right) _{a=a_{0}}<0\) where \(p=\psi \left( a,\sigma \right) \) is the variable equation of state [28, 29].
Data Availability
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The paper is theoretical and required no data.]
References
M.S. Morris, K.S. Thorne, Am. J. Phys. 56, 395 (1988)
M.S. Morris, K.S. Thorne, U. Yurtsever, Phys. Rev. Lett. 61, 1446 (1988)
D. Hochberg, M. Visser, Phys. Rev. Lett. 81, 746 (1998)
T. Harko, F.S.N. Lobo, M.K. Mak, S.V. Sushkov, Phys. Rev. D 87, 067504 (2013)
F.S.N. Lobo, Class. Quantum Gravity 25, 175006 (2008)
S. Capozziello et al., Phys. Rev. D 86, 127504 (2012)
C. Bambi et al., Phys. Rev. D 93, 064016 (2016)
G.U. Varieschi, K.L. Ault, Int. J. Mod. Phys. D 25, 1650064 (2016)
F. Duplessis, D.A. Easson, Phys. Rev. D 92, 043516 (2015)
P.K. Sahoo, P.H.R.S. Moraes, P. Sahoo, Eur. Phys. J. C 78, 46 (2018)
P.K.F. Kuhfittig, J. Korean Phys. Soc. 70, 962 (2017)
P.K.F. Kuhfittig, Indian J. Phys. 92, 1207 (2018)
C. Barcelo, M. Visser, Phys. Lett. B 466, 127 (1999)
F. Willenborg, S. Grunau, B. Kleihaus, J. Kunz, Phys. Rev. D 97, 124002 (2018)
R. Shaikh, Phys. Rev. D 92, 024015 (2015)
R. Shaikh, S. Kar, Phys. Rev. D 94, 024011 (2016)
R. Shaikh, S. Kar, Phys. Rev. D 96, 044037 (2017)
M. Visser, Phys. Rev. D 39, 3182 (1989)
M. Visser, Nucl. Phys. B 328, 203 (1989)
F.S.N. Lobo, P. Crawford, Class. Quantum Gravity 21, 391 (2004)
F.S.N. Lobo, Class. Quantum Gravity 21, 4811 (2004)
F.S.N. Lobo, Gen. Relativ. Gravit. 37, 2023 (2005)
E. Poisson, M. Visser, Phys. Rev. D 52, 7318 (1995)
E.F. Eiroa, Phys. Rev. D 78, 024018 (2008)
S.H. Mazharimousavi, M. Halilsoy, Phys. Lett. B 710, 489 (2012)
B. Bertotti, Phys. Rev. D 116, 1331 (1959)
I. Robinson, Bull. Acad. Pol. 7, 351 (1959)
N.M. Garcia, F.S.N. Lobo, M. Visser, Phys. Rev. D 86, 044026 (2012)
V. Varela, Phys. Rev. D 92, 044002 (2015)
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
Here we revisit the two well-known TSWs and study the status of the NEC by applying the main equation (8).
(i) For the first example we try the Schwarzschild black hole for the bulk spacetime where \(f\left( r\right) =1-\frac{2M}{r}\) and \(h\left( r\right) =r^{2}.\) The master equation (8) reduces to
upon which only for \(2M<a_{0}\le 3M\) the NEC is satisfied.
(ii) Our second example is the Reissner–Nordström black hole to be the bulk spacetime. In this case, \(f\left( r\right) =1-\frac{2M}{r}+\frac{Q^{2}}{ r^{2}}\), \(h\left( r\right) =r^{2}\) and the NEC becomes
Taking into account that \(a_{0}>r_{h}\) where
is the radius of the event horizon, (A.2) reveals
In summary, we have shown that for the Schwarzschild bulk spacetime the radius of the throat \(a_{0}\) should lie in the interval \(\left( 2M,3M\right] \) in order to have NEC satisfied. For TSW constructed in RN bulk spacetime \( a_{0}\in \left( M+\sqrt{M^{2}-Q^{2}},\frac{3}{2}\left( M+\sqrt{M^{2}-\frac{8 }{9}Q^{2}}\right) \right] \) for having NEC respected.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Mazharimousavi, S.H. Thin-shell wormhole satisfying the null-energy condition unconditionally. Eur. Phys. J. C 82, 496 (2022). https://doi.org/10.1140/epjc/s10052-022-10459-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-022-10459-x