1 Introduction

Physical problems involving gravitational collapse have been well studied since the pioneering work of Oppenheimer and Snyder [1]. In an effort to improve models, a non-empty exterior spacetime was included [2] which lead to Vaidya’s well-known solution for a radiation-filled exterior spacetime [3]. Modelling has required the setting of part of the gravitational framework according to physically viable potentials, with the remaining part often being determined through equations of state, and more recently through gravitational decoupling [4, 14]. This has been a method for closing the systems of equations which arise in applying general relativity and other gravity theories.

The concept of complexity has now also become useful in the modelling of self-gravitating systems. Complexity is used in many branches of science, and as such does not seem to have a rigorous definition [5]. Perhaps a bit tautological, but a system which is complex avoids simplification and thus makes its description somewhat removed from an idealised one. Thus idealised systems such as a perfect crystal and an ideal gas are used as a basis and reference point, endowed with the condition of vanishing complexity. This connection with the examples of idealised systems was used in building the original definition of statistical complexity [6]. A condensed matter crystal requires minimal data in its description, namely identification of a repeating unit. Application of the space-group symmetry then generates the crystal. As a result of structural defects and thermal energy, there is no perfect crystal in nature, nevertheless crystallised matter has a relatively low entropy and minimal complexity. At the opposite end of the spectrum, an ideal gas requires a knowledge of the positions and trajectories of every particle and so the data is maximal. Yet both of these systems have zero complexity. Within the context of condensed matter physics, complexity has been defined as a product of the “information content” and the degree of “disequilibrium” of a system. For a crystal, the information content is minimal but the system is far from equilibrium. The reverse situation occurs for an ideal gas, thus vanishing complexity may be obtained for both of these systems via a product definition. This is the so-called statistical measure of complexity as given by López-Ruiz et al. [6]. This formulation of complexity, and extensions thereof [7], have been used in discerning equations of state and investigating the structure of compact objects [8, 9].

A different approach has been taken in the context of spherically symmetric, self-gravitating relativistic fluids [10]. In this case, the fluid system is considered to be least complex if it is homogeneous in energy density and isotropic in pressure. A definition of complexity is then based on macroscopic quantities, in contrast to a statistical definition in which the information content is calculated according to the populations of microstates. In addition, disequilibrium does not provide meaningful insight into systems undergoing gravitational collapse since the reference point of equilibrium is in general unattainable, the end point of collapse being the formation of an event horizon beyond which no further information may be gleaned within the confines of general relativity.

The orthogonal splitting of the Riemann tensor has been performed and found to yield various scalar functions [5, 11, 12]. In performing this process, five structure scalars are attained, one of which is well-suited to a definition of complexity. The complexity factor, so defined, links the pressure anisotropy to the energy density inhomogeneity. It is interesting to note that of these structure scalars, it is not always the same one that is linked to complexity. This is the case in \(f(R,T,R_{\mu \nu },T^{\mu \nu })\) gravity [13]. Much progress has already been made in using the complexity factor as a constraint for the closure of the systems of equations arising in gravitational models for static systems. Investigations of complexity have assisted in generating new solutions [15] and recently utilised within the framework of the gravitational decoupling method [4, 14].

Recent studies of complexity in both general relativity and higher theories of gravity have focused on static systems. In our study, we consider the case of radiating collapse and how the complexity factor evolves in this scenario. The theoretical framework for including heat flux in the computation of complexity has already been setup by Herrera and co-workers [10] and we apply a physically viable, radiating model in order to investigate the behaviour of this dynamical complexity factor. The inclusion of a dynamical complexity factor could provide a further means of investigating the evolution of gravitational collapse in addition to (in)stability [16,17,18] and dynamical forces [19, 20].

2 The field equations

The most general, spherically symmetric line element is given by

$$\begin{aligned} ds^2 = -A^2dt^2 + B^2 dr^2 + C^2 r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2) \end{aligned}$$
(1)

where the gravitational potentials are in general both spatially and temporally dependent. In modelling gravitational collapse, we consider the matter distribution to be shear-free in addition to spherically symmetric. This is a reasonable assumption when modelling a relativistic, radiating star and requires that \(\partial _t log(B/C) = 0\). We make use of a line element in which the potentials are separable in terms of space and time coordinates as done by Sharma and Das [21]. With the coordinates \(({x}^\alpha ) = (t, r, \theta , \phi )\) this line element, for the interior spacetime of the stellar model, takes the form

$$\begin{aligned} ds^2= & {} -A_0^2(r)dt^2 + f^2(t)\nonumber \\&\times \left[ B_0^2(r)dr^2 + r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2) \right] . \end{aligned}$$
(2)

We see that this line element obeys the shear-free condition. In terms of the general line element, we have the association

$$\begin{aligned} A = A_0(r), B = B_0(r)f(t), C = f(t).\end{aligned}$$

This type of gravitational formalism in which the spatial and temporal parts are separated and written as a product is popular in gravitational collapse modelling [22, 23]. The spatial part is often determine by imposing an equation of state and the temporal part, via the heat flux boundary condition. We consider a model which represents a spherically symmetric, shear-free fluid configuration with heat flux. For our model, the energy–momentum tensor for the stellar fluid takes the form

$$\begin{aligned} T_{\alpha \beta }= & {} (\rho + p_t)u_\alpha u_\beta + p_t g_{\alpha \beta } + (p_r - p_t)\chi _\alpha \chi _\beta \nonumber \\&+ q_\alpha u_\beta + q_\beta u_\alpha \end{aligned}$$
(3)

where \(\rho \) is the energy density, \(p_r\) and \(p_t\) are the radial and tangential stresses respectively, \(q^\alpha = (0, q, 0, 0)\) is the heat flux vector assumed to flow in the radial direction due to spherical symmetry, \(u^\alpha \) is the fluid four-velocity and \(\chi ^a\) is a unit space-like four-vector along the radial direction. The following relations need to be satisfied

$$\begin{aligned} u^\alpha u_\alpha = -1, u^\alpha q_\alpha = 0, \chi ^\alpha \chi _\alpha = 1, \chi ^\alpha u_\alpha = 0. \end{aligned}$$

An equivalent, canonical form of the energy momentum tensor is given by

$$\begin{aligned} T_{\alpha \beta }= & {} \rho u_\alpha u_\beta + \hat{p}h_{\alpha \beta } + \left( p_r - p_t \right) \left( \chi _\alpha \chi _\beta - \frac{1}{3}h_{\alpha \beta }\right) \nonumber \\&+ q\left( u_\alpha \chi _\beta + \chi _\alpha u_\beta \right) \end{aligned}$$
(4)

where \(\hat{p} = \frac{1}{3}\left( p_r + 2p_t \right) \) and the projection tensor \(h_{\alpha \beta } = g_{\alpha \beta } + u_\alpha u_\beta \). This form of the energy momentum tensor is more convenient in developing the explicit forms of the structure scalars arising from the splitting of the Riemann tensor.

The fluid collapse rate \(\Theta = u^\alpha _{;\alpha }\) of the stellar model is given by

$$\begin{aligned} \Theta = 3\frac{\dot{B}}{AB}, \end{aligned}$$
(5)

where dots represent differentiation with respect to t.

One must proceed with caution when exploring shear-free fluids. It has been demonstrated that the shear-free condition is unstable [24] in the sense that a shear-free fluid can mimic shearing behaviour in the presence of density inhomogeneities and dissipation. A measure of the stability of the shear-free condition is encoded in the scalar \( {Y_{TF}}\)

$$\begin{aligned} Y_{TF}= & {} 16\pi \eta \sigma + 8\pi (p_t - p_r) \nonumber \\&+ \frac{4\pi }{(Cr)^3}\int _0^r (Cr)^3\left( \rho ' - 3q\frac{B^2}{A}\frac{\dot{C}}{C}\right) dr \end{aligned}$$
(6)

where \(\sigma \) is the shear-scalar, \(p_t\) and \(p_r\) are the tangential and radial pressures respectively, \(\rho \) is the energy density and q is the heat flux. This is a prelude to the main topic of our study. The scalar \( {Y_{TF}}\) is a combination of localised pressure anisotropy, energy density inhomogeneities, dissipative fluxes such as heat flow and shear viscosity. In the absence of shear viscosity \(\eta \) (if internal friction between layers of the collapsing fluid is to be ignored) there can be an increase in the absolute value of the shear scalar induced by density inhomogeneities and heat flux dissipation. We also see that energy density inhomogeneity is responsible for deviations from an initial shear-free profile. These deviations can be enhanced in the presence of heat dissipation within the stellar core.

We now present the nonzero components of the Einstein field equations for the line element (2). In geometrised units (G = c = 1) we obtain

$$\begin{aligned} 8\pi \rho= & {} \frac{1}{f^2}\left[ \frac{1}{r^2}-\frac{1}{r^2B_0^2}+\frac{2B_0'}{r B_0^3}\right] +\frac{3\dot{f^2}}{A_0^2f^2}, \end{aligned}$$
(7)
$$\begin{aligned} 8\pi p_r= & {} \frac{1}{f^2}\left[ -\frac{1}{r^2}+\frac{1}{r^2B_0^2}+\frac{2A_0'}{r A_0B_0^2}\right] \nonumber \\&- \frac{1}{A_0^2}\left[ 2\frac{\ddot{f}}{f}+\frac{\dot{f^2}}{f^2}\right] , \end{aligned}$$
(8)
$$\begin{aligned} 8\pi p_t= & {} \frac{1}{f^2}\left[ \frac{A_0''}{A_0B_0^2}+\frac{A_0'}{r A_0B_0^2}-\frac{B_0'}{r B_0^3}-\frac{A_0'B_0'}{A_0B_0^3}\right] \nonumber \\&-\frac{1}{A_0^2}\left[ 2\frac{\ddot{f}}{f}+\frac{\dot{f^2}}{f^2}\right] , \end{aligned}$$
(9)
$$\begin{aligned} 8\pi q= & {} -\frac{2A_0'\dot{f}}{A_0^2B_0^2f^3}. \end{aligned}$$
(10)

Equations (7)–(9) may be written in the form

$$\begin{aligned} \rho= & {} \frac{\rho _0}{f^2}+\frac{3\dot{f^2}}{8\pi A_0^2f^2}, \end{aligned}$$
(11)
$$\begin{aligned} p_r= & {} \frac{p_{r0}}{f^2}-\frac{1}{8\pi A_0^2}\left[ 2\frac{\ddot{f}}{f}+\frac{\dot{f^2}}{f^2}\right] , \end{aligned}$$
(12)
$$\begin{aligned} p_t= & {} \frac{p_{t0}}{f^2}-\frac{1}{8\pi A_0^2}\left[ 2\frac{\ddot{f}}{f}+\frac{\dot{f^2}}{f^2}\right] , \end{aligned}$$
(13)

where \(\rho _0\), \(p_{r0}\) and \(p_{t0}\) denote the energy density, radial pressure and tangential pressure respectively of the initial static configuration. These are given by

$$\begin{aligned} 8\pi \rho _0= & {} \left[ \frac{1}{r^2}-\frac{1}{r^2B_0^2}+\frac{2B_0'}{r B_0^3}\right] , \end{aligned}$$
(14)
$$\begin{aligned} 8\pi p_{r0}= & {} \left[ -\frac{1}{r^2}+\frac{1}{r^2B_0^2}+\frac{2A_0'}{r A_0B_0^2}\right] , \end{aligned}$$
(15)
$$\begin{aligned} 8\pi p_{t0}= & {} \left[ \frac{A_0''}{A_0B_0^2}+\frac{A_0'}{r A_0B_0^2}-\frac{B_0'}{r B_0^3}-\frac{A_0'B_0'}{A_0B_0^3}\right] . \end{aligned}$$
(16)

The anisotropy parameter is defined as

$$\begin{aligned} \Delta = \left( p_t - p_r \right) . \end{aligned}$$
(17)

We see that in terms of our gravitational formalism, this simplifies to

$$\begin{aligned} \Delta (r, t) = \frac{\Delta _0 (r)}{f^2 (t)} \end{aligned}$$
(18)

where

$$\begin{aligned} \Delta _0 (r)= & {} \frac{1}{8\pi }\bigg [\frac{A''_0}{A_0 B^2 _0} - \frac{A'_0}{rA_0 B^2 _0} - \frac{B' _0}{rB^3 _0} - \frac{A' _0 B' _0}{A_0 B^3 _0} \nonumber \\&- \frac{1}{r^2 B^2 _0} + \frac{1}{r^2} \bigg ] \end{aligned}$$
(19)

The framework is now in place for setting up the initial static configuration. In our study, we specify the potential \(B_0\) according to the Vaidya–Tikekar (V–T) ansatz and make use of a linear equation of state. The V–T potential is suitable for modelling superdense compact objects, and a linear equation of state is a reasonable approximation [25]. Our initial static configuration is used to model an unstable neutron star which collapses to form a black hole remnant.

3 Junction conditions

In modelling the gravitational collapse of compact stellar objects with heat flux, we make use of an exterior spacetime described by Vaidya’s outgoing solution [3] given by

$$\begin{aligned} ds^2= & {} - \left( 1 - \frac{2m(\upsilon )}{\textsf {r}}\right) d\upsilon ^2 - 2d\upsilon d\textsf {r}\nonumber \\&+ \textsf {r}^2 \left( d\theta ^2 + \sin ^2\theta d\phi ^2 \right) . \end{aligned}$$
(20)

The quantity m(\(\upsilon \)) represents the Newtonian mass of the gravitating body as measured by an observer at infinity, as a function of the retarded time \(\upsilon \). The metric given by (20) is the unique spherically symmetric solution of the Einstein field equations for radiation in the form of a null fluid. The Einstein tensor for the line element (20) is given by

$$\begin{aligned} G_{\alpha \beta } = -\frac{2}{\textsf {r}^2}\frac{dm}{d\upsilon } \delta ^0_\alpha \delta ^0_\beta .\end{aligned}$$
(21)

The energy momentum tensor for null radiation assumes the form

$$\begin{aligned} T_{\alpha \beta } = {\Phi }w_{\alpha }w_{\beta }, \end{aligned}$$
(22)

where the null four-vector is given by \(w_\alpha = (1, 0, 0, 0)\). Thus from (21) and (22) we have

$$\begin{aligned} {\Phi } = -\frac{2}{\textsf {r}^2}\frac{dm}{d\upsilon }, \end{aligned}$$
(23)

for the energy density of the null radiation. Since the star is radiating energy to the exterior spacetime we must have \(\displaystyle \frac{dm}{d\upsilon }< 0 \).

The necessary conditions for the smooth matching of the interior spacetime to the exterior spacetime was first presented by Santos [27]. The associated junction conditions for the line elements (2) and (20) are given by

$$\begin{aligned} \left( p_r\right) _{\Sigma }= & {} \left( q B_0 f\right) _{\Sigma } \end{aligned}$$
(24)
$$\begin{aligned} m(\upsilon )= & {} \left[ \frac{r f}{2} \left( 1 - \frac{1}{B_0^2} + \frac{(r \dot{f})^2}{A_0^2}\right) \right] _{\Sigma } \end{aligned}$$
(25)

where \(\Sigma \) represents the boundary between the interior and exterior spacetimes.

4 A Vaidya–Tikekar static configuration

Vaidya and Tikekar [28] have developed realistic compact stellar models according to the gravitational potential formulation given by

$$\begin{aligned} B_0^2(r) = \frac{1 - K(r^2/L^2)}{1 - (r^2/L^2)} \end{aligned}$$
(26)

where K is a spheroidal parameter which allows for departure from spherical symmetry with respect to the radial coordinate. This formulation has been shown to be suitable for modelling superdense stellar matter and is less prone to instability due to anisotropy in pressure towards the surface. Following Sharma et al. [25], we employ a linear equation of state, \(p_r = \alpha \rho - \beta \), together with the Vaidya–Tikekar potential. Using the standard time-independent Einstein field equations, we obtain

$$\begin{aligned} A_0^2(r) = J \left( 1 - r^2/L^2\right) ^n \left( 1 - K r^2/L^2 \right) ^\alpha e^{K\left( L^2 - r^2\right) \beta /2} \end{aligned}$$
(27)

where

$$\begin{aligned} n = \frac{1}{2}\left( -1 - 3\alpha + L^2 \beta + K(1 + \alpha - L^2 \beta ) \right) \end{aligned}$$
(28)

and J is a constant to be determined through matching of both potentials at the boundary. Matching of the internal metric to a Schwarzschild exterior at the boundary provides

$$\begin{aligned} L^2 = \frac{R^2 \left( 2KM - KR + R\right) }{2M} . \end{aligned}$$
(29)

The surface energy density is given by

$$\begin{aligned} \rho _s = \frac{\left( 1 - K\right) \left( 3 - K R^2 /L^2 \right) }{L^2 \left( 1 - K R^2 /L^2 \right) ^2} \end{aligned}$$
(30)

and surface density parameter

$$\begin{aligned} \beta = \alpha \rho _s . \end{aligned}$$
(31)

We choose the standard value \(\alpha = 1/3\) which then sets \(\rho _s = 4\mathscr {B}\) where \(\mathscr {B}\) is the MIT Bag constant. The linear equation of state, incorporating the Bag constant, has been a popular choice in modelling relativistic stars [26].

Table 1 Model parameters of initial unstable static configuration (\(M = 2.015 M_\odot \); \(R = 9.384 km\))
Full size table

5 Temporal dependence of the collapse process

We make use of the boundary condition \((p_r)_\Sigma = (q B)_\Sigma \) for establishing the temporal dependence of the collapse process. Making use of (10) and (12) with the static part set to zero since \((p_{r0})_\Sigma = 0\), we obtain

$$\begin{aligned} 2 f \ddot{f} + \dot{f}^2 - 2 a \dot{f} = 0 \end{aligned}$$
(32)

where the temporal dependence parameter, which has units of acceleration, is given by

$$\begin{aligned} a = \left( \frac{A_0' }{B_0}\right) _\Sigma . \end{aligned}$$
(33)

An integral of (32) is given by

$$\begin{aligned} \dot{f} = 2a\left( 1 - \frac{1}{\sqrt{f}} \right) \end{aligned}$$
(34)

in which the integration constant was set so that \(f = 1\) represents the initial static configuration at \(t = - \infty \). This can be further integrated to obtain

$$\begin{aligned} t = \frac{1}{a}\left[ \frac{f}{2} + \sqrt{f} + \ln (1 - \sqrt{f}) \right] . \end{aligned}$$
(35)

The temporal dependence of the collapse process has been modelled in a similar way previously [22, 29] and is well-adapted to models linked to realistic equations of state [22]. The second derivative of f is given by

$$\begin{aligned} \ddot{f} = -\frac{2a^2}{f^2}\left( 1 - \sqrt{f}\right) \end{aligned}$$
(36)

which is useful for writing the field equations in derivative-free form.

It is necessary to determine the lower limit of f at which the event horizon is formed. This is determined by examining the asymptotic behaviour of the surface redshift, given by

$$\begin{aligned} z_\Sigma = \left[ \frac{d\upsilon }{d\tau }\right] _\Sigma - 1 = \left[ \frac{1}{B_0} + r\dot{f}\right] ^{-1}_\Sigma - 1 \end{aligned}$$
(37)

where \(\tau \) is the proper time defined on the surface boundary. Divergence of \(z_\Sigma \) leads to

$$\begin{aligned} f_{bh} = \left( \frac{2M}{R}\right) ^2 \end{aligned}$$
(38)

which gives the time of formation of the black hole.

6 A dynamical model

We utilise a model describing the gravitational collapse of an unstable neutron star of radius \(R = 9.384 km\) and mass \(M = 2.015 M_\odot \) with the gravitational formalism used previously by Bogadi et al. [20]. The collapse of unstable neutron stars to form black holes has been previously investigated [22, 30]. The model parameters are shown in Table 1 with the spheroidal parameter (K) set at the standard value of \(K = -2\) as initially proposed by Vaidya and Tikekar [28] and a second model with a more radially asymmetric setting of \(K = -5\) chosen for comparison. Values of the MIT Bag constant \(\mathscr {B}\) are calculated from \(\rho _s = \rho (r = R)\) and are a bit higher than the more common values around \(60 MeV/fm^3\). Higher MIT Bag constants have been utilised in studies of strange stars [31, 32] wherein it is noted that a higher value softens the equation of state.

The temporal dependence parameter, a, is calculated to be

$$\begin{aligned} a = \left( \frac{A_0' }{B_0}\right) _{9.384 km} = 0.03377 km^{-1} \end{aligned}$$
(39)

The mass function (25) is given by

$$\begin{aligned} m(r, f) = f m_0 (r) + 2 r^3 \frac{a^2}{A_0(r)^2}\left( 1 - \sqrt{f} \right) ^2 \end{aligned}$$
(40)

where

$$\begin{aligned} m_0(r)= & {} 4\pi \int {\rho _0(r) r^2}dr= r^3 \left[ \frac{R^3}{M} +\frac{2K}{1 - K}\left( R^2 - r^2 \right) \right] ^{-1} \end{aligned}$$
(41)

is the mass of the initial configuration. The temporal function, evaluated at the time of horizon formation, gives \(f_{bh} = 0.4018\).

7 Dynamical complexity

We give a brief overview of the main mathematical features which may be found by retracing the steps back from the most recent definition of the complexity factor for dissipative self-gravitating systems, given by Herrera et al. [10].

Fig. 1
figure 1

Complexity factor: components and sum

Full size image

In four-dimensional spacetime, unit time-like vector fields enable an orthogonal splitting (also known as 3+1 decomposition) of a tensor. In particular, the Riemann tensor which describes the curvature of the spacetime manifold, can be used to generate the following tensors, namely

$$\begin{aligned} Y_{\alpha \beta }= & {} R_{\alpha \gamma \beta \delta }u^\gamma u^\delta \end{aligned}$$
(42)
$$\begin{aligned} Z_{\alpha \beta }= & {} \frac{1}{2}\eta _{\alpha \gamma \epsilon \rho }{R^{\epsilon \rho }}_{\beta \delta }u^\gamma u^\delta \end{aligned}$$
(43)
$$\begin{aligned} X_{\alpha \beta }= & {} \frac{1}{2}{\eta _{\alpha \gamma }}^{\epsilon \rho }R^*_{\epsilon \rho \beta \delta }u^\gamma u^\delta \end{aligned}$$
(44)

where

$$\begin{aligned} R^*_{\alpha \beta \gamma \delta }= & {} \frac{1}{2}\eta _{\epsilon \rho \gamma \delta }{R_{\alpha \beta }}^{\epsilon \rho } \end{aligned}$$
(45)

and \(\eta _{\alpha \beta \gamma \delta }\) is the Levi-Civita tensor which gives the four-dimensional volume element. This orthogonal splitting was first studied by Bel [11] and then followed up by Gómez-Lobo [12]. Herrera et al. [33] did further calculations in order to express the above tensors in terms of the physical quantities according to the Einstein field equations so that the following may be obtained:

$$\begin{aligned} Y_{\alpha \beta }= & {} \frac{4\pi }{3} \left( \rho + p_r + 2p_t \right) h_{\alpha \beta } \nonumber \\&+ 4\pi \left( p_r - p_t \right) \left( \chi _\alpha \chi _\beta - \frac{1}{3}h_{\alpha \beta } \right) + E_{\alpha \beta } \end{aligned}$$
(46)
$$\begin{aligned} Z_{\alpha \beta }= & {} \frac{\kappa }{2} q \chi ^\gamma u^\delta \eta _{\delta \alpha \gamma \beta } \end{aligned}$$
(47)
$$\begin{aligned} X_{\alpha \beta }= & {} \frac{\kappa }{3} \rho h_{\alpha \beta } + \frac{\kappa }{2}\left( p_r - p_t \right) \left( \chi _\alpha \chi _\beta - \frac{1}{3}h_{\alpha \beta } \right) \nonumber \\&- E_{\alpha \beta } \end{aligned}$$
(48)

where the Weyl tensor is given in terms of its electric part, namely \(E_{\alpha \beta } = C_{\alpha \gamma \beta \delta } u^\gamma u^\delta \) for spherically symmetric systems. The Weyl tensor may be further expressed as

$$\begin{aligned} E_{\alpha \beta } = E\left( \chi _\alpha \chi _\beta - \frac{1}{3}h_{\alpha \beta }\right) \end{aligned}$$
(49)

where the amplitude E is calculated via the gravitational potentials according to

$$\begin{aligned} E= & {} \frac{1}{2A^2}\bigg [\frac{\ddot{C}}{C} - \frac{\ddot{B}}{B} - \left( \frac{\dot{C}}{C} - \frac{\dot{B}}{B}\right) \left( \frac{\dot{A}}{A} + \frac{\dot{C}}{C}\right) \bigg ] \nonumber \\&+ \frac{1}{2B^2}\bigg [\frac{A''}{A} - \frac{C''}{C} - \frac{2C'}{rC}+ \left( \frac{1}{r} + \frac{B'}{B} + \frac{C'}{C}\right) \nonumber \\&\times \left( \frac{1}{r} +\frac{C'}{C} - \frac{A'}{A}\right) \bigg ] - \frac{1}{2r^2C^2}. \end{aligned}$$
(50)

In terms of our shear-free metric we obtain

$$\begin{aligned} E= & {} \frac{1}{2B_0^2 f^2}\left[ \frac{A_0''}{A_0} + \left( \frac{1}{r} + \frac{B_0'}{B_0}\right) \left( \frac{1}{r} - \frac{A_0'}{A_0}\right) \right] - \frac{1}{2r^2f^2}.\nonumber \\ \end{aligned}$$
(51)

Now, an additional way of expressing tensors (42)-(44) gives rise to five structure scalars (\(X_T, X_{TF}, Y_T, Y_{TF}, Z\)) as follows,

$$\begin{aligned} Y_{\alpha \beta }= & {} \frac{1}{3}Y_T h_{\alpha \beta } + Y_{TF}\left( \chi _\alpha \chi _\beta - \frac{1}{3}h_{\alpha \beta }\right) \end{aligned}$$
(52)
$$\begin{aligned} X_{\alpha \beta }= & {} \frac{1}{3}X_T h_{\alpha \beta } + X_{TF}\left( \chi _\alpha \chi _\beta - \frac{1}{3}h_{\alpha \beta }\right) \end{aligned}$$
(53)
$$\begin{aligned} Z= & {} \sqrt{Z_{\alpha \beta }Z^{\alpha \beta }} = \sqrt{32}\pi q . \end{aligned}$$
(54)

The scalars \(X_T = X_\gamma ^\gamma \) and \(Y_T = Y_\gamma ^\gamma \) are the traces of their respective tensors. The trace-free parts (\( X_{TF} , Y_{TF}\)) may be determined by comparison with Eqs. (46) and (48) and are

$$\begin{aligned} Y_{TF}= & {} 4\pi \Delta + E \end{aligned}$$
(55)
$$\begin{aligned} X_{TF}= & {} 4\pi \Delta - E \end{aligned}$$
(56)

where \(\Delta = p_t - p_r\).

The structure scalar \(Y_{TF}\) has been identified by Herrera et al. [10] as the complexity factor. Further use of the field equations and the Misner and Sharp mass function provide the integral form for \(Y_{TF}\),

$$\begin{aligned} Y_{TF} = 8\pi \Delta + \frac{4\pi }{(Cr)^3}\int _0^r (Cr)^3\left( \rho ' - 3q\frac{B^2}{A}\frac{\dot{C}}{C}\right) dr. \end{aligned}$$
(57)

As applied to our shear-free, separable potential model, we calculate the complexity factor to be

$$\begin{aligned} Y_{TF} = 8\pi \Delta + \frac{4\pi f}{C^3}\int _0^r \left( r^3 \rho _0 ' \right) dr \end{aligned}$$
(58)

where \(\rho _0\) is the static energy density as defined in Sect. 2. We note that the dissipative term in the integral cancels with the time-varying part of the energy density gradient. Equation (58) can be integrated to yield

$$\begin{aligned} Y_{TF} = 8\pi \Delta + \frac{1}{f^2}\left( 4\pi \rho _0 - \frac{3m_0(r)}{r^3}\right) . \end{aligned}$$
(59)

Thus, apart from the anisotropic parameter \(\Delta \), the complexity factor is described in terms of static quantities. For further analysis, we set

$$\begin{aligned} Y_1= & {} 8\pi \Delta \nonumber \\ Y_2= & {} \frac{1}{f^2}\left( 4\pi \rho _0 - \frac{3m_0(r)}{r^3}\right) \end{aligned}$$
(60)

and identify component \(Y_2\) as the energy density inhomogeneity.

Fig. 2
figure 2

Complexity factor temporal progression

Full size image
Fig. 3
figure 3

Complexity factor versus co-moving radial coordinate

Full size image

8 Discussion

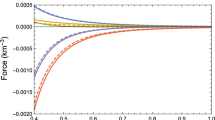
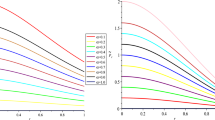
We now turn our attention to studying the evolution of the terms contributing to \(Y_{TF}\). In Fig. 1 we have plotted the components of the complexity factor at the surface as a function of the temporal progression parameter f, for spheroidal parameter \(K= -2\) and \(K= -5\) respectively. In Fig. 1a we observe that the anisotropy is positive, i.e., the radial pressure dominates the tangential pressure while contributions from the density inhomogeneities are negative. This interplay between these two components tends to lead to a vanishing of the complexity factor throughout the evolution of the collapsing star. For \(K = - 5\), which is a further departure from spherical symmetry than the \(K = -2\) model, we observe that complexity is close to zero for early times (\(f = 1\)) and becomes increasingly negative for late times. In Fig. 2 we display the behaviour of the complexity factor as a function of the temporal parameter f for different values of the radial coordinate. For \(K = -2\) we observe that \(Y_{TF}\) is positive at the surface for all time. For the inner collapsing shells located at R/4 and R/2 respectively, the complexity factor becomes negative for all time. This trend is further enhanced as the star departs from spherical symmetry. In Fig. 3 we observe the departure from zero complexity for fixed epochs, viz., early collapse and late-time collapse close to the time of formation of the horizon. It is clear that the fluid is driven further away from vanishing complexity closer to the time of formation of the horizon. This trend has also been observed in terms of the Tolman–Oppenheimer–Volkoff (TOV) forces at play during dynamical collapse. There is a strong connection between the evolution of the complexity factor (sum of anisotropy and inhomogeneity) and the TOV forces (anisotropic, gravitational and hydrostatic forces) [20]. Figure 4 displays the behavior of the complexity factor for \(K = -2\) as a function of the radial and temporal coordinates. We note that \(Y_{TF}\) is smoothly behaved at each interior point of the stellar configuration. For late times, the complexity factor changes sign due to the interplay between pressure anisotropy and density inhomogeneity. The deviation from zero complexity can also be linked to the interplay between the TOV forces within the collapsing fluid.

Fig. 4
figure 4

Complexity factor progression for \(K = -2\)

Full size image

9 Conclusion

In this work we investigated the dynamics of the complexity factor during the evolution of a shear-free radiating sphere undergoing gravitational collapse. We showed that for a shear-free metric in which the potentials are separated into their spatial and temporal components, the dissipative contribution to the complexity factor is cancelled by the time-dependent contribution of the inhomogeneity of the energy density. The complexity factor could then be expressed as a sum of two components viz., contributions from the pressure anisotropy and density inhomogeneities. We utilized the generalized Vaidya–Tikekar solution as the initial static configuration and studied the evolution of the complexity factor as collapse ensued. Several observations were made regarding departure from zero complexity:

  1. (1)

    Deviation from spherical symmetry (larger magnitudes of the spheroidal parameter) leads to enhanced disequilibrium.

  2. (2)

    When the star loses hydrostatic equilibrium, it moves into a regime of increasing complexity due to the interplay between the pressure anisotropy and density inhomogeneity.

  3. (3)

    In this particular model, the magnitude of the complexity increases for all time and at each interior point of the stellar configuration.

For shear-free fluids with separable metric functions, the dissipative contributions to the complexity factor are annihilated by terms from the density inhomogeneity. From a physical standing we can think of the energy radiated in the form of a radial heat flux as being counterbalanced by the collapsing shells with inhomogeneous densities. This highlights the inertial effect of the heat flux which plays an important role in radiating collapse [34]. Furthermore, the contributions of the complexity factor mimic the TOV forces within the stellar fluid [20]. We believe that our findings are novel and show for the first time, in a dynamical collapse model the generation of increased complexity.