1 Introduction

In general theory of relativity, many observations ensure that our universe is undergoing an accelerated expansion. To explain this discovered phenomenon, the universe is supposed to be filled with dark energy within the framework of Einstein’s theory of relativity. Dark energy is the exotic energy part with negative pressure and covers about 72 per cent of this total cosmic energy. The best clarification for dark energy is modelled by cosmological constant [1,2,3,4], which is a term added to Einstein’s field equations (EFEs). This term acts as a perfect fluid with an equation of the state \(\varpi =-1\) and the energy density is associated with the quantum vacuum. Phantom energy is a theoretical type of dark energy satisfying the equation of state \(P=\varpi \rho \) and \(\varpi <-1\) where P and \(\rho \) are denoted by pressure and energy density, respectively. To perceive phantom dark energy, one can change the sign before the kinetic expression of a scalar field known as the phantom scalar field [5]. Phantom fields were first presented in Hoyle’s form and found as a solution for EFEs follow by the variation of Lagrangian densities with the negative sign of kinetic terms. This sort of exotic field is explored in scalar and electromagnetic fields by [6]. In the past few years, the phantom fields only provide the theoretical motivation but recent discoveries in cosmological observations have provided the opportunity to discuss its physical properties [7]. Aside from different investigations in cosmology, the impact of the phantom field in BH physics has widely been examined [8].

Many authors [9, 10] have discovered a phantom field model which has negative dynamic energy and understands its evolution by considering \(\varpi <-1\). Although the presentation of a phantom field causes numerous theoretical issues, for example, the violation of some well-known energy conditions and a rapid vacuum decay [11], it is still interesting as it is the best-fitted model in current observations. The phantom scalar fields have been investigated in the classical and quantum field theory by many authors [12]. A scalar field with negative kinetic energy might represent an explicit threat to the stability of the vacuum states [13].

Over the last few years, the thermodynamical properties of BH are an active area of research in theoretical physics [14, 15]. In general relativity and modern physics, there are many similarities between the physical properties of the black holes (BHs) and the laws of thermodynamics. Moreover, BH physics is the most important topic in general relativity and quantum gravity [16,17,18]. Investigation of the thermodynamic functions of the charged AdS BH confirmed that there exists a closed relationship between astrophysical signatures and the liquid–gas framework. The first invention in this line is Hawking-Page phase-transition [19], which illustrates the phase-transition among the thermal AdS space and consequently the Schwarzschild AdS BH. Particularly, Reissner–Nordström (RN) AdS BH presents first-order phase transitions whose critical behaviour is much like the consolidated matter [20, 21]. Chamblin et al. investigated the phase-transition of RN-AdS BHs [22] and found a close relationship between charged AdS BHs and consequently the fluid gas system.

Recently, Kubiznk and Mann [25] generalized this connection by analyzing the P–V criticality within the extended phase space along with the thermodynamical Pressure and thermodynamical quantity [20]. In this aspect, one can find a detailed discussion about the concept of cosmological constant treated as a thermodynamical pressure and the similarity between phase transitions, liquid–gas systems and other important astrophysical signatures, see in detail, [26, 30, 31]- [37]. The thermodynamical properties of a BH are intensively studied in the literature, see in [42,43,44,45]. It is known that the specific heat of the Schwarzschild BH is usually negative and the BH is thermodynamically unstable. On the other hand, the RN BH contains two regions, positive and negative. Positive regions describe the stability of the BH and therefore the negative region represents the instability of the system. Davies discussed the phase-transition in BH thermodynamics and consequently, find the second-order phase-transition in the divergencies of specific heat [46, 47]. Husain and Mann [48] indicate that specific heat of the BH turns into positive when phase transition approaches the Plank Scale [49]. Another achievement in BHs physics was the perception of a phase-transition [50] in charged AdS BHs, like that found in a VdW liquid–gas system. Recognizing the importance of thermodynamics in AdS space, we will study the background of dynamic phantom AdS BHs and discuss the small-large BH phase transition. There are also various strategies for examining the structure of a dynamic phantom BH system close to a critical point [31].

Our aim in this paper is to explain the thermodynamical properties of the dynamic phantom AdS BH and additionally examine the critical behaviour and stability for different values of state parameter \(a^2\). Next, we discuss the P–V criticality and find the exact universal number of VdW gas/fluids which shows the presence of inter-molecular forces in gas. Moreover, we also investigate Gibbs free energy G and discuss its swallow-tail behaviour of the dynamic phantom AdS BH. This work is presented as follows. In Sect. 2, we discuss the solution of the dynamic phantom AdS BH metric. In Sect. 3, we examine the thermodynamics of the dynamic phantom AdS BH. In Sect. 4, we examine the critical behaviour by utilizing the P–V Criticality. In Sect. 5, we investigate Joule–Thomson expansion for dynamic phantom AdS BH. In Sect. 6, we discuss thermal stability and in Sect. 7, we find the Gibbs free energy G and discuss the Swallow-tail behaviour [18, 22].

Fig. 1
figure 1

The metric function W(r) for distinct values of \(\Lambda \) and e at fixed \(g=0.6\) and \(M=1\). Left Panel: \(a^2=1\) and right panel: \(a^2=2\)

Full size image

2 Dynamic phantom AdS black hole solution

The Einstein-Hilbert with massless phantom fields with a negative sign of cosmological constant is given by

$$\begin{aligned} S=\frac{1}{16 \pi G} \int d^4 x \sqrt{-g}\left[ R-2 \Lambda +\frac{1}{2} \sum _{i=1}^2 (\partial \Psi _i)^2\right] . \end{aligned}$$
(1)

In the above equation, Gravitational constant is denoted by G and \(\Psi _i\) is the phantom massless scalar fields [5]. In 4D, the connection among the cosmological constant \(\Lambda \) with negative sign and charged AdS radius curvature l is given as follows

$$\begin{aligned} \Lambda =-\frac{3}{l^2}. \end{aligned}$$
(2)

The equations of the Einstein’s field within the presence of cosmological constant \(\Lambda \) corresponding with action (1) read

$$\begin{aligned} T_{\mu \nu } = R_{\mu \nu } -\frac{1}{2} g^{\mu \nu } R+ \Lambda g^{\mu \nu }, \end{aligned}$$
(3)

where the energy momentum tensor is

$$\begin{aligned} T_{\mu \nu } =\sum _{i=1}^{2} \left[ - \nabla _{\mu }\Psi _i \nabla _{\nu }\Psi _i +\frac{1}{2} g_{\mu \nu } (\nabla {\Psi _i})^2\right] . \end{aligned}$$
(4)

The equation of motion is given as

$$\begin{aligned} \nabla ^{2}\Psi _i=0. \end{aligned}$$
(5)

It is important to mention here the features of Ricci flat horizon on this framework with that metric is given as

$$\begin{aligned} ds^2=-W(r) dt^2+\frac{1}{W(r)} dr^2+r^2(dx^{2}+dy^{2}). \end{aligned}$$
(6)

With this metric, one has the non-zero part of Ricci tensor given as follows [5, 54]:

$$\begin{aligned} R_{tt}= & {} \frac{1}{2}W W''+\frac{1}{r}W W', \end{aligned}$$
(7)
$$\begin{aligned} R_{rr}= & {} \frac{1}{2}\frac{W''}{W}+\frac{1}{r}\frac{W'}{W}, \end{aligned}$$
(8)
$$\begin{aligned} R_{xx}= & {} R_{yy}=-(W+rW'), \end{aligned}$$
(9)

where \(W'\), \(W''\) are first and second derivatives w. r. t. r, respectively. We can write Ricci scalar as:

$$\begin{aligned} R= & {} g^{tt}R_{tt}+g^{rr}R_{rr}+g^{ij}R_{ij}\nonumber \\= & {} -W''-\frac{4}{r} W'-\frac{2}{r^2} W, \end{aligned}$$
(10)

where t and r are the independent coordinates of the fields. Scalar fields as a component of transverse coordinates:

$$\begin{aligned} \Psi _1= & {} b\mathbf{x }, \end{aligned}$$
(11)
$$\begin{aligned} \Psi _2= & {} b\mathbf{y }, \end{aligned}$$
(12)

where b is constant. One can observe that the equation of the motions satisfied matter and gravitational fields if W(r) takes in the form:

$$\begin{aligned} W(r)=a^2- \frac{1}{3} r^2 \Lambda - \frac{2M}{r}, \end{aligned}$$
(13)

where M is the parameter concerning the mass of the solution. Indeed, this solution narrates an AdS BHs with a Ricci flat horizon. One can notice the impact of state parameter \(a^2\) in the solution of phantom fields. In the absence of the phantom scalar fields (\(a=0\)), in Einstein gravity, the solution decreases to AdS BH solution with Ricci flat horizon.

3 Dynamic phantom AdS black hole thermodynamics

The solution (13) can be generalized by utilizing the electric charge e and magnetic charge g from the Maxwell field. Within the sight of Maxwell field in action Eq. (1), the dynamic phantom AdS BH solution is given by

$$\begin{aligned} W(r)=a^2-\frac{1}{3} r^2 \Lambda -\frac{2M}{r}+\frac{e^2 + g^2}{r^2}, \end{aligned}$$
(14)

where W(r) is the metric function of dynamic phantom AdS BH [55] The BH event horizon can be calculated by taking \(W(r)=0\), which provides the mass in terms of horizon [49, 56]

$$\begin{aligned} M=\frac{\Lambda r_+^4-3a^2 r_+^2-3e^2-3g^2}{-6r_+}. \end{aligned}$$
(15)

The graphical representation of the metric function of dynamic phantom AdS BH is presented in Fig. 1 for distinct values of cosmological constant \(\Lambda \) [57, 58]. For \(a^2=1\), we find the maximum of two roots and for \(a^2=2\), we have a maximum of three roots.

The Bekenstein–Hawking entropy of dynamic phantom AdS BH is given by [59]

$$\begin{aligned} S_{BH}= \pi r_+^2. \end{aligned}$$
(16)

We can express the BH mass by using the area law [16, 18]

$$\begin{aligned} M(S,\Lambda )=\frac{-3\pi e^2-3\pi g^2-3\pi S a^2+\Lambda S^2}{-6\sqrt{S} \pi ^{\frac{3}{2}}}. \end{aligned}$$
(17)

With the interpretation that the pressure P is associated to cosmological constant \(\Lambda \) as [20]

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }. \end{aligned}$$
(18)

Moreover, by using Eqs. (17) and (18) we get

$$\begin{aligned} M(S,P)=\frac{8P S^2+3\pi e^2+3\pi g^2+3S a^2}{6\sqrt{\pi } \sqrt{S}}. \end{aligned}$$
(19)

The thermal property of the dynamic phantom AdS BH is temperature and it is easy to point out that Mass M, Hawking Temperature T and Entropy S of the dynamic phantom AdS BH from the first law of BH thermodynamics.

$$\begin{aligned} T= \frac{\partial M}{\partial S}. \end{aligned}$$
(20)

The Hawking Temperature can be calculated as [60,61,62]

$$\begin{aligned} T= \frac{1}{4 \sqrt{\pi S}} \left( a^2 - \frac{\pi (e^2 + g^2)}{S} +8PS\right) . \end{aligned}$$
(21)

4 P–V criticality

Here we will explore the P–V criticality of the dynamic phantom AdS BH. The significant relationship between the cosmological constant and thermodynamical pressure in Eq. (18) produces significant outcomes in VdWs like behaviour and first-order phase transition. The VdW fluid is the first, simplest and most extensively used model of an associating system of particles that show a phase transition. A first-order phase transition appears when the VdW theory of the pressure (P) versus volume (V) isotherms is complemented by the Maxwell construction [63] to define the regions of coexistence of gas.

By using Eq. (21), one can find

$$\begin{aligned} P=\frac{T}{2r_+}-\frac{a^2}{8 \pi r_{+}^2}+ \frac{e^2 + g^2}{8 \pi r_{+}^4}. \end{aligned}$$
(22)

Since we want to compare Eq. (22) with van der Waals equation and further applying series expansion to van der Waals equation with inverse of specific volume V, one can identify the specific volume V with \(r_+\) of the BHs i.e. \(V= 2r_+\) [66, 68, 69]. Hence, one can find

$$\begin{aligned} P=\frac{T}{V}-\frac{a^2}{2 \pi V^2}+ \frac{2(e^2 + g^2)}{ \pi V^4}. \end{aligned}$$
(23)

We can calculate the critical points from Eq. (23) by utilizing the following conditions [14, 38, 39].

$$\begin{aligned} \frac{\partial P}{\partial V}= & {} 0, \nonumber \\ \frac{\partial ^2 P}{\partial V^2}= & {} 0. \end{aligned}$$
(24)

The corresponding critical temperature \(T_c\), critical volume \(V_c\), and critical pressure \(P_c\) are given below

$$\begin{aligned} T_c= & {} \frac{a^3}{3\pi \sqrt{24e^2 + 24g^2}},~~~V_c=\frac{\sqrt{24e^2 + 24g^2}}{a},\nonumber \\ P_c= & {} \frac{a^4}{96\pi (e^2 + g^2)}. \end{aligned}$$
(25)

These formulas of critical values lead us to the critical compressibility factor [40]

$$\begin{aligned} \frac{P_c V_c}{T_c}=0.375000=\frac{3}{8}. \end{aligned}$$
(26)

This ratio represents the critical compressibility factor which measures the behaviour of the ideal fluid and that is perfectly matched with that of the VdW gas/fluids model and known as the universal number and modelled for all fluids [14]. Meanwhile, for the VdW fluid, one can construct a universal dimensionless quantity \(\frac{P_c V_c}{T_c}\) by employing the essential thermodynamic quantities, with \(V_c\) being the critical specific volume [18, 74]. In RN AdS BH, that ratio is also equivalent to VdW gas. Hence, dynamic phantom AdS BH also allows another signature of VdW like connections within the critical phenomena [41, 50].

For \(T<T_c\), an oscillating part of the isotherm represents the unstable region where the isothermal compressibility is negative, i.e.,

$$\begin{aligned} k_T = -\frac{1}{V}\frac{\partial V}{\partial P}\mid _T < 0. \end{aligned}$$
(27)

This instability is replaced by an isobar (the horizontal line) via the Maxwell equal area construction, \( \oint V \,dP = 0\), indicating that the SBH and LBH have a first-order phase transition. The small-large BH transition region, calculated by Maxwell construction has the forms [51]

$$\begin{aligned} {\tilde{T}}^2= & {} \frac{{\tilde{P}}(3-\sqrt{{\tilde{P}}})}{2}, \end{aligned}$$
(28)
$$\begin{aligned} {\tilde{P}}= & {} \frac{7+6 {\tilde{V}}^\frac{2}{3}-4( \sqrt{3+6 {\tilde{V}}^\frac{2}{3})}}{ {\tilde{V}}^ \frac{4}{3}}, \end{aligned}$$
(29)

where the reduced thermodynamic variables are defined as

$$\begin{aligned} {\tilde{T}}=\frac{T}{T_c},~~~{\tilde{P}}=\frac{P}{P_c},~~~{\tilde{V}}=\frac{V}{V_c}. \end{aligned}$$
(30)

It is worthwhile to note that the two phases of small and large BHs cannot be distinguished above the critical point [52, 53].

Fig. 2
figure 2

P–V plot of dynamic phantom AdS BH with \(e=0.2\), \(g=0.6\), \(a^2=1\) (left) and \(a^2=2\) (right). In both graphs the isotherm decreases from top to bottom. The zeroth and first order phase transition are characterized different colors. The isobar (black thin line) remedy unphysical locally and globally unstable regime

Full size image

The plot pressure vs volume by utilizing the Eq. (23) in Fig. 2 shows the behaviour like the VdW gas/fluids model. The left and right figures correspond to the case of fixed electric \(e=0.2\) and magnetic charges \(g=0.6\), respectively. The critical temperature curve is depicted by the red dotted line. The lower dashed-dotted line corresponds to a small temperature \(T<T_c\), which divides the curve into three branches of BH, one unstable and two stable configurations. These two stable configurations have a positive compression coefficient (P decreases as V increases). We also have an unstable region with a negative compression coefficient (P increases as V increases) between these two regions at which the BH of intermediate size can represent the mixture of liquid and gas phases. In a high-temperature case \(T>T_c\), the BHs behave like an ideal gas and no phase transition occurs. We notice that by increasing the value of the state parameter the pressure increased and also shifted towards the singularity [40, 70, 71].

Fig. 3
figure 3

Hawking temperature T versus Entropy S at constant electric charge \(e=0.1\) and magnetic charge \(g=0.4\). Left panel: \(a^2=1\) and right panel: \(a^2=2\)

Full size image

Now, we focus on studying the T–S plots of the dynamic phantom AdS BH in Fig. 3 [14, 18, 49]. In the left panel: the temperature shows critical behaviour in the region \(0.47<S<2.5 \).

In the right panel: the temperature shows critical behaviour when \(0.22<S<0.9\). The behaviour of the isotherm resembles the VdW fluids. One can notice that by increasing the state parameter \(a^2\), the temperature also increases which indicates that the state parameter plays an important role in the stability of dynamic phantom AdS BH.

Table 1 At \(a^2=1\) and \(e=0.1\)
Full size table
Table 2 At \(a^2=1\) and \(g=0.6\)
Full size table

Moreover, we observe that the effect of different parameters on important physical quantities of dynamic phantom AdS BH. In Tables 1, 2, 3 and 4, we observe that by increasing the charge \(T_c\) and \(P_c\) shows the decreasing behavior while \(V_c\) increases and importantly the ratio is equal to the universal number of VdW gas model of all fluids. We also observe that by increasing the state parameter all critical values of physical quantities increased significantly.

Next, we discuss the critical exponents which help us to describe the behavior of a system near the critical point. The critical exponents \(\alpha , \beta , \gamma , \delta \) can be expressed in terms of power law, as [66, 67]:

$$\begin{aligned}&C_v= T \Big (\frac{\partial S }{\partial T}\Big )_v \propto \mid t\mid ^{-\alpha }, \end{aligned}$$
(31)
$$\begin{aligned}&\eta \propto \mid t\mid ^{\beta }, \end{aligned}$$
(32)
$$\begin{aligned}&k_T \propto \mid t\mid ^{-\gamma }, \end{aligned}$$
(33)
$$\begin{aligned}&\mid P-P_c\mid \propto \mid V-V_c\mid ^{\delta }, \end{aligned}$$
(34)

where \(\alpha , \beta , \gamma \) and \(\delta \) characterize the behaviour of specific heat at constant volume, order parameter, isothermal compressibility and pressure, respectively. One can easily find the critical exponents for dynamic phantom AdS BHs are \(\alpha =0, \beta =\frac{1}{2}, \gamma =1\) and \(\delta =3\) which are exactly equal to the critical exponents of van der Waals liquid–gas system. These components are independent of each other [40]. It also provides additional property for dynamic phantom AdS BH.

Table 3 At \(a^2=2\) and \(e=0.1\)
Full size table
Table 4 At \(a^2=2\) and \(g=0.6\)
Full size table
Fig. 4
figure 4

Inversion curves for dynamic phantom AdS BH. Left Panel: \(a^2=1\) and right panel: \(a^2=2\)

Full size image
Fig. 5
figure 5

Inversion and isenthalpic curves for dynamic phantom AdS BH for \(a^2=1\)

Full size image

5 Joule–Thomson expansion

Fig. 6
figure 6

Inversion and isenthalpic curves for dynamic phantom AdS BH for \(a^2=2\)

Full size image

Here, we discuss the Joule–Thomson expansion for dynamic phantom AdS BH. It is well known that the BH mass is considered as an enthalpy in AdS space [26]. During the expansion process, the characteristic of the expansion is that temperature changes with pressure, and enthalpy remains constant. It means that our isenthalpic curves are constant. We know from [27, 28] that the mass of the BH is determined as enthalpy in the AdS space, so the mass of the BH remains constant during the expansion process. To investigate the Joule–Thomson expansion, its coefficient serves as an important physical quantity whose sign can be utilized to determine whether heating or cooling will occur. For a fixed charge, the Joule–Thomson coefficient is given as follows [29],

$$\begin{aligned} \mu = \Big (\frac{\partial T}{\partial P}\Big )_M=\frac{1}{C_p}\Big [T \Big (\frac{\partial v}{\partial T}\Big )\Big ] -v. \end{aligned}$$
(35)
Fig. 7
figure 7

Event horizon of dynamic phantom AdS BH for \(a^2=1\). A: \(e^2=0.36\), \(g^2=0.64\), B: \(e^2=0.04\), \(g^2=1.96\), C: \(e^2=1\), \(g^2=9\), D: \(e^2=4\), \(g^2=16\)

Full size image

The equation of temperature can be written in term of volume as

$$\begin{aligned} T_i= & {} \frac{6^{1/3}\Big (12P v^{4/3} \pi ^{2/3} + 6^{1/3} v^{2/3} \pi ^{1/3} a- \frac{2}{3}6^{2/3} \pi (e^2 + g^2)\Big )}{ 12\pi v}, \nonumber \\= & {} \frac{8\pi P r_+^4 + a r_+^2-(e^2 + g^2)}{4\pi r_+^3} , \end{aligned}$$
(36)

and the inversion temperature is calculated by utilizing Eq. (35)

$$\begin{aligned} T_i= & {} \frac{-12 6^{1/3} P v^{5/3} \pi ^{2/3} + 6^{2/3} v \pi ^{1/3} a- 12 v^{1/3} \pi (e^2 + g^2)}{36 \pi v^{4/3}}, \nonumber \\= & {} \frac{8\pi P r_+^4 - a r_+^2+ 3e^2 + 3g^2}{12\pi r_+^3}. \end{aligned}$$
(37)

By subtracting Eq. (37) from (36), on can obtain

$$\begin{aligned} {2a r_+^2}+{8 \pi P r_+^4}- 3(e^2 + g^2)=0, \end{aligned}$$
(38)

and solving the above equation, the real positive root is given by

$$\begin{aligned} r_+= \frac{\sqrt{2 \pi P\Big (-a+\sqrt{24\pi P (e^2 + g^2)+a^2}\Big )}}{4\pi P}. \end{aligned}$$
(39)

By using this root and Eq. (36), the inversion temperature is given as

$$\begin{aligned} T_i= \frac{\sqrt{2 P} \Big (-a\sqrt{24\pi P (e^2 + g^2) +a^2}+16\pi (e^2+ g^2) P + a^2\Big )}{2\sqrt{\pi }\Big ({-a+\sqrt{24\pi P (e^2 + g^2) +a^2}}\Big )^{\frac{3}{2}}}.\nonumber \\ \end{aligned}$$
(40)

In Fig. 4, inversion curves are presented for various values e and g. There is only a lower inversion curve. The branch above the inversion curve is the cooling region, and the branch below the inversion curve is the heating region. In contrast to Van der Waals fluids, the expression inside the square root in Eq. (40) is always positive, so this curve does not terminate at any point.

Fig. 8
figure 8

Event horizon of dynamic phantom AdS BH for \(a^2=2\). A: \(e^2=0.36\), \(g^2=0.64\), B: \(e^2=0.04\), \(g^2=1.96\), C: \(e^2=1\), \(g^2=9\), D: \(e^2=4\), \(g^2=16\)

Full size image

Next, we plot isenthalpic, i.e constant mass, curves in the T–P plane. From Eqs. (19) and (23), one can get the isenthalpic curves in the T–P plane. In Figs. 5 and 6, inversion and isenthalpic curves are presented for \(a^2=1\) and \(a^2=2\), respectively. Cooling happens in a region where isenthalpic curves have a positive slope over the inversion curves. Heating occurs in the region where the sign of the slope changes under the inversion curves. It is very important to discuss the naked singularities for dynamic phantom AdS BH.

In Figs. 7 and 8, we plot \(r_+\) versus mass (enthalpy) and pressure. We present four 3D plots, which relate to \(e=0.6,0.2,1,2\) and \(g=0.8,1.4,3,4\), respectively. The regions can be seen that denote the naked singularities in Figs. 7 and 8. One can’t think about Joule–Thomson expansion because of the absence of an event horizon for a naked singularity. For instance, we cannot characterize event horizon for \(e=2\), \(g=4\) and \(M\ge 2\). For these values, an event horizon is imaginary and it relates to naked singularity, the isenthalpic curves in the T–P plane are imaginary [64].

6 Thermal stability

Furthermore, we want to explore thermal stability which is the most important thermodynamic property that indicates the system’s behaviour after a small deviation among thermodynamical parameters. Specific heat is the most significant physical quantity in thermodynamics, which shows the thermal stability and instability of the system. Positive specific heat shows the stability and a negative value of specific heat show instability of the system. Conventionally, we find the specific heat for dynamic phantom AdS BHs in two different ways. First, the specific heat of the dynamic phantom AdS BHs at constant volume are stated as

$$\begin{aligned} C_V= T \Big (\frac{\partial S }{\partial T}\Big )_V=0. \end{aligned}$$
(41)

From Eq. (41), one can notice that if V and S are constants then isochoric processes are additionally adiabatic for dynamic phantom AdS BH due to the connection between volume and entropy [18]. Secondly, at constant pressure Specific heat [14] can be written as, Eq. (42),

$$\begin{aligned} C_p= & {} T \Big (\frac{\partial S }{\partial T}\Big )_P, \end{aligned}$$
(42)
$$\begin{aligned} C_p= & {} \frac{-2 S \Big (-8P S^2+\pi e^2+\pi g^2-S a^2\Big )}{8P S^2+3\pi e^2+3\pi g^2-S a^2}. \end{aligned}$$
(43)
Fig. 9
figure 9

\(C_p\) versus S with \(a^2 = 1\), \(e=0.2\) and \(g=0.6\). Left panel: \(P=P_c\), middle panel: \(P>P_c\) and right panel: \(P<P_c\)

Full size image
Fig. 10
figure 10

\(C_p\) versus S with \(a^2 = 2\), \(e=0.2\) and \(g=0.6\). Left panel: \(P=P_c\), middle panel: \(P>P_c\) and right panel: \(P<P_c\)

Full size image

In Fig. 9, for \(a^2 = 1\), we plot \(C_p -S\) to find the order of Phase-transition for the dynamic phantom AdS BH. We observe that there is no singularity for \(P>P_c\), find one singularity at \(P=P_c\) and produces two singularities at \(P<P_c\). In the left panel, there are two unique regions separated by a singularity i.e. SBH and LBH lie in positive specific heat. At \(P=P_c\), SBH and LBH are thermodynamically stable. The middle panel shows the most important finding for dynamic phantom AdS BH is the singularity disappears at \(P>P_c\), In the right panel, we have two singularities at \(P<P_c\) which divides the region into three parts i.e. SBH and LBH lie in the positive region which shows the stability while IBH lies in the negative Specific heat that presents the unstability of the system [14, 72]. In Fig. 10, for \(a^2 = 2\), we observe a similar behavior as in Fig. 9. It is important to mention here that by increasing the state parameter overall stability of the system is also increased which provides evidence that the state parameter plays a vital role in the stability of the system.

Furthermore, one can analyze other response functions such as the volume expansivity \(\beta \) is given by [64, 73]

$$\begin{aligned} \beta = \frac{1}{V}\Big (\frac{\partial V }{\partial T}\Big )_P. \end{aligned}$$
(44)

The volume expansivity \(\beta \) for dynamic phantom AdS BH is given by

$$\begin{aligned} \beta = \frac{4S^{\frac{3}{2}} \sqrt{\pi }}{8PS^2 +3 \pi (e^2 + g^2)-S a^2} \cong \frac{1}{P}. \end{aligned}$$
(45)

The isothermal compressibility \(\kappa \) is as follows

$$\begin{aligned} \kappa _T = - \frac{1}{V}\Big (\frac{\partial V }{\partial P}\Big )_T. \end{aligned}$$
(46)

By utilizing Eq. (23), the isothermal compressibility \(\kappa \) for dynamic phantom AdS BH is given as

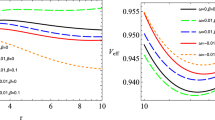
$$\begin{aligned} \kappa _T = \frac{4S^{\frac{5}{2}} \sqrt{\pi }}{2\pi T S^2 +2 \pi ^{\frac{3}{2}}\sqrt{S} (e^2 + g^2)-S^{\frac{3}{2}} \pi a^2} \cong \frac{1}{T} \end{aligned}$$
(47)

We also plot the curves of \(\beta -S\), \(\kappa -S\) in Figs. 11, 12, 13, 14, respectively. We can see from these curves that there is an infinite peak in the dynamic phantom AdS BH. In Figs. 11, 12, we plot \(\beta - S\) to describe the phase transition of the dynamic phantom AdS BH. In Fig. 11, for \(a^2=1\), at \(P=P_c\), one can locate two singular points, which divide the graph into two regions i.e. SBH and LBH lie in positive region. The singularity disappears at \(P>P_c\) and \(P<P_c\) shows two singular points at \(S=5.1\), \(S=14.5\) which divides the region into three parts i.e. SBH, IBH and LBH. In Fig. 12, for \(a^2=2\), the plot shows similar behaviour. We also observe that by increasing the value of state parameter \(a^2\) the singularity moves towards the origin. The surprising results \(\beta \cong \frac{1}{P}\) and \(\kappa \cong \frac{1}{T}\) are obtained for dynamic phantom AdS BHs which resembles ideal gas.

Fig. 11
figure 11

\(\beta \) versus S with \(a^2 = 1\), \(e=0.2\) and \(g=0.6\). Left panel: \(P=P_c\), middle panel: \(P>P_c\) and right panel: \(P<P_c\)

Full size image
Fig. 12
figure 12

\(\beta \) versus S with \(a^2 = 2\), \(e=0.2\) and \(g=0.6\). Left panel: \(P=P_c\), middle panel: \(P>P_c\) and right panel: \(P<P_c\)

Full size image

In Figs. 13, 14, for \(a^2=1\), we plot \(\kappa - S\) at \(T=T_c\) and \(T<T_c\), the singularity points are \(S=7.2, 7.9\) and \(S=4.1, 19.7\), respectively. The singularity disappears at \(T>T_c\). In Fig. 14, for \(a^2=2\), the plot shows similar behaviour as in Fig. 13. We also observe that by increasing the value of state parameter \(a^2\) the singularity moves towards the origin. From these graphs, One can conclude the behaviour of state parameter \(a^2\) plays an important role.

Fig. 13
figure 13

\(\kappa \) versus S with \(a^2 = 1\), \(e=0.2\) and \(g=0.6\). Left panel: \(T=T_c\), middle panel: \(T>T_c\) and right panel: \(T<T_c\)

Full size image
Fig. 14
figure 14

\(\kappa \) versus S with \(a^2 = 2\), \(e=0.2\) and \(g=0.6\). Left panel: \(T=T_c\), middle panel: \(T>T_c\) and right panel: \(T<T_c\)

Full size image

7 Gibbs free energy

Finally, we discuss the behaviour of Gibbs free energy G, which is the important parameter to finding the thermodynamical phase transition. Gibbs energy \(G=M-TS\) [14, 74] is a thermodynamic Potential that can be calculated by utilizing Eqs. (19), (21),

$$\begin{aligned} G=M-TS= \frac{-8P S^2+9\pi e^2+9\pi g^2+3S a^2}{12 \sqrt{S \pi }}. \end{aligned}$$
(48)
Fig. 15
figure 15

G versus S with \(e=0.2\), \(g=0.6\). Left panel: \(a^2=1\) and right panel: \(a^2=2\)

Full size image

We investigate the behaviour of G vs S in Fig. 15 and also discuss the stability and instability of the dynamic phantom AdS BH. In the left and right figures, we can see the behaviour of the parameter in which the Gibbs free energy at critical pressure \(P_c=0.00828\) produces a local minimum near a critical value of S. We observe that the overall stability of the system increased for higher values of the state parameter. One can find the local minima near the critical value of S at critical pressure, also the local minima shifted towards the singularity for higher values of state parameter \(a^2\).

Fig. 16
figure 16

Gibbs free energy G versus Temperature T for the fixed Pressure and \(e=0.2\), \(g=0.6\). Left panel: \(a^2=1\) and right panel: \(a^2=2\)

Full size image
Fig. 17
figure 17

Gibbs energy vs Temperature for the fixed Pressure, \(e=0.1\) and \(g=0.2\). left panel: \(a^2=1\), right panel: \(a^2=2\)

Full size image

The VdW like phase-transition between two distinct phases is characterized by a Swallow-tail shape in Figs. 16 and 17. In the case of dynamic phantom AdS BH solutions, such behaviour represents a SBH and LBH phase-transition [66, 75]. In these figures, we observe that swallow-tail behaviour shows only below the critical pressure \(P<P_c\) which shows the unstability of the system, while \(P\ge P_c\) swallow-tail behaviour vanishes which shows the stability of the system. It is important to mention here the overall system stability increases by considering the higher values of the state parameter which shows the vital role of the state parameter in dynamic phantom AdS BH. By comparing both Figs. 16, 17, we can conclude that Swallow-tail appears only below the critical pressure and it vanishes for \(P \ge P_c\) which is the significant finding of the dynamic phantom AdS BH.

8 Conclusion

In this work, we have investigated the thermodynamics, criticality, Joule Thomson Expansion and Gibbs free energy of the dynamic phantom AdS BH. The electric charge e has a phantom nature because the electromagnetic energy density that enters the corresponding action is negative [7]. The investigation of thermodynamic behaviour has uncovered several interesting results and P–V criticality, Joule Thomson Expansion, specific heat, response functions and Gibbs free energy also produce the most interesting and significant results of the dynamic phantom AdS BH [70]. We have also obtained different thermodynamic parameters like critical temperature \(T_c\), critical pressure \(P_c\) and critical volume \(V_c\) by utilizing Eq. (25) for dynamic phantom AdS BH.

The significant result \(\frac{P_c V_c}{T_c}\) is obtained by utilizing critical values [77] which models the VdW gas/fluid, that is exactly matched to 3/8 also known as the Universal number for dynamic phantom AdS BH. This ratio represents the critical compressibility factor which measures the behaviour of the ideal fluid and that is perfectly matched with VdW gas/fluids model [14]. This factor model the intermolecular forces in gases. It is important to mention here that this ratio remains the same at 3/8 by variating the state parameter \(a^2\).

Next, we have presented the Joule–Thomson expansion for dynamic phantom AdS BHs. BHs generally cool above the inversion curve and heat below the inversion curve during the Joule–Thomson expansion. Cooling and heating regions were displayed for different values of the charge e, g and mass M (enthalpy) [24]. We have also investigated the naked singularity which is not suitable for Joule–Thomson expansion because of the absence of an event horizon [64, 65].

Moreover, the \(C_p\) vs S produces the second order, first order and zero-order phase transitions at \(P<P_c\), \(P=P_c\) and \(P>P_c\), respectively. A phase transition is described through divergences in second moments like specific heat and compressibility in statistical mechanics. The presence of local minimum in the \(G-S\) plot shows a thermodynamic instability [14]. We have explored the other response functions \(\beta \) volume expansibility and \(\kappa _T\) isothermal compressibility which produces similar findings like \(C_p\) [73]. The surprising results \(\beta \cong \frac{1}{P}\) and \(\kappa \cong \frac{1}{T}\) are obtained for dynamic phantom AdS BHs which resemble ideal gas.

Furthermore, we can see that the G surface demonstrates the characteristic of Swallow-tail behaviour, which indicates the occurrence of VdW like SBH/LBH phase transition below the critical pressure \(P<P_c\) in the corresponding system while at critical pressure \(P\ge P_c\), the Swallow-tail behaviour vanishes [74]. It is worth mentioning that the system is stable at \(P>P_c\) and higher values of state parameters. Hence, the state parameter \(a^2\) plays a vital role in the stability of dynamic phantom AdS BH.