Echoes from asymmetric wormholes and black bounce

Abstract

The time evolutions of the field perturbations in certain asymmetric wormhole and black bounce backgrounds are investigated. It is found that the echo signals arise only in some wormhole cases. We examine the influences of these wormhole echoes by their mass and charge, as well as the asymmetry of spacetime. The results show that a massive wormhole with smaller charge is easier to observe echo signals. Particularly, the asymmetry of wormhole spacetime causes lower frequency echoes. Besides, analytical results show that the negative regions of effective potentials are enclosed by the black hole horizons for a class of symmetric black bounce metrics. This suggests the stability of these symmetric metrics.

1 Introduction

Black holes and wormholes are two typical fascinating solutions of General Relativity. Recently, progress in astrophysical experiments has attracted a lot of interest in black hole physics. Two breakthroughs in this field are the first image of a black hole with the Event Horizon Telescope [1,2,3] and the observation of gravitational waves from a binary black hole merger [4]. Especially, there is a growing number of detected cases of GWs reported by LIGO Scientific Collaboration and Virgo Collaboration [5,6,7], which provides a lot of concrete examples to study the properties of black holes.

However, many studies pointed out that there is no sufficient evidence to claim that the GWs ringdown signals come from black holes [8, 9]. In Ref. [9] and earlier research in Ref. [10], the authors suggested that the horizonless objects can mimic black holes in the sense of initial ringdown signals. The compact horizonless objects involve neutron stars [11], boson stars [12] and wormholes [9, 13,14,15,16,17] and so on. The original concept of wormholes is proposed by Ludwig Flamm in 1916 [18]. Then Morris and Thorne systemically studied the properties of traversable wormholes [19]. They found that the existence of traversable wormhole needs exotic matters. Ellis [20] and Bronnikov [21] obtained the first eponymous wormhole solution respectively by introducing a free phantom scalar as the exotic matter. Due to the widespread interest in wormhole physics [22,23,24,25,26,27], it has a great motivation to distinguish black holes with wormholes. A useful way to achieve this goal is to perturb the objects and then observe the time evolution of the perturbation. When black holes or wormholes are perturbed, they radiate GWs based on the initial conditions of the perturbations. After that, they reduce to damped oscillations with complex frequencies. The modes of oscillations are the so-called quasinormal modes (QNMs), which encode information on the evolutions. Researches on the QNMs of various black hole and wormhole solutions are quite prominent [28,29,30,31,32,33,34,35]. There is an intriguing phenomenon called echoes in QNMs. The echoes are generated by the reflected waves of the system, in which a sudden increase of amplitudes in QNM spectrums appears. We should note, however, that not all black holes or wormholes can generate echoes after perturbations. An interesting direction is to use the features of echoes to examine the properties of black holes and wormholes. For example, Refs. [36, 37] pointed out that echoes arise from black holes if there are local Lorentz symmetry violations or discontinuities in the effective potentials. Reference [14] studied the echoes of two wormhole models, they found that there are obvious echo signals in wormhole geometries. Also, echoes from wormhole/black hole transition were considered in the brane-world model [38]. In a recent paper [39], the authors presented an interesting discussion on the echoes from wormholes.

On the other hand, it is necessary to investigate the differences between black holes and wormholes in the same circumstance. To do this, we need to find the theories that admit both the black hole and wormhole solutions. A natural candidate is the regular black hole. A regular black hole means that there is no singularity inside the event horizons. Simpson and Visser proposed a new concept named black bounce recently [40]. This new concept was inspired by Bardeen’s regular black hole and similar to Bronnikov’s dark universe [41]. Simpson and Visser suggested a two parameters metric, which can describe traversable wormholes and black bounces regarding the values of the parameters. The black bounce mechanism and the Simpson–Visser (SV) metric have caused concern among physicists. Later, Huang and Yang (HY) obtained a charged wormhole/black bounce solution in the Einstein-Maxwell-scalar theory [42]. In their theory, the wormhole/black bounce is supported by the phantom fields. Although there are some disputes, the phantom fields play important role in many aspects of physics, such as string theory [43, 44], dark energy models [45, 46] and particle physics [47]. One may argue that the phantom fields will cause negative energies and hence become a sign of instabilities. However, Ref. [48] argued that such instabilities can be cured. Then Lobo et al. [49] constructed a novel black bounce spacetimes (LRSSV metric). The observable properties, such as the gravitational lensing [50,51,52] and perturbation echoes [53, 54], of the SV metric and the LRSSV metric are studied. Especially in Ref. [53], they investigated the SV metric and suggested that the black hole/wormhole transition is characterized by the echoes. A similar conclusion is presented with respect to the LRSSV metric [54].

It should be mentioned that the SV metric and the LRSSV metric are both symmetric. Then the symmetry of the metrics leads to the symmetric effective potential in the perturbed equation. Being distinct from the above symmetric metrics, the HY metric involves asymmetric cases. It is worth examining how an asymmetric metric affects the time evolution of the perturbations.

In this paper, we would like to draw attention to the evolution of (a)symmetric black bounces when they are perturbed. We found that in symmetric black bounce metrics (SV metric and LRSSV metric and a special case in HY metric), the negative regions of effective potentials are enclosed by the black hole horizons. On the other hand, the asymmetry of metrics leads to the asymmetric effective potentials in the case of the HY metric, such that the negative regions could appear the outside the black hole horizons. In Refs. [53, 54], they listed all the possible shapes of the effective potential in the SV metric and the LRSSV metric. Here we choose two common shapes of all the possible effective potentials, namely the single-peak and the two-peak forms, to compare the difference. Note that the single-peak potentials can not produce any echoes, we mainly care about the two-peak potentials in the present work. For the symmetric metrics, we can only adjust the depth of the well between the two peaks. On the other hand, in the asymmetric metrics the relative height of the two peaks can also be adjusted. These results lead us to a deeper understanding of the time evolution of the perturbations.

The paper is organized as follows. In Sect. 2, we make a brief review of the symmetric and the asymmetric wormhole/black bounce metrics. In Sect. 3, we derive the perturbation equations for general spherically symmetric metrics, and then introduce the finite difference method to solve those perturbation equations. The effective potentials in different metrics are analyzed in Sect. 4. The time-domain profiles of the perturbations evolved in the asymmetric spacetime are presented in Sect. 5. Finally, the conclusion and discussion are given in Sect. 6.

2 Review of black bounce solutions

A spherically symmetric ansatz with wormhole throat-like geometry takes the form

$$\begin{aligned} ds^2=-h(x)dt^2+h^{-1}(x)dx^2+(x^2+q^2)d\Omega ^2_{2}, \end{aligned}$$

(1)

where

$$\begin{aligned} d\Omega ^2_{2}=d\theta ^2+\sin ^2 \theta d\phi ^2. \end{aligned}$$

(2)

For the Simpson–Visser (SV) metric, we have [40]

$$\begin{aligned} h(x)=h_{sv}=1-{\textstyle {\frac{\scriptstyle 2m}{\scriptstyle \sqrt{x^2+q^2}} } }. \end{aligned}$$

(3)

This metric describes a traversable wormhole or a black bounce up to the value of parameter q. Specifically, it can be used to describe a traversable wormhole for $q>2m$ or a regular black hole for $0<q<2m$. It is obvious that the metric has x to $-x$ symmetry, such that it depicts a symmetric wormhole or regular black hole. In the regular black hole case, there is a wormhole throat-like geometry in $x=0$. This geometry is a spacelike hypersurface, while the wormhole throat usually is timelike. Simpson and Visser treat this geometry as a bounce into a future incarnation of the Universe [40].

There is another symmetric metric proposed by Lobo et al. [49]. They consider a charged solution from the Einstein gravity with the matter sector as an anisotropic fluid. The LRSSV metric is given by the same form as (1) and

$$\begin{aligned} h(x)=h_{l}=1-{\textstyle {\frac{\scriptstyle 2m}{\scriptstyle (x^4+q^4)^{1/4}} } }. \end{aligned}$$

(4)

The properties of this metric are very similar to the SV metric. It also has the x to $-x$ symmetry and describes symmetric spacetimes. When $q>2m$, it depicts a charged traversable wormhole; When $0<q<2m$, it depicts a black bounce.

Huang and Yang (HY) introduced a phantom scalar as the matter sector in the Einstein-Maxwell-phantom scalar theory [42], then obtained an asymmetric black bounce solution. The Lagrangian for this theory is given by

$$\begin{aligned}&{\mathcal {L}}=\sqrt{-g}(R+{\textstyle {\frac{\scriptstyle 1}{\scriptstyle 2} } }(\partial \phi )^2-{\textstyle {\frac{\scriptstyle 1}{\scriptstyle 4} } }Z^{-1}F^2),\nonumber \\&Z=\gamma _1 \cos \phi +\gamma _2 \sin \phi . \end{aligned}$$

(5)

The phantom field is defined by flapping the sign of kinetic term in Lagrangian, then it is easy to see the scalar field is phantom-like everywhere. When the coupling function Z becomes negative somewhere, the Maxwell field is also phantom-like. The phantom fields as exotic matters support wormhole throats. Recently, an asymmetric wormhole solution without exotic matters is found in Ref. [55] and its QNMs and echoes have been studied in Ref. [56].

Within the ansatz (1), the HY solution is given by

$$\begin{aligned} h(x)= & {} 1-{\textstyle {\frac{\scriptstyle \gamma _2 Q^2 x}{\scriptstyle 4q(x^2+q^2)} } }+{\textstyle {\frac{\scriptstyle \gamma _1 Q^2}{\scriptstyle 4 (x^2+q^2)} } },\nonumber \\ \phi= & {} \phi (x,q), \quad A=\xi (x,q,Q)dt,\nonumber \\ \phi= & {} 2\arccos ({\textstyle {\frac{\scriptstyle x}{\scriptstyle \sqrt{x^2+q^2}} } }),\qquad \xi '={\textstyle {\frac{\scriptstyle QZ}{\scriptstyle x^2+q^2} } }, \end{aligned}$$

(6)

where $x\in (-\infty ,+\infty )$. It follows that the solution (6) is asymptotic to flat in $x\rightarrow \pm \infty$. It is easy to reduce the solution to the Ellis wormhole solution in the limit $Q\rightarrow 0$. We need to emphasize that we won’t take the parameter q to be zero in this paper. The mass M and the electric charge $Q_e$ of the solution [42]

$$\begin{aligned} M={\textstyle {\frac{\scriptstyle \gamma _2Q^2}{\scriptstyle 8q} } },\qquad Q_e=\gamma _1 Q. \end{aligned}$$

(7)

The HY metric characterizes traversable wormholes, if and only if

$$\begin{aligned} Q^2<{\textstyle {\frac{\scriptstyle 8q^2(\gamma _1+\sqrt{\gamma _1^2+\gamma _2^2})}{\scriptstyle \gamma _2^2} } }. \end{aligned}$$

(8)

Although the two asymptotic regions at $x\rightarrow \pm \infty$ are both flat, the spacetime curvatures are different in the vicinity of the wormhole throat. It means that the HY metric is an asymmetric solution. When the charge decreases or mass increases, the spacetime geometry in the vicinity of $x=0$ becomes more and more asymmetric.

When

$$\begin{aligned} Q^2\ge {\textstyle {\frac{\scriptstyle 8q^2(\gamma _1+\sqrt{\gamma _1^2+\gamma _2^2})}{\scriptstyle \gamma _2^2} } }, \end{aligned}$$

(9)

the HY metric characterizes regular black holes. It can depict two types of regular black holes in this situation. Type I regular black hole looks like an RN black hole, which has outer and inner horizon but the curvature singularity at $x=0$ is replaced by a wormhole throat. Type II regular black hole is a black bounce where the bounce occurs at $x=0$ and the two horizons are located on both sides of the bounce.

Specially, if $\gamma _2=0$, the function h in metric (6) reduces to

$$\begin{aligned} h(x)=1-{\textstyle {\frac{\scriptstyle Q^2}{\scriptstyle 4 (x^2+q^2)} } }, \end{aligned}$$

(10)

where we set $\gamma _1=-1$ without loss of generality. This is an analogy with the SV metric (3) and the LRSSV metric (4). When $2q<Q$, it depicts a black bounce; when $2q=Q$, it depicts a one-way wormhole; when $2q>Q$, it depicts a traversable wormhole.

3 Perturbations and finite difference method

In general, there are usually three types of perturbations, namely scalar, electromagnetic and gravitational field perturbations. One of the goals of this work is to discuss how the asymmetry of spacetimes affects the results of the perturbations. Note that the gravitational fields and the scalar fields behave similarly. And hence we study the scalar field perturbations as a proxy for the gravitational perturbations [14].

The equation of motion (E.O.M) of a massless scalar field $\phi$ is given by

$$\begin{aligned} {\textstyle {\frac{\scriptstyle 1}{\scriptstyle \sqrt{-g}} } }\partial _\mu (\sqrt{-g}g^{\mu \nu }\partial _\nu \phi )=0. \end{aligned}$$

(11)

We could separate the scalar field $\phi$ into two parts, which are the spherical harmonics $Y_{l,m}$ and the radial part $\psi (t,x)$,

$$\begin{aligned} \phi =\underset{l,m}{\Sigma }{\textstyle {\frac{\scriptstyle \psi (t,x)}{\scriptstyle \sqrt{x^2+q^2}} } }Y_{l,m}, \end{aligned}$$

(12)

where l denotes the angular number and m denotes the azimuthal number. Then the E.O.M of the scalar field (11) reduces to

$$\begin{aligned}&-\frac{\partial ^2 \psi (t,x)}{\partial t^2} + \frac{1}{h(x)^2} \frac{\partial ^2 \psi (t,x)}{\partial x^2} + h(x) h^{\prime }(x) \frac{\partial \psi (t,x)}{\partial x}\nonumber \\&-\frac{h(x) \bigg ( q^2 h(x)+(q^2+x^2)(l(l+1)+x h^{\prime }(x))\bigg )}{(q^2+x^2)^2} \psi (t,x)=0.\nonumber \\ \end{aligned}$$

(13)

Here we introduce the tortoise coordinate $x_*$. The tortoise coordinate $x_*$ is defined by

$$\begin{aligned} dx_*={\textstyle {\frac{\scriptstyle 1}{\scriptstyle h(x)} } }dx. \end{aligned}$$

(14)

It is also worth mentioning that the tortoise coordinate $x_*$ is monotonically increasing with x but avoids the horizon. And hence (11) becomes the wave function in the time domain, namely

$$\begin{aligned} -{\textstyle {\frac{\scriptstyle \partial ^2 \psi (t,x)}{\scriptstyle \partial t^2} } }+{\textstyle {\frac{\scriptstyle \partial ^2 \psi (t,x)}{\scriptstyle \partial x_*^2} } }-V(x) \psi (t,x)=0, \end{aligned}$$

(15)

where

$$\begin{aligned} V(x)=\frac{h(x)\bigg (q^2 h(x)+(q^2+x^2)(l(l+1)+x h^{\prime }(x))\bigg )}{(q^2+x^2)^2}. \end{aligned}$$

(16)

Furthermore, we could rewrite $\psi (t,x)$ as $\Psi (x) \exp (-i \omega _{l,n}t)$ ,where $e^{-i \omega t}$ is the time evolution of the scalar field. Then we obtain the wave function in the frequency domain, namely

$$\begin{aligned} {\textstyle {\frac{\scriptstyle d^2\Psi (x)}{\scriptstyle dx_*^2} } }+(\omega _{l,n}^2-V(x))\Psi (x)=0. \end{aligned}$$

(17)

where n denotes the overtone number. The $\omega _{l,n}$ is a complex number that characterizes the frequency of QNMs.

The effective potential, as known as the Regge–Wheeler potential, can be rewritten as the following form

$$\begin{aligned} V(x)=h(x)F(x), \end{aligned}$$

(18)

with

$$\begin{aligned} F(x)={\textstyle {\frac{\scriptstyle 1}{\scriptstyle (q^2+x^2)^2} } }\bigg ( q^2 h(x)+(q^2+x^2)(l+l^2+x h'(x))\bigg ).\nonumber \\ \end{aligned}$$

(19)

As we will see as follows, the time evolution of the perturbed fields is strongly related to the effective potential V.

In order to solve the perturbation equation (15) numerically, we use the finite difference method. The details of the method could be found in Ref. [14].

We discretize the coordinates $t=i \Delta t$ and $x_*=j \Delta x_*$, where the i and j are integers. As the result, $\psi (t,x_*)$ becomes $\psi (i\Delta t,j\Delta x_*)$. After making $\Delta t$ and $\Delta x_*$ to be constant, we can replace $\psi (i\Delta t,j\Delta x_*)$ with $\psi (i,j)$. In a similar way, $V(x_*)= V(j \Delta x_*)= V(j)$. Then the discretized form of equation (15) becomes

$$\begin{aligned}&-\frac{\psi (i+1,j)-2\psi (i,j)+\psi (i-1,j)}{\Delta t^2}\nonumber \\&+\frac{\psi (i,j+1)-2\psi (i,j)+\psi (i,j-1)}{\Delta x_*^2}\nonumber \\&-V(j)\psi (i,j)=0. \end{aligned}$$

(20)

According to Ref. [57], we consider the initial Gaussian distribution $\psi (t=0,x_*)=e^{- \frac{(x_*- {\bar{a}})^2}{2 b^2}}$ and $\psi (t<0,x_*)=0$. In the present work, we take $b=1$ and the value of ${\bar{a}}$ will be chosen accordingly. Then we can derive the evolution of $\psi$ by

$$\begin{aligned} \psi (i+1,j)= & {} -\psi (i-1,j)\nonumber \\&+\bigg (2-2 \frac{\Delta t^2}{\Delta x_* ^2}- \Delta t^2 V(j) \bigg ) \psi (i,j)\nonumber \\&+ \frac{\Delta t^2}{\Delta x_* ^2} \bigg (\psi (i,j+1)+\psi (i,j-1) \bigg ). \end{aligned}$$

(21)

The von Neumann stability conditions require that [57]

$$\begin{aligned} \Delta t / \Delta x_*<1. \end{aligned}$$

(22)

In the present paper, we set $\Delta t / \Delta x_*=0.5$. The setting is the same with Refs. [57] and [14]. We use the usual boundary conditions here:

$$\begin{aligned} \psi (t,x_*)|_{x_*\rightarrow -\infty }=e^{-\mathrm{i}{\omega x_*}},\qquad \psi (t,x_*)|_{x_*\rightarrow +\infty }=e^{\mathrm{i}{\omega x_*}}.\nonumber \\ \end{aligned}$$

(23)

The physical interpretation of this boundary condition is that there are only ingoing waves in $x\rightarrow -\infty$ and outgoing waves in $x\rightarrow \infty$.

4 Effective potential

Before we solve the discretized equation (21) with the numerical method and show the main results in the next section, it is necessary to discuss the effective potentials V with different metrics.

Based on (18), the behavior of the effective potential V(x) is determined by the roots of the following three equations:

$$\begin{aligned} h(x)= & {} 0, \end{aligned}$$

(24)

$$\begin{aligned} F(x)= & {} 0, \end{aligned}$$

(25)

$$\begin{aligned} \frac{d V(x)}{dx}= & {} 0, \end{aligned}$$

(26)

where the roots of Eq. (24) determine the existence and the positions of the horizons, the roots of Eqs. (24) and (25) describe the transformations of the sign of V(x), and the roots of Eq. (26) represent the extreme points of V(x).

As a studied in Ref. [58], the exponentially growing QNMs could appear when the effective potential V satisfies a sufficient condition (33). This is a signal of the instability of the systems. In what follows, we will point out that there are no negative regions outside the black hole horizons in the cases of symmetric black bounce, which suggests the stability of these symmetric metrics. But this argument could be broken in the asymmetric black bounce cases (see Appendix A for details).

4.1 Symmetric spacetimes

As we mentioned above, the SV metric, the LRSSV metric and the HY metric with $\gamma _2=0$ are both symmetric solutions. It is worth noting that $\gamma _2=0$ corresponds to the solution with zero mass. A symmetric wormhole with zero mass is acceptable, such as the famous Ellis wormhole [20].

As the conclusions of Ref. [53], there are two shapes of effective potentials in the SV metric. The two-peaks shapes happen only in certain traversable wormhole cases, namely $q>2m$. It follows that the black bounce cases have only single-peak shapes of the effective potential and hence there are no echoes. The LRSSV metric holds a similar conclusion, besides a new three-peaks shape arises in the traversable wormhole cases. Let’s expand the effective potential V at the two asymptotic regions, namely $x\rightarrow \pm \infty$, we found that the above two symmetric metrics have the same form. For any $l\ne 0$ perturbation, it leads to the same leading term of the effective potential V, namely

$$\begin{aligned} V(\pm \infty )={\textstyle {\frac{\scriptstyle l(l+1)}{\scriptstyle x^2} } }+\cdots \end{aligned}$$

(27)

When $l=0$, the leading term changes to

$$\begin{aligned} V(\pm \infty )=2m({\textstyle {\frac{\scriptstyle 1}{\scriptstyle x^2} } })^{3/2}+\cdots \end{aligned}$$

(28)

Keeping this in mind, it is clear that the effective potentials tend to $0^+$ no matter $x\rightarrow +\infty$ or $x\rightarrow -\infty$ . We would use this conclusion to prove that there are no negative regions of the effective potentials outside of the horizons in the cases of the SV metric, the LRSSV metric and the HY metric of $\gamma _2=0,\gamma _1<0$.

The SV metric, the LRSSV metric and the HY metric of $\gamma _2=0,\gamma _1<0$ share the following form of h(x):

$$\begin{aligned} h(x) = 1- \frac{A}{(x^{2N}+q^{2N})^B} \end{aligned}$$

(29)

where $A>0$, $B>0$ and N is a positive integer. Let us assume that the roots of h(x) locate at $x=\pm x_0$. Then we have $h(x)>0$ for $x>|x_0|$ and $h(x)<0$ for $x<|x_0|$, since $h(x)>0$ for $x\rightarrow \pm \infty$. On the other hand, it can be easily verified that $xh'(x) \ge 0$. Therefore the roots of $F(x)=0$ can only appear in the region $x\le |x_0|$, and $F(x_0)=0$ only happens for $x_0 =0$ and $l=0$.

From the above arguments, we arrive at the conclusion that the transformation of the sign of V(x) only happens between the two horizons. Combining with the asymptotic behavior of V(x), it is positive when $x\rightarrow \pm \infty$. Because for $l\ne 0$ the leading term of V at the boundaries are the same with (27). For $l=0$, the leading term becomes

$$\begin{aligned} V(\pm \infty )={\textstyle {\frac{\scriptstyle q^2-Q^2 \gamma _1/2}{\scriptstyle x^4} } }+\cdots . \end{aligned}$$

(30)

Thus the negative region of the effective potential only appears between the two horizons. This suggests the stability of these symmetric metrics.

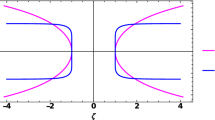
To sum up, we show that there are no negative regions of the effective potentials outside the horizons in all the three symmetric metrics. We use the illustrations, varying with q, to exhibit our conclusion more intuitively in Fig. 1. For a certain value of q, the red dashed line denotes how many peaks and wells of the effective potential V(x) while the blue solid line denotes how many horizons. Based on such profiles, we found that for a large q the three metrics give rise to traversable wormholes that possess a single peak of effective potential at the wormhole throat. When q decreases, more peaks emerged. To be specific, there are two peaks in the SV metric and the HY metric with $\gamma _2=0$ and three peaks in the LRSSV metric. For a small q, there are two symmetric black hole horizons emerge and each side of the horizon has only one peak.

Fig. 1

Roots of (24) (blue solid line), (25) (green dotted line) and (26)(red dashed line) of the three symmetric metrics. From top to bottom, they correspond to the SV metric, the LRSSV metric and the HY metric with $\gamma _2=0$ respectively. The left column shows the case of $l=0$ while the right column shows the case of $l=1$

Fig. 2

The effective potentials and the corresponding time evolution profiles with different $\gamma _2$. We set $q=1.65,\gamma _1=-10,l=2,Q=1$

Fig. 3

The effective potentials and the corresponding time evolution profiles with different l. We set $q=1.6,\gamma _1=-10,\gamma _2=2,Q=1$

Fig. 4

The effective potentials and the corresponding time evolution profiles with different M. We set $\gamma _1=-10,\gamma _2=2,l=2,Q=1$

Fig. 5

The effective potentials and the corresponding time evolution profiles with different $Q_e$. We set $M=0.147059,\gamma _1=-10,\gamma _2=2,l=2$

4.2 Asymmetric spacetimes

When $\gamma _2\ne 0$, the HY metric describes an asymmetric spacetime. It should be noted that the asymptotic behavior of V(x) becomes

$$\begin{aligned} V(\pm \infty )={\textstyle {\frac{\scriptstyle l(l+1)}{\scriptstyle x^2} } }-{\textstyle {\frac{\scriptstyle (-1+l+l^2)Q^2 \gamma _2}{\scriptstyle 4q x^3} } }+\cdots \end{aligned}$$

(31)

If $l\ne 0$, the leading term is the same with the above symmetric cases and the effective potential V(x) in two asymptotic regions both tend to $0^+$. But in the cases of $l=0$, we find that

$$\begin{aligned} V(\pm \infty )={\textstyle {\frac{\scriptstyle Q^2 \gamma _2}{\scriptstyle 4q x^3} } }+\cdots \end{aligned}$$

(32)

It follows that $V(+\infty )$ and $V(-\infty )$ have always different signs. In fact, $V(+\infty )$ tends to $0^+$ and $V(-\infty )$ tends to $0^{-}$. Comparing with the symmetric cases in the above section, we may conclude that, for the s-wave ($l=0$) perturbations, the asymmetry of spacetime causes negative regions of the effective potentials outside the horizons. The negative region perhaps relates to unstable or stable situation. The existence of the unstable modes dependents on whether the depth of the gap is sufficient to form a bound state with negative energy. We discuss the details of the stability in Appendix A.

In this work, we concentrate on the black bounce and wormhole cases and hence ignore the RN-like black hole cases. Moreover, we do not interest in the structures inside black hole horizons. Within these assumptions, there are only single-peak shapes and two-peaks shapes. These two shapes are good examples to illustrate how the asymmetry affects the time evolution of the perturbations. The single-peak cases involve all the black bounce cases and some wormhole cases.

The two-peaks cases arise in certain traversable wormhole geometries. The left column of Figs. 2, 3, 4 and 5 show the shapes of these two-peaks cases with different parameters. We should emphasize that the implications of each parameter are different. $\gamma _2$ arises in the coupling function $Z(\phi )$ of the Lagrangian. l is the eigenvalue of the spherical harmonics $Y_{l,m}$, which corresponds to the angular momentum of the perturbation fields. The scalar parameter q relates to the mass M of the wormhole when we fix Q. The parameter Q is proportional to the electrical charge $Q_e$ of the wormhole.

5 Quasinormal modes and echoes

The frequencies of QNMs are complex numbers that depict the properties of compact objects when spacetimes against perturbations. The real and imaginary parts of QNMs frequencies (QNFs) describe oscillation frequency and damping rate in the time-domain profiles of $\psi$ respectively. Here we use the Prony method to calculate the QNFs.

The QNFs for different angular numbers l, wormhole mass M and charge $Q_e$ are shown in Tables 1 and 2. As we will see in what follows, echoes appear in double-peaks potentials. Hence the QNFs have different values for each echo and we don’t show them in the tables. We can see that in Table 1 the imaginary parts of QNFs have maximum values for different l, while in Table 2 the real and imaginary parts of QNFs both have maximum values. As examples, some time-profiles of QNMs in Tables 1 and 2 are presented in Appendix B. One can see that the tendency of our data matches the behavior of time-domain profiles in Figs. 8 and 9.

Table 1 The QNM frequencies with different $Q_e$. We set $M=0.147059,\gamma _1=-10,\gamma _2=2$

Table 2 The QNM frequencies with different M. We set $Q_e=-10,\gamma _1=-10,\gamma _2=2$

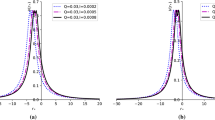
We would like to show the important results of the time-evolution profiles that contain echo signals now. For the two-peak profiles, as we present in Fig. 2, 3, 4 and 5, we classify the situations with different $\gamma _2, l, M, Q_e$. The two-peak cases can produce echoes. The left columns of these figures show the effective potential $V(x_*)$ while the right columns show the corresponding time evolution profiles. Based on those profiles, we sum up our results as follows:

• Theoretical parameter $\gamma _2$ relates to the coupling strength between the scalar field and the electromagnetic field. When $\gamma _2=0$, there are two symmetric peaks in $V(x_*)$. With the increase of $\gamma _2$, these two peaks become further and further, and thus lead to a broad well. We should note that one of the peaks becomes higher while another peak becomes lower. The corresponding QNMs profile suggests that larger $\gamma _2$ leads to lower frequency but larger amplitude echoes. The first echo signal after the initial ringdown arises earlier for smaller $\gamma _2$. One may expect to observe large amplitudes when $\gamma _2$ becomes large.

• When we use the scalar waves with different angular momentum l to perturb the same wormholes, the height of the effective potential changes. Larger l gives rise to higher peaks. Interestingly, changing l does not significantly affect the width between the two peaks. According to the QNMs profiles, we can see that smaller l leads to higher frequencies of the echoes. The amplitudes of the echoes become smaller with larger l. With smaller l, we can detect the first echo signal earlier.

• The wormhole mass M strongly affects the width of the two peaks. An intriguing feature is that changing the mass of the wormholes does not significantly alter the height of the two peaks. A larger mass leads to a broader width and a deeper well in the two-peak effective potential. The corresponding QNMs profiles suggest that larger mass wormholes have larger amplitude and lower frequency echoes. The wormhole mass relates to the parameters Q and q. Here we fix Q and vary q to change wormhole mass.

• As a charged solution, we would like to discuss how the electric charge of the wormhole affects the time evolution after a scalar field perturbation. As we can see in Fig. 5, with the increase of the electric charge, the peaks of the effective potential become lower. A wormhole with a smaller electric charge could create more obvious signals of echoes.

6 Conclusion and discussion

In this paper, we investigated the time evolution of the symmetric and asymmetric regular black holes after a scalar field perturbation, based on three black bounce solutions. The SV metric and the LRSSV metric and the $\gamma _2=0$ case of HY metric both describe symmetric traversable wormholes or black bounces. But if $\gamma _2\ne 0$, the HY metric becomes an asymmetric solution, which leads to the different sides of the wormhole throat or black bounce.

We considered the scalar field perturbations as a proxy for the GWs in the present work. We derived a general form of the effective potential for the spherically symmetric metric with throat-like geometry. We analyzed the effective potentials in both symmetric and asymmetric metrics. In conclusion, we found that the negative regions of the effective potentials only arise inside the black hole horizons in symmetric black bounce cases. This situation is changed in asymmetric black bounce cases, namely, they admit a negative region outside the black hole horizons.

We used the finite difference method to solve the time evolution equation of the perturbations. We showed our numerical results of QNFs in Tables 1 and 2. The time-domain profiles are shown in Figs. 2, 3, 4 and 5. As some references have pointed out, the symmetric black bounce cases do not produce echo signals. Our results support this argument and show that it is also valid even in the asymmetric black bounce cases. All these features characterize the properties of the (a)symmetric wormholes with two-peak effective potentials.

When the effective potential has two peaks, it form a well. These situations can happen in some wormhole cases. Such shapes of the effective potentials admit echoes after the perturbations. We studied the relationship of the theoretical parameter, the angular momentum of the perturbed waves, the mass and the electric charge of the wormholes with the properties of the echoes respectively. According to the numerical results, we may therefore conclude that massive wormholes with smaller charges are easier to observe echo signals after the scalar perturbations. Increase with $\gamma _2$ aggravates the asymmetry of the effective potentials, which leads to lower frequency but larger amplitude echoes. The angular momentum l of the perturbed waves changes the height of the peaks, while it has no significant influence on the widths of effective potentials. We found that larger l leads to lower frequency echoes.

Fig. 6

In the left column, roots of (24) (blue solid line), (25) (green dotted line) and (26) (red dashed line) of the asymmetric wormhole case in the HY metric. We set $\gamma _1=1, \gamma _2=1, Q=1, l=0$. Under these parameters, it represents the asymmetric wormholes for $q>0.2275$ and the effective potentials are asymptotic to $0^-$ in $x\rightarrow \infty$. The right column presents two examples with negative regions of the effective potentials

Fig. 7

Time-domain profiles with the same parameters with Fig. 6

As we mentioned above, the HY metric can describe RN-like black holes. We didn’t touch on this situation in the present paper. For future work, one can go further to investigate the time evolution after the scalar field, electromagnetic field, and gravitational field perturbations of the HY metric or other asymmetric spacetime geometries.

Appendices

Appendix

A Discussion on the stabilities of massless scalar perturbations in asymmetric wormholes

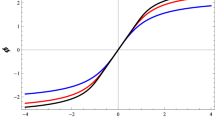
In Sect. 4, we pointed out that the asymmetric wormholes allow negative regions in effective potentials. For example, we show a plot of roots and the corresponding effective potentials of the asymmetric metric case in Fig. 6. In this appendix, we would like to discuss the influence of the negative regions on the stabilities of the asymmetric wormholes.

Fig. 8

The time evolution profiles with different $Q_e$. We set $l=2, M =0.147059, \gamma _1=-10, \gamma _2=2$

Fig. 9

The time evolution profiles with different M. We set $l=2, Q_e=-10, \gamma _1=-10, \gamma _2=2$

According to Ref. [59], the unstable modes arise if

$$\begin{aligned} \int ^{+\infty }_{-\infty }{\textstyle {\frac{\scriptstyle V}{\scriptstyle h} } }dx<0\rightarrow I\equiv \int ^{+\infty }_{-\infty }F(x)dx<0. \end{aligned}$$

(33)

For simplicity, we consider the s-wave($l=0$) perturbation. Now F(x) reduce to

$$\begin{aligned} F= & {} {\textstyle {\frac{\scriptstyle 1}{\scriptstyle 4q(q^2+x^2)^3} } }\big ( 4q^5-2q Q^2 x^2\gamma _1+q^3(4x^2+ _1 Q^2)\nonumber \\&-2\gamma _2 q^2Q^2 x+\gamma _2 Q^2 x^3\big ). \end{aligned}$$

(34)

Integrating this function, we have

$$\begin{aligned} I={\textstyle {\frac{\scriptstyle (16q^2+\gamma _1 Q^2)\pi }{\scriptstyle 32q^3} } }. \end{aligned}$$

(35)

The wormhole cases in the HY metric must satisfy an inequality in (8). Under the assumption $q\ge 0$, it is easy to see that these two inequalities (8) and (33) are incompatible. In fact this argument is also valid for $l\ne 0$ because the l term in (19) is always positive. Therefore, we can conclude that the integration I is always positive for wormholes in the HY metric.

Thus we can see that it is hard to determine whether the asymmetric wormholes are stable under the perturbations. Nevertheless, our numerical results show that at least in a large parameter region the wormholes are stable. As examples, two time-domain profiles are shown in Fig. 7.

B Time-domain profiles of QNMs

In Figs. 8 and 9, we show the time-domain profiles of wormhole geometry with the parameter values in Tables 1 and 2 respectively. It is obvious that the data of those tables are consistent with the time-domain profiles.