1 Background

The inclusion of higher powers of curvature corrections in Einstein’s theory of gravity (ETG) attracted a lot of attention as it describes a new way for the quantization of gravitational field. ETG comes out to be a non-renormalizable theory, however, it is possible to construct a renormalizable one [1] if one makes higher power curvature corrections. In the case of AdS/CFT correspondence, new couplings among the operators of the dual CFT are formed as a result of these corrections and a more generalized class of dual CFTs is introduced [2,3,4]. The most interesting modified theory containing higher power of curvature corrections is the Lovelock gravity [5]. This theory possesses a remarkable property that it reduces to ETG in four dimensions. It should be noted that this theory at linear level is free of ghosts because the differential equations of motion are still second order. The Einstein–Gauss–Bonnet gravity theory can be formed by including only the first nontrivial higher curvature term in the gravity Lagrangian along with the cosmological constant and ETG terms. The action function describing the Einstein–Gauss–Bonnet gravity (or Lovelock gravity of order two) can also be derived from the low energy effective action of string theory [6,7,8].

Although the Lovelock gravity is truly a higher dimensional generalization of ETG, it possesses some unwanted features as well. First, for spacetime dimensions greater than four, the time evolution of fields does not appear uniquely: given a surface at some initial instant \(t=t_0\), the fields at values t greater than \(t_0\) cannot be completely specified from the equations of motion. This is due to the involvement of higher powers of velocities in the action functional [9, 10]. Second, along with cosmological and Newtonian constants, the action contains \([(d+1)/2]\) arbitrary coupling parameters as well [11]. This arbitrariness makes it difficult to investigate the properties of black holes and construct explicit solutions for the field equations. Apart from these problems, some physical consequences of these arbitrary parameters were also reported. For example, (i) the field equations have at most \(n-1\) different solutions, (ii) all of them possess horizons corresponding to both signs of energy, and (iii) the entropy is not monotonically increasing function of horizon radius, so that violation of the second law of thermodynamics appears. Due to these consequences, it is convenient to make a special choice for the arbitrary Lovelock coupling parameters. Therefore, Bañados, Teitelboim and Zanelli proposed a suitable choice for these parameters due to which an explicit solution can easily be obtained. On the basis of this specific choice, a new special case of Lovelock gravity known as dimensionally continued gravity (DCG) was constructed [11]. Recently, many exact dimensionally continued black hole solutions have been derived [11,12,13,14]. The thermodynamic and physical properties associated with these black holes have also been studied [11,12,13,14,15,16,17,18].

The most fascinating and exciting gravitating objects which appear in any gravity theory are black holes whose physical properties could provide new insights for the formulation of quantum gravity. Hence, it is important to investigate black hole solutions and their thermodynamic behaviour in different theories of gravity. In recent decades, physics of black holes in diverse dimensions, in particular, the black holes of Lovelock gravity got a lot of attention. For example, solutions representing Lovelock black holes in the presence of different matter sources have been derived in literature [16, 19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. In this paper, we are interested in studying dimensionally continued Lovelock black holes with a cloud of strings. We also study thermodynamics of such black holes under the effects of one-dimensional strings. It is concluded that the mass, temperature and specific heat associated with DCG black holes could have exciting features in the presence of string parameter, however the entropy remains unchanged. It may be noted that black holes with a cloud of strings are physically significant as the universe is assumed to be composed of these one-dimensional objects which are considered to be fundamental objects in nature. Here, we study the gravitational effects of matter which is in the form of a configuration of strings. The relationship between counting string states and black hole entropy was first described by Strominger and Vafa in Ref. [39]. Letelier demonstrated that the model of a configuration of strings can be considered as perfect fluids [40]. After this black hole solutions in different theories were derived under this assumption. The very first solution describing a generalized Schwarzschild black hole surrounded by strings was determined by Letelier [40]. He then generalized the string-cloud model by introducing the pressure that forms this cloud and obtained a Petrov–Pirani type solution of the gravitational field equations [41, 42]. The Gauss–Bonnet and Lovelock black holes have also been investigated in a string-cloud model [43,44,45,46]. It was also shown that the spacetime contains string fluid matter around static spherically symmetric object when the mass of the black hole is taken as a function of radial coordinate [47, 48]. Recently, a black hole solution of Rastall gravity in a string-cloud model has also been found [49].

There is a significant evidence from recent astronomical observations that our universe is expanding at an accelerating rate. Currently, it is believed that this acceleration is due to the existence of an exotic thing known as dark energy. According to recent cosmological observations, dark energy fills all of space with negative pressure and almost 70 percent of the energy density of universe is composed of it [50,51,52]. A time evolving, spatially non-homogeneous component having negative pressure called quintessence can be taken as a candidate for dark energy [53, 54]. It is defined by the equation of state which relates the pressure \(p_q\) and density \(\rho _q\) by \(p_q = \omega _q \rho _q\) , where the parameter \(\omega _q\) has the range \(-1< \omega _q < -1/3\) [55,56,57]. It is worthwhile to mention here that it cannot be considered as the only candidate which causes the acceleration. One among different other contenders which can generate the accelerated expansion is the cosmological constant [58, 59]. In the presence of dark energy and black holes in the universe it is significant to investigate the effects of quintessence on black holes. The presence of quintessential dark energy in the black hole surrounding could produce some consequences at astrophysical scales, for instance, out-coming null rays from distant stars are more deviated as compared to the situation when no quintessence is present [60]. In the scenario of quintessence around gravitating objects, the first solution of the gravitational field equations was computed by Kiselev [61]. Generalizations of Kiselev solution have also been worked out, for example, charged [62], Nariai [63, 64] and higher dimensional black holes [65]. Studies related to quasi-normal modes for these black holes in the presence of quintessence [65, 66], and their thermodynamics [65, 67,68,69] have also been undertaken. It is shown that the thermodynamic quantities are modified by quintessence, while black hole entropy remains unchanged.

The Event Horizon Telescope (EHT) [70] supports the current theoretical analysis of black hole shadows based on recent astronomical observations. It is also confirmed that black hole shadows can now directly be observed through EHT. The effect of accelerated expansion of the universe on the shadow of a black hole has been studied [71]. Similarly, the shadows of black holes influenced by quintessential dark energy have also been considered [72, 73]. The generalized form of Kiselev solutions with axially symmetric background was also determined [74, 75]. Recently, thermodynamics and Hawking radiations of Lovelock black holes in quintessence background have been studied [76]. Similarly, uncharged and charged Lovelock black holes with both quintessential dark energy and string-cloud matter have also been analyzed [77,78,79]. The combined effects of the cloud of strings and quintessence on thermodynamic criticality of black holes have also been investigated [80, 81]. Similarly, the shadow and photon sphere of a black hole with both quintessence and configuration of strings has been examined [82].

The well known no-hair theorems say that it is impossible to obtain asymptotically flat conformal hairy black hole solution in ETG [83, 84]. However, when the cosmological constant is zero, the existence of hairy black holes in \((3+1)\) dimensions is possible where the real scalar field is divergent at the horizon [85]. For higher d-dimensional spacetimes, such that \(d>4\), it is stated that these gravitating objects simply do not exist [86]. Three- and four-dimensional non-asymptotically flat black holes for which the conformal scalar field is analytic everywhere were recently introduced [87, 88]. Until recently higher dimensional black holes with scalar hair were not found which are subject to no-go results [89]. Recently, gravitational field has been non-minimally coupled to real scalar field for the investigation of such black holes [90, 91]. The action function in this regard can be written as

$$\begin{aligned} I_s&=\int d^dx\sqrt{-g}\sum _{p=0}^{p_{max}}\nonumber \\&\quad \times \bigg (b_p\psi ^{d-4p} \delta ^{\mu _1\ldots \mu _{2p}}_{\nu _1\ldots \nu _{2p}}S^{\nu _1\nu _2}_{\mu _1\mu _2}\ldots S^{\nu _{2p-1}\nu _{2p}}_{\mu _{2p-1}\mu _{2p}}\bigg ), \end{aligned}$$
(1.1)

where

$$\begin{aligned} \begin{aligned} S^{\gamma \alpha }_{\mu \nu }&=\psi ^2R^{\gamma \alpha }_{\mu \nu }-2\delta ^{[\gamma }_{[\mu } \delta ^{\alpha ]}_{\nu ]}\nabla _{\beta }\psi \nabla ^{\beta }\psi -4\psi \delta ^{[\gamma }_{[\mu }\nabla _{\nu ]}\nabla ^{\alpha ]}\psi \\&\quad +8\delta ^{[\gamma }_{[\mu }\nabla _{\nu ]}\psi \nabla ^{\alpha ]}\psi . \end{aligned} \end{aligned}$$
(1.2)

Here \(p_{max}=[\frac{d-1}{2}]\) such that the brackets represent the integer part of \((d-1)/2\), \(\delta ^{\mu _1\ldots \mu _{2p}}_{\nu _1\ldots \nu _{2p}}\) is the generalized Kronecker delta, g is the determinant of the metric tensor \(g_{\mu \nu }\), \(\psi \) is the scalar field and \(R^{\alpha }_{\mu \nu \gamma }\) represents components of the Riemann tensor.

It should be noted that the theory generated by the above action is also ghost-free since both the gravitational and scalar field equations are of order two. When \(p=1\) or in case of four dimensions, the conformal scalar field in action (1.1) has a potential defined by \(V(\psi )=\frac{\lambda }{4!}\psi ^4\) so that the non-minimal coupling term in the total action becomes \((-1/12)R\psi ^2\) [91]. Several solutions of the field equations describing black holes with scalar hair have been determined in Refs. [91,92,93,94,95]. Note that, the scalar field configuration gives finite values in the exterior geometry as well as on the horizon. It is also concluded that these black holes are more physical and thermodynamically stable as compared to those with no conformal scalar hair [92, 93]. The thermodynamic properties of nonlinear electrically charged dimensionally continued hairy black holes are deeply studied in Ref. [96]. In addition to this, nonlinear magnetically charged dimensionally continued black holes have been studied in Ref. [97]. Motivated by the above background, in this paper, we study dimensionally continued hairy black holes under the effects of quintessence and a cloud of strings. It is important to note that the black hole solutions derived in this paper generalize the pure Lovelock black holes [45, 46, 77] into the case of dimensionally continued gravity coupled to conformal scalar field.

We make the outline of this paper as follows: In Sect. 2, the Lovelock gravity is non-minimally coupled to a scalar field. The higher dimensional black holes in the presence of quintessence and cloud of strings are also briefly reviewed. Then the Lovelock field equations for the case of DCG are solved and the effects of quintessence and cloud of strings on the black holes with conformal scalar hair are studied. In Sect. 3 we focus on thermodynamics of dimensionally continued black holes. Using thermodynamic quantities, validation of the extended first law and Smarr’s relation is examined. In Sect. 4, we briefly study black holes with a cloud of strings and quintessence in general Lovelock-scalar gravity. Finally, the concluding remarks are given in Sect. 5.

2 Dimensionally continued hairy black holes

The action describing the Lovelock-scalar gravity with matter sources is given by

$$\begin{aligned} I= & {} \frac{1}{16\pi G}\int d^dx\sqrt{-g}\bigg [\sum _{p=0}^{p_{max}}\frac{1}{2^p}\delta ^{\mu _1\ldots \mu _{2p}}_{\nu _1\ldots \nu _{2p}} \nonumber \\&\times \bigg (\alpha _p R^{\nu _1\nu _2}_{\mu _1\mu _2}\ldots R^{\nu _{2p-1}\nu _{2p}}_{\mu _{2p-1}\mu _{2p}} +16\pi G b_p\psi ^{d-4p}S^{\nu _1\nu _2}_{\mu _1\mu _2}\nonumber \\&\ldots S^{\nu _{2p-1}\nu _{2p}}_{\mu _{2p-1} \mu _{2p}}\bigg )+4\pi GL_M\bigg ], \end{aligned}$$
(2.1)

where G is Newton’s constant, \(L_M\) stands for the Lagrangian density of matter, Lovelock coefficients \(\alpha _p\) are arbitrary constants and \(b_p\) are conformal coupling constants. The components \(S^{\alpha \beta }_{\mu \nu }\) defined by (1.2) transform homogeneously under the conformal transformation defined by \(g_{\mu \nu }\rightarrow \omega ^2g_{\mu \nu }\) and \(\psi \rightarrow \omega ^{-1}\psi \) as \(S^{\alpha \beta }_{\mu \nu }\rightarrow \omega ^{-4}S^{\alpha \beta }_{\mu \nu }\). The action (2.1) will give the description of DCG if the coefficients \(\alpha _p\) are defined as [11, 15]

$$\begin{aligned} \alpha _p=\left( \begin{array}{c} n-1 \\ p \end{array} \right) \frac{(d_1-2p)!}{d_2!l^{-2(p+1-n)}}, \end{aligned}$$
(2.2)

where for simplicity we used the notation \(d_k=d-k\) and the positive integer n corresponds to \(d=2n+1\) in odd dimensions while \(d=2n+2\) in even dimensions. It is worthwhile to note that DCG becomes Born–Infeld gravity in even critical dimensions and Chern–Simons gravity in odd spacetime dimensions [11,12,13]. Varying the action (2.1) with respect to the metric components, \(g_{\mu \nu }\), implies

$$\begin{aligned}&\sum _{p=0}^{p_{max}}\frac{\alpha _p}{2^{p+1}}\delta ^{\nu \lambda _1\ldots \lambda _{2p}}_{\mu \rho _1\ldots \rho _{2p}} R^{\rho _1\rho _2}_{\lambda _1\lambda _2}\ldots R^{\rho _{2p-1}\rho _{2p}}_{\lambda _{2p-1} \lambda _{2p}}=-16\pi GT^{(M)\nu }_{\mu }\nonumber \\&\qquad -16\pi GT^{(S)\nu }_{\mu }, \end{aligned}$$
(2.3)

where \(T^{(M)\nu }_{\mu }\) symbolizes the components of the energy–momentum tensor such that

$$\begin{aligned} T^{(M)}_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta I_M}{\delta g^{\mu \nu }}, \end{aligned}$$
(2.4)

in which \(I_M\) stands for the action representing the contributions of matter in the spacetime geometry while \(T^{(S)\nu }_{\mu }\) denotes components of the energy–momentum tensor of the scalar field such that

$$\begin{aligned} \begin{aligned} T^{(S)\nu }_{\mu }&=\sum _{p=0}^{p_{max}}\frac{b_p}{2^{p+1}}\psi ^{d-4p} \delta ^{\nu \lambda _1\ldots \lambda _{2p}}_{\mu \rho _1\ldots \rho _{2p}} S^{\rho _1\rho _2}_{\lambda _1\lambda _2}\ldots S^{\rho _{2p-1}\rho _{2p}}_{\lambda _{2p-1} \lambda _{2p}}. \end{aligned}\nonumber \\ \end{aligned}$$
(2.5)

By varying the action with respect to the scalar field, we can get equations of motion as

$$\begin{aligned} \sum _{p=0}^{p_{max}}(d-2p)b_p\psi ^{d_1-4p}\delta ^{\sigma _1\ldots \sigma _{2p}}_{\gamma _1\ldots \gamma _{2p}}S^{\gamma _1\gamma _2}_{\sigma _1 \sigma _2}\ldots S^{\gamma _{2p-1}\gamma _{2p}}_{\sigma _{2p-1}\sigma _{2p}}=0.\nonumber \\ \end{aligned}$$
(2.6)

The trace of the tensor (2.5) would be zero if one imposes Eq. (2.6). This is consistent with the conformal invariance of the theory. In order to include effects of the cloud of strings in the background, we need to give a brief review of the theory on the cloud of strings. The Nambu–Goto action of a string evolving in a spacetime is written as

$$\begin{aligned} I_{st}= \int _{\Sigma }L_{st}d\xi ^{0}d\xi ^{1}, L_{st}=\mu (-{\overline{h}})^{\frac{1}{2}}, \end{aligned}$$
(2.7)

where \(\mu \) is a positive constant related to the tension of the string, and \(\xi ^0\) and \(\xi ^1\) are the timelike and spacelike coordinates, respectively. These coordinates parametrize the world sheet \(\Sigma \). Also, \({\overline{h}}\) denotes the determinant of the induced metric associated with \(\Sigma \) given by

$$\begin{aligned} {\overline{h}}_{ab}= g_{\mu \nu }\frac{\partial x^{\mu }}{\partial \xi ^a}\frac{\partial x^{\nu }}{\partial \xi ^b}. \end{aligned}$$
(2.8)

Associated with the world sheet of string \(\Sigma \), we can define the bivector as

$$\begin{aligned} \Sigma _{\alpha \beta }=\epsilon ^{ab}\frac{\partial x^{\alpha }}{\partial \xi ^a}\frac{\partial x^{\beta }}{\partial \xi ^a}, \end{aligned}$$
(2.9)

where \(\epsilon _{ab}\) refers to the two-dimensional Levi-Civita tensor. Within this context, it is possible to write the Lagrangian density for a string as

$$\begin{aligned} L_{st}=\mu \bigg (-\frac{1}{2}\Sigma ^{\alpha \beta }\Sigma _{\alpha \beta } \bigg )^{\frac{1}{2}}, \end{aligned}$$
(2.10)

from which one can obtain the energy–momentum tensor for one string as

$$\begin{aligned} T^{(st)\alpha \beta }=\mu \frac{\Sigma ^{\alpha \sigma }\Sigma ^{\beta }_{\sigma }}{\sqrt{-{\overline{h}}}}. \end{aligned}$$
(2.11)

Hence, associated with the cloud of strings, we can write the energy–momentum tensor as

$$\begin{aligned} T^{(C)\alpha \beta }=\rho _C \frac{\Sigma ^{\alpha \sigma }\Sigma ^{\beta }_{\sigma }}{\sqrt{-{\overline{h}}}}, \end{aligned}$$
(2.12)

where \(\rho _C\) denotes the proper density corresponding to the cloud of strings while \(\rho _C/\sqrt{-{\overline{h}}}\) is called the gauge invariant density. Moreover, by employing the identities

$$\begin{aligned} \Sigma ^{\mu [\alpha }\Sigma ^{\beta \gamma ]}=0, \nabla _{\mu }\Sigma ^{\mu [\alpha }\Sigma ^{\beta \gamma ]}=0, \Sigma ^{\mu \alpha }\Sigma _{\alpha \beta }\Sigma ^{\beta \nu }={\overline{h}} \Sigma ^{\nu \mu },\nonumber \\ \end{aligned}$$
(2.13)

one can show that \(\partial _{\mu }(\sqrt{-g}\rho _C\Sigma ^{\mu \nu })=0\). So, the energy–momentum tensor for the configuration of strings becomes

$$\begin{aligned} T^{(C)\nu }_{\mu }=-\frac{a}{r^2}[1,1,0,0]. \end{aligned}$$
(2.14)

The generalized Schwarzschild black hole with a cloud of strings [40] has the line element

$$\begin{aligned} ds^2= & {} -\bigg (1-\frac{2M}{r}-a\bigg )+\bigg (1-\frac{2M}{r}-a\bigg )^{-1}+r^2d \theta ^2\nonumber \\&+r^2\sin ^{2}\theta d\phi ^2. \end{aligned}$$
(2.15)

One can easily verify the above metric by solving Einstein’s equations with (2.14). The generalized Schwarzschild–Tangherlini solution within this setup is written as [44]

$$\begin{aligned} \begin{aligned} ds^2&=-\bigg (1-\frac{16\pi M}{d_2\Sigma _{d_2}r^{d_3}}-\frac{2a}{d_2r^{d_4}}\bigg )dt^2\\&\quad +\bigg (1-\frac{16\pi M}{d_2\Sigma _{d_2}r^{d_3}}-\frac{2a}{d_2r^{d_4}}\bigg )^{-1}dr^2+r^2 (h_{ij}dx^idx^j), \end{aligned}\nonumber \\ \end{aligned}$$
(2.16)

where

$$\begin{aligned} \Sigma _{d_2}=\frac{2\pi ^{\frac{d_1}{2}}}{\Gamma [\frac{d_1}{2}]}, \end{aligned}$$
(2.17)

stands for the volume of \(d_2\)-dimensional hyper-surface. The components of the energy–momentum tensor needed for the line element (2.16) are given by

$$\begin{aligned} T^{(C)\nu }_{\mu }=-\frac{a}{r^{d_2}}[1,1,0,0,\ldots ,0]. \end{aligned}$$
(2.18)

Note that, M signifies the black hole’s mass and the parameter a is related to the strength of the cloud.

The line element of the four-dimensional black hole surrounded by quintessence [61] can be expressed as

$$\begin{aligned} ds^2= & {} -\bigg (1-\frac{2M}{r}-\frac{q}{r^{3\omega _q+1}}\bigg )+\bigg (1-\frac{2M}{r} -\frac{q}{r^{3\omega _q+1}}\bigg )^{-1}\nonumber \\&+r^2d\theta ^2+r^2\sin ^{2}\theta d\phi ^2, \end{aligned}$$
(2.19)

where q refers to the parameter of the quintessential matter. The energy density \(\rho _q\) corresponding to this case is given by

$$\begin{aligned} \rho _q=-\frac{3q\omega _q}{2r^{3(\omega _q+1)}}. \end{aligned}$$
(2.20)

The components of the energy–momentum tensor for the quintessential matter are defined as

$$\begin{aligned} T^{(q)t}_{t}=T^{(q)r}_r=\rho _q, \quad T^{(q)\theta }_{\theta }=T^{(q)\phi }_{\phi }=-\frac{1}{2}\rho _q(3\omega _q+1).\nonumber \\ \end{aligned}$$
(2.21)

Similarly, the generalized Schwarzschild–Tangherlini black hole in the presence of quintessence [26] is defined by the lime element

$$\begin{aligned} \begin{aligned} ds^2&=-\bigg (1-\frac{16\pi M}{d_2\Sigma _{d_2}r^{d_3}}-\frac{q}{r^{d_1\omega _q+d_3}}\bigg )dt^2\\&\quad +\bigg (1-\frac{16\pi M}{d_2\Sigma _{d_2}r^{d_3}}-\frac{q}{r^{d_1\omega _q+d_3}}\bigg )^{-1}dr^2+r^2 (h_{ij}dx^idx^j). \end{aligned}\nonumber \\ \end{aligned}$$
(2.22)

The components of the energy–momentum tensor required for this solution are written as

$$\begin{aligned} T^{(q)t}_{t}= & {} T^{(q)r}_r=\rho _q=-\frac{q\omega _qd_1d_2}{2r^{d_1(\omega _q+1)}}, \nonumber \\ T^{(q)\theta _k}_{\theta _k}= & {} -\frac{1}{d_2}\rho _q(d_1\omega _q+1), \end{aligned}$$
(2.23)

where \(k=1,2,3,\ldots ,d-2\).

Let us choose a static and spherically symmetric line element as

$$\begin{aligned} ds^2=-g(r)dt^2+\frac{dr^2}{g(r)}+r^2d\Sigma ^{2}_{d_2}, \end{aligned}$$
(2.24)

where \(d\Sigma ^{2}_{d_2}\) refers to the line element of \(d_2\)-dimensional boundary surface whose curvature is equal to a constant value \(d_2d_3\kappa \). Here, \(\kappa \) is a constant such that the cases \(\kappa =0,1,-1\), correspond to flat, spherical and hyperbolic horizon topologies, respectively. This sub-manifold possesses a volume \(\Sigma _{d_2}\), whose value in the case of a spherical horizon topology is given by (2.17). Choosing the scalar field configuration in the form

$$\begin{aligned} \psi (r)=\frac{N}{r}, \end{aligned}$$
(2.25)

the function \(\psi (r)\) will be the solution of equations of motion (2.6) if N satisfies

$$\begin{aligned} \sum _{p=1}^{p_{max}}pb_p\frac{d_1!}{(d_1-2p)!}N^{2-2p}=0, \end{aligned}$$
(2.26)

and

$$\begin{aligned} \sum _{p=1}^{p_{max}}b_p\frac{d_1!(d^2-d+4p^2)}{(d_1-2p)!}N^{-2p}=0. \end{aligned}$$
(2.27)

The above equations show that there is one unknown, N, so one of the equations defines a constraint on constants \(b_p\). Hence, by choosing values of the coefficients \(\alpha _p\) from (2.2), using the line element (2.24), the energy–momentum tensor components related to string-cloud (2.18) and quintessence (2.23) along with Eqs. (2.5), (2.6) and (2.25)–(2.27) for scalar field configuration, we have found the following solution for DCG field equations (2.3)

$$\begin{aligned} \begin{aligned} g(r)&=\kappa +\frac{r^2}{l^2}-r^2\bigg [\frac{16\pi G M}{\Sigma _{d_2}r^{d_1}}+\frac{\delta _{d,2n-1}}{r^{d_1}}+\frac{16\pi d_2G H_A}{r^d}\\&\quad -\frac{8\pi G q d_2}{r^{1+d_1\omega _q}}-\frac{16\pi G a}{r^{d_2}}\bigg ]^{\frac{1}{n-1}},\end{aligned} \end{aligned}$$
(2.28)

where

$$\begin{aligned} H_A=\sum _{p=0}^{p_{max}}b_p\frac{d_2!N^{d-2p}}{(d_2-2p)!}. \end{aligned}$$
(2.29)
Fig. 1
figure 1

The plot of g(r) (Eq. (2.28)) vs r for fixed values of \(l=1\), \(M=10^3\), \(\delta _{d,2n-1}=100\), \(\omega _q=-0.7\), \(\Sigma _{d-2}=1\), \(q=0.2\), \(a=0.05\) and \(H_A=0.5\)

Full size image
Fig. 2
figure 2

The plot of g(r) (Eq. (2.28)) vs r for fixed values of \(l=1\), \(M=10^3\), \(\delta _{d,2n-1}=100\), \(\omega _q=-0.7\), \(\Sigma _{d-2}=1\), \(n=2\), \(d=6\) and \(H_A=0.5\)

Full size image

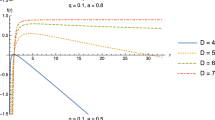
The constant M in the resulting metric function refers to the mass of the object and the additive constant \(\delta _{d,2n-1}\) would correspond to those values for which the condition \(M\rightarrow 0\) makes the gravitating object shrink. The behaviour of solution (2.28) for different values of spacetime dimensions is shown in Fig. 1. The horizon’s locations are determined by those values for which the curve meets the horizontal axis. Similarly, Fig. 2 shows that the parameters a and q affect the location of the event horizon and behaviour of the metric function as well. Selecting \(b_p=0\) or by using \(H_A\rightarrow 0\), the new family of dimensionally continued black holes with no scalar hair in a quintessence and string-cloud background can be described. Moreover, the hairy black hole solution in the absence of any matter sources can be determined by choosing \(q=0\) and \(a=0\). The metric function (2.28) shows that the hairy black holes exist only for \(d\ge 5\) because in four-dimensional geometry Eqs. (2.26)–(2.27) cannot be satisfied when any of the conformal coupling constants \(b_p\) is not equal to zero. Hence, it is noted that dimensionally continued hairy black holes with a cloud of strings and quintessence do not exist in four dimensions. Thus, we should emphasize that the metric function (2.28) has the same behaviour as determined in Refs. [96, 97].

The curvature invariants for the chosen ansatz (2.19) are calculated as

$$\begin{aligned} \begin{aligned} R(r)&=\bigg [d_2d_3\bigg (\frac{\kappa -g(r)}{r^2}\bigg )-\frac{d^2g}{dr^2} -\frac{2d_2}{r}\frac{dg}{dr}\bigg ],\end{aligned} \end{aligned}$$
(2.30)

and

$$\begin{aligned} \begin{aligned} K(r)&=\bigg [2d_2d_3\bigg (\frac{\kappa -g(r)}{r^2}\bigg )^2-\bigg (\frac{d^2g}{dr^2}\bigg )^2+\frac{2d_2}{r^2}\bigg (\frac{dg}{dr}\bigg )^2\bigg ]. \end{aligned}\nonumber \\ \end{aligned}$$
(2.31)

It is straightforward to verify that both the curvature scalars associated with the metric function (2.28) are divergent in the limit \(r\rightarrow 0\). This implies that there is a true curvature singularity in the spacetime.

3 Thermodynamics of black holes

In order to discuss thermodynamic properties of dimensionally continued hairy black holes with a cloud of strings and quintessence backgrounds, we compute thermodynamic quantities in terms of the horizon radius \(r_+\). Consider, for simplicity, the case of spherical black holes, \(\kappa =1\). From the condition \(g(r_+)=0\), we are able to write the expression for finite mass as

$$\begin{aligned} M= & {} \frac{\Sigma _{d_2}}{16\pi G}\bigg [r_+^{d_1}\bigg (\frac{1}{r_+^2}+\frac{1}{l^2}\bigg )^{n-1} -\delta _{d,2n-1}-\frac{16\pi G H_Ad_2}{r_+} \nonumber \\&+16\pi G a r_++\frac{8\pi Gqd_2r_+^{d_1}}{r_+^{1+d_1\omega _q}}\bigg ]. \end{aligned}$$
(3.1)
Fig. 3
figure 3

The plot of mass M (Eq. (3.1)) vs \(r_+\) for chosen values of \(l=1\), \(\delta _{d,2n-1}=100\), \(\omega _q=-0.5\), \(\Sigma _{d-2}=1\), \(q=0.5\), \(a=0.05\) and \(H_A=1\)

Full size image
Fig. 4
figure 4

The plot of mass M (Eq. (3.1)) vs \(r_+\) for chosen values of \(l=1\), \(\delta _{d,2n-1}=10\), \(\omega _q=-0.5\), \(\Sigma _{d-2}=1\), \(n=2\), \(d=5\) and \(H_A=1\)

Full size image

Figures 3 and 4 show the behaviour of the black hole mass in terms of \(r_+\) for different values of parameters d, q and a. Note that, corresponding to all the positive values of M in (3.1), there may exist one or more horizons. However, the mass of the extremal black hole can be obtained from the conditions \(g(r)=0\) and \(dg/dr=0\). So, we have

$$\begin{aligned} M_e= & {} \frac{\Sigma _{d_2}}{16\pi G d_1}\bigg [2r_e^{d_3}\bigg (\!\frac{1}{r_e^2}+\frac{1}{l^2}\!\bigg )^{-n}\! -\delta _{d,2n-1}d_1-\!\frac{16\pi G H_A dd_2}{r_e} \nonumber \\&+16\pi G a r_ed_2+\frac{8\pi Gqd_2(1+d_1\omega _q)r_e^{d_2}}{r_e^{d_1\omega _q}}\bigg ]. \end{aligned}$$
(3.2)

The Hawking temperature [98] is defined as \(T_H=\kappa _s/2\pi \) where \(\kappa _s\) stands for surface gravity. Therefore, for the hairy black hole structures described by Eq. (2.28), we obtain the temperature as

$$\begin{aligned} T_{H}= & {} -\frac{1}{2\pi r_+}+\frac{r_+^{2n-2}l^{2n-4}}{4\pi (n-1)\big (l^2+r_+^2\big )^{n-2}}\bigg [\frac{16\pi G H_Ad_2}{r_+^{d_{-1}}}\nonumber \\&+\frac{16\pi G a(2d-3)}{r_+^{d_1}} +\frac{d_1r_+^{2n-3}l^{2n-2}}{\big (l^2+r_+^2\big )^{n-1}} \nonumber \\&+\frac{8\pi Gqd_2(d_1(1-\omega _q)-1)}{r_+^{d_1\omega _q+2}}\bigg ]. \end{aligned}$$
(3.3)
Fig. 5
figure 5

The plot of temperature \(T_H\) (Eq. (3.3)) vs \(r_+\) for fixed values of \(l=1\), \(\delta _{d,2n-1}=100\), \(\omega _q=-0.7\), \(\Sigma _{d-2}=1\), \(q=0.2\), \(a=0.05\) and \(H_A=0.5\)

Full size image
Fig. 6
figure 6

The plot of temperature \(T_H\) (Eq. (3.3)) vs \(r_+\) for fixed values of \(l=1\), \(\delta _{d,2n-1}=100\), \(\omega _q=-0.7\), \(\Sigma _{d-2}=1\), \(n=2\), \(d=6\) and \(H_A=0.5\)

Full size image

The plot of temperature \(T_H\) for different values of the spacetime dimension is depicted in Fig. 5. Similarly, Fig. 6 describes the effects of quintessence and string-cloud on temperature of the black hole. The positivity of temperature for the values of \(r_+\) implies that black holes of such horizon radii are physical. The entropy of the black hole (2.28) can be obtained by employing Wald’s formulation [99, 100], and we can write

$$\begin{aligned} S=-2\pi \oint d^{d_2}x\sqrt{{\overline{\gamma }}}\frac{\partial L}{\partial R_{abcd}}\epsilon _{ab}\epsilon _{cd}, \end{aligned}$$
(3.4)

in which L refers to Lovelock Lagrangian density, \({\overline{\gamma }}\) is the determinant of the induced metric \({\overline{\gamma }}_{ab}\) defined on the horizon and \(\epsilon _{ab}\) stands for the binormal. Thus, the entropy corresponding to metric function (2.28) can be obtained as

$$\begin{aligned} \begin{aligned} S&=\frac{\Sigma _{d_2}}{4G}\sum _{p=1}^{p_{max}}\frac{pb_pd_2!N^{d-2p}}{(d-2p)!} +\frac{(n-1)\Sigma _{d_2}r_+^d}{4G(d-2n+2)}\\&\quad \times \bigg (\frac{1}{r_+^2} +\frac{1}{l^2}\bigg )^{n-1}F_1\bigg [1,\frac{d}{2},\frac{d-2n+4}{2},\frac{-r_+^2}{l^2}\bigg ], \end{aligned} \end{aligned}$$
(3.5)

where \(F_1\) symbolizes the Guassian hypergeometric function. It should be noted that the contribution of background matter i.e. quintessence and cloud of strings comes from terms containing \(r_+\) through Eq. (3.1) in the above mathematical expression of Wald entropy. Again, this behaviour is similar to that obtained in Refs. [96, 97] where effects of the nonlinear electromagnetic field (matter sources considered in [96, 97]) comes from the value of \(r_+\) through the expression of black hole’s mass. The extended first law [26, 67, 94] corresponding to the dimensionally continued hairy black hole with quintessential dark energy in a string-cloud model can be written as

$$\begin{aligned} \begin{aligned} dM&=T_HdS+A_ada+Wdq+\sum _{p=0}^{p_{max}}{\overline{B}}^{(p)}db_p. \end{aligned} \end{aligned}$$
(3.6)

Note that, \(A_a\) and W are conjugate quantities associated with the parameters of strings a and quintessential dark energy q, respectively. These quantities are mathematically expressed as

$$\begin{aligned} \begin{aligned} A_a&=\frac{\partial M}{\partial a}=\Sigma _{d_2}r_+, \end{aligned} \end{aligned}$$
(3.7)

and

$$\begin{aligned} \begin{aligned} W&=\frac{\partial M}{\partial q}=\frac{d_2\Sigma _{d_2}}{2r_+^{1+d_1(\omega _q-1)}}. \end{aligned} \end{aligned}$$
(3.8)

Similarly, \({\overline{B}}\)’s are conjugated to conformal coupling constants b’s and are determined as

$$\begin{aligned} \begin{aligned} {\overline{B}}^{(p)}=-\frac{\Sigma _{d_2}}{r_+}\sum _{p=0}^{p_{max}} \frac{4d_2!}{(d_2-2p)!N^{2p-d}}. \end{aligned} \end{aligned}$$
(3.9)

Similarly, the generalized Smarr’s relation [26, 94, 101] associated with the above thermodynamic quantities takes the form

$$\begin{aligned} \begin{aligned} d_3M&=d_2T_HS+d_4A_aa+(d_3+\omega _qd_1)Wq\\&\quad +d_2\sum _{p=0}^{p_{max}} {\overline{B}}^{(p)}b_p.\end{aligned} \end{aligned}$$
(3.10)

We have noted earlier that all the conformal coupling parameters \(b's\) are not independent because of the two constraints (2.26) and (2.27) on metric function (2.28). Therefore, it must be emphasized here that variations of \(b's\) in the generalized first law (2.30) are not all independent.

The specific heat capacity [102] can be defined as

$$\begin{aligned} C_H=T_{H}\frac{dS}{dT_H}. \end{aligned}$$
(3.11)

Differentiating the expression of Hawking temperature (3.3) with respect to \(r_+\) yields

$$\begin{aligned} \frac{\partial T_H}{\partial r_+}&=\frac{1}{2\pi r_+^2}-\frac{(n-2)l^{2n-4}r_+G_1(r_+)}{2\pi (n-1)(l^2+r_+^2)^{n-1}} \nonumber \\&\quad +\frac{l^{2n-4}}{4\pi (n-1)(l^2+r_+^2)^{n-2}}\bigg (\frac{dG_1}{dr_+}\bigg ), \end{aligned}$$
(3.12)

where

$$\begin{aligned} G_1(r_+)&=\frac{16\pi G H_A d_2}{r_+^{d-2n+3}}+\frac{16\pi G a (2d-3)}{r_+^{d-2n+1}}+\frac{d_1l^{2n-2}r_+^{4n-5}}{(l^2+r_+^2)^{n-1}} \nonumber \\&\quad +\frac{8\pi G q d_2(d_1(1-\omega _q)-1)}{r_+^{d_1\omega _q-2n+4}}, \end{aligned}$$
(3.13)

and

$$\begin{aligned} \frac{dG_1}{dr_+}&=-\frac{16\pi G H_Ad_2(d-2n+3)}{r_+^{d-2n+4}} \nonumber \\&\quad +\frac{8\pi G qd_2(d_1(1-\omega _q)-1)}{(2n-4-d_1\omega _q)^{-1}r_+^{d_1\omega _q-2n+5}} \nonumber \\&\quad +\frac{16\pi G a(3-2d)(d-2n+1)}{r_+^{d-2n+2}} \nonumber \\&\quad +\frac{d_1l^{2n-2}(4n-5)r_+^{4n-6}}{(l^2+r_+^2)^{n-1}} \nonumber \\&\quad -\frac{d_1(2n-2)l^{2n-2}r_+^{4n-4}}{(r_+^2+l^2)^n}. \end{aligned}$$
(3.14)

Substitution of Wald entropy (3.5), temperature (3.11) and Eq. (3.12) into (3.11) yields the expression for the specific heat

$$\begin{aligned} C_H= & {} \frac{(n-1)\Sigma _{d_2}r_+^{d-2n+2}(r_+^2+l^2)^{n-1}Z_1(r_+) \big (r_+l^{2n-4}G_1(r_+)-2(n-1)(r_+^2+l^2)^{n-2}\big )}{8Gl^{2n}(d-2n+2)(d-2n+4)}\nonumber \\&\times \frac{1}{(n-1)(r_+^2+l^2)^{n-1}-l^{2n-4}(n-2)r_+^3G_1(r_+) +2l^{2n-4}r_+^2(r_+^2+l^2)dG_1/dr_+}, \end{aligned}$$
(3.15)

where

$$\begin{aligned} \begin{aligned} Z_1(r_+)&=l^2(d-2n+4)(r_+^2d+l^2(d-2n+2))F_1\\&\quad \times \bigg [1,\frac{d}{2},\frac{d-2n+4}{2}, -\frac{r_+^2}{l^2}\bigg ]\\&\quad -2r_+^2d(r_+^2+l^2)F_1\bigg [2,1+\frac{d}{2},3-n +\frac{d}{2},-\frac{r_+^2}{l^2}\bigg ].\end{aligned} \end{aligned}$$
(3.16)
Fig. 7
figure 7

The plot of specific heat \(C_H\) (Eq. (3.15)) vs \(r_+\) for fixed values of \(l=1\), \(G=1\), \(\delta _{d,2n-1}=10\), \(\omega _q=-0.7\), \(\Sigma _{d-2}=100\), \(q=0.2\), \(a=0.05\) and \(H_A=0.5\)

Full size image
Fig. 8
figure 8

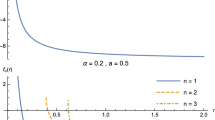
The plot of \(\frac{dT_H}{dr_+}\) (Eq. (3.12)) vs \(r_+\) for fixed values of \(l=1\), \(G=1\), \(\delta _{d,2n-1}=100\), \(\omega _q=-0.7\), \(\Sigma _{d-2}=1\), \(q=3.5\), \(a=1.5\) and \(H_A=0.5\)

Full size image
Fig. 9
figure 9

The plot of specific heat \(C_H\) (Eq. (3.15)) vs \(r_+\) for fixed values of \(l=1\), \(G=1\), \(\delta _{d,2n-1}=100\), \(\omega _q=-0.7\), \(\Sigma _{d-2}=1\), \(n=2\), \(d=5\) and \(H_A=0.5\)

Full size image
Fig. 10
figure 10

The plot of \(\frac{dT_H}{dr_+}\) (Eq. (3.12)) vs \(r_+\) for fixed values of \(l=1\), \(\delta _{d,2n-1}=100\), \(\omega _q=-0.7\), \(\Sigma _{d-2}=1\), \(n=3\), \(d=8\) and \(H_A=0.5\)

Full size image

The specific heat capacity is helpful for the investigation of local thermodynamic stability. The behaviour of specific heat (3.15) in different spacetime dimensions is shown in Fig. 7. When \(C_H\) becomes negative then the black hole does not exist. However, the region in which it is positive implies that there is local thermodynamic stability of the black hole. The first order phase transition of the black hole corresponds to those horizon radii for which the curve of specific heat \(C_H\) meets the \(r_+\)-axis. The second order phase transitions take place at those values for which the specific heat capacity is not convergent. One can also check this type of phase transitions from Fig. 8. So, when Hawking temperature has an extremum, \(dT_H/dr_+=0\), the specific heat is singular and the second order phase transitions take place. The effects of quintessence and cloud of strings on the local thermodynamic stability and phase transitions of black holes can also be seen from Figs. 9 and 10. Gibb’s free energy density [102] is defined by

$$\begin{aligned} G(r_+)&=M-T_H S=\frac{\Sigma _{d_2}}{16\pi G}\bigg [r_+^{d_1}\bigg (\frac{1}{r_+^2}+\frac{1}{l^2}\bigg )^{n-1} -\delta _{d,2n-1}\nonumber \\&\quad -\frac{16\pi G H_Ad_2}{r_+} +16\pi G a r_++\frac{8\pi Gqd_2r_+^{d_1}}{r_+^{1+d_1\omega _q}}\bigg ] \nonumber \\&\quad -\bigg [-\frac{1}{2\pi r_+}+\frac{r_+^{2n-2}l^{2n-4}}{4\pi (n-1)\big (l^2+r_+^2\big )^{n-2}}\nonumber \\&\quad \times \bigg (\frac{16\pi G H_Ad_2}{r_+^{d+1}}+\frac{16\pi G a(2d-3)}{r_+^{d_1}}\nonumber \\&\quad +\frac{8\pi G q d_2(d_1(1-\omega _q)-1)}{r_+^{d_1\omega _q+2}}\nonumber \\&\quad +\frac{d_1r_+^{2n-3}l^{2n-2}}{\big (l^2+r_+^2\big )^{n-1}}\bigg )\bigg ]\bigg [H_1+\frac{(n-1)\Sigma _{d_2}r_+^d}{4G(d-2n+2)}\nonumber \\&\quad \times \bigg (\frac{1}{r_+^2}+\frac{1}{l^2}\bigg )^{n-1} F_1\bigg [1,\frac{d}{2},\frac{d-2n+4}{2},\frac{-r_+^2}{l^2}\bigg ]\bigg ], \end{aligned}$$
(3.17)

where

$$\begin{aligned} H_1=\frac{\Sigma _{d_2}}{4G}\sum _{p=1}^{p_{max}}\frac{pb_pd_2!N^{d-2p}}{(d-2p)!}. \end{aligned}$$
(3.18)
Fig. 11
figure 11

The plot of Gibb’s energy G (Eq. (3.17)) vs \(r_+\) for fixed values of \(l=0.9\), \(H_1=100\), \(\delta _{d,2n-1}=10\), \(\omega _q=-0.5\), \(\Sigma _{d-2}=1\), \(d=7\) and \(H=1\)

Full size image

Note that in the above expression of Gibb’s free energy density, \(F_1\) denotes the Guassian hypergeometric function. The global stability of a black hole can be explored from the negativity of this thermodynamic quantity. The behaviour of Gibb’s free energy as a function of \(r_+\) for different values of quintessence and string-cloud parameters is shown in Fig. 11. One can clearly see the regions where the black holes are enjoying global thermodynamic stability.

4 Lovelock hairy black holes

The polynomial equation generating solutions that describe Lovelock hairy black holes with quintessence and string-cloud background can be determined as

$$\begin{aligned} P\big [\frac{\kappa -g(r)}{r^2}\big ]&=\sum _{p=0}^{p_{max}}{\overline{\alpha }}_p \bigg [\frac{\kappa -g(r)}{r^2}\bigg ]^p\nonumber \\&=\frac{16\pi G M}{d_2\Sigma _{d_2}r^{d_1}}-\frac{8\pi G q}{r^{d_1(1+\omega _q)}}\nonumber \\&\quad -\frac{16\pi G a}{d_2r^{d_2}}+\frac{16\pi G H_A}{r^d}, \end{aligned}$$
(4.1)

where the contribution of scalar configuration (2.29) and energy–momentum tensors corresponding to quintessence (2.23) and cloud of strings (2.18) have been used in construction of the above polynomial equation. Note that for simplicity we have also used

$$\begin{aligned} {\overline{\alpha }}_0&=\frac{\alpha _0}{d_1d_2}, {\overline{\alpha }}_1=1,\nonumber \\ {\overline{\alpha }}_p&=\prod _{i=3}^{2p}d_i\alpha _p. \end{aligned}$$
(4.2)

It is worthwhile to mention here that the general expression for \({\overline{\alpha }}_p\) in the above holds only in case of \(p>1\). Different black hole solutions can be constructed from the above polynomial equation.

The mass of black hole associated with Eq. (4.1) is written as

$$\begin{aligned} M&=\frac{d_2\Sigma _{d_2}}{16\pi G}\bigg [\sum _{p=o}^{p_{max}}{\overline{\alpha }}_p\kappa ^pr_+^{d_1-2p}+\frac{8\pi G q}{r_+^{d_1\omega _q}}+\frac{16\pi G ar_+}{d_2} \nonumber \\&\quad -\frac{16\pi G H_A}{r_+}\bigg ]. \end{aligned}$$
(4.3)

The Hawking temperature corresponding to the black hole characterized by Eq. (4.1) can be expressed as

$$\begin{aligned} T_{H}(r_+)&=\frac{1}{4\pi \Xi (r_+)}\bigg [\sum _{p=0}^{n-1}\frac{{\overline{\alpha }}_p\kappa ^p(d_1-2p)}{r_+^{2p+1}}+\frac{16\pi G H_A}{r_+^{d+1}} \nonumber \\&\quad +\frac{16\pi G a}{d_2r_+^{d_1}}-\frac{8\pi G qd_1\omega _q}{r_+^{d_1\omega _q+d}}\bigg ], \end{aligned}$$
(4.4)

where \(\Xi (r_+)\) is defined by

$$\begin{aligned} \Xi (r_+)=\sum _{p=0}^{p_{max}}\frac{p{\overline{\alpha }}_p\kappa ^{p-1}}{r_+^{2p}}. \end{aligned}$$
(4.5)

The entropy for these black holes can be calculated again by Wald’s method as

$$\begin{aligned} S= & {} \frac{(d-2)\Sigma _{d-2}}{4G}\sum _{p=1}^{p_{max}}p\kappa ^{p-1} \bigg (\frac{{\overline{\alpha }}_p}{d-2p}r_+^{d-2p}\nonumber \\&+\frac{b_p(d-3)!N^{d-2p}}{(d-2p)!}\bigg ). \end{aligned}$$
(4.6)

Using entropy (4.6) and temperature (4.4), it is straightforward to compute heat capacity as

$$\begin{aligned} C_H&=\frac{\Xi (r_+)d_2\Sigma _{d_2}\bigg (\sum _{p=0}^{p_{max}}p\kappa ^{p-1} {\overline{\alpha }}_pr_+^{d_1-2p}\bigg )}{4G\bigg (\Delta _1(r_+)\Xi (r_+)-\Delta _2(r_+)d \Xi /dr_+\bigg )}\nonumber \\&\quad \times \bigg [\sum _{p=0}^{p_{max}}\frac{{\overline{\alpha }}_p \kappa ^p(d_1-2p)}{r_+^{2p+1}}\nonumber \\&\quad +\frac{16\pi G a}{d_2r_+^{d_1}}-\frac{8\pi G q\omega _qd_1}{r_+^{d+d_1\omega _q}}+\frac{16\pi G H_A}{r_+^{d+1}}\bigg ], \end{aligned}$$
(4.7)

where

$$\begin{aligned} \Delta _1(r_+)&=\frac{8\pi G q \omega _qd_1(d+d_1\omega _q)}{r_+^{d+1+d_1\omega _q}}\nonumber \\&\quad -\sum _{p=o}^{p_{max}} \frac{{\overline{\alpha }}_p\kappa ^p(2p+1)(d_1-2p)}{r_+^{2p+2}} \nonumber \\&\quad -\frac{16\pi G H_A (d+1)}{r_+^{d+2}}-\frac{16\pi G ad_1}{d_2r_+^d}, \end{aligned}$$
(4.8)
$$\begin{aligned} \Delta _2(r_+)&=\sum _{p=0}^{p_{max}}\frac{{\overline{\alpha }}_p\kappa ^p(d_1-2p)}{r_+^{2p+1}}-\frac{8\pi G q \omega _qd_1}{r_+^{d_1\omega _q+d}}+\frac{16\pi G a}{d_2r_+^{d_1}} \nonumber \\&\quad +\frac{16\pi G H_A}{r_+^{d+1}}, \end{aligned}$$
(4.9)

and

$$\begin{aligned} \begin{aligned} \frac{d\Xi }{dr_+}&=-2\sum _{p=1}^{p_{max}}\frac{p^2{\overline{\alpha }}_p \kappa ^{p-1}}{r_+^{2p+1}}. \end{aligned} \end{aligned}$$
(4.10)

One can easily determine hairy black hole solutions in any nth-order Lovelock gravity from the polynomial equation (4.1). For example, the Gauss–Bonnet hairy black hole can be illustrated by simply putting \({\overline{\alpha }}_2\ne 0\) and \({\overline{\alpha }}_p=0\) for \(p\ge 3\) in Eq. (4.1) as follows

$$\begin{aligned} \begin{aligned} f_{\pm }(r)&=\kappa +\frac{r^2}{2{\overline{\alpha }}_2}\bigg [1\pm \sqrt{\zeta (r)}\bigg ], \end{aligned} \end{aligned}$$
(4.11)

where

$$\begin{aligned} \begin{aligned} \zeta (r)&=1-4{\overline{\alpha }}_2{\overline{\alpha }}_0 +4{\overline{\alpha }}_2{\overline{\alpha }}_0\bigg (\frac{16\pi G M}{d_2\Sigma _{d_2}r^{d-1}}-\frac{8\pi G q}{r^{d_1(1+\omega _q)}}\\&\quad -\frac{16\pi G a}{d_2r^{d_2}}+\frac{16\pi G H_A}{r^d}\bigg ).\end{aligned} \end{aligned}$$
(4.12)

5 Summary and conclusion

In this work we focused on the new solutions of Lovelock-scalar gravity in the background of quintessence and a configuration of strings. The Lovelock gravity is non-minimally coupled to a conformal scalar field, and the matter sources for gravity were taken in the form of quintessence and a cloud of strings. A specific choice of DCG for the Lovelock coefficients is used and the gravitational field equations are solved. The metric function (2.28) representing dimensionally continued hairy black hole with quintessence and a cloud of strings is calculated. Moreover, we also examined thermodynamics of the hairy black holes. The finite mass of black hole, Hawking temperature, specific heat capacity and Gibb’s free energy are calculated in terms of the event horizon radius. It is shown that the thermodynamic quantities are significantly affected by the contributions of quintessence and cloud of strings except for the Wald entropy which remains unchanged. We considered the entropy S, parameter of strings a, quintessence parameter q and conformal coupling coefficients \(b's\) as extensive thermodynamic variables and computed their conjugate quantities as well. We used these quantities for validation of the generalized first law and Smarr’s relation. We also performed thermodynamic stability analysis from both local and global points of views. The results for Hawking temperature and heat capacity in different spacetime dimensions have also been presented graphically. The region of positive heat capacity and Hawking temperature shows that there is local thermodynamic stability of the black holes. It is shown that larger DCG hairy black holes are more stable than the smaller ones because as \(r_+\) increases both the heat capacity and Hawking temperature also increase. The possibility of both the first and second order phase transitions is also visible from the plots of specific heat capacity. Further, global thermodynamic stability of black holes can be analysed from the plot of Gibb’s free energy as a function of \(r_+\).

Finally, the hairy black holes of general Lovelock theory in the presence of quintessential dark energy and string-cloud model are also studied. In order to do this, we determined the Lovelock polynomial equation which can generate d-dimensional black hole solutions of any nth-order Lovelock theory. The thermodynamic quantities corresponding to this polynomial equation have also been computed.

It is worthwhile to note that for \(H_A=0\) or \(b_p=0\), the metric function (2.28) again describes a new class of dimensionally continued non-hairy black holes surrounded by quintessence and a cloud of strings. Similarly, topological black holes obtained in Ref. [77] can also be recovered from polynomial equation (4.1) for \(H_A=0\). Moreover, by taking \(q=a=0\), the metric function in each case describes neutral black holes with scalar hair.

It might be very significant to study the phenomenon of thermal fluctuations, Hawking radiations, quasi-normal modes and greybody factors in the framework of a cloud of strings and quintessence. Similarly, the study of charged black holes, black branes and cylindrical black holes within this setup could also be very interesting.