1 Introduction

In recent years, the study of cosmological issues such as dark energy and dark matter has gradually intensified. Meanwhile, a large number of questions need to be solved urgently. These issues require the support of new astronomical observations. The discovery of the gravitational wave burst event GW150914 [1, 2] marks the arrival of the era of gravitational-wave astronomy. It has opened up a whole new window for human beings to study extreme physical processes and phenomena such as strong gravitational fields, extremely dense objects, extremely high-energy processes, and the very early universe.

One of the biggest cosmological surprises in recent years was the discovery that the Universe is presently undergoing a phase of accelerated expansion [3,4,5]. The reason for this behavior is still a complete mystery.

If the Universe is homogeneous and isotropic on large scales, all contributions to the cosmological energy-momentum tensors can be characterized by their energy density \(\rho (z)\) and pressure p(z). Accelerated expansion requires that \(\rho +3p<0\). This can be achieved by introducing a so-called “dark energy” component with negative pressure in addition to the usual pressureless matter. One of the main challenges of observational cosmology is to characterize the properties of this dark energy. The homogeneous and isotropic aspects of dark energy are completely determined by the equation of state \(w_{\mathrm{DE}}(z)\equiv p_{\mathrm{DE}}(z)/\rho _{\mathrm{DE}}(z)\) which links its pressure and energy density. The primary goal of observational dark energy studies is to measure the functional form of \(w_{\mathrm{DE}}(z)\).

The GW signal from a compact-binary object provides a unique way to measure the luminosity distance to the source with high precision. Such binary sources are often referred to as standard sirens (analogous to the electromagnetic standard candle). With the redshift information determined by an electromagnetic follow-up observation, the standard siren can be an accurate tracer of the cosmic expansion [6]. The gravitational wave signal can give the luminosity distance \(d_L\) of the wave source, the electromagnetic counterpart of gravitational waves can give the redshift z, the \(d_L\)-z relation characterizes the expansion history of the universe [7] and is the basis for calculating the Hubble parameter H(z) and the dark energy equation of state \(w_{\mathrm{DE}}(z)\).

Current experiments detect the dark energy equation of state by measuring the luminosity distances to supernovae or the angular diameter distance to the last scattering surface via the cosmic microwave background (CMB) peak positions. These distances are linked to \(w_{\mathrm{DE}}(z)\) through a double integration, rendering them rather insensitive to rapid variations of the equation of state. The required modeling can lead to strong biases that are difficult to detect and quantify [8, 9]. Direct measurement of the Hubble parameter H(z) would facilitate the derivation of \(w_{\mathrm{DE}}(z)\) immensely and allow for a more direct comparison with model predictions [10, 11].

Based on the above discussion, we purpose a novel method to obtain the Hubble parameters directly from the anisotropy of the luminosity distance, considering the anisotropy of the gravitational wave signal, on the premise of simulating the gravitational wave \(d_L\) data detected by DECIGO [12, 13] in the future.

In the case of DECIGO, the detectors orbit the Sun with a period of one sidereal year and constitute four clusters, each of which consists of three spacecraft exchanging laser beams with the others. Two of the four clusters are located at the same position to enhance correlation sensitivity to a gravitational-wave background, and the other two are separated on the Earth orbit to enhance the angular resolution so that we can easily identify the host galaxy of each NS binary via the electromagnetic follow-up observations. Based on this setup, Cutler and Holz have shown that cosmological parameters can be accurately measured by DECIGO with a precision of 1% [14].

In the first section of this paper, we introduce the current research status in this area. And in the second section, we first obtain the luminosity distance \(d_L\) by simulating the gravitational wave sources, and obtain the Hubble parameter H(z) from the luminosity distance, and then obtain the dark energy equation of state \(w_{\mathrm{DE}}\) by both model-dependent and model-independent methods, and introduce the specific method of simulation and the Cosmic Chronometer data(CC data). In the third section, we calculate \(w_{\mathrm{DE}}\) from the gravitational wave data model independently and then constrain three dark energy models with the gravitational wave data, the CC data, and the combination of them respectively. Also, we place constraints on the direction and amplitude of anisotropy, assuming that its origin is not exactly known. The concluding remarks are given in the forth section.

2 Methodology

2.1 The dipole anisotropy of \(d_L\)

We consider the luminosity distance to some astronomical objects measured at redshift z and angular position \({\varvec{n}}\) [15, 16]. Generally, the observations of many objects over the sky enable us to map out the angular distribution of luminosity distance \(d_L(z,{\varvec{n}})\), and no directional dependence appears if the observer is at a cosmological rest-frame (i.e., CMB rest-frame) in a homogeneous universe. However, there exist tiny anisotropies in \(d_L\) arising from the matter inhomogeneities of the large-scale structure and the local motion of the observer [14, 17]. The dominant component of anisotropies in the dipole is induced by the peculiar velocity of the observer, and the contribution to the higher multipoles coming from the weak gravitational lensing effect is small.

Assuming that \(d_L(z,{\varvec{n}})\) data have been obtained, the \(d_L(z,{\varvec{n}})\) can be Legendre decomposed to the first order: [15, 16]:

$$\begin{aligned} d_L(z, {\varvec{n}})&= d_L^{(0)}(z) + d_L^{(1)}(z)\left( {\varvec{n}} \cdot {\varvec{e}}\right) , \end{aligned}$$
(1)
$$\begin{aligned} d_L^{(0)}(z)&= \frac{1}{4\pi }\int d{\varvec{n}} d_L(z, {\varvec{n}}), \end{aligned}$$
(2)
$$\begin{aligned} d_L^{(1)}(z)&= \frac{3}{4\pi }\int d{\varvec{n}}\left( {\varvec{n}} \cdot {\varvec{e}}\right) d_L(z, {\varvec{n}}), \end{aligned}$$
(3)

where \({\varvec{e}}={\varvec{e}}(\theta _e,\phi _e)\) is the most significant direction of each anisotropy of the data, \(d_L^{(0)}\) is the background photometric distance and \(d_L^{(1)}\) is the anisotropic part, which mainly originates from the Doppler effect of the observer motion [15]:

$$\begin{aligned} d_L^{(0)}(z)&= (1 + z) \int _0^z\frac{dz^\prime }{H(z^\prime )}, \end{aligned}$$
(4)
$$\begin{aligned} d_L^{(1)}(z)&= \frac{|{\varvec{v}}_0|(1 + z)^2}{H(z)}. \end{aligned}$$
(5)

where \({\varvec{v}}_0\) is the velocity of the earth’s motion, \({\varvec{e}} = {\varvec{v}}_0 / |{\varvec{v}}_0|\), \(|{\varvec{v}}_0|= 369.1 \pm 0.9\) km/s [16, 18], assuming that the most important cause of the anisotropy of the gravitational wave signal originates from the motion of the Earth, other effects can be neglected. This value of \(v_0\) is constrained from CMB. By the way, although different observations may yield different values of \(v_0\), in the present paper, only its order of magnitude matters.

However, the anisotropy of the gravitational-wave signal may not just originate from the motion of the Earth, in which case we cannot directly assume that \({\varvec{v}}_0\) is known, and therefore it is necessary to investigate the accuracy of the constraint of the gravitational wave signal on the anisotropy.

2.1.1 Suppose \(v_0\) is known

Suppose \({\varvec{v}}_0\) is known, H(z) can be obtained directly from \(d_L^{(1)}(z)\) according to Eq. (5). Neglecting the error of \({\varvec{v}}_0\) [16]:

$$\begin{aligned} \frac{\sigma _H(z)}{H(z)} = \frac{\sigma _{d_L}^{(1)}(z)}{d_L^{(1)}(z)} = \sqrt{3}\left[ \frac{d_L^{(0)}(z)}{d_L^{(1)}(z)}\right] \left[ \frac{\sigma _{d_L}^{(0)}(z)}{d_L^{(0)}(z)}\right] . \end{aligned}$$
(6)

Usually \(d_L^{(0)}(z)/d_L^{(1)}(z)\) is of the order of \(10^2 \sim 10^3\), so a large amount of data is needed. As is stated by [11, 16], this method requires \(10^5 \sim 10^6\) samples to measure H(z) with the accuracy of a few percent. Otherwise, the analysis should be conducted in conjunction with other observations, such as [18]. This method is independent of cosmological modeling and only pursues a flat FRW metric.

2.1.2 Suppose \({v}_0\) is unknown

Suppose \({\varvec{v}}_0\) is unknown, which indicates that the anisotropy of the gravitational wave signal may not only originate from the motion of the Earth. According to Eqs. (1) and Eq. (5), one can restrict \(\varvec{\lambda } = \{v_0, \theta _e, \phi _e\}\) with \(d_L(z,{\varvec{n}})\) data, \(v_0 = |{\varvec{v}}_0|\)

$$\begin{aligned} \chi ^2_{{\varvec{v}}_0} = \sum _i^{N_{\mathrm{GW}}} \frac{\left[ d_L^{\mathrm{th}}(z_i, {\varvec{n}}_i; \varvec{\lambda }) - d_{L, i}\right] ^2}{\sigma ^2_{d_L, i}}. \end{aligned}$$
(7)

\(d^{\mathrm{th}}_L\) is defined in Eq. (1).

The simulation of GW detection is described in Sect. 2.3. For similar studies see [19] (supernova) [20] (gravitational waves).

2.2 Method for calculating the equation of state of dark energy

After obtaining the Hubble parameters H(z) by luminosity distance \(d_L\), we get the dark energy equation of state \(w_{\mathrm{DE}}(z)\) by two methods, model-dependent and model-independent.

2.2.1 Model-independent

For the model-independent approach, we do not need to pressume the specific form of the dark energy equation of state \(w_{\mathrm{DE}}(z)\). For a flat universe consist of only dark energy and dark matter, the relationship between \(w_{\mathrm{DE}}(z)\) and H(z) can be given according to the Friedmann equation

$$\begin{aligned} {w_{\mathrm{DE}}(z) =\frac{2/3 (1 + z) H H^\prime - H^2}{H^2 - H_0^2 \Omega _m (1 + z)^3},} \end{aligned}$$
(8)

where \(H^\prime =dH/dz\). In addition to H(z) and its derivative, there is only one parameter combination of \(H^2_0\Omega _m\) in the formula. And this parameter combination can be measured exactly by the Planck satellite. Therefore, we can calculate \(w_{\mathrm{DE}}(z)\) based only on the relationship between H(z) and \(w_{\mathrm{DE}}(z)\) given by the Friedmann equation.

2.2.2 Model-dependent

We constrain the dark energy model with the measured H(z), for the model-dependent approach. Assume a functional form of \(w_{\mathrm{DE}}(z)\), such as CPL, JBP, etc., which contains pending parameters \(w_0\), \(w_a\), etc.

The parameter restriction means that the theoretical value of H(z) is calculated using the assumed \(w_{\mathrm{DE}}(z)\) and compared with the observed value to find the parameter value that makes the theory and observation most compatible. In Bayesian theory, the criterion of “conformity” is the minimum value of \(\chi ^2\).

Constrain cosmological model (parameter \({\varvec{p}}\)):

$$\begin{aligned} \chi ^2_{\mathrm{GW}} = \sum _i^{N_{\mathrm{GW}}} \frac{\left[ H^{\mathrm{th}}(z_i; {\varvec{p}}) - H_i\right] ^2}{\sigma ^2_{H, i}}. \end{aligned}$$
(9)

The general form of the \(\chi ^2\) function: (theoretical value - observed value / error\()^2\), above \(H^{\mathrm{th}}(z;{\varvec{p}})\) is obtained from the parameterization of \(w_{\mathrm{DE}}(z;{\varvec{p}})\), see Sect. 2.5.

The Bayesian analysis of parameters is conducted via open-source Fortran code CosmoMC [21].

Fig. 1
figure 1

Redshift distribution of simulated data (histogram) and theoretical merging rate (curve)

Full size image

2.3 Mock data

The gravitational wave detector we simulate is DECIGO, the observation time \(T_{\mathrm{obs}} = 10\) year, and the simulated wave source type is a binary neutron star system (BNS) with the electromagnetic counterpart.

  1. 1.

    Choose the flat \(\Lambda \)CDM model with parameters \(\{H_0 = 67.8\) km/s/Mpc, \(\Omega _m = 0.331\}\) as the fiducial model. Simulate the wave source distribution (Fig. 1), and calculate the error of \(d_L\).

    The redshifts of BNS are drawn from the distribution

    $$\begin{aligned} {} R_z(z) = \frac{R_{\mathrm{merge}}(z)}{1+z}\frac{dV(z)}{dz} = \frac{4 \pi d_{\mathrm{L}}^2(z) R_{\mathrm{merge}}(z)}{(1 + z)^3 H(z)}, \end{aligned}$$
    (10)

    where the second equality originates from the definition of comoving volume. The merger rate of BNS, dubbed \(R_{\mathrm{merge}}(z)\), is the convolution of NS formation rate \(R_{\mathrm{f}}\) and the time-delay probability \(P_{\mathrm{d}}\) [22, 23]:

    $$\begin{aligned} R_{\mathrm{merge}}(z) \propto \int _{t_{\mathrm{min}}}^{t_{\mathrm{max}}}R_{\mathrm{f}}\left[ t(z) - t_{\mathrm{d}}\right] \ P_{\mathrm{d}}\left( t_{\mathrm{d}}\right) dt_{\mathrm{d}}. \end{aligned}$$
    (11)

    It is often assumed that \(P_{\mathrm{}}(t_{\mathrm{d}}) \propto t_{\mathrm{d}}^{-1}\), and \(\{t_{\mathrm{min}}, t_{\mathrm{max}}\} = \{20\mathrm{Myr}, t_H\}\), \(t_H\) is the Hubble time, and \(R_{\mathrm{f}}\) follows the star formation rate

    $$\begin{aligned} \mathrm{SFR}(z) = k\frac{a \exp [b(z-z_{\mathrm{m}})]}{a-b+b \exp [a(z-z_{\mathrm{m}})]}, \end{aligned}$$
    (12)

    where the parameters \(\{k, a, b, z_{\mathrm{m}}\}\) take the values of ‘Fiducial + PopIII’ model [24].

    As for other parameters, the sky position \({\hat{\varvec{n}}} = {\hat{\varvec{n}}}(\theta , \phi )\), time and phase of coalescence \((t_c, \phi _c)\) are sampled from uniform distributions. The component masses of BNS follow Gaussian distribution \(N(1.33, 0.09)M_{\mathrm{sun}}\) according to [25]. The calculation of SNR and error budget basically follow those of [16, 26]. With the sampled source parameters, we are readily to calculate the SNR of each event via

    $$\begin{aligned} \rho ^2 = 4\sum _{i = 1}^8 \int _{f_{min}}^{f_{max}}\frac{|{\tilde{h}}_i(f)|^2}{P(f)}df, \end{aligned}$$
    (13)

    where \({\tilde{h}}_i(f)\) is the Fourier GW waveform of the \(i^{th}\) interferometer, whose explicit expression is given in [16, 27], and DECIGO captures 8 interferometric signals in total. P(f) stands for the noise spectrum (see [16] for the fitting form of DECIGO). Following [16], \(f_{min} = 0.233 M_z^{-5/8} T_{obs}^{-3/8}\),where \(M_z = (1 + z) M_{c}\) is the redshifted chirp mass in the \(M_{sun}\) unit, and \(f_{max} = 100\)Hz. We set the SNR threshold as \(\rho _{\mathrm{threshold}} = 8\). According to [18, 28], the number of BNS merger detected by DECIGO in 10 year is \(\sim 10^6\), which is sufficient for measuring H(z) with acceptable precision. Following the results of previous research, in this paper, the total number of simulated BNS sources is \(10^6\).

    Further, the instrumental error of parameter labeled a reads

    $$\begin{aligned} \sigma _{a, \mathrm{ins}} = \sqrt{(\Gamma ^{-1})_{aa}}, \end{aligned}$$
    (14)

    where \(\Gamma \) is the Fisher matrix, defined as

    $$\begin{aligned} \Gamma _{ab} = 4\sum _{i = 1}^8 \Re \int _{f_{min}}^{f_{max}}\frac{\partial _a {\tilde{h}}^*_i(f) \partial _b {\tilde{h}}_i(f)}{P(f)}df. \end{aligned}$$
    (15)

    The redshifts of sources can be acquired independently via extra information from electromagnetic (EM) counterparts [29, 30], or with statistical methods [31,32,33]. We optimistically assume that the redshifts of all detected BNS are acquired.

  2. 2.

    Add the errors caused by gravitational lensing and peculiar velocity of source (see Eqs. (2.10) and (2.11) of [18]), thus

    $$\begin{aligned} \sigma ^2_{d_L} = \sigma ^2_{d_L, \mathrm{ins}} + \sigma ^2_{d_L, \mathrm{len}} + \sigma ^2_{d_L, \mathrm{pv}}, \end{aligned}$$
    (16)

    where

    $$\begin{aligned} \frac{\sigma _{d_L, \mathrm{len}}}{d_L}&= 0.066\left[ \frac{1 - (1 + z)^{-0.25}}{0.25}\right] ^{1.8}, \end{aligned}$$
    (17)
    $$\begin{aligned} \frac{\sigma _{d_L, \mathrm{pv}}}{d_L}&= \left|1 - \frac{(1 + z)^2}{H(z)d_L(z)} \right|\sigma _{\mathrm{v, gal}}, \end{aligned}$$
    (18)

    with \(\sigma _{\mathrm{v, gal}} = 300\) km/s.

    So far, we have obtained the isotropic part (\(0^{th}\) order) of GW data points, each consisting of 3 aspects \(\{z_\alpha , d_{L, \alpha }^{(0)}, \sigma _{d_L, \alpha }^{(0)}\}\).

  3. 3.

    Compute the error of H(z) according to Eq. (5) and (6) to get the simulation data \(\{z_\alpha , H_\alpha , \sigma _{H, \alpha }\}\). To be specific, \(\sigma _{H, \alpha }\) can be computed via Eq. (6), where \(d_L^{(1)}\) is given by Eq. (5), and these calculations only depend on the fiducial cosmological model and the isotropic \(d_L\) data. Furthermore, the simulated \(H_\alpha \) data is the sum of the fiducial value of H and a random error generated from Gaussian distribution \({\mathcal {N}}(0, \sigma _{H, \alpha })\).

  4. 4.

    The wave sources are uniformly distributed throughout the day without loss of generality, setting \({\varvec{e}} = {\varvec{e}}(\pi / 4, \pi / 4)\) of the simulated data. According to Eqs. (1) and (5), adding dipole to \(d_L^{(0)}\) in step 2, we get the data with each anisotropy \(\{z_\alpha , {\varvec{n}}_\alpha , d_{L, \alpha }, \sigma _{d_L, \alpha }\}\) to restrict \({\varvec{v}}_0\).

2.4 Cosmic chronometer

The CC data is a collection of Hubble parameters obtained with a model-independent method named differential age (DA) [34]. Specifically, the age differences \(\Delta t\) of galaxies located at different redshifts (separated by \(\Delta z\)) are measured, and the Hubble parameter is calculated from \(\Delta z / \Delta t\) according to

$$\begin{aligned} H(z) = -\frac{1}{1+z}\frac{\Delta z}{\Delta t}. \end{aligned}$$
(19)

The CC data are also \(\{z_i, H_i, \sigma _{H, i}\}\) measurements obtained using model-independent means (e.g. [35]). Purposes of introducing CC data:

  1. 1.

    Compare with simulated data.

  2. 2.

    Joint restricted cosmological model. \(\chi ^2 = \chi ^2_{\mathrm{GW}} + \chi ^2_{\mathrm{CC}}\), where

    $$\begin{aligned} \chi ^2_{\mathrm{CC}} = \sum _i^{N_{\mathrm{CC}}} \frac{\left[ H^{\mathrm{th}}(z_i; {\varvec{p}}) - H_i\right] ^2}{\sigma ^2_{H, i}}. \end{aligned}$$
    (20)

This paper uses 31 CC observations summarized in [35].

Table 1 The \(1\sigma \) ranges of cosmological parameters. left: \(\Lambda \)CDM, middle: \(\omega \)CDM, right: JBP
Full size table

2.5 DE models

H(z) for general dark energy

$$\begin{aligned} \frac{H^2}{H_0^2}= & {} \Omega _m (1 + z)^3 + (1 - \Omega _m) \exp \nonumber \\&\times \left[ 3\int _0^z \frac{1 + w_{\mathrm{DE}}(z^\prime )}{1 + z^\prime }dz^\prime \right] . \end{aligned}$$
(21)
  1. 1.

    \(\Lambda \)CDM:

    \(w_{\mathrm{DE}} = -1\), \({\varvec{p}} = \{\Omega _m, H_0\}\)

  2. 2.

    wCDM:

    \(w_{\mathrm{DE}} = w_0\), \({\varvec{p}} = \{\Omega _m, H_0, w_0\}\)

  3. 3.

    Jassal–Bagla–Padmanabhan (JBP) [36]:

    \(w_{\mathrm{DE}}(z) = w_0 + w_a z/(1 + z)^2\), \({\varvec{p}} = \{\Omega _m, H_0, w_0, w_a\}\)

3 Results

3.1 Model-independent DE

When using the model-independent methods to calculate \(w_{\mathrm{DE}}(z)\) from the simulated H(z) data. For error analysis, the main techniques are differential derivatives and statistical methods.

We segment the redshift and label each segment with i, then calculate the weighted average \(H(z_i)\) and the average error \(\sigma _{H}(z_i)\) within each segment, and differentiate the derivatives. Assuming that \(H_0^2\Omega _m\) is known, e.g. measured by Planck, we can calculate \(w_{\mathrm{DE}}(z_i)\) according to the formula (8), sample and calculate the error of \(w_{\mathrm{DE}}(z_i)\).

We average \(H(z_\alpha )\) and \(\sigma _H(z_\alpha )\) within each bin to get \(H(z_i)\) and \(\sigma _H(z_i)\), where \(z_\alpha \in (z_i - \Delta z / 2, z_i + \Delta z / 2)\). The derivative \(H^\prime (z_i)\) in Eq. (8) is calculated via the central difference method:

$$\begin{aligned} H^\prime (z_i)&= \frac{H(z_{i + 1}) - H(z_{i - 1})}{2\Delta z}. \end{aligned}$$
(22)
Fig. 2
figure 2

\(w_{\mathrm{DE}}(z)\) within each segment, error bars indicate \(1\sigma \) errors and the first three points have been enlarged to show. Dotted lines are the baseline model (\(\Lambda \)CDM, \(w_{\mathrm{DE}} = -1\))

Full size image

For example, by uniformly dividing the redshift range \(z\in (0, 3)\) into 10 bins, the resulting \(w_{\mathrm{DE}}\) is shown in Fig. 2. The calculated results are consistent with the fiducial model (\(\Lambda \)CDM) in the \(1\sigma \) range, indicating that GW has the potential of giving an unbiased model-independent measurement of \(w_{\mathrm{DE}}\). To be more specific, higher accuracy can be achieved in the first three bins, compared to the results at the other redshifts.

Note that the errors of \(w_{\mathrm{DE}}\) are proportional to \(N_i^{-1/2}\), \(N_i\) being the numbers of binned events. Our current choice of bins is based on the attempt to both reflect the local property of \(w_{\mathrm{DE}}\) (at least at the low redshifts) and keep the errors to an acceptable range.

3.2 Constraint on cosmological models

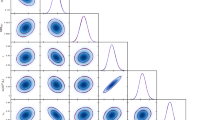
The cosmological models are constrained with CC, GW, and CC + GW data, respectively. The results are as follows (each contour plot represents the joint distribution of two parameters with \(1\sigma \) errors in the inner circle, \(2\sigma \) in the outer circle, and the \(1\sigma \) ranges of parameters are shown in Table 1).

  1. 1.

    \(\Lambda \)CDM model, results in Fig. 3 (top left), Table 1 (left column).

  2. 2.

    wCDM model, results in Fig. 3 (top right), Table 1 (middle column).

  3. 3.

    JBP model, results in Fig. 3 (bottom left), Table 1 (right column).

Fig. 3
figure 3

Constraints on the cosmological parameters and anisotropy. top left: \(\Lambda \)CDM, top right: wCDM, bottom left: JBP, bottom right:anisotropy

Full size image

We, therefore, believe that the accuracy of the gravitational wave data is comparable to the existing CC data, allowing for effective parameter constraints. Meanwhile, the joint constraint of gravitational wave data and CC data can further improve the precision of the parameters. By comparing the results of different models, it is evident that, as the number of parameters increases, the errors of parameters also increase. Moreover, since H(z) derived from GW data and directly taken from CC data share the same dependence on parameters, the degeneracy between parameters (e.g. \(H_0\) and \(\Omega _m\)) can not be relieved by the combination of these two data sets.

3.3 Constraint on anisotropy

The anisotropy of the gravitational wave signal may not only originate from the motion of the Earth, and it has the potential for revealing other aspects of the universe, such as the distribution of matter and the property of gravity. Therefore, it is necessary to predict the constraining ability of gravitational wave data on the direction and amplitude of anisotropy. Fixing the \(\Lambda \)CDM model and cosmological parameters, and restricting \({\varvec{v}}_0\), the results are shown in Fig. 3(lower right), Table 2.

It can be seen that gravitational wave data can give precise limits on \({\varvec{v}}_0\). The resulting \(v_0\), \(\theta _e\), and \(\phi _e\) are consistent with the fiducial values within the \(1\sigma \) range, thus, again it turns out that GW data can faithfully reflect the underlying model parameters. The relative precision of \(v_0\) is \(1.62\%\), which is an order of magnitude larger than CMB (\(0.24\%\)), but still a quite precise measurement. We have only considered flat \(\Lambda \)CDM as the cosmological model since the aim of this section is to illustrate the constraining ability of GW data on anisotropy, and the influence of changing the background model would be just moderate.

Table 2 The \(1\sigma \) ranges of the amplitude and direction of anisotropy
Full size table

4 Conclusion

In this paper, we propose a novel method to calculate the equation of state of dark energy \(w_{\mathrm{DE}}(z)\). We simulate the gravitational wave data detected by future gravitational wave detectors and obtain information about their redshift distribution and luminosity distance \(d_L\). We obtain the Hubble parameter H(z) by direct calculation instead of integration while considering its anisotropy, and further calculate the dark energy equation of state \(w_{\mathrm{DE}}(z)\) from both model-related and model-independent cases. Also, we consider the case when \(\varvec{v_0}\) is unknown, using a fixed dark energy model and cosmological parameters to constrain \({\varvec{v}}_0\). By the calculation of the model-independent approach, we obtain that the calculated results are consistent with the fiducial model (\(\Lambda \)CDM) in the \(1\sigma \) range, indicating that GW has the potential of giving an unbiased model-independent measurement of \(w_{\mathrm{DE}}\). For the model-dependent approach, after the introduction of CC data, we constrain the cosmological model with, CC, GW, CC+GW data, respectively, and prove that the accuracy of gravitational wave data is close to the existing CC data, which can effectively constrain the parameters and the joint constrain of gravitational wave and CC data can further improve the accuracy of the parameters. By comparing the results of different models, it is evident that as the number of parameters increases, the errors of parameters also increase. While the gravitational wave can give accurate restrictions on \({\varvec{v}}_0\). The resulting \(v_0\), \(\theta _e\), and \(\phi _e\) are consistent with the fiducial values within the \(1\sigma \) range, and the relative precision of \(v_0\) is \(1.62\%\), which is an order of magnitude larger than CMB (\(0.24\%\)), but still a quite precise measurement.