1 Introduction

In the year 1915, Albert Einstein has published his most important work by equating gravity with geometry. In the later years, it was experimentally/observationally verified [1] and is being used by researchers all over the globe as a stepping stone to understand the Universe in a better way. This theory gave rise to bizarre events like gravitational lensing, black holes, gravitational waves, wormholes etc. Among them, wormhole geometry is another solution of Einstein’s Field Equations (EFE) apart from black hole solution that connects two distinct space-time of the same or different universes widely separated. The first wormhole solution, the Einstein–Rosen bridge, was proposed by Albert Einstein and Nathan Rosen [2]. However, it was not paid much attention because the wormhole was non-traversable and considered only a theoretical solution. In 1973, Ellis showed a wormhole having spherical symmetry with the help of a ghost massless scalar field [3]. Later Morris and Thorne developed a theoretical traversable wormhole which, unlike the Einstein–Rosen bridge, does not contain any singularity or event horizons [4]. Matt Visser and Maccone have shown that inter universe travel is possible with the help of traversable stable wormholes [5, 6].

Recent discoveries about the Universe has revealed that all the planets, stars and visible matter comprise around \(5\%\) of the total matter and energy, where the rest is dominated by dark matter(DM) and dark energy, among which 27 % is dark matter. Although this DM does not interact with photons like normal baryonic matter, but only has gravitational effects. Astronomer Zwicky in the year 1933, first determined the existence of DM in a distant galaxy cluster [7, 8]. The presence of DM in the Milky Way galaxy was first speculated by Oort [16, 17] and later confirmed observationally by Diemand and Springel [9, 10]. In the later years, further experiments regarding the rotational curve of outer regions of galaxies and gravitational microlensing were conducted to understand the DM distribution [11]. Dark matter is an important entity for the fabrication of wormholes. The DM density profile proposed by researchers over the year plays a significant role in theoretically developing a fully stable and traversable wormhole.

This research aims to investigate the existence of wormhole geometry only in the bulge and the halo region of MWG. The bulge is the core of the Milky Way galaxy formed with compact stars, also seen in other spiral galaxies. The core of MWG contains a supermassive black hole around which a large numbers of old star clusters are there. This galactic centre is known as the bulge, and it roughly extends to 0.5 kpc [12]. Studies conducted by Mamon et al. [13] of the mass and shape of the dark galactic halo revealed that the core of the galaxy is being dominated by baryonic matter rather than dark matter. In 2011, studies of Martinez-Valpuesta showed that the galactic centre must have separate flat long bar components that are twisted according to the barred bulge of the galaxy [14]. The halo of the Milky Way Galaxy (MWG) comprises old stars and globular star clusters. Although at the disk of the MWG star formations take place, the halo has less gas to offer. Thus no star formation takes place [15]. As DM may be an important entity for the formation of wormholes, the halo of MWG is analyzed along with the Universal Rotational Curve. Studies revealed DM being dominant in the halo region of the MWG, thus it may be the best candidate to harbour wormhole structures.

Global monopole charge is a topological defect that came into existence due to the phase transition mechanism in the early universe [18]. It is the result due to global O(3) symmetry breaking of the self-coupling triplet of scalar fields \(\phi ^a\) that belongs to objects like cosmic strings, domain walls etc. It is an important topic in modern physics and has caught the attention of researchers to investigate its space-time geometry [19,20,21,22]. Studies have shown that this kind of topological defect contains negative gravitational potential [23]. The global monopole charge has also been used in cosmology [24,25,26]. This paper deals with a new kind of Morris Thorne wormhole solution with a global monopole charge in \(3+1\) gravity minimally coupled to a triplet of scalar fields. Sarkar et al. and Jusufi analyzed the stability of wormholes with global monopole charge with MacMillan DM profile in the bulge of MWG [27, 28]. Whereas we have used pseudo-isothermal, Novarro-Frank-White(NFW) and Universal Rotational Curve (URC) DM profile in the bulge and halo region of the MWG to check the existence of wormholes under this DM profiles along with global monopole charge.

2 Einstein’s field equations with global monopole charge and wormhole metric

The formulation of the Einstein field equations with global monopole charge obtained from \(3+1\) dimensional action without considering the cosmological constant minimally coupled triplet scalar field (\(\hbox {c}=\hbox {G}=1\)) is given by

$$\begin{aligned} S=\int \left( \frac{\mathscr {R}}{2 k}+\mathscr {L} \right) \sqrt{-g} d^4 x +S_m \end{aligned}$$
(1)

where \(k=8 \pi \). Lagrangian density of a self-coupling scalar triplet \(\phi ^a\) is given by

$$\begin{aligned} {\mathscr {L}}= - \frac{\lambda }{4}(\phi ^2 -\eta ^2)^2 -\frac{1}{2} \sum _a g^{ij} \partial _i \phi ^a \partial _j \phi ^a \end{aligned}$$
(2)

where \(\hbox {a}=1,2,3\) and \(\eta \), \(\lambda \) are scale of gauge-symmetry breaking, self interaction term respectively. Field configuration described by monopole is described as

$$\begin{aligned} \phi ^a = \frac{\eta }{r} f(r) x^a \end{aligned}$$
(3)

where the variable \(x^a\) is defined as \((r sin\theta cos\phi , r sin\theta sin\phi , rcos\theta )\) so that \(\sum _a x^a x^2 = r^2\).

Since our main interest lies in analysing traversable wormholes in the MWG, we consider a Morris–Thorne wormhole in four-dimensional spacetime. The wormhole metric in Schwarzschild coordinate is denoted by [29]

$$\begin{aligned} ds^2 = -e^{2\phi (r)} dt^2 + \frac{d r^2}{1-\frac{b(r)}{r}} + r^2 (d\theta ^2+sin^2\theta d\phi ^2) \end{aligned}$$
(4)

where \(\phi (r)\) and b(r) are the redshift and shape functions, respectively. Determination of these functions is very important to examine the wormhole geometry. The redshift function must be finite since the Morris–Thorne wormhole is devoid of any singularity and event horizons. In the equation, the minimum value of r is \(r_{th}\), also known as the throat radius of the wormhole. The shape function must obey the relation \(b(r_{th})=r_{th}\). The redshift function and shape function must be well defined beyond \(r>r_{th}\) for the wormhole to be traversable. The flare out condition must also be satisfied by the shape function b(r), given by,

$$\begin{aligned} \frac{b(r)-r b'(r)}{b^2(r)} > 0 \end{aligned}$$
(5)

for \(r>r_{th}\) in which \(b'(r_{th}) <1\). By using the field configuration, the Lagrangian density can be written in terms of f(r) as

$$\begin{aligned} \mathscr {L} = -\left( 1-\frac{b(r)}{r}\right) \frac{\eta ^2 (f')^2}{2} -\frac{\eta ^2 f^2}{r^2}-\frac{\lambda \eta ^4}{4}(f^2-1)^2\nonumber \\ \end{aligned}$$
(6)

and the Euler-Lagrangian equation for the field f(r) is

$$\begin{aligned}&\left( 1-\frac{b(r)}{r}\right) f'' + f' \left[ \left( 1-\frac{b(r)}{r}\right) \frac{2}{r}+\frac{1}{2}\left( \frac{b-b' r}{r^2}\right) \right] \nonumber \\&\quad -f\left[ \frac{2}{r^2}+\lambda \eta ^2(f^2-1)\right] =0 \end{aligned}$$
(7)

From Eq. (2), the energy momentum tensor can be obtained as

$$\begin{aligned} \bar{T_{ij}}=\partial _i\phi ^a\partial _j\phi ^a -\frac{1}{2} g_{ij}g^{\mu \nu }\partial _\mu \phi ^a\partial _\nu \phi ^a -\frac{g_{ij}\lambda }{4}(\phi ^2 -\eta ^2)^2 \nonumber \\ \end{aligned}$$
(8)

Now, from Eq. (8) all the four components of Energy-Momentum tensor are as follows:

$$\begin{aligned} \bar{T}^t_ t= & {} -\eta ^2\left[ \frac{f^2}{r^2}+\left( 1-\frac{b(r)}{r}\right) \frac{(f')^2}{2} +\frac{\lambda \eta ^2}{4}(f^2-1)^2\right] \nonumber \\ \end{aligned}$$
(9)
$$\begin{aligned} \bar{T}^r_ r= & {} -\eta ^2\left[ \frac{f^2}{r^2}+\left( 1-\frac{b(r)}{r}\right) \frac{(f')^2}{2} +\frac{\lambda \eta ^2}{4}(f^2-1)^2\right] \nonumber \\ \end{aligned}$$
(10)
$$\begin{aligned} \bar{T}^\theta _ \theta= & {} \bar{T}^\phi _\phi \nonumber \\= & {} -\eta ^2\left[ \left( 1-\frac{b(r)}{r}\right) \frac{(f')^2}{2} +\frac{\lambda \eta ^2}{4}(f^2-1)^2\right] \end{aligned}$$
(11)

As seen in Eq. (7), it is very complex to find an exact analytical solution. So the approximation of \(f(r)\rightarrow 1\) outside the wormhole is enough to simplify it to get the solution. Therefore, the reduced energy-momentum components are written as

$$\begin{aligned} \bar{T}^t_t=\bar{T}^r_r=-\frac{\eta ^2}{r^2} , \bar{T}^\theta _\theta =\bar{T}^\phi _\phi = 0 \end{aligned}$$
(12)

Now, we know that the Einstein field equation is

$$\begin{aligned} G_{\mu \nu } = \mathscr {R}_{\mu \nu } -\frac{1}{2} g_{\mu \nu } \mathscr {R} = 8\pi T_{\mu \nu } \end{aligned}$$
(13)

where \(T_{\mu \nu }\) is the sum of the energy-momentum tensor of anisotropic fluid part and matter field part. Therefore, it can be written as

$$\begin{aligned} T_{\mu \nu } =T^0_{\mu \nu } + \bar{T}_{\mu \nu } \end{aligned}$$
(14)

The components of the energy-momentum part of the anisotropic fluid are

$$\begin{aligned} {T^\mu _\nu }^ {(0)} =(-\rho , P_r, P_\theta , P_\phi ) \end{aligned}$$
(15)

Solving the Einstein field equation for Morris–Thorne wormhole metric, the components we get are,

$$\begin{aligned} G^t_t= & {} -\frac{b'(r)}{r^2} \end{aligned}$$
(16)
$$\begin{aligned} G^r_r= & {} - \frac{b(r)}{r^3}+2\left( 1-\frac{b(r)}{r}\right) \frac{\phi '}{r} \end{aligned}$$
(17)
$$\begin{aligned} G^\theta _\theta= & {} G^\phi _\phi = \left( 1-\frac{b(r)}{r}\right) \left\{ \phi '' + (\varPhi ')^2 - \frac{b'(r) r - b(r)}{2r(r-b)}\phi ' \right. \nonumber \\&\left. - \frac{b(r)' r -b(r)}{2 r^2(r-b)}+\frac{\phi '}{r} \right\} \end{aligned}$$
(18)

Now, combining the Einstein field equation for the wormhole along with the Global Monopole Charge, the solutions can be written as

$$\begin{aligned} \rho (r)= & {} \frac{1}{8\pi } \left( \frac{b'(r)}{r^2} - 8 \pi \eta ^2 \right) \end{aligned}$$
(19)
$$\begin{aligned} P_r(r)= & {} \frac{1}{8\pi }\left[ \left( 1-\frac{b(r)}{r}\right) \left( \frac{1}{r^2}+\frac{2\phi '(r)}{r}\right) -\frac{1}{r^2} +\frac{8\pi \eta ^2}{r^2}\right] \end{aligned}$$
(20)
$$\begin{aligned} P_t(r)= & {} \frac{1}{8\pi }\left( 1-\frac{b(r)}{r}\right) \phi ''(r) +\left( 1-\frac{b(r)}{r}\right) \phi '^2(r) \nonumber \\&+\frac{1}{2}\left( \frac{b(r)}{r^2}-\frac{b'(r)}{r}\right) \phi '(r) +\frac{1}{r}\left( 1-\frac{b(r)}{r}\right) \phi '(r) \nonumber \\&+\frac{1}{2r}\left( \frac{b(r)}{r^2}-\frac{b'(r)}{r}\right) \end{aligned}$$
(21)

where \(\rho \) is the energy density, \(P_r\) is the radial pressure and \(P_t\) is the transverse pressure. We have used \(\hbox {c}=\hbox {G}=1\) and \(\hbox {f}=\hbox {f(r)}\).

3 Different dark matter profiles

Sarkar et al. [27] has recently able to shown the wormhole geometry in the bulge of MWG using the Mc Millan DM profile. We have considered three possible DM profiles to generalize and maximize the probability of wormhole geometry supported by our galaxy–the NFW, pseudo-isothermal and URC profile.

The NFW profile as studied by Novarro et al. [30]. represented the dark matter profile which is defined by

$$\begin{aligned} \rho _{nfw}(r) = \frac{\rho _0}{\frac{r}{r_0}\left( 1+\frac{r}{r_0}\right) ^2} \end{aligned}$$
(22)

where, \(\rho _0\) and \(r_0\) is the core density and the core radius respectively. This profile along with the Global Monopole Charge (GMC) will be used for both the bulge and the halo region of the Milky Way galaxy to investigate its effect in wormhole geometry.

Now, we take another DM profile known as the Pseudo-Isothermal, represented by,

$$\begin{aligned} \rho _{iso}(r) = \frac{\rho _0}{1+\left( \frac{r}{r_0}\right) ^2} \end{aligned}$$
(23)

Although this profile is not used in the determination of wormhole in the galactic halo because the wormhole does not satisfy the flare out condition and the necessary violation needed for the NEC.

The URC or Burkert DM density profile along with the Global Monopole Charge is also considered for the investigation of wormhole geometry in both the bulge and halo of MWG. The density relation is given by,

$$\begin{aligned} \rho _{urc}(r) = \frac{\rho _0 r_0^3}{(r+r_0)(r^2+r_0^2)} \end{aligned}$$
(24)

where \(r_0\) and \(\rho _0\) are the core radius and density respectively.

4 Null energy condition and redshift function

In analyzing the formation of traversable wormhole geometry, the Null energy condition (NEC) is of utmost importance. The violation of NEC must be satisfied by the anisotropic matter content in the wormhole [31,32,33]. The NEC can be expressed in terms of general relativity as \(T_{\mu \nu }{v^\mu } {v^\nu } \ge 0\), where \(n^\mu \) is a null vector [34] represented by \(\rho (r) +P_r(r) \ge 0\). Thus for the violation of NEC \(v^\mu \le 0\), and verification of this condition, one must know the \(P_r(r)\), and from Eq. (20), it is evident that the knowledge of the redshift function is necessary to compute the radial pressure and thus determine the violation of NEC. We have used three redshift functions for more generalization of our model. For the redshift function

$$\begin{aligned} \phi (r) =0 \end{aligned}$$
(25)

is called the tidal force [35]. Since the function is finite, it does not have any event horizons or singularity. By taking \(\phi =0\), we have shown that this redshift function satisfies the violation of NEC along with Global Monopole Charge (\(\eta \)) ranges from \(0\le \eta \le 0.006\). Thus the DM content in the bulge and halo of the Milky Way galaxy is well enough to sustain wormhole geometry in the two regions.

The second redshift function is taken as

$$\begin{aligned} \phi =\frac{\tau }{r} \end{aligned}$$
(26)

where \(\tau \) is an non zero constant and remains finite for \(r>0\). This kind of redshift function also does not have an event horizon. Moreover, substituting the redshift function in Eq. (20), we have obtained total NEC violation for all the dark matter profiles in both the bulge and halo of the Milky Way galaxy.

The final redshift function is obtained from the flat rotational curve of galaxies. In the studies of Chandrasekhar and Landau [36, 37] the tangential velocity for stable circular geodesic motion can be represented by \((v^\varPhi )^2 = r \phi '(r)\). Rahaman et al. [38] proposed a theoretical function to describe the flat rotational curve which is

$$\begin{aligned} v^\varPhi = \alpha \ r e^{(-k_1r)} + \beta [1-e^{(-k_2r)}] \end{aligned}$$
(27)

where r is the distance in kpc and \(v^\varPhi \) is the velocity in Km/s. Now by using the above equation, the redshift function can be easily obtained as

$$\begin{aligned} \phi (r)&= -\frac{\alpha ^2 r}{2 k_1 e^{(2k_1r)}} - \frac{\alpha ^2}{4 k_1^2 e^{(2k_1r)}} - \frac{2 \alpha \beta }{k_1 e^{(k_1 r)}} \nonumber \\&\quad + \frac{2\alpha \beta e^{(-k_1 r- k_2 r)}}{k_1 +k_2} + \beta ^2 ln(r) \nonumber \\&\quad + 2\beta ^2 E_i(1, k_2 r) - \beta ^2 E_i(1,2k_2 r) +D \end{aligned}$$
(28)

where E[x,y] is exponential integral function and D is the integration constant and the value of the parameters to be \(k_1=k_2=1\).\(\alpha = 0.8\),\(\beta = 0.001\). Similar to the previous redshift function, we used it to find the radial pressure and it is seen to violate the NEC condition for all the dark matter profiles we have considered. This will prove that the DM profiles considered in our articles are appropriate to sustain wormhole geometry in both the bulge and halo of the Milky Way Galaxy. Moreover, the Global Monopole Charge is studied in the recent paper of Rahaman. et al. shows that the tendency of the NEC violation decreases with the increase of \(\eta \).

4.1 Embedding surface of the wormhole

The embedding surface is defined by z(r) function and is described by the following equation

$$\begin{aligned} \frac{dz(r)}{dr}=\pm \left( \frac{r}{b(r)}-1\right) ^{-\frac{1}{2}} \end{aligned}$$
(29)

The above function is not a conversing function at \(b(r_{th}) =r_{th}\) instead it becomes vertical at the throat of the wormhole. In this paper, the embedding function is plotted in a 3D graph to get the full visualization of the wormhole for each case.

5 Existence of wormhole geometries in the bulge of Milky Way galaxy

5.1 Wormhole using NFW dark matter profile in the galactic bulge

Core radius and core density is taken as \(\rho _0 = 0.004 \,\,{\text {kpc}}^{-2}\) and \(r_0 = 2\,\,{\text {kpc}}\). We can get the throat radius, \(r_{th} = 1.7 \,\,{\text {kpc}}\) from the linear graph \(b-r\) with r where \(b-r\) cuts the r axis.

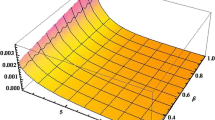
The shape function for the wormhole geometry is obtained as shown in Fig. 1a.

$$\begin{aligned} b(r)= 8\pi \left[ \frac{\eta ^2 r^3}{3} + \frac{r_0^4 \rho _0}{r_0 +r} + r_0^3 \rho _0 log(r_0 +r)\right] + A \end{aligned}$$
(30)

where A is int. constant and is determined by using the boundary condition \(b(r_{th})=r_{th}\).

Fig. 1
figure 1

The shape function b(r) with respect to r(kpc) and \(\eta \) is plotted by using \(\rho _0\) = 0.004 \(kpc^{-2}\), \(r_0 = 2 \) kpc for a NFW profile : \(r_{th} = 1.7\) kpc b Pseudo-Isothermal profile : \(r_{th} = 1 \) kpc (c)URC profile : \(r_{th} = 1.1 \) kpc

Full size image

In Figs. 2a and 3a, the flare out condition is satisfied by taking \(0 \le \eta \le 0.006\) as done by S. Sarkar et. al. in the article [27]. We can see \(\frac{b}{r} < 1\) and \(\frac{b-r. b'}{b^2} <1\) are satisfied.

Fig. 2
figure 2

The ratio \(\frac{b(r)}{r}\) with respect to r(kpc) and \(\eta \) is plotted by using \(\rho _0\) = 0.004 \(kpc^{-2}\), \(r_0 = 2 \) kpc for a NFW profile : \(r_{th} = 1.7\) kpc, b Pseudo-Isothermal profile : \(r_{th} = 1 \) kpc, c URC profile : \(r_{th} = 1.1 \) kpc

Full size image
Fig. 3
figure 3

The function \(\frac{b(r)- r \times b'(r)}{b^2(r)}\) with respect to r(kpc)and \(\eta \) is plotted by using \(\rho _0\) = 0.004 \(kpc^{-2}\), \(r_0 = 2 \) kpc for a NFW profile : \(r_{th} = 1.7\) kpc, b Pseudo-Isothermal profile : \(r_{th} = 1 \) kpc, c URC profile : \(r_{th} = 1.1 \) kpc

Full size image

In the above graphs, if the GMC \(\eta \) is taken to be 0, it will represent the Einstein gravity without any topological defect. Now using Eq. (25) in Eq. (20) to find the \(P_r\) of the matter of wormhole for investigating the NEC is given by

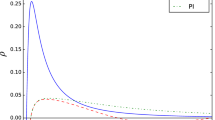
$$\begin{aligned} P_r(r)&= -\frac{1}{ r^3 (r_0 +r)}(r_0(-0.118057 \nonumber \\&\quad + \eta ^2(1.125 +r-0.33\times r^3))\nonumber \\&\quad +r(-0.11+\eta ^2(1.125 +r -0.33\times r^3))-r_0^4 \rho _0 \nonumber \\&\quad + r_0^3(-r_0-r)\rho _0 ln(r_0+r)) \end{aligned}$$
(31)

Thus, the NEC is violated as can be confirmed by the plot in Fig. 4a.

Fig. 4
figure 4

NEC with respect to r(kpc) and \(\eta \) is plotted by using \(\rho _0\) = 0.004 \(kpc^{-2}\), \(r_0 = 2 \) kpc, \(r_{th} = 1.7\) kpc, \(k_1=k_2=1\), \(\alpha =0.8\), \(\beta =0.001\) and \(\tau = 2.5\) for NFW profile

Full size image

The radial pressure of the wormhole obtained by using Eq. (26) in Eq. (20) as

$$\begin{aligned} P_r(r)= & {} -\frac{1}{ 8 \pi r^3 }\left\{ -r+8\eta ^2\pi r +(r-5) \left\{ 1-\frac{1}{r}\left\{ 2.9671 \right. \right. \right. \nonumber \\&+\eta ^2(-28.274+8.377 r^3) +\frac{8 r_0^4 \pi \rho _0}{r_0 + r}\nonumber \\&\left. \left. \left. +8 r_0^3 \pi \rho _o log(r_0 +r) \right\} \right\} \right\} \end{aligned}$$
(32)

and the NEC is also violated as can be inferred from Fig. 4b.

The final expression for the radial pressure is obtained by using Eq. (28) in Eq. (20).

$$\begin{aligned} \begin{aligned} P_r(r)&= -\frac{1}{ 8 \pi r^3 }\left\{ \frac{8 \pi \eta ^2}{r^2} -\frac{1}{r^2} \right. \\&\quad + \left( \frac{1}{r^2} +\frac{2(e^{-k_1r}\alpha r + (1-e^{-k_2 r} \beta )^2}{r^2}\right) \\&\quad \times \left( 1-\frac{1}{r}\left( 2.967-28.27 \eta ^2\right. \right. \\&\quad + \left. \left. \left. 8\pi \left( \frac{\eta ^2 r^3}{3} + \frac{r_0^4 \rho _0}{r_0 + r}+ r_0^3\rho _0 log(r_0+r)\right) \right) \right) \right\} \end{aligned} \end{aligned}$$
(33)

Similarly the violation of null energy is shown in Fig. 4c.

Figure 7a shows the embedding diagram of the wormhole and Fig. 8a shows the full visualization of the wormhole structure.

5.2 Wormhole using pseudo-isothermal dark matter profile in the galactic bulge

Core radius and core density is taken as \(\rho _0 = 0.004\,\, {\text {kpc}}^{-2}\) and \(r_0 = 2\,\, {\text {kpc}}\). We can get the throat radius, \(r_{th} = 1\,\, {\text {kpc}}\) from the linear graph \(b-r\) with r where \(b-r\) cuts the r axis.

Figure 1b shows the variation of the shape function for the wormhole.

The expression for the shape function as obtained for the pseudo-isothermal DM profile coupled with the global monopole charge is given by

$$\begin{aligned} b(r)&= 0.970 - 8.377 \eta ^2+8 \pi \left\{ \frac{\eta ^2 r^3}{3} \right. \nonumber \\&\quad \left. +r_0^2 r \rho _0 - r_0^3\rho _0 Tan^{-1}\left( \frac{r}{r_0}\right) \right\} \end{aligned}$$
(34)

Now, in Fig. 3b, the flare out condition \(\frac{b(r) -r\times b'(r)}{b^2(r)} < 1\) is being satisfied. And Fig. 2b it is shown that \(\frac{b(r)}{r} <1\).

Fig. 5
figure 5

NEC with respect to r(kpc) and \(\eta \) is plotted by using \(\rho _0\) = 0.004 \(kpc^{-2}\), \(r_0 = 2 \) kpc, \(r_{th} = 1\) kpc, \(k_1=k_2=1\), \(\alpha =0.8\), \(\beta =0.001\) and \(\tau = 2.5\) for pseudo-isothermal profile

Full size image

Moving over to the most important condition for the sustainability of the wormhole structure in any location of the universe, i.e. the NEC violation condition using the three redshift functions obtained in Sect. 4. Similarly, the radial pressure for all the three redshift functions is computed, and then the violation of NEC is checked. The \(P_r(r)\) for the function \(\phi =0\) is given by

$$\begin{aligned} P_r(r)= & {} \frac{1}{r^3} \left\{ -0.038 +\eta ^2 \bigl \{0.33 +r - 0.333\times r^3\bigr \}\right. \nonumber \\&\left. - r_0^2 r \rho _0 + r_0^3 \rho _0 tan^{-1}\left( \frac{r}{r_0}\right) \right\} \end{aligned}$$
(35)

Figure 5a represents the violation of the NEC for the radial pressure computed in Eq. (36).

For the second redshift function \(\phi =\frac{\tau }{r}\), the new radial pressure \(P_r(r)\) is computed as

$$\begin{aligned} P_r(r)= & {} -\frac{1}{8\pi r^4} \left\{ r^2 -8 \eta ^2 \pi r^2 + 8.37758( r - 2\tau )\bigl \{0.115 \right. \nonumber \\&\left. \left. - 0.1193 r + \eta ^2 (r^3 -1)+ 3 r_0^2 r \rho _0 \right. \right. \nonumber \\&\left. \left. - 3 r_0^3 \rho _0 Tan^{-1}\left( \frac{r}{r_0}\right) \right\} \right\} \end{aligned}$$
(36)

This radial pressure when added with the DM density profile to check for the violation of NEC shows clear result of violating the NEC condition as evident from Fig. 5b.

Finally using the redshift function in Eq. (28) which has been obtained from the flat rotational curve, the radial pressure \(P_r(r)\) is expressed as,

$$\begin{aligned} P_r(r)\!=\! & {} \frac{1}{8\pi r^3}\Bigg \{-r +8\pi \eta ^2 r \!+\! \Bigg \{1+2(8 e^{-k_1 r} r \alpha +\beta e^{-k_2 r} \beta )^2\Bigg \}\nonumber \\&\times \Bigg \{-0.9707 +r+\eta ^2 (8.377 -8.377 r^3)\nonumber \\&- 25.1327 r_0^2 r \rho _0 +25.1327 r_0^3 \rho _0 tan^{-1}\left( \frac{r}{r_0}\right) \Bigg \}\Bigg \} \end{aligned}$$
(37)

Using the above equation the NEC is satisfied for the final redshift function too. It is plotted in Fig. 5c.

Figures 7b and 8b shows the embedding diagram and the full visualization of the wormhole in the galactic bulge respectively.

5.3 Wormhole using URC dark matter profile in the galactic bulge

Finally, the URC or Burkert dark matter profile is analysed to support the wormhole structure in the bulge of the Milky Way galaxy. The EFE are solved by coupling them with the Global Monopole Charge. The core radius and core density is taken as the same i.e. \(\rho _0 = 0.004\,\, {\text {kpc}}^{-2}\) and \(r_0 = 2\,\, {\text {kpc}}\). We can get the throat radius, \(r_{th} = 1.1 \,\, {\text {kpc}}\) from the linear graph \(b-r\) with r where \(b-r\) cuts the r axis.

Figure 1c shows the variation of the shape function with the global monopole charge and distance.

The expression of shape function of the wormhole obtained from the URC dark matter profile is given as

$$\begin{aligned} b(r)\!=\! & {} 8\pi \left\{ \frac{\eta ^2 r^3}{3} \!+\!\frac{1}{2} r_0^3\rho _0 tan^{-1}\left( \frac{r_0}{r}\right) \!+\!\frac{1}{2} r_0^3 \rho _0 log[r_0+r]\right. \nonumber \\&\left. + \frac{1}{4} r_0^3 \rho _0 log[r_0^2+r^2]\right\} + A \end{aligned}$$
(38)

where, A is the integral constant that is derived by imposing the boundary condition of \(b(r_{th}) = r_{th}\). The flare out condition is satisfied as evident from the Figs. 3c and 2c shows \(\frac{b(r)}{r} \le 1\). The value of \(\eta \) is taken to be from \(0 \le \eta \le 0.006\)

Fig. 6
figure 6

NEC with respect to r(kpc) and \(\eta \) is plotted by using \(\rho _0\) = 0.004 \(kpc^{-2}\), \(r_0 = 2 \) kpc, \(r_{th} = 1\) kpc, \(k_1=k_2=1\), \(\alpha =0.8\), \(\beta =0.001\) and \(\tau = 2.5\) for URC profile

Full size image

Now, the other important condition, i.e. the NEC, is being checked for violation. To check the violation of NEC, the radial pressure \(P_r(r)\) is needed to be computed with the help of the three redshift functions obtained in Eqs. (25, 26, 28). Expression for \(P_r(r)\) obtained for \(\phi =0\) is

$$\begin{aligned} P_r(r)= & {} -\frac{1}{12 r^3}\Bigg \{-12 \eta ^2 r +4 \eta ^2 r^3 \nonumber \\&+ 6 r_0^3 \rho _o tan^{-1}\frac{r_0}{r} \nonumber \\&+ 6r_0^3 \rho _0 log[r_0+r] +3 r_0^3 \rho _0 log[r_0^2+r^2]\Bigg \} \end{aligned}$$
(39)

The violation of NEC can be observed using this radial function plotted in Fig. 6a. The \(P_r(r)\) expression as obtained from the second redshift function \(\phi =\frac{\tau }{r}\) is represented as

$$\begin{aligned} P_r(r)= & {} \frac{1}{8\pi } \left\{ \frac{8\eta ^2\pi }{r^2} -\frac{1}{r^2}+\left( \frac{1}{r^2}-\frac{5}{r^3}\right) \right. \nonumber \\&\times \left\{ 1 -\frac{8 \pi }{r} \left\{ \frac{\eta ^2 r^3}{3} +\frac{r_0^3 \rho _0}{2} tan^{-1}\left( \frac{r_0}{r}\right) \right. \right. \nonumber \\&\left. \left. \left. + \frac{r_0^3 \rho _0}{2} log[r_0+r] + \frac{r_0^3 \rho _0}{2} log[r_0^2+r^2]\right\} \right\} \right\} \end{aligned}$$
(40)

The NEC violation for this particular redshift function is demonstrated in the Fig. 6b. The \(P_r(r)\) expression as obtained from the redshift function, and \(\phi \) obtained from flat rotational curve is represented as

$$\begin{aligned} P_r(r)= & {} \frac{1}{8\pi } \left\{ \frac{8\eta ^2\pi }{r^2}-1+(1+2(8 e^{-k_1 r}r \alpha + \beta -e^{-k_2 r}\beta )^2)\right. \nonumber \\&\times \left\{ 1-\frac{2 \pi }{3r} \left\{ 4\eta ^2 r^3 + 6 r_0^3 \rho _0 tan^{-1}\left( \frac{r_0}{r}\right) \right. \right. \nonumber \\&\left. \left. + 6 r_0^3 \rho _0 log[r_0 +r]+ 3 r_0^3 \rho _0 log[r_0^2 +r^2]\right\} \right\} \end{aligned}$$
(41)

The NEC violation for this particular redshift function is demonstrated in the Fig. 6c.

Fig. 7
figure 7

Embedding diagram for the wormhole at the centre bulge with \(\eta =0.003\) for a NFW profile : \(r_{th} = 1.7\) kpc, b Pseudo-Isothermal profile : \(r_{th} = 1 \) kpc, c URC profile : \(r_{th} = 1.1 \) kpc

Full size image
Fig. 8
figure 8

Full visualization of wormhole structure for a NFW profile : \(r_{th} = 1.7\) kpc, b Pseudo-Isothermal profile : \(r_{th} = 1 \) kpc, c URC profile : \(r_{th} = 1.1 \) kpc

Full size image

The embedding diagram and the full visualization of the wormhole in the galactic bulge for URC is shown in Figs. 7c and 8c.

6 Existence of wormhole geometries in the galactic halo of Milky Way Galaxy

6.1 Wormhole geometry using NFW dark matter profile in the galactic halo

In this section, the NFW dark matter density profile for the galactic halo is used for investigating the existence of wormhole geometry in the outer halo of the Milky Way galaxy. The core density \(\rho _0\) = 0.05 \(kpc^{-2}\) and core radius \(r_0\) = 1kpc are as per article by Rahaman et al. [38].

We can get the throat radius, \(r_{th} = 1.7 kpc\) from the linear graph \(b-r\) with r where \(b-r\) cuts the r axis and b(r)-r \(\le \) 0 for \(r> r_{th}\).

The shape function is same as that of central bulge with varying parameters. It is denoted by

$$\begin{aligned} b(r)= 8\pi \left[ \frac{\eta ^2 r^3}{3} + \frac{r_0^4 \rho _0}{r_0 +r} + r_0^3 \rho _0 log(r_0 +r)\right] + S \end{aligned}$$
(42)

where S is the integration constant. The variation of shape function with the distance and the Global Monopole Charge is demonstrated in Fig. 9a.

Fig. 9
figure 9

The shape function b(r) with respect to r(kpc) and \(\eta \) is plotted by using \(\rho _0\) = 0.05 \(kpc^{-2}\), \(r_0 = 1 \) kpc with \(0\le \eta \le 0.006\) for a NFW profile: \(r_{th} = 1.7\) kpc, b URC profile: \(r_{th} = 1 \) kpc

Full size image

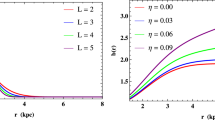
Now, in the Figs. 10a and 11a, the flare out conditions of the wormhole are satisfied.

Fig. 10
figure 10

The function \(\frac{b(r)}{r}\) with respect to r(kpc) and \(\eta \) is plotted by using \(\rho _0\) = 0.05 \(kpc^{-2}\), \(r_0 = 1 \) kpc with \(0\le \eta \le 0.006\) for a NFW profile: \(r_{th} = 1.7\) kpc, b URC profile: \(r_{th} = 1 \) kpc

Full size image
Fig. 11
figure 11

The function \(\frac{b(r)- r \times b'(r)}{b^2(r)}\) with respect to r(kpc)and \(\eta \) is plotted by using \(\rho _0\) = 0.05 \(kpc^{-2}\), \(r_0 = 1 \) kpc with \(0\le \eta \le 0.006\) for a NFW profile : \(r_{th} = 1.7\) kpc, b URC profile : \(r_{th} = 1 \) kpc

Full size image

Now the violation of NEC is checked by using the expression of the \(P_r(r)\) obtained in Eqs. (39, 40, 41) and plotting the NEC in Fig. 12.

Fig. 12
figure 12

NEC with respect to r(kpc) and \(\eta \) is plotted by using \(\rho _0\) = 0.05 \(kpc^{-2}\), \(r_0 = 1 \) kpc, \(r_{th} = 1.7\) kpc, \(k_1=k_2=1\), \(\alpha =0.8\), \(\beta =0.001\) and \(\tau = 2.5\) for NFW profile

Full size image
Fig. 13
figure 13

NEC with respect to r(kpc) and \(\eta \) is plotted by using \(\rho _0\) = 0.05 \(kpc^{-2}\), \(r_0 = 1 \) kpc, \(r_{th} = 1.7\) kpc, \(k_1=k_2=1\), \(\alpha =0.8\), \(\beta =0.001\) and \(\tau = 2.5\) for URC profile

Full size image

Thus from the above figures, it is evident that the NFW dark matter profile coupled with the Global Monopole Charge has the suitable fuel for the supporting and existing wormhole structures in the halo of the Milky Way galaxy. Fig. 14a shows the embedding graph for the Halo of Milky Way for NFW dark matter profile. Figure 15a shows full visualization of the wormhole.

Fig. 14
figure 14

Embedding diagram for the wormhole at the centre bulge with \(\eta =0.003\) for a NFW profile: \(r_{th} = 1.7\) kpc, b URC profile : \(r_{th} = 1 \) kpc

Full size image
Fig. 15
figure 15

Full visualization of wormhole structure for a NFW profile : \(r_{th} = 1.7\) kpc, b URC profile : \(r_{th} = 1 \) kpc

Full size image

6.2 Existence of wormhole in the galactic halo using URC dark matter profile

The final dark matter profile that we are considering for our research for the existence of wormholes structure in our Milky Way galaxy is the URC profile.

The core radius and core density is taken as \(\rho _0 = 0.05 kpc^{-2}\) and \(r_0 = 1kpc\). We can get the throat radius, \(r_{th} = 1 kpc\) from the linear graph \(b-r\) with r where \(b-r\) cuts the r axis.

The expression for the shape function is same as that of Eq. (38) with only the external parameters has been changed. The graphical representation of the shape function is given in Fig. 9b.

Now, the shape function is tested for the flare out conditions and is verified from Figs. 10b, 11b, that it obeys the flare out condition.

Finally the NEC is checked for violation by plotting \(\rho +p\) against r and \(\eta \). They are demonstrated in Fig. 13.

Embedding function for this particular wormhole is constructed as shown in Fig. 14b and the full visualization of the Wormhole is shown in Fig. 15b.

7 Wormhole in the expanding universe

It is well known now that our Universe is expanding with an acceleration due to the effect of dark energy. The main factor determining the behaviour of wormholes in an expanding Universe is that the violation of NEC i.e. \((\rho +P)<0\). This indicates that the energy density increases with expanding cosmic time to an infinite value. Pedro has performed the detailed calculations. Gonzales Diaz and F. Pedro [40] has investigated the evolution of the circumference, throat and the embedding surface and has shown that the wormhole will inflate with time as the Universe expands. Inspiring with that we have also investigated similar circumstances and try to check how the global monopole charge affects the expansion of the wormhole’s physical attributes. The equation describes the de-Sitter scale factor for the expanding Universe, [40]

$$\begin{aligned} g(t)^2=e^{2\chi t} \end{aligned}$$
(43)

where \(\chi =\sqrt{\varLambda /3}\) and \(\varLambda =2.036\times 10^{-35}\;s^{-2} \) is the cosmological constant. The state factor is given by \(p=\omega \rho \) and \(\omega <-1\). Thus, the Morris–Thorne wormhole metric in an expanding Universe changes to

$$\begin{aligned} ds^2=-e^{2\varPhi (r)}dt^2+g(t)^2\left( \frac{dr^2}{1-\frac{K(r)}{r}}+r^2d\varOmega ^2\right) \end{aligned}$$
(44)

Throat radius of the wormhole is denoted by \(r_{th}\), so the proper circumference in the accelerating Universe is given by

$$\begin{aligned} c=r_{th}\int _0^{2\pi }d\phi g(t)=2\pi r_{th}g(t) \end{aligned}$$
(45)

This explicitly shows that the expansion of the circumference is only depends on the scale factor of the expanding Universe with a quintessence field, and the GMC has no effect. The variation of the proper radial distance between two arbitrary large points has been computed. The de-Sitter scale factor g(t) and the GMC depends on time. The equation is described as

$$\begin{aligned} d(t)=\pm \int _{r_A}^{r_B}\frac{dr}{\sqrt{1-b(r)/r}} \end{aligned}$$
(46)

The below diagram (Fig. 16) shows that the radial distance increases with time and the topological defect.

Fig. 16
figure 16

Variation of proper radial distance

Full size image

Similarly, since the embedded function’s evaluation is same as radial distance, the embedding function also increases with the expansion of the Universe. Moreover, after evaluating the wormholes for an expanding Universe, if we look at the first case where the wormhole has zero redshift function with no tidal force, the new Eq. (44) represents the de-Sitter metric for the expanding Universe.

8 Conclusion

This article investigates the existence of a wormhole in the bulge and halo of the Milky Way galaxy. Three different Dark matter profiles are taken for the investigation. Previous studies have shown the importance of Dark matter in constructing wormholes since it violates the null energy condition. Although NEC violation has not been artificially demonstrated in the laboratory, the DM is theorized to violate the NEC. The three Dark matter profiles taken are pseudo-Isothermal, Burkert and NFW. For generalization, the topological defect from the early universe, i.e. the global monopole charge, is considered to broaden the possibility of a wormhole in the Milky Way galaxy. Sarkar et al. have previously studied the existence of wormholes using Mc Millan DM profile. Thus we have considered other DM profiles for this article. Studies by M. Kalam et al [39] has also shown the supporting of wormhole geometry in the halo of different massive spiral and dwarf galaxies. Thus, our study in this article further enforces the works on supporting wormhole geometry in our galaxy’s halo and central bulge.

Fig. 17
figure 17

Variation of NEC due to Global monopole charge, \(\hbox {r}=1.8\) kpc

Full size image

This article shows that the pseudo isothermal, Burkert and NFW DM profiles coupled with the global monopole charge accurately supports the wormhole structure in the central bulge region. The shape function gives the wormhole’s embedded function and, upon its rotation along the z-axis, gives the full visualization of the wormhole structure. Interestingly, the throat radius for all the models is obtained between 1 to 2 kpc. The flare out conditions have also been satisfied by the above dark matter profiles, another important criterion for wormhole geometry. The NEC has been checked using three redshift functions for more generalization: tidal force, rotational redshift function, and redshift function obtained from the Universal rotational curve. All the redshift functions corresponding to \(e^\phi \) are finite. NEC has been checked individually for the redshift functions and is duly satisfied. However, the presence of a Global monopole charge is seen to minimize the violation of NEC, as shown in Fig. 16. Figure 8 shows the full visualization of the wormhole.

Contrary to the supporting of wormhole structure by different DM profiles coupled with the GMC in the bulge of the Milky Way galaxy, only two among these three in our study have been found to support wormhole geometry in the galactic halo region. The pseudo isothermal DM profile failed to violate the NEC when coupled with the global monopole charge. The existence of wormhole geometry has been successfully investigated for the NFW and URC dark matter profile. Figures 10 and 11 shows the satisfaction of the flare out conditions and Figs. 12 and 13 shows the violation of NEC by the three redshift functions individually. The throat radius of the wormholes is determined to be around 1 to 2 kpc. Finally, the embedding graph and the full visualization of the wormhole structures have been constructed in Figs. 14 and 15.

The wormholes are deemed traversable for a human being if the tidal gravitational forces acting are very small. Arguments have been made regarding some black hole solutions mimicking wormholes. Our study is intended to inspire researchers and scientists to investigate the existence of wormholes in the bulge and the halo of our galaxy, as it is entirely theoretically possible for them to exist. Scientist can search for several clues within our galaxy to confirm the presence of wormhole structure, which includes, first pinpointing areas of the galaxy that contains enough dark matter for NEC violation then searching for the iron \(K_\alpha \) line profiles that are emitted from accretion disks formed due to traversable wormholes [94], gravitational microlensing of background universe due to the presence of traversable wormholes, a gravitational anomaly in trajectories of nearby wormhole objects due to the gravitational effect of objects circulating near the wormhole in another space [95] and formulation of gravitational waves that will be generated upon objects traversing a wormhole. Since the analytical study about the existence of wormholes in our universe in this paper papers proves the existence of wormhole geometry with a wider generalized case.