1 Introduction

Wormholes describe an incredible spacetime structure of joining two separate parts of the same world or universes. Einstein field equations perform like the pillar towards the concept of wormholes and were first exploited by Flamm [1]. Later, a new twist was added by Einstein and Rosen  [2] in this regard.

Einstein and Rosen endorsed the concept of spacetime deformation through a geometrical approach as elementary particles like electrons are governed by a geometrical structure now known as Einstein Rosen Bridge (ERB). The ERB was indicated to be unstable  [3,4,5,6,7,8] for the topological defects mainly by global monopoles, which could be a part of galaxies with spiral arms having dark matter. Traversable wormholes have previously been extensively studied by Ellis  [7, 8] and Bronnikov [9] and several others. Clement  [10] obtained a class of wormhole solutions in higher dimensional gravitation theory coupled to a repulsive type scalar field. But interest in wormhole solutions of GR inflated after the remarkable work of Morris and Thorne [11]. Wormholes with thin shells were developed by Visser  [12]. Energy momentum tensors of exotic matter explain the phenomenon i.e. the cosmos complies with certain energy rules, and in this context, we can sense that the sustainability of wormholes plays a major source of concern. The geometry of traversable wormhole in particular necessitates the presence of a material of an exotic kind at the throat of the wormhole (to maintain the spacetime area open). The empirical study for the representation of wormhole throat has been inspected in terms of the graphical system in the present article. Species of exotic matter such as this do not obey the laws of physics, such as the null energy condition (NEC) and the average energy condition(ANEC) [12]. It is hypothesised that such stuff exists within the setting of quantum field theory in terms of vacuum polarization. This vacuum polarization effect of quantum fields plays a noteworthy role in the background of monopole geometry and, as a result, it can noticeably modify the metric responsible for the spacetime near it. In a pioneering work, Hiscock [13, 14] investigated the analysis of the backreaction of Energy–momentum tensor of vacuum based on a space-time metric perturbed by linear terms. The stress-energy tensor of every massless conformal collection within the spacetime of a stationary particle, the free quantum fields exist although spherically symmetric global monopoleFootnote 1 can be obtained upto an unknown numerical constant. Correction of the metric system to the first order for exteriors of such a monopole can be obtained by perturbatively solving the semiclassical linearised Einstein equations. The projection values of vacuum stress energy tensors in quantum fields can be visualised as equal quantity to the Einstein tensor in the reference frame of gravitational quantum theory based on semiclassical principles [15]. Hiscock  [13] specifically studied the quantum effects caused by the monopole background in the matter fields for the scalar field. The exact solution of the space-time outside of a global monopole’s core exist in the semi-classical approach. The findings demonstrate that gravitational vacuum polarisation effects may drastically change the value of the monopole core mass on symmetry breaking scales close to the Planck energy.

In the second part we discuss the steadiness of the wormhole solutions. Field approximation solution  [15] in terms of semiclassical gravitational effects of global monopole leads to the exact solution. This solution has an intriguing property that, under some circumstances, it corresponds to a wormhole in spacetime with a particular throat radius. Spacetime of a global monopole with semi-classical effects, which exerts no gravitational force, creates a wormhole geometry in spacetime. This result is in agreement with Hiscock monopole (weak field approximations). Based on the wormhole spacetime geometry, the linear perturbation approach is one method for checking stability assessments throughout the wormhole throat introduced by Visser and Poisson  [16]. Wormholes have been studied from a variety of perspectives, such as thin-shell wormholes  [16], Traversable Wormhole by Teo  [17], wormholes with phantom energy  [18], a Lorentzian wormhole that is traversable and has a cosmological constant  [19], wormholes in Eddington-inspired Born–Infeld  [20,21,22], wormholes in f(R, T) gravity  [23], wormholes from cosmic strings gravity etc. But Topological defectsFootnote 2 are an interesting part of cosmic strings which can be explained with a similar prediction for the existence by phase transition mechanism of particle physics in the early universe  [24]. The spherically symmetric phenomenon known as the global monopole by the scalar field triplet that is self-coupling Ïa is one specific example of a topological defect. Numerous articles have explored the global monopole for the spacetime metric along with the definition [25, 26, 28,29,30,31]. In this article or paper we will observe the monopole effect as a topological defect through the passage of Einasto Density profile model  [32,33,34], an anisotropic fluid minimally connected to a triplet of scalar fields in the 1+3 gravity theory.

  In the setting of an extensive dark matter halos, the Einasto profile outperforms other solitary two-parameter models such as the Navarro, Frenk, and White (NFW)  [35]. One issue with this profile is that the surface mass density is non-analytical for general Einasto index values. However, the Einasto halo model has so far shown the best fit  [36] for the observed rotating curve and may therefore be regarded a new standard model for wormhole, DM halos. The Einasto model also fits the surface brightness of elliptical galaxies quite well.

2 Einstein’s field equations

In this section, we shall propound the Einstein field equations with global monopole charge and semiclassical effects. To do so, we consider a \((3+1)\) dimensional action without a cosmological constant as

$$\begin{aligned} S=\int \sqrt{-g}\left( \mathcal {L}+\frac{\Re }{16\pi } \right) d^4x+S_m \end{aligned}$$
(1)

Here and in the following, we adopt the geometrical unit i.e. \(G = c = 1\), both dimensionless.

For a self-coupling scalar triplet \(\phi ^a\) the Lagrangian density is given as [37]

$$\begin{aligned} \mathcal {L}=-\frac{\lambda }{4}(\phi ^2-\eta ^2)^2-\frac{1}{2}\sum _a g^{ij}\partial _i\phi ^a\partial _j\phi ^a \end{aligned}$$
(2)

Here, \(\lambda \) is the self-interaction term, \(\eta \) is the scale of a gauge-symmetry breaking and \(a = 1,~2,~3\). The field configuration with monopole is given as

$$\begin{aligned} \phi ^a=\frac{\eta }{r}f(r)x^a \end{aligned}$$
(3)

where \(x^a=(r\sin \theta \cos \phi ,~r\sin \theta \sin \phi ,~r\cos \theta )\) such that \(\sum _ax^ax^2 = r^2.\)

Now, to proceed for finding the wormhole solutions we consider the Morris–Thorne traversable wormhole space-time [11] as

$$\begin{aligned} ds^2 = e^{2\phi (r)}dt^2-\left( 1-\frac{b(r)}{r}\right) ^{-1}dr^2-r^2(d\theta ^2 + sin^2\theta d\phi ^2). \end{aligned}$$
(4)

Here, \(\phi (r)\) and b(r) are called the redshift function and shape function, respectively. To construct the traversable wormholes, the redshift function \(\phi (r)\) and shape function b(r) need to satisfy the following conditions: (i) \(\phi (r)\) should not contain any event horizon i.e. it is finite everywhere after the wormhole throat \(r = r_{th}\), where \(b(r_{th}) = r_{th}\) and (ii) \(b(r)/r < 1\) and \(b^{\prime }(r) < 1\) (Flare-out condition) for \(r>r_{th}\).

Now, the Lagrangian density in terms of f(r) can be written as

$$\begin{aligned} \mathcal {L}=-\frac{\eta ^2 f^2}{r^2}-\frac{\lambda \eta ^4}{4}(f^2-1)^2-\left( 1-\frac{b(r)}{r}\right) \frac{\eta ^2(f^\prime )^2}{2}\nonumber \\ \end{aligned}$$
(5)

Further, for the field f(r), the Euler-Lagrange equation gives

$$\begin{aligned}{} & {} \left( 1-\frac{b(r)}{r}\right) f^{\prime \prime }+ \left[ \left( \frac{b(r)-rb^\prime (r)}{2r^2}\right) +\frac{2}{r}\left( 1-\frac{b(r)}{r}\right) \right] f^\prime \nonumber \\{} & {} \quad -\left[ \frac{2}{r^2}+\lambda \eta ^2(f^2-1)\right] f=0 \end{aligned}$$
(6)

The energy–momentum tensor is obtained from Eq. (2) as

$$\begin{aligned} \bar{T}_{ij}= \partial _i\phi ^a\partial _j\phi ^a-\frac{1}{2}g_{ij} g^{\mu \nu }\partial _\mu \phi ^a\partial _\nu \phi ^a-\frac{g_{ij}\lambda }{4}(\phi ^2-\eta ^2)^2 \end{aligned}$$
(7)

The above Eq. (7) gives the following results

$$\begin{aligned} \bar{T}_t^t= & {} -\eta ^2\left[ \frac{f^2}{r^2}+\left( 1-\frac{b}{r}\right) \frac{(f^{\prime })^2}{2}+\frac{\lambda \eta ^2}{4}(f^2-1)^2\right] ,\nonumber \\ \bar{T}_r^r= & {} -\eta ^2\left[ \frac{f^2}{r^2}-\left( 1-\frac{b}{r}\right) \frac{(f^{\prime })^2}{2}+\frac{\lambda \eta ^2}{4}(f^2-1)^2\right] ,\nonumber \\ \bar{T}_\theta ^\theta= & {} \bar{T_\phi ^\phi }=-\eta ^2\left[ \left( 1-\frac{b}{r}\right) \frac{(f^{\prime })^2}{2}+\frac{\lambda \eta ^2}{4}(f^2-1)^2\right] .\nonumber \end{aligned}$$

Due to the complicated form of Eq. (6), we consider \(f(r)\rightarrow 1\) outside the wormhole to solve the Eq. (6) and, therefore, the corresponding components of energy–momentum read as

$$\begin{aligned} \bar{T}_t^t=\bar{T}_r^r\simeq -\frac{\eta ^2}{r^2},~~ \bar{T}_\theta ^\theta =\bar{T}_\phi ^\phi \simeq 0 .\nonumber \end{aligned}$$

The Einstein field equations are written as

$$\begin{aligned} G_{ij}=R_{ij}-\frac{1}{2}g_{ij}R=8\pi \mathcal {T}_{ij},\nonumber \end{aligned}$$

where \(\mathcal {T}_{ij}\) is the total energy–momentum tensor of the dark matter fluid and global monopole with the quantum effects due to monopole background in matter fields. The Einstein field equations can be expressed as

$$\begin{aligned} \mathcal {T}_{ij}=T_{ij}^{(0)}+\bar{T}_{ij}+\langle \bar{T}_{ij}\rangle \nonumber \end{aligned}$$

It is known that the Lagrangian is conformally invariant in classical theory and as a result, we have the vanishing trace of the energy stress tensor. However, in the case of quantized theory, it achieves a trace through renormalization. This trace irregularity is a geometrical scalar that contains derivatives of the metric tensor.

Fig. 1
figure 1

(Left) The density function \(\rho (r)\) is plotted corresponding to \(\rho _0 = 0.005\) and \(r_0 = 2~ kpc\) and (Right) the shape function b(r) is plotted corresponding to \(L = 2\), \(\rho _0 = 0.005,~ r_0 = 2~ kpc,~ r_{th} = 1 ~kpc, ~ B = 0.01 \) and \( h = 1\)

Full size image

The anomaly due to the trace of the vacuum stress energy for a conformally coupled massless free field is specified as [13]

$$\begin{aligned} T^\mu _\nu= & {} \frac{1}{2880\pi ^2}\left[ a C_{ijkl} C^{ijkl} + b ( R_{ij} R^{ij} \right. \nonumber \\{} & {} \left. -\frac{1}{3} R^2) + c~\square R + d R^2 \right] \end{aligned}$$
(8)

Here a, b, c, and d are constants depending upon the concerning conformal scalar field. The remaining symbols are the standard notations in Riemannian geometry.

Now the vacuum expectation values of stress-energy tensors of the quantum fields take part as contribute to the energy–momentum tensor components in the Einstein field equations. Hiscock[13] studied the quantum effects due to monopole background in the matter fields. He has found the vacuum expectation value of the stress-energy tensor of a conformally coupled massless scalar field of the space-time as

$$\begin{aligned} \langle Tij \rangle = \frac{\hbar }{r^{4}} diag [B,~ (A + B ), ~(A + B ), ~(A + B )] \end{aligned}$$
(9)

where

$$\begin{aligned} A= & {} \frac{1}{1440\pi ^2}\left[ n_{sc} +3n_{sp} + 12n_{vd}\right. \nonumber \\{} & {} \times \left. { 12 n_{v\xi } ( 2\alpha ^2 + 1)/ ( 3\alpha ^2 -1)}\right] ( 1 - \alpha ^2 )( 3\alpha ^2 -1)^{-4}\nonumber \\ \end{aligned}$$
(10)

Here, \(n_{sc}\), \(n_{sp}\), \(n_{vd}\) \(n_{v\xi }\) represent the number of scalars, two-component spinor, dimensionally regularized vector and concerning zeta function regularized vector fields, respectively. Similar to A, B is a dimensionless constant depending on \(\eta \) and the number and spin of the concerning component fields and \(\hbar \approx 2.612 \times 10^{-66}\) cm\(^2\).

In this study, we consider an anisotropic matter distribution. The components of the energy–momentum tensor for anisotropic matter fluid are given as follows

$$\begin{aligned} {T_j^i}~^{(0)}=\left[ -\rho (r), \mathcal {P}_r(r), \mathcal {P}_\theta (r), \mathcal {P}_\phi (r)\right] .\nonumber \end{aligned}$$

The Einstein tensor components for the metric (4) are

$$\begin{aligned} G_t^t= & {} -\frac{b^{\prime }(r)}{r^2},\\ G_r^r= & {} -\frac{b(r)}{r^3}+2\left[ 1-\frac{b(r)}{r}\right] \frac{\Phi ^{\prime }}{r},\\ G_\theta ^\theta= & {} \left( 1-\frac{b(r)}{r}\right) \left[ \Phi ^{\prime \prime }+(\Phi ^{\prime })^2\right. \\{} & {} \left. -\frac{b^{\prime }r-b}{2r(r-b)}\Phi ^{\prime }-\frac{b^{\prime }r-b}{2r^2(r-b)}+\frac{\Phi ^{\prime }}{r}\right] ,\\ G_\phi ^\phi= & {} G_\theta ^\theta . \end{aligned}$$

Therefore, the Einstein field equations with the Global Monopole Charge and Semiclassical effects can be written as

$$\begin{aligned} \rho (r)= & {} \frac{1}{8\pi }\left[ \frac{b^\prime (r)}{r^2}-\frac{8\pi \eta ^2}{r^2} + \frac{8 \pi B \hbar }{r^4}\right] , \end{aligned}$$
(11)
$$\begin{aligned} \mathcal { P}_r(r)= & {} \frac{1}{8\pi }\left[ \left( 1-\frac{b(r)}{r}\right) \left( \frac{1}{r^2}+\frac{2\phi ^\prime (r)}{r}\right) \right. \nonumber \\{} & {} \left. -\frac{1}{r^2}+\frac{8\pi \eta ^2}{r^2} - \frac{8 \pi ( A+B) \hbar }{r^4}\right] , \end{aligned}$$
(12)
$$\begin{aligned} \mathcal {P}_t(r)= & {} \frac{1}{8\pi } \left( 1-\frac{b(r)}{r}\right) \phi ^{\prime \prime }(r)+\left( 1-\frac{b(r)}{r}\right) {\phi ^\prime }^2(r)\nonumber \\{} & {} +\frac{1}{2}\left( \frac{b(r)}{r^2}-\frac{b^\prime (r)}{r}\right) \phi ^\prime (r) +\frac{1}{r}\left( 1-\frac{b(r)}{r}\right) \phi ^\prime (r)\nonumber \\{} & {} +\frac{1}{2r}\left( \frac{b(r)}{r^2}-\frac{b^\prime (r)}{r} \right) + \frac{8 \pi ( A+B) \hbar }{r^4}. \end{aligned}$$
(13)

where \(\prime \) stands for \(\frac{d}{dr}\).

3 Wormhole formation

In this section, we are going to find the wormhole solution of Einstein’s field equations supported by the Einasto DM density profile in the galactic halo. The Einasto DM density profile is given as [38,39,40]

$$\begin{aligned} \rho (r) = \rho _0 e^{-\frac{2}{L} \left[ \left( \frac{r}{r_0}\right) ^L -1 \right] } \end{aligned}$$
(14)

where \(\rho _0\) and \(r_0\) are the core density and core radius of the galactic halo, respectively and L is a positive constant.

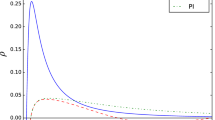
The behaviour of the density profile (14) is demonstrated in Fig. 1 (left) for \(\rho _0\) = 0.005 and \(r_0\) = 1 kpc with L = 2, 3, 4 and 5, respectively. Figure 1 (left) ensures that the density profile is positive and decreasing in nature, which makes the sense of matter density. Here, we make an assumption that the matter density of the wormhole is the profile density of the Einasto. So, on using the density profile (14) in the Eq. (11) and the condition \(b(r_{th}) = r_{th}\), we obtain the following shape function

$$\begin{aligned} b(r)= & {} \frac{8\pi }{Lr}\left[ B\hbar L+Lr^2\eta ^2-\rho _0 r^4 e^{2/L}g(r)\right] \nonumber \\{} & {} +\frac{1}{Lr_{th}}\left[ L\left( r^2_{th}(1-8\pi \eta ^2)-8\pi B\hbar \right) \right. \nonumber \\{} & {} \left. +8\pi \rho _0 r^4_{th}e^{2/L}g(r_{th})\right] \end{aligned}$$
(15)

where

$$\begin{aligned} g(r)=E\left[ \frac{-3+L}{L},\frac{2}{L}\left( \frac{r}{r_0}\right) ^L\right] . \end{aligned}$$
(16)

E[m, x] being the exponential integral function defined as

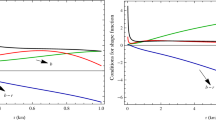
$$\begin{aligned} E[m,x] = \int _0^1 e^{-\frac{x}{z}}z^{m-2}dz; ~~~x > 0. \end{aligned}$$
(17)

In order to maintain the wormhole structure, the shape function (15) needs to satisfy the conditions mentioned in Sect. 2. It is clear from Fig. 1 (right) that the shape function obtained here is positive and monotonically increasing in nature after the wormhole throat \(r_{th} = 1\) kpc. Moreover, Fig. 2 indicates that \(b(r)/r < 1\) (the figure in the left) and \(db(r)/dr < 1\) after the wormhole throat \(r_{th}\) = 1 kpc corresponding to \(\eta \) = {0, 0.03, 0.06, 0.09} with \(L = 2\), \(\rho _0\) = 0.005, \(r_{0}\) = 2 kpc, \(B = 0.01\), \(\hbar = 1\). Therefore, shape function presented here is suitable to construct the wormhole structure in the galactic halo by satisfying all the necessary conditions. It is noted that, the values of all parameters are increasing for increasing values of global monopole charge \(\eta \).

Fig. 2
figure 2

(Left) The function b(r)/r and (Right) the function db(r)/dr are plotted corresponding to \(L = 2\), \(\rho _0 = 0.005,~ r_0 = 2 ~kpc,~ r_{th} = 1 ~kpc, ~ B = 0.01 \) and \( h = 1\)

Full size image
Fig. 3
figure 3

(Left) NEC1 and (Right) NEC2 corresponding to \(C = 1.5\) and \(\alpha = 1\) along with \(L = 2\), \(\rho _0 = 0.005,~ r_0 = 2 ~kpc,~ r_{th} = 1 ~kpc, ~ B = 0.01 ~ A = 0.0015\) and \( h = 1\), respectively

Full size image

4 Null energy condition

In this section, we consider the matter content of the wormhole to check whether it violates the null energy condition (NEC) as the violation of NEC is an essential condition to sustain the wormhole structure. According to GTR, the NEC reads as \(\rho (r) + \mathcal {P}_r(r)\ge 0\), and hence the matter content of wormhole violates NEC if \(\rho (r) + \mathcal {P}_r(r) < 0\) for \(r > r_{th}\).

In order to check the NEC, we need to compute the radial pressure \(\mathcal {P}_r(r)\) from Eq. (12) and to do so, here, we shall consider different redshift functions \(\phi (r)\).

4.1 NEC1: redshift function \(\phi (r)\) = C

The function \(\phi (r) = C\), constant is suitable as a redshift function due to its regular behavior with respect to the radial coordinate r. It is noted that the function \(\phi (r) = C\) is called the tidal force whenever \(C = 0\) and, here, we will proceed with positive values of C. This redshift function and the shape function given in Eq. (15) simultaneously produce the explicit expression of radial pressure from Eq. (12) as

$$\begin{aligned} \mathcal {P}_r(r)= & {} -\frac{1}{8 r^4}\left[ 8 B \hbar \left( 2-\frac{r}{r_{th}}\right) +rr_{th} \left( \frac{1}{\pi }-8 \eta ^2\right) +8 A\hbar \right] \nonumber \\ {}{} & {} +\frac{\rho _0e^{\frac{2}{L}}}{Lr^3}\left[ r^3g(r)-r^3_{th}g(r_{th})\right] \end{aligned}$$
(18)

The left panel of Fig. 3 shows that \(\rho (r) + \mathcal {P}_r(r) < 0\) after the wormhole throat \(r_{th} = 1\)kpc corresponding to global monopole charge \(\eta \) = {0, 0.03, 0.06, 0.09} with \(C = 1.5\), \(L = 2\), \(\rho _0\) = 0.005, \(r_{0}\) = 2 kpc, \(B = 0.01\), \(\hbar = 1\). Therefore, the matter content of wormhole i.e. the DM represented by the Einasto density profile is good enough to hold the wormhole structures in the galactic halo.

4.2 NEC2: redshift function \(\phi (r) = \frac{\alpha }{r}\)

The function \(\phi (r) = \alpha /r\) [41], \(\alpha \) being a non-zero constant, is also suitable as a redshift function, since it is regular for \(r > 0\) i.e. it avoids the event horizon after the wormhole throat. For this redshift function, Eq. (12) gives the radial pressure as

$$\begin{aligned} \mathcal {P}_r(r)= & {} \frac{1}{8\pi Lr^5 r_{th}}\big [L (8\pi B\hbar (r(r - 2\alpha ) + 2r_{th}(\alpha -r)) \nonumber \\{} & {} + r_{th} r (-8 A \hbar \pi + (r_{th}r - 2r_{th}\alpha + 2r\alpha ) (8\pi \eta ^2-1)))\nonumber \\{} & {} -8\pi \rho _o r_{th} e^{2/L} r (r - 2\alpha )(r^3_{th}g(r_{th})-r^3g(r))\big ]. \end{aligned}$$
(19)

The above radial pressure together with the matter density profile (14) violates the NEC, clear from the right panel of Fig. 3. Indeed, the DM content of the wormhole gives the essential fuel to sustain the wormhole structure in the galactic halo. Further, from the same right panel of Fig. 3, one can see that whenever global monopole charge \(\eta \) increases the level of violation of NEC decreases i.e. the increasing global monopole charge \(\eta \) can reduce the probability of violation of NEC.

4.3 NEC3: redshift function \(\phi ^\prime (r) = {v^\Phi }^2 / r\)

The tangential galactic rotational velocity \(v^{\Phi }(r)\) in the equatorial is obtained in terms of the redshift function \(\phi \) form the flat curve as [42, 43]

$$\begin{aligned} v^{\Phi }(r) = \sqrt{r\phi ^\prime (r)} \end{aligned}$$
(20)

Here, we shall consider the tangential galactic rotational velocity in the region of the DM as [44, 45]

$$\begin{aligned} v^{\Phi }(r)=s(1-e^{-\mu r})+w r e^{-\beta r} \end{aligned}$$
(21)

where s, w, \(\mu \) and \(\beta \) are positive constants.

Upon using the above tangential galactic rotational velocity in (20) one can find the following redshift function

$$\begin{aligned} \phi (r)= & {} s^2\left\{ \ln (r)+2E[1,\beta r]-E[1,2\beta r]\right\} \nonumber \\{} & {} +C_1-\frac{w^2e^{-2\mu r}}{2\mu }\left[ r+\frac{1}{2\mu }\right] \nonumber \\{} & {} -2sw e^{-\mu r}\left[ \frac{1}{\mu }-\frac{1e^{-\beta r}}{(\mu +\beta ) }\right] \end{aligned}$$
(22)

where \(C_1\) is an integration constant. The above redshift function given in Eq. (22) provides the following radial pressure

$$\begin{aligned} \mathcal {P}_r(r)= & {} \frac{1}{8\pi r^4}\Big [8\pi (r^2\eta ^2{-}\hbar (A{+}B)){+}\frac{1}{Lr_th}\{L(8\pi B\hbar (r{-}r_{th})\nonumber \\{} & {} +rr_{th}(8\pi \eta ^2(r_{th}-r)))-8\pi \rho _o r_{th} r e^{2/L}(r_{th}^3g(r_{th})\nonumber \\{} & {} -r^3g(r))\}{-}\frac{k(r)}{L\mu r_{th}}\{L(r_{th}{-}r)(8\pi B\hbar {+}rr_{th}(1{-}8\pi \eta ^2))\nonumber \\{} & {} +8\pi \rho _o r e^{2/L}(r_{th}^3g(r_{th})-r^3g(r))\}\Big ], \end{aligned}$$
(23)

where,

$$\begin{aligned} k(r)&{=}&2we^{{-}2r(\mu {+}\beta )}\{{-}2\mu sre^{r(\mu {+}\beta )}{+}\mu w e^{2\mu r}(1{+}e^{2\beta r}{-}2e^{\beta r})\nonumber \\{} & {} -re^{2\beta r}(w(\mu r-1)-4\mu s)\}. \end{aligned}$$
(24)

The graphical demonstration of \(\rho (r) + p_r (r)\) is shown in the right panel of Fig. 4, which confirms that it is negative after the wormhole throat \(r_{th} = 1~ kpc\) i.e. the NEC is completely violated. Consequently, the wormhole containing DM content is widely supporting to sustain the wormhole structure.

Fig. 4
figure 4

(Left) NEC3 corresponding to \(D = 0.05, ~ \mu = \beta = 0.2,~ w = 0.1,~ s = 0.002\), \(L = 2\), \(\rho _0 = 0.005,~ r_0 = 2 ~kpc,~ r_{th} = 1 ~kpc, ~ B = 0.01~ A = 0.0015 \) and \( h = 1\). (Right) The total amount of ANEC violating matter at the wormhole throat is plotted with respect to the global monopole charge \(\eta \)

Full size image

5 Amount of average null energy condition violating matter

According to the Visser et al. [46], the total amount of average null energy condition (ANEC) violating matter can be defined as

(25)

where, \(dv = r^2 \sin \theta dr d\theta d\phi \). Here, our aim is to check the dependence of the wormhole containing total amount of ANEC violating matter on the global monopole charge \(\eta \). Now, the dependence of the total amount of ANEC on \(\eta \) is actually the dependence of the integrand \(I_F =r^2[\rho (r)+\mathcal {P}_r(r)]\) on \(\eta \) near the wormhole’s throat. For each of our proposed wormhole solutions, the value of integrand \(I_F\) at the wormhole throat is obtained as \(I_F = -0.0408 + \eta ^2\) corresponding to considered values of constant for each of the cases. Interestingly, the result shows that the total amount of ANEC violating matter depends on the global monopole charge \(\eta \) and it can be minimized by minimizing values of \(\eta \), which is also clear from Fig. 4 (right).

Table 1 Numerical values of the embedding surface z(r) corresponding to the global monopole charge \(\eta \) = {0, 0.03, 0.06, 0.09} with \(\rho _0 = 0.005,~kpc, r_{0} = 2~kpc~ L = 2,~ B = 0.01, ~ \hbar = 1, ~r_{th}^+ = 1.1~kpc\)
Full size table

6 Embedding surface and proper-radial distance of wormhole

Here, we are going to discuss two important features of the wormhole structure, namely the embedding surface and the proper-radial distance of the wormhole.

6.1 Embedding surface

We consider the two dimensional hypersurface \( H~:~\theta = \pi /2,~t\) = constant for the visualization of wormhole geometry. Now, the line element at the considered hypersurface H is given by

$$\begin{aligned} ds_H^2 = \left( 1-\frac{b(r)}{r}\right) ^{-1}dr^2+r^2d\phi ^2 \end{aligned}$$
(26)

On account of the hypersurface H, the above metric can be embedded into the following three dimensional Euclidean space

$$\begin{aligned} ds_H^2 = \left[ 1+\left( \frac{dz(r)}{dr}\right) ^2\right] dr^2+r^2d\phi ^2 \end{aligned}$$
(27)

Comparing Eqs. (26) and (27) we get a differential equation of the embedding surface z(r) as

$$\begin{aligned} \frac{dz(r)}{dr} = \pm \left( \frac{r}{b(r)}-1\right) ^{-\frac{1}{2}} \end{aligned}$$
(28)

Eventually, the above Eq. (28) gives the expression of embedding surface z(r) in the following integral form

$$\begin{aligned} z(r) = \pm \int _{r_{th}^+}^r \left( \frac{r}{b(r)}-1\right) ^{-\frac{1}{2}} \end{aligned}$$
(29)

where \(r_{th}^+\) is the nearest distance after the wormhole throat. Now, we solve the above integration numerically due to the complicated form of our introduced shape function (15). It is noted that the numerical technique is applied for \(r_{th}^+ = 1.1~ kpc\) and the obtained results are given Table 1. Further, the graphical demonstration of z(r) is depicted in the left panel of Fig. 5 which corresponds to \(\eta = \{0, 0.09\}\) with \(L = 2\), \(\rho _0 = 0.005\), \(r_0 = 2\) kpc, \(r_{th} = 1\) kpc, \(B = 0.01\) and \(\hbar = 1\). Also, Fig. 8 shows the full visualization diagram of the wormhole corresponding to only \(\eta = 0.09\).

Fig. 5
figure 5

The embedding surface z(r) (Left) and proper-radial distance L(r) (Right) are plotted corresponding to \(L = 2\), \(\rho _0 = 0.005,~ r_0 = 2 ~kpc,~ r_{th} = 1 ~kpc, ~ B = 0.01 \) and \( \hbar = 1\)

Full size image
Table 2 Numerical values of the proper-radial distance L(r) corresponding to the global monopole charge \(\eta \) = {0, 0.03, 0.06, 0.09} with \(\rho _0 = 0.005,~kpc, r_{0} = 2~kpc~ L = 2,~ B = 0.01, ~ \hbar = 1, ~r_{th}^+ = 1.1~kpc\)
Full size table

6.2 Proper-radial distance

The proper radial distance of wormhole is defined as

$$\begin{aligned} L(r) = \pm \int _{r_{th}^+}^r \left( 1-\frac{b(r)}{r}\right) ^{-\frac{1}{2}} \end{aligned}$$
(30)

Here, we calculate the value of L(r) using the numerical technique with the lower limit \(r_{th}^+ = 1.1~ kpc\) and the obtained results are provided in Table 2. Moreover, the diagram of the proper radial distance L(r) for our solution is shown in Fig. 8 (right).

7 Asymptotic flatness

The asymptotic flatness of the wormhole structures is ensure by (i) \(b(r)/r\rightarrow 0\) as \(r\rightarrow \infty \) and (ii) \(e^{2\phi (r)}\) \(\rightarrow 1\) as \(r\rightarrow \infty \). Corresponding to the choice of \(L = 2\), \(\rho _0 = 0.005,~ r_0 = 2 ~kpc,~ r_{th} = 1 ~kpc, ~ B = 0.01 \) and \( h = 1\), we obtain \(b(r)/r = \frac{1}{r}[1.9 +0.25/r-25.13(1-r)\eta ^2-0.17 r^3 E\left[ -1/2, r^2/4\right] \) and it tends to zero as r tends to infinity for any values of \(\eta \), which is also clear from the left panel of the Fig. 2. Now, \(e^{2\phi (r)}\) \(\rightarrow 1\) whenever \(r\rightarrow \infty \) only for the second choice of redshift function. Consequently, this redshift function generates the asymptotically flat wormhole. For the first and third choices of redshift functions \(\phi (r)\), \(e^{2\phi (r)}\) does not tend to unity as \(r\rightarrow \infty \) and hence these represent non-asymptotically flat wormholes. As a result, the wormhole structures matched with the external Schwarzschild solution. It is noted that in the case of \(\phi (r) = C\), when \(C = 0\) it gives the asymptotically flat wormhole but in this context, we have chosen non-zero C. The exterior Schwarzschild solution is given as

$$\begin{aligned} ds^2= & {} - \left( 1-\frac{2M}{r}\right) dt^2+\left( 1-\frac{2M}{r}\right) ^{-1}dr^2\nonumber \\{} & {} +r^2(d\theta ^2 + \text {sin}^2\theta d\phi ^2), \end{aligned}$$
(31)

where M denotes the wormhole mass.

Comparing the wormhole metric (4) with the external Schwarzschild solution (31) at some \(r = R > r_s\) (\(r_s\) is the Schwarzschild radius) we get \(b(R)=2M\) and \(\phi (R)=\frac{1}{2}\ln (1-2M/R)\). Therefore, for first and third choices of redshift functions, we obtain the following values of constants

$$\begin{aligned} C= & {} \frac{1}{2}\ln (1-2M/R) \end{aligned}$$
(32)
$$\begin{aligned} C_1= & {} \frac{1}{2}\ln (1-2M/R)+\frac{w^2e^{-2\mu R}}{2\mu }\left[ R+\frac{1}{2\mu }\right] \nonumber \\{} & {} +2sw e^{-\mu R}\left[ \frac{1}{\mu }-\frac{1e^{-\beta R}}{(\mu +\beta ) }\right] \nonumber \\{} & {} -s^2\left[ \ln (r)+2E[1,\beta R]-E[1,2\beta R]\right] \end{aligned}$$
(33)

Indeed, for these choices of C and \(C_1\) with \(b(R)=2M\) the respective non-asymptotically flat wormhole solutions matched with the external Schwarzschild solution at some \(r = R > r_s\). Further, these wormholes representing metric reads as

$$\begin{aligned} ds^2= & {} - e^{2\Phi (r)}dt^2+\left( 1-\frac{b(r)}{r}\right) ^{-1}dr^2\nonumber \\{} & {} +r^2(d\theta ^2 + \text {sin}^2\theta \,d\phi ^2), \quad \text {for}\quad r<R \end{aligned}$$
(34)

and

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{b(R)}{r}\right) dt^2+\left( 1-\frac{b(R)}{r}\right) ^{-1}dr^2\nonumber \\{} & {} +r^2(d\theta ^2 + \text {sin}^2\theta \,d\phi ^2), \quad \text {for}\quad r\ge R. \end{aligned}$$
(35)
Fig. 6
figure 6

(Left) The different forces are plotted corresponding to the redshift function of NEC1 and (Right) the different forces are plotted corresponding to the redshift function of NEC2

Full size image

8 Equilibrium analysis

Any astrophysical object stays in an equilibrium position under the action of different forces by satisfying the generalized Tolman–Oppenheimer–Volkoff (TOV) equation. The generalized TOV equation in wormhole spacetime can be written as

$$\begin{aligned}{} & {} -\frac{1}{r}[M_g(r)\{\rho (r)+\mathcal {P}_r(r)\}]\phi (r)(1-b(r)/r)-\frac{d\mathcal {P}_r(r)}{dr}\nonumber \\{} & {} \quad +\frac{2}{r}(\mathcal {P}_t(r)-\mathcal {P}_r(r))=0, \end{aligned}$$
(36)

where \(M_g(r)\) represents the effective gravitational mass that spread from the wormhole throat to some radius r. Also, on using the Tolman-Whittaker formula and the Einstein field equations, \(M_g(r)\) is derived as

$$\begin{aligned} M_g(r)=r\phi '(r)[\phi (r)(1-b(r)/r)]^{-1}~. \end{aligned}$$
(37)

where prime denotes differentiation with respect to r. Inserting this value of \(M_g(r)\) in Eq. (36), the TOV equation reads as

$$\begin{aligned}{} & {} -\phi '(r)\{\rho (r)+\mathcal {P}_r(r)\}-\frac{d\mathcal {P}_r(r)}{dr}+\frac{2}{r}\{\mathcal {P}_t(r)-\mathcal {P}_r(r)\}=0. \end{aligned}$$
(38)
$$\begin{aligned}{} & {} \text {i.e.} ~~~~~F_g(r)+F_h(r)+F_a(r)=0, \end{aligned}$$
(39)

Here, \(F_g(r) = -\phi '(r)\{\rho (r)+\mathcal {P}_r(r)\}\), \(F_h(r) = -\frac{d\mathcal {P}_r(r)}{dr}\) and \(F_a(r) = \frac{2}{r}[\mathcal {P}_t(r)-\mathcal {P}_r(r)]\), are called gravitational, hydrostatic and anisotropic forces, respectively. Now, to analyze the equilibrium condition, the graphical demonstrations of three different forces for respective wormholes are depicted in Figs. 6 and 7. In the case of redshift function \(\phi (r) = C\), \(F_g(r)\) is zero and hence the wormhole solution achieves the equilibrium position under the action \(F_h(r)\) and \(F_a(r)\) (see Fig. 6 (left)). However, corresponding to the redshift functions \(\phi (r) = \alpha /r\) and obtained from the flat rotational curve the wormhole solutions stay in equilibrium position under the simultaneous action of \(F_g(r)\), \(F_h(r)\) and \(F_a(r)\), clear from Figs. 6 (right) and 7. Also, Fig. 7 shows that \(F_g(r)\) is very small in these cases, so, here, the anisotropic force plays an important to achieve the equilibrium position.

Fig. 7
figure 7

The different forces are plotted corresponding to redshift function of NEC3

Full size image
Fig. 8
figure 8

The embedding diagram of wormhole corresponding to \(\eta = 0.09\)

Full size image

9 Discussions and conclusion

It is true that the study of wormhole geometry created an enthusiastic stir among theoretical researchers over the last few years. As a result, the wormholes are found in the galactic halo region supported by the NFW, URF, and Isothermal DM density profiles. In this article, for the first time, we have introduced the wormhole structures in the galactic halo supported by the Einasto DM density profile and global monopole charge with semiclassical effects.

The Einasto DM density profile creates a suitable redshift function to represent wormhole-like geometry: The obtained redshift function is positive and increasing in behavior, clear from Fig. 1 (right) and it is less than the radial coordinate r after the wormhole throat (see the Fig. 2 (left)) corresponding to global monopole charge \(\eta = \{0, 0.03, 0.06, 0.09\}\) along with \(L = 2\), \(\rho _0 = 0.005\), \(r_0 = 2\) kpc, \(r_{th}\) = 1 kpc, \(\hbar = 1\) and the semiclassical effect \(B = 0.01\), and also, the reported shape function satisfies the flare-out condition (see the Fig. 2 (right)). It is noted that for fixed values of semiclassical effect \(B = 0.01\), the shape function and its essential conditions are increasing for increasing value of \(\eta \).

The anisotropic DM content within the wormholes gives the appropriate environment to sustain the wormhole structures by violating the NEC: The NEC has checked for three redshift functions \(\phi = C, ~ \alpha / r\) and obtained from the flat rotational curve. For each of the three redshift functions, the NEC is violated, which is clear from Figs. 3 and 4 (right). In the violation of NEC, the global monopole charge \(\eta \) plays an important role with the fixed values of semiclassical effects \(A = 0.0015\) and \(B = 0.01\), the chance of violation of NEC decreases for increasing values of \(\eta \) (see the Figs. 3 and 4 (right)). Moreover, the total amount of ANEC violating matter in the wormhole can be minimized by minimizing the value of \(\eta \) (see Fig. 4 (right)).

Two important features of wormhole namely, embedding surface z(r) and proper radial distance L(r) are analyzed for our reported solutions. We have estimated the numerical values of z(r) and L(r) using the numerical technique corresponding to \(\eta = \{0, 0.03, 0.06, 0.09\}\) with \(L = 2\), \(\rho _0 = 0.005\), \(r_0 = 2\) kpc, \(r_{th}^+\) = 1.1 kpc, \(\hbar = 1\) and the semiclassical effect \(B = 0.01\), given in Tables 1 and 2, respectively. The graphical behaviors of z(r) and l(r) are shown in Fig. 5 only for \(\eta = 0\) and 0.09, and also, the full visualization 4D diagram of wormhole only for \(\eta = 0.09\) is shown in Fig. 8.

The asymptotic flatness of our wormhole solutions is discussed: Only for the redshift function \(\phi (r) = \alpha /r\) the solutions represent asymptotically flat wormhole spacetime and this result is not dependent on the global monopole charge \(\eta \). Further, the wormhole geometries corresponding to the first and third choices of redshift functions are not asymptotically flat as both these cases \(e^{2\phi (r)}\) do not tend to 1 whenever \(r\rightarrow \infty \). Consequently, these asymptotically non-flat wormhole geometries are matched with the external Schwarzschild solutions at some \(r = R>\) the Schwarzschild radius.

We have also analyzed the equilibrium for the reported wormhole solutions: The gravitational force \(F_g(r)\) becomes zero for the redshift function \(\phi (r) = C\). Therefore, the wormhole solutions, in this case, are in the equilibrium position under the action \(F_h(r)\) and \(F_a(r)\) (see Fig. 6 (left)). However, for the redshift functions \(\phi (r) = \alpha /r\) and obtained from flat rotational curve the wormhole solutions stay in equilibrium position under the simultaneous action of \(F_g(r)\), \(F_h(r)\) and \(F_a(r)\), which is clear from Figs. 6 (right) and 7. It is noted that the forces are dependent on the global monopole charge \(\eta \) for fixed values of semiclassical effects \(A = 0.01\) and \(B = 0.015\), clear from Figs. 6 and 7. The anisotropic force increases, the hydrostatic force decreases, and the gravitational force becomes zero in the first case and decreases for the second two cases for increasing values of \(\eta \).

To make it a more compatible proposal of wormhole solutions in the galactic halo, we are going to compare our model with the results in Refs. [26, 27]. In the study of Sarkar et al. [26], the wormhole structures are found in the bulge of the Milky Way galaxy situated on the MacMillan DM density profile with global monopole charge \(\eta \). They have found that the global monopole charge \(\eta \) has a crucial effect on the violation of NEC and on the asymptotic flatness of the wormhole structures. Also, they have shown that the total amount of averaged NEC violating matter depends on \(\eta \). Das et al. [27] studied the wormhole geometries in the halo and bulge of the Milky Way Galaxy by considering pseudo-isothermal, NFW and Universal Rotational Curve (URC) DM density profiles along with global monopole charge. In their study, they investigated the effect of global monopole charge in the presented solutions. In this article, we present the wormhole-like geometries in the local universe as the galactic halo supported by the Einasto DM density profile and global monopole charge with semiclassical effects. Here, we can see that for fixed values of semiclassical effects \(A = 0.01\), \(B = 0.015\), there are crucial effects of global monopole charge as mentioned above in the presented solutions.

Finally, all the successful results of our proposed solutions ensure that the wormhole geometries supported by the Einasto DM density profile and global monopole charge with semiclassical effects exist in the galactic halo. Therefore, the scientific community may get inspiration from this study to do fruitful further research work in the future.