1 Introduction

Cosmic inflation is a period of accelerated expansion of the early universe and an attractive mechanism for explaining the observed structures in the universe. It provides a solution to several puzzles, so-called cosmological problems, including the horizon, flatness, and monopole problems [1,2,3,4,5]. Current observations favor the inflationary paradigm for its prediction of an almost scale-invariant spectrum of primordial curvature perturbations imprinted in the cosmic microwave background (CMB) radiation and the large scale structure formations data [6,7,8,9]. The simplest model of inflation describes the period of exponential expansion of the early universe being driven by the slow-roll of a single scalar field known as the inflaton. To match the CMB temperature anisotropy measurements and give rise to a sufficient amount of inflation, the models of inflation share the flatness of the inflaton potential as a common feature among them [10, 11]. This nontrivial requirement of flatness of inflaton potential creates fine-tuning problems, in particular, quantum corrections in the absence of a symmetry generically spoil the flatness of the potential, which is known as the \(\eta \)-problem.

In particle physics model of inflation, the flatness of the potential should be protected against radiative corrections that can arise from the inflaton self-interactions or from its coupling to matter fields, responsible for reheating the universe after inflation [12,13,14]. To protect the flatness of the inflaton potential against the radiative corrections, the symmetries of a system play an important role – e.g., as for the standard model Higgs field, supersymmetry can provide a natural protection against the radiative corrections [13, 14]. If the inflaton is a pseudo-scalar axion, the axionic (shift) symmetry, \(\phi \rightarrow \phi +\text {constant}\), is another possible symmetry that protects the flatness of the inflaton potential. In this case, the inflaton potential arises from the breaking of a (global) shift symmetry, and the couplings of inflaton to matter fields do not affect the inflaton potential as long as the shift symmetry is respected. This mechanism was originally proposed in Ref. [12] as natural inflation, and its implications in light of the observational data, as well as implementations in the other theories, have been discussed in Refs. [12,13,14,15,16,17,18,19,20,21,22,23,24,25]. In the natural inflation model, a rolling inflaton has a flat potential due to shift symmetries. Whenever a global symmetry is spontaneously broken, Nambu Goldstone bosons arise, with a potential that is exactly flat. However, the inflaton cannot roll and drive inflation if the shift symmetry is exact. Thus, to drive inflation, there must be additional explicit symmetry breaking hence these particles become pseudo-Nambu Goldstone bosons, with “nearly” flat potentials exactly as required by inflation [16]. The resulting inflaton potential is generally of the form \(V(\phi )=\varLambda ^4[1+\cos (\phi /f)]\), where f is called the decay constant and is constrained by the observational data [12, 15, 16]. Despite its well established theoretical motivation and a simple form of the potential, the natural inflation model is disfavored at greater than 95% confidence by the observational data [10, 11, 26, 27], especially after the recent announcement of the improved Planck + BICEP/Keck 2018 data [28]. Although the original model, in which the scalar field is minimally coupled to gravity, is now disfavored by current observational constraints, some variants of natural inflation, including the generalized and multi-field versions, were proposed and discussed in Refs. [14, 29,30,31,32], and references therein. The inflationary predictions in those extended models can be modified and, in general, be consistent with observations.

Adopting the original natural inflation potential without any modification – e.g., \(V(\phi )=\varLambda ^4[1+\cos (\phi /f)]\), we investigate natural inflation for the cosmological models with the derivative self-interaction of the inflaton field and inflaton’s kinetic coupling to gravity via the Einstein tensor. The cosmological model of our interest was proposed in Ref. [33] (see Refs. [34, 35] for its applications) as a subclass of G-inflation framework [36], which is based on the Horndeski (equivalently, generalized Galileon) theory [37, 38], i.e., the most general scalar-tensor theory with second-order field equations avoiding the Ostrogradski instability [39], see Ref. [40] for a review. A unique feature of considering inflaton’s derivative self-interaction and its kinetic coupling with gravity is that the gravitationally enhanced friction mechanism works for steep potentials [41,42,43,44,45,46]. Thus, it motivates us to investigate whether it is possible to reconcile the predictions of natural inflation with the CMB observations in the setting of inflaton’s derivative self-interaction and its kinetic coupling with gravity scenario.

After inflation, it is usually assumed that the inflaton coherently oscillates at the minimum of its potential, decaying and transferring its energy to a relativistic plasma of the standard model particles [47,48,49]. This post-inflationary process that populates our universe with ordinary matter is known as reheating, see Ref. [50] for a review. Because there are no direct cosmological observations are traceable from reheating, the physics of reheating is highly uncertain and unconstrained. Thus, this post-inflationary era depends heavily on models of inflation. It was pointed out in the literature that consideration of reheating may provide additional constraints to inflationary perdictions [51,52,53,54,55]. In this work, for our model, we follow the approaches proposed in Refs. [29, 51,52,53,54,55,56,57,58] to perform the analyses on the reheating parameters, including the equation of state, the duration, and the temperature of reheating. Then, using the link between these parameters of reheating and the observable quantities of inflation, we provide constraints on the inflationary predictions of natural inflation in light of current observational data [10, 11, 28].

This paper is organized as follows. We start Sect. 2 by setting up our model with the derivative self-interaction of the scalar field and the kinetic coupling between the scalar field and gravity, which belongs to the subclass of Horndeski’s theory of gravity. Then, in the same section, we derive the background equations of motion, as well as the observable quantities; including power spectra of tensor and scalar modes, \(\mathcal {P}_S\) and \(\mathcal {P}_T\), respectively, their spectral tilts \(n_S\) and \(n_T\), and the tensor-to-scalar ratio r in the slow-roll scenario of inflation. Based on our analytic results obtained in Sect. 2, we place the observational constraints on \(n_S\) and r predictions of natural inflation in Sect. 3 and show that the natural inflation model is now consistent with the latest observational data, mainly due to the suppressed tensor-to-scalar ratio. In Sect. 4, we impose the effects of reheating to the predictions of natural inflation. The results of the section implies that the reheating parameters, the equation of state \(\omega _{re}\) and the temperature \(T_{re}\) at the end of reheating, significantly affect the duration of inflation \(N_k\) hence the \(n_S\) and r. We conclude our work and provide some implications of our findings in Sect. 5.

2 Background and perturbation dynamics

The action for the cosmological model that we investigate in this work is give as [33,34,35]

$$\begin{aligned} S&= \int d^{4}x\sqrt{-g} \left[ \frac{M_p^2}{2} R - \frac{1}{2} \left( g^{\mu \nu }-\frac{\alpha }{M^3}g^{\mu \nu }\partial _\rho \partial ^\rho \phi \right. \right. \nonumber \\&\left. \quad \left. + \frac{\beta }{M^2} G^{\mu \nu }\right) \partial _\mu \phi \partial _\nu \phi - V(\phi ) \right] , \end{aligned}$$
(1)

where \(M_p=2.44\times 10^{18}\)GeV is the reduced Planck mass and \(V(\phi )\) is the inflaton potential, and M is the mass scale making \(\alpha \) and \(\beta \) dimensionless constants. In the limit \((\alpha , \beta )\rightarrow 0\), the Einstein gravity with a minimal coupling to the scalar field is recovered. Thus, the case with \((\alpha , \beta )\ne 0\) reflects the deviation from the general relativity. While Refs. [33,34,35] discuss the scalar field dependent coupling function \(\xi (\phi )\) for the \(\alpha \)-term in Eq. (1), we consider such the coupling to be a constant; namely, \(\xi (\phi )=1\), in the present study for simplicity.

Varying the action with respect to metric \(g_{\mu \nu }\) and \(\phi \), one obtains the Einstein and field equations

$$\begin{aligned}&G_{\mu \nu }= \frac{1}{M_p^2} T_{\mu \nu } , \end{aligned}$$
(2)
$$\begin{aligned}&\partial _\mu \partial ^\mu \phi - V_{,\phi } + \frac{\alpha }{M^3} \left( \partial _\mu \partial _\nu \phi \partial ^\mu \partial ^\nu \phi -\partial _\mu \partial ^\mu \phi \partial _\nu \partial ^\nu \phi \right. \nonumber \\&\quad \left. +R_{\mu \nu }\partial ^\mu \partial ^\nu \phi \right) +\frac{\beta }{M^2} G_{\mu \nu }\partial ^\mu \partial ^\nu \phi =0 , \end{aligned}$$
(3)

respectively, where the \(G_{\mu \nu }=R_{\mu \nu }-g_{\mu \nu }R/2\) is the Einstein tensor,

(4)

is the energy momentum tensor, \(\square \phi \equiv \partial _\mu \partial ^\mu \phi \), and \(V_{,\phi }\equiv dV(\phi )/d\phi \). In a spatially flat Friedman-Robertson-Walker universe with metric

$$\begin{aligned} ds^2=-dt^2+a(t)^2\delta _{ij}dx^i dx^j , \end{aligned}$$
(5)

where a(t) is a scale factor, the background and field equations are obtained as

$$\begin{aligned}&3M_p^2H^2 = \frac{1}{2} \dot{\phi }^2 +V(\phi ) +\frac{3\alpha }{M^3}H\dot{\phi }^3 -\frac{9\beta }{2M^2}\dot{\phi }^2 H^2 , \end{aligned}$$
(6)
$$\begin{aligned}&M_p^2\left( 2\dot{H}+3H^2 \right) = -\frac{1}{2}\dot{\phi }^2 +V +\frac{\alpha }{M^3}\dot{\phi }^2\ddot{\phi }\nonumber \\&\quad -\frac{\beta }{2M^2}\dot{\phi }^2\left( 2\dot{H} +3H^2 +4H\frac{\ddot{\phi }}{\dot{\phi }} \right) , \end{aligned}$$
(7)
$$\begin{aligned}&\ddot{\phi } +3H\dot{\phi } + V_{,\phi } +\frac{3\alpha }{M^3}\dot{\phi }^2 \left( \dot{H} + 3H^2 + 2 H \frac{\ddot{\phi }}{\dot{\phi }} \right) \nonumber \\&\quad -\frac{3\beta }{M^2} H \dot{\phi }\left( 2\dot{H} +3H^2 +H\frac{\ddot{\phi }}{\dot{\phi }}\right) =0 , \end{aligned}$$
(8)

where the overdot denotes the derivative with respect to time t. To investigate the slow-roll inflation, we take so called the slow-roll conditions that read \(V(\phi )\gg \dot{\phi }^2\) and \(\ddot{\phi }\ll 3H\dot{\phi }\) into account and introduce the following slow-roll parameters

$$\begin{aligned} \epsilon _1 \equiv -\frac{\dot{H}}{H^2} ,\quad \epsilon _2 \equiv -\frac{\ddot{\phi }}{H\dot{\phi }} ,\quad \epsilon _3 \equiv \frac{\dot{\phi }^2}{2M_p^2H^2} , \end{aligned}$$
(9)

which assumed to be small, \(\epsilon _{i}\ll 1\) where \(i=1,2,3\), during inflation. Equation (8) can, therefore, be rewritten in terms of these parameters as

$$\begin{aligned}&3H\dot{\phi }\left[ 1-\frac{1}{3}\epsilon _2 +\frac{3\alpha }{M^3} H\dot{\phi }\left( 1-\frac{\epsilon _1}{3}-\frac{2\epsilon _2}{3}\right) \right. \nonumber \\&\quad \left. -\frac{3\beta }{M^2} H^2\left( 1-\frac{2\epsilon _1}{3}-\frac{\epsilon _2}{3}\right) \right] = -V_{,\phi } . \end{aligned}$$
(10)

Thus, under the slow-roll conditions, Eqs. (6) and (8) can be approximated as

$$\begin{aligned} 3M_p^2H^2\simeq V , \quad 3H\dot{\phi } \left( 1+\mathcal {A}\right) \simeq -V_{,\phi } , \end{aligned}$$
(11)

where

$$\begin{aligned} \mathcal {A}=\frac{3\alpha }{M^3} H\dot{\phi }-\frac{3\beta }{M^2} H^2 . \end{aligned}$$
(12)

In Eq. (11), \((1+\mathcal {A})\) should be positive not to violate the null energy condition. As one can see from Eq. (12) that the function \(\mathcal {A}\) encodes the information about the additional interactions; the derivative self-interaction of the scalar field (the first term) and the kinetic coupling between the scalar field and gravity (the second term) that we introduced in Eq. (1), and it becomes zero if both terms cancel each other, which indicates the complete absence of these additional interactions in our model. To weigh the contributions of each term in Eq (12) during inflation, we introduce a parameter defined by

$$\begin{aligned} \gamma \equiv \frac{\alpha }{\beta M} \frac{ \dot{\phi }}{H} . \end{aligned}$$
(13)

If the kinetic coupling between the scalar field and gravity is much stronger (or weaker) than the derivative self-interaction of the scalar field during inflation, \(|\gamma |\ll 1\) (or \(|\gamma |\gg 1\)). Thus, the equally important contributions from both interactions indicate \(|\gamma |\sim \mathcal {O}(1)\). Equation (12) can be rewritten in terms of \(\gamma \) as

$$\begin{aligned} \mathcal {A}=3\beta (\gamma -1)\frac{H^2}{M^2} . \end{aligned}$$
(14)

Here, if the \(\gamma \) equals unity, the \(\mathcal {A}\) becomes zero, which, as discussed, indicates the absence of the additional interactions. The resulting spectrum for the CMB mode would be the same as that in slow-roll inflation in GR. If the \(\mathcal {A}\) is non-zero, one can consider two different limiting cases; \(|\mathcal {A}|\ll 1\) and \(\mathcal {A}\gtrsim 1\), respectively, during inflation. When \(|\mathcal {A}|\ll 1\), Eq. (11) leads to the slow-roll approximated equations for standard single-field inflation in the Einstein gravity. Although the \(|\mathcal {A}|\ll 1\) case could be interesting to investigate as it can be treated perturbatively in the slow-roll parameters, its effect deviating from standard slow-roll inflation in general relativity (GR) would be small, if not negligible. It is, therefore, worth investigating the second case where \(\mathcal {A}\gtrsim 1\) to account for the effects of additional interactions encoded in the \(\mathcal {A}\). Thus, our interest in this work is to consider the case where \(\mathcal {A}\gtrsim 1\), while \(|\gamma |\sim \mathcal {O}(1)\). From Eq. (14), condition \(\mathcal {A}\gtrsim 1\) implies that

$$\begin{aligned} \frac{H^2}{M_p^2}\gtrsim \frac{1}{3\beta (\gamma -1)}\frac{M^2}{M_p^2} , \end{aligned}$$
(15)

where \(\beta (\gamma -1)>0\) with \(|\gamma |\sim \mathcal {O}(1)\) is assumed. To satisfy the sufficient condition to avoid from quantum gravity that reads \(H^2/M_p^2\ll 1\), the condition \(M^2/M_p^2\ll 3\beta (\gamma -1)\) should also hold for our model, and we will examine the parameter space that satisfies this condition in the next section.

The amount of inflation is quantified by the number \(N_k\) of e-folds, which reads

$$\begin{aligned} N_k = \int _\phi ^{\phi _e} \frac{H}{\dot{\tilde{\phi }}} d\tilde{\phi } \simeq \frac{1}{M_p^2}\int _{\phi _e}^\phi \frac{V}{V_{,\tilde{\phi }}}\left( 1+\mathcal {A}\right) d\tilde{\phi } , \end{aligned}$$
(16)

where \(\phi _e\) is the scalar-field value at the end of inflation and is to be estimated by solving \(\epsilon _1(\phi _e)\equiv 1\).

The linear perturbation analysis for our model Eq. (1) is carried out in Refs. [33, 35], see Ref. [36] for more general cases, and the observable quantities, including power spectra of the scalar (\(\mathcal {P}_S\)) and tensor (\(\mathcal {P}_T\)) modes, their spectral tilts (\(n_S\) and \(n_T\), respectively), and the tensor-to-scalar ratio r, are computed on the large scale \(c_S k |\tau |\ll 1\) as

$$\begin{aligned} \mathcal {P}_S&= \frac{k^3}{2\pi ^2}\left| \frac{\nu _k}{z_S}\right| ^2 \simeq \frac{H^2}{8\pi ^2 M_p^2 c_S^3 \epsilon _V}\left( 1+\mathcal {A}\right) , \end{aligned}$$
(17)
$$\begin{aligned} \mathcal {P}_T&= \frac{k^3}{\pi ^2}\sum _{\lambda =x, +}\left| \frac{\mu _{\lambda ,k}}{z_T}\right| ^2 \simeq \frac{H^2}{2\pi ^2 M_p^2 c_T^3} , \end{aligned}$$
(18)
$$\begin{aligned} n_S-1&= \frac{d\ln \mathcal {P}_S}{d\ln k} = 3-2\mu _S \nonumber \\&\simeq \frac{1}{1+\mathcal {A}} \left[ 2\eta _V -2\epsilon _V\left( 4- \frac{1}{1+\mathcal {A}}\right) \right] ,\end{aligned}$$
(19)
$$\begin{aligned} n_T&= \frac{d\ln \mathcal {P}_T}{d\ln k} = 3-2\mu _T \simeq -\frac{2\epsilon _V}{1+\mathcal {A}} ,\end{aligned}$$
(20)
$$\begin{aligned} r&= \frac{\mathcal {P}_T}{\mathcal {P}_S} \simeq \frac{16\epsilon _V}{1+\mathcal {A}} , \end{aligned}$$
(21)

where \(\epsilon _V \equiv M_p^2\left( V_{,\phi }/V\right) ^2/2\) and \(\eta _V\equiv M_p (V_{,\phi \phi }/V)\), and \(c_{S, T}^2\sim 1+\mathcal {O}(\epsilon _1)\simeq 1\), see Refs. [33, 35] for further details. Based on these findings, we place observational constraints on the natural inflation model in the following sections. In the standard single field inflation scenario in the general relativity, which is \(\mathcal {A}\ll 1\) limit of our model, the theoretical predictions of natural inflation on \(n_S\) and r has been disfavored by observational data [10, 11, 28]. Thus, in the following section, we place observational constraints on natural inflation in the \(\mathcal {A}\gg 1\) limit and show that the model is now consistent with the current observations even at \(1\sigma \) (\(68\%\) confidence) level.

Fig. 1
figure 1

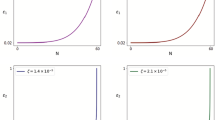
Left: the exponent of an argument of \(\mathcal {W}\)-function in Eq. (31) as a function of \(\varDelta \) and \(N_k\). The solid, dashed, and dot-dashed lines correspond to \(N_k=50\), 55, and 60, respectively. The the exponent grows from \(-\infty \) to \(-1\), the horizontal black solid line, as the \(\varDelta \) increases from 0 to \(\infty \). Right: the \(\mathcal {W}_0(x)\) branch as a function of \(\varDelta \) and \(N_k\), which gives \(|\cos (\phi /f)|\le 1\) in Eq. (31)

Full size image

3 Observational constraints

In the presence of the derivative self-interaction of the scalar field and its kinetic coupling with the Einstein tensor, we place observational constraints on natural inflation. Since natural inflation in the GR limit, where \(\mathcal {A}=0\) (equivalently, \(\gamma =1\)), is well discussed in Refs. [10, 11, 26, 27] and references therein, we investigate the \(\mathcal {A}\gg 1\) case, from now on, to account for the significant deviation from the standard slow-roll inflation scenario in GR. In this and next section, we consider the \(\mathcal {A}\gg 1\) limit of our analytic results of the previous section. Thus, it is worth emphasizing that results in this and the following sections correspond only to the \(\gamma \ne 1\) case.Footnote 1 The potential for natural inflation reads

$$\begin{aligned} V(\phi ) = \varLambda ^4 \left[ 1+ \cos \left( \frac{\phi }{f} \right) \right] , \end{aligned}$$
(22)

where the energy density \(\varLambda ^4\) and the decay constant f are the parameters of the model with dimensions of mass. In the limit \(f\rightarrow \infty \), the potential behaves like pure power laws, e.g., \(V(\phi )\sim m^2\phi ^2\) where m is an energy scale that plays the role of \(\varLambda \) [29]. For natural inflation, the number \(N_k\) of e-fold is obtained from Eq. (16) as

$$\begin{aligned} N_k = \varDelta \left[ \mathcal {F}\left( \phi _e\right) - \mathcal {F}\left( \phi \right) \right] , \end{aligned}$$
(23)

where

$$\begin{aligned} \varDelta = \beta (\gamma -1) \frac{f^2 \varLambda ^4}{M^2 M_p^4} , \end{aligned}$$
(24)

and

$$\begin{aligned} \mathcal {F}\left( \phi \right) = \cos {\left( \frac{\phi }{f}\right) } + 4\ln {\sqrt{\pm \frac{1}{2} \left[ 1-\cos {\left( \frac{\phi }{f}\right) }\right] }} . \end{aligned}$$
(25)

Here, we choose “\(+\)” sign in Eq. (25) since the quantity under the square root should be positive. To obtain Eq. (23), we assumed \(\mathcal {A}\gg 1\) in Eq. (16). By using the condition that \(\epsilon _1(\phi _e)=1\), we obtain the scalar-field value \(\phi _e\) at the end of inflation as

$$\begin{aligned} \cos {\left( \frac{\phi _e}{f}\right) } = \frac{4}{1\pm \sqrt{16\varDelta +1}}-1 , \end{aligned}$$
(26)

where we choose “\(+\)” sign for reason that \(|\cos (\phi _e/f)|\le 1\). Substituting Eq. (26) into Eq. (25), we obtain

$$\begin{aligned}&\mathcal {F}\left( \phi _e\right) = 2\ln \left[ \frac{1+8\varDelta -\sqrt{16\varDelta +1}}{8\varDelta }\right] \nonumber \\&\quad -\frac{1+4\varDelta -\sqrt{16\varDelta +1}}{4\varDelta } . \end{aligned}$$
(27)

Consequently, the potential value at the end of inflation gets

$$\begin{aligned} V(\phi _{e}) = \left( \frac{\sqrt{16\varDelta +1}-1}{4\varDelta }\right) \varLambda ^4 . \end{aligned}$$
(28)

For the potential in Eq. (22), the spectral index for scalar modes and the tensor-to-scalar ratio are obtained from Eqs. (19) and (21) as

$$\begin{aligned} n_S&=1 - \frac{2\left[ 2-\cos {\left( \frac{\phi }{f}\right) } \right] }{\varDelta \left[ 1+\cos {\left( \frac{\phi }{f}\right) }\right] ^2} , \end{aligned}$$
(29)
$$\begin{aligned} r&=\frac{8\left[ 1-\cos {\left( \frac{\phi }{f}\right) } \right] }{\varDelta \left[ 1+\cos {\left( \frac{\phi }{f}\right) }\right] ^2} . \end{aligned}$$
(30)

Using Eq. (23), we obtain

$$\begin{aligned} \cos {\left( \frac{\phi }{f}\right) } = 1+ 2\mathcal {W}\left( \pm e^{\frac{1}{2}\left( \mathcal {F}\left( \phi _e\right) -\frac{N_k+\varDelta }{\varDelta }\right) } \right) , \end{aligned}$$
(31)

where \(\mathcal {W}(x)\) is the product logarithm function, also known as the Lambert \(\mathcal {W}\) function, and both \(\varDelta \) and \(N_k\) are positive constants. Let us first consider the positive sign for the argument of \(\mathcal {W}\)-function in Eq. (31). As the \(\varDelta \) increases from 0 to \(\infty \), while the number of e-folds of inflation is fixed to be \(N_k\sim 60\), the exponent increases from \(-\infty \) to \(-1\), see the left panel of Fig. 1. Thus, the argument of \(\mathcal {W}(x)\) takes a value in a range \(0\le x\le 1/e\) and, consequently, the \(\mathcal {W}(x)\) takes a value between zero and \(\mathcal {W}(1/e)\simeq 0.2784\). As a result from Eq. (31), we obtain \(\cos (\phi /f)\ge 1\), and the scalar field becomes complex-valued, which we are not interested in in this work. Let us now consider the negative sign in Eq. (31). Again, as the \(\varDelta \) increases from 0 to \(\infty \) for a fixed \(N_k\), the argument of \(\mathcal {W}(x)\) decreases in a range \(0\ge x \ge -1/e\). In that case, there are two branches of real values of \(\mathcal {W}(x)\). Following Ref. [59], we denote the branch satisfying \(\mathcal {W}(x)\le -1\) by \(\mathcal {W}_{-1}(x)\) and the branch satisfying \(-1\le \mathcal {W}(x)\le 0\) by \(\mathcal {W}_0(x)\). For the \(\mathcal {W}_{-1}(x)\) branch, we obtain \(\cos (\phi /f)\le -1\) from Eq. (31), in which the scalar field is also complex-valued. Lastly, we obtain \(|\cos (\phi /f)|\le 1\) for the \(\mathcal {W}_{0}(x)\) branch. Thus, for our further study, we choose the negative sign in Eq. (31) and the \(\mathcal {W}_0(x)\) branch where \(-1\le \mathcal {W}(x)\le 0\), and then \(|\cos {(\phi /f)}|\le 1\), see the right panel of Fig. 1.

Although we have several free parameters; including \(\alpha \), \(\beta \), and M, coming from our model, and \(\varLambda \) and f, from the choice of inflaton potential, our result shows that the theoretical predictions of \(n_S\) and r depend only on a single parameter \(\varDelta \), which is given in Eq. (24). Thus, it is effectively one parameter model, and we plot in the left panel of Fig. 2 the theoretical predictions of our model based on Eqs. (29) and (30) for natural inflation.

Fig. 2
figure 2

Left: the \(n_S-r\) plot for natural inflation with potential given in Eq. (22). The shaded regions present the \(1\sigma \) (dark blue) and \(2\sigma \) (light blue) contours of the latest Planck+BICEP/Keck 2018 data [28]. The diagonal gray lines indicate the different values of \(\varDelta \) within the interval \(15\le \varDelta \le 4500\), increasing from bottom left to top right with a step of 10. For the orange line, \(\varDelta =20\). The purple lines represent the number \(N_k\) of e-folds during inflation; \(N_k=50\) (dotted), 60 (dashed), and 70 (solid). Right: the parameter space of \(\beta (\gamma -1)\) vs. \(M^2/M_p^2\) from Eq. (24), where the black line corresponds to the cutoff scale \(M^2/M_p^2=3\beta (\gamma -1)\). The gray shaded region is the allowed parameter space satisfying \(M^2/M_p^2\lesssim 3\beta (\gamma -1)\). For the blue- and red-shaded regions, we set \(\varDelta =15\) and \(\varDelta =28\), respectively, and vary the \(f/M_p\) value within the range of \(0.3\le \log _{10}(f/M_p) \le 2.5\) adopted from Planck paper [10, 11], the value increases from solid to dashed boundaries

Full size image

The shaded dark- and light-blue regions represent the \(1\sigma \) and \(2\sigma \) confidence contours of the Planck+BICEP/Keck 2018 data [28], respectively. The diagonal gray lines indicate the different values of \(\varDelta \); for example, \(\varDelta =20\) for the orange line. The purple lines represent the number \(N_k\) of e-folds during inflation; \(N_k=50\) (dotted), 60 (dashed), and 70 (solid). The values of r and \(n_S\) decrease/increase along the purple lines as the \(\varDelta \) value decreases/increases. The figure shows that natural inflation is now compatible with the observational data if the kinetic coupling between gravity and the scalar field and the derivative self-interaction of the scalar field are taken into account during inflation. For our model to be consistent with the observational data at \(1\sigma \)/\(2\sigma \) level, the duration of inflation is preferred to be \(N_k\gtrsim 60\)/\(N _k\gtrsim 50\). The ranges of \(\varDelta \) compatible with the data are \(18\lesssim \varDelta \lesssim 25\) (\(1\sigma \) confidence) and \(25\lesssim \varDelta \lesssim 45\) (\(2\sigma \) confidence) for \(N_k=60\)(dashed line), the most conservative value for duration of inflation. Having obtained the range of \(\varDelta \) values in agreement with the observational data, we can search for the parameter space of other parameters using Eq. (24).

The amplitude of the scalar power spectrum is well determined to be \(\mathcal {P}_S(k_*)=2.0989\times 10^{-9}\) (TT, TE, EE + lowE + lensing) at the pivot scale \(k_*=0.05\, \text {Mpc}^{-1}\) [10, 11]. Thus, we can use Eq. (17) to obtain the \(\varLambda \) parameter. First, we write Eq. (17) in the following form

$$\begin{aligned} \mathcal {P}_S(k_*)&= \frac{\varDelta }{12 \pi ^2}\frac{\varLambda ^4}{M_p^4} \left[ 1+\cos \left( \frac{\phi }{f}\right) \right] ^3\left[ 1-\cos \left( \frac{\phi }{f}\right) \right] ^{-1}\nonumber \\&=2.0989\times 10^{-9} , \end{aligned}$$
(32)

where \(\cos (\phi /f)\) is given in Eq. (31) in terms of \(N_k\) and \(\varDelta \). The \(N_k\) can be expressed in terms of \(n_S\) and \(\varDelta \) after substituting Eq. (31) into Eq. (29), which then reads

$$\begin{aligned} N_k&= \varDelta \left\{ \mathcal {F}(\phi _e) - \ln \left[ \exp \left( \frac{1-(n_S-1)\varDelta +\sqrt{1-6(n_S-1)\varDelta }}{(n_S-1)\varDelta }\right) \right. \right. \nonumber \\&\quad \times \left. \left. \left( \frac{1-2(n_S-1)\varDelta +\sqrt{1-6(n_S-1)\varDelta }}{2(n_S-1)\varDelta }\right) ^2 \right] \right\} . \end{aligned}$$
(33)

Thus, we obtain \(\varLambda (n_S, \varDelta )\) from Eq. (32) as

$$\begin{aligned} \frac{\varLambda ^4}{M_p^4}= & {} -\frac{3\pi ^2}{\varDelta }\mathcal {P}_S(k_*) \left( 1+ \mathcal {W}\left[ -\sqrt{\exp \left( \mathcal {F}\left( \phi _e\right) -\frac{N_k+\varDelta }{\varDelta }\right) }\right] \right) ^{-3}\nonumber \\&\quad \times \mathcal {W}\left[ -\sqrt{\exp \left( \mathcal {F}\left( \phi _e\right) -\frac{N_k+\varDelta }{\varDelta }\right) }\right] . \end{aligned}$$
(34)

For the central \(n_S=0.9649\) value from the Planck TT, TE, EE + lowE + lensing data [10, 11], Eq. (34) gives \(2.7331\times 10^{-3}\le \varLambda /M_p\le 5.1006\times 10^{-3}\) for the \(15\le \varDelta \le 28\) range. The corresponding range of tensor-to-scalar ratio is \(0.0035\le r \le 0.036\), which is compatible with the latest constraint on \(r_{0.05}<0.036\) at \(95\%\) confidence [28].

Substituting Eq. (34) into Eq. (24), we plot the parameter space of \(\beta (\gamma -1)\) vs. \(M^2/M_p^2\) in the right panel of Fig. 2. The black solid line indicates cutoff scale \(M^2/M_p^2=3\beta (\gamma -1)\). The gray shaded region presents the allowed parameter space from Eq. (15) satisfying the sufficient condition \(M^2/M_p^2\ll 3\beta (\gamma -1)\) to avoid the quantum gravity. For plotting the blue- and red-shaded regions, we adopt the \(n_S=0.9649\) and \(0.3\le \log _{10}(f/M_p) \le 2.5\) from the Planck paper [10, 11]. The value of \(f/M_p\) increases from solid to dashed boundaries, while we set \(\varDelta =15\) and \(\varDelta =28\) for the blue and red regions, respectively. Since we consider \(\gamma \ne 1\) case; hence \(\beta \ne 0\), in this study, the divergence occurring at \(\beta (\gamma -1)=0\) is not physical. In other words, the \(\gamma =1\) case should be treated separately. The left panel of Fig. 2 shows that the CMB data prefer the positive values of \(\varDelta \), which indicates the \(\beta (\gamma -1)\) in Eq. (24) must also be positive. Therefore, \(\beta >0\) for \(\gamma >1\) and \(\beta <0\) for \(\gamma <1\) in the right panel of Fig. 2, respectively. Thus, we conclude from Fig. 2 that the natural inflation model is now consistent with the latest observational data for a broad range of model parameters. In the following section, to put further constraints to the inflationary predictions for natural inflation, we impose reheating considerations after inflation.

Fig. 3
figure 3

The \(n_S-T_{re}\) (bottom) and \(n_S-N_{re}\) (top) plots for natural inflation with potential given in Eq. (22). The yellow shaded region indicates the current \(1\sigma \) range of \(n_S=0.9649\pm 0.0042\) (\(68\%, TT, TE, EE+lowE+lensing\)) from Planck data [10, 11]. The pink and brown shaded regions indicate the \(T_{re}\le 100\)GeV and \(T_{re}\le 10\)MeV energy scales, respectively. The \(\omega _{re}\) values residing inside the shaded regions are favored

Full size image
Fig. 4
figure 4

The \(n_S-r\) plot for natural inflation with potential given in Eq. (22). The shaded regions are the same as Fig. 2

Full size image

4 Reheating constraints

Inflation ends when equation-of-state parameter becomes \(\omega _{\text {inf}}=-1/3\). The standard inflationary cosmology then assumes that, after inflation, the universe undergoes a phase of reheating, during which the inflaton field coherently oscillates at the minimum of its potential, decaying and transferring its energy to a relativistic plasma, and populates the universe with ordinary matter. As for the reheating phase, we follow the approaches proposed in Refs. [29, 51,52,53,54,55,56,57,58], especially [29, 56], in which the present day observations are related to the evolution of the inflaton field during inflation. The key is the relation between the comoving scale k today and that during inflation. In other words, the comoving Hubble radius, \(a_k H_k=k\), exiting the horizon is associated with that of present time by

$$\begin{aligned} \ln \frac{k}{a_0 H_0} = \ln \frac{(a H)_{k}}{(aH)_{e}}+\ln \frac{(a H)_{e}}{(a H)_{re}}+\ln \frac{(a H)_{re}}{(aH)_{eq}} + \ln \frac{(a H)_{eq}}{a_0 H_0} . \end{aligned}$$
(35)

The number of e-folds during each inflation, reheating, and radiation dominated epoch; \(N_k=\ln (a_{e}/a_{k})\), \(N_{re}=\ln (a_{re}/a_{e})\), and \(N_{RD}=\ln (a_{eq}/a_{re})\), respectively, can be used to simplify Eq. (35) as

$$\begin{aligned} \ln \frac{k}{a_0H_0}=-N_k-N_{re}-N_{RD}+\ln \frac{a_{eq}}{a_0}+\ln \frac{H_k}{H_{0}} , \end{aligned}$$
(36)

where “\(a_\text {eq}\)” is the scale factor at the matter and radiation equality, and the subscript “0” denotes the present day value of each quantity. The Hubble parameter during inflation is obtained from Eq. (18) with an assumption \(\mathcal {P}_T(k_*)=r \mathcal {P}_S(k_*)\) to be \(H_k=\sqrt{2}\pi M_p(r\mathcal {P}_S)^{1/2}c_T^{3/2}\), where \(c_T\simeq 1\) for our case. The ratio between the energy density \(\rho _{e}\) at the end of the inflation and the energy density \(\rho _{re}\) at the end of the reheating depends on the equation-of-state parameter and the duration of reheating and is

$$\begin{aligned} \frac{\rho _{re}}{\rho _{e}}=e^{-3(1+\omega _{re})N_{re}} . \end{aligned}$$
(37)

The energy density \(\rho _{e}\) at the end of inflation is then computed from the modified Friedmann equations Eq. (11) to be \(\rho _e\simeq V(\phi _e)\). Assuming the conservation of entropy and the current neutrino temperature, \(T_{\nu ,0}=(4/11)^{1/3}T_0\), the energy density at reheating is

$$\begin{aligned} \rho _{re}=\frac{\pi ^2g_{re}}{30}T_{re}^4 , \end{aligned}$$
(38)

where

$$\begin{aligned} T_{re}=\left( \frac{43}{11g_{s,re}}\right) ^{\frac{1}{3}}\frac{a_0}{a_{re}} T_0 . \end{aligned}$$
(39)

The number of e-folds during reheating can be obtained from Eq. (37) with Eqs. (38) and (36) as

$$\begin{aligned} N_{re}&=\frac{4}{1-3\omega _{re}}\Bigg [-N_k-\ln \frac{k}{a_0T_0}-\frac{1}{4}\ln \frac{30}{\pi ^2g_{re}} -\frac{1}{3}\ln \frac{11g_{s,re}}{43} \nonumber \\&\quad -\frac{1}{4}\ln V(\phi _e)+\frac{1}{2}\ln \left( 2\pi ^2 M_p^2r\mathcal {P}_S\right) \Bigg ] . \end{aligned}$$
(40)

The corresponding reheating temperature, \(T_{re}\), is

$$\begin{aligned} T_{re}^4=\left( \frac{30}{\pi ^2g_{re}}\right) V(\phi _e)e^{-3(1+\omega _{re})N_{re}} . \end{aligned}$$
(41)

Assuming the effective equation-of-state parameter \(\omega _{re}\) is functionally constant, we plot the temperature \(T_{re}\) and the duration of reheating as functions of the spectral index \(n_S\) in Fig. 3. The left and right panels correspond to two different values of \(\varDelta \). In each figure, we choose four different values of \(\omega _{re}\); namely, \(\omega _{re}=-1/3\) (red), \(\omega _{re}=0\) (blue), \(\omega _{re}=0.25\) (black), and \(\omega _{re}=1\) (green). The smallest \(\omega _{re}=-1/3\) value is required for inflation end, while the largest \(\omega _{re}=1\) one, the most conservative upper limit, comes from the causality. Thus, the \(\omega _{re}\) value varies within the interval of \(-1/3\le \omega _{re}\le 1\). The background yellow shaded region presents the current \(1\sigma \) range of \(n_S=0.9649\pm 0.0042\) (\(68\%, TT, TE, EE+lowE+lensing\)) from Planck data [10, 11]. The pink and brown shaded regions with \(T_{re}\le 100\)GeV and \(T_{re}\le 10\) MeV indicate the constraints on energy scales the electroweak and the big-bang nucleosynthesis, respectively. The \(\omega _{re}\) values residing inside the shaded regions are favored. The curves of all \(\omega _{re}\) intersect at \((n_S, T_{re}^{max}) = (0.9634, 3.04\times 10^{15} \text {GeV})\) for \(\varDelta =20\) and \((n_S, T_{re}^{max}) = (0.9698, 3.26\times 10^{15} \text {GeV})\) for \(\varDelta =40\) and indicate the instantaneous reheating (\(N_{re}=0\)) for our model. The instantaneous reheating temperature \(T^{max}_{re}\) and corresponding spectral index \(n_S\) values slightly increase as the \(\varDelta \) value increases, which is due to the potential energy value at the end of inflation depends on the value of \(\varDelta \), see Eqs. (28) and (41). By matching the lines of the same colors in both upper and lower panels, one can estimate the duration and corresponding temperature of reheating. Thus, for given \(\omega _{re}\), the figure shows that the longer the reheating lasts, the lower the temperature gets at the end of reheating. For the increasing direction of \(n_S\), the \(T_{re}\) increases, while the \(N_{re}\) decreases, toward the intersecting point for \(\omega _{re}<1/3\). As for the case of \(\omega _{re}>1/3\), the \(T_{re}\) decreases, while \(N_{re}\) increases, away from the intersecting point of all lines.

In Eq. (33), the duration \(N_k\) of inflation is expressed in terms of \(n_S\) and \(\varDelta \). Also, the \(n_S\) can be expressed in terms of reheating parameters, including \(\omega _{re}, N_{re}\), and \(T_{re}\). Thus, by taking the reheating considerations into account, we plot \(n_S-r\) predictions once again in Fig. 4 for the same values of \(\omega _{re}\) as Fig. 3. Since \(N_{re}\) and \(T_{re}\) are related to each other, we choose \(T_{re}\) as another reheating parameter in Fig. 3. As it is in Fig. 2, the underlying diagonal gray lines correspond to the different values of \(\varDelta \), and it increases from bottom left to top right within the interval of \(20\le \varDelta \le 40\). The purple lines are some reference values of \(N_k\). As the labels indicate in each panel, the different colors on the diagonal lines correspond to the different values of \(T_{re}\). The main implication of this figure is that both the \(\omega _{re}\) and the \(T_{re}\) at the end of reheating provide us with information about how long inflation had to be lasted to be compatible with the CMB observations. For example, if \(\omega _{re}<1/3\), inflation cannot last longer than \(N_k\simeq 57\) e-folds due to our reheating considerations. Thus, the prediction of \(n_S\) and r is only \(2\sigma \) consistent with the observations. Conversely, the duration of inflation must be longer than \(N_k\gtrsim 57\) for \(\omega _{re}>1/3\). As a result, the theoretical prediction of our model is still consistent with the CMB data, the \(n_S\) and r values residing inside \(1\sigma \) contour. The turning point is the instantaneous reheating with \(N_{re}=0\), which also indicates \(\omega _{re}=1/3\). Since reheating must have occurred instantaneously after inflation, the estimated duration of inflation is \(N_k\simeq 57\) e-folds, the exact value is slightly different for different \(\varDelta \) values as the figure shows. Figure 4 also shows that the CMB data prefer different ranges of reheating temperature depending on the values of \(\omega _{re}\). For equation of state approaching \(\omega _{re}\simeq 1/3\), the reheating temperature from as low as a few MeV to as large as \(10^{15}\)GeV can be achieved.

5 Conclusions

For a cosmological model described by Eq. (1), where the derivative self-interaction of a scalar field and its kinetic coupling with gravity is presented, we placed observational constraints on the natural inflation model. Then, we investigated the effects of reheating on the inflationary predictions. The interactions we introduced in this work are assumed to give equally important contributions during inflation such that \(|\gamma |\sim \mathcal {O}(1)\) in Eq. (13). The main analytic results of inflationary predictions for our model are obtained in Eqs. (17)–(21), where the presence of \(\mathcal {A}\) indicates the non-zero effects of the interactions mentioned above. These equations do not depend on details of inflaton potential. To give a sizable effect during inflation, deviating from the standard single-field inflation model in Einstein gravity, the \(\mathcal {A}\) should be \(\mathcal {A}\gtrsim 1\). Equation (11) shows that the additional interactions in our model significantly enhance the gravitational friction. Consequently, the tensor-to-scalar ratio is suppressed by a factor of \(1+\mathcal {A}\) in Eq. (21). The suppression is more significant if \(\mathcal {A}\gg 1\); hence, the inflationary predictions can be compatible with the observations.

In Sect. 3, in light of the latest observational data [10, 11, 28], we discussed the theoretical predictions of the natural inflation model with potential given in Eq. (22). Although we have several free parameters, the observable quantities of natural inflation depend only on a single parameter \(\varDelta \) as defined in Eq. (24). In the \(n_S-r\) plane in Fig. 2, we showed that the natural inflation model is now compatible with the observational data for a certain parameter range, mainly due to the suppressed tensor-to-scalar ratio r. For the predictions to be consistent with data at \(1\sigma \) (\(68\%\) confidence) level, natural inflation is supposed to last slightly longer (\(N_k\gtrsim 60\)) than usually assumed. The right panel of Fig. 2 shows the parameter space of M and \(\gamma \) parameters that provides the right value for the amplitude of the CMB spectrum.

Imposing the effective equation-of-state \(\omega _{re}\) parameter to be constant after inflation, we estimated the duration and the temperature of reheating in terms of inflationary parameters in Eqs. (40) and (41), respectively. In Fig. 3, we plotted Eqs. (40) and (41) as a function of \(n_S\) for given \(\varDelta \) and \(\omega _{re}\) values. The figure shows that the broad ranges of \(\omega _{re}\) and \(\varDelta \) give compatible results with the CMB predictions on \(n_S\). The combined result with Fig. 4 implies that, if \(\omega _{re}>1/3\), inflation can last long enough – i.e., having \(N_*\gtrsim 60\). Thus, it is more compatible with the CMB data, the predictions residing inside the \(1\sigma \) contour, see Fig. 4 for \(\omega _{re}=1\). For the \(\omega _{re}<1/3\) cases, the maximum number of e-folds in natural inflation is \(N_k\simeq 57\); hence the predictions reside inside the \(2 \sigma \) contour only, see Fig. 4 for \(\omega _{re}=-1/3,\,0,\) and 0.25 cases. Our result also shows that the broad range of reheating temperatures, from as low as \(\sim \mathcal {O}(10)\) MeV to as large as \(\sim \mathcal {O}(10^{15})\) GeV, can be achieved at the end of reheating if the equation of state is closer to 1/3. The maximum reheating temperature is \(T_{re}^{max}\simeq 3\times 10^{15}\) GeV, corresponding to an instantaneous reheating scenario for which \(\omega _{re}=1/3\) and \(N_{re}=0\).

We conclude that the effects of reheating to inflationary predictions are important to tighten the parameter space of observable quantities, breaking degeneracy between inflationary predictions that otherwise overlap in the \(n_S-r\) plane. We also found it is interesting to investigate the phenomenological details of reheating for the \(\omega _{re}\gtrsim 1/3\). According to our result, in that case, inflation can last longer than usually assumed; hence more consistent with the CMB data, and the broad range of reheating temperature is also accessible.