1 Introduction

Based on the observations carried out by Reiss and Perlmutter [1, 2] the current universe is in an accelerated expansion phase. The reason behind it can be considered as the existence of cosmological constant \(\Lambda \). But the dynamic behaviour of \(\Lambda \) and computing the value of it in a quantum field theoretic way opens the paths of extended scenarios. One of which is to keep general relativity based on gravitation theory while considering new, exotic matter, which explains the dark energy (DE) concept [3,4,5]. The other is to extend the theory of gravity whose special case is general relativity with extended degree of freedom to get the explanation about the accelerated universe [6,7,8,9].

Using the holographic Principle (HP), one intriguing possibility for explaining the genesis and nature of dark energy can be obtained at a cosmological framework [10,11,12]. G.’t Hooft [10] presented the well-known concept of holographic principle based on investigations of black hole thermodynamics [13, 14]. This asserts that a hologram corresponding to a theory on the volume’s border can be used to represent the whole information contained in a spatial volume. HP was used to solve the DE problem by proposing the concept of holographic dark energy (HDE) model [15]. According to HDE model, on the universe’s edge, the reduced Plank’s mass \(M_p\equiv \dfrac{1}{\sqrt{8\pi G}}\), where G denotes the universal gravitational constant of Newton and universe’s future event horizon L [15] are the physical quantities on which the dark energy density \(\rho _d\) depends . The DE model equipped with HP (HDE) supports the current cosmological observations [15,16,17,18,19,20,21] and extensively studied [22,23,24,25,26]. Also, observational data are in agreement with the concept of HDE [27,28,29,30,31].

Due to the long-range nature of gravity and the unpredictable structure of spacetime, many extended entropy formalisms have been employed to investigate gravitational and cosmic phenomena. In order to study gravitational and cosmic systems through the concepts of generalized statistical mechanics, the Tsallis’s entropy [32, 33] plays a central role. Kaniadakis, on the other hand, presented generalized Boltzmann–Gibbs entropy through single parameter, known as Kaniadakis entropy [34, 35] and studied by Niki and Sharma [36, 37] using the concepts of future event horizon and apparent horizon respectively. This is the consequence of a unified and self-consistent relativistic statistical theory that retains the core properties of normal statistical theory. The usual Maxwell–Boltzmann statistics is continuously deformed by a single parameter leading to the extended statistical theory, whose limiting case is the standard statistical theory. In this manuscript we will apply the Tsallis entropy concept to formulate new Tsallis holographic dark energy (NTHDE) by considering the future event horizon as an IR cut-off and investigate its cosmic implications. The study of NTHDE carried out by [38,39,40] is based on the consideration of Hubble horizon as an IR cut-off which could not recover the standard HDE model for which Tsallis entropy should become the standard entropy but it is not. Large parameter values could represent the universe’s evolution. Such a consideration results in more deviation from the standard entropy. This difference is due to the Hubble horizon acting as an IR cut-off. As a result, in this paper, we develop a consistent formulation of NTHDE to get a well-defined extension of conventional HDE, which is the limiting case when the Tsallis entropy becomes the conventional Bekenstein Hawking entropy.

In Sect. 2, by formulating the NTHDE expression, the differential equation for specific DE density parameter \(\Omega _d\), expressions for deceleration parameter and equation of state (EoS) parameter are obtained analytically. Section 3 is devoted to studying cosmological behaviour. In Sect. 4, a discussion on the obtained results is carried out with a concluding summary.

2 New Tsallis holographic dark energy

NTHDE formulation will be established here. The DE density \(\rho _d\), the entropy S of black hole with radius L and the largest theory’s distance L connected by the relation \(\rho _d L^4\le S\) is the key idea for HDE formulation [15, 16]. For usual Bekenstein–Hawking entropy \(S_{BH}\propto (4G)^{-1}A=\pi G^{-1}L^2\) with Newton’s gravitational constant G. The standard HDE \(\rho _d=3c^2M_p^2L^{-2}\) with model parameter c is the saturation of the above inequality. As a result, a modified HDE model is obtained by modifying the entropy.

If \(k_B=1\) and a distribution has W states with Gibbs and Shannon entropies, then the expression for each state is same and given by

$$\begin{aligned} S=-\sum _{i=1}^W P_i \,{\mathrm {ln}}(P_i). \end{aligned}$$
(1)

The Von-Neumann entropy or the quantum mechanical equivalent of (1) is

$$\begin{aligned} S=-{\mathrm {Tr}} [\rho \, {\mathrm {ln}}(\rho )]. \end{aligned}$$
(2)

For classical systems, (2) supports Boltzmann’s proposal in phase space with state density \(\rho \). The Bekenstein–Hawking entropy \(\left( \equiv S_{BH}=\dfrac{A}{4}\right) \) is obtained by applying (2) to a pure gravitational system where A is system’s area [41]. By assumption that the degrees of freedom are dispersed on the horizon where no particular priority for each other is specified [42, 43], all \(P_i\)’s are equal and \(P_i=\dfrac{1}{W}\). Both (1) and (2) implies the Boltzmann’s entropy (\(S={\mathrm {ln}}(W)\)) and hence we get the expression for horizon entropy [44]

$$\begin{aligned} S_{BH}=\dfrac{A}{4}={\mathrm {ln}}(W)\rightarrow W={\mathrm {e}}^{\left( \dfrac{A}{4}\right) }. \end{aligned}$$
(3)

The Tsallis entropy is defined by [45]

$$\begin{aligned} S_n^T=\dfrac{1}{1-n}\sum _{i=1}^W (P_i^n-P_i)=\dfrac{W^{1-n}-1}{1-n}, \end{aligned}$$
(4)

where \(P_i=\dfrac{1}{W}\), n is an unknown parameter (non-extensive) and as \(n\rightarrow 1, S_n^T\rightarrow S\). The parameter n may also have its roots in quantum features of gravity. Using (3), (4) and \(1-n=\delta \), we get

$$\begin{aligned}&S_n^T=\dfrac{1}{1-n}\left[ {\mathrm {e}}^{(1-n)S_{BH}}-1\right] , \nonumber \\&S_\delta ^T=\dfrac{2\,{\mathrm {e}}^{\left( \dfrac{\delta \,S_{BH}}{2}\right) }}{\delta } {\mathrm {sinh}} \left( \dfrac{\delta \,S_{BH}}{2} \right) . \end{aligned}$$
(5)

As \(\delta \rightarrow 0\) the standard Bekenstein–Hawking entropy is recovered. As expected the usual Bekenstein–Hawking entropy is obtained as a limiting case of Tsallis entropy and hence \(\delta \ll 1\) i.e. \(\delta \in (-1,1)\). The Eq. (5) in its expanded and truncated form is given by

$$\begin{aligned} S_\delta ^T=S_{BH}+\dfrac{\delta \, S_{BH}^2}{2}+\dfrac{\delta ^2 \, S_{BH}^3}{6}+{\mathcal {O}}(\delta ^3). \end{aligned}$$
(6)

Clearly, the first term of (6) is the standard entropy. Using (6) and \(\rho _d L^4\le S\), we get

$$\begin{aligned} \rho _d=\dfrac{3 c^2 M_p^2}{L^2}+\dfrac{3 c_1^2 \delta M_p^4}{2}+\dfrac{3 c_2^2 \delta ^2 M_p^6 L^2}{6}, \end{aligned}$$
(7)

where \(c,\,c_1,\, c_2\) are constants. For \(\delta =0,\) the Eq. (7) leads to standard HDE, i.e \(\rho _d= \dfrac{3 c^2 M_p^2}{L^2}\). By letting \(\dfrac{3 c_1^2 \delta }{2}=\delta _1\) and \(\dfrac{3 c_2^2 \delta ^2}{6}=\delta _2^2\), Eq. (7) can be rewritten by absorbing \(c_1\) and \(c_2\) in \(\delta \) as

$$\begin{aligned} \rho _d=\dfrac{3 c^2 M_p^2}{L^2}+ \delta M_p^4 + \delta ^2 M_p^6 L^2. \end{aligned}$$
(8)

By considering the geometry of Friedmann–Robertson–Walker (FRW) model to be homogeneous, isotropic and flat with metric described by

$$\begin{aligned} {\mathrm {d}}s^2=\delta _{ij} {\mathrm {d}}x^i {\mathrm {d}}x^ja^2(t) -{\mathrm {d}}t^2 , \end{aligned}$$
(9)

with a scaling factor a(t) that varies with cosmic time. To investigate an HDE model the largest distance L of the theory is needed. According to Li and Hsu [15, 46], \(L\ne H^{-1}\) is the need for an HDE model to be consistent and standard. The Hubble horizon is expressed as \(H^{-1}={\dot{a}}(t)^{-1} \, a(t)\). Future event horizon as offered by Li [15] is expressed as

$$\begin{aligned} r_h=a(t)\int _{t}^\infty \frac{{\mathrm {d}}y}{a(y)}=a(t)\int _{a(t)}^\infty \frac{{\mathrm {d}}a}{H\left[ a(y)\right] ^2} . \end{aligned}$$
(10)

In [38, 39], \(L=H^{-1}\) is considered as IR-cutoff and the parameter \(\delta \) is \({\mathcal {O}} \left( 10^3\right) \). Such a high value of \(\delta \) leads to high deviation from basic Bekenstein–Hawking entropy. We want to construct NTHDE consistently in this paper, thus we utilize the future event horizon \(r_h\) as L in (8) and get the NTHDE density as

$$\begin{aligned} \rho _d=\dfrac{3 c^2 M_p^2}{r_h^2}+ \delta M_p^4 + \delta ^2 M_p^6 r_h^2 . \end{aligned}$$
(11)

Friedmann’s equations for a universe made up of perfect fluids such as DE and dark matter are expressed by

$$\begin{aligned}&3 M_p^2 H^2=\rho _m+\rho _d , \end{aligned}$$
(12)
$$\begin{aligned}&-2 M_p^2 {\dot{H}}=P_m+P_d+\rho _m+\rho _d , \end{aligned}$$
(13)

where \(P_d\) represents NTHDE pressure, \(\rho _m\) represents dark matter energy density, and \(P_m\) represents dark matter pressure. The dark matter conservation equation is as follows:

$$\begin{aligned} {\dot{\rho }}_m+3 H (\rho _m + P_m)=0 . \end{aligned}$$
(14)

The fractional DE and dark matter density parameters are defined as

$$\begin{aligned} \Omega _d= & {} \frac{\rho _d}{3 M_p^2 H^2} , \end{aligned}$$
(15)
$$\begin{aligned} \Omega _m= & {} \frac{\rho _m}{3 M_p^2 H^2} \end{aligned}$$
(16)

respectively. Using the Eq. (11) in (15), we get a fourth degree equation in \(r_h\). By considering \(r_h\) to be positive and taking the limit \(\delta \rightarrow 0\) the standard HDE \(\int _{x}^\infty \frac{{\mathrm {d}}x}{Ha}=\dfrac{c}{H a \sqrt{\Omega _d}}\) is obtained. Hence such a value of \(r_h\) is considered and expressed by

$$\begin{aligned} r_h=\left( \dfrac{3 H^2 \Omega _d-\delta M_p^2-\sqrt{(3 H^2 \Omega _d-\delta M_p^2)^2-12 c^2 \delta ^2 M_p^4 } }{2 \delta ^2 M_p^4} \right) ^{\dfrac{1}{2}}.\nonumber \\ \end{aligned}$$
(17)

Using Eqs. (10) and (17), we get

$$\begin{aligned}&\int _{x}^\infty \frac{{\mathrm {d}}x}{Ha}\nonumber \\&\quad = \dfrac{1}{a}\left( \dfrac{3 H^2 \Omega _d-\delta M_p^2-\sqrt{(3 H^2 \Omega _d-\delta M_p^2)^2-12 c^2 \delta ^2 M_p^4 } }{2 \delta ^2 M_p^4} \right) ^{\dfrac{1}{2}}, \end{aligned}$$
(18)

where \(a={\mathrm {e}}^x\).

Now we consider the physically intriguing dust matter scenario for which the matter EoS parameter is zero. If we consider the present matter energy density to be \(\rho _{m_0}\) for current scale factor \(a_0=1\), Eq. (14) gives

$$\begin{aligned} \rho _m=\dfrac{\rho _{m_0}}{a^3}. \end{aligned}$$
(19)

Using Eq. (19) into (16) we get

$$\begin{aligned} \Omega _m=\dfrac{\Omega _{m_0} H_0^2}{H^2a^3}, \end{aligned}$$
(20)

where \(H_0\) is the present value of the Hubble parameter.

Using Eq. (20) and the Friedmann equation \(\Omega _d+\Omega _m=1\) we get

$$\begin{aligned} \dfrac{1}{Ha}=\dfrac{\sqrt{a (1-\Omega _d)}}{ H_0\sqrt{\Omega _{m_0}}}. \end{aligned}$$
(21)

Substituting Eq. (21) into (18) we get

$$\begin{aligned}&\int _{x}^\infty \dfrac{\sqrt{a (1-\Omega _d)}}{ H_0\sqrt{\Omega _{m_0}}} {\mathrm {d}}x\nonumber \\&\quad = \dfrac{1}{a}\left( \dfrac{3 H^2 \Omega _d-\delta M_p^2-\sqrt{(3 H^2 \Omega _d-\delta M_p^2)^2-12 c^2 \delta ^2 M_p^4 } }{2 \delta ^2 M_p^4} \right) ^{\dfrac{1}{2}}. \end{aligned}$$
(22)

Differentiating Eq. (22) with respect to ‘x’ we get

$$\begin{aligned} \Omega _d '&= \Omega _d (1-\Omega _d)\left[ 3-\dfrac{2\left( {\mathcal {I}}-2 \delta ^2 M_p^6 {\mathcal {J}} \right) }{{\mathcal {I}} +\delta M_p^4}\right. \nonumber \\&\quad \times \left. \left\{ 1-\sqrt{3} \left( \dfrac{M_p^2 \Omega _d}{\left( {\mathcal {I}}+\delta M_p^4 \right) {\mathcal {J}}} \right) ^{\dfrac{1}{2}}\right\} \right] , \end{aligned}$$
(23)

where

$$\begin{aligned} {\mathcal {I}}= & {} \dfrac{3\, {\mathrm {e}}^{-3x} H_0^2 M_p^2 \Omega _{m_0} \Omega _d }{1-\Omega _d}-\delta M_p^4,\\ {\mathcal {J}}= & {} \dfrac{{\mathcal {I}}-\sqrt{{\mathcal {I}}^2-12 c^2 \delta ^2 M_p^8}}{2 \, \delta ^2 M_p^6}. \end{aligned}$$

For flat spatial geometry and dust matter, the differential equation (23) describes the evolution of NTHDE. As a limit on considering \(\delta \rightarrow 0\) we get \({\mathcal {J}}=\dfrac{3 c^2 }{{\mathcal {I}}}\), which implies (23) to recover the differential equation of standard HDE [47], i.e. \(\Omega _d ' = \Omega _d (1-\Omega _d) \left( 1+\dfrac{2}{c}\sqrt{\Omega _d}\right) \) and can be solved analytically.

Now we will consider the EoS parameter for NTHDE defined by \(w_d=\dfrac{P_d}{\rho _d}\). As the matter sector is conserved. The Eq. (14) and the Friedmann equations (12), (13) implies the DE sector to be conserved, i.e.

$$\begin{aligned} {\dot{\rho }}_d+3 H \rho _d (1+w_d)=0. \end{aligned}$$
(24)

Differentiating (11) w.r.t. ‘t’ results

$$\begin{aligned} {\dot{\rho }}_d=-\dfrac{2\, M_p^2 \left( 3 c^2 -\delta ^2 M_p^4 r_h^4 \right) \dot{r_h}}{r_h^3} . \end{aligned}$$
(25)

From Eq. (10) we get

$$\begin{aligned} {\dot{r}}_h=H r_h-1. \end{aligned}$$
(26)

Using Eqs. (25) and (26) we get the expression for \(r_h\) in terms of \(\rho _d\) given by

$$\begin{aligned} r_h=\left[ \dfrac{\rho _d - \delta M_p^4 -\sqrt{\left( \rho _d-\delta M_p^4 \right) ^2-12 c^2 \delta ^2 M_p^8}}{2 \delta ^2 M_p^6} \right] ^{\dfrac{1}{2}}. \end{aligned}$$
(27)

Using Eqs. (15), (21) and (25) to (27), we get

$$\begin{aligned} w_d&= -1 -2 \left( \dfrac{M_p^6 \, \Omega _d}{3\left( {\mathcal {I}}+\delta M_p^4 \right) ^3}\right) ^{\dfrac{1}{2}} \left( \dfrac{\delta ^2 M_p^4 {\mathcal {J}}^2-3c^2}{{\mathcal {J}}^{\dfrac{3}{2}}} \right) \nonumber \\&\quad \times \left[ -1+\left( \dfrac{\left( {\mathcal {I}}+\delta M_p^4\right) {\mathcal {J}}}{3 M_p^2 \Omega _d} \right) ^{\dfrac{1}{2}} \right] . \end{aligned}$$
(28)

Clearly the standard HDE is recovered by letting \(\delta \rightarrow 0\) i.e. as \(\delta \rightarrow 0, \, w_d \rightarrow \dfrac{-1}{3}-\dfrac{2 \sqrt{\Omega _d}}{3 c}\). In general, we can highlight that \(w_d\) can behave either like quintessence or quintom which shows the richness of the current model.

The parameter describing deceleration behaviour can be expressed as

$$\begin{aligned} q&=-\dfrac{{\dot{H}}}{H^2}-1\nonumber \\&=\dfrac{3\,w_d \Omega _d+1}{2}. \end{aligned}$$
(29)

3 Cosmological evolution of NTHDE

In Sect. 2, we derived the differential equation describing the evolutionary behaviour of NTHDE density parameter, corresponding expressions for EoS and deceleration parameters. Now we will discuss the detailed cosmological behaviour for results obtained in the previous section. The numerical solution for the differential equation (23) reflects various evolutionary features of \(\Omega _d\) for redshift z by the transformation \(x={\mathrm {ln}} \left( \dfrac{1}{1+z} \right) \) with initial condition \(\Omega _d (x=0)=\Omega _d[0]\approx 0.7\). And hence by virtue of Friedmann equation \(\Omega _{m_0}\approx 0.3\).

Fig. 1
figure 1

NTHDE density parameter \(\Omega _d\) with \(\delta =0.2\) and \(c=0.8\) to 1.2 is plotted w.r.t. redshift z by considering \(\Omega _d[z=0] \approx 0.7, \, M_p^2=1 \)

Full size image
Fig. 2
figure 2

NTHDE density parameter \(\Omega _d\) with \(c=0.7\) and \(\delta =0.1\) to 0.5 is plotted w.r.t. redshift z by considering \(\Omega _d[z=0] \approx 0.7, \, M_p^2=1 \)

Full size image

The Figs. 1 and 2 shows the DE density parameter plots against the redshift z. In Fig. 1, we have considered \(\delta =0.2\) fixed with varying c values. Figure 2 is plotted by considering \(c=0.7\) fixed and varying \(\delta \). As we can see from both the graphs, the current model may give the universe’s needed thermal history, i.e. in the past matter dominated, current domination of \(70\%\) by DE and in future fully dominated by DE only.

Fig. 3
figure 3

The evolution of EoS parameter \(w_d\) of NTHDE with \(\delta =0.2\) and \(c=0.8\) to 1.2 is plotted w.r.t. redshift z by considering \(\Omega _d[z=0] \approx 0.7, \, M_p^2=1 \)

Full size image
Fig. 4
figure 4

The evolution of EoS parameter \(w_d\) of NTHDE with \(c=0.7\) and \(\delta =0.1\) to 0.5 is plotted w.r.t. redshift z by considering \(\Omega _d[z=0] \approx 0.7, \, M_p^2=1 \)

Full size image

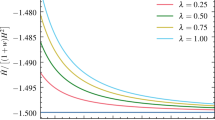
Figures 3 and 4 represent EoS parameters for the NTHDE model. Which shows that the current value of \(w_d\) resides in the vicinity of \(-1\), which is consistent with the observational data. Now we’ll look at how the model parameters \(\delta \) and c affect the DE’s EoS parameter \(w_d\). In Fig. 3 we have plotted \(w_d\) for \(\delta =0.2\) and different c values. As can be seen, for \(c<1\) values, \(w_d\) always enters the phantom regime in the far future. While \(c>1\) completely lies in the quintessence region. \(c=1\) corresponds to the \(\Lambda \)CDM model. In addition, we show \(w_d\) for constant \(c=0.7\) and different \(\delta \) values in Fig. 4. We have an intriguing pattern here with rising \(\delta \), \(w_d\) remains almost the same at times around the current ones. To get the far future value of \(w_d\), i.e. for \(z \rightarrow -1\) Eq. (28) indicates the combined dependence on \(\delta \) and c. In conclusion NTHDE leads to some fascinating cosmic phenomenology where \(w_d\) shows behaviours like quintessence, or like quintom.

Fig. 5
figure 5

The deceleration parameter q with \(\delta =0.2\) and \(c=0.8\) to 1.2 is plotted w.r.t. redshift z by considering \(\Omega _d[z=0] \approx 0.7, \, M_p^2=1 \)

Full size image
Fig. 6
figure 6

The deceleration parameter q with \(c=0.7\) and \(\delta =0.1\) to 0.5 is plotted w.r.t. redshift z by considering \(\Omega _d[z=0] \approx 0.7, \, M_p^2=1 \)

Full size image

Figures 5 and 6 describe the deceleration parameter q behaviour against z. Figure 5 is plotted by fixing \(\delta \) to be 0.2 and varying c values. While Fig. 6 is based on varying \(\delta \) and fixed \(c=0.7\). It confirms the universe to enter an accelerated phase for \(z\approx 0.6\). Which is in full agreement with the observational data supported by [1, 2]. The inner plot of Fig. 6 shows a close-up of the outer plot in which the difference can be seen. They are not exactly identical but difference is very small. Similar is the case with the Figs. 2 and 4.

Fig. 7
figure 7

The NTHDE density parameter \(\Omega _d\) and dark matter density parameter \(\Omega _m\) is depicted. The graph is plotted against the redshift z by considering \(\delta =0.2, \, c=0.9, \, \Omega _d[z=0] \approx 0.7, \, M_p^2=1 \). Where the present time corresponds to \(z=0\)

Full size image

4 Conclusive remarks

In the present work we formulated the HDE model in which Tsallis entropy, a one-parameter generalization of Boltzmann–Gibbs entropy, is used. Such a concept is derived from a consistent relativistic statistical theory. A parameter \(\delta \) is used to distinguish deviations from conventional entropy expressions. The consistent NTHDE model is obtained by applying IR cutoff in terms of future event horizon and the Tsallis entropy, to the standard HDE model. The parameter \(\delta \) is responsible for such an extension with usual HDE as a limiting case \(\delta \rightarrow 0\). We derived the differential equation to describe the evolutionary behaviour of dark energy density parameter \(\Omega _d\) which investigates possible cosmic applicability of NTHDE. On considering today’s universe to be dominated \(70\%\) by DE, Fig. 7, clearly indicates the full domination of the universe by DE in the far future. In addition, the analytical formulations of the deceleration parameter and the EoS parameter are obtained. As per the observation from NTHDE’s EoS parameter, the parameters c and \(\delta \) describe the diversified behaviour of the model i.e. pure quintessence for \(c>1\), quintom for \(c<1\) (in near or far future) and \(\Lambda \)CDM for \(c=1\). The trend shown by the deceleration parameter q for the model, possesses interesting cosmological descriptions such as the universe’s thermal history from dark matter to DE. The transition from decelerated to accelerated phase happens at \(z \approx 0.6\). Finally, because of consistent formulation and versatile behaviour, the NTHDE leads to standard HDE as a limiting case, which is the biggest advantage of the model.

Indeed, the use of such entropies is in the early stages [48]. The existence of long-range interactions in systems is a basic reason to use such entropies in describing the systems [45]. General relativity (GR) is not the final form of the gravitational theory. GR satisfies Bekenstein entropy, and thus, one may expect that other entropies should be satisfied by the final form of the gravitational theory. Such attempts can at least help us get some estimations about the final form of gravitational field equations. It seems that there is a connection between the quantum aspects of gravity and non-extensivity [49,50,51,52,53,54,55,56]. There are various works claiming that various problems are solved (at least, solved better) by considering such entropies which may be a clue to understand the thermodynamics of spacetime, gravity, and related phenomena [48, 57,58,59,60,61,62,63]. HDE is a great hypothesis to reconcile quantum field theory and gravity, a hope to solve the DE problem. Therefore, such papers may at least help us find a proper mathematical model for the density profile of DE, a result which is so vital to overcome the problems such as the nature and behavior of DE, DM, spacetime, and the final form of gravitational theory. Indeed, one may consider such entropies as well as the Loop Quantum Gravity entropy as the sub-classes of a general entropy [64].

As the origin and behavior of DE are not completely known, and moreover, due to the weakness of GR in describing DE, and also since HDE based Bekenstein entropy is not capable to describe DE, we think that it is too soon to confine ourselves to small values of \(\delta \). More observations and studies are still needed to get and apply this limitation.

In order for the NTHDE to be a successful alternative to describe the DE, the model parameters must be constrained. Such constraints can be obtained using the observational data from the Hubble parameter, CMB, BAO, and SNIa. The phase-space can be analyzed to understand the global dynamics of the DE.