Perturbative QCD analysis of neutral B-meson decays into $\sigma \sigma , \sigma f_0$ and $f_0 f_0$

Abstract

The decays of $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$, with $\sigma$ and $f_0$ denoting the light scalar mesons $f_0(500)$ and $f_0(980)$ in the two-quark picture, are studied in the perturbative QCD approach based on $k_T$ factorization. With the referenced value of the mixing angle $|\varphi | \sim 25^\circ$ for the $\sigma -f_0$ mixing in the quark-flavor basis, it is of great interest to obtain that: (a) these neutral B-meson decays into $\sigma \sigma , \sigma f_0$, and $f_0 f_0$ have large branching ratios in the order of $10^{-6}{-}10^{-4}$, which mean the possibly constructive interferences existed in the decays with different flavor states, and then are expected to be tested at the Large Hadron Collider beauty and/or Belle-II experiments in the (near) future; (b) the large direct CP violations could be easily found in the $B_d^0 \rightarrow \sigma \sigma , f_0 f_0$ and $B_{d,s}^0 \rightarrow \sigma f_0$ decays, which indicate the considerable interferences between the tree and the penguin decay amplitudes involved in these four modes, and would be confronted with the future measurements; (c) these neutral B-meson decays could be examined through the secondary decay chain $\sigma /f_0 \rightarrow \pi ^+ \pi ^-$, namely, the four-body decays of $B_{d,s}^0 \rightarrow (\pi ^+ \pi ^-)_{\sigma (f_0)} (\pi ^+ \pi ^-)_{\sigma (f_0)}$ with still large branching ratios. On the other side, it seems that other 4 four-body decays of $B_d^0 \rightarrow (\pi ^+ \pi ^-)_{\sigma } (K^+ K^-)_{f_0}$, $B_s^0 \rightarrow (\pi ^+ \pi ^-)_{\sigma (f_0)} (K^+ K^-)_{f_0}$, and $B_s^0 \rightarrow (K^+ K^-)_{f_0} (K^+ K^-)_{f_0}$ could also be detected at the relevant experiments, if the $f_0 \rightarrow K^+ K^-$ could be identified from the $\phi \rightarrow K^+ K^-$ clearly. The (near) future experimental confirmations with good precision would help to further study the perturbative and/or nonperturbative QCD dynamics involved in these considered decay modes, as well as to explore the intrinsic characters of these scalar mesons $\sigma$ and/or $f_0$ and to constrain both of the magnitude and the sign of $\varphi$.

1 Introduction

The light scalars have arisen a great of interest at both aspects of theory and experiment due to the fact that they have the same spin-parity quantum number, i.e., $J^{P}=0^{+}$, as that of the QCD vacuum. However, the inner structure of the light scalars is still in controversy theoretically, though the first observation of the light scalar $f_0(980)$¹ state was made by the Belle [1] and BABAR [2] Collaborations through the decay mode of $B \rightarrow f_0 K$. Nevertheless, one is still inspired to explore the light scalars in the decay products of the heavy B mesons naturally because of the much larger phase space, with comparison to those produced in the $D_{(s)}$ meson decays. Therefore, investigating on their production in B decays could be a unique insight to study their underlying structure indeed.

In the conventional quark model, namely, the two-quark picture, a meson is composed of one quark and one antiquark, i.e., $q\bar{q}$, with different coupling of the orbital and spin angular momenta [3,4,5]. Nowadays, the structure of the S-wave ground state mesons has almost been determined unambiguously, though the $\eta$ and $\eta ^\prime$ ones contain the possible component of gluonium (or pseudoscalar glueball) with different extent [6,7,8,9]. But, the components of the P-wave mesons can not be easily determined, especially of the light scalar states such as $a_0(980)$, $\kappa$ or $K_0^*(800)$, $\sigma$ or $f_0(500)$, and $f_0(980)$. Theoretically, many proposals such as $q \bar{q}$, $\bar{q}\bar{q} q q$, meson-meson bound states, etc. on classifying these light scalars are presented. It seems that the inner structure is still not well established (for a review, see e.g., Refs. [10,11,12]). Currently, two different scenarios, namely, Scenario-1 (S1) and Scenario-2 (S2), are proposed to classify the light scalars [13]. More specifically, the light $\sigma$ and $f_0$ are viewed as the $q\bar{q}$ mesons in S1, while as the four-quark states in S2. It is necessary to note that the latter structure is too complicated to be studied in the factorization approach and could not be quantitatively predicted. Therefore, we will work in S1 for the $\sigma$ and $f_0$ to give several quantitative predictions.

The scalar $\sigma$ and $f_0$ are believed to be made of the superposition of strange and non-strange quark contents, based on the measurements of $D_s^+ \rightarrow f_0 \pi ^+$, $\phi \rightarrow f_0 \gamma$, $J/\psi \rightarrow f_0 \omega$, $J/\psi \rightarrow f_0 \phi$, etc. [12]. For more detail, please see Refs. [10,11,12,13,14, 14,15,16,17], and references therein. Hence, analogous to the pseudoscalar $\eta -\eta '$ mixing in the two-quark picture, the physical $\sigma$ and $f_0$ states can also be described by a $2\times 2$ rotation matrix with a mixing angle $\varphi$ in the quark-flavor basis, namely,

$$\begin{aligned} \left( \begin{array}{c} \sigma \\ f_0 \\ \end{array} \right) = \left( \begin{array}{cc} \cos {\varphi } &{} -\sin {\varphi } \\ \sin {\varphi } &{} \;\;\;\cos {\varphi } \end{array} \right) \left( \begin{array}{c} f_n\\ f_s \\ \end{array} \right) . \end{aligned}$$

(1)

where $f_n \equiv \frac{u\bar{u} + d\bar{d}}{\sqrt{2}}$ and $f_s\equiv s\bar{s}$ are the quark-flavor states. It is necessary to mention that the possible scalar glueball components involved in the $\sigma /f_0$ mesons [6] are left for future investigations elsewhere. Currently, various measurements on the mixing angle $\varphi$ have been derived and summarized in the literature with a wide range of values, for example, see Refs. [13, 18,19,20]. However, an explicit upper limits on the magnitude of the mixing angle is set as $|\varphi |<31^\circ$ according to the recent Large Hadron Collider beauty (LHCb) measurements in the B meson decays into $\sigma$ and $f_0$, i.e., the $B_d^0 \rightarrow J/\psi \sigma$ and $B_s^0 \rightarrow J/\psi f_0$ decays, within two-quark structure description [21]. On the basis of these data, by also assuming the $\sigma$ and $f_0$ as $q\bar{q}$ mesons, a slightly small value of the mixing angle $|\varphi |< 29^\circ$ (90% CL) was proposed by Stone and Zhang [22]. In Ref. [23], one of our authors (X.L.) and his collaborators found that the mixing angle $\varphi$ could be further constrained around $25^\circ$ through clarifying the experimental data of the $B_d^0 \rightarrow J/\psi f_0(\rightarrow \pi ^+ \pi ^-)$ and $B_s^0 \rightarrow J/\psi \sigma /f_0(\rightarrow \pi ^+ \pi ^-)$ channels in the two-quark structure for these two light scalars, except for the challenging $B_d^0 \rightarrow J/\psi \sigma (\rightarrow \pi ^+ \pi ^-)$. Of course, it is unfortunate that the $B_{d,s}^0 \rightarrow J/\psi \sigma /f_0$ decays could only provide the information about the magnitude of $\varphi$ but with a two-fold ambiguity on the sign. Therefore, as stated in [23], this ambiguity is expected to be resolved through the studies of other $B \rightarrow M \sigma (f_0)$ decays with M denoting the open-charmed or light hadrons, once the related measurements are available with high precision.

Presently, several $B \rightarrow \sigma /f_0 (P,V)$ (here, P and V denote the pseudoscalar and vector meson, respectively) decays have been measured experimentally [12, 24]. And the related investigations, for instance, see [25,26,27,28,29,30,31,32,33,34,35], are also performed with different approaches/methods theoretically. With the great development of LHCb and Belle-II experiments [36], more and more modes involving one and/or two scalar states in the B meson decays are expected to be measured with good precision in the near future. Therefore, we will systematically study the neutral B-meson decays into $\sigma \sigma , \sigma f_0$, and $f_0 f_0$, i.e., the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays, by employing the perturbative QCD (PQCD) approach [37,38,39] based on the $k_T$ factorization theorem. In Ref. [40], Liang and Yu have analyzed the CP-averaged branching ratios and CP-violating parameters of the $B_s^0 \rightarrow \sigma \sigma$ and $B_s^0 \rightarrow f_0 f_0$ channels in the PQCD approach. However, it is noted that the branching ratio of the $B_s^0 \rightarrow \sigma \sigma$ mode is similar to that of the $B_s^0 \rightarrow a_0(980)^0 a_0(980)^0$ one, which seems a bit strange to us that the interferences from the $B_s^0 \rightarrow f_n f_s$ and $f_s f_s$ decay amplitudes did not contribute evidently. In this work, we will take the possibly considerable interferences arising from the mixed $f_s$ state with the referenced value of the mixing angle $\varphi \sim 25^\circ$ [23], namely, the contributions from the $B_s^0 \rightarrow f_n f_s$ and $B_s^0 \rightarrow f_s f_s$ decay amplitudes, into account to make reliable predictions in the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ channels.

The paper is organized as follows. In Sect. 2, we present the formalism of the PQCD approach and the related calculations of the considered $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays in a simplified form. Then the numerical calculations and phenomenological discussions on the related results will be made explicitly in Sect. 3. The main conclusions and a short summary will be finally given in Sect. 4.

2 Perturbative calculations

It is well known that the decay amplitude of non-leptonic B meson decays is determined by the effective and reliable evaluation on the hadronic matrix element. At the current time, the community provide some standard factorization approaches/methods, in which the QCD factorization approach [41,42,43,44], the PQCD approach, and the soft-collinear effective theory [45] are the three more popular tools based on QCD dynamics presently. Frankly speaking, due to the existence of the end-point singularities, the QCD factorization approach and the soft-collinear effective theory have to parameterize several Feynman amplitudes in the non-factorizable emission and annihilation diagrams, which finally result in large uncertainties theoretically. While the PQCD approach, by keeping the transverse momentum ($k_T$) of the valence quark, successfully conquers the end-point singularities that exist in the collinear factorization theorem. Based on the $k_T$ factorization theorem and armed with the $k_T$ [46, 47] (threshold [48, 49]) resummation techniques, the resultant Sudakov factor S (the jet function J) could help us to kill the end-point singularities (smear the double logarithmic divergences). Then the PQCD approach can be well applied to calculate the hadronic matrix element of the non-leptonic B meson decays. The decay amplitude could be factorized into the convolution of the hard kernel associated with the wave functions of the initial (B) and final ($M_1$ and $M_2$) mesons as follows:

$$\begin{aligned} {\mathcal {A}} \sim \Phi _B \otimes H \otimes S \otimes J \otimes \Phi _{M_1} \otimes \Phi _{M_2}, \end{aligned}$$

(2)

where the hard kernel H can be calculated perturbatively in the PQCD approach, while the wave functions $\Phi$, containing the light-cone distribution amplitudes, are universal for all modes, although non-perturbative in nature. With the PQCD approach, the non-factorizable emission diagrams and the annihilation ones can also be perturbatively calculated, besides the factorizable emission diagrams. And what’s more, the annihilation diagrams perturbatively evaluated in the PQCD approach can provide a large strong phase that could well explain the CP-violating asymmetries in the B meson decays [50], for example, in the $B \rightarrow K \pi$ ones [37, 51], which have been confirmed in relevant measurements [12, 24] at BABAR, Belle, and LHCb experiments. More detail and the recent developments of the PQCD approach could be found in the literature, for example, see Refs. [52,53,54,55,56,57,58].

At the quark level, the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays are induced by the $\bar{b} \rightarrow \bar{d}$ or $\bar{b} \rightarrow \bar{s}$ transitions, respectively. The weak effective Hamiltonian $H_\mathrm{eff}$ for these decays can be written as [59],

$$\begin{aligned} H_\mathrm{eff}= & {} {G_F\over \sqrt{2}}\Bigg \{V_{ub}^*V_{uq} \left[ C_1(\mu )O_1^{u}(\mu ) +C_2(\mu )O_2^{u}(\mu )\right] \nonumber \\&- V_{tb}^*V_{tq} \sum _{i=3}^{10}C_i(\mu )O_i(\mu )\Bigg \}, \end{aligned}$$

(3)

with the Fermi constant $G_F=1.16639\times 10^{-5}~\mathrm{GeV}^{-2}$, the light $q = d, s$ quark, and Wilson coefficients $C_i(\mu )$ at the renormalization scale $\mu$. The local four-quark operators $O_i(i=1,\ldots ,10)$ are written as

• Tree operators

  $$\begin{aligned} O_1^{u}= & {} (\bar{q}_\alpha u_\beta )_{V-A}(\bar{u}_\beta b_\alpha )_{V-A},\nonumber \\ O_2^{u}= & {} (\bar{q}_\alpha u_\alpha )_{V-A}(\bar{u}_\beta b_\beta )_{V-A}; \end{aligned}$$

  (4)

• QCD penguin operators

  $$\begin{aligned} O_3= & {} (\bar{q}_\alpha b_\alpha )_{V-A}\sum _{q'}(\bar{q}'_\beta q'_\beta )_{V-A},\nonumber \\ O_4= & {} (\bar{q}_\alpha b_\beta )_{V-A}\sum _{q'}(\bar{q}'_\beta q'_\alpha )_{V-A},\nonumber \\ O_5= & {} (\bar{q}_\alpha b_\alpha )_{V-A}\sum _{q'}(\bar{q}'_\beta q'_\beta )_{V+A},\nonumber \\ O_6= & {} (\bar{q}_\alpha b_\beta )_{V-A}\sum _{q'}(\bar{q}'_\beta q'_\alpha )_{V+A}; \end{aligned}$$

  (5)

• Electroweak penguin operators

  $$\begin{aligned} O_7= & {} \frac{3}{2}(\bar{q}_\alpha b_\alpha )_{V-A}\sum _{q'}e_{q'}(\bar{q}'_\beta q'_\beta )_{V+A},\nonumber \\ O_8= & {} \frac{3}{2}(\bar{q}_\alpha b_\beta )_{V-A}\sum _{q'}e_{q'}(\bar{q}'_\beta q'_\alpha )_{V+A},\nonumber \\ O_9= & {} \frac{3}{2}(\bar{q}_\alpha b_\alpha )_{V-A}\sum _{q'}e_{q'}(\bar{q}'_\beta q'_\beta )_{V-A},\nonumber \\ O_{10}= & {} \frac{3}{2}(\bar{q}_\alpha b_\beta )_{V-A}\sum _{q'}e_{q'}(\bar{q}'_\beta q'_\alpha )_{V-A}, \end{aligned}$$

  (6)

with the color indices $\alpha , \ \beta$ and the notations $(\bar{q}'q')_{V\pm A} = \bar{q}' \gamma _\mu (1\pm \gamma _5)q'$. The index $q'$ in the summation of the above operators runs through the active quarks $u,\;d,\;s$, c, and b. It is worth mentioning that since we work in the framework of the PQCD approach at leading order [${\mathcal {O}}(\alpha _s)$], it is natural to use the Wilson coefficients at leading order correspondingly. For the renormalization group evolution of the Wilson coefficients from higher scale to lower scale, the formulas as given in Refs. [37, 38] will be adopted directly.

Fig. 1

Leading order Feynman diagrams for the neutral B-meson decays into $\sigma \sigma , \sigma f_0$, and $f_0 f_0$ within the framework of PQCD

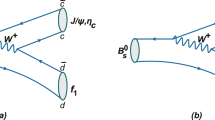
In Fig. 1, it is clear to see the Feynman diagrams for the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays in the leading order PQCD framework and to observe that these diagrams could be classified into two kinds of topologies, namely, the emission ones with Fig. 1a, b being the factorizable-emission(fe) diagrams and Fig. 1c, d being the non-factorizable-emission(nfe) diagrams, and the annihilation ones with Fig. 1e, f being the non-factorizable-annihilation (nfa) diagrams and Fig. 1g, h being the factorizable-annihilation (fa) diagrams, respectively. Several two-body non-leptonic $B \rightarrow SS$ (S stands for the scalar meson) decays have been studied in the PQCD approach by different groups [40, 60,61,62,63,64], and the analytic expressions for the factorization formulas and the decay amplitudes have been presented explicitly in the literature. One just need to identify the scalar meson as the specific $\sigma$ and/or $f_0$ one to obtain easily the corresponding information of the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays considered in this work. Thus, for the sake of simplicity, we do not present the aforementioned formulas in this paper. The interested readers can refer, for example, to Ref. [60] for detail.

By including the essential contributions arising from the operators as presented in the Eqs. (4)–(6), then the decay amplitudes of the considered $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays could be written straightforwardly as follows:

• 1. For $B_d^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays.

  For the sake of convenience, we take the $B_d^0 \rightarrow \sigma f_0$ decay as an example to explain the procedure obtaining the decay amplitudes analytically. The decay amplitudes for the $B_d^0$ meson decaying into the quark-flavor states $f_n f_n$, $f_n f_s$, and $f_s f_s$ can be easily written as follows:

  $$\begin{aligned}&2 A(B_d^0 \rightarrow f_n f_n) = V_{ub}^* V_{ud} \biggl \{ a_2 f_{B_d^0} F_{fa} \nonumber \\&\quad + C_2 (M_{nfe} + M_{nfa} ) \biggr \} - V_{tb}^* V_{td} \biggl \{ \left( a_6 -\frac{1}{2} a_8 \right) \bar{f}_{f_n} F^{P_2}_{fe} \nonumber \\&\quad + \biggl [2 a_3+a_4+ 2a_5 +\frac{1}{2}(a_7 + a_{9}- a_{10})\biggr ] f_{B_d^0} F_{fa} \nonumber \\&\quad + \left( a_6 - \frac{1}{2} a_8\right) f_{B_d^0} F_{fa}^{P_2} \nonumber \\&\quad +\biggl [C_3 + 2 C_4 - \frac{1}{2} (C_9 -C_{10})\biggr ] (M_{nfe} \nonumber \\&\quad + M_{nfa}) +\left( C_5 -\frac{1}{2} C_7\right) (M_{nfe}^{P_1} + M_{nfa}^{P_1}) \nonumber \\&\quad +\left( 2 C_6 + \frac{1}{2} C_8\right) (M_{nfe}^{P_2} + M_{nfa}^{P_2} )\biggr \}, \end{aligned}$$

  (7)
  $$\begin{aligned}&\sqrt{2} A(B_d^0 \rightarrow f_n f_s)= -V_{tb}^* V_{td} \biggl \{ \left( C_4 -\frac{1}{2} C_{10}\right) {M}_{nfe} \nonumber \\&\qquad +\left( C_6 - \frac{1}{2} C_8\right) {M}_{nfe}^{P_2} \biggr \}, \end{aligned}$$

  (8)
  $$\begin{aligned}&A(B_d^0 \rightarrow f_s f_s)= -V_{tb}^* V_{td} \biggl \{ \biggl [a_3+a_5- \frac{1}{2} (a_7 + a_9)\biggr ] \nonumber \\&\quad \times f_{B_d^0} F_{fa} +\left( C_4 -\frac{1}{2} C_{10}\right) M_{nfa} +\left( C_6 - \frac{1}{2} C_8\right) M_{nfa}^{P_2} \biggr \}. \end{aligned}$$

  (9)

  with $f_{B_d^0}$ and $\bar{f}_{f_n}$ being the decay constant of initial $B_{d}^0$ meson and the scalar decay constant of the final flavor state $f_n$. Notice that the vector decay constants $f_{f_n}$ and $f_{f_s}$ are naturally zero due to the neutral scalar mesons with the charge conjugation invariance not being produced by the vector current, which consequently result in the exact zero factorizable emission contribution $F_{fe}$ in the above decay amplitudes. It needs to point out that these three equations denote the contributions with $B_d^0 \rightarrow \sigma (f_n)$ transition and here the coefficients, namely, 2, $\sqrt{2}$, and 1, in front of the amplitudes $A(B_d^0 \rightarrow f_n f_n)$, $A(B_d^0 \rightarrow f_n f_s)$, and $A(B_d^0 \rightarrow f_s f_s)$ as correspondingly presented in the Eqs. (7)–(9) are from the flavor wave function of $f_n$ and $f_s$. When the $\sigma (f_n)$ and $f_0(f_n)$ states exchange their positions, then these three equations could give the contributions with $B_d^0 \rightarrow f_0(f_n)$ transition in a same form. All the contributions with both of the $B_d^0 \rightarrow \sigma (f_n)$ and the $B_d^0 \rightarrow f_0(f_n)$ transitions will lead to the decay amplitude with physical state, i.e., ${\mathcal {A}}(B_d^0 \rightarrow \sigma f_0)$. In the above formulas, i.e., Eqs. (7)–(9), the “F” and “M” stand for the amplitudes coming from the factorizable and non-factorizable diagrams associated with the $(V-A)(V-A)$ operators, the $F^{P_1}$ and $M^{P_1}$ stand for the amplitudes coming from the factorizable and non-factorizable diagrams associated with the $(V-A)(V+A)$ operators, and the $F^{P_2}$ and $M^{P_2}$ stand for the amplitudes coming from the factorizable and non-factorizable diagrams associated with the $(S-P)(S+P)$ operators that through Fierz transformation of the $(V-A)(V+A)$ ones, respectively. And the $a_i$ is the standard combination of the Wilson coefficients $C_i$ defined as follows [65]:

  $$\begin{aligned} a_1= & {} C_2 + \frac{C_1}{3},\quad a_2 = C_1 + \frac{C_2}{3}; \end{aligned}$$

  (10)
  $$\begin{aligned} a_i= & {} \left\{ \begin{array}{ll} C_i + C_{i+1}/3 &{}\quad (i=3,5,7,9), \\ C_i + C_{i-1}/3 &{}\quad (i=4,6,8,10), \end{array} \right. \end{aligned}$$

  (11)

  where $C_2 \sim 1$ is the largest one among all the Wilson coefficients.

  By taking the mixing of $\sigma$ and $f_0$ in the quark-flavor basis into account, the decay amplitude for the physical state of $B_d^0 \rightarrow \sigma f_0$ is then

  $$\begin{aligned}&{\mathcal {A}}(B_d^0 \rightarrow \sigma f_0)=\biggl [A(B_d^0 \rightarrow f_n f_n)-A(B_d^0 \rightarrow f_s f_s)\biggr ]\sin (2\varphi ) \nonumber \\&\qquad +\,A(B_d^0 \rightarrow f_n f_s)\cos (2\varphi ), \end{aligned}$$

  (12)

  Similarly, the $B_d^0 \rightarrow \sigma \sigma$ and $B_d^0 \rightarrow f_0 f_0$ decay amplitudes could be written straightforwardly as,

  $$\begin{aligned}&\sqrt{2} {\mathcal {A}}(B_d^0 \rightarrow \sigma \sigma )= 2 A(B_d^0 \rightarrow f_n f_n)\cos ^2\varphi \nonumber \\&\quad +2 A(B_d^0 \rightarrow f_s f_s)\sin ^2\varphi -A(B_d^0 \rightarrow f_n f_s)\sin (2\varphi ), \end{aligned}$$

  (13)
  $$\begin{aligned}&\sqrt{2} {\mathcal {A}}(B_d^0 \rightarrow f_0 f_0) = 2 A(B_d^0 \rightarrow f_n f_n)\sin ^2\varphi \nonumber \\&\quad +\,2 A(B_d^0 \rightarrow f_s f_s)\cos ^2\varphi +A(B_d^0 \rightarrow f_n f_s)\sin (2\varphi ). \nonumber \\ \end{aligned}$$

  (14)

  It is clear to see that these expressions of the decay amplitudes for the considered modes are consistent with those for the neutral B-meson decays into the $\eta \eta '$, $\eta \eta$, and $\eta ' \eta '$ in the pseudoscalar sector. For example, please see Ref. [66] for detail.

• 2. For $B_s^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays.

  Analogously, the decay amplitudes of $B_s^0 \rightarrow f_n f_n$, $f_n f_s$, and $f_s f_s$ can be written as,

  $$\begin{aligned}&2 A(B_s^0 \rightarrow f_n f_n)= V_{ub}^*V_{us}\biggl \{ a_2 f_{B_s^0} F_{fa} + C_2 M_{nfa} \biggr \}\nonumber \\&\qquad - V_{tb}^*V_{ts} \biggl \{\left( 2C_4 + \frac{1}{2} C_{10}\right) M_{nfa} \nonumber \\&\qquad + \biggl [2(a_3+a_5)+\frac{1}{2}(a_7+a_9)\biggr ] f_{B_s^0} F_{fa}\nonumber \\&\qquad +\left( 2C_6 + \frac{1}{2} C_{8}\right) M_{nfa}^{P_2} \biggr \}, \end{aligned}$$

  (15)
  $$\begin{aligned}&\sqrt{2} A(B_s^0 \rightarrow f_n f_s)=V_{ub}^*V_{us} \biggl \{ C_2 M_{nfe} \biggr \} - V_{tb}^*V_{ts} \nonumber \\&\quad \times \biggl \{ \left( 2C_4 + \frac{1}{2} C_{10}\right) M_{nfe} + \left( 2C_6 + \frac{1}{2} C_8\right) M_{nfe}^{P_2}\biggr \}, \end{aligned}$$

  (16)
  $$\begin{aligned}&A(B_s^0 \rightarrow f_s f_s)= -V_{tb}^*V_{ts}\biggl \{ \left( a_6 -\frac{1}{2} a_8 \right) \bar{f}_{f_s} F^{P_2}_{fe} \nonumber \\&\quad +\left( C_6 - \frac{1}{2} C_8\right) (M_{nfe}^{P_2} +M_{nfa}^{P_2} ) \nonumber \\&\quad +\biggl [a_3+a_4+a_5-\frac{1}{2}(a_7+a_9+a_{10}) \biggr ] f_{B_s^0} F_{fa} \nonumber \\&\quad +\left( a_6-\frac{1}{2}a_8\right) f_{B_s^0} F_{fa}^{P_2} \nonumber \\&\quad +\biggl [C_3 +C_4-\frac{1}{2}(C_9+C_{10})\biggr ] \nonumber \\&\quad \times ( M_{nfe} +M_{nfa} ) +\left( C_5 - \frac{1}{2} C_7\right) (M_{nfe}^{P_1} +M_{nfa}^{P_1} ) \biggr \}, \end{aligned}$$

  (17)

  with $f_{B_s^0}$ and $\bar{f}_{f_s}$ being the decay constant of the initial $B_s^0$ meson and the scalar decay constant of the final flavor state $f_s$. Then, we could give the decay amplitudes for the physical states similarly,

  $$\begin{aligned}&{\mathcal {A}}(B_s^0 \rightarrow \sigma f_0) \nonumber \\&\quad =\biggl [A(B_s^0 \rightarrow f_n f_n) - A(B_s^0 \rightarrow f_s f_s)\biggr ] \nonumber \\&\qquad \times \sin (2\varphi )+ A(B_s^0 \rightarrow f_n f_s) \cos (2\varphi ), \end{aligned}$$

  (18)
  $$\begin{aligned}&\sqrt{2} {\mathcal {A}}(B_s^0 \rightarrow \sigma \sigma ) \nonumber \\&\quad = 2 A(B_s^0 \rightarrow f_n f_n)\cos ^2\varphi -A(B_s^0 \rightarrow f_n f_s) \sin (2\varphi ) \nonumber \\&\qquad +2 A(B_s^0 \rightarrow f_s f_s) \sin ^2\varphi , \end{aligned}$$

  (19)
  $$\begin{aligned}&\sqrt{2} {\mathcal {A}}(B_s^0 \rightarrow f_0 f_0) \nonumber \\&\quad = 2 A(B_s^0 \rightarrow f_n f_n)\sin ^2\varphi +A(B_s^0 \rightarrow f_n f_s) \sin (2\varphi ) \nonumber \\&\qquad +2 A(B_s^0 \rightarrow f_s f_s) \cos ^2\varphi . \end{aligned}$$

  (20)

It is easy to see from the above six decay amplitudes as shown in Eqs. (12)–(14) and (18)–(20) that these decay channels could not only constrain the magnitude but also identify the sign for the $\sigma$ and $f_0$ mixing angle $\varphi$ by the help of the future measurements with good precision, due to the possibly significant interferences among the $B_{d,s}^0 \rightarrow f_n f_n$, $B_{d,s}^0 \rightarrow f_n f_s$, and $B_{d,s}^0 \rightarrow f_s f_s$ decay amplitudes.

3 Numerical results and discussions

Now, we come to the numerical calculations of the CP-averaged branching ratios and the CP-violating asymmetries of the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays in the PQCD approach. Several comments on the nonperturbative inputs are presented essentially as follows:

• (1) For the neutral B mesons, the wave functions (and the distribution amplitudes) and the decay constants are same as those extensively utilized, for example, in Refs. [37, 38, 60, 66], but with the updated lifetimes $\tau _{B_d^0} = 1.52$ ps and $\tau _{B_s^0} = 1.509$ ps [12]. The masses of $B_d^0$ and $B_s^0$ mesons are $m_{B_d^0} = 5.28$ GeV and $m_{B_s^0} = 5.37$ GeV [12], respectively. The recent developments on the B-meson distribution amplitude could be found in the literature, e.g., [67,68,69,70,71,72]. The effects induced by these mentioned distribution amplitudes could be left for the (near) future investigations with definitely precise data.

• (2) For the light scalar flavor states, namely, $f_n$ and $f_s$, the decay constants and the Gegenbauer moments in the distribution amplitudes have been derived in the QCD sum rule method [25] and their values at the renormalization scale $\mu =1$ GeV are adopted same as those in Ref. [23], specifically, the scalar decay constants $\bar{f}_{f_n} \simeq 0.35$ GeV and $\bar{f}_{f_s} \simeq 0.33$ GeV, and the Gegenbauer moments $B_1^n = -0.92 \pm 0.08$, $B_3^n = -1.00 \pm 0.05$, and $B_{1,3}^s \simeq 0.8 B_{1,3}^n$ [25]. Moreover, the masses for the physical states $\sigma$ and $f_0$ and the flavor states $f_n$ and $f_s$ are same as those utilized in Ref. [23], i.e., $m_\sigma = 0.5$ GeV, $m_{f_0} = 0.98$ GeV, $m_{f_n} = 0.99$ GeV, and $m_{f_s} = 1.02$ GeV, respectively.²

• (3) For the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, we also adopt the Wolfenstein parametrization at leading order, i.e., up to $\mathcal{O}(\lambda ^4)$,

  $$\begin{aligned} V_{\text{ CKM }}= & {} \left( \begin{array}{ccc} 1-\frac{1}{2}\lambda ^2 \qquad &{} \lambda \qquad &{} A\lambda ^3(\rho -i\eta ) \\ -\lambda \qquad &{} 1-\frac{1}{2}\lambda ^2 \qquad &{} A\lambda ^2\\ A\lambda ^3(1-\rho -i\eta ) \qquad &{} -A\lambda ^2 \qquad &{} 1 \end{array}\right) +{\mathcal {O}}(\lambda ^4), \nonumber \\ \end{aligned}$$

  (21)

  but with the updated parameters $A=0.836$, $\lambda =0.22453$, $\bar{\rho }= 0.122^{+0.018}_{-0.017}$, and $\bar{\eta }= 0.355^{+0.012}_{-0.011}$ [12], in which $\bar{\rho }\equiv \rho ( 1- \frac{\lambda ^2}{2})$ and $\bar{\eta }\equiv \eta (1- \frac{\lambda ^2}{2})$.

3.1 CP-averaged branching ratios

Now, we present the numerical results of the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays in the PQCD approach at leading order. Firstly, the PQCD predictions of the CP-averaged branching ratios at the referenced value of the mixing angle $\varphi \sim 25^\circ$ can be read as follows:

$$\begin{aligned}&{\mathcal {B}}(B_d^0 \rightarrow \sigma \sigma )= 4.15^{+0.77}_{-0.63}(\omega _B) ^{+1.13}_{-0.95}(B^n_i) ^{+0.05}_{-0.04}\nonumber \\&\quad \times (B^s_i) ^{+0.36}_{-0.37}(\varphi ) ^{+0.19}_{-0.13}(a_t) ^{+0.21}_{-0.18}(V) \times 10^{-5}, \end{aligned}$$

(22)

$$\begin{aligned}&{\mathcal {B}}(B_d^0 \rightarrow \sigma f_0)= 2.66^{+0.62}_{-0.50}(\omega _B) ^{+0.61}_{-0.52}\nonumber \\&\quad \times (B^n_i) ^{+0.11}_{-0.10}(B^s_i) ^{+0.24}_{-0.26}(\varphi ) ^{+0.22}_{-0.16}(a_t) ^{+0.11}_{-0.09}(V) \times 10^{-5}, \qquad \end{aligned}$$

(23)

$$\begin{aligned}&{\mathcal {B}}(B_d^0 \rightarrow f_0 f_0)= 3.36^{+0.54}_{-0.46}(\omega _B) ^{+0.77}_{-0.67}(B^n_i) ^{+0.09}_{-0.09}\nonumber \\&\quad \times (B^s_i) ^{+1.26}_{-1.00}(\varphi ) ^{+0.36}_{-0.25}(a_t) ^{+0.09}_{-0.08}(V) \times 10^{-6}, \qquad \end{aligned}$$

(24)

and

$$\begin{aligned}&{\mathcal {B}}(B_s^0 \rightarrow \sigma \sigma )= 1.88^{+0.36}_{-0.29}(\omega _B) ^{+0.33}_{-0.27}\nonumber \\&\quad \times (B^n_i) ^{+0.10}_{-0.09}(B^s_i) ^{+0.16}_{-0.16}(\varphi ) ^{+0.29}_{-0.23}(a_t) ^{+0.01}_{-0.01}(V) \times 10^{-4}, \end{aligned}$$

(25)

$$\begin{aligned}&{\mathcal {B}}(B_s^0 \rightarrow \sigma f_0)= 1.22^{+0.00}_{-0.00}(\omega _B) ^{+0.06}_{-0.05}\nonumber \\&\quad \times (B^n_i) ^{+0.13}_{-0.12}(B^s_i) ^{+0.04}_{-0.01}(\varphi ) ^{+0.37}_{-0.27}(a_t) ^{+0.00}_{-0.00}(V) \times 10^{-4}, \end{aligned}$$

(26)

$$\begin{aligned}&{\mathcal {B}}(B_s^0 \rightarrow f_0 f_0)= 5.31^{+1.16}_{-0.87}(\omega _B) ^{+0.29}_{-0.28}\nonumber \\&\quad \times (B^n_i) ^{+0.62}_{-0.58}(B^s_i) ^{+0.17}_{-0.19}(\varphi ) ^{+1.09}_{-0.85}(a_t) ^{+0.01}_{-0.01}(V) \times 10^{-4}. \nonumber \\ \end{aligned}$$

(27)

It is clearly seen that the CP-averaged branching ratios of the considered $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays vary from $10^{-6}$ to $10^{-4}$ in the PQCD approach at leading order. Generally speaking, the largest uncertainties of these theoretical predictions arise from the Gegenbauer moments $B_i^n$ and $B_i^s(i=1,3)$, which are lack of effective constraints at both of the experimental and the theoretical aspects currently, in the distribution amplitudes of the final states $f_n$ and $f_s$, as well as from the shape parameter $\omega _B$ in those of the initial neutral B-mesons.³ To estimate the possible contributions at higher order, a factor $a_t =1.0 \pm 0.2$ for the hard scale $t_\mathrm{max}$, namely, from 0.8t to 1.2t, is introduced to the numerical calculations, and the resultant results could be considered as one of the sources of theoretical errors. The sensitivity of the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decay rates to the mixing angle $\varphi$ between the flavor states $f_n$ and $f_s$ is also presented. The variation of $\varphi$ is taken as 10% of the central value, namely, $\varphi =25^\circ \pm 2.5^\circ$, which lead to the relatively smaller theoretical uncertainties in general, except for that in the $B_d^0 \rightarrow f_0 f_0$ mode. Moreover, it is clear to see that the branching ratios of the $B_d^0$ channels are more sensitive than those of the $B_s^0$ ones to the variations of the CKM parameters $V(\bar{\rho }, \bar{\eta })$, which is mainly because both of $|V_{ub}^*V_{ud}|$ and $|V_{tb}^*V_{td}|$ are in the same order, namely, $10^{-3}$, while $|V_{ub}^*V_{us}|$ is less than $|V_{tb}^*V_{ts}|$ with a factor near 50. It is noted that two of the considered decays in this work, i.e., $B_s^0 \rightarrow \sigma \sigma$ and $B_s^0 \rightarrow f_0 f_0$, have ever been investigated in Ref. [40]. However, we find that the predicted values about their branching ratios are a bit smaller than ours in this work, especially for the $B_s^0 \rightarrow \sigma \sigma$ mode with a highly small decay rate, namely, $4.35^{+1.75}_{-1.50} \times 10^{-6}$. Certainly, it is worth mentioning that the Gegenbauer moments $B_1$ and $B_3$ of the flavor states $f_n$ and $f_s$ used in Ref. [40] are different to those adopted in this work, and the scalar decay constants $\bar{f}_{f_n}$ and $\bar{f}_{f_s}$ are slightly larger than those taken in our evaluations. We expect the future measurements at LHCb and/or Belle-II could test these predictions given by different groups.

In light of these large theoretical errors induced by the hadronic parameters, for the convenience of future experimental measurements with good precision, several interesting ratios are defined by employing the above branching ratios in the PQCD approach presented in the Eqs. (22)–(24) and (25)–(27). In principle, the uncertainties could be cancelled in the ratios to a great extent, although the aforementioned hadronic inputs cannot be isolated from the decay amplitudes. The relevant ratios can be read as follows:

$$\begin{aligned}&R_{d\sigma }^{\sigma /f_0}\equiv \frac{\mathcal{B}(B_d^0 \rightarrow \sigma \sigma )}{\mathcal{B}(B_d^0 \rightarrow \sigma f_0)}= 1.56^{+0.07}_{-0.06}(\omega _B) ^{+0.06}_{-0.07}(B^n_i) ^{+0.05}_{-0.04}\nonumber \\&\quad \times (B^s_i) ^{+0.02}_{-0.00}(\varphi ) ^{+0.05}_{-0.05}(a_t) ^{+0.01}_{-0.02}(V), \end{aligned}$$

(28)

$$\begin{aligned}&R_{df_0}^{\sigma /f_0}\equiv \frac{\mathcal{B}(B_d^0 \rightarrow \sigma f_0)}{\mathcal{B}(B_d^0 \rightarrow f_0 f_0)}= 7.92^{+0.49}_{-0.47}(\omega _B) ^{+0.05}_{-0.01}\nonumber \\&\quad \times (B^n_i) ^{+0.11}_{-0.09}(B^s_i) ^{+2.25}_{-1.64}(\varphi ) ^{+0.12}_{-0.18}(a_t) ^{+0.11}_{-0.08}(V), \end{aligned}$$

(29)

$$\begin{aligned}&R_{d}^{\sigma /f_0}\equiv \frac{\mathcal{B}(B_d^0 \rightarrow \sigma \sigma )}{\mathcal{B}(B_d^0 \rightarrow f_0 f_0)}= 12.35^{+0.27}_{-0.21}(\omega _B) ^{+0.45}_{-0.47}\nonumber \\&\quad \times (B^n_i) ^{+0.22}_{-0.18}(B^s_i) ^{+3.67}_{-2.59}(\varphi ) ^{+0.58}_{-0.68}(a_t) ^{+0.29}_{-0.25}(V), \end{aligned}$$

(30)

$$\begin{aligned}&R_{s\sigma }^{\sigma /f_0}\equiv \frac{\mathcal{B}(B_s^0 \rightarrow \sigma \sigma )}{\mathcal{B}(B_s^0 \rightarrow \sigma f_0)}= 1.54^{+0.30}_{-0.24}(\omega _B) ^{+0.19}_{-0.16}(B^n_i) ^{+0.09}_{-0.08}\nonumber \\&\quad \times (B^s_i) ^{+0.08}_{-0.12}(\varphi ) ^{+0.20}_{-0.18}(a_t) ^{+0.01}_{-0.01}(V), \end{aligned}$$

(31)

$$\begin{aligned}&R_{sf_0}^{f_0/\sigma }\equiv \frac{\mathcal{B}(B_s^0 \rightarrow f_0 f_0)}{\mathcal{B}(B_s^0 \rightarrow \sigma f_0)}= 4.35^{+0.95}_{-0.71}(\omega _B) ^{+0.05}_{-0.05}\nonumber \\&\quad \times (B^n_i) ^{+0.14}_{-0.16}(B^s_i) ^{+0.00}_{-0.12}(\varphi ) ^{+0.34}_{-0.32}(a_t) ^{+0.01}_{-0.01}(V), \end{aligned}$$

(32)

$$\begin{aligned}&R_{s}^{f_0/\sigma }\equiv \frac{\mathcal{B}(B_s^0 \rightarrow \ f_0 f_0)}{\mathcal{B}(B_s^0 \rightarrow \sigma \sigma )}= 2.82^{+0.07}_{-0.03}(\omega _B) ^{+0.29}_{-0.28}\nonumber \\&\quad \times (B^n_i) ^{+0.21}_{-0.20}(B^s_i) ^{+0.16}_{-0.13}(\varphi ) ^{+0.13}_{-0.12}(a_t) ^{+0.01}_{-0.01}(V), \end{aligned}$$

(33)

$$\begin{aligned}&R_{s/d}^{\sigma \sigma } \equiv \frac{\mathcal{B}(B_s^0 \rightarrow \sigma \sigma )}{\mathcal{B}(B_d^0 \rightarrow \sigma \sigma )} =4.53^{+0.02}_{-0.01}(\omega _B) ^{+0.51}_{-0.35}(B^n_i) ^{+0.19}_{-0.17}\nonumber \\&\quad \times (B^s_i) ^{+0.02}_{-0.01}(\varphi ) ^{+0.47}_{-0.43}(a_t) ^{+0.18}_{-0.20}(V), \end{aligned}$$

(34)

$$\begin{aligned}&R_{s/d}^{\sigma f_0} \equiv \frac{\mathcal{B}(B_s^0 \rightarrow \sigma f_0)}{\mathcal{B}(B_d^0 \rightarrow \sigma f_0)}=4.59^{+1.06}_{-0.87}(\omega _B) ^{+0.85}_{-0.69}\nonumber \\&\quad \times (B^n_i) ^{+0.37}_{-0.36}(B^s_i) ^{+0.45}_{-0.25}(\varphi ) ^{+0.93}_{-0.79}(a_t) ^{+0.16}_{-0.19}(V), \end{aligned}$$

(35)

$$\begin{aligned}&R_{s/d}^{f_0 f_0} \equiv \frac{\mathcal{B}(B_s^0 \rightarrow f_0 f_0)}{\mathcal{B}(B_d^0 \rightarrow f_0 f_0)}=1.58^{+0.08}_{-0.05}(\omega _B) ^{+0.29}_{-0.23}\nonumber \\&\quad \times (B^n_i) ^{+0.14}_{-0.14}(B^s_i) ^{+0.59}_{-0.39}(\varphi ) ^{+0.14}_{-0.15}(a_t) ^{+0.04}_{-0.04}(V) \times 10^2. \end{aligned}$$

(36)

One could easily observe that the errors induced by the nonperturbative inputs of the above ratios are indeed much smaller due to the effective cancellation, except for those of the ratios $R_{d f_0}^{\sigma /f_0}$, $R_d^{\sigma /f_0}$, and $R_{s/d}^{f_0 f_0}$ because the $B_d^0 \rightarrow f_0 f_0$ decay rate is highly sensitive to the mixing angle $\varphi$. These ratios are expected to be examined in the (near) future experiments at LHCb and/or Belle-II.

Table 1 The factorization decay amplitudes (in units of $10^{-3}$ GeV$^{3}$) of the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays with the mixing angle $\varphi \sim 25^\circ$ in the PQCD approach at leading order, where only the central values are quoted for clarifications

As aforementioned, the neutral B-meson decays into $\sigma \sigma , \sigma f_0, f_0 f_0$ would contain the three decay amplitudes of $B_{d,s}^0 \rightarrow f_n f_n$, $B_{d,s}^0 \rightarrow f_n f_s$, and $B_{d,s}^0 \rightarrow f_s f_s$ with different ratios when the light scalar $\sigma /f_0$ are treated as superposition of the $f_n$ and $f_s$ flavor states, which could bring the possibly constructive or destructive interferences into the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays. Within the theoretical uncertainties, the results of the branching ratios for these neutral B-meson decays into $\sigma \sigma , \sigma f_0$, and $f_0 f_0$ by adding various errors in quadrature could be written explicitly as follows:

$$\begin{aligned} \mathcal{B}(B_d^0 \rightarrow \sigma \sigma )= & {} 4.15^{+1.44}_{-1.22} \times 10^{-5},\nonumber \\ \mathcal{B}(B_s^0 \rightarrow \sigma \sigma )= & {} 1.88^{+0.60}_{-0.49} \times 10^{-4}; \end{aligned}$$

(37)

$$\begin{aligned} \mathcal{B}(B_d^0 \rightarrow \sigma f_0)= & {} 2.66^{+0.94}_{-0.79} \times 10^{-5}, \nonumber \\ \mathcal{B}(B_s^0 \rightarrow \sigma f_0)= & {} 1.22^{+0.40}_{-0.30} \times 10^{-4} ; \end{aligned}$$

(38)

$$\begin{aligned} \mathcal{B}(B_d^0 \rightarrow f_0 f_0)= & {} 3.36^{+1.62}_{-1.32}\times 10^{-6}, \nonumber \\ \mathcal{B}(B_s^0 \rightarrow f_0 f_0)= & {} 5.31^{+1.74}_{-1.39}\times 10^{-4}. \end{aligned}$$

(39)

Within still large errors, the branching ratios show that $\mathcal{B}(B_d^0 \rightarrow \sigma \sigma ) \sim \mathcal{B}(B_d^0 \rightarrow \sigma f_0) > \mathcal{B}(B_d^0 \rightarrow f_0 f_0)$, and $\mathcal{B}(B_s^0 \rightarrow \sigma \sigma ) \sim \mathcal{B}(B_s^0 \rightarrow \sigma f_0) < \mathcal{B}(B_s^0 \rightarrow f_0 f_0)$. The main reason is that the $f_n (f_s)$ component dominates the $\sigma (f_0)$ state. In terms of the central values of the branching ratios, the relation $\mathcal{B}(B_d^0 \rightarrow \sigma \sigma )> \mathcal{B}(B_d^0 \rightarrow \sigma f_0) > \mathcal{B}(B_d^0 \rightarrow f_0 f_0)$ is easily understood. However, it is slightly strange that $\mathcal{B}(B_s^0 \rightarrow \sigma \sigma ) > \mathcal{B}(B_s^0 \rightarrow \sigma f_0)$, which is attributed to the different interferences from the flavorful states $f_n f_n, f_n f_s,$ and $f_s f_s$.

To see the contributions from the diagrams in every topology explicitly, we present the factorization amplitudes of the considered neutral B-meson decays into $\sigma \sigma , \sigma f_0, f_0 f_0$ in Table 1, in which we just quote the central values for clarifications. The quantities ${\mathcal {A}}_{fe}$, ${\mathcal {A}}_{nfe}$, ${\mathcal {A}}_{nfa}$, and ${\mathcal {A}}_{fa}$ are defined to denote the factorization decay amplitudes arising from the factorizable emission, the nonfactorizable emission, the nonfactorizable annihilation, and the factorizable annihilation diagrams with physical final states, respectively. Specifically, every factorization amplitude includes all the possible contributions induced by the $(V-A)(V-A)$, $(V-A)(V+A)$, and $(S-P)(S+P)$ currents. For the sake of the simplicity, in association with the Eqs. (7)–(12), the factorization amplitude ${\mathcal {A}}_{fe}$ in the $B_{d,s}^0 \rightarrow \sigma f_0$ decay is taken as an example to clarify the meaning of these four quantities as presented in Table 1 explicitly as follows,

$$\begin{aligned}&{\mathcal {A}}_{fe}(B_d^0 \rightarrow \sigma f_0) \equiv \biggl [ A_{fe}(B_d^0 \rightarrow f_n f_n) - A_{fe}(B_d^0 \rightarrow f_s f_s) \biggr ]\nonumber \\&\qquad \times \sin (2\varphi ) + A_{fe}(B_d^0 \rightarrow f_n f_s) \cos (2\varphi ) \nonumber \\&\quad = A_{fe}(B_d^0 \rightarrow f_n f_n) \sin (2\varphi ) \nonumber \\&\quad = \frac{1}{2} \sin (2\varphi )\biggl \{ - V_{tb}^* V_{td} (a_6 -\frac{1}{2}a_8) \bar{f}_{f_n} F_{fe}^{P_2} \biggr \}, \end{aligned}$$

(40)

and

$$\begin{aligned}&{\mathcal {A}}_{fe}(B_s^0 \rightarrow \sigma f_0)\equiv \biggl [ A_{fe}(B_s^0 \rightarrow f_n f_n) \nonumber \\&\qquad - A_{fe}(B_s^0 \rightarrow f_s f_s) \biggr ]\sin (2\varphi ) +A_{fe}(B_s^0 \rightarrow f_n f_s) \cos (2\varphi ) \nonumber \\&\quad = - A_{fe}(B_s^0 \rightarrow f_s f_s) \sin (2\varphi ) \nonumber \\&\quad = \sin (2\varphi )\biggl \{ V_{tb}^* V_{ts} \left( a_6 -\frac{1}{2}a_8\right) \bar{f}_{f_s} F_{fe}^{P_2} \biggr \}. \end{aligned}$$

(41)

And the other three quantities ${\mathcal {A}}_{nfe}$, ${\mathcal {A}}_{nfa}$, and ${\mathcal {A}}_{fa}$ could also be expressed in a similar manner. It is interesting to notice that the conventionally large contributions from the factorizable emission diagrams in the $B \rightarrow PP, PV, VV$ decays disappeared naturally due to the zero vector decay constants $f_{f_n}$ and $f_{f_s}$ in these $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays. In sharp contrast, as stated in Refs. [31, 60, 62,63,64], there are large non-factorizable contributions in the B-meson decays into the final states involving scalar meson(s). In particular, due to the anti-asymmetric leading-twist distribution amplitude of the scalars, the non-factorizable emission diagrams with a significant cancellation between Fig. 1c and d in the pseudoscalar and/or vector sector now become with a dramatic enhancement in the scalar sector, which result further in the large branching ratios as presented in the Eqs. (37)–(39).

Furthermore, to see clearly the interferences arising from the flavorful states, namely, $B_{d,s}^0 \rightarrow f_n f_n, f_n f_s, f_s f_s$, in these $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ modes, we also present the decay amplitudes of the neutral B-meson decays into the flavorful and physical final states respectively in Tables 2 and 3. At the same time, the amplitudes induced by the tree operators and the penguin operators are also differentiated. From Eqs. (15)–(20) and Table 2, it is evident to observe that, due to the purely large non-factorizable emission contributions in the $B_s^0 \rightarrow f_n f_s$ decay amplitudes, the slightly constructive (destructive) interferences between the $B_s^0 \rightarrow f_n f_n$ and $B_s^0 \rightarrow f_n f_s$ amplitudes consequently lead to a bit larger (smaller) $B_s^0 \rightarrow \sigma \sigma (B_s^0 \rightarrow \sigma f_0)$ decay rate.

Table 2 The decay amplitudes (in units of $10^{-3}$ GeV$^{3}$) of the neutral B-meson decays into the flavorful final states $f_n f_n, f_n f_s$, and $f_s f_s$ in the PQCD approach at leading order, where only the central values are quoted for clarifications

Table 3 The decay amplitudes (in units of $10^{-3}$ GeV$^{3}$) of the neutral B-meson decays into physical final states $\sigma \sigma , \sigma f_0$, and $f_0 f_0$ in the PQCD approach at leading order, where only the central values are quoted for clarifications. The mixing angle $\varphi$ is taken as $25^\circ$

It is necessary to point out that the $f_0$ state can decay into $\pi ^+ \pi ^-$, as well as into $K^+ K^-$, with the decay rates [21, 73,74,75,76]

$$\begin{aligned} \mathcal{B}(f_0 \rightarrow \pi ^+ \pi ^-)= & {} 0.45^{+0.07}_{-0.05}, \end{aligned}$$

(42)

and

$$\begin{aligned} \mathcal{B}(f_0 \rightarrow K^+ K^-)= & {} 0.16^{+0.04}_{-0.05}, \end{aligned}$$

(43)

respectively. Notice that the following assumptions have been made: the decays of $f_0$ are governed by the $f_0 \rightarrow \pi \pi$ and KK modes, and the relations of the decay rates are $\Gamma (f_0\rightarrow \pi ^0 \pi ^0) = \frac{1}{2} \Gamma (f_0 \rightarrow \pi ^+ \pi ^-)$ and $\Gamma (f_0 \rightarrow K^0 \bar{K}^0) = \Gamma (f_0 \rightarrow K^+ K^-)$. Moreover, the branching ratio for the $\sigma \rightarrow \pi ^+ \pi ^-$ channel could be $\mathcal{B}(\sigma \rightarrow \pi ^+ \pi ^-) \simeq 0.67 \pm 0.07$ [23]. Therefore, one can obtain the following rich four-body decay channels ⁴ with the possible resonances $\sigma$ and $f_0$ via strong decays into $\pi ^+ \pi ^-$ in the considered $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ channels:

$$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) \sigma (\rightarrow \pi ^+ \pi ^-) )\nonumber \\&\quad \equiv \mathcal{B}(B_d^0 \rightarrow \sigma \sigma ) \mathcal{B}(\sigma \rightarrow \pi ^+ \pi ^-)\mathcal{B}(\sigma \rightarrow \pi ^+ \pi ^-) \nonumber \\&\quad = 1.86 ^{+0.35+0.51+0.02+0.16+0.09+0.09+0.19+0.19}_{-0.28-0.43-0.02-0.17-0.06-0.08-0.19-0.19} \times 10^{-5}, \end{aligned}$$

(44)

$$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad \equiv \mathcal{B}(B_d^0 \rightarrow \sigma f_0) \mathcal{B}(\sigma \rightarrow \pi ^+ \pi ^-)\mathcal{B}(f_0 \rightarrow \pi ^+ \pi ^-) \nonumber \\&\quad = 0.80 ^{+0.19+0.18+0.03+0.07+0.07+0.03+0.08+0.12}_{-0.15-0.16-0.03-0.08-0.05-0.03-0.08-0.09} \times 10^{-5}, \end{aligned}$$

(45)

$$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow f_0(\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad \equiv \mathcal{B}(B_d^0 \rightarrow f_0 f_0) \mathcal{B}(f_0 \rightarrow \pi ^+ \pi ^-) \mathcal{B}(f_0 \rightarrow \pi ^+ \pi ^-) \nonumber \\&\quad = 0.68 ^{+0.11+0.16+0.02+0.26+0.07+0.02+0.11+0.11}_{-0.09-0.13-0.02-0.20-0.05-0.02-0.08-0.08} \times 10^{-6}, \end{aligned}$$

(46)

$$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) \sigma (\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad \equiv \mathcal{B}(B_s^0 \rightarrow \sigma \sigma ) \mathcal{B}(\sigma \rightarrow \pi ^+ \pi ^-)\mathcal{B}(\sigma \rightarrow \pi ^+ \pi ^-) \nonumber \\&\quad = 0.84 ^{+0.16+0.15+0.05+0.07+0.13+0.00+0.09+0.09}_{-0.13-0.12-0.04-0.07-0.10-0.00-0.09-0.09} \times 10^{-4}, \end{aligned}$$

(47)

$$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad \equiv \mathcal{B}(B_s^0 \rightarrow \sigma f_0) \mathcal{B}(\sigma \rightarrow \pi ^+ \pi ^-) \mathcal{B}(f_0 \rightarrow \pi ^+ \pi ^-) \nonumber \\&\quad = 0.37 ^{+0.00+0.02+0.04+0.01+0.11+0.00+0.04+0.06}_{-0.00-0.02-0.04-0.00-0.08-0.00-0.04-0.04} \times 10^{-4}, \end{aligned}$$

(48)

$$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow f_0(\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad \equiv \mathcal{B}(B_s^0 \rightarrow f_0 f_0) \mathcal{B}(f_0 \rightarrow \pi ^+ \pi ^-) \mathcal{B}(f_0 \rightarrow \pi ^+ \pi ^-) \nonumber \\&\quad = 1.08 ^{+0.23+0.06+0.13+0.03+0.22+0.00+0.17+0.17}_{-0.18-0.06-0.12-0.04-0.17-0.00-0.12-0.12} \times 10^{-4}, \end{aligned}$$

(49)

in which the last two errors come from the uncertainties of the $\sigma /f_0$ decay width. All the above modes in association with large numerical results would be explored at the LHCb and/or Belle-II experiments with good precision in the future. Moreover, though the $f_0$ resonance coming from the $K^+ K^-$ invariant mass could not be easily detected at the experimental aspects since the $f_0$ state is usually buried under the tail of the $\phi$ one, it is essential for us to present the possible channels induced by the $f_0 \rightarrow K^+ K^-$ decay as follows:

$$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow K^+ K^-))\nonumber \\&\quad \equiv \mathcal{B}(B_d^0 \rightarrow \sigma f_0) \mathcal{B}(\sigma \rightarrow \pi ^+ \pi ^-) \mathcal{B}(f_0 \rightarrow K^+ K^-) \nonumber \\&\quad = 0.29 ^{+0.07+0.06+0.01+0.03+0.02+0.01+0.03+0.07}_{-0.05-0.05-0.01-0.03-0.02-0.01-0.03-0.09}\nonumber \\&\qquad \times 10^{-5}, \end{aligned}$$

(50)

$$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow f_0(\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow K^+ K^-)) \nonumber \\&\quad \equiv \mathcal{B}(B_d^0 \rightarrow f_0 f_0) \mathcal{B}(f_0 \rightarrow \pi ^+ \pi ^-) \mathcal{B}(f_0 \rightarrow K^+ K^-) \nonumber \\&\quad = 0.24 ^{+0.04+0.05+0.01+0.09+0.03+0.01+0.04+0.06}_{-0.03-0.05-0.01-0.07-0.02-0.01-0.03-0.08}\nonumber \\&\qquad \times 10^{-6}, \end{aligned}$$

(51)

$$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow f_0(\rightarrow K^+ K^-) f_0(\rightarrow K^+ K^-)) \nonumber \\&\quad \equiv \mathcal{B}(B_d^0 \rightarrow f_0 f_0) \mathcal{B}(f_0 \rightarrow K^+ K^-) \mathcal{B}(f_0 \rightarrow K^+ K^-) \nonumber \\&\quad = 0.09 ^{+0.01+0.02+0.00+0.03+0.01+0.00+0.02+0.02}_{-0.01-0.02-0.00-0.03-0.01-0.00-0.03-0.03}\nonumber \\&\qquad \times 10^{-6}, \end{aligned}$$

(52)

$$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow K^+ K^-))\nonumber \\&\quad \equiv \mathcal{B}(B_s^0 \rightarrow \sigma f_0) \mathcal{B}(\sigma \rightarrow \pi ^+ \pi ^-) \mathcal{B}(f_0 \rightarrow K^+ K^-) \nonumber \\ \nonumber \\&\quad = 0.13 ^{+0.00+0.01+0.01+0.00+0.04+0.00+0.01+0.03}_{-0.00-0.01-0.01-0.00-0.03-0.00-0.01-0.04}\nonumber \\&\qquad \times 10^{-4}, \end{aligned}$$

(53)

$$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow f_0(\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow K^+ K^-)) \nonumber \\&\quad \equiv \mathcal{B}(B_s^0 \rightarrow f_0 f_0) \mathcal{B}(f_0 \rightarrow \pi ^+ \pi ^-) \mathcal{B}(f_0 \rightarrow K^+ K^-) \nonumber \\&\quad = 0.38 ^{+0.08+0.02+0.04+0.01+0.08+0.00+0.06+0.10}_{-0.06-0.02-0.04-0.01-0.06-0.00-0.04-0.12}\nonumber \\&\qquad \times 10^{-4}, \end{aligned}$$

(54)

$$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow f_0(\rightarrow K^+ K^-) f_0(\rightarrow K^+ K^-)) \nonumber \\&\quad \equiv \mathcal{B}(B_s^0 \rightarrow f_0 f_0) \mathcal{B}(f_0 \rightarrow K^+ K^-) \mathcal{B}(f_0 \rightarrow K^+ K^-) \nonumber \\&\quad = 0.14 ^{+0.03+0.01+0.01+0.00+0.03+0.00+0.03+0.03}_{-0.02-0.01-0.01-0.00-0.02-0.00-0.04-0.04}\nonumber \\&\qquad \times 10^{-4}. \end{aligned}$$

(55)

It is clearly seen that the last three $B_s^0$-meson decay modes have large branching ratios and are expected to be examined in the near future.

Fig. 2

Dependence of the CP-averaged $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ branching ratios on $\varphi$ in the PQCD approach, in which the red-solid line, the blue-dashed line, and the magenta-dotted line correspond to the final states of $\sigma \sigma$, $\sigma f_0$, and $f_0 f_0$, respectively

To provide more information to better constrain the magnitude and the sign of the mixing angle $\varphi$, we plot the variation of the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decay rates with the mixing angle in the range of $\varphi \in [-90^\circ , 90^\circ ]$ (see Fig. 2), through which we could find the differences between the results around $+25^\circ$ and $-25^\circ$, and further obtain the information about the sign of the mixing angle $\varphi$ once the related experiments could provide stringent examinations. From Fig. 2b, an interesting variation could be observed that, when the mixing angle are taken as $-25^\circ$, the relation of the two branching ratios $\mathcal{B}(B_s^0 \rightarrow \sigma \sigma )$ and $\mathcal{B}(B_s^0 \rightarrow \sigma f_0)$ could change from $\mathcal{B}(B_s^0 \rightarrow \sigma \sigma )[1.88 \times 10^{-4}] > \mathcal{B}(B_s^0 \rightarrow \sigma f_0)[1.22 \times 10^{-4}]$ at $\varphi \sim + 25^\circ$ to $\mathcal{B}(B_s^0 \rightarrow \sigma \sigma )[8.75 \times 10^{-5}] < \mathcal{B}(B_s^0 \rightarrow \sigma f_0) [3.43 \times 10^{-4}]$ evidently at $\varphi \sim -25^\circ$. The underlying reason is that the previously constructive (destructive) interferences at $\varphi \sim +25^\circ$ become the presently destructive (constructive) ones at $\varphi \sim -25^\circ$ between the flavorful states $B_s^0 \rightarrow f_n f_n$ and $B_s^0 \rightarrow f_n f_s$, which finally result in the considerable change in the $B_s^0 \rightarrow \sigma \sigma$ and $B_s^0 \rightarrow \sigma f_0$ decay rates. Maybe the precise tests in the future on this relation could help us to distinguish the correct sign of the mixing angle $\varphi$ in the $\sigma -f_0$ mixing.

In order to provide the referenced predictions for the future measurements, even to find the possible hints for the magnitude and/or sign of $\varphi$, it is essential to present the results at $\varphi \sim -25^\circ$ for all the above observables that have been shown. Various predictions in the PQCD approach are presented in order:

• The CP-averaged branching ratios at $\varphi \sim - 25^\circ$,

  $$\begin{aligned} \mathcal{B}(B_d^0 \rightarrow \sigma \sigma )= & {} 5.10^{+1.75}_{-1.49} \times 10^{-5}, \nonumber \\ \mathcal{B}(B_s^0 \rightarrow \sigma \sigma )= & {} 8.75^{+3.20}_{-2.83} \times 10^{-5}; \end{aligned}$$

  (56)
  $$\begin{aligned} \mathcal{B}(B_d^0 \rightarrow \sigma f_0)= & {} 1.69^{+0.67}_{-0.57} \times 10^{-5}, \nonumber \\ \mathcal{B}(B_s^0 \rightarrow \sigma f_0)= & {} 3.43^{+1.54}_{-1.17} \times 10^{-4}; \end{aligned}$$

  (57)
  $$\begin{aligned} \mathcal{B}(B_d^0 \rightarrow f_0 f_0)= & {} 3.61^{+1.14}_{-0.92} \times 10^{-6}, \nonumber \\ \mathcal{B}(B_s^0 \rightarrow f_0 f_0)= & {} 4.10^{+1.13}_{-0.86} \times 10^{-4}. \end{aligned}$$

  (58)

• Several ratios at $\varphi \sim - 25^\circ$,

  $$\begin{aligned}&R_{d\sigma }^{\sigma /f_0}\equiv \frac{\mathcal{B}(B_d^0 \rightarrow \sigma \sigma )}{\mathcal{B}(B_d^0 \rightarrow \sigma f_0)} = 3.02^{+0.36}_{-0.31},\nonumber \\&\quad R_{df_0}^{\sigma /f_0} \equiv \frac{\mathcal{B}(B_d^0 \rightarrow \sigma f_0)}{\mathcal{B}(B_d^0 \rightarrow f_0 f_0)} = 4.68^{+0.74}_{-0.79}, \end{aligned}$$

  (59)
  $$\begin{aligned}&R_{d}^{\sigma /f_0}\equiv \frac{\mathcal{B}(B_d^0 \rightarrow \sigma \sigma )}{\mathcal{B}(B_d^0 \rightarrow f_0 f_0)} = 14.13^{+2.38}_{-2.65}, \nonumber \\&\quad R_{s\sigma }^{\sigma /f_0}\equiv \frac{\mathcal{B}(B_s^0 \rightarrow \sigma \sigma )}{\mathcal{B}(B_s^0 \rightarrow \sigma f_0)}= 0.26^{+0.06}_{-0.07}, \end{aligned}$$

  (60)
  $$\begin{aligned}&R_{s}^{f_0/\sigma }\equiv \frac{\mathcal{B}(B_s^0 \rightarrow \ f_0 f_0)}{\mathcal{B}(B_s^0 \rightarrow \sigma \sigma )} = 4.69^{+1.35}_{-1.04}, \nonumber \\&\quad R_{sf_0}^{f_0/\sigma }\equiv \frac{\mathcal{B}(B_s^0 \rightarrow f_0 f_0)}{\mathcal{B}(B_s^0 \rightarrow \sigma f_0)}= 1.20^{+0.42}_{-0.36}, \end{aligned}$$

  (61)
  $$\begin{aligned}&R_{s/d}^{\sigma \sigma } \equiv \frac{\mathcal{B}(B_s^0 \rightarrow \sigma \sigma )}{\mathcal{B}(B_d^0 \rightarrow \sigma \sigma )}=1.72^{+0.51}_{-0.43} ,\nonumber \\&\quad R_{s/d}^{\sigma f_0} \equiv \frac{\mathcal{B}(B_s^0 \rightarrow \sigma f_0)}{\mathcal{B}(B_d^0 \rightarrow \sigma f_0)}=20.30^{+6.35}_{-5.36}, \end{aligned}$$

  (62)
  $$\begin{aligned}&R_{s/d}^{f_0 f_0} \equiv \frac{\mathcal{B}(B_s^0 \rightarrow f_0 f_0)}{\mathcal{B}(B_d^0 \rightarrow f_0 f_0)}=1.14^{+0.31}_{-0.30} \times 10^2. \end{aligned}$$

  (63)

• Possible four-body decays to $(\pi ^+ \pi ^-)_{\sigma (f_0)}(\pi ^+\pi ^-)_{f_0(\sigma )}$ at $\varphi \sim - 25^\circ$,

  $$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) \sigma (\rightarrow \pi ^+ \pi ^-) )\nonumber \\&\quad = 2.29^{+0.85}_{-0.75} \times 10^{-5}, \end{aligned}$$

  (64)
  $$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad = 0.51^{+0.22}_{-0.18} \times 10^{-5}, \end{aligned}$$

  (65)
  $$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow f_0(\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad = 0.73^{+0.16}_{-0.22} \times 10^{-6}, \end{aligned}$$

  (66)
  $$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) \sigma (\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad = 3.93^{+1.55}_{-1.40} \times 10^{-5}, \end{aligned}$$

  (67)
  $$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad = 1.03^{+0.51}_{-0.38} \times 10^{-4}, \end{aligned}$$

  (68)
  $$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow f_0(\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow \pi ^+ \pi ^-))\nonumber \\&\quad = 0.83^{+0.29}_{-0.22} \times 10^{-4}. \end{aligned}$$

  (69)

• Possible four-body decays with $f_0 \rightarrow K^+ K^-$ at $\varphi \sim - 25^\circ$,

  $$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow K^+ K^-)) \nonumber \\&\quad = 0.18^{+0.09}_{-0.09} \times 10^{-5}, \end{aligned}$$

  (70)
  $$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow f_0(\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow K^+ K^-))\nonumber \\&\quad = 0.26^{+0.11}_{-0.11} \times 10^{-6}, \end{aligned}$$

  (71)
  $$\begin{aligned}&\mathrm{BR}(B_d^0 \rightarrow f_0(\rightarrow K^+ K^-) f_0(\rightarrow K^+ K^-)) \nonumber \\&\quad = 0.09^{+0.04}_{-0.05} \times 10^{-6}, \end{aligned}$$

  (72)
  $$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow K^+ K^-))\nonumber \\&\quad = 0.38^{+0.19}_{-0.17} \times 10^{-4}, \end{aligned}$$

  (73)
  $$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow f_0(\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow K^+ K^-)) \nonumber \\&\quad = 0.30^{+0.12}_{-0.12} \times 10^{-4}, \end{aligned}$$

  (74)
  $$\begin{aligned}&\mathrm{BR}(B_s^0 \rightarrow f_0(\rightarrow K^+ K^-) f_0(\rightarrow K^+ K^-)) \nonumber \\&\quad = 0.10^{+0.05}_{-0.05} \times 10^{-4}. \end{aligned}$$

  (75)

All the above predictions in the PQCD approach await the future tests with good precision at LHCb and/or Belle-II, etc.

3.2 CP-violating asymmetries

Now, let us turn to analyze the CP-violations of the neutral B-meson decays into $\sigma \sigma , \sigma f_0$, and $f_0 f_0$ in the PQCD approach. In the analysis of the CP-violating asymmetries for the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays, the effects of neutral $B_{d,s}^0-\bar{B}_{d,s}^0$ mixing should be taken into account. The CP-violating asymmetries of $B_{d,s}^0(\bar{B}_{d,s}^0) \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays are time dependent and can be defined as

$$\begin{aligned} A_\mathrm{CP}\equiv & {} \frac{\Gamma \left( \bar{B}_{d,s}^0(\Delta t) \rightarrow f_\mathrm{CP}\right) - \Gamma \left( B_{d,s}^0(\Delta t) \rightarrow f_\mathrm{CP}\right) }{ \Gamma \left( \bar{B}_{d,s}^0(\Delta t) \rightarrow f_\mathrm{CP}\right) + \Gamma \left( B_{d,s}^0(\Delta t) \rightarrow f_\mathrm{CP}\right) }\nonumber \\= & {} A_\mathrm{CP}^\mathrm{dir} \cos (\Delta m_{d,s} \Delta t) + A_\mathrm{CP}^\mathrm{mix} \sin (\Delta m_{d,s} \Delta t), \end{aligned}$$

(76)

where $\Delta m_{d,s}$ is the mass difference between the two $B_{d,s}^0$ mass eigenstates, $\Delta t =t_\mathrm{CP}-t_{tag}$ is the time difference between the tagged $B_{d,s}^0$ ($\bar{B}_{d,s}^0$) and the accompanying $\bar{B}_{d,s}^0$ ($B_{d,s}^0$) with opposite b flavor decaying to the final CP-eigenstate $f_\mathrm{CP}$ at the time $t_\mathrm{CP}$. The direct and mixing-induced CP-violating asymmetries $A_\mathrm{CP}^\mathrm{dir}$ and $A_\mathrm{CP}^\mathrm{mix}$ can be written as

$$\begin{aligned} A_\mathrm{CP}^\mathrm{dir}\equiv \frac{ \left| \lambda _\mathrm{CP}^{d,s}\right| ^2-1 }{1+\left| \lambda _\mathrm{CP}^{d,s}\right| ^2}, \quad A_\mathrm{CP}^\mathrm{mix}\equiv \frac{ 2 \mathrm{Im} (\lambda _\mathrm{CP}^{d,s})}{1+\left| \lambda _\mathrm{CP}^{d,s}\right| ^2}, \end{aligned}$$

(77)

where the CP-violating parameter $\lambda _\mathrm{CP}^{d,s}$ can be read as

$$\begin{aligned} \lambda _\mathrm{CP}^{d}\equiv & {} \eta _f \; \frac{V_{tb}^*V_{td}}{V_{tb}V_{td}^*} \cdot \frac{ \langle f_\mathrm{CP} |H_\mathrm{eff}|\bar{B}_{d}^0\rangle }{\langle f_\mathrm{CP} |H_\mathrm{eff}|B_{d}^0\rangle }, \nonumber \\ \lambda _\mathrm{CP}^{s}\equiv & {} \eta _f \; \frac{V_{tb}^*V_{ts}}{V_{tb}V_{ts}^*} \frac{ \langle f_\mathrm{CP} |H_\mathrm{eff}|\bar{B}_{s}^0\rangle }{\langle f_\mathrm{CP} |H_\mathrm{eff}|B_{s}^0\rangle }, \end{aligned}$$

(78)

with the CP-eigenvalue of the final states $\eta _f = +1$. Notice that, for the strange B-meson decays, due to the presence of a non-negligible $\Delta \Gamma _s$, a non-zero ratio $(\Delta \Gamma /\Gamma )_{B_s^0}$ is expected in the standard model [79, 80]. Thus, for $B_s^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays, the $\Delta \Gamma _s$-induced CP-violation $A_\mathrm{CP}^{\Delta \Gamma _s}$ can be defined as follows [80]:

$$\begin{aligned} A_\mathrm{CP}^{\Delta \Gamma _s} \equiv \frac{ 2 \mathrm{Re} ( \lambda _\mathrm{CP}^{s})}{1+\left| \lambda _\mathrm{CP}^{s}\right| ^2}. \end{aligned}$$

(79)

The above three quantities describing the CP violations in $B_s^0$ meson decays shown in Eqs. (77) and (79) satisfy the following relation,

$$\begin{aligned} |A_\mathrm{CP}^\mathrm{dir}|^2+ |A_\mathrm{CP}^\mathrm{mix}|^2 + |A_\mathrm{CP}^{\Delta \Gamma _s}|^2= 1. \end{aligned}$$

(80)

By the numerical evaluations, the direct and the mixing-induced CP-violating asymmetries $A_\mathrm{CP}^\mathrm{dir}$ and $A_\mathrm{CP}^\mathrm{mix}$ for the $B_d^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays are collected as

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{dir}(B_d^0 \rightarrow \sigma \sigma ) = -74.66 ^{+4.82}_{-4.58}(\omega _B) ^{+4.57}_{-5.38}(B_i^n) ^{+0.51}_{-0.51}\nonumber \\&\quad \times (B_i^s) ^{+1.27}_{-1.33}(\varphi ) ^{+4.80}_{-5.32}(a_t) ^{+2.53}_{-2.35}(V) \times 10^{-2}, \end{aligned}$$

(81)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{dir}(B_d^0 \rightarrow \sigma f_0) = -37.22 ^{+2.89}_{-3.50}(\omega _B) ^{+2.69}_{-3.54}(B_i^n) ^{+1.45}_{-1.39}\nonumber \\&\quad \times (B_i^s) ^{+2.49}_{-2.27}(\varphi ) ^{+2.89}_{-3.76}(a_t) ^{+1.45}_{-1.46}(V) \times 10^{-2}, \end{aligned}$$

(82)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{dir}(B_d^0 \rightarrow f_0 f_0) = -65.96 ^{+3.29}_{-2.88}\nonumber \\&\quad \times (\omega _B) ^{+3.68}_{-4.18}(B_i^n) ^{+1.31}_{-1.38}(B_i^s) ^{+3.30}_{-4.41}(\varphi ) ^{+0.19}_{-0.19}\nonumber \\&\quad \times (a_t) ^{+1.85}_{-1.92}(V) \times 10^{-2}; \end{aligned}$$

(83)

and

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{mix}(B_d^0 \rightarrow \sigma \sigma ) = -41.67 ^{+3.84}_{-3.43}(\omega _B) ^{+5.50}_{-3.87}(B_i^n) ^{+2.34}_{-2.23}\nonumber \\&\quad \times (B_i^s) ^{+3.77}_{-3.44}(\varphi ) ^{+1.26}_{-0.09} (a_t) ^{+5.44}_{-5.16}(V) \times 10^{-2}, \end{aligned}$$

(84)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{mix}(B_d^0 \rightarrow \sigma f_0) = -92.77 ^{+1.56}_{-1.14}(\omega _B) ^{+1.52}_{-0.74}\nonumber \\&\quad \times (B_i^n) ^{+0.71}_{-0.58}(B_i^s) ^{+1.24}_{-0.97} (\varphi ) ^{+1.78}_{-0.45}(a_t) ^{+0.77}_{-0.58}(V) \times 10^{-2}, \end{aligned}$$

(85)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{mix}(B_d^0 \rightarrow f_0 f_0) = -74.31 ^{+3.38}_{-3.28}(\omega _B) ^{+5.11}_{-3.68}(B_i^n) ^{+1.60}_{-1.45}\nonumber \\&\quad \times (B_i^s) ^{+4.86}_{-3.20}(\varphi ) ^{+2.00}_{-0.64}(a_t) ^{+1.61}_{-1.54}(V) \times 10^{-2}. \end{aligned}$$

(86)

The large direct CP-violating asymmetries indicate that these $B_d^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays contain the large tree amplitudes and the large penguin amplitudes simultaneously, which could be evidently seen from the decay amplitudes as shown in Table 3 and then lead to significant interferences between these two amplitudes. In light of the predicted large decay rates around $10^{-6}{-}10^{-5}$ in the PQCD approach, it is expected that these large direct CP-violating asymmetries in the considered neutral $B_d^0$-meson decays into $\sigma \sigma$, $\sigma f_0$, and $f_0 f_0$ could be confronted with the relevant experiments in the future.

Fig. 3

Dependence of the direct CP-violating asymmetries $A_\mathrm{CP}^\mathrm{dir}(B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0)$ on $\varphi$ in the PQCD approach, in which the red-solid line, the blue-dashed line, and the magenta-dotted line correspond to final states $\sigma \sigma$, $\sigma f_0$, and $f_0 f_0$, respectively

And the direct, the mixing, and the $\Delta \Gamma _s$-induced CP violations $A_\mathrm{CP}^\mathrm{dir}$, $A_\mathrm{CP}^\mathrm{mix}$, and $A_\mathrm{CP}^\mathrm{\Delta \Gamma _s}$ for the $B_s^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays predicted in the PQCD approach are as follows:

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow \sigma \sigma ) = -4.10 ^{+0.07}_{-0.01}(\omega _B) ^{+0.28}_{-0.22}(B_i^n) ^{+0.19}_{-0.17}\nonumber \\&\quad \times (B_i^s) ^{+0.54}_{-0.54}(\varphi ) ^{+0.56}_{-0.46}(a_t) ^{+0.13}_{-0.13}(V) \times 10^{-2}, \end{aligned}$$

(87)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow \sigma f_0) = -11.76 ^{+1.46}_{-1.65}(\omega _B) ^{+1.26}_{-1.25}(B_i^n) ^{+0.17}_{-0.16}\nonumber \\&\quad \times (B_i^s) ^{+1.34}_{-0.62}(\varphi ) ^{+1.64}_{-1.71} (a_t) ^{+0.36}_{-0.40}(V) \times 10^{-2}, \end{aligned}$$

(88)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow f_0 f_0) = 4.55 ^{+0.09}_{-0.19}(\omega _B) ^{+0.15}_{-0.17}(B_i^n) ^{+0.10}_{-0.10}\nonumber \\&\quad \times (B_i^s) ^{+0.27}_{-0.31}(\varphi ) ^{+0.30}_{-0.28}(a_t) ^{+0.15}_{-0.15}(V) \times 10^{-2}. \end{aligned}$$

(89)

and

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{mix}(B_s^0 \rightarrow \sigma \sigma ) = 11.50 ^{+0.65}_{-0.61}(\omega _B) ^{+0.51}_{-0.61}(B_i^n) ^{+0.08}_{-0.08}\nonumber \\&\quad \times (B_i^s) ^{+0.09}_{-0.17}(\varphi ) ^{+0.79}_{-0.74}(a_t) ^{+0.38}_{-0.36}(V) \times 10^{-2}, \end{aligned}$$

(90)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{mix}(B_s^0 \rightarrow \sigma f_0) = 3.36 ^{+0.06}_{-0.25}(\omega _B) ^{+0.61}_{-0.47}(B_i^n) ^{+0.18}_{-0.17}\nonumber \\&\quad \times (B_i^s) ^{+2.71}_{-2.37}(\varphi ) ^{+0.22}_{-0.07}(a_t) ^{+0.11}_{-0.12}(V) \times 10^{-2}, \end{aligned}$$

(91)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{mix}(B_s^0 \rightarrow f_0 f_0) = 2.87 ^{+0.53}_{-0.58}(\omega _B) ^{+0.42}_{-0.45}(B_i^n) ^{+0.03}_{-0.05}\nonumber \\&\quad \times (B_i^s) ^{+0.38}_{-0.38}(\varphi ) ^{+0.50}_{-0.52}(a_t) ^{+0.09}_{-0.09}(V) \times 10^{-2}. \end{aligned}$$

(92)

and

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{\Delta \Gamma _s}(B_s^0 \rightarrow \sigma \sigma ) = 99.25 ^{+0.07}_{-0.07}(\omega _B) ^{+0.07}_{-0.05}(B_i^n) ^{+0.02}_{-0.01}\nonumber \\&\quad \times (B_i^s) ^{+0.01}_{-0.00}(\varphi ) ^{+0.11}_{-0.11}(a_t) ^{+0.05}_{-0.05}(V) \times 10^{-2}, \end{aligned}$$

(93)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{\Delta \Gamma _s}(B_s^0 \rightarrow \sigma f_0) = 99.25 ^{+0.16}_{-0.20}(\omega _B) ^{+0.15}_{-0.18}(B_i^n) ^{+0.01}_{-0.01}\nonumber \\&\quad \times (B_i^s) ^{+0.20}_{-0.21}(\varphi ) ^{+0.18}_{-0.23}(a_t) ^{+0.04}_{-0.05}(V) \times 10^{-2}, \end{aligned}$$

(94)

$$\begin{aligned}&A_\mathrm{CP}^\mathrm{\Delta \Gamma _s}(B_s^0 \rightarrow f_0 f_0) = 99.86 ^{+0.01}_{-0.01}(\omega _B) ^{+0.01}_{-0.02}(B_i^n) ^{+0.00}_{-0.01}\nonumber \\&\quad \times (B_i^s) ^{+0.02}_{-0.03}(\varphi ) ^{+0.02}_{-0.03}(a_t) ^{+0.00}_{-0.01}(V) \times 10^{-2}. \end{aligned}$$

(95)

Different from the $B_d^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays, the highly smaller direct CP-violating asymmetries are obtained for the corresponding $B_s^0$ decays in the PQCD approach. As seen from the related decay amplitudes in Table 3, the fact is that, relative to the suppressed (enhanced) CKM matrix element $|V_{td}|(|V_{ud}|)$ in the $B_d^0$ decays, the enhanced (suppressed) one $|V_{ts}|(|V_{us}|)$ in the $B_s^0$ decays contributes to the penguin (tree) amplitudes remarkably, which eventually weakened the interferences between the tree and penguin amplitudes. Nevertheless, a bit large direct CP violation $A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow \sigma f_0) \sim -10\%$, associated with the large branching ratio $\mathcal{B}(B_s^0 \rightarrow \sigma f_0) \sim 10^{-4}$, could be tested at the LHCb and/or Belle-II experiments in the (near) future.

Similarly, we also plot the variation of the direct CP-violating asymmetries $A_\mathrm{CP}^\mathrm{dir}$ of the neutral B-meson decays into $\sigma \sigma$, $\sigma f_0$, and $f_0 f_0$ with the mixing angle $\varphi \in [-90^\circ , 90^\circ ]$ in Fig. 3. It is noted that, for the $B_d^0$-meson decays, their direct CP violations shown in Fig. 3a slightly change from near $-40\% \sim -70\%$ at $\varphi \sim + 25^\circ$ to about $-60\% \sim -70\%$ at $\varphi \sim - 25^\circ$; however, for the $B_s^0$-meson decays, their direct CP violations presented in Fig. 3b vary dramatically with a total sign-changed, specifically, $A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow \sigma \sigma )$ from $-4\%$ to $+ 7\%$, $A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow \sigma \sigma )$ from $-12\%$ to $+ 7\%$, and $A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow \sigma \sigma )$ from $+ 5\%$ to $- 6\%$, respectively. Therefore, we here also present the CP-violating asymmetries for the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays at $\varphi \sim -25^\circ$ in the PQCD approach explicitly as follows:

• For the $B_d^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays,

  $$\begin{aligned} A_\mathrm{CP}^\mathrm{dir}(B_d^0 \rightarrow \sigma \sigma )= & {} -57.38^{+6.91}_{-7.91} \times 10^{-2}, \nonumber \\ A_\mathrm{CP}^\mathrm{mix}(B_d^0 \rightarrow \sigma \sigma )= & {} -78.41^{+4.83}_{-3.85} \times 10^{-2}, \end{aligned}$$

  (96)
  $$\begin{aligned} A_\mathrm{CP}^\mathrm{dir}(B_d^0 \rightarrow \sigma f_0)= & {} -66.68^{+9.15}_{-10.08} \times 10^{-2}, \nonumber \\ A_\mathrm{CP}^\mathrm{mix}(B_d^0 \rightarrow \sigma f_0)= & {} -41.18^{+12.96}_{-10.58} \times 10^{-2}, \end{aligned}$$

  (97)
  $$\begin{aligned} A_\mathrm{CP}^\mathrm{dir}(B_d^0 \rightarrow f_0 f_0)= & {} -71.77^{+13.74}_{-11.31} \times 10^{-2}, \nonumber \\ A_\mathrm{CP}^\mathrm{mix}(B_d^0 \rightarrow f_0 f_0)= & {} 67.40^{+8.22}_{-10.62} \times 10^{-2}. \end{aligned}$$

  (98)

• For the $B_s^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays,

  $$\begin{aligned} A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow \sigma \sigma )= & {} 6.83^{+0.56}_{-0.47} \times 10^{-2}, \nonumber \\ A_\mathrm{CP}^\mathrm{mix}(B_s^0 \rightarrow \sigma \sigma )= & {} 8.69^{+1.17}_{-1.25} \times 10^{-2}, \end{aligned}$$

  (99)
  $$\begin{aligned} A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow \sigma f_0)= & {} 6.58^{+0.93}_{-0.88} \times 10^{-2}, \nonumber \\ A_\mathrm{CP}^\mathrm{mix}(B_s^0 \rightarrow \sigma f_0)= & {} 7.04^{+1.55}_{-1.66} \times 10^{-2}, \end{aligned}$$

  (100)
  $$\begin{aligned} A_\mathrm{CP}^\mathrm{dir}(B_s^0 \rightarrow f_0 f_0)= & {} -6.45^{+1.46}_{-1.51} \times 10^{-2}, \nonumber \\ A_\mathrm{CP}^\mathrm{mix}(B_s^0 \rightarrow f_0 f_0)= & {} 2.24^{+0.75}_{-0.69} \times 10^{-2}, \end{aligned}$$

  (101)

  and

  $$\begin{aligned} A_\mathrm{CP}^\mathrm{\Delta \Gamma _s}(B_s^0 \rightarrow \sigma \sigma )= & {} 99.39^{+0.12}_{-0.14} \times 10^{-2}, \nonumber \\ A_\mathrm{CP}^\mathrm{\Delta \Gamma _s}(B_s^0 \rightarrow \sigma f_0)= & {} 99.53^{+0.12}_{-0.10} \times 10^{-2}, \end{aligned}$$

  (102)
  $$\begin{aligned} A_\mathrm{CP}^\mathrm{\Delta \Gamma _s}(B_s^0 \rightarrow f_0 f_0)= & {} 99.77^{+0.09}_{-0.12} \times 10^{-2}. \end{aligned}$$

  (103)

By combining all the numerical results on the CP-averaged branching ratios and the CP violations for the neutral B-meson decays into $\sigma \sigma$, $\sigma f_0$, and $f_0 f_0$ at both of $\varphi \sim +25^\circ$ and $\varphi \sim -25^\circ$ in the PQCD approach, it is expected that the near future experiments could find some useful information on the magnitude and/or the sign of the mixing angle $\varphi$, especially in the $B_s^0 \rightarrow \sigma \sigma$ and $\sigma f_0$ channels.

4 Conclusions and summary

In this paper, we have investigated the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0,$ and $f_0 f_0$ decays through calculating the observables such as the CP-averaged branching ratios and the CP-violating asymmetries within the framework of PQCD approach. Due to the undetermined inner structure of the light scalars below 1 GeV in the hadron sector, we made this PQCD analysis by considering the $\sigma$ and $f_0$ as the conventional two-quark-structure mesons in the product of B meson decays. With the referenced value $\sim \pm 25^\circ$ of the mixing angle $\varphi$ in the quark-flavor basis, the numerical results in the PQCD formalism show that all the six decay channels of neutral B-meson decays into $\sigma \sigma , \sigma f_0$, and $f_0 f_0$ have large decay rates and are expected to be confronted with the related experiments through the four-body modes with $\sigma /f_0 \rightarrow \pi ^+ \pi ^-$ in the (near) future. Of course, if the $f_0 \rightarrow K^+ K^-$ could be identified clearly from the tail of the $\phi \rightarrow K^+ K^-$, then some of the four-body modes such as $B_{d,s}^0 \rightarrow \sigma (\rightarrow \pi ^+ \pi ^-) f_0(\rightarrow K^+ K^-)$ and $B_s^0 \rightarrow f_0(\rightarrow \pi ^+ \pi ^-/ K^+ K^-) f_0(\rightarrow K^+ K^-)$ could also be examined in the future experiments. It is worth mentioning that, different from those in the $B \rightarrow PP, PV, VV$ decays, the non-factorizable emission diagrams of the $B_{d,s}^0 \rightarrow \sigma \sigma , \sigma f_0, f_0 f_0$ decays in this work give large contributions because of the anti-symmetric behavior of the leading-twist distribution amplitude of the scalar mesons. The effective constraints from experiments and/or the reliable calculations from Lattice QCD are very important for studying the light scalars in the heavy meson decays. Relative to the $B_s^0$ decays with suppressed tree amplitudes, the significant interferences between both of the large tree and penguin amplitudes in the $B_d^0$ decays contribute to the large direct CP violations. It is expected that these related PQCD analyses could provide useful information to constrain both magnitude and sign of the mixing angle $\varphi$ between the $\sigma$ and $f_0$ with the help of the future precise measurements. Honestly speaking, the determination of the mixing angle $\varphi$ with its magnitude and sign indeed rely on the sound constraints on the light-cone distribution amplitudes of scalar flavor states $f_n$ and $f_s$ at both of theoretical and experimental aspects. Of course, the possible final state interactions or re-scattering effects, though existed as they should be, have to be left for future studies elsewhere.