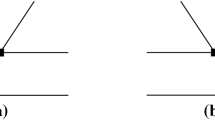Phenomenological studies on neutral B-meson decays into $J/\psi f_1$ and $\eta _c f_1$

Abstract

The axial-vector mesons $f_1(1285)$ and $f_1(1420)$ are particularly viewed as the mixtures of flavor states $f_n$ and $f_s$ with mixing angle $\varphi$. In order to determine this angle, we study the $B_{d,s}^0\rightarrow J/\psi f_1(1285,1420)$ and $B_{d,s}^0\rightarrow \eta _c f_1(1285,1420)$ decays in perturbative QCD (PQCD) approach, including the effects of vertex corrections, nonfactorizable diagrams and penguin operators. Not only the branching fractions, but also the direct CP asymmetries and the polarization fractions are calculated. It is found that the branching fractions of these decays are large enough to be measured in the running LHCb and Belle-II experiments. Moreover, in comparison with the observed ${\mathcal {B}}(B_{d,s}^0 \rightarrow J/\psi f_1(1285))$, $B_s^0 \rightarrow (J/\psi , \eta _c) f_1(1420)$ decays have large branching fractions, which could be measured promisingly through $f_1(1420) \rightarrow K_S^0 K^\pm \pi ^\mp$ in experiments. We also propose several ratios that could be used to further constrain the absolute value of the mixing angle $\varphi$, but its sign cannot be determined yet in these decays. The direct CP asymmetries of these decays indicate the penguin pollution in the $B_d^0 \rightarrow (J/\psi , \eta _c) f_1$ decays cannot be neglected. We acknowledge that there are large theoretical uncertainties arising from the distribution amplitudes of axial-vector mesons and charmonium states, and more precise nonperturbative parameters are called. The comparisons between our results and future experimental data would help us to understand the nature of $f_1$ states and to test the PQCD approach.

1 Introduction

In the quark model, two nonets of $J^P = 1^+$ axial-vector mesons are expected as the orbital excitation of the ${\bar{q}}q$ system. In terms of the spectroscopic notation $^{2S+1}L_J$, there are two types of P-wave axial-vector mesons, namely, $^{3}P_{1}$ and $^{1}P_{1}$. These two nonets have distinctive C quantum numbers for the corresponding neutral mesons, $C=+$ and $C=-$, respectively [1,2,3]. The light axial-vector $f_1$ states, namely, $f_1(1285)$ and $f_1(1420)$, accompanied with $a_{1}(1260)$ and $K_{1A}$, are categorized as the $1^{++}$ multiplets, while the $1^{+-}$ multiplets incorporate $b_{1}(1235), h_{1}(1170), h_{1}(1380)$ and $K_{1B}$ [4, 5]. Although lots of efforts have been made to investigate these light axial-vectors [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], our understanding on their natures is still far from satisfactory [6]. Similar to the $\eta -\eta ^\prime$ mixing in the pseudoscalar sector, two physical $f_1$ mesons (For convenience, we will adopt $f_1$ to denote the $f_1(1285)$ and $f_1(1420)$ mesons in the following context, unless otherwise stated.) are generally viewed as the mixtures of two flavor states $f_n( \equiv ({\bar{u}} u+ {\bar{d}} d)/{\sqrt{2}})$ and $f_s( \equiv {\bar{s}} s)$ with a single mixing angle $\varphi$, which can be written as

$$\begin{aligned} \left( \begin{array}{c} f_1(1285)\\ f_1(1420) \\ \end{array} \right)= & {} \left( \begin{array}{cc} \cos {\varphi } &{} -\sin {\varphi } \\ \sin {\varphi } &{} \; \;\ \cos {\varphi } \end{array} \right) \left( \begin{array}{c} f_{n}\\ f_{s} \\ \end{array} \right) . \end{aligned}$$

(1)

However, both the magnitude and the sign of the mixing angle $\varphi$ have not been determined yet. In addition, in light of Gell-mann–Okubo mass relation, this mixing angle $\varphi$ could provide constraints to the unique mixing between the $K_{1A}(1^3P_1)$ and $K_{1B}(1^1P_1)$ states for the axial-vector strange $K_1$ mesons [1]. In order to study the mixing angle $\varphi$, besides the $f_1$ mesons decays, the productions of $f_1$ mesons in the nonleptonic decays of heavy mesons could also be used. With this strategy, many B decays to $f_1$ have been explored in the literature [13, 14, 20,21,22,23,24,25,26].

In 2013, LHCb collaboration reported their first measurements of the branching fractions of $B_{d,s}^0 \rightarrow J/\psi f_1(1285)$ decays as follows [27],

$$\begin{aligned}&{\mathcal {B}}(B_d^0 \rightarrow J/\psi f_1(1285))_{\mathrm{Exp}}=(8.37^{+2.10}_{-2.09}) \times 10^{-6}, \end{aligned}$$

(2)

$$\begin{aligned}&{\mathcal {B}}(B_s^0 \rightarrow J/\psi f_1(1285))_{\mathrm{Exp}}=(7.14^{+1.36}_{-1.41}) \times 10^{-5}, \end{aligned}$$

(3)

where the uncertainties from different sources have been added in quadrature. It is found that the uncertainties are still large, and are expected to be reduced in the on-going LHCb and Belle-II experiments. Using the SU(3) symmetry and neglecting the contributions from penguin operators, the mixing angle $\varphi$ was extracted to be $\varphi ^{\mathrm{Exp}}= \pm (24.0^{+3.1+0.6} _{-2.6-0.8})^\circ$ [27]. In Ref. [20], two of us (Liu and Xiao) had studied $B_s^0 \rightarrow J/\psi f_1(1285)$ decay and obtained $|\varphi ^{\mathrm{Theo}}| \sim 15^\circ$, where the large errors arose from large theoretical uncertainties of the branching fraction. Although both $|\varphi ^{\mathrm{Theo}}|$ and $|\varphi ^{\mathrm{Exp}}|$ locate in the range proposed by Stone and Zhang [18], the evident discrepancy still demands further explorations.

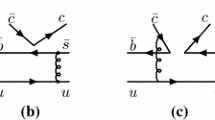
It is the purpose of this article to analyze the $B_{d,s}^0 \rightarrow J/\psi f_1$ decays and to search for new observables for determination of the mixing angle, and the quark level Feynman diagrams for these decays are illustrated in Fig. 1. The B-meson decays with a charmonium state have been studied extensively in the QCD-inspired approaches [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43]. In this article we focus on the perturbative QCD (PQCD) approach to non-leptonic B-decays [44,45,46]. It is a model-independent framework that systematically disentangles short-distance (perturbative) from long-distance (non-perturbative) effects based on the $k_T$ factorization, and the basic concepts will be given in next section. It is found that for the color-suppressed modes, the contributions beyond leading order (LO) play important roles in explaining the experimental data. For instance, $B \rightarrow J/\psi V$ and $B \rightarrow \eta _c V$ decays have been studied in PQCD approach in Refs. [42, 43] associated with the next-to-leading order (NLO) contributions, namely, the vertex corrections and the NLO Wilson coefficients, and the theoretical predictions are improved to basically agree with current data [4, 5]. Recently, the Sudakov factor for charmonium that plays critical roles in suppressing the long-distance contributions was derived, which affects the observables of the decays with charmonium remarkably [47, 48]. With above new ingredients, we will reexamine the decays $B_s^0 \rightarrow J/\psi f_1$ [20] and evaluate the modes $B_d^0 \rightarrow J/\psi f_1$ and $B^0 \rightarrow \eta _c f_1$ for the first time, and will provide predictions of the branching fractions, polarization fractions, relative phases and CP asymmetries. Within the experimental data, the branching fractions could help us constrain $|\varphi |$ effectively, while other observables are helpful to further understand the QCD of $f_1$. Moreover, as pointed out in Refs. [12,13,14,15], the QCD behavior of $1^{++}$ axial-vector meson is very similar to that of $1^{--}$ vector, then it is natural to expect some important information provided by the considered $B_s^0$ decay modes, relative to the golden channel $B_s^0 \rightarrow J/\psi \phi$. For example, $B_s^0 \rightarrow J/\psi f_1(1420)$ and $B_s^0 \rightarrow \eta _c f_1(1420)$ decays might serve as the alternative channels to explore the $B_s^0-{\bar{B}}_s^0$ mixing phase $\phi _s$ in a supplementary manner, provided that the mixing angle has been well determined by other ways. After all, it is an unarguable fact that the exclusive decays of neutral B-meson into charmonium have attracted great attention in the past decades at both theoretical and experimental aspects, as they can play special roles in studies of CP asymmetries [49] and $B^0-{\bar{B}}^0$ mixing phases.

Fig. 1

Leading quark-level Feynman diagrams for neutral B-meson decays into $J/\psi f_1$ and $\eta _c f_1$

The paper is organized as follows. In Sect. 2, we shortly review the formalism of PQCD approach in association with the meson wave functions, and then present the perturbative calculations of considered decays. The analytic expressions of decay amplitudes are also collected in this section. In Sect. 3, we perform the numerical evaluations and discuss the theoretical results. Finally, a brief summary of this work is given in Sect. 4.

2 Formalism and perturbative QCD calculations

We consider the B meson at rest for simplicity. For the decays $B^0 \rightarrow M_{c{\bar{c}}} f_1$ with $M_{c{\bar{c}}}$ denoting the $J/\psi$ and $\eta _c$, $M_{c{\bar{c}}}$ and $f_{1}$ are assumed to move in the plus and minus z-directions, respectively. In the light-cone coordinate, the B meson momentum $P_1$, the charmonium momentum $P_2$ and $f_1$ meson momentum $P_3$ are taken to be:

$$\begin{aligned}&P_{1}=\frac{m_{B}}{\sqrt{2}}(1, 1, \mathbf{0}_{T}), \quad P_{2}= \frac{m_{B}}{\sqrt{2}}(1-r_{3}^{2}, r_{2}^{2}, \mathbf{0}_{T}), \nonumber \\&P_{3}=\frac{m_{B}}{\sqrt{2}}(r_{3}^{2}, 1-r_{2}^{2}, \mathbf{0}_{T}), \end{aligned}$$

(4)

and the polarization vectors $\epsilon _2$ of $J/\psi$ and $\epsilon _3$ of $f_1$ as,

$$\begin{aligned} \epsilon _{2L}= & {} \frac{1}{\sqrt{2(1-r_{3}^{2})} r_{2}}(1-r_{3}^{2}, -r_{2}^{2}, \mathbf{0}_{T}),\!\! \quad \epsilon _{2T}=(0,0, \mathbf{1}_{T}) ,\nonumber \\ \end{aligned}$$

(5)

and

$$\begin{aligned} \epsilon _{3L}= & {} \frac{1}{\sqrt{2(1-r_{2}^{2})} r_{3}}(-r_{3}^{2}, 1-r_{2}^{2}, \mathbf{0}_{T}), \!\!\quad \epsilon _{3T}=(0,0, \mathbf{1}_{T}), \nonumber \\ \end{aligned}$$

(6)

where the ratios $r_{2}=m_{M_{c{\bar{c}}}}/m_{B}$ and $r_{3}=m_{f_{1}}/m_{B}$. Due to the conservation of the angular momentum, only the longitudinal polarization vector $\epsilon _{3L}$ of $f_1$ contributes to the $B^0 \rightarrow \eta _c f_1$ decays. Denoting the (light-)quark momenta in the $B^0$, $M_{c{\bar{c}}}$ and $f_{1}$ mesons as $k_{1}$, $k_{2}$ and $k_{_{3}}$ correspondingly, we then have

$$\begin{aligned} \begin{aligned} k_{1}&= (x_{1}P_{1}^{+}, 0, \mathbf{k}_{1T}) = \left( \frac{m_{B}}{\sqrt{2}} x_{1}, 0, \mathbf{k}_{1T}\right) ,\\ k_{2}&=(x_{2}P_{2}^{+}, x_{2}P_{2}^{-}, \mathbf{k}_{2T}) = \left( \frac{m_{B}}{\sqrt{2}} x_{2}(1-r_{3}^{2}), \frac{m_{B}}{\sqrt{2}} x_{2} r_{2}^{2}, \mathbf{k}_{2T}\right) , \\ k_{3}&=(x_{3}P_{3}^{+}, x_{3}P_{3}^{-}, \mathbf{k}_{3T}) = \left( \frac{m_{B}}{\sqrt{2}} x_{3}r_{3}^{2}, \frac{m_{B}}{\sqrt{2}} x_{3}(1-r_{2}^{2}), \mathbf{k}_{3T}\right) . \end{aligned} \end{aligned}$$

(7)

For the considered decays $B^0 \rightarrow M_{c{\bar{c}}} f_1$, the effective Hamiltonian $H_{\mathrm{eff}}$ could be read as [50]

$$\begin{aligned} H_{\mathrm{eff}}= & {} \frac{G_F}{\sqrt{2}} \left\{ V^*_{cb}V_{cq} \left[ C_1(\mu )O_1^{c}(\mu ) +C_2(\mu )O_2^{c}(\mu ) \right] \right. \nonumber \\&\left. - V^*_{tb}V_{tq} \left[ \sum _{i=3}^{10}C_i(\mu )O_i(\mu ) \right] \right\} , \end{aligned}$$

(8)

where the light quark $q=d$ or s, the Fermi constant $G_F=1.16639\times 10^{-5}~{\mathrm{GeV}}^{-2}$, $V_{ij}$ represents the Cabibbo–Kobayashi–Maskawa (CKM) matrix element, and $C_i(\mu )$ is Wilson coefficients corresponding to the effective operator $O_i$ at the renormalization scale $\mu$. The local four-quark operators $O_i(i=1,\ldots ,10)$ are given as

• Tree operators

  $$\begin{aligned}&O_1^{c} =(\bar{q}_\alpha c_\beta )_{V-A}(\bar{c}_\beta b_\alpha )_{V-A}, \nonumber \\&O_2^{c} =(\bar{q}_\alpha c_\alpha )_{V-A}(\bar{c}_\beta b_\beta )_{V-A}, \end{aligned}$$

  (9)

• QCD penguin operators

  $$\begin{aligned}&O_3 =(\bar{q}_\alpha b_\alpha )_{V-A}\sum _{q'}(\bar{q}'_\beta q'_\beta )_{V-A}, \nonumber \\&O_4 = (\bar{q}_\alpha b_\beta )_{V-A}\sum _{q'}(\bar{q}'_\beta q'_\alpha )_{V-A}, \nonumber \\&O_5 = (\bar{q}_\alpha b_\alpha )_{V-A}\sum _{q'}(\bar{q}'_\beta q'_\beta )_{V+A}, \nonumber \\&O_6 = (\bar{q}_\alpha b_\beta )_{V-A}\sum _{q'}(\bar{q}'_\beta q'_\alpha )_{V+A}. \end{aligned}$$

  (10)

• Electroweak penguin operators

  $$\begin{aligned}&O_7 = \frac{3}{2}(\bar{q}_\alpha b_\alpha )_{V-A}\sum _{q'}e_{q'}(\bar{q}'_\beta q'_\beta )_{V+A},\nonumber \\&O_8 = \frac{3}{2}(\bar{q}_\alpha b_\beta )_{V-A}\sum _{q'}e_{q'}(\bar{q}'_\beta q'_\alpha )_{V+A}, \nonumber \\&O_9 = \frac{3}{2}(\bar{q}_\alpha b_\alpha )_{V-A}\sum _{q'}e_{q'}(\bar{q}'_\beta q'_\beta )_{V-A},\nonumber \\&O_{10}= \frac{3}{2}(\bar{q}_\alpha b_\beta )_{V-A}\sum _{q'}e_{q'}(\bar{q}'_\beta q'_\alpha )_{V-A}, \end{aligned}$$

  (11)

where $\alpha$ and $\beta$ are the color indices and $q^\prime$ are the active quarks at the scale $m_b$, i.e. $q^\prime =(u,d,s,c,b)$. The left handed current is defined as $({\bar{q}}^{\prime }_{\alpha } q^{\prime }_{\beta } )_{V-A}= {\bar{q}}^{\prime }_{\alpha } \gamma _\nu (1-\gamma _5) q^{\prime }_{\beta }$ and the right handed current $({\bar{q}}^{\prime }_{\alpha } q^{\prime }_{\beta } )_{V+A}= {\bar{q}}^{\prime }_{\alpha } \gamma _\nu (1+\gamma _5) q^{\prime }_{\beta }$. For convenience, the combination $a_{i}$ of the Wilson coefficients is defined as [46, 51]

$$\begin{aligned}&a_1= C_2+C_1/3,\quad a_3= C_3+C_4/3,\quad a_5= C_5+C_6/3,\nonumber \\&\quad a_7= C_7+C_8/3,\quad a_9= C_9+C_{10}/3,\nonumber \\&a_2= C_1+C_2/3,\quad a_4= C_4+C_3/3,\quad a_6= C_6+C_5/3,\nonumber \\&\quad a_8= C_8+C_7/3,\quad a_{10}= C_{10}+C_{9}/3. \end{aligned}$$

(12)

Under the factorization hypothesis, the amplitude of $B^0 \rightarrow M_{c{\bar{c}}} f_1$ decay in PQCD can be written conceptually as follows [44,45,46],

$$\begin{aligned}&{\mathcal {A}}(B^0 \rightarrow M_{c{\bar{c}}} f_1) \sim \int \!\! d x_1 d x_2 d x_3 b_1 d b_1 b_2 d b_2 b_3 d b_3 \nonumber \\&\quad \times \mathrm{Tr} [ C(t) \Phi _{B}(x_1, b_1) \Phi _{M_{c{\bar{c}}}}(x_2, b_2) \Phi _{f_1}(x_3, b_3) \nonumber \\&\quad \times H(x_i, b_i, t) S_t(x_i)\, e^{-S(t)}], \end{aligned}$$

(13)

where C(t) stands for the corresponding Wilson coefficient. $x_{i}(i=1,2,3)$ denotes the fraction of momentum carried by (light-)quark inside the meson, and $b_{i}$ is the conjugate space coordinate of transverse momentum $k_{iT}$. The wave function $\Phi$ describes the hadronization of quark and antiquark into a meson, and it is nonperturbative in nature but universal. The hard kernel $H(x_i, b_i, t)$ involves the dynamics associated with the effective “six-fermion interaction” by exchanging a hard gluon [44, 45, 52, 53], where t is the largest energy scale involved in the hard part. The rest two factors, namely, the Sudakov factor $e^{-S(t)}$ and the jet function $S_t(x_i)$ as shown in the above Eq. (13), play important roles on the effective evaluations of B-meson decay amplitude in PQCD, which is based on the $k_T$ factorization theorem. The Sudakov factor $e^{-S(t)}$ suppresses the soft dynamics effectively, which makes perturbative calculation of the hard part H applicable at intermediate scale [54, 55]. The jet function $S_t(x_i)$ smears the endpoint singularities with threshold resummation technique [56, 57]. Recently, the Sudakov factor for charmonium up to the next-to-leading-logarithm accuracy has been derived in Refs. [47, 48], where the effects of the charm quark mass are also included. In this work, we will adopt the new factor. Besides, more concepts of PQCD can be found in Ref. [58]. In recent years, several developments on this approach have been obtained, for a review, see, e.g. [59, 60].

2.1 Meson wave functions

As aforementioned, the nonperturbative meson wave functions and the related distribution amplitudes are the most important inputs in PQCD, which are universal and usually determined within the experimental data or the nonperturbative techniques, such as QCD sum rule or Lattice QCD.

For the B meson wave function, we adopt the form used widely in the literature [44, 45, 52, 53, 58], which is expressed as

(14)

$N_c=3$ being the color factor. $\phi _B$ is the leading-twist B-meson distribution amplitude, and x and $\mathbf{k}_T$ are the momentum fraction and the intrinsic transverse momentum of light quark in B meson, respectively. The subscripts $\alpha$ and $\beta$ are the color indices.

For charmonium states $J/\psi$ and $\eta _c$, their wave functions have been studied within the non-relativistic QCD approach [61]. For the vector $J/\psi$ meson, the longitudinal and transverse wave functions are given as,

(15)

(16)

Here, $\epsilon _{L}$ and $\epsilon _{T}$ are the two polarization vectors of $J/\psi$, $\phi ^{L}_{J/\psi }(x)$ and $\phi ^{T}_{J/\psi }(x)$ are the twist-2 distribution amplitudes, while $\phi ^{t}_{J/\psi }(x)$ and $\phi ^{v}_{J/\psi }(x)$ are the twist-3 ones. For the pseudoscalar $\eta _{c}$ meson, its wave function could be read as,

(17)

where $\phi _{\eta _{c}}^{v}(x)$ and $\phi _{\eta _{c}}^{s}(x)$ are the twist-2 and twist-3 distribution amplitudes, respectively.

For the light axial-vector $f_{q}$ with $q=n$ or s, its wave function could be written as follows [12, 62],

(18)

(19)

where x denotes the momentum fraction carried by quark in $f_q$, $n=(1,0,\mathbf{0}_T)$ and $v=(0,1,\mathbf{0}_T)$ are the dimensionless lightlike vectors, the Levi-Cività tensor $\epsilon ^{\mu \nu \alpha \beta }$ is conventionally taken as $\epsilon ^{0123}=1$. It should be stressed that $m_{f_q}$ stands for the mass of $f_q$ obtained through the following mass relations [63],

$$\begin{aligned} m_{f_n}^2= & {} m_{f_1(1285)}^2 \cos ^2\varphi + m_{f_1(1420)}^2 \sin ^2\varphi , \end{aligned}$$

(20)

$$\begin{aligned} m_{f_s}^2= & {} m_{f_1(1285)}^2 \sin ^2\varphi + m_{f_1(1420)}^2 \cos ^2\varphi , \end{aligned}$$

(21)

with $m_{f_1(1285)}$ and $m_{f_1(1420)}$ being the masses of physical states $f_1(1285)$ and $f_1(1420)$, respectively.

For the sake of simplicity, the distribution amplitudes in the above wave functions have been collected in Appendix A. With the above essential hadronic inputs, we can then proceed with perturbative calculations of the $B^0 \rightarrow M_{c{\bar{c}}} f_1$ decay amplitudes within the framework of PQCD approach.

2.2 Perturbative calculations

It can be seen from Fig. 1 that for the $B_d^0 \rightarrow M_{c{\bar{c}}} f_1$ decays, the spectator d quark enters the final axial vector meson $f_1$, therefore only $f_n$ component contributes to the decays with mixing angles. Similarly, only $f_s$ component contributes to the $B_s^0 \rightarrow M_{c{\bar{c}}} f_1$ decays. According to the effective Hamiltonian Eq. (8), the lowest-order (LO) Feynman diagrams are summarized in Fig. 2 for $B \rightarrow M_{c{\bar{c}}} f_1$ decays, where the first two diagrams are called factorizable and the last two diagrams are the non-factorizable diagrams. Due to the fact that the behavior of axial vector in $B \rightarrow M_{c{\bar{c}}} f_1$ decays is very similar to that of vectors, the amplitudes F for the factorizable diagrams and M for the nonfactorizable ones are almost same as those of decays $B \rightarrow (J/\psi , \eta _c) V$ decays. In this case, we will not list them in current work, and the readers are referred to Refs. [42, 43] for detail. It should be stressed that the term $\sqrt{1-r_2^2}$ in the denominator of the longitudinal polarization vector $\epsilon _{3L}$ is kept in Eq. (6), while it has been neglected in Ref. [42].

Fig. 2

Typical Feynman diagrams for neutral B-meson decays into $J/\psi f_{1}$ and $\eta _c f_1$ at LO in the PQCD approach

Fig. 3

Vertex corrections to neutral B-meson decays into $J/\psi f_{1}$ and $\eta _c f_1$

In Refs. [28,29,30,31,32,33,34,35, 37], it was found that for the color-suppressed processes, such as B-meson decays into charmonium states, the vertex corrections play so important roles in explaining the experimental data that cannot be neglected. For this reason, the vertex corrections in $B^0 \rightarrow M_{c{\bar{c}}} f_1$ decays as illustrated in Fig. 3 should be included, and their effects are embodied by modifying the Wilson coefficients in the factorizable emission diagrams, leading to the effective Wilson coefficients $\tilde{a}_i^h (i=2,3,5,7,9)$ as follows,

$$\begin{aligned} a_2\rightarrow & {} \tilde{a}_{2}^{h} = a_2 +\frac{\alpha _{s}}{4\pi }\frac{C_{F}}{N_{c}}C_{2} \biggl (-18+12\ln \frac{m_{b}}{\mu }+f_{I}^{h}\biggr ), \end{aligned}$$

(22)

$$\begin{aligned} a_3\rightarrow & {} \tilde{a}_{3}^{h} = a_3 +\frac{\alpha _{s}}{4\pi }\frac{C_{F}}{N_{c}}C_{4} \biggl (-18+12\ln \frac{m_{b}}{\mu }+f_{I}^{h}\biggr ), \end{aligned}$$

(23)

$$\begin{aligned} a_5\rightarrow & {} \tilde{a}_{5}^{h} = a_5 +\frac{\alpha _{s}}{4\pi }\frac{C_{F}}{N_{c}}C_{6} \biggl (6-12\ln \frac{m_{b}}{\mu }-f_{I}^{h}\biggr ), \end{aligned}$$

(24)

$$\begin{aligned} a_7\rightarrow & {} \tilde{a}_{7}^{h} = a_7 +\frac{\alpha _{s}}{4\pi }\frac{C_{F}}{N_{c}}C_{8} \biggl (6-12\ln \frac{m_{b}}{\mu }-f_{I}^{h}\biggr ), \end{aligned}$$

(25)

$$\begin{aligned} a_9\rightarrow & {} \tilde{a}_{9}^{h} = a_9 +\frac{\alpha _{s}}{4\pi }\frac{C_{F}}{N_{c}}C_{10} \biggl (-18+12\ln \frac{m_{b}}{\mu }+f_{I}^{h}\biggr ). \nonumber \\ \end{aligned}$$

(26)

In above formulae, the function $f_{I}^{h}$ with helicities $h=0,\pm$ are defined as:

$$\begin{aligned} f_{I}^{0}= & {} f_{I}+g_{I}(1-r_{2}^{2}), \quad f_I^{\pm }=f_{I}, \end{aligned}$$

(27)

where the explicit expressions for the functions $f_I$ and $g_I$ can be found in Ref. [29].

We also note that in the LO calculations we used the LO Wilson coefficients $C_{i}(m_{W})$ and the LO renormalization group evolution matrix $U(t,m)^{(0)}$ for the Wilson coefficient associating with the LO running coupling $\alpha _{s}$,

$$\begin{aligned} \alpha _{s}(t)=\frac{4\pi }{\beta _{0}\ln [t^{2}/\Lambda _\mathrm{QCD}^{2}]}, \end{aligned}$$

(28)

where $\beta _{0}=(33-2N_{f})/3$. In the NLO contributions, it is natural for us to adopt the NLO Wilson coefficients $C_{i}(m_{W})$ and the NLO renormalization group evolution matrix $U(t,m,\alpha )$ with the running coupling $\alpha _{s}(t)$ at two-loop [50],

$$\begin{aligned} \alpha _{s}(t)\!=\!\frac{4\pi }{\beta _{0}\ln (t^{2}/\Lambda _\mathrm{QCD}^{2})}\cdot \left\{ 1-\frac{\beta _{1}}{\beta _{0}^{2}}\cdot \frac{\ln [\ln (t^{2}/\Lambda _\mathrm{QCD}^{2})]}{\ln (t^{2}/\Lambda _\mathrm{QCD}^{2})}\right\} ,\nonumber \\ \end{aligned}$$

(29)

where $\beta _{1}=(306-38N_{f})/3$. For the hadronic scale $\Lambda _\mathrm{QCD}$, $\Lambda _\mathrm{QCD}^{(4)}=0.287$ GeV (0.326 GeV) could be arrived within $\Lambda _\mathrm{QCD}^{(5)}=0.225$ GeV for the LO (NLO) case. In addition, we set $\mu _{0}=1.0$ GeV [64] as the lower cut-off for the hard scale t.

With the amplitudes of each diagrams in Fig. 2, the amplitude of $B^0 \rightarrow J/\psi f_{q}$ decay could be written as

$$\begin{aligned}&\xi A^{\sigma }(B_{d(s)}^0 \rightarrow J/\psi f_{n(s)}) = F_{J/\psi }^{\sigma } \biggl \{ V_{cb}^* V_{cd(s)} \tilde{a}^\sigma _{2}\nonumber \\&\quad -V_{tb}^* V_{td(s)} \biggl ( \tilde{a}^\sigma _{3}+\tilde{a}^\sigma _{5} +\tilde{a}^\sigma _{7}+\tilde{a}^\sigma _{9}\biggr ) \biggr \} \nonumber \\&\quad +M_{J/\psi }^\sigma \biggl \{V_{cb}^* V_{cd(s)} C_{2} -V_{tb}^* V_{td(s)}\nonumber \\&\quad \times \biggl ( C_{4}-C_{6}-C_{8}+C_{10}\biggr ) \biggr \}, \end{aligned}$$

(30)

with $\xi =\sqrt{2}$ and $\xi =1$ for $f_n$ and $f_s$, respectively. The superscript $\sigma (= L, N, T)$ denotes the helicity state of the final states. Combining above amplitude and the quark-flavor mixing scheme as shown in Eq. (1), we finally obtain the amplitudes of the $B^0 \rightarrow J/\psi f_{1}$ decays,

• (1) For $B_d^0 \rightarrow J/\psi f_1$ decays,

  $$\begin{aligned} {\mathcal {A}}^{\sigma }(B_{d}^{0}\rightarrow J/\psi f_{1}(1285))= & {} A^{\sigma }(B_{d}^{0}\rightarrow J/\psi f_{n}) \cos \varphi ,\nonumber \\ \end{aligned}$$

  (31)
  $$\begin{aligned} {\mathcal {A}}^{\sigma }(B_{d}^{0}\rightarrow J/\psi f_{1}(1420))= & {} A^{\sigma }(B_{d}^{0}\rightarrow J/\psi f_{n}) \sin \varphi .\nonumber \\ \end{aligned}$$

  (32)

• (2) For $B_s^0 \rightarrow J/\psi f_1$ decays,

  $$\begin{aligned} {\mathcal {A}}^{\sigma }(B_{s}^{0}\!\rightarrow \! J/\psi f_{1}(1285))= & {} - A^{\sigma }(B_{s}^{0}\rightarrow J/\psi f_{s}) \sin \varphi , \nonumber \\ \end{aligned}$$

  (33)
  $$\begin{aligned} {\mathcal {A}}^{\sigma }(B_{s}^{0}\!\rightarrow \! J/\psi f_{1}(1420))= & {} A^{\sigma }(B_{s}^{0}\rightarrow J/\psi f_{s}) \cos \varphi . \nonumber \\ \end{aligned}$$

  (34)

Now, we turn to the amplitudes of $B^0 \rightarrow \eta _c f_1$ decays. Similarly, the amplitudes of $B^0 \rightarrow \eta _{c} f_{1}$ decays at NLO could be obtained straightforwardly by replacing the information of vector $J/\psi$ with that of pseudoscalar $\eta _c$ in Eqs. (30)–(34). Of course, only the longitudinal contributions of $f_1$ mesons contribute to the $B^0 \rightarrow \eta _c f_1$ decays, because of the conservation of the angular momentum. Therefore, we have

$$\begin{aligned}&\xi A(B_{d(s)}^{0} \rightarrow \eta _{c} f_{n(s)}) = F_{\eta _c} \biggl \{ V_{cb}^{*} V_{cd(s)} \tilde{a}_{2}-V_{tb}^{*} V_{td(s)}\nonumber \\&\quad \times \biggl ( \tilde{a}_{3}- \tilde{a}_{5}- \tilde{a}_{7}+ \tilde{a}_{9}\biggr ) \biggr \} \nonumber \\&\quad \!\!+M_{\eta _c} \biggl \{V_{cb}^{*} V_{cd(s)} C_{2} \!-\!V_{tb}^{*} V_{td(s)} \biggl ( C_{4}\!-\!C_{6}\!-\!C_{8}\!+\!C_{10}\biggr ) \biggr \}.\nonumber \\ \end{aligned}$$

(35)

Here, the effective Wilson coefficients $\tilde{a}_i$ have included the related vertex corrections with new functions $f^\prime _I$ and $g^\prime _I$ that arise from $\eta _c$ emission [30]. The explicit expressions of $f^{(\prime )}_{I}$ and $g^\prime _I$ can be found in Refs. [29, 30, 42, 43]. Also, the amplitudes of $B^0 \rightarrow \eta _c f_{1}$ decays could be read as follows,

• (1) For $B_d^0 \rightarrow \eta _c f_1$ decays,

  $$\begin{aligned} {\mathcal {A}}(B_{d}^{0}\rightarrow \eta _c f_{1}(1285))= & {} A(B_{d}^{0}\rightarrow \eta _c f_{n}) \cos \varphi , \end{aligned}$$

  (36)
  $$\begin{aligned} {\mathcal {A}}(B_{d}^{0}\rightarrow \eta _c f_{1}(1420))= & {} A(B_{d}^{0}\rightarrow \eta _c f_{n}) \sin \varphi . \end{aligned}$$

  (37)

• (2) For $B_s^0 \rightarrow \eta _c f_1$ decays,

  $$\begin{aligned} {\mathcal {A}}(B_{s}^{0}\rightarrow \eta _c f_{1}(1285))= & {} - A(B_{s}^{0}\rightarrow \eta _c f_{s}) \sin \varphi , \end{aligned}$$

  (38)
  $$\begin{aligned} {\mathcal {A}}(B_{s}^{0}\rightarrow \eta _c f_{1}(1420))= & {} A(B_{s}^{0}\rightarrow \eta _c f_{s}) \cos \varphi . \end{aligned}$$

  (39)

As a matter of fact, using these decay channels, we can only extract the absolute value $|\varphi |$ of the mixing angle. In order to determine its sign, we have to resort to other decays that the interference between $f_n$ and $f_s$ is involved, such as $B \rightarrow M f_1$ with M being the open-charmed and charmless mesons [41].

3 Numerical results and discussions

In this section, we will perform numerical calculations based on the given analytic expressions to estimate the experimental observables in the $B^0 \rightarrow M_{c{\bar{c}}} f_1$ decays, such as the branching fractions and the direct CP asymmetries. Furthermore, the results of the polarization fractions in the decays $B^0 \rightarrow J/\psi f_1$ are also discussed.

3.1 Input parameters

In the numerical calculations, the input parameters such as meson masses (GeV), decay constants (GeV) and B-meson lifetimes (ps) will be listed [4, 12, 63]:

$$\begin{aligned}&m_W = 80.41, \quad m_{B_d^0}= 5.28, \quad m_{B_s^0}= 5.37, \quad \nonumber \\&\quad m_b = 4.8 , \quad m_{c} = 1.50 , \nonumber \\&f_{J/\psi } = 0.405\pm 0.014 , \quad f_{\eta _{c}}=0.42\pm 0.05, \quad \nonumber \\&\quad f_{f_{n}} = 0.193 ^{+0.043}_{-0.038} , \quad f_{f_{s}} = 0.230 \pm 0.009,\nonumber \\&m_{J/\psi }=3.097, \quad m_{f_{1}(1285)} = 1.28, \quad \nonumber \\&\quad m_{f_{1}(1420)}= 1.43, \quad m_{\eta _{c}} = 2.98,\nonumber \\&\tau _{B_d^0}= 1.519, \quad \tau _{B_s^0}= 1.515. \end{aligned}$$

(40)

For CKM matrix elements, we adopt the Wolfenstein parameterization [65] and the updated parameters [4]: $A=0.790$, $\lambda =0.22650$, ${\bar{\rho }}=0.141_{-0.017}^{+0.016}$, ${\bar{\eta }}=0.357_{-0.011}^{+0.011}$, in which ${\bar{\rho }} \equiv \rho ( 1- \frac{\lambda ^2}{2})$ and ${\bar{\eta }} \equiv \eta (1- \frac{\lambda ^2}{2})$.

3.2 $B \rightarrow J/\psi f_1$

We firstly focus on the $B^0 \rightarrow J/\psi f_1$ decays. The branching fraction of $B^0 \rightarrow J/\psi f_{1}$ decay can be written as

$$\begin{aligned} {\mathcal {B}}(B^0 \rightarrow J/\psi f_1) = \tau _{B} \frac{G_{F}^{2}|\mathbf {p_c}|}{16 \pi m^{2}_{B} } \sum _{\sigma =L,N,T} {\mathcal {A}}^{(\sigma )\dagger } {\mathcal {A}}^{(\sigma )}, \end{aligned}$$

(41)

where $\tau _{B}$ is the lifetime of neutral B-meson, $|\mathbf {p_c}|\equiv |\mathbf {p_{2z}}|=|\mathbf {p_{3z}}|$ is the three-momentum of the two outgoing final states in the center-of-mass frame of B meson and ${\mathcal {A}}^\sigma$ denotes the helicity amplitudes of $B^0 \rightarrow J/\psi f_1$ modes as given in Eqs. (31)–(34).

For the mixing angle $\varphi$, we take both $|\varphi ^{\mathrm{Theo}}| \sim 15^\circ$ and $|\varphi ^{\mathrm{Exp}}| \sim 24^\circ$ as typical values to predict the ${\mathcal {B}}(B^0 \rightarrow J/\psi f_1)$ and further discuss them phenomenologically. By employing the decay amplitudes and various inputs, the CP-averaged branching fractions in the PQCD approach at NLO with uncertainties are presented in Table 1. We acknowledge that there are many uncertainties in our calculations, and four kinds of uncertainties are included here. The first uncertainties are from the wave function of B meson, and we adopt the variations of shape parameters $\omega _{B_d^0} = 0.40 \pm 0.04$ GeV and $\omega _{B_s^0} = 0.50 \pm 0.05$ GeV for $B_d^0$ and $B_s^0$, respectively. The second uncertainties come from the nonperturbative parameters in the wave functions of the final states, such as decay constants and the Gegenbauer moments, which are given in Appendix A. The third uncertainties arise from the higher-order and higher-power corrections, which are characterized by varying the running hard scale $t_{\mathrm{max}}$ with 20%, namely, from 0.8 to 1.2 t in the hard kernel. The last errors are induced by the variations of $|\varphi ^{\mathrm{Theo}}|=(15.0 \pm 1.5)^\circ ~( |\varphi ^{\mathrm{Exp}}| = (24.0^{+3.2}_{-2.7})^\circ )$, respectively. From this table, one finds that all theoretical results agree roughly with the available measurements in $2\sigma$ standard deviations. Additionally, the changes induced by the mixing angle $|\varphi |$ are plagued by uncertainties arising from other parameters. In this regard, in order to determine the mixing angle $|\varphi |$, more stringent constraints from other observables are required. We also note that the large branching fractions of the $B^0 \rightarrow J/\psi f_1$ decays are expected to be tested at LHCb and Belle-II experiments [66] in future.

Table 1 The CP-averaged branching ratios for neutral B-meson decays into $J/\psi f_1$ in the PQCD approach

The decays $B_s^0 \rightarrow J/\psi f_1(1285,1420)$ have been investigated previously by two of us (Liu and Xiao) in Ref. [20] by including the vertex corrections. Comparing the new results with previous ones, we find all results agree with each other with uncertainties, and the acceptable differences are from the effects from the new ingredients in Sudakov factor. Furthermore, for comparison, we also take the decay $B_s^0 \rightarrow J/\psi f_1(1285)$ as an example and calculate its branching fractions for different values of $|\varphi |$ without vertex corrections and new ingredients in Sudakov factor, and the results are given as

$$\begin{aligned}&{\mathcal {B}}(B_{s}^0 \rightarrow J/\psi f_1(1285))|_{\varphi \sim 15^\circ } \nonumber \\&\quad = (0.32^{+0.09+0.05+0.05+0.06}_{-0.07-0.05-0.05-0.06})\times 10^{-4}, \end{aligned}$$

(42)

$$\begin{aligned}&{\mathcal {B}}(B_{s}^0 \rightarrow J/\psi f_1(1285))|_{\varphi \sim 24^\circ } \nonumber \\&\quad =(0.78^{+0.22+0.12+0.12+0.21}_{-0.17-0.13-0.10-0.16})\times 10^{-4}. \end{aligned}$$

(43)

It is obvious that the vertex corrections can enhance the branching fractions remarkably, because the Wilson coefficient ${\tilde{a}}_2$ is much larger than $a_2$, which has been also shown in Refs. [28, 32]. We also note that the uncertainties from the scale t are declined from 30 and 5%, as we expected.

We also acknowledge that our NLO calculation are incomplete. In principle, the NLO contributions should contain both the vertex corrections and hard spectator scattering (HS) amplitudes. For the charmless B meson decays, the NLO effects of HS have been explored partly [59, 67, 68]. However, for the decays with charm quark, the calculations of NLO corrections of HS are very complicated because the new scale $m_c$ is involved, and we shall left it as our future work.

On the experimental side, $\varphi ^{\mathrm{Exp}} = \pm (24.0^{+3.1+0.6} _{-2.6-0.8}) ^\circ$ was extracted through partial-wave analysis only with ${\mathcal {B}}(f_1(1285) \rightarrow 2\pi ^+ 2\pi ^-) = 0.109 \pm 0.006$ [27], by assuming the SU(3) flavor symmetry and neglecting the penguin contributions in $B_d^0 \rightarrow J/\psi f_1(1285)$ and $B_s^0 \rightarrow J/\psi f_1(1285)$ decays. As aforementioned, $f_1(1285)$ state could mix with $f_1(1420)$, then it could also be contributed through other partial-wave analysis, for example, $f_1(1285) \rightarrow K_S^0 K^+ \pi ^-$ [26]. With the theoretical predictions and experimental measurements of ${\mathcal {B}}(B_s^0 \rightarrow J/\psi f_1(1285))$ and ${\mathcal {B}}(f_1(1285) \rightarrow K{\bar{K}} \pi ) = 0.090 \pm 0.004$ [4], the magnitude of ${\mathcal {B}}(B_s^0 \rightarrow J/\psi f_1(1285)(\rightarrow K_S^0 K^\pm \pi ^\mp ))$ is about $10^{-6} \sim 10^{-5}$, which is measurable in the on-going LHCb and Belle-II experiments. Meanwhile, combining our results and the available experimental data ${\mathcal {B}}(f_{1}(1285) \rightarrow \eta \pi ^{+} \pi ^{-}) =0.35_{-0.15}^{+0.15}$ [4] and ${\mathcal {B}}(f_1(1420) \rightarrow K_S^0 K^\pm \pi ^\mp ) \approx 0.64_{-0.06}^{+0.06}$ [25], we then estimate ${\mathcal {B}}(B^0 \rightarrow J/\psi f_1(1285)(\rightarrow \eta \pi ^+ \pi ^-))$ and ${\mathcal {B}}(B^0 \rightarrow J/\psi f_1(1420)(\rightarrow K_S^0 K^+ \pi ^-))$ as

$$\begin{aligned}&{\mathcal {B}}(B_d^0 \rightarrow J/\psi (\eta \pi ^+\pi ^-)_{f_1(1285)})\nonumber \\&\quad \equiv {\mathcal {B}}(B_d^0 \rightarrow J/\psi f_1(1285))\nonumber \\&\qquad \cdot \, {\mathcal {B}}(f_1(1285) \rightarrow \eta \pi ^+ \pi ^-) \approx \biggl \{\begin{array}{ll} (1.07^{+0.84}_{-0.70}) \times 10^{-5}\\ (0.96^{+0.75}_{-0.63}) \times 10^{-5} \end{array},\nonumber \\ \end{aligned}$$

(44)

$$\begin{aligned}&{\mathcal {B}}(B_s^0 \rightarrow J/\psi (\eta \pi ^+\pi ^-)_{f_1(1285)})\nonumber \\&\quad \equiv {\mathcal {B}}(B_s^0 \rightarrow J/\psi f_1(1285)) \nonumber \\&\qquad \cdot \, {\mathcal {B}}(f_1(1285) \rightarrow \eta \pi ^+ \pi ^-) \approx \biggl \{\begin{array}{ll} (0.31^{+0.21}_{-0.18}) \times 10^{-4} \\ (0.77^{+0.54}_{-0.47}) \times 10^{-4} \end{array},\nonumber \\ \end{aligned}$$

(45)

$$\begin{aligned}&{\mathcal {B}}(B_d^0 \rightarrow J/\psi (K_S^0 K^+ \pi ^-)_{f_1(1420)})\nonumber \\&\quad \equiv {\mathcal {B}}(B_d^0 \rightarrow J/\psi f_1(1420)) \nonumber \\&\quad \cdot \, {\mathcal {B}}(f_1(1420) \rightarrow K_S^0 K^+ \pi ^-) \approx \biggl \{\begin{array}{ll} (1.27^{+0.88}_{-0.68}) \times 10^{-6} \\ (3.15^{+2.24}_{-1.72}) \times 10^{-6} \end{array},\nonumber \\ \end{aligned}$$

(46)

$$\begin{aligned}&{\mathcal {B}}(B_s^0 \rightarrow J/\psi (K_S^0 K^+ \pi ^-)_{f_1(1420)})\nonumber \\&\quad \equiv {\mathcal {B}}(B_s^0 \rightarrow J/\psi f_1(1420)) \nonumber \\&\qquad \cdot \, {\mathcal {B}}(f_1(1420) \rightarrow K_S^0 K^+ \pi ^-) \approx \biggl \{\begin{array}{ll} (0.73^{+0.36}_{-0.28}) \times 10^{-3} \\ (0.65^{+0.33}_{-0.25}) \times 10^{-3} \end{array},\nonumber \\ \end{aligned}$$

(47)

where all uncertainties have been added in quadrature. In above results, the upper and the lower entries correspond to the results obtained with $|\varphi ^{\mathrm{Theo}}| \sim 15^\circ$ and $|\varphi ^{\mathrm{Exp}}| \sim 24^\circ$, respectively. (In the following context, the similar presentation will be adopted implicitly, unless otherwise stated.) The results of Eqs. (44)–(47) are expected to be tested at LHCb and Belle-II experiments in the near future, and they could further provide more additional constraints on $|\varphi |$ and rich information for understanding the nature of $f_1$.

In PDG [4], the branching fractions of $B_d^0 \rightarrow J/\psi \rho ^0$ and $B_s^0 \rightarrow J/\psi \phi$ have been well measured as

$$\begin{aligned}&{\mathcal {B}}(B_{d}^0 \rightarrow J/\psi \rho ^0) = (2.55^{+0.18}_{-0.16})\times 10^{-5}, \nonumber \\&{\mathcal {B}}(B_{s}^0 \rightarrow J/\psi \phi ) = (1.04^{+0.04}_{-0.04})\times 10^{-3}. \end{aligned}$$

(48)

These branching fractions with high precision can be used for normalizations in studying $B \rightarrow J/\psi f_1$ decays. Theoretically, both branching fractions have been calculated in PQCD at NLO [42], and the results are given as

$$\begin{aligned}&{\mathcal {B}}(B_{d}^0 \rightarrow J/\psi \rho ^0) = (2.98^{+0.81}_{-0.69})\times 10^{-5}, \nonumber \\&{\mathcal {B}}(B_{s}^0 \rightarrow J/\psi \phi ) = (1.07^{+0.33}_{-0.29})\times 10^{-3}, \end{aligned}$$

(49)

where the uncertainties arising from different sources have been added in quadrature. Considering ${\mathcal {B}}(\phi \rightarrow K^+ K^-) = 0.492 \pm 0.005$ and ${\mathcal {B}}(\rho ^0 \rightarrow \pi ^+ \pi ^-) \sim 100\%$ [4], we then obtain the branching fractions of $B_s^0 \rightarrow J/\psi \phi (\rightarrow K^+ K^-)$ and $B_d^0 \rightarrow J/\psi \rho ^0 (\rightarrow \pi ^+ \pi ^-)$ decays as follows,

$$\begin{aligned}&{\mathcal {B}}(B_{s}^0 \rightarrow J/\psi (K^{+} K^{-})_{\phi }) \equiv {\mathcal {B}}(B_{s}^0 \rightarrow J/\psi \phi ) \nonumber \\&\quad \cdot \,{\mathcal {B}}(\phi \rightarrow K^{+}K^{-}) \approx (0.53^{+0.16}_{-0.14}) \times 10^{-3}, \end{aligned}$$

(50)

$$\begin{aligned}&{\mathcal {B}}(B_{d}^0 \rightarrow J/\psi (\pi ^{+} \pi ^{-})_{\rho ^0}) \equiv {\mathcal {B}}(B_{d}^0 \rightarrow J/\psi \rho ^0) \nonumber \\&\quad \cdot \,{\mathcal {B}}(\rho ^0 \rightarrow \pi ^{+} \pi ^{-}) \approx (2.98^{+0.81}_{-0.69}) \times 10^{-5}. \end{aligned}$$

(51)

Then, four ratios could be defined as follows,

$$\begin{aligned}&R_{s}^{J/\psi }[f_{1}(1420)/\phi ] \equiv \frac{{\mathcal {B}}(B_{s}^{0} \rightarrow J/\psi f_{1}(1420)) }{{\mathcal {B}}(B_{s}^0 \rightarrow J/\psi \phi ) } \nonumber \\&\quad \approx \biggl \{\begin{array}{cc} 1.07^{+0.34}_{-0.25} \\ 0.95^{+0.31}_{-0.23} \end{array}, \end{aligned}$$

(52)

$$\begin{aligned}&R_{d}^{J/\psi }[f_{1}(1285)/\rho ^0]\equiv \frac{{\mathcal {B}}(B_{d}^{0} \rightarrow J/\psi f_{1}(1285))}{{\mathcal {B}}(B_{d}^0 \rightarrow J/\psi \rho ^0)}\nonumber \\&\quad \approx \biggl \{\begin{array}{cc} 1.02^{+0.55}_{-0.42} \\ 0.92^{+0.49}_{-0.37} \end{array}, \end{aligned}$$

(53)

and

$$\begin{aligned} R_{\pi }^{J/\psi }\equiv & {} \frac{{\mathcal {B}}(B_s^0 \rightarrow J/\psi (K_S^0 K^+ \pi ^-)_{f_1(1420)})}{{\mathcal {B}}(B_{s}^0 \rightarrow J/\psi (K^{+} K^{-})_{\phi }) } \nonumber \\\approx & {} \biggl \{\begin{array}{cc} 1.38^{+0.48}_{-0.34} \\ 1.23^{+0.41}_{-0.30} \end{array}, \end{aligned}$$

(54)

$$\begin{aligned} R_\eta ^{J/\psi }\equiv & {} \frac{{\mathcal {B}}(B_d^0 \rightarrow J/\psi (\eta \pi ^+\pi ^-)_{f_1(1285)})}{{\mathcal {B}}(B_{d}^0 \rightarrow J/\psi (\pi ^{+} \pi ^{-})_{\rho ^0})}\nonumber \\\approx & {} \biggl \{\begin{array}{cc} 0.36^{+0.24}_{-0.21} \\ 0.32^{+0.22}_{-0.19} \end{array}. \end{aligned}$$

(55)

All the above results could be tested in LHCb and Belle-II experiments. As far as the central values are concerned, because the behaviors of $f_1$ meson are very similar to those of $\rho /\phi$ [12,13,14,15], the results indicate that $f_n(f_s)$ state should predominately govern the $f_1(1285)(f_1(1420))$ meson, that is, the small $|\varphi |$ is preferred.

In Ref. [27], after neglecting the contributions from penguin operators and assuming the SU(3) flavor symmetry, LHCb estimated the angle $\varphi$ with the relation

$$\begin{aligned}&\tan ^2\varphi \nonumber \\&\quad \approx \frac{1}{2}\frac{{\mathcal {B}}(B_{s}^{0} \rightarrow J/\psi f_{1}(1285))}{{\mathcal {B}}(B_{d}^{0} \rightarrow J/\psi f_{1}(1285))} \frac{\tau _0}{\tau _s}\frac{|V_{cd}|^2}{|V_{cs}|^2} \frac{\Phi (m_{B_d},m_{J/\psi },m_{f_{1}(1285)})}{\Phi (m_{B_s},m_{J/\psi },m_{f_{1}(1285)})},\nonumber \\ \end{aligned}$$

(56)

where the phase space factor is given as $\Phi (a,b,c)=\left[ (a^2-(b+c)^2)(a^2-(b-c)^2)\right] ^{\frac{3}{2}}$. In fact, the corrections from penguin operators are about $15\%$ [33], and SU(3) asymmetry is particularly estimated to be about $30\%$. Without above uncertainties, we define two ratios and evaluate them as

$$\begin{aligned}&R_{d}^{J/\psi }\equiv \frac{{\mathcal {B}}(B_{d}^{0} \rightarrow J/\psi f_{1}(1285))}{{\mathcal {B}}(B_{d}^{0} \rightarrow J/\psi f_{1}(1420))}\nonumber \\&\quad = \frac{\Phi (m_{B_d},m_{J/\psi },m_{f_{1}(1285)})}{\Phi (m_{B_d},m_{J/\psi },m_{f_{1}(1420)})}\cdot \cot ^2\varphi \approx \biggl \{\begin{array}{rr} 15.33^{+0.15}_{-0.14} \\ 5.55^{+0.06}_{-0.04} \end{array}, \nonumber \\ \end{aligned}$$

(57)

$$\begin{aligned}&R_{s}^{J/\psi }\equiv \frac{{\mathcal {B}}(B_{s}^{0} \rightarrow J/\psi f_{1}(1420))}{{\mathcal {B}}(B_{s}^{0} \rightarrow J/\psi f_{1}(1285))}\nonumber \\&\quad = \frac{\Phi (m_{B_s},m_{J/\psi },m_{f_{1}(1420)})}{\Phi (m_{B_s},m_{J/\psi },m_{f_{1}(1285)})}\cdot \cot ^2\varphi \approx \biggl \{\begin{array}{rr} 12.81^{+0.17}_{-0.18} \\ 4.62^{+0.08}_{-0.03} \end{array}.\nonumber \\ \end{aligned}$$

(58)

Such two ratios with small uncertainties could also be used to determine $|\varphi |$ in future, if $f_{1}(1285)$ and $f_{1}(1420)$ are believed to be two-quark states.

Now we turn to other observables such as the polarization fractions and the direct CP asymmetries in $B^0 \rightarrow J/\psi f_1$ decays. With the helicity amplitudes shown in Eqs. (31)–(34), a set of transversity amplitudes, namely, the longitudinal one ${\mathcal {A}}_L$, the parallel one ${\mathcal {A}}_{\parallel }$, and the perpendicular one ${\mathcal {A}}_{\perp }$, can be defined respectively as follows,

$$\begin{aligned} {\mathcal {A}}_{L}={\mathcal {A}}_{L}, \quad {\mathcal {A}}_{\parallel }=\sqrt{2} {\mathcal {A}}_{N},\quad {\mathcal {A}}_{\perp }=r_{2}r_{3}\sqrt{2(\kappa ^{2}-1)}{\mathcal {A}}_{T}, \nonumber \\ \end{aligned}$$

(59)

with the ratio $\kappa =P_{2} \cdot P_{3}/(m_{J/\psi }m_{f_1})$. The polarization fractions $f_{L}$ and $f_T$ in $B^0 \rightarrow J/\psi f_1$ decays can be defined as follows [69],

$$\begin{aligned}&f_{L}\equiv \frac{|{\mathcal {A}}_{L}|^2}{|{\mathcal {A}}_L|^2+|{\mathcal {A}}_{||}|^2+|{\mathcal {A}}_{\perp }|^2}, \qquad \nonumber \\&f_T \equiv \frac{|{\mathcal {A}}_{||}|^2+ |{\mathcal {A}}_\perp |^2}{|{\mathcal {A}}_L|^2+|{\mathcal {A}}_{||}|^2+|{\mathcal {A}}_{\perp }|^2} = f_\parallel + f_\perp , \end{aligned}$$

(60)

which satisfy the relation of $f_{L}+f_{T}=1$. The relative phases $\phi _{\parallel }$ and $\phi _\perp$ (in units of rad) are thus obtained as follows,

$$\begin{aligned} \phi _{\parallel }= & {} \arg \frac{{\mathcal {A}}_{\parallel }}{{\mathcal {A}}_{L}}, \quad \phi _{\perp }=\arg \frac{{\mathcal {A}}_{\perp }}{{\mathcal {A}}_{L}}. \end{aligned}$$

(61)

In PQCD, these observables of $B^0 \rightarrow J/\psi f_1$ decays are calculated, and the results are given as

$$\begin{aligned}&f_{L}(B_{d}^{0} \rightarrow J/\psi f_{1}(1285)) = (44.6^{+13.9}_{-10.4})\%,\nonumber \\&f_{L}(B_{d}^{0} \rightarrow J/\psi f_{1}(1420)) = (45.8^{+13.8}_{-10.4}) \%, \nonumber \\&f_{L}(B_{s}^{0} \rightarrow J/\psi f_{1}(1285)) = (45.1^{+14.1}_{-10.7}) \%, \nonumber \\&f_{L}(B_{s}^{0} \rightarrow J/\psi f_{1}(1420)) = (46.2^{+14.0}_{-10.9}) \%, \end{aligned}$$

(62)

and

$$\begin{aligned}&\phi _{\parallel }(B_d^0 \rightarrow J/\psi f_1)=2.11_{-0.05}^{+0.05}, \nonumber \\&\phi _{\perp }(B_d^0 \rightarrow J/\psi f_1)=1.99_{-0.07}^{+0.05}, \nonumber \\&\phi _{\parallel }(B_s^0 \rightarrow J/\psi f_1)=2.15_{-0.06}^{+0.09}, \nonumber \\&\phi _{\perp }(B_s^0 \rightarrow J/\psi f_1)=2.01_{-0.06}^{+0.06}, \end{aligned}$$

(63)

in which various errors have been added in quadrature. Though these quantities are the ratios of (squared) decay amplitudes, the nonperturbative parameters, especially the Gegenbauer moment $a_1^\perp$ in the distribution amplitudes of $f_n$ and $f_s$ and the charm quark mass $m_c$, take large theoretical uncertainties. We also note that the longitudinal polarization fractions and transverse ones are almost equal, due to the helicity flip. Such phenomenon has been confirmed in $B_s\rightarrow J/\psi \phi$ and $B_d\rightarrow J/\psi K^*$ decays [42, 70, 71]. All these observables will also be tested in experiments.

The direct CP asymmetry $A_{\mathrm{CP}}^{\mathrm{dir}}$ of $B^0 \rightarrow J/\psi f_1$ decays is defined as

$$\begin{aligned} A_{\mathrm{CP}}^{\mathrm{dir}}\equiv & {} \frac{|\overline{\mathcal {A}} (\overline{B}^0\rightarrow {\overline{f}})|^2 - |{\mathcal {A}}(B^0\rightarrow f)|^2}{|\overline{\mathcal {A}}(\overline{B}^0\rightarrow {\overline{f}})|^2+|{\mathcal {A}}(B^0\rightarrow f)|^2}, \end{aligned}$$

(64)

where ${\mathcal {A}}$ stand for the decay amplitudes of $B^0 \rightarrow J/\psi f_{1}$, while $\overline{\mathcal {A}}$ describe the corresponding charge conjugation ones. With the obtained amplitudes, we calculate the direct CP asymmetries and present the results as

$$\begin{aligned}&A_{\mathrm{CP}}^{\mathrm{dir}}(B_{d}^{0} \rightarrow J/\psi f_{1}) = A_{\mathrm{CP}}^{\mathrm{dir}}(B_d^0 \rightarrow J/\psi f_n) \nonumber \\&\quad =(-5.86^{+4.54}_{-5.52}) \times 10^{-3}, \end{aligned}$$

(65)

$$\begin{aligned}&A_{\mathrm{CP}}^{\mathrm{dir}}(B_{s}^{0} \rightarrow J/\psi f_{1}) = A_{\mathrm{CP}}^{\mathrm{dir}}(B_{s}^{0} \rightarrow J/\psi f_s) \nonumber \\&\quad =(2.24^{+2.41}_{-1.97}) \times 10^{-4}. \end{aligned}$$

(66)

Meanwhile, the direct CP asymmetries in each polarization can also be studied as [72]

$$\begin{aligned} A_{\mathrm{CP}}^\mathrm{dir,\alpha }= & {} \frac{\bar{f}_{\alpha }-f_{\alpha }}{\bar{f}_{\alpha }+f_{\alpha }} \quad (\alpha =L, \parallel , \perp ), \end{aligned}$$

(67)

where ${\bar{f}}_\alpha$ is the polarization fraction for the corresponding ${\bar{B}}$ decays in Eq. (60). In this work, the direct CP asymmetries for $B^0 \rightarrow J/\psi f_{1}$ decays at each polarization are collected as follows,

• for $B_{d}^{0} \rightarrow J/\psi f_{1}$ modes (in units of $10^{-3}$),

  $$\begin{aligned}&A_{\mathrm{CP}}^\mathrm{dir,L}= -5.05_{-7.83}^{+5.82}, \quad A_{\mathrm{CP}}^\mathrm{dir,\parallel } = -6.38_{-4.46}^{+4.02} ,\nonumber \\&A_{\mathrm{CP}}^\mathrm{dir,\perp } = -6.78_{-4.07}^{+3.55} , \end{aligned}$$

  (68)

• for $B_{s}^{0} \rightarrow J/\psi f_{1}$ modes (in units of $10^{-4}$),

  $$\begin{aligned}&A_{\mathrm{CP}}^\mathrm{dir,L} = 1.69_{-2.17}^{+2.86} , \quad A_{\mathrm{CP}}^\mathrm{dir,\parallel } = 2.58_{-2.03}^{+2.35} , \nonumber \\&A_{\mathrm{CP}}^\mathrm{dir,\perp } = 2.89_{-1.72}^{+2.05} . \end{aligned}$$

  (69)

All uncertainties from various parameters in above results have been added in quadrature. It is obvious that the direct CP violations for $B_d^0 \rightarrow J/\psi f_1$ decays are a few percent within errors, however, which are still too small to be detected in the running LHCb and Belle-II experiments.

3.3 $B^0 \rightarrow \eta _c f_1$

Different from the decays of $B^0 \rightarrow J/\psi f_1$, $B^0 \rightarrow \eta _c f_1$ decays have only the longitudinal contributions because of the conservation of the angular momentum. By employing the decay amplitudes as presented in Eqs. (36)–(39), the corresponding branching ratio can be expressed as follows,

$$\begin{aligned} {\mathcal {B}}(B^0 \!\rightarrow \! \eta _c f_1) \!=\! \tau _{B} \cdot \frac{G_F^2}{32\pi m_B} (1\!-\!r_{\eta _c}^2) |{\mathcal {A}}(B^0\! \rightarrow \! \eta _c f_1)|^2,\nonumber \\ \end{aligned}$$

(70)

with $r_{\eta _c} = m_{\eta _c}/m_{B^0}$. Similar to ${\mathcal {B}}(B^0 \rightarrow J/\psi f_1)$, the theoretical predictions of ${\mathcal {B}}(B^0 \rightarrow \eta _c f_1)$ at both $|\varphi ^{\mathrm{Theo}}|$ and $|\varphi ^{\mathrm{Exp}}|$ in PQCD approach are presented in Table 2, where the sources of errors are also similar to those in $B^0 \rightarrow J/\psi f_1$ modes but with $f_{\eta _c} = 0.42 \pm 0.05$ GeV. Within the large theoretical errors, the $B^0 \rightarrow \eta _c f_1$ decay rates at $|\varphi ^{\mathrm{Theo}}| \sim 15^\circ$ are generally consistent with those at $|\varphi ^{\mathrm{Exp}}| \sim 24^\circ$. These decays have not been measured yet currently, and are expected to be tested in the near future.

Table 2 The CP-averaged branching ratios $B^0 \rightarrow \eta _c f_1$ in PQCD approach

Comparing $B^0 \rightarrow J/\psi f_1$ and $B^0 \rightarrow \eta _c f_1$ decays, we have

$$\begin{aligned}&\frac{{\mathcal {B}}(B_{d}^{0} \rightarrow J/\psi f_{1}(1285))}{{\mathcal {B}}(B_{d}^{0}\rightarrow \eta _{c} f_{1}(1285))} \approx 4.00^{+1.29}_{-0.85}, \nonumber \\&\frac{{\mathcal {B}}(B_{s}^{0} \rightarrow J/\psi f_{1}(1285))}{{\mathcal {B}}(B_{s}^{0} \rightarrow \eta _{c} f_{1}(1285))} \approx 4.14^{+1.48}_{-0.90} , \nonumber \\&\frac{{\mathcal {B}}(B_{d}^{0} \rightarrow J/\psi f_{1}(1420))}{{\mathcal {B}}(B_{d}^{0} \rightarrow \eta _{c} f_{1}(1420))} \approx 3.86^{+1.27}_{-0.82} ,\nonumber \\&\frac{{\mathcal {B}}(B_{s}^{0} \rightarrow J/\psi f_{1}(1420))}{{\mathcal {B}}(B_{s}^{0} \rightarrow \eta _{c} f_{1}(1420))} \approx 4.01^{+1.51}_{-0.90}. \end{aligned}$$

(71)

It is noticeable that these ratios are all about 4, which attributes to the large contributions from the transverse polarization. The measurements of such kinds of ratios in future could help us to test the polarization mechanism.

Analogous to the decays $B^0 \rightarrow J/\psi f_1$, we also define four ratios in $B^0 \rightarrow \eta _c f_1$ modes as follows,

$$\begin{aligned}&R_{d}^{\eta _c} \equiv \frac{{\mathcal {B}}(B_{d}^{0} \rightarrow \eta _{c} f_{1}(1285))}{{\mathcal {B}}(B_{d}^{0} \rightarrow \eta _{c} f_{1}(1420))} \nonumber \\&\quad = \frac{\Phi (m_{B_d},m_{\eta _c},m_{f_{1}(1285)})}{\Phi (m_{B_d},m_{\eta _c},m_{f_{1}(1420)})} \cdot \cot ^2\varphi , \end{aligned}$$

(72)

$$\begin{aligned}&R_{s}^{\eta _c} \equiv \frac{{\mathcal {B}}(B_{s}^{0} \rightarrow \eta _{c} f_{1}(1420))}{{\mathcal {B}}(B_{s}^{0} \rightarrow \eta _{c} f_{1}(1285))}\nonumber \\&\quad = \frac{\Phi (m_{B_s},m_{\eta _c},m_{f_{1}(1420)})}{\Phi (m_{B_s},m_{\eta _c},m_{f_{1}(1285)})} \cdot \cot ^2\varphi , \end{aligned}$$

(73)

$$\begin{aligned}&R_{sd}^{\eta _c}[f_1(1285)]\equiv \frac{{\mathcal {B}}(B_{s}^{0} \rightarrow \eta _{c} f_{1}(1285))}{{\mathcal {B}}(B_{d}^{0} \rightarrow \eta _{c} f_{1}(1285))}\nonumber \\&\quad = \frac{\tau _{B_s^0}}{\tau _{B_d^0}} \cdot \frac{\Phi (m_{B_s},m_{\eta _c},m_{f_{1}(1285)})}{\Phi (m_{B_d},m_{\eta _c},m_{f_{1}(1285)})} \nonumber \\&\qquad \cdot \,\frac{|{\mathcal {A}}(B_s^0 \rightarrow \eta _c f_s)|^2}{|{\mathcal {A}}(B_d^0 \rightarrow \eta _c f_n)|^2} \cdot \tan ^2\varphi \end{aligned}$$

(74)

$$\begin{aligned}&R_{sd}^{\eta _c}[f_1(1420)]\equiv \frac{{\mathcal {B}}(B_{s}^{0} \rightarrow \eta _{c} f_{1}(1420))}{{\mathcal {B}}(B_{d}^{0} \rightarrow \eta _{c} f_{1}(1420))}\nonumber \\&\quad = \frac{\tau _{B_s^0}}{\tau _{B_d^0}} \cdot \frac{\Phi (m_{B_s},m_{\eta _c},m_{f_{1}(1420)})}{\Phi (m_{B_d},m_{\eta _c},m_{f_{1}(1420)})} \nonumber \\&\qquad \cdot \,\frac{|{\mathcal {A}}(B_s^0 \rightarrow \eta _c f_s)|^2}{|{\mathcal {A}}(B_d^0 \rightarrow \eta _c f_n)|^2} \cdot \cot ^2\varphi , \end{aligned}$$

(75)

which can be used to constrain the absolute value of the mixing angle $\varphi$. In PQCD, these above ratios could be calculated from Table 2, and the results are given as

$$\begin{aligned}&R_{d}^{\eta _c} \approx \biggl \{\begin{array}{cc} 14.81^{+3.12}_{-2.36}\\ 5.34^{+1.02}_{-0.92} \end{array},\quad R_{s}^{\eta _c} \approx \biggl \{\begin{array}{cc} 13.21^{+2.73}_{-2.13} \\ 4.78^{+0.91}_{-0.84} \end{array},\nonumber \\&R_{sd}^{\eta _c}[f_1(1285)]\approx \biggl \{\begin{array}{cc} 2.81^{+1.32}_{-0.94} \\ 7.77^{+3.76}_{-2.56} \end{array}, \nonumber \\&\quad R_{sd}^{\eta _c}[f_1(1420)] \approx \biggl \{\begin{array}{cc} (5.50^{+2.64}_{-1.83}) \times 10^{2}, \\ (1.98^{+0.99}_{-0.72}) \times 10^{2}, \end{array} \end{aligned}$$

(76)

where all uncertainties are added in quadrature.

Since the branching fractions of $B_{d,s}^0 \rightarrow J/\psi f_1(1285)$ decays were measured with ${\mathcal {B}}(f_1(1285) \rightarrow 2\pi ^+ 2\pi ^-) =0.109_{-0.006}^{+0.006}$, we also propose the analogous measurements on $B_{d,s}^0 \rightarrow \eta _c f_1(1285)(\rightarrow 2\pi ^+ 2\pi ^-)$, whose branching fractions are estimated to be

$$\begin{aligned}&{\mathcal {B}}(B_d^0 \rightarrow \eta _{c} (2\pi ^+2\pi ^-)_{f_1(1285)}) \equiv {\mathcal {B}}(B_d^0 \rightarrow \eta _{c} f_1(1285)) \nonumber \\&\quad \cdot \, {\mathcal {B}}(f_1(1285) \rightarrow 2\pi ^+2\pi ^-) \approx \biggl \{\begin{array}{cc} ( 0.84^{+0.71}_{-0.54}) \times 10^{-6} \\ ( 0.75^{+0.64}_{-0.48}) \times 10^{-6} \end{array}, \nonumber \\\end{aligned}$$

(77)

$$\begin{aligned}&{\mathcal {B}}(B_s^0 \rightarrow \eta _{c} (2\pi ^+2\pi ^-)_{f_1(1285)}) \equiv {\mathcal {B}}(B_s^0 \rightarrow \eta _{c} f_1(1285)) \nonumber \\&\quad \cdot \, {\mathcal {B}}(f_1(1285) \rightarrow 2\pi ^+2\pi ^-) \approx \biggl \{\begin{array}{cc} ( 0.24^{+0.19}_{-0.14}) \times 10^{-5} \\ ( 0.58^{+0.49}_{-0.36}) \times 10^{-5} \end{array}.\nonumber \\ \end{aligned}$$

(78)

Meanwhile, with the large widths of $f_1(1285) \rightarrow \eta \pi ^+ \pi ^-$ and $f_1(1420) \rightarrow K_S^0 K^+ \pi ^-$, the branching fractions of $B^0 \rightarrow \eta _c f_1(1285)(\rightarrow \eta \pi ^+ \pi ^-)$ and $B^0 \rightarrow \eta _c f_1(1420)(\rightarrow K_s^0 K^+ \pi ^-)$ decays are also calculated to be

$$\begin{aligned}&{\mathcal {B}}(B_d^0 \rightarrow \eta _{c} (\eta \pi ^+\pi ^-)_{f_1(1285)}) \equiv {\mathcal {B}}(B_d^0 \rightarrow \eta _{c} f_1(1285)) \nonumber \\&\quad \cdot \, {\mathcal {B}}(f_1(1285) \rightarrow \eta \pi ^+ \pi ^-) \approx \biggl \{\begin{array}{cc} ( 2.67^{+2.54}_{-2.06}) \times 10^{-6} \\ ( 2.39^{+2.27}_{-1.84}) \times 10^{-6} \end{array},\nonumber \\ \end{aligned}$$

(79)

$$\begin{aligned}&{\mathcal {B}}(B_s^0 \rightarrow \eta _{c} (\eta \pi ^+\pi ^-)_{f_1(1285)}) \equiv {\mathcal {B}}(B_s^0 \rightarrow \eta _{c} f_1(1285)) \nonumber \\&\quad \cdot \, {\mathcal {B}}(f_1(1285) \rightarrow \eta \pi ^+ \pi ^-) \approx \biggl \{\begin{array}{cc} ( 0.75^{+0.68}_{-0.56}) \times 10^{-5} \\ ( 1.86^{+1.71}_{-1.37}) \times 10^{-5} \end{array},\nonumber \\ \end{aligned}$$

(80)

$$\begin{aligned}&{\mathcal {B}}(B_d^0 \rightarrow \eta _{c} (K_S^0 K^+ \pi ^-)_{f_1(1420)}) \equiv {\mathcal {B}}(B_d^0 \rightarrow \eta _{c} f_1(1420)) \nonumber \\&\quad \cdot \, {\mathcal {B}}(f_1(1420) \rightarrow K_S^0 K^+ \pi ^-) \approx \biggl \{\begin{array}{cc} ( 3.30^{+2.90}_{-2.22}) \times 10^{-7} \\ ( 0.82^{+0.72}_{-0.56}) \times 10^{-6} \end{array},\nonumber \\ \end{aligned}$$

(81)

$$\begin{aligned}&{\mathcal {B}}(B_s^0 \rightarrow \eta _{c} (K_S^0 K^+ \pi ^-)_{f_1(1420)}) \equiv {\mathcal {B}}(B_s^0 \rightarrow \eta _{c} f_1(1420)) \nonumber \\&\quad \cdot \, {\mathcal {B}}(f_1(1420) \rightarrow K_S^0 K^+ \pi ^-) \approx \biggl \{\begin{array}{cc} ( 1.82^{+1.40}_{-1.07}) \times 10^{-4} \\ ( 1.63^{+1.26}_{-0.96}) \times 10^{-4} \end{array}.\nonumber \\ \end{aligned}$$

(82)

It is obvious that the decays $B_s^0 \rightarrow \eta _c f_1(1285)(\rightarrow 2\pi ^+ 2\pi ^-)$, $B^0 \rightarrow \eta _c f_1(1285)(\rightarrow \eta \pi ^+ \pi ^-)$ and $B_s^0 \rightarrow \eta _c f_1(1420)(\rightarrow K_S^0 K^+ \pi ^-)$ with large decay rates could be observed in the running LHCb and Belle-II experiments. Once these predictions would be confirmed experimentally, then the mixing angle $\varphi$ between the $f_1(1285)$ and $f_1(1420)$ mixing could receive more constraints, though they still suffer from large theoretical uncertainties induced by the hadronic parameters in the $f_n$ and $f_s$ light-cone distribution amplitudes.

In measuring the branching fractions of $B_{d,s}^0 \rightarrow \eta _c f_1$ decays, we can also select the modes $B_d^0 \rightarrow \eta _c \rho ^0$ and $B_s^0 \rightarrow \eta _c \phi$ for normalization. Theoretically, the ${\mathcal {B}}(B_d^0 \rightarrow \eta _c \rho ^0)$ and ${\mathcal {B}}(B_s^0 \rightarrow \eta _c \phi )$ in Ref. [43] are updated, and the results are presented as follows,

$$\begin{aligned}&{\mathcal {B}}(B_{d}^0 \rightarrow \eta _{c} \rho ^0)= (7.92^{+3.67}_{-3.04}) \times 10^{-6}, \nonumber \\&{\mathcal {B}}(B_{s}^0 \rightarrow \eta _{c} \phi ) = (3.57^{+1.81}_{-1.41} )\times 10^{-4}, \end{aligned}$$

(83)

which are slightly smaller than but consistent with previous predictions [43]. The updated ${\mathcal {B}}(B_s^0 \rightarrow \eta _c \phi )$ still agrees well with data ${\mathcal {B}}(B_s^0 \rightarrow \eta _c \phi )=(5.0\pm 0.9 )\times 10^{-4}$ [4] within errors, but the branching fraction of $B_{d}^0 \rightarrow \eta _{c} \rho ^0$ have not been measured so far. Within $\rho ^0 \rightarrow \pi ^+ \pi ^-$ and $\phi \rightarrow K^+ K^-$, we then obtain the following results as,

$$\begin{aligned}&{\mathcal {B}}(B_{d}^0 \rightarrow \eta _{c} (\pi ^{+} \pi ^{-})_{\rho ^0}) \equiv {\mathcal {B}}(B_{d}^0 \rightarrow \eta _{c} \rho ^0) \nonumber \\&\quad \cdot \,{\mathcal {B}}(\rho ^0 \rightarrow \pi ^{+} \pi ^{-}) \approx (7.92^{+3.67}_{-3.04}) \times 10^{-6}, \end{aligned}$$

(84)

$$\begin{aligned}&{\mathcal {B}}(B_{s}^0 \rightarrow \eta _{c} (K^{+} K^{-})_{\phi }) \equiv {\mathcal {B}}(B_{s}^0 \rightarrow \eta _{c} \phi ) \nonumber \\&\quad \cdot \,{\mathcal {B}}(\phi \rightarrow K^{+}K^{-}) \approx (1.76^{+0.89}_{-0.69}) \times 10^{-4}. \end{aligned}$$

(85)

In order to search for $B^0 \rightarrow \eta _c f_1$ decays, we also calculate the following ratios

$$\begin{aligned}&R_d^{\eta _c}[f_{1}(1285)/\rho ^0]\equiv \frac{{\mathcal {B}}(B_{d}^{0} \rightarrow \eta _{c} f_{1}(1285))}{{\mathcal {B}}(B_{d}^0 \rightarrow \eta _{c} \rho ^0)} \nonumber \\&\quad \approx \biggl \{\begin{array}{cc} 0.96^{+0.39}_{-0.31} \\ 0.86^{+0.35}_{-0.27} \end{array}, \end{aligned}$$

(86)

$$\begin{aligned}&R_s^{\eta _c}[f_{1}(1420)/\phi ]\equiv \frac{{\mathcal {B}}(B_{s}^{0} \rightarrow \eta _{c} f_{1}(1420))}{{\mathcal {B}}(B_{s}^0 \rightarrow \eta _{c} \phi )} \nonumber \\&\quad \approx \biggl \{\begin{array}{cc} 0.80^{+0.08}_{-0.08} \\ 0.71^{+0.06}_{-0.06} \end{array}, \end{aligned}$$

(87)

and

$$\begin{aligned} R^{\eta _c}_{\pi }\equiv & {} \frac{{\mathcal {B}}(B_s^0 \rightarrow \eta _{c} (K_S^0 K^+ \pi ^-)_{f_1(1420)})}{{\mathcal {B}}(B_{s}^0 \rightarrow \eta _{c} (K^{+} K^{-})_{\phi })} \approx \biggl \{\begin{array}{cc} 1.03^{+0.14}_{-0.13} \\ 0.93^{+0.11}_{-0.12} \end{array} ,\nonumber \\ \end{aligned}$$

(88)

$$\begin{aligned} R^{\eta _c}_{\eta }\equiv & {} \frac{{\mathcal {B}}(B_d^0 \rightarrow \eta _{c} (\eta \pi ^+\pi ^-)_{f_1(1285)})}{{\mathcal {B}}(B_{d}^0 \rightarrow \eta _{c} (\pi ^{+} \pi ^{-})_{\rho ^0})} \approx \biggl \{\begin{array}{cc} 0.34^{+0.20}_{-0.18} \\ 0.30^{+0.18}_{-0.16} \end{array} .\nonumber \\ \end{aligned}$$

(89)

These ratios are also expected to be examined in future.

Lastly, we shall study the direct CP asymmetries of $B^0 \rightarrow J/\psi f_1$ decays. Based on the definition in Eq. (64), the numerical results can be given as

$$\begin{aligned}&A_{\mathrm{CP}}^{\mathrm{dir}}(B_{d}^{0} \rightarrow \eta _{c} f_{1}) = A_{\mathrm{CP}}^{\mathrm{dir}}(B_{d}^{0} \rightarrow \eta _{c} f_n) \nonumber \\&\quad = (7.53^{+1.07}_{-0.98}) \times 10^{-2}, \end{aligned}$$

(90)

$$\begin{aligned}&A_{\mathrm{CP}}^{\mathrm{dir}}(B_{s}^{0} \rightarrow \eta _{c} f_{1}) = A_{\mathrm{CP}}^{\mathrm{dir}}(B_{s}^{0} \rightarrow \eta _{c} f_s) \nonumber \\&\quad = (-4.33^{+0.60}_{-0.66}) \times 10^{-3}. \end{aligned}$$

(91)

It is shown that the direct CP asymmetries of $B \rightarrow \eta _c f_1$ are as large as a few percent, and are an order of magnitude larger than those of $B^0 \rightarrow J/\psi f_1$ decays. The measurements of such asymmetries in the running LHCb and Belle-II experiments are helpful for understanding the nature of $f_1$ states and testing the PQCD approach.

4 Summary

We have made reexaminations on $B^0 \rightarrow J/\psi f_1$ and the first time studies on $B^0 \rightarrow \eta _c f_1$ decays in the framework of PQCD, where $f_1=f_1(1280)$ and $f_1(1420)$ are viewed as the mixtures of $f_n$ and $f_s$ with mixing angle $\varphi$. In this work, the contributions of vertex corrections, nonfactorizable diagrams and penguin operators are all included. It is found that the branching fractions of these decays are large enough to be measured in the running LHCb and Belle-II experiments. We also note that the $B^0 \rightarrow \eta _c f_1(1285)$ and $B_s^0 \rightarrow (J/\psi , \eta _c) f_1(1420)$ decays could be analyzed within the secondary decay chains $f_1(1285) \rightarrow 2\pi ^+ 2\pi ^-$, $f_1(1285) \rightarrow \eta \pi ^+ \pi ^-$ and $f_1(1420) \rightarrow K_S^0 K^+ \pi ^-$. In addition, we proposed several ratios that could be used to constrain the mixing angle $\varphi$, but its sign cannot be determined in these decays. We also studied the direct CP asymmetries in these decays, and results indicate the large penguin pollution in the $B_d^0 \rightarrow (J/\psi , \eta _c) f_1$ decays. It should be emphasized that there are large theoretical uncertainties arising from the nonperturbative parameters, especially from the distribution amplitudes of axial-vector mesons and charmonium states, and more precise parameters from nonperturbative QCD approaches are needed. The comparisons between our results and future experimental data would help us to understand the nature of $f_1$ states and to test the PQCD approach.

Appendices

Appendix A: Distribution amplitudes

In the conjugate $\mathbf{b}$ space of transverse momentum $\mathbf{k}_T$, the related B meson distribution amplitude $\phi _B(x,\mathbf{b})$ could be given as

$$\begin{aligned} \phi _{B}(x,\mathbf{b})= & {} N_{B}x^2(1\!-\!x)^2 \exp \biggl [-\frac{1}{2}\left( \frac{x m_{B}}{\omega _{B}}\right) ^2 \!-\!\frac{\omega _{B}^2 \mathbf{b}^2}{2}\biggr ] ,\nonumber \\ \end{aligned}$$

(92)

where $\omega _B$ is the shape parameter of $\phi _B(x,\mathbf{b})$. $N_B$ is the normalization factor, which is correlated with the decay constant $f_{B}$ satisfying the following relation,

$$\begin{aligned} \int _0^1 dx \phi _{B}(x, \mathbf{b}=0) = \frac{f_{B}}{2 \sqrt{2N_c}}. \end{aligned}$$

(93)

The shape parameter $\omega _B$ has been well constrained as $\omega _B = 0.4$ GeV [73] for the $B_d^0$ meson and $\omega _B =0.5$ GeV [46] for the $B_s^0$ meson, respectively. With the decay constants $f_{B_d^0} = 0.21$ GeV and $f_{B_s^0} = 0.23$ GeV, the normalization factors could be obtained as $N_{B_d^0} = 101.445$ and $N_{B_s^0} = 63.67$ correspondingly. The recent developments on the B-meson distribution amplitude with high twists can be found in [74,75,76,77,78]. The effects induced by these newly developed distribution amplitudes will be left for future investigations together with highly precise measurements.

For $J/\psi$ meson, the explicit forms for the distribution amplitudes of twist-2 $\phi _{J/\psi }^{L,T}(x)$ and twist-3 $\phi _{J/\psi }^{t,v}(x)$ could be read as [61],

$$\begin{aligned} \phi _{J/\psi }^{L}(x)= & {} \phi _{J/\psi }^{T}(x)=9.58\frac{f_{J/\psi }}{2\sqrt{2N_{c}}}x(1-x)\nonumber \\&\times \biggl [\frac{x(1-x)}{1-2.8x(1-x)}\biggl ]^{0.7}, \nonumber \\ \phi _{J/\psi }^{t}(x)= & {} 10.94\frac{f_{J/\psi }}{2\sqrt{2N_{c}}}(1-2x)^{2}\biggl [\frac{x(1-x)}{1-2.8x(1-x)}\biggl ]^{0.7}, \nonumber \\ \phi _{J/\psi }^{v}(x)= & {} 1.67\frac{f_{J/\psi }}{2\sqrt{2N_{c}}}[1+(2x-1)^{2}]\biggl [\frac{x(1-x)}{1-2.8x(1-x)}\biggl ]^{0.7},\nonumber \\ \end{aligned}$$

(94)

where x describes the distribution of charm quark momentum in $J/\psi$ meson and $f_{J/\psi }$ is the decay constant.

And the twist-2 $\phi _{\eta _c}^v(x)$ and the twist-3 $\phi _{\eta _c}^s(x)$ distribution amplitudes for $\eta _c$ meson are collected as follows [61],

$$\begin{aligned} \phi _{\eta _{c}}^{v}(x)= & {} 9.58\frac{f_{\eta _{c}}}{2\sqrt{2N_{c}}}x(1-x)\biggl [\frac{x(1-x)}{1-2.8x(1-x)}\biggl ]^{0.7}, \end{aligned}$$

(95)

$$\begin{aligned} \phi _{\eta _{c}}^{s}(x)= & {} 1.97\frac{f_{\eta _{c}}}{2\sqrt{2N_{c}}}\biggl [\frac{x(1-x)}{1-2.8x(1-x)}\biggl ]^{0.7}, \end{aligned}$$

(96)

with the $\eta _c$ decay constant $f_{\eta _c}$ and x being the momentum fraction of charm quark in $\eta _c$ meson.

For the axial-vector meson $f_1$, the twist-2 light-cone distribution amplitudes, i.e., $\phi _{f_q}(x)$ and $\phi _{f_q}^T(x)$, can be expanded as the Gegenbauer polynomials [62]:

$$\begin{aligned} \phi _{f_q}(x)= & {} \frac{f_{f_q}}{2\sqrt{2N_c}} 6 x (1-x) \left[ 1 + a_{2}^\parallel \, \frac{3}{2} ( 5(2x-1)^2 - 1 ) \right] , \nonumber \\ \end{aligned}$$

(97)

$$\begin{aligned} \phi _{f_q}^T(x)= & {} \frac{f_{f_q}}{2\sqrt{2N_c}}6 x (1-x) \left[ 3 a_{1}^\perp \, (2x-1) \right] . \end{aligned}$$

(98)

And the twist-3 light-cone distribution amplitudes will be used in the following form [62],

$$\begin{aligned}&\phi _{f_q}^s(x)=\frac{f_{f_q}}{4\sqrt{2N_c}} \frac{d}{dx}\Biggl [ 6x (1-x) ( a_{1}^\perp (2x-1) )\Biggr ], \nonumber \\&\phi _{f_q}^t(x)=\frac{f_{f_q}}{2\sqrt{2N_c}}\Biggl [ \frac{3}{2}\,a_{1}^\perp \,(2x-1) (3 (2x-1)^2-1)\Biggr ], \nonumber \\&\phi _{f_q}^v(x)=\frac{f_{f_q}}{2\sqrt{2N_c}} \Biggl [\frac{3}{4} (1+(2x-1)^2) \Biggr ], \qquad \nonumber \\&\quad \phi _{f_q}^a(x) = \frac{f_{f_q}}{8\sqrt{2N_c}} \frac{d}{dx}\Biggl [6 x (1-x) \Biggr ], \end{aligned}$$

(99)

where $f_{f_q}$ is the decay constant of quark-flavor state $f_{q}$ [62] and $a_2^\parallel$ and $a_1^\perp$ are the Gegenbauer moments in the $f_q$ distribution amplitudes [12].

Appendix B: Related functions in the PQCD approach

The threshold resummation function is universal and is usually parameterized in a simplified form as [56]

$$\begin{aligned} S_{t}(x)=\frac{2^{1+2c}\Gamma (3/2+c)}{\sqrt{\pi }\Gamma (1+c)}[x(1-x)]^{c}, \end{aligned}$$

(100)

with $c = 0.4\pm 0.1$ and this factor is normalized to unity.

In the calculation, the Sudakov factor for (a) and (b) in Fig. 2 is symbolled as $S_{ab}(t)$, and one for (c) and (d) is $S_{cd}(t)$. The expression are given as the following,

$$\begin{aligned}&S_{ab}(t)=s(x_{1}P_{1}^{+},b_{1})+ s(x_{3}P_{3}^{-},b_{3})\nonumber \\&\quad +s((1-x_{3})P_{3}^{-},b_{3}) -\frac{1}{\beta _{1}}\nonumber \\&\quad \times \biggl [\frac{5}{6}\ln \frac{\ln (t/\Lambda )}{-\ln (b_{1}\Lambda )}+\ln \frac{\ln (t/\Lambda )}{-\ln (b_{3}\Lambda )}\biggl ], \end{aligned}$$

(101)

$$\begin{aligned}&S_{cd}(t)=s(x_{1}P_{1}^{+},b_{1})+ s_c(x_{2}P_{2}^{+},b_{2})\nonumber \\&\quad +s_c((1-x_{2})P_{2}^{+},b_{2}) + s(x_{3}P_{3}^{-},b_{1})\nonumber \\&\quad +s((1-x_{3})P_{3}^{-},b_{1}) -\frac{1}{\beta _{1}}\nonumber \\&\quad \times \biggl [\frac{11}{6}\ln \frac{\ln (t/\Lambda )}{-\ln (b_{1}\Lambda )}+\ln \frac{\ln (t/\Lambda )}{-\ln (m_c\Lambda )}\biggl ], \end{aligned}$$

(102)

where the functions s(q, b) and $s_c(q,b)$ could be found in Refs. [45] and [47], respectively.