Glueballs at high temperature within the hard-wall holographic model

Abstract

In this investigation an holographic description of the deconfined phase transition of scalar and tensor glueballs is presented within the so called hard-wall model. The spectra of these bound states of gluons have been calculated from the linearized Einstein equations for a graviton propagating from a thermal $AdS_5$ space to an AdS Black-Hole. In this framework, the deconfined phase is reached via a two steps mechanism. We propose that the transition between the AdS thermal sector to the BH is described via a first order phase transition, with discontinuous masses at the critical temperature, which has been determined by Herzog’s method of regulating the free energy densities. Then, the glueball masses diverge with increasing T in the BH phase and thus lead to deconfined states à la Hagedorn.

1 Introduction

A successful strategy for applying the AdS/CFT correspondence and holography [1, 2] to hadron physics is the so-called bottom-up approach. In this framework, one starts from some non perturbative features of QCD and attempts to construct its five-dimensional holographic dual. One implements duality in nearly conformal conditions defining QCD on the four dimensional boundary and introducing a bulk space which is a slice of $AdS_5$ whose size is related to $z_0 \sim 1/\Lambda _{QCD}$ [3,4,5,6,7]. This is the so called hard-wall (HW) approximation. Later on, in order to reproduce the Regge trajectories of the hadronic spectrum, the so called soft-wall model was introduced [8, 9]. Within the bottom-up strategy and in both, hard-wall and the soft-wall approaches, glueballs arising from the correspondence of fields in $AdS_5$ have been studied [10,11,12,13,14]. However, we have recently proposed the calculations of the spectrum of the scalar and tensor glueballs under the assumption that in this holographic approach, the dual operator to the glueballs could be the graviton, the latter thus plays a significant role to describe the lowest lying glueballs. We have studied the problem in hard and the graviton soft-wall models and found an excellent description of the data with very few parameters [15,16,17,18]. The main result of these investigations is that we do not need to introduce additional fields into any $AdS_5$ to describe the glueballs, the gravitons indeed satisfy the duality boundary conditions and are able to describe the elementary scalar and tensor glueball spectra. Due to the exploratory nature of the the present investigation, the HW AdS/QCD model has been used to study the deconfinement phase transition. Since we have proposed that the scalar and tensor glueball spectrum is associated to the graviton of the theory [15, 18], it is therefore natural to generalize this association to the graviton propagating in a black-hole (BH) space. Thus, in the following we have studied the graviton spectrum when a BH background is considered in order to describe the mass dependence on the temperature of the environment and compare the new result with the previous calculations. We recall that much research has been carried out to determine the deconfinement temperature and the behaviour of the glueball and meson spectra after the phase transition [19,20,21].

In the present analysis, we found out that the deconfinement phase is reached via a two steps mechanism. We propose a strategy to describe the transition from the AdS thermal phase, i.e. the low temperature region, to the BH sector, i.e. the high temperature sector. In particular, the Hawking-Phase phase transition is a first order phase transition at the temperature obtained by Herzog [22]. These calculations have been extended to the excited states.

Table 1 Energy modes for the scalar glueball with Dirichlet (D) and Neumann (N) boundary conditions [15]

Table 2 Scalar glueball masses [MeV] from lattice calculations by MP [25], YC [26] and LTW [27] and the recent analysis SDTK [28]

Fig. 1

Scalar and tensor glueball spectrum obtained within the hard-wall model. The solid lines correspond to Dirichlet boundary conditions ($z_0=L_d^{-1} =250$ MeV) and the dashed lines correspond to Neumann boundary conditions ($z_0=L_n^{-1} =290$ MeV). The full circles represent the scalar LQCD masses, the squares the large N limit scalar LQCD masses and the triangles the tensor LQCD masses [15]

2 Scalar and tensor glueballs at zero temperature

In this investigation, we consider the holographic description of glueball states via the hard-wall model. Virtues and inconveniences of this model have been thoroughly discussed, e.g., in Refs. [3, 6, 8, 15]. Here we start from the gravity action:

$$\begin{aligned} \mathcal {I} = \frac{1}{16 \pi G_5} \int d^5x~\sqrt{-\bar{g}} \; [R + 2 \Lambda ], \end{aligned}$$

(1)

where R is the Ricci curvature and $\Lambda$ the corresponding cosmological constant. It can be easily shown that:

$$\begin{aligned} ds^2= \frac{L^2}{z^2} (dt^2 +d \mathbf {x}^2 +dz^2) \end{aligned}$$

(2)

is a solution of the Einstein–Hilbert equations if $\Lambda = -6/L^2$. The equation of motion (EoM) for a graviton propagating in the thermal $AdS_5$ space can be obtained from the Einstein equation for a perturbation in this space. By performing a linear expansion

$$\begin{aligned} \bar{g}_{ab} = g_{ab} + h_{ab} \end{aligned}$$

(3)

one obtains the graviton equations of motion [23, 24]. We report here the result presented in Ref. [15] for the scalar component of the graviton obtained from the standard $AdS_5$ metric, i.e., at $T=0$:

$$\begin{aligned} \frac{d ^2\phi (z)}{d z^2} - \frac{3}{z} \frac{d \phi (z)}{d z} + M^2 \phi (z) = 0, \end{aligned}$$

(4)

where M is the mass of the scalar gravitons. In the HW model, the confinement is realized by restricting the maximum value of $z \le z_0$ at which one imposes either Dirichlet or Neumann boundary conditions. The exact solution of the above equation has been shown in Ref. [15] and the corresponding modes, in units of 1/L, are shown in Table 1. As discussed in Ref. [15], in the $AdS_5$ space, the scalar and tensor graviton equations are the same for the HW model.

Moreover, in Ref. [15], the energy scale has been determined by fitting the lattice data of scalar and tensor glueballs, shown in Table 2. Results are also displayed in Fig. 1. Let us remind that in the hard-wall model the scale is given by $z_0=L$, i.e. the confinement parameter. The fit leads to $z_0 =L_d=1/250$ MeV$^{-1}$, for the Dirichlet boundary conditions, while for the Neumann ones $z_0 =L_N=1/290$ MeV$^{-1}$.

In closing this section, we compare the scalar and tensor glueball spectra obtained from different holographic models. We report in Table 3 some numerical results. As one can see, holographic approaches are powerful tools to explore the glueball spectra. However, as discussed in, e.g. Refs. [9, 11, 29], the standard Soft-Wall (SW) models, where scalar fields dual to the glueball are considered, cannot describe the overall spectrum, in particular they cannot reproduce the ground and higher excited states at the same time. Therefore, modifications, as those of Refs. [9, 11, 14, 29, 30], have been developed. However, although the agreement with lattice data has been improved, with respect to the SW model, also in these cases, a global overall good descriptions of scalar and tensor glueballs for low and excited states has not been reached. We mention the model of Ref. [31] which reproduces well the lowest modes if the first exotic state is skipped. Among the modifications of the SW model we also recall the recent GSW model of Ref. [15] capable of describing the overall scalar and tensor glueball spectrum. Moreover, as already stated, due to the exploratory nature of the present work, we focus on the HW [7, 32] model, which, despite its simplicity, reproduces quite well the glueball spectra.

Table 3 Scalar and tensor glueball masses [MeV] from holographic models. In the model related to the last line, corresponding to Ref. [31], the first exotic mode has been skipped

Table 4 Some theoretical estimates of the critical temperature $T_c$

3 The glueball deconfinement phase transition

In this section the glueball deconfinement phase transition mechanism, realised within the HW model, is described. Within this approach, the first step, towards the deconfinement, corresponds to a Hawking-Page  [33] first order phase transition between the AdS thermal space, see Eq. (2), at low temperature and an asymptotically AdS geometry containing a black hole

$$\begin{aligned} ds^2 = \frac{L^2}{z^2} (f(z) dt^2 + d \mathbf {x}^2 + f^{-1} (z) dz^2), \end{aligned}$$

(5)

at high temperature. Here $f(z)= 1-{z^4}/{z_h^4}$, thus $z_h$ determines the Hawking’s temperature of the black hole solution $T_h = 1/(\pi z_h)$. The comparison between the free energy densities of both phases leads to a critical temperature [22]:

(6)

where again $z_0$ is the infrared cut-off determining confinement and the phase transition is characterized by the relation $z_0^4 = 2z_h^4$ [22]. Thus as the temperature increases, the AdS thermal becomes unstable and the black-hole becomes stable. At $T_c$, the BH horizon forms inside the AdS cavity, between the boundary and the infrared cut-off , at a radius $z_h< z_0$. Here, from Eq. (6), the temperature can be determined from $z_0$. In the present analysis we consider $z_0$ obtained from the previous fit of the scalar and tensor glueball spectra. Numerically, we obtain $T_c= 95$ MeV for Dirichlet boundary conditions, and $T_c= 110$ MeV for Neumann boundary conditions. In Table 4, some lattice data and previous calculations of $T_c$ are reported for comparisons. As one can see, the above results are distant from those in Table 4. Nevertheless, if one evaluates $T_c$, from Eq. (6), by fixing $z_0$ according to the average of lowest glueball mass, see Table 2, then a more realistic value could be found, i.e.: $T_c \sim 125$ MeV for Dirichlet boundary conditions and $T_c \sim 165$ MeV for Neumann boundary conditions. However, by comparing the above results with those in Table 4, one can realise that apparently the HW model needs further improvements, since data related to gluodynamics lead to higher critical temperatures. In the future we could consider other models, such those of Refs. [11, 14, 15, 18, 29, 34], to calculate $T_c$. Other authors have used experimental values of the meson spectroscopy to fit the deconfinement temperature. In the hard-wall model the result is also too low $T_c \sim 125$ MeV, however they obtain higher values for the soft wall model $T_c > 160$ MeV [19, 20, 22, 35].

4 Scalar and tensor glueballs beyond the critical temperature

In this section, we present the mode equations and solutions for scalar and tensor glueball states dual to gravitons propagating in both the thermal $AdS_5$ and black-hole spaces. We expect that beyond the critical temperature the BH horizon forms inside the AdS cavity between the boundary and $z_0$, $z_0>z_h$. We now have to construct the equations of motion for the gravitons with the black hole metric, Eq. (5). To this aim, use has been made of the procedure discussed above for $QCD_3$. Then the EoM for the scalar graviton reads

$$\begin{aligned}&\frac{d^2\phi (z)}{dz^2} + \left( \frac{2}{z} - \frac{5 z_h^4-z^4}{z (z_h^4-z^4)}\right) \frac{d \phi (z)}{dz}\nonumber \\&\quad + \left( \frac{M^2 z_h^4}{z_h^4-z^4}+ \frac{ 256 z^6 z_h^4}{(z_h^4-z^4)(6 z_h^4-2z^4)^2}\right) \phi (z) = 0. \end{aligned}$$

(7)

and for the scalar graviton becomes

$$\begin{aligned} \frac{d^2\phi (z)}{dz^2} + \left( \frac{2}{z} - \frac{5 z_h^4-z^4}{z (z_h^4-z^4)}\right) \frac{d \phi (z)}{dz} + \frac{M^2 z_h^4}{z_h^4-z^4} \phi (z) = 0, \end{aligned}$$

(8)

Furthermore, the tensor graviton EoM is the same as that of an external scalar field in the BH space [23, 24]. One should notice that, at variance with the mode equations obtained in the $AdS_5$ sector [15], in this case the scalar graviton has a different mode equation with respect to that for the tensor graviton and external scalar field due to an additional potential term.

For the sake of simplicity, a constant $\lambda$ is introduced in front of the additional potential term in Eq. (7) so that: $\lambda = 1$ corresponds to the scalar graviton EoM and $\lambda =0$ corresponds to tensor graviton and external field EoM:

$$\begin{aligned}&\frac{d^2\phi (z)}{dz^2} + \left( \frac{2}{z} - \frac{5 z_h^4-z^4}{z (z_h^4-z^4)}\right) \frac{d \phi (z)}{dz}\nonumber \\&\quad + \left( \frac{M^2 z_h^4}{z_h^4-z^4}+ \lambda \frac{ 256 z^6 z_h^4}{(z_h^4-z^4)(6 z_h^4-2z^4)^2}\right) \phi (z) = 0. \end{aligned}$$

(9)

4.1 Solutions to the equation of motion in the BH background

As one might expect, Eq. (9) requires a delicate numerical analysis. In order to study the temperature dependence, a useful change of variable $w=z/z_h$ leads to

$$\begin{aligned}&\frac{d^2\phi (w)}{dw^2} + \left( \frac{2}{w} - \frac{5 -w^4}{w (1 - w^4)}\right) \frac{d \phi (w)}{dw} \nonumber \\&\quad + \left( \frac{\tilde{\mu }^2 }{1 - w^4}- \lambda \frac{ 256 w^6}{(1- w^4)(6 -2 w^4)^2}\right) \phi (w) = 0, \end{aligned}$$

(10)

where the quantity $\mu = M z_h$ is introduced. In order to find the modes of this equation, one needs to integrate it from $w=0$ towards the horizon. It is therefore useful to study the the behavior at $w=z=0$:

$$\begin{aligned} \phi (w) \sim A w^4 + B \end{aligned}$$

(11)

where A, B are integration constants. For simplicity one can set, without loosing generality, $A=1$ and $B=0$ fixing thus the outgoing solution. The changing of the values of A and B leads only to a modification of the shape of the mode function keeping the energy modes fixed. This feature will be explicitly shown later on after the resolution of the equation.

Further, the equation must be the integrated from the horizon inward and then one needs to match the outward and inward solutions and to determine the value of the energy mode. In order to study the behaviour of the solution close to the horizon, needed for the numerical integration, another change of variable is useful: $v =1 - w^4$. Equation (10) now becomes:

(12)

where $v \rightarrow 0$ at the horizon, i.e. $w \rightarrow 1$. The regular solution at $v=0$ has the form of $\phi (v) = \sum _0^\infty a_n v^n$. Substituting this ansatz into the equation and keeping only terms up to order 3, one obtains recurrence relations for $a_i$, with $i \ge 1$, the latter functions of the independent $a_0$ coefficient. For the three first modes one has:

$$\begin{aligned}&a_1 =- \frac{(16 \lambda +\mu ^2 )a_0 }{16} \nonumber \\&a_2= \frac{ (16 \lambda - 3 \mu ^2 ) a_0 -(32 \lambda + 2 \mu ^2 ) a_1}{128 } \nonumber \\&a_3 = -\frac{ (80 \lambda + 15 \mu ^2 ) a_0 + (64 \lambda - 12 \mu ^2 ) a_1 - (128 \lambda + 8 \mu ^2 ) a_2}{1152 }. \end{aligned}$$

(13)

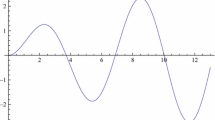
The approximate solution with the four first terms and its derivative is used as initial condition for the numerical program at v close to zero. In Fig. 2 the AdS thermal solutions for the Dirichlet and Neumann boundary conditions, whose mode values are $\mu _d =5.136$ and $\mu _n=3.832$ respectively, are shown for $z_0 = z_h$. Let us remark that this choice is just an example. In addition, also the AdS Black-Hole solution, obtained by matching the outward and inward solutions for $\lambda = 1$ (corresponding to the scalar glueball), is displayed. The matching numerically occurs for $\mu =5.487$ and $a_0 = -0.179$. These two parameters, fixed the by matching, determine uniquely the solution. For the moment being we focus our attention on the scalar glueball. The tensor case will be addressed later on. In order to proceed to the study of the behaviour of the solution, beyond the phase transition, it is important to discuss the A, B independence of the mass modes. The B case is straight forward since the change of B simply implies a displacement of $\phi$. The numerical A dependence is shown in Fig. 3 where the mode function is displayed for $A= 0.5, 1, 1.5, 2.0$ for the same value of $\mu =5.487$. As one can see, the matching is found for different values of $a_0= -0.091, -0.179, -0.271, -0.370$. From the figure, one should realise that the energy modes are determined by the zero of the mode functions which is reached at the same w for all values of A.

Fig. 2

The scalar glueball mode function as a function of $w=z/z_h$. The dashed curve corresponds to Dirichlet (d) boundary conditions with mode value $\mu _d = 5.136$ in the AdS thermal sector and for $z_0=L=z_h$. Dot-dashed line, same of the dashed one, but for the Neumann (n) boundary conditions and $\mu _n = 3.832$. The solid-dotted curve corresponds to the black-hole AdS graviton solution. The solid part of the latter curve is related to the outward solution and the dotted curve to the inward one. At matching the mode value is $\mu =5.487$ and the intercept with the black-hole radius occurs for $a_0= -0.179$

Fig. 3

The solution of the differential Eq. (10) for $\mu = 5.487$ and different values of $A = 0.5$ (dotted), 1 (solid), 1.5 (dashed), 2.0 (dot-dashed) and $B=0$. The mode functions keep the same mass mode value but with different intercepts $a_0= -0.091, -0.179, .0.276, -0.370$

The next step is to study the energy mode values as a function of the energy scale given by the HW model, i.e., $z_0=L$. In this way we will obtain the temperature dependence of the modes from the BH radius. To this aim, we introduce a new variable $u=z/z_0$. The differential equation becomes:

$$\begin{aligned}&\frac{d^2\phi (u)}{du^2} + \left( \frac{2}{u} - \frac{5 u_h^4 -u^4}{u (u_h^4-u^4)}\right) \frac{d \phi (u)}{du} \nonumber \\&\quad + \left( \frac{\tilde{\mu }^2 u_h^4}{u_h^4-u^4} + \lambda \frac{ 256 u^6 u_h^4}{(u_h^4-u^4)(6u_h^4 -2 u^4)^2}\right) \phi (u) = 0. \end{aligned}$$

(14)

where now $\tilde{\mu } = M z_0$ and $u_h=z_h/z_0$. One of the main advantages of moving to the w and u variables is that Eqs. (10,14) have no direct dependence on any dimensional external parameter thus the solution, for the lowest mode, is unique and can be simply obtained for $z_0=z_h$, i.e. $u_h=1$.

Fig. 4

The mass mode of the lowest scalar glueball state as a function of $u_h$. The left figure for the Dirichlet boundary conditions, while the right one for the Neumann boundary conditions. Here it is highlighted the behaviour before and after the adimensional Herzog’s critical temperature, . In the AdS thermal phase we assume constant temperature dependence

Table 5 Energy modes for the scalar glueball in the BH phase at $u_h=1$

On the other hand side, in order to obtain the intercept, $a_0$, at the BH radius, it is necessary, again, to change variable: $\omega = u_h^4- u^4$. When $z \sim z_h$ then $v \sim \omega$ and the solution behaves like: $\phi (z) \sim \sum _0^n \tilde{a}_n(z_0 ^4\omega )^n= \sum _0^n a_n (z_h^4 v)^n$, therefore $\tilde{a}_n z_0^{4n} = a_n z_h^{4n}$, thus

$$\begin{aligned} \tilde{\mu }&= M z_0 = M z_h \frac{z_0}{z_h} = \mu /u_h = 5.487/u_h, \end{aligned}$$

(15)

$$\begin{aligned} \tilde{a}_0&= a_0 \frac{z_0^4}{z_h^4} = a_0 /u_h^4 = -0.179/u_h^4. \end{aligned}$$

(16)

Changing from the w variable to the u variable one can obtain the temperature dependence of the mode functions $\tilde{\mu }$ as given by Eq. (15).

4.2 Hard-wall phase transition à la Herzog [22]

Thanks to the above result, it is now possible to describe the phase transition from the AdS thermal to the AdS BH. In Fig. 4 we plot the AdS BH scalar glueball mass as a function of $u_h$, which is basically the inverse of the temperature, and then we extrapolate the AdS thermal mass at $T=0$ ($u_h \rightarrow \infty$) toward $u_h \rightarrow 0$, assuming a very small temperature dependence in the hard-wall model [20] stopping at Herzog’s value [22]. As one can see, there is a mass difference at the boundary which is relatively large: $\Delta \mu _d =1.389$, corresponding to 347 MeV for the Dirichlet condition and $\Delta \mu _n =2.693$, corresponding to 781 MeV, for the Neumann one. Before closing this section, let us now study the excited modes and how they behave at the phase transition. To this aim, the higher modes have been calculated in the BH sector, which determines the high temperature dependence. The first five modes are shown in Table 5 for $u_h=1$. Moreover, the BH modes are compared with those obtained in the AdS thermal sector, at the Herzog’s phase transition , in Table 6. The full dependence of the modes on $u_h$ is shown in Fig. 5.

Table 6 The energy modes for the scalar glueball AdS BH, at the phase transition and the AdS thermal modes at $T=0$

The results shown in Table 6 can be now converted into physical glueball masses. In terms of energy units, as already discussed, the fit of the glueball spectrum leads to $z_0^{-1}=L_d^{-1} = 250$ MeV and $z_0^{-1}=L^{-1}_n = 290$ MeV, see Table 7. One should notice that the mass differences at the phase transition is smaller for the Dirichlet solutions w.r.t. the Neumann ones. Moreover this quantity diminishes for the excitations. In closing, the main approximation here assumed is the constancy of the dependence of the modes with temperature in the AdS thermal phase. In this scenario, there seems to be a first order phase transition, beyond the Herzog’s temperature, Eq. (6), where the deconfinement mechanism manifests itself in this model by a high rise in the masses of the states as the temperature increases, being the masses proportional to the latter, see for example Eq. (15). Furthermore, following Hagedorn [44], at some point the energy of the deconfined gluons will be smaller than that of the bound states, and there the transition to the quark gluon plasma (QGP) will be reached. Thus in this model, the transition from hadronic matter (HM) to QGP seems to be a two step process, a first order phase transition from hadronic matter to highly massive glueballs (hadrons in general) and then a transition to QGP at higher temperatures. In some sense we are reminded of the scenario described by Shuryak and Zahed [45] where one expects some glueball enhancement mechanisms to appear [46]. For the seek of clarity, the left panel of Fig. 5 has been displayed again but showing directly the energy modes as function of the temperature in units of ${1}/{z_0}$, i.e. $T={1}/{(\pi u_h)}$, see Fig. 6. The importance of this figure lies in the AdS BH phase, which will repeat itself in all other scenarios. The different excited states have divergent linear trajectories, thus their masses separate more and more, leaving space for other intermediate states, which could be associated to colour bound states, which our colourless model does not contain, in line with the two step phase transition already mentioned.

Table 7 The masses in MeV units of the scalar AdS BH glueballs, at the phase transition and the AdS thermal modes at $T=0$ with scales $L_d^{-1} =250$ MeV and $L^{-1}_n = 290$ MeV

Fig. 5

The spectrum of the scalar glueballs, in both sides of the phase transition, for the Dirichlet condition (left panel) and the Neumann one (right panel). We are assuming here that in the AdS thermal phase the masses of the particles almost remain constant

Fig. 6

Same of Fig. 5 but the modes are now functions of the temperature in unit of the energy scale, i.e., $T={1}/(\pi u_h)$

4.3 Tensor glueballs

Finally, let us now discuss the tensor components. We recall that the tensor glueball states and the scalar glueballs are degenerate in this model in the $AdS_5$. However, the mode equation in the BH AdS background is different from that of the scalar graviton equation, see Eqs. (8,7). In Table 8 we compare the masses of both the glueball components in the BH AdS sector at the phase transition and, in Fig. 7, the temperature dependence of the the tensor graviton spectrum (dashed) and the scalar graviton spectrum (solid) are respectively displayed. As one can see, the effect of the additional term, proportional to $\lambda$ in Eq. (9), is small. Moreover, the scalar modes become lighter than the tensor ones as expected. Therefore, we can conclude, that the deconfinement phase transition mechanism for the tensor glueballs follows the one already described for the scalar case. Before closing this section, we can interpret the above results in view of the HW model used. Indeed, as already stated in Sect. 4, the external scalar field EoM in the BH background is the same of that of the tensor component in the same space. Therefore, by comparing the spectra presented in this section with those of the scalar graviton, e.g. see Fig. 7, we prove that the modes of the scalar graviton have lower masses than those of the scalar external field in the BH space. Such a feature is consistent with the analysis of, e.g. Ref. [23].

Table 8 The masses of the scalar and tensor AdS BH glueballs, at the phase transition with scales $L_d^{-1} =250$ MeV and $L^{-1}_n = 290$ MeV

Fig. 7

The tensor glueball spectrum (dashed line) in the AdS BH sector, i.e., below the horizon, as a function of $u_h$, compared with that of scalar glueballs (solid lines)

5 Conclusions

In this investigation the scalar and tensor glueball spectra have been calculated within the holographic Hard-Wall model. In particular we have studied the equation of motion for a graviton propagating first in a thermal AdS space and then in a AdS Black-Hole in order to describe the glueball masses as a function of the temperature. The scalar and tensor components are degenerate in AdS at $T=0$. However, when the BH background is considered, such degeneracy is lost, and the tensor glueballs become heavier. The energy scale of the HW model has been fixed by fitting lattice data of the glueball spectrum. Such a fit is quite good in particular when Dirichlet boundary conditions are used. Starting from these results, the mode energies of glueballs have been calculated in both the AdS thermal and BH spaces. The outcomes of these evaluations have been used to propose a mechanism to describe the transition from the AdS thermal sector to the BH one. If the masses do not depend strongly on the temperature in the AdS thermal phase and at Herzog’s critical temperature a first order Hawking-Page phase transition, between the low temperature AdS thermal phase and a high temperature BH phase, takes place. Finally, the real transition to a purely deconfined state is described by a sharp rise of the mass of the glueballs beyond $T_c$.

The results of this investigation are quite dependent on the behaviour of the modes in the AdS thermal phase, but not so in the AdS BH phase, where the solutions of the EoM are completely determined by the behaviour of the equations at the horizon. We can conclude that deconfinement is realized following Hagendorn’s mechanism [44], consisting in a rapid rise of the mass of the hadron states until they become heavier than a system of unconfined gluons, forcing the glueballs to change from bound states to unbound free particles. The resulting scenario is similar to that described by Shuryak and Zahed [45] for a transition to an intermediate phase of heavy colour bound states before the true deconfinement to QGP takes over.

This investigation makes use of a specific model and it should be carried out in more sophisticated models like the soft-wall or/and the graviton soft-wall models. However, we expect that a similar behaviour beyond the horizon will take place there, with a rapid rising of the mode values in the AdS BH phase. In order to determine the type of phase transition, a temperature dependence study of the modes in the AdS thermal phase should be also performed.

Schrödinger solutions

It has been shown that Eq. (10) can be transformed into a Schrödinger type equations by changing the function $\phi (z) = \beta (z) \chi (z)$ where $\beta {z}= z^2 z_h^2\sqrt{\frac{z_h-z}{z_h(z_h^4-z^4)}}$ followed by a change of variable $z= z_h/(1+e^y)$ of the form

$$\begin{aligned} - \chi ''(y) = V(y) \,\chi (y), \end{aligned}$$

(17)

where

$$\begin{aligned} V(y)&= \frac{1}{4} +\frac{e^{2y} (15(1+ e^y)^8 -30(1+e^y )^4 -1}{4 (1+e^y)^2 ((1+e^y)^4-1)^2} \nonumber \\&\quad - \frac{\mu ^2 e^{2y}}{(1-e^y)^4 -1} - \lambda \frac{64(1+e^y)^2 e^{2y}}{ (1+e^y)^4-1) (3(1+e^y)^4-1)^2}, \end{aligned}$$

(18)

where $y \in (-\infty , \infty )$ [23, 24]. We have solved this differential equation numerically by starting from $-\infty$ towards the right, and from $\infty$ towards the left and matching the solutions. In order to do so we need the behavior of the potential which is

$$\begin{aligned} \lim _{y \rightarrow -\infty } V(y)&\rightarrow \left( \frac{5}{4} -\frac{\mu ^2}{4} - 4\lambda \right) e^y, \end{aligned}$$

(19)

$$\begin{aligned} \lim _{y \rightarrow +\infty } V(y)&\rightarrow 4. \end{aligned}$$

(20)

These limits tell us that the solution of the equation behaves at the limits as

$$\begin{aligned} \lim _{y \rightarrow -\infty } \chi (y)&\rightarrow - e^{\delta e^y}, \end{aligned}$$

(21)

$$\begin{aligned} \lim _{y \rightarrow +\infty } \chi (y)&\rightarrow \gamma e^{-\dfrac{2y}{\sqrt{\gamma }}}. \end{aligned}$$

(22)

We fix $\delta = \frac{5}{4} -\frac{\mu ^2}{4} - 4\lambda$ and we vary $\mu = M z_h$ and $\gamma$ to find the match. For $\gamma = 1.089$ we get the match shown in Fig. 8 exactly at $\mu = 5.51$ to be compared to 5.487 for the method above. It is clear that this technique for solving the problem might be useful for the use of WKB methods but one looses the physical insight compared to our way of solving the problem, which establishes an direct comparison between the modes and mode functions in the AdS thermal phase and in the AdS BH phase.

Fig. 8

We show the match between the left and right branches of the solution to the Schrödinger equation Eq. (17 for the lightest scalar glueball