1 Introduction

The study of distant Type Ia supernovae [1,2,3,4] has changed our perception about the evolution of the universe drastically and it was found that the universe is going through an accelerated expansion at present. The observations of the cosmic microwave background radiation [5, 6], large-scale structure [7, 8], baryon acoustic oscillations [9] and Planck data [10, 11] confirm the accelerated expansion of the universe. These observations suggest that about 70% of the energy content of the universe is in the form of a mysterious component, which violates the strong energy condition, called dark energy (DE). A number of DE models have been proposed in the literature but the \(\Lambda \)CDM model is the simplest and most successful model of DE. However, despite excellent features, it has some theoretical problems like the coincidence and fine-tuning problems [12]. The major problem with the \(\Lambda \)CDM model based on Einstein’s general relativity arises when it is applied at the quantum level. According to Einstein, space time is warped by the matter and energy in it, but quantum physics says the matter and energy exists in multiple states simultaneously. So, where is the gravitational field? In recent papers [13, 14], the authors have shown that the \(\Lambda \)CDM model has some major tension with recent observations and it may not be the best description of our universe. Therefore, it is time to explore all the possibilities for a better understanding of the universe.

Modified theories of gravity have been considered as an alternative to general relativity (GR) and play an important role in the study of the evolution of the universe. A natural extension of GR is Brans–Dicke (BD) theory, introduced by Brans and Dicke [15] in 1961. In this theory, the gravitational constant G is no longer a constant, and is replaced by a scalar field \(\phi (t)=(8\pi G)^{-1}\), called the BD scalar field. The BD scalar field plays a vital role in BD theory, and various cosmological phenomena have been studied using a power law form of the BD scalar field [16,17,18,19,20]. In the literature, it has been shown by a number of authors [21,22,23] that the power law form \(\phi \propto a^n\), where a represents the cosmic scale factor, of the BD scalar field leads to a constant deceleration parameter (DP). Therefore, the well known phase transition of the universe from deceleration to acceleration cannot be achieved using a power law form. However, a number of authors [17,18,19, 24, 25] have obtained a time-dependent DP for the same assumption of \(\phi \). Kumar and Singh [26] discussed this problem of constant DP associated with the power law form, and proposed a logarithmic form of the BD scalar field. A number of authors have considered the logarithmic form to explain various aspects of cosmological evolution [27,28,29,30,31]. In the present paper, we are interested to discuss the evolution of the universe in BD theory without taking any specific form of BD scalar field and also to find a suitable form of BD scalar field for the model under consideration in the paper.

Dynamical DE candidates, which contains some significant properties of quantum gravity, are able to present a unified model of the universe and explain some problems of modern cosmology like the coincidence problem [32]. The dynamical DE models based on the holographic principle, introduced by ’t Hooft [33] and further discussed by Susskind [34], have garnered a lot of attention to explain the accelerated expansion and problems of the \(\Lambda \)CDM model. These models of DE are known as holographic dark energy (HDE) models. It was shown [35] that the formation of black holes puts an upper bound on the DE density in the formalism of quantum field theory. According to Li [36], if \(\rho _{h}\) is the quantum zero-point energy density caused by a short distance cut-off, the total energy in a region of size L should not exceed the mass of a black hole of the same size. Taking the largest IR cut-off L to saturate the inequality, the author obtained \(\rho _{h}=3c^2 M_{p}^2 L^{-2}\), where c is a dimensionless constant and \(M_{p}\) stands for the reduced Planck mass. A number of authors have discussed various aspects of HDE [37,38,39,40,41,42,43].

In the present paper, we consider the concept of HDE is the framework of BD theory. First, we demonstrate how the assumption \(\phi \propto a^n\) naturally leads to a constant DP which is not able to describe the phase transition. Further, without using any specific form of the BD scalar field, we obtain the value of the scale factor and corresponding value of \(\phi \) for HDE model. We obtain the value of the DP by using the value of the scale factor and discuss the possible evolution of the universe. Further, we are interested to discuss dissipative behavior of HDE in BD theory. Therefore, we consider viscous HDE. More precisely, we are interested to know whether the non-interacting viscous HDE may play the role of interacting HDE.

Dissipation is a natural phenomenon of the cosmic fluid and plays a significant role in the evolution of the universe. Scalar dissipative processes of the cosmic fluid may be treated via the relativistic theory of bulk viscosity. The phenomenon of bulk viscosity arises in the cosmological fluid when the fluid expands (contracts) too fast, due to which the system is out of thermal equilibrium. Then, the effective pressure become negative to restore the thermal equilibrium [44]. Therefore, it is natural to consider bulk viscosity in an accelerating universe. In the literature, bulk viscosity has been discussed to study early time inflation, as well as late time acceleration due to its ability to produce an effective negative pressure [45,46,47,48,49,50,51,52]. We show that the non-interacting viscous HDE with Hubble length as IR cuf-off can explain the phase transition (deceleration to acceleration) in contrast to non-interacting non-viscous HDE [17, 18]. This also shows that viscous HDE may play the role of interacting HDE in the framework of BD theory.

Sahni et al. [53] introduced a robust analysis to discriminate among DE models, known as statefinder diagnosis. The statefinder is a geometrical diagnostic, and allows us to characterize the properties of DE in a model-independent manner. It is dimensionless and is constructed from the scale factor of the universe and its time derivatives only. The statefinder diagnosis is able to successfully discriminate between a wide range of DE models, including the cosmological constant, quintessence, k-essence, Chaplygin gas and braneworld models. Statefinder diagnosis plays a particularly important role for modified gravity theories such as scalar–tensor models and braneworld models of DE, for which the equation of state is not a fundamental physical entity. Thus, it is important to compare our DE models with existing ones. Therefore, we obtain the value of the statefinder parameters r and s, and plot \(r-s\) and \(r-q\) trajectories to compare both of our models, interacting HDE and non-interacting viscous HDE, with existing models.

The paper is organized as follows. HDE with Hubble horizon as an IR cut-off is the subject of the next section in the framework of BD theory. We demonstrate that \(\phi \propto a^n\) is not a suitable choice to explain the phase transition of the universe. Further, we find the scale factor a and the corresponding value of \(\phi \). We obtain the expression of the DP q to study the possible evolution of the universe. Further, we apply statefinder diagnostics to compare our model with existing models. Section 3 is devoted to the study of viscous HDE. We obtain the value of a, \(\phi \) and q as in Sect. 2. Further, we discuss statefinder diagnostics in the model. In Sect. 4, we present a summary of our results.

2 Holographic dark energy in Brans–Dicke theory

The action for BD theory in the Jordan frame is given by

$$\begin{aligned} S=\int d^{4}x\sqrt{-g}\left[ \frac{1}{2}\left( -\phi R+\frac{\omega }{\phi }g^{\mu \nu }\partial _{\mu }\phi \; \partial _{\nu }\phi \right) +{\mathcal {L}}_{m}\right] ,\nonumber \\ \end{aligned}$$
(1)

where R, g and \({\mathcal {L}}_{m}\) represent the Ricci scalar curvature, determinant of the metric tensor \(g_{\mu \nu }\) and the matter Lagrangian density, respectively. Here, \(\phi \) and \(\omega \) denote the BD scalar field and BD coupling parameter, respectively. From a theoretical point of view, there are no constraints on the coupling parameter \(\omega \). Observational constraints vary depending upon the method being used. Solar system bounds are \(\omega > 40{,}000\) [54] whereas cosmological scale bounds are very low [55,56,57]. In this theory, the Newtonian constant G is replaced with a time dependent scalar field \(\phi \) such that \(\phi =(8\pi G)^{-1}\). The dimensionless parameter \(\omega \) is introduced to represent a coupling between the scalar field and gravity. In the Jordan frame, the scalar field and matter field do not interact, and matter minimally couples to the metric.

We assume a homogeneous and isotropic flat Friedmann–Lemaitre–Robertson–Walker (FLRW) space-time to discuss the evolution of the Universe. The FLRW line element is given by

$$\begin{aligned} ds^{2}=dt^{2}-a^{2}(t)\left[ \frac{dr^{2}}{1- r^2}+r^{2}(d\theta ^{2}+\sin ^2\theta \; d\phi ^2)\right] , \end{aligned}$$
(2)

where a is the cosmic scale factor. We assume that the universe is filled with pressureless dark matter (DM) and HDE. We exclude baryonic matter and radiation due to their negligible contribution to the total energy budget during late time evolution. In the above formalism, the Brans–Dicke field equations take the form

$$\begin{aligned}&H^2+H\frac{{\dot{\phi }}}{\phi }-\frac{\omega }{6}\frac{{\dot{\phi }}\;^2}{\phi \;^2}=\frac{\rho _{m}+\rho _{h}}{3\phi }, \end{aligned}$$
(3)
$$\begin{aligned}&2\frac{\ddot{a} }{a}+H^2+2 H\frac{{\dot{\phi }}}{\phi }+\frac{\omega }{2}\frac{{\dot{\phi }}\;^2}{\phi \;^2}+\frac{\ddot{\phi }}{\phi }=\frac{-p_{h}}{\phi }, \end{aligned}$$
(4)

where \(\rho _{m}\), \(\rho _{h}\) and \(p_{h}\) stand for the energy density of DM, energy density of HDE and pressure of HDE, respectively. The evolution of the BD scalar field \(\phi \) follows the wave equation

$$\begin{aligned} \ddot{\phi }+3H{\dot{\phi }}=\frac{\rho _{m}+\rho _{h}-3p_{h}}{2\omega +3}. \end{aligned}$$
(5)

Using Eqs. (3)–(5), we obtain the combined energy conservation equation as follows [16, 17]:

$$\begin{aligned} {\dot{\rho }}+3H(\rho +p)=0, \end{aligned}$$
(6)

where \(\rho =\rho _{m}+\rho _{h}\) and \(p=p_{h}\).

2.1 Power law form and constant deceleration parameter

To discuss DE models including HDE and models without DE in the framework of BD theory, there is a general tendency to assume \(\phi \propto a^n\). Now, we will show that this assumption leads to a constant value of DP which does not depend on which candidate of DE is being considered. It does also not depend on whether it is non-interacting or interacting DE. Combining the Eqs. (3)–(5) and using the assumption \(\phi \propto a^n\), we obtain a single equation as follow:

$$\begin{aligned} 2\frac{\ddot{a}}{a}(3-n\omega )+H^2(6-4 n \omega -n^2\omega )=0. \end{aligned}$$
(7)

In cosmology, the DP is defined as \(q=-\frac{\ddot{a}}{aH^2}\). Therefore, one can find the value of q from Eq. (7) directly as

$$\begin{aligned} q=-\frac{\ddot{a}}{aH^2}=\frac{(6-4n\omega -n^2\omega )}{2(3-n\omega )}. \end{aligned}$$
(8)

It is evident that a constant DP is obtained irrespective of the matter content of the universe for the assumption \(\phi \propto a^n\). One can observe, whatever the candidate of DE we choose, non-interacting or interacting, we will get the same Eq. (7) and the same value of DP. However, a number of authors [17,18,19, 24, 25] have obtained a time-dependent DP for the same assumption of \(\phi \), taking different forms of DE. This problem of the power law form was addressed in the paper [26], and the authors proposed a logarithmic form of the BD scalar field which is free from this problem.

2.2 Interacting HDE, BD scalar field and deceleration parameter

In the present paper, we are not going to take any one of the available forms of the BD scalar field. Rather, we are interested to find an appropriate form of it for the HDE model. We assume interaction between the pressureless DM and HDE as taken by [17]. Now, the conservation equations of pressureless DM and HDE are given by

$$\begin{aligned}&{\dot{\rho }}_{m}+3H\rho _{m}=Q, \end{aligned}$$
(9)
$$\begin{aligned}&{\dot{\rho }}_{h}+3H(\rho _{h}+p_{h})=-Q, \end{aligned}$$
(10)

where Q denotes the interaction term between DM and HDE. For \(Q>0\), there is energy transfer from HDE to DM and there is energy transfer from DM to HDE for \(Q<0\). In the literature, Q has been assumed to be proportional to the Hubble parameter, i.e., \(Q \propto H\) to maintain the interaction term Q as a function of a quantity with units of inverse of time multiplied with the energy density. Therefore, we assume \(Q=\Gamma \rho _{h}\) as taken by [17, 19], where \(\Gamma \) stands for the interaction rate. Here, we do not restrict \(\Gamma \) to be a positive quantity as in the above cited papers. We are interested to study the effects of the energy transfer from both sides on the evolution of the universe, i.e., energy transfer from HDE to DM as well as from DM to HDE. Therefore, for this requirement, we have taken \(\Gamma \) such that it can take both the sign, positive and negative. We consider HDE with Hubble length \(L^{-1}=H\) as IR cut-off as taken by [17, 19]:

$$\begin{aligned} \rho _{h}=3c^2M_{p}^2H^2, \end{aligned}$$
(11)

where c is a dimensionless constant and \(M_{p}\) stands for the reduced Planck mass, and has the value \(M_{p}^2=\frac{1}{8\pi G}\). In BD theory, we know that Newton’s gravitational constant G is no more a constant, but we assume \(M_{p}\) as a constant in HDE (11) as taken in papers [17, 19]. It may be noticed from the equation for \(\rho _{h}\) that there are no theoretical restrictions on the constant c, except that it has to be of the order of the reduced Planck mass \(M_{p}\). We consider the equation of state (EoS) of HDE as \(p_{h}=w\rho _{h}\), where w is the EoS parameter. Now, we are interested to find the value of \(\phi \) rather than assuming it. One way is that we assume the scale factor like a power or exponential law, and using Eqs. (3)–(5) separately or together, find the value of \(\phi \). But, this will be just a reconstruction of the BD scalar field and then there will be no significance to the HDE. Conversely, if we use HDE (11) in Eqs. (3)–(5), then also we will not get any fruitful result. Therefore, we find the scale factor from the energy conservation equation (10) of the HDE using the form (11) for the HDE.

Using the value of Q and Eq. (11), Eq. (10) reduces to

$$\begin{aligned} \dot{H}+\frac{3}{2}(1+w)H^2+\Gamma H=0. \end{aligned}$$
(12)

Here, we obtain a single evolution equation for the Hubble parameter. It may be seen from this equation that the constant c from Eq. (11) does not appear. Hence there are no further restrictions on c. On solving Eq. (12), we get the value of H in terms of cosmic time t as

$$\begin{aligned} H=\frac{e^{-\frac{\Gamma }{2}t}}{c_{0}-\frac{3(1+w)}{\Gamma }e^{-\frac{\Gamma }{2}t}}, \end{aligned}$$
(13)

where \(c_{0}\) is a constant of integration. On solving Eq. (13), one can obtain scale factor as

$$\begin{aligned} a=c_{1}\left[ c_{0}-\frac{3(1+w)}{\Gamma }e^{-\frac{\Gamma }{2}t}\right] ^{\frac{2}{3(1+w)}}, \end{aligned}$$
(14)

where \(c_{1}>0\) is an another constant of integration. The non-negative of \(c_1\) is the consequence of calculation because it appears under the logarithmic function which is not defined for negative values. We can rewrite the scale factor as

$$\begin{aligned} a=a_{0}\left[ 1-\frac{3(1+w)H_{0}}{\Gamma }(e^{-\frac{\Gamma }{2}(t-t_0)}-1)\right] ^{\frac{2}{3(1+w)}}, \end{aligned}$$
(15)

where \(a_{0}\) and \(H_{0}\) denote the present value of the Hubble parameter and the scale factor at the time \(t_{0}\), the present value of time when the HDE begins to dominate. From Eq. (9), we obtain the value of the DM energy density as

$$\begin{aligned} \rho _{m}= & {} \frac{M_{p}^2\;c^2\; \Gamma }{\frac{3(1+w)}{\Gamma }-(\frac{1}{H_{0}}+\frac{3(1+w)}{\Gamma })e^{\frac{\Gamma }{2}t}}\nonumber \\&-\frac{3\;t}{e^{\frac{3(1+w)}{\Gamma }-(\frac{1}{H_{0}}+\frac{3(1+w)}{\Gamma })e^{\frac{\Gamma }{2}t}}}\;c_{2}, \end{aligned}$$
(16)

where \(c_{2}\) is a constant of integration. Now, using the values of \(\rho _{h}\) and \(\rho _{m}\) in the wave equation (5), one can find the value of the BD scalar field \(\phi \). For simplicity we let \(c_{2}=0\), however, the solution also exists for a nonzero value of \(c_{2}\). On solving Eq. (5), we obtain the value of \(\phi \) as

$$\begin{aligned} \phi (t)= & {} -\frac{M_{p}^2\;c^2\;\Gamma }{3}\;t\nonumber \\&+\frac{M_{p}^2\;c^2\;(1-3w)}{(2\omega +3) \left[ \left( \frac{1}{H}+\frac{3(1+w)}{\Gamma }\right) e^{\frac{\Gamma }{2}t}-\frac{3(1+w)}{\Gamma }\right] }\;t\nonumber \\&-\frac{3}{2}t\left[ \left( \frac{1}{H}+\frac{3(1+w)}{\Gamma }\right) e^{\frac{\Gamma }{2}t}-\frac{3(1+w)}{\Gamma }\right] \nonumber \\&\times e\;^{\left[ \left( \frac{1}{H}+\frac{3(1+w)}{\Gamma }\right) e^{\frac{\Gamma }{2}t}-\frac{3(1+w)}{\Gamma }\right] }\;c_{3}+c_{4}, \end{aligned}$$
(17)

where \(c_{3}\) and \(c_{4}\) are constants of integration. We have obtained the scale factor a and the BD scalar field \(\phi \) corresponding to HDE with Hubble length as IR cut-off. Now, using the value of the scale factor, we obtain the value of the DP (q) to discuss the evolution of the universe. The expression of the DP for the scale factor (15) is as follows:

$$\begin{aligned} q=\left[ \frac{\Gamma }{2H_{0}}+\frac{3(1+w)}{2}\right] e^{\frac{\Gamma }{2}(t-t_0)}-1. \end{aligned}$$
(18)

Here, we obtain a dynamic DP whose value depends on the interaction rate (\(\Gamma \)) and the EoS parameter of HDE (w). Both the parameters \(\Gamma \) and w play an important role in the evolution of the universe. If \(\Gamma >0\) and w lies in the quintessence region, i.e. \(-1<w<-1/3\), then there are two possible evolutions of the universe. We obtain a phase transition from early time acceleration (inflation) to deceleration for \((\frac{\Gamma }{2H_{0}}+\frac{3(1+w)}{2})<1\), and decelerated expansion through out the evolution for \((\frac{\Gamma }{2H_{0}}+\frac{3(1+w)}{2})>1\). If w lies in the phantom region, i.e. \(w<-1\), then there are three possible evolutions of the universe. Two possible evolutions are same as in the quintessence region with the same conditions. In the third possibility, we obtain a negative value of q throughout the evolution with the condition \((\frac{\Gamma }{2H_{0}}+\frac{3(1+w)}{2})<0\), i.e. \(\Gamma <-3(1+w)H_{0}\). Thus, we get recent accelerated expansion of the universe which is not possible in the quintessence region. Here, our results show that \(\Gamma >0\) is not an appropriate choice to discuss the recent phase transition of the universe, however, we can obtain the recent accelerated expansion in the phantom region.

Fig. 1
figure 1

The figure of deceleration parameter q against cosmic time t has been plotted for \(H_0\) = 10

Full size image

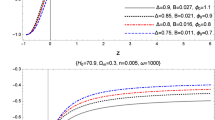
A viable model must accommodate the phase transition rather than only showing acceleration. It seems that the assumption \(\Gamma >0\) has been considered by several authors to deal with an important issue, viz., why is the observational value of the vacuum energy (DE) 120 orders smaller than the value predicted by quantum physics? Let us now discuss the case when \(\Gamma <0\). In this case, we obtain recent accelerated expansion for both the quintessence and the phantom HDE. To achieve the recent phase transition, the parameters must satisfy the condition \((\frac{\Gamma }{2H_{0}}+\frac{3(1+w)}{2})>1\), i.e. \(w>-\frac{1}{3}-\frac{\Gamma }{3H_{0}}\). As we have taken \(\Gamma <0\), we obtain \(w>-\frac{1}{3}\). The energy transfer from DM to HDE, due to the choice \(\Gamma <0\), is responsible for the result \(w>-\frac{1}{3}\) required to explain the recent phase transition. The value of \(\Gamma \) should be very small (\(\Gamma<<<1\)) to obtain the phase transition at late times. Therefore, we can achieve \(w\approx -\frac{1}{3}\). We observe that phantom HDE is not suitable to accommodate the phase transitions of the universe for both positive and negative values of \(\Gamma \). Further, we observe that the quintessence HDE successfully describes the phase transition from early time acceleration (inflation) to deceleration for \(\Gamma >0\). However, to accommodate the recent phase transition (deceleration to acceleration) for \(\Gamma <0\), the EoS parameter has the value below the quintessence divide (\(w>-\frac{1}{3}\)). The evolution of the DP for various values of the model parameters has been shown in Fig. 1. It may be seen that the desired behaviour of a transition from deceleration to acceleration is obtained for \(\Gamma < 0\) and \(w > -\frac{1}{3}\).

2.3 Statefinder Diagnosis

Sahni et al. [53] introduced a robust analysis to discriminate among DE models known as statefinder diagnosis which was further discussed by Alam et al. [58] in detail. The authors presented a new diagnostic pair \(\{r, s\}\) which is geometrical in nature as it is constructed from the space-time metric directly. The pair r and s are known as statefinder parameters. The statefinder pair \(\{r, s\}\) provides a very comprehensive description of the dynamics of the universe and consequently the nature of DE. For the \(\Lambda \)CDM model and the SCDM model, the statefinder pair \(\{r,s\}\) has the fixed value \(\{1, 0\}\) and \(\{1, 1\}\), respectively. The statefinder pair \(\{r,s\}\) is defined as, respectively,

$$\begin{aligned} r=\frac{\dddot{a}}{aH^3},\quad s=\frac{r-1}{3(q-1/2)}. \end{aligned}$$
(19)

In our model, we obtain the value of the statefinder parameters using the value of the scale factor a given by (15) and the value of the DP q given by (18) as follows

$$\begin{aligned} r= & {} \frac{e^{\Gamma (t-t_0)}}{4H_0^2}\Big [(1-3 H_0(1+w)(e^{-\frac{\Gamma (t-t_0)}{2}}-1))\nonumber \\&\times (\Gamma +3H_0(1+w)+6H_0 w(e^{-\frac{\Gamma (t-t_0)}{2}}))\nonumber \\&+ 2H_0(1+3w)(2+3w) e^{-\Gamma (t-t_0)}\Big ], \end{aligned}$$
(20)
$$\begin{aligned} s= & {} \frac{e^{\Gamma (t-t_0)}}{(2\Gamma H_0+6(1+w)H_0^2)e^{\frac{\Gamma (t-t_0)}{2}}-18H_0^2}\nonumber \\&\times \Big [\Big \{(1-3 H_0(1+w)(e^{-\frac{\Gamma (t-t_0)}{2}}-1))\nonumber \\&\times (\Gamma +3H_0(1+w)+6H_0 w(e^{-\frac{\Gamma (t-t_0)}{2}}))\nonumber \\&+2H_0(1+3w)(2+3w) e^{-\Gamma (t-t_0)}\Big \}-1\Big ]. \end{aligned}$$
(21)

We have plotted the \(r-s\) trajectories in Fig. 2. The points plotted on upper boundary of the figure represent the values of \(\{r, s\}\) for the \(\Lambda \)CDM model which is \(\{1, 0\}\) and for the SCDM model which is \(\{1, 1\}\). In Fig. 2a, we have plotted \(r-s\) trajectories for a negative interaction rate \(\Gamma = -0.1\) and in Fig. 2b, we have plotted \(r-s\) trajectories for a positive interaction rate \(\Gamma =0.005\). We observe in Fig. 2a, where \(\lambda < 0\), that in the late time evolution, the trajectories show quintessence-like behavior and approache the \(\Lambda \)CDM model (See Alam et al. [58]). In Fig. 2b, where \(\lambda > 0\), we observe that the trajectories for \(w > -1\) look like those in Fig. 2a, but start with higher negative values of r and higher positive values of s. Further, the trajectories move towards the \(\Lambda \)CDM model at late times, but never reach there. The trajectories of phantom HDE (\(w<-1\)) in Fig. 2b behave differently and approach the \(\Lambda \)CDM model at late times, which is shown by trajectory (5) in the figure.

The \(r-q\) trajectories have been plotted in Fig. 3. The straight line in the figure has been plotted to show the evolution of the \(r-q\) trajectory for the \(\Lambda \)CDM model and the fixed point values of \(\{r, q\}\) for the steady-state (SS) model and the SCDM model having the values \(\{1, -1\}\) and \(\{1, 0.5\}\), respectively. We have plotted \(r-q\) trajectories for a negative interaction rate \(\Gamma = -0.1\) in Fig. 3a and for a positive interaction rate \(\Gamma =0.01\) in Fig. 3a. It has been observed in Fig. 3a that for smaller negative values of the EoS parameter w, the trajectories behave like quintessence during late time evolution. But as we increase the negative value of w, the trajectories deviate more and more from quintessence behavior. In Fig. 3b, we observe that for small negative values of w, the trajectories behave almost like quintessence at early times, but do not approach the SS model at late times, whereas the quintessence model approaches the SS model at late times. As we increase the negative values of w, greater deviation from quintessence has been observed. Even, phantom HDE shows totally different behavior from the quintessence HDE shown by trajectory (5) in the figure.

Fig. 2
figure 2

The \(r-s\) trajectories has been plotted in the figure. We have taken \(H_0=10\) and \(t_0=1\) to plot the trajectories. The figure a is plotted for negative value of interaction rate \(\Gamma =-0.1\) and the figure b is plotted for positive value of interaction rate \(\Gamma =0.005\). In figure (a), the trajectories 1, 2, 3, and 4 are plotted for \(w=-0.35\), \(w=-0.5\), \(w=-0.7\), and \(w=-0.9\), respectively. In figure (b), the trajectories 1, 2, 3, 4 and 5 are plotted for \(w=-0.6\), \(w=-0.7\), \(w=-0.8\), \(w=-0.9\) and \(w=-1.2\), respectively

Full size image
Fig. 3
figure 3

The \(r-q\) trajectories has been plotted in the figure. We have taken \(H_0=10\) and \(t_0=1\) to plot the trajectories. The figure a is plotted for negative value of interaction rate \(\Gamma =-0.1\) and the figure b is plotted for positive value of interaction rate \(\Gamma =0.01\). In figure (a), the trajectories 1, 2, 3, 4 and 5 are plotted for \(w=-0.35\), \(w=-0.5\), \(w=-0.7\), \(w=-0.8\) and \(w=-1.1\), respectively. In figure (b), the trajectories 1, 2, 3, 4 and 5 are plotted for \(w=-0.6\), \(w=-0.7\), \(w=-0.8\), \(w=-0.9\) and \(w=-1.1\), respectively

Full size image

3 Viscous holographic dark energy in Brans–Dicke theory

In an isotropic and homogeneous FLRW model, the dissipative process may be treated via the relativistic theory of bulk viscosity proposed by Eckart [59] and later on pursued by Landau and Lifshitz [60]. It has been found that only the bulk viscous fluid remains compatible with the assumption of large scale homogeneity and isotropy. The other processes, like shear and heat conduction, are directional mechanisms and they decay as the universe expands. Bulk viscosity has been studied in the literature to discuss inflation as well as the recent acceleration of the universe. It also plays an important role to explain the phase transition of the universe, particle creation, the photon to baryon ratio in the universe and to avoid the initial singularity [45,46,47,48,49,50,51,52]. We do not know the exact nature of DE yet except its negative pressure and it might be viscous in nature. Therefore, it will be interesting to discuss the bulk viscous nature of HDE. The main purpose behind considering bulk viscous HDE in BD theory is to find the answer to the question: Can the non-interacting bulk viscous HDE play the role of interacting HDE? The concept of viscous DE has been discussed extensively in the literature, e.g., [39, 61,62,63]. Due to viscous effects, the effective pressure of HDE is given by \(P_{eff}=p_{h}+\Pi \), where \(\Pi \) denotes the change due to bulk viscosity. According to Eckart theory [59], \(\Pi =-3\zeta H\), where \(\zeta \) stands for the coefficient of bulk viscosity. Here, we consider \(\zeta >0\) to satisfy the second law of thermodynamics. Now, we have the Friedmann equations and the wave equation for BD theory as follows:

$$\begin{aligned}&H^2+H\frac{{\dot{\phi }}}{\phi }-\frac{\omega }{6}\frac{{\dot{\phi }}\;^2}{\phi \;^2}=\frac{\rho _{m}+\rho _{h}}{3\phi }, \end{aligned}$$
(22)
$$\begin{aligned}&2\frac{\ddot{a} }{a}+H^2+2 H\frac{{\dot{\phi }}}{\phi }+\frac{\omega }{2}\frac{{\dot{\phi }}\;^2}{\phi \;^2}+\frac{\ddot{\phi }}{\phi }=\frac{-P_{eff}}{\phi }, \end{aligned}$$
(23)
$$\begin{aligned}&\ddot{\phi }+3H{\dot{\phi }}=\frac{\rho _{m}+\rho _{h}-3P_{eff}}{2\omega +3}. \end{aligned}$$
(24)

3.1 Non-interacting HDE, BD scalar field and deceleration parameter

In Sect. 2, we have discussed non-viscous HDE interacting with DM. In this section, we assume that there is no interaction between DM and viscous HDE. Therefore, the energy density of viscous HDE and DM conserve separately. The conservation equations of the viscous HDE and DM are given by

$$\begin{aligned}&{\dot{\rho }}_{m}+3H\rho _{m}=0, \end{aligned}$$
(25)
$$\begin{aligned}&{\dot{\rho }}_{h}+3H(\rho _{h}+P_{eff})=0. \end{aligned}$$
(26)

There are a number of choices available for bulk viscosity coefficient \(\zeta \) in the literature. One of the important forms of it is \(\zeta =\zeta _0 + \zeta _1 H\) which is a combination of two forms \(\zeta _0\) (constant) and \(\zeta \propto H\). This motivation can be traced in fluid mechanics where the transport/viscosity phenomenon is involved with velocity \(\dot{a}\) which is related to the expansion rate H. As the system of field equations of BD theory is complex, therefore, for simplicity we choose a constant coefficient of bulk viscosity, i.e., \(\zeta =\zeta _{0}\), where \(\zeta _1=0\). In the paper [64], the authors have shown using observations that \(0< \zeta _0 < 3\) when \(\zeta _1=0\). Therefore, firstly, we have taken \(\zeta _0> 0\) in our model as this is required to satisfy the second law of thermodynamics as mentioned above. Secondly, in [64], it has been shown that \(0< \zeta _0 < 3\) to satisfy observations, and we adopt this condition here also. With the help of Eq. (11), Eq. (26) reduces to

$$\begin{aligned} \dot{H}+\frac{3}{2}(1+w)H^2-\frac{3\zeta _{0}}{2c^2 M_{p}^2} H=0. \end{aligned}$$
(27)

On solving Eq. (27), we get the value of H in terms of cosmic time t as

$$\begin{aligned} H=\frac{e^{\frac{3\zeta _{0}}{2\;M_{p}^2\;c^2}t}}{c_{5}+\frac{M_{p}^2\;c^2\;(1+w)}{\zeta _{0}}e^{\frac{3\zeta _{0}}{2\;M_{p}^2\;c^2}t}}, \end{aligned}$$
(28)

where \(c_{5}\) is a constant of integration. On solving Eq. (28), one can obtain the scale factor as

$$\begin{aligned} a=c_{6}\left[ c_{5}+\frac{M_{p}^2\;c^{2}(1+w)}{\zeta _{0}}\;e^{\frac{3\zeta _{0}}{2\;M_{p}^2\;c^2}t}\right] ^{\frac{2}{3(1+w)}}, \end{aligned}$$
(29)

where \(c_{6}>0\) is an another constant of integration. The non-negative of \(c_6\) is the consequence of calculation because it appears under the logarithmic function which is not defined for negative values. We can rewrite the scale factor as

$$\begin{aligned} a=a_{0}\left[ 1+\frac{M_{p}^2\;c^{2}(1+w)H_{0}}{\zeta _{0}}\;(e^{\frac{3\zeta _{0}}{2\;M_{p}^2\;c^2}(t-t_0)}-1)\right] ^{\frac{2}{3(1+w)}},\nonumber \\ \end{aligned}$$
(30)

where \(a_{0}\) and \(H_{0}\) denotes the present value of the scale factor and the Hubble parameter at time \(t_{0}\), the present value of time where the HDE begins to dominate. We obtain the scale factor in exponential form as in the case of non-viscous interacting HDE in Sect. 2. From Eq. (22), we obtain the value of the energy density of the DM \(\rho =\frac{A}{a^3}\), where A is a constant of integration. Now, we obtain the value of \(\phi \) from the wave equation (21) for the scale factor given by Eq. (27) as follows:

$$\begin{aligned} \phi= & {} \frac{1}{3}e^{-\frac{3\zeta _{0}}{M_{p}^2\;c^2}t}\left[ \frac{1}{H_{0}}+\frac{M_{p}^2\;c^2(1+w)}{\zeta _{0}} (e^{\frac{3\zeta _{0}}{M_{p}^2\;c^2}t}-1)\right] ^{-\frac{2(2+w)}{1+w}}\nonumber \\&\times t\;\Big [\frac{(\zeta _{0}-M_{p}^2\;c^2(1+w)H_{0})^3A}{(2\omega +3)\zeta _{0}^3\;a_{0}^3\;H_{0}^{\frac{5+3w}{1+w}}}\nonumber \\&+\;\frac{3A\;M_{p}^2\;c^2(1+w)(\zeta _{0}-M_{p}^2\;c^2(1+w)H_{0})^2}{(2\omega +3)\zeta _{0}^3\;a_{0}^3\;H_{0}^{\frac{2(2+w)}{1+w}}} e^{\frac{3\zeta _{0}}{M_{p}^2\;c^2}t}\;t\nonumber \\&+\frac{A\;M_{p}^6\;c^6(1+w)^3}{(2\omega +3)\zeta _{0}^3\;a_{0}^3\;H_{0}^{\frac{2}{1+w}}} e^{\frac{9\zeta _{0}}{M_{p}^2\;c^2}t}\;t\nonumber \\&+\;\frac{3\;M_{p}^2\;c^2(w^2+2w+3)}{(2\omega +3)\zeta _{0}} e^{\frac{9\zeta _{0}}{M_{p}^2\;c^2}t}\nonumber \\&\times \left( \frac{1}{H_{0}}+\frac{M_{p}^2\;c^2(1+w)}{\zeta _{0}} (e^{\frac{3\zeta _{0}}{M_{p}^2\;c^2}t}-1)\right) ^{\frac{2}{1+w}}\;t\nonumber \\&+\;\frac{(\zeta _{0}-M_{p}^2\;c^2(1+w)H_{0})}{\zeta _{0}H_{0}}e^{\frac{6\zeta _{0}}{M_{p}^2\;c^2}t}\nonumber \\&\times \Big (\frac{3A\;M_{p}^4\;c^4(1+w)^2}{(2\omega +3)\zeta _{0}^2\;a_{0}^3\;H_{0}^{\frac{2}{1+w}}}+ \frac{3M_{p}^2\;c^2(1-3w)}{(2\omega +3)}\nonumber \\&\times \; \big (\frac{1}{H_{0}}+\frac{M_{p}^2\;c^2(1+w)}{\zeta _{0}} \times (e^{\frac{3\zeta _{0}}{M_{p}^2\;c^2}t}-1)\big )^{-\frac{2)}{1+w}}\Big )t\nonumber \\&-\Big (\frac{1}{H_{0}}+\frac{M_{p}^2\;c^2(1+w)}{\zeta _{0}}\nonumber \\&\times \;c_{7}\;(e^{\frac{3\zeta _{0}}{M_{p}^2\;c^2}t}-1)\Big )^{\frac{(5+3w)}{1+w}}t\; \;\;e^{\Big (\frac{-3e^{\frac{-3\zeta _{0}t}{M_{p}^2c^2}t}}{\frac{1}{H_{0}}+\frac{M_{p}^2\;c^2(1+w)}{\zeta _{0}} (e^{\frac{3\zeta _{0}}{M_{p}^2\;c^2}t}-1)}\Big )} \nonumber \\&+\;3\zeta _{0}e^{\frac{3\zeta _{0}}{M_{p}^2\;c^2}t}\left( \frac{1}{H_{0}}+\frac{M_{p}^2\;c^2(1+w)}{\zeta _{0}} (e^{\frac{3\zeta _{0}}{M_{p}^2\;c^2}t}-1)\right) ^{\frac{2(2+w)}{1+w}}\nonumber \\&\times t+c_{8}\Big ], \end{aligned}$$
(31)

where \(c_7\) and \(c_8\) are integration constants. This is the form of \(\phi \) for viscous non-interacting HDE.

The DP for this model is given by

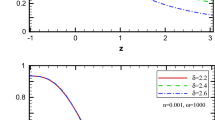
$$\begin{aligned} q=\frac{3\left[ 1+w-\frac{\zeta _{0}}{M_{p}^2\;c^2\;H_{0}}\right] }{2\;e^{\frac{3\zeta _{0}}{2M_{p}^2\;c^2}(t-t_0)}}-1. \end{aligned}$$
(32)

Here, we obtain a time dependent DP as obtained in the case of non-viscous interacting HDE. We observe that the sufficiently large value of the bulk viscous coefficient (\(\zeta _{0}\)) can accelerate the expansion of the universe irrespective of whether the HDE is of quintessence type or of phantom type. Further, if the HDE is of phantom type, i.e., \(w<-1\), then this is sufficient to accelerate the expansion irrespective of the bulk viscous coefficient (\(\zeta _{0}\)). To accommodate the recent phase transition from deceleration to acceleration, the parameters must satisfy the condition \(\frac{3}{2}\left[ 1+w-\frac{\zeta _{0}}{M_{p}^2\;c^2\;H_{0}}\right] >1\), i.e., \(w>-\frac{1}{3}+\frac{\zeta _{0}}{M_{p}^2\;c^2\;H_{0}}\). We observe that non-interacting bulk viscous HDE produces the same type of results as in the case of non-viscous interacting HDE for \(\Gamma <0\). Therefore, bulk viscosity may play the role of interaction for HDE and can explain acceleration as well as the phase transition of the universe. The evolution of DP for various values of the model parameters has been shown in Fig. 4. We notice that for some values of the parameters it is possible to get a suitable form of q which is positive early on, representing deceleration, and negative at later epochs, representing acceleration.

Fig. 4
figure 4

The figure of deceleration parameter q against cosmic time t has been plotted for \(M_p = 1\), \(c = 1\) and \(H_0\) = 10

Full size image

3.2 Statefinder diagnosis

Let us apply the statefinder diagnosis to the viscous HDE model also. We obtain the expression of the statefinder parameter r as follows

$$\begin{aligned} r= & {} e^{-\frac{3\zeta _0 t}{M_p^2 c^2}}\Bigg [\frac{9 \zeta _0^2}{4M_p^4 c^4 H_0^2}e^{\frac{3\zeta _0 t_0}{M_p^2 c^2}}-\frac{9 \zeta _0}{4M_p^2 c^2 H_0}e^{\frac{3\zeta _0 t_0}{2M_p^2 c^2}}\nonumber \\&\times \Bigg ((w-1)e^{\frac{3\zeta _0 t}{2M_p^2 c^2}}+2(1+w)e^{\frac{3\zeta _0 t_0}{M_p^2 c^2}}\Bigg )\nonumber \\&+ \Bigg ( e^{\frac{3\zeta _0 t}{M_p^2 c^2}}+\frac{c^2(1+w)^2 M_p^2}{4\zeta _0} e^{\frac{3\zeta _0t}{M_p^2 c^2}}\nonumber \\&-9 (1-w^2) e^{\frac{3\zeta _0(t+t_0)}{2M_p^2 c^2}}\Bigg )\Bigg ]. \end{aligned}$$
(33)

The expression of the statefinder parameter s can be obtained easily from the formula \(s=\frac{r-1}{3(q-\frac{1}{2})}\) using the values of q and r from Eqs. (32) and (33), respectively. We have plotted the \(r-s\) trajectories in Fig. 5a and the \(r-q\) trajectories in Fig. 5b. In Fig. 5a, the trajectories behave like quintessence for \(w>-1\); however, for \(w<-1\) the trajectories have higher positive value of r and negative value of s, and approach the \(\Lambda \)CDM model at late times like the Chaplygin gas model. In Fig. 5b, we observe that all the trajectories show quintessence like behavior in the late time evolution. Moreover, the trajectories show almost quintessence behavior for smaller negative values of w. Thus, we observe that the viscous HDE model shows more similarity with the quintessence model than the interacting HDE model.

Fig. 5
figure 5

The figure a plots the \(r-s\) trajectories and the figure b plots the \(r-q\) trajectories. We have taken \(H_0=10\), \(M_p=1\), \(c=1\) and \(t_0=1\) to plot the trajectories. In figure (a), the trajectory 1 is plotted for \(w = -0.35\) and \(\zeta = 1/5\), the trajectory 2 is plotted for \(w = -0.5\) and \(\zeta = 1/3\), the trajectory 3 is plotted for \(w = -0.6\) and \(\zeta = 1/3\) and the trajectory 4 is plotted for \(w = -1.03\) and \(\zeta = 1/3\). In figure (b), we have taken \(\zeta = 1/2\) and the trajectories 1, 2, 3, 4 and 5 are plotted for \(w = -0.2\), \(w = -0.33\), \(w = -0.4\), \(w = -0.5\) and \(w = -0.6\), respectively

Full size image

4 Conclusion

To resolve the mysteries of cosmology like the recent accelerated expansion and the cosmic coincidence problem, the concept of HDE in the framework of BD theory has been studied in the literature. In BD theory, a number of authors have obtained a time dependent deceleration parameter using various forms of DE and taking the assumption \(\phi \propto a^n\) [17,18,19, 24, 25]. In the present paper, we demonstrate that the assumption \(\phi \propto a^n\) naturally leads to a constant deceleration parameter, irrespective of the form of DE in BD theory. Taking into account this problem with power law form, a logarithmic form was introduced in [26]. We have considered HDE with Hubble length as IR cut-off in the framework of BD theory, and we do not use any specific form of the BD scalar field. We obtain the value of the scale factor and corresponding value of \(\phi \) for the HDE model. As the assumption \(\phi \propto a^n\) in Brans–Dicke theory is not suitable to study the phase transition of the universe; therefore, we have found a suitable value of \(\phi \) for HDE. Further, we discuss the possible evolution of the universe using the DP and apply statefinder diagnosis to compare our model with existing standard models.

First, we consider a non-viscous interacting HDE model and obtain the value of the scale factor. Further, the expression of the BD scalar field \(\phi \) has been obtained with the help of values of scale factor and energy density of the HDE in the wave equation of the BD scalar field \(\phi \). We obtain the DP to discuss the evolution of the non-viscous interacting HDE model. Using the DP, we observe that if there is an energy transfer from HDE to DM, i.e. \(\Gamma >0\), then both quintessence and phantom HDE are viable candidates to describe the early time phase transition (inflation to deceleration) under suitable constraints on the parameters as given in Sect. 2. However, phantom HDE may accommodate the recent accelerated expansion for \(\Gamma >0\) but is not able to describe the recent phase transition. For \(\Gamma <0\), we observe the accelerated expansion throughout the evolution for both quintessence and phantom HDE. To accommodate the recent phase transition, the HDE must not cross the quintessence divider, i.e., \(w>-\frac{1}{3}\). Our results show that we can obtain the recent accelerated expansion in the phantom region for \(\Gamma >0\) and \(\Gamma <0\), in the quintessence region for \(\Gamma <0\), but the recent phase transition is possible for the quintessence region only. As is well known, the phase transition is an integral part of cosmic history. Therefore, to achieve the recent phase transition HDE must not cross the quintessence divider. The statefinder diagnostic has been applied to compare our model with existing standard models. We observe that the trajectories for \(\lambda <0\) show more similarities with trajectories of the quintessence model than the trajectories for \(\lambda >0\). We also observe that as we increase the negative value of w, the trajectories deviate more and more form quintessence.

Further, we consider viscous HDE with constant bulk viscous coefficient \(\zeta =\zeta _{0}\), and assume that there is no interaction between the HDE and DM. As in the case of interacting HDE for \(\Gamma <0\), we observe the recent phase transition for non-interacting bulk viscous HDE below the quintessence region, i.e, for \(w>-1/3\). The justification for \(w>-1/3\) is the bulk viscous nature of the HDE adding the extra negative pressure to the effective pressure. As w passes the boundary line of the quintessence region (\(w\le -1/3\)), the effective negative pressure becomes sufficient to accelerate the universe throughout the evolution, which rules out the decelerated expansion of evolution. In the quintessence and phantom region, we have observed the accelerated expansion of the universe. Thus, We observe that non-interacting bulk viscous HDE produces almost the same type of results as in the case of non-viscous interacting HDE. Therefore, bulk viscosity may play the role of interaction for HDE and can explain acceleration as well as the phase transition of the universe. Further, we apply the statefinder diagnosis to the viscous HDE model. In this model, we observe that the trajectories of both \(r-s\) and \(r-q\) show more similarity with the quintessence model than the interacting HDE model.