1 Introduction

Compact objects provide extreme conditions in terms of gravity and density and thus are unique astrophysical laboratories for studying general relativity and interactions at the super nuclear density. In general, compact objects exist in binaries comprising either two neutron stars (NS–NS binaries) or a black hole (BH) and a neutron star (NS) (BH–NS binaries). The merger of these objects generates huge gravitational waves which have been experimentally verified in the recent times.

A neutron star provides a perfect place for investigating the nature of particle interactions at very high densities in a natural way [1]. Neutron stars (NS) are compact objects of very high energy density having approximate masses \(1.5~M_{\odot }\) and radii \(10^{5}\) times smaller than the Sun’s radius. Therefore, they are perfectly natural systems to study nuclear matter properties at high densities. In fact, density inside the core of an NS can be as high as several times the density that is reached inside a heavy atomic nucleus [2]. Despite attempts of several decades, we still lack a proper understanding of the thermodynamical behaviour inside a compact star. The extreme conditions at the interior of a compact star comprising matter of uncertain composition have prompted many investigators to study its gross macroscopic properties within the framework of General Relativity. In order to understand the microscopic properties, physical quantities such as NS masses and radii have been used as important tools to constrain its EOS.

This article explores the possibility of introducing tidal deformation as one of the astrophysically observable macroscopic properties that can be used to study the interior of a NS [3]. Like any other extended object, a NS is tidally deformed under the influence of an external tidal field. The tidal deformability measures the star’s quadrupole deformation in response to a companion perturbating star [4]. The induced quadrupole moment of the neutron star affects the binding energy of the system and increases the rate of emission of gravitational waves [5,6,7]. Tidal deformability plays an important role in the observation of coalescing NS with gravitational waves and has been used to probe the internal structure of NS. The TLN characterizes how easy or difficult it would be to deform a NS away from sphericity [8, 9]. The TLN can be computed by following the standard methods available in the literature [10,11,12,13,14].

The tidal behaviour of a NS has been observed to have a direct bearing on the emitted gravitational wave signal. The advanced LIGO [15] and advanced Virgo [16] gravitational-wave detectors have made their first observation of a binary NS inspiral [17], an event known as GW170817. Subsequently, another signal emitted during a neutron star binary coalescence, known as GW190425, was detected. The latter signal was much weaker than GW170817 as it was originated from a much greater distance [18]. Such observational data can be used to constraint many physical properties of NS such maximum masses and radii [19,20,21,22,23,24,25,26,27,28,29]. In particular, the LIGO observational data may lead to the theoretical insight into the TLN [17].

In gravitational wave astronomy, the tidal deformability characterized by TLN [10], can be used to analyze the physical features of the merging objects [30]. The TLN, in particular, is used to constrain the EOS of the NS [28, 30]. To understand the methods of estimating the TLN, we refer to the citations [14, 31,32,33]. The algorithm can also be extended to slowly rotating extended compact objects [33,34,35,36,37,38]. Note that even though the TLN of a Schwarzschild black hole is zero [31, 32, 39,40,41], it does not vanish for a Kerr BH [42]. For relatively less compact objects, the dominant contribution to the tidal deformability comes from the even parity quadrupole term l, which starts to impact the phase of the GW signal emitted in a binary at the fifth post-Newtonian (5PN) order [43]. The leading order (6PN) term of even-parity tidal deformability has also been calculated [44]. A method to calculate the odd-parity (or gravitomagnetic or mass-current) tidal deformability was proposed independently by Damour and Nagar [31] and Binnington and Poisson [32]. The choice of fluid properties also affects the odd-parity tidal deformability [33] as shown by Pani et al. [45]. The pioneer in this field was Yagi [46] who, for the first time, estimated the impact of odd-parity tidal deformability on the gravitational waves phase evolution and then extended the work by analyzing the signal from GW170817 [47].

In this paper, we develop a method to estimate the TLN for a spherically symmetric and anisotropic relativistic star in static equilibrium. In a compact object, pressures may be different in radial and transverse directions and the difference of radial pressure (\(p_r\)) and tangential pressure (\(p_t\)) is defined as pressure anisotropy. Incorporating anisotropy into the matter distribution of compact objects, numerous anisotropic stellar models have been developed and investigated which include the investigations carried out in references [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72] and Raposo et al. [73]; amongst others. Ruderman [74] and Canuto [75] have shown that anisotropy may develop inside highly dense, compact stellar objects due to a variety of factors. Kippenhahn and Weigert [76] showed that in relativistic stars, anisotropy might occur due to the existence of a solid core or type 3A superfluid. Strong magnetic fields can also generate an anisotropic pressure inside a self-gravitating body [77]. Anisotropy may also develop due to the slow rotation of fluids [78]. A mixture of perfect and a null fluid may also be represented by an effective anisotropic fluid model [79]. Local anisotropy may occur in astrophysical objects for various reasons such as viscosity, phase transition [80], pion condensation [81] and the presence of strong electromagnetic field [82]. The factors contributing to the pressure anisotropy have also been discussed by Dev and Gleiser [83, 84] and Gleiser and Dev [85]. Ivanov [86] pointed out that influences of shear, electromagnetic field etc. on self-bound systems can be absorbed if the system is considered to be anisotropic. Self-bound systems composed of scalar fields, the so-called ‘boson stars’ are naturally anisotropy [87]. Wormholes [88] and gravastars [89, 90] are also naturally anisotropic. The shearing motion of the fluid can be considered as one of the reasons for the presence of anisotropy in a self-gravitating body [91]. Bowers and Liang [92] have extensively discussed the underlying causes of pressure anisotropy in the stellar interior and analyzed the effects of anisotropic stress on the equilibrium configuration of relativistic stars. Therefore, we find it worthwhile to investigate the impacts of anisotropic stress on sources of gravitational waves. Alternatively, for an estimated TLN of the source, the technique can also be used to constrain the anisotropy of the source of a given mass and radius. Earlier, Biswas and Bose [93] used the gravitational wave (GW) and electromagnetic (EM) observation of GW170817 to constrain the extent of pressure anisotropy. Many applications of TLN in neutron stars have also been explored by Yagi and Yunes [8].

The paper is organized as follows: In Sect. 2, the methodology of determining the TLN is discussed. Section 3 provides a particular stellar model which is used to get an estimate of the TLN. In Sect. 4, the TLN \(k_2\) for a wide range of masses and radii is provided. The range of values of \(k_2\) for a fixed compactness \({\mathscr {C}}\) possessing anisotropic stress is investigated. Section 5 summarizes the main results and provides some prospects of future investigation in this direction.

2 Tidal Love number

We consider a static spherically symmetric neutron star (NS) immersed in an external tidal field. In response to the tidal field, the star will be deformed by the tidal force by developing a multipolar structure. This kind of situation occurs in coalescing binary systems where the gravitational field of its companion tidally deforms each component. The TLN characterizes the deformability of the NS away from sphericity [94]. For mathematical simplicity, in our calculation, we shall restrict ourselves to quadrupole moments \({\mathscr {Q}}_{ij}\) only. This is reasonable if the two binary neutron stars remain sufficiently far away from each other. In such a situation, the quadrupole moment (\(l = 2\)) dominates over the multiple moments. \({\mathscr {Q}}_{ij}\) can be related to the external tidal field \({\mathscr {E}}_{ij}\) as [95]

$$\begin{aligned} {\mathscr {Q}}_{ij} = - \Lambda {\mathscr {E}}_{ij}, \end{aligned}$$
(1)

where \(\Lambda \) is the tidal deformability of the neutron star and it is related to the TLN \(k_{2}\) as [95]

$$\begin{aligned} k_{2} = \dfrac{3}{2}\Lambda \, R^{-5}. \end{aligned}$$
(2)

The TLN is dimensionless. The quadrupole fields \({\mathscr {Q}}_{ij}\) and \({\mathscr {E}}_{ij}\) can be expanded in tensor spherical harmonics \({\mathscr {Y}}_{ij}^{lm}\) as:

$$\begin{aligned} {\mathscr {E}}_{ij}&= \sum _{m = -2 }^{2} {\mathscr {E}}_{m} {\mathscr {Y}}_{ij}^{2m} = {\mathscr {E}}_{0} {\mathscr {Y}}_{ij}^{20} = {\mathscr {E}} {\mathscr {Y}}_{ij}^{20} , \end{aligned}$$
(3)
$$\begin{aligned} {\mathscr {Q}}_{ij}&= \sum _{m = -2 }^{2} {\mathscr {Q}}_{m} {\mathscr {Y}}_{ij}^{2m} = {\mathscr {Q}}_{0} {\mathscr {Y}}_{ij}^{20} = {\mathscr {Q}} {\mathscr {Y}}_{ij}^{20}. \end{aligned}$$
(4)

In the second equality, the coordinate system was so oriented that the term became symmetric in \(\phi \). Subsequently, the only component that is non-vanishing is the \(m = 0\) component. We can rewrite Eq. (1) as

$$\begin{aligned} {\mathscr {Q}} = - \Lambda {\mathscr {E}}. \end{aligned}$$
(5)

Now the background metric \(^{(0)}g_{\mu \nu }(x^{\nu })\) corresponding to the neutron star, with a small perturbation \(h_{\mu \nu }(x^{\nu })\) due to external tidal field, gets modified as

$$\begin{aligned} g_{\mu \nu }\left( x^{\nu }\right) =^{(0)} g_{\mu \nu }\left( x^{\nu }\right) +h_{\mu \nu }\left( x^{\nu }\right) . \end{aligned}$$
(6)

We write the background geometry of the spherical static star in the standard form

$$\begin{aligned} {}^{\left( 0\right) } ds^{2}&=^{\left( 0\right) } g_{\mu \nu }dx^{\mu }dx^{\nu } \nonumber \\&=-e^{2 \nu (r) }dt^{2}+e^{2 \lambda (r) }dr^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\right) . \end{aligned}$$
(7)

For the linearized metric perturbation \(h_{\mu \nu }\), using the method as in Refs. [93, 96], we restrict ourselves to static \(l = 2, \, m=0\) even parity perturbation. With these assumptions, the perturbed metric becomes

$$\begin{aligned} h_{\mu \nu }=&{\text {diag}}\left[ H_{0}(r) e^{2 \nu }, H_{2}(r) e^{2 \lambda },\right. \nonumber \\&\left. r^{2} K(r), r^{2} \sin ^{2} \theta K(r)\right] Y_{2 0}(\theta , \phi ) \end{aligned}$$
(8)

where \(H_{0}(r), H_{2}(r)\) and K(r) are radial functions to be determined by the perturbed Einstein field equations.

For the spherically static metric (7), the stress-energy tensor is given by [97,98,99,100]

$$\begin{aligned} {}^{(0)}T_{\chi }^{\xi }=\left( \rho +p_{t}\right) u^{\xi } u_{\chi }+p_{t} g_{\chi }^{\xi }+\left( p_{r}-p_{t}\right) \eta ^{\xi } \eta _{\chi }, \end{aligned}$$
(9)

where \(\eta ^{i}\) is the space-like vector and the vector \(u^{i}\) represents fluid 4-velocity. The quantities satisfy the relations \(u^{\xi } u_{\xi } = -1\), \(\eta ^{\xi } \eta _{\xi } = 1\) and \(\eta ^{\xi } u_{\xi } = 0 \). The quantities \(\rho \), \(p_r\) and \(p_t\) represent density, radial pressure and tangential pressure, respectively.

Furthermore, the energy–momentum tensor is perturbed by a perturbation tensor \(\delta T_{\chi }^{\xi }\) which is defined as

$$\begin{aligned} T_{\chi }^{\xi } = ^{(0)}T_{\chi }^{\xi } + \delta T_{\chi }^{\xi }. \end{aligned}$$
(10)

The non-zero components of \(T_{\chi }^{\xi }\) are:

$$\begin{aligned} T_{t}^{t}&= - \dfrac{d\rho }{dp_{r}} \,\, \delta p_{r}\,\, Y(\theta ,\phi )- \rho (r), \end{aligned}$$
(11)
$$\begin{aligned} T_{r}^{r}&= \delta p_{r}(r) Y(\theta ,\phi )+ p_{r}(r), \end{aligned}$$
(12)
$$\begin{aligned} T_{\theta }^{\theta }&= \frac{dp_{t}}{dp_{r}} \delta p_{r}(r) Y(\theta ,\phi )+ p_{t}(r), \end{aligned}$$
(13)
$$\begin{aligned} T_{\phi }^{\phi }&= \frac{dp_{t}}{dp_{r}} \delta p_{r}(r) Y(\theta ,\phi )+ p_{t}(r). \end{aligned}$$
(14)

With these perturbed quantities, we write the perturbed Einstein Field Equations as

$$\begin{aligned} G_{\chi }^{\xi } = 8 \pi T_{\chi }^{\xi }, \end{aligned}$$
(15)

where we assume \(G = c =1\) and the Einstein tensor \(G_{\chi }^{\xi } \) is calculated using the metric \(g_{\chi \xi } \).

2.1 Derivation of the master equation and expression for TLN

Using the background field equations \(^{(0)}G_{\chi }^{\xi } = 8 \pi ^{(0)}T_{\chi }^{\xi }\), we obtain the following results:

$$\begin{aligned} {}^{(0)}G_{t}^{t}&= 8 \pi ^{(0)}T_{t}^{t},\nonumber \\ \Rightarrow \lambda '(r)&= \frac{8 \pi r^2 e^{2 \lambda (r)} \rho (r)-e^{2 \lambda (r)}+1}{2 r}, \end{aligned}$$
(16)
$$\begin{aligned} {}^{(0)}G_{r}^{r}&= 8 \pi ^{(0)}T_{r}^{r},\nonumber \\ \Rightarrow \nu '(r)&= \frac{8 \pi r^2 p_{r}(r) e^{2 \lambda (r)}+e^{2 \lambda (r)}-1}{2 r}. \end{aligned}$$
(17)

Note that \(\nabla _{\xi }^{(0)}T_{\chi }^{\xi } = 0 \). Choosing \(\xi = r\), we obtain

$$\begin{aligned} p_{r}'(r) = \frac{-r p_{r}(r) \nu '(r)-2 p_{r}(r)+2 p_{t}(r)-r \rho (r) \nu '(r)}{r}. \end{aligned}$$
(18)

For the perturbed metric, using Einstein equations (15), we get the following results:

$$\begin{aligned}&G_{\theta }^{\theta } - G_{\phi }^{\phi } = 0 \Rightarrow H_{0}(r) = H_{2}(r) = H(r), \end{aligned}$$
(19)
$$\begin{aligned}&G_{r}^{\theta } =0 \Rightarrow K' = H' +2 H \nu ' , \end{aligned}$$
(20)
$$\begin{aligned}&G_{\theta }^{\theta } + G_{\phi }^{\phi } = 8 \pi (T_{\theta }^{\theta } + T_{\phi }^{\phi }), \nonumber \\&\quad \Rightarrow \delta p_{r} = \frac{H(r) e^{-2 \lambda (r)} \left( \lambda '(r)+\nu '(r)\right) }{8 \pi \frac{dp_{t}}{dp_{r}} r}. \end{aligned}$$
(21)

Now, using the identity

$$\begin{aligned}&\dfrac{\partial ^{2} Y(\theta ,\phi )}{\partial \theta ^{2}} + cot(\theta ) \dfrac{\partial Y(\theta ,\phi )}{\partial \theta }\\&\qquad + \csc ^2(\theta ) \dfrac{\partial ^{2} Y(\theta ,\phi )}{\partial \phi ^{2}} = -6 Y(\theta ,\phi ), \end{aligned}$$

and Eqs. (16), (17), (18), (19), (20) and (21), we obtain the master equation for H(r) as

$$\begin{aligned}&- \frac{1}{e^{-2 \lambda (r)} Y(\theta ,\phi )} \left[ G_{t}^{t} - G_{r}^{r}\right] \nonumber \\&\quad = - \frac{8 \pi }{e^{-2 \lambda (r)} Y(\theta ,\phi )} \left[ T_{t}^{t} - T_{r}^{r}\right] \nonumber \\&\quad \Rightarrow H''(r) + {\mathscr {R}} H'(r) + {\mathscr {S}} H(r) =0, \end{aligned}$$
(22)

where,

$$\begin{aligned} {\mathscr {R}}&= - \left( \frac{-e^{2 \lambda (r)}-1}{r}-4 \pi r e^{2 \lambda (r)} (p_{r}(r)-\rho (r))\right) , \end{aligned}$$
(23)
$$\begin{aligned} {\mathscr {S}}&= - \left( \frac{4 e^{2 \lambda (r)}+e^{4 \lambda (r)}+1}{r^2}+64 \pi ^2 r^2 p_{r}(r)^2 e^{4 \lambda (r)}\right. \nonumber \\&\quad + 16 \pi e^{2 \lambda (r)} \left( p_{r}(r) \left( e^{2 \lambda (r)}-2\right) -p_{t}(r)-\rho (r)\right) \nonumber \\&\quad \left. +\frac{-4 \pi \frac{d\rho }{dp_{r}} e^{2 \lambda (r)} (p_{r}(r)+\rho (r))-4 \pi e^{2 \lambda (r)} (p_{r}(r)+\rho (r))}{\frac{dp_{t}}{dp_{r}}}\right) . \end{aligned}$$
(24)

The exterior region of the static spherically symmetric star will be described by the Schwarzschild metric and hence by setting, \(\rho = 0,\, p_{r} = 0, \, p_t=0\) and \(e^{2 \lambda } = 1/(1- 2 M/r)\), the master equation (22) takes the form

$$\begin{aligned}&-H''(r)-\frac{2 (M-r) H'(r)}{r (2 M-r)}\nonumber \\&\quad +\frac{2 H(r) \left( 2 M^2-6 M r+3 r^2\right) }{r^2 (r-2 M)^2} =0. \end{aligned}$$
(25)

The solution to this second-order differential equation (25) is obtained as [9]

$$\begin{aligned} H(r)&=\dfrac{1}{2 M^2 r (2 M-r)}\left[ c_2 \left( -2 M \left( 2 M^3+4 M^2 r\right. \right. \right. \nonumber \\&\quad \left. -9 M r^2+3 r^3\right) -3 r^2 (r-2 M)^2 \log \left( \frac{r}{M}-2\right) \nonumber \\&\quad \left. \left. +3 r^2 (r-2 M)^2\times \log \left( \frac{r}{M}\right) \right) \right] + \frac{3 c_1 r (2 M-r)}{M^2}, \end{aligned}$$
(26)

where, \(c_1\) and \(c_2\) are integration constants. In order to get the expression for these constants, we make a series expansion of Eq. (26) as

$$\begin{aligned} H(r) = -\frac{3 c_1 r^2}{M^2}+\frac{6 c_1 r}{M}-\frac{c_2 \left( 8 M^3\right) }{5 r^3}+{\mathscr {O}}\left( \left( \frac{1}{r}\right) ^4\right) . \end{aligned}$$
(27)

Now, in the star’s local asymptotic rest frame, at large r the metric coefficient \(g_{tt}\) is given by [95, 101, 102]

$$\begin{aligned} \frac{\left( 1-g_{t t}\right) }{2}&=-\frac{M}{r}-\frac{3 {\mathscr {Q}}_{i j}}{2 r^{3}}\left( n^{i} n^{j}-\frac{1}{3} \delta ^{i j}\right) +{\mathscr {O}}\left( \frac{1}{r^{3}}\right) \nonumber \\&\quad +\frac{1}{2} {\mathscr {E}}_{i j} x^{i} x^{j}+ {\mathscr {O}}(r^{3}), \end{aligned}$$
(28)

where \(n^{i} = x^{i}/r\). Matching the asymptotic solution using Eq. (27) together with the expansion of Eq. (28) and using Eq. (1), we obtain

$$\begin{aligned} c_1 = - \frac{M^2 {\mathscr {E}}}{3}, \quad c_2 = \frac{15 {\mathscr {Q}}}{8 M^3}. \end{aligned}$$
(29)

Subsequently, the expression for TLN \(k_2\) can be obtained by using Eqs. (2), (26), (29) and also using the expression for H(r) and its derivatives at the star’s surface \(r=R\) as

$$\begin{aligned} k_2 = [8 (1-2 {\mathscr {C}})^2 {\mathscr {C}}^5 (2 {\mathscr {C}} (y-1)-y+2)]/ X, \end{aligned}$$
(30)

where,

$$\begin{aligned} X&= 5(2 {\mathscr {C}} ({\mathscr {C}} (2 {\mathscr {C}} ({\mathscr {C}} (2 {\mathscr {C}} (y+1)+3 y-2)\nonumber \\&\quad - 11 y+13)+3 (5 y-8))\nonumber \\&\quad \left. -3 y+6) +3 (1-2 {\mathscr {C}})^2 (2 {\mathscr {C}} (y-1)\right. \nonumber \\&\quad -y+2) \log \left( \frac{1}{{\mathscr {C}}}-2\right) \nonumber \\&\quad \left. -3 (1-2 {\mathscr {C}})^2 (2 {\mathscr {C}} (y-1)-y+2) \log \left( \frac{1}{{\mathscr {C}}}\right) \right) . \end{aligned}$$
(31)

Note that \({\mathscr {C}} (= \frac{M}{R})\) and y depend on \(r,\, H(r)\) and it’s derivatives evaluated at R in the form

$$\begin{aligned} \left. y =\dfrac{r H'(r)}{H(r)}\right| _{r = R}. \end{aligned}$$
(32)

To calculate the TLN \(k_2\) for a particular compact star, we need to specify a model which we can be utilized to calculate y and subsequently \(k_2\) for a particular NS of given mass M and radius R.

3 Choice of a physically acceptable model

3.1 Einstein field equations

To describe the interior of a static and spherically symmetric relativistic star, we take the line element in coordinates \((x^{a}) = (t,r,\theta ,\phi )\) as given in Eq. (7).

We also assume an anisotropic matter distribution for which the energy–momentum tensor is assumed in the form as given in the Eq. (9).

The energy density \(\rho \), the radial pressure \(p_r\) and the tangential pressure \(p_t\) are measured relative to the comoving fluid velocity \(u^i = e^{-\nu }\delta ^i_0.\) For the line element (7), the independent set of Einstein field equations are then obtained as

$$\begin{aligned} 8 \pi \rho= & {} \frac{1}{r^{2}} \left[ r(1-e^{-2\lambda }) \right] ', \end{aligned}$$
(33)
$$\begin{aligned} 8 \pi p_r= & {} - \frac{1}{r^{2}} \left( 1-e^{-2\lambda } \right) + \frac{2\nu '}{r}e^{-2\lambda } , \end{aligned}$$
(34)
$$\begin{aligned} 8 \pi p_t= & {} e^{-2\lambda }\left( \nu '' + \nu '^{2} + \frac{\nu '}{r}- \nu '\lambda ' - \frac{\lambda '}{r} \right) , \end{aligned}$$
(35)

where primes (\('\)) denote differentiation with respect to r. The system of equations determines the behaviour of the gravitational field of an anisotropic imperfect fluid sphere. The mass contained within a radius r of the sphere is defined as

$$\begin{aligned} m(r)= 4 \pi \int _0^r\omega ^2 \rho (\omega )d\omega . \end{aligned}$$
(36)

We define, \(\Delta = p_t-p_r\) as the measure of anisotropy. The anisotropic stress will be directed outward (repulsive) when \(p_t > p_r\) (i.e., \( \Delta > 0\)) and inward when \(p_t < p_r\) (i.e., \(\Delta < 0\)).

3.2 A particular anisotropic model

Any well-behaved, physically viable stellar model can be used to find the TLN \(k_2\) in our construction. For example, Jiang and Yagi [103] have used the Tolman VII model to analyze the relationship between the TLN with the moment of inertia and compactness of the star. The same model was also used by them for the description of neutron star interiors, where the authors introduced central density as an input to fine-tune the observables [104]. The authors have also used the tidal measurement of binary stars for probing the GW propagation [105]. To calculate the TLN, we choose a particular model, which is an anisotropic generalization of the Korkina and Orlyanskii solution III obtained earlier by [106]. To examine the physical acceptability of the solution, we first write the variables which are obtained as

$$\begin{aligned} e^{2\nu }= & {} A^2(1+aCr^2)^2, \end{aligned}$$
(37)
$$\begin{aligned} e^{2\lambda }= & {} \Big [1-BCr^2(1+3aCr^2)^{-2/3}-\alpha Cr^2 (1+aCr^2)^{-1} \nonumber \\&\times (1+3aCr^2)^{-2/3} \Big ]^{-1}, \end{aligned}$$
(38)
$$\begin{aligned} 8 \pi \Delta= & {} \frac{\alpha C^2 a r^2(1+3aC r^2)^{1/3}}{(1+a C r^2)^3}. \end{aligned}$$
(39)

The line element (7) then takes the form

$$\begin{aligned} ds^{2}= & {} -A^2(1+aCr^2)^2 dt^{2} \nonumber \\&+ \Big [1-B C r^2(1+3 a C r^2)^{-2/3} -\alpha C r^2 (1+a C r^2)^{-1} \nonumber \\&\times (1+3 a C r^2)^{-2/3} \Big ]^{-1}dr^{2} + r^{2}(d\theta ^{2} + \sin ^{2}{\theta } d\phi ^{2}).\nonumber \\ \end{aligned}$$
(40)

The model contains five constants namely, a, A, B, C and \(\alpha \) three of which do get fixed by the boundary conditions. The parameter a that appears as a free parameter in the solutions provided by [106], without any loss of generality, can be set to \(a=1\). The other free parameter \(\alpha \) provides the measure of anisotropy. For an isotropic sphere (\(\alpha =0\)), if we set \(B=0\) and \(C=1\), the metric (40) reduces to

$$\begin{aligned} ds^{2} = -A^2(1+ar^2)^2 dt^{2} + dr^{2} + r^{2}(d\theta ^{2} + \sin ^{2}{\theta } d\phi ^{2}), \end{aligned}$$
(41)

which is the Korkina and Orlyanskii solution III [107]. In other words, the solution (40) obtained by [106] is an anisotropic generalization of the solution of [107]. Consequently, this particular solution provides a tool to investigate the anisotropic effects on the TLN. Physical quantities in this model are obtained as

$$\begin{aligned} 8 \pi \rho&= \frac{B C \eta _{1}^2 (3 + 5 a C r^2) + C (3 + a C r^2 (6 - a C r^2)) \alpha }{\eta _{1}^2 \eta _{2}^{\frac{5}{3}}}, \end{aligned}$$
(42)
$$\begin{aligned} 8 \pi p_r&= -\frac{C (B \eta _{1} \psi _{1} + \alpha + a (-4 \eta _{2}^{\frac{2}{3}} + C r^2 (-4 a \eta _{2}^{\frac{2}{3}} + 5 \alpha )))}{\eta _{1}^2 \eta _{2}^{\frac{2}{3}}}, \end{aligned}$$
(43)
$$\begin{aligned} 8 \pi p_t&= \dfrac{1}{\eta _{1}^3 \eta _{2}^{\frac{2}{3}}} \times \Big [C (-B \eta _{1}^2 \psi _{1} + a (4 \eta _{2}^{\frac{2}{3}} + C r^2 (2 a (4 \eta _{2}^{\frac{2}{3}} \nonumber \\&\quad + C r^2 (2 a \eta _{2}^{\frac{2}{3}} - \alpha )) - 5 \alpha )) - \alpha ) \Big ], \end{aligned}$$
(44)
$$\begin{aligned} 8 \pi \Delta&= \frac{a C^2 r^2 \eta _{2}^{\frac{1}{3}} \alpha }{\eta _{1}^3}, \end{aligned}$$
(45)
$$\begin{aligned} m(r)&= \frac{C r^3 (B + a B C r^2 + \alpha )}{2 \eta _{1} \eta _{2}^{\frac{2}{3}}}, \end{aligned}$$
(46)

where, \(\psi _{1} = (1 + 5 a C r^2)\), \(\eta _{1} = (1 + a C r^2)\) and \(\eta _{2} =(1 + 3 a C r^2) \).

3.3 Physical acceptability of the solution

Before using the solutions, let us first examine the physical acceptability of the solution:

  1. (i)

    In this model, we have \((e^{2\nu (r)})'_{r=0}=(e^{2\lambda (r)})'_{r=0}=0 \) and \(e^{2\nu (0)}=A^2,~ e^{2\lambda (0)}=1\); these imply that the metric is regular at the centre \(r=0\).

  2. (ii)

    Since \( 8 \pi \rho (0)= 3\,C(B+\alpha )\) and \( 8 \pi p_r(0)=8 \pi p_t(0)=C (4a-B- \alpha )\), the energy density, radial pressure and tangential pressure will be non-negative at the centre if we choose the parameters satisfying the condition \(a>\frac{B+\alpha }{4}\).

  3. (iii)

    The interior solution (7) should be matched to the exterior Schwarzschild metric

    $$\begin{aligned} ds^2= & {} - \left( 1 - \frac{2M}{r} \right) dt^2 +\left( 1 - \frac{2M}{r} \right) ^{-1} dr^2 \nonumber \\&+ r^2 (d\theta ^2 +\sin ^2\theta d\phi ^2), \end{aligned}$$
    (47)

    across the boundary of the star \(r=R\), where M is the total mass of the sphere which can be obtained directly from Eq. (36) as

    $$\begin{aligned} M=m(R)=\frac{C R^3(B+a B C R^2+\alpha )}{2 (1+2 a C R^2)(1+3 a C R^2)^{\frac{2}{3}}}. \end{aligned}$$

    Matching of the line elements (40) and (47) at the boundary \(r=R\) yields,

    $$\begin{aligned} \left( 1 - \frac{2M}{R} \right)= & {} 1-\frac{\alpha CR^2}{(1+aCR^2)(1+3 a C R^2)^{\frac{2}{3}}} \nonumber \\&-\frac{B C R^2}{(1+3 a C R^2)^{\frac{2}{3}}}, \end{aligned}$$
    (48)
    $$\begin{aligned} \left( 1 - \frac{2M}{R} \right)= & {} A^2(1+a C R^2)^2. \end{aligned}$$
    (49)

    Using the junction conditions, we determine the constants \(A, \, B, \, C\) as

    $$\begin{aligned} A= & {} \frac{(5 M -2 R)}{2\sqrt{R(R-2 M)}}, \end{aligned}$$
    (50)
    $$\begin{aligned} C= & {} \frac{M}{a R^2(2 R-5 M)}, \end{aligned}$$
    (51)
    $$\begin{aligned} B= & {} -\frac{(5 M-2R)[2^{\frac{8}{3}}a(\frac{M-R}{5 M -2R})^{\frac{2}{3}}(2 M -R)+R \alpha ]}{2R(2 M-R)}.\nonumber \\ \end{aligned}$$
    (52)
  4. (iv)

    The gradient of density, radial pressure and tangential pressure are respectively obtained as

    $$\begin{aligned} 8 \pi \frac{d\rho }{dr}&=\dfrac{1}{A_{1}} \times \left( 2 a C^2 r (-10 B \eta _{1}^4 + (-15 + a C r^2 \right. \nonumber \\&\quad \left. (-53 + a C r^2 (-49 + 5 a C r^2))) \alpha )\right) , \end{aligned}$$
    (53)
    $$\begin{aligned} 8 \pi \frac{dp_r}{dr}&=-\frac{1}{A_{2}} (2 a C^2 r (-2 B \eta _{1} \eta _{3} + a (4 \eta _{2}^{\frac{2}{3}} \nonumber \\&\quad + C r^2 (a (16 \eta _{2}^{2/3} + C r^2 (12 a \eta _{2}^{2/3}\nonumber \\&\quad - 25 \alpha )) - 8 \alpha )) + \alpha )), \end{aligned}$$
    (54)
    $$\begin{aligned} 8 \pi \frac{dp_t}{dr}&=\frac{1}{\eta _{1}^4 \eta _{2}^{\frac{5}{3}}}\times (4 a C^2 r (B \eta _{1}^2 \eta _{3} + a (-2 \eta _{2}^{\frac{2}{3}} \nonumber \\&\quad + C r^2 (6 \alpha + a (-10 \eta _{2}^{\frac{2}{3}} + C r^2 (17 \alpha + a (-14 \eta _{2}^{\frac{2}{3}} \nonumber \\&\quad + C r^2 (-6 a \eta _{2}^{\frac{2}{3}} + 5 \alpha )))))))), \end{aligned}$$
    (55)

    where, \(\eta _{3} = (-1 + 5 a^2 C^2 r^4)\), \(A_{1} = \eta _{1}^3 \eta _{2}^{\frac{8}{3}}\) and \(A_{2} = \eta _{1}^3 \eta _{2}^{\frac{5}{3}}\).

    The decreasing nature of these quantities is shown graphically.

  5. (v)

    Within a stellar interior, it is expected that the speed of sound should be less than the speed of light i.e., \( 0 \le \frac{dp_r}{d\rho }\le 1\) and \( 0 \le \frac{dp_t}{d\rho }\le 1\).

    In this model, we have

    $$\begin{aligned} \frac{dp_r}{d\rho }&=-\frac{1}{(-10 B \eta _{1}^4 + (-15 + a C r^2 (-53 + a C r^2 \eta _{4})) \alpha )}\nonumber \\&\quad \times \Big [\eta _{2} (-2 B \eta _{1} \eta _{3} + a (4 \eta _{2}^{\frac{2}{3}} + C r^2 (a (16 \eta _{2}^{\frac{2}{3}} \nonumber \\&\quad +C r^2 (12 a \eta _{2}^{\frac{2}{3}} - 25 \alpha )) - 8 \alpha )) + \alpha ) \Big ], \end{aligned}$$
    (56)
    $$\begin{aligned} \frac{dp_t}{d\rho }&=\frac{- 1}{( 10 B \eta _{1}^5 + 15 \alpha + a C r^2 (68 + a C r^2 (102 + a C r^2 \eta _{5})) \alpha )} \nonumber \\&\quad \times \Big [ 2 \eta _{2} (B \eta _{1}^2 \eta _{3} + a (-2 \eta _{2}^{\frac{2}{3}} + C r^2 (6 \alpha + a (-10 \eta _{2}^{\frac{2}{3}} \nonumber \\&\quad + C r^2 (17 \alpha + a (-14 \eta _{2}^{\frac{2}{3}} + C r^2 (-6 a \eta _{2}^{\frac{2}{3}} + 5 \alpha ))))))) \Big ], \end{aligned}$$
    (57)

    where, \(\eta _{4} = (-49 + {5aCr}^{2})\) and \(\eta _{5} = (44 - {5aCr}^{2})\).

    By choosing the model parameters appropriately, it can be shown that this requirement is also satisfied in this model.

  6. (vi)

    Fulfillment of the energy conditions for an anisotropic fluid i.e., \(\rho +p_r+2p_t\ge 0\), \(\rho +p_r \ge 0\) and \(\rho +p_t \ge 0\) can also be shown graphically to be satisfied in this model.

Fig. 1
figure 1

Density profile at the stellar interior

Full size image
Fig. 2
figure 2

Radial and tangential pressure profiles at the stellar interior

Full size image
Fig. 3
figure 3

Radial and transverse component of sound speed at the stellar interior

Full size image
Fig. 4
figure 4

Fulfillment of energy condition at the stellar interior

Full size image
Fig. 5
figure 5

Radial variation of anisotropy at the stellar interior

Full size image
Fig. 6
figure 6

Radial variation of adiabatic index at the stellar interior

Full size image
Fig. 7
figure 7

Radial variation of mass at the stellar interior

Full size image
Fig. 8
figure 8

Nature of Equation of state (EOS) at the stellar interior

Full size image
Fig. 9
figure 9

Forces in equilibrium at the stellar interior

Full size image

3.4 Physical behaviour of the model

The simple elementary functional forms of the physical quantities help us to make a detailed study of the physical behaviour of the star. Most importantly, the solution contains an ‘anisotropic switch’ \(\alpha \), which allows us to investigate the impact of anisotropy. We analyze the physical behaviour of the model by using the values of masses and radii of observed pulsars as input parameters. We consider the data available from the pulsar \( PSR J0030+0451\) whose estimated mass and radius are \(M = 1.34 ~M_{\odot }\) and \(R = 12.71~\text {km}\), respectively [108]. Even though systematic errors in the measurements of neutron star masses and radii can not be ignored [109] for the assumed set of values, we determine the constants for two different values of the anisotropic factor \(\alpha \). For an isotropic case (\(\alpha =0\)), we obtain the constants \(B = 3.03291,~C = 0.000787453,~A=0.736378\); assuming the star to be composed of an anisotropic fluid distribution (we assume \(\alpha =1.5\)), the constants are calculated as \(A=0.736378,~B = 1.70219,~C = 0.000787453\). Making use of these values, we show graphically the nature of all the physically meaningful quantities in Figs. 1, 2, 3, 4, 5, 6, 7 and 8. The plots clearly show that all the quantities comply with the requirements of a real star. In particular, the figures highlight the effect of anisotropy on the gross physical behaviour of the compact star. Figure 9 shows that the configuration is stable under the combined effects of three different types of forces.

Fig. 10
figure 10

\(k_2\) is plotted against \({\mathscr {C}} \) for different \(\alpha \)

Full size image
Fig. 11
figure 11

\(V_r ^2 (R) \) and \(V_t ^2 (R)\) plotted against \({\mathscr {C}}\) for different \(\alpha \) values

Full size image
Table 1 The maximum limit of \({\mathscr {C}}\) and its corresponding \(k_2\) for \(\alpha >2 \)
Full size table
Fig. 12
figure 12

\(k_2\) is plotted against \({\mathscr {C}}\) for different \(\alpha \) values. Only physically allowed range of \(\alpha \) and \({\mathscr {C}}\) are considered here

Full size image
Fig. 13
figure 13

(Top) \(k_2\) plotted against different masses M for different \(\alpha \) at \(R = 10\, km\), (Bottom) \(k_2\) plotted against different masses M with different radii R for a fixed value of \(\alpha = 2\)

Full size image
Fig. 14
figure 14

(Top) \(k_2\) plotted against different radii R for different values of \(\alpha \) of a star of fixed mass \(M = 1.5 \, M_{\odot }\), (Bottom) \(k_2\) plotted against different radii R and masses M for a fixed value of \(\alpha = 2\)

Full size image
Fig. 15
figure 15

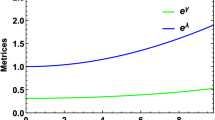
y is plotted against \(\alpha \) assuming different compact star masses and radii provided in the Table 2. Only physically allowed range of \(\alpha \) is considered

Full size image
Fig. 16
figure 16

\(k_2\) is plotted against \(\alpha \) assuming different compact star masses and radii provided in the Table 2. Only physically allowed range of \(\alpha \) has been considered

Full size image

4 Numerical calculation of TLN

Using the method employed in reference [110], we now calculate the numerical value of \(k_2\) for a particular neutron star. We first rewrite the master equation (22) using the Eq. (32) as

$$\begin{aligned} r y' +y^2 + (r {\mathscr {R}} - 1) y + r^2 {\mathscr {S}} = 0. \end{aligned}$$
(58)

From Eq. (30), at \({\mathscr {C}} = 0\) we expect \(k_2 = 0\). This implies that \(y(0) = 2\). Moreover, in the horizon formation limit \({\mathscr {C}} = 0.5\), the TLN \(k_2\) vanishes for all values of y.

In order to solve the differential equation (58), we use the initial condition \(y(0) = 2\) in addition to the expression for \({\mathscr {R}}, \, {\mathscr {S}}\) using Eqs. (23) and (24), respectively. Using the initial condition and Eqs. (38), (42), (43) and (44) for a particular NS, Eq. (58) can be solved and subsequently using Eq. (30), the TLN \(k_2\) can be calculated. One can also find the analytical

Table 2 y and \(k_2\) for \(\alpha = 0\) and the corresponding maximum value of \(\alpha \) are evaluated for different compact objects. The masses and radii of the compact stars are in accordance to references [112, 113]
Full size table

expression for y(r) in terms of compactness factor \({\mathscr {C}}\) and anisotropy \(\alpha \). Employing this technique, we plot the relation between \(k_2\) and compactness factor \({\mathscr {C}}\) for different values of \(\alpha \) as shown in the Fig. 10. We note that \(k_2\) increases gradually with increasing \({\mathscr {C}}\) up to a certain value and then decreases with further increase of \({\mathscr {C}}\). The range numerical value of \(k_2\) resembles with the Ref. [111]. For a NS having compactness \({\mathscr {C}} < 0.34\) and \(\alpha \le 2\), the above scheme can be used to calculate the TLN in this model.

For \(\alpha > 2\), a discontinuity arises in the plot of \(k_2\) vs \({\mathscr {C}}\). To address this problem, we set a maximum limit on \({\mathscr {C}}\) for a particular \(\alpha > 2\), using the ‘physical acceptability’ conditions discussed earlier. One can check that for all range of values of \({\mathscr {C}} <0.34\), \(\rho (r=0), \rho (r= R), p_r(r = 0), p_r(r = R), p_t(r = 0), p_t(r = R) \ge 0\). The energy condition \(\rho + p_r + 2 p_t \ge 0\). Therefore, the maximum limit on \({\mathscr {C}}\) can be calculated from the condition \(0 \le \dfrac{dp_r}{d \rho } \le 1\) and \(0 \le \dfrac{d p_t}{d \rho } \le 1\). For different values of \(\alpha \), \(V_r ^2(R) = \dfrac{dp_r}{d \rho }\) and \(V_t ^2(R) = \dfrac{d p_t}{d \rho } \) are plotted against \({\mathscr {C}}\) in Fig. 11. It then becomes easy to evaluate the maximum limit on \({\mathscr {C}}\) for different \(\alpha \) from the plot. For example, in Fig. 11, we note that for \(0 \le \alpha \le 2\), the range of compactness is \(0 \le {\mathscr {C}} \le 0.4\). For \(0 \le \alpha \le 2\), Fig. 10 shows that \(0 \le {\mathscr {C}} \le 0.34\). In Table 1, the maximum value of \({\mathscr {C}}\) for different \(\alpha \) is given.

For \(\alpha > 2 \), variation of the TLN \(k_2\) against \({\mathscr {C}}\) is shown in Fig. 12. In Table 1, the numerical values of the TLN \(k_2\) is shown for different \(\alpha \) values.

In the Fig. 13, (Top) \(k_2\) is plotted against mass M for different values of \(\alpha \) at \(R = 10\, km\), (Bottom) \(k_2\) is plotted against mass M for different radii R at a fixed value of \(\alpha = 2\). In the Fig. 14, (Top) \(k_2\) is plotted against radius R for different \(\alpha \) values having a fixed mass \(M = 1.5 \, M_{\odot }\) and (Bottom) \(k_2\) is plotted against R for different masses M for a fixed value of \(\alpha = 2\).

In the Fig. 15, variation of y with respect to \(\alpha \) is plotted for different compact stars. In this case, the range of \(\alpha \) is assumed to be \(0 \le \alpha < 4\). In Fig. 16, \(k_2\) is plotted against \(\alpha \). Physically acceptable range of \(\alpha \) has been calculated numerically. Obviously, the maximum value of \(\alpha \) is not the same for different class of compact stars. In Table 2, the maximum value of \(\alpha \) is calculated for different neutron stars and the corresponding \(k_2\) is also shown. In Fig. 16, we note that the TLN increases monotonically with increasing \(\alpha \) for stars having different compactness. In Table 2, \(k_2\) is calculated for \(\alpha = 0\) for different compact objects.

5 Discussion

In this paper, we have presented a technique to measure the TLN of a compact object when subjected to an external tidal field. Conversely, if the TLN is known, our method can be used to constrain the anisotropic stress of a compact star of a given mass and radius. The possible role of anisotropy vis-a-vis matter distribution of the star on the TLN has been analyzed. Our investigation clearly shows that TLN is influenced by anisotropic stress. It remains to be seen whether such impacts can be observationally realized. In our model, we focused on the quadrapolar ‘even parity TLN \(k_2\). However, one can also calculate higher-order TLN as well as magnetic TLN. Effects of other factors such as EOS, electromagnetic field etc. on the TLN needs further probe and will carried out elsewhere.