1 Introduction

Inspired by the Dirac oscillator [1], the Klein–Gordon (KG) oscillator [2, 3] has been a subject of intensive research in the last few decades. For example, the KG-oscillator in the Gödel and Gödel-type space-time backgrounds (e.g., [1,2,3,4,5,6,7,8]), in cosmic string space-time and Kaluza–Klein theory backgrounds (e.g., [9,10,11,12,13]), in Som-Raychaudhuri [14], in the (2+1)-dimensional Gürses space-time backgrounds (e.g., [15,16,17,18]), etc. The reader may find a sufficiently comprehensive sample of references on the historical progress background of this issue in [10, 16, 19,20,21,22,23,24]. The KG-oscillator in the (2+1)-dimensional Gürses space-time backgrounds is the focal point of the current methodical proposal.

On the other hand, the introduction of Mathews–Lakshmanan oscillator [25] has activated intensive research studies on “effective” position-dependent mass (PDM in short), both in classical and quantum mechanics [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. PDM is a metaphoric manifestation of the coordinate deformation/transformation [29,30,31]. Nevertheless, Khlevniuk [34] has argued that a point mass in the curved space may effectively be transformed into a PDM in Euclidean space. Such coordinate transformation/deformation affects, in turn, the form of the canonical momentum in classical and the momentum operator in quantum mechanics (e.g., [29, 30, 33, 37] and related references therein). In classical mechanics, it has been shown that negative the gradient of the potential force field is no longer the time derivative of the canonical momentum \(p=m\left( x\right) \dot{x}\), but it is rather related to the time derivative of the pseudo-momentum (also called Noether momentum) \(\pi \left( x\right) =\sqrt{m\left( x\right) }\dot{x}\) [30]. In quantum mechanics, however, the PDM momentum operator is constructed [33] and used to find the PDM creation and annihilation operators for the Schrödinger oscillator [29]. It would be interesting, therefore, to investigate the effects of such PDM recipe [29, 30, 33, 37] on the KG-oscillator in the (2+1)-dimensional Gürses space-time backgrounds with a confinement.

The KG-oscillator in a (1+2)-dimensional Gürses space-time backgrounds was investigated by Ahmed [16, 17], without a confinement (i.e., the scalar type interaction \(S\left( r\right) =0\) in \( m\longrightarrow m+S\left( r\right) \)). In the current methodical proposal, however, we consider the KG-oscillator confined in a Cornell-type scalar potential (i.e., \(S\left( r\right) \) of (14) below, which is commonly used in quarkonium spectroscopy [19, 43]) in a (2+1)-dimensional Gürses space-time backgrounds. We discuss the confined KG-oscillator in a Gürses space-time background (i.e. Gürses space-time metric \(ds^{2}\) (1) at specific Gürses parametric settings) and report the corresponding exact solution in Sect. 2. Therein, we discuss and report the effects of the vorticity parameter (i.e., \(\Omega \) in (1) below) on the energies levels through the reported Figs. 1, 2, 3 and 4. Such figures exhibit some interesting features like, energy levels crossings, partial clustering of positive and negative energy levels, and shifting the energy gap upwards or downwards. In Sect. 3, we consider the confined KG-oscillator in a generalized deformed (2+1)-dimensional Gürses space-time background. We show that the resulting confined-deformed KG-oscillator is, in fact, invariant and isospectral with that in the (2+1)-dimensional Gürses space-time background of Sect. 1. We discuss, in Sect. 4, a confined-deformed KG-oscillator from a (2+1)-dimensional Gürses to yet another Gürses space-time backgrounds. That is, the deformation in the (2+1)-dimensional Gürses space-time metric \(d\tilde{s}^{2}\) is chosen so that it belongs to a another Gürses space-time metric but with different Gürses-type parametric settings. Moreover, we consider (in Sect. 5) a confined-deformed KG-oscillator from Gürses to a pseudo-Gürses space-time backgrounds. The notion of pseudo-Gürses space-time metric is manifested by the fact that its parametric settings do not belong to the set of parameters of Gürses space-time metric, but it can be transformed into Gürses space-time metric within a transformation (26) below. The resulting confined-deformed KG-oscillators are found to admit invariance and isospectrality with the confined KG-oscillator in a (2+1)-dimensional Gürses space-time background discussed in Sect. 2. Our concluding remarks are given in Sect. 6.

2 Confined Klein–Gordon oscillator in a (2+1)-dimensional Gürses space-time background

In this section, we recollect the basic formulation of the KG-oscillator in a (2+1)-dimensional Gürses space-time background. Hence, we consider the (2+1)-dimensional Gürses space-time metric [15]

$$\begin{aligned} ds^{2}= & {} -dt^{2}+dr^{2}-2\Omega r^{2}dtd\theta +r^{2}\left( 1-\Omega ^{2}r^{2}\right) d\theta ^{2}\nonumber \\= & {} g_{\mu \nu }dx^{\mu }dx^{\nu };\quad \mu ,\nu =0,1,2 \end{aligned}$$
(1)

with \(a_{_{0}}=b_{_{0}}=e_{_{0}}=1\), \(b_{_{1}}=c_{_{0}}= \lambda _{_{0}}=0\), and the vorticity \(\Omega =-\mu /3\), in the Gürses metric

$$\begin{aligned} ds^{2}=-\phi dt^{2}+2qdtd\theta +\frac{h^{2}\psi -q^{2}}{a_{_{0}}}d\theta ^{2}+\frac{1}{\psi }dr^{2} \end{aligned}$$
(2)

(i.e., as in Eq. (5) of [15]), where

$$\begin{aligned} \phi= & {} a_{_{0}},\quad \psi =b_{_{0}}+\frac{b_{_{1}}}{r^{2}}+\frac{3\lambda _{_{0}} }{4}r^{2},\nonumber \\ q= & {} c_{_{0}}+\frac{e_{_{0}}\mu }{3}r^{2},\quad h=e_{_{0}}r,\quad \lambda _{_{0}}=\lambda +\frac{\mu ^{2}}{27}. \end{aligned}$$
(3)

The covariant and contravarian metric tensors in this case, respectively, read

$$\begin{aligned} g_{\mu \nu }= & {} \left( \begin{matrix} -1 &{} 0 &{} -\Omega r^{2} \\ 0 &{} 1 &{} 0 \\ -\Omega r^{2} &{} \,0 &{} \,r^{2}\left( 1-\Omega ^{2}r^{2}\right) \end{matrix} \right) \nonumber \\\Longleftrightarrow & {} g^{\mu \nu }=\left( \begin{matrix} -\left( 1-\Omega ^{2}r^{2}\right) &{} 0 &{} -\Omega \\ 0 &{} 1 &{} 0 \\ -\Omega &{} \,0 &{} \,\frac{1}{r^{2}} \end{matrix} \right) ;\nonumber \\&\quad \det \left( g\right) =-r^{2}. \end{aligned}$$
(4)

Under such setting, the KG-equation, with a scalar confinement \(S\left( r\right) \) (i.e., \(m\longrightarrow m+S\left( r\right) \)), is given by

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu }\left( \sqrt{-g}g^{\mu \nu }\partial _{\nu }\Psi \right) =\left( m+S\left( r\right) \right) ^{2}\Psi . \end{aligned}$$
(5)

Moreover, we may now couple the KG-oscillator using the recipes in [20, 21] and allow the momentum operator to indulge the oscillator through

$$\begin{aligned} p_{\mu }\longrightarrow p_{\mu }+i\eta \chi _{\mu }, \end{aligned}$$
(6)

with \(\eta \) denoting the frequency of the oscillator and \(\chi _{\mu }=\left( 0,r,0\right) \). This would, in effect, transform KG-equation (5) into

$$\begin{aligned}&\frac{1}{\sqrt{-g}}\left( \partial _{\mu }+\eta \chi _{\mu }\right) \left[ \sqrt{-g}g^{\mu \nu }\left( \partial _{\nu }{-}\eta \chi _{\nu }\right) \Psi \right] \nonumber \\&\quad =\left( m+S\left( r\right) \right) ^{2}\Psi . \end{aligned}$$
(7)

Which consequently yields

$$\begin{aligned}&\left\{ -\partial _{t}^{2}+\left( \Omega \,r\,\partial _{t}-\frac{1}{r} \partial _{\theta }\right) ^{2}+\partial _{r}^{2}+\frac{1}{r}\partial _{r}\right. \nonumber \\&\quad \left. -\eta ^{2}r^{2}-2\eta -\left( m+S\left( r\right) \right) ^{2} \right\} \Psi =0. \nonumber \\ \end{aligned}$$
(8)

A textbook substitution in the form of

$$\begin{aligned}&\Psi \left( t,r,\theta \right) =\exp \left( i\left[ \ell \theta -Et\right] \right) \psi \left( r\right) \nonumber \\&\quad =\exp \left( i\left[ \ell \theta -Et\right] \right) \frac{R\left( r\right) }{\sqrt{r}} \end{aligned}$$
(9)

would result in a one-dimensional Schrödinger-like KG-oscillator with a confinement S(r) so that

$$\begin{aligned}&R^{\prime \prime }\left( r\right) +\left[ \lambda -\frac{\left( \ell ^{2}-1/4\right) }{r^{2}}-\tilde{\omega }^{2}r^{2}-2mS\left( r\right) -S\left( r\right) ^{2}\right] \nonumber \\&\quad R\left( r\right) =0, \end{aligned}$$
(10)

where

$$\begin{aligned} \lambda =E^{2}-2\,\Omega \,\ell \,E-2\eta -m^{2}{; \ }\tilde{\omega } ^{2}=\Omega ^{2}E^{2}+\eta ^{2}. \end{aligned}$$
(11)

Obviously, Eq. (10) represents, with \(S(r)=0\), the 2-dimensional radial harmonic oscillator with an effective oscillation frequency \(\tilde{\omega }\) and consequently inherits its textbook eigenvalues

$$\begin{aligned} \lambda =2 \tilde{\omega }\left( 2n_{r}+\left| \ell \right| +1\right) \end{aligned}$$
(12)

and radial eigenfunctions

$$\begin{aligned} R\left( r\right)\sim & {} r^{\left| \ell \right| +1/2}\exp \left( -\frac{ \tilde{\omega }r^{2}}{2}\right) L_{n_{r}}^{\left| \ell \right| }\left( \tilde{\omega }r^{2}\right) \nonumber \\\Longleftrightarrow & {} \psi \left( r\right) \sim r^{\left| \ell \right| }\exp \left( -\frac{\tilde{\omega }r^{2}}{ 2}\right) L_{n_{r}}^{\left| \ell \right| }\left( \tilde{\omega } r^{2}\right) , \end{aligned}$$
(13)

where \(L_{n_{r}}^{\left| \ell \right| }\left( z\right) \) are the generalized Lagueree polynomials. At this point we may move further and use a Cornell-type scalar potential

$$\begin{aligned} S\left( r\right) =Ar+\frac{B}{r} \end{aligned}$$
(14)

so that equation (10) now reads

$$\begin{aligned}&R^{\prime \prime }\left( r\right) +\left[ \tilde{\lambda }-\frac{\left( \tilde{\ell }^{2}-1/4\right) }{r^{2}}-\beta ^{2}r^{2}-2mAr-\frac{2mB}{r} \right] \nonumber \\&\quad R\left( r\right) =0, \end{aligned}$$
(15)

where

$$\begin{aligned} \tilde{\lambda }= & {} E^{2}-2\,\Omega \,\ell \,E-2\eta -m^{2}-2AB, \, \tilde{\ell }^{2}=\ell ^{2}\nonumber \\&+B^{2},\quad \beta ^{2}=\Omega ^{2}E^{2}+\eta ^{2}+A^{2}. \end{aligned}$$
(16)

Equation (15) admits a finite/bounded solution in the form of biconfluent Heun functions

$$\begin{aligned} R\left( r\right)\sim & {} \mathcal {\,}r^{\left| \tilde{\ell }\right| +1/2}\,\exp \left( -\frac{\beta ^{2}r^{2}+2Amr}{2\,\beta }\right) H_{B}\nonumber \\&\times \left( 2\left| \tilde{\ell }\right| ,\frac{2mA}{\beta ^{3/2}}, \frac{A^{2}m^{2}+\tilde{\lambda }\,\beta ^{2}}{\beta ^{3}},\frac{4mB}{\sqrt{ \beta }},\sqrt{\beta }\,r\right) . \nonumber \\ \end{aligned}$$
(17)

The biconfluent Heun function \(H_{B}\left( \alpha ',\beta ',\gamma ',\delta ',z\right) \) of (17) becomes a polynomial of degree \(n'\) [44] if and only if

$$\begin{aligned} \alpha '-\gamma '-2=2\,n'; \,n'\ge 0, \end{aligned}$$
(18)

where, \(\alpha '=2|\tilde{\ell }|\) is a non-negative integer, \(\beta '=\frac{2mA}{\beta ^{3/2}}\), \(\gamma '=\frac{A^{2}m^{2}+\tilde{\lambda }\,\beta ^{2}}{\beta ^{3}}=\frac{\tilde{\lambda }}{\beta }\), \(\delta '=\frac{4mB}{\sqrt{\beta }}\), and \(z=\sqrt{\beta }\,r\). This would indeed offer not only a finite wavefunction but also a quantization recipe with some irrational quantum number \(n'\ge 0\) that needs to be correlated with the traditional radial quantum number \(n_r=0,1,2,\ldots \) (i.e., number of nodes in the radial wavefunction). In so doing, one may argue that the solution in (17) should collapse into that in (13), with the eigenvalues of (12), when the confining potential is switched off (i.e., \(A=B=0\)). This should always be the natural tendency of the solution of the more general problem of (15). Under such confinement parametric settings, the biconfluent Heun function of (17) would (using the Kummer relation [44]) yield

$$\begin{aligned}&H_{B}\left( \alpha ',0,\gamma ',0,z\right) \nonumber \\&\quad ={_{1}F_{1}}\left( \left( \frac{1}{2}+\frac{\alpha '}{4}-\frac{\gamma '}{4}\right) ,\left( 1+\frac{\alpha '}{2}\right) ,z^2\right) , \end{aligned}$$
(19)

Now, the condition that the confluent hypergeometric function becomes a polynomial of degree \(n_{r}\ge 0\) (i.e, \({_{1}F_{1}}\left( -n_r,1+\frac{\alpha '}{2},z^2\right) \) ) and finite everywhere is satisfied by the assumption that \(\frac{1}{2}+\frac{\alpha '}{4}-\frac{\gamma '}{4}=-n_r\) [44,45,46]. Consequently, we may now recast (19) in its finite polynomial form as

$$\begin{aligned}&H_{B}\left( \alpha ',0,\alpha '+2(2n_r+1),0,z\right) \nonumber \\&\quad ={_{1}F_{1}}\left( -n_r,\left( 1+\frac{\alpha '}{2}\right) ,z^2\right) \nonumber \\&\quad =n_r!\,\frac{\Gamma (1+\frac{\alpha '}{2})}{\Gamma (1+\frac{\alpha '}{2}+n_r)}\,L^{\frac{\alpha '}{2}}_{n_r}(z^2);\;n_r\ge 0. \end{aligned}$$
(20)

Obviously, our results in (13) and (12) are now retrieved up to a multiplicity constant that can be absorbed in the normalization constant. Hence, our irrational quantum number \(n'\) of (18) finds its fine tuning into a regular quantum number so that \(n'=2n_r\ge 0\). This would in turn establish the relation between \(\alpha '\) and \(\gamma '\) required to make our biconfluent Heun function in (17) a polynomial of degree \(n'=2n_{r}\ge 0\) and allows us to rewrite condition (18) as

$$\begin{aligned} \frac{1}{2}+ & {} \frac{\alpha '}{4}-\frac{\gamma '}{4}=-n_r\Longleftrightarrow \gamma '=4n_r+\alpha '\nonumber \\+ & {} 2\Longleftrightarrow \alpha '=\gamma '-2(2n_r+1), \end{aligned}$$
(21)

Therefore, for our \(H_{B}\left( \alpha ',\beta ',\gamma ',\delta ',z\right) \) in (17) to imply a quantum mechanically viable and acceptable solution, we adopt the parametric relation (21). This would consequently yield that

$$\begin{aligned} \frac{A^{2}m^{2}+\tilde{\lambda }\,\beta ^{2}}{\beta ^{3}}= & {} 2\left( 2n_{r}+\left| \tilde{\ell }\right| +1\right) \Longleftrightarrow \tilde{\lambda }\nonumber \\= & {} 2\beta \left( 2n_{r}+\left| \tilde{\ell }\right| +1\right) -\frac{m^{2}A^{2}}{\beta ^{2}}. \end{aligned}$$
(22)

In this case, we get the relation for the energy eigenvalues as

$$\begin{aligned}&E^{2}-2\,\Omega \,\ell \,E-2\eta -m^{2}-2AB+\frac{m^{2}A^{2}}{\left( \Omega ^{2}E^{2}+\eta ^{2}+A^{2}\right) }\nonumber \\&\quad =2\left( \Omega ^{2}E^{2}+\eta ^{2}+A^{2}\right) ^{1/2}\left( 2n_{r}+\left| \tilde{\ell }\right| +1\right) . \end{aligned}$$
(23)
Fig. 1
figure 1

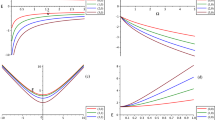
For \(\eta =m=1\) we show \(E_{n_r,\ell }\) of (23) against the vorticity parameter \(\Omega \) and for \(\ell =0,\pm 1,\pm 2\). In a–c we show the KG-oscillator energies without the confinement (i.e., \(A=B=0\)) for \(n_r=0,1,2\), respectively. In d–f we show the parametric effects of the Cornell confinement (14) on the KG-oscillator energies with \(n_r=0\) for \((A=1, B=0)\), \((A=0, B=1)\), and \((A=1,B=1)\), respectively

Full size image

One should notice that this result collapses into that in (12) when the parameters A and B of the Cornell potential (14) are set zeros. Yet, the wave function in (17) would yield that of (13) for \(A=B=0\). On the other hand, the Gürses metric (1) suggests that the range of the radial coordinate is restricted to \(0\le r < 1/\vert \Omega \vert \), otherwise the particle will be outside the light-cone (which should be avoided). However, at the limit \(\vert \Omega \vert \rightarrow 0\) the range of r is stretched so that \(0\le r < \infty \) becomes a viable range as well. Nevertheless, the above two conditions, (21 and \(0\le r < 1/\vert \Omega \vert \)) would therefore allow normalization and secure the finiteness of the corresponding wavefunctions [22, 45,46,47,48]. Moreover, it is obvious that the energy equation (23) is hard to solve analytically, not impossible though. Yet, it is clear that the second term \((-2\,\Omega \,\ell \,E\)) on the L.H.S. plays a critical role in shaping the fate of energy levels’ \(E_{n_r,\ell }\) structure when plotted against the vorticity parameter \(\Omega \) for some different parametric values, and against the oscillator frequency \(\omega \). This term is, in fact, associated to the non-inertial effect of rotating frames and resembles the so called Sagnac-type effect (cf. e.g. [46, 47]). Nevertheless, the role of this term \((-2\,\Omega \,\ell \,E_{\pm })\) is identified (± stands for positive and negative energy regions, respectively ) as follows: (i) the positive energy \(E_+\), with \(\Omega \) and \(\ell \) are both positive or both negative, will be boosted upward for \(\ell \ne 0\), whereas (ii) the negative energy \(E_-\), with positive/negative \(\Omega \) and negative/positive \(\ell \), the energy levels are boosted downward for \(\ell \ne 0\).

Fig. 2
figure 2

For \(\eta =m=1\) we show \(E_{n_r,\ell }\) of (23) against the vorticity parameter \(\Omega \) at \(n_r=0,1,2,3,4\). In a–e we show the KG-oscillator energies with the Cornell confinement (14) (i.e., \(A=B=1\)) for \(\ell =0,1,-1,3,10\), respectively. In f we show the KG-oscillator energies without the Cornell confinement (14) (i.e., \(A=B=0\)) at \(\ell =10\)

Full size image

This is documented in Figs. 1 and 2. In Fig. 3, we observe that the effect of the second term is clearly exemplified through shifting the energy gap upwards (when \(\Omega \) and \(\ell \) are both positive e or both negative) and downwards (when \(\Omega \) is negative/positive and \(\ell \) is positive/negative, respectively). As a result, we observe that the energy levels crossings (documented in Fig. 1), the energy levels partial clustering (documented in Fig. 2b–f), and the energy gap shifting (documented in Fig. 3a, b) are unavoidable manifestations in the process. Furthermore, when \(\ell =0\) the second term effect dies out and the spectrum retains its regular ordering format, but remains infected with the effect of the vorticity parameter though.

3 Confined KG-oscillator in a deformed (2+1)-dimensional Gürses space-time background

In this section, we consider that the (2+1)-dimensional Gürses space-time metric (1) is deformed in such a way that

$$\begin{aligned} ds^{2}\longrightarrow d\tilde{s}^{2}=-\left( dt+\Omega \,\tilde{r}^{2}d \tilde{\theta }\right) ^{2}+\tilde{r}^{2}d\tilde{\theta }^{2}+d\tilde{r}^{2}. \end{aligned}$$
(24)

Then the corresponding confined KG-oscillator is given, with \(\tilde{\chi } _{\mu }=\left( 0,\sqrt{m(r)}\tilde{r},0\right) \), by

$$\begin{aligned}&\frac{1}{\sqrt{-\tilde{g}}}\left( \,\tilde{\partial }_{\mu }+\eta \,\tilde{ \chi }_{\mu }\right) \left[ \sqrt{-\tilde{g}}\tilde{g}^{\mu \nu }\left( \, \tilde{\partial }_{\nu }-\eta \,\tilde{\chi }_{\nu }\right) \Psi \left( t, \tilde{r},\tilde{\theta }\right) \right] \nonumber \\&\quad =\left( m+A\tilde{r}+\frac{B}{\tilde{ r}}\right) ^{2}\Psi \left( t,\tilde{r},\tilde{\theta }\right) . \end{aligned}$$
(25)

We may now use the transformation

$$\begin{aligned} \tilde{r}=\int \sqrt{m\left( r\right) }dr=\sqrt{Q\left( r\right) }r{; \ }d\tilde{\theta }=d\theta \text {.} \end{aligned}$$
(26)

to connect the deformed Gürses space-time (24) with the formal one in (1). Moreover, the relation between \(m\left( r\right) \) and \(Q\left( r\right) \) is given by

$$\begin{aligned} \frac{d\tilde{r}}{dr}=\sqrt{m\left( r\right) }=\sqrt{Q\left( r\right) } \left( 1+\frac{Q^{\prime }\left( r\right) }{2Q\left( r\right) }r\right) \end{aligned}$$
(27)

In this case, the deformed Gürses metric (24) reads

$$\begin{aligned} d\tilde{s}^{2}= & {} -\left( dt+\Omega \,Q\left( r\right) r^{2}d\theta \right) ^{2}\nonumber \\&+Q\left( r\right) r^{2}d\theta ^{2}+m\left( r\right) dr^{2}, \end{aligned}$$
(28)

and consequently the corresponding space-time metric tensor is

$$\begin{aligned} \tilde{g}_{\mu \nu }=\left( \begin{matrix} -1\, &{} 0 &{} -\Omega \,Q\left( r\right) r^{2} \\ 0 &{} \,m\left( r\right) &{} 0 \\ -\Omega \,Q\left( r\right) r^{2} &{} 0 &{} \,\,Q\left( r\right) r^{2}\left( 1-\Omega ^{2}Q\left( r\right) r^{2}\right) \end{matrix} \right) , \nonumber \\ \end{aligned}$$
(29)

with its determinant \(\det \left( \tilde{g}\right) =-m\left( r\right) Q\left( r\right) r^{2}\) and its inverse

$$\begin{aligned} \tilde{g}^{\mu \nu }=\left( \begin{matrix} -\left( 1-\Omega ^{2}Q\left( r\right) r^{2}\right) &{} 0 &{} -\Omega \, \\ 0 &{} \frac{1}{m\left( r\right) }\, &{} 0 \\ -\Omega \, &{} 0 &{} \,\,\frac{1}{Q\left( r\right) r^{2}} \end{matrix} \right) . \end{aligned}$$
(30)

The deformed (2+1)-dimensional space-time metric (28) may very well be called a pseudo-Gürses metric for it may return to the Gürses one through reversing the transformation recipe.

Fig. 3
figure 3

For \(A=B=m=1\) we show the confined KG-oscillator energies \(E_{n_r,\ell }\) of (23) against the oscillator frequency \(\eta \) at \(n_r=0,1,2,3,4\). In a for \((\Omega =1, \ell =2)\), b for \((\Omega =-1, \ell =2)\), and c for \((\Omega =2, \ell =0)\)

Full size image

Under such settings, one may, in a straightforward manner, obtain

$$\begin{aligned}&\frac{d^{2}}{d\tilde{r}^{2}}R\left( \tilde{r}\right) +\left[ \tilde{\lambda } -V_{eff}\left( \tilde{r}\right) \right] R\left( \tilde{r}\right) =0;\nonumber \\&V_{eff}\left( \tilde{r}\right) =\frac{\left( \tilde{\ell }^{2}-1/4\right) }{\tilde{r}^{2}} +\beta ^{2}\tilde{r}^{2}+2mA\tilde{r}+\frac{2mB}{\tilde{r}}, \end{aligned}$$
(31)

which immediately inherits the form of (17) so that

$$\begin{aligned}&R\left( \tilde{r}\right) =R\left( \sqrt{Q\left( r\right) }r\right) = \mathcal {N\,}\left( \sqrt{Q\left( r\right) }r\right) ^{\left| \tilde{\ell }\right| +1/2}\,\nonumber \\&\quad \times \exp \left( -\frac{\beta ^{2}Q\left( r\right) r^{2}+2Am \sqrt{Q\left( r\right) }r}{2\,\beta }\right) \nonumber \\&\quad \times \,H_B\left( 2\,\left| \tilde{\ell }\right| ,\frac{2mA}{ \beta ^{3/2}},\frac{A^{2}m^{2}+\lambda \beta ^{2}}{\beta ^{3}},\frac{4mB}{ \sqrt{\beta }},\sqrt{\beta }\sqrt{Q\left( r\right) }r\right) \nonumber \\ \end{aligned}$$
(32)

Next, with \(R\left( \tilde{r}\right) =R\left( \tilde{r}\left( r\right) \right) =m\left( r\right) ^{-1/4}\phi \left( r\right) \), equation (31) reads

$$\begin{aligned}&\left( \frac{1}{\sqrt{m\left( r\right) }}\frac{d}{dr}\frac{1}{\sqrt{m\left( r\right) }}\frac{d}{dr}\right) m\left( r\right) ^{-1/4}\phi \left( r\right) \nonumber \\&\quad + \left[ \lambda -V_{eff}\left( \tilde{r}\right) \right] m\left( r\right) ^{-1/4}\phi \left( r\right) =0. \end{aligned}$$
(33)

Now multiplying from the left by \(m\left( r\right) ^{1/4}\) we get

$$\begin{aligned}&\left( m\left( r\right) ^{-1/4}\frac{d}{dr}m\left( r\right) ^{-1/2}\frac{d}{ dr}m\left( r\right) ^{-1/4}\right) \phi \left( r\right) \nonumber \\&\quad +\left[ \lambda -V_{eff}\left( \tilde{r}\left( r\right) \right) \right] \phi \left( r\right) =0, \end{aligned}$$
(34)

where

$$\begin{aligned} V_{eff}\left( \tilde{r}\left( r\right) \right)= & {} \frac{\left( \tilde{\ell } ^{2}-1/4\right) }{Q\left( r\right) r^{2}}+\beta ^{2}Q\left( r\right) r^{2}\nonumber \\&+2mA\sqrt{Q\left( r\right) }r+\frac{2mB}{\sqrt{Q\left( r\right) }r} \end{aligned}$$
(35)

that admits isospectrality with the one dimensional Schrödinger-like confined KG-oscillator in (15) with its eigenvalues given in (23) and its eigen functions given by (32). Hence the radial wave function is eventually given by

$$\begin{aligned} \psi \left( \tilde{r}\right)= & {} \psi \left( \sqrt{Q\left( r\right) }r\right) = \frac{R\left( \sqrt{Q\left( r\right) }r\right) }{\sqrt{\sqrt{Q\left( r\right) }r}}\nonumber \\= & {} \frac{f\left( r\right) ^{-1/4}\phi \left( r\right) }{\sqrt{ \sqrt{Q\left( r\right) }r}}. \end{aligned}$$
(36)

Obviously, the confined KG-oscillators of (34) and that of (15) are isospectral and share the same energy eigenvalues of (23), therefore. Yet we may safely conclude that the two confined KG-oscillators in a the (2+1)-dimensional Gürses to deformed-Gürses space-time backgrounds, (7) and (25), respectively, are invariant and isospectral. Moreover, one should notice that equation (34) resembles an effective position-dependent mass (PDM) particles in the one-dimensional von Roos PDM Hamiltonian [26] with Mustafa and Mazharimusavi parametric settings [29, 32, 33]).

4 Confined-deformed KG-oscillator from a (2+1)-dimensional Gürses to a Gürses space-time backgrounds

Let us rewrite the deformed (2+1)-dimensional Gürses space-time metric (28), using the transformation recipe in (26), as

$$\begin{aligned} d\tilde{s}^{2}= & {} -dt^{2}-2\Omega \,Q\left( r\right) r^{2}dt\,d\theta \nonumber \\&+Q\left( r\right) r^{2}\left( 1-\Omega ^{2}\,Q\left( r\right) r^{2}\right) d\theta ^{2}+m\left( r\right) dr^{2}, \end{aligned}$$
(37)

and compare it with (2) of [15] to imply, that \(a_{_{0}}=1,\)

$$\begin{aligned} \psi =\frac{1}{m\left( r\right) },\quad q=\frac{\mu }{3}Q\left( r\right) r^{2}=c_{_{0}}+\frac{e_{_{0}}\mu }{3}r^{2}. \end{aligned}$$
(38)

Consequently, our Q(r) reads

$$\begin{aligned} Q\left( r\right) =e_{_{0}}+\frac{3c_{_{0}}}{\mu r^{2}}\Longleftrightarrow Q\left( r\right) r^{2}=e_{_{0}}r^{2}+\frac{3c_{_{0}}}{\mu }, \end{aligned}$$
(39)

to imply, through (27), that

$$\begin{aligned} m\left( r\right) =\frac{\mu e_{_{0}}^{2}r^{2}}{\mu e_{_{0}}r^{2}+3c_{_{0}}} \Longleftrightarrow \psi =\frac{1}{m(r)}=\frac{1}{e_{_{0}}}+\frac{3c_{_{0}}}{\mu e_{_{0}}^{2}r^{2}}. \nonumber \\ \end{aligned}$$
(40)

Obviously, the resulted parametric structures agree with those of Gürses [15] in (2), where

$$\begin{aligned} b_{_{0}}=\frac{1}{e_{_{0}}},\quad b_{_{1}}=\frac{3c_{_{0}}}{\mu e_{_{0}}^{2}},\quad \lambda _{_{0}}=0,\quad h=e_{_{0}}r. \end{aligned}$$
(41)

Then the corresponding metric tensor is given by

$$\begin{aligned} \tilde{g}_{\mu \nu }=\left( \begin{matrix} -1\, &{} 0 &{} -\Omega \,\left( e_{_{0}}r^{2}+\frac{3c_{_{0}}}{\mu } \right) \\ 0 &{} \,\left( \frac{\mu e_{_{0}}^{2}r^{2}}{\mu e_{_{0}}r^{2}+3c_{_{0}}} \right) &{} 0 \\ -\Omega \,\left( e_{_{0}}r^{2}+\frac{3c_{_{0}}}{\mu } \right) &{} 0 &{} \,\,\left( e_{_{0}}r^{2}+\frac{3c_{_{0}}}{\mu } \right) \left( 1-\Omega ^{2}\left( e_{_{0}}r^{2}+\frac{3c_{_{0}}}{\mu } \right) \right) \end{matrix} \right) , \end{aligned}$$
(42)

with \(\det (\tilde{g})=-e_{_{0}}^{2}r^{2}\), and its inverse

$$\begin{aligned} \tilde{g}^{\mu \nu }=\left( \begin{matrix} -\left( 1-\Omega ^{2}\left( e_{_{0}}r^{2}+\frac{3c_{_{0}}}{\mu } \right) \right) &{} 0 &{} -\Omega \, \\ 0 &{} \left( \frac{\mu e_{_{0}}r^{2}+3c_{_{0}}}{\mu e_{_{0}}^{2}r^{2}}\right) \, &{} 0 \\ -\Omega \, &{} 0 &{} \,\,\frac{1}{\left( e_{_{0}}r^{2}+\frac{3c_{_{0}}}{\mu } \right) } \end{matrix} \right) \nonumber \\ \end{aligned}$$
(43)

Moreover, we may now report the corresponding confined-deformed KG-oscillator in the deformed Gürses space-time (37) background as

$$\begin{aligned}&\left( \left( \frac{\mu e_{_{0}}^{2}r^{2}}{\mu e_{_{0}}r^{2}+3c_{_{0}}} \right) ^{-1/4}\frac{d}{dr}\left( \frac{\mu e_{_{0}}^{2}r^{2}}{\mu e_{_{0}}r^{2}+3c_{_{0}}}\right) ^{-1/2}\right. \nonumber \\&\quad \times \left. \frac{d}{dr}\left( \frac{\mu e_{_{0}}^{2}r^{2}}{\mu e_{_{0}}r^{2}+3c_{_{0}}}\right) ^{-1/4}\right) \phi \left( r\right) \nonumber \\&\quad +\left[ \tilde{\lambda }-V\left( \tilde{r}\left( r\right) \right) \right] \phi \left( r\right) =0, \end{aligned}$$
(44)

where

$$\begin{aligned} V\left( r\right)= & {} V\left( \tilde{r}\left( r\right) \right) =\frac{\left( \tilde{\ell }^{2}-1/4\right) }{\left( e_{_{0}}+\frac{3c_{_{0}}}{\mu r^{2}} \right) r^{2}}+\beta ^{2}\left( e_{_{0}}+\frac{3c_{_{0}}}{\mu r^{2}}\right) r^{2}\nonumber \\&+2mA\sqrt{\left( e_{_{0}}+\frac{3c_{_{0}}}{\mu r^{2}}\right) }r+\frac{ 2mB}{\sqrt{\left( e_{_{0}}+\frac{3c_{_{0}}}{\mu r^{2}}\right) }r}. \end{aligned}$$
(45)

This confined-deformed KG-oscillator is isospectral and invariant with that of (15) and, therefore, shares the eigen energies given in (23). The corresponding eigenfunctions are readily given in (32) with \( Q\left( r\right) \) and \(m\left( r\right) \) are as defined in (39) and (40), respectively. The confined KG-oscillators, (44) and (15), in Gürses space-time backgrounds are invariant and isospectral, therefore.

5 Confined-deformed KG-oscillator from a pseudo-Gürses to a Gürses space-time backgrounds

In this section, we consider a deformation in the radial coordinate through

$$\begin{aligned} \sqrt{Q\left( r\right) }r=ar+\frac{b}{r}\Longleftrightarrow Q\left( r\right) r^2=\left( ar+\frac{b}{r}\right) ^{2}, \end{aligned}$$
(46)

which would, through the correlation in (27), imply that

$$\begin{aligned} m\left( r\right) =\left( a-\frac{b}{r^{2}}\right) ^{2}. \end{aligned}$$
(47)
Fig. 4
figure 4

a Corresponds to Fig. 1a but with the vorticity parameter \(\Omega \in [-0.05,0.05]\), b corresponds to Fig. 3e but with the vorticity parameter \(\Omega \in [-0.5,0.5]\), and c corresponds to b above but with \(\Omega \in [-5,0.5]\)

Full size image

Consequently, Eq. (34) yields

$$\begin{aligned}&\left( \left( a-\frac{b}{r^{2}}\right) ^{-1/2}\frac{d}{dr}\left( a-\frac{b}{ r^{2}}\right) ^{-1}\frac{d}{dr}\left( a-\frac{b}{r^{2}}\right) ^{-1/2}\right) \phi \left( r\right) \nonumber \\&\quad +\left[ \lambda -V_{1}\left( r\right) \right] \phi \left( r\right) =0, \end{aligned}$$
(48)

where \(V\left( r\right) \) is now given by (35) as

$$\begin{aligned} V_{1}\left( r\right)= & {} \frac{\left( \tilde{\ell }^{2}-1/4\right) }{\left( ar+b/r\right) ^{2}}+\beta ^{2}\left( ar+\frac{b}{r}\right) ^{2}\nonumber \\&+2mA\left( ar+ \frac{b}{r}\right) . \end{aligned}$$
(49)

Such confined-deformed KG-oscillators, (48) and (15), in pseudo-Gürses to Gürses space-time backgrounds are invariant and isospectral, therefore. Moreover, this system corresponds to a (2+1)-dimensional pseudo-Gürses deformed space-time metric (28) of the form

$$\begin{aligned} d\tilde{s}^{2}= & {} -\left( dt+\Omega \,\left( ar+\frac{b}{r}\right) ^{2}d\theta \right) ^{2}\nonumber \\&+\left( ar+\frac{b}{r}\right) ^{2}d\theta ^{2}+\left( a-\frac{b}{ r^{2}}\right) ^{2}dr^{2}, \end{aligned}$$
(50)

The notion of pseudo-Gürses space-time metric is manifested by the fact that this metric may yield a Gürses space-time like metric (1) (discussed in Sect. 1) if the transformation is reversed. Having said that, it is obvious that the only feasible Gürses to Gü rses space-time metric backgrounds case is the one discussed Sect. 4, where \(Q\left( r\right) \) and \(m\left( r\right) \) are, respectively, given by (39) and (40). Any other structure for \( Q\left( r\right) \) and \(m\left( r\right) \) in (28) should be classified as pseudo-Gürses to Gürses space-time metric backgrounds.

6 Concluding remarks

In this study, we have considered (in Sect. 2) the KG-oscillator confined in a Cornell-type scalar potential \(S\left( r\right) \) of (14) in some (2+1)-dimensional Gürses space-time backgrounds. We started with a confined KG-oscillator in a Gürses space-time background (i.e. Gürses space-time metric \(ds^{2}\) (1) at specific parametric settings) and reported the corresponding exact solution in (17) and (23). Hereby, we argue that the natural tendency of a physically viable solution of a more general case ( confined KG-oscillator in our case) should necessarily collapse into that of a less complicated KG-oscillator ones in (12) and (13), when the confinement parameters are switched off. So is the tendency of our reported exact solution in (17) and (23).

To observe the effect of the vorticity parameter \(\Omega =-\mu /3\) (in our case) on the energy levels \(E_{n_r,\ell }\), we have reported \(E_{n_r,\ell }\) (23) versus \(\Omega \) in Figs. 1 and 2, and \(E_{n_r,\ell }\) vs \(\eta \) (the KG-oscillator frequency) in Fig. 3. The mathematical structure as well as the reported figures document the critical role of the second term, \((-2\,\Omega \,\ell \,E)\) on the L.H.S. of (23), in shaping the energies of the confined KG-oscillator. This effect is summarized as follows: (i) the positive energy \(E_+\), with \(\Omega \) and \(\ell \) are both positive or both negative, is boosted upward for \(\ell \ne 0\), (ii) the negative energy \(E_-\), with positive/negative \(\Omega \) and negative/positive \(\ell \), respectively, is boosted downward for \(\ell \ne 0\), and (iii) for a fixed \(\Omega \) the energy gap is shifted upwards (for positive \(\Omega \) and \(\ell \)) and downwards (for negative \(\Omega \) and \(\ell \)), whilst the gap increases as the KG-oscillator frequency \(\eta \) increases. As a result of such effects, the energy levels crossings (documented in Fig. 1), the energy levels clustering (documented in Fig. 2b–f), and the energy gap shifting (documented in Fig. 3a, b) are unavoidable natural manifestations in the process. Moreover, to figure out how the energy levels behave near \(\Omega =0\) (i.e., flat space-time background) we have also reported Fig. 4. Figure 4a corresponds to Fig. 1a but with the vorticity parameter \(\Omega \in [-0.05,0.05]\). Obviously, at \(\Omega =0\) the energy levels admit degeneracy as follows: \(E_{0,0},E_{0,\pm 1},E_{0,\pm 2}\) form bottom to top for the positive energies and from top to bottom for negative energies. As we move far from \(\Omega =0\), we see that \(E_{0,+1}\) and \(E_{0,-1}\) switch their ordering in moving from \(\Omega >0\) to \(\Omega <0\) regions (similar behaviour occurs for all \(E_{n_{r}>0,+|\ell |}\) and \(E_{n_{r}>0,-|\ell |}\) states). To make sure that energy levels clustering do not indulge levels crossings we plot Fig. 4b, c, they correspond to Fig. 3e but with the vorticity parameter \(\Omega \in [-0.5,0.5]\) and \(\Omega \in [-5,0.5]\), respectively. Clearly, for a fixed value of the magnetic quantum number \(\ell =\pm |\ell |\), no energy levels crossings are observed and the energy levels just cluster without ordering change.

Next, we have considered (in Sect. 3) the confined KG-oscillator in a general deformation of the (2+1)-dimensional Gürses space-time background (28). Hereby, we have shown that the resulting confined and deformed KG-oscillator is invariant and isospectral with of the confined KG-oscillator (15) in the (2+1)-dimensional Gürses space-time background (1). We have further considered (in Sect. 4) a confined and deformed KG-oscillator in a deformed (2+1)-dimensional Gürses (28) to a Gürses space-time backgrounds (2). That is, the deformation in the (2+1)-dimensional Gürses space-time metric \(d\tilde{s}^{2}\) (28) is chosen so that it belongs to a another Gürses space-time metric (but with different Gürses-type parametric setting) in (2). We have shown that such a confined and deformed KG-oscillator is invariant and isospectral with of the confined KG-oscillator (15) in the (2+1)-dimensional Gürses space-time background (1). Finally, we have considered (in Sect. 5) a confined and deformed KG-oscillator in pseudo-Gürses to Gürses space-time backgrounds. The notion of pseudo-Gürses space-time metric is manifested by the fact that its parametric settings do not belong to Gürses space-time (2) metric but it can be transformed into Gürses space-time metric (1) within the transformation (26). Once again we have shown that such a confined and deformed KG-oscillator is invariant and isospectral with of the confined KG-oscillator (15) in the (2+1)-dimensional Gürses space-time background (1).

Finally, the current methodical proposal implicitly indulges a new form of topological defects in cosmic string space-time or in the geometrical theory of topological defects in condensed matter that may lead to some interesting features to be explored. To the best of our knowledge, within the above methodical proposal settings, such KG-oscillators in the backgrounds of (2+1)-dimensional Gürses to Gürses or to pseudo-Gürses space-time metric have never been reported elsewhere.