Curing tachyonic tree-level syndrome in NMSSM light-singlet scenarios

Abstract

Models with an extended Higgs sector open up the phenomenological possibility of additional scalars, beyond the SM-like boson observed by the LHC, with mass at or below the electroweak scale. Such scenarios are in particular viable in the presence of electroweak-singlet spin-0 fields, as expected for instance in the context of the NMSSM. Given that the size of radiative corrections can substantially affect the Higgs potential, a negative squared mass at the tree level does not necessarily yield a tachyonic spectrum at the physical level, but only indicates a failure of the tree-level description for calculational purposes. We explain how to tackle this technical issue in the example of the NMSSM, in scenarios with light $\mathcal {CP}$-odd or $\mathcal {CP}$-even singlet-dominated states and show how loop corrections to the Higgs masses and decay widths can be derived with the regularized Lagrangian. We further explore how the same flexibility in the definition of tree-level parameters can be exploited to circumvent large deviations of the tree-level spectrum from the kinematical setup in Higgs decays, or to estimate the theoretical uncertainty associated with the discrepancy between tree-level and physical Higgs spectra. The latter is of particular relevance for the properties of the SM-like Higgs boson in supersymmetry-inspired models.

1 Introduction

The investigation of the Higgs properties at the LHC  [1,2,3] places limits on the phenomenology of models with extended Higgs sectors, which should accommodate a state with characteristics roughly Standard-Model (SM)-like at $125.25\pm 0.17$ GeV  [4,5,6,7]. While such a condition (up to the exact mass value) is almost automatically fulfilled in scenarios with decouplingly heavy new physics, it should be examined with care in the presence of additional light states. Direct searches of the latter, as well as observables in electroweak (EW) or flavor physics, are of course relevant tests of such configurations as well. In order to exploit the growing collection of experimental limits and constrain the parameter space of models beyond the SM (BSM) in a quantitative fashion, precision calculations are needed on the theoretical side. As a result, the mass of the SM-like state in supersymmetric (SUSY) extensions of the SM  [8, 9] has been the object of considerable study in the last few decades – we refer the reader to the recent review  [10] for an overview of the corresponding literature. This one observable is however far from sufficient for a survey of the properties of the Higgs sector at the EW scale in non-minimal models.

In this paper, we focus on the Next-to-Minimal SUSY SM (NMSSM)  [11, 12], and more specifically on scenarios involving a light singlet-dominated state, i.e.  with mass below that of the observed SM-like Higgs boson, which is one of the trademarks of Higgs physics in this particular model  [13,14,15,16]. We refer the curious reader to e.g.  the comparatively recent works concerning searches at colliders in Refs. [17,18,19,20,21,22,23,24,25,26,27,28] as well as discussions in the context of singlino Dark Matter in Refs. [29,30,31,32,33,34,35,36,37]. For simplicity, we only consider the R-parity, $Z_3$- and $\mathcal {CP}$-conserving version of the Lagrangian, but the methods and results that we develop here can easily be extended to variants and even to distinct models. We aim at extending our work on controlled predictions for the Higgs masses and decays at the full one-loop (1L)/leading two-loop (2L) order in the NMSSM  [38,39,40,41,42] – similar projects have also been presented in e.g.  Refs. [43,44,45,46,47,48,49,50,51,52,53,54].

Our main interest in the present discussion consists in addressing a technical difficulty that routinely arises in the presence of light scalar states, namely the fact that the associated tree-level squared-mass becomes negative while continuity suggests that the physical squared mass (as estimated from the inclusion of radiative corrections) would remain positive. As the evaluation of loop functions with tachyonic spectrum is problematic and a standard processing of the parameter points with negative mass-squared thus fails, such benchmarks are often dismissed, while there is nothing intrinsically wrong with them, only with the chosen description at tree level. After a fashion, this issue is just an extension of the one raised in the Coleman–Weinberg mechanism  [55]. We address this ‘tachyonic tree-level syndrome’ in the context of the NMSSM in scenarios involving light singlet-dominated $\mathcal {CP}$-even or $\mathcal {CP}$-odd states. We further investigate the light-Higgs decays and the properties of the SM-like state for these scenarios and tackle analogous problems caused by the discrepancy between the tree-level and the physical spectrum at the level of the three-point functions. We also insist on the accuracy that can be achieved in such calculations at four-loop (4L) QCD and 1L EW/SUSY order: the latter can considerably degrade in the presence of light singlet-dominated $\mathcal {CP}$-even states, limiting the testability of corresponding scenarios at colliders.

In Sect. 2 we describe our strategy to circumvent the immediate difficulty of an artificial tachyonic spectrum at tree level and illustrate the workings of this method over a few scenarios involving light $\mathcal {CP}$-odd or $\mathcal {CP}$-even singlet-dominated states. The decays of the light-Higgs state are investigated in Sect. 3: in particular, we insist on the difficulty to accurately assess the singlet–doublet mixing in 1L calculations in scenarios with a light $\mathcal {CP}$-even singlet. The phenomenology of the SM-like state is discussed in Sect. 4, where we highlight the impact of various sources of theoretical uncertainty in BSM theories. Both SM-like and NMSSM-specific decay channels are considered at this level. The achievements of the paper are summarized in the conclusions of Sect. 5.

2 The ‘tachyonic tree-level syndrome’ and its cure

In models with extended Higgs sectors, in particular the NMSSM, several Higgs states may take a mass at the EW scale or below without necessarily endangering the limits from collider searches. However, as the hierarchies in the spectrum generate large logarithms in loop effects, radiative corrections to the masses may be comparable to the tree-level values (or larger), raising the question of how to interpret a tachyonic tree-level mass: does it signal an instability of the selected minimum of the scalar potential, incompatible with the phenomenology? Or is it just an artifact of the tree-level description that radiative corrections can mend? We investigate this issue below over several examples borrowed to the NMSSM phenomenology.

2.1 Scenarios with a light $\mathcal {CP}$-odd Higgs

To state the issue in a clear fashion, we first turn to NMSSM configurations where a light $\mathcal {CP}$-odd Higgs emerges. We remind the form of the tree-level mass matrix for the $\mathcal {CP}$-odd Higgs sector (after rotating out the Goldstone boson):¹

$$\begin{aligned} {{\mathcal {M}}}_{\text {odd},11}^{2}&= M^2_A \equiv M_{H^{\pm }}^2-M_W^2+\lambda ^2\,v^2\,, \end{aligned}$$

(1a)

$$\begin{aligned} {{\mathcal {M}}}_{\text {odd},22}^{2}&= M_A^2\left( \frac{\lambda \, v}{2\,\mu _{\text {eff}}}\,s_{2\beta }\right) ^2 \!\!- 3\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}\,A_{\kappa } \!+\! \frac{3}{2}\,\kappa \,\lambda \,v^2\,s_{2\beta }\,, \end{aligned}$$

(1b)

$$\begin{aligned} {{\mathcal {M}}}_{\text {odd},12}^{2}&= M_A^2\,\frac{\lambda \, v}{2\,\mu _{\text {eff}}}\, s_{2\beta } - 3\,\kappa \,v\,\mu _{\text {eff}}\,. \end{aligned}$$

(1c)

While the doublet component (${{\mathcal {M}}}_{\text {odd},11}^{2}$) is typically heavy in realistic scenarios, due to constraints on the $\mathcal {CP}$-even and charged sectors, see e.g.  Refs. [56,57,58,59,60,61], the singlet entry (${{\mathcal {M}}}_{\text {odd},22}^{2}$) can take values at the EW scale and below – even close to zero – in a phenomenologically more realistic way because of the elusive nature of singlet-dominated matter at colliders. Technically, a low-mass value easily emerges when $A_{\kappa }\!\rightarrow 0$, with two more motivated limits where the light pseudo-scalar can be viewed as the pseudo-Goldstone boson of an approximate global U(1) symmetry.

We first consider an NMSSM scenario corresponding to the Peccei–Quinn (PQ) limit of the model, with $|\kappa /\lambda |\ll 1$: $\kappa =-0.02$, $\lambda =0.4$, $M_{H^{\pm }}\!=2.5$ TeV, $t_{\beta }=5$, $\mu _{\text {eff}}\approx -480$ GeV and we vary $A_{\kappa }\in [-60,60]$ GeV. Then, terms violating the $U(1)_{\text {PQ}}$ symmetry – with charge assignment $Q^{\text {PQ}}_S+Q^{\text {PQ}}_{H_u}+Q^{\text {PQ}}_{H_d}{\mathop {=}\limits ^{!}}0$ for the singlet S and doublet-Higgs fields $H_{u,d}$ – are suppressed in the Higgs potential and a comparatively light singlet-dominated pseudo-scalar Higgs state $a^S = h_4$ is thus expected. With $A_{\kappa }\! > rsim -6$ GeV, the mass-squared $m_{a^S}^2$ of this state becomes negative at the tree level in the considered scenario.

Let us now turn to the radiative corrections. Our renormalization scheme has been described in Ref. [38] and employs vanishing tadpoles, on-shell (OS) conditions for SM-fermion and EW-gauge-boson masses, as well as $M_{H^{\pm }}^2$, while remaining parameters are renormalized in the $\overline{\text {DR}}$ scheme, with renormalization scale $\mu _{\text {ren}}\!=m_t$. In the pseudo-scalar Higgs sector, we restrict ourselves to corrections of 1L order (since those are currently the only fully exploitable radiative corrections for a singlet-dominated $\mathcal {CP}$-odd state – see however Ref. [45] as well as the recent Ref. [49]), and evaluate them with the expansion-and-truncation method at fixed-order described in Refs. [41, 42], thus avoiding dependence of observable quantities on gauge-fixing parameters and on the chosen field renormalization. The Feynman diagrams are computed with the help of FeynArts  [62] and FormCalc  [63, 64]. Loop functions are evaluated with LoopTools  [64]. The doublet-dominated pseudo-scalar is evidently very far in mass and the mixing of the singlet-dominated state with the EW neutral current proves numerically negligible, justifying the use of a non-degenerate framework for the derivation of mass corrections. As the SUSY spectrum becomes relevant at the radiative level, we specify that the squarks of third generation take mass at $\mathord {\sim }\,1.5$ TeV, while $M_3=2$ TeV and $A_t\sim -2.5$ TeV – for convenience, the input of all the scenarios that we investigate is collected in Appendix A. However, for the singlet-dominated states, 1L corrections primarily originate in the Higgs and higgsino/singlino sectors. Then, the physical mass of the light $\mathcal {CP}$-odd Higgs (as estimated at 1L order) for $A_{\kappa }\lesssim -6$ GeV – i.e.  in the limit $m^2_{a^S}\!\rightarrow 0^+$ – evaluates to ${\approx }\,70$ GeV, suggesting that the ‘tachyonic boundary’ at $A_{\kappa }\approx -6$ GeV is non-essential.

Parameter points with $A_{\kappa } > rsim -6$ GeV cannot be directly processed in the formalism described above, because the derivation of radiative corrections would require extending the definition of loop functions for tachyonic masses (and external momenta). On the other hand, such points cannot be dismissed on a robust phenomenological basis and are just unexplorable in this setup. In view of the technical issue at hand, one would be tempted to simply regularize the tree-level spectrum by adding an ad-hoc contribution to the tree-level mass-squared term, restoring its positivity, and then subtracting this quantity at the radiative level: such a solution has been existing for years within the public package NMSSMTools  [65,66,67], which employs an effective-potential approach to the calculation of the Higgs spectrum. Nevertheless, the explicit insertion of an infrared (IR) mass-cutoff in the lagrangian raises further concerns, as such a term violates several symmetries at tree level, including the EW gauge symmetry (since the light state contains a small doublet component).² In a ‘Feynman-diagrammatic’ description taking into account Higgs-to-Higgs mass corrections, it is therefore preferable to address the question in a formally more robust fashion.

As we stated before, the issue actually originates in the tree-level description of the parameter point, rather than in the scenario itself. In other words, the tree-level parameters, i.e.  the chosen renormalization scheme, are just ill-suited for the description of such scenarios, so that one simply needs to translate the problem to a more convenient scheme. Numerous choices are a priori possible. Nevertheless, in the $Z_3$-conserving NMSSM, a natural handle on the masses of the singlet-dominated Higgs states is the parameter $A_{\kappa }$ – see Eq. (1). We thus shift its tree-level value $A_{\kappa }^{\text {orig}}\rightarrow A_{\kappa }^{\text {mod}}\equiv A_{\kappa }^{\text {orig}}+A_{\kappa }^{\text {shift}}$ and correspondingly subtract the shift at the level of the counterterm $\delta A_{\kappa }^{\text {orig}}\rightarrow \delta A_{\kappa }^{\text {mod}}\equiv \delta A_{\kappa }^{\text {orig}} - A_{\kappa }^{\text {shift}}+\mathcal {O}(\text {2L})$, ensuring that we are still describing the original point in parameter space (at the perturbative order under control). The value of $A_{\kappa }^{\text {shift}}$ is chosen such that the tree-level $\mathcal {CP}$-odd mass-squared in the modified scheme is positive, $m^{2\,\text {mod}}_{a^S}>0$. It is obvious from the form of the mass matrix that (as long as $\kappa \ne 0$)³ $A_{\kappa }^{\text {shift}}$ can be chosen to accommodate any value of $m^{2\,\text {mod}}_{a^S}$. Nevertheless, we also know from physical intuition that the farther this value stands away from the physical mass, i.e.  the pole of the propagator, the slower the perturbative series converges, so that a wise choice of $m^{2\,\text {mod}}_{a^S}$ would select its value close to the OS scheme for the light singlet – for which, however, the conversion factor from the original scheme cannot be determined without regularizing the tree-level spectrum first. In addition, $A_{\kappa }^{\text {shift}}$ should remain of a magnitude allowing its interpretation as a quantity of 1L order – this can be controlled with the requirement that large cancellations be absent from the combination of tree-level and radiative contributions to the mass of the light-singlet state.

Fig. 1

Mass predictions for the light $\mathcal {CP}$-odd Higgs $a^S$ in the scenario of the PQ limit, plotted against the tree-level mass-squared of the original scheme. Left: Mass predictions in the original scheme (red), and in two modified schemes with $A_{\kappa }$ shifted so that $m^2_{a^S}$ remains above 49 GeV (scheme A, dashed) or above 2.6 GeV (scheme B, dotted). Right: Differences in mass predictions between scheme A (dashed) or B (dotted) with the OS scheme. The predictions of scheme B and the original scheme essentially coincide for $m^2_{a^S}>0$

In Fig. 1, we show the predicted pseudo-scalar mass $M_{a^S}$ at 1L in the considered scenario as a function of the tree-level mass-squared in the original renormalization scheme, $m^2_{a^S}$. The calculation in the original scheme (red curve) is only defined for positive $m^2_{a^S}$ (for illustrational purpose, the loop-corrected mass is replaced by 0 for negative $m^2_{a^S}$). Two modified schemes A and B are considered in green, which essentially implement an IR-cutoff on the tree-level pseudo-scalar mass with $m^{\text {(A)}}_{a^S}>49$ GeV (dashed curve) and $m^{\text {(B)}}_{a^S}>2.6$ GeV (dotted curve) – through the manipulations on the renormalization of $A_{\kappa }$ that are described above. Both extend the validity of the mass prediction well into the negative-$m^2_{a^S}$ region and largely coincide with one another, despite the very different choice of IR-cutoff for the pseudo-scalar mass.

In the plot on the right of Fig. 1, we show the difference of the loop-corrected masses predicted in schemes A and B with respect to the OS scheme (i.e.  $A_\kappa ^{\text {mod}}{\mathop {=}\limits ^{!}}A_{\kappa }^{\text {OS}}$ ensuring $m_{a^S}^{\text {OS}}{\mathop {=}\limits ^{!}}M_{a^S}^{\text {OS}}$; in practice, this condition is approximately fulfilled by means of an iterative algorithm that converges to the exact value).⁴ This quantity typically remains of order 100 MeV in the considered scenario, and exceeds this magnitude only for scheme A in the limit $M_{a^S}\!\rightarrow 0$, where the corresponding tree-level mass $m_{a^S}^{\text {(A)}}$ is comparatively far from the physical mass and the hierarchy as compared to the EW scale becomes more relevant. In the region with $m^2_{a^S}\!>0$, scheme B (with a very low IR-cutoff) hardly differs from the original scheme, while the predictions of scheme A (with a higher cutoff) depart from those of the original scheme by effects of $\mathcal {O}(10\text {\,MeV})$. Naively, we expect scheme A to perform better in the regime with a heavier $M_{a^S}$, while scheme B should offer a better depiction of the physics situation when $M_{a^S}\!=\mathcal {O}(1\text {\,GeV})$. The OS scheme serves as our reference, but its definition requires some further operations as compared to the other two. However, in this specific scenario, all these schemes perform quite similarly. We stress that perturbative corrections in all schemes are of limited usefulness in the regime with tree-level mass $m_{a^S}\lesssim m_c$ (or more essentially for $M_{a^S}\!\lesssim m_c$) where interactions with strongly-interacting matter are not captured by the partonic picture. In fact, the description at q–${\bar{q}}$ thresholds already calls for a more detailed analysis – see e.g.  Ref. [69] and references therein.

We consider another example in Fig. 2, corresponding to the R-symmetry limit of the NMSSM – i.e.  with the parametrization in Eq. (1): $A_{\kappa }\rightarrow 0$, $M_A^2-2\,(\kappa /\lambda )\,\mu _{\text {eff}}^2/s^2_{2\beta }\rightarrow 0$ – where again the light $a^S = h_4$ can be viewed as the pseudo-Goldstone boson of a global $U(1)_R$ symmetry with charge assignment satisfying $2\,Q^{R}_S-Q^{R}_{H_u}-Q^{R}_{H_d}{\mathop {=}\limits ^{!}}0$. Here, $\kappa =0.4$, $\lambda =0.2$, $M_{H^{\pm }}\!=1.75$ TeV, $t_{\beta }=10$, $\mu _{\text {eff}}=400$ GeV and we vary $A_{\kappa }\in [-2,0.5]$ GeV. The tree-level mass of the lightest $\mathcal {CP}$-odd Higgs becomes tachyonic for $A_{\kappa } > rsim -0.05$ GeV while the 1L-corrected mass is still ${\approx }\,24$ GeV. We again consider two modified schemes A and B with IR-cutoffs at 59 GeV and 2.9 GeV on the singlet-Higgs mass $m_{a^S}$, respectively. In this case, the mass predictions of scheme A (with a higher IR-cutoff) depart from those of the OS scheme (or those of scheme B) more significantly than in the first example in the low-mass regime: the difference reaches several GeV; this is in part due to the choice of a higher cutoff in scheme A, less suited to describe light states. In addition, the non-negligible value of $\kappa$ in the chosen benchmark both generates a hierarchy in the singlet/singlino sector and makes corresponding 1L corrections to the pseudo-scalar mass sensitive to this splitting. However, the qualitative agreement remains acceptable and, in any case, the regularization always improves on the unpredictive original scheme. In fact, these variations with the choice of scheme also shed some light on the uncertainties at stake in the mass predictions for the light Higgs states at the considered order: it is indeed not surprising that, when the tree-level mass is far from the physical one (in relative value), the convergence of the perturbative series is slow, hence the theoretical uncertainty is large at 1L order.

Fig. 2

Mass predictions for the light $\mathcal {CP}$-odd Higgs $a^S$ in the scenario of the R-symmetry limit, plotted against the tree-level mass-squared of the original scheme. The conventions are similar to those of Fig. 1, up to adjustments in the definition of the modified schemes

Finally, a low pseudo-scalar Higgs mass can also be achieved ‘accidentally’, typically with a small value of $A_{\kappa }$. The Higgs/higgsino spectrum is then a priori  more free than in the PQ- and R-symmetry limit. We also stress that radiative corrections to the squared mass of the light Higgs $a^S$ are not systematically positive, as in the examples above. Nevertheless, variations in the scheme may still be of interest, e.g.  in order to bring the tree-level spectrum closer to the physical situation or to assess theoretical uncertainties: the analysis of the Higgs decays will illustrate these points in Sects. 3 and 4.

2.2 Scenarios with a light $\mathcal {CP}$-even Higgs

Another phenomenological possibility is that of a light $\mathcal {CP}$-even state. We first remind the form of the $\mathcal {CP}$-even mass matrix in the base of gauge eigenstates:

$$\begin{aligned} {{\mathcal {M}}}_{\text {even},11}^{2}&= M^2_A\,s_{\beta }^2+M_Z^2\,c_{\beta }^2\,, \end{aligned}$$

(2a)

$$\begin{aligned} {{\mathcal {M}}}_{\text {even},22}^{2}&= M^2_A\,c_{\beta }^2+M_Z^2\,s_{\beta }^2\,, \end{aligned}$$

(2b)

$$\begin{aligned} {{\mathcal {M}}}_{\text {even},33}^{2}&= M_A^2\left( \frac{\lambda \,v}{2\,\mu _{\text {eff}}}\,s_{2\beta }\right) ^2 + \frac{\kappa }{\lambda }\,\mu _{\text {eff}} \left( A_{\kappa } +4\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}\right) \nonumber \\&\quad - \frac{1}{2}\,\kappa \,\lambda \, v^2\,s_{2\beta }\,, \end{aligned}$$

(2c)

$$\begin{aligned} {{\mathcal {M}}}_{\text {even},12}^{2}&= -\frac{1}{2}\left( M_A^2+M_Z^2-2\,\lambda ^2\,v^2\right) s_{2\beta }\,, \end{aligned}$$

(2d)

$$\begin{aligned} {{\mathcal {M}}}_{\text {even},13}^{2}&= \lambda \,v \left[ 2\,\mu _{\text {eff}}\,c_{\beta } - \left( \frac{M_A^2}{\mu _{\text {eff}}}\,s_{2\beta } + 2\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}\right) s_{\beta }\right] , \end{aligned}$$

(2e)

$$\begin{aligned} {{\mathcal {M}}}_{\text {even},23}^{2}&= \lambda \,v \left[ 2\,\mu _{\text {eff}}\,s_{\beta } - \left( \frac{M_A^2}{\mu _{\text {eff}}}\,s_{2\beta } + 2\,\frac{\kappa }{\lambda }\,\mu _{\text {eff}}\right) c_{\beta }\right] . \end{aligned}$$

(2f)

Once again, the singlet entry ${{\mathcal {M}}}_{\text {even},33}^{2}$ can be small in the limit where the PQ-breaking scales $A_{\kappa }$ and $(\kappa /\lambda )\,\mu _{\text {eff}}$ are at the EW scale or below. In fact, in the PQ-inspired scenario of the previous section, the spectrum contains a light $\mathcal {CP}$-even singlet-dominated state with mass $\mathord {\sim }\,50$ GeV at tree level, and reaching 90–100 GeV at 1L order. In addition, an accidental cancellation between the terms contributing to ${{\mathcal {M}}}_{\text {even},33}^{2}$ is possible, allowing for a light $\mathcal {CP}$-even state without a light pseudo-scalar simultaneously. In this case, as the low mass is not guaranteed by a symmetry, radiative corrections are expected to have a sizable impact.

From the phenomenological perspective, a complication emerges in the presence of a light $\mathcal {CP}$-even state, as its mixing with the SM-like state should not excessively alter the properties of the latter: this tends to imply either a very suppressed $\lambda$ or a correlation between $\mu _{\text {eff}}$, $M_A$ and $t_{\beta }$; the latter can be deduced from the form of ${{\mathcal {M}}}_{\text {even},13}^{2}$ and $\mathcal{M}_{\text {even},23}^{2}$. As this relation is not guaranteed by a symmetry, there is limited control over the singlet–doublet mixing at the radiative level.

Fig. 3

Mass predictions for the light $\mathcal {CP}$-even Higgs $h^S$ in the scenario CPE1 with $\lambda =\kappa =0.05$, plotted against the tree-level mass-squared of the original scheme. The conventions are similar to those of Fig. 1, up to adjustments in the definition of the modified schemes

We first consider a scenario with comparatively low values of $\lambda$ and $\kappa$ (for commodity, we will refer to it as CPE1 below): $\lambda =\kappa =0.05$, $M_{H^{\pm }}\!=4.8$ TeV, $t_{\beta }=10$, $\mu _{\text {eff}}=500$ GeV and $A_{\kappa }$ in the range $[-2003,-1990]$ GeV; squark masses are at 1.5 TeV and the associated trilinear couplings at $-2.4$ TeV. The heavy-doublet and $\mathcal {CP}$-odd singlet-dominated states then receive multi-TeV masses, leaving two light $\mathcal {CP}$-even Higgs bosons: the SM-like $h^{\text {SM}}= h_2$ and the singlet-dominated $h^S= h_1$. The latter two are largely decoupled at the tree level, with mixing-squared at the level of $10^{-4}$. For $A_{\kappa }\lesssim -2$ TeV, the tree-level mass-squared $m_{h^S}^2$ of the light singlet becomes negative while the predicted physical mass $M_{h^S}$ is still at ${\approx }\,34$ GeV. Once again, the scheme of $A_{\kappa }$ can be adapted to perform the mass calculation in the pseudo-tachyonic region, employing $A_{\kappa }^{\text {shift}}$ to stabilize the $\mathcal {CP}$-even singlet mass this time: this is shown in Fig. 3. There, we again consider two schemes A and B implementing an IR-cutoff on $m_{h^S}$ at $\mathord {\sim }\,65$ GeV (scheme A) or $\mathord {\sim }\,5$ GeV (scheme B), as well as the OS scheme. All provide qualitatively compatible results, although the low-mass regime shows larger deviations.

The solution addressing the pseudo-tachyonic region is therefore identical to the case of a light $\mathcal {CP}$-odd state, with the only difference that the shift in $A_{\kappa }$ is performed in the opposite direction. In principle, a complication affecting this method is possible in scenarios where both the $\mathcal {CP}$-odd and $\mathcal {CP}$-even singlet-dominated states are very light (or tachyonic): then, the shift of $A_{\kappa }$ may not suffice to obtain positive tree-level masses for both states simultaneously (the shift a priori  acts in opposite directions for each, compare Eqs. (1b) and (2c)). Then, one may attempt to regularize the full tree-level spectrum by also altering the renormalization scheme for the other $Z_3$-conserving singlet scale $(\kappa /\lambda )\,\mu _{\mathrm {eff}}$. Alternatively, one may simply add a quartic singlet coupling ${\hat{\kappa }}^2\,|S|^4$ to the Higgs potential as a handle on the $\mathcal {CP}$-even mass, while $A_{\kappa }$ is determined by the regularization of the $\mathcal {CP}$-odd mass. We will not investigate such scenarios in detail below, although we will demonstrate the use of the extended Higgs potential for the PQ-inspired scenario of the previous subsection at the level of the Higgs decays of the SM-like state.

Fig. 4

Mass predictions for the light $\mathcal {CP}$-even Higgs $h^S$ in the scenario CPE2, plotted against the tree-level mass-squared of the original scheme. The conventions are similar to those of Fig. 1, up to adjustments in the definition of the modified schemes

A second illustration is shown in Fig. 4 for a large value of $\lambda$ (the scenario is labelled CPE2 below). In this case, $\kappa =0.05$, $\lambda =0.5$, $M_{H^{\pm }}\!=1.225$ TeV, $t_{\beta }=2$, $\mu _{\text {eff}}=500$ GeV and $A_{\kappa }$ in the range $[-500,-380]$ GeV. The soft-breaking sfermion mass parameters are unchanged as compared to the earlier scenarios, but the trilinear soft-breaking couplings are now set to 2.1 TeV. While $\kappa \ll \lambda$, the scale of the PQ-symmetry-breaking terms is comparatively high and the lightest $\mathcal {CP}$-odd Higgs takes a mass above 200 GeV. In the $\mathcal {CP}$-even sector, the full range of $A_{\kappa }$ leads to a tachyonic tree-level mass for the singlet-dominated scalar $h^S = h_1$: $m_{h^S}$ vanishes at $A_{\kappa }\approx -283$ GeV, but the corresponding 1L-corrected mass then reads $M_{h^S}\approx 103$ GeV, demonstrating the large magnitude of the radiative corrections and the artificial nature of the tachyonic boundary at the tree level. In Fig. 4, the mass prediction at 1L is plotted in a scheme A with a high IR-cutoff of 65 GeV (dashed green) and a scheme B (dotted green) with a low IR-cutoff of $\mathord {\sim }\,3$ GeV. The original scheme (red) does not provide results in the considered range.

3 Properties of the light Higgs at 1L order

The regularization of the tree-level spectrum through the redefinition of the renormalization scheme further allows to compute the decay properties of the light state at the radiative level. In fact, it allows to tackle another issue appearing at the level of the three-point functions: the tree-level Higgs mass may be smaller than the sum of the masses of the final states (while the physical mass is larger), thus causing problems with the evaluation of the loop integrals with LoopTools.⁵ This problem is not fundamental in nature, but associated with the implemented numerical method. It would thus be possible to repair the evaluation of three-point functions to address all kinematical configurations. On the other hand, we may worry about the accuracy of an evaluation that is performed in a regime comparatively different from the actual one, i.e.  with tree-level Higgs masses significantly below the loop-corrected physical values, especially if it displaces the external momenta with respect to poles of the internal propagators. Employing a loop-corrected mass in the 1L amplitudes is a straightforward method for dealing with this issue without the need to address the problematic regime, but it endangers the invariance of observables with respect to gauge-fixing parameters and field renormalization, as argued in Ref. [41], hence resulting in limited improvement in terms of accuracy. Therefore, it is useful to bypass the problem in a more consistent way and compute Higgs decays in a scheme that directly places the tree-level masses in a kinematically allowed configuration: the OS scheme appears as the most convenient choice and also probably the most predictive, since it brings the tree-level spectrum in accordance with the physical configuration.

In view of the considered spectra and restricting ourselves to the partonic picture, the accessible final states to the decays of the light singlet-dominated state at 1L essentially consist of SM-fermion pairs at next-to-leading order (NLO), as well as gluon and photon pairs at leading order (LO), including further radiation of photons and gluons: we directly consider the inclusive fermionic decay widths with respect to QCD and QED  [70, 71], including up to $\mathcal {O}(\alpha _s^4)$ corrections  [72, 73] – see also the short overview in Ref. [74] – as well as QCD corrections to the diphoton ($\gamma \gamma$) and digluon (gg) channels  [75, 76]. Due to the hierarchy of Yukawa couplings, the $b{\bar{b}}$ channel is expected to dominate if kinematically accessible, with important decays into $\tau ^+\tau ^-$, gg and $c{\bar{c}}$ below the b–${\bar{b}}$ threshold. Nevertheless, such a partonic picture is over-simplistic at Higgs masses similar to twice the bottom mass and below, and the interaction of the Higgs state with hadronic matter should then be considered in a non-perturbative fashion: we refer the reader to e.g.  Refs. [77, 78] for a discussion of effects at q–${\bar{q}}$ thresholds, as well as Ref. [79] for the chiral limit. While we restrict ourselves to the partonic description here, this should thus be seen only as the perturbative step in a more involved path to the actual decay widths at low mass.

3.1 Case of a light $\mathcal {CP}$-odd Higgs

The decays of the light singlet-dominated pseudo-scalar $a^S = h_4$ into SM matter proceed at tree level through its subleading doublet component. The latter is suppressed by the high mass of the doublet component, $M_A\approx M_{H^{\pm }}\!\gg M_Z$. The exact choice of $M_A$ is not free in the R-symmetry limit, as it is largely determined by the defining condition of this limit, i.e.  $M_A^2\approx 2\,(\kappa /\lambda )\,\mu _{\text {eff}}^2/s^2_{2\beta }$. A less immediate condition also arises in the PQ-limit in order to avoid large mixing in the $\mathcal {CP}$-even sector: $M_A^2\approx 4\,\mu _{\text {eff}}^2/s^2_{2\beta }$. Correspondingly, the size of the doublet component in $a^S$ at tree level evaluates to ${\approx }\,0.03$ and ${\approx }\,0.02$ in the two scenarios of Sect. 2.1, leading to reduced decay widths (and a suppressed direct production cross-section at colliders). Though moderate in these examples, the value of $t_{\beta }>1$ further favors the decays into down-type quarks and leptons.

The decay widths into $b{\bar{b}}$, $\tau ^+\tau ^-$, $c{\bar{c}}$, gg and $\gamma \gamma$ are shown as a function of the physical Higgs mass in Fig. 5 for the two proposed benchmarks. Calculation in the original scheme (dashed lines) not only fails when the tree-level mass turns negative, but already when it falls under threshold (although the physical mass is above), due to the aforementioned difficulty in the evaluation of three-point loop functions with LoopTools. Further spurious effects develop when the tree-level mass is small (visible mostly in the digluon and diphoton channels). Now allowing for a change of scheme via a shift of $A_{\kappa }$, it is most natural to select the OS condition on the mass of the light singlet as defining the framework for the Higgs decays: the tree-level masses then immediately satisfy the expected kinematical relations and only genuine hierarchies are present in the calculation of the radiative corrections. The corresponding predictions for the decay widths are shown as solid lines and exhibit the expected behavior down to $M_{a^S}\!=0$.

Fig. 5

Partial decay widths of the light $\mathcal {CP}$-odd state $a^S$ in the scenarios of Sect. 2.1: PQ- (left) and R-symmetry limit (right). The solid curves are obtained in the scheme with the renormalization of $A_{\kappa }$ determined by the OS condition on the mass of the light singlet $a^S$. The decays in the original scheme are shown with dashed lines

Radiative corrections to the decay widths into fermions are dominated by QCD effects (when applicable): these involve first an ultraviolet (UV) logarithm that we absorb within the definition of the Yukawa couplings  [70], then further non-logarithmic finite corrections amounting to $\mathcal {O}(10$–$30\%)$ of the tree-level widths. QED and EW/Yukawa contributions remain at the percent level – with the exception of $a^S\rightarrow c{\bar{c}}$ in the R-symmetry limit, where they reach $15\%$ due to the $t_{\beta }$-suppression of the Born-level amplitude. Yet, it may be worthwhile to underline that such mild EW/Yukawa contributions result from large cancellations between the vertex diagrams and the loop corrections on the external Higgs line, so that a separate processing of both, e.g.  by defining an effective mixing matrix – see e.g.  Ref. [38] – would lead to sizable non-predictive effects. We already emphasized this point in Ref. [41]. In addition, the large contributions of Higgs-mixing type do not come about as the consequence of large mixing among the $\mathcal {CP}$-odd states – the latter remains of order $10^{-3}$, legitimizing the use of a non-degenerate formalism – but originate in the much larger decay amplitude of doublet-dominated states into SM matter. Finally, we also observe a good agreement of the fermionic widths derived in the OS scheme with those obtained in the original scheme in the region where the latter produces a well-behaved spectrum: this illustrates the weak dependence of the decay width on the tree-level Higgs mass, which is itself related to the small size of the EW corrections. In fact, a much larger dependence would emerge if we did not factor out QCD corrections and employ a physical Higgs mass in the corresponding piece, in lieu  of the tree-level mass.

The decays into gluon and photon pairs, emerging directly at 1L order, are much more sensitive to the employed tree-level Higgs mass, as can be seen from the ‘horns’ developing in the original scheme at the limit of its applicability. This artificial sensitivity to the tree-level mass is expected to disappear with the inclusion and resummation of higher orders. This lengthy procedure could be bypassed by directly upgrading the tree-level Higgs mass to its physical value. This is possible here because no genuine weak corrections contribute at the corresponding order, only fermion loops; in the $\mathcal {CP}$-even case, an upgrade of the Higgs couplings to Goldstone bosons would also be needed under penalty of violating the Ward identity and generating further large spurious effects, see Ref. [41]. Instead of following this procedure, we work in the scheme with an OS Higgs mass, which conveniently circumvents such complications.

Other schemes with modified $A_{\kappa }$ can also be employed for the calculation of the Higgs decay widths, as long as the tree-level spectrum does not violate the kinematical setup of the considered process. Here, we tested the modified schemes A of Sect. 2.1, with a relatively high IR-cutoff on the tree-level Higgs mass, as well as a scheme C with IR-cutoff ${\approx }\,12$ GeV (still above the $b{\bar{b}}$ threshold). Deviations with respect to the OS scheme are essentially contained in the derived value of the physical mass $M_{a^S}$ – see the comparisons in Fig. 1 and Fig. 2. Once considered as function of this mass, the predictions of the decay widths into fermions for both modified schemes agree with the OS scheme at the level of $\mathord {\lesssim }\,10\%$ of the magnitude of the EW contributions. Again, this illustrates the very loose dependence of these decay channels on the chosen tree-level mass. Nevertheless, for the diphoton and digluon final states, where 1L is the LO, the choice of tree-level mass (hence, of scheme) has a critical impact on the decay widths, as we discussed already.

3.2 Case of a light $\mathcal {CP}$-even Higgs

The case of a light singlet-dominated $\mathcal {CP}$-even state is much more difficult to quantitatively describe at 1L, due to the radiative mixing with the SM-like state. As the singlet component does not couple to the SM decay products, the corresponding decays of the singlet-dominated state are indeed governed by its (in phenomenologically realistic scenarios) subdominant doublet component, generated either at tree level or through radiative corrections. In the $\mathcal {CP}$-odd sector, the singlet–doublet mixing was well under control already at tree level, because of the large mass of the heavy-doublet state, thus making the mass-splitting comparatively clean. It is not so in the $\mathcal {CP}$-even sector, because of the simultaneous presence of two light states with masses heavily depending on radiative corrections, so that the mass-splitting can easily be shifted by $\mathcal {O}(100\%)$ by 1L (and even 2L) effects. In other words, the tree-level description of the light states is very far from the physical configuration and would require the inclusion of higher orders for a precise prediction of the phenomenology. As it is, the convergence of the perturbative series is too slow to quantitatively assess the mixing of the singlet- and SM-like Higgs at 1L.

Let us clarify this point first. The tree-level couplings of the light singlet to SM matter are governed by the mixing angles emerging in the diagonalization of the mass matrix of Eq. (2):

$$\begin{aligned} U_{11}&\approx -\frac{c_{\beta }}{m^2_{h_1}\!-m^2_{h_2}}\left[ c_{\beta }\,{{\mathcal {M}}}_{\text {even},13}^{2}+s_{\beta }\,{{\mathcal {M}}}_{\text {even},23}^{2} \right] \nonumber \\&\quad - \frac{s_{\beta }}{m^2_{h_1}\!-m^2_{h_3}}\left[ s_{\beta }\,{{\mathcal {M}}}_{\text {even},13}^{2}-c_{\beta }\,{{\mathcal {M}}}_{\text {even},23}^{2} \right] , \end{aligned}$$

(3a)

$$\begin{aligned} U_{12}&\approx -\frac{s_{\beta }}{m^2_{h_1}\!-m^2_{h_2}}\left[ c_{\beta }\,{{\mathcal {M}}}_{\text {even},13}^{2}+s_{\beta }\,{{\mathcal {M}}}_{\text {even},23}^{2} \right] \nonumber \\&\quad + \frac{c_{\beta }}{m^2_{h_1}\!-m^2_{h_3}}\left[ s_{\beta }\,{{\mathcal {M}}}_{\text {even},13}^{2}-c_{\beta }\,{{\mathcal {M}}}_{\text {even},23}^{2} \right] . \end{aligned}$$

(3b)

In phenomenologically realistic scenarios, considering e.g.  the constraints placed by LEP on a light Higgs boson  [80], these objects will typically be small, of the order of $\mathord {\lesssim }\,10^{-1}$. However, the Higgs spectrum is only marginally controlled at tree level, e.g.  $m^2_{h_{1,2}}$ may be shifted by $\mathord { > rsim }\,100\%$ at 1L, so that $U_{11}$ and $U_{12}$ are complemented by a significant loop-induced mixing (potentially of comparable magnitude to the tree-level values). At 1L, the radiative mixing enters the decay amplitudes via the LSZ reduction as

(4)

where $i\in \{2,3\}$ and ${\hat{\Sigma }}^{(1)}_{1i}$ are the renormalized off-diagonal self-energies at 1L. This expansion remains a priori  valid as long as $\mathcal {Z}_{1i}\ll 1$. In particular, the denominator $m_{h_1}^2\!-m_{h_i}^2$ should be evaluated at the tree level in this object in order to preserve the independence from gauge-fixing parameters after combination with vertex corrections  [41]. We stress that $\mathcal {Z}_{1i}$ is a scheme-, gauge- and field-dependent quantity appearing as an intermediate step in the calculation, so that it should not be over-interpreted. Nevertheless, its physical meaning makes it clear that, the farther this 1L object stands from an estimate using the genuine physical spectrum, the larger the corrections left to higher orders are expected to be. Here, in the case of light states, we observe that 1L (and even 2L) effects would shift the denominator by $\mathcal {O}(100\%)$; this indicates that higher-order corrections to the mixing would be numerically comparable to the 1L version in Eq. (4), which itself competes with the tree-level mixing, as we argued above. This is but one obvious problem of the fashion in which the Higgs mixing is assessed at 1L. In fact, the numerator of $\mathcal {Z}_{1i}$ is also unstable under radiative corrections, because it is calculated with the unrealistic tree-level Higgs couplings and mixing angles. In other words, the loop expansion converges too slowly to claim reliable results at 1L in the perturbative calculation performed in the SUSY model.

One can attempt to capture the contributions of the Higgs mixing to the decay widths in more quantitative fashions. A first strategy would amount to resorting to the mixing formalism described in Refs. [41, 42]. Although $\big |{\hat{\Sigma }}^{(1)}_{12}\big |\ll \big |m_{h_1}^2\!-m_{h_2}^2\big |$ in the considered scenarios, the closeness in mass of $h_1$ and $h_2$ in view of the magnitude of the mass corrections at 1L legitimates the use of this approach: the external momentum entering the self-energies may indeed be expanded in the vicinity of $m_{h_1}^2$, $m_{h_2}^2$ or $\big (m_{h_1}^2+m_{h_2}^2\big )/2$ indifferently. The advantage of this technique is that the 1L mixing is pre-included in a loop-corrected rotation matrix for the tree-level fields, which in particular takes into account the large radiative mass corrections while keeping the dependence on field counterterms and gauge-fixing parameters to a minimum; we refer the reader to Refs. [41, 42] for a more detailed discussion. Nevertheless, this mixing matrix is still calculated with the unrealistic tree-level spectrum, meaning that large higher-order contributions are still expected to correct the off-diagonal self-energies, i.e.  the numerator of $\mathcal {Z}_{1i}$.

Alternatively, we can attempt to adapt the renormalization scheme, in order to yield a tree-level Higgs spectrum closer to the actual physical situation. We have already described above how the mass of the light singlet could be brought OS through a re-definition of $A_{\kappa }$. The status of the mass of the SM-like state is a priori  somewhat more delicate, because, at the tree level, it cannot be set to its physical value through a simple change of renormalization condition on the original parameters of the model.⁶ Nevertheless, following the suggestion of Ref. [41] (see in particular the appendix), one may generalize the Higgs potential of the model to an effective ‘non-SUSY’ version, thus allowing for an OS renormalization of the neutral-Higgs masses. In this approach, one introduces quartic Higgs couplings $\ell _i$, $i\in \{1,\ldots ,7\}$, in the Higgs-doublet sector – additional terms for the singlets could be considered as well, see Ref. [81] – together with their counterterms $\delta \ell _i$, and matches the corresponding model to the SUSY potential.⁷ Yet, in the present paper, instead of following the unwieldy matching conditions derived from the identification of observables as in Ref. [41] – this requires the introduction of a broad set of observables, hence increasing the reliance on calculations performed in the original description – we resort to the more convenient requirement that the bare parameters should be unchanged in both models, i.e.  $\ell _i+\delta \ell _i=\mathcal {O}(\text {2L})$, similarly to the condition that we imposed on $A_{\kappa }$ at the level of the singlet masses. Moreover, given that we specialize in the phenomenology of light states, we need only introduce a non-vanishing $\ell _2$ (the coupling multiplying the new $|H_u|^4$ operator), characterized by OS conditions on the mass of the SM-like Higgs; all the other $\ell _i$ are kept equal to 0 (and $\overline{\text {DR}}$). This choice is not unique but convenient, as it allows for a straightforward determination of the $\ell _i$-s; it is also physically meaningful since the large top/stop corrections to the SM-like mass indeed mostly project onto $\ell _2$. In practice we determine $\ell _2$ by the condition

$$\begin{aligned} \det {\Big [\mathcal {M}^2_{\text {even}} + 2\,\ell _2\,v^2\,s^2_{\beta }\,\mathcal {E}^{22} - M^2_{h^{\text {SM}}}\,\mathbb {1}\Big ]}{\mathop {=}\limits ^{!}}0\,, \end{aligned}$$

(5)

where $\mathcal {M}^2_{\text {even}}$ is the original (NMSSM) $\mathcal {CP}$-even mass matrix at tree level – see Eq. (2) – and $\mathcal {E}^{22}$ is defined by its matrix elements: $(\mathcal {E}^{22})_{ij}=\delta _{i2}\,\delta _{j2}$ for $i,j\in \{1,2,3\}$. The parameter $M^2_{h^{\text {SM}}}$ is the physical squared Higgs mass of the SM-like state derived in the original scheme and taking into account effects beyond 1L (e.g.  $\alpha _t\,\alpha _s$, $\alpha _t^2$ corrections, UV-resummation, etc.  [44,45,46,47,48,49, 82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116]). After taking into account this non-zero $\ell _2$, the Higgs states of the modified scheme are denoted as $\breve{h\,}\!_{I}=\breve{U}_{Ij}\,h^0_j$, $h^0_j\in \{\phi _1,\phi _2,\phi _s\}$ (the $\mathcal {CP}$-even gauge eigenstates), together with the new tree-level diagonalization matrix $\breve{{\mathbf {U}}}$; one of the states of the modified scheme takes the tree-level mass $M_{h^{\text {SM}}}$. The counterterm associated to $\ell _2$ should satisfy $\delta \ell _2\approx -\ell _2$. At the same time, it is constrained by the OS definition of the SM-like Higgs-boson mass: $\breve{\Sigma }_{II}\big (M^2_{h^{\text {SM}}}\big ) - \delta \mathcal {M}^{2\,\text {NMSSM}}_{II} - 2\,\delta \big (\ell _2\,v^2\big )\,s^2_{\beta }\,\breve{U}_{I2}^2$ must have a vanishing real part (up to higher-order effects), where $\breve{\Sigma }_{II}$ represents the diagonal self-energy associated with the field $\breve{h\,}\!_{I}$, and $\delta \mathcal {M}^{2\,\text {NMSSM}}_{II}$ the NMSSM-like counterterm projected onto the $\breve{h\,}\!_{I}$-direction. There is an ambiguity at this level, because we determine $\ell _2$ after including several higher-order effects to the Higgs self-energies, while we compute the decays at 1L order. In these conditions, we regard the choice (the superscript $^{(1)}$ signaling restriction to the 1L order)

$$\begin{aligned} 2\,\delta \big (\ell _2\,v^2\big )\,s^2_{\beta }\,\breve{U}_{I2}^2{\mathop {=}\limits ^{!}} \Re \mathfrak {e}{\left[ \breve{\Sigma }^{(1)}_{II}\big (M^2_{h^{\text {SM}}}\big ) - \delta ^{(1)}\mathcal {M}^{2\,\text {NMSSM}}_{II}\right] } \end{aligned}$$

(6)

as the most consistent one, although it violates the cancellation of $\ell _2+\delta \ell _2$ by the full magnitude of the effects beyond 1L. Alternatively, the following condition, with $I_0$ indexing the SM-like state in the original scheme, would satisfy $\ell _2+\delta \ell _2\approx 0$ almost exactly:

$$\begin{aligned}&2\,\delta \big (\ell _2\,v^2\big )\,s^2_{\beta }\,\breve{U}_{I2}^2 {\mathop {=}\limits ^{!}} \Re \mathfrak {e}{\left[ \breve{\Sigma }^{(1)}_{II}\big (M^2_{h^{\text {SM}}}\big ) - \delta ^{(1)}\mathcal {M}^{2\,\text {NMSSM}}_{II}\right] } \nonumber \\&\quad - \Re \mathfrak {e}{\left[ {\hat{\Sigma }}_{I_0I_0}^{(1)}\big (m^2_{h_{I_0}}\big )\right] } - 2\,\ell _2\,v^2\,s^2_{\beta }\,\breve{U}_{I2}^2\,. \end{aligned}$$

(7)

However, in this case, we would also need to include in the computation of diagrams (e.g.  off-diagonal Higgs self-energies or triple-Higgs vertex) pieces that numerically mimic the impact of the leading 2L contributions. In Higgs decays into SM final states, we find the choice between Eq. (6) or Eq. (7) to have a numerically marginal impact. This concludes the description of this formalism, in which we expect a better convergence of the perturbative series of radiative corrections, because the tree-level spectrum is closer to its physical configuration, hence resums large radiative corrections within the tree-level mixing angles (controlling the Higgs couplings), as well as in the new operator $\ell _2\,|H_u|^4$ encoding the correspondence between spectrum and Higgs-to-Higgs couplings.

Fig. 6

Partial $b{\bar{b}}$ decay widths of the light $\mathcal {CP}$-even state $h^S$ in the scenario CPE1 of Sect. 2.2 with $\lambda =\kappa =0.05$

We now examine the situation in the scenario CPE1 with a small value of $\lambda$. The singlet–doublet mixing remains below $10^{-2}$ at tree level and the 1L mixing between $h^S = h_1$ and $h^{\text {SM}} = h_2$ is of comparable magnitude (though slightly larger, depending on the scheme and point in parameter space): the production of the light singlet at LEP is a priori  suppressed by about $10^{-4}$ as compared to an SM Higgs at the same mass. We focus on the $b{\bar{b}}$ decay channel in Fig. 6. In the plot on the left, all calculations are performed with the original SUSY Lagrangian and the expansion formalism, and only the scheme defining $A_{\kappa }$ is changed: OS condition on the light singlet mass in the blue curve, tree-level singlet mass set to a fixed value (65 GeV in dashed light-green, 15 GeV in dotted dark-green), or the original $\overline{\text {DR}}$  condition in red (failing for masses below 35 GeV, as explained in Sect. 2.2). All predictions provide a very roughly comparable order of magnitude, but the dispersion already indicates the lack of control over the singlet–doublet mixing: occasional cancellations of the predicted decay width reflect destructive interferences between tree-level and 1L amplitudes, which however do not intervene at the same point in parameter space in the different schemes. In particular, the points with $m_{h^S}\! > rsim 75$ GeV lead to a near-degeneracy between $h^S$ and $h^{\text {SM}}$ at tree level, which, however, is very far from the actual kinematical configuration, hence they receive a poor description.

In the plot on the right, $A_{\kappa }$ is always fixed by the OS scheme for the light-singlet mass. For reference, the solid blue curve of the left plot is repeated here; several other approaches are applied to attempt and control the singlet–doublet mixing. The dashed cyan curve is obtained with the original NMSSM Lagrangian, employing the mixing formalism with a loop-corrected rotation matrix. The predicted width is similar, though somewhat suppressed, to those of the plot on the left. The other two curves employ a modified Lagrangian including an $\ell _2$ coupling determined by an OS condition for the mass of the SM-like state: the solid orange line is derived with the strict perturbative expansion while the dashed yellow one adds contributions in the mixing formalism. The corresponding predictions for the decay widths are suppressed with respect to those of the left plot. This can be understood as a consequence of working with states that have well-separated masses already at tree level, hence suppressing the Higgs-mixing contributions mediated by off-diagonal self-energies. Our belief is that mixing effects are more properly resummed in this procedure with OS masses. However, this debate cannot be decided at 1L order and we must therefore admit our incapacity to provide precise results for the decays of the light $\mathcal {CP}$-even singlet in this scenario. All that can be performed is to set an upper bound on the magnitude of the width. We do not show the other decay channels: all the fermionic ones lead to a comparable situation to that of $b{\bar{b}}$; as to the bosonic channels, the description at EW LO can be regarded as even less reliable.

The scenario CPE2 with large $\lambda =0.5$ is considered in Fig. 7. In this case, the 1L mixing between $h^S = h_1$ and $h^{\text {SM}} = h_2$ completely dominates over the tree-level one (of order $\mathord {\sim }\,10^{-2}$): it reaches up to $\mathord {\sim }\,0.4$ in the strict-expansion approach at $m_{h^S}\!\approx 75$ GeV, reflecting the unrealistic situation of near-degeneracy with the $\mathord {\sim }\,88$ GeV SM-like Higgs at the tree level. A more realistic assessment of the mixing via the effective mixing matrix or the OS scheme for the SM-like Higgs returns values of $\mathord {\sim }\,10^{-1}$. This still corresponds to production cross-sections at the percent level of that of a SM Higgs boson at LEP. However, given that the tree-level mixing is close to zero and the 1L mixing subsequently appears as the LO, observing also that the latter is ill-controlled, i.e.  strongly dependent on the chosen scheme, no clear predictivity can be reached at the level of the decay widths. In fact, the dominant radiative mixing generates a negative contribution to the width that is larger than the tree-level width; positivity in this scenario can only be reached by also including a 1L$^2$ term, but this in turn indicates that the achieved prediction is compatible with 0. The various approaches for modeling the Higgs mixing then lead to relatively diverse results, of which only a rough upper bound on the decay widths can be extracted. This strong disparity is illustrated in Fig. 7 for the $b{\bar{b}}$ channel. For the blue curve, with only $h^S$ renormalized OS, the mixing with the SM-like state is unrealistically intense, especially when $m_{h^S}\!\rightarrow m_{h^{\text {SM}}}$, i.e.  at the rightmost end of the plot. If the masses of both $h^S$ and $h^{\text {SM}}$ are processed OS (orange line), the radiative mixing remains much smaller and leads to a better-behaved prediction. These trends persist in the mixing formalism (dashed curves), where we should see the impact of the tree-level description of the mixing angles on the derivation of the mixing matrix. Nevertheless, the general shape of the dashed curves clearly contradicts the destructive interferences between Born-level and 1L amplitudes that are suggested by the strict expansion approach. We must thus conclude that the predicted widths for the light singlet in this scenario are once again dominated by the uncertainties.

Fig. 7

Partial $b{\bar{b}}$ decay widths of the light $\mathcal {CP}$-even state $h^S$ in the scenario CPE2 of Sect. 2.2 with $\lambda =10\,\kappa =0.5$

Table 1 SM input. Masses correspond to pole values, except when indicated as $\overline{\text {MS}}$

As long as one focuses on points with suppressed singlet–doublet mixing at tree level, the radiative mixing can be expected to be comparatively large, since it is only protected by the EW symmetry, which is clearly broken at the considered scales. Then, as we showed above, a quantitative assessment of the singlet–doublet mixing is problematic at 1L, forbidding precise predictions for the decays of the singlet-dominated state until higher-order corrections are fully available. Cleaner results are likely to emerge in scenarios with a larger singlet–doublet mixing at tree level and dominant with respect to the radiative mixing. Such scenarios are however of lesser phenomenological interest.

4 Properties of the SM-like Higgs boson

The characteristics of the SM-like Higgs boson are of particular interest, since experiments have been accumulating data on corresponding observables. While we do not aim at a comprehensive discussion of the associated phenomenology in the NMSSM here – our benchmarks are only meant for illustration of the calculation of radiative corrections – we can attempt to assess to which extent the presence of new physics (light or heavy) affects the properties of the Higgs boson at the radiative level. A detailed understanding of the precision achieved in corresponding calculations then appears as critical in order to avoid over-interpreting apparent deviations in the predicted central values. We thus discuss these features in some details below.

4.1 SM input and SM Higgs decays

SM fermion masses and EW measurements determine a significant portion of the parameters of the model. Here, we use comparatively recent experimental input  [7, 117], which is summarized in Table 1. Parameters that are given in the minimal subtraction scheme ($\overline{\text {MS}}$) are such only from the perspective of QCD, and not with respect to EW, Yukawa or SUSY corrections. We perform the $\overline{\text {MS}}$ running for quark masses and the strong coupling constant to 4L order (as well as the $\overline{\text {MS}}$–OS conversion), employing to that purpose the code RunDec  [118, 119]. By varying the input of Table 1 within experimental error bands and studying the impact of this variation on observables, one would derive the associated parametric uncertainty: we will not discuss the latter below, and regard the SM input as though it were ‘exact’.

Our processing of the EW input is the one commonly employed in SM and BSM calculations, but we detail it here for completeness. All the EW quantities (gauge couplings, masses of the EW gauge bosons, weak mixing angle, EW v.e.v. – hence Yukawa couplings – etc.) are defined from the following three input quantities: the fine-structure constant $\alpha$ and the masses of the EW gauge bosons $M_{W,Z}$. The latter two are renormalized OS at their experimentally measured value. $\alpha$ is renormalized in the Thomson limit, so that $\alpha (0)$ would appear as the natural input. However, due to the sizable dependence of the associated counterterms on hadronic physics, it is customary to prefer either the measurement at the Z pole, $\alpha (M_Z)=\alpha (0)\big (1-\Delta \alpha (M_Z)\big )^{-1}$, or the Fermi constant, $\alpha _{G_F}\equiv \big (\sqrt{2}/\pi \big )\,G_F\,M_W^2\,\big (1-M_W^2/M_Z^2\big )=\alpha (0)\,(1+\Delta r)$, as more robust input for EW physics: the non-perturbative effects in the electric charge counterterm are then absorbed within the calculable quantities $\Delta \alpha (M_Z)$ or $\Delta r$.

The shift $\Delta \alpha (M_Z)\approx 5.9\cdot 10^{-2}$ can be extracted from data of $e^+e^-$ scattering with means of the optical theorem  [120, 121]. The corrections to the muon decay width, $\Delta r$, have been computed in the NMSSM  [122,123,124]. Here, we define $\Delta r=\Delta r_{\text {SM}}^{\text {(4L)}}+\big (\Delta r_{\text {NMSSM}}^{\text {(1L)}}-\Delta r_{\text {SM}}^{\text {(1L)}}\big )$; the object $\Delta r_{\text {SM}}^{\text {(4L)}}\approx 3.76\cdot 10^{-2}$ includes up to leading 4L effects calculated in the SM and is obtained from the fit formulae of Refs. [125, 126], providing a precision of permil level on this quantity. We note in passing that the inclusion of higher-order contributions in the SM, i.e.  the difference $\Delta r_{\text {SM}}^{\text {(4L)}}-\Delta r_{\text {SM}}^{\text {(1L)}}\approx 0.8\cdot 10^{-2}$, could be misleading in observables computed at 1L order, since it is not clear that SM(-like) loop corrections of higher order to such observables would not compensate with those introduced through $\Delta r_{\text {SM}}^{\text {(4L)}}-\Delta r_{\text {SM}}^{\text {(1L)}}$. We regard this as a first source of higher-order uncertainty on the EW corrections. Coming back to the calculation of $\Delta r$, a few classes of higher-order BSM contributions to $\Delta r$ in SUSY models have been computed in Refs. [127,128,129,130] and exploited in the context of the NMSSM before  [123, 124]. Nevertheless, we restrict ourselves to strict 1L contributions from new physics here. The latter typically contribute to $\Delta r$ at the level of $\mathcal {O}(10^{-3})$ in the considered scenarios.

In practice, we present only results obtained with the parameter $\alpha _{G_F}$ as defined above in this paper. Nevertheless, also performing the calculation in the scheme associated with $\alpha (M_Z)$ provides a useful alternative in order to assess the uncertainty associated with the choice of $\alpha$. As $\alpha _{G_F}$ and $\alpha (M_Z)$ differ by $\delta \alpha /\alpha \sim 2.2\%$, the calculation a priori  cannot claim a precision narrower than this value on the last controlled EW order. We count this uncertainty, dominated by effects of SM-type, as being of the parametric class.

Before considering new-physics effects to the Higgs decays, it seems desirable to analyze the situation in the SM beforehand, and evaluate corresponding decay widths at exactly the same order as later in the BSM model to serve as a reference. We consider the following channels (for an SM Higgs boson $H^{\text {SM}}$ with OS mass $M_{H^{\mathrm {SM}}}$):

• Decays into quarks ($b{\bar{b}}$, $c{\bar{c}}$) and leptons ($\tau ^+\tau ^-$): we evaluate these channels at the same order as commonly done in the SM  [117], i.e.  we include QCD corrections to 4L order – see e.g.  Refs. [72, 73] or the summary in Ref. [74], taking also finite-fermion-mass effects into account at 1L  [70, 71] – as well as QED and EW corrections at 1L. The corresponding theoretical uncertainty has been evaluated to below $1\%$ in Ref. [117] at the level of the branching ratios, which are expected to be largely insensitive to the choice of input for $\alpha$. Our results for the fermionic Higgs decay widths employing $\alpha _{G_F}$ are consistent with those published by the LHC Cross-section Working Group  [117, 131], obtained with HDECAY  [132, 133], up to a few permil. However, we stress that the choice of $\alpha (M_Z)$ for input affects the decay widths by 1–$2\%$, to which further parametric uncertainty should be added, from e.g.  $\alpha _s$ or the fermion masses – the latter typically amount to the percent level  [131].

• Decays into EW gauge bosons (WW, ZZ): for an SM Higgs boson, these decays proceed off-shell and in fact approximate the more complete decay channels with four fermions in the final state. Given that a full 1L analysis in the NMSSM is beyond our current means, we employ a tree-level description – see e.g.  Eqs. (37–39) in Ref. [74]. The standard in the SM is given by the calculation of Prophecy4f  [134,135,136], with an estimated theoretical uncertainty below percent  [117]. The corrections to the tree-level results are of order $5\%$. In our NMSSM scenarios, we rescale the results for the SM-like Higgs accordingly, which is a way of putting SM-like effects under control.

• Radiative decays into gauge bosons ($\gamma \gamma$, gg): we evaluate these decay widths at leading EW order, including $\mathcal {O}(\alpha _s)$ corrections to the diphoton channel  [75] and up to $\mathcal {O}\big (\alpha _s^5\big )$ corrections to the digluon channel  [137] – the $\mathcal {O}\big (\alpha _s^3\big )$ SUSY corrections  [76] will be included in the NMSSM as well. We directly consider the digluon width with radiation of five light-quark flavors, even though at least bottom (and possibly charm) quarks should lead to a distinguishable final state. In these conditions, the uncertainty from EW higher orders is dominant, amounting to $\mathcal {O}(20\%)$ for the diphoton channel. Comparison with HDECAY, where 2L EW corrections are included for the SM Higgs decays, reveals that the leading EW order for the diphoton channel has an improved predictivity after rescaling of the decay width by a factor $\big (\alpha (0)/\alpha _{G_F}\big )^2$; we apply this correction. Our prediction in the digluon channel remains $\mathord {\sim }\,6\%$ off. Beyond its impact on the total width, this latter decay channel is mostly relevant as an estimate of the effective Higgs coupling to gluons, which is relevant for Higgs production at hadron colliders.

We present our results for the decays of a SM Higgs boson with a mass of 125.25 GeV in the second column of Table 2. We stress that they are not meant as state-of-the-art evaluations of these Higgs properties in the SM, but only as reference for comparison with BSM results that are calculated at a similar order in the loop expansion. There, we consider the decay widths rather than the branching ratios, the latter being more useful for comparison with experiment. The reason for this choice is that the channels known with least precision in our calculation (bosonic channels) contaminate the total width, hence increase the theoretical uncertainty for the more precisely known (fermionic) channels. In addition, non-standard channels also contribute to the total width in the NMSSM. Thus, a comparison with the SM is easier at the level of the decay widths.

4.2 Mass and decays of the SM-like Higgs boson into SM particles

Now we turn to the SM-like Higgs boson of the considered NMSSM scenarios. A first observable that has received considerable attention is the mass of this particular state  [10]. Radiative corrections of Yukawa-type have a sizable impact on these predictions. We are in a position to include corresponding effects at the 2L level and resum UV logarithms for heavy-squark spectra according to the description in Ref. [42]. EW and NMSSM-specific effects are included at 1L. A large value of $\lambda$ generates a contribution already at tree level, which is mostly relevant for moderate $t_{\beta }$; in the considered benchmarks, this amounts to an effect of at most a few GeV in the PQ-scenario with $t_{\beta }=5$ and $\mathord {\sim }\,20$ GeV in the scenario CPE2 with $t_{\beta }=2$. On the other hand, we do not observe any significant NMSSM-specific effect at 1L in the considered scenarios. The properties of the squark sector offer an obvious handle on the SM-like Higgs mass observable, almost independently from the characteristics of the singlet Higgs, and we chose soft masses and trilinear couplings so as to accommodate a central value of the mass prediction compatible with 125.25 GeV. Higher-order uncertainties are dominated by EW logarithms at 2L, large squark-mixing effects, as well as NMSSM-specific contributions of 2L order. All these factors accumulate to a higher-order uncertainty at the GeV level  [113, 138, 139]. Furthermore, alternating the schemes for the input of $\alpha$ between $\alpha _{G_F}$ and $\alpha (M_Z)$ results in variations of $\mathcal {O}(1\%)$, dominated by the fluctuations of the uncorrected $\alpha _q\,\alpha _s$ contributions. In turn, these theoretical and parametric uncertainties on the mass determination can be regarded as a parametric uncertainty at the level of the Higgs decays (which we ignore below).

The SM-like decay channels listed in Sect. 4.1 can be considered to the end of testing the emergence of BSM physics in Higgs interactions. New physics intervenes here in two different fashions:

• 1. SUSY and THDM effects decouple in the limit of heavy $M_{H^{\pm }}$ and $M_{\text {SUSY}}$. The EW symmetry protects the relation between the mass of the SM fermions or gauge bosons and the couplings of the SM-Higgs component (i.e.  the exact $SU(2)_{\text {L}}$ partner of the Goldstone bosons) to these same particles; radiative corrections projecting onto that direction are thus ‘invisible’ to a large extent. Contributions to orthogonal directions are suppressed as $v^2/M_{H^{\pm }}^2$, where only the THDM sector causes deviations at tree level. The SUSY sector intervenes at the loop level, hence generates contributions that are suppressed with an additional loop factor, although partially compensated by a UV-logarithm. In the scenarios under consideration, with $M_{H^{\pm }}$ and $M_{\text {SUSY}}$ in the TeV range, the contributions from heavy new physics are thus expected to remain at the percent level, i.e.  they are at most comparable to the theoretical uncertainty achieved in the calculation of the decay widths.

• 2. Light-singlet states may affect the phenomenology of the SM-like Higgs in several fashions. First, they open new decay channels, which we discuss in the next subsection. Then, mixing of the SM-like Higgs with a singlet-dominated state leads to an exchange of properties between the two states: with $\mathcal {CP}$-conservation, this effect concerns only scenarios with a light $\mathcal {CP}$-even singlet. We have discussed in Sect. 3.2 how the lack of control on this mixing at 1L forbade a quantitative determination of the decay widths for the singlet-dominated state. The situation of the SM-like Higgs is less critical, since the Born-level amplitude is expected to be dominant. However, the accuracy of the predicted decay widths is bound to suffer from the unclear status of the mixing.

  These are the essential effects that we aim at assessing in the considered scenarios.

The evaluation of the decay widths follows the description given in Sect. 4.1 at the level of the SM-like Higgs boson, i.e.  includes complete 1L contributions (now also involving the SUSY and extended-Higgs sectors) – except for the WW and ZZ channels, which remain at tree level – as well as higher-order QCD corrections to the same available order as in the SM. However, several new features need to be considered when interpreting the results and estimating the uncertainty budget:

• In order to avoid introducing artificial symmetry-violating effects and explicit dependence of the observable on the choice of field renormalization, one should evaluate the loop functions in the expansion formalism described in e.g.  Refs. [41, 42]. In other words, the external momenta entering the loop functions need always be expanded in the vicinity of the tree-level spectrum.

• As we observed before, the mass of the SM-like Higgs boson of the SUSY model cannot be renormalized OS using only the original parameters of the SUSY Lagrangian, in contrast to the situation in the SM. As is well-known, the tree-level mass is typically below $M_Z$, even though NMSSM-specific effects can circumvent this bound at large $\lambda$ and low $t_{\beta }\lesssim 2$. This means that the tree-level spectrum is always significantly away from the actual kinematical configuration, and that 1L (and even 2L) mass-shifts can be comparable to the tree-level mass. This is of limited consequence for processes where EW effects are controlled at NLO, i.e.  the Higgs decays into SM fermions in our description. However, we have already seen in Fig. 5 that this feature is problematic for the diphoton and digluon channels, where only the EW LO is known. This difficulty can be circumvented by upgrading the tree-level Higgs mass to its physical value in all its occurrences, i.e.  in external momenta as well as in the Higgs potential used in the contributing loops. The latter can be achieved straightforwardly in the digluon and diphoton case as only the Higgs-couplings to charged Goldstone bosons need an upgrade then  [39, 140] – it is much more involved in the general case  [41]. Here, we resort to the ‘cleaner’ method described in Sect. 3.2, introducing new parameters in the Higgs potential that allow for an OS renormalization of the SM-like Higgs mass. For all decay channels, comparison of the widths derived with the original spectrum and those obtained with an OS SM-like Higgs allows to estimate the impact of the unrealistic tree-level spectrum on the accuracy of the predictions.

• We must also account for the limited control over the Higgs mixing at 1L in scenarios containing a light singlet-dominated state $h^S = h_1$, as explained in Sect. 3.2. Once again, we can consider several approaches in order to assess the impact of these mixing effects at the level of the decays of the SM-like Higgs $h^{\text {SM}} = h_2$: first, given that $\big |{\hat{\Sigma }}^{(1)}_{21}\big |\ll \big |m_{h_2}^2\!-m_{h_1}^2\big |$ in the considered scenarios, the strict perturbative expansion generally falls in its regime of validity; then, it is also possible to resort to the mixing formalism of Refs. [41, 42], which is legitimate in view of the comparable magnitude of tree-level and 1L contributions to the mass-splitting; finally, we can redefine the Higgs potential so as to allow for an OS definition of the relevant Higgs masses, as explained above. We reserve our opinion as to which method provides the most reliable results, a question that can only be decided through the inclusion of higher-order contributions to the decay widths.

• In the case of Higgs decays into EW gauge bosons, where the actual calculation is at tree level, the rescaling by the more complete SM result of Prophecy4f remains somewhat meaningful in that non-SM-Higgs components do not couple to W-s and Z-s at tree level, so that corresponding BSM contributions (by new particles with mass $M_{\text {BSM}}$) would be suppressed by both a factor $v^2/M_{\text {BSM}}^2$ and a loop factor. Nevertheless, the difficulty of quantitatively assessing the singlet–doublet mixing in the presence of a light $\mathcal {CP}$-even singlet limits the reliability of such a tree-level estimate in corresponding scenarios. In addition, we stress that the light singlets open up new contributions to the four-fermion decays: these are counted separately and discussed in the following subsection.

For all these reasons, it is clear that the precision achieved in the calculation of the decay widths is necessarily inferior to that associated with the SM at the same order. A reduction of the theoretical uncertainties below percent level would thus require the inclusion of higher orders. In the presence of a light $\mathcal {CP}$-even singlet mixing with the SM-like state, the higher-order uncertainty may be even significantly larger than percent, due to the lack of control on radiative mixing.

Table 2 Decay widths of the SM-like Higgs candidate in the standard channels, for the SM (second column) and the scenarios of Sects. 2 and 3. The mass of the SM-like Higgs is 125.25 GeV. The five first rows provide details on the chosen input and scheme: value of $A_{\kappa }$ in the original scheme, chosen renormalization of $A_{\kappa }$, $\ell _2$ and $\hat{\kappa }^2$ for the calculation (see text for the definition of these couplings), use of a mixing formalism for the system of the $\mathcal {CP}$-even singlet-like and SM-like Higgs bosons

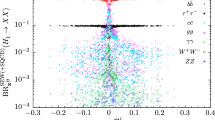
Predictions for the decay widths into SM-particles (we do not consider light fermions or $Z\gamma$) are collected in Table 2 for the considered scenarios. As these properties hardly depend on the variation of $A_{\kappa }$ that we performed in the earlier sections (at least as long as the tree-level masses of $h_1$ and $h_2$ are not too close), we only show results for the value $A_{\kappa }{\mathop {=}\limits ^{!}}-1.5$ GeV in the R-symmetry-inspired scenario, $-40$ GeV in the PQ-inspired scenario, $-1994$ GeV in the scenario CPE1 with $\lambda =\kappa =0.05$, $-438$ GeV in the scenario CPE2 with $\lambda =10\,\kappa =0.5$. We observe that all the decay widths are consistent with an SM interpretation (see second column) within a few percent (i.e.  a magnitude comparable to the theoretical uncertainty).

For the scenario in the R-symmetric limit, we perform the calculation of the decay widths both with the original SUSY Lagrangian and in the version with extended Higgs potential and OS SM-like Higgs (i.e.  $\ell _2\ne 0$): numerical differences are minor except for the diphoton and digluon channels, where the version with extended Higgs potential is a priori  more trustworthy. For the fermionic decays, we observe that the sizable difference between tree-level and physical masses for the SM-like Higgs $h^{\text {SM}} = h_1$ costs somewhat more than $0.5\%$ on the accuracy of the prediction. Now turning to the phenomenology, the comparison of the fermionic decay widths seems to indicate that the SM-like Higgs of this scenario has a slightly increased affinity for decays into down-type fermions. However, the magnitude of this effect ($\mathord {\sim }\,2\%$) is relatively small, comparable in size to the uncertainty, and might not be preserved at higher order. Similarly, the small increase of these fermionic decay widths as compared to their SM counterparts is not really exploitable at the level of the branching ratios, since the apparent constancy of the decay widths into EW gauge bosons is likely an artifact of the tree-level description in these channels. The slight reduction of the digluon decay width agrees with the impression of a somewhat reduced coupling to top quarks, even though the large theoretical uncertainty there forbids any definite conclusion. Similarly, little can be deduced from the diphoton decay channel at 1L, as the large range of variation between the OS and original schemes ($\mathord {\sim }\,30\%$) illustrates the significant uncertainties at this order of the calculation. The rather clean situation in this scenario without a light $\mathcal {CP}$-even singlet-dominated state thus demonstrates the deterioration of the precision due to the instability of the Higgs potential with respect to radiative corrections in SUSY-inspired models. Working in an effective framework where the various Higgs masses can be renormalized OS probably improves the prediction, since it allows to expand the perturbative series from a position in parameter space that is closer to the physical situation, hence promises a faster convergence of the series. On the other hand, such a procedure explicitly violates the form of the softly-broken SUSY potential, implying a lesser regularity of the radiative corrections.

For the scenario in the PQ-limit, the situation is complicated by the presence of a comparatively light $\mathcal {CP}$-even singlet $h^S = h_1$ with tree-level mass $\mathord {\sim }\,50$ GeV and $\mathord {\sim }\,90$–100 GeV at 1L. This state has a coupling to EW gauge bosons at the level of $10^{-2}$ (dominated by 1L effects) of that of a SM Higgs at the same mass, so that its production at LEP is heavily suppressed. In this scenario, the impossibility to reliably quantify the mixing with the SM-like state $h^{\text {SM}} = h_2$ at 1L order is illustrated by the wide spread of predictions in the fermionic channels, reaching $\mathord {\sim }\,3\%$ (for channels supposedly known with better than $1\%$ accuracy in the SM, discarding the parametric uncertainty). Here, we considered on one side the strict expansion formalism, with the original Lagrangian, with an OS SM-like Higgs or with both an OS SM-like Higgs and an OS $\mathcal {CP}$-even singlet, on the other side, the mixing formalism with the original Lagrangian or with an OS SM-like Higgs. As explained above, the OS condition on the SM-like Higgs mass is obtained through the introduction of a non-vanishing $\ell _2$. To renormalize also the $\mathcal {CP}$-even singlet mass OS in this scenario, we introduce an additional quartic singlet term ${\hat{\kappa }}^2\,|S|^4$ to the Lagrangian, together with its counterterm $\delta {\hat{\kappa }}^2\approx -{\hat{\kappa }}^2$, in a very similar fashion ($A_{\kappa }$ is already needed to control the light $\mathcal {CP}$-odd mass). This choice is natural as the mass of the $\mathcal {CP}$-even singlet indeed proceeds mostly from such a quartic coupling in the PQ-limit. All these operations a priori  aim at controlling the mass-splitting and Higgs mixing already at tree level. Simultaneously, by altering the strength of the Higgs coupling, the OS procedures also slightly modify the magnitude of the 1L corrections: these effects are a priori  legitimate, provided the added operators adequately model the impact of the radiative corrections. In contrast, the mixing formalism accounts for the modified mass-splitting without altering the strength of the Higgs couplings. These differences in treatment account for the disparity of the predictions, which can only be resolved after inclusion of full higher-order corrections to the Higgs decays. Once again, the 1L EW description of the digluon and diphoton decay widths proves insufficient to accurately characterize these channels.

In the scenario CPE1 with a light $\mathcal {CP}$-even Higgs and small $\lambda$, the various considered approaches give very similar results in the fermionic channels. The question of working with an SM-like Higgs $h^{\text {SM}} = h_2$ that is renormalized OS or that possesses the far-away tree-level mass of the SUSY potential affects these decay widths by at most a few permil. Indeed, although the singlet–doublet mixing is not well known in absolute value for this benchmark, its general order of magnitude at tree and 1L level, $U_{21}=\mathcal {O}(10^{-2})=\mathcal {Z}_{21}$, cannot significantly threaten the dominant SM-like amplitude – which it affects as $\mathord {\sim }\,\big (1-1/2\,\mathcal {Z}_{21}^2\big )\,\mathcal {A}^{\text {SM}}$. The resulting effects thus remain negligible. This situation contrasts violently with that of the singlet-dominated state $h^S = h_1$, which we presented in the previous section. The digluon and diphoton decay channels still illustrate the impact of the tree-level description inherited from the SUSY construction (which is quite different from the physical situation in this scenario) on the precision of the radiative widths.

In the scenario CPE2 with large $\lambda$, the impact of the mixing effect is larger than in CPE1, and leads to a dispersion of the predicted decay widths at the percent level. Nevertheless, the general order of magnitude of the decay widths for the SM-like state $h^{\text {SM}} = h_2$ is once again under control (contrarily to the case of the light singlet $h^S = h_1$).

4.3 Interplay with the light singlets

The presence of light-singlet states $a^S$ ($\mathcal {CP}$-odd) or $h^S$ ($\mathcal {CP}$-even) modifies the phenomenology of the SM-like Higgs $h^{\text {SM}}$. The most obvious effect consists in the opening of the kinematical window for the unconventional decay into a pair of light singlets. The latter could be sizable, in general, as the mass scales in the Higgs potential are frequently larger than those of SM particles. In such a case, the properties of the SM-like state would be shadowed by the unconventional channels, leading to inconsistency or tension with the experimental measurements. At the technical level, the calculation of the Higgs-to-Higgs decays raises a difficulty that is not unlike the one discussed in Sect. 3. The evaluation of the loop-functions with LoopTools is indeed problematic if the tree-level Higgs masses verify $m_{h^{\text {SM}}}\!<2\,m_{a^S\!,h^S}$: this results in an effective (unphysical) upper limit on the mass of the light singlet allowing for the calculation of the decay width. An obvious fix, similar to our strategy enabling the mass determination in pseudo-tachyonic regions, consists in restricting ourselves to renormalization schemes for $A_{\kappa }$ where the considered decay is kinematically allowed already at tree level. Below, we consider two schemes where the singlet mass is set to $\mathord {\sim }\,43.5$ GeV (scheme A$^{\prime }$) or $\mathord {\sim }\,3$ GeV (scheme B$^{\prime }$) at tree level. In addition, if we allow for quartic Higgs parameters beyond the SUSY potential, it becomes possible to renormalize both the light singlet and the SM-like Higgs OS, as we discussed before, in which case the tree-level masses trivially satisfy the kinematical conditions already at tree level. On the other hand, the recourse to the mixing formalism in the presence of light $\mathcal {CP}$-even singlet-dominated states is made about impossible by the technical difficulty in evaluating the three-point functions, as also $m_{h^S}\!>2\,m_{a^S\!,h^S}$ would then be needed for competitive use of LoopTools.

Fig. 8

Predictions for the decay widths $\Gamma [h^{\text {SM}}\rightarrow a^Sa^S]$ (first row) and $\Gamma [h^{\text {SM}}\rightarrow Z\,a^S]$ (second row) in the scenarios with light pseudo-scalars of Sect. 2.1: PQ-limit (left) and R-symmetric limit (right). Several schemes are considered: a without modifying the Higgs potential, $A_{\kappa }$ is fixed so that the tree-level mass of the light $\mathcal {CP}$-odd state is kept equal to 43.5 GeV (scheme A$^{\prime }$; dashed green curves) or to 3 GeV (scheme B$^{\prime }$; dotted green curves). b after introduction of a coupling $\ell _2$ to the Higgs potential, the mass of the SM-like Higgs is renormalized OS, while $A_{\kappa }$ is fixed by the OS condition on the mass of the light $\mathcal {CP}$-odd singlet (orange curves). c in the PQ-limit, in the presence of a light $\mathcal {CP}$-even Higgs, the mass of the latter can also be brought OS after introduction of a quartic singlet coupling ${\hat{\kappa }}^2$ (pink line)

In the scenarios with light $\mathcal {CP}$-odd Higgs $a^S = h_4$ that we introduced in Sect. 2.1, the approximate symmetries imposed on the Higgs potential constrain the triple-Higgs couplings $g^{\text {PQ}}_{h^{\text {SM}}a^Sa^S}$ (PQ-limit) and $g^{R}_{h^{\text {SM}}a^Sa^S}$ (R-symmetry limit). Under the assumption of a subleading doublet component in the light singlet and a subleading singlet component in the SM-like state, it is possible to derive

$$\begin{aligned}&g^{\text {PQ}}_{h^{\text {SM}}a^Sa^S}\! \approx 9\,\sqrt{2}\,\kappa \,\lambda \,v\,s_{\beta }\,c_{\beta }\,, \end{aligned}$$

(8a)

$$\begin{aligned}&g^{R}_{h^{\text {SM}}a^Sa^S}\! \approx \frac{3\,\lambda ^2\,v}{2\,\sqrt{2}\,\kappa \,\mu _{\text {eff}}}\nonumber \\&\quad \times \left\{ 6\,\kappa \,s_{2\beta }\left( \frac{M_A^2\,s_{2\beta }}{2\,\mu _{\text {eff}}} - \frac{\kappa }{\lambda }\,\mu _{\text {eff}}\right) + \left( \lambda - \kappa \,s_{2\beta }\right) A_{\kappa }\right\} . \end{aligned}$$

(8b)

It thus appears that these couplings are proportional to those parameters that vanish in the exact R-symmetry or PQ-limits. However, with our particular choice of U(1)-breaking parameters, it is clear that $g^{R}_{h^{\text {SM}}a^Sa^S}$ receives an extra $\lambda \,v/\mu _{\text {eff}}$ suppression while $g^{\text {PQ}}_{h^{\text {SM}}a^Sa^S}\!=\mathcal {O}(m_b)$: consequently, the unconventional decay channel is potentially important in the PQ-inspired scenario despite the coupling being apparently protected by a symmetry. In this latter case, however, the radiative corrections are also likely to unsettle the tree-level picture, because of the proximity in mass of the $\mathcal {CP}$-even singlet and the SM-like state: the assumption of a negligible singlet component in the SM-like Higgs then appears as a fine-tuning matter and can be challenged by mixing effects at the loop order. Unfortunately, these are ill-controlled at 1L, as already explained before, and would require a higher-order calculation for a quantitative estimate of their impact on the phenomenology of the considered scenario.

In the first row of Fig. 8, we consider the Higgs-to-Higgs decay $h^{\text {SM}}\!\rightarrow a^Sa^S$ in the two scenarios with light $\mathcal {CP}$-odd Higgs $a^S = h_4$, with approximate PQ- (left) or R-symmetry (right). Calculations in scheme A$^{\prime }$ and B$^{\prime }$ give very similar predictions with deviations at typically $1\%$ (dashed and dotted green lines). 1L effects amount to $\mathcal {O}(10\%)$ in the PQ-like benchmark and a few percent in the R-symmetric scenario. Therefore, the inclusion of radiative corrections does not destabilize the tree-level amplitudes in these schemes. Differences are more marked if we renormalize both the $\mathcal {CP}$-odd singlet and the SM-like Higgs OS (orange), especially in the PQ-scenario, where the decay width is reduced. This effect is not completely unexpected as the resummation of mass effects in the Higgs potential simultaneously affects the Higgs-to-Higgs couplings, and the PQ-scenario is more sensitive to radiative corrections due to the presence of the light $\mathcal {CP}$-even singlet at $\mathord {\sim }\,100$ GeV. Renormalizing also the mass of the latter OS (pink curve) further widens the scope of predictions for the Higgs-to-Higgs decay. We must thus conclude that the inclusion of higher orders is needed to control the uncertainties of about $100\%$ for this channel in the PQ-inspired scenario – while the situation is comparatively tame in the scenario with approximate R-symmetry. Now looking at the magnitude of the predicted $h^{\text {SM}}\!\rightarrow a^Sa^S$ decay width, we observe that it remains below $2\%$ of the total width of the SM Higgs, in the R-symmetric scenario, thus defying the sensitivity of detection at the LHC. In the PQ-scenario, however, $\Gamma [h^{\text {SM}}\!\rightarrow a^Sa^S]$ could reach $\mathord {\sim }\,1$ MeV at low $M_{a^S}$, leading to tensions with the measured Higgs properties. Nevertheless, as we stressed above, the large theoretical uncertainty does not allow to unquestionably associate this phenomenology to the investigated point in parameter space.

Another possible decay channel is $h^{\text {SM}}\!\rightarrow Z\,a^S$. In this case, given that $m_{h^{\text {SM}}}\!\lesssim M_Z$ at tree level, the difficulty of LoopTools in evaluating loop functions becomes critical, and the only consistent mean at our disposal for computing the decay width (without actually repairing the evaluation of three-point functions) consists in renormalizing the mass of $h^{\text {SM}}$ OS through the introduction of a non-vanishing $\ell _2$ in the Higgs potential. The results are shown in the second row of Fig. 8 (solid orange curves) and the predicted widths are clearly subleading. In the scenario with approximate PQ-symmetry, we may also renormalize the mass of the light $\mathcal {CP}$-even singlet OS via the introduction of the quartic parameter ${\hat{\kappa }}^2$: corresponding results are indistinguishable from those where the mass of $h^S$ is computed in the original scheme (so that we do not present the corresponding results in the plot). On the other hand, the 1L amplitude dominates the process, as is demonstrated by the inclusion of the 1L$^2$ term (dashed orange curves). This shows that the decay width is controlled by effects of 2L order. The situation is less critical in the scenario with approximate R-symmetry (right-hand side) but the 1L$^2$ contribution is still comparable to the strict 1L width, hinting at the need to include 2L corrections for a reliable control of the decay width.

At the 1L order, also the tree-level three-body decays $h^{\text {SM}}\!\rightarrow a^Sf{\bar{f}}$, with $f\in \{b,\tau \}$, are a priori relevant  [40]. However, our results showed no significative contribution at the numerical level beyond that of the OS $h^{\text {SM}}\!\rightarrow a^Sa^S$ channel. This is consistent with the absence of a hierarchy between the masses of the decaying Higgs and of the EW gauge bosons, forbidding the emergence of large Sudakov logarithms. The PQ-inspired scenario also contains a relatively light singlino-dominated state $\chi _1^0$ with mass $\mathord {\sim }\,43$ GeV, allowing for the a priori  invisible decay channel $h^{\text {SM}}\!\rightarrow \chi _1^0\,\chi _1^0$: its width is at $\mathcal {O}{(1\,\text {MeV})}$, and depends on the details of the singlet–doublet mixing. We do not investigate it further in this article, as such channels are not the focus of our discussion.

Fig. 9

Predictions for the decay widths $\Gamma [h^{\text {SM}}\!\rightarrow h^Sh^S]$ in the scenarios with light scalars of Sect. 2.2: CPE1 with low value of $\lambda$ (left), CPE2 with large value of $\lambda$ (right). The considered schemes are comparable to those of Fig. 8

In the scenarios of Sect. 2.2, with a light $\mathcal {CP}$-even state $h^S = h_1$ and no symmetry protecting the Higgs sector (or a symmetry that is broken at a scale comparable to the EW one), the reliability of the predictions for the Higgs-to-Higgs decays at 1L can be expected to be poor, similarly to what was observed for the singlet–doublet mixing in Sect. 3.2. The corresponding results are displayed in Fig. 9. The plot on the left shows that, in the scenario CPE1 with small $\lambda$, the choice of scheme leads to predictions for $\Gamma [h^{\text {SM}}\!\rightarrow h^Sh^S]$ ranging from negligible values to percent level of the SM total width below the kinematical threshold. This suggests in any case that the unconventional Higgs decay would be difficult to identify at the LHC. In the plot on the right, the scenario CPE2 with large $\lambda$ leads, under threshold, to large decay widths, incompatible with the measured Higgs properties. In this case, the Born-level amplitude dominates the process and sets the general scale of the decay width, although the variation induced by the choice of scheme suggests an uncertainty of $\mathcal {O}(10\%)$. $\mathcal {CP}$-conservation forbids the $h^{\text {SM}}\!\rightarrow Z\,h^S$ decay in these scenarios.

As a last comment about the limited precision achieved at 1L in the prediction of these Higgs-to-Higgs decays, we observed that variations on the definition of the quark masses (a priori a 2L matter) were liable to produce shifts of $\mathcal {O}{(100\%)}$ at the level of the widths, e.g.  in scenario CPE1, emphasizing the large uncertainty which we illustrated above only through alternating descriptions of the tree-level Higgs spectra.

5 Conclusions

In this paper, we have shown how apparent tachyonic masses in the tree-level spectrum of the NMSSM could (sometimes) be seen as an artificial problem related to an inadequate choice of renormalization scheme. In the specific case of the $Z_3$-conserving NMSSM with a light $\mathcal {CP}$-even or $\mathcal {CP}$-odd singlet-dominated state, the renormalization of $A_{\kappa }$ is a natural handle on such a mass, and generally allows for the selection of a scheme with a well-defined tree-level spectrum. An OS renormalization of the light state is even possible, and may prove a viable strategy in order to resum logarithms caused by such a light-singlet mass.

The choice of a renormalization scheme with well-defined tree-level spectrum also allows to calculate further physical properties of the light Higgs bosons, in particular their decay widths or their impact on the phenomenology of the SM-like state. There, we showed several additional difficulties that the mismatch between tree-level and physical spectra could cause, in particular the occasional emergence of three-point functions corresponding to ‘unphysical’ configurations (i.e.  with the sum of masses of the decay products exceeding the one of the decaying particle at tree level) or the slow convergence of the perturbative series in the presence of a light singlet-dominated $\mathcal {CP}$-even state (causing masses, mixing matrices and couplings to take tree-level values very far from the actual situation). The use of OS renormalization conditions and the introduction, if needed, of additional non-SUSY parameters to the Higgs potential often alleviate these problems, or at least shed some light on the uncertainties at stake.

The scenarios that we considered in this paper are strictly meant as illustration of the computational issues that we wished to discuss and should not be understood as presenting a comprehensive picture of the NMSSM phenomenology in light-Higgs scenarios. Nevertheless, it is tempting to emphasize a few general features of such physical configurations. The main two effects are the opening of new decay channels for the SM-like state and, if the light state is $\mathcal {CP}$-even, the exchange of singlet and doublet properties via mixing. We have stressed, however, how these two features were not necessarily so well controlled at the considered orders achieved in the calculation.

The theoretical sources of uncertainty are necessarily more numerous in BSM models than in the SM. In this respect, we have discussed how the comparatively large difference between tree-level and physical mass for the SM-like state of the SUSY model could amount to a few permil uncertainty in fermionic decays at NLO and up to $\mathord {\sim }\,30\%$ for the digluon and diphoton decays at (QCD-corrected) LO. While we believe that this feature is improved by the inclusion of additional quartic couplings in the Higgs potential, allowing for an OS renormalization of the relevant masses (but departing from the SUSY framework), this gain for the convergence of the perturbative series is only likely to be verifiable after the actual inclusion of higher-order corrections to the decay widths. In addition, reliable predictions at the level of the branching ratios require homogeneous control over all the leading decay channels, failing which, the uncertainty of the less accurate widths contaminate all other channels. In the case of SM-like states in SUSY models, this suggests going beyond the approximation of off-shell $h^{\text {SM}}\!\rightarrow WW^*,ZZ^*$ at tree-level. Finally, the lack of control over the singlet–doublet mixing in scenarios with a light $\mathcal {CP}$-even singlet could seriously hinder the predictivity of calculations at 1L, both at the level of the properties of the light Higgs and in assessing the deviations with respect to the SM for widths of the SM-like state (in scenarios with large $\lambda$). There again, only higher orders could satisfactorily improve the reliability of the predictions and prepare such scenarios with light singlet-dominated states to a meaningful comparison with precise experimental measurements, as expected from future $e^+e^-$ colliders.

Appendices

Input

See Table 3

Table 3 NMSSM input for the various scenarios considered in this paper. The remaining parameters, $M_1=450$ GeV, $M_2=700$ GeV, $M_3=2$ TeV, and the quadratic soft SUSY-breaking terms governing the sfermion masses, $m_{\tilde{f}}=1.5$ TeV, are not varied. The renormalization scale for $\overline{\text {DR}}$  parameters is $m_t$

Regularization of the tachyonic lagrangian with a mass cutoff

In this appendix, instead of regularizing the tachyonic tree-level mass by a scheme transformation on $A_{\kappa }$, we directly insert mass-cutoffs $\mu _{h^S}$ and $\mu _{a^S}$ in the lagrangian density:

$$\begin{aligned} \mathcal {L}_{\text {NMSSM}}\rightarrow \mathcal {L}_{\text {NMSSM}} - \tfrac{1}{2}\left( \text {max}[\mu ^2_{a^S},m^2_{a_S}] - m^2_{a_S}\right) \big (a^S\big )^2\nonumber \\ - \tfrac{1}{2}\left( \text {max}[\mu ^2_{h^S},m^2_{h_S}] - m^2_{h_S}\right) \big (h^S\big )^2,\nonumber \\ \end{aligned}$$

(9)

as implemented in e.g.  NMSSMTools. The mass shifts are then correspondingly subtracted from the 1L corrections to the masses. Due to the small doublet component contained in the light singlet-dominated state, this operation violates the gauge symmetry, so that the considered lagrangian is no longer renormalizable. As a consequence, 1L amplitudes require an ad hoc renormalization to achieve UV-finiteness, with observables explicitly depending on this unphysical UV-regulator. In practice, we insert an $\overline{\text {MS}}$-like counterterm together with a logarithmic finite piece $\ln \mu _R^2/\mu _{\text {UV}}^2$ (resetting the renormalization scale $\mu _R$ to $\mu _{\text {UV}}$ for this specific counterterm), and study the dependence on this UV-regularization through variations of $\mu _{\text {UV}}$.

Obviously, the loss of renormalizability could have dramatic consequences for the predictivity of the calculations performed with this recipe. This is why we prefer a regularization based on a scheme conversion for the parameter $A_{\kappa }$. Nevertheless, if the regularized mass indeed corresponds to a singlet-dominated state (which is the realistic scenario in practice), the violation of the EW symmetry, hence the dependence on the UV-cutoff, is suppressed in proportion to the small doublet component squared of the light state, and also in proportion to the size of the shift between IR-cutoff and tachyonic tree-level mass-squared. This could still have a large impact on observables that are very sensitive to EW symmetry breaking. However, as far as Higgs masses are concerned, one can anticipate only mild consequences.

Fig. 10

Mass shifts between the two different methods for regularizing tachyonic tree-level masses are shown for the scenario of Fig. 2. The IR-cutoffs for scheme A (orange), $\mu _{a^S}=59$ GeV, and scheme B (blue), $\mu _{a^S}=2.9$ GeV, are set to the same values as derived from the cutoffs on $A_{\kappa }$ in Sect. 2.1. The UV-cutoff for the unphysical counterterm in the method of direct mass regularization is set to the tree-level Higgs mass (solid), or the SUSY scale at $\mathord {\sim }\,1.5$ TeV (dashed)

We illustrate this discussion with Fig. 10, where we consider the mass of the light $\mathcal {CP}$-odd Higgs in the scenario of Fig. 2. More precisely, we compare the mass predictions at 1L by the two different methods, employing $A_\kappa ^{\text {mod}}$ or $\mu _{a^S}$, when using the same value of the regularized tree-level mass. The difference of both predictions, $\Delta M_{a^S}^{\text {X}}$, is displayed for scheme A (orange) and scheme B (blue) of Sect. 2.1. The UV-cutoff $\mu _{\text {UV}}$ is varied between the light Higgs mass at tree level, $\mu _{a^S}\in \{59\,\text {GeV},\,2.9\,\text {GeV}\}$, and the SUSY scale at $\mathord {\sim }\,1.5$ TeV, leading to the band of predictions between the solid and dashed lines. We observe that the typical magnitude of the shifts remains of a size that is comparable to the uncertainty resulting from the choice of scheme in Fig. 2. A direct regularization of the mass thus leads to numerically acceptable results in this scenario. In addition, we see that the shifts in the results become larger for higher values of the mass-cutoff (orange curves), where the explicit symmetry-breaking parameter is larger. It is thus desirable to maintain the mass-cutoff to values as low as possible.

We will not discuss here the additional dependence of the mass observable on gauge-fixing. In spite of the comparatively limited consequences of non-renormalizability on the mass observable at the numerical level (in this example), we advise caution in the use of such a symmetry-breaking regularization. We also stress that, through an altered connection between masses and couplings, the introduction of a mass-cutoff represents an independent source of breaking for the approximate R- or PQ-symmetries.