1 Introduction

One of the intriguing asymmetries in nature is the empirical absence of magnetic monopoles. Their nonexistence breaks the Maxwellian duality symmetry. Their theoretical existence can nevertheless be put by hand in the Abelian theory. It was Dirac [1] who first seriously considered the monopole’s physical existence by showing that it can explain how electric charge is quantized. In doing so, he necessarily introduced the existence of an unphysical string describing the singularity of the monopole. This singularity seems to be an artifact of the Abelian gauge group.

While the monopole can be added in the Abelian gauge theory, it must exist in certain non-Abelian gauge formalisms. Wu and Yang [2] proposed a magnetic monopole without a singular string using the non-Abelian SU(2) gauge theory. Later, ’t Hooft [3] and Polyakov [4] introduced a magnetic monopole as a topological soliton, which shows that the SU(2) gauge theory allows a finite-energy monopole solution. For an excellent review on magnetic monopoles as topological solitons see, for example, [5, 6]. Unfortunately, the correct non-Abelian construction for electroweak unification in nature is based on the \(SU(2)\times U(1)_Y\) Weinberg–Salam model [7, 8], whose vacuum manifold is a 3-sphere, \(\mathcal {M}=SU(2)\times U(1)/U(1)\cong \mathbb {S}^3\). Thus, the second homotopy group is trivial, \(\pi _2\left( \mathbb {S}^3\right) =\mathbb {I}\).

Upon closer inspection, it is revealed that the vacuum manifold of the bosonic sector of Weinberg–Salam theory can have a non-contractible loop [9], suggesting the existence of monopole defects. This is made precise by Cho and Maison [10], who realized that the extra U(1) hypercharge can be viewed as a gauged \(C\mathbb {P}^1\), thus resulting in \(\pi _2\left( C\mathbb {P}^1\right) =\mathbb {Z}\). The Cho–Maison (CM) monopole, however, suffers from the singularity of energy due to its Coulombic (point-like) U(1) hypercharge. This singularity can be understood if we view the CM monopole as a hybrid between the U(1) (singular) Dirac and the SU(2) (regular) t’Hooft–Polyakov monopoles [11, 12]. In spite of this, recent investigation has shown that the perturbation spectra of this electroweak monopole do not contain any negative mode, and are thus stable [13]. It was originally hoped that the infinite energy could be made finite by either embedding it into a larger (say, SU(5)) Grand Unified Theory (GUT) group [14] or coupling it with gravity [15].

An extensive experimental search for magnetic monopoles has been conducted, for example by the MoEDAL collaboration [16,17,18,19,20,21,22]. The CM monopole becomes a prominent candidate, since it emerges from the realistic electroweak unification group. However, to detect its existence, we need its mass estimate, and it is not so trivial given the singularity of the energy. In [12], Cho, Kim, and Yoon (CKY) proposed three ways to estimate the mass bound: dimensional argument, scaling argument, both of which are backed up by ultraviolet (UV) regularization. Their calculation shows that the monopole mass is around 4 TeV \(\lesssim \) \(M_W\lesssim 7\) TeV, which should be accessible to MoEDAL. The CKY UV regularization is based on the non-minimal coupling between the Higgs and the U(1)-gauge fields, \(\mathcal {L}\ni \epsilon \left( |H|\right) B_{\mu \nu }B^{\mu \nu }\) with \(\varepsilon \left( |H|\right) \propto |H|^8\). Ellis, Mavromatos, and You (EMY) [23] found that such power-law \(\epsilon \) regulator phenomenologically contradicts the Higgs decay \(H\rightarrow \gamma \gamma \) [24]. Instead, they proposed more general polynomial functions whose coefficients are determined by requiring that \(\epsilon \) satisfies the principle of maximum entropy (PME) [23]. This approach gives a theoretical prediction that the electroweak magnetic monopole can be observed with a mass of \(\lesssim 5.5\) TeV.

It is well known that in the limit of vanishing potential, the monopole is stable with globally minimum energy. This is the Bogomolny–Prasad–Sommerfield (BPS) limit [25, 26]. Blaschke and Beneš were the first to show that the CKY model has a BPS state in its spectrum [27]. Using the Bogomolny formalism [25], they calculated the lower bound of the energy to be \(M_W\sim 2.37\) TeV. Employing a different regularization mechanism, Zhang, Zhou, and Cho (ZZC) obtained an energy bound around 3.75 TeV [28], but in the BPS state, it approaches 2.37 TeV. Interestingly, the ZZC model allows the existence of non-unique BPS states. With different Bogomolny equations they show that they could obtain the energy bound of 2.98 TeV. The non-uniqueness of the BPS state in the ZZC model of an electroweak monopole is truly remarkable. The t’Hooft–Polyakov monopole and all its non-canonical variants (see [29,30,31]) have a single BPS energy lower bound. To the best of our knowledge, the CM electroweak monopole in this ZZC regularization model is the first soliton with non-unique BPS energy. Further investigating the other possible sector of BPS states in this ZZC model is precisely the aim of this work.

In this paper we try to construct other possible BPS configurations in the ZZC electroweak monopole by employing one of the Bogomolny formalisms. The paper is organized as follows. In Sect. 2 we briefly review the electroweak monopole. To obtain the BPS equations, we employ one of the Bogomolny formalisms. This method is reviewed in Sect. 3. We apply the Bogomolny method to the electroweak monopole with an electromagnetic permittivity regulator in Sect. 4. In Sect. 5 we discuss several alternative proposals for electroweak monopole regularization and the existence of their BPS states. Finally, in Sect. 6 we discuss our results.

2 The electroweak monopole: a review

Here, we briefly review the existence of the magnetic monopole in electroweak theory. The discussion closely follows Refs. [10, 32].

The electroweak theory is described by the \(SU(2)\times U(1)_Y\) Weinberg–Salam model [7, 8] whose Lagrangian consists of the following four parts:

$$\begin{aligned} \mathcal {L}_{EW}=\mathcal {L}_{h}+\mathcal {L}_{g}+\mathcal {L}_{f}+\mathcal {L}_{y}. \end{aligned}$$
(1)

Here, \(\mathcal {L}_{h}\), \(\mathcal {L}_{g}\), \(\mathcal {L}_{f}\), and \(\mathcal {L}_{y}\) denote the scalar Englert–Brout–Higgs, the Abelian and non-Abelian gauge, the fermionic, and the interactions between the fermions Lagrangians, respectively:

where \({\hat{D}}_{\mu }\) is the \(SU(2)\times U(1)_Y\) covariant derivative,

$$\begin{aligned} {\hat{D}}_{\mu } H&\equiv \left( \partial _{\mu } - i\frac{g}{2}\sigma ^a A_{\mu }^a-i\frac{g'}{2}B_{\mu }\right) H\\&=\left( D_{\mu }-i\frac{g'}{2}B_{\mu }\right) H. \end{aligned}$$

The Englert–Brout–Higgs field H is responsible for the \(SU(2)\times U_Y (1)\rightarrow U_{\text {em}}(1)\) symmetry breaking, where \(U_{\text {em}}(1)\) is the Abelian gauge group for electromagnetism. The vector potential \(A_\mu ^a\) and \(B_\mu \) in the field strength tensors \(F_{\mu \nu }^a\) (\(a=1,2,3\)) and \(G_{\mu \nu }\), respectively, are the gauge fields from SU(2) and hypercharge \(U_Y(1)\).

The Cho–Maison monopole can be found in the bosonic sector of the Lagrangian (1):

$$\begin{aligned} \mathcal {L}= & {} \mathcal {L}_{h}+\mathcal {L}_{g}\nonumber \\= & {} -|{\hat{D}}_{\mu }H|^2-\frac{\lambda }{2}\left( H^\dagger H -\frac{\mu ^2}{\lambda }\right) ^2\nonumber \\{} & {} -\frac{1}{4}F_{\mu \nu }^a F^{a\mu \nu }-\frac{1}{4}G_{\mu \nu } G^{\mu \nu }\nonumber \\= & {} -\frac{1}{2}(\partial _{\mu } \rho )^2-\frac{\rho ^2}{2}|D_{\mu } \xi |^2-\frac{\lambda }{8}(\rho ^2-\rho _0^2)^2\nonumber \\{} & {} -\frac{1}{4}F_{\mu \nu }^a F^{a\mu \nu }-\frac{1}{4}G_{\mu \nu } G^{\mu \nu }, \end{aligned}$$
(2)

where in the last line the field H is decomposed into the Higgs field \(\rho \) and the unit doublet \(\xi \), \(H\equiv \left( \rho /\sqrt{2}\right) \xi \) with \(\xi ^\dagger \xi =1\). We also define \(\rho _0\equiv \sqrt{2\mu ^2/\lambda }\) to be the expectation value of the Higgs field in a vacuum. The most general ansatz for the CM monopole compatible with spherical symmetry is as follows [10, 28, 32]:

$$\begin{aligned} \rho= & {} \rho (r),\quad \xi = i \begin{pmatrix} \sin \left( \theta /2\right) e^{-i\varphi }\\ -\cos \left( \theta /2\right) \end{pmatrix},\nonumber \\ {\hat{n}}= & {} -\xi ^\dagger \varvec{\sigma }\xi ={\hat{r}},\quad C_{\mu }=-\frac{1}{g}\left( 1-\cos \theta \right) \partial _\mu \varphi \nonumber \\ \textbf{A}_{\mu }= & {} \frac{1}{g}A(r)\partial _\mu t {\hat{r}}+\frac{1}{g}\left( f(r)-1\right) {\hat{r}}\times \partial _\mu {\hat{r}},\nonumber \\ B_{\mu }= & {} \frac{1}{g'}B(r)\partial _\mu t -\frac{1}{g'}\left( 1-\cos \theta \right) \partial _\mu \varphi . \end{aligned}$$
(3)

Note that for the case of a pure magnetic monopole, \(A(r)=B(r)=0\). The gauge ansatz \(A_\mu ^a\) and \(B_\mu \) in (3) can be written in the complete form:

$$\begin{aligned} \textbf{A}_t= & {} (0,0,0) = \textbf{A}_r, \\ \textbf{A}_{\theta }= & {} \frac{1-f(r)}{g}\left( \sin \varphi ,-\cos \varphi ,0\right) ,\\ \textbf{A}_{\varphi }= & {} \frac{1-f(r)}{g}\sin \theta \left( \cos \varphi \cos \theta ,\sin \varphi \cos \theta ,-\sin \theta \right) ,\\ B_t= & {} 0=B_r=B_{\theta },\quad B_{\varphi }=-\frac{1}{g'}\left( 1-\cos \theta \right) . \end{aligned}$$

The unitary transformation \(\xi \rightarrow U\xi =\begin{pmatrix} 0\\ 1 \end{pmatrix}\) allows one to define physical gauge fields consisting of the electromagnetic field \(A_\mu ^{(\text {em})}\), and the charged and the neutral bosons \(W_{\mu }\) \(Z_\mu \), respectively:

$$\begin{aligned} A_{\mu }^{(em)}= & {} e\left( \frac{1}{g^2}A(r)+\frac{1}{{g'}^2}B(r)\right) \partial _{\mu } t-\frac{1}{e}\left( 1-\cos \theta \right) \partial _{\mu } \varphi ,\nonumber \\ W_{\mu }= & {} \frac{i}{g}\frac{f(r)}{\sqrt{2}}e^{i\varphi } \left( \partial _{\mu } \theta + i\sin \theta _W \partial _{\mu } \varphi \right) ,\nonumber \\ Z_{\mu }= & {} \frac{e}{gg'}\left( A(r)-B(r)\right) \partial _{\mu } t. \end{aligned}$$
(4)

The Lagrangian (1) in terms of the physical fields can be rewritten as

$$\begin{aligned} \mathcal {L}=&-\frac{1}{2} \left( \partial _{\mu }\rho \right) ^2-\frac{\lambda }{8}\left( \rho ^2-\rho _0^2\right) ^2\nonumber \\&-\frac{1}{4} {F'}^2_{\mu \nu }-\frac{1}{4}G_{\mu \nu }^2-\frac{1}{2}|D'_{\mu } W_{\nu } - D'_{\nu } W_{\mu }|^2\nonumber \\&-\frac{g^2}{4}\rho ^2 W^*_{\mu } W^{\mu } - \frac{g^2+{g'}^2}{8}\rho ^2 Z^2_{\mu }\nonumber \\&+ig F'_{\mu \nu } W^{*\mu }W^\nu +\frac{g^2}{4}\left( W^*_{\mu } W_{\nu }-W^*_{\nu } W_{\mu }\right) ^2\nonumber \\ =&-\frac{1}{2}\left( \partial _{\mu } \rho \right) ^2-\frac{\lambda }{8}\left( \rho ^2-\rho _0^2\right) ^2\nonumber \\&-\frac{1}{4} {F_{\mu \nu }^{(\text {em})}}^2 -\frac{1}{4} Z_{\mu \nu }^2 -\frac{g^2}{4}\rho ^2 W_{\mu }^* W^{\mu } -\frac{g^2+ {g'}^2}{8}\rho ^2 Z_{\mu }^2 \nonumber \\&-\frac{1}{2}|\left( D_{\mu }^{(\text {em})}{+}i e\frac{g}{g'}Z_{\mu }\right) W_{\nu }{-}\left( D_{\nu }^{(\text {em})}{+}i e\frac{g}{g'}Z_{\nu }\right) W_{\mu }|\nonumber \\&+i e \left( F_{\mu \nu }^{(\text {em})}+\frac{g}{g'}Z_{\mu \nu }\right) {W^*}^{\mu } W^{\nu } \nonumber \\&+\frac{g^2}{4}\left( W_{\mu }^* W_{\nu }-W_{\nu }^* W_{\mu }\right) , \end{aligned}$$
(5)

where

$$\begin{aligned} D'_{\mu }\equiv & {} \partial _{\mu } + i g A'_{\mu },\\ D_{\mu }^{\text {em}}\equiv & {} \partial _{\mu } + i e A_{\mu }^{\text {(em)}}, \\ F'_{\mu \nu }= & {} \partial _{\mu } A'_{\nu } - \partial _{\nu } A'_{\mu },\\ A'_{\mu }= & {} A_{\mu } + C_{\mu },\\ C_{\mu }= & {} -\frac{2 i}{g} \xi ^\dagger \partial _{\mu } \xi , \end{aligned}$$

and e (defined to be the electric charge) is related to the coupling constants g and \(g'\) by

$$\begin{aligned} e= \frac{g g'}{\sqrt{g^2 + {g'}^2}}. \end{aligned}$$
(6)

The corresponding field equations are

$$\begin{aligned} \rho ''+\frac{2}{r}\rho '-\frac{1}{2r^2}f^2 \rho= & {} \frac{\lambda }{2}\left( \rho ^2-\rho _0^2\right) \rho -\frac{1}{4}\left( B-A\right) ^2 \rho ,\nonumber \\ f''-\frac{1}{r^2}\left( f^2-1\right) f= & {} \frac{g^2}{4}\rho ^2 f -A^2 f. \end{aligned}$$
(7)

The simplest nontrivial solution of (7) is when \(A(r)=B(r)=f(r)=0\), \(\rho =\rho _0\equiv \sqrt{2} \mu /\sqrt{\lambda }\), and the EM gauge becomes

$$\begin{aligned} A_{\mu }^{(em)}=-\frac{1}{e}\left( 1-\cos \theta \right) \partial _{\mu } \varphi , \end{aligned}$$
(8)

that is, a point-like magnetic monopole with the magnetic charge \(4\pi /e\).

A more general solution can be obtained when A(r), B(r), and f(r) are nonzero, satisfying the boundary conditions

$$\begin{aligned} \rho (0)&=0,\quad f(0)=1,\quad A(0)=0, \quad B(0)=b_0,\nonumber \\ \rho (\infty )&=\rho _0,\quad f(\infty )=0,\quad A(\infty )=B(\infty )=A_0, \end{aligned}$$
(9)

where \(0\le A_0 \le e\rho _0\) and \(0\le b_0 \le A_0\). This condition describes a Cho–Maison dyon with the electric charge \(q_e\) and magnetic charge \(q_m\),

$$\begin{aligned} q_e= & {} -\frac{8\pi }{e}\sin ^2\theta _W \int _0^\infty f^2 A\,\textrm{d}r=\frac{4\pi }{e}A_1, \nonumber \\ q_m= & {} \frac{4\pi }{e}. \end{aligned}$$
(10)

Here \(A_1\) is the coefficient of 1/r term in the asymptotic expansion of A(r),

$$\begin{aligned} A(r)\rightarrow A_0+\frac{A_1}{r}+\cdots . \end{aligned}$$
(11)

The ansatz (4) gives the energy of monopole (\(A(r)=B(r)=0\)) in the form

$$\begin{aligned} E= & {} E_0+E_1, \end{aligned}$$
(12)
$$\begin{aligned} E_0\equiv & {} 4\pi \int _0^\infty \frac{\textrm{d}r}{2r^2}\left\{ \frac{1}{g'^2}+ \frac{1}{g^2}\left( f^2-1\right) ^2\right\} ,\end{aligned}$$
(13)
$$\begin{aligned} E_1\equiv & {} 4\pi \int _0^\infty \textrm{d}r \left\{ \frac{1}{2}\left( r\rho '\right) ^2+\frac{\lambda }{8}r^2 \left( \rho ^2-\rho _0^2\right) ^2\right. \nonumber \\{} & {} \left. +\frac{1}{g^2}f'^2+\frac{1}{4}f^2 \rho ^2\right\} . \end{aligned}$$
(14)

Applying the boundary conditions (9) for \(\rho \) and f, \(E_1\) approaches a finite value

$$\begin{aligned} E_1\approx 4.1 \text { TeV}, \end{aligned}$$
(15)

but \(E_0\rightarrow \infty \) at the origin. This condition implies that there is no lower bound energy for this monopole, hence no BPS equations.

3 BPS Lagrangian method for a monopole

The Bogomolny formalism is a convenient way of solving a soliton’s second-order field equations by reducing them into first order. The corresponding equations and solutions are known as the BPS equations and BPS states, respectively. For a monopole, the BPS state corresponds to the vanishing of the potential (\(\lambda \rightarrow 0\)) while keeping the Higgs vacuum expectation value (VEV) finite: \(\mu /\sqrt{\lambda }\rightarrow \) const. [25, 26], thus preserving the nontrivial topology.

The original Bogomolny mechanism was more of a smart guess trick of completing the square. Over the years there have been numerous proposals on constructing a systematic algorithm for obtaining the BPS equations (see, for example, [33,34,35]). Among them is the so-called BPS Lagrangian method, initially used for some vortex models [36]. This formalism was used for obtaining BPS states of some exotic magnetic monopoles in [37]. In this method, the BPS equations are the solutions of

$$\begin{aligned} \mathcal {L}-\mathcal {L}_\textrm{BPS}=0. \end{aligned}$$
(16)

The brief review of this method is explained below.

In spherical coordinates where the system depends only on the radial coordinate r, the total static energy in the BPS limit is the difference of a BPS energy function in the limit \(r\rightarrow \infty \) and \(r\rightarrow 0\) [35]

$$\begin{aligned} E_\textrm{BPS}=Q(r\rightarrow \infty )-Q(r\rightarrow 0)=\int _0^\infty \textrm{d}Q. \end{aligned}$$
(17)

According to the work by Atmaja, Prasetyo, and Ramadhan [36, 37], \(Q=\eta \pi P(\rho ) F(f)\) is the suitable choice for the BPS energy function in many models of vortices (\(\eta =2\)) and monopoles (\(\eta =4\)), where \(\rho (r)\) and f(r) are the components of the ansatz that depend on r. We can write \(\mathcal {L}_{BPS}\) as

$$\begin{aligned} \mathcal {L}_\textrm{BPS}&=-\frac{1}{4\pi r^2}\frac{\textrm{d}Q}{\textrm{d}r}=-\frac{1}{r^2}\frac{\textrm{d}}{\textrm{d}r}\left\{ P(\rho )F(f)\right\} \nonumber \\&=-\frac{1}{r^2}\left\{ \frac{\textrm{d}P}{\textrm{d}\rho }\rho '(r) F(f)+P(\rho )\frac{\textrm{d} F}{\textrm{d} f}f'(r)\right\} , \end{aligned}$$
(18)

with \(\rho '(r)\equiv \textrm{d}\rho /\textrm{d}r\) and \(f'(r)\equiv \textrm{d}f/\textrm{d}r\). We can see that \(\mathcal {L}_\textrm{BPS}\) consists of the first-order derivative of \(\rho (r)\) and f(r), so Eq. (16) is a polynomial of \(\rho '(r)\) and \(f'(r)\).

In the model where the static Lagrangian of the monopole is a quadratic function of \(\rho '(r)\) and \(f'(r)\), Eq. (16) gives

$$\begin{aligned}&\left\{ \rho '(r)-G_1^{(1)}[\rho ,f,f'(r)]\right\} \left\{ \rho '(r)-G_1^{(2)}[\rho ,f,f'(r)]\right\} =0 \text { or } \nonumber \\&\left\{ f'(r)-G_3^{(1)}[\rho ,f,\rho '(r)]\right\} \left\{ f'(r)-G_3^{(2)}[\rho ,f,\rho '(r)]\right\} =0. \end{aligned}$$
(19)

If we choose to solve the roots of \(\rho '(r)\) first, then to obtain a unique expression of \(\rho '(r)\), we restrict \(G_1^{(1)}-G_1^{(2)}=0\). This in turn can be rearranged to give us

$$\begin{aligned} \left\{ f'(r)-G_2^{(1)}[\rho ,f]\right\} \left\{ f'(r)-G_2^{(2)}[\rho ,f]\right\} =0, \end{aligned}$$
(20)

which give us one expression of \(f'(r)\) by \(G_2^{(1)}-G_2^{(2)}=0\). This model must be valid for all r. Therefore, if \(G_2^{(1)}-G_2^{(2)}\) is written as the polynomial of r,

$$\begin{aligned} G_2^{(1)}-G_2^{(2)}\equiv \sum _n a_n r^n=0, \end{aligned}$$
(21)

we obtain some conditions for both \(F(f) \textrm{d}P/\textrm{d}\rho \) and \(P(\rho ) \textrm{d}F/\textrm{d}f\) from \(a_n=0, \forall n\). The BPS equations are obtained from solving these conditions for both and substituting the results into \(\rho '(r)\) and \(f'(r)\).

Note that, in general, we cannot always express \(\mathcal {L}_\textrm{BPS}\) proportionally as a total differential of the boundary term, as in Eq. (18). A more general expression for \(\mathcal {L}_\textrm{BPS}\) can be written as

$$\begin{aligned} \mathcal {L}_\textrm{BPS}=- Q_\rho (\rho ,f) \frac{ \rho '(r)}{r^2}-Q_f(\rho ,f) \frac{ f'(r)}{r^2}, \end{aligned}$$
(22)

where \(Q_\rho \) and \(Q_f\) are generally functions of both \(\rho \) and f. In this case, the total energy (E) and the topological charge (Q) cannot be directly inferred. The definition of topological charge, however, is still well defined, since it depends solely on the homotopy of the vacuum manifold. In this paper we shall encounter the BPS electroweak monopole where Eq. (18) does not hold.

4 Bogomolny formalism for Cho–Maison monopole with permittivity regularization

As an attempt to regularize the singular CM monopole, ZZC [28] proposed a non-canonical kinetic term on the U(1) gauge sector of the Lagrangian (5) by introducing a non-vacuum electromagnetic permittivity \(\epsilon (\rho )\),

$$\begin{aligned} \mathcal {L}= & {} -\frac{1}{2}\left( \partial _{\mu } \rho \right) ^2-\frac{\lambda }{8}\left( \rho ^2-\rho _0^2\right) ^2-\frac{1}{4}\epsilon (\rho ){F_{\mu \nu }^{(em)}}^2\nonumber \\{} & {} -\frac{1}{2}\left| \left( D_{\mu }^{(em)}{+}ie\frac{g}{g'}Z_{\mu }\right) W_{\nu }{-}\left( D_{\nu }^{(em)}{+}ie\frac{g}{g'}Z_{\nu }\right) W_{\mu } \right| ^2\nonumber \\{} & {} -\frac{1}{4}Z_{\mu \nu }^2-\frac{g^2}{4}\rho ^2 W_{\mu }^* W^{\mu } -\frac{g^2+g'^2}{8}\rho ^2 Z_{\mu }^2\nonumber \\{} & {} +ie\left( F_{\mu \nu }^{(em)}+\frac{g}{g'}Z_{\mu \nu }\right) {W^*}^{\mu } W^{\nu } + \nonumber \\{} & {} \frac{g^2}{4}\left( W^*_{\mu } W_{\nu }-W^*_{\nu } W_{\mu }\right) ^2. \end{aligned}$$
(23)

Using the ansatz (4), the monopole field equations are

$$\begin{aligned}{} & {} \rho ''+\frac{2}{r}\rho '-\frac{1}{2r^2}f^2 \rho \nonumber \\{} & {} \quad =\frac{\lambda }{2}\left( \rho ^2-\rho _0^2\right) \rho -\frac{1}{4}\left( B-A\right) ^2 \rho \nonumber \\{} & {} \qquad +\frac{\epsilon }{2}\left[ \frac{1}{e^2 r^4}-e^2\left( \frac{A'}{g^2}+\frac{B'}{g'^2}\right) \right] ,\nonumber \\{} & {} f''-\frac{1}{r^2}\left( f^2-1\right) f=\frac{g^2}{4}\rho ^2 f -A^2 f. \end{aligned}$$
(24)

The boundary condition is determined by considering the total energy:

$$\begin{aligned} E= & {} E_0+E_1, \end{aligned}$$
(25)
$$\begin{aligned} E_0\equiv & {} 4\pi \int _0^\infty \frac{\textrm{d}r}{2r^2}\left\{ \frac{\epsilon }{e^2}+ \frac{1}{g^2}f^2\left( f^2-2\right) \right\} ,\end{aligned}$$
(26)
$$\begin{aligned} E_1\equiv & {} 4\pi \int _0^\infty \textrm{d}r \left\{ \frac{1}{2}\left( r\rho '\right) ^2+\frac{\lambda }{8}r^2\left( \rho ^2-\rho _0^2\right) ^2\right. \nonumber \\{} & {} \quad \left. +\frac{1}{g^2}f'^2+\frac{1}{4}f^2 \rho ^2\right\} . \end{aligned}$$
(27)

It is evident that \(E_0\) is divergent at the origin (\(r\rightarrow 0\)). This divergence can be removed by introducing a power-law function of \(\epsilon (\rho )\) [28]:

$$\begin{aligned} \epsilon= & {} \left( \frac{\rho }{\rho _0}\right) ^n\left\{ c_0+c_1\left( \frac{\rho }{\rho _0}\right) +\cdots \right\} ,\end{aligned}$$
(28)
$$\begin{aligned} \rho (r\rightarrow 0)\approx & {} r^\delta \left( h_0+h_1 r+\cdots \right) , \end{aligned}$$
(29)

where \(\delta \) can be determined from Eq. (24):

$$\begin{aligned} \delta =\frac{\sqrt{3}-1}{2},\quad n>\frac{2}{\delta }=2\left( \sqrt{3}+1\right) \simeq 5.46. \end{aligned}$$
(30)

In this condition, the first term in \(E_0\) is finite near the origin. To make the second term in \(E_0\) finite, we need \(f(0)=0\) or \(\sqrt{2}\). However, both conditions do not result in finite energy. The solution to remove the singularity of Eq. (25) is to combine the two divergent terms. Defining

$$\begin{aligned} \epsilon =\epsilon _0 +\epsilon _1,\ \epsilon _0=\frac{g'^2}{g^2+g'^2}=\frac{e^2}{g^2},\ \epsilon _1\simeq \left( \frac{\rho }{\rho _0}\right) ^n, \end{aligned}$$
(31)

the singular energy \(E_0\) can be written as

$$\begin{aligned} E_0= 4\pi \int _0^\infty \frac{\textrm{d}r}{2e^2 r^2}\left\{ \epsilon _0\left( f^2-1\right) ^2+\epsilon _1\right\} . \end{aligned}$$
(32)

Thus, ZZC shows that the CM monopole energy is finite by taking \(f(r\rightarrow 0)=1\). This boundary condition is similar to the CKY case [12].

Applying the BPS Lagrangian method into this model, Eq. (32) and the ansatz (4)can be used to rewrite the Lagrangian as

$$\begin{aligned} \mathcal {L}= & {} -\frac{{\rho '}^2}{2}- \frac{1}{2e^2 r^4}\left( \epsilon _0 \left( f^2-1\right) ^2 +\epsilon _1 \right) \nonumber \\{} & {} -\frac{{f'}^2}{g^2 r^2}-\frac{f^2 \rho ^2}{4r^2}-V(\rho ). \end{aligned}$$
(33)

Here, we add a potential term of the Higgs \(V(\rho )\). In this method, we do not a priori assume that \(V=0\). Instead, such condition (to be precise, \(V=\) const.) appears as a constraint for the BPS equations to exist (see, for example, [36, 37]).

Putting the Lagrangians (22) and (33) into Eq. (16), we end up with algebraic equations for \(\rho '(r)\) and \(f'(r)\). Solving \(\rho '(r)\) first yields

$$\begin{aligned} \rho '_\pm =\frac{Q_\rho }{r^2}\pm \frac{1}{2r^2}\sqrt{-8r^4 V+4 Q_\rho ^2-\frac{4}{e^2}\left( \epsilon _0\left( f^2-1\right) ^2+\epsilon _1\right) -2r^2 f^2 \rho ^2 +8 Q_f r^2 f'-\frac{8r^2 {f'}^2}{g^2}}. \end{aligned}$$
(34)

Demanding the two roots to be equal (\(\rho '_+=\rho '_-\)) results in a quadratic equation for \(f'\), whose solution is

$$\begin{aligned}{} & {} f'_\pm =\frac{g^2 Q_f}{2}\pm \frac{g}{er}\sqrt{e^2\left( 2Q_\rho ^2 +g^2 Q_f^2 r^2\right) -2\left( \epsilon _0 \left( f^2-1\right) ^2+\epsilon _1\right) -e^2 r^2\left( 4r^2 V+f^2\rho ^2\right) }. \end{aligned}$$
(35)
Fig. 1
figure 1

The BPS Eqs. (40) and (41) for \(n = 6, 10, 20, 30\), and \(n = \infty \). The solutions for the Eq. (24) for \(n=6\) (with \(A(r)=B(r)=0\)) [28] are represented by dashed lines

Full size image

Again, the two roots will be equal (\(f'_+=f'_-\)) if the terms inside the square root equal zero. The resulting equation can be written as a power series of r:

$$\begin{aligned}{} & {} 2\left[ e^2 Q_\rho ^2-\left( \epsilon _0\left( f^2-1\right) ^2+\epsilon _1\right) \right] \nonumber \\{} & {} \quad +e^2 r^2\left( g^2 Q_f^2-f^2 \rho ^2\right) -4e^2 r^4 V=0. \end{aligned}$$
(36)

Equation (36) is satisfied only when

$$\begin{aligned} V= & {} 0,\end{aligned}$$
(37)
$$\begin{aligned} Q_\rho= & {} \pm \frac{1}{e}\sqrt{ \epsilon _0\left( f^2-1\right) ^2+\epsilon _1}=\pm \sqrt{\frac{ \left( f^2-1\right) ^2}{g^2}+\frac{\epsilon _1}{e^2}},\nonumber \\\end{aligned}$$
(38)
$$\begin{aligned} Q_f= & {} \pm \frac{\rho f}{g}. \end{aligned}$$
(39)

Therefore, the BPS equations for this monopole are

$$\begin{aligned} \rho '= & {} \pm \frac{1}{r^2}\sqrt{\frac{ (f^2-1)^2}{g^2}+\frac{\epsilon _1}{e^2}},\end{aligned}$$
(40)
$$\begin{aligned} f'= & {} \pm \frac{1}{2}g\rho f. \end{aligned}$$
(41)

Equations (40) and (41) are the main results of our work. They are distinct BPS equations and cannot be reduced to Eq. (44) or (50) in the ZZC model [28]. Note that Eq. (40) and the energy (32) depend on the power of n via \(\epsilon _1 = \left( \rho /\rho _0\right) ^n\). Choosing a different regularization function, \(\epsilon _1\), amounts to having BPS solutions with smaller energy. In the limit of \(n\rightarrow \infty \), the total energy converges to a finite value, \(E\rightarrow 3.569\) GeV.

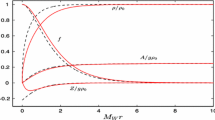
In Fig. 1 we present the solutions of Eq. (40) and (41) for several values of n up to \(n\rightarrow \infty \).

As can be seen, small n produces more diffuse BPS solutions. As n increases, the field profiles become more localized. As a comparison, we plot the solution of the second-order field Eq. (24) for \(n=6\).

The total energy (Eq. (25)), after setting \(\lambda = 0\), can be written as

$$\begin{aligned} E= & {} 4\pi \int _0^\infty \textrm{d}r \left\{ \frac{1}{2} r^2 {\rho '}^2 + \frac{1}{2e^2 r^2}\left( \epsilon _0 (f^2-1)^2 +\epsilon _1 \right) \right. \nonumber \\{} & {} \left. +\frac{1}{g^2} {f'}^2+\frac{1}{4} f^2 \rho ^2\right\} \nonumber \\= & {} 4\pi \int _0^\infty \textrm{d}r \left\{ \frac{1}{2} r^2 \left( \frac{1}{r^2}\sqrt{\frac{ (f^2-1)^2}{g^2}+\frac{\epsilon _1}{e^2}}\right) ^2 \right. \nonumber \\{} & {} \left. + \frac{\left( \epsilon _0 (f^2-1)^2 +\epsilon _1 \right) }{2e^2 r^2}+\frac{1}{g^2} \left( \frac{1}{2}g\rho f\right) ^2+\frac{f^2 \rho ^2}{4} \right\} \nonumber \\\ge & {} 4\pi \int _0^\infty \textrm{d}r \left\{ \frac{ (f^2-1)^2}{g^2 r^2}+\frac{\epsilon _1}{e^2 r^2} +\frac{f^2 \rho ^2}{2} \right\} . \end{aligned}$$
(42)

The bound is saturated by Eqs. (40) and (41).

In Fig. 2 we show the plots of energy densities for several values of n. Since \(\epsilon _1=(\rho /\rho _0)^n\), we have an energy bound which depends on n. The value of this bound decreases as n increases. Note that the energy densities at \(r\rightarrow 0\) are very high due to the \(\epsilon _1\) term. In the limit where \(n\rightarrow \infty \), the integral of the \(\epsilon _1\) term becomes negligible, and we have the lowest bound for the total energy.

Fig. 2
figure 2

The energy density (42) for \(n = 6, 10, 20, 30\), and \(n = \infty \)

Full size image

5 Some regularization alternatives for the Cho–Maison monopole and their BPS states

In the previous section we showed how the BPS state of the CM monopole in the ZZC model could be obtained by means of the BPS Lagrangian method. Since the ZZC model [28] is just one toy model to regularize the singularity, it is by no means unique. In this section we shall discuss several other regularization possibilities in the literature and establish their corresponding Bogomolny equations.

5.1 Born–Infeld extension in the hypercharge sector

The spirit of “regularization” seems to rely on adding nonlinear interactions into the field configurations. When talking about nonlinear fields, one natural choice is the Born–Infeld field theory [38]. Arunasalam and Kobakhidze [39] proposed the the Born–Infeld extension to the hypercharge sector of the Lagrangian  (2):

$$\begin{aligned} \mathcal {L}= & {} -|{\hat{D}}_{\mu }H|^2-\frac{\lambda }{2}\left( H^\dagger H -\frac{\mu ^2}{\lambda }\right) ^2-\frac{1}{4}F_{\mu \nu }^a F^{a\mu \nu }\nonumber \\{} & {} +\beta ^2\left[ 1-\sqrt{-\textrm{det}\left( \eta _{\mu \nu }+\frac{1}{\beta }G_{\mu \nu }\right) }\right] \nonumber \\= & {} -|{\hat{D}}_{\mu }H|^2-\frac{\lambda }{2}\left( H^\dagger H -\frac{\mu ^2}{\lambda }\right) ^2-\frac{1}{4}F_{\mu \nu }^a F^{a\mu \nu }\nonumber \\{} & {} +\beta ^2\left[ 1-\sqrt{1+\frac{1}{2\beta ^2}G_{\mu \nu }G^{\mu \nu }-\frac{1}{16\beta ^4}(G_{\mu \nu }\tilde{G }^{\mu \nu })^2}\right] ,\nonumber \\ \end{aligned}$$
(43)

where \(\tilde{G}^{\mu \nu }\equiv \frac{1}{2}\epsilon ^{\mu \nu \alpha \beta }G_{\alpha \beta }\) is the Hodge dual of the field strength tensor \(G_{\mu \nu }\), and \(\beta \) is the Born–Infeld parameter with the unit of \(\text {mass}^2\). In the limit \(\beta \rightarrow \infty \), the Lagrangian goes back to Eq. (2).

The field equations are

$$\begin{aligned} \rho ''+\frac{2}{r}\rho '-\frac{f^2}{2r^2}\rho= & {} \lambda \left( \frac{\rho ^2}{2}-\frac{\mu ^2}{\lambda }\right) \rho ,\nonumber \\ f''-\frac{f^2-1}{r^2}f= & {} \frac{g^2}{4}\rho ^2 f, \end{aligned}$$
(44)

which is the same as Eq. (7) when \(A=B=0\). The energy is

$$\begin{aligned} E= & {} E_0 + E_1, \end{aligned}$$
(45)
$$\begin{aligned} E_0\equiv & {} \int _0^\infty \textrm{d}r\, \beta ^2 \left\{ \sqrt{(4\pi r^2)^2+\frac{h_Y^2}{\beta ^2}}-4\pi r^2\right\} ,\end{aligned}$$
(46)
$$\begin{aligned} E_1\equiv & {} 4\pi \int _0^\infty \textrm{d}r \left\{ \frac{(f^2-1)^2}{2g^2 r^2}+\frac{1}{2}(r\rho ')^2+\frac{f'^2}{g^2}\right. \nonumber \\{} & {} \left. +\frac{\lambda r^2}{8}(\rho ^2-\rho _0^2)^2+\frac{1}{4}f^2\rho ^2\right\} , \end{aligned}$$
(47)

with \(h_Y\equiv 4\pi /g'\) the hyper-magnetic charge of the monopole. \(E_1 \approx 4.1\) TeV as before, while \(E_0\) is finite due to the Born–Infeld modification. Its value is

$$\begin{aligned} E_0\approx \frac{\pi ^{3/2}}{3\Gamma \left( \frac{3}{4}\right) ^2}\sqrt{\frac{\beta h_Y^3}{4\pi }}=\frac{4\pi ^{5/2}}{3\Gamma \left( \frac{3}{4}\right) ^2}\sqrt{\frac{\beta }{g'^3}}\approx 72.8\sqrt{\beta }, \end{aligned}$$
(48)

where they use \(g'=0.357\). This shows that the monopole energy depends on the parameter \(\beta \). The magnetic field is \(q_m=4\pi /e\). The numerical value of \(\beta \) can be obtained from experiments. With the constraint from the Pb–Pb scattering at LHC [40] and considering the \(\cos \theta _W\) factor in the sector, \(\sqrt{\beta } > rsim 90\text { GeV}\). Therefore,

$$\begin{aligned} E=4.1\text { TeV}+72.8\sqrt{\beta }\approx 10.6\text { TeV}. \end{aligned}$$
(49)

Since the monopole has finite energy, it is then legitimate to ask about its BPS states.

The Lagrangian (43) can be written, using the BPS Lagrangian method, asfunction of r only:

$$\begin{aligned} \mathcal {L}= & {} \mathcal {L}_s + \mathcal {L}_{BI},\nonumber \\ \mathcal {L}_s\equiv & {} -\frac{{\rho '}^2}{2}- \frac{(f^2-1)^2}{2g^2 r^4}-\frac{{f'}^2}{g^2 r^2}-\frac{f^2 \rho ^2}{4r^2}-V(\rho ),\nonumber \\ \mathcal {L}_{BI}\equiv & {} \beta ^2 \left( 1-\sqrt{1+\frac{1}{{g'}^2 r^4 \beta ^2}}\right) , \end{aligned}$$
(50)

where \(\mathcal {L}_{BI}\) comes from the hypercharge sector. The lowest energy bound is given by (48), and since \(\mathcal {L}_{BI}\) is independent of \(\rho (r)\) and f(r), it does not enter into the formalism \(\mathcal {L}_s-\mathcal {L}_{BPS}=0\). Solving it for \(\rho '(r)\), we have

$$\begin{aligned} \rho '(r)_{\pm }=\frac{Q_\rho }{r^2}\pm \frac{1}{2 r^2}\sqrt{4 Q_\rho ^2 - \frac{4}{g^2} (f^2-1)^2-8 r^4 V-2 r^2 f^2 \rho ^2 + 8 Q_f r^2 f'-\frac{8r^2 {f'}^2}{g^2}}, \end{aligned}$$
(51)

from which the roots of \(f'(r)\) can be deduced:

$$\begin{aligned} f'(r)_\pm =\frac{g^2 Q_f}{2}\pm \frac{1}{2r}\sqrt{ 2g^2 Q_\rho ^2 -2(f^2-1)^2 + g^4 Q_f^2 r^2 - 4g^2 r^4 V -g^2 r^2 \rho ^2 f^2}. \end{aligned}$$
(52)

We then have a polynomial equation in the power of r:

$$\begin{aligned}{} & {} 2\left[ g^2 Q_\rho ^2 - (f^2-1)^2\right] - 4g^2 r^4 V \nonumber \\{} & {} \quad + g^2 r^2 \left[ g^2 Q_f^2 - f^2 \rho ^2\right] =0. \end{aligned}$$
(53)

The fourth-order term gives \(V=0\). The zeroth-order and the second-order terms yield, respectively,

$$\begin{aligned} Q_\rho= & {} \pm \frac{f^2-1}{g},\end{aligned}$$
(54)
$$\begin{aligned} Q_f= & {} \pm \frac{\rho f}{g}. \end{aligned}$$
(55)

We have the BPS equations of the form

$$\begin{aligned} \rho '= & {} \pm \frac{f^2-1}{g r^2} ,\end{aligned}$$
(56)
$$\begin{aligned} f'= & {} \pm \frac{1}{2} g \rho f . \end{aligned}$$
(57)

These results confirm the BPS equations obtained by [41]. Note that the difference between these BPS states and that of t’Hoof–Polyakov is the appearance of the factor 1/2, which makes them unable to be solved analytically. We present their numerical solutions in Fig. 3. The BPS solutions are rather more diffuse than the corresponding solutions to the Euler–Lagrange field equations (44).

Fig. 3
figure 3

Solid lines: the numerical solutions to the BPS equations (56) and (57). Dashed lines: the solutions to the Euler–Lagrange equations (44)

Full size image

5.2 Born–Infeld extension in both SU(2) and U(1) sectors

Modifying the hypercharge sector with nonlinear electrodynamics, despite being useful in terms of the regularization objective, is rather trivial from the BPS point of view. This is because such term does not enter in the BPS condition (16). A more interesting case is when the Born–Infeld extension is applied not only to the hypercharge but also to the SU(2) Yang–Mills sectors. This model was proposed by Arunasalam, Collison, and Kobakhidze (ACK) [42].

The corresponding Lagrangian can be written as

$$\begin{aligned} \mathcal {L}= & {} \mathcal {L}_s + \mathcal {L}_\textrm{BI1}+\mathcal {L}_\textrm{BI2},\nonumber \\ \mathcal {L}_s\equiv & {} -\frac{{\rho '}^2}{2}-\frac{f^2 \rho ^2}{4r^2}-V(\rho ),\nonumber \\ \mathcal {L}_\textrm{BI1}\equiv & {} \beta _1^2 \left( 1-\sqrt{1+\frac{(f^2-1)^2}{g^2 \beta _1^2 r^4}+\frac{2{f'}^2}{g^2 \beta _1^2 r^2}}\right) ,\nonumber \\ \mathcal {L}_\textrm{BI2}\equiv & {} \beta _2^2 \left( 1-\sqrt{1+\frac{1}{{g'}^2 r^4 \beta _2^2}}\right) . \end{aligned}$$
(58)

Since, like before, \(\mathcal {L}_\textrm{BI2}\) does not contribute to the field solutions, the BPS equations can be written as \((\mathcal {L}_s +\mathcal {L}_\textrm{BI1})-\mathcal {L}_\textrm{BPS}=0\). Solving it for \(\rho '(r)\),

$$\begin{aligned}{} & {} \rho '_{\pm } =\frac{Q_\rho }{r^2}\pm \sqrt{\frac{Q_\rho ^2}{r^4}+2\left( V - \beta _1^2 + \frac{f^2 \rho ^2}{4r^2}-\frac{Q_f f'}{r^2}+\sqrt{\beta _1^4+\frac{1}{2}\beta _1^2 \left( \frac{2(f^2-1)^2}{g^2 r^4}+\frac{4 {f'}^2}{g^2 r^2}\right) }\right) }. \end{aligned}$$
(59)

This can be used to solve \(f'(r)\):

$$\begin{aligned} f'_\pm = \frac{K+\sqrt{\frac{128 \beta _1^2}{r^2} D_2}}{L}, \end{aligned}$$
(60)

where

$$\begin{aligned} D_2\equiv & {} 4 g^2 Q_\rho ^4 - 16 g^2 r^8 (2 \beta _1^2 - V) V \nonumber \\{} & {} +4 g^2 r^2 (2 Q_f^2 - 4 Q_f^2 f^2 + 2 Q_f^2 f^4 - Q_\rho ^2 f^2 \rho ^2)\nonumber \\{} & {} + r^4 (-16 \beta _1^2 + 16 g^2 Q_\rho ^2 \beta _1^2 + 32 \beta _1^2 f^2 \nonumber \\{} & {} - 16 \beta _1^2 f^4 - 16 g^2 Q_\rho ^2 V + g^2 f^4 \rho ^4)\nonumber \\{} & {} + 8 g^2 r^6 (g^2 Q_f^2 \beta _1^2 - \beta _1^2 f^2 \rho ^2 + f^2 V \rho ^2),\nonumber \\ K\equiv & {} - g^2 Q_f \left( \frac{16 Q_\rho ^2}{r^2} + 32 r^2 \beta _1^2 - 32 r^2 V - 8 f^2 \rho ^2 \right) ,\nonumber \\ L\equiv & {} 2 (16 g^2 Q_f^2 - 32 r^2 \beta _1^2). \end{aligned}$$
(61)

Setting \(D_2=0\), the coefficient for the eighth-order power constrains the potential to be constant, \(V=0\) or \(2 \beta _1^2\). From the sixth-order term we have

$$\begin{aligned} Q_f=\pm \frac{\rho f \sqrt{\beta _1^2 - V}}{g \beta _1}. \end{aligned}$$
(62)

Choosing \(V=2 \beta _1^2\) gives an imaginary value for \(Q_f\), so we choose \(V=0\). Substituting these results to \(D_2\) gives

$$\begin{aligned} D_2= & {} 4 g^2 Q_\rho ^4+4 g^2 r^2 (2 Q_f^2 - 4 Q_f^2 f^2 + 2 Q_f^2 f^4 \nonumber \\{} & {} - Q_\rho ^2 f^2 \rho ^2)+r^4 (-16 \beta _1^2 + 16 g^2 Q_\rho ^2 \beta _1^2 + 32 \beta _1^2 f^2 \nonumber \\{} & {} - 16 \beta _1^2 f^4 + g^2 f^4 \rho ^4), \end{aligned}$$
(63)

with

$$\begin{aligned} Q_f=\pm \frac{\rho f}{g}. \end{aligned}$$

We can immediately see that there is an incompatibility here with nontrivial BPS equations. The zeroth-order power of Eq. (63) implies that \(Q_\rho =0\), while the second- and fourth-order terms yield, respectively,

$$\begin{aligned} Q_\rho= & {} \pm \left\{ \frac{\sqrt{2} (f^2-1)}{g},\ \frac{\sqrt{16 \beta _1^2 (f^2-1)^2 - g^2 \rho ^2 f^2}}{4 g \beta _1}\right\} .\nonumber \\ \end{aligned}$$
(64)

These three \(Q_{\rho }\) conditions cannot be consistently satisfied unless f(r) and \(\rho (r)\) are constants,

$$\begin{aligned} f=\pm 1,\quad \rho =0. \end{aligned}$$
(65)

We conclude that within this BPS Lagrangian method, there is no BPS state for the ACK model of the electroweak monopole.

5.3 Generalized electroweak monopole

As our last attempt, we can generalize the “regulators” in Eq. (23) by introducing two functions dependent on the scalar field, \(W(\rho )\) and \(G(\rho )\). These act as the multiplier to the Lagrangian, which will generalize the model from Eq. (23). In the context of the t’Hooft–Polyakov monopole, this mechanism was discussed by in [29, 30], and its BPS Lagrangian method was elaborated in [37].

The Lagrangian, in the case of monopole (\(A(r)=B(r)=0\)), is

$$\begin{aligned} \mathcal {L}= & {} -G(\rho )\left( \frac{1}{2}(\partial _\mu \rho )^2+\frac{g^2}{4}\rho ^2 W_\mu ^* W^\mu \right) \nonumber \\{} & {} -V(\rho )-W(\rho ) \bigg (\frac{1}{4}\epsilon (\rho ){F_{\mu \nu }^{(em)}}^2\nonumber \\{} & {} +\frac{1}{2}\bigg |D_{\mu }^{(em)}W_\nu -D_{\nu }^{(em)} W_\mu \bigg |^2 -ie F_{\mu \nu }^{(em)}{W^*}^\mu W^\nu \nonumber \\{} & {} -\frac{g^2}{4}(W^*_\mu W_\nu -W^*_\nu W_\mu )^2\bigg ). \end{aligned}$$
(66)

This is the generalized version of the non-singular electroweak monopole with non-vacuum electromagnetic permittivity (23). Using the ansatz (4), the Lagrangian reads

$$\begin{aligned} \mathcal {L}= & {} -G(\rho ) \left( \frac{{\rho '}^2}{2} +\frac{f^2 \rho ^2}{4r^2}\right) \nonumber \\{} & {} - W(\rho )\left[ \frac{1}{2e^2 r^4}\left\{ \epsilon _0 (f^2-1)^2 +\epsilon _1 \right\} +\frac{{f'}^2}{g^2 r^2}\right] -V.\nonumber \\ \end{aligned}$$
(67)

From \(\mathcal {L}-\mathcal {L}_{BPS}=0\), we have

$$\begin{aligned} \rho '_\pm= & {} \frac{Q_\rho }{G r^2}\pm \frac{1}{2 G r^2}\bigg \{4 Q_\rho ^2-G \bigg (8r^4 V\nonumber \\{} & {} +\frac{4}{e^2} W\left( \epsilon _0(f^2-1)^2+\epsilon _1\right) +2 G r^2 f^2 \rho ^2 \nonumber \\{} & {} -8 Q_f r^2 f'+\frac{8 r^2 W {f'}^2}{g^2}\bigg )\bigg \}^\frac{1}{2}. \end{aligned}$$
(68)

Solving for \(f'(r)\), we have

$$\begin{aligned} f'_\pm= & {} \frac{g^2 Q_f}{2 W}\pm \frac{g}{e \sqrt{G} r W}\bigg \{e^2\left( 2 W Q_\rho ^2 +g^2 G Q_f^2 r^2\right) \nonumber \\{} & {} -2GW^2\left( \epsilon _0 \left( f^2-1\right) ^2+\epsilon _1\right) \nonumber \\{} & {} \quad -e^2 r^2 G W\left( 4r^2 V +f^2 G \rho ^2\right) \bigg \}^\frac{1}{2}. \end{aligned}$$
(69)

The terms inside the square root satisfy

$$\begin{aligned}{} & {} -32 e^4 G r^8 V W^2 + 16 e^2 r^4 W^2 \nonumber \\{} & {} \qquad \times \bigg (e^2 Q_\rho ^2 - G W \left( \epsilon _0 (f^2-1)^2 + \epsilon _1\right) \bigg ) \nonumber \\{} & {} \qquad + 8 e^4 G r^6 W\left( g^2 Q_f^2 - f^2 G W \rho ^2\right) =0. \end{aligned}$$
(70)

The eighth-order term yields \(V=0\). The fourth-order and the sixth-order terms give, respectively,

$$\begin{aligned} Q_\rho= & {} \pm \sqrt{G W}\sqrt{\frac{ (f^2-1)^2}{g^2}+\frac{\epsilon _1}{e^2}}, \end{aligned}$$
(71)
$$\begin{aligned} Q_f= & {} \pm \frac{\sqrt{G W}\rho f}{g}. \end{aligned}$$
(72)

The BPS equations are thus

$$\begin{aligned} \rho '= & {} \pm \frac{1}{r^2} \sqrt{\frac{W}{G}} \sqrt{\frac{ (f^2-1)^2}{g^2}+\frac{\epsilon _1}{e^2}},\end{aligned}$$
(73)
$$\begin{aligned} f'= & {} \pm \frac{1}{2}g\rho f \sqrt{\frac{G}{W}}. \end{aligned}$$
(74)

The energy bound of this monopole can be found in a similar way as in Eq. (42). Substituting Eqs. (73) and (74) into the Lagrangian (66) and integrating it gives

$$\begin{aligned} E= & {} 4\pi \int _0^\infty \textrm{d}r\left\{ G(\rho ) \left[ \frac{r^2{\rho '}^2}{2} +\frac{f^2 \rho ^2}{4}\right] \right. \nonumber \\{} & {} \left. + W(\rho )\left[ \frac{1}{2e^2 r^2}\left\{ \epsilon _0 (f^2-1)^2 +\epsilon _1 \right\} +\frac{{f'}^2}{g^2 }\right] \right\} \nonumber \\= & {} 4\pi \int _0^\infty \textrm{d}r \left\{ G(\rho ) \left[ \frac{W(\rho )}{2 G(\rho ) r^2}\left( \frac{ (f^2-1)^2}{g^2}+\frac{\epsilon _1}{e^2}\right) \right. \right. \nonumber \\{} & {} \left. +\frac{f^2 \rho ^2}{4}\right] + W(\rho )\left[ \frac{1}{2e^2 r^2}\left\{ \epsilon _0 (f^2-1)^2 +\epsilon _1 \right\} \right. \nonumber \\{} & {} \left. \left. +\frac{G(\rho )}{W(\rho )} \frac{\rho ^2 f^2}{4} \right] \right\} \nonumber \\\ge & {} 4\pi \int _0^\infty \textrm{d}r \left\{ W(\rho ) \left( \frac{ (f^2-1)^2}{g^2 r^2}+\frac{\epsilon _1}{e^2 r^2} \right) \right. \nonumber \\{} & {} \left. +G(\rho ) \frac{f^2 \rho ^2}{2} \right\} . \end{aligned}$$
(75)

The bound is determined by the forms of \(G(\rho )\) and \(W(\rho )\).

6 Conclusions

The possible existence of a magnetic monopole in electroweak theory is what makes the Cho–Maison monopole theoretically appealing. However, its singular energy problem must be resolved before any serious experimental result can be claimed. Zhang, Zhou, and Cho in [28] regularize the electroweak monopole by means of renormalization of the “bare” electromagnetic permittivity. Once the finite energy is achieved, it is only natural to ask whether the BPS solutions that saturate the lowest energy bound exist. In this paper we employ the BPS Lagrangian method to systematically generate such solutions.

The nature of the electroweak Cho–Maison monopole opens up degeneracy in its BPS states, not found in the t’Hooft–Polyakov case. ZZC reported that for a given regularized Lagrangian, there can exist at least two sets of BPS equations, each having a different energy bound. Using the BPS Lagrangian method, we report a new set of BPS equations within the ZZC model, Eqs. (40) and (41). These equations are not reducible to the known BPS states in the ZZC paper [28] The solutions depend on n, the polynomial power of the permittivity expansion. The corresponding energy bound (in the limit of \(n\rightarrow \infty \)) is \(E\simeq 3.569\) GeV. This value is higher than the lowest energy bound predicted by ZZC, but still within the allowed theoretical window.

In this work we also consider several other regularization proposals and apply the BPS method to extract their corresponding BPS states. The first is the Born–Infeld extension in the hypercharge sector [39]. In this model, the Born–Infeld modification does not enter the field equations but does regularize the energy. We obtain the BPS equations (56) and (57), which are the same as those obtained in [41], and only differ from the t’Hooft–Polyakov equations by a factor of 1/2. An immediate extension to the first model is an electroweak monopole with Born–Infeld form in both the hypercharge and Yang–Mills sectors. This model was considered in [42]. The SO(3) counterpart of this monopole can be found, for example, in [43]. Our investigation reveals that within the BPS Lagrangian method, no nontrivial configuration for \(\rho (r)\) and f(r) exists. It seems that having the Born–Infeld form in both the gauge sectors is too restrictive for the existence of the BPS state. For the last model we study, we construct a “generalized electroweak monopole” in the same spirit as in [29, 30], having non-canonical kinetic terms whose generalized functions G and W depend only on the Higgs field and not on its derivative. The resulting BPS equations have the factor of \(\sqrt{W/G}\) in both \(\rho '(r)\) and \(1/f'(r)\), as shown in Eqs. (73) and (74).

Finally, we should comment on the limitation of the Bogomolny method we employ. It is surprising that the method gives us a new set of distinct BPS equations, Eqs. (40) and (41). But what is more intriguing is that they are the only BPS solutions for the ZZC model of the electroweak monopole using this mechanism. Surely this means that the method cannot probe the possible existence of other BPS solutions. Secondly, it is well known that every topological soliton solution is labeled by its topological charge, and there is a relation between the BPS energy and the charge. However, in this BPS method, the direct relation seems to be absent. The BPS Lagrangian \(\mathcal {L}_\textrm{BPS}\) cannot be expressed as a total differential, whose integral does not give us the boundary term (i.e, the topological charge),

$$\begin{aligned} E_\textrm{BPS}\ne Q. \end{aligned}$$
(76)

Lastly, this method fails to give us the BPS equations for the ACK model [42] described by the Lagrangian (58). The method leads to three incompatible conditions for the function \(Q_{\rho }\), which amounts to having trivial solutions (65). At the moment it is not yet clear whether this failure is due to the BPS method or to the structure of the non-Abelian Born–Infeld monopole itself. The Grandi–Moreno–Schaposnik monopole [43] is not known to have BPS states. In any case, Atmaja in [44] suggests how to generalize the \(\mathcal {L}_\textrm{BPS}\) by introducing non-boundary terms. These terms can later be determined from the constraints of the system. It would be interesting to see whether this approach can be applied to the electroweak monopole case to solve our problems. This will be the topic of our forthcoming publications.