Abstract
We construct nonassociative quasi-stationary solutions describing deformations of Schwarzschild black holes, BHs, to ellipsoid configurations, which can be black ellipsoids, BEs, and/or BHs with ellipsoidal accretion disks. Such solutions are defined by generic off-diagonal symmetric metrics and nonsymmetric components of metrics (which are zero on base four dimensional, 4-d, Lorentz manifold spacetimes but nontrivial in respective 8-d total (co) tangent bundles). Distorted nonassociative BH and BE solutions are found for effective real sources with terms proportional to \(\hbar \kappa \) (for respective Planck and string constants). These sources and related effective nontrivial cosmological constants are determined by nonlinear symmetries and deformations of the Ricci tensor by nonholonomic star products encoding R-flux contributions from string theory. To generate various classes of (non) associative /commutative distorted solutions we generalize and apply the anholonomic frame and connection deformation method for constructing exact and parametric solutions in modified gravity and/or general relativity theories. We study properties of locally anisotropic relativistic, optically thick, could and thin accretion disks around nonassociative distorted BHs, or BEs, when the effects due to the rotation are negligible. Such configurations describe angular anisotropic deformations of axially symmetric astrophysical models when the nonassociative distortions are related to the outer parts of the accretion disks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Motivations for nonassociative geometry, physics and gravity
Nonassociative algebras and nonassociative and noncommutative theories have a long and diverse history in mathematics and physics. We cite [1,2,3,4,5] for introductions and reviews of results beginning with the middle of the nineteenth century up to last few years containing various developments and applications in quantum field/gravity and string theories. For instance, the algebra octonions is an example of noncommutative Jordan algebras which provided the first example of appearance of nonassociativity in physics. Papers [6, 7] are for early approaches to nonassociative quantum mechanics, and [8,9,10,11,12,13,14,15,16] are for further developments and references on noassociative algebras and mathematical particle physics.
In open string theories, nonassociative structures are present due to a non-vanishing background 2-form in the world volume of a D-brane. Such structures exist also for closed strings, for instance, as consequences of flux compactification with non-trivial three-form and related non-geometric backgrounds. Various related and/or alternative approaches to noncommutative geometric flows, noncommutative and nonassociative gravity and gauge theories, membranes and double field theory, etc. were studied in [12, 17,18,19,20,21,22,23,24] and references therein. In this work, we do not attempt to review all subjects on nonassociative physics and gravity and do not provide a comprehensive list of references, which can be found in [3,4,5, 25, 26].
A few years ago a geometric approach leading to nonassociative gravity, with star product (in brief, \(\star \)) deformations determined by R-flux backgrounds of string theory and modelled on a phase space \({\mathcal {M}}\) enabled with nonassociative geometric objects, has been provided and elaborated in [3, 4]. A unique nonassociative Levi-Civita connection (LC-connection \(\nabla ^{\star }),\) which is torsionless and compatible with respective \(\star \)-deformed symmetric and nonsymmetric metric structures, was derived in [4]. In that work the nonassociative geometric constructions were performed in a form which is covariant under the quasi-Hopf algebra [27] generated by infinitesimal diffeomorphisms on twisted nonassociative phase space. The nonassociative vacuum gravitational equations,
were introduced for star deformations of the standard Ricci tensor in general relativity, GR, to a nonassociative \(Ric^{\star }[\nabla ^{\star }]\), where \(\nabla ^{\star }\) is defined and computed on \({\mathcal {M}}\). The coefficient formulas were derived for Moyal–Weyl products formulated with respect to tensor products involving coordinate bases extended on phase space. Abstract definitions of fundamental geometric objects were provided in [3, 4] but without details on arbitrary frame and coframe (dual frame) decompositions. Here we note that in the mentioned approach the coefficient formulas for nonassociative geometric and physical objects on phase spaces depend both on spacetime and momentum like coordinates (the last ones are with respective multiplications on complex unity \(i^{2}=-1\)).
One of the original motivations for developing nonassociative geometric models was to construct a nonassociative theory of gravity on a spacetime V encoding \({\star }\)–deformations via certain type R-flux contributions from string/brane theory, or other type theories. For physical applications, we can consider V as a four dimensional, 4-d, spacetime Lorentz manifold using fundamental geometric objects defined as in GR. We can elaborate also on various models of modified commutative and noncommutative gravity theories, MGTs, which can be for 5-d, or 6-d, base spacetimes. The geometry of a (total) nonassociative phase space \({\mathcal {M}}\) can be modelled on a cotangent bundle \(T^{*}V\) enabled with star product and R-flux deformations. In [4], it was obtained also a very important result for computing the Ricci tensor of nonassociative gravity in a form with parametric decomposition on \(\hbar ,\) the Planck constant, and \( \kappa :=\ell _{s}^{3}/6\hbar \). In theories modelled on effective phase spaces, \(\kappa \) can be considered as a string constant to be determined by experimental data or from some theoretic assumptions. Projecting nonassociative geometric models from phase space to spacetime, \({\mathcal {M}} \rightarrow V\), with \(\nabla ^{\star }\rightarrow \ ^{V}\nabla ,\) we can compute star parametric deformations of the nonassociative Ricci tensor, \( Ric^{\star }[\nabla ^{\star }]\rightarrow Ric^{\circ }[\ ^{V}\nabla ]\), when
describes real star R-flux deformations induced on base spacetime V. In these formulas, \(Ric[\ ^{V}\nabla ]\) is the usual Ricci tensor of a LC-connection \(\ ^{V}\nabla \) for a pseudo-Riemannian metric \( g=\{g_{no}(x^{k})\}\) of signature \((+++-)\) on a spacetime V; coordinate spacetime indices run values \(i,j,k,...=1,2,3,4;\) partial derivatives \( \partial _{j}=\partial /\partial x^{j}\) define a local coordinate base/frame. In our notations, the anti-symmetric tensor \({\mathcal {R}}^{jkm}\) defines R-flux contributions via some nontrivial constant values with respect to a chosen coordinate basis \(\partial _{n}\) (such a tensor may depend on space and cofiber coordinates for frame transforms on \({\mathcal {M}}\) ); and the anti-symmetric tensor \(B_{jkm}\) is a functional of respective operators and geometric objects.Footnote 1 The Eqs. (1) and (2) present starting points for constructing models of nonassociative gravity theory which encode the low-energy effective dynamics of closed strings in so-called non-geometric backgrounds.
1.2 Geometric methods for constructing exact and parametric solutions in nonassociative gravity
Geometric and physical models on (non) associative phase spaces are formulated for geometric objects depending both on spacetime and phase coordinates, for instance, with metrics \(g_{\alpha \beta }(x^{i},p_{a}),\) where indices \(\alpha ,\beta ,...=1,2,...8,\) are used as total phase space ones; \(i,j,k,..=1,2,3,4\) are used for spacetime indices and \( a,b,c,...=5,6,7,8\) are cofiber ones. The nonassociative gravity models elaborated in [3, 4] may be considered as certain nonassociative generalizations and modifications (in some special cases with LC-connections and coordinate frames) of (non) commutative Finsler–Lagrange–Hamilton and higher dimension (super) string gravity theories, various MGTs, studied in a series of our works [28,29,30], see recent reviews and methods of constructing exact solutions in phase spaces in [31, 32].
In Refs. [3, 4], there were emphasized three tasks for further developments of nonassociative gravity which we approach in our research program (in this and partner works [25, 26], and future ones):
-
1.
construct exact/parametric solutions of nonassociative vacuum gravitational equations (1);
-
2.
study further generalizations for nontrivial matter sources; and
-
3.
elaborate on possible applications of such theories in modern particle physics, cosmology and astrophysics.
The main technical difficulty in elaborating on above directions of research is that all types of modified (non) associative/commutative gravitational and geometric flow theories are described by sophisticated nonlinear systems of partial differential equations, PDEs, with coupling and mixing of indices of geometric objects. To find exact and parametric solutions we have to use certain coordinate and frame decompositions. Such (non) associative/ commutative tensor and product coupling and/or mixing are consequences of various conditions and constraints imposed on coefficients. For example, the star products are defined via contractions with R-flux coefficients \({\mathcal {R}}^{jkm}\) and the metric compatibility and zero torsion conditions are introduced for the LC-connection. In GR, a decoupling of Einstein equations is possible, for instance, for diagonal metric ansatz depending on one space variable (radial type). As a result, the vacuum and nonvacuum gravitational equations stated as systems of nonlinear PDEs transform into respective systems of decoupled ordinary differential equations, ODEs. For such assumptions, it is possible to construct black hole, BH, solutions; when there are considered additional spherical symmetry and asymptotic conditions resulting in the Newton gravitational potential of a point mass particle. This method can be generalized in certain forms for generating, for instance, BHs with rotation and nontrivial sources (we can consider a nontrivial cosmological constant); for wormholes; with nontrivial algebraic structures, in cosmological models, when metrics depend on a time like variable etc. The bulk of physically important exact and parametric solutions described, for instance, in standard monographs [33,34,35,36], are constructed for certain very special type ansatz (usually diagonalizable via coordinate transforms) transforming PDEs into ODEs with decoupling of tensor coefficients. There were studied also certain cases with solitonic gravitational metrics for various classes of nonlinear waves when PDEs are solved using other geometric and analytic techniques. Such methods can not be applied if our aim is to find exact solutions with generic off-diagonal metricsFootnote 2 of type \(g_{kj}(x^{i})\) and/or \(g_{\alpha \beta }(x^{i},p_{a})\) depending on some spacetime/phase space coordinates, generalized connections and/or LC-connections, even we project all geometric objects and equations on a GR background.
In a series of works [31, 32, 37, 38], see also references therein, we developed the so-called anholonomic frame and connection deformation method, AFCDM (in previous works, we wrote AFDM) to a level which allows us to prove some general decoupling and integrability properties of modified gravitational field and geometric flow equations on phase spaces. For nonassociative vacuum gravity models on star deformed \(V \rightarrow {\mathcal {M}}\), and with effective sources determined by R-fluxes of type (2), we elaborated nonholonomic versions of nonassociative geometry and gravity in two partner works [25, 26]. The main idea of the AFCDM is to redefine the geometric constructions on \( {\mathcal {M}}\) and V in certain nonholonomic bases,Footnote 3 when using an auxiliary linear connection \(\widehat{{\mathbf {D}}}^{\star }=\nabla ^{\star }+\widehat{\mathbf {Z }}^{\star }\) we can prove certain general decoupling properties of physically important systems of PDEs. This way, we can generate certain very general classes of exact/parametric solutions determined by generic off-diagonal symmetric and nonsymmetric metrics, respectively, \({}_{\star }^{\parallel }\mathfrak {\check{g}}\) and \({}_{\star }^{\parallel }{\mathfrak {a}}\). Such metrics depend, in principle, on all phase space coordinates, with coefficients parameterized by off-diagonal matrices \(g_{\alpha \beta }(x^{i},p_{a})\). In explicit form, the coordinate and parametric dependencies are determined by respective classes of generating functions and generating (effective) sources. For vacuum nonassociative gravitational equations, a general decoupling property was proven in [26] for a large class of quasi-stationary solutions with Killing symmetry on \(\partial _{4}=\partial _{t}\) on the first two shells for nonholonomic dyadic decompositions of \({\mathcal {M}}\). The results of that paper will be used for further developments and applications of nonassociative geometric methods in modern gravity, cosmology and astrophysics, non-standard particle theories, etc., by constructing nonassociative locally anisotropic BH and cosmological solutions generalizing the constructions reviewed in [32].
The nonassociative vacuum phase equations (1) and related spacetime equations (2) can be considered as some 4-d curved spacetime Einstein equations with an effective real source proportional to \( \hbar \kappa \) encoding star deformations and R-fluxes from a generalized co-fiber dynamics projected on V. Re-defining such systems of nonlinear PDEs in nonholonomic variables, we can construct generic off-diagonal quasi-stationary solutions (when the coefficients of metrics and connections depend only on space coordinates in certain adapted systems of reference). There is a rigorous proof in [26] that nonassociative vacuum Einstein equations (1) can be decoupled in general form for quasi-stationary phase spaces and a nontrivial cosmological constant. Using such a decoupling property and respective classes of nonlinear symmetries, we can encode the cofiber dynamics into real effective R-flux sources as in (2) and/or cosmological constants. As a result, we work self-consistently with 4-d Einstein equations for nonassociative distortions of off-diagonal components of metrics. Exact and parametric solutions (locally anisotropic quasi-stationary and/or cosmological ones) can be constructed applying the AFCDM method and results of [32] redefined in this work for real sources with R-fluxes. Using off-diagonal real nonholonomic vacuum configurations, we can compute also as parametric induced values respective nonsymmetric components of star-deformed metrics and complex parametric sources. This formalism can be elaborated independently for the first two nonholonomic dyadic shells on a 4-d spacetime. In general, there are 4 dyadic oriented shells on a 8-d phase space and such methods are elaborated in [26]. Those formulas will be used in our further partner works in order to construct, for instance, nonassociative BH and solitonic solutions on 8-d phase spaces generalizing some respective classes of solutions from [37, 38].
1.3 Main purposes of the paper
In this work, we concentrate on a particular class of black hole, BH, and black ellipsoid, BE, configurations with thin accretion disks determined by nonassociative distorted solutions in 4-d modified gravity encoding effective R-flux sources as in (2). The first goal is to construct such generic off-diagonal parametric solutions in explicit form and consider the conditions when quasi-stationary metrics describe BEs (which are different from the Kerr metrics) and may transform into Schwarzschild like BH configurations. It should be noted that the spacetime in the vicinity of respective horizons with zero effective cosmological constants may remain vacuum if we relax the condition of asymptotically flatness for quasi-stationary R-flux distorted metrics. We proved that BEs can be stable in various variants of modified (non) commutative gravity and geometric flow theories (including associative gravity models with nonsymmetric metrics, string gravity etc.) and in GR with spacetime and/or matter distortions [29, 39, 40]. Those constructions were for nonholonomic generalizations of Chandrasekhar’s equilibrium conditions and formulas on stability of BH solutions [41]. We can extend the geometric constructions and methods for solutions constructed in this paper because we use the same AFCDM but for different types of effective sources which can be stabilized by corresponding classes of nonholonomic constraints.
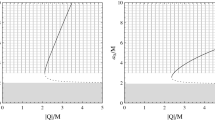
The second goal of this paper is to study in brief the properties of relativistic thin disks around nonassociative distorted Schwarzschild BHe and BEs up to the quadrupole approximations. For associative and commutative models, such constructions are reviewed in [42, 43]. The effective R-flux source can be treated similarly to an external mass type distribution resulting in distortions with contributions of the outer parts of the disk. Self-gravity and star product deformation effects play also important roles. Using the nonassociative distorted geometry, we can also study the inner part of locally anisotropic thin accretion disks. In this paper, the anisotropy will be stated by dependencies on an angular type space coordinate \(x^{3}=\phi .\) For respective classes of generating functions, we can describe stable ellipsoidal orbits encoding contributions from effective R-flux sources.
The plan of the article work is as follows: in Sect. 2, we outline necessary results on nonassociative geometry and effective R-sources for vacuum gravitational equations with nonholonomic 2 + 2 decoupling. Section 3 is devoted to explicit constructions of quasi-stationary 4-d generic off-diagonal and BH and BE solutions encoding nonassociative star deformation and R-flux real effective sources. We study possible physical effects of locally anisotropic thin accretion discs around nonassociative BEs and BHs determined by nonassociative distortions in Sect. 4. Conclusions are provided in Sect. 5.
2 Nonholonomic 2 + 2 spacetime splitting and nonassociative vacuum Einstein equations
The geometric preliminaries on nonassociative star R-flux deformations presented in this section refer to a four dimensional, 4-d, nonholonomic spacetime projection of the nonholonomyc dyadic phase space geometry and vacuum gravity formulated for 8-d (co) tangent Lorentz bundles in [26]. Such associative and commutative geometric methods for 6–10 dimensions are elaborated in details and reviewed in [31, 32, 40]. For a phase space \({\mathcal {M}}\) enabled with nonholonomic dyadic shell \(s=1,2,3,4\) structure corresponding to a conventional nonholonomic (2 + 2)+ (2 + 2) splitting (in brief, called a s-decomposition), it is possible to prove a general decoupling property of nonassociative vacuum gravitational equations formulated for a canonical distinguished connection \(\widehat{{\mathbf {D}}}^{\star }=\nabla ^{\star }+\widehat{{\mathbf {Z}}}^{\star }\). Such a nonassociative linear distinguished connection, d–connection, can be nonholonomically constrained for zero distortions, \(\widehat{{\mathbf {Z}}} ^{\star }=0,\) to \(\nabla ^{\star }\). This can be used for generating solutions of the nonassociative Einstein equations for a Levi Civita, LC, connection with nontrivial cosmological constants and effective R-flux sources generalizing the methods and solutions presented in [32]. On 4-d nonholonomic spacetimes V with a corresponding nonholonomic (2 + 2)-splitting, the nonassociative vacuum equations (1) with real R-flux induced sources (2) can be solved using star deformations of constructions from [37, 38], considered for shells \(s=1,2.\)
2.1 Nonassociative nonholonomic star products from real R-flux sources, metrics and connections
In the partner works [25, 26], the nonassociative vacuum Einstein equations from [3, 4] were re-defined and generalized in canonical nonholonomic variables on a phase space modeled as a cotangent Lorentz bundle \({\mathcal {M}}=T_{\parallel }^{*}\mathbf {V.}\) Such variables are enabled with nonlinear connection, N-connection structure \(\ ^{\parallel }{\mathbf {N}}\) and a N-adapted star product defined with respect to general frame structures. That allowed to develop the AFCDM and prove a general decoupling property and construct exact and parametric solutions in nonassociative gravity when the geometric constructions are adapted to a s-connection structure \({}_{s}^{\parallel }{\mathbf {N}}\) and a nonholonomic s-decomposed nonassociative phase space \({\mathcal {M}}=T_{s\parallel }^{*}\mathbf { V.}\)Footnote 4
2.1.1 Nonlinear connections with dyadic splitting and nonassociative star product
We outline for nonholonomic spacetime shells \(s=1\) and 2 the definitions and necessary formulas from Sect. 2.1 of [26].
Nonholonomic dyadic decomposition (s-decomposition):
We can define in global form (2 + 2) + (2 + 2) nonholonomic splitting of phase spaces considering respective classes of N–connection structures (s-connections, with \(s=1,2\) when \(s=3,4\) contribute indirectly via certain effective sources):
Such dyadic decompositions into conventional 2-dim nonholonomic distributions of TTV, \(TT^{*}V\) and \(TT_{\parallel }^{*}V\) involve dimensions \(\dim (\ ^{1}hT^{*}V)=\dim (\ ^{2}vT^{*}V)=\dim (\ ^{3}cT^{*}V)=(\ ^{4}cT^{*}V)=2\) and \(\dim (\ ^{1}hT_{\parallel }^{*}V)=\dim (\ ^{2}vT_{\parallel }^{*}V)=\dim (\ ^{3}cT_{\parallel }^{*}V)=(\ ^{4}cT_{\parallel }^{*}V)=2\), where, for instance, left up labels like \(\ ^{1}h,\ ^{3}c\) etc. state that using nonholonomic (equivalently, anholonomic and/or non-integrable) distributions we split respective 8-d total spaces into oriented 2-d shells with numbers 1, 2, 3 and 4.
On a Lorentz spacetime manifold \({\mathbf {V}},\) nonholonomic dyadic splitting with N-connections (3) are defined locally by coefficients \({}_{2}^{\parallel }{\mathbf {N}}=\{N_{i_{1}}^{i_{2}}(x^{i_{1}},x^{a_{2}})\}\) used for constructing N-elongated bases (N-/s-adapted bases),
where we follow the conventions for dyadic indices and coordinates stated in footnote 4.
For dual shell s-adapted bases to (4), s-cobases, we have
defined by the same N-connection coefficients and respective s-decomposition which can be considered on spacetime and extended on phase spaces.
2.1.2 Nonassociative star product and dyadic s-structures
In our partner works [25, 26], we generalized for nonholonomic phase spaces endowed with N- /s–connection structure the definition of nonassociative star product. For coordinate bases, such formulas transform respectively into those presented is section 2 of [3] and section 2 of [4]. Here we provide necessary definitions for shells \(s=1,2\).
Considering a full phase space \({\mathcal {M}}\) containing a spacetime direction \(\ ^{\shortmid }{\mathbf {e}}_{i_{s}}\) and a momentum like cofiber direction \(\ ^{\shortmid }e^{b_{s}},\) see formulas (4), for any two functions \(\ z(x,p)\) and \(\ q(x,p),\) we define a nonholonomic s-adapted star product \(\star _{s}\):
In these formulas, the constant \( \ell \) defines the R-flux contributions for a antisymmetric \(R^{i_{s}j_{s}a_{s}}\) background in string theory, with s-indices. We can restrict the definitions for any \(s=1\) and \( s=2,\) when the R-flux contracts with momentum like coordinates in an un-stated explicit form if you consider only the base spacetime V. In these formulas, the tensor product \(\otimes \) is used in a s-adapted form indicating on which factor of \(z\otimes q\) the s-adapted derivatives act with the dot form (for many computations with small parametric decompositions on \(\hbar \) and \(\kappa = \ell _{s}^{3}/6\hbar ,\) the tensor products turn into usual multiplications).
2.1.3 Symmetric and nonsymmetric spacetime s-metric structures and star deformations
For total phase space models, a (pseudo) Riemannian symmetric metric on cotangent Lorentz bundle \(T^{*}V\) is defined by a tensor \(\ ^{\parallel }g=\{\ ^{\parallel }g_{\alpha \beta }\}\in \) \(TT^{*}V\otimes TT^{*}V\) of local signature \((+,+,+,-;+,+,+,-).\) Such a metric structure can be expressed in a nonholonomic dyadic form for shells \( s=1,2,3,4\) as a s-metric on phase space \({\mathcal {M}}={\mathbf {T}} _{\parallel }^{*}\mathbf {V.}\) We state nonholonomic 2 + 2 decompositions of geometric objects on the first two shells \(s=1,2\) if we consider symmetric tensor products of s-bases \(\ ^{\parallel }\mathbf {\ e }^{\alpha _{2}}\in T_{2}^{*}{\mathbf {T}}_{\parallel }^{*}\mathbf {V }\) (4),
For star products and R-flux deformations to nonassociative geometry, symmetric metrics transform, in general, into symmetric and nonsymmetric ones [3, 4] (for nonholonomic N-/s-adapted constructions, see respectively [25, 26]). We use such s-adapted parameterizations (s-metrics)
On spacetime V and considering coordinate bases, when \(\ ^{\parallel } {\mathbf {e}}^{\alpha _{2}}\rightarrow \ ^{\parallel }e^{\alpha _{2}}=d\ ^{\parallel }u^{\alpha _{2}}\in hT_{\parallel }^{*}V\), we can omit the shell/dyadic label s. Respective star deformed metric structures can be written in generic off-diagonal forms,
The coefficients in above formulas are related via frame transforms,
relating respective dyadic decompositions with off-diagonal matrices.
2.1.4 Canonical s-connections, (2 + 2)-splitting, and distortions of LC-connections
Choosing a s-metric \({}_{s}^{\parallel }{\mathbf {g}}\) \(\rightarrow {}_{2} {\mathbf {g}}\) (7), we can define two important linear connections and respective phase space and spacetime projections:

A s-operator \({}_{s}^{\parallel }\widehat{{\mathbf {D}}}=(h_{1}\ ^{\parallel }\widehat{{\mathbf {D}}},\ v_{2}\ ^{\parallel }\widehat{ {\mathbf {D}}},\ c_{3}\ ^{\parallel }\widehat{{\mathbf {D}}},\ c_{4}\ ^{\parallel }\widehat{{\mathbf {D}}})\) acts on tangent spaces of phase space, i.e. on \(T{\mathbf {T}}_{\parallel }^{*}{\mathbf {V}},\) with dyadic (co) vertical splitting, being a s-connection adapted to a N–/s-connection structure \({}_{s}^{\parallel }\mathbf {N.}\) Such linear (affine) connections and N-connections and their s-torsion are nonholonomic when the torsions of type \(\ ^{\parallel }\widehat{{\mathcal {T}}},\) etc. are computed in standard form. We use “hat” labels in order to emphasize that such s-adapted values are determined by a s-metric structure following certain nonholonomic constraints involving (partial) zero torsion and metric compatibility conditions. When such values are computed on the spacetime shells \(s=1\) and 2 and trivial co-fibers \(c_{3}\) and \(c_{4},\) we can omit the label “\(^{\parallel \text {''}}\) and write \({}_{2}\widehat{ {\mathbf {D}}}=(h_{1}\widehat{{\mathbf {D}}},\ v_{2}\widehat{{\mathbf {D}}}).\) The LC-connection \(\ ^{\parallel }\mathbf {\nabla =}\) \({}_{s}^{\parallel }\mathbf {\nabla }\) and its spacetime projection \({}_{2} \mathbf {\nabla }\) are not a d-/ or s-connections because such linear connections do not preserve any N-/s-connection splitting and/or dyadic decompositions under parallel transports in respective phase space and spacetime.
In [25, 26], we provide all abstract and N- / s-adapted formulas for canonical s-connections and their distortions on \(T{\mathbf {T}} _{\parallel }^{*}\mathbf {V.}\) Here, we consider some important nonholonomic formuls for 2 + 2 spacetime splitting and \({}_{2}^{\parallel }\widehat{{\mathbf {D}}}\) which are important for our further considerations. We can check by straightforward computations that the respective conditions from (11) are satisfied by such s-coefficients,
We can compute a canonical distortion relation to a canonical s-connection, or respective spacetime canonical d-connection,
For instance, the distortion s-tensor, \({}_{s}^{\parallel }\widehat{ {\mathbf {Z}}}= \{\ ^{\parallel }\widehat{{\mathbf {Z}}}_{\ \beta _{s}\gamma _{s}}^{\alpha _{s}} [\ ^{\parallel }\widehat{{\mathbf {T}}}_{\ \beta _{s}\gamma _{s}}^{\alpha _{s}}]\}\) from (13) is an algebraic combination of the coefficients the canonical torsion s-tensor \({}_{s}^{\parallel }\widehat{{\mathcal {T}}}=\{\ ^{\parallel }\widehat{ {\mathbf {T}}}_{\ \beta _{s}\gamma _{s}}^{\alpha _{s}}\}\) of \({}_{s}^{\parallel }\widehat{{\mathbf {D}}}.\) Similar algebraic combinations can be defined for the nonholonomic spacetime projections with \(s=1,2\).
2.1.5 Canonical nonholonomic Ricci and Einstein d-tensors for (2 + 2)-splitting
For all types of linear connections defined in (11), we can define and compute in standard forms as in metric-affine geometry respective torsions, see details on (non) associative formulations in [25, 26]. Here we provide necessary formulas without details on computations of s-adapted coefficients of torsions and curvatures using derivatives and contractions with s-connection and s-metric coefficients. For a nonholonomic spacetime (2 + 2)-splitting, there are considered fundamental geometric objects like torsions \({}_{\nabla }^{2}{\mathcal {T}}=0\) and \({}_{2}\widehat{{\mathcal {T}}},\) and curvature, \({}_{\nabla }^{2}\mathcal {R }=\{{}_{\nabla }R_{\ \beta _{2}\gamma _{2}\delta _{2}}^{\alpha _{2}}\}\) and \( {}_{2}^{\parallel }\widehat{{\mathcal {R}}}=\{\ ^{\parallel }\widehat{ {\mathbf {R}}}_{\ \beta _{2}\gamma _{2}\delta _{2}}^{\alpha _{2}}\},\) s-tensors.
The canonical Ricci s-tensor on the first two shells, \({}_{2}\widehat{ {\mathcal {R}}}ic=\{\widehat{{\mathbf {R}}}_{\ \beta _{2}\gamma _{2}}:=\ \widehat{ {\mathbf {R}}}_{\ \alpha _{2}\beta _{2}\gamma _{s}}^{\gamma _{2}}\}\), is characterized by such a splitting of s-adapted coefficients,
Using two linear connections (11), we define two different scalar curvatures,
The modified Einstein equations for \(({}_{2}\mathbf {g,}{}_{2}\widehat{ {\mathbf {D}}})\) on \({\mathbf {T}}_{2\parallel }^{*}{\mathbf {V}}\) with a nontrivial cosmological constant \(\ ^{\parallel }\lambda \) can be postulated using the same geometric principles as in GR.Footnote 5 In abstract geometric form (see, for instance, [33]), re-defining the geometric constructions for nonholonomic Lorentz manifolds/(co) bundles [31], we write
The value \({}_{2}{\widehat{E}}n=\{\ {\widehat{E}}_{_{\alpha _{2}\beta _{2}}}\}\) is by definition the canonical Einstein d-tensor. The cosmological constant \( \ ^{\parallel }\lambda \) encodes as an effective source certain contributions from cofiber dynamics of phase space. If we completely ignore such possible contributions, we should write \(\ ^{\parallel }\lambda =\) \(\lambda \) and work with nonholonomic 2 + 2 splitting and Einstein manifolds for the canonical d-connection. It should be emphasized that \({}_{2}\widehat{{\mathbf {D}}}({}_{2}{\widehat{E}} n)\ne 0.\) This means that the conservation laws on nonholonomic manifolds are subjected to additional non-integrable constraints (similar constructions are considered in nonholonomic mechanics). Using distortions (13), we can always nonholonomically deform such systems of nonlinear PDEs into equivalent ones, \({}_{2}{\widehat{E}}n\rightarrow {}_{\nabla }En,\) when \({}_{2}\nabla ({}_{\nabla }En)=0.\) Such canonical s-distortions are determined by respective distortions of the curvature and Ricci tensors,
In these formulas, the distortion s-tensors \({}_{\nabla }\widehat{{\mathcal {Z}} }\) and \({}_{\nabla }\widehat{{\mathcal {Z}}}ic\) are correspondingly determined by \(({}_{2}\widehat{{\mathbf {Z}}},{}_{2}\mathbf {g)}\) on a (pseudo) Riemannian phase background with LC-connection \(\ ^{2}\nabla \) encoding the N-connection coefficients for a nonholonomic 2 + 2 splitting. We omit abstract and cumbersome s-adapted/coordinate formulas for such s-objects and respective geometric and physical systems of PDEs. Finally, we note that all geometric constructions can be performed equivalently working with different geometric data \(\left( {}_{2}{\mathbf {g}},\ ^{2}\nabla \right) \) and/or \(({}_{2}{\mathbf {g}},{}_{2}{\mathbf {N}},{}_{2}\widehat{{\mathbf {D}}})\) if we prescribe a zero, or non-zero cosmological constant of type \(\ ^{\parallel }\lambda \) or \(\lambda .\)
2.2 Nonholonomic geometry of star deformed spacetime (non) symmetric d-metrics
In [3, 4], nonassocitative geometric models determined by R-flux star deformations are elaborated in coordinate frames and beginning with a flat (co) fiber metric \(\mathbf {\ ^{\parallel }} \eta .\) Star products \(\star \) are defined in terms of coordinate bases \( \mathbf {\ ^{\parallel }\partial }\) when nonassociative generalizations of (pseudo) Riemann geometry are constructed with symmetric, \({}_{\star }^{\parallel }g,\) and nonsymmetric, \({}_{\star }^{\parallel } \mathsf {G,}\) star-metric structures and a related nonassociative variant of LC-connection \(\mathbf {\ ^{\parallel }}\nabla ^{\star }.\) Conventionally, there are considered star-deformations of geometric structures when \((\ ^{\parallel }\eta ,\ ^{\parallel }\partial ,\ ^{\parallel }\nabla )\rightarrow (\star \ ,\ {\mathcal {A}}^{\star },{}_{\star }^{\parallel }g,{}_{\star }^{\parallel }{\mathsf {G}},\ \ ^{\parallel }\partial \ ^{\parallel }\nabla ^{\star }),\) when the constructions are adapted to quasi-Hopf algebras \(\ {\mathcal {A}}^{\star }\), or other type algebraic and geometric structures. In such an approach, it is difficult technically to decouple physically important systems of nonlinear PDEs.
2.2.1 Convention 2 for nonassociative phases with nonholonomic spacetime shells
In our recent partner works [25, 26], we followed Convention 2 on constructing nonassociative nonholonomic geometries which allow the application of the AFCDM for constructing exact solutoins of graviational and geometric flow equations. In this paper, we adapt those assumptions for study nonholonomic vacuum Einstein equations with 2 + 2 splitting and effective sources encoding star and R-flux contributions form the total 8-d phase space.
Convention 2 (extended) on nonholonomic constraints from nonassociative phase spaces to spacetime configurations: On phase spaces, star products (6) are defined via nonholonomic dyadic decompositions on \(\ ^{\parallel }{\mathbf {e}}_{\alpha _{s}}\) with R-flux terms and there are computed respective star deformations of canonical s-adapted geometric objects into nonassociative ones, with symmetric, \({}_{\star s}^{\parallel }{\mathbf {g}}\), and nonsymmetric, \({}_{\star s}^{\parallel }\mathbf {{\mathfrak {g}}}\), star s-metrics and canonical star s-connection \({}_{s}^{\parallel }{\mathbf {D}}^{\star },\) see definitions below (details are provided in [25, 26]). The nonholonomic dyadic star deformations of geometric canonical s-structures and their projections on the spacetime shells \(s=1,2\) are defined by such star transforms of geometric data:

for \(\ ^{\parallel }{\mathbf {D}}^{\star }=\ ^{\parallel }\nabla ^{\star }+\ ^{\parallel }\widehat{{\mathbf {Z}}}^{\star }\) and \({}_{s}^{\parallel }{\mathbf {D}}^{\star }=\ ^{\parallel }\nabla ^{\star }+{}_{s}^{\parallel }\widehat{{\mathbf {Z}}}^{\star }\) with respective spacetime 2 + 2 splitting \({}_{2}{\mathbf {D}}^{\star }={}_{2}\nabla ^{\star }+{}_{2}\widehat{{\mathbf {Z}}}^{\star }.\) This convention with transforms (17) allows us to construct large classes of generic off-diagonal solutions on 4-d spacetimes with effective sources encoding nonassociative R-flux distortions.
2.2.2 Nonsymmetric and symmetric 2 + 2 metrics and their inverses
In [26], metric s-structures in nonassociative nonholonomic differential geometry and related quasi-Hopf s-structures are studied on 8-d phase spaces. A star metric symmetric s-tensor (8) for shells \( s=1,2,3,4,\) on phase space, and \(s=1,2\) on h-v-decompositions, with R-flux induced terms on a Lorentz base manifold can be represented in the form
where the geometric objects on spacetime shells do not depend on co-fiber coordinates only on some special s-adapted bases. In general, R-flux terms connect and mix indices of all shells and we need additional assumptions on how to extract spacetime geometric objects with dependencies only on \( x^{\alpha _{2}}\) coordinates. We can work with background metrics with flat cofiber components \(c^{3}\) and \(c^{4}\) when the s-connection structure is prescribed to be nontrivial only for \(s=1,2.\) In our approach, there are considered real-valued s-adapted coefficients \({}_{\star }^{\parallel } {\mathbf {g}}(\ ^{\parallel }{\mathbf {e}}_{\alpha _s},\ ^{\parallel } {\mathbf {e}}_{\beta _s})= {}_{\star }^{\parallel }{\mathbf {g}}_{\alpha _s \beta _s}= {}_{\star }^{\parallel }{\mathbf {g}}_{\beta _s \alpha _s}\in {\mathcal {A}}_{s}^{\star }\), with respective restrictions for \(s=1,2.\) Such a s-metric and respective nonholonomic constraints for \({}_{\star s}^{\parallel }\mathbf {g\rightarrow }{}_{\star 2}^{\parallel } {\mathbf {g}}\) are both compatible with a star s-connection \({}_{s}^{\parallel }{\mathbf {D}}^{\star }\rightarrow {}_{2}^{\parallel } {\mathbf {D}}^{\star }\) if the conditions
are satisfied. We shall consider below how star deformations of s-connections and their shell projections are defined and computed, see details in [25, 26].
The models of nonassociative geometry and gravity formulated in [3, 4] involve “non-geometric” constructions when R-flux deformations result in nonsymmetric metric structures. Such geometric off-diagonal and/or d-/s-objects have to be considered additionally to the symmetric metric. A nonsymmetric metric on phase space \({\mathbf {T}} _{\parallel }^{*}{\mathbf {V}}\) with restrictions to shells \(s=1,2,\) can be defined in generic off-diagonal form with respect to local coordinate bases when
Such coefficients define, respectively, some nonsymmetric \(8\times 8\) and \( 4\times 4\) matrices but on the spacetime shells the coefficients are determined by \({\mathcal {R}}_{\quad \alpha _{2}}^{\tau \xi }\)-coefficients even \({}_{\star }^{\parallel }g_{\alpha _{2}\beta _{2}}\) are constrained to depend only on spacetime coordinates \(x^{\beta _{2}}\).
With respect to s-adapted bases \(\ ^{\parallel }{\mathbf {e}}_{\xi _{s}}\rightarrow \ ^{\parallel }{\mathbf {e}}_{\xi _{2}}\) and tensor products of their dual s-bases, a nonsymmetric s-metric structure (9) can be parameterized in a \([(2\times 2)+(2\times 2)]+\) \([(2\times 2)+(2\times 2)] \) block form which can be nonholonomically restricted to a matrix \([2\times 2]+\) \([2\times 2],\) when
Such formulas are similar to (19) but we underline the R-flux coefficients because they are re-written in s-adapted form \(\overline{ {\mathcal {R}}}_{\quad \alpha _{s}}^{\tau _{s}\xi _{s}}\) in order generate a star nonsymmetric generalization of the commutative s-metric (7). On total phase space, we can write \({}_{\star s}^{\parallel }{\mathfrak {g}} ={}_{\star }^{\parallel }{\mathfrak {g}}_{\alpha _{s}\beta _{s}}\star _{s}(\ ^{\parallel }{\mathbf {e}}^{\alpha _{s}}\otimes _{\star s}\ ^{\parallel }{\mathbf {e}}^{\beta _{s}})={}_{\star }^{\parallel } {\mathsf {G}}_{\alpha \beta }\star (\ d\ ^{\parallel }u^{\alpha }\otimes _{\star }d\ ^{\parallel }u^{\beta })\), where \({}_{\star }^{\parallel }{\mathfrak {g}}_{\alpha _{s}\beta _{s}}\ne {}_{\star }^{\parallel }{\mathfrak {g}}_{\beta _{s}\alpha _{s}}\) and \({}_{\star }^{\parallel }{\mathsf {G}}_{\alpha \beta }\ne {}_{\star }^{\parallel }{\mathsf {G}}_{\beta \alpha }.\) We can also consider nonholonomic constraints for \(s=1,2,\)
from which we can find off-diagonal \({}_{\star }^{\parallel }{\mathsf {G}} _{\alpha _{2}\beta _{2}}\) but such coefficients in coordinate bases may depend not only on \(x^{\beta _{2}}\) but also on cofiber coordinates \( p_{a_{3}}\) and \(p_{a_{4}},\) for \(s=3,4.\)
In [25, 26], we elaborated a nonholonomic and s-adapted geometric formalism for quasi-Hopf s-structures, It generalized the holonomic procedure for constructing inversions of matrices for a star quasi-Hopf algebra \({\mathcal {A}}^{\star }\) formulated in [4]. So, working in coordinates, or s-adapted frames, we can compute, for instance, the inverse matrix \(\ ^{\parallel }\overline{{\mathsf {G}}} ^{-1}=\{{}_{\star }^{\parallel }{\mathsf {G}}^{\alpha \beta }\}\) of a matrix \(\ ^{\parallel }\overline{{\mathsf {G}}}=\{{}_{\star }^{\parallel }{\mathsf {G}}_{\alpha \beta }\}\) as a solution of algebraic equations \({}_{\star }^{\parallel }{\mathsf {G}}^{\alpha \beta }\cdot {}_{\star }^{\parallel }{\mathsf {G}}_{\beta \gamma }={}_{\star }^{\parallel }{\mathsf {G}}_{\gamma \beta }\cdot \) \({}_{\star }^{\parallel }{\mathsf {G}}^{\beta \alpha }=\delta _{\beta }^{\alpha }.\) In geometric series, such matrix formulas are of type
which \({\mathcal {R}}_{\quad \tau }^{\mu \nu }\) constructing via nonholonomic transforms. We can write similar formulas in block s-forms for various matrices constructed from s-adapted coefficients of a nonsymmetric star s-metric \({}_{\star }^{\parallel }{\mathfrak {g}}_{\alpha _{s}\beta _{s}}\) and, respectively, of a symmetric star d-metric \({}_{\star }^{\parallel }{\mathbf {g}}_{\alpha _{s}\beta _{s}}.\)
2.2.3 Star deformed LC-connections, canonical s-connections and spacetime projections
Using a star d-metric \({}_{\star }^{\parallel }{\mathbf {g}}\) (8) with spacetime shells \(s=1,2\) nonholonomic constraints (projections) to \({}_{2\star }^{\parallel }\mathbf {g,}\) and applying tedious computations with star product (6), following Convention 2 (17), we can define and compute star deformations of respective LC- and canonical s-connections from (11). Such details are contained for all shells on phase spaces in our partner work [26]. Here we present some important formulas stated in additional forms for spacetime shells which allow us to and work in equivalent forms with two different linear connections both on total phase spaces and on spacetimes encoding R-fluxes and star deformations:

In these formulas, decompositions \({}_{s}^{\parallel }\widehat{ {\mathbf {D}}}^{\star }=(h_{1}\ ^{\parallel }\widehat{{\mathbf {D}}}^{\star },\ v_{2}\ ^{\parallel }\widehat{{\mathbf {D}}}^{\star },\ c_{3}\ ^{\parallel }\widehat{{\mathbf {D}}}^{\star },\ c_{4}\ ^{\parallel } \widehat{{\mathbf {D}}}^{\star })\) and \({}_{2}\widehat{{\mathbf {D}}}^{\star }=(h_{1}\ \widehat{{\mathbf {D}}}^{\star },\ v_{2}\ \widehat{{\mathbf {D}}}^{\star })\) are considered for respective nonholonomic dyadic horizontal and (co) vertical splitting, which define s-connections adapted to respective nonlinear s–connection structures \({}_{s}^{\parallel }\mathbf { N\rightarrow {}_{2}{\mathbf {N}}.}\)Footnote 6 Such canonical s-connection and d-connection satisfy the metricity conditions (18) and involve some “mixing shells” nontrivial torsion coefficients of \(\ ^{\parallel }\widehat{{\mathcal {T}}} ^{\star },\) and \(\ \widehat{{\mathcal {T}}}^{\star }.\) Pure shell torsion coefficients vanish in s-adapted (co) frames \(\ ^{\parallel }{\mathbf {e}} _{\alpha _{s}}\rightarrow {\mathbf {e}}_{\alpha _{2}}\) (4) and \(\ ^{\parallel }{\mathbf {e}}^{\alpha _{s}}\rightarrow {\mathbf {e}}^{\alpha _{2}}\) (5). The torsion s-tensor of any s-connection can be defined in standard form as for any affine (linear) connection and subjected to respective star deformations (see below some necessary formulas; more details are presented in [25, 26]).
The R-flux s-adapted contributions are proportional to \(\kappa \), can be computed both on total phase space with nontrivial projections on spacetime shells using respective s-adapted frames and symmetric s-metric coefficients,
We note that formulas (24) involve higher shells (with \(s=3,4\)) contributions on spacetime shells \(s=1,2\) even we work in s-adapted frames. Using (5), we can define and compute in complete parametric form the s-adapted coefficients of the star canonical s-connection \({}_{s}^{\parallel }\widehat{{\mathbf {D}}}^{\star }=\{\ ^{\parallel } \widehat{\mathbf {\Gamma }}_{\star \alpha _{s}\beta _{s}}^{\gamma _{s}}\}\) and respective spacetime components. For simplicity, we provide only the formulas for spacetime 2 + 2 decompositions if they do not encode certain higher shell mixing, \(\widehat{\mathbf {\Gamma }}_{\star \alpha _{2}\beta _{2}}^{\gamma _{2}}=\ {}_{[0]}\widehat{\mathbf {\Gamma }}_{\star \alpha _{2}\beta _{2}}^{\gamma _{2}}+i\kappa {}_{[1]}\widehat{\mathbf {\Gamma }} _{\star \alpha _{2}\beta _{2}}^{\gamma _{2}}=(\ {\widehat{L}}_{\star j_{1}k_{1}}^{i_{1}},\ \ {\widehat{L}}_{\star b_{2}\ k_{1}}^{a_{2}},\ \widehat{C }_{\star \ j_{1}c_{2}}^{i_{1}\ },{\widehat{C}}_{\star b_{2}c_{2}}^{a_{2}})\). The nonsymmetric s-metric \({}_{\star }^{\parallel }{\mathfrak {g}}_{\alpha _{s}\beta _{s}}\) (20) is subjected to such conditions
In these formulas, the s-components of \({}_{[0]}^{\parallel }\widehat{ \mathbf {\Gamma }}_{\star \tau _{s}\alpha _{s}\beta _{s}}\) are determined by formulas (12) using the respective (inverse) symmetric star metric, when \({}_{[1]}^{\parallel }\widehat{\mathbf {\Gamma }}_{\star \alpha _{s}\beta _{s}\mu _{s}}\) and \({}_{[1]}^{\parallel }\widehat{ \mathbf {\Gamma }}_{\star \alpha _{2}\beta _{2}\mu _{2}}\) (24) involve respective s-compositions of \({}_{\star }^{\parallel }{\mathbf {g}} _{\beta _{s}\tau _{s}}\) and \(_{\star }^{\parallel }{\mathbf {g}}_{\beta _{2}\tau _{2}}.\)
All definitions and formulas from [3, 4] can be rewritten in s-adapted form if \(\ ^{\parallel }\partial _{\alpha }\rightarrow \ ^{\parallel }{\mathbf {e}}_{\alpha _{s}}\) and \(\ ^{\parallel }\partial _{\alpha _{2}}\rightarrow \ ^{\parallel } {\mathbf {e}}_{\alpha _{2}}\) as we prove in [25, 26]. Similarly to (13), we can compute s-adapted coefficients of nonassociative star deformed LC-connections to respective canonical s-connections,
In explicit form, the s-adapted coefficients of distortion s-tensor are some algebraic functionals on s-adapted torsion \({}_{2}{\mathcal {T}}^{\star }=\{\ ^{\parallel }\widehat{{\mathbf {T}}}_{\ \star \beta _{2}\gamma _{2}}^{\alpha _{2}}\}\), for instance, \({}_{2\star }^{\parallel } \widehat{{\mathbf {Z}}}=\{\ ^{\parallel }\widehat{{\mathbf {Z}}}_{\ \star \beta _{2}\gamma _{2}}^{\alpha _{2}}[\ ^{\parallel }\widehat{{\mathbf {T}}} _{\ \star \beta _{2}\gamma _{2}}^{\alpha _{2}}]\}.\) We omit such formulas in this work because they are not used for constructing exact and parametric solutions.
Using nonholonomic dyadic decompositions, we can describe equivalently in coordinated frames or s-adapted frames any model of nonassociative phase geometry and gravity determined by a nonsymmetric s-metric structure and spacetime projections \({}_{\star }^{\parallel }{\mathfrak {g}}_{\alpha _{s}\beta _{s}}\rightarrow {}_{\star }{\mathfrak {g}}_{\alpha _{2}\beta _{2}}.\) For any given s-connection and R-flux s-coefficients data, we can consider only the respective symmetric star s-metrics \({}_{\star }^{\parallel } {\mathbf {g}}_{\alpha _{s}\beta _{s}}\rightarrow {}_{\star }{\mathbf {g}}_{\alpha _{2}\beta _{2}}.\) Such nonassociative geometric models with (non) symmetric s-metrics can be described equivalently both in terms of the star LC-connections \(\ ^{\parallel }\nabla ^{\star }\rightarrow \) \(\nabla ^{\star }\) and/or the star canonical s-connections \({}_{s}^{\parallel } \widehat{{\mathbf {D}}}^{\star }\rightarrow {}_{2}\widehat{{\mathbf {D}}}^{\star }. \) The main idea of the AFCDM is that for constructing exact and parametric solutions of physically important systems of PDEs is more convenient to work with nonassociative nonholonomic dyadic canonical geometric data \(({}_{\star s}^{\parallel }{\mathfrak {g}},{}_{s}^{\parallel }\widehat{{\mathbf {D}}}^{\star })\rightarrow ({}_{\star 2} {\mathfrak {g}},{}_{2}\widehat{{\mathbf {D}}}^{\star }).\) We can redefine the constructions in terms of star deformed LC-configurations using s-distortions (26) and extract nonassociative LC-configurations imposing respective zero s-torsion conditions
There are large classes of nontrivial solutions with zero torsion coefficients (\(\ ^{\parallel }\widehat{{\mathbf {T}}}_{\ \star \beta _{s}\gamma _{s}}^{\alpha _{s}}=0\) and \(\ \widehat{{\mathbf {T}}}_{\ \star \beta _{2}\gamma _{2}}^{\alpha _{2}}=0),\) and the respective coefficients of geometric s-objects solve the equations (27). In general, such solutions contain certain nonzero anholonomy coefficients computed on any (dual) s-shell and on spacetime shells. This states that respective (non) symmetric s-metrics can be written in local coordinate forms as generic off-diagonal matrices. We can not diagonalize such matrices by coordinate transforms on a finite spacetime or phase space region if the integrability conditions are not satisfied, i.e. if there are nonzero anholonomy coefficients.
2.3 Parametric decompositions of nonassociative Riemann and Ricci s-tensors
We re-formulate for spacetime shells with h1-v2 decompositions the formulas from section 3.3 of [26].
2.3.1 Star and parametric (2 + 2)-deformed canonical curvature d-tenors
The nonassociative canonical Riemann s-tensor can be computed in standard (non) associative forms for the (star) canonical s-connection coefficients \(\ ^{\parallel }\widehat{\mathbf {\Gamma }}_{\star \alpha _{s}\beta _{s}}^{\gamma _{s}}\) (25). For shells \(s=1,2\) and using “hat” s-adapted variables with mixing on certain \(s=3,4\) indices, we have
These formulas are h1-v2 decompositions with s-adapted “hat” coefficients of formulas (A.15), (38) and (39) defined in [26].
Parametric decompositions of the star canonical s-connections can be written in s-form on all phase space shells :
with respective formulas for \(s=1,2.\) Using such parametric formulas for ( 28), we compute
Such nonholonomic dyadic decompositions of (non) associative/ commutative canonical Riemann s-tensors and their star deformations on \({\mathcal {M}}= {\mathbf {T}}_{s\parallel }^{*}{\mathbf {V}}\) and \({\mathbf {V}}\) with \( s=1,2,\) can be priscribed for sun nonholonomic configrations when values \({}_{[00]}^{\parallel }\widehat{\mathcal {\Re }}_{\quad \alpha _{s}\beta _{s}\gamma _{s}}^{\star \mu _{s}}\rightarrow {}_{[00]}^{\parallel } \widehat{\mathcal {\Re }}_{\quad \alpha _{2}\beta _{2}\gamma _{2}}^{\star \mu _{2}}\) define “hat” variants of “not star deformed” curvature s-tensors for the respective canonical s-connections \(\ ^{\parallel }{\widehat{\Gamma }} _{\star \alpha _{s}\tau _{s}}^{\mu _{s}}\rightarrow \ ^{\parallel } {\widehat{\Gamma }}_{\star \alpha _{2}\tau _{2}}^{\mu _{2}}\) (11).
2.3.2 Parametric decomposition of star canonical Ricci s-tensors and spacetime distortions
Contracting on the fist and forth indices in formulas (28) and using formulas with\(\ ^{\parallel }{\widehat{\Gamma }}_{\star \alpha _{s}\gamma _{s}}^{\mu _{s}}\rightarrow \ ^{\parallel }{\widehat{\Gamma }} _{\star \alpha _{2}\gamma _{2}}^{\mu _{2}},\) we define and compute the h1-v2 s-components of the the nonassociative canonical Ricci s-tensor,
The parametric decompositions of such s-adapted coefficients are expressed:
In appendix A.3.3 of [26], it is shown how to compute parametric [00],[01],[10], and [11] canonical Ricci s-coefficients for all s-coefficients from (30).
We can nonholonomic dyadic distributions with \({}_{[00]}^{\parallel } \widehat{{\mathbf {R}}}ic_{\alpha _{2}\beta _{2}}^{\star }= \widehat{{\mathbf {R}}} _{\ \alpha _{2}\beta _{2}}\) (14) but other parametric [01, 10, 11] when \(\left\lceil \hbar ,\kappa \right\rceil \) components contain nonassociative and noncommutative contributions from star product deformations on phase space and which can be real or complex ones. In result, we can express the star s-deformed Ricci s-tensor in parametric h1-v2- form
Such formulas encode nonassociative parametric deformations of the canonical Ricci s-tenor which, in general, are computed for all shells \(s=1,2,3,4.\) We can chose an associative and commutative solution \(\ ^{\parallel } {\mathbf {g}}_{\alpha _{s}\beta _{s}}\) (7) of nonholonomic dyadic vacuum Einstein equations (15). Then, we can compute \({}_{\star }^{\parallel }{\mathbf {g}}_{\alpha _{s}\beta _{s}}\) (8) and R-flux and star canonical s-deformations (20) to \({}_{\star }^{\parallel }{\mathfrak {g}}_{\tau _{s}\gamma _{s}}\) (9). Projections to h1-v2 shells can be considered for \({}_{\star }^{\parallel }{\mathfrak {g}}_{\tau _{2}\gamma _{2}}\) (21). For such computations, we consider \({}_{2}^{\parallel }\widehat{{\mathcal {K}}} ic=\{\ ^{\parallel }\widehat{{\mathbf {K}}}_{\ \beta _{2}\gamma _{2}}\left\lceil \hbar ,\kappa \right\rceil \},\) when nonassociative distortions of Ricci s-tensors of type \(\ ^{\parallel }\widehat{\mathbf { K}}_{\ \beta _{s}\gamma _{s}}\left\lceil \hbar ,\kappa \right\rceil \) for \( s=3,4\) are encoded in (31) using certain effective sources and/or cosmological constants. This is possible because of nonlinear symmetries relating generating functions and generating (effective) sources on total phase spaces, see details in section 5.4 of [26]. In this work, we shall search for solutions of nonassociative vacuum Einstein equations with R-flux deformations of Lorentz spacetimes involving parametric decompositions of type (31).
2.4 Nonassociative vacuum Einstein equations with real R-flux source
The goal of this subsection is to show how star deformations of nonholonomic 2 + 2 vacuum Einstein equations (15) transform into systems of nonlinear PDEs with effective R-flux sources computed in coordinate bases in [4]. We consider the nonholonomic dyadic formalism, elaborated in [26] for nonassociative geometry in s-adapted form for R-flux, and star modifications of vacuum phase space gravitational equations with (effective) cosmological constant.
2.4.1 Nonassociative R-flux spacetime deformations with (non) symmetric s-metrics
A nonsymmetric star s-metric can be expressed in the form
where \({}_{\star }^{\parallel }\mathfrak {\check{g}}_{\alpha _{2}\beta _{2}}\) is the symmetric part and \({}_{\star }^{\parallel }{\mathfrak {a}} _{\alpha _{s}\beta _{s}}\) is the anti-symmetric part of star and R-flux deformations of spacetime s-metrics for \(s=1,2\) (for total phase space computations, see section 4.1.1 and formulas (17), (A.20) in [26] ). We have
We chose in such formulas \({}_y{\star }^{\parallel }{\mathfrak {a}}_{\alpha _{s}\beta _{s}}^{[0]}=0\) for nonassociative star deformations of commutative theories with symmetric metrics. Here we note that for nonassociative geometric models we have to apply a more sophisticate procedure for computing inverse metrics and/or s-metrics, see respective details in [4, 26]. The symmetric and nonsymmetric parts of a nonsymmetric inverse s-metric with parametric decompositions can be written similarly to
when, in general, \({}_{\star }^{\parallel }\mathfrak {\check{g}}^{\alpha _{s}\beta _{s}}\) is not the inverse to \({}_{\star }^{\parallel } \mathfrak {\check{g}}_{\alpha _{s}\beta _{s}}\) and \({}_{\star }^{\parallel }{\mathfrak {a}}^{\alpha _{s}\beta _{s}}\) is not inverse to \( {}_{\star }^{\parallel }{\mathfrak {a}}_{\alpha _{s}\beta _{s}}\).
2.4.2 Vacuum gravitational equations for star deformed canonical s-connections
In general, a (non) associative canonical Ricci s-tensor \(\mathbf {\mathbf { \mathbf {\mathbf {\ ^{\parallel }}}}}\widehat{\mathbf {\mathbf {\mathbf { {\mathbf {R}}}}}}ic_{\mu _{s}\nu _{s}}^{\star }\) is not symmetric. We can define and compute the nonassociative nonholonomic canonical Ricci scalar curvature following formulas
with respective symmetrization and anti-symmetrization with multiple 1/2.
For total phase spaces, such constructions are provided in details in section 4 of [26] for the nonassociative vacuum Einstein equations of a nonassociative star s-metric \({}_{\star }^{\parallel } {\mathfrak {g}}_{\alpha _{s}\beta _{s}}\) (32) defined by s-adapted star deformations using the convention (17) and formulas (23) for the nonholonomic associative Einstein equations (15). Respective systems of nonlinear PDEs can be written in a form emphasizing explicitly the symmetric and nonsymmetric components of s-metric,
From the second system of equations, we observe that if we impose the nonholonomic conditions that
the s-adapted R-fluxes generate decoupled nonsymmetric components of s–metrics \({}_{\star }^{\parallel }{\mathfrak {a}}_{\mu _{s}\nu _{s}}[ \overline{{\mathcal {R}}}_{\quad \beta _{s}}^{\tau _{s}\xi _{s}}\ \mathbf { ^{\parallel }e}_{\xi _{s}}{}_{\star }^{\parallel }{\mathbf {g}}_{\tau _{s}\alpha _{s}}]\) (34) for arbitrary symmetric solutions \({}_{\star }^{\parallel }\mathfrak {\check{g}}_{\mu _{s}\nu _{s}}={}_{\star }^{\parallel }{\mathfrak {g}}_{\mu _{s}\nu _{s}}[{}_{\star }^{\parallel }{\mathbf {g}}_{\beta _{s}\tau _{s}},\overline{{\mathcal {R}}} _{\quad \beta _{s}}^{\tau _{s}\xi _{s}}\ \mathbf {^{\parallel }e}_{\xi _{s}}{}_{\star }^{\parallel }{\mathbf {g}}_{\tau _{s}\alpha _{s}}]\) of ( 33), where respective s–coefficients are constructed as functionals. The symmetric part can taken to be a solution of
which is a star s-adapted deformation of (15). The symmetric solutions of such PDEs of zero order on parameters \(\hbar \) and \(\kappa \) can be used as prime ones for generating general (non) symmetric solutions with parametric dependence in nonassociative gravity and geometric flow theories, see next section.
We can use formulas (35) and impose nonholonomic constraints
encoding the contributions from shells \(s=3,4\) into an effective cosmological constant \(\ ^{\parallel }\lambda ={}_{s}^{\parallel }\lambda \mathbf {\mathbf {\mathbf {\mathbf {\ }}}}\) (for any s), when there are also nontrivial R-flux effective sources on shells \(s=1,2;\) for nontrivial quasi-stationary configurations with prescribed effective sources
In this work, we consider only real spacetime nonholonomic star R-flux deformations characterize by star s-deformed Ricci s-tensor in parametric h1-v2- form (31). In such models, the higher shell \(s=3,4\) dynamics with respective data for \(\ {}_{s}^{\parallel }\Upsilon \) and \( {}_{s}^{\parallel }{\mathbf {K}}\) are encoded into effective \(\mathbf { \mathbf {\mathbf {\mathbf {\ ^{\parallel }}}}}\lambda \) from (38), which can be prescribed in order to have certain compatibility with some experimental data or higher order theoretical computations.
The system of real spacetime s-adapted spacetime projections of parametric nonassociative gravitational equations (37) with sources (39) transforms into
To solve such systems of nonlinear PDEs with parametric sources we can apply AFCDM method for constructing exact and parametric solutions of dimensions 2 + 2. For instance, we can construct (off-) diagonal black hole and cosmological solutions following the technique summarized in [37], see references therein. Prescribing any values for generating sources \({}_{s}^{\parallel }{\mathcal {K}}=\left[ {}_{1}^{\parallel } {\mathcal {K}},{}_{2}^{\parallel }{\mathcal {K}}\right] ,\) for \(s=1,2,\) in ( 40), we can decouple and solve in certain general forms such systems of nonlinear PDEs.
The main difference of this paper from our previous works on (non) commutative MGTs and geometric flow models on Lorentz manifolds and projected is that in this article we consider a special type of effective parametric sources determined by star R-flux deformations with
as we computed in formulas (77) of [26]. In these formulas, \(\ ^{\parallel }\widehat{\mathbf {\Gamma }}_{\ j_{2}k_{2}}^{r_{2}}\) are computed as in (12) for
If we find an exact/parametric solution \({\mathbf {g}}_{i_{2}j_{2}}(x^{k_{2}})\) of (40) for any prescibed generating source data \( \left[ {}_{1}^{\parallel }{\mathcal {K}},{}_{2}^{\parallel }\mathcal {K }\right] \) encoding an effective cosmological constant \(\ ^{\parallel }\lambda \) and parameters \(\hbar \) and \(\kappa ,\) we can compute in explicit form the real R-flux sources (41) on a Lorentz spacetime base. Such solutions are also characterized by associated complex values of the Ricci s-tensor which can be computed but do not contribute as real spacetime R-flux deformations. Such solutions are also charaterized by nontrivial complex components of associated nonsymmetric metrics, i.e. by \({}_{\star }^{\parallel }\mathfrak {\check{g}}_{\alpha _{2}\beta _{2}}\) (33) and \({}_{\star }^{\parallel }{\mathfrak {a}}_{\alpha _{2}\beta _{2}}\) (34) computed respectively for data (42). In our further partner works, we shall consider such solutions for total phase spaces when complex configurations may play a substantial role. For simplicity, in this article we restrict our considerations only for possible 4-d spacetime real R-flux deformations.
3 Quasi-stationary configurations encoding nonassociative string R-fluxes and gravity
The main goal of this work is to extend the AFCDM to applications in nonassociative vacuum gravity described by dyadic equations (40) with effective sources (41) and prove a general decoupling property of such nonlinear systems of PDEs. We shall integrate corresponding equations in a general off-diagonal metric form for quasi-stationary spacetime metrics encoding in parametrical form nonassociative star R-flux deformations. In explicit form, we shall construct a new class of black ellipsoid configurations determined by nonassociative effective R-flux sources. We consider for spacetime shells \( s=1,2\) the methods and results outlined in [26], section 5, and [37] (see there sections on quasi-stationary off-diagonal solutions and black hole, BH, configurations).
3.1 Decoupling of nonassociative quasi-stationary solutions
We can prove an important decoupling property of the system of modified vacuum Einstein equations (40) with effective sources induced in parametric forms by nonassociative star R-flux deformations on shells \(s=1,2,\) for a class of generic off-diagonal metrics with Killing symmetry on \(\partial _{4}=\partial /\partial y^{4}= \partial _{t}=\partial /\partial t\).Footnote 7 For BH solutions and their nonassociative deformations, we can use standard spacetime spherical coordinates with \(\ ^{\shortmid }u^{1}=x^{1}=r,\ ^{\shortmid }u^{2}=x^{2}=\theta , \ ^{\shortmid }u^{3}=y^{3}=\varphi ,\ ^{\shortmid }u^{4}=y^{4}=t)\) when the phase space dynamics is encoded in effective cosmological constants and prescribed \({}_{1}^{\parallel } {\mathcal {K}}\) and \({}_{2}^{\parallel }{\mathcal {K}}\) in \(\ ^{\parallel }{\mathbf {K}}_{~j_{2}}^{i_{2}}=\ \delta _{~j_{2}}^{i_{2}}{}_{s}^{\parallel }{\mathcal {K}}\) (39) constrained on spacetime shells. Those parametrization of (effective) nonassociative and associative sources were stated in a quasi-stationary form. In explicit form, \({}_{s}^{\parallel }{\mathcal {K}}\) should be chosen a form which is compatible with some experimental and/o observational data or computed for some models of string theory.
For an associative and commutative s-metric \({}_{s}^{\parallel }\mathbf { g}=\ ^{\parallel }{\mathbf {g}}_{\alpha _{s}\beta _{s}}\ ^{\parallel } {\mathbf {e}}^{\alpha _{s}}\otimes \ ^{\parallel }{\mathbf {e}}^{\beta _{s}}\) (42) with spacetime projection to \({}_{2}^{\parallel } {\mathbf {g}}=\ ^{\parallel }{\mathbf {g}}_{\alpha _{2}\beta _{2}}\ ^{\parallel }{\mathbf {e}}^{\alpha _{2}}\otimes \ ^{\parallel } {\mathbf {e}}^{\beta _{2}}\) (7), we consider a quasi-stationary ansatz for a linear quadratic element,
where the s-adapted coefficients for the s-metric are parameterized in the form
Such coefficients will encode additional parametric dependencies on \(\hbar \) and \(\kappa \) which will be computed in next sections for respective classes of exact/parametric solutions. We shall use “hat” labels on s-metric and N-connection coefficients for a stationary ansatz which will be used for computing the s-adapted coefficients of a respective canonical s-connection \( {}_{2}^{\parallel }\widehat{{\mathbf {D}}}\) (11) with coefficients (12).
The N-adapted co-bases \(\ \widehat{{\mathbf {e}}}^{\alpha _{2}}=({\mathbf {e}} ^{i_{1}}=dx^{i_{1}},\widehat{{\mathbf {e}}}^{a_{2}}=d\ y^{a_{2}}+{\widehat{N}}_{\ i_{1}}^{a_{2}}dx^{i_{1}})\) (5), with
are determined by N-connection coefficients \({\widehat{N}}_{j_{1}}^{3}={}_{2}w_{j_{1}}=\ w_{j_{1}}(r,\theta ,\varphi ),\ N_{j_{1}}^{4}={}_{2}n_{j_{1}}=\ n_{j_{1}}(r,\theta ,\varphi )\).
We can use the term “stationary” for metrics with coefficients which in certain adapted coordinates do not depend on respective time like coordinates but contain some off-diagonal terms, for instance, as for rotating Kerr BH [33,34,35,36]. In our approach, there are considered more general nonholonomic configurations (not only with coordinate rotating frames). The h1-v2 part (i.e. the first 4 components for a Lorentz manifold base) in (7) is of stationary type. The term “quasi-stationary” can be used for s-metric ansatz with associated N-connection s-structure which is nonholonomic and encode in local anisotropic form R-flux contributions from a phase space dynamics.
We shall use short notations for partial derivatives when, for instance, \( \partial _{1}q=q^{\bullet },\partial _{2}q=q^{\prime },\partial _{3}q=\partial _{\varphi }q=q^{\diamond }\) and construct quasi-stationary configurations for \(g_{4}^{\diamond }\ne 0.\)Footnote 8 Explicit computations of the canonical Ricci s-tensor (14) for \({}_{s}^{\parallel }\widehat{{\mathbf {D}}}\) (12) for a s-metric (7) allows to write the system of vacuum s-adapted gravitational equations (40)
On shells \(s=1\) and \(s=2,\) with \(i_{1},k_{1}...=1,2,\) the dependence on string parameter \(\kappa \) is determined by some formulas (39) related algebraically via some frame transforms to (41). For such two generating source ansatz \({}_{1}^{\parallel } {\mathcal {K}}\) and \({}_{2}^{\parallel }{\mathcal {K}},\) we restrict nonholonomically the class of possible real R-flux deformations. This will allow to find exact solutions in explicit form.
Using (43), (14) and (15), we find such formulas for shell components of quasi-stationary phase spaces,
The nonassociative vacuum gravitational field equations (40), written in geometric form as (44), computed for a quasi-stationary s-metric ansatz (7) decouple in a 2 + 2:
These equations can be solved recurrently because possess an explicit decoupling property on both shells \(s=1\) and 2. The first equation in (45) is a 2-d Poisson equation which can be solved in certain general forms for any prescribed source \({}_{1}^{\parallel }{\mathcal {K}}\) encoding parametric R-flux contributions. Prescribing \({}_{2}^{\parallel }{\mathcal {K}}\) and \(g_{3}\) (or \(g_{4}\)) on second shell \( s=2,\) we can find integrating respective nonlinear equation relating such coefficients and determine \(g_{4}\) (or \(g_{3}\)). This allows us to compute the coefficients \(\alpha _{i_{1}},{}_{2}\beta \) and \({}_{2}\gamma \) and determine the N-connection coefficients from respective linear algebraic equations for \(\ w_{j_{1}};\) and integrating two times in the last system of equations in order to compute \(n_{k_{1}}.\)
3.2 Integrability for nonassociative quasi-stationary vacuum deformations
3.2.1 Quasi-stationary solutions with (non) associative induced canonical s-torition
The system (45) can be integrated in general form by coefficients of such a quasi-stationary quadratic linear form,
The coefficients of such an off-diagonal metric are determined by
Any such off-diagonal solution depends in parametric form on \(\hbar ,\kappa \) for any R-flux nonassociative data encoded in \(~_{s}^{\parallel } {\mathcal {K}}\). The canonical s-torsion structure \(\ \widehat{{\mathbf {T}}}_{\ \alpha _{2}\beta _{2}}^{\gamma _{2}}\) of respective \({}_{2}\widehat{\mathbf {D }}=\ \nabla +{}_{2}\widehat{{\mathbf {Z}}}\) is not trivial for a general (46), see similar details on computing such s-adapted coefficients which are similar to those presented in [32, 37].
Let us discuss the difference of quasi-stationary solutions (46) for any class of stationary solutions (for black holes, wormholes etc.) outlined in [33,34,35,36] etc. In those monographs, the Einstein equations are transformed for certain special diagonal ansatz into systems of nonlinear ODEs depending on one space like variable (such ansatz are studied similarly in various MGTs). The general solutions of such second order ODEs depend on two integration constants which are defined from additional physical considerations, for instance, to get some asymptotic limits to the Newton gravity potential, or to modify the constructions for certain nontrivial cosmological constants etc. Nonassociative R-flux deformations of the GR vacuum structures result in more general classes of nonlinear PDEs which can not be transformed in a general form to ODEs. We have to apply a generalized AFCDM which allow to construct off-diagonal quasi-stationary solutions, when the coefficients of d-metrics depend at least on three space coordinates via respective integration functions (not only on integration constants) and on generating functions and generating sources. There are parametric dependencies on various (non) commutative / associative quantum/string parameters etc. The solutions are constructed as exact ones by for certain stated values of parameters for corresponding effective sources. In such cases, we have to prescribe integration/generation functions and effective sources in certain explicit form in order to have compatibility with certain experimental/observational data. This is possible for such types of nonholonomic constraints and N-adapted frames and canonical distortions of (non) linear connections, which allow a self-consistent causal physical descriptions of new classes of quasi-stationary solutions and their nonholonomic deformations.
3.2.2 Spacetime LC-configurations encoding nonassociative parametric R-fluxes
We have to impose additional nonholonomic constraints on generating functions and effective sources in order to extract zero torsion LC-configurations for a \(\ ^{\parallel }\nabla \) generated constrained on a spacetime encoding a nontrivial real R-flux structure. A class of solutions (46) can be constrained in such a form that up to orders \(\hbar ,\kappa \) and \(\hbar \kappa ,\) for star deformations of respective connections, there are satisfied the conditions \({}_{\star }^{\parallel 2}\widehat{{\mathbf {Z}}}=0,\) i. e. \({}_{2}^{\parallel }\widehat{{\mathbf {D}}}_{\mid {}_{s}^{\parallel } \widehat{{\mathbf {T}}}=0}^{\star }= \ ^{\parallel }\nabla ^{\star },\) see (27). By straightforward computations, we can verify that such equations are solved by such s-metric and N-connection coefficients:
Let us analyze the most important LC-conditions on respective classes of generating functions and generating sources from (47): If we prescribe a shell generating function \({}_{2}\Psi ={}_{2}{\check{\Psi }} (\hbar ,\kappa ,x^{i_{1}},y^{3}),\) for which \([\partial _{i_{1}}({}_{2}\check{ \Psi })]^{\diamond }=\partial _{i_{1}}({}_{2}{\check{\Psi }})^{\diamond },\) we can solve explicitly the conditions for \(w_{j_{1}}\) in (47) if \({}_{2}^{\parallel }{\mathcal {K}}=const,\) or for a functional \({}_{2}^{\parallel }{\mathcal {K}}(\hbar ,\kappa ,x^{i},y^{3})= {}_{2}^{\parallel }{\mathcal {K}}[{}_{2}{\check{\Psi }}].\) The third class of conditions in (47), \(\partial _{i_{1}}w_{j_{1}}=\partial _{j_{1}}w_{i_{1}},\) can be solved in parametric form for any generating function \({}_{2}\check{A}={}_{2}\check{A}(\hbar ,\kappa ,x^{k},y^{3})\) for which \(w_{i_{1}}=\check{w}_{i_{1}}=\partial _{i_{1}}{}_{2}\Psi /({}_{2}\Psi )^{\diamond }=\partial _{i_{1}}{}_{2}\check{A}.\) The forth class of values can be solved by any \(n_{i_{1}}(x^{k_{1}})=\partial _{i_{1}}n(x^{k_{1}}).\) We summarize these formulas in the form:
For subclasses of s-coefficients determined by data (48), the quadratic line element (46) transforms into
Any solution (49) defines a LC-variant of (46) for quasi-stationary spacetime solutions with R-flux contributions encoded in \({}_{1}^{\parallel }{\mathcal {K}}\) and \({}_{2}^{\parallel }{\mathcal {K}}.\) This way, we generate exact solutions of the systems of nonassociative vacuum Einstein equations (40) for \(\ ^{\parallel }\nabla ^{\star }\) and reduced to (44) with spacetime \(\ ^{\parallel }\nabla ^{\star }\rightarrow \nabla ^{\star }.\)
3.2.3 Nonlinear symmetries for stationary generating functions and R-flux sources
We can change the spacetime nonassociative generating data with generating functions and effective sources and a prescribed cosmological constant, \(({}_{2}\Psi (\hbar ,\kappa ,x^{i_{1}},y^{3}),\ ~_{2}^{\parallel }\mathcal {K }(\hbar ,\kappa , x^{i_{1}},y^{3}))\leftrightarrow ({}_{2}\Phi (\hbar ,\kappa ,x^{i_{1}},y^{3}),{}_{2}\Lambda _{0})\), if there are used such nonlinear transforms:
Using nonlinear symmetries (50), we can write the quadratic element (46) in an equivalent form encoding the nonlinear symmetries of generating functions and generating sources of R-flux or a respective effective cosmological constant,
for indices: \(i_{1},j_{1},k_{1},...=1,2;i_{2},j_{2},k_{2},...=1,2,3,4\) and
In a similar form, we can define nonlinear symmetries for generating functions and R-flux sources and introduce effective cosmological constants \( {}_{s}^{\parallel }\Lambda _{0}\) for LC-configurations and quasi-stationary s-metrics (49).
Finally, we note that nonlinear transforms (50) induce nonlinear symmetries for the symmetric part of the star deformed s-metric (33) and other geometric s-objects which may involve both real and complex components. For the chosen class of quasi-stationary spacetime s-metrics, the nonsymmetric part of star deformed s-metrics (34) is still constrained to be zero for such re-definitions of generating functions and sources but certain nontrivial components can be computed on shells \(s=3,4\) on (co) tangent Lorentz bundles.
3.3 Nonholonomic dyadic deformations into parametric solutions
In this section, we adapt for 4-d base spacetimes with shells \(s=1,2\) dyadic decompositions the results for 8-d phase space nonassociative gravity models from Appendix B [26]. Such extensions of the AFCDM are important for constructing exact and parametric locally anisotropic BH solutions of the system of nonlinear PDEs (45) generated by nonassociative star nonholonomic deformations and related effective R-flux sources. There are provided formulas for certain general quasi-stationary d-metrics encoding nonassociative deformations. We also derive formulas for such nonholonomic configurations which are defined as small parametric nonassociative distortions of Schwarzschild metrics via respective “gravitational polarization” functions. It is possible to prescribe such generating functions with ellipsoid symmetry when the generic off-diagonal solutions describe distorted black ellipsoids, BEs, and other type small nonholonomic deformations of static BHs in so-called Weyl coordinates.
3.3.1 Using some d-metric coefficients as generating functions
The nonlinear symmetries (50) can be written in the form:
As a result, we conclude that the quadratic elements for quasi-periodic solutions (46) and/or (51) can be rewritten equivalently in terms of generating data \((g_{4};{}_{1}^{\parallel } {\mathcal {K}},{}_{2}^{\parallel }{\mathcal {K}},{}_{s}^{\parallel }\Lambda ),\)
The parametric dependence, signs and integration functions/constants in above formulas have to be chosen in some forms which are compatible with experimental/observational data or corrections from R-fluxes in string theories.
We can restrict the class generic off-diagonal solutions (52) to LC-configurations if we use as a generating function any coefficient \( \check{g}_{4}(\hbar ,\kappa ,x^{i_{1}},y^{3})\) and nonlinear symmetries involving (48) for quasi-stationary solutions (49). For such zero torsion solutions, the R-flux contributions of effective sources \( {}_{2}^{\parallel }{\mathcal {K}}\) are encoded correspondingly in the N-connection coefficients \({}_{2}^{\parallel }\check{A}.\)
3.3.2 Polarization functions for nonassociative prime and target spacetime d-metrics
We can elaborate on associative/commutative models of gravity on a nonholonomic Lorentz manifold enabled with nonholonomic dyadic structure, \(\ ^{\parallel }{\mathbf {e}}^{\alpha _{2}}\in T_{2}^{*}{\mathbf {T}}^{*} {\mathbf {V}}\) (4) and defined by a prime d-metric \({}_{2}\mathbf {\mathring{g}}\) structure (7), with possible star deformations to respective symmetric and nonsymmetric s-metrics of type (8) and (9). For such constructions, we can consider trivial shells \(s=3,4\) enabled with (co) fiber Minkowski metric structure. In N-adapted form, we parameterize such a spacetime d-metric for \(s=1,2\) in the form
To label coefficients of prime d-metrics and related geometric d-objects, we shall use left/right/up labels with a small circle. In general, a prime \({}_{2}\mathbf {\mathring{g}}\) (53) my be, or not, a solution of certain gravitational field equations in a MGT or GR. In this work, we consider that \({}_{2}\mathbf {\mathring{g}}\) is a Schwarzschild metric written in some adapted coordinates which allow to apply the AFCDM and construct generic off-diagonal solutions for some target metrics. We can always consider phase space extensions of prime d-metrics resulting in parametric R-flux deformations to nonassociative configurations following formulas \({}_{\star }^{\parallel }\mathfrak {\check{g}}_{\mu _{s}\nu _{s}}^{\circ }=({}_{\star }^{\parallel }\mathfrak {\check{g}} _{i_{1}j_{1}}^{\circ },{}_{\star }^{\parallel }\mathfrak {\check{g}} _{a_{2}b_{2}}^{\circ },{}_{\star }^{\parallel }\mathfrak {\check{g}} _{\circ }^{a_{3}b_{3}},{}_{\star }^{\parallel }\mathfrak {\check{g}} _{\circ }^{a_{4}b_{4}})\) (33) and \({}_{\star }^{\parallel } {\mathfrak {a}}_{\mu _{s}\nu _{s}}^{\circ }=(0,0,{}_{\star }^{\parallel } {\mathfrak {a}}_{c_{3}b_{3}}^{\circ },{}_{\star }^{\parallel }{\mathfrak {a}} _{c_{4}b_{4}}^{\circ })\) (34), when the star-metrics are parametric extensions of some associative and commutative s-metrics.
For nontrivial R-flux and star deformations, we can study nonassociative parametric nonholonomic deformations of a prime metric \({}_{2}\mathbf { \mathring{g}}\) (53) to nonlinear quadratic elements determined by target quasi-stationary d-metrics \({}_{2}^{\parallel }\mathbf { g,}\) which can be parameterized in any necessary form (46), (51), or (52). Such a target \({}_{2}^{\parallel }{\mathbf {g}}\) is a solution of the nonassociative vacuum Einstein equations represented in any form (40), (43), or (45). Nonholonomic star s-deformations of type “prime to target” s-metrics can be described in terms of gravitational polarization (\(\eta - \)polarization) functions,
when the target d-metrics are parameterized in the form
We emphasize that any multiple \(\eta \ \mathring{g}\) in (54) may depend on mixed (higher) shell coordinates and various parameters, sources, etc. To apply the AFCDM for constructing solutions we have to use products subjected to the condition that the target d-metrics, for instance, is of type (52) or any equivalent form. The term “gravitational polarization” is used because for \(\eta \)-deformations with a small parameter, we can generate new classes of exact/parametric solutions, for instance, of black hole/ellipsoid type but with effective polarization of fundamental physical constants. Such diagonal and off-diagonal solutions were constructed in (non) commutative MGTs, see [29,30,31,32, 37] and reference therein. By straightforward computations, we can check that any solution (52) can be parameterized in a form (54) and described by a nonlinear quadratic element with explicit dependence on \(\eta \)-polarizations,
where the polarization functions are determined by generating data \(\psi (\hbar ,\kappa ,x^{i_{1}})\) and \(^{\parallel }\eta _{4}(\hbar ,\kappa ,x^{i_{1}},y^{3}).\) We keep left labels “\( {\parallel }''\) for such spacetime configurations in order to emphasize that the coefficients encode certain R-flux deformations in the (co) tangent bundle.
3.3.3 Parametric nonassociative transforms to quasi-stationary spacetime metrics
The nonassociative vacuum gravitational field equations can be projected on spacetime background, in instance, in the form (44). Such nonlinear system of PDEs involve in parametrical form an effective R-flux source (41). Similar geometric constructions were considered in our previous works [30,31,32, 37] for (other types) effective sources with parametric deformations on a small parameter \(\varepsilon ,0\le \varepsilon <1.\) In [26], we proved that the same AFCDM can be applied for a quasi-stationary s-metric ansatz on total phase spaces when as a small parameter it is considered the string constant, \(\varepsilon \rightarrow \kappa .\) For the goals of this paper, we adapt those constructions for generating parametric spacetime solutions with gravitational polarizations depending in N-adapted form only on space coordinates.
Let us consider parametric \(\kappa \)–decompositions of the \(\eta \) -polarization functions in a d-metric (55) resulting in quasi-stationary solutions of type (46) and/or (51):
These formulas for star parametric deformations of a d-metric and N-connection structure on \(_{2}{\mathbf {T}}_{\parallel }^{*}{\mathbf {V}} \) can be written in the form
where \(\zeta \)- and \(\chi \)-coefficients for deformations (56) are generated by nonholonomic deformation data
For quasi-stationary configurations, \(\ ^{\parallel }\eta _{2}\) and \(\ ^{\parallel }\eta _{4}\) are considered as generating functions. In a more general context, we can consider\(\ ^{\parallel }g_{2}\) and \(\ ^{\parallel }g_{4}\) as generating functions and, for small parametric deformations, we can take \(\ ^{\parallel }\chi _{2}\) and \(\ ^{\parallel }\chi _{4}\) as generating functions.
We can compute parametric deformations following such a procedure: For \( s=1,\) we consider \(\ \ ^{\parallel }\zeta _{i_{1}}=(\ ^{\parallel } \mathring{g}_{i_{1}})^{-1}e^{\psi _{0}(x^{k_{1}})}\) and \(\ ^{\parallel }\chi _{i_{1}}=(\ ^{\parallel }\mathring{g}_{i_{1}})^{-1}\ ^{\psi }\ ^{\parallel }\chi (x^{k_{1}})\), where
for \(\psi _{0}(x^{k_{1}})\) and \(\ ^{\parallel }\chi (x^{k_{1}})\) defined by a solution of a 2-d Poisson equation (45). For \(s=2\) we have generating functions \(\ ^{\parallel }\zeta _{4}\) and \(\ ^{\parallel }\chi _{4};\) generating source and cosmological constant, respectively,\(\ ~_{2}^{\parallel }{\mathcal {K}}\) and \({}_{2}^{\parallel }\Lambda _{0};\) integration functions\({}_{1}^{\parallel }n_{k_{1}}\) and \({}_{2}^{\parallel }n_{k_{1}};\) and certain prescribed data for a prime s-metric, \((^{\parallel } \mathring{g}_{3},\ ^{\parallel }\mathring{g}_{4};\ ^{\parallel } \mathring{N}_{i_{1}}^{3},\ ^{\parallel }\mathring{N}_{k_{1}}^{4}).\) After tedious computations, we express
Introducing above coefficients with \(\kappa \)-decomposition instead of \(\eta \)-coefficients of (55), we obtain respective nonlinear quadratic elements for quasi-stationary solutions encoding nonassociative star R-flux deformations. In next subsection, there are provided such formulas for such distortions of Schwarzschild BHs. This subclass of quasi-stationary solutions consist a restriction on shells \(s=1,2\) of the phase space solutions from Appendix B, formulas (B.7) in [26] (in that works, the solutions are with \(\eta \)-polarization functions depending also on phase space coordinates).
3.4 Nonassociative distorted black holes and black ellipsoids
Our goal is to construct exact quasi-stationary solutions encoding in parametric form nonassociative nonholonomic (ellipsoid) deformations of the Schwarzschild spacetime. Such solutions are obtained by assuming that existence of a R-flux effective matter source (41).
3.4.1 Prime metrics as a distorted Schwarzschild BH
Let us introduce on spacetime \({\mathbf {V}}\) local (prolate spheroidal) coordinates
and consider a prime d-metric \({}_{2}\mathbf {\mathring{g}}^{W}= \left( \ \ \mathring{g}_{i_{1}}^{W},\ \ \mathring{g}_{a_{2}}^{W},\mathring{N} _{i_{1}}^{Wa_{2}}\right) \) (53) (with a label W referring to Weyl coordinates (58)) with such parameterizations of nontrivial coefficients:
To avoid coordinate singularities and non-compatible constraints for nonholonomic and/or off-diagonal deformation in d-metrics of type (56), we can consider such coordinate transforms \(u^{\alpha _{2}^{\prime }}\rightarrow u^{\alpha _{2}^{\prime }}(u^{\alpha _{2}}),\) when \(\mathring{N}_{i_{1}^{\prime }}^{a_{2}^{\prime }}(u^{\beta _{2}^{\prime }})=0 \) transform into some coefficients \(\mathring{N}_{i_{1}}^{a_{2}}(u^{ \beta _{2}})\ne 0\) of necessary smooth class, preserving a respective (2 + 2) splitting for the same d-metric possessing a horizon for \(x=1\) and singularity for \(x=-1.\) In (59), the parameter \(M_{0}\) can be identified as the BH mass. We use also distortion functions which can be expressed in terms of Legendre polynomials \(P_{l}\) (of the first kind, see details in [41, 43, 45]),
where \(P_{l}:=P_{l}(xy/{\check{\rho }})\) for \({\check{\rho }}=\sqrt{x^{2}+y^{2}-1}\) . In these formulas \(a_{l}\in {\mathbb {R}}\) are called multipole moments defining a distortion due, in our case, to an effective R-flux source. The Schwarzschild spacetime is recovered for \(a_{l}=0,\) \(a_{1}=1\) is considered as the dipole moment, \(a_{2}:=\mathring{q}\) is the quadrupole moment, etc. for higher momenta which describe deviations from the spherically symmetric shape of a central compact object.Footnote 9
3.4.2 Target d-metrics for distorted nonassociative black ellipsoids
For small \(\kappa \)-ellipsoidal deformations with
for \(\ ^{\parallel }\chi _{1}=\ ^{\parallel }\chi _{2}=\ ^{\parallel }\chi (x^{i_{1}}),\) we can define values
The coefficients (in Weyl coordinates) of a target d-metric \({}_{2}{\mathbf {g}} ^{W}\mathbf {=}\left( \ \ g_{i_{1}}^{W},\ \ g_{a_{2}}^{W},N_{i_{1}}^{Wa_{2}}\right) \) with geometric data (59 ) for a nonholonomic deformation for \({}_{2}\mathbf {\mathring{g}=}\left( \ \ \mathring{g}_{i_{1}}^{W},\ \ \mathring{g}_{a_{2}}^{W},\mathring{N} _{i_{1}}^{Wa_{2}}\right) \) (59) can be written in the form
where we changed labels from (56) as \(\ \ ^{\parallel }\zeta _{\alpha }\rightarrow \ ^{W}\zeta _{\alpha },\ ^{\parallel }\zeta _{i_{1}}^{a_{2}}\rightarrow \ ^{W}\zeta _{i_{1}}^{a_{2}},\ ^{\parallel }\chi _{4}\rightarrow \ ^{W}\chi _{4},\) etc. in order to emphasize that we use Weyl coordinates and begin deformations of a prime Weyl metric.
In result, we generate a family of such quasi-stationary off-diagonal solutions
In this quadratic element, the parametric deformations (57) are computed for the prime metric (59), when the effective R-sources are computed as functionals \(~_{s}^{W}\mathcal {K=}~_{s}^{\parallel } {\mathcal {K}}[{}_{2}{\mathbf {g}}^{W},{}_{W}^{\parallel }\widehat{\mathbf { \Gamma }}_{\ i_{2}k_{2}}^{m_{2}},{}_{s}^{\parallel }\Lambda ,\hbar \kappa \overline{{\mathcal {R}}}]\) following formulas (40 ) with effective sources (41) determined by \(\ ^{W}\widehat{ \mathbf {\Gamma }}_{\ i_{2}k_{2}}^{m_{2}}=\ ^{\parallel }\widehat{ \mathbf {\Gamma }}_{\ i_{2}k_{2}}^{m_{2}}[{}_{2}{\mathbf {g}}^{W}],\)\({}_{2} \mathbf {g=}{}_{2}^{W}{\mathbf {g}}\) and \({}_{2}^{W}\mathbf {\mathring{g}}=(\ \mathring{g}_{\alpha }^{W})\),
Putting together above coefficients (63), we express the quadratic linear element (62) for nonassociative R-flux distorted Schwarzschild BH in the form:
We can prescribe solutions (65) with ellipsoidal configurations for generating functions of type
for a smooth function \({\underline{\chi }}(x,y)\) (in particular, \(\underline{ \chi }\) can be a constant) and constants \(\omega _{0}\) and \(\phi _{0}.\) Such d-metrics have an ellipsoidal horizon with eccentricity \(\kappa \) stated by the equation \(x=1+\kappa \ ^{W}\chi _{4}(x,y,\phi )\) of zero horizon when the coefficients before \(\ ^{W}\zeta _{4}\ \exp [2\mathring{\psi }(x,y)]\{dt+...dx^{i}\}^{2}\) in (62). The integration and generating functions and generating source for such d-metrics are defined as in (51) but for the case when the term \(\ ^{W}\zeta _{4}(1+\kappa \ ^{e}\chi _{4})\) is considered as a generating function as in (52) (see also respective nonlinear symmetries involving (48) for quasi-stationary solutions (49)). We can restrict the class generic off-diagonal solutions of type (65) (equivalently (62)), in particular, with ellipsoidal horizons (66) in order to extract to LC-configurations with zero torsion, when the R-flux contributions of effective sources \({}_{2}^{W}{\mathcal {K}}\) are encoded correspondingly in the N-connection coefficients of type \({}_{2}^{\parallel }\check{A}.\)
Finally, we note that black ellipsoid, BE, solutions were studied in details in a series of our former works, for instance, see [29, 40]. Such BE distorted configurations can be prescribed to obey well-defined stability conditions as in [39]. The stability and instability of some small parametric deformations depend on the type generating and integration functions are used for constructing respective exact/parametric solutions.
4 Thin accretion disks around nonassociative black ellipsoids
A series of important astrophysical phenomena (for active galactic nuclei and/or X-ray binaries) are related to accretion of matter onto BHs. This topic has been discussed intensively in modern literature, see reviews of results in [42,43,44,45]. In addition to numerical simulations, the approach to finding analytical solutions to accretion disk models and for BH – disk systems in GR and various MGTs is essential for study and understanding properties of such gravitational and astrophysical models. In this section, we concentrate on accretion onto compact objects for a particular class of BH and BE like solutions in nonassociative gravity theories with star R-flux distortions. Such nonholonomic configurations are defined in the presence of external effective matter sources defined for axially symmetric prescribed constraints (40) on effective R-flux sources (41). This is analogous to external axially symmetric distributions of some effective mass outside the horizon. To study such models we use classes of solutions (62) and (65) of the nonassociative nonholonomic and parametric deformed vacuum Einstein equations (45). For such solutions, we can consider generating functions for black ellipsoid configurations (66) and impose zero torsion conditions (47) via generating data (48) resulting in metrics of type (49). All constructions simplify to the Schwarzschild solution for holonomic (diagonalizable, with trivial N-connection structure) configurations and if the R-flux source is zero. A quasi-stationary nonassociative star R-flux spacetime in the vicinity of an (ellipsoidal, or other type smooth distorted) horizon is described by an off-diagonal vacuum metric with the cost of relaxing the assumption of asymptotically flatness for respective nonholonomic modifications of the Einstein equations.
4.1 Approximations and equations for locally anisotropic thin disk models
The structure of thin accretion disks and respective equations can be defined in a simple form using prolate coordinates (58) which can easily transformed into distorted Schwarzschild coordinates easily. We can follow all assumptions and formulas from section III of [43] but using locally anisotropic Weyl coefficients (61) as nonholonomic deformations of Legendre polynomical formulas (60), when
determined \(\kappa \)-parametrically by generating functions \(\ ^{\parallel }\chi (x^{i_{1}})\) and \(^{\parallel }\chi _{3}(x^{i_{1}},\phi ).\) We can elaborate on standard thin disk models and consider small nonholonomic and/or off-diagonal \(\kappa \)-deformations. This results in geometrically thin, optically thick, and cold accretion disks which be described as certain ellipsoid like quasi-stationary configurations. Effectively, such locally anisotropic accretion effects can modelled as standard ones in GR but (in well defined cases) self-consistently embedded in a nonassociative \(\kappa \)-distorted vacuum, when all formulas are written with respect to N-adapted bases.
Let us analyze three fundamental equations encoding nonassociative contributions and governing the radial structure of thin disk models. We adopt the coordinates with \(c=1,\) \(G=1\) and \(M_{0}=1\). The first equation (in N-adapted bases) for the particle number conservation are R-distorted
where the distortion d-tensor \(\widehat{{\mathbf {Z}}}_{\alpha _{2}}\) defines real canonical s-deformations of the LC connection by respective nonassociative R-deformations as in formulas (26). In this formula, \({\mathbf {u}}^{\alpha _{2}}\) is the velocity d-vector of a fluid and \( \rho \) is its mass density. Such a (nonholonomic) conservation law means that we expect that the mass accretion rate is constant in certain N-adapted frames.
We can introduce the second fundamental equation (for the radial momentum) as a component of the relativistic Navier-Stokes equations and their canonical N-adapted deformation,
where \(\widehat{{\mathbf {h}}}^{\alpha _{2}\beta _{2}}:={\mathbf {u}}^{\alpha _{2}} {\mathbf {u}}^{\beta _{2}}+\widehat{{\mathbf {g}}}^{\alpha _{2}\beta _{2}}\) is the projection d-tensor defining the spacial d-metric which is normal to \( {\mathbf {u}}_{\alpha _{2}}.\) Such quasi-stationary values can be defined if \( \widehat{{\mathbf {g}}}^{\alpha _{2}\beta _{2}}\) is determined, for instance, by a vacuum solution (62) encoding nonassociative star deformations. The stress-energy d-tensor \({\mathbf {T}}^{\beta _{2}\gamma _{2}}\) is for the accreting fluid type matter which is different from the effective nonassociative R-flux source (41).
The third energy conservation equation is
where the stress-energy d-tensor is parameterized in N-adapted form as
In this formula, h is the enthalpy density (defined as the sum of internal energy per unit proper volume and the pressure over the rest mass density); P is the pressure; the d-vector \({\mathbf {q}}^{\beta _{2}}\) describes the transverse energy flux; and the viscous stress energy tensor \({\mathbf {S}} ^{\beta _{2}\gamma _{2}}=-2{\widetilde{\lambda }}\mathbf {\sigma }^{\beta _{2}\gamma _{2}}\) is taken in a relativistic form without no bulk viscosity, where \({\widetilde{\lambda }}\) is the dynamical viscosity and \(\mathbf {\sigma } ^{\beta _{2}\gamma _{2}}\) is the shear d-tensor. In the thin disk approximation and with respect to N-adapted frames using prolate coordinates with \(x^{1}=r\) and \(x^{3}=\phi \), one approximates
In coordinate frames and for LC–configurations, we obtain the formula (24) from [43]. In next subsection, we summarize certain important formulas and results from sections III.B and IV of that work using Convention 2 extended in the form (17), which allows us to transform (non) associative geometric constructions from coordinate bases to N-adapted ones, and inversely.
4.2 Thin accretion disk around nonassociative distorted quasi-stationary BEs
The system of fundamental equations (67)–(69) and respective N-adapted energy transport law, the equation of state and opacity, allow us to derive in dyadic variables the system of nonlinear algebraic equations for the thin disk model [47, 48]. Let us introduce such important values compute per unit mass of geodesic circular motion in equatorial planes (when \(\theta =\pi /2,\) or \(y=0\) in Weyl coordinates (58)):
Above boldface values are defined and computed in N-adapted prolated frames for any solution (62) and/or (65) encoding nonassociative R-flux effects but circle values are in prolated coordinate frames for prime data \(({}_{2}\mathbf {\mathring{g}}^{W},\mathring{\nabla })\) ( 59).
We omit long N-adapted calculations which are similar to the coordinate ones in [43] (see there all assumptions on thermodynamic models for thin disk accretion) and provide such results for most important physical quantities appearing in the equations of the thin disk model:
where the dipole moment \(a_{2}:=\mathring{q}\) from (60) is used, and the nonassociative polarized mass \(\check{M}(x,0,\phi )\) is determined by formula (61). All such formulas are valid locally, in some neighborhood of the horizon \(y=1\) and have physical meaning for real values which impose some constraints on the range of coordinate x (considering a prescribed value \(\mathring{q}\)).
Analyzing formulas (70) we conclude that possible nonassociative real R-flux distortions do not change nearly the horizon the disk energy of a locally anisotropic BH (or BE for polarizations of type (66 )) but may result in string constant \(\kappa \)-polarizations on \(\phi \) of the angular momentum and angular velocity, \({\mathbf {L}}\) and \({\varvec{\Omega }}\) , via \(\check{M}(x,0,\phi ).\) So, in principle, nonassociative R-flux modifications can be observed in certain thin disk accretion processes by additional rotation on \(\phi \) effects which can be of ellipsoid type polarization. For a fixed value \(\phi _{0}\) and vanishing \(\mathring{q},\) we have monotonically decreasing function \({\varvec{\Omega }}(\phi _{0},r)\) of the radius. Such a BH, or BE, is surrounded by a mass distribution “embedded” into a nonassociative deformed gravitational vacuum, when after some distance the behaviour of \({\varvec{\Omega }}(\phi ,r)\) manifests the existence both of an external matter and effective R-flux source. There is a extremum when the influence of the surrounding matter becomes strong when the local solution is no longer valid. Here we note that for \(\mathring{q}<0\) such an extremum can appear within a valid range of radial coordinates with real \(\mathbf {E,L,}\) and \({\varvec{\Omega }} .\) For \(\mathring{q}>0,\) such an extremum is usually outside the valid range even the additional dependence on x and \(\phi \) in \(\check{M}\) may open some new possibilities comparing to the case \(\check{M}=M_{0}.\)
Here we note that the inner edge of the standard thin disk model in [43] is assumed to be at the Innermost Stable Circular Orbit (ISCO; it is also called the marginally stable orbit). Let us analyze the location of the ISCO in the nonassociative distorted Schwarzschild spacetime. The reflection symmetry states such a conditions for existence of geodesics in the equatorial plane: \(a_{2l-1}=0,\) for \(l>0,\) but this does not give any new in the study of quadrupoles for prime configurations (60). Similarly, the nonassociative gravitational polarization for quasi-stationary solutions does not result in contributions to the effective potential of R-flux modified Schwarzschild BH because
which is equivalent to formula (49) in [43]. The main results of the thin disk models for distorted Schwarzschild BH are described and plotted in section V with figures 1-8 of that work. Comparing with the usual Schwarzschild spacetimes in GR, we should mention that formulas for \(\mathbf { E,L,}\) \({\varvec{\Omega }}\) and \(\ ^{Eff}V\) characterizing nonassociative BHs and BEs are only valid locally, i.e. in the vicinity of the horizon. So, we have only considered the inner part of the respective disks in such (non) associative and nonholonomically deformed spacetimes. The choice of the quadrupole (additionally to ellipsoidal R-flux distortions) imposes respective limits o which points we can extend the thin disk solutions. Finally, we conclude that the solutions for static BHs in GR extend to certain quasi-stationary ones when observable thin disk effects are \(\kappa \) -polarized on \(\phi \) with nontrivial contributions to the angular momentum and angular velocity, \({\mathbf {L}}\) and \({\varvec{\Omega }} ,\) via nonlinear gravitational locally anisotropic polarizations of mass \(\check{M}(x,0,\phi ).\)
5 Summary and conclusions
5.1 Main results
In this work, we constructed and discussed new classes of exact and parametric solutions for four dimensional, 4-d, black holes, BHs, and black ellipsoids, BEs, with distortions encoding nonassociative star deformations and R-flux effective sources from string theory. Such nonassociative vacuum solutions are described by generic off–diagonal symmetric metrics when certain nonsymmetric metric components \({}_{\star }^{\parallel }{\mathfrak {a}}_{\mu _{s}\nu _{s}}\) (34) contain nontrivial contributions for higher shells in corresponding 8-d nonassociative phase spaces. Our geometric method of constructing solutions in modified gravity theories and GR (see [26] and references therein, on AFCDM and applications) was extended to a level bearing direct relevance to observable nonassociative contributions using for relativistic thin disk models around such compact objects. We computed the most important quantities (energy, angular momentum, and angular velocity) for the most important physical quantities characterizing the thin disk model. The results of this paper prove that the main differences of such formulas in nonassociative gravity and GR are consequences of different types of nonholonomic structures resulting in angular anisotropies on \(\phi \) (in prolate coordinates); generic off-diagonal terms; and, for respective symmetries of generating functions) ellipsoidal type deformations, of BH horizons and thin accretion disks.
In the face-on case, we found that using nonholonomic frames, analytic approximations with effective cosmological constants for 8-d phase spaces, via nonlinear symmetries and parametric decompositions on string constant of nonassociative geometric objects we obtain effective real sources encoding contributions of star R-flux deformations. Such 8-d and 4-d nonassociative vacuum Einstein equations were originally proposed in [3, 4]. We have disentangled the roles of phase and spacetime nonassociative vacuum gravitational dynamics using nonholonomic dyadic decompositions and restricting the class of effective sources encoding star deformations. Such 4-d gravitational models can be studied independently up to a level when we have to compute nonsymmetric metrics coefficients, involve generalized phase space nonlinear symmetries and analyze explicitly certain higher dimension contributions. The BH and BE solutions constructed in this work define certain nonassociative generalizations of some classes of solutions in noncommutative and string gravity [30].
5.2 Concluding remarks and perspectives
Our work does not attempt to perform a complete study of BH solutions in nonassociative gravity with R-fluxes. Instead, we use simple toy models which provide intuition for possible geometric effects of nonassociative distortions for the 4-d Schwarzschild solution and imprints on related thin disks accretion effects. The techniques on generating exact and parametric nonassociative quasi-stationary phase space solutions elaborated in [26] can be applied to classes of of solutions in 8-d and 10-d phase spaces found in [32, 40] and construct new classes of nonassociative phase space and string BH and BE solutions, generalizing the Tangherlini and higher dimension Kerr metrics.
Here we note that only for some very special effective ellipsoid / spheroid horizons, the BHs and BEs can be characterized by corresponding Bekenstein–Hawking thermodynamic models. For more general classes of quasi-stationary and locally anisotropic solutions, we have to elaborate on nonassociative generalizations of relativistic geometric flow theory and Grigory Perelman’s entropic functionals and statistical/information thermodynamics [38]. In particular, we can treat the 4-d sector of nonassociative stationary vacuum gravitational solutions as relativistic Lorentz–Ricci solitons. This will allow to compute corresponding thermodynamical variables determined by R-flux distortions and encoding star product deformations and off-diagonal (non) symmetric effects. To study nonassociative (non) symmetric metric contributions, geometric and information flows (see related associative and commutative results in [37]) is a project for our future research.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The paper does not use associated data.]
Notes
We follow the Einstein convention rule with summation on up-low repeating indices, when left up, or low labels will be used for stating that certain geometric objects are defined on a some spaces, regions, for certain conditions etc. Here we note that we elaborate a different system of notation for coordinates, abstract and coordinate indices, and geometric objects for nonassociative gravity. In coordinate form, the R-flux deformation of the Ricci tensor (2) is given by formulas (5.90) and (1.3) in [4]. We shall provide in next section some generalized formulas for nonholonomic frames and a canonical distinguished connection distorting the LC-connection to certain configurations which allow to construct exact and parametric solutions.
Which can not be diagonalized by coordinate transforms in a finite spacetime/ phase space region.
i.e. non-integrable, equivalently anholonomic/nonholonomic; for details and definitions see above cited works and next section.
In this series of works on nonassociative nonholonomic geometry and gravity, we follow such conventions and notations for local real (spacetime and total phase space) and complex (co) fiber coordinates:
$$\begin{aligned}&\text{ on }\,\,{\mathbf {V}} \text{ and } {}_{s}{\mathbf {V}}:x=\{x^{i}\}=~_{s}x= \{x^{i_{s}}\}\\&\quad =(x^{i_{1}},x^{a_{2}}\rightarrow y^{a_{2}})=(x^{i_{2}}), \text{ with } x^{4}=t, \\&\quad \text{ where } i,j,...=1,2,3,4; \text{ shells }:\ \\&\quad s=1: \text{ when } i_{1},j_{1},...=1,2;s=2,a_{2},b_{2},...=3,4; \\&\quad \text{ on } T{\mathbf {V}} \text{ and } T_{s}\mathbf {{\mathbf {V}}}:\ u=(x,y)=\{u^{\alpha }=(u^{k}=x^{k},\ u^{a}=y^{a})\} \\&\quad ={}_{s}u =(~_{s}x,~_{s}y)=\{u^{\alpha _{s}}=(u^{k_{s}}=x^{k_{s}},\ u^{a_{s}}=y^{a_{s}})\}\\&=(x^{i_{1}},x^{i_{2}},x^{a_{3}}\rightarrow y^{a_{3}},x^{a_{4}}\rightarrow y^{a_{4}}), \text{ shells } \\&\quad s=1,2,3,4, \text{ where } \alpha ,\beta ,...=1,2,...8;a,b,...=5,6,7,8;a_{3},b_{3},...\\&\quad =(5,6);\ a_{4},b_{4},..=(7,8); \\&\quad \text{ on } T^{*}{\mathbf {V}} \text{ and } T_{s}^{*} {\mathbf {V}}: \ \ ^{\shortmid }u{=}(x,\ ^{\shortmid }p){=}\{\ u^{\alpha }{=}(u^{k}{=} x^{k},\ \ ^{\shortmid }p_{a}=p_{a})\} \\&\quad =({}_{3}^{\shortmid }x,{}_{4}^{\shortmid }p)=\{\ ^{\shortmid }u^{\alpha }=(\ ^{\shortmid }u^{k_{3}}=\ ^{\shortmid }x^{k_{3}},\ \ ^{\shortmid }p_{a_{4}}=p_{a_{4}})\} \\&\quad = {}_{s}^{\shortmid }u=( {}_{s}x,{}_{s}^{\shortmid }p) =\{\ ^{\shortmid }u^{\alpha _{s}}=(x^{k_{s}}, \ ^{\shortmid }p_{a_{s}}=p_{a_{s}})\}\\&\quad \quad =(x^{i_{1}},x^{i_{2}}, \ ^{\shortmid }p_{a_{3}}=p_{a_{3}},\ \ ^{\shortmid }p_{a_{4}}=p_{a_{4}}), \\&\quad =({}_{3}^{\shortmid }u~={}_{3}^{\shortmid }x,{}_{4}^{\shortmid }p)= \{\ ^{\shortmid }u^{\alpha _{3}} =(x^{i_{1}},x^{i_{2}},\ \ ^{\shortmid }x^{i_{3}}\rightarrow ~\ ^{\shortmid }p_{a_{3}}),\ \ ^{\shortmid }p_{a_{4}}\},\\&\quad \text{ where } \ \ ^{\shortmid }x^{\alpha _{3}}=(x^{i_{1}},x^{a_{2}},\ \ ^{\shortmid }p_{a_{3}}=p_{a_{3}}). \\&\quad \text{ on } T_{\parallel }^{*}{\mathbf {V}} \text{ and } T_{\parallel s}^{*}{\mathbf {V}}: \ ^{\parallel }u{=}(x,\ ^{\parallel }p){=}\{\ ^{\parallel }u^{\alpha }{=}(u^{k}{=}x^{k},\ ^{\parallel }p_{a}=(i\hbar )^{-1}p_{a})\} \\&\quad = ({}_{3}^{\parallel }x,{}_{4}^{\parallel }p)=\{\ ^{\parallel }u^{\alpha }=(^{\parallel }u^{k_{3}}=\ ^{\parallel }x^{k_{3}},\ ^{\parallel }p_{a_{4}}=(i\hbar )^{-1}p_{a_{4}})\} \\&\quad = {}_{s}^{\parallel }u=(~_{s}x,{}_{s}^{\parallel }p) = \{\ ^{\parallel }u^{\alpha _{s}}=(x^{k_{s}},\ \ ^{\parallel }p_{a_{s}}=(i\hbar )^{-1}p_{a_{s}})\}\\&=(x^{i_{1}},x^{i_{2}}, \ ^{\parallel }p_{a_{3}}=(i\hbar )^{-1}p_{a_{3}},\ ^{\parallel }p_{a_{4}}=(i\hbar )^{-1}p_{a_{4}}), \\&\quad =({}_{3}^{\parallel }u~{=}{}_{3}^{\parallel }x,{}_{4}^{\parallel }p){=}\{\ ^{\parallel }u^{\alpha _{3}}{=}(x^{i_{1}},x^{i_{2}},\ ^{\parallel }x^{i_{3}}\rightarrow ~^{\parallel }p_{a_{3}}),\ ^{\parallel }p_{a_{4}}\}, \text{ where } \\&\quad \ ^{\parallel }x^{\alpha _{3}}=(x^{i_{1}},x^{i_{2}},\ \ ^{\parallel }p_{a_{3}}=(i\hbar )^{-1}p_{a_{3}}). \end{aligned}$$Boldface indices are used for spaces and geometric objects enabled with (adapted to) N-connection structure. Our notations are different from the spacetime coordinates with momentum like variables considered in [3, 4] and we consider a N- and/or s-adapting of formulas for considering quasi-Hopf structures. An up (or low, on convenience), label “\(\ ^{\parallel }\)” is used in our papers for distinguishing coordinates with “complexified momenta” from real phase coordinates \(\ ^{\shortmid }u^{\alpha }=(x^{k},p_{a})\) on \(T^{*}\mathbf { V,}\) see similar conventions in Finsler–Lagrange–Hamilton geometry [31]. The formalism of N- and s-adapted labels and respective abstract or frame coefficient notations is elaborated in such a way that allows to use unified “symbolic” nonholonomic geometric calculus and many proofs by analogy.
We keep the label “\({\parallel }''\) if this constant is taken for the total phase space but the geometric objects are nonholonomically constrained on shells \(s=1,2\) and/or projected on a nonholonomic Lorentz base.
In brief, such formulas are with respective h1-v2-c3-c4 and h1-v2 decompositions.
Similar decoupling properties can be proven for so-called locally anisotropic cosmological solutions with Killing symmetry on \(\partial _{3}=\partial /\partial y^{3},\) for higher dimensions, and for more general assumptions when generic off-diagonal spacetime and/or phase space s-metrics depend on all coordinates, see details in [32, 37] and references therein. For simplicity, we omit such geometric constructions in this work.
If such conditions are note imposed, we can fine more special classes of exact and parametric solutions with another type of nonlinear and nonholonomic structures, possible singularities etc. but the corresponding formulas are quite cumbersome and do not allow general explicit integration of modified Einstein equations. We do not study such solutions in this work.
We consider that in the presence of an external static and axially symmetric matter distribution the exterior of a BH is described as a distorted Schwarzschild solution as in [44]. In such a case, a prime metric (59) defines a static vacuum solution with a regular event horizon but such a metric is not asymptotically flat [41, 43] . We can consider Schwarzschild coordinates \(x=r/M_{0}-1\) and \(y=\cos \theta \) and related them to the Weyl coordinates \(\rho =\sqrt{r(r-2M_{0})}\sin \theta \) and \(z=(r-M_{0})\cos \theta .\) In such variables, a prime metric ( 59) can be written as a Weyl metric
$$\begin{aligned} d\mathring{s}^{2}=e^{2[\gamma (\rho ,z)-\psi (\rho ,z)]}(d\rho ^{2}+dz^{2})+e^{-2\psi (\rho ,z)}\rho ^{2}d\phi ^{2}-e^{2\psi (\rho ,z)}dt^{2}. \end{aligned}$$For a Schwarzschild solution, we have \(\mathring{\psi }=\frac{1}{2}\ln \frac{ x-1}{x+1}\) and \(\ \mathring{\gamma }=\frac{1}{2}\ln \frac{x^{2}-1}{x^{2}-y^{2} },\) when \(\rho =M_{0}\sqrt{(x^{2}-1)(1-y^{2})}\) and \(z=M_{0}xy\), see details in [46] and section II of [43].
References
R.D. Schafer, An Introduction to Nonassociative Algebras (Dover Publications, New York, 1995)
J.C. Baez, The octonions. Bull. Am. Math. Soc. 39, 145–202 (2002) arXiv:math-ra/0105155 [Erratum: 42 (2005) 2013]
R. Blumenhagen, M. Fuchs, Towards a theory of nonassociative gravity. JHEP 1601, 039 (2016). arXiv:1604.03253
P. Aschieri, M. Dimitrijević Ćirić, R.J. Szabo, Nonassociative differential geometry and gravity with non-geometric fluxes. JHEP 02, 036 (2018). arXiv:1710.11467
R.J. Szabo, An introduction to nonassociative physics. Published in: PoS CORFU2018, 100 (2019).arXiv:1903.05673
P. Jordan, Über Eine Klasse Nichassociativer Hyperkomplexer Algebre, Nachr. Ges. Wiss. Göttingen, 569-575 (1932)
P. Jordan, J. von Neumann, E. Wigner, On algebraic generalization of the quantum mechanical formalism. Ann. Math. 35, 29–64 (1934)
D.F. Kurdgelaidze, The foundation of nonassociative classical field theory. Acta Phys. Hung. 57, 79 (1985)
S. Okubo, Introduction to Octonion and other Non-associative Algebras in Physics (Cambridge University Press, Cambridge, 1995)
C. Castro Perelman, The noncommutative and nonassociative geometry of octonionic spacetime, modified dispersion relations and grand unification. J. Math. Phys. 48, 073517 (2007)
C. Castro Perelman, Octonionic ternary gauge field theories revisited, IJGMMP, 1450013 (2014)
D. Mylonas, P. Schupp, R.J. Szabo, Membrane sigma-models and quantization of non-geometric flux backgrounds. JHEP 09 (2012). arXiv:1207.0926
D. Mylonas, P. Schupp, R.J. Szabo, Non-geometric fluxes, quasi-Hopf twist deformations and nonassociative quantum mechanics. J. Math. Phys. 55, 122301 (2014). arXiv:1312.1621
V.G. Kupriyanov, D.V. Vassilevich, Nonassociative Weyl star products. JHEP 1509, 102 (2015). arXiv:1506.02329
V.G. Kupriyanov, Non-associative star products and quantization of non-geometric backgrounds in string and M-theory. PoS CRFU2017, 200 (2018). arXiv:1804.10161
M. Günaydin, D. Lüst, E. Malek, Non-associativity in non-geometric string and M-theory background, the algebra of octonions, and missing momentum models. JHEP 1611, 027 (2016). arXiv:1607.06474
P. Bouwknegt, K. Hannabuss, V. Mathai, Nonassociative tori and applications to T-duality. Commun. Math. Phys. 264, 41–69 (2006). arXiv:hep-th/o412092
L. Alvarez-Gaume, F. Meyer, M.A. Vazquez-Mozo, Comments on noncommutative gravity. Nucl. Phys. B 753, 92–127 (2006). arXiv:hep-th/0605113
D. Lüst, T-duality and closed string non-commutative (doubled) geometry. JHEP 12, 084 (2010). arXiv:1010.1361
R. Blumenhagen, E. Plauschinn, Nonassociative gravity in string theory? J. Phys. A 44, 015401 (2011). arXiv:1010.1263
C. Condeescu, I. Florakis, C. Kounnas, D. Lü st, Gauged supergravities and non-geometric Q/R-fluxes from asymmetric orbifold CFT’s. JHEP 10, 057 (2012). arXiv:1307.0999
R. Blumenhagen, M. Fuchs, F. Haßler, D. Lüst, R. Sun, Non-associative deformations of geometry in double field theory. JHEP 04, 141 (2014). arXiv:1312.0719
V.G. Kupriyanov, \(L_{\infty }\)-Bootstrap approach to non-commutative gauge theories. Fortsch. Phys. 67, 1910010 (2019). arXiv:1903.02867
V.G. Kupriyanov, Non-commutative deformations of Chern–Simons theory. Eur. Phys. J. C 80, 42 (2020). arXiv:1905.08753
S. Vacaru, E.V. Veliev, L. Bubuianu, Nonassociative nonholonomic geometry of phase spaces with star R-flux deformations and (non) symmetric metrics. Fortschr. Physik 69, 2100029 (2021)
E.V. Veliev, L. Bubuianu, S.I. Vacaru, Decoupling and integrability of nonassociative vacuum phase space gravitational equations with star and R-flux parametric deformations. Fortschr. Physik 69, 2100030 (2021)
V.G. Drinfeld, Quasi-Hopf algebras. Algebraic Anal. 1(6), 114–148 (1989)
S. Vacaru, Superstrings in higher order extensions of Finsler superspaces. Nucl. Phys. B 434, 590–656 (1997). arXiv:hep-th/9611034
S. Vacaru, Exact solutions with noncommutative symmetries in Einstein and gauge gravity. J. Math. Phys. 46, 042503 (2005). arXiv:gr-qc/0307103
S. Vacaru, Finsler black holes induced by noncommutative anholonomic distributions in Einstein gravity. Class. Quantum Gravity 27, 105003 (2010). arXiv:0907.4278 [math-ph]
L. Bubuianu, S. Vacaru, Axiomatic formulations of modified gravity theories with nonlinear dispersion relations and Finsler–Lagrange–Hamilton geometry. Eur. Phys. J. C 78, 969 (2018)
L. Bubuianu, S. Vacaru, Black holes with MDRs and Bekenstein–Hawking and Perelman entropies for Finsler–Lagrange–Hamilton spaces. Ann. Phys. N. Y. 404, 10–38 (2019). arXiv:1812.02590
C.W. Misner, K.S. Thorn, J.A. Wheeler, Gravitation (Freeman, San Francisco, 1973)
S.W. Hawking, C.F.R. Ellis, The Large Scale Structure of Spacetime (Cambridge University Press, Cambridge, 1973)
R.W. Wald, General Relativity (Universtiy of Chicago Press, Chicago, 1984)
D. Kramer, H. Stephani, E. Herdlt, M.A.H. MacCallum, Exact Solutions of Einstein’s Field Equations, 2d edn. (Cambridge University Press, Cambridge, 2003)
L. Bubuianu, S. Vacaru, Deforming black hole and cosmological solutions by quasiperiodic and/or pattern forming structures in modified and Einstein gravity. Eur. Phys. J. C 78, 393 (2018). arXiv:1706.02584
I. Bubuianu, S.I. Vacaru, E.V. Veliev, Entropy functionals and thermodynamics of relativistic geometric flows, stationary quasi-periodic Ricci solitons, and gravity. Ann. Phys. N. Y. 423, 168333 (2020). arXiv:1903.04920
S. Vacaru, Perturbations and stability of black ellipsoids. Int. J. Mod. Phys. D 12, 461–478 (2003). arXiv:gr-qc/0206016
S. Vacaru, K. Irwin, Off-diagonal deformations of Kerr metrics and black ellipsoids in heterotic supergravity. Eur. Phys. J. C 77, 17 (2017). arXiv:1608.01980
S. Chandrasekhar, The Mathematical Theory of Black Holes (Oxford University Press, Oxford, 2002)
M.A. Abramowicz, P. ChrisFragile, Foundations of black hole accretion disk theory. Living Rev. Relativ. 16(1), 1 (2013)
Shokoufe Faraji, E. Hackmann, Thin accretion disk around the distorted Schwarzschild black hole. Phys. Rev. D 101, 023002 (2020). arXiv:2010.02786v2
R. Geroch, J.B. Hartle, Distorted black holes. J. Math. Phys. 23, 680–692 (1982)
N. Bretón, T.E. Denisova, V.S. Manko, A Kerr black hole in the external gravitational field. Phys. Lett. A 230, 7–11 (1997)
H. Quevedo, Multipole moments in general relativity static and stationary vacuum solutions. Fortschr. Physik 38, 733–840 (1990)
I.D. Novikov, K.S. Thorne, Astrophysics of black holes. In: C. Dewitt, B.S. Dewitt, editors, Black Holes (Les Astres Occlus, 1973), pp. 343-450
G. Compère, R. Oliveri, Self-similar accretion in thin discs around near-extremal black holes. MNRAS 468, 4351–4361 (2017)
Acknowledgements
This work develops for nonassociative geometry and gravity some research programs on geometry and physics supported during 2006–2015 by senior fellowships at the Perimeter Institute and Fields Institute (Ontario, Canada), CERN (Geneva, Switzerland) and Max Planck Institut für Physik/Werner Heisenberg Institut, München (Germany). SV is grateful to professors V. G. Kupriyanov, D. Lüst, N. Mavromatos, J. Moffat, D. Singleton and P. Stavrinos for respective hosting of short/long terms visits, seminars, and/or discussing important ideas and preliminary results.
Author information
Authors and Affiliations
Additional information
Address for post correspondence in 2020–2021 as a visitor senior researcher at YF CNU Ukraine is: Yu. Gagarin street, 37-3, Chernivtsi, Ukraine, 58008; authors are listed in alphabetic order when equal contributions are assumed.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Bubuianu, L., Vacaru, S.I. & Veliev, E.V. Nonassociative black ellipsoids distorted by R-fluxes and four dimensional thin locally anisotropic accretion disks. Eur. Phys. J. C 81, 1145 (2021). https://doi.org/10.1140/epjc/s10052-021-09921-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09921-z