1 Introduction

A gravitational singularity at the center of black holes is usually mathematically ill-defined because it can cause the curvature to diverge. Since the divergence can affect the validity of the causality law of spacetime, the singularity should always be hidden inside the black hole and is not allowed to appear in spacetime. In other words, an observer at infinity cannot detect any information from the singularity. To ensure well-define spacetime and the validity of the causality law, Penrose [1] proposed the weak cosmic censorship conjecture (WCCC). This conjecture postulates that the singularity should be surrounded by the event horizon and can never be exposed to spacetime.

Although the WCCC is suggested for any black hole, the general demonstration for the WCCC is notoriously difficult. Moreover, the validity of the conjecture also depends on the research technique. A notable gedanken experiment attempting to destroy Kerr black holes was proposed by Wald [2]. For Kerr black holes, the angular momentum should be bounded by the mass as \(J \le M^2\) when the event horizon of the black hole is guaranteed. To destroy Kerr black holes, a process whereby a test particle with sufficient angular momentum falls into Kerr black holes is considered. If the particle successfully drops into the black hole, the value of the angular momentum can exceed the boundary, and the existence of the event horizon will no longer be guaranteed. In this situation, a naked singularity will emerge in spacetime, and the WCCC for Kerr black holes is no longer valid. Fortunately, it was shown that when the particle carries the angular momentum sufficient to over-spin the Kerr black hole, it cannot be captured by the black hole due to the centrifugal force. This means that the WCCC for Kerr black holes cannot be violated under this process. Since this method was introduced, it has been used to examine the WCCC for other kinds of black holes [3,4,5,6,7]. However, the method has an inherent defect because the interaction between the particle and the background spacetime is not considered. Moreover, Hubeny [8] proposed that using the above method, violation of the WCCC might occur if one suitably adds the particle to a slightly non-extremal black hole. Therefore, to solve the defect, Sorce and Wald [9] proposed a new version of the gedanken experiment to examine the WCCC for Kerr–Newman black holes. In this experiment, the interaction between the black hole spacetime and matter fields outside the black hole was sufficiently considered. In this way, the black hole and matter fields are regarded as a complete dynamical system, while the process by which matter fields pass through the event horizon to perturb the black hole can be treated as a dynamical evolution process of the system. From this perspective, it was shown that the WCCC for near-extremal Kerr–Newman black holes cannot be as easily violated under the second-order approximation of the matter field perturbation. Furthermore, based on the new version of the gedanken experiment, the WCCC has also been demonstrated to be valid for other kinds of black holes [10,11,12,13].

For three-dimensional Bañados–Teitelboim–Zanelli (BTZ) black holes, the singularity at the center of the black hole is called a conical singularity. However, a conical singularity is not similar to a canonical singularity because it does not cause the spacetime curvature to diverge [14]. This means that a conical singularity does not influence the well-defined spacetime and the validity of the causality law. Moreover, an assumption was proposed in Ref. [15] which states that if black holes do not have a canonical singularity, the black hole will not need to obey the requirement of the WCCC. Due to the specific property of the conical singularity, investigating the WCCC for charged BTZ black holes is the best way to examine the assumption. Therefore, according to Ref. [14], the WCCC for rotated BTZ black holes was examined using the new version of the gedanken experiment. It was shown that after perturbation of the matter fields, the WCCC for rotated BTZ black holes cannot be violated. However, in this investigation, the Maxwell field is not contained in the spacetime, and the cosmological constant is not treated as a dynamical variable. Therefore, following our previous work [16], the cosmological constant is regarded as a portion of matter fields, while black holes and matter fields can be seen as a complete dynamical system using the new version of the gedanken experiment. In this case, the cosmological constant should be regarded as a dynamical variable. From this perspective, we will examine the WCCC for charged BTZ black holes under the second-order approximation of the perturbation to comprehensively check the assumption.

The paper is organized as follows. In Sect. 2, we discuss the spacetime geometry of charged BTZ black holes under the perturbation of matter fields. In Sect. 3, based on the Iyer–Wald formalism, we derive the first-order and the second-order perturbation inequalities of the black hole. In Sect. 4, using the first-order optimal option and the second-order inequality, we examine the WCCC for charged BTZ black holes under the second-order approximation of the perturbation. The paper ends with conclusions in Sect. 5.

2 Perturbed geometry of charged BTZ black holes

For the three-dimensional Einstein–Maxwell–AdS gravitational theory, the Lagrangian three-form is

$$\begin{aligned} {\varvec{L}}=\frac{1}{16 \pi } \left( R-2\Lambda - F^{ab}F_{ab} \right) {\varvec{\epsilon }}, \end{aligned}$$
(1)

where R is the Ricci scalar, \(\Lambda \) is the cosmological constant with a negative value, \({\varvec{F}}=d {\varvec{A}}\) is the strength of the electromagnetic field, \({\varvec{A}}\) is the gauge potential of the electromagnetic field, and \({\varvec{\epsilon }}\) is the volume element of the three-dimensional spacetime. From the Lagrangian, a class of static spherically symmetric solutions describing charged BTZ black holes is given as

$$\begin{aligned}&{\mathrm{d}}s^2 = -f(r) {\mathrm{d}}v^2 + 2 {\mathrm{d}}v {\mathrm{d}}r + r^2 {\mathrm{d}}\varphi ^2,\nonumber \\&{\varvec{A}} = -Q \ln \left( r \sqrt{-\Lambda } \right) {\mathrm{d}}v, \quad {\varvec{F}} = \frac{Q}{r} {\mathrm{d}}v \wedge {\mathrm{d}}r, \end{aligned}$$
(2)

where the blackening factor f(r) is

$$\begin{aligned} f(r) = -M - Q^2 \ln \left( - \Lambda r^2 \right) -\Lambda r^2. \end{aligned}$$
(3)

The parameters M and Q in f(r) correspond to the mass and the electric charge of the black hole. The radius of the event horizon \(r_h\) is the largest root of the equation \(f(r) = 0\). According to the radius of the event horizon, the area, surface gravity, and electric potential for the event horizon are further given as

$$\begin{aligned} A_{{\mathcal {H}}} = 2 \pi r_h, \quad \kappa = \frac{f^\prime \left( r_h \right) }{2}, \quad \Phi _{{\mathcal {H}}} = \frac{Q}{r_h}. \end{aligned}$$
(4)

Subsequently, we should first consider a process to examine the WCCC of charged BTZ black holes. In this process, matter fields pass through the event horizon and fall into the black hole. We further suggest that the cosmological constant can be regarded as an effective parameter determined by the matter source coupling to the Einstein–Maxwell gravity. This implies that the cosmological constant can be treated as a portion of matter fields. Moreover, the spacetime geometry of the black hole and matter fields can be seen as a complete dynamical system. From Eq. (1), the Lagrangian of this dynamical system can be rewritten as

$$\begin{aligned} {\varvec{L}} = \frac{1}{16 \pi } \left( R- F_{ab} F^{ab} \right) {\varvec{\epsilon }} + {\varvec{L}}_{\text {mt}}, \end{aligned}$$
(5)

where \({\varvec{L}}_{\text {mt}}\) is the Lagrangian of matter fields. From the Lagrangian, the Einstein–Maxwell–AdS gravitational theory can be efficiently derived again when there is a static solution of matter fields such that

$$\begin{aligned} T_{ab}= - \frac{\Lambda }{8 \pi } g_{ab}, \end{aligned}$$
(6)

where \(T_{ab}\) is the stress–energy tensor of matter fields. Since the cosmological constant is contained in matter fields, when matter fields fall into the black hole, their value can vary with the process. This suggests that the cosmological constant should be considered a dynamical variable in this situation.

To simplify the calculation and discussion, we only consider the case in which the configuration of matter fields is spherically symmetric. When the spacetime of the black hole and matter fields is treated as the complete dynamical system, the configurations of the metric \(g_{ab}\), the gauge potential of the electromagnetic field \({\varvec{A}}\), and matter fields can be uniformly described by a symbol \(\alpha \). The variation of the configurations with the process can be labeled a one-parameter family, i.e., \(\alpha (\lambda )\). For the case of \(\lambda = 0\), \(\alpha (0)\) represents the configuration of the dynamical fields on the background spacetime which is a charged BTZ black hole. When the change in \(\lambda \) with the process is small enough, the process can be treated as a perturbation. Therefore, under the perturbation, the equation of motion in this one-parameter family can be written as

$$\begin{aligned}&R_{ab} (\lambda ) - \frac{1}{2} R(\lambda ) g_{ab} (\lambda ) = 8 \pi \left[ T_{ab}^{\text {EM}} + T_{ab} (\lambda ) \right] , \nonumber \\&\nabla _a^{(\lambda )} F^{ab} (\lambda ) = 4 \pi j^a(\lambda ), \end{aligned}$$
(7)

where \(j^a\) is the current of the electric charge, and \(T_{ab}^{\text {EM}}\) is the stress–energy tensor of the electromagnetic field, which can be expressed as

$$\begin{aligned} T_{ab}^{\text {EM}} = \frac{1}{4 \pi } \left[ F_{ac} F_b^{\ c} - \frac{1}{4} g_{ab} F_{cd} F^{cd} \right] . \end{aligned}$$
(8)

The metric of spacetime during the perturbation can be generally written as

$$\begin{aligned} {\mathrm{d}}s^2 = - f(v, r, \lambda ) {\mathrm{d}}v^2 + 2 \mu (v, r, \lambda ) {\mathrm{d}}v {\mathrm{d}}r + r^2 {\mathrm{d}} \varphi ^2, \end{aligned}$$
(9)

where \(\mu (v, r, \lambda )\) is an arbitrary function. When \(f(v, r, 0) = f(r)\) and \(\mu (v, r, 0) = 1\), the metric will degenerate into the case of the background spacetime.

Following the train of thought proposed by Sorce and Wald, we also suggest that the perturbation should satisfy two conditions. The first is that the bifurcation surface B is not affected by the perturbation. The second is that the perturbation should satisfy the stability condition. This condition means that after perturbation of the matter fields, the spacetime geometry can also be described by the class of charged BTZ solutions. In other words, the solutions of the equation of motion after the perturbation are still described by Eq. (2), and the parameters M, Q, and \(\Lambda \) are replaced by \(M(\lambda )\), \(Q(\lambda )\), and \(\Lambda (\lambda )\), respectively, i.e.,

$$\begin{aligned}&{\mathrm{d}}s^2 (\lambda ) = -f(r, \lambda ) {\mathrm{d}}v^2 + 2 {\mathrm{d}}v \, {\mathrm{d}}r + r^2 {\mathrm{d}} \varphi ^2, \nonumber \\&{\varvec{A}} = - Q (\lambda ) \ln \left( r \sqrt{-\Lambda (\lambda )} \right) {\mathrm{d}}v, \quad {\varvec{F}}(\lambda ) = \frac{Q(\lambda )}{r} {\mathrm{d}}v \wedge {\mathrm{d}}r, \end{aligned}$$
(10)

where the blackening factor \(f(r, \lambda )\) is

$$\begin{aligned} f(r, \lambda ) = -M(\lambda ) - Q^2 (\lambda ) \ln \left[ -\Lambda (\lambda ) r^2 \right] - \Lambda (\lambda ) r^2. \end{aligned}$$
(11)

In addition, when the stability condition is satisfied, the stress–energy tensor of matter fields at sufficiently late time should have a similar form as Eq. (6), i.e.,

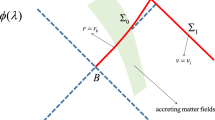
$$\begin{aligned} T_{ab} (\lambda ) = - \frac{\Lambda (\lambda )}{8 \pi } g_{ab} (\lambda ). \end{aligned}$$
(12)

The currents with the energy, the electric charge, and the cosmological constant are supposed to pass through a finite portion of the future event horizon and drop into the black hole to ensure that the two conditions are satisfied. So we can always choose a hypersurface \(\Sigma = {\mathcal {H}} \cup \Sigma _1\) on spacetime. For the hypersurface, \({\mathcal {H}}\) is a part of the event horizon which starts from the bifurcation surface B and continues along the future event horizon until the section of the event horizon \(B_1\) at a sufficiently late time. After that, the hypersurface becomes spacelike and goes to asymptotic infinity through the isochronous surface \(\Sigma _1\). Since the hypersurface \(\Sigma \) is independent of the parameter \(\lambda \), \(r_h\) is always the radius of the event horizon of the background spacetime. In addition, due to the stability condition, the spacetime geometry on the hypersurface \(\Sigma _1\) can be described by Eq. (10) directly.

3 Perturbation inequalities for charged BTZ black holes

Starting with this section, we would like to examine the WCCC for charged BTZ black holes under perturbation of the matter fields. Before examining the WCCC, the first-order and second-order perturbation inequalities should be derived. According to the Iyer–Wald formalism [17], we focus mainly on the Lagrangian three-form \({\varvec{L}}\) of three-dimensional Einstein–Maxwell gravitational theory and use the off-shell variation to obtain the two perturbation inequalities. For the theory of gravity, since the dynamical fields consist of the Lorentz signature metric \(g_{ab}\) and the electromagnetic field \({\varvec{A}}\), we also use the unified symbol \(\phi \) to represent the configuration of the dynamical field operators, i.e., \(\phi =\left( g_{ab}, {\varvec{A}} \right) \). When we consider the perturbation of the matter fields, the changing behavior of the configuration can also be described by the one-parameter family \(\lambda \), i.e., \(\phi (\lambda )\), while the variation of the quantity \(\eta \) related to the dynamical fields \(\phi \) is defined by

$$\begin{aligned} \delta \eta = \left. \frac{{\mathrm{d}} \eta (\lambda )}{{\mathrm{d}} \lambda } \right| _{\lambda =0}, \quad \delta ^2 \eta = \left. \frac{{\mathrm{d}}^2 \eta (\lambda )}{{\mathrm{d}} \lambda ^2} \right| _{\lambda =0}. \end{aligned}$$
(13)

Using the off-shell variation, the first-order variation of the Lagrangian \({\varvec{L}}\) is formally given as

$$\begin{aligned} \delta {\varvec{L}} = {\varvec{E}}_{\phi } \delta \phi + {\mathrm{d}} \varvec{\Theta }(\phi , \delta \phi ), \end{aligned}$$
(14)

where \({\varvec{E}}_{\phi } = 0\) is the equation of motion of the on-shell fields related to the Lagrangian \({\varvec{L}}\), and \({\varvec{\Theta }}\) is called the symplectic potential two-form which is locally constructed out of \(\phi \) and its derivatives. In Einstein–Maxwell gravity, from the Lagrangian

$$\begin{aligned} {\varvec{L}} = \frac{1}{16 \pi } \left( R- F_{ab} F^{ab} \right) {\varvec{\epsilon }}, \end{aligned}$$
(15)

the equation of motion is formally given as

$$\begin{aligned} {\varvec{E}}_{\phi } \delta \phi = - {\varvec{\epsilon }} \left[ \frac{1}{2} T^{ab} \delta g_{ab} + j^a \delta A_a \right] \end{aligned}$$
(16)

with

$$\begin{aligned} T_{ab} = \frac{1}{8 \pi } \left( R_{ab} - \frac{1}{2} R g_{ab} \right) - T_{ab}^{\text {EM}}, \quad j^a = \frac{1}{4 \pi } \nabla _a F^{ab}, \end{aligned}$$
(17)

where \(T_{ab}\) and \(j^a\) are the stress–energy tensor and the electric current of matter fields, respectively. For the background spacetime, the form of the stress–energy tensor is similar to Eq. (6). The total symplectic potential two-form \({\varvec{\Theta }}(\phi , \delta \phi )\) in Eq. (14) can be decomposed into two parts which represent the part of gravity and the part of the electromagnetic field, respectively,

$$\begin{aligned} {\varvec{\Theta }}_{ab} = {\varvec{\Theta }}_{ab}^{\text {GR}} + {\varvec{\Theta }}_{ab}^{\text {EM}}, \end{aligned}$$
(18)

where

$$\begin{aligned}&{\varvec{\Theta }}_{ab}^{\text {GR}} = \frac{1}{16 \pi } {\varvec{\epsilon }}_{cab} g^{cd} g^{ef} \left( \nabla _f \delta g_{de} - \nabla _d \delta g_{ef} \right) ,\nonumber \\&{\varvec{\Theta }}_{ab}^{\text {EM}} = - \frac{1}{4 \pi } {\varvec{\epsilon }}_{cab} F^{cd} \delta A_d. \end{aligned}$$
(19)

Using the symplectic potential, the symplectic current two-form can be defined as

$$\begin{aligned} {\varvec{\omega }} (\phi , \delta _1 \phi , \delta _2 \phi ) = \delta _1 {\varvec{\Theta }} (\phi , \delta _2 \phi ) - \delta _2 {\varvec{\Theta }} (\phi , \delta _1 \phi ). \end{aligned}$$
(20)

Since the symplectic potential can be linearly decomposed as the gravitational part and the electromagnetic part, the symplectic current can also be decomposed as the two parts, i.e.,

$$\begin{aligned} {\varvec{\omega }} = {\varvec{\omega }}^{\text {GR}} + {\varvec{\omega }}^{\text {EM}}. \end{aligned}$$
(21)

The specific expression of the two parts is respectively given as

$$\begin{aligned}&{\varvec{\omega }}_{ab}^{\text {GR}} = \frac{1}{16 \pi } {\varvec{\epsilon }}_{cab} w^c,\nonumber \\&{\varvec{\omega }}_{ab}^{\text {EM}} = \frac{1}{4 \pi } \left[ \delta _2 \left( {\varvec{\epsilon }}_{cab} F^{cd} \right) \delta _1 A_d - \delta _1 \left( {\varvec{\epsilon }}_{cab} F^{cd} \right) \delta _2 A_d \right] . \end{aligned}$$
(22)

For the gravitational part, we denote

$$\begin{aligned} w^{a}=P^{a b c d e f}\left( \delta _{2} g_{b c} \nabla _{d} \delta _{1} g_{e f}-\delta _{1} g_{b c} \nabla _{d} \delta _{2} g_{e f}\right) \end{aligned}$$
(23)

with

$$\begin{aligned} P^{a b c d e f}= & {} g^{a e} g^{f b} g^{c d}-\frac{1}{2} g^{a d} g^{b e} g^{f c}-\frac{1}{2} g^{a b} g^{c d} g^{e f}\nonumber \\&-\frac{1}{2} g^{b c} g^{a e} g^{f d}+\frac{1}{2} g^{b c} g^{a d} g^{e f}. \end{aligned}$$
(24)

We set \(\zeta ^a\) as an infinitesimal generator of the diffeomorphism. Replacing \(\delta \) with \({\mathcal {L}}_{\zeta }\) in Eq. (14), one can define the Noether current two-form \(\varvec{J}_{\zeta }\) associated with \(\zeta ^a\) as

$$\begin{aligned} \varvec{J}_{\zeta } = {\varvec{\Theta }} \left( \phi , {\mathcal {L}}_{\zeta } \phi \right) - \zeta \cdot {\varvec{L}}. \end{aligned}$$
(25)

In addition, it is shown that the Noether current can also be represented as [2]

$$\begin{aligned} \varvec{J}_{\zeta } = {\varvec{C}}_{\zeta } + d {\varvec{Q}}_{\zeta }, \end{aligned}$$
(26)

where \({\varvec{Q}}_{\zeta }\) is called the Noether charge, and \({\varvec{C}}_{\zeta } = \zeta \cdot {\varvec{C}}\) are the constraints of the theory. If \(C_a = 0\), the dynamical fields will satisfy the equations of motion. In the theory of Einstein–Maxwell gravity, the Noether charge can be decomposed into two parts as well that represent the conservation charge of the gravity and the electric charge of the electromagnetic field, i.e.,

$$\begin{aligned} {\varvec{Q}}_{\zeta } = {\varvec{Q}}_{\zeta }^{\text {GR}} + {\varvec{Q}}_{\zeta }^{\text {EM}}, \end{aligned}$$
(27)

where the specific expression of the \({\varvec{Q}}_{\zeta }^{\text {GR}}\) and \({\varvec{Q}}_{\zeta }^{\text {EM}}\) can respectively be given as

$$\begin{aligned}&\left( {\varvec{Q}}_{\zeta }^{\text {GR}} \right) _{a} = - \frac{1}{16 \pi } {\varvec{\epsilon }}_{abc} \nabla ^b \zeta ^c,\nonumber \\&\left( {\varvec{Q}}_{\zeta }^{\text {EM}} \right) _{a} = - \frac{1}{8 \pi } {\varvec{\epsilon }}_{abc} F^{bc} A_d \zeta ^d. \end{aligned}$$
(28)

Meanwhile, the constraints \({\varvec{C}}_{abc}\) in Eq. (26) are defined as

$$\begin{aligned} {\varvec{C}}_{abc} = {\varvec{\epsilon }}_{dbc} \left( T_a^{\ d} + A_a j^d \right) . \end{aligned}$$
(29)

To investigate the perturbation that comes from the spherically symmetric matter fields, the diffeomorphism generated by the static Killing vector field \(\xi ^a = \left( \partial / \partial v \right) ^a\) on the background spacetime is involved. Due to the diffeomorphism, a gauge condition that makes the coordinates \(\left( v, r, \phi \right) \) fixed under the variation can be chosen. This means that under the gauge condition, the Killing vector is invariable under the variation, i.e., \(\delta \xi ^a = 0\). Therefore, taking the first-order variations of Eqs. (25) and (26), the first-order variational identity can be expressed as

$$\begin{aligned} {\mathrm{d}} \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi , \delta \phi \right) \right]= & {} {\varvec{\omega }} \left( \phi , \delta \phi , {\mathcal {L}}_\xi \phi \right) - \xi \cdot {\varvec{E}}_{\phi } \delta \phi \nonumber \\&- \delta {\varvec{C}}_\xi . \end{aligned}$$
(30)

Furthermore, taking the variation on the above identity again, the second-order variational identity can also be obtained as

$$\begin{aligned}&{\mathrm{d}} \left[ \delta ^2 {\varvec{Q}}_\xi - \xi \cdot \delta {\varvec{\Theta }} \left( \phi , \delta \phi \right) \right] = {\varvec{\omega }} \left( \phi , \delta \phi , {\mathcal {L}}_\xi \delta \phi \right) \nonumber \\&\quad - \xi \cdot {\varvec{E}}_{\phi } \delta ^2 \phi - \xi \cdot \delta {\varvec{E}}_{\phi } \delta \phi - \delta ^2 {\varvec{C}}_\xi , \end{aligned}$$
(31)

where we have used the fact that \({\mathcal {L}}_\xi \phi = 0\) for the background dynamical fields.

In the following, according to Eqs. (30) and (31), we will derive the first-order and second-order perturbation inequalities, respectively. Furthermore, based on the two inequalities, we will examine the WCCC for charged BTZ black holes under the second-order approximation of the matter fields perturbation.

3.1 The first-order perturbation inequality

We first calculate the integral form of the first-order variational identity to derive the first-order perturbation inequality. Integrating the first-order variational identity on the hypersurface \(\Sigma \) and utilizing the condition \({\mathcal {L}}_\xi \phi = 0\), we have

$$\begin{aligned}&\int _{\Sigma } {\mathrm{d}} \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi , \delta \phi \right) \right] \nonumber \\&\quad +\int _\Sigma \xi \cdot {\varvec{E}}_{\phi } \delta \phi + \int _\Sigma \delta {\varvec{C}}_\xi = 0. \end{aligned}$$
(32)

Considering the property whereby the hypersurface \(\Sigma \) consists of a portion of the event horizon \({\mathcal {H}}\) and the spacelike hypersurface \(\Sigma _1\), and using the Stokes’ theorem, the integral form of the first-order variational identity can be decomposed as

$$\begin{aligned}&\int _{S_c} \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi , \delta \phi \right) \right] - \int _{B} \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi , \delta \phi \right) \right] \nonumber \\&\quad + \int _{\Sigma _1} \xi \cdot {\varvec{E}}_{\phi } \delta \phi + \int _{\Sigma _1} \delta {\varvec{C}}_\xi \nonumber \\&\quad + \int _{{\mathcal {H}}} \xi \cdot {\varvec{E}}_{\phi } \delta \phi + \int _{{\mathcal {H}}} \delta {\varvec{C}}_\xi = 0. \end{aligned}$$
(33)

When the cosmological constant is regarded as a variable, the divergence term will appear as the result of the integral on the spacelike infinity. In order to formally obtain the result of the integral, we will choose a cut-off sphere \(S_c\) with radius \(r_c\) to replace the asymptotic infinity boundary of \(\Sigma _1\). Moreover, we will take the limitation such that the cut-off sphere \(S_c\) approaches asymptotic infinity again to obtain the final result.

Following a similar consideration as Ref. [9], the gauge condition of the electromagnetic field, \(\xi ^a \delta A_a = 0\), on the event horizon \({\mathcal {H}}\) can also be imposed. However, on the hypersurface \(\Sigma _1\), the gauge condition cannot be used to calculate quantities related to \(\delta {\varvec{A}}\) and \(\delta ^2 {\varvec{A}}\) because the specific expression of the gauge potential,

$$\begin{aligned} {\varvec{A}}(\lambda ) = -Q(\lambda ) \ln \left( r \sqrt{- \Lambda (\lambda )} \right) {\mathrm{d}}v, \end{aligned}$$
(34)

does not satisfy the gauge condition on the hypersurface \(\Sigma _1\). Therefore, we need to find another method to calculate the relevant quantities. Since the strength of electromagnetic \({\varvec{F}}(\lambda )\) is gauge-invariant, it is reasonable for us to calculate the quantities which contain the gauge potential on hypersurface \(\Sigma _1\) using the electromagnetic strength. In the following calculation, we use only the specific expression of \({\varvec{F}}(\lambda )\) and neglect the expression of the gauge potential \({\varvec{A}}(\lambda )\) on the hypersurface \(\Sigma _1\).

The volume element on the hypersurface \(\Sigma _1\) can be written as

$$\begin{aligned} {\varvec{\epsilon }} = r {\mathrm{d}}v \wedge {\mathrm{d}}r \wedge {\mathrm{d}}\varphi . \end{aligned}$$
(35)

Since the expression of \({\varvec{\epsilon }} \) does not contain the parameter \(\lambda \), this implies that the variation of the element volume is vanishing, i.e., \(\delta {\varvec{\epsilon }} = 0\). According to the equation of motion, the stress–energy tensor \(T_{ab}\) and electric current \(j^a\) on \(\Sigma _1\) can be expressed as

$$\begin{aligned} T_{ab}(\lambda ) = - \frac{\Lambda (\lambda )}{8 \pi } g_{ab} (\lambda ), \quad j^a (\lambda ) = 0. \end{aligned}$$
(36)

Firstly, we consider the first term in Eq. (33). As mentioned above, the Noether charge and the symplectic potential are both decomposed as the gravity part and the electromagnetic field part. This means that the first term can also be decomposed into the two parts,

$$\begin{aligned}&\int _{S_c} \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} (\phi , \delta \phi ) \right] \nonumber \\&\quad = \int _{S_c} \left[ \delta {\varvec{Q}}_\xi ^{\text {GR}} - \xi \cdot {\varvec{\Theta }}^{\text {GR}} \left( \phi , \delta \phi \right) \right] \nonumber \\&\qquad + \int _{S_c} \left[ \delta {\varvec{Q}}_\xi ^{\text {EM}} - \xi \cdot {\varvec{\Theta }}^{\text {EM}} (\phi , \delta \phi ) \right] . \end{aligned}$$
(37)

For the gravity part, from Eqs. (19) and (28), using the specific expression of the metric in Eq. (10), we can obtain

$$\begin{aligned}&\int _{S_c} \left[ \delta {\varvec{Q}}_\xi ^{\text {GR}} - \xi \cdot {\varvec{\Theta }}^{\text {GR}} \left( \phi , \delta \phi \right) \right] \nonumber \\&\quad = \frac{1}{8} \left[ \frac{Q^2}{\Lambda } \delta \Lambda +2 Q \delta Q \ln \left( -\Lambda r_c^2\right) +\delta M+\delta \Lambda r_c^2 \right] . \end{aligned}$$
(38)

For the electromagnetic field part, using Eqs. (19) and (28), the integrand can be written as

$$\begin{aligned}&\delta {\varvec{Q}}_\xi ^{\text {EM}} - \xi \cdot {\varvec{\Theta }}^{\text {EM}} (\phi , \delta \phi ) \nonumber \\&\quad = - \frac{1}{8 \pi } {\varvec{\epsilon }}_{abc} \left( \delta F^{bc} A_d \xi ^d + F^{bc} \delta A_d \xi ^d + 2 F^{cd} \delta A_d \xi ^b \right) . \end{aligned}$$
(39)

Substituting the specific expression of the strength of the electromagnetic field into Eq. (39), we find the following relation between the second term and the third term

$$\begin{aligned} -{\varvec{\epsilon }}_{abc} F^{bc} \delta A_d \xi ^d = 2 {\varvec{\epsilon }}_{abc}F^{cd} \delta A_d \xi ^b = 2 Q \delta A_d \xi ^d (d \phi )_a.\nonumber \\ \end{aligned}$$
(40)

This implies that the last two terms in the integrand can cancel each other exactly, and only the integrand of the electromagnetic part remains as the first term. Hence, the result of the integral can be expressed as

$$\begin{aligned}&\int _{S_c} \left[ \delta {\varvec{Q}}_\xi ^{\text {EM}} - \xi \cdot {\varvec{\Theta }}^{\text {EM}} (\phi , \delta \phi ) \right] \nonumber \\&\quad = - \frac{1}{8 \pi } \int _{S_c} {\varvec{\epsilon }}_{abc} \delta F^{bc} A_d \xi ^d = - \frac{1}{4} \left[ Q \delta Q \ln \left( - \Lambda r_c^2 \right) \right] . \end{aligned}$$
(41)

Combining Eq. (38) with Eq. (41), the integral result of the first term in Eq. (33) is

$$\begin{aligned} \int _{S_c} \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} (\phi , \delta \phi ) \right] = \frac{1}{8} \left( \delta M + \frac{Q^2}{\Lambda } \delta \Lambda +\delta \Lambda r_c^2 \right) . \end{aligned}$$
(42)

According to the condition wherein the perturbation cannot influence the bifurcation surface B, the second term in Eq. (33) can be directly neglected.

Secondly, we will calculate the integrals on the hypersurface \(\Sigma _1\). For the third term in Eq. (33), substituting Eqs. (16) and (36) into it, we have

$$\begin{aligned} \int _{\Sigma _1} \xi \cdot {\varvec{E}}_{\phi } \delta \phi= & {} - \int _{\Sigma _1} \xi \cdot {\varvec{\epsilon }} \left[ \frac{1}{2} T^{ab} \delta g_{ab} + j^a \delta A_a \right] \nonumber \\= & {} \frac{\Lambda (\lambda )}{16 \pi } \int _{\Sigma _1} \xi \cdot {\varvec{\epsilon }}g^{ab} \delta g_{ab}. \end{aligned}$$
(43)

From the expression of the metric, we can obtain the condition \(g^{ab} \delta g_{ab} = 0\). This condition implies that the integral of the third term is equal to zero.

In order to evaluate the fourth term of Eq. (33), we should calculate the constraints on \(\Sigma _1\) firstly. According to Eq. (29), the expression of the Killing vector contracting with the constraints on the hypersurface \(\Sigma _1\) can be specifically written as

$$\begin{aligned} \left[ {\varvec{C}}_\xi (\lambda ) \right] _{bc}= & {} {\varvec{\epsilon }}_{dbc} \left[ T_a^{\ d} (\lambda ) \xi ^a + A _a j^d (\lambda ) \xi ^a \right] \nonumber \\= & {} - \frac{\Lambda (\lambda ) r}{8 \pi } ({\mathrm{d}}r)_b \wedge ({\mathrm{d}}\phi )_c. \end{aligned}$$
(44)

Taking the variation on the above expression and integrating it on the hypersurface \(\Sigma _1\), the fourth term can be obtained as

$$\begin{aligned} \int _{\Sigma _1} \delta {\varvec{C}}_\xi = - \frac{\delta \Lambda }{4} \int _{r_h}^{r_c} r {\mathrm{d}}r = \frac{\delta \Lambda }{8} \left( r_h^2 - r_c^2 \right) . \end{aligned}$$
(45)

Finally, we turn to calculate the integrals on the event horizon \({\mathcal {H}}\). For the fifth term in Eq. (33), the integral result is directly equal to zero because the Killing vector contracting with the volume element vanishes on the event horizon \({\mathcal {H}}\). For the sixth term of Eq. (33), according to the definition of the constraints and \(j(0) = 0\) on the background spacetime, using the expression of the gauge potential \({\varvec{A}}\), we have

$$\begin{aligned} \int _{{\mathcal {H}}} \delta {\varvec{C}}_\xi= & {} \delta \int _{{\mathcal {H}}} \left[ {\varvec{\epsilon }}_{dbc} \left( T_a^{\ d} (\lambda ) \xi ^a + A _a \xi ^a j^d (\lambda ) \right) \right] \nonumber \\= & {} - \delta \left[ \int _{{\mathcal {H}}} \tilde{{\varvec{\epsilon }}} \mu (v, r_h) T_{ad} (\lambda ) \xi ^a ({\mathrm{d}}r)^d \right] \nonumber \\&- \frac{1}{2} Q \ln \left( - \Lambda r_h^2 \right) \delta \left( \int _{{\mathcal {H}}} {\varvec{\epsilon }}_{dbc} j^d \right) , \end{aligned}$$
(46)

where we have denoted the volume element of the event horizon as \(\tilde{{\varvec{\epsilon }}} = {\mathrm{d}}v \wedge \hat{{\varvec{\epsilon }}}\), and \(\hat{{\varvec{\epsilon }}} = r {\mathrm{d}} \varphi \) is the volume element of a cross-section of the event horizon. According to the electromagnetic part of the equation of motion, we can then obtain

$$\begin{aligned} \delta \left( \int _{{\mathcal {H}}} {\varvec{\epsilon }}_{dbc} j^d \right)= & {} \frac{1}{4 \pi } \delta \left( \int _{{\mathcal {H}}} {\varvec{\epsilon }}_{dbc} \nabla _a F^{da} \right) \nonumber \\= & {} \frac{1}{8 \pi } \delta \left( \int _{B_1} {\varvec{\epsilon }}_{dbc}F^{db}- \int _{B} {\varvec{\epsilon }}_{dbc} F^{db} \right) \nonumber \\= & {} - \frac{\delta Q}{2}. \end{aligned}$$
(47)

Therefore, Eq. (46) can be reduced as

$$\begin{aligned}&\int _{{\mathcal {H}}} \delta {\varvec{C}}_\xi = \frac{1}{4} Q \delta Q \ln \left( - \Lambda r_h^2 \right) \nonumber \\&\quad - \delta \left[ \int _{{\mathcal {H}}} \tilde{{\varvec{\epsilon }}} \mu (v, r_h) T_{ae} (\lambda ) \xi ^a ({\mathrm{d}}r)^e \right] . \end{aligned}$$
(48)

Substituting Eqs. (42), (45), and (48) into Eq. (33), the integral form of the first-order variational identity can be written as

$$\begin{aligned}&\delta M + \frac{Q^2}{\Lambda } \delta \Lambda + r_h^2 \delta \Lambda + 2 Q \delta Q \ln \left( - \Lambda r_h^2 \right) \nonumber \\&\quad = 8 \delta \left[ \int _{{\mathcal {H}}} \tilde{{\varvec{\epsilon }}} \mu (v, r_h) T_{ae} (\lambda ) \xi ^a ({\mathrm{d}}r)^e \right] . \end{aligned}$$
(49)

To derive the first-order perturbation inequality, we should determine the connection between the right-hand side of Eq. (49) and the null energy condition. During the perturbation, since we consider the process wherein the spherically symmetric matter fields fall into charged BTZ black holes, a null vector field can be chosen as

$$\begin{aligned} l^a (\lambda ) = \xi ^a + \beta (\lambda ) r^a, \end{aligned}$$
(50)

where

$$\begin{aligned} r^a = \left( \frac{\partial }{\partial r} \right) ^a, \quad \beta (\lambda ) = \frac{f(v, r_h, \lambda )}{2 \mu (v, r_h, \lambda )}. \end{aligned}$$
(51)

Using the null vector field, the null energy condition during the perturbation process can generally be expressed as

$$\begin{aligned} T_{ab} (\lambda ) l^a (\lambda ) l^b (\lambda ) \ge 0. \end{aligned}$$
(52)

It can be demonstrated that the null energy condition should satisfy the following relation

$$\begin{aligned} T_{ab} (\lambda ) l^a (\lambda ) l^b (\lambda )= & {} \mu (v, r_h, \lambda ) T_{ab} (\lambda ) \xi ^a ({\mathrm{d}}r)^b + \beta (\lambda )^2 \nonumber \\&\quad \times T_{ab} (\lambda ) r^a r^b. \end{aligned}$$
(53)

Utilizing the fact that \(\beta (0) = 0\) for the background spacetime, the null energy condition under the first-order approximation can be obtained as

$$\begin{aligned}&\int _{{\mathcal {H}}} T_{ab}(\lambda ) l^a (\lambda ) l^b (\lambda ) dv \wedge \tilde{{\varvec{\epsilon }}} \nonumber \\&\quad \simeq \lambda \delta \left[ \int _{{\mathcal {H}}} \tilde{{\varvec{\epsilon }}} \mu (v, r_h) T_{ab} \xi ^a ({\mathrm{d}}r)^b \right] \ge 0. \end{aligned}$$
(54)

Substituting Eq. (54) into Eq. (49), the integral form of the first-order variational identity can be reduced as

$$\begin{aligned} \delta M + \frac{Q^2}{\Lambda } \delta \Lambda + r_h^2 \delta \Lambda + 2 Q \delta Q \ln \left( - \Lambda r_h^2 \right) \ge 0. \end{aligned}$$
(55)

This inequality is called the first-order perturbation inequality.

Since the main objective of our investigation is to examine the WCCC for charged BTZ black holes under a second-order approximation to check the assumption that if a black hole does not have a canonical singularity, it does not need to satisfy the requirement of the WCCC. When the first-order perturbation inequality is satisfied, this indicates that the WCCC cannot be violated under the first-order approximation of the perturbation, while the higher-order approximation can be largely neglected. However, if a first-order perturbation inequality is chosen as an optimal option, i.e.,

$$\begin{aligned} \delta M + \frac{Q^2}{\Lambda } \delta \Lambda + r_h^2 \delta \Lambda + 2 Q \delta Q \ln \left( - \Lambda r_h^2 \right) = 0, \end{aligned}$$
(56)

the WCCC cannot be examined under the first-order approximation, and the second-order approximation needs to be further considered in this situation. In addition, the optimal option also implies that the energy flux through the event horizon vanishes under the first-order approximation of perturbation.

3.2 The second-order perturbation inequality

To consider the second-order approximation of the perturbation, we should sequentially derive the second-order perturbation inequality. Integrating the second-order variational identity on the hypersurface \(\Sigma \), Eq. (31) can be written as

$$\begin{aligned}&\int _{\Sigma } \delta \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi , \delta \phi \right) \right] + \int _{\Sigma } \delta ^2 {\varvec{C}}_\xi \nonumber \\&\quad + \int _{\Sigma } \delta \left( \xi \cdot {\varvec{E}}_{\phi } \delta \phi \right) - \int _{\Sigma } {\varvec{\omega }} \left( \phi , \delta \phi , {\mathcal {L}}_\xi \delta \phi \right) = 0. \end{aligned}$$
(57)

According to Stokes’ theorem, and utilizing the property of the hypersurface \(\Sigma \), the integral expression can be decomposed as

$$\begin{aligned}&\int _{S_c} \delta \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi , \delta \phi \right) \right] - \int _{B} \delta \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi , \delta \phi \right) \right] \nonumber \\&\quad + \int _{{\mathcal {H}}} \delta ^2 {\varvec{C}}_\xi + \int _{\Sigma _1} \delta ^2 {\varvec{C}}_\xi + \int _{\Sigma _1} \delta \left( \xi \cdot {\varvec{E}}_{\phi } \delta \phi \right) \nonumber \\&\quad + \int _{{\mathcal {H}}} \delta \left( \xi \cdot {\varvec{E}}_{\phi } \delta \phi \right) - {\mathcal {E}}_{{\mathcal {H}}} \left( \phi , \delta \phi \right) - {\mathcal {E}}_{\Sigma _1} \left( \phi , \delta \phi \right) = 0,\nonumber \\ \end{aligned}$$
(58)

where

$$\begin{aligned} {\mathcal {E}}_{{\mathcal {H}}} \left( \phi , \delta \phi \right)= & {} \int _{{\mathcal {H}}} {\varvec{\omega }} \left( \phi , \delta \phi , {\mathcal {L}}_\xi \delta \phi \right) , \nonumber \\ {\mathcal {E}}_{\Sigma _1} \left( \phi , \delta \phi \right)&{=}&\int _{\Sigma _1} {\varvec{\omega }} \left( \phi , \delta \phi , {\mathcal {L}}_\xi \delta \phi \right) . \end{aligned}$$
(59)

In the integral form of the second-order variational identity, we can see that, except for the last two terms, any term in Eq. (58) only takes the variation again on the corresponding term in the first-order variational identity. Therefore, we can use the integral result directly in the first-order variational identity to evaluate the integral of the second-order perturbation inequality.

As with the first-order variational identity, the first term in Eq. (58) can also be decomposed into the gravity part and the electromagnetic field part. From Eqs. (38) and (41), the integrand of the two parts can be obtained as

$$\begin{aligned}&\delta \left[ \delta {\varvec{Q}}^{\text {GR}}_\xi - \xi \cdot {\varvec{\Theta }}^{\text {GR}} \left( \phi , \delta \phi \right) \right] \nonumber \\&\quad = \frac{1}{16 \pi } \left[ \delta ^2 M + r^2 \delta ^2 \Lambda + \frac{Q^2}{\Lambda } \delta ^2 \Lambda - \frac{Q^2}{\Lambda ^2} \delta \Lambda ^2+ \frac{4Q}{\Lambda } \delta Q \delta \Lambda \right. \nonumber \\&\qquad \left. + 2 Q \delta ^2 Q \ln \left( - \Lambda r^2 \right) + 2 \delta Q^2 \ln \left( - \Lambda r^2 \right) \right] ({\mathrm{d}}\phi )_a, \end{aligned}$$
(60)

and

$$\begin{aligned}&\delta \left[ \delta {\varvec{Q}}^{\text {EM}}_\xi - \xi \cdot {\varvec{\Theta }}^{\text {EM}} \left( \phi , \delta \phi \right) \right] \nonumber \\&\quad = - \frac{1}{8 \pi } {\varvec{\epsilon }}_{abc} \delta ^2 F^{bc} A_d \xi ^d - \frac{1}{8 \pi }{\varvec{\epsilon }}_{abc} \delta F^{bc} \delta A_d \xi ^d \nonumber \\&\quad = - \frac{1}{8 \pi } Q \delta ^2 Q \ln \left( - \Lambda r^2 \right) ({\mathrm{d}}\phi )_a - \frac{1}{8 \pi }{\varvec{\epsilon }}_{abc} \delta F^{bc} \delta A_d \xi ^d. \end{aligned}$$
(61)

Integrating the above two equations on the hypersurface \(S_c\), respectively, and summing the integral results of the two parts, the result of the first term in Eq. (58) can be given as

$$\begin{aligned}&\int _{S_c} \delta \left[ \delta {\varvec{Q}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi , \delta \phi \right) \right] \nonumber \\&\quad = \frac{1}{8} \left[ \delta ^2 M + r_c^2 \delta ^2 \Lambda + \frac{Q^2}{\Lambda } \delta ^2 \Lambda - \frac{Q^2}{\Lambda ^2} \delta \Lambda ^2\right. \nonumber \\&\qquad \left. + \frac{4Q}{\Lambda } \delta Q \delta \Lambda + 2 \delta Q^2 \ln \left( - \Lambda r_c^2 \right) \right] - {\mathcal {Y}} \left( \phi , \delta \phi \right) , \end{aligned}$$
(62)

where

$$\begin{aligned} {\mathcal {Y}} \left( \phi , \delta \phi \right) = \frac{1}{8 \pi } \int _{S_c} {\varvec{\epsilon }}_{abc} \delta F^{bc} \delta A_d \xi ^d. \end{aligned}$$
(63)

Based on the definition of the constraints (29) and \(j(0) = 0\) on the background spacetime, the second-order variation of the Killing vector contracting with the constraints can be expressed as

$$\begin{aligned} \delta ^2 {\varvec{C}}_\xi= & {} \delta ^2 \left( {\varvec{\epsilon }}_{dbc} \mu (v, r_h) T_{a}^{\, d} \xi ^a \right) \nonumber \\&+{\varvec{\epsilon }}_{dbc} \left( 2 \xi ^a \delta A_a \delta j^d + \xi ^a A_a \delta ^2 j^d \right) . \end{aligned}$$
(64)

Integrating Eq. (64) on the event horizon \({\mathcal {H}}\), using the result of Eq. (47) and the gauge condition \(\xi ^a \delta A_a = 0\), the integral result of the third term in Eq. (58) is

$$\begin{aligned} \int _{{\mathcal {H}}} \delta ^2 {\varvec{C}}_\xi= & {} - \delta ^2 \left( \int _{{\mathcal {H}}} \tilde{{\varvec{\epsilon }}} \mu (v, r_h) T_{ad} \xi ^a (dr)^d \right) \nonumber \\&+ \frac{1}{4} Q \delta ^2 Q \ln \left( - \Lambda r_h^2 \right) . \end{aligned}$$
(65)

From the result of Eq. (44), the fourth term can be directly calculated as

$$\begin{aligned} \int _{\Sigma _1} \delta ^2 {\varvec{C}}_\xi = - \frac{\delta ^2 \Lambda }{4} \int _{r_h}^{r_c} r {\mathrm{d}}r = \frac{\delta ^2 \Lambda }{8} \left( r_h^2 - r_c^2 \right) . \end{aligned}$$
(66)

Based on the condition \(g^{ab}(\lambda ) \delta g_{ab} (\lambda ) = 0\) and the fact that \(\xi ^a\) contracting with the volume element is zero on the event horizon \({\mathcal {H}}\), we have

$$\begin{aligned} \int _{\Sigma _1} \delta \left( \xi \cdot {\varvec{E}}_{\phi } \delta \phi \right) = \int _{{\mathcal {H}}} \delta \left( \xi \cdot {\varvec{E}}_{\phi } \delta \phi \right) = 0. \end{aligned}$$
(67)

For the seventh term, since the symplectic current can be decomposed as the gravitational part and the electromagnetic part, its integral can be decomposed as the two parts as well, i.e.,

$$\begin{aligned} {\mathcal {E}}_{{\mathcal {H}}} = \int _{{\mathcal {H}}} {\varvec{\omega }}^{\text {GR}} + \int _{{\mathcal {H}}} {\varvec{\omega }}^{\text {EM}}. \end{aligned}$$
(68)

For the integral of the gravitational part, according to the specific expression of the metric in Eq. (9), the integral can be directly calculated as

$$\begin{aligned} \int _{{\mathcal {H}}} {\varvec{\omega }}^{\text {GR}}= & {} - \frac{r_h}{2} \int _{v_0}^{v_1} {\mathrm{d}}v \Bigg [\delta \mu (v, r_h) \partial _v \delta f (v, r_h)\nonumber \\&\qquad - \partial _v \delta \mu (v, r_h) \delta f(v, r_h)\Bigg ] \nonumber \\= & {} \frac{r_h}{2} \delta \mu (v_1, r_h) \delta f(v_1, r_h) = 0, \end{aligned}$$
(69)

where we have used the optimal option of the first-order approximation.

To evaluate the integral of the electromagnetic part, the specific expression of the symplectic current of the electromagnetic part should first be considered. Based on the definition, the symplectic current of the electromagnetic field can be expressed as

$$\begin{aligned} \omega _{ab}^{\text {EM}}&= \frac{1}{4 \pi } {\varvec{\epsilon }}_{cab} \left[ \delta A_d {\mathcal {L}}_\xi \delta F^{cd} - \delta F^{cd} {\mathcal {L}}_\xi \delta A_d \right] \nonumber \\&+ \frac{1}{4 \pi } \left[ \left( {\mathcal {L}}_\xi \delta {\varvec{\epsilon }}_{cab} F^{cd} \delta A_d - \delta {\varvec{\epsilon }}_{cab} F^{cd} {\mathcal {L}}_\xi \delta A_{d} \right) \right] . \end{aligned}$$
(70)

The expressions of the electromagnetic field strength in Eq. (10) indicates that if the index c in the volume element is chosen as the component of r, i.e., \(({\mathrm{d}}r)_c\), after contracting \(({\mathrm{d}}r)_c\) with \(F^{cd}\), a proportional relation between the result of the contraction and the Killing vector can be obtained as \(({\mathrm{d}}r)_c F^{cd}\propto - \xi ^d\). According to the proportional relation and the gauge condition \(\xi ^a \delta A_a = 0\) on the event horizon, we can find that the last two terms in Eq. (70) both vanish, and Eq. (70) can be reduced as

$$\begin{aligned} \omega _{cab}^{\text {EM}} = \frac{1}{4 \pi } {\mathcal {L}}_\xi \left( {\varvec{\epsilon }}_{cab} \delta A_d \delta F^{cd} \right) - \frac{1}{2 \pi } {\varvec{\epsilon }}_{cab} \delta F^{cd} {\mathcal {L}}_\xi \delta A_d.\nonumber \\ \end{aligned}$$
(71)

For the first term in Eq. (71), it will not appear in the final expression of the integral because it only contains a boundary term after the integration, and the boundary term will not contribute to \({\mathcal {E}}_{{\mathcal {H}}}\). Using the gauge condition \(\xi ^a \delta A_a = 0\) again on the event horizon, the expression of Eq. (68) can finally be simplified as

$$\begin{aligned} {\mathcal {E}}_{{\mathcal {H}}}= & {} \frac{1}{2 \pi } \int _{{\mathcal {H}}} \tilde{{\varvec{\epsilon }}} ({\mathrm{d}}r)_c \delta F^{cd} {\mathcal {L}}_\xi \delta A_d \nonumber \\= & {} \frac{1}{2 \pi } \int _{{\mathcal {H}}} \left[ \tilde{{\varvec{\epsilon }}} ({\mathrm{d}}r)_a \xi ^b \delta F^{ac} \delta F_{bc} + \tilde{{\varvec{\epsilon }}} ({\mathrm{d}}r)_a \delta F^{ac} \nabla _c (\xi ^b \delta A_b) \right] \nonumber \\= & {} \frac{1}{2 \pi } \int _{{\mathcal {H}}} \tilde{{\varvec{\epsilon }}} ({\mathrm{d}}r)_a \xi ^b \delta F^{ac} \delta F_{bc}. \end{aligned}$$
(72)

On the other hand, based on the stress–energy tensor of the electromagnetic field, the result of Eq. (72) can be rewritten as

$$\begin{aligned} {\mathcal {E}}_{{\mathcal {H}}} = \delta ^2 \left( \int _{{\mathcal {H}}} \varvec{\tilde{\epsilon }} \mu (v, r_h) T_{ab}^{\text {EM}} \xi ^a ({\mathrm{d}}r)^b \right) . \end{aligned}$$
(73)

Therefore, combining Eqs. (62), (65), (66), (67), and (73), the second-order variational identity can be obtained as

$$\begin{aligned}&\frac{1}{8} \Bigg [\delta ^2 M + r_h^2 \delta ^2 \Lambda + \frac{Q^2}{\Lambda } \delta ^2 \Lambda \nonumber \\&\quad - \frac{Q^2}{\Lambda ^2} \delta \Lambda ^2 + \frac{4Q}{\Lambda } \delta Q \delta \Lambda + 2 \delta Q^2 \ln \left( - \Lambda r_c^2 \right) \nonumber \\&\quad + 2 Q \delta ^2 Q \ln \left( -\Lambda r_h^2 \right) \Bigg ] \nonumber \\&\quad - \delta ^2 \left[ \int _{{\mathcal {H}}} \varvec{\tilde{\epsilon }} \mu (v, r_h) \left( T_{ab}^{\text {EM}} + T_{ab} \right) ({\mathrm{d}}r)^a \xi ^b \right] \nonumber \\&\quad - {\mathcal {E}}_{\Sigma _1} \left( \phi , \delta \phi \right) - {\mathcal {Y}} \left( \phi , \delta \phi \right) = 0. \end{aligned}$$
(74)

Next we will evaluate the last two terms \({\mathcal {E}}_{\Sigma _1} \left( \phi , \delta \phi \right) \) and \({\mathcal {Y}} \left( \phi , \delta \phi \right) \) in Eq. (74) to obtain the complete expression of the second-order variational identity. From the expressions of \({\mathcal {E}}_{\Sigma _1} \left( \phi , \delta \phi \right) \) and \({\mathcal {Y}} \left( \phi , \delta \phi \right) \), we can see that the two quantities depend only on the first-order variation of the dynamical fields, and the integral is implemented only on the hypersurface \(\Sigma _1\). Following the method in Ref. [9], an auxiliary spacetime should be introduced to calculate the two terms. Since the auxiliary spacetime involves only the dynamical fields and their first-order variation, the first-order variation of the dynamical fields \(\delta \phi \) can be labeled \(\delta \phi ^{\text {BTZ}}\), where \(\phi ^{\text {BTZ}}\) represents the dynamical fields in the auxiliary spacetime. Therefore, we can replace \(\delta \phi \) with \(\delta \phi ^{\text {BTZ}}\) in the expression of the two quantities, i.e.,

$$\begin{aligned} {\mathcal {E}}_{\Sigma _1} (\phi , \delta \phi )= & {} {\mathcal {E}}_{\Sigma _1} (\phi , \delta \phi ^{\text {BTZ}} ), \nonumber \\ {\mathcal {Y}}(\phi , \delta \phi )= & {} {\mathcal {Y}}(\phi , \delta \phi ^{\text {BTZ}} ). \end{aligned}$$
(75)

According to the stability condition, the spacetime geometry still belongs to the class of charged BTZ solutions after the perturbation, and the changing behavior of the configurations of the dynamical fields can be described by the one-parameter family \(\lambda \). Therefore, after the perturbation process, the solutions of the equation of motion in the auxiliary spacetime can be directly written as

$$\begin{aligned} {\mathrm{d}}s_{\text {BTZ}}^2 (\lambda )= & {} - f^{\text {BTZ}} (r, \lambda ) {\mathrm{d}}v^2 + 2 {\mathrm{d}}v \, {\mathrm{d}}r + r^2 {\mathrm{d}} \varphi ^2, \nonumber \\ {\varvec{A}}(\lambda )= & {} - Q^\text {BTZ}(\lambda ) \ln \left( r \sqrt{- \Lambda ^\text {BTZ}(\lambda )} \right) {\mathrm{d}}v, \nonumber \\ {\varvec{F}} (\lambda )= & {} \frac{Q^{\text {BTZ}}(\lambda )}{r} {\mathrm{d}}v \wedge {\mathrm{d}}r, \end{aligned}$$
(76)

where the blackening factor \(f^{\text {BTZ}} (r, \lambda )\) is

$$\begin{aligned} f^{\text {BTZ}}(r, \lambda )= & {} -M^{\text {BTZ}}(\lambda ) - \left[ Q^{\text {BTZ}} (\lambda ) \right] ^2 \ln \left[ -\Lambda ^{\text {BTZ}}(\lambda ) r^2 \right] \nonumber \\&-\Lambda ^{\text {BTZ}}(\lambda ) r^2. \end{aligned}$$
(77)

Since only the first-order variation of the dynamical fields is contained in the auxiliary spacetime, and the higher-order variation does not exist, the parameters \(M^{\text {BTZ}} (\lambda )\), \(Q^{\text {BTZ}} (\lambda )\), and \(\Lambda ^{\text {BTZ}} (\lambda )\) under the first-order approximation can be expanded as

$$\begin{aligned}&M^{\text {BTZ}} (\lambda ) = M + \lambda \delta M, \nonumber \\&Q^{\text {BTZ}} (\lambda ) = Q + \lambda \delta Q, \nonumber \\&\Lambda ^{\text {BTZ}} (\lambda ) = \Lambda + \lambda \delta \Lambda , \end{aligned}$$
(78)

where \(\delta M\), \(\delta Q\), and \(\delta \Lambda \) are chosen to agree with the values of the first-order approximation. This implies that the relation \(\delta ^2 M = \delta ^2 Q = \delta ^2 \Lambda = {\mathcal {E}}_{{\mathcal {H}}}(\phi , \delta \phi ) = 0\) will be given naturally in the auxiliary spacetime. Based on the above discussions, the two terms \({\mathcal {E}}_{\Sigma _1} \left( \phi , \delta \phi \right) \) and \({\mathcal {Y}} \left( \phi , \delta \phi \right) \) can be directly evaluated in the auxiliary spacetime.

Using Stokes’ theorem, the integral of the second-order variational identity can be written as

$$\begin{aligned}&\int _{S_c} \delta \left[ \delta {\varvec{Q}}^{\text {BTZ}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi ^{\text {BTZ}}, \delta \phi ^{\text {BTZ}} \right) \right] \nonumber \\&\quad - \int _{B_1} \delta \left[ \delta {\varvec{Q}}^{\text {BTZ}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi ^{\text {BTZ}}, \delta \phi ^{\text {BTZ}} \right) \right] \nonumber \\&\quad + \int _{\Sigma _1} \delta ^2 {\varvec{C}}_\xi ^{\text {BTZ}} + \int _{\Sigma _1} \delta \left( \xi \cdot {\varvec{E}}^{\text {BTZ}}_{\phi } \delta \phi ^{\text {BTZ}} \right) \nonumber \\&\quad - {\mathcal {E}}_{\Sigma _1} \left( \phi ^{\text {BTZ}}, \delta \phi ^{\text {BTZ}} \right) = 0. \end{aligned}$$
(79)

For the third and fourth terms in Eq. (79), because \(\delta ^2 M = \delta ^2 Q = \delta ^2 \Lambda = 0\), we can easily demonstrate that

$$\begin{aligned} \int _{\Sigma _1} \delta ^2 {\varvec{C}}_\xi ^{\text {BTZ}} = \int _{\Sigma _1} \delta \left( \xi \cdot {\varvec{E}}^{\text {BTZ}}_{\phi } \delta \phi ^{\text {BTZ}} \right) = 0. \end{aligned}$$
(80)

Therefore, Eq. (79) can be reduced as

$$\begin{aligned}&\int _{S_c} \delta \left[ \delta {\varvec{Q}}^{\text {BTZ}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi ^{\text {BTZ}}, \delta \phi ^{\text {BTZ}} \right) \right] \nonumber \\&\qquad - \int _{B_1} \delta \left[ \delta {\varvec{Q}}^{\text {BTZ}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi ^{\text {BTZ}}, \delta \phi ^{\text {BTZ}} \right) \right] \nonumber \\&\quad = {\mathcal {E}}_{\Sigma _1} \left( \phi ^{\text {BTZ}}, \delta \phi ^{\text {BTZ}} \right) . \end{aligned}$$
(81)

Using the result of Eq. (62) and the gauge condition \(\xi ^a \delta A^{\text {BTZ}}_a = 0\) on the event horizon, the first and second terms of Eq. (81) can be obtained as

$$\begin{aligned}&\int _{S_c} \delta \left[ \delta {\varvec{Q}}^{\text {BTZ}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi ^{\text {BTZ}}, \delta \phi ^{\text {BTZ}} \right) \right] \nonumber \\&\quad = \frac{1}{8} \left[ - \frac{Q^2}{\Lambda ^2} \delta \Lambda ^2 + \frac{4Q}{\Lambda } \delta Q \delta \Lambda + 2 \delta Q^2 \ln \left( - \Lambda r_c^2 \right) \right] \nonumber \\&\qquad - {\mathcal {Y}} \left( \phi ^{\text {BTZ}}, \delta \phi ^{\text {BTZ}} \right) , \end{aligned}$$
(82)

and

$$\begin{aligned}&\int _{B_1} \delta \left[ \delta {\varvec{Q}}^{\text {BTZ}}_\xi - \xi \cdot {\varvec{\Theta }} \left( \phi ^{\text {BTZ}}, \delta \phi ^{\text {BTZ}} \right) \right] \nonumber \\&\quad = \frac{1}{8} \left[ - \frac{Q^2}{\Lambda ^2} \delta \Lambda ^2 + \frac{4Q}{\Lambda } \delta Q \delta \Lambda + 2 \delta Q^2 \ln \left( - \Lambda r_h^2 \right) \right] .\nonumber \\ \end{aligned}$$
(83)

Substituting Eqs. (82) and (83) into Eq. (81), we have

$$\begin{aligned}&{\mathcal {E}}_{\Sigma _1} (\phi , \delta \phi ) + {\mathcal {Y}} (\phi , \delta \phi ) \nonumber \\&\quad = \frac{1}{8} \left[ 2 \delta Q^2 \ln \left( - \Lambda r_c^2 \right) - 2 \delta Q^2 \ln \left( - \Lambda r_h^2 \right) \right] . \end{aligned}$$
(84)

Finally, substituting Eq. (84) into Eq. (74), the complete expression of the second-order variational identity can be obtained as

$$\begin{aligned}&\delta ^2 M + r_h^2 \delta ^2 \Lambda + \frac{Q^2}{\Lambda } \delta ^2 \Lambda - \frac{Q^2}{\Lambda ^2} \delta \Lambda ^2 + \frac{4Q}{\Lambda } \delta Q \delta \Lambda \nonumber \\&\qquad \quad + 2 \delta Q^2 \ln \left( - \Lambda r_h^2 \right) + 2 Q \delta ^2 Q \ln \left( -\Lambda r_h^2 \right) \nonumber \\&\quad = 8 \delta ^2 \left[ \int _{{\mathcal {H}}} \varvec{\tilde{\epsilon }} \mu (v, r_h) \left( T_{ab}^{\text {EM}} + T_{ab} \right) ({\mathrm{d}}r)^a \xi ^b \right] . \end{aligned}$$
(85)

According to Eq. (53) and \(T_{ab}(0) = 0\) for the background spacetime, using the optimal option of the first-order approximation, the null energy condition under the second-order approximation can be given as

$$\begin{aligned}&\int _{{\mathcal {H}}} T_{ab} (\lambda ) l^a (\lambda ) l^b (\lambda ) {\mathrm{d}}v \wedge \tilde{{\varvec{\epsilon }}}\nonumber \\&\quad \simeq \frac{\lambda ^2}{2} \delta ^2 \left( \int _{{\mathcal {H}}} \tilde{{\varvec{\epsilon }}} \mu (v, r_h) T_{ab} \xi ^a ({\mathrm{d}}r)^b \right) \ge 0. \end{aligned}$$
(86)

Substituting Eq. (86) into Eq. (85), the second-order variational identity becomes an inequality, i.e.,

$$\begin{aligned}&\delta ^2 M + r_h^2 \delta ^2 \Lambda + \frac{Q^2}{\Lambda } \delta ^2 \Lambda \nonumber \\&\qquad \quad - \frac{Q^2}{\Lambda ^2} \delta \Lambda ^2 + \frac{4Q}{\Lambda } \delta Q \delta \Lambda + 2 \delta Q^2 \ln \left( - \Lambda r_h^2 \right) \nonumber \\&\qquad \quad + 2 Q \delta ^2 Q \ln \left( -\Lambda r_h^2 \right) \ge 0, \end{aligned}$$
(87)

which is called the second-order perturbation inequality.

Thus far, the first-order and second-order perturbation inequalities have both been obtained. In the following, based on the two perturbation inequalities, we will examine the WCCC for charged BTZ black holes under the second-order approximation of the perturbation to check whether the conical singularity should still be surrounded by the event horizon and hidden inside the black hole.

4 Gedanken experiment to examine nearly extremal charged BTZ black holes

In the following, based on the first-order and second-order perturbation inequalities, we would like to examine the WCCC for charged BTZ black holes under the second-order approximation of the perturbation. According to the stability condition, the spacetime geometry on the hypersurface \(\Sigma _1\) still belongs to the class of charged BTZ solutions. Therefore, testing the WCCC is equivalent to testing whether the event horizon exists after the perturbation. If the event horizon exists, the geometry on \(\Sigma _1\) can be described by charged BTZ black holes. This means that the WCCC cannot be violated under the perturbation of the matter fields.

Fig. 1
figure 1

Plot of the blackening factor f(r) for different values of mass M when \(Q = 1\) and \(\Lambda = -1\)

Full size image

Figure 1 shows that the event horizon of the black hole exists when the minimal value of the blackening factor f(r) is negative. If the sign of the minimal value of f(r) becomes positive, the event horizon will disappear, while the naked singularity will be exposed to spacetime. This implies that examining the WCCC for charged BTZ black holes is equivalent to checking the sign of the minimal value of \(f \left( r, \lambda \right) \) in Eq. (11). Therefore, we define a function

$$\begin{aligned} h (\lambda ) \equiv f \left( r_m \left( \lambda \right) , \lambda \right) \end{aligned}$$
(88)

to represent the minimal value of the blackening factor, where \(r_m \left( \lambda \right) \) is defined as the position of the minimal value of the function \(f \left( r, \lambda \right) \), and its value can be determined by

$$\begin{aligned} \partial _r f \left( r_m \left( \lambda \right) , \lambda \right) = 0. \end{aligned}$$
(89)

Meanwhile, Eq. (89) also gives the following relation

$$\begin{aligned} \Lambda = -\frac{Q^2}{r_m^2}. \end{aligned}$$
(90)

Considering the second-order approximation of the matter fields perturbation, the expression of \(h(\lambda )\) can be expanded with respect to the parameter \(\lambda \) at \(\lambda = 0\). The specific expression of \(h(\lambda )\) under the second-order approximation is

$$\begin{aligned} h(\lambda )= & {} -M - 2 Q^2 \ln \left| Q \right| - Q^2 - \lambda \left( \delta M + 4 Q \delta Q \ln \left| Q \right| \right) \nonumber \\&- 2 \lambda ^2 \left[ \frac{2 Q \delta Q \delta r_m}{r_m} + \Lambda \delta r_m^2 + r_m \delta r_m \delta \Lambda \right] \nonumber \\&- \frac{\lambda ^2}{2} \left[ \delta ^2 M + 4 \left( Q \delta ^2 Q + \delta Q^2 \right) \ln \left| Q \right| \right. \nonumber \\&\left. - \frac{Q^2}{\Lambda ^2} \delta \Lambda ^2 + \frac{4 Q}{\Lambda } \delta Q \delta \Lambda \right] , \end{aligned}$$
(91)

where we have used Eq. (90) to simplify the expression. Taking the first-order variation of Eq. (89) and using Eq. (90) as well, the first-order variation of \(r_m\) can be expressed as

$$\begin{aligned} \delta r_m = \frac{r_m}{Q} \delta Q + \frac{r_m^3}{2 Q^2} \delta \Lambda . \end{aligned}$$
(92)

Substituting Eq. (92) into Eq. (91), the second-order expansion of \(h(\lambda )\) can be simplified as

$$\begin{aligned} h(\lambda )&= -M+Q^2-2Q^2 \ln \left| Q \right| + \lambda \left( \delta M + 4 Q \delta Q \ln \left| Q \right| \right) \nonumber \\&\quad -\lambda ^2 \left[ \frac{\delta ^2 M}{2} + 2 \delta Q^2 + 2 \left( \delta Q^2 + Q \delta ^2 Q \right) \ln \left| Q \right| \right] . \end{aligned}$$
(93)

Following a similar idea as in Ref. [9], a small parameter \(\epsilon \) which should agree with the first-order approximation of the matter fields perturbation is introduced. For nearly extremal charged BTZ black holes, the minimal value of the blackening factor \(r_m\) and the radius of the event horizon \(r_h\) satisfy the relation \(r_m = (1 - \epsilon ) r_h\). Using this relation, Eq. (89) can be written as

$$\begin{aligned} f^\prime \left( r_h \right) = \epsilon r_h f^{\prime \prime } \left( r_h \right) \end{aligned}$$
(94)

under the first-order approximation of \(\epsilon \). The minimal value of the blackening factor \(f \left( r_m, \lambda \right) \) under the second-order approximation of \(\epsilon \) is expressed as

$$\begin{aligned} f \left( r_m \right)= & {} f \left( r_h \left( 1-\epsilon \right) \right) \nonumber \\= & {} - \epsilon r_h f^\prime \left( r_h \right) + \frac{\epsilon ^2 r_h^2}{2} f^{\prime \prime } \left( r_h \right) \nonumber \\= & {} - \frac{1}{2} \epsilon ^2 r_h^2 f^{\prime \prime } \left( r_h \right) . \end{aligned}$$
(95)

Substituting the specific expression of f(r) into the result of Eq. (95), we have

$$\begin{aligned} -M + Q^2 - 2 Q^2 \ln \left| Q \right| = \epsilon ^2 \left( r_h^2 \Lambda - Q^2\right) . \end{aligned}$$
(96)

Utilizing the first-order optimal option and the second-order perturbation inequality, combining the above results, the expression of \(h(\lambda )\) under the second-order approximation is reduced as

$$\begin{aligned} h(\lambda )\le & {} \left( r_h^2 \Lambda - Q^2\right) \epsilon ^2 + \left( 4 Q \delta Q+2 r_h^2 \delta \Lambda \right) \epsilon \lambda \nonumber \\&-\frac{\left( 2 Q \delta Q + r_h^2 \delta \Lambda \right) ^2}{2 Q^2} \lambda ^2. \end{aligned}$$
(97)

In addition, under the zero-order approximation of \(\epsilon \), we have the following relation

$$\begin{aligned} r_h = r_m = \sqrt{-\frac{Q^2}{\Lambda }}. \end{aligned}$$
(98)

Combining Eq. (98) with Eq. (97), the function \(h(\lambda )\) can finally be written as

$$\begin{aligned} h(\lambda ) \le -\frac{( \lambda Q \delta \Lambda +2 \epsilon \Lambda Q - 2 \lambda \Lambda \delta Q)^2 }{2 \Lambda ^2}. \end{aligned}$$
(99)

Equation (99) shows that the value of \(h(\lambda )\) is negative under the second-order approximation. This illustrates that the event horizon still exists and that the WCCC for a charged BTZ black hole cannot be violated during the perturbation of matter fields. This result also implies that even if the singularity at the center of the black hole is conical, it should also be surrounded by the event horizon of the black hole and cannot be exposed to spacetime.

5 Conclusions

Based on the new version of the gedanken experiment proposed by Sorce and Wald, we examine the WCCC for charged BTZ black holes under a second-order approximation of the perturbation of the matter fields to check the assumption that if a black hole does not have a canonical singularity, it does not need to satisfy the requirement of the WCCC. In our investigation, we consider a process wherein the spherically symmetric matter fields pass through the event horizon to perturb charged BTZ black holes. During the perturbation, the cosmological constant is regarded as a portion of the matter fields, while the spacetime geometry of the black hole and matter fields can be seen as a complete dynamical system. In this situation, the cosmological constant should be considered a dynamical variable. In addition, a stability condition is proposed to examine the WCCC, which states that the spacetime geometry still belongs to the class of charged BTZ solutions after the perturbation. According to the stability condition and the null energy condition, the first-order and second-order perturbation inequalities are derived. Then, using the optimal option of the first-order approximation and the second-order perturbation inequality, based on the stability condition and the null energy condition, the WCCC for charged BTZ black holes under the second-order approximation of the perturbation is examined. The result shows that the event horizon of charged BTZ black holes still exists after the perturbation of the matter fields, and the WCCC for charged BTZ black holes cannot be violated. It also illustrates that even if the conical singularity does not cause the spacetime curvature to diverge, it still should be surrounded by the event horizon and hidden inside the black hole.