1 Introduction

As a most fascinating prediction of General relativity, black hole has always attracted much interests for a long time [1,2,3,4,5]. In particular, an international collaboration of Event Horizon Telescope (EHT) has recently observed that the first shadow image of a supermassive black hole in the centre of M87 has been captured through the very long baseline interferometer experiment [6,7,8,9,10,11]. And, the second image with inclusion of the magnetic fields and the plasma properties has also been imaged in this year [12, 13]. This fact receives a wide cheer of scientific community since it can give rise to some significant breakthroughs on fundamental properties of black hole. From the image of M87, it shows that there are a dark interior at the core of image, and outside of which is a compact asymmetric ring. In general, the dark interior is now called as black hole shadow, while the outside bright ring is known as photon ring.

The light ray emitted from the infinity will be deflected as a result of the strong gravitational field when it passes through the near region of black hole. The photon will asymptotically moved to the bound photon orbit if the curvature of the deflected light approach to that of the critical curve. The bound photon orbit is the so-called photon sphere, which can cast a shadow of black hole. The curvature of the deflected light is referred to the impact parameter, i.e., the critical curve corresponds to the critical impact parameter \(b_p\). For Schwarzschild case, the photon sphere and the critical impact parameter are found to be 3M and \(3\sqrt{3}M\), respectively. So far, the study of shadow of black holes and wormholes has received more and more interests in recent year since the first calculations of shadow [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]. The shadow of the Schwarzschild black hole was first studied by Synge and Luminet, and then Bardeen investigated the D-shape shadow for Kerr black hole in 1973 [73,74,75,76]. In modified gravity theories, the shadows cast by the non-rotating and rotating black holes are studied for different values of the parameter [20, 21]. Different from the single shadow, double shadows of black holes and wormholes have also been presented in [16, 43]. And, the effect of the Melvin magnetic field and the plasma on the structure of shadow have been carefully addressed, and references therein [52, 53]. However, it should be pointed out that there are always various kinds of matters existed in real universe, thereby the near region of black hole would arise various accretions naturally, instead of remain the vacuum. Combined with this facts, when Schwarzschild black hole surrounded by a simple model of spherically symmetric accretion, the properties of image has been carefully studied in 2019, and the results show that the accretion has no influence on the shadow size [77]. In this case, the optical appearance of shadow with two photon spheres in a Hairy Black Hole has been presented in [78], where the smaller photon sphere is considered to be the shadow boundary. For another model of accretion, namely the optically thin and geometrically thin disk, the later studies [79,80,81,82,83,84,85,86,87] show that the size of shadow is closely related to the position of the accretion, and the bright region outside of shadow are always composed of direct emission, lensing rings and photon rings. With this consideration, an optically observational signature of the asymmetric thin-shell wormhole has been thoroughly investigated, which shows that this signature can be used to distinguish wormholes from black holes [88]. And, one also finds that the polarized image of black hole produced by photon coupled to Weyl tensor is very important to understand the thin accretion disk [89]. Hence one can see that, it is still very necessary and important to study the shadow of black holes with inclusion of various models of accretions and the other possible factors.

To explain the accelerated-inflation problem without of dark energy and dark matter, Buchdahl in 1970 proposed a type of modified gravity theory, namely the f(R) gravity theory [90,91,92,93]. Since then, many efforts have devoted to study the f(R) gravity theories [94,95,96,97,98,99,100,101,102,103]. In 2012, one has obtained a global monopole black hole solution in f(R) theory [94]. Effects of the f(R) parameter on the thermodynamic properties and strong gravitational lensing of black hole have been discussed by Man and Cheng [95, 96]. And in the context of f(R) theory, one has used the standard procedure of the reconstructive approach to derive a d-dimensional black hole solution with a spherically symmetric string cloud configuration [97]. The space-time geometry generated by a f(R) global monopole black hole has also been investigated in the metric-affine formalism [98]. In addition, the Hawking-Page phase transition in this system are inspected with particular attention in 2019 [99]. Nevertheless, the shadows and rings of the f(R) black hole surrounded by various accretions remains unclear. So, our aim in this paper is to focus on this issue. In particular, under the illumination of virous accretions, we will numerically study the observational appearances as seen by an observer located at the asymptotic infinity and the certain region out of black hole, and reveal the effects of the global monopole parameter and f(R) parameter on observational appearances of black hole.

The organization of the paper is as follows: In Sect. 2, we will first study the effective potential and photon orbits of a f(R) global monopole black hole. Section 3 is devoted to investigate shadows and rings of thin disk emission in this spacetime. In Sect. 4, observational appearances of black hole surrounded by the static and infalling spherical accretions will be carefully discussed. Finally, Sect. 5 ends up with some conclusions and discussions.

2 The effective potential and photon orbits of f(R) global monopole black hole

At first, we in this section will first to study the effective potential of a f(R) black hole with a global monopole. The Lagrangian with inclusion of the global monopole can be expressed as

$$\begin{aligned} {\mathcal {L}}= \frac{1}{2}(\partial _\mu \phi ^a)(\partial ^\mu \phi _a)-\frac{1}{4}\lambda ( \phi ^a\phi ^a-\eta ^2 )^2, \end{aligned}$$
(1)

and the self-coupling triplet of scalar fields presents a global monopole, which is

$$\begin{aligned} \phi ^a= \eta h(r) \frac{x^a}{r}, \end{aligned}$$
(2)

where, \(\eta \) and \(\lambda \) are all the model parameters, h(r) is a dimensionless function, and \(x^a x^a = r^2\). In f(R) gravity theory, the action coupled to a matter field can written as

$$\begin{aligned} S= \frac{1}{2\kappa }\int d^4 x \sqrt{-g}f(R) + S_m. \end{aligned}$$
(3)

f(R) represents the analytical function of the Ricci scalar and \(\kappa = 8\pi G\) with G is the Newton gravitational constant. \(S_m\) is the action associated with the matter fields, which is \(S_m = \int d^4x \sqrt{-g} {\mathcal {L}}\). In this case, a spherically symmetric solution has been obtained, it is

$$\begin{aligned} ds^2=A(r) d t^2 - \frac{1}{B(r)} d r^2 - r^2 (d \theta ^2 + {\sin ^2\theta } d \phi ^2), \end{aligned}$$
(4)

with

$$\begin{aligned} A(r) = B(r) = 1 - \frac{2GM}{r} - 8\pi G \eta ^2 - \psi _0 r. \end{aligned}$$
(5)

The factor \(\psi _0\) originated from the f(R) theory of gravity represents the deviation of standard general relativity. And, the linear correction \(\psi _0 r\ll 1\), which is very different from black holes in de Sitter spacetime. The part with a global monopole \(8\pi G \eta ^2\) is also very small, which is approximately equal to \( 10^{-5}\). As the conditions \(\psi _0\rightarrow 0\) and \(\eta \rightarrow 0\) satisfied, this black hole will naturally reduce to the schwarzschild black hole. By solving the equation \(B(r)=0\), we have

$$\begin{aligned} r_{\pm } = \frac{1}{\psi _0}\left( 1 - 8\pi \eta ^2 \pm \sqrt{ (1-8\pi \eta ^2)^2 - 8M\psi _0} \right) . \end{aligned}$$
(6)

For simplicity, here the Newton constant G has been set to 1. It is clear that there are two horizons(\(r_+\) and \(r_-\)) of f(R) global monopole black hole, the smaller one is the event horizon \(r_-=r_h\), another is supposed to be the cosmological horizon \(r_+=r_c\). In the next, our aim is to study the null geodesic of f(R) global monopole black hole. Generally, here we consider the situation that the motion of a particle located at the equatorial plane(\(\theta =\pi /2\)). So, it is easy to obtain the Lagrangian \({\mathcal {L}}\) for a particle in this spacetime, which is

$$\begin{aligned} {\mathcal {L}}=\frac{1}{2}g_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }=\frac{1}{2}\left[ -A(r)\dot{t}^2+\frac{\dot{r}^2}{B(r)}+r^2\dot{\phi }^2\right] , \end{aligned}$$
(7)

where, \(\dot{x}^{\mu } = \frac{\partial {x}^{\mu }}{\partial \lambda }\) is the four-velocity of the photon and \(\lambda \) is the affine parameter. In this spacetime, there exists two Killing fields \(\partial _t\) and \(\partial _\phi \), which correspond to two conserved quantities, namely the energy E and the orbital angular momentum L, respectively. They areFootnote 1

$$\begin{aligned} -E = \frac{\partial {\mathcal {L}}}{\partial \dot{t}} = -A(r)\dot{t}, \quad L = \frac{\partial {\mathcal {L}}}{\partial \dot{\phi }} = r^2 \dot{\phi }. \end{aligned}$$
(8)

Meanwhile, by considering \(g_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }= 0\) for null geodesic, then solving Eq. (7) with the aid of Eq. (8), it yields

$$\begin{aligned}&\dot{t}=\frac{1}{b_{c} \left[ 1 - \frac{2M}{r} - 8\pi \eta ^2 - \psi _0 r \right] }, \end{aligned}$$
(9)
$$\begin{aligned}&\dot{\phi } = \pm \frac{1}{r^2} , \end{aligned}$$
(10)
$$\begin{aligned}&\dot{r}^2= \frac{1}{b_{ c}^2} - \frac{1}{r^2}\left[ 1 - \frac{2M}{r} - 8\pi \eta ^2 - \psi _0 r \right] . \end{aligned}$$
(11)

Here, \(b_c = \frac{|L|}{E}\) is the impact parameter, the affine parameter \(\lambda \) is redefined as \(\lambda /|L|\), and the sign ± represents the counterclockwise and clockwise direction of the light ray. By introducing the effective potential \(V_{{ eff}}\) into (11), then we have

$$\begin{aligned} \dot{r}^2+V_{{eff}}=\frac{1}{b_{c}^2}, \end{aligned}$$
(12)

where,

$$\begin{aligned} V_{{ eff}}=\frac{1}{r^2}\left[ 1 - \frac{2M}{r} - 8\pi \eta ^2 - \psi _0 r \right] . \end{aligned}$$
(13)

Considering the photon sphere condition \(\dot{r} = 0\) and \(\ddot{r}=0\), \(V_{{ eff}}\) should satisfy the condition

$$\begin{aligned} V_{{eff}}=\frac{1}{b_{ c}^2}, \quad V_{{ eff}}'=0. \end{aligned}$$
(14)

The sign \('\) represents the derivative with respect to r. In a four-dimensional symmetric black hole, this condition can be rewrote as

$$\begin{aligned} r_p{}^2=b_{ p}^2 A(r),\quad 2 b_p^2 A(r)^2=r_p^3 A'(r). \end{aligned}$$
(15)

In Eq. (14), \(b_p\) and \(r_p\) are the impact parameter and radius of the photon sphere, respectively. By choosing different values of \(\eta \) and \(\psi _0\), the numerical results of the event horizon \(r_h\), the cosmological horizon \(r_c\), the radius \(r_p\) and impact parameter \(b_{p}\) of photon sphere have been shown in Table 1. From it, one can see that the cosmological horizon \(r_c\) decreases when the f(R) parameter \(\psi _0\) increased, and it will vanish as \(\psi _0 = 0\). However, the event horizon \(r_h\), the radius \(r_p\) and impact parameter \(b_{p}\) of photon sphere are all increases with increase of the \(\eta \) and \(\psi _0\). This implies that the f(R) global monopole black hole does not only have the cosmological horizon, but also the event horizon is larger than that of Schwarzschild black hole.

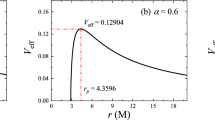
Table 1 The numerical results of the event horizon \(r_h\), the cosmological horizon \(r_c\), the radius \(r_p\) and impact parameter \(b_{p}\) of photon sphere, where the value of M is set to 1
Full size table

By taking \(\eta =0.07\) and \(\psi _0=0.003\) as an example, the effective potential \(V_{eff}\) has been intuitively shown in Fig. 1.

Fig. 1
figure 1

The effective potential \(V_{eff}\) and impact parameter \(b_c\) versus r

Full size image

From Fig. 1, one can see that the effective potential \(V_{eff}\) has its value existed only when r is greater than or equal to the value of event horizon \(r_h\). At the event horizon, the value of \(V_{eff}\) is zero. From this point to the photon sphere \(r_p\), it increases monotonously and gets to the maximum value at the photon sphere. Then, it will gradually decrease to zero with the increase of r from photon sphere to infinity. In this sense, the potential \(V_{eff}\) will naturally produce the potential barrier for the entering light rays. When light rays at the position of observer emitted in the radially inward direction, some of them (namely, \(b_c > b_p\)) will encounter with the potential barrier and will be reflected by it. This region at where those light rays located corresponds to region 1 in Fig. 1. And, some of them (namely, \(b_c < b_p\)) will not encounter the potential barrier and will drop into black hole finally. This region is related to region 3 in Fig. 1. Moreover, there still exists an interesting region, namely region 2, in which light rays (namely, \(b_c = b_p\)) will asymptotically approach to the orbit of the photon sphere, and then circle around black hole infinitely many times. On the other hand, it is obvious that the effective potential \(V_{eff}\) decreases in f(R) global monopole black hole by comparing with Schwarzschild black hole.

To carefully address the trajectories of light ray, here we use the Eqs. (10) and (11) to reexpress the motion equation of photon, it is

$$\begin{aligned} \frac{{dr}}{d \phi }=\pm r^2\sqrt{\frac{1}{b_{ c}^2} - \frac{1}{r^2}\left[ 1 - \frac{2M}{r} - 8\pi \eta ^2 - \psi _0 r \right] }. \end{aligned}$$
(16)

With a rearrangement of r, i.e., \(u=1/r\), the above equation can be expressed as

$$\begin{aligned} {\mathcal {H}}(u,b)\equiv \frac{d u}{d \phi }=\sqrt{\frac{1}{b_{ c}^2} - u^2\left[ 1 - {2M u} - 8\pi \eta ^2 - \frac{\psi _0}{u} \right] }. \end{aligned}$$
(17)

Using the ray-tracing code, the trajectories of light ray are shown in Fig. 2 with the aid of Eq. (17).

Fig. 2
figure 2

The trajectories of light ray for different values of \(\eta \) and \(\psi _0\) in the polar coordinates \((r, \phi )\)

Full size image

The spacing of impact parameter \(b_c\) in Fig. 2 are all chosen as \(\frac{1}{5}\). The solid disk represents the black hole, while the dashed grey circle is the photon orbit. When the impact parameter \(b_c < b_p\) (region 3 in Fig. 1), the photon will be captured by black hole. The trajectories of those photons correspond to the black line that shown in Fig. 2. On the contrary, if \(b_c > b_p\) (region 1 in Fig. 1), the photon will be reflected back and move to infinity. And, its trajectories correspond to the green line in Fig. 2. While \(b_c = b_p\) (region 2 in Fig. 1), the photon will revolve around black hole infinitely many times. The trajectories of those photons approximately correspond to the red line in Fig. 2. More importantly, it is clear from Fig. 2 that the incident light rays are almost parallel to the abscissa axis for subfigure (a), while are more or less sloping for subfigures (b) and (c). The reason is that there is no cosmological horizon existed in (a), thereby the observer is assumed to be located at the infinity. But for (b) and (c), due to the existence of cosmological horizon, the location of the observer is fixed to \(\frac{r_c}{6}\) in Fig. 2.Footnote 2 In addition, the global monopole parameter \(\eta \) and the f(R) parameter \(\psi _0\) produce an obvious influence of trajectories of light rays that cannot be ignored.

3 Shadows and rings of thin disk emission

For a real universe, it is general considered that black hole surrounded by various matters. In this case, the study of shadows and rings of black hole will be more interesting. Therefore, we in this section will investigate the shadows and rings of f(R) global monopole black hole when it surrounded by an optically and geometrically thin disk accretion.

3.1 Direct emission, Lensed ring and photon ring

As described by Gralla et al. [79], when one traced the light ray from the observer backwards towards the black hole, the emissions with different value of \(b_c\) will give rise to different appearances of the black hole to a distant observer. According to the orbital plane azimuthal angle \(\phi \), the total number of orbits \(n=\phi /{2 \pi }\) as a function of the impact parameter \(b_c\) has been defined to distinguish the trajectories of light rays emitted from the north pole direction. There exists three cases for different values of n. They are direct emission, lensing ring and photon ring respectively, which correspond to \(n<3/4\), \(3/4<n<5/4\) and \(n>5/4\). And, the corresponding trajectories of light rays will intersect with the equatorial plane once, twice and more than twice, respectively. For a f(R) black hole with the global monopole, we have taken the following choice of \(\eta \) and \(\psi _0\) as the examples to present the regions of direct emission, lensing ring and photon ring in Eqs. (18)–(20).

$$\begin{aligned}&{\begin{matrix} \eta =0.07 \\ \psi _0 = 0 \end{matrix} }\Rrightarrow {\left\{ \begin{array}{ll} \text {Direct emission:}\ n<3/4,~ b_c<6.03652 ~ \text {and} ~ b_c>8.10645 \\ \text {Lensing ring:}\ 3/4<n<5/4,~ 6.03652<b_c<6.31170 ~~ \text {and}~6.39278<b_c<8.10645 , \\ \text {Photon ring:}\ n>5/4,~ 6.31170<b_c<6.39278 \end{array}\right. } \end{aligned}$$
(18)
$$\begin{aligned}&{\begin{matrix} \eta =0 \\ \psi _0=0.003 \end{matrix}}\Rrightarrow {\left\{ \begin{array}{ll} \text {Direct emission:}\ n<3/4,~ b_c<5.09467 ~ \text {and} ~ b_c>6.05219 \\ \text {Lensing ring:}\ 3/4<n<5/4,~ 5.09467<b_c<5.25955 ~ \text {and} ~5.29556<b_c<6.05219 , \\ \text {Photon ring:}\ n>5/4,~ 5.25955<b_c<5.29556 \end{array}\right. } \end{aligned}$$
(19)
$$\begin{aligned}&{\begin{matrix} \eta =0.07 \\ \psi _0 = 0.003 \end{matrix}}\Rrightarrow {\left\{ \begin{array}{ll} \text {Direct emission:}\ n<3/4,~ b_c<6.16715 ~ \text {and} ~ b_c> 7.73130 \\ \text {Lensing ring:}\ 3/4<n<5/4,~ 6.16715<b_c<6.42633 ~ \text {and} ~ 6.49637<b_c<7.73130 . \\ \text {Photon ring:}\ n>5/4,~ 6.42633<b_c<6.49637 \end{array}\right. } \end{aligned}$$
(20)

It is obvious from the above equations that two parameters \(\eta \) and \(\psi _0\) all enlarge the regions of direct emission, lensing ring and photon ring by comparing with that of Schwarzschild black hole. In the following Fig. 3, we take a more careful attention to show the trajectories of light ray, where the regions of direct emissions and rings are emphasized.

Fig. 3
figure 3

Behavior of photons in the f(R) global monopole black hole as a function of the impact parameter \(b_c\)

Full size image

The first line directly shows the fractional number of orbits n versus the impact parameter \(b_c\), where the singularities always occur at \(b_c = b_p\). And, the corresponding trajectories of light rays in the f(R) global monopole black hole are presented in the second line. In this line, the direct, lensing ring and photon ring trajectories correspond to the red line, blue line and green line, for which the related spacings of \(b_c\) reads 1/5, 1/50 and 1/500, respectively. Similarly to Fig. 2, the photon orbit is the dashed grey line and black hole is presented as a solid disk.

3.2 Observed specific intensities and transfer functions

After discussing direct emissions and rings in the f(R) global monopole black hole, our aim in this subsection is to investigate the observed specific intensity of the thin-disk accretion, which viewed in a face-on orientation. Here, the thin disk is assumed to be lied in the equatorial plane of f(R) global monopole black hole. And, the emissions from it are isotropically in the rest frame of static worldlines. In this case, when the static observer located at the north pole, the observed specific intensity can be wrote as the following form. It is

$$\begin{aligned} I_{obs}(r)= \left[ 1 - \frac{2M}{r} - 8\pi \eta ^2 - \psi _0 r \right] ^{3/2} I_{em}(r). \end{aligned}$$
(21)

Here, we have defined \(I_{obs}(r)\) as the observed specific intensity and its frequency as \(\nu \), while \(I_{em}(r)\) as the emitted specific intensity and its frequency as \(\nu _e\). The total observed specific intensity can be reexpressed as

$$\begin{aligned} I(r)&= \int I_{obs}(r)d\nu \nonumber \\&=\int \left[ 1 - \frac{2M}{r} - 8\pi \eta ^2 - \psi _0 r\right] ^2 I_{em}(r) d\nu _e \nonumber \\&= \left[ 1 - \frac{2M}{r} - 8\pi \eta ^2 - \psi _0 r\right] ^2 I_{emi}(r). \end{aligned}$$
(22)

The relationship \(\nu = A(r)^{1/2} \nu _e\) has been used to simplify Eq. (22). The total emitted specific intensity \(I_{emi}(r)\) is an integral of \( I_{em}(r)\) with respect to \(\nu _e\), i.e., \(I_{emi}(r) = \int I_{em}(r) d\nu _e\). Since the thin disk lies in the equatorial plane, the light rays emitted from the north pole will intersect with the disk. So, the brightness will be picked up by the light rays for each intersection. When the photons emitted from thin disk, the light rays located at the regions of lensed rings (which are the blue lines in Fig. 3) will intersect with the opposite side of the disk once. Those rays will pick up the additional brightness once. For the light rays located at the regions of photon rings (which are the green lines in Fig. 3), it does not only intersect with the opposite side of the disk, but also with the front side. Those rays will pick up the additional brightness twice. In view of this, the total observed intensity should be regarded as a sum of those intensities from each intersection. So,

$$\begin{aligned} I(r) =\left[ 1 - \frac{2M}{r} - 8\pi \eta ^2 - \psi _0 r\right] ^2 \sum _n I_{emi}(r)|_{r=r_n(b_c)}. \end{aligned}$$
(23)

The function \(r_n(b_c)\) is the radial location at which the light rays intersect with the disk. It is referred as the transfer function, where \(n=1,2,3\ldots .\) At each point of \(b_c\), there will produce a slope of the transfer function \(dr/{db_c}\), which represents the demagnification factor. Note that, the absorption of brightness which may abate the observation intensity has been neglected here. In Fig. 4, we have plotted the first three transfer functions \(r_n(b)\) with respect to the impact parameter \(b_c\) for the f(R) global monopole black hole.

Fig. 4
figure 4

The first three transfer functions for the f(R) global monopole black hole

Full size image

In Fig. 4, the red, blue and green lines correspond to the first(\(n=1\)), second(\(n=2\)) and third(\(n=3\)) transfer function, respectively. The slope of those lines are very different. For the red line, the value of its slope is in the neighbourhood of 1. So, this line is related to the direct image of the disk, which represents the redshifted source profile. While, the blue line’s slope increase quickly and is much greater than 1, thereby this line is related to the lensing ring (with the photon ring included in), which represents the image of the back side of the disk that has been largely demagnified. For the green line, its slope is close to infinity. This line is related to the photon ring. So, it implies that the image of the front side of the disk is extremely demagnified. Similar to previous figures, it is easy to see that the transfer function depends on the global monopole parameter \(\eta \) and the f(R) parameter \(\psi _0\) closely.

3.3 Observational appearances of direct emissions and rings

Based on above discussions, our aim in this subsection is continue to study the observed specific intensity with some typical toy-model functions. Firstly, we assume that the emissions of the thin disk occur at the innermost stable circular orbit and the emitted function \( I_{emi}(r)\) of it is a decay function suppressed by the second power. In this case, the emitted function \(I'_{{emi}}(r)\) is assumed to be

$$\begin{aligned} I'_{{emi}}(r) ={\left\{ \begin{array}{ll}\left( \frac{1}{r-(r_{isco}-1)}\right) ^2, &{} r>r_{{isco}} \\ 0, &{}r \le r_{{isco}} \end{array}\right. }. \end{aligned}$$
(24)

With the help of Eq. (23), the corresponding observed intensity of direct emissions and rings for the f(R) global monopole black hole have been intuitively shown in Fig. 5.

Fig. 5
figure 5

Observational appearances of the thin disk for the function \(I'_{{emi}}(r)\)

Full size image

In Fig. 5, the left, middle and right column correspond to the emitted function \(I'_{{emi}}(r)\), the observed specific intensity I(r) and the corresponding observational appearances of the thin disk under various choices of parameters \(\eta \) and \(\psi _0\). From the left column, it is obvious that the emissions peaked sharply at \( r \thicksim 6.8M\) for subfigure (a)(\(r \thicksim 6.4M \) for subfigure (b) and \(r \thicksim 7.7M \) for subfigure (c)), and then decayed quickly with the increase of r. From middle column, one can see that the observed intensities of direct image are very similar to the emitted intensities, and the peaks of it move to the position \(b_c \thicksim 8.2M \) for the case (a)(\(b_c \thicksim 7.7M \) for the case (b) and \(b_c \thicksim 9.6M \) for the case (c)) due to the gravitational lensing. The lensing ring as an image of the disk’s back side is found to in the range of \( 6.8M \thicksim 7.6M\) for (a)(\( 5.6M \thicksim 6.1M\) for (b) and \( 6.9M \thicksim 7.7M\) for (c)). This thin region makes a small contribution to the total observed intensity. Also, the photon ring as a more narrow region located at the position \(b_c\thicksim 6.3M\) for (a)(\(b_c\thicksim 5.3M\) for (b) and \(r\thicksim 6.4M\) for (c)). The intensity of this ring is so small that it is hard to see it in the right column. Also, we find that the parameter \(\eta \) decreased the observed intensity of direct emission, while \(\psi _0\) increased it. For the lensing ring, two parameters all cut down the observed intensity, even if they hardly affect the intensity of photon ring. From the right column, the corresponding shadows and rings can be seen in Fig. 5, where the hardly saw photon rings will appear by enlarging the plot.

Secondly, when the thin disk located at the photon sphere, we assume the emitted function \(I_{emi}(r)\) is an exponential decay function. In this situation, the emitted function \(I''_{emi}(r)\) is

$$\begin{aligned} I''_{emi}(r) ={\left\{ \begin{array}{ll}\frac{2-\tanh (r-r_p)}{2 \exp {(r-r_p)}}, &{} r> r_{p} \\ 0, &{}r \le r_{p} \end{array}\right. }. \end{aligned}$$
(25)

In a similar way, the corresponding observed intensity of direct emissions and rings can be easily obtained, which have been plotted in Fig. 6.

Fig. 6
figure 6

Observational appearances of the thin disk for the function \(I''_{{emi}}(r)\)

Full size image

From left column of Fig. 6, the peak of emission occurs at \(r \thicksim 3.4M\) for case (a)(\(r \thicksim 3.1M\) for case (b) and \(r \thicksim 3.4M\) for case (c)). The observed intensity I(r) of direct emissions peaks near the position \(b_c \thicksim 4.5M\) for case (a)(\(b_c \thicksim 4M\) for case (b) and \(b_c \thicksim 4.7M\) for case (c)). Interestingly, the direct emissions, the lensing ring as well as photon ring in the middle column overlapped at the region \(6.3M \thicksim 8M\) for case (a)(\(5.3M \thicksim 6M\) for case (b) and \(6.4M \thicksim 7.2M\) for case (c)). However, it shows that the lensing ring and photon ring are indistinguishable for case (a) and (b) while distinguishable for case (c). Similar to the function \(I'_{emi}(r)\), the lensing ring also contributes a small part to the total observed intensity, and photon ring remains an ignorable part. Meanwhile, we find that the parameters \(\eta \) and \(\psi _0\) all decreased observed intensities of direct emission and rings. The related shadows and rings are clearly presented at the right column of Fig. 6.

Thirdly, by considering the thin disk lies in the position of the event horizon, we assume \(I_{emi}(r)\) is a more or less moderate decay function. In this consideration, the emitted function \(I'''_{emi}(r)\) can be read as

$$\begin{aligned} I'''_{emi}(r) ={\left\{ \begin{array}{ll} \frac{\frac{\pi }{2}-\tan ^{-1}(r-(r_{isco}-1))}{\frac{\pi }{2}+\tan ^{-1}(r_{p})}, &{} r>r_+ \\ 0, &{}r \le r_+ \end{array}\right. }. \end{aligned}$$
(26)

Similarly, we in Fig. 7 have presented the corresponding shadows and rings of this geometrically and optically thin disk.

Fig. 7
figure 7

Observational appearances of the thin disk for the function \(I'''_{{emi}}(r)\)

Full size image

In Fig. 7, the emission of the disk decayed slowly and spread to the position \(r \thicksim 2.3M\) for case (a)(\(r \thicksim 2.1M\) for case (b) and \(r \thicksim 2.3M\) for case (c)). In this sense, the observed intensity of direct emission occurs at \(b_c \thicksim 3.4M\) for case (a)(\(b_c \thicksim 3M\) for case (b) and \(b_c \thicksim 3.5M\) for case (c)). It shows in the middle column that the case (a) is very similar to that of the Schwarzschild black hole, where the lensing ring and photon ring are indistinguishable and they superimposed on the direct image. But unlike Schwarzschild black hole, there is only a peak for case (b) since the peak of direct emission and rings are all superimposed and very close. And interestingly, we also found in case (c) that the peaks of direct emission, lensing and photon ring are all distinguishable, which locate at the \(b_c \thicksim 6.6M\), 6.4M and 6.8M respectively. Similarly, \(\eta \) and \(\psi _0\) all decreased observed intensities of direct emission and rings as before. The right column of Fig. 7 shows the corresponding shadows and rings for different value of \(\eta \) and \(\psi _0\).

4 Shadows and photon spheres with spherical accretions

Besides the thin disk, there also may exist various kinds of spherical accretions around black hole. In view of this, we will continue to investigate the shadows of f(R) global monopole black hole surrounded by the static and infalling spherical accretions in this section.

4.1 The static spherical accretion

When the static accretion surrounded the f(R) global monopole black hole, the observed intensity for a distant observer can be expressed as

$$\begin{aligned} I(\nu _o) = \int _l g^3 \cdot j(\nu _e) \cdot d\ell _{prop}. \end{aligned}$$
(27)

And in current context, we have

$$\begin{aligned}&g = A(r)^{1/2}, \end{aligned}$$
(28)
$$\begin{aligned}&j(\nu _e)\propto \frac{\delta (\nu _e - \nu _m)}{r^2},\end{aligned}$$
(29)
$$\begin{aligned}&d\ell _{prop} = \sqrt{ \frac{1}{A(r)} +r^2\left( \frac{d\phi }{dr}\right) ^2}dr. \end{aligned}$$
(30)

The symbol l, g, \(j(\nu _e)\) and \(d\ell _{prop}\) represent the trajectory of emitted photons, the redshift factor, the emissivity per unit volume in the rest frame, and the infinitesimal proper length, respectively. And, \(\nu _o\), \(\nu _e\) are the observed and emitted photon frequency, where \(\nu _o\) is assumed to be the frequency when the emitter radiate photons monochromatically. With the aid of Eqs. (16), (28), (31) and (32), the observed intensity for a static observer can be obtained as

$$\begin{aligned} I_{obs}(\nu _o) = \int _l \frac{A(r)^{3/2}}{r^2} \sqrt{\frac{1}{A(r)} + r^2 \left( \frac{d\phi }{dr} \right) }dr. \end{aligned}$$
(31)

In the context of the static accretion, it is obvious that the obtained luminosity of the f(R) global monopole black hole is a function of r. Since the radius r connected with the impact parameter \(b_c\) with in trajectory equation Eq. (17), we can plot the observed luminosity with respect to \(b_c\) in Fig. 8 to intuitively show the shadows and photon spheres of the f(R) global monopole black hole.

Fig. 8
figure 8

The specific intensity \(I_{obs}(\nu _o)\) seen by a distant observer for a static spherical accretion

Full size image

From Fig. 8, it is easy to see from the first row that, the observed intensity quickly increase to the maximum value firstly and then gradually decrease to a lower value with the increase of the impact parameter \(b_c\). Since the photon will revolve many times around the black hole, the maximum value of \(I_{obs}(\nu _o)\) occurs at \(b_c = b_p\). When \(b_c < b_p\), the observed intensity is very smallFootnote 3 because the photon will be absorbed by the black hole in this case. For \(b_c > b_p\), the refracted light rays that contributed to \(I_{obs}(\nu _o)\) become less with \(b_c\), thereby the observed intensity decrease naturally. The corresponding shadows and photon spheres cast by the black hole in the (x, y) plane are shown in second row of Fig. 8. More importantly, one can see that the global monopole parameter \(\eta \) and f(r) parameter \(\psi _0\) indeed decrease the intensity of \(I_{obs}(\nu _o)\), although they increase the radius of the photon sphere \(b_p\).

4.2 The infalling spherical accretion

Considering the fact that the accretion matters are always dynamical, it is also interesting to investigate the shadows and photon spheres when the f(R) global monopole black hole surrounded by the infalling spherical accretion. Similar to the static spherical accretion, the expression of the observed intensity for a distant observer Eq. (27) still holds true for the infalling spherical accretion. While in this case, the redshift factor should be rewritten as

$$\begin{aligned} g = \frac{\kappa _\alpha \cdot v_{obs}^\alpha }{\kappa _\beta \cdot v_{emi}^\beta }, \end{aligned}$$
(32)

where, \(\kappa ^\mu \equiv \dot{x}_\mu \) is the four-velocities of the photon, which can be found in Eqs. (9)–(11). And, \(v_{obs}^\mu \equiv (1,0,0,0)\) represents the four-velocities of the static observer. While, the four-velocities of the infalling accretion is \(v_{emi}^\mu \), which is given by

$$\begin{aligned} v_{emi}^t {=}\frac{1}{A(r)}, \quad v_{emi}^r{=}{-}\sqrt{1-A(r)}, \quad v_{emi}^\theta {=}0, \quad v_{emi}^\phi {=}0. \end{aligned}$$
(33)

The proper distance in this case reads

$$\begin{aligned} d \ell _{prop} = \frac{1}{g} \frac{\kappa _t}{|\kappa _r|} dr. \end{aligned}$$
(34)

In addition, here the emissivity \(j(\nu _e)\) in Eq. (29) remains unchanged. By using Eqs. (32)–(34), the observed intensity for a static observer in the context of the infalling spherical accretion can be obtained, which is

$$\begin{aligned} I_{obs}(\nu _o) \propto \int _l \frac{g^3}{r^2} \frac{\kappa _t}{|\kappa _r|} dr. \end{aligned}$$
(35)

In a similar way, the shadows and photon spheres of the f(R) global monopole black hole cast by the infalling accretion have been presented in Fig. 9.

Fig. 9
figure 9

The specific intensity \(I_{obs}(\nu _o)\) seen by a distant observer for an infalling accretion

Full size image

Similar to the case of the static accretion, the infalling accretion emission is also sharply peaked at \(b_c=b_p\), and then decrease slowly with the increase of \(b_c\), which are shown in the first row of Fig. 9. The parameter \(\eta \) more or less decreases the intensity of \(I_{obs}(\nu _o)\), while parameter \(\psi _0\) increases it obviously. By comparing the second row of Fig. 9 with that of Fig. 8, it can be saw that the central region inside the photon sphere of the corresponding shadows for the infalling accretion are darker than that for the static accretion, which is a result of the Doppler effect. In addition, we can also find that the region outside the photon sphere is brighter for infalling accretion, which caused by the reason that \(I_{obs}(\nu _o)\) decreased slower than that of the static accretion as \(b_c > b_p\).

5 Conclusions and discussions

In this paper, by considering three simple models of accretions, we have numerically investigated observational appearances of a f(R) global monopole black hole when the observer located at the asymptotic infinity and the certain region out of black hole. At first, we studied the effective potential and photon orbits of a f(R) global monopole black hole, and analysed the trajectories of light rays emitted from the north pole direction. Then, when emissions emitted from an optically and geometrically thin disk in the near region of black hole, the observational appearances of Direct emissions and rings have been carefully addressed with the aid of some typical toy-model functions. Finally, we also discussed shadows and photon spheres of black hole surrounded by the static and infalling spherical accretions. Throughout of this paper, the effect of the global monopole parameter \(\eta \) and f(R) parameter \(\psi _0\) on shadows, rings and photon spheres of this black hole are clearly emphasized.

The result shows that the event horizon \(r_h\), the radius \(r_p\) and impact parameter \(b_p\) of photon sphere are all increases with increase of \(\eta \) and \(\psi _0\), while the cosmological horizon \(r_c\) decreases. And, the effective potential decreases in the f(R) global monopole black hole by comparing with that of Schwarzschild black hole. For the thin-disk accretion, it turns out that the location of direct emission occurs at \(b_c < 6.16715\) and \(b_c>7.73130M\) for \(\eta = 0.07\) and \(\psi _0 = 0.003\), and the ranges of lensing ring are \( 6.16715M< b_c < 6.42633M\) and \( 6.49637M< b_c < 7.73130M\), while photon ring is within the scope of \(6.42633M< b_c < 6.49637M \). The related results for other two cases of \(\eta \) and \(\psi _0\) have been presented in Eqs. (18) and (19). Those regions as well as the corresponding trajectories of light ray are clearly presented in Fig. 3. Based on the first three transfer functions, when the emission function is \(I'_{{emi}}(r)\), one can see from Fig. 5 that the observed intensities of direct image, lensing ring and photon ring peaked at \(b_c \sim 9.6M\), 6.9M and 6.4M, for subfigure (c) respectively. For the emission function \(I''_{{emi}}(r)\), it shows that lensing ring and photon ring are indistinguishable for case (a) and (b) while distinguishable for case (c) in Fig. 6. Those rings are all superimposed on the direct emission at the region \(6.4M \sim 7.2M\) for case (c). For \(I'''_{{emi}}(r)\), as the emissions extended to the region of event horizon in Fig. 7, it shows in case (c) that the peaks of direct emission, lensing and photon ring are distinguishable, which locate at the \(bc\sim 6.6M\), 6.4Mand 6.8M, respectively. And, they are more or less indistinguishable for case (a) and (b). More importantly, we can conclude that the direct image is always similar to the emission profile, and contributes a dominant part of the total observed intensity. While, lensing ring and photon ring that around black hole shadow, always make a small contribution and a negligible contribution, for all three toy-model functions. For the static and infalling spherical accretions, we find that shadows and photon spheres cast by a f(R) global monopole black hole in the (x,y) plane are always similar. But, the brightness of shadow in the infalling accretion is darker than that in the static accretion, which caused by the Doppler effect. And, the brightness of photon sphere with infalling spherical accretion decreased slower than that of the static one. In addition, it shows that parameter \(\psi _0\) increases the observed intensity for infalling accretion, although two parameters(\(\eta \) and \(\psi _0\)) all decrease the observed intensity in static case. In a word, observational appearances of a f(R) global monopole black hole surrounded by various accretions present some very different features so that it can be used for us to distinguish black holes from different gravity theories.

On the other hand, we in principle are also possible to constrain the f(R) parameter \(\psi _0\) by using the shadow of M87 detected by the Event Horizon Telescope. Based on the discussions [55, 104, 105], the diameter of the shadow in units of mass for M87 has been obtained, which is \(d_{M87} \equiv D \cdot \delta / M \approx 11 \pm 1.5 \), where D and \(\delta \) are the angular size of the shadow and the distance to M87, respectively. Within 1\(\delta \) and 2\(\delta \) uncertainties, it is easy to see that the ranges of the diameter locate at the regions \(9.5 \sim 12.5 \) and \(8 \sim 14\). So, this range may give rise to some upper or lower limits to black hole parameters. Combined with this fact, we can expect to set an upper limit on the f(R) parameter \(\psi _0\) by using the shadow of a f(R) global monopole black hole. By computing the diameter of the resulting shadow, when the parameter \(\eta = 0.01\), it is easy for us to find that the upper limits of the parameter \(\psi _0\) are \(\psi _0 \approx 0.034M\) for 1\(\delta \) uncertainties and \(\psi _0 \approx 0.051M\) for 2\(\delta \) uncertainties. The detailed analysis of the observational constraints on black hole parameters will be carefully addressed in our next work. In a conclusion, it is true that black hole shadow can indeed present some observational constraints on the related parameters of black hole. In addition, there may also exists an optically thin but geometrically thick accretion around the black hole. Therefore, it is interesting for us to further discuss the observational appearances of black hole in the near future.