Dynamics of charged test particles around quantum-corrected Schwarzschild black holes

Abstract

We investigate neutral and charged test particles’ motions around quantum-corrected Schwarzschild black holes immersed in an external magnetic field. Taking the innermost stable circular orbits of neutral timelike particles into account, we find that the black holes can mimic different ranges of the Kerr black hole’s spin |a/M| from 0.15 to 0.99. Our analysis of charged test particles’ motions suggests that the values of the angular momentum l and the energy $E^{2}$ are slightly higher than Schwarzschild black holes. The allowed regions of the $(l,E^{2})$ demonstrate that the critical energy $E^{2}_{c}$ divides the charged test particle’s bounded trajectory into three types. With the help of a Monte Carlo method, we study the charged particles’ probabilities of falling into the black holes and find that the probability density function against l depends on the signs of the particles’ charges. Finally, the epicyclic frequencies of the charged particles are considered with respect to the observed twin peak quasi-periodic oscillations frequencies. Our results might provide hints for distinguishing quantum-corrected Schwarzschild black holes from Schwarzschild ones by using the dynamics of charged test particles around the strong gravitational field.

1 Introduction

A lot of evidences for the presence of black holes have been proved by gravitational waves [1,2,3,4,5,6], x-ray binaries (see Refs. [7, 8] references therein) and imaging the shadow of the supermassive black hole [9,10,11,12,13,14]. As the strong gravitational field in our Universe, black holes are predicted by Einstein’s general relativity (GR) and contain central singularities and the event horizons. However, the central singularity makes GR invalid and the event horizon causes the information paradox. These black holes give us a perfect chance to probe the problems of the singularities, the event horizons and even breakdown of GR (see Refs. [15, 16] and references therein). They also provide ideal laboratories for testing fundamental gravity theories in the strong gravitational field [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51].

To address the problems of singularities and event horizons, we are still looking for a self-consistent and full theory of quantum gravity. Before that, some influences of quantum behaviors on black holes should be first investigated for this purpose. For the sake of removing singularities, there exist some efficient methods to bring out quantum effects in the 4D spacetime of black holes by replacing singularities with regular cores [52,53,54,55], introducing quasi black holes [56,57,58,59,60] and using quantum pressures to construct one kind of bouncing geometry [61,62,63]. In order to erase the event horizons, “compact quantum objects” [64], “exotic compact objects” [65] and quantum dynamics for these objects [66] are attentively taken into account. A lot of properties between quantum effects and the spacetime of gravitation have been extensively studied (see Refs. [67,68,69,70,71,72,73,74], for details). And some black holes with quantum characteristics have been proposed under the frameworks of renormalization group [75,76,77,78,79], the loop quantum gravity [80, 81], effective field theories [82,83,84], and noncommutative geometry [85,86,87,88].

We will mainly concentrate on quantum-corrected Schwarzschild black holes in this investigation. Inspired by the spherically symmetric quantum fluctuations of the metric and the matter field, quantum-corrected Schwarzschild black holes have been developed by Ref. [89]. In this black hole, due to the quantum deformation, the 4D theory of gravity with the standard Einstein–Hilbert action reduces to the effective 2D dilaton gravity [90, 91]. The corresponding central singularity moves to one finite distance and turn into a divergent sphere. This character is quite different from the classical Schwarzschild black holes. Some intriguing properties in quantum-corrected Schwarzschild black holes were well studied in the quasinormal modes [92,93,94], the tunneling process [95], the geodesics and periodic orbits [96], the strong and weak deflection gravitational lensing [97], and thermal stability and energy conditions [98,99,100,101,102,103]. However, charged test particles’ bounded trajectories in quantum-corrected Schwarzschild black holes are missing, which needs to perform more detailed studies.

In some cases of astrophysics, when a black hole has an accretion disk or is orbited by a nearby neutron star, one magnetic field could exist near the black hole. Due to the fact that a black hole has no a magnetic field of its own, an external magnetic field is always considered. When black holes are surrounded by an external magnetic field, the charged test particles’ motions could be affected [104,105,106,107,108,109] and result in chaotic behaviors [110,111,112,113,114,115,116,117,118,119,120]. Motivated by exploring the nature of jets and winds coming from an active galactic nucleus [121,122,123], much attentions have been devoted to investigating the motion of a charged test particle and following its bound orbit around a black hole immersed in an external magnetic field in some modified gravity theories [124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140]. In fact, magnetic field strengths can be induced by different sources and the relevant properties have drawn much attention [141,142,143,144,145]. In the present work, at the first step, we will consider the simple case: charged test particles around one quantum-corrected Schwarzschild black hole immersed in an external asymptotically uniform magnetic field, which can not change the curvature of the 4D spacetime.

On the other hand, quasi-periodic oscillations (QPOs) are promising to provide insights into the structure of 4D spacetime in the strong gravitational field [146,147,148,149,150,151,152,153,154,155,156,157,158]. QPOs appear as peaks in the power density spectra of the low mass X-ray binary systems such as a stellar mass black hole or a neutron star, where twin high-frequency QPOs with the 3:2 frequency ratio have been observed [159]. Some possible mechanisms for the production of twin peak QPOs have been proposed, which include resonance [159,160,161], relativistic precession [162,163,164], basic p-mode oscillations for a small accretion torus [165], and relativistic diskoseismology [166,167,168]. Although there is still no consensus on which physical mechanism is responsible for the production of twin peak QPOs, their frequencies are directly related to the characteristic orbital frequencies of a timelike particle, which are respectively orbital (Keplerian) frequency, radial epicyclic frequency, and vertical epicyclic frequency (see Refs. [7, 8], for reviews). Since these epicyclic frequencies are only determined by the metric and independent of the complicated astrophysical processes of the accretion, they might present an opportunity to measure possible deviations from GR and to detect some quantum effects.

The remainder of the paper is organized as follows. Sect. 2 is devoted to briefing the quantum-corrected Schwarzschild metric and its geodesics. In Sect. 3, we describes dynamics of charged particles around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field. In Sect. 4, we mainly concentrate on studying charged particles’ bounded trajectories and their probabilities of falling into the black holes. In Sect. 5, the epicyclic frequencies of the quasicircular motion around the black holes in the present of the external magnetic field are investigated. Finally, in Sect. 6, conclusions and discussion are outlined.

2 Metric and geodesics

Inspired by the spherically symmetric quantum fluctuations of the metric and the matter field, quantum-corrected Schwarzschild black holes have been developed by Ref. [89]. In this solution, the 4D theory of gravity with the standard Einstein–Hilbert action reduces to the effective 2D dilaton gravity. In this section, we will first briefly review the metric in quantum-corrected Schwarzschild black holes (see Refs. [89,90,91, 98], for details). And, then, the corresponding geodesics will be derived and discussed.

The standard Einstein–Hilbert action reads

$$\begin{aligned} \mathscr {S}=\int \mathrm {d}^{4}x\sqrt{-g}\bigg [\frac{R}{16\pi G}+\mathscr {L}_{M}\bigg ], \end{aligned}$$

(1)

where $g\equiv \mathrm {det}(g_{\mu \nu })$ and R respectively denote the determinant of the metric tensor and the Ricci scalar in the 4D spacetime. G is the gravitational constant and $\mathscr {L}_{M}$ is the Lagrangian of the matter. Then the spherically symmetric reduction for the 4D spacetime can be described by

$$\begin{aligned} \mathrm {d}s^{2}_{(4)}=\mathrm {d}s^{2}_{(2)}+\frac{2G}{\pi }\mathrm {e}^{-2\phi }\mathrm {d}\varOmega ^{2}, \end{aligned}$$

(2)

where $\mathrm {d}\varOmega ^2=\mathrm {d}\theta ^{2}+\sin ^{2}\theta \mathrm {d}\varphi ^{2}$ and $\phi$ is the dilaton field. The radial part in Eq. (2) is expressed in terms of $\phi$, which serves as the 2D diffeomorphism. Following Ref. [91], the action for the 2D dilaton gravity is

$$\begin{aligned} \mathscr {S}=\frac{1}{2\pi }\int \mathrm {d}^{2}x\sqrt{-g}\bigg [\mathrm {e}^{-2\phi }R+2\mathrm {e}^{-2\phi }(\nabla \phi )^{2}+\frac{\pi }{G}\bigg ]. \end{aligned}$$

(3)

By introducing $U(\phi )$, the action for the renormalization can be written as

$$\begin{aligned} \mathscr {S}=\frac{1}{2\pi }\int \mathrm {d}^{2}x\sqrt{-g}\bigg [\mathrm {e}^{-2\phi }R+2\mathrm {e}^{-2\phi }(\nabla \phi )^{2}+\frac{\pi }{G}U(\phi )\bigg ].\nonumber \\ \end{aligned}$$

(4)

The divergences can be resolved through the following 2D nonlinear $\sigma$ model [98]

$$\begin{aligned} \mathscr {S}= & {} -\frac{1}{2\pi }\int \mathrm {d}^{2}X\sqrt{-\hat{g}(X)}\bigg [\frac{1}{2}\varPhi (X)\hat{R}+T(X)\nonumber \\&+G_{\mu \nu }(X)\hat{\nabla }X^{\mu }\hat{\nabla }X^{\nu }\bigg ], \end{aligned}$$

(5)

in which $\hat{g}_{\mu \nu }$ and $\hat{G}_{\mu \nu }$ denote respectively the fiducial metric and the target space one. T and $\varPhi$ are the tachyon field and the dilaton. By using the vanishing $\beta$ function [90], $\beta ^{U}=\partial _{t}U$ and $t=\ln (\mu /\mu _{0})$ [89], the renormalized potential $U(\phi )$ is

$$\begin{aligned} U(\phi )=\frac{\mathrm {e}^{-\phi }}{\sqrt{\mathrm {e}^{-2\phi }-\frac{4}{\pi }G^{*}}}, \end{aligned}$$

(6)

in which $G^{*}\equiv G\ln (\mu /\mu _{0})$ and $\mu$ is the scale parameter. We can obtain the metric for quantum-corrected Schwarzschild black holes of the action (4) as follows

$$\begin{aligned} f(x)= & {} -\frac{2}{x}+\frac{1}{x}\int ^{x}U(x)\mathrm {d}x=-\frac{2}{x}+\frac{\sqrt{x^{2}-b^{2}}}{x}, \end{aligned}$$

(7)

where we set $M=1$ and $b^{2}\equiv 4G^{*}/\pi$. The spacetime for quantum-corrected Schwarzschild black holes can be expressed as

$$\begin{aligned} \mathrm {d}s^{2}= & {} g_{tt}\mathrm {d}t^{2}+g_{xx}\mathrm {d}x^{2}+g_{\theta \theta }\mathrm {d}\theta ^{2}+g_{\varphi \varphi }\mathrm {d}\varphi ^{2}\nonumber \\\equiv & {} -f(x)\mathrm {d}t^{2}+\frac{1}{f(x)}\mathrm {d}x^{2} + x^{2}\mathrm {d}\varOmega ^{2}. \end{aligned}$$

(8)

In the metric (8), it needs to satisfy $x\ge b$. We can see that the parameter b has a relationship with a redefinition of the gravitational constant $G^{*}$ and comes from the effective two-dimensional dilaton gravity. When the quantum-corrected effect disappears, namely $b=0$, the metric (8) agrees with the Schwarzschild one. If $b\ne 0$, the event horizon ($x_{H}=\sqrt{4+b^{2}}$) in the black holes is always larger than the one of Schwarzschild black holes. The corresponding central singularity moves to one finite distance and turn into a divergent sphere, so that the spacetime for quantum-corrected Schwarzschild black holes is formed from two asymptotically flat world sheets and looks like regular [89].

Fig. 1

The Ricci scalar, the square of Ricci tensor and the Kretschmann scalar as a function of the radius x for the quantum-corrected Schwarzschild metric

The Ricci scalar, the square of Ricci tensor and the Kretschmann scalar in the spacetime (8) can be derived as

$$\begin{aligned} R= & {} g^{\mu \nu }R_{\mu \nu }\nonumber \\= & {} \frac{2(x^2-b^2)^{\frac{3}{2}}-2x^3+3b^2x}{x^2(x^2 - b^2)^{\frac{3}{2}}}, \end{aligned}$$

(9)

$$\begin{aligned} R^{2}= & {} R_{\mu \nu }R^{\mu \nu }\nonumber \\= & {} \frac{8x^6 - 20b^2x^4 + 17b^4x^2 - 4b^6 -8x\left( x^2 - b^2\right) ^{\frac{5}{2}}}{2x^4\left( x^2 - b^2\right) ^3},\nonumber \\\end{aligned}$$

(10)

$$\begin{aligned} \mathscr {K}^{2}= & {} R_{\mu \nu \sigma \rho }R^{\mu \nu \sigma \rho }\nonumber \\= & {} -\frac{8(x^5+2x^4-2b^2x^3-9b^2x^2+b^4x+6b^4)}{x^6(x^2-b^2)^{\frac{3}{2}}}\nonumber \\&+\bigg [8x^8+16x^7-(28b^2-48)x^6-48b^2x^5\nonumber \\&+b^2(49b^2 - 144)x^4+48b^4x^3-b^4(40b^2-144)x^2\nonumber \\&-16b^6x+12b^8-48b^6\bigg ]\bigg [(x^2-b^2)^{3}x^6\bigg ]^{-1}. \end{aligned}$$

(11)

These scalars show some properties from quantum-corrected Schwarzschild spacetime. From Eqs. (9)–(11), the Ricci scalar, the square of Ricci tensor and the Kretschmann scalar are directly affected by the parameter b. When $b\rightarrow 0$, the behaviors of three scalars reduce to the ones of Schwarzschild spacetime. When $b\rightarrow \infty$, we have $x\rightarrow \infty$ due to the condition $x\ge b$ in the quantum-corrected Schwarzschild spacetime, then it indicates that three scalars tend to zero. The values of R, $R^{2}$ and $\mathscr {K}^{2}$ as a function of x for the quantum-corrected Schwarzschild metric are shown in Fig. 1. While three scalars diverge at the center of the black holes, R, $R^{2}$ and $\mathscr {K}^{2}$ all go to zero when $x>x_{H}$.

For a neutral timelike particle in the spacetime (8), its Lagrangian for geodesics in the equatorial place $\theta =\pi /2$ is

$$\begin{aligned} 2\mathscr {L}=-f(x)\dot{t}^{2}+\frac{1}{f(x)}\dot{x}^{2}+x^{2}\dot{\varphi }^{2}=-1, \end{aligned}$$

(12)

where “$\cdot$” denotes taking derivative against an affine parameter such as $\tau$. Then, we obtain two conserved quantities as follows

$$\begin{aligned} E= & {} f(x)\dot{t},\end{aligned}$$

(13)

$$\begin{aligned} l= & {} x^{2}\dot{\varphi }. \end{aligned}$$

(14)

From Eq. (12) and the above conserved quantities, it yields

$$\begin{aligned} \dot{x}^{2}=E^{2}-V_{\mathrm {eff}}, \end{aligned}$$

(15)

where the effective potential is

$$\begin{aligned} V_{\mathrm {eff}}=\bigg (-\frac{2}{x}+\frac{\sqrt{x^2-b^2}}{x}\bigg )\bigg (1+\frac{l^2}{x^2}\bigg ). \end{aligned}$$

(16)

The above equation gives the innermost stable circular orbits (ISCO) [169] by

$$\begin{aligned} V_{\mathrm {eff}}=E^{2},\quad \partial _{x}V_{\mathrm {eff}}=0,\quad \partial _{x}\partial _{x}V_{\mathrm {eff}}=0. \end{aligned}$$

(17)

For ISCO in quantum-corrected Schwarzschild black holes, $x_{\mathrm {ISCO}}$, $l_{\mathrm {ISCO}}$ and $E_{\mathrm {ISCO}}$ increase with the increase of b [96]. And the values of $x_{\mathrm {ISCO}}$, $l_{\mathrm {ISCO}}$ and $E_{\mathrm {ISCO}}$ are larger than the ones in the Schwarzschild black hole (see Ref. [96] for details). ISCO plays an important role in astrophysics and contributes to modeling a rotating Kerr black hole. In the following part, we will show that quantum-corrected Schwarzschild black holes could mimic the rotating Kerr black hole at the same ISCO radius $x_{\mathrm {ISCO}}$.

Fig. 2

The degeneracy graphs of the ISCO radius between Kerr spin a and the parameter b. Left: ISCO radius vs Kerr spin a and the parameter b. Right: Kerr spin a vs the parameter b with providing the same ISCO radius

For ISCO around the Kerr black hole, retrograde and prograde orbits had been formulated as follows [170]

$$\begin{aligned} r^{\mathrm {Kerr}}_{\mathrm {ISCO}}= & {} 3+Z_{2}\pm \sqrt{(3-Z_{1})(3+Z_{1}+2Z_{2})}, \end{aligned}$$

(18)

with

$$\begin{aligned} Z_{1}= & {} 1+\bigg (\root 3 \of {1+a}+\root 3 \of {1-a}\bigg )\root 3 \of {1-a^{2}}, \end{aligned}$$

(19)

$$\begin{aligned} Z_{2}= & {} \sqrt{3a^2+Z^{2}_{1}}. \end{aligned}$$

(20)

If quantum-corrected Schwarzschild black holes could mimic the rotating Kerr black hole at the same ISCO radius, it yields

$$\begin{aligned} x_{\mathrm {ISCO}}=r^{\mathrm {Kerr}}_{\mathrm {ISCO}}. \end{aligned}$$

(21)

Then, we can plot the degeneracy graphs of the ISCO radius $x_{\mathrm {ISCO}}$ with respect to the Kerr spin a and the parameter b in the quantum-corrected Schwarzschild black hole (see Fig. 2). The left panel in Fig. 2 shows that the ISCO radius increases with a and b. It also illustrates the relationship between the parameter b and the spin parameter a at the same ISCO radius for the test particles (see the right panel in Fig. 2). It clearly suggests that different values of b can mimic different range of the spin |a/M| from 0.15 to 0.99 with $0<b\le 2.23$. Especially, according to the astronomical observations of the accretion disks, we have $|a/M|\simeq 0.99$. We find that quantum-corrected Schwarzschild black holes with $b\approx 2.23$ could mimic this rapidly rotating. It makes quantum-corrected Schwarzschild black holes quite different from renormalized group improved Schwarzschild black hole [127], which can mimic the rotation parameter of Kerr black hole up to 0.31. This character might also be used to distinguish quantum-corrected Schwarzschild black holes from others.

Fig. 3

The energy efficiency $\eta$ with respect to the parameter b in quantum-corrected Schwarzschild black holes

It is well known that the Novikov–Thorne model [171, 172] is the standard model for relativistic, thin-disc accretion around a black hole, which is governed by the test particle’s circular geodesics around the black hole. The energy efficiency $\eta$ for the accretion disk is defined as follows

$$\begin{aligned} \eta =1-E_{\mathrm {ISCO}}, \end{aligned}$$

(22)

where $E_{\mathrm {ISCO}}$ is the test particle’s energy at ISCO. The efficiency $\eta$ implies that the maximum value for the particle’s energy could be extracted as radiation when the particle falls into the black hole from the accretion disk. Based on Eq. (22), Fig. 3 shows $\eta$ with respect to b, indicating that the energy efficiency decreases to $\sim 5\%$ with the increase of b from 0 to infinity. It means that the effect of the quantum-corrected Schwarzschild spacetime on the accretion disc radiation is unreasonable and unmeasurable.

Fig. 4

The azimuthal component of the external magnetic field $B^{\hat{\theta }}$ normalized to its asymptotic value $B_{0}$ with respect to x

3 Dynamics of charged particles

In some cases of astrophysics, when a black hole has an accretion disk, one external magnetic field could exist near the black hole. The charged test particles’ motions will be affected. In this section, we will study dynamics of charged particles in the quantum-corrected Schwarzschild black hole surrounded by an external magnetic field, which include dynamics equations, effective potentials, ISCO and the allowed regions of the particles’ angular momentum and energy for bound orbits.

An asymptotically uniform magnetic field is the simplest case. Generally, the real case for the structure of the magnetic field is more complicated. However, at the first step, we will consider the quantum-corrected Schwarzschild black hole surrounded by an external asymptotically uniform magnetic field. This situation has been pioneered by Ref. [104]. By using the method of Ref. [104], we assume that the external asymptotically uniform magnetic field $B_{0}$ is perpendicular to the equatorial plane $\theta =\pi /2$. Then the electromagnetic four potentials are

$$\begin{aligned} A_{\varphi }= & {} \frac{1}{2}B_0 x^2 \sin ^2{\theta }, \end{aligned}$$

(23)

$$\begin{aligned} A_{t}= & {} A_{x} = A_{\theta } = 0. \end{aligned}$$

(24)

With the help of $F_{\mu \nu }\equiv A_{\nu ,\mu }-A_{\mu ,\nu }$, the electromagnetic field tensor has the following nonzero components

$$\begin{aligned} F_{x\varphi }= & {} B_0 x\sin ^2{\theta }, \end{aligned}$$

(25)

$$\begin{aligned} F_{\theta \varphi }= & {} B_0x^2 \sin {\theta } \cos {\theta }. \end{aligned}$$

(26)

Then, for a proper observer, the orthonormal components of the magnetic field around quantum-corrected Schwarzschild black holes can be derived by using the following formula

$$\begin{aligned} B^{\alpha } = \frac{1}{2} \eta ^{\alpha \beta \delta \lambda } F_{\beta \delta }u_{\lambda }, \end{aligned}$$

(27)

where $u_{\lambda }$ is the four-velocity of the proper observer and $\eta _{\alpha \beta \delta \lambda }$ is the pseudotensorial form of the Levi-Civita symbol $\epsilon _{\alpha \beta \delta \lambda }$ [169]. Then, we obtain

$$\begin{aligned} B^{\hat{r}} = B_0\cos {\theta },\quad B^{\hat{\theta }} = \sqrt{f(x)}B_0\sin {\theta }. \end{aligned}$$

(28)

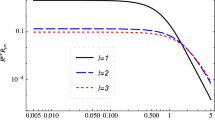
It means that $B^{\hat{\theta }}$ depends on the metric coefficient f(x) and is directly affected by the parameter b in the quantum-corrected Schwarzschild spacetime. Figure 4 shows $B^{\hat{\theta }}/B_{0}$ with respect to x. It suggests that the azimuthal component of the external magnetic field $B^{\hat{\theta }}$ decreases with the increase of b.

Fig. 5

The effective potential $V_{\mathrm {eff}}$ for $l>0$ as a function of x for charged test particles around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field

Now, we consider dynamics equations of a charged test particle with electric charge q around quantum-corrected Schwarzschild black holes immersed in the magnetic field $B_{0}$. The corresponding Hamilton–Jacobi equation [169] reads

$$\begin{aligned} g^{\mu \nu }\left( \frac{\partial S}{\partial x^{\mu }} - qA_{\mu } \right) \left( \frac{\partial S}{\partial x^{\nu } } - qA_{\nu }\right) = -m^2, \end{aligned}$$

(29)

in which m is the charged test particle’s mass. The action S is

$$\begin{aligned} S = -Et + L\varphi + S_x(x) + S_{\theta }(\theta ), \end{aligned}$$

(30)

where t and $\varphi$ are two Killing variables. We have

$$\begin{aligned}&\dot{t}=\frac{E}{f(x)}, \end{aligned}$$

(31)

$$\begin{aligned}&\dot{\varphi }=\frac{l}{x^2\sin ^{2}\theta }-\omega _{B} ,\end{aligned}$$

(32)

$$\begin{aligned}&\frac{1}{f(x)}\dot{x}^2+x^{2}\dot{\theta }^{2}=-2U(x,\theta ,E,l,\omega _{B}) \end{aligned}$$

(33)

with

$$\begin{aligned}&U(x,\theta ,E,l,\omega _{B})\nonumber \\&\quad = -\frac{E^2}{2f(x)} + \frac{1}{2}\left( \frac{l}{x\sin {\theta }} - \omega _B x \sin {\theta }\right) ^2 + \frac{1}{2}, \end{aligned}$$

(34)

where $\omega _{B}=qB_{0}/(2m)$ is the cyclotron frequency and denotes the interactions between the charged particle and the magnetic field. On the equational plane with $\theta =\pi /2$ for Eq. (33), it yields

$$\begin{aligned} \dot{x}^{2}= & {} -2f(x)U(x,\pi /2,E,l,\omega _{B})\nonumber \\\equiv & {} E^2 -V_{\mathrm {eff}}, \end{aligned}$$

(35)

with

$$\begin{aligned} V_{\mathrm {eff}} = \bigg (-\frac{2}{x}+\frac{\sqrt{x^2-b^2}}{x}\bigg )\left[ 1+ \left( \frac{l}{x} - \omega _{B}x \right) ^2\right] . \end{aligned}$$

(36)

By comparison between Eq. (16) for the neutral particle and Eq. (36), the effective potential for the charged particle depends not only on b but also on $\omega _{B}$. This also means that charged particle motions around the black holes can be affected by magnetic fields as a result of the Lorenz force. In Eq. (36), l can be negative or positive. When $l>0$, the Lorentz force is repulsive. While $l<0$, the Lorentz force is attractive. In comparison to neutral test timelike particles [96], charged test particles’ motions around quantum-corrected Schwarzschild black holes immersed in the magnetic field happen without the marginally bound orbits (MBO) and have their typical bound orbits. We will investigate the effective potential, its first and its second derivatives.

Fig. 6

Radial dependence of l and $E^{2}$ with different values of b and $\omega _{B}$. Red, blue and green colors denote respectively $\omega _{B}=0$, 0.05 and -0.01. Solid, dashed and dotted lines denote respectively $b=0$, 0.5, 1

Fig. 7

$x_{\mathrm {ISCO}}$ (left), $l_{\mathrm {ISCO}}$ (middle) and $E_{\mathrm {ISCO}}$ (right) of charged test particles around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field with respect to $\omega _{B}$ and b for ISCO. The horizontal lines denote $x_{\mathrm {ISCO}}$, $l_{\mathrm {ISCO}}$ and $E_{\mathrm {ISCO}}$ of neutral test timelike particles around the black holes

We plot the effective potential $V_{\mathrm {eff}}$ (or $E^{2}$) for $l>0$ as a function of x for charged test particles around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field. In Fig. 5, each row shares the same values of b while each column has the same $\omega _{B}$. The first column in Fig. 5 shows the situations for the neutral test timelike particles and bound orbits for the neutral particles always lie between ISCO and MBO [96]. For the charged test particles ($\omega _{B}\ne 0$), the values of the effective potential can be much larger than one. Their bound orbits lie between unstable circular orbits and stable circular orbits, which corresponds to the minimum and the maximum of the effective potential (see Ref. [105] for details). For example, with $\omega _{B}=0.1$ and $b=0$, there is no circle orbit in the green curve and there is ISCO in the red curve. Only in the blue curve, there exists stable and unstable circular orbits corresponding to the maximum and the minimum of $V_{\mathrm {eff}}$. And the bound orbit in the blue curve has $E^{2}_\mathrm {max}(x_\mathrm {max}=3.02)=1.15$ and $E^{2}_\mathrm {min}(x_\mathrm {min}=6.81)=0.72$. When $\omega _{B}=0.2$ and $b=0.5$, the blue curve also has the bound orbit, in which the minimum and the maximum of the effective potential (or $E^{2}$) are respectively 0.83 and 0.60.

Therefore, the energy of any bound orbit for the charged particle ($E_{\mathrm {OB}}$) is between the minimum and the maximum of the effective potential, namely, $E_{\mathrm {min}}<E_{\mathrm {OB}}<E_{\mathrm {max}}$. For a given bound orbit of $E_{\mathrm {OB}}$, it suggests that there are two roots of the radius in the curve of the effective potential, respectively $x_{1}$ and $x_{2}$. And we always obtain $x_{1}<x_\mathrm {min}<x_{2}$. It is also means that the charged test particle’s radius is between $x_{1}$ and $x_{2}$ (see Ref. [105], for details). It is interesting to note that $\partial _{x}V_{\mathrm {eff}}(x_{c})=\omega _{B}(b^2/\sqrt{l/\omega _{B}-b^2}+2)/l$ when $x_{c}=\sqrt{l/\omega _{B}}$. In the following section, it will be found that $E^{2}_{c}=V_{\mathrm {eff}}(x_{c})$ is the critical energy, which is used to distinguish between different behaviors of bounded trajectories for the charged test particles around quantum-corrected Schwarzschild black holes.

For charged test particles, based on the first two expressions in Eq. (17), we derive l and $E^{2}$ for the charged particles’ circular orbits as

$$\begin{aligned} l_{\pm }= & {} \frac{x}{\mathscr {Z}x-2}\left( \omega _B\mathscr {Z}x^2 \pm \mathscr {Q} \right) , \end{aligned}$$

(37)

$$\begin{aligned} E_{\pm }^2= & {} \frac{2f(x)}{\left( \mathscr {Z}x-2 \right) ^2}\left[ 2-\mathscr {Z}x +4\omega _B^2x^2 \pm 2\omega _Bx\mathscr {Q} \right] , \end{aligned}$$

(38)

where

$$\begin{aligned} \mathscr {Q}^2= & {} 2\mathscr {Z}x + x^2\left( 4\omega _B^2 - \mathscr {Z}^2 \right) , \end{aligned}$$

(39)

$$\begin{aligned} \mathscr {Z}= & {} \partial _x \ln {f(x)}. \end{aligned}$$

(40)

From Eqs. (37)–(38), it is noted that the values of l and $E^{2}$ have two sets of solutions and these two solutions possess symmetry, namely, $\left( l,E^{2}\right) _{+}\left( \omega _B > 0 \right) =\left( -l,E^{2}\right) _{-}\left( \omega _B < 0 \right)$. Figure 6 gives the angular momentum and energy for charged test particles’ circular orbits against x with different values of b and $\omega _{B}$. Red, blue and green colors denote respectively $\omega _{B}=0$, $\omega _{B}=0.05$ and $\omega _{B}=-0.01$. Solid, dashed and dotted lines denote respectively $b=0$, $b=0.5$, $b=1$. From Fig. 6, we can see that the energy $E^{2}$ with $\omega _{B}<0$ with the fixed x is larger than the energy $E^{2}$ with $\omega _{B}=0$. And the case for $\omega _{B}>0$ is opposite. It is also shown that, when $x>6$ and x is fixed, the angular momentum l with $\omega _{B}>0$ is larger than l with $\omega _{B}<0$. And l with $\omega _{B}>0$ and $\omega _{B}<0$ with the fixed x is always larger than the case with $\omega _{B}=0$. Furthermore, it suggests that the values of l and $E^{2}$ for circle orbits with $b\ne 0$ are slightly higher than the values of Schwarzschild black holes.

ISCO is a minimal radius permitting stable circular motions around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field and is defined as Eq. (17). For the ISCO, $x_{\mathrm {ISCO}}$ (left), $l_{\mathrm {ISCO}}$ (middle) and $E_{\mathrm {ISCO}}$ (right) of charged test particles with respect to $\omega _{B}$ and b are plotted in Fig. 7. It shows that the values of $x_{\mathrm {ISCO}}$ increase with the increase of b and decrease with the increase of $|\omega _{B}|$. And the values of $E_{\mathrm {ISCO}}$ and $l_{\mathrm {ISCO}}$ increase with the increase of b and decrease with the increase of $\omega _{B}$. It means that, by choosing the appropriate values of $\omega _{B}$ and b, the ISCO behavior of charged test particles around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field can mimic the dynamics of the neutral timelike particles around the classical Schwarzschild black hole.

Fig. 8

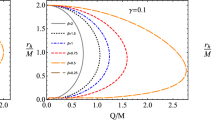
The allowed regions (in shadow) of the $(l,E^{2})$ for charged particles’ bound orbits around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field with two cases: (a) $b=0.5,~\omega _{B}=0.5$; (b) $b=1,~\omega _{B}=0.5$. The red curves denote $E^{2}_{\mathrm {max}}$ and the green curves denote $E^{2}_{\mathrm {min}}$, while the blue curves denote the critical energy $E^{2}_{c}$

According to the above discussion and Ref. [105], for a given l ($l>0$), the energy of the charged particle’s bound orbit belongs to the region between $E^{2}_{\mathrm {min}}(x_{\mathrm {min}})$ and $E^{2}_{\mathrm {max}}(x_{\mathrm {max}})$. And the radius x for the bound orbit of a fixed energy $E_{\mathrm {OB}}$ belongs to the region of $[x_{1},x_{2}]$. We have $x_{\mathrm {max}}\le x_{1}\le x_{\mathrm {min}}\le x_{2}$, where $x_{1}$ and $x_{2}$ are two roots of the radius in the curve of the effective potential for the bound orbit of a fixed energy $E_{\mathrm {OB}}$. It also shows that the bound orbits for charged test particles around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field have a range for energies with a fixed l. This allows us to plot the regions of $(l,E^{2})$ for the bound orbits. Figure 8 illustrates that the allowed regions (in shadow) of the $(l,E^{2})$ for charged particles’ bound orbits around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field with two cases: (a) $b=0.5,~\omega _{B}=0.5$; (b) $b=1,~\omega _{B}=0.5$. The red curve denotes $E^{2}_{\mathrm {max}}$ and the green curve denotes $E^{2}_{\mathrm {min}}$. From this figure, the purple region decreases with the increase of b, while the gray region is opposite. Noted that the blue curve denotes the critical energy $E^{2}_{c}$ with $x=x_{c}=\sqrt{l/\omega _{B}}$. The critical energy determines the behavior of the charged test particle’s bounded trajectory [105]. In the gray region of Fig. 8, the particles’ motion trajectory has no curls. In the purple region of Fig. 8, however, the particles’ motion trajectory has curls. When $E^{2}_{\mathrm {OB}}=E^{2}_{c}$, the particles’ motion trajectory is critical (blue) one and has cusps. We will show these properties in the next section.

Fig. 9

Three types for charged test particles in the weak gravitational field of magnetized quantum-corrected Schwarzschild black holes: a no curls, b cusps, c curls

4 Charged particles’ bounded trajectories and their probabilities of falling into the black holes

The motion of charged particles around black holes is a useful tool to test modified gravity theories and plays an important role to get an insight into black holes physics (see Refs. [7, 8, 15, 16, 124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140] and references therein). Particularly, in the presence of the external magnetic field, charged test particles’ trajectories are affected not only by the gravitational field of the black hole, but also by the magnetic field surrounding the black hole. It makes charged particles’ trajectories exhibit different properties from neutral timelike particles’ ones. In this section, we firstly investigate charged test particles’ bounded trajectories around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field. Furthermore, we study their probabilities of falling into quantum-corrected Schwarzschild black holes by using a Monte Carlo method.

Fig. 10

Charged test particles’ bounded trajectories around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field with $b=0.5$, $\omega _{B}=0.001$ and $l=-3.98$. With $l<0$ (the Lorentz force is attractive), it presents the same zoom-whirl behavior as the neutral timelike particles’ motions

Fig. 11

Three types for charged test particles’ bounded trajectories around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field with $l>0$ (the Lorentz force is repulsive). The first column has curls with the condition $E^{2}>E^{2}_{c}$, corresponding to the purple regions in Fig. 8. The middle column has cusps with the condition $E^{2}=E^{2}_{c}$, corresponding to the blue curves in Fig. 8. The last column has no curls with the condition $E^{2}<E^{2}_{c}$, corresponding to the gray regions in Fig. 8

In the weak gravitational field for the metric (8), we obtain $f(x)\approx 1-2/x-b^{2}/(2x^{2})+\mathscr {O}(b^{4}/x^{4})$ in the form of a Taylor expansion in b/x. From Eqs. (35) and (36), it yields

$$\begin{aligned} \ddot{x}= & {} \frac{l^2}{x^3} - \omega _B^2 x - g , \end{aligned}$$

(41)

with $g = 1/x^2 + b^2/2x^3$. Set a point $(x_{0},\phi _{0})$ and introduce the local coordinates $(\bar{x},\bar{y})$ near the point, where $\bar{x}$ is directed clockwise and $\bar{y}$ is directed along the radius. In addition, we assume $\bar{x}\ll x_{0}$ and $\bar{y}\ll x_{0}$ with respect to $\delta t$ and have

$$\begin{aligned} x \approx x_0 + \bar{y},\quad \phi \approx \phi _0 - \bar{x}/x_0. \end{aligned}$$

(42)

With the above approximation, Eqs. (41) and (32) become

$$\begin{aligned} \ddot{\bar{y}}= & {} -\varOmega ^2 \bar{y} - g_0, \end{aligned}$$

(43)

$$\begin{aligned} \dot{\bar{x}}= & {} \varOmega \bar{y} \end{aligned}$$

(44)

where $l=\omega _{B}x^{2}_{0}$, $\varOmega =2\omega _{B}$ and $g_0 = 1/x_0^2 + b^2/2x_0^3$. When $b=0$, it returns to the result of Ref. [105]. Then, Eqs. (43) and (44) give the following solution

$$\begin{aligned} \bar{y}(\tau )= & {} c_0\cos {(\varOmega t)} - \frac{g_0}{\varOmega ^2}, \end{aligned}$$

(45)

$$\begin{aligned} \bar{x}(\tau )= & {} c_0\sin {(\varOmega t)} - \frac{g_0}{\varOmega }t, \end{aligned}$$

(46)

where the initial conditions are $\bar{x}(0) = 0$,$\bar{y}(0) = c_0 - g_0/\varOmega ^2$. For the weak gravitational field in quantum-corrected Schwarzschild metric, Fig. 9 shows that there exist three types motions for charged test particles in the weak gravitational field of magnetized quantum-corrected Schwarzschild black holes on the $(\bar{x},\bar{y})$ plane. If $c_{0}<g_{0}/\varOmega ^{2}$, the particle’s motion has no curls. If $c_{0}>g_{0}/\varOmega ^{2}$, the particle’s motion has curls. When $c_{0}=g_{0}/\varOmega ^{2}$, the particle’s motion is critical one and has cusps. This situation is very similar to that of classical Schwarzschild black holes.

In the strong gravitational field, charged test particles’ bounded trajectories are more interesting for the applications of astrophysics. For the charged test particles around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field, based on Eqs. (32) and (35), $\varDelta \varphi$ takes the form

$$\begin{aligned} \varDelta \varphi =2\int ^{x_{2}}_{x_{1}}\frac{l-\omega _{B}x^{2}}{x^{2}\sqrt{E^{2}-V_{\mathrm {eff}}}}\mathrm {d}x, \end{aligned}$$

(47)

where the effective potential $V_{\mathrm {eff}}$ is given by Eq. (36). According to the discussion below Eq. (36), the Lorentz force is attractive when $l<0$. By taking $b=0.5$, $\omega _{B}=0.001$ and $l=-3.98$ as an example, we can plot the figure of the charged test particles’ bounded trajectories around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field based on Eq. (47) (see Fig. 10). It presents the same zoom-whirl behavior as the neutral timelike particles’ motions in Ref. [96]. However, when $l>0$, the Lorentz force is repulsive. It shows different characters. From Eq. (47), charged test particles’ bounded trajectories with $l>0$ can be solved by numerical integration and be shown as Fig. 11. In the figure, each row shares the same values of b and l while each column has the similar bounded trajectories for the charged test particles. The critical energy $E^{2}_{c}$ divides the charged test particles’ bounded trajectories into three types. For the middle column in Fig. 11, the energy is $E^{2}_{c}$, corresponding to the blue curves in Fig. 8. The particles’ motions for the critical energy have cusps. For the first column in the figure, $E^{2}>E^{2}_{c}$, corresponding to the purple regions in Fig. 8. In this case, the particles’ motions have curls. On the contrary, for the last column with $E^{2}<E^{2}_{c}$, the particles’ motions have no curls, which is corresponding to the gray regions in Fig. 8. While the behaviors in quantum-corrected Schwarzschild black holes are very similar to that of classical Schwarzschild black holes, there exist different energies for charged test particles’ motions between quantum-corrected Schwarzschild black holes and Schwarzschild ones. Although the bounded trajectories are not directly observable, their energies for the bound orbits might be able to show promise as a benefit to signal extraction from the some observations in radio and gravitational waves.

If the particles’ energies and angular momentums are less than the ones of ISCO around the black holes, the particles will plunge into the black holes. In what follows, we mainly focus on these charged test particles’ probabilities of falling into quantum-corrected Schwarzschild black holes by using a Monte Carlo method. As the first step, we neglect the involved plasma processes without introducing a magnetosphere. Our purpose is to study whether oppositely charged particles of falling into the black hole have the different probabilities.

If we fixed b and $\omega _{B}$ in the equational plane with $\theta =\pi /2$, the initial conditions $(t_{0},x_{0},\varphi _{0},U^{\mu }_{0})$ control the charged test particles’ motions, their energies and angular momentums. Since the quantum-corrected Schwarzschild metric (8) is a static and spherically symmetric, it yields $t_{0}=\varphi _{0}=0$. The allowable regions for the test particles satisfy the condition $\dot{x}^{2}\ge 0$. The plane of $\dot{x}^{2}$ vs x is divided into several regions with $\dot{x}^{2}\ge 0$. When the event horizon and the initial positions lie in the same region with $\dot{x}^{2}\ge 0$ [173], the charge test particles can fall into the black holes. For the particles with $U^{x}_{0}<0$, they can also fall into the black holes [173]. For the other situations, however, the particles will keep away from the center of the black hole and never fall into quantum-corrected Schwarzschild black holes (see Ref. [173], for details).

Fig. 12

The probability density functions of the initial state distributions with respect to x, E, l and $U^{t}_{0}$ in quantum-corrected Schwarzschild black holes

Fig. 13

The probability density functions of falling into quantum-corrected Schwarzschild black holes with respect to x, E, l and $U^{t}_{0}$

Setting $b=0.5$ and $\omega _{B}=\pm 0.25$, we analysis the probability density function of the initial state distribution. For the initial state $x_{0}$, we assume that it uniformly takes random value from the range $(x_{H},x_{\mathrm {max}})$, where $x_{\mathrm {max}}=10$. For the initial states $U^{x}_{0}$, $U^{\theta }_{0}$ and $U^{\varphi }_{0}$, we assume that they uniformly take random values from the range $(-v_{\mathrm {max}},v_{\mathrm {max}})$, where $v_{\mathrm {max}}=1$. $U^{t}_{0}$ can be obtained by the relationship $g_{\alpha \beta }U^{\alpha }U^{\beta }=-1$. It is worth noting that the values of b, $\omega _{B}$, $x_{\mathrm {max}}$ and $v_{\mathrm {max}}$ are all arbitrarily and do not affect our final results. We take $10^{5}$ random numbers and the range of the fixed parameter is 0.5 in the present work.

Figure 12 indicates that the probability density functions of the initial state distributions with respect to x, E, l and $U^{t}_{0}$ in quantum-corrected Schwarzschild black holes. From Fig. 12a, the probability density function of $x_{0}$ is the uniform distribution. However, the probability density functions of E, l and $U^{t}_{0}$ are not. In addition, the probability density functions of E and $U^{t}_{0}$ are independent of the particles’ charges. In Fig. 12c, we see that the probability density function of l depends on the signs of the particles’ charges. Based on the above initial condition distributions, we can discuss the charged particles’ probabilities of falling into quantum-corrected Schwarzschild black holes. Fig. 13 shows the probability density functions for charged particles falling into the black holes with respect to x, E, l and $U^{t}_{0}$. From Fig. 13a, it suggests that the charged particles closer to the black holes are easier to fall into the black holes. From Fig. 13b–d, the charged particles are easier to fall into the black hole when $E\sim 1$, $l\sim (-5,5)$ and $U^{t}_{0}\sim (2,4)$. However, only the probability density function with respect to l depends on the signs of the particles’ charges.

5 Epicyclic frequencies of charged particles

Fig. 14

The epicyclic frequencies for quantum-corrected Schwarzschild black holes (“QC”) and Schwarzschild ones (“Sch”) immersed in an external uniform magnetic field. Black solid vertical lines denote the positions of 3:2 resonance in between $\nu _{x}$ and $\nu _{\varphi }$, black dotted vertical lines denote the positions of 3:2 resonance in between $\nu _{\theta }$ and $\nu _{x}$ and black dashed vertical lines denote the positions of 3:2 resonance in between $\nu _{\theta }$ and $\nu _{\varphi }$

Fig. 15

The epicyclic frequencies for quantum-corrected Schwarzschild black holes (“QC”) and Schwarzschild ones (“Sch”) immersed in an external uniform magnetic field. Black solid vertical lines denote the positions of 3:2 resonance in between $\nu _{x}$ and $\nu _{\varphi }$, black dotted vertical lines denote the positions of 3:2 resonance in between $\nu _{\theta }$ and $\nu _{x}$ and black dashed vertical lines denote the positions of 3:2 resonance in between $\nu _{\theta }$ and $\nu _{\varphi }$

The galactic microquasars consist of one accretion disk surrounding a stellar mass black hole, which can emit jets with X-rays. In this kind of astrophysical system, the high-frequency QPOs are usually observed in pairs of the lower $f_{L}$ and upper $f_{U}$ frequencies of twin peaks in the power spectra. And the twin QPOs for $f_{U}:f_{L}$ exhibit the exact 3:2 frequency ratio. Although there is still no consensus on which physical mechanism is responsible for the production of twin peak QPOs, their frequencies are related to the characteristic orbital frequencies of a timelike particle, which are respectively orbital (Keplerian) frequency $\nu _{\varphi }$, radial epicyclic frequency $\nu _{x}$, and vertical epicyclic frequency $\nu _{\theta }$ (see Refs. [7, 8], for reviews). In this section, we mainly focus on the twin high-frequency QPOs which are modeled as one quantum-corrected Schwarzschild black hole immersed in an external asymptotically uniform magnetic field with charged particles.

We consider a charged test particle with the stable circular orbit $x_{0}$. When the charged particle is slightly displaced from $x_{0}$, the epicyclic motion happens around the mean orbit. For small displacements, $x=x_{0}+\delta x$ and $\theta =\pi /2+\delta \theta$ at the linear order, where $\delta x$ and $\delta \theta$ are small radial and vertical displacements around the mean orbit. In addition, we assume that there exists no non-linear effects coupling the the radial and the vertical modes. Then, we have

$$\begin{aligned}&\delta \ddot{ x} + \bar{\omega }_x^2 \delta x = 0, \end{aligned}$$

(48)

$$\begin{aligned}&\delta \ddot{\theta } + \bar{\omega }_{\theta }^2 \delta \theta = 0, \end{aligned}$$

(49)

where $\bar{\omega }_x$ and $\bar{\omega }_{\theta }$ denote respectively radial epicyclic frequency and vertical epicyclic frequency measured by a local observer. The local orbital frequency $\bar{\omega }_{\varphi }$ mainly depends on $\dot{\varphi }$ [see Eq. (32)]. The fundamental frequencies measured by the local observer can be found as

$$\begin{aligned} \bar{\omega }_x^2= & {} \frac{1}{g_{xx}}\frac{\partial ^2 U(x,\theta ,E,l,\omega _{B})}{\partial x^2}, \end{aligned}$$

(50)

$$\begin{aligned} \bar{\omega }_{\theta }^2= & {} \frac{1}{g_{\theta \theta }}\frac{\partial ^2 U(x,\theta ,E,l,\omega _{B})}{\partial \theta ^2},\end{aligned}$$

(51)

$$\begin{aligned} \bar{\omega }_{\varphi }= & {} \frac{1}{g_{\varphi \varphi }}\bigg (l-\omega _{B}x^{2}\bigg ), \end{aligned}$$

(52)

with the metric (8) and Eq. (34). From the above equations, for a distant observer, we can derive the fundamental frequencies $\nu _{x}$, $\nu _{\theta }$ and $\nu _{\varphi }$ measured by the observer at infinity as follows

$$\begin{aligned} \nu = \bigg (\frac{1}{2\pi } \frac{c^3}{GM}\bigg )\bigg [\frac{\bar{\omega }}{(-g^{tt})E}\bigg ], \end{aligned}$$

(53)

where $\bar{\omega }$ is determined respectively by $\bar{\omega }_x$, $\bar{\omega }_{\theta }$ and $\bar{\omega }_{\varphi }$, and we switch the dimension (G, M, c) back in order to discuss the epicyclic frequencies and mass-limit microquasars under quantum-corrected Schwarzschild black holes.

Fig. 16

The upper frequency $f_{U}$(Hz) and mass $M/M_{\odot }$ relations for different parameters b and $\omega _{B}$ with the case of $\nu _{\theta }:\nu _{x}=3:2$. And GRO 1655-40, XTE 1550-564 and GRS 1915+105 are respectively denoted by red, blue and green horizontal lines

Based on Eq. (53), we can plot the epicyclic frequencies for various parameter b in quantum-corrected Schwarzschild black holes immersed in an external uniform magnetic field with different parameters $\omega _{B}$ and make a comparison with classical Schwarzschild ones immersed in an external uniform magnetic field, see Figs. 14 and 15. Here we take $M=10M_{\odot }$ as an example. These figures show the radial epicyclic frequency $\nu _{x}$, the vertical epicyclic frequency $\nu _{\theta }$ and the orbital frequency $\nu _{\phi }$ against x. Black solid vertical lines denote the positions of 3:2 resonance in between $\nu _{x}$ and $\nu _{\varphi }$, black dotted vertical lines denote the positions of 3:2 resonance in between $\nu _{\theta }$ and $\nu _{x}$ and black dashed vertical lines denote the positions of 3:2 resonance in between $\nu _{\theta }$ and $\nu _{\varphi }$. From Figs. 14 and 15, it is clearly shown that the substantial difference between the three fundamental frequencies depends on b, $\omega _{B}$ and the positions of the stable circular orbits. It can cause the 3:2 resonance shifts (see Figs. 14 and 15).

The ratio of twin frequencies $f_{U}:f_{L}=3:2$ has been observed in the three galactic microquasars: GRS 1915+105, XTE 1550-564 and GRO 1655-40 [159]. One interpretation is to identify the upper frequency $f_{U}$ with $\nu _{\theta }$ and the lower frequency $f_{L}$ with $\nu _{x}$. Other interpretations are to either identify $f_{U}=\nu _{x}$ and $f_{L}=\nu _{\varphi }$ or identify $f_{U}=\nu _{\theta }$ and $f_{L}=\nu _{\varphi }$. These are shown in the vertical lines of Figs. 14 and 15. In order to compare with the classical Schwarzschild black holes and detect some possible quantum effects, under quantum-corrected Schwarzschild black holes, we present the effects of the parameter b on the relations between the upper frequency $f_{U}$(Hz) and mass $M/M_{\odot }$ with respect to the data of three galactic microquasars (see Fig. 16). Here we consider the case of $f_{U}:f_{L}=\nu _{\theta }:\nu _{x}$. And GRO 1655-40, XTE 1550-564 and GRS 1915+105 are respectively denoted by red, blue and green horizontal lines in Fig. 16. In Fig. 16, it is also shown that the parameter b best fits the data of the above observations with a non vanishing magnetic field. It means that QPOs might be very promising tools to distinguish quantum-corrected Schwarzschild black holes from Schwarzschild ones.

6 Conclusions and discussion

In the paper, we mainly focus on the dynamics of test particles around quantum-corrected Schwarzschild black holes. For neutral timelike particles, we analysis the spacetime characters of the Ricci scalar R, the square of Ricci tensor $R^{2}$ and the Kretschmann scalar $\mathscr {K}^{2}$. While three scalars diverge at the center of quantum-corrected Schwarzschild black holes, R, $R^{2}$ and $\mathscr {K}^{2}$ all go to zero when $x>x_{H}$ with different values of b, where the parameter b has a relationship with a redefinition of the gravitational constant $G^{*}$ and comes from the effective two-dimensional dilaton gravity. When the timelike particle’s motion lies in ISCO, we find that quantum-corrected Schwarzschild black holes with $0<b\le 2.23$ can mimic different range of the Kerr black hole’s spin |a/M| from 0.15 to 0.99. It means that the observability at ISCO (directly or indirectly) might be used to distinguish quantum-corrected Schwarzschild black holes from others.

Then, we consider the dynamics for charged test particles around quantum-corrected Schwarzschild black holes immersed in an external uniform magnetic field. Our analysis of charged test particles’ motions suggests that the values of the angular momentum l and the energy $E^{2}$ are slightly higher than Schwarzschild black holes. For the ISCO of the charged test particles, it shows that the values of $x_{\mathrm {ISCO}}$ increase with the increase of b and decrease with the increase of $|\omega _{B}|$. It means that, by choosing the appropriate values of $\omega _{B}$ and b, the ISCO behavior of charged test particles around quantum-corrected Schwarzschild black holes immersed in an external asymptotically uniform magnetic field can mimic the dynamics of the neutral timelike particles around the classical Schwarzschild black hole.

With the analysis of the allowed regions of $(l,E^{2})$, charged test particles’ bounded trajectories around quantum-corrected Schwarzschild black holes immersed in an external uniform magnetic field are investigated. With $l<0$, it appears the same zoom-whirl behavior as the neutral timelike particle’s motion in Ref. [96]. When $l>0$, the critical energy $E^{2}_{c}$ divides the charged test particle’s bounded trajectory into three types. While the behaviors in quantum-corrected Schwarzschild black holes are very similar to that of classical Schwarzschild black holes, there exist different energies for charged test particles’ motions between quantum-corrected Schwarzschild black holes and Schwarzschild ones. Furthermore, by using a Monte Carlo method, we study the charged particles’ probabilities of falling into the black holes and find that the probability density function against l depends on the signs of the particles’ charges.

Meanwhile, the epicyclic frequencies of the charged particles are considered with respect to the observed twin peak quasi-periodic oscillations frequencies. These results show that the epicyclic frequencies in quantum-corrected Schwarzschild black holes immersed in an external uniform magnetic field have different frequencies from Schwarzschild ones. Especially, some fundamental frequencies for special cases are very close to upper and lower frequencies in the three Galactic microquasars: GRS 1915+105, XTE 1550-564 and GRO 1655-40. It is also shown that the parameter b best fits the data of the above observations with a non vanishing magnetic field. It means that QPOs might be very promising tools to distinguish quantum-corrected Schwarzschild black holes from Schwarzschild ones.

Our results might provide hints for distinguishing quantum-corrected Schwarzschild black holes from Schwarzschild ones by using the dynamics of charged test particles around the strong gravitational field. In the present work, the dynamics in quantum-corrected Schwarzschild black holes without spin is investigated. In fact, the metric with spin will also lead to a 3:2 frequency ratio [157]. Another open issue for quantum-corrected Schwarzschild black holes is the motion of magnetized particles in the black holes as in the case of Refs.[127, 130, 137]. We will leave the detailed research on the above issues in our next step.