1 Introduction

The Fermilab collaboration released new result of the E989 for muon anomalous magnetic moment (\(g-2\)) which now, combined with the measurement of the E821 [1, 2], amounts to [3]

$$\begin{aligned} \Delta a_\mu =a_\mu ^{exp}-a_\mu ^{SM}=(25.1\pm 5.9)\times 10^{-10}, \end{aligned}$$
(1)

which has an approximate \(4.2\sigma \) discrepancy from the SM prediction.

Two-Higgs-doublet model (2HDM) is a simple extension of SM by including one more electroweak Higgs doublet field. The \(\Delta a_\mu \) discrepancy can be easily explained in the lepton-specific 2HDM [4,5,6,7,8,9,10,11,12,13,14,15,16] and aligned 2HDM [17,18,19,20,21,22,23,24,25,26]. However, in the decay \(\tau \rightarrow \mu \nu \bar{\nu }\), the tree-level diagram mediated by the charged Higgs gives negative contribution, which will lead to the deviation of the lepton flavor universality (LFU) in \(\tau \) decays [13,14,15]. Besides, a scalar with the \(\mu \)–\(\tau \) lepton flavor violation (LFV) interactions can accommodate the \(\Delta a_\mu \) discrepancy by the one-loop contribution [27,28,29,30,31,32,33,34,35,36,37,38,39,40]. Meanwhile, the extra Higgs doublet with the \(\mu \)–\(\tau \) LFV interactions can alleviate the discrepancy of LFU in \(\tau \) decays [34]. In this paper, we consider relevant theoretical and experimental constraints, including the lepton flavor universality (LFU) in the \(\tau \) decays and multi-lepton event searches at the LHC, and examine the possibilities of explaining the \(\Delta a_\mu \) discrepancy reported by Fermilab in the 2HDM with a discrete \(Z_4\) symmetry in which an inert Higgs doublet field (\(H,~A,~H^\pm \)) has the lepton flavor violation \(\mu \)–\(\tau \) interactions. Ref. [36] applied the model to discuss the E821 result of \(\Delta a_\mu \) discrepancy and focused on the case of \(m_H>\) 200 GeV. Different from the Ref. [36], in this paper we try to use a light H to explain the muon \(g-2\) combining the LFU in the \(\tau \) decays and multi-lepton event searches at the LHC.

The rest of the paper is organized as follows. In Sect. 2 we introduce the model briefly. In Sect. 3 we discuss the muon \(g-2\), the LFU in \(\tau \) decays, the exclusion limits of multi-lepton event searches at the LHC, and other relevant constraints. In Sect. 4, we show the allowed and excluded parameter space. Finally, we give our conclusion in Sect. 5.

2 The 2HDM with \(\mu \)–\(\tau \)-philic Higgs doublet

The SM is extended by adding an inert Higgs doublet \(\phi _2\) under an abelian discrete \(Z_4\) symmetry, and the \(Z_4\) charge assignment is shown in Table 1 [34].

Table 1 The \(Z_4\) charge assignment of \(\mu \)–\(\tau \)-philic 2HDM
Full size table

The scalar potential is expressed as

$$\begin{aligned} \mathrm {V}= & {} Y_1 (\phi _1^{\dagger } \phi _1) + Y_2 (\phi _2^{\dagger } \phi _2)+ \frac{\lambda _1}{2} (\phi _1^{\dagger } \phi _1)^2 + \frac{\lambda _2}{2} (\phi _2^{\dagger } \phi _2)^2 \nonumber \\&+ \lambda _3 (\phi _1^{\dagger } \phi _1)(\phi _2^{\dagger } \phi _2) + \lambda _4 (\phi _1^{\dagger } \phi _2)(\phi _2^{ \dagger } \phi _1) \nonumber \\&+ \left[ \frac{\lambda _5}{2} (\phi _1^{\dagger } \phi _2)^2 + \mathrm h.c.\right] . \end{aligned}$$
(2)

Although \(\lambda _5\) is the only potentially complex parameter, it can be rendered real with a phase redefinition of one of the two Higgs fields. Therefore, \(\lambda _5\) could be real without loss of generality. The two complex scalar doublets \(\phi _1\) and \(\phi _2\) take the form

$$\begin{aligned} \phi _1= \left( \begin{array}{c} G^+ \\ \frac{1}{ \sqrt{2}}\,(v+h+iG^0) \end{array} \right) , \ \ \ \phi _2=\left( \begin{array}{c} H^+ \\ \frac{1}{\sqrt{2 }}\,(H+iA) \end{array}\right) . \end{aligned}$$

The vacuum expectation value (VEV) of the \(\phi _1\) field is v=246 GeV, while the \(\phi _2\) field has zero VEV. The \(Y_1\) is calculated using the minimization condition of the scalar potential.

$$\begin{aligned} Y_1=-\frac{1}{2}\lambda _1 v^2. \end{aligned}$$
(3)

The \(G^0\) and \(G^+\) indicate Nambu–Goldstone bosons eaten by the gauge bosons. The A and \(H^+\) represent the mass eigenstates of the CP-odd Higgs boson and charged Higgs boson, whose masses are written as

$$\begin{aligned} m_{H^\pm }^2 = Y_2+\frac{\lambda _3}{2} v^2, ~~~m_{A}^2 = m_{H^\pm }^2 +\frac{1}{2}(\lambda _4-\lambda _5) v^2. \end{aligned}$$
(4)

Therefore, their masses are

$$\begin{aligned} m_{h}^2 = \lambda _1 v^2\equiv (125~\mathrm{GeV })^2, ~~~m_{H}^2 = m_{A}^2+ \lambda _5 v^2. \end{aligned}$$
(5)

We obtain the masses of fermions via the Yukawa interactions with \(\phi _1\),

$$\begin{aligned} - {{\mathcal {L}}} = y_u\overline{Q}_L \, \tilde{{ \phi }}_1 \,U_R + y_d\overline{Q}_L\,{\phi }_1 \, D_R + y_\ell \overline{L}_L \, {\phi }_1 \, E_R + \text{ h.c. } \nonumber \!\!\!\!\!\!\!\!\!\\ \end{aligned}$$
(6)

Here \(Q_L^T = (u_{Li},d_{Li})\), \(L_L^T=(\nu _{Li},\ell _{Li})\), and \(\widetilde{\phi }_{1} = i\tau _2 \phi _{1}^* \), where i is generation index. \(E_R\), \(U_R\), and \(D_R\) represent the three generation charged lepton, right-handed fields of the up-type quark and down-type quark, respectively. Under the \(Z_4\) symmetry, the lepton Yukawa matrix \(y_\ell \) to be diagonal. As a result, the lepton fields (\(L_L\), \(E_R\)) are mass eigenstates.

Under the \(Z_4\) symmetry, the \(\phi _2\) is allowed to have \(\mu \)–\(\tau \) interactions [34],

$$\begin{aligned} - {{\mathcal {L}}}_{LFV}= & {} \sqrt{2}~\rho _{\mu \tau } \,\overline{L^\mu _{L}} \, {\phi }_2 \,\tau _R \, + \sqrt{2}~\rho _{\tau \mu }\, \overline{L^\tau _{L}} \, {\phi }_2 \,\mu _R \, + \, \text{ h.c. } \nonumber \\ \end{aligned}$$
(7)

The interactions of Eq. (7) lead to the \(\mu \)–\(\tau \) LFV couplings of H, A, and \(H^\pm \).

If the new Yukawa couplings \(\rho _{\mu \tau }\) and \(\rho _{\tau \mu }\) are complex, the model will give additional contributions to the electric dipole moment (EDM) of muon via the same diagram for muon \(g-2\). The current experimental bound on muon EDM is [41]

$$\begin{aligned} \frac{\mid d_\mu \mid }{e} < 1.9 \times 10^{-19}\, \mathrm{cm}, \end{aligned}$$
(8)

which can impose an upper limit on the imaginary part of \(\rho _{\mu \tau }\rho _{\tau \mu }\). For simplicity, we take the CP-conserving Yukawa matrix, namely that \(\rho _{\mu \tau }\) and \(\rho _{\tau \mu }\) are real.

The SM-like Higgs h has the same tree-level couplings to fermions and gauge boson as the SM, and has no \(\mu \)–\(\tau \) LFV coupling. The H, A, and \(H^\pm \) have the \(\mu \)–\(\tau \)-philic Yukawa couplings and no other Yukawa couplings. There are no cubic interactions with ZZ,  WW for the neutral Higgses A and H.

3 Muon \(g-2\), LFU in \(\tau \) decays, LHC data, and relevant constraints

In our numerical calculations, the input parameters are \(\lambda _2\), \(\lambda _3\), \(m_h\), \(m_H\), \(m_A\) and \(m_{H^\pm }\). The values of \(\lambda _1\), \(\lambda _4\) and \(\lambda _5\) can be determined according to Eqs. (4, 5), and \(m_h\) is fixed at 125 GeV. The key parameters are scanned over in the following ranges:

$$\begin{aligned}&\!\!\!0< \rho _{\mu \tau }=\rho _{\tau \mu }\equiv \rho<1.0,~5~\mathrm{GeV}<m_H<115~\mathrm{GeV},\nonumber \\&\!\!\!130~\mathrm{GeV}< m_A< 900~ \mathrm{GeV},~90~ \mathrm{GeV}<m_{H^{\pm }} < 900~ \mathrm{GeV}. \nonumber \\ \end{aligned}$$
(9)

We choose \(\rho <1.0\) to maintain the perturbativity of the new Yukawa couplings. For \(m_H < m_A\), the contribution of H to muon \(g-2\) can overcome that of A, and leads to a positive contribution to the muon \(g-2\). When the mass of H (A) is closed to that of h, the signal data of the 125 GeV Higgs will constrain the couplings of H (A). Therefore, we take \(m_H<115\) GeV and \(m_A > 130\) GeV. When \(m_H\) is much larger than \(m_\tau \), the corresponding contributions to muon \(g-2\) can be approximately given by a simple expression. As a result, \(m_H>\) 5 GeV is taken. Considering the searches for the charged Higgs at the LEP [42], we require \(m_{H^{\pm }}> 90\) GeV.

The \(\lambda _2\), which controls the quartic couplings of additional Higgses, does not affect the observables studied in this paper. We choose \(\lambda _3=\lambda _4+\lambda _5\) which leads the hHH coupling to vanish. The tree-level couplings of the SM-like Higgs h to the SM particles are exactly same to the SM, and there is no exotic decay mode. Since the extra Higgses do not couple to quarks, we may safely neglect the bounds of meson observable. \(\textsf {HiggsBounds}\) [43] is used to implement the exclusion constraints from the searches for the neutral and charged Higgs at the LEP at 95% confidence level. In addition, we consider other observables and constraints:

  1. (1)

    Theoretical constraints and the oblique parameters. We use the \(\textsf {2HDMC}\) [44] to implement the theoretical constraints from the unitarity, vacuum stability and perturbativity of coupling-constant, as well as the oblique parameters (S, T, U). The recent fit results of the oblique parameters [45] are

    $$\begin{aligned}&S=0.02\pm 0.10, ~~~T=0.07\pm 0.12,\nonumber \\&U=0.00 \pm 0.09, \end{aligned}$$
    (10)

    with the correlation coefficients of

    $$\begin{aligned} \rho _{ST} = 0.92, ~~\rho _{SU} = -0.66, ~~\rho _{TU} = -0.86. \end{aligned}$$
    (11)

    They favor parameter spaces with small mass splitting between \(H^\pm \) and H or A.

  2. (2)

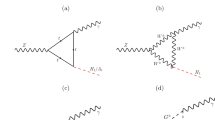
    Muon \(g-2\) anomaly. In the model, the new contribution to \(\Delta a_{\mu }\) comes from the one-loop diagrams containing the \(\mu \)–\(\tau \) LFV coupling of H and A [28],

    $$\begin{aligned} \Delta a_{\mu } = \frac{m_\mu m_\tau \rho ^2}{8\pi ^2} \left[ \frac{ (\log \frac{m_H^2}{m_\tau ^2} - \frac{3}{2})}{m_H^2} -\frac{\log ( \frac{m_A^2}{m_\tau ^2}-\frac{3}{2})}{m_A^2} \right] . \nonumber \\ \end{aligned}$$
    (12)

    The Eq. (12) shows that the new contributions are positive for \(m_A>m_H\). This is reason why we take \(m_A > m_H\) in our calculations.

  3. (3)

    Lepton universality in the \(\tau \) lepton decays. The strictest constraints are from the measurements on ratios of pure leptonic processes, and two ratios from semi-hadronic processes, \(\tau \rightarrow \pi /K \nu \) and \(\pi /K \rightarrow \mu \nu \),

    $$\begin{aligned}&\left( g_\tau \over g_\mu \right) ^2 \equiv \bar{\Gamma }( \tau \rightarrow e \nu \bar{\nu })/ \bar{\Gamma }(\mu \rightarrow e \nu \bar{\nu }),\nonumber \\&\left( g_\tau \over g_e \right) ^2 \equiv \bar{ \Gamma }(\tau \rightarrow \mu \nu \bar{\nu })/ \bar{\Gamma }(\mu \rightarrow e \nu \bar{\nu }),\nonumber \\&\left( g_\mu \over g_e \right) ^2 \equiv \bar{ \Gamma }(\tau \rightarrow \mu \nu \bar{\nu })/ \bar{\Gamma }(\tau \rightarrow e \nu \bar{ \nu }), \end{aligned}$$
    (13)

    where \(\bar{\Gamma }\) denotes the partial width normalized to corresponding SM value. In this model, we have

    $$\begin{aligned}&\bar{\Gamma }(\tau \rightarrow \mu \nu \bar{\nu })= (1+\delta _\mathrm{loop}^\tau )^2~(1+\delta _\mathrm{loop}^\mu )^2+\delta _\mathrm{tree},\nonumber \\&\bar{\Gamma }(\tau \rightarrow e \nu \bar{\nu })= (1+\delta _\mathrm{loop}^\tau )^2,\nonumber \\&\bar{\Gamma }(\mu \rightarrow e \nu \bar{\nu })= (1+\delta _\mathrm{loop}^\mu )^2. \end{aligned}$$
    (14)

    Here \(\delta _\mathrm{tree}\) is from the tree-level diagram mediated by the charged Higgs,

    $$\begin{aligned} \delta _\mathrm{tree}=4\frac{m_W^4\rho ^4}{g^4 m_{H^{\pm }}^4}, \end{aligned}$$
    (15)

    which can give a positive correction to \(\tau \rightarrow \mu \nu \bar{\nu }\). \(\delta _\mathrm{loop}^\mu \) and \(\delta _\mathrm{loop}^\tau \) are the corrections to vertices \(W\bar{\nu _{\mu }}\mu \) and \(W\bar{\nu _{\tau }}\tau \) from the one-loop diagrams containing A, H, and \(H^\pm \), respectively. As we assume \(\rho _{\mu \tau }=\rho _{\tau \mu }\) in the lepton Yukawa matrix, we have \(\delta _\mathrm{loop}^\tau =\delta _\mathrm{loop}^\mu \). Following the results of [13, 15, 34],

    $$\begin{aligned} \delta _\mathrm{loop}^\tau =\delta _\mathrm{loop}^\mu ={1 \over 16 \pi ^2} {\rho ^2} \left[ 1 + {1\over 4} \left( H(x_A) + H(x_H) \right) \right] ,\nonumber \\ \end{aligned}$$
    (16)

    where \(H(x_\phi ) \equiv \ln (x_\phi ) (1+x_\phi )/(1-x_\phi )\) with \(x_\phi =m_\phi ^2/m_{H^{\pm }}^2\). In our model,

    $$\begin{aligned} \left( g_\tau \over g_\mu \right) =\left( g_\tau \over g_\mu \right) _K = \left( g_\tau \over g_\mu \right) _\pi . \end{aligned}$$
    (17)

    The results obtained by the HFAG collaboration are [46]

    $$\begin{aligned}&\left( g_\tau \over g_\mu \right) \!=\!1.0011 \pm 0.0015,\left( g_\tau \over g_e \right) \!=\! 1.0029 \pm 0.0015,\nonumber \\&\left( g_\mu \over g_e \right) \!=\! 1.0018 \pm 0.0014,\left( g_\tau \over g_\mu \right) _\pi \!\!\!=\! 0.9963 \pm 0.0027,\nonumber \\&\left( g_\tau \over g_\mu \right) _K = 0.9858 \pm 0.0071, \end{aligned}$$
    (18)

    with correlation matrix of

    $$\begin{aligned} \left( \begin{array}{ccccc} 1 &{} \quad 0.53 &{}\quad -0.49 &{}\quad 0.24 &{}\quad 0.12 \\ 0.53 &{}\quad 1 &{}\quad 0.48 &{}\quad 0.26 &{}\quad 0.10 \\ -0.49 &{}\quad 0.48 &{}\quad 1 &{}\quad 0.02 &{}\quad -0.02 \\ 0.24 &{}\quad 0.26 &{}\quad 0.02 &{} \quad 1 &{}\quad 0.05 \\ 0.12 &{}\quad 0.10 &{}\quad -0.02 &{}\quad 0.05 &{} \quad 1 \end{array} \right) . \end{aligned}$$
    (19)

    We perform a \(\chi ^2_\tau \) fit for the five observables. The eigenvalues of covariance matrix constructed from the data of Eq. (18) and Eq. (19) are absent, so we remove the corresponding degree in the calculation. In following discussions, we require \(\chi ^2_\tau <\chi ^2_\tau |_\mathrm{SM} = 12.3\), i.e. giving better explanation than SM.

  4. (4)

    Lepton universality in the Z boson decays. The experimental values of the ratios of the Z leptonic decay branching fractions are [47]:

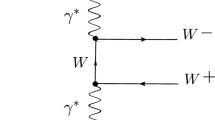
    $$\begin{aligned} {\Gamma _{Z\rightarrow \tau ^+ \tau ^- }\over \Gamma _{Z\rightarrow e^+ e^- }}= & {} 1.0019 \pm 0.0032, \end{aligned}$$
    (20)
    $$\begin{aligned} {\Gamma _{Z\rightarrow \mu ^+ \mu ^-}\over \Gamma _{Z\rightarrow e^+ e^- }}= & {} 1.0009 \pm 0.0028. \end{aligned}$$
    (21)

    The correlation coefficient is 0.63. In our model, the new contributions to the decay widths of \(Z\rightarrow \mu ^+ \mu ^-\) and \(Z \rightarrow \tau ^+\tau ^-\) are from the one-loop diagrams containing the extra Higgs bosons. The ratio of Eq. (20) is given as [13, 15, 34]

    $$\begin{aligned} {\Gamma _{Z\rightarrow \tau ^+ \tau ^- }\over \Gamma _{Z\rightarrow e^+ e^- }} \approx 1.0+ {2 g_L^e\mathrm{Re}(\delta g^\mathrm{loop}_L)+ 2 g_R^e\mathrm{Re}(\delta g^\mathrm{loop}_R) \over {g_L^e}^2 + {g_R^e}^2 }, \,\nonumber \\ \end{aligned}$$
    (22)

    where \(g_R^e=0.23\) and \(g_L^e=-0.27\). The one-loop corrections \(\delta g^\mathrm{loop}_L\) and \(\delta g^\mathrm{loop}_R\) are from

    $$\begin{aligned} \delta g^\mathrm{loop}_L= & {} {1\over 16\pi ^2} \rho ^2 \, \bigg \{ -{1\over 2} B_Z(r_A)- {1\over 2} B_Z(r_H) -2 C_Z(r_A, r_H) \nonumber \\&+ s_W^2 \left[ B_Z(r_A) + B_Z(r_H) + {\tilde{C}}_Z(r_A) + {\tilde{C}}_Z(r_H) \right] \bigg \},\nonumber \\ \delta g^\mathrm{loop}_R= & {} {1\over 16\pi ^2} \rho ^2 \, \bigg \{ 2 C_Z(r_A, r_H) - 2 C_Z(r_{H^\pm }, r_{H^\pm }) + {\tilde{C}}_Z(r_{H^\pm }) \nonumber \\&- {1\over 2} {\tilde{C}}_Z(r_A) - {1\over 2} {\tilde{C}}_Z(r_H) \nonumber \\&+ s_W^2 \left[ B_Z(r_A) + B_Z(r_H) + 2 B_Z(r_{H^\pm })\right. \nonumber \\&\left. +{\tilde{C}}_Z(r_A) + {\tilde{C}}_Z(r_H) + 4C_Z(r_{H^\pm },r_{H^\pm }) \right] \bigg \}, \end{aligned}$$
    (23)

    where \(r_\phi = m_\phi ^2/m_Z^2\), \(\phi =A,H, H^\pm \), and

    $$\begin{aligned} B_Z(r)= & {} -{\Delta _\epsilon \over 2} -{1\over 4} + {1\over 2} \log (r), \end{aligned}$$
    (24)
    $$\begin{aligned} C_Z(r_1,r_2)= & {} {\Delta _\epsilon \over 4} -{1\over 2} \int ^1_0 d x \int ^x_0 d y\, \log [ r_2 (1-x)\nonumber \\&+ (r_1 -1) y + x y], \end{aligned}$$
    (25)
    $$\begin{aligned} {\tilde{C}}_Z(r)= & {} {\Delta _\epsilon \over 2}+{1\over 2} - r\big [1+\log (r) \big ]\nonumber \\&+r^2 \big [ \log (r) \log (1+r^{-1}) \nonumber \\&-\mathrm{Li_2}(-r^{-1}) \big ] \nonumber \\&-{i \pi \over 2} \left[ 1 - 2r + 2r^{2}\log (1+r^{-1}) \right] . \end{aligned}$$
    (26)

    Besides, \(\Gamma _{Z\rightarrow \mu ^+ \mu ^-}\) equals to \(\Gamma _{Z\rightarrow \tau ^+ \tau ^- }\) for \(\rho _{\mu \tau }=\rho _{\tau \mu }\). (5) The multi-lepton searches at the LHC. The H, A, and \(H^{\pm }\) are mainly produced at the LHC via the electroweak processes:

    $$\begin{aligned} pp\rightarrow&W^{\pm *} \rightarrow H^\pm A, \end{aligned}$$
    (27)
    $$\begin{aligned} pp\rightarrow&W^{\pm *} \rightarrow H^\pm H, \end{aligned}$$
    (28)
    $$\begin{aligned} pp\rightarrow&Z^* \rightarrow HA, \end{aligned}$$
    (29)
    $$\begin{aligned} pp\rightarrow&Z^*/\gamma ^* \rightarrow H^+H^-. \end{aligned}$$
    (30)
    $$\begin{aligned} pp\rightarrow&Z \rightarrow \tau ^\pm \mu ^\mp H. \end{aligned}$$
    (31)

    For compressed spectrum, the main decay modes of H, A, and \(H^{\pm }\) are

    $$\begin{aligned} H\rightarrow \tau ^{\pm }\mu ^{\mp },~~~A\rightarrow \tau ^{\pm }\mu ^{\mp },~~~H^\pm \rightarrow \tau ^\pm \nu _\mu , \mu ^\pm \nu _\tau .\nonumber \\ \end{aligned}$$
    (32)

    For \(m_A~(m_{H^{\pm }}) > m_H +m_Z\), the following exotic decay modes will open,

    $$\begin{aligned} A\rightarrow HZ, ~~~~H^\pm \rightarrow H W^\pm . \end{aligned}$$
    (33)

    We use MG5_aMC-2.4.3 [48] to simulate above processes at 13 TeV LHC, with PYTHIA6 [49] for parton shower and hadronization, Delphes-3.2.0 [50] for fast detector simulation, and Fastjet [52] for jet reconstruction. Then we impose the constraints from all the ATLAS and CMS analysis at the 13 TeV LHC in the latest CheckMATE 2.0.28 [51]. The analysis we implemented in our previous works [36, 53] are also included. Besides, we implement the recently published analyses of searching for events with final states of three or more leptons using 137 fb\(^{-1}\) LHC data [54]. It improves significantly the limits on new physical particles that decay to leptons. The signal regions of 4lI, 4lJ and 4lK, which require 4 leptons with one or two hadronical \(\tau \) leptons in the final states, are most sensitive to our samples, because the main decay modes of H, A, and \(H^{\pm }\) are lepton dominated.

4 Results and discussions

Fig. 1
figure 1

The surviving samples satisfying the constraints of ”pre-muon \(g-2\)” and \(\chi ^2_\tau<\) 12.3 projected on the plane of \(\rho \) versus \(m_{H^\pm }\)

Full size image

Firstly, we impose the constraints of ”pre-muon \(g-2\)” (including the theory and the oblique parameters constraints, the exclusion limits from the searches for Higgs at LEP), and display the surviving samples with \(\chi ^2_\tau<\) 12.3 fitting the data of LFU in \(\tau \) decays in Fig. 1. For a very small \(\rho \), the new contributions to \(\tau \) decays disappear. Therefore, the value of \(\chi ^2_\tau \) approaches to the SM value, 12.3. The discrepancy of LFU in \(\tau \) decays can be alleviated by enhancing \(\Gamma (\tau \rightarrow \mu \nu \bar{\nu })\). From Eq. (14), we can find that \(\tau \rightarrow \mu \nu \nu \) receives the corrections from the one-loop diagram and tree-level diagram mediated by the charged Higgs. According to Eq. (16), the former tends to give the negative corrections and enhance the value of \(\chi ^2_\tau \). According to Eq. (15), the latter gives the positive corrections and reduce the value of \(\chi ^2_\tau \). In order to obtain \(\chi ^2_\tau<\) 12.3 for a large \(m_{H^\pm }\), a large \(\rho \) is required to make the contributions of tree-level diagram to overcome those of one-loop diagram since the contributions of tree-level diagram are suppressed by \(m_{H^\pm }\). For \(\chi ^2_\tau<\) 9.7, \(\rho \) is always required to increase with \(m_{H^\pm }\) and be larger than 0.11.

Fig. 2
figure 2

The surviving samples satisfying the constraints of ”pre-muon \(g-2\)” and muon \(g-2\) anomaly projected on the planes of \(\rho \) versus \(m_{H}\) and \(\rho \) versus \(\Delta m\)

Full size image
Fig. 3
figure 3

The surviving samples satisfying the constraints of ”pre-muon \(g-2\)”, muon \(g-2\) anomaly, \(\chi ^2_\tau<\) 12.3, and Z decays

Full size image
Fig. 4
figure 4

The surviving samples on the planes of \(m_H\) versus \(m_A\), \(\rho \) versus \(m_H\), and \(\chi ^2_\tau \) versus \(m_{H^\pm }\). All the samples satisfy the constraints of ”pre-muon \(g-2\)”, muon \(g-2\) anomaly, \(\chi ^2_\tau<\) 12.3, and Z decays. The bullets and squares are excluded and allowed by the direct searches at the LHC

Full size image

After further imposing the constraints of muon \(g-2\) anomaly, we project the surviving samples on the planes of \(\rho \) versus \(m_H\) and \(\rho \) versus \(\Delta m\) (\(\Delta m=m_A-m_H\)) in Fig. 2. From the Eq. (12), we can find that \(\Delta a_\mu \) receives a positive correction from the diagrams containing H and a negative correction from ones involving A. As a result, \(\Delta a_\mu \) is sizable enhanced by a large mass splitting between \(m_A\) and \(m_H\) (\(\Delta m\)), and favors \(\rho \) to decrease with an increase of \(\Delta m\), as shown in the right panel of Fig. 2. In addition, the Eq. (12) shows that the contributions of the diagrams containing H and A to \(\Delta a_\mu \) are respectively suppressed by \(m_H^2\) and \(m_A^2\). Therefore, \(\Delta a_\mu \) favors \(\rho \) to increase with \(m_H\), as shown in the left panel of Fig. 2. The \(\Delta a_\mu \) discrepancy can be explained in the parameter space of \(0.005<\rho <0.12\) and 5 GeV \(<m_H<\) 115 GeV.

In Fig. 3, we show the surviving samples after imposing the constraints of ”pre-muon \(g-2\)”, muon \(g-2\), \(\chi ^2_\tau<\) 12.3, and Z decays. Since the muon \(g-2\) anomaly favors \(0.005<\rho <0.12\), most of the parameter space satisfying \(\chi _\tau ^2<\) 12.3 are excluded. From Fig. 3, we find that a small \(\chi ^2_\tau \) favors a large \(m_H\) and a small \(m_{H^\pm }\). Since the \(\Delta a_\mu \) discrepancy favors a large \(\rho \) for a large \(m_{H}\), and such large \(\rho \) can enhance the width of \(\tau \rightarrow \mu \nu \nu \) and reduce the value of \(\chi ^2_\tau \).

After imposing the constraints of the direct searches at the LHC, the surviving samples of Fig. 3 are projected on Fig. 4. We find that the direct searches at the LHC impose a stringent upper bound on \(m_H\), \(m_H<20\) GeV, and allow 130 GeV \(<m_A~(m_{H^\pm })<\) 610 GeV. It is caused by the multi-lepton searches described in Sect. 3, especially the CMS searches for the direct production of charginos and neutralinos in signatures with two/three or more leptons [54, 55]. The most sensitive signal regions require four leptons including up to two hadronically decaying tau leptons, as in our model the HA pair production leads to \(\tau \tau \mu \mu \) final state. However, for a light H, the \(\tau \mu \) from H decays become too soft to be distinguished at detector, while the \(\tau \mu \) from H in \(A/H^\pm \) decays are collinear because of the large mass splitting between H and \(A/H^\pm \). In addition, in the low \(m_{H}\) region, the \(A/H^\pm \rightarrow H Z/W^\pm \) decays can dominate over the \(A\rightarrow \tau \mu \) and \(H^\pm \rightarrow \tau \nu _\mu , \mu \nu _\tau \). Thus, in the region of \(m_{H}<20\) GeV, the acceptance of above signal region for final state containing collinear \(\tau \mu \) + Z/W boson quickly decreases. For 5 GeV \(<m_H<\) 20 GeV, the \(\Delta a_\mu \) discrepancy favors 0.005 \(<\rho<\) 0.014. As a result, the new contributions to the \(\tau \) decays are very small, and the \(\chi ^2_\tau \) approaches to the value of SM, 12.3.

In our calculation, we always assume \(\rho _{\mu \tau }=\rho _{\tau \mu }\). If the relation is not satisfied, the \(\rho ^2\) in the Eq. (12) for \(\Delta a_{\mu }\) is replaced with \(\rho _{\mu \tau }\rho _{\tau \mu }\). For the calculation of LFU in \(\tau \) decays, the \(\rho ^4\) of the Eq. (15) for \(\delta _\mathrm{tree}\) is replaced with \(\rho _{\mu \tau }^2\rho _{\tau \mu }^2\), and the one-loop correction \(\delta _\mathrm{loop}^\tau \) does not equal to the \(\delta _\mathrm{loop}^\mu \). For the calculation of the Z decays, the \(\rho ^2\) of the Eq. (23) for \(\delta g^\mathrm{loop}_L\) and \(\delta g^\mathrm{loop}_R\) are respectively replaced with \(\rho _{\tau \mu }^2\) and \(\rho _{\mu \tau }^2\). If one of \(\mid \rho _{\mu \tau }\mid \) and \(\mid \rho _{\tau \mu }\mid \) is very small, the other is required to be large enough to explain the muon \(g-2\) and LFU in \(\tau \) decays, which is more easily constrained by the perturbativity and Z decays than the case of \(\rho _{\mu \tau }=\rho _{\tau \mu }\).

In order to fit the observed data of neutrino masses and mixings, the \(Z_4\) flavor symmetry in the model must be broken [34, 56]. One may introduce a SM singlet scalar S with \(Z_4\) charge i and three right-handed neutrinos (\(N_{eR}\), \(N_{\mu R}\), \(N_{\tau R}\)) with (\(1,~i,~-i\) ). The interaction terms relevant to neutrino sector are then given by

$$\begin{aligned} -{{\mathcal {L}}}_{N}&= \frac{1}{2} \begin{pmatrix} \overline{N_{eR}^{c}}&\overline{N_{\mu R}^{c}}&\overline{N_{\tau R}^{c}} \end{pmatrix} \begin{pmatrix} M_{1} &{}\quad y_{12} S^{*} &{}\quad y_{13}S \\ y_{12} S^{*} &{} &{}\quad M_{23} \\ y_{13} S &{}\quad M_{23} &{} \end{pmatrix} \begin{pmatrix} N_{e R}^{} \\ N_{\mu R}^{} \\ N_{\tau R}^{} \end{pmatrix} \nonumber \\&\qquad +\begin{pmatrix} \overline{L_{e}}&\overline{L_{\mu }}&\overline{L_{\tau }} \end{pmatrix} \begin{pmatrix} y_{e1}^{} \phi _1 &{} &{} \\ &{}\quad y_{\mu 2}^{} \phi _1 &{}\quad y_{\mu 3}\phi _2 \\ &{} y_{\tau 2} \phi _2 &{}\quad y_{\tau 3}^{}\phi _1 \end{pmatrix} \begin{pmatrix} N_{eR}^{} \\ N_{\mu R}^{} \\ N_{\tau R}^{} \end{pmatrix}\nonumber \\&\qquad +\text {h.c.} \end{aligned}$$
(34)

We assume the singlet S to have a VEV \(\varepsilon \), which breaks the \(Z_{4}\) symmetry. Thus, the total neutrino mass matrix has the structure

$$\begin{aligned} M_{\nu } \propto \begin{pmatrix} {{\mathcal {O}}}(\varepsilon ^{0}) &{}\quad {{\mathcal {O}}}(\varepsilon ) &{}\quad {{\mathcal {O}}}(\varepsilon ) \\ {{\mathcal {O}}}(\varepsilon ) &{}\quad {{\mathcal {O}}}(\varepsilon ^{2}) &{}\quad {{\mathcal {O}}}(\varepsilon ^{0})\\ {{\mathcal {O}}}(\varepsilon ) &{}\quad {{\mathcal {O}}}(\varepsilon ^{0}) &{}\quad {{\mathcal {O}}}(\varepsilon ^{2}) \end{pmatrix}. \end{aligned}$$
(35)

At the leading order of \({{\mathcal {O}}}(\varepsilon ^{0})\), the neutrino mass matrix has non-zero values only in (1, 1), (2, 3), and (3, 2) elements. We can diagonalize this mass matrix by using a unitary matrix (PMNS matrix). Because of the vanishing (2, 2) and (3, 3) elements at the order of \({{\mathcal {O}}}(\varepsilon ^{0})\), the model can naturally predict a large \(\theta _{23}\) mixing angle. Therefore, such extension of model can relax the constraints of neutrino data sizably.

5 Conclusion

In the 2HDM with an abelian discrete \(Z_4\) symmetry, one Higgs doublet has the same interactions with fermions as the SM, and another inert Higgs doublet only has the \(\mu \)–\(\tau \) LFV interactions. After imposing various relevant theoretical and experimental constraints, especially for the multi-lepton search at the LHC, we found that the model can explain the \(\Delta a_\mu \) discrepancy within \(2\sigma \) confidence level in the region of 5 GeV \(<m_H<20\) GeV, 130 GeV \(< m_A~(m_{H^\pm })<\) 610 GeV, and 0.005 \(<\rho<\) 0.014. Meanwhile, the \(\chi ^2_\tau \) fitting the data of LFU in the \(\tau \) decays approaches to the SM prediction.