A study of traversable wormhole solutions in extended teleparallel theory of gravity with matter coupling

Abstract

This study is devoted to explore the physical aspects of wormhole geometry under embedded class-1 spacetime in $f(T,\tau )$ gravity, where $\tau$ denotes the trace of the energy-momentum tensor and T is the torsion. We derive the embedded class-1 solutions by considering spherically symmetric static spacetime. The shape function is calculated in the framework of embedded class-1 spacetime. It is necessary to mention here that the calculated shape function can be used in other modified theories of gravity. To complete this study, we take diagonal and off-diagonal tetrad, and try to build a comparison by considering the validity region of energy conditions in embedded class-1 spacetime. The embedded surface diagram is given to understand the connection between the two different regions of spacetime. The validity regions of all the energy conditions are calculated. A detailed graphical analysis is provided for validity regions of all the energy conditions. The presence of exotic matter is confirmed in both the cases as the null energy condition is violated.

1 Introduction

Some concrete results admit that the Universe is undergoing a continuous and accelerating expansion [1,2,3,4,5,6,7,8,9,10]. An ambiguous and mysterious force famous as Dark Energy (DE) with negative pressure is alleged responsible as a strong candidate for this rapid accelerated expansion phenomenon of the Universe. Some other approaches may also be available to counter this mysterious DE. But a more prominent approach to understanding this reversed pressure force is to modify the the Einstein theory of gravity known as general relativity (GR). To service this motivation, a lot of modifications of GR such as f(R) gravity, f(T) gravity etc have been proposed [11,12,13]. Considering teleparallel equivalent of GR (TEGR) as a starting point, one can approach the modified gravity theory with matter-coupling. As a choice, Harko et al. [14], have suggested such matter-coupled theory named as $f(T, \tau )$ gravity. In this particular modification, gravitational Lagrangian is composed by the arbitrary function comprising the torsion scalar T and trace $\tau$ of the energy-momentum tensor. The $f(T,\tau )$ modification [15,16,17,18,19,20,21,22], explains gravity in a completely different way while compared to other torsion or curvature-based gravity theories, which is formulated from the tetrad field. Two types of tetrads were suggested in [67]. In the current work we use both tetrad formalism cases, i.e., diagonal and off-diagonal tetrad.

An interesting topic in modern cosmology is the discussion about the existence and formation of wormholes solutions. A wormhole (WH) is a short tunnel or passage to connect two or more different parts of the same or departing Universes. Primarily they were proposed as a mechanism to understand GR [23]. Optimistic observational confirmations about the existence of WHs in GR have been presented in literature [24,25,26,27,28,29,30]. A recent study [31], mentioned two types of WHs characterized as static and dynamic. The confirmation of exotic matter can be checked from the violation of null energy condition (NEC) [23, 32]. This violation of the energy conditions is one of the core requirement for the existence of a WH structure. It was challenging for researchers to construct the WH solutions in GR. Whereas GR admits WH solutions, it requires modifying the matter part with the necessary inclusion of additional term (as a known fact, normal matter satisfies the energy conditions that is an adverse condition for the existence of WHs). So the inclusion of extra terms permits the violation of energy conditions by providing the environment for WHs in GR. Einstein and Rosen [33], in 1935, expressed the mathematical formalism for WHs in GR and suggested the WH solutions famed as Lorentzian wormholes or Schwarzchild wormholes. Numerous authors in literature [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] have developed WH solution by generating different admissible and viable results with the inclusion of several types of exotic fluids like quintom, scalar field models, non-commutative geometry and electromagnetic field, and discussed the energy conditions for different modified theories of gravity. Some valuable stable results for WHs without the inclusion of exotic matter are also discussed in the literature [49, 50].

Morris and Thorne [23], expressed that the human being can travel through the throat of a WH. They discussed the static and spherically symmetric WHs in GR theory by presenting traversable WHs basic formulation. The study presented by Morris et al. [23], claims that the presence of exotic matter has an important contribution in the structural formation of WHs in the case GR. This exotic matter is a source of repulsive force having EoS $\omega <-1/3$. Recent studies also support this concept by taking it as a deriving source of accelerated expansion of our Universe. During the last century, GR remained a successful theory. Only addition of cosmological constant or other sources like Chaplygin gas or the quintessence fields etc. is needed to elaborate accelerated expansion of the observable Universe. But some other ways are also available to explain the DE by modification of gravity. Some WH solutions in modified gravity theories have been studied in literature [51,52,53,54,55,56]. In this study, we apply the principle of $f(T,\tau )$ gravity to calculate the WH solutions. For this purpose, we apply the renowned Karmarkar condition (KC) under embedded spacetime by following the work presented in the literature [57, 59]. Karmarkar [60], developed a condition of embedding class-1 spacetime for a static and spherically symmetric line element. A lot of work is presently showing the compact object configurations based on KC. Kuhfittig [57], have developed a WH geometry by utilizing KC and shown that the embedding approach may also provide the foundation for detailed WH solutions. In a recent work Farasat and Iffat [58], have explored WH solutions in $f\!(R)$ gravity by using Karmarkar condition.

We structure our paper as follows. In Sect. 2 of this paper, we present the traversable WH geometry embedding formalism. In Sect. 3 we discuss the basics of $f(T,\tau )$ gravity and field equations for the WH geometry. In Sect. 4 we write some necessary detail about our WH solutions using diagonal tetrad. In Sect. 5 we discuss the WH solutions using off-diagonal tetrad. And in the last part we conclude our discussion about the obtained WH solutions.

Fig. 1

shows the evolution of embedding diagram

2 The geometry of traversable wormhole and embedding diagram

Our motive in this study is to discuss WH solutions using KC with embedded class-1 spacetime. For this purpose, we start with spherically symmetric and static spacetime with the following line element

$$\begin{aligned} ds^{2}=e^{\nu (r)}dt^{2}-e^{\lambda (r)} dr^{2}-r^{2} d\theta ^{2}-r^{2}\sin ^{2}\theta d\phi ^{2} , \end{aligned}$$

(1)

where, $\nu (r)$ and $\lambda (r)$ only functions of the radial coordinate r. The nonzero components of the Riemann curvature tensor are expressed as

$$\begin{aligned} {\mathcal {R}}_{\mu \upsilon \eta \gamma }=\Sigma (\Lambda _{\varsigma \eta }\Psi _{\upsilon \gamma } - \Upsilon _{\mu \gamma }\Upsilon _{\nu \eta }), \end{aligned}$$

with

$$\begin{aligned} 0=\Upsilon _{\mu \nu };n-\Upsilon _{\nu \eta };\nu . \end{aligned}$$

These values intimate the space-like or time-like manifold. The Karmarkar condition [60], is expressed as

$$\begin{aligned} {\mathcal {R}}_{2323}{\mathcal {R}}_{1414}={\mathcal {R}}_{1224}{\mathcal {R}}_{1334}+ {\mathcal {R}}_{1212}{\mathcal {R}}_{3434}, \end{aligned}$$

(2)

where, ${\mathcal {R}}_{2323}\ne {\mathcal {R}}_{1414}\ne 0$. From Eq. (2) we get the differential equation after plugging the Riemann tensor components as:

$$\begin{aligned}&-\left( \nu '(r) \lambda '(r)+\nu '(r)^2-2 \left( \nu ''(r)+\nu '(r)^2\right) \right) \nonumber \\&\quad +\frac{\nu '(r) \lambda '(r)}{1-e^{\lambda (r)}}=0, \quad e^{\lambda (r)}\ne 1 \end{aligned}$$

(3)

By employing integration on Eq. (3) we get a following relation

$$\begin{aligned} e^{\lambda (r)}=1+Ae^{\nu (r)}\nu ^{'2}(r) \end{aligned}$$

(4)

where A is an integration constant. The WH geometry is given as:

$$\begin{aligned} ds^{2}=e^{\nu (r)}dt^{2}-\frac{1}{1-\frac{S(r)}{r}}dr^{2}-r^{2}d\theta ^{2}-r^{2}sin^{2}\theta d\phi ^{2}.\nonumber \\ \end{aligned}$$

(5)

We call the metric function $\nu (r)$ the red-shift function as $\nu (r)\rightarrow 0$ when $r \rightarrow \infty$. In this discussion we assume the red-shift function as [61, 62]

$$\begin{aligned} \nu (r)=-\frac{2 \zeta }{r}, \end{aligned}$$

(6)

where $\zeta$ is an arbitrary constant. From Eqs. (1) and (5) we can get the following relation for the shape function

$$\begin{aligned} e^{\lambda (r)}=Log\Bigg [\frac{r}{r-S(r)}\Bigg ]. \end{aligned}$$

(7)

Here S is known as the WH shape function. By using Eqs. (4, 5, 7) we can derive the shape function, which is calculated as

$$\begin{aligned} S(r)=r-\frac{r^{5}}{r^{4}+4\zeta ^{2}A e^{-\frac{2 \zeta }{r}} }. \end{aligned}$$

(8)

According to Morris [23], the shape function for a traversable WH solution should meet the necessary limitations i.e (1). $S(r) - r = 0$ at $r = r_{0}$, (2). $\frac{S(r)-rS^{'}(r)}{S(r)} > 0$ as $r=r_{0}$, (3). $S^{'}(r)<1$ and (4). $\frac{S(r)}{r}\rightarrow 0$ as $r\rightarrow \infty$, where $r_0$ is called WH throat radius and r is the radial coordinate such as $r_0< r <\infty$. To tackle with the problem a free parameter L is introduced by adding it in Eq. (8). In the new form it is $S(r)=r-\frac{r^{5}}{r^{4}+4\zeta ^{2}A e^{-\frac{2 \zeta }{r}} }+L$. By utilizing the above Eq. (1) we get $A=\frac{r_{0}^{4}(r_{0}-L)}{4 \zeta ^{2}e^{\frac{-2\zeta }{r}}}$. By considering these values of unknowns Eq. (8) takes the new form as

$$\begin{aligned} S(r)=r-\frac{r^{5}}{r^{4}+r_{0}^{4}(r_{0}-L)}+L,\quad 0<L<r_{0}. \end{aligned}$$

(9)

Now, we discuss the embedding surface diagram and extract the specifically required conditions to symbolize the embedded wormhole configuration. To take specific spherical symmetric space-time with an equatorial slice, we use $\theta =2\pi$ and $t = const.$ in Eq. (1), which then becomes

$$\begin{aligned} ds^{2}= \left( 1-\frac{S(r)}{r}\right) ^{-1}dr^{2}+r^{2}d\phi ^{2}, \end{aligned}$$

(10)

Equation (10) can be embedded into 3-D Euclidean spacetime with cylindrical symmetry, which is expressed as

$$\begin{aligned} ds^{2}_{\Xi }= dg^{2}+dr^{2}+r^{2}d\phi ^{2}. \end{aligned}$$

(11)

The above Eq. (11) can be rewritten as

$$\begin{aligned} ds^{2}_{\Xi }= \bigg (1+\bigg (\frac{dg}{dr}\bigg )^{2}\bigg )dr^{2}+r^{2}d\phi ^{2}. \end{aligned}$$

(12)

By matching Eqs. (10–12), we get the following relation

$$\begin{aligned} \frac{dg}{dr}=\pm \left( \frac{r}{S(r)}-1\right) ^{-1/2}. \end{aligned}$$

(13)

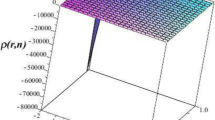
The embedded surface diagram is shown in Fig. 1. The connection between upper Universe $g>0$ and Lower Universe $g<0$ at $r_{0}$ can be confirmed from Fig. 1.

In order to complete this study, we discuss the energy conditions, i.e., weak energy condition (WEC), null energy condition (NEC), dominant energy condition (DEC), and strong energy condition (SEC), are defined as:

$$\begin{aligned}&WEC:\,\rho \ge 0,\quad \rho +p_r\ge 0,\quad \rho +p_t\ge 0,\nonumber \\&NEC:\rho +p_r\ge 0,\quad \rho +p_t\ge 0,\nonumber \\&DEC:\,\rho \ge 0,\quad \rho -|p_r|\ge 0,\quad \rho -|p_t|\ge 0,\nonumber \\&SEC:\,\rho +p_r\ge 0,\quad \rho +p_t\ge 0,\quad \rho +p_r+2p_t\ge 0. \end{aligned}$$

The above bounds in $f(T,\tau )$ gravity are satisfied by the normal matter. To explore the WH construction, we shall examine the validity regions for energy bounds. The invalid region of NEC confirms the violation, which is the necessary requirement for WH construction.

3 $f(T,\tau )$ gravity

The Lagrangian or action is considered a foundation in the basic formulation of any theory of gravity. The $f(T,\tau )$ theory is the extended form of f(T) theory with minimal matter coupling $\tau$. The action for $f(\tau , T)$ gravity is written as

$$\begin{aligned} s=\int dx^{4} e\lbrace \frac{1}{2k^{2}} f(T,\tau )+{\mathcal {L}}_{(M)}\rbrace , \end{aligned}$$

(14)

where, $e= det\left( e_{\mu }^{A}\right) =\sqrt{-g}$, $k^{2}=8\pi G =1$ and, $\tau = \delta _{\gamma }^{\varepsilon \alpha }\tau _{\varepsilon \alpha }^{\gamma }=[\rho ,-p_r,-p_t,-p_t]$. Here, ${\mathcal {L}}_{m}$ based on tetrad field represents the Lagrangian density. Some important aspects, ie., contorsion, torsion, and super potential are necessary for the $f(T,\tau )$ theory, which are given as:

$$\begin{aligned} T^{\lambda }_{\varepsilon \upsilon }= & {} e_{\vartheta }{}^{\lambda }(\partial _{\varepsilon }e^\vartheta {}_\upsilon -\partial _{\upsilon }e^\vartheta {}_{\varepsilon }), \end{aligned}$$

(15)

$$\begin{aligned} K^{\varepsilon \upsilon }_{\lambda }= & {} -\frac{1}{2}\left( T^{\varepsilon \upsilon }{}_{\lambda }-T^{\upsilon \varepsilon }{}_{\rho }-T_{\lambda } {}^{\varepsilon \upsilon }\right) , \end{aligned}$$

(16)

$$\begin{aligned} S_{\lambda }{}^{\varepsilon \upsilon }= & {} \frac{1}{2}\left( K^{\varepsilon \upsilon }{}_{\lambda }+\delta ^{\varepsilon }{}_{\lambda }{T^{\gamma \varepsilon }{}_{\gamma }}-\delta ^{\upsilon }{}_{\lambda } {T^{\gamma \varepsilon }{}_{\gamma }}\right) . \end{aligned}$$

(17)

where T defines the Lagrangian density as:

$$\begin{aligned} T=T^{\lambda }{}_{\kappa \upsilon }S_{\lambda }{}^{\kappa \upsilon }. \end{aligned}$$

(18)

4 CASE-I (diagonal tetrad)

The calculations of field equations for this theory are based on tetrad, which is a key element in torsional theories of gravity. The diagonal tetrad is calculated as:

$$\begin{aligned} e_{\gamma }^{\eta } =\Bigg [e^{\frac{\nu (r)}{2}},e^{\frac{\lambda (r)}{2}},r,r\sin \theta \Bigg ], \end{aligned}$$

(19)

where $e=e^{\nu (r)+\lambda (r)}r^{2}\sin \theta$. The relativistic anisotropic source of fluid is expressed as

$$\begin{aligned} \overset{\text {e-m}}{\tau }_{\alpha \psi }=(\rho +p_{t})u_{\alpha }u_{\psi }-p_{t}g_{\alpha \psi }+(p_{r}-p_{t})v_{\alpha }v_{\psi }, \end{aligned}$$

(20)

where $u_{\alpha }=e^{\frac{a}{2}}\delta _{\alpha }^{0}$ and $v_{\alpha }=e^{\frac{b}{2}}\delta _{\alpha }^{1}$. The energy density, and the pressure components are expressed by $\rho$, $p_{r}$, and $p_{t}$ respectively. By using the spherically symmetric spacetime and anisotropic source of matter with the action of $f(T, \tau )$ theory, we get the following set of equations

$$\begin{aligned}&\Big [e^{-1}\partial _{\varepsilon }(e e_{a}^{\alpha }S_{\alpha }^{\psi \varepsilon })+e_{a}^{\alpha } T^{\varepsilon }_{a\alpha }S_{\varepsilon }^{a \psi }\Big ]f_{T}\nonumber \\&\quad +e_{a}^{\alpha }S_{\alpha }^{\psi \varepsilon } (f_{TT}\partial _{\varepsilon }T+f_{T \tau }\partial _{\varepsilon }\tau )\nonumber \\&\quad +\frac{e_{a}^{\psi }f}{4}- \left( \frac{e_{a}^{\alpha }\tau _{\alpha }^\psi +p_{t}e_{a}^{\psi }}{2}\right) f_{\tau }=\frac{e_{a}^{\alpha }\overset{\textit{e-m}}{T}_{\alpha }^{\psi }}{4}. \end{aligned}$$

(21)

Torsion scalar T in Eq. (18) is calculated as

$$\begin{aligned} \tau (r)=\frac{2 e^{-\lambda (r)} \left( \nu '(r)+\frac{1}{r}\right) }{r}. \end{aligned}$$

(22)

After utilizing Eqs. (15–17, 22) in Eq. (21) we get the following expressions for energy density and pressure components

$$\begin{aligned} \rho= & {} -\frac{e^{-\lambda (r)}}{r}\left( f_{\tau \tau } \tau '+f_{\tau \text { T}} T '\right) \nonumber \\&-\left( \tau (r)-\frac{1}{r^2}-\frac{e^{-\lambda (r)} \left( \lambda '(r)+\nu '(r)\right) }{r}\right) \frac{f_\tau }{2}+\frac{f}{4}\nonumber \\&-\frac{1}{2} f_{T } (p_t+\rho ), \end{aligned}$$

(23)

$$\begin{aligned} p_r= & {} \left( \tau (r)-\frac{1}{r^2}\right) \frac{f_\tau }{2}-\frac{f}{4}+\frac{f_{T }}{2}(p_t-p_r), \end{aligned}$$

(24)

$$\begin{aligned} p_t= & {} \frac{e^{-\lambda (r)}}{2}\left( \frac{\nu '(r)}{2}+\frac{1}{r}\right) \left( f_{\tau \tau } \tau '+f_{\tau \text {T}} T'\right) \nonumber \\&+\Bigg [\frac{\tau (r)}{2}+e^{-\lambda (r)}\Bigg [\frac{\nu ''(r)}{2}+\left( \frac{\nu '(r)}{4}+\frac{1}{2 r}\right) \nonumber \\&\times \bigg [\nu '(r)-\lambda '(r)\bigg ]\Bigg ]\Bigg ]\frac{f_\tau }{2}-\frac{f}{4} . \end{aligned}$$

(25)

Fig. 2

Shows the evolution of energy density $\rho$

The above field equations are based on diagonal tetrad, which is only compatible with the linear model of $f(T,\tau )$ gravity. Any other form of model of $f(T,\tau )$ gravity follows some solar constraints [63, 64], in case of diagonal choice of tetrad. By taking into account the choice of tetrad we apply linear model of the form $f=\alpha T(r)+\beta (\tau )(r)+\phi$. Where $\alpha$ is any arbitrary constant, $\beta$ is coupling parameter and $\phi$ is cosmological constant calculated in [65]. After solving Eqs. (23–25) and Eq. (22) and considering the function of $f(T,\tau )$ theory we get the split form of $\rho$, $p_r$ and $p_t$

$$\begin{aligned} \rho= & {} -\frac{1}{4 (\beta -1) (\beta +2) r^2}\Big [e^{-\lambda (r)} \Big [2 \alpha \beta -4 \alpha +\alpha \beta r^2 \lambda '(r) \nu '(r) \nonumber \\&-2 \alpha \beta r^2 \nu ''(r)-\alpha \beta r^2 \nu '(r)^2+\beta r^2 \phi e^{\lambda (r)}+2 r^2 \phi e^{\lambda (r)}\nonumber \\&- \alpha \beta r \lambda '(r)-2 \alpha \beta e^{\lambda (r)}-3 \alpha \beta r \nu '(r)+4 \alpha r \lambda '(r)+4 \alpha e^{\lambda (r)}\Big ]\Big ],\nonumber \\ \end{aligned}$$

(26)

$$\begin{aligned} p_r= & {} \frac{1}{4 (\beta -1) (\beta +2) r^2}\Big [e^{-\lambda (r)} \Big [2 \alpha \beta -4 \alpha +\alpha \beta r^2 \lambda '(r) \nu '(r)\nonumber \\&-2 \alpha \beta r^2 \nu ''(r)-\alpha \beta r^2 \nu '(r)^2+\beta r^2 \phi e^{\lambda (r)}+2 r^2 \phi e^{\lambda (r)} \nonumber \\&+ 3 \alpha \beta r \lambda '(r)-2 \alpha \beta e^{\lambda (r)}+\alpha \beta r \nu '(r)+4 \alpha e^{\lambda (r)}4 \alpha r \nu '(r)\Big ]\Big ], \end{aligned}$$

(27)

$$\begin{aligned} p_t= & {} \frac{1}{4 (\beta -1) (\beta +2) r^2}\Big [e^{-\lambda (r)} \Big [-2 \alpha \beta +\alpha r^2 \lambda '(r) \nu '(r)\nonumber \\&-2 \alpha r^2 \nu ''(r)-\alpha r^2 \nu ' (r)^2+\beta r^2 \phi e^{\lambda (r)}+2 r^2 \phi e^{\lambda (r)}+\alpha \beta r \lambda '(r)\nonumber \\&+2 \alpha \beta e^{\lambda (r)}-\alpha \beta r \nu '(r)+2 \alpha r \lambda '(r)-2 \alpha r \nu '(r)\Big ]\Big ]. \end{aligned}$$

(28)

By incorporating Eqs. (6,7), the components of WH geometry we obtain the final expressions representing solutions in form of density $\rho$, radial pressure $p_r$ and tangential pressure $p_t$:

$$\begin{aligned} \rho= & {} \frac{1}{4 \left( \beta ^2+\beta -2\right) r^5}\nonumber \\&\times \Bigg [r \left( -(\beta +2) r^4 \phi -2 \alpha \beta \zeta (r-2 \zeta ) +\alpha r ((\beta -4) r-2 \beta \zeta ) S'(r)\right) \nonumber \\&+\alpha \beta \left( -4 \zeta ^2+r^2+4 \zeta r\right) S(r)\Bigg ], \end{aligned}$$

(29)

$$\begin{aligned} p_r= & {} \frac{1}{4 \left( \beta ^2+\beta -2\right) r^5}\nonumber \\&\times \Bigg [r \left( (\beta +2) r^4 \phi \right. \nonumber \\&\left. -2 \alpha \zeta (2 \beta \zeta -5 \beta r+4 r)+\alpha \beta r (2 \zeta +3 r) S'(r)\right) \nonumber \\&+\alpha S(r) \left( 4 \beta \zeta ^2+(4-5 \beta ) r^2+4 (2-3 \beta ) \zeta r\right) \Bigg ], \end{aligned}$$

(30)

$$\begin{aligned} p_t= & {} \frac{1}{4 \left( \beta ^2+\beta -2\right) r^5}\nonumber \\&\times \Bigg [r \left( (\beta +2) r^4 \phi -2 \alpha \zeta (2 \zeta +(\beta -2) r)\right. \nonumber \\&\left. +\alpha r (2 \zeta + (\beta +2) r) S'(r)\right) \nonumber \\&+\alpha S(r) \left( 4 \zeta ^2+ (\beta -2) r^2+2 (\beta -3) \zeta r\right) \Bigg ]. \end{aligned}$$

(31)

Fig. 3

Shows the evolution of $\rho +p_r$

After replacing the shape function from Eq. (9) in above equations we get

$$\begin{aligned} \rho= & {} \frac{1}{4 \left( \beta ^2+\beta -2\right) r^5}\nonumber \\&\Big [r \Big [\frac{\alpha r r_{0}^4 (L-r_{0}) \left( r_{0}^4 (L-r_{0})+3 r^4\right) ((\beta -4) r-2 \beta \zeta )}{\left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}\nonumber \\&-(\beta +2) r^4 \phi \nonumber \\&-2 \alpha \beta \zeta (r-2 \zeta )\Big ]+\alpha \beta \left( -4 \zeta ^2+r^2+4 \zeta r\right) \nonumber \\&\times \left( -\frac{r^5}{-L r_{0}^4+r^4+r_{0}^5}+L+r\right) \Big ], \end{aligned}$$

(32)

$$\begin{aligned} p_r= & {} \frac{1}{4 \left( \beta ^2+\beta -2\right) r^5}\nonumber \\&\Big [r \Big [\frac{\alpha \beta r r_{0}^4 (L-r_{0}) (2 \zeta +3 r) \left( r_{0}^4 (L-r_{0})+3 r^4\right) }{\left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}\nonumber \\&+(\beta +2) r^4 \phi -2 \alpha \zeta (2 \beta \zeta \nonumber \\&+(4-5 \beta ) r)\Big ]+\alpha \left( -\frac{r^5}{-L r_{0}^4+r^4+ r_{0}^5}+L+r\right) \nonumber \\&\times \left( 4 \beta \zeta ^2+(4-5 \beta ) r^2+4 (2-3 \beta ) \zeta r\right) \Big ], \end{aligned}$$

(33)

$$\begin{aligned} p_t= & {} \frac{1}{4 \left( \beta ^2+\beta -2\right) r^5}\nonumber \\&\Big [r \Big [\frac{\alpha r r_{0}^4 (L-r_{0}) \left( r_{0}^4 (L-r_{0})+3 r^4\right) (2 \zeta +(\beta +2) r)}{\left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}\nonumber \\&+(\beta +2) r^4 \phi -2 \alpha \zeta (2 \zeta \nonumber \\&+(\beta -2) r)\Big ]+\alpha \left( -\frac{r^5}{-L r_{0}^4+r^4+r_{0}^5} +L+r\right) \nonumber \\&\left( 4 \zeta ^2+(\beta -2) r^2+2 (\beta -3) \zeta r\right) \Big ]. \end{aligned}$$

(34)

The energy conditions for the diagonal case are given in the Appendix I.

Fig. 4

Shows the evolution of $\rho -p_r$

Fig. 5

Shows the evolution of $\rho +p_t$

Fig. 6

Shows the evolution of $\rho -p_t$

Fig. 7

Shows the evolution of $\rho +p_r +2p_t$

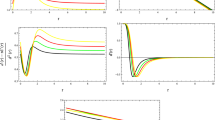
It can be confirmed from the left panel of Fig. 2 that the energy density, i.e., $\rho \ge 0$ in $r_{0}\le r <3.5$ and $\rho < 0$ in $3.5 \le r \le 7$ with $0 <\alpha \le 10$ for the specific value of $\beta =10$. It is also noticed from the same panel $\rho \le 0$ in $r_{0}\le r <3.5$ and $\rho > 0$ in $3.5 \le r \le 7$ with $-10 <\alpha \le 0$ for the specific value of $\beta =10$. The right panel of Fig. 2 provides the valid region of energy density with $\alpha =5$ for $-10 \le \beta \ge 10$. It can be seen from the left part of Fig. 3 that the expression, i.e., $\rho +p_{r}\le 0$ in $r_{0} \le r <5$ for $0< \alpha \le 10$ with $\beta =10$. The expression $\rho +p_{r}$ is also noticed negative in $5 \le r \le 7$ for $-10< \alpha \le 0$ with $\beta =10$. It can be checked from the right part of Fig. 3 that $\rho +p_{r}\le 0$ in $r_{0} \le r <5$ for $-2< \beta \le 10$ with $\alpha =5$. Further, $\rho +p_{r}$ is also seen negative in $5 \le r \le 7$ for $-10< \beta \le -2$ with $\alpha =5$. The negative and invalid region of $\rho +p_{r}$ shows the violation of null energy condition. The violation of null energy condition confirms the presence of exotic matter, which is necessary requirement for the compatible and traversability for the WH existence. The valid region for $\rho -p_{r}$ can be verified from the Fig. 4 by left and right apart for the different choices of involved parameters. Figures 5 and 6 provide the detail of valid region for $\rho +p_{t}$ and $\rho -p_{t}$ respectively. The valid region for the strong energy condition is shown in Fig. 7 for the different ranges of involved parameters. All the energy conditions for diagonal tetrad are summarized in Table 1.

Table 1 Summery of energy conditions in extended teleparallel gravity with diagonal tetrad

5 CASE-II (OFF-diagonal tetrad)

TEGR has a unanimous geometric formulation for the gesticulations of gravitational field. The root formulation of this theory is dependent on the tetrad field. The known reality about these fields is that they are generic ingredients to link the Dirac spinor fields with the gravitational field, also tetrad fields provide a detailed explanation about the reference frames in line element over a manifold. Generally, without the boundary conditions imposed on the tetrad fields, TEGR is invariant under the global Lorentz group SO(3,1) structure. Therefore, gauge transformations cannot exclude the six degrees of freedom furnished by the tetrad fields (which is genuinely relative to the metric tensor) like the Einstein–Cartan theory, as it exhibits local SO(3,1) symmetry. Contrarily, reference frame is designed based on the six ingredients of the acceleration tensor [66], which is the main source for specification of inertial anticipations of the frame. It is valuable to express that in TEGR the tetrad framework governs both the gravitational field and reference frame. As the $f(T,\tau )$ gravity is dependent on the coupling of matter term $\tau$ with the torsion T, so the tetrad framework is essential in the set up of this matter coupled theory. In development of field equations, tetrad contributes as a defining role. In view of Tamanini and Boehmer [67], two types of tetrads can be used as good and bad (poor) tetrads. Use of diagonal tetrad is not a suitable choice as it forces some solar system constraints [63, 64]. Here, in this section we inject good tetrad in field equations. to minimize the discrepancies of diagonal tetrad.

$$\begin{aligned} e_{\gamma }^{\eta } = \begin{pmatrix} e^{\frac{\nu (r)}{2}} &{} 0 &{} 0 &{}0\\ 0 &{} e^{\frac{\lambda (r)}{2}}\sin \theta \cos \phi &{} r\cos \theta \cos \phi &{} -r\sin \theta \sin \phi \\ 0 &{} e^{\frac{\lambda (r)}{2}}\sin \theta \sin \phi &{} r\cos \theta \sin \phi &{} r\sin \theta \cos \phi \\ 0 &{} e^{\frac{\lambda (r)}{2}}\cos \theta &{} -r\sin \theta &{} 0 \end{pmatrix} \end{aligned}$$

(35)

where e describes $e_{\gamma }^{\eta }$ which is given as $e^{\nu (r)+\lambda (r)}r^{2}\sin \theta$. Torsion T(r) and its derivative $T'(r)$ relative to “r”, calculated from Eq. (18) in case of the off diagonal tetrads are given by

$$\begin{aligned} T(r)= & {} \frac{2 e^{-\lambda (r)} \left( e^{\frac{\lambda (r)}{2}}-1\right) \left( e^{\frac{\lambda (r)}{2}}-r \nu '(r)-1\right) }{r^2}, \end{aligned}$$

(36)

$$\begin{aligned} T'= & {} -\frac{4 e^{-\lambda (r)} \left( e^{\frac{\lambda (r)}{2}}-1\right) \left( e^{\frac{\lambda (r)}{2}}-r \nu '(r)-1\right) }{r^3}\nonumber \\&+\frac{e^{-\frac{\lambda (r)}{2}} \lambda '(r) \left( e^{\frac{\lambda (r)}{2}}-r \nu '(r)-1\right) }{r^2}\nonumber \\&-\frac{2 e^{-\lambda (r)} \left( e^{\frac{\lambda (r)}{2}}-1\right) \lambda '(r) \left( e^{\frac{\lambda (r)}{2}}-r \nu '(r)-1\right) }{r^2}\nonumber \\&+\frac{1}{r^2}2 e^{-\lambda (r)} \left( e^{\frac{\lambda (r)}{2}}-1\right) \nonumber \\&\Bigg [\frac{1}{2} e^{\frac{\lambda (r)}{2}} \lambda '(r)-r \nu ''(r)-\nu '(r)\Bigg ]. \end{aligned}$$

(37)

Generalized field equations of $f(T,\tau )$ gravity for off diagonal tetrad by using Eqs. (20, 21) and (35) in form of $\rho$, $p_r$ and $p_t$

$$\begin{aligned} \rho= & {} -\frac{e^{-\frac{\lambda (r)}{2}} \left( e^{-\frac{\lambda (r)}{2}}-1\right) \left( f_{\text {TT}} T'+f_{\text {T}\tau } \tau '\right) }{r}\nonumber \\&-\frac{1}{2} f_T \left( -\frac{e^{-\lambda (r)} \left( 1-r \lambda '(r)\right) }{r^2}-\frac{1}{r^2}+\frac{T(r)}{2}\right) +\frac{f}{4}+\frac{1}{2} f_{\tau } \nonumber \\&\times (p_t+\rho ), \end{aligned}$$

(38)

$$\begin{aligned} p_r= & {} \left( \frac{e^{-\lambda (r)} \left( r \nu '(r)+1\right) }{r^2}-\frac{1}{r^2}+\frac{T(r)}{2}\right) \frac{f_T}{2}\nonumber \\&-\frac{f}{4}-\frac{1}{2} f_{\tau } (p_{t}-p_{r}), \end{aligned}$$

(39)

$$\begin{aligned} p_t= & {} \frac{1}{2} e^{-\lambda (r)} \left( -\frac{e^{\frac{\lambda (r)}{2}}}{r}+\frac{\nu '(r)}{2}+\frac{1}{r}\right) \left( f_{\text {TT}} T'+f_{\text {T}\tau } \tau '\right) \nonumber \\&+ \Big [e^{-\lambda (r)} \left( \left( \frac{\nu '(r)}{4}+\frac{1}{2 r}\right) \left( \nu '(r)-\lambda '(r)\right) +\frac{\nu ''(r)}{2}\right) \nonumber \\&+\frac{T(r)}{2}\Big ]\frac{f_T}{2} -\frac{f}{4}. \end{aligned}$$

(40)

Fig. 8

Shows the evolution of energy density $\rho$

Fig. 9

Shows the evolution of $\rho +p_r$

In our discussion we use a generic $f(T,\tau )$ model which involves higher powers of torsion and is defined as

$$\begin{aligned} f(T,\tau )=\alpha T^{n}(r)+\beta \tau (r)+\phi , \end{aligned}$$

(41)

where $\alpha$, $\beta$ and $\phi$ are unknown and real arbitrary constant as explained in section-IV and $n\ne 0$. TEGR is recovered if we set these parameters $\alpha =n=1$, $\beta =\phi =0$. By putting $n=2$ and $\phi =0$ we receive a model $f(T,\tau )=\alpha T^{2}(r)+\beta \tau (r)$, which had already been used in Harko et al. [14], to study the cosmic aspects. In literature [21, 22], authors worked on the linear choice of torsion i.e., $n=1$ which we use in section-IV. However, in this section we presented results for quadratic contribution of torsion by choosing $n=2$ by reducing the Eq. (41) as $f(T,\tau )=\alpha T^{2}(r)+\beta \tau (r)+\phi$. After replacing the WH geometry from Eq. (6, 7) and values from Eqs. (36–37) along with trace term $\tau =\rho -p_r-2p_t$ and by using the model (41) for $n=2$, we split Eqs. (38–40) as WH solutions in the form of $\rho ,\;\;p_r,\;\;p_t$ as:

$$\begin{aligned} \rho= & {} \frac{(g_{2}(r))^2}{4 (\beta -2) (\beta -1) r^6}\nonumber \\&\Bigg [-60 \alpha \beta +72 \alpha +g_3(r) g_4(r)+g_5(r)\nonumber \\&+\frac{192 \alpha \beta \zeta \sqrt{g_{1}(r)}}{r}- g_6(r)+g_(7)\Bigg ], \end{aligned}$$

(42)

$$\begin{aligned} p_r= & {} \frac{(g_2(r))^2}{4 (\beta -2) (\beta -1) r^6}\nonumber \\&\Bigg [-36 \alpha \beta +24 \alpha +g_8(r) g_9(r)-g_{10}(r)\nonumber \\&+\frac{64 \alpha \beta \zeta \sqrt{g_1(r)}}{r}-g_{11}(r)+g_{12}(r)\Bigg ], \end{aligned}$$

(43)

$$\begin{aligned} p_t= & {} \frac{(g_{2}(r))^2}{4 (\beta -2) (\beta -1) r^6} \Bigg [12 \alpha \beta -24 \alpha +\frac{1}{g_{2}(r)}g_{13}(r)\nonumber \\&+g_{14}(r)+g_{15}(r)+g_{16}(r)\Bigg ], \end{aligned}$$

(44)

where $g_i(r)$, $\{i=1,\ldots ,16\}$ are given in the Appendix II. The energy conditions for the off-diagonal case are given in the Appendix III.

Fig. 10

Shows the evolution of $\rho -p_r$

Fig. 11

Shows the evolution of $\rho +p_t$

Fig. 12

Shows the evolution of $\rho -p_t$

Fig. 13

Shows the evolution of $\rho +p_r +2p_t$

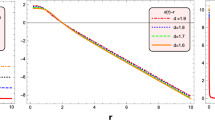
It can be observed from the left panel of Fig. 8 that $\rho \ge 0$ in $r_{0}\le r <2.8$ and $\rho < 0$ in $2.8 \le r \le 7$ with $0 <\alpha \le 10$ with $\beta =10$. It is also perceived from the same panel $\rho \le 0$ in $r_{0}\le r <2.8$ and $\rho > 0$ in $2.8 \le r \le 7$ with $-10 <\alpha \le 0$ with $\beta =10$. The right panel of Fig. 8 provides the valid region of energy density with $\alpha =5$ for $-10 \le \beta \ge 10$. It can be checked from the left part of Fig. 9 that $\rho +p_{r}\le 0$ in $r_{0} \le r <3.2$ for $2< \alpha \le 10$ with $\beta =10$. The null energy condition, i.e., $\rho +p_{r}$ is also seen negative in $3.2 \le r \le 7$ for $-10< \alpha \le 2$ with $\beta =5$. It is verified from the right portion of Fig. 9 that $\rho +p_{r}\le 0$ in $3.2 \le r <7$ for $2< \beta \le 10$ with $\alpha =5$. Further, $\rho +p_{r}$ is also observed negative in $3.2 \le r \le 7$ for $-10< \beta \le 2$ with $\alpha =5$. The invalid region of $\rho +p_{r}$ from Fig. 9 shows the negative region which violate the null energy condition. The invalidity of null energy condition approaches to the presence of the exotic matter, which is fundamental requirement for for the WH existence. The positive region for $\rho -p_{r}$ can be confirmed from the Fig. 10 by the both penal. Figures 11 and 12 express the valid and invalid regions for both $\rho +p_{t}$ and $\rho -p_{t}$ respectively. The valid and invalid regions for the strong energy condition are shown in Fig. 13 for the different ranges of involved parameters. All the energy conditions for off-diagonal tetrad are summarized in Table 2.

Table 2 Summery of energy conditions in extended teleparallel gravity with off-diagonal tetrad

6 Equilibrium analysis

Here we provide the equilibrium analysis for two different models in $f(T,\tau )$ gravity. For this purpose, we shall consider the Tolman–Oppenheimer–Volkoff (TOV) equation for $f(T,\tau )$ gravity which is defined as

$$\begin{aligned}&\frac{2\Delta }{r}-\frac{dp_{r}}{dr}-\frac{a'}{2}(\rho +p_r)\nonumber \\&-\frac{(2\beta )}{\beta +1} \left( -\frac{1}{4} \frac{dp_{r}}{dr}-\frac{dp_{t}}{dr}+\frac{\frac{d \rho }{dr}}{4}\right) =0. \end{aligned}$$

(45)

The above TOV equation can be rearranged as, ${\mathcal {F}}_g +{\mathcal {F}}_h+{\mathcal {F}}_a+{\mathcal {F}}_e=0$ where ${\mathcal {F}}_g= \frac{a'(r)}{2}(\rho +p_r)$, ${\mathcal {F}}_h= \frac{dp_{r}}{dr}$, ${\mathcal {F}}_a= \frac{2\Delta }{r}$, and ${\mathcal {F}}_e=\frac{(2\beta )}{\beta +1} \left( -\frac{1}{4} \frac{dp_{r}}{dr}-\frac{dp_{t}}{dr}+\frac{\frac{d \rho }{dr}}{4}\right)$. Here ${\mathcal {F}}_a$, ${\mathcal {F}}_h$, ${\mathcal {F}}_g$ and ${\mathcal {F}}_e$ represent the anisotropic, hydrostatic, gravitational forces, and extra force, respectively.

Fig. 14

Shows the balanced behavior of of $F_i$

The balancing behavior of four the different forces via TOV equation can be checked from Fig. 14 for both the diagonal and off-diagonal cases under particulars values of the involved parameters. In both the cases, it is observed that balanced behavior of the TOV equation provides the stable configuration for the existence of WHs.

7 Conclusion

The main focus of this work was to investigate the WH solutions in $f(T,\tau )$ gravity. In this paper, we carried the useful discussion for WH geometry in the embedded class-1 spacetime. As the first attempt, we derived the embedded class-1 solutions by taking spherically symmetric static spacetime with an anisotropic source of matter. The shape function is calculated in the framework of embedded class-1 spacetime. A debate regarding the existence of the wormhole and the construction of its solutions with different aspects is among the most interesting challenges in modern astrophysics. Recently, Falco et al. [68, 69] discussed the equations of motion of a test particle in the equatorial plane around a WH geometry influenced by a radiation field in the precise of general relativistic and in extended gravity by considering Poynting–Robertson effect. They have established a diagnostic to distinguish a black hole from a WH, which numerous and different observational data can quickly be reinforced. Falco and his coauthors [70] have presented an approach to reconstruct WH solutions through extended theories of gravity in the weak gravitational field limit. In the weak-field limit, GR reduces to the Newtonian theory. Still, the observations on the rotational curves and mass to light ratios of some galaxies displayed a clear departure from the standard explanation. Therefore, to address such an issue, modified theories of gravity have been proposed. The geodesic structure for the traversable WH is discussed by Chakraborty and his coauthor Pradhan [71]. They have also shown the Keplerian frequency for the WH geometry. In this continuation, Falco and his collaborators [72] have calculated epicyclic frequencies for WH geometries. Further, they have checked the physical implications of their proposed epicyclic methods. All the necessary properties for the existence of WH in the current analysis, are satisfied for the particulars values of the involved parameters, which are reported in [58]. In the current analysis, we explored the following necessary aspects for the WH discussion:

• In this work, we have calculated the filed equations for $f(T,\tau )$ gravity with both the diagonals for the anisotropic source of matter for the WH spacetime.

• We have provided a detailed discussion for embedded spacetime to be a class-1 solution. We have also combined the basic concept of class-1 spacetime with the spherically symmetric static spacetime and successfully calculate the shape function under the embedded spacetime.

• The embedding surface diagram for embedded WH configuration is presented as Fig. 1 undertake the specific spherically symmetric spacetime with an equatorial slice, we used $\theta =2\pi$ and $t = const.$ via Eq. (1).

• We have calculated the validity region for the energy conditions in the framework of diagonal and off-diagonal tetrads. For the diagonal case, the valid region of energy conditions, $\rho$, $\rho +p_{r}$, $\rho -p_{r}$, $\rho +p_{t}$, $\rho -p_{t}$, and $\rho +p_{r}+2p_{t}$ for $-10\le \alpha <10$ with $\beta =10$ is provided in Figs. 2, 3, 4, 5, 6 and 7. From the same Figs. 3, 4, 5, 6 and 7, we have also checked the validity of region with $-10\le \beta <10$ with $\alpha =5$ for all the energy conditions.

• For the off-diagonal case, the valid region of expressions $\rho$, $\rho +p_{r}$, $\rho -p_{r}$, $\rho +p_{t}$, $\rho -p_{t}$, and $\rho +p_{r}+2p_{t}$ for $-10\le \alpha <10$ with $\beta =10$ is presented in Figs. 8, 9, 10, 11, 12, and 13. Further, we have also verified the positive region with $-10\le \beta <10$ with $\alpha =5$ for all the above mentioned expression, which is also provided in Figs. 8, 9, 10, 11, 12, and 13.

• In both the cases, the invalid region of $\rho +p_{r}$ shows the violation of NEC. The violating behavior of NEC confirms the presence of the exotic matter. The presence of the exotic matter shows the supremacy and physical acceptability of embedded spacetime in the study of WH solutions in $f(T,\tau )$ gravity.

• The stability analysis is provided via TOV equation for $f(T,\tau )$ gravity in Fig. 14.

• All the energy conditions for diagonal and off-diagonal tetrad are summarized in Tables 1 and 2 respectively.

It can be concluded that the embedded class-1 is suitable for the WH geometry, which means that the obtained solutions in the background of $f(T,\tau )$ gravity are viable due to the presence of the exotic matter.

Appendices

Appendix I

$$\begin{aligned} \rho +p_r= & {} \frac{1}{(\beta +2) r^4 \left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}\nonumber \\&\times \Big [2 \alpha \zeta \left( r_{0}^4 (r_{0}-L)+r^4\right) \nonumber \\&\times \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) \nonumber \\&-\alpha r \left( L^3 r_{0}^8-2 L^2 r_{0}^9+L r^8+2 r^4 r_{0}^5 (L+2 r)\right. \nonumber \\&\left. -2 L r^4 r_{0}^4 (L+2 r)+L r_{0}^{10}\right) \Big ], \end{aligned}$$

(46)

$$\begin{aligned} \rho -p_r= & {} \frac{\alpha L \left( -4 \beta \zeta ^2+(3 \beta -2) r^2+4 (2 \beta -1) \zeta r\right) +r^3}{2 \left( \beta ^2+\beta -2\right) r^5} \nonumber \\&\times \Big [\frac{2 \alpha }{\left( r_{0}^4 (r_{0}-L)+r^4\right) ^2} \Big [r_{0}^4 (L-r_{0}) \nonumber \\&\times \left( (\beta -2) r_{0}^4 (L-r_{0})-(3 \beta +2) r^4\right) \nonumber \\&+\zeta r^3 \left( (2-3 \beta ) r^4-(\beta +2) r_{0}^4 (L-r_{0})\right) +2 \beta \zeta ^2 r^2 \nonumber \\&\times \left( r_{0}^4 (r_{0}-L)+r^4\right) \Big ]-(\beta +2) r^2 \phi \Big ]\Big ], \end{aligned}$$

(47)

$$\begin{aligned} \rho + p_t= & {} \frac{\alpha }{2 (\beta +2) r^5 \left( r_{0}^4 (r_{0}-L)+r^4\right) ^2} \nonumber \\&\times \Big [2 \zeta ^2 \left( r_{0}^4 (r_{0}-L)+r^4\right) \nonumber \\&\times \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) +r^2\nonumber \\&\times \left( L^2 r_{0}^8 (L+2 r)+L r^8+2 r^4 r_{0}^5 (L-r)\right. \nonumber \\&\left. +2 L r^4 r_{0}^4 (r-L)+r_{0}^{10} (L+2 r)-2 L r_{0}^9 (L+2 r)\right) \nonumber \\&+\zeta r \left( 3 L^3 r_{0}^8-6 L^2 r_{0}^9+r^8 (3 L-2 r)\right. \nonumber \\&\left. +2 r^4 r_{0}^5 (3 L+r)-2 L r^4 r_{0}^4 (3 L+r)+3 L r_{0}^{10}\right) \Big ], \end{aligned}$$

(48)

$$\begin{aligned} \rho - p_t= & {} \frac{2 \alpha L \left( -2 (\beta +1) \zeta ^2+r^2+(\beta +3) \zeta r\right) +2 r^3}{4 \left( \beta ^2+\beta -2\right) r^5}\nonumber \\&\times \Big [\frac{2 \alpha }{\left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}\Big [-r_{0}^4 (r_{0}-L)\nonumber \\&\quad \times \left( r_{0}^4 (r_{0}-L)-5 r^4\right) \nonumber \\&\quad -\zeta r^3 \left( (2 \beta +1) r_{0}^4 (L-r_{0})+r^4\right) \nonumber \\&\quad +(\beta +1) \zeta ^2 r^2 \left( r_{0}^4 (r_{0}-L)+r^4\right) \Big ]-(\beta +2) r^2 \phi \Big ],\nonumber \\ \end{aligned}$$

(49)

$$\begin{aligned} \rho + p_r+2p_t= & {} \frac{1}{2 \left( \beta ^2+\beta -2\right) r^5 \left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}\nonumber \\&\times \Big [\alpha \left( -L^3\right) r_{0}^8 \left( -4 \zeta ^2+ \beta r^2+2 (\beta +1) \zeta r\right) +L^2 r_{0}^4 \nonumber \\&\times \left( (\beta +2) r^5 r_{0}^4 \phi +2 \alpha \right. \nonumber \\&\times \left( 2 (\beta +1) \zeta r \left( r^4+r_{0}^5\right) -4 \zeta ^2 \left( r^4+r_{0}^5\right) \right. \nonumber \\&\left. \left. +\beta r^2 \left( r^4+r r_{0}^4 +r_{0}^5\right) \right) \right) \nonumber \\&-L \Big [2 (\beta +2) r^5 r_{0}^4 \phi \left( r^4+r_{0}^5\right) \nonumber \\&+\alpha \Big [2 \zeta r \Big [(\beta +1) r^8+ (\beta -4) r^5 r_{0}^4+2 (\beta +1) r^4 r_{0}^5 \nonumber \\&+(\beta +1) r_{0}^{10}\Big ]-4 \zeta ^2 \Big [r^8+r^5 r_{0}^4+2 r^4 r_{0}^5 +r_{0}^{10}\Big ]\nonumber \\&+\beta r^2 \Big [r^8-10 r^5 r_{0}^4+2 r^4 r_{0}^5+4 r r_{0}^9\nonumber \\&+r_{0}^{10}\Big ]\Big ]\Big ]+(\beta +2) r^5 \phi \left( r^4+r_{0}^5\right) ^2\nonumber \\&+2 \alpha r^3 \Big [\beta r_{0}^5 \left( r_{0}^5-5 r^4\right) \nonumber \\&+\zeta r^3 \left( \beta r^4+(\beta -4) r_{0}^5 \right) \nonumber \\&-2 \zeta ^2 r^2 \left( r^4+r_{0}^5\right) \Big ]\Big ]. \end{aligned}$$

(50)

Appendix II

$$\begin{aligned} g_1(r)= & {} \frac{r}{\frac{r^5}{r_{0}^4 (r_{0}-L)+r^4}-L},\quad g_2(r)=L-\frac{r^5}{r_{0}^4 (r_{0}-L)+r^4},\\ g_3(r)= & {} \frac{4 \alpha (3 \beta -4) \left( \sqrt{g_{1}(r)}-1 \right) ^{2} (2 \zeta +r)}{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) },\\ g_4(r)= & {} \Big [L^3 r_{0}^8-2 L^2 r_{0}^4 \left( r^4+r_{0}^5\right) \\&+ L \left( r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5+r_{0}^{10}\right) +4 r^5 r_{0}^5\Big ],\\ g_5(r)= & {} \frac{16 \alpha \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( (\beta -2) \sqrt{g_{1}(r)}+2\right) }{r^2},\;\;\;\;\;\\ g_6(r)= & {} \frac{8 \alpha \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( 3 \beta \left( \sqrt{g_{1}(r)}-3\right) +8\right) }{r},\\ g_7(r)= & {} 48 \alpha \beta (g_{1}(r))^{3/2}+160 \alpha \beta \sqrt{g_{1}(r)}\\&-\frac{256 \alpha \zeta \sqrt{g_{1}(r)}}{r}- 64 \alpha (g_{1}(r))^{3/2}\\&-192 \alpha \sqrt{g_{1}(r)}-\frac{\beta r^6 \phi }{(g_{2}(r))^2}\\&+\frac{2 r^6 \phi }{(g_{2}(r))^2}-\frac{4 \alpha \beta r^2}{(g_{2}(r))^2}+\frac{8 \alpha r^2}{(g_{2}(r))^2}\\&+\frac{96 \alpha \beta \zeta }{g_{2}(r)}+\frac{144 \alpha \beta r}{g_{2}(r)}-\frac{128 \alpha \zeta }{g_{2}(r)}\\&-\frac{176 \alpha r}{g_{2}(r)}-\frac{96 \alpha \beta \zeta }{r}+\frac{128 \alpha \zeta }{r},\\ g_8(r)= & {} \frac{4 \alpha \beta \left( \sqrt{g_1(r)}-1\right) ^2 (2 \zeta +r)}{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) },\\ g_9(r)= & {} \Big [L^3 r_{0}^8-2 L^2 r_{0}^4\left( r^4+r_{0}^5\right) \\&+L \left( r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5+r_{0}^{10}\right) +4 r^5 r_{0}^5\Big ],\\ g_{10}(r)= & {} \frac{16 \alpha \zeta ^2 \left( \sqrt{g_1(r)}-1\right) \left( -4 \beta +(\beta -2) \sqrt{g_1(r)}+6\right) }{r^2},\\ g_{11}(r)= & {} \frac{8 \alpha \zeta \left( \sqrt{g_1(r)}-1\right) \left( -11 \beta +3 (3 \beta -4) \sqrt{g_1(r)}+12\right) }{r},\\ g_{12}(r)= & {} 16 \alpha \beta (g_1(r))^{3/2}+96 \alpha \beta \sqrt{g_1(r)}\\&-64 \alpha \sqrt{g_1(r)}+\frac{\beta r^6 \phi }{(g_2(r))^2}\\&-\frac{2 r^6 \phi }{(g_2(r))^2}+\frac{4 \alpha \beta r^2}{(g_2(r))^2}-\frac{8 \alpha r^2}{(g_2(r))^2}\\&+\frac{32 \alpha \beta \zeta }{g_2(r)}+\frac{80 \alpha \beta r}{g_2(r)}\\&-\frac{48 \alpha r}{g_2(r)}-\frac{32 \alpha \beta \zeta }{r},\\ g_{13}(r)= & {} \Big [4 \alpha \left( \frac{4 r^5 r_{0}^4 (L-r_{0})}{\left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}-L\right) \\&\times \Big [\frac{4 (\beta -1) \zeta ^2 \left( 2 \sqrt{g_{1}(r)}-3\right) }{r^2}\\&-\frac{2 \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( -8 \beta +(2 \beta -3) \sqrt{g_{1}(r)}+9\right) }{r}\\&+(6-5 \beta ) \left( \sqrt{g_{1}(r)}-1\right) ^2\Big ]\Big ],\\ g_{14}(r)= & {} \frac{8 \alpha \zeta \left( \sqrt{g_{1}(r)}-1\right) }{r} \Big [-3 \beta +(\beta +2) \sqrt{g_{1}(r)}\\&-\frac{4 (\beta -1) r}{g_{2}(r)}-\frac{16 (\beta -1) \zeta }{r}+2\Big ],\\ g_{15}(r)= & {} \frac{32 \alpha (\beta -1) \zeta ^3 \left( \sqrt{g_{1}(r)}-1\right) }{r^3}\\&- \frac{16 \alpha \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( -\beta +(2 \beta -3) \sqrt{g_{1}(r)}+3\right) }{r^2}\\&-\frac{128 \alpha \beta \zeta \sqrt{g_{1}(r)}}{r},\\ g_{16}(r)= & {} 16 \alpha \beta (g_{1}(r))^{3/2}-32 \alpha \beta \sqrt{g_{1}(r)}\\&+ \frac{192 \alpha \zeta \sqrt{g_{1}(r)}}{r}+64 \alpha \sqrt{g_{1}(r)}\\&+\frac{\beta r^6 \phi }{(g_{2}(r))^2}-\frac{2 r^6 \phi }{(g_{2}(r))^2}\\&-\frac{12 \alpha \beta r^2}{(g_{2}(r))^2}+\frac{8 \alpha r^2}{(g_{2}(r))^2}\\&-\frac{64 \alpha \beta \zeta }{g_{2}(r)}-\frac{16 \alpha \beta r}{g_{2}(r)}+\frac{96 \alpha \zeta }{g_{2}(r)}\\&+\frac{48 \alpha r}{g_{2}(r)}+\frac{64 \alpha \beta \zeta }{r}-\frac{96 \alpha \zeta }{r}. \end{aligned}$$

Appendix III

$$\begin{aligned}&\rho +p_r=\frac{\alpha (g_{2}(r))^2}{(\beta -2) (\beta -1) r^6} \Big [-24 \beta +\frac{\beta \left( \sqrt{g_{1}(r)}-1\right) ^2 (2 \zeta +r)}{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) } \Big [L^3 r_{0}^8-2 L^2 r_{0}^4 \left( r^4+r_{0}^5\right) \nonumber \\&\quad + L \left( r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5+r_{0}^{10}\right) +4 r^5 r_{0}^5\Big ]+\frac{(3 \beta -4) \left( \sqrt{g_{1}(r)}-1\right) ^2 (2 \zeta +r)}{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) }\nonumber \\&\quad \times \Big [L^3 r_{0}^8- 2 L^2 r_{0}^4 \left( r^4+r_{0}^5\right) +L \left( r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5+r_{0}^{10}\right) +4 r^5 r_{0}^5\Big ]+\frac{4 \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( (\beta -2) \sqrt{g_{1}(r)}+2\right) }{r^2}\nonumber \\&\quad -\frac{4 \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( -4 \beta +(\beta -2) \sqrt{g_{1}(r)}+6\right) }{r^2}+\frac{64 \beta \zeta \sqrt{g_{1}(r)}}{r} -\frac{2 \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( 3 \beta \left( \sqrt{g_{1}(r)}-3\right) +8\right) }{r}\nonumber \\&\quad -\frac{2 \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( -11 \beta +3 (3 \beta -4) \sqrt{g_{1}(r)}+12\right) }{r} +16 \beta (g_{1}(r))^{3/2}+64 \beta \sqrt{g_{1}(r)}-\frac{64 \zeta \sqrt{g_{1}(r)}}{r}\nonumber \\&-16 (g_{1}(r))^{3/2}-64 \sqrt{g_{1}(r)}+\frac{32 \beta \zeta }{g_{2}(r)}+\frac{56 \beta r}{g_{2}(r)}-\frac{32 \zeta }{g_{2}(r)} -\frac{56 r}{g_{2}(r)}-\frac{32 \beta \zeta }{r}+\frac{32 \zeta }{r}+24\Big ], \end{aligned}$$

(51)

$$\begin{aligned}&\rho -p_r=\frac{(g_{2}(r))^2}{2 (\beta -2) (\beta -1) r^6} \Big [-12 \alpha \beta +24 \alpha +\frac{2 \alpha (3 \beta -4) \left( \sqrt{g_{1}(r)}-1\right) ^2 (2 \zeta +r)}{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) } \Big [L^3 r_{0}^8-2 L^2 r_{0}^4\nonumber \\&\quad \times \left( r^4+r_{0}^5\right) +L \left( r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5+r_{0}^{10}\right) +4 r^5 r_{0}^5\Big ]-\frac{2 \alpha \beta \left( \sqrt{g_{1}(r)}-1\right) ^2 (2 \zeta +r)}{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) }\nonumber \\&\quad \times \Big [L^3 r_{0}^8-2 L^2 r_{0}^4 \left( r^4+r_{0}^5\right) +L \left( r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5+r_{0}^{10}\right) +4 r^5 r_{0}^5\Big ]\nonumber \\&\quad +\frac{8 \alpha \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( (\beta -2) \sqrt{g_{1}(r)}+2\right) }{r^2} +\frac{8 \alpha \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( -4 \beta +(\beta -2) \sqrt{g_{1}(r)}+6\right) }{r^2}\nonumber \\&\quad +\frac{4 \alpha \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( -11 \beta +3 (3 \beta -4) \sqrt{g_{1}(r)}+12\right) }{r}+\frac{64 \alpha \beta \zeta \sqrt{g_{1}(r)}}{r}-\frac{4 \alpha \zeta \left( \sqrt{g_{1}(r)}-1\right) }{r}\nonumber \\&\quad \times \left( 3 \beta \left( \sqrt{g_{1}(r)}-3\right) +8\right) +16 \alpha \beta (g_{1}(r))^{3/2} +32 \alpha \beta \sqrt{g_{1}(r)}-\frac{128 \alpha \zeta \sqrt{g_{1}(r)}}{r}-32 \alpha (g_{1}(r))^{3/2}-64 \alpha \sqrt{g_{1}(r)} \nonumber \\&\quad -\frac{\beta r^6 \phi }{(g_{2}(r))^2} +\frac{2 r^6 \phi }{(g_{2}(r))^2}-\frac{4 \alpha \beta r^2}{(g_{2}(r))^2}+\frac{8 \alpha r^2}{(g_{2}(r))^2} +\frac{32 \alpha \beta \zeta }{g_{2}(r)}+\frac{32 \alpha \beta r}{g_{2}(r)} -\frac{64 \alpha \zeta }{g_{2}(r)}-\frac{64 \alpha r}{g_{2}(r)}-\frac{32 \alpha \beta \zeta }{r}+\frac{64 \alpha \zeta }{r}\Big ], \end{aligned}$$

(52)

$$\begin{aligned}&\rho +p_t=\frac{\alpha (g_{2}(r))^2 }{(\beta -2) (\beta -1) r^6}\Big [-12 \beta +\frac{\left( \frac{4 r^5 r_{0}^4 (L-r_{0})}{\left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}-L\right) }{g_{2}(r)} \Bigg [\frac{4 (\beta -1) \zeta ^2 \left( 2 \sqrt{g_{1}(r)}-3\right) }{r^2}\nonumber \\&\quad -\frac{2 \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( -8 \beta +(2 \beta -3) \sqrt{g_{1}(r)}+9\right) }{r} +(6-5 \beta ) \left( \sqrt{g_{1}(r)}-1\right) ^2\Bigg ]\nonumber \\&\quad +\frac{2 \zeta \left( \sqrt{g_{1}(r)}-1\right) }{r}\times \Big [-3 \beta +(\beta +2) \sqrt{g_{1}(r)}-\frac{4 (\beta -1) r}{g_{2}(r)}-\frac{16 (\beta -1) \zeta }{r}+2\Big ]\nonumber \\&\quad +\frac{(3 \beta -4) \left( \sqrt{g_{1}(r)}-1\right) ^2 (2 \zeta +r) \left( L^3 r_{0}^8-2 L^2 r_{0}^4 \left( r^4+r_{0}^5\right) +L \left( r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5+r_{0}^{10}\right) +4 r^5 r_{0}^5\right) }{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) }\nonumber \\&\quad +\frac{8 (\beta -1) \zeta ^3 \left( \sqrt{g_{1}(r)}-1\right) }{r^3} +\frac{4 \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( (\beta -2) \sqrt{g_{1}(r)}+2\right) }{r^2}-\frac{4 \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) }{r^2} \Big [-\beta \nonumber \\&\quad +(2 \beta -3) \sqrt{g_{1}(r)}+3\Big ] +\frac{16 \beta \zeta \sqrt{g_{1}(r)}}{r} -\frac{2 \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( 3 \beta \left( \sqrt{g_{1}(r)}-3\right) +8\right) }{r} +16 \beta (g_{1}(r))^{3/2}\nonumber \\&\quad +32 \beta \sqrt{g_{1}(r)}-\frac{16 \zeta \sqrt{g_{1}(r)}}{r}-16 (g_{1}(r))^{3/2}-32 \sqrt{g_{1}(r)} -\frac{4 \beta r^2}{(g_{2}(r))^2}+\frac{4 r^2}{(g_{2}(r))^2} +\frac{24 \beta \zeta }{g_{2}(r)}-\frac{16 \beta \zeta }{g_{2}(r)} +\frac{36 \beta r}{g_{2}(r)}\nonumber \\&\quad -\frac{4 \beta r}{g_{2}(r)}-\frac{8 \zeta }{g_{2}(r)}-\frac{32 r}{g_{2}(r)} -\frac{8 \beta \zeta }{r}+\frac{8 \zeta }{r}+12\Big ], \end{aligned}$$

(53)

$$\begin{aligned}&\rho -p_t=\frac{(g_{2}(r))^2}{2 (\beta -2) (\beta -1) r^6} \Big [-36 \alpha \beta +48 \alpha -\frac{2 \alpha \left( \frac{4 r^5 r_{0}^4 (L-r_{0})}{\left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}-L\right) }{g_{2}(r)} \Big [\frac{4 (\beta -1) \zeta ^2 \left( 2 \sqrt{g_{1}(r)}-3\right) }{r^2}\nonumber \\&\quad -\frac{2 \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( -8 \beta +(2 \beta -3) \sqrt{g_{1}(r)}+9\right) }{r}+(6-5 \beta ) \left( \sqrt{g_{1}(r)}-1\right) ^2\Big ]-\frac{4 \alpha \zeta \left( \sqrt{g_{1}(r)}-1\right) }{r}\nonumber \\&\quad \times \left( -3 \beta +(\beta +2) \sqrt{g_{1}(r)}-\frac{4 (\beta -1) r}{g_{2}(r)}-\frac{16 (\beta -1) \zeta }{r}+2\right) \nonumber \\&\quad +\frac{2 \alpha (3 \beta -4) \left( \sqrt{g_{1}(r)}-1\right) ^2 (2 \zeta +r) \left( L^3 r_{0}^8-2 L^2 r_{0}^4 \left( r^4+r_{0}^5\right) +L \left( r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5+r_{0}^{10}\right) +4 r^5 r_{0}^5\right) }{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) }\nonumber \\&\quad -\frac{16 \alpha (\beta -1) \zeta ^3 \left( \sqrt{g_{1}(r)}-1\right) }{r^3} +\frac{8 \alpha \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( (\beta -2) \sqrt{g_{1}(r)}+2\right) }{r^2} +\frac{8 \alpha \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) }{r^2}\nonumber \\&\quad \times \left( -\beta +(2 \beta -3) \sqrt{g_{1}(r)}+3\right) \frac{160 \alpha \beta \zeta \sqrt{g_{1}(r)}}{r} -\frac{4 \alpha \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( 3 \beta \left( \sqrt{g_{1}(r)}-3\right) +8\right) }{r}\nonumber \\&\quad + 16 \alpha \beta (g_{1}(r))^{3/2}+96 \alpha \beta \sqrt{g_{1}(r)} -\frac{224 \alpha \zeta \sqrt{g_{1}(r)}}{r}-32 \alpha (g_{1}(r))^{3/2}-128 \alpha \sqrt{g_{1}(r)} -\frac{\beta r^6 \phi }{(g_{2}(r))^2} +\frac{2 r^6 \phi }{(g_{2}(r))^2}\nonumber \\&\quad +\frac{4 \alpha \beta r^2}{(g_{2}(r))^2}+\frac{48 \alpha \beta \zeta }{g_{2}(r)}+\frac{32 \alpha \beta \zeta }{g_{2}(r)}+\frac{72 \alpha \beta r}{g_{2}(r)} +\frac{8 \alpha \beta r}{g_{2}(r)} - \frac{112 \alpha \zeta }{g_{2}(r)}-\frac{112 \alpha r}{g_{2}(r)} -\frac{80 \alpha \beta \zeta }{r}+\frac{112 \alpha \zeta }{r}\Big ], \end{aligned}$$

(54)

$$\begin{aligned}&\rho +p_r+2p_t=\frac{(g_{2}(r))^2}{2 (\beta -2) (\beta -1) r^6} \Big [-36 \alpha \beta +24 \alpha +\frac{4 \alpha \left( \frac{4 r^5 r_{0}^4 (L-r_{0})}{\left( r_{0}^4 (r_{0}-L)+r^4\right) ^2}-L\right) }{g_{2}(r)} \times \Big [\frac{4 (\beta -1) \zeta ^2 \left( 2 \sqrt{g_{1}(r)}-3\right) }{r^2}\nonumber \\&\quad -\frac{2 \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( -8 \beta +(2 \beta -3) \sqrt{g_{1}(r)}+9\right) }{r} +(6-5 \beta ) \left( \sqrt{g_{1}(r)}-1\right) ^2\Big ]+ \frac{8 \alpha \zeta \left( \sqrt{g_{1}(r)}-1\right) }{r}\nonumber \\&\quad \times \left( -3 \beta +(\beta +2) \sqrt{g_{1}(r)}-\frac{4 (\beta -1) r}{g_{2}(r)}-\frac{16 (\beta -1) \zeta }{r}+2\right) \nonumber \\&\quad +\frac{2 \alpha \beta \left( \sqrt{g_{1}(r)}-1\right) ^2 (2 \zeta +r) \left( L^3 r_{0}^8-2 L^2 r_{0}^4 \left( r^4+r_{0}^5\right) +L \left( r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5+r_{0}^{10}\right) +4 r^5 r_{0}^5\right) }{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) }\nonumber \\&\quad +\frac{2 \alpha (3 \beta -4) \left( \sqrt{g_{1}(r)}-1\right) ^2 (2 \zeta +r)}{r \left( r_{0}^4 (r_{0}-L)+r^4\right) \left( L^2 r_{0}^4-L \left( r^4+r_{0}^5\right) +r^5\right) } \times \Big [L^3 r_{0}^8-2 L^2 r_{0}^4 \left( r^4+r_{0}^5\right) +L \Big [r^8-4 r^5 r_{0}^4+2 r^4 r_{0}^5\nonumber \\&\quad + r_{0}^{10}\Big ]+4 r^5 r_{0}^5\Big ]+\frac{32 \alpha (\beta -1) \zeta ^3 \left( \sqrt{g_{1}(r)}-1\right) }{r^3} +\frac{8 \alpha \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( (\beta -2) \sqrt{g_{1}(r)}+2\right) }{r^2}\nonumber \\&\quad -\frac{8 \alpha \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) \left( -4 \beta +(\beta -2) \sqrt{g_{1}(r)}+6\right) }{r^2}-\frac{16 \alpha \zeta ^2 \left( \sqrt{g_{1}(r)}-1\right) }{r^2} \Big [-\beta +(2 \beta -3)\nonumber \\&\quad \times \sqrt{g_{1}(r)}+3\Big ]-\frac{4 \alpha \zeta \left( \sqrt{g_{1}(r)}-1\right) \left( 3 \beta \left( \sqrt{g_{1}(r)}-3\right) +8\right) }{r}\nonumber \\&\quad -\frac{4 \alpha \zeta \left( \sqrt{g_{1}(r)}-1\right) }{r} \Big [-11 \beta +3 (3 \beta -4) \sqrt{g_{1}(r)}+12\Big ] +48 \alpha \beta (g_{1}(r))^{3/2}+96 \alpha \beta \sqrt{g_{1}(r)} \nonumber \\&\quad +\frac{64 \alpha \zeta \sqrt{g_{1}(r)}}{r}-32 \alpha (g_{1}(r))^{3/2} -64 \alpha \sqrt{g_{1}(r)}+\frac{\beta r^6 \phi }{(g_{2}(r))^2} -\frac{2 r^6 \phi }{(g_{2}(r))^2}-\frac{12 \alpha \beta r^2}{(g_{2}(r))^2}+\frac{8 \alpha r^2}{(g_{2}(r))^2}\nonumber \\&\quad +\frac{64 \alpha \beta \zeta }{g_{2}(r)}-\frac{64 \alpha \beta \zeta }{g_{2}(r)}+\frac{112 \alpha \beta r}{g_{2}(r)}-\frac{16 \alpha \beta r}{g_{2}(r)}+\frac{32 \alpha \zeta }{g_{2}(r)} -\frac{64 \alpha r}{g_{2}(r)}-\frac{32 \alpha \zeta }{r}. \end{aligned}$$

(55)