1 Introduction

Deflection of light signals near massive celestial bodies was the most convincing phenomenon that helped establishing General Relativity (GR) as the correct description of gravity [1]. Nowadays deflection of signals by gravity is almost exclusively used in gravitational lensing (GL), which has become a powerful tool in astrophysics and cosmology. GL has been used to constrain not only properties of the lens, such as the mass distribution of galaxy [2,3,4], the structure of dark matter halos [5,6,7], accretion of materials [8, 9], but also those of the source, such as supernova explosion mechanism [10, 11]. Observables in GL can also correlate with properties of signal particles forming the GL images [12].

Traditionally, GL observations were always done using light signals of various wavelength. However, with the discovery of neutrinos form SN1987A [13, 14] and more recently from blazer TXS 0506 + 056 [15, 16], and the discovery of gravitational waves (GW) due to binary black hole (BH)/neutron star mergers [17,18,19], especially the GBR+GW dual observation [20], it is clear that neutrinos and GW can also act as messengers to have GL effects. Unlike light rays, both neutrinos and GWs in some theories beyond GR are timelike signals. Even for light rays in the real Universe, it was known that their propagation becomes timelike in a cold non-magnetized plasma [21]. The deflection and GL of these signals could have qualitatively different features comparing to null signals and therefore require separate treatment.

In (strong) GL observations, the apparent angle of the images and the time delay between them are two most important observables that were widely used to reveal information about the lens, source and messenger. For both neutrino and GW observatories, currently their angular resolution are both too low to distinguish different images. However, the time measurement for these signals are usually very precise, reaching \({\mathcal {O}}(1)\) [ns] for neutrino events [22, 23] and \({\mathcal {O}}(1)\) [ms] for GW observations [20]. Therefore theoretical study and corresponding observations on time delay in GLs of these signals might bear fruit earlier than resolving different images formed by them. While for light rays propagating in plasma medium, the influence of the plasma on time delay was studied for Shapiro time delay of radio signals through the solar corona [24, 25].

In this work, we study time delay of timelike and null signals with general asymptotic velocity in the strong field limit (SFL) in static and spherically symmetric (SSS) spacetimes. In this limit, the signal’s trajectory approaches the critical particle/photon sphere and the signal might loop around the central lens many time before reaching the detector, forming series of relativistic images from each side of the lens. The time delay of light signal in SSS spacetimes in this limit has been studied by Bozza in Ref. [26] as a distance estimator and then followed by many researchers in particular spacetimes or gravitational theories [27,28,29,30,31,32,33,34,35,36,37]. In this work, we not only extend it to arbitrary signal velocity, but develop a trackable way to calculate the total travel time and time delay to any desired order, which was never done before. Moreover, we also show that the time delay is given by a simple formula, Eq. (36), allowing a very simple and intuitive understanding, i.e., Eq. (37).

The work is organized as follows. In Sect. 2, we develop the perturbative method used for the computation of the total travel time in the SFL. We will show that the total travel time takes a quasi-power series form, which is then used in Sect. 3 to find the time delay between different images. We emphasize that unlike the time delay computed using numerical integration, results here are for arbitrary SSS metric and the effect of any spacetime parameter can be recognized easily from them. It is also shown that the time delay equals to the circumference of the particle sphere divided by the local velocity of the signal and then multiplied by the redshift factor and the winding number. In Sect. 4, we then apply these results to the Hayward BH spacetime and study the dependence of the time delay on the spacetime charge parameter l and signal velocity v. The result reveals that the time delay can be used to constrain l quite well but not v since for both supernova neutrinos and GWs, their speeds have been well constrained to be extremely close to light speed.

2 The perturbation method

The perturbative method we used here to calculate the total travel time is adapted from Ref. [38] which was to calculate the deflection angle in the SFL, while here this method is used to a different integral. Therefore in this section, we will first recap the essential steps to help understanding the method, and then apply it to the suitable integral defining the total travel time of the signal.

We start from the most general SSS metric described by

$$\begin{aligned} {\mathrm {d}}s^2=-A(r) {\mathrm {d}}t^2 + B(r) {\mathrm {d}}r^2 + C(r) ({\mathrm {d}}\theta ^2 + \sin ^2 \theta {\mathrm {d}}\phi ^2), \end{aligned}$$
(1)

where \((t,~r,~\theta ,~\phi )\) are coordinates and A,  B,  C are metric functions depending on r only. The corresponding geodesic equations can always be transformed to the equatorial plane \(( \theta = \pi /2)\), and then become

$$\begin{aligned}&{\dot{r}}^2 = \frac{\left( \frac{E^2}{A(r)}-\kappa \right) C(r) - L^2 }{B(r) C(r)}, \end{aligned}$$
(2)
$$\begin{aligned}&{\dot{t}} = \frac{E}{A(r)}, \end{aligned}$$
(3)
$$\begin{aligned}&{\dot{\phi }} = \frac{L}{C(r)}, \end{aligned}$$
(4)

where \(\kappa =0,~1\) for massless and massive signals respectively and L,  E are the angular momentum and energy of the signal (per unit mass). L and E can relate to the impact parameter b and the asymptotic velocity v of the signal by

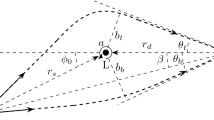
$$\begin{aligned} L=\frac{bv}{\sqrt{1-v^2}},\quad E=\frac{1}{\sqrt{1-v^2}}. \end{aligned}$$
(5)

The travel time from a source at \(r=r_s\) to a detector at \(r=r_d\) (see Fig. 1), after using Eqs.  (2) and (3), is then

$$\begin{aligned} t= & {} \sum _{i=s,d} \int _{r_0}^{r_i} \frac{{\dot{t}}}{{\dot{r}}}{\mathrm {d}}r=\sum _{i=s,d} \int _{r_0}^{r_i} \frac{E \sqrt{B(r)C(r)}}{L A(r)}\nonumber \\&\cdot \, \frac{L}{\sqrt{\left( \frac{E^2}{A(r)}-\kappa \right) C(r) - L^2 } } {\mathrm {d}}r, \end{aligned}$$
(6)

where \(r_0\) is the closest approach of the trajectory to the lens. According to Eq. (2), \(r_0\) satisfies \({\dot{r}}|_{r=r_0}=0\), i.e.,

$$\begin{aligned} \left( \frac{E^2}{A(r_0)}-\kappa \right) C(r_0) - L^2 = 0. \end{aligned}$$
(7)

Together with Eq. (5), this provides a relation connecting the closest approach \(r_0\) and the impact parameter b

$$\begin{aligned} \frac{1}{b}=\frac{\sqrt{E^2-\kappa }}{L}=\sqrt{\frac{E^2-\kappa }{\left( \frac{E^2}{A(r_0)} - \kappa \right) C(r_0) }}. \end{aligned}$$
(8)

On the other hand, when \(r_0\) or b is small enough, the signal will spiral into a compact sphere, the particle (or photon) sphere, and not escape back to infinity. The radius \(r_c\) of this sphere is defined as the critical point of the denominator of Eq. (6)

$$\begin{aligned} {\mathrm {d}}\left[ \left( \frac{E^2}{A(r)}-\kappa \right) C(r) \right] / {\mathrm {d}}r |_{r=r_c}=0. \end{aligned}$$
(9)

If \(r_0\) approaches \(r_c\) from above, we call the corresponding b the critical impact parameter and denote it by \(b_c\). Using Eq. (8), it is related to \(r_c\) by

$$\begin{aligned} \frac{1}{b_c}=\sqrt{\frac{E^2-\kappa }{\left( \frac{E^2}{A(r_c)} - \kappa \right) C(r_c) }}. \end{aligned}$$
(10)

The total travel time (6) in the SFL is difficult to compute exactly even for the simpler SSS spacetimes and therefore approximation methods are desired. In Ref. [38] we have developed a perturbative way to expand a similar integral for the computation of signal’s deflection angle. Here we adapt that method to the computation of the total travel time in the SFL. First, we define a function p(x) inspired by Eq. (8) as

$$\begin{aligned} p\left( x \right) = \frac{1}{b_c} - \sqrt{ \frac{E^2 - \kappa }{ \left( \frac{E^2}{A\left( 1/x \right) } - \kappa \right) C\left( 1/x\right) } }, \end{aligned}$$
(11)

and define its inverse function as q(x). From Eq. (8), it is clear that

$$\begin{aligned} p\left( \frac{1}{r_0}\right) =\frac{1}{b_c}-\frac{1}{b}\equiv \frac{a}{b_c}, \quad \text {where}\ a\equiv 1-\frac{b_c}{b} \end{aligned}$$
(12)

so that taking its inverse function we have

$$\begin{aligned} \frac{1}{r_0} = q\left( \frac{1}{b_c} - \frac{1}{b} \right) = q\left( \frac{1-b_c/b}{b_c} \right) . \end{aligned}$$
(13)

We then can do the following change of variables in Eq. (6) from r to \(\xi \) connected by function q or p

$$\begin{aligned} \frac{1}{r}=q\left( \frac{\xi }{b_c}\right) ,~\text {i.e.,}~p\left( \frac{1}{r}\right) =\frac{\xi }{b_c}. \end{aligned}$$
(14)

Note that although the analytical form of p(x) is clear once the metric functions are given, the inversion process to find q(x) is not always analytically possible. Fortunately, what is required in our later computation is the series expansion of q(x) and it can always be worked out using the Lagrange inversion theorem from the series form of p(x). Under this change of variables, and noticing Eqs. (11) and (12), the integration limits and various factors in the integrand of Eq. (6) are changed according to

$$\begin{aligned}&r_0 \rightarrow 1-\frac{b_c}{b}= a,~r_i \rightarrow b_c p\left( \frac{1}{r_i}\right) \equiv \eta _i,~i=s,d, \end{aligned}$$
(15a)
$$\begin{aligned}&\frac{L}{\sqrt{\left( \frac{E^2}{A(r)}-\kappa \right) C(r)-L^2}} \rightarrow \frac{1-\xi }{\sqrt{\left( \frac{b_c}{b}\right) ^2 - \left( \xi -1\right) ^2 } }, \end{aligned}$$
(15b)
$$\begin{aligned}&\frac{E \sqrt{B(r)C(r)}}{L A(r)} \rightarrow \frac{\sqrt{B(1/q)C(1/q)}}{bvA(1/q)}, \end{aligned}$$
(15c)
$$\begin{aligned}&{\mathrm {d}}r \rightarrow -\frac{q'}{q^2} \frac{{\mathrm {d}}\xi }{b_c}, \end{aligned}$$
(15d)

where \(q=q\left( \frac{\xi }{b_c}\right) \) and \(q'\) is its derivative. Here the \(\eta _{s,d}\) are nothing but the sine value of the apparent angles of the signal at the source and detector respectively [45]. In the SFL and large \(r_{s,d}\) limit, we have \(a\rightarrow 0^+\) and \(\eta _{s,d}\rightarrow 1^-\) respectively. Grouping these terms together, we obtain the transformed total travel time as

$$\begin{aligned} t= & {} \sum _{i=s,d} \int _{a}^{\eta _i} \frac{\sqrt{B(1/q)C(1/q)}}{A(1/q)} \nonumber \\&\cdot \, \frac{\xi -1}{\sqrt{\left( 2-a-\xi \right) \left( \xi -a\right) } } \cdot \frac{(1-a)q'}{vb_c^2q^2} {\mathrm {d}}\xi . \end{aligned}$$
(16)

Note that this form of t depends on the impact parameter b through the parameter a and on the source/detector radius through \(\eta _{s,d}\). Its dependence on all other parameters of the spacetime is through the metric functions and the critical impact parameter \(b_c\), which also appears in \(q=q(\xi /b_c)\).

2.1 Perturbative expansion of total travel time

The beauty of the above change of variables (14) is that it transforms the large integration range to a finite range and allow the resultant integrand to be expanded in the small \(\xi \) limit, so that an perturbative integration can be carried out.

To see how the expansion is carried out, we first split the integrand into two factors, \(\frac{1}{\sqrt{\xi -a}}\) and \(y(\xi )\) with

$$\begin{aligned} y(\xi )=\frac{\sqrt{B(1/q)C(1/q)}}{A(1/q)} \cdot \frac{\xi -1}{\sqrt{2-a-\xi } } \cdot \frac{(1-a)q'}{vb_c^2q^2}. \end{aligned}$$
(17)

The factor \(\frac{1}{\sqrt{\xi -a}}\) will be directly integrated later while the factor \(y(\xi )\) should be further treated. Since in the SFL, the main part of the total time is contributed from the integration near small \(\xi \), we can further split \(y(\xi )\) into two factors and expand them in the small \(\xi \) limit, i.e.,

$$\begin{aligned}&\frac{1}{\sqrt{2-a-\xi } }=\sum _{n=0}^{\infty } \frac{(2n-1)!!}{(2n)!!}\frac{\xi ^n}{(2-a)^{n+\frac{1}{2}}}, \end{aligned}$$
(18a)
$$\begin{aligned}&\frac{\sqrt{B(1/q)C(1/q)}}{A(1/q)} \frac{ \left( \xi -1 \right) (1-a)q'}{vb_c^2q^2} =(1-a) \sum _{n=-1}^{\infty } f_n \xi ^{\frac{n}{2}}, \end{aligned}$$
(18b)

where in Eq. (18b) the index starts from \(-1\) because of the \(q'\) term, and the \(f_n\) are the expansion coefficients that can be worked out once the metric functions are known. We point out that it is in expansion (18b) that the series form of \(q(\xi /b_c)\) is needed and can be obtained using the Lagrange inversion theorem from the series expansion of p(x). We also emphasize that the coefficients \(f_n\) will not depend on the initial/boundary conditions of the trajectory, such as the impact parameter b and \(r_{s,d}\), but only on the metric functions and spacetime parameters therein.

Collecting these expansions according to the powers of \(\xi \), we see that \(y(\xi )\) becomes

$$\begin{aligned} y(\xi )=\sum _{n=-1}^{\infty } \frac{1-a}{\left( 2-a\right) ^{[\frac{n+1}{2}]+\frac{1}{2}}} \sum _{m=0}^{[\frac{n+1}{2}]} y_{n,m} a^m \xi ^{n/2}, \end{aligned}$$
(19)

where a sum over a finite terms of \(a^m\) appears because different powers of the denominator factor \((2-a)\) in Eq. (18a) mix into the coefficient of the same \(\xi ^{n/2}\) power. The coefficients \(y_{n,m}\) can be obtained from the coefficients \(f_n\) and other factors in Eqs. (18) but their exact forms are too tedious to show here. Further substituting Eq. (19) into the total time, we finally get

$$\begin{aligned} t=\sum _{i=s,d} \sum _{n=-1}^{\infty } \sum _{m=0}^{[\frac{n+1}{2}]} \frac{1-a}{\left( 2-a\right) ^{[\frac{n+1}{2}]+\frac{1}{2}}} y_{n,m} a^m \int _{a}^{\eta _i} \frac{\xi ^{n/2}}{\sqrt{\xi -a}}{\mathrm {d}}\xi . \nonumber \\ \end{aligned}$$
(20)

The integrability of this formula relies on the integration of the form \(\int _{a}^{\eta _i} \frac{\xi ^{n/2}}{\sqrt{\xi -a}}{\mathrm {d}}\xi \). Fortunately, this kind of integrals can always be worked out for integers n, and the results are given in Eq. (A1) in Appendix A. Using these results, the total travel time t becomes

$$\begin{aligned} t&=\sum _{i=s,d} \sum _{k=0}^{\infty } \sum _{m=0}^{k} \frac{\left( 1-a\right) a^m}{\left( 2-a\right) ^{k+\frac{1}{2}}} \Bigg \{ y_{2k-1,m} \nonumber \\&\quad \cdot \,\frac{a^kC_{2k}^k}{4^k} \Bigg [ -\ln a +2 \ln \left( \sqrt{\eta _i}+\sqrt{\eta _i-a}\right) \nonumber \\&\quad +\, \sum _{j=1}^{k}\frac{ 4^j \eta _i^j }{j a^j C_{2j}^{j}} \sqrt{1-\frac{a}{\eta _i}}\,\Bigg ] + y_{2k,m} \nonumber \\&\quad \cdot \,\sum _{j=0}^{k} \frac{2 C_{k}^{j}a^{k-j}\left( \eta _i-a\right) ^{j+1/2}}{2j+1} \Bigg \}. \end{aligned}$$
(21)

Here the first and second terms in the curly bracket are due to the integration of odd and even powers of \(\xi ^{n/2}\) respectively. It is also important to notice that all the dependence of t on a and \(\eta _{s,d}\) in this formula has been shown explicitly, and the coefficients \(y_{n,m}\) only contain the signal kinetic parameter v and spacetime parameters through \(b_c\).

It is not difficult to notice that all the functions involved in t are quite elementary. Because of this, in the SFL (i.e, \(b\rightarrow b_c^+,~a\rightarrow 0^+\)), it can be further expanded into a quasi-power series of small a

$$\begin{aligned} t=\sum _{k=0}^\infty \left[ C_k \ln a+D_k(\eta _s,\eta _d)\right] a^k, \end{aligned}$$
(22)

where in the coefficient of each order of \(a^k\), there is only one term that contains \(\ln a\). The coefficients \(C_k\) and \(D_k\) can be worked out from Eq. (21) and it is seen that only the \(D_k\)’s (but not the \(C_k\)’s) depend on \(\eta _{s,d}\). This total time (22) resembles the same form as the deflection angle in the SFL in Ref. [38], although their coefficients \(C_k\) and \(D_k\) will be different. When the source and detector radius \(r_{s,d}\) are not infinite, then in the \(a\rightarrow 0\) limit, there is only one divergent term in t contributed by the \({\mathcal {O}}(a)^0\) order. To the \({\mathcal {O}} \left( a \right) ^0\) order, one can also directly recognize from Eq. (21) that only the \(m=k=0\) terms contribute. The result to this order is

$$\begin{aligned} t (r_s,r_d,b)&= \sum _{i=s,d}\left\{ - \frac{\sqrt{2}}{2} y_{-1,0} \ln a + \frac{\sqrt{2}}{2} y_{-1,0} \ln \left( 4 \eta _i \right) \right. \nonumber \\&\quad \left. +\sum _{n=0}^{\infty } \frac{y_{n,0}}{2^{\left[ \frac{n+1}{2}\right] +\frac{1}{2}}} \cdot \frac{2 \eta _i^{\frac{n+1}{2}}}{n+1} \right\} + {\mathcal {O}}\left( a\right) ^1. \end{aligned}$$
(23)
$$\begin{aligned}&= C_0\ln a +D_0(\eta _s,\eta _d)+{\mathcal {O}}\left( a\right) ^1 \end{aligned}$$
(24)

from which we can read off the coefficients \(C_0\) and \(D_0\) in Eq. (22) as

$$\begin{aligned}&C_0 = - \sqrt{2} y_{-1,0} , \end{aligned}$$
(25)
$$\begin{aligned}&D_0(\eta _s,\eta _d)=\sum _{i=s,d}\left[ \frac{\sqrt{2}}{2} y_{-1,0} \ln \left( 4 \eta _i \right) + \sum _{n=0}^{\infty } \frac{y_{n,0}}{2^{\left[ \frac{n+1}{2}\right] +\frac{1}{2}}} \cdot \frac{2 \eta _i^{\frac{n+1}{2}}}{n+1} \right] . \end{aligned}$$
(26)

Later on, we will use the total time (23) to calculate the time delay between different relativistic images in the SFL. Different images correspond to different impact parameters and consequently, different a, but their \(r_{s,d}\) and other spacetime parameters are exactly the same. This also implies that when subtracting two total times along the trajectories with slightly different b, the \(D_0\) term will not contribute to the time delay at this order.

2.2 Computing coefficients \(y_{n,m}\)

From the relation (13) and the change of variables (14) we knew that the \(\xi \rightarrow 0^+\) limit is also the \(r_0\rightarrow r_c^+,~b\rightarrow b_c^+\) limit. Therefore the expansions (18) at small \(\xi \) or equivalently the coefficients \(y_{n,m}\) should also be determined from the series expansion of the metric functions at \(r=r_c\). Assuming these expansions are

$$\begin{aligned} A(r\rightarrow r_c)&= \sum _{n=0}^{\infty } a_n (r-r_c)^n, \end{aligned}$$
(27a)
$$\begin{aligned} B(r\rightarrow r_c)&= \sum _{n=0}^{\infty } b_n (r-r_c)^n, \end{aligned}$$
(27b)
$$\begin{aligned} C(r\rightarrow r_c)&= \sum _{n=0}^{\infty } c_n (r-r_c)^n, \end{aligned}$$
(27c)

where \(a_i,~b_i\) and \(c_i\) are the coefficients, then the very definition of \(r_c\) in Eq. (9) becomes a constraint between the first few coefficients

$$\begin{aligned} c_1\left( \frac{E^2}{a_0} - \kappa \right) = \frac{a_1 c_0 E^2}{a_0^2}. \end{aligned}$$
(28)

The impact parameter in Eq. (10) can also be expressed using \(a_0\) and \(c_0\) as

$$\begin{aligned} b_c=\frac{1}{v} \sqrt{\frac{c_0}{a_0} \left( 1 - a_0 + v^2 a_0 \right) }. \end{aligned}$$
(29)

Using these metric expansions and going through the process from Eqs. (17) to (19), the \(y_{n,m}\)’s can be computed. In particular, the first two \(y_{n,0}\) are found to be

$$\begin{aligned} y_{-1,0}&=\frac{1}{\sqrt{2}v a_0} \sqrt{\frac{b_0 c_0}{T_2} }, \end{aligned}$$
(30a)
$$\begin{aligned} y_{0,0}&= -\frac{b_c \left[ \left( 2 a_1 b_0 c_0 - a_0 b_1 c_0 -a_0 b_0 c_1\right) T_2 + 2 a_0 b_0 c_0 T_3 \right] }{2 v a_0^2 \sqrt{b_0 c_0} T_2^2 }, \end{aligned}$$
(30b)

where

$$\begin{aligned} T_2&= \frac{1}{v^2 a_0} \left[ c_2 \left( 1 - a_0 + a_0 v^2 \right) - \frac{ a_1 c_1 + a_2 c_0 }{a_0} + \frac{a_1^2 c_0}{a_0^2} \right] , \end{aligned}$$
(31a)
$$\begin{aligned} T_3&= \frac{1}{v^2 a_0} \left[ c_3 \left( 1 - a_0 + a_0 v^2 \right) - \frac{ a_1 c_2 + a_2 c_1 + a_3 c_0 }{a_0}\right. \nonumber \\&\left. \quad + \frac{a_1^2 c_1 + 2 a_1 a_2 c_0 }{a_0^2} - \frac{a_1^3 c_0 }{a_0^3} \right] . \end{aligned}$$
(31b)

Higher order \(y_{n,0}~(n>0)\) and \(y_{n,m}~(m>0)\) can also be readily computed but are too long to be presented here. However from these higher orders, we are able to assert that for general n, \(y_{n,0}\) is determined by the metric expansion coefficients up to \(a_{n+3}\), \(b_{n+1}\) and \(c_{n+3}\).

3 Time delay in the SFL

In time measurement in GL, what is measured is not the total travel time but the time delay between different images of the source. For GL in the SFL, a typical path is illustrated in Fig. 1. There will exist two basic kinds of time delay: the time delay between signals from the same side of the lens but with different winding numbers around the center, and the time delay between signals from different sides of the lens but with the same winding number around the center. A general time delay, which we denote as \(\Delta t_{n,m}~(n,m\in {\mathbb {Z}})\) to represent the time delay between images winding around the center counter-clockwisely n and m times, should be a combination of the former two basic time delays. Using Eq. (24), this time difference can be written as

$$\begin{aligned} \Delta t_{n,m}= & {} t(r_s,r_d,b_n)-t(r_s,r_d,b_m)\nonumber \\= & {} C_0\ln \left[ \frac{1-b_c/b_n}{1-b_c/b_m}\right] +{\mathcal {O}}(a)^1, \end{aligned}$$
(32)

where \(b_n\) and \(b_m\) are the impact parameters of the two images. Note the \(D_0a^0\) term in Eq. (24) does not affect the time delays since it is independent of b and therefore the same for all trajectories. Furthermore, here n,  m could be negative integers if the winding is indeed clockwise (although \(b_n\) and \(b_m\) are always positive). Note that the case that winding does not actually happen corresponds to the weak field limit of the time delay and was considered in our previous work [39].

Fig. 1
figure 1

The GL in the SFL. \((r_d,\phi _d)\) and \((r_s,\phi _s)\) are respectively the radial and angular coordinates of the detector D and source S. The signal winds clockwisely one loop around the lens L. b is the impact parameter and the shadow stands for the BH

Full size image

Clearly, in order to compute the time delay, we shall find the corresponding impact parameters for the images in the SFL first. For this purpose, we will directly use the result from Eq. (38) of Ref. [38],

$$\begin{aligned} b_{n} = \frac{b_c}{1-{\mathrm {Exp}}\left[ \frac{-\left( 2|n|+1+\mathrm {sign}(n) \right) \pi +D_{a0}+\mathrm {sign}(n) \Delta \phi _{sd} }{-C_{a0}} \right] }, \end{aligned}$$
(33)

where \(\Delta \phi _{sd}=\phi _s-\phi _d\) is the difference between the angular coordinates \(\phi _s\) of the source and \(\phi _d\) of the detector (see Fig. 1). The coefficient

$$\begin{aligned} C_{a0}=-b_c\sqrt{b_0/(c_0T_2)}, \end{aligned}$$
(34)

while the coefficient \(D_{a0}\) is given in Eq. (28) of Ref. [38] and does not contribute to the time delay, as we will show in Eq. (36).

Now substituting Eq. (33) into (32) and after a small simplification we have

$$\begin{aligned} \Delta t_{n,m}= & {} \frac{2\pi C_0}{C_{a0}}\Bigg \{ \left( |n|- |m|\right) \nonumber \\&+\frac{ \left[ \mathrm {sign}(n)-\mathrm {sign}(m)\right] (\pi - \Delta \phi _{sd})}{2\pi } \Bigg \} \end{aligned}$$
(35)
$$\begin{aligned}= & {} \frac{2\pi \sqrt{c_0}}{\sqrt{1-a_0(1-v^2)}}\frac{1}{\sqrt{a_0}} \Bigg \{ \left( |n|- |m|\right) \nonumber \\&+\frac{ \left[ \mathrm {sign}(n)-\mathrm {sign}(m)\right] (\pi - \Delta \phi _{sd})}{2\pi } \Bigg \} \end{aligned}$$
(36)

where \(C_0\) in Eq. (25), \(C_{a0}\) in Eq. (34) and \(b_c\) in Eq. (29) are substituted and simplified. It is seen that the time delay depends only on the following parameters: the metric expansion coefficients \(a_0,~c_0\), the asymptotic signal velocity v and an angular factor determined by the number of loops n,  m and angular coordinate difference \(\Delta \phi _{sd}\), but not on the finite distance \(r_i\) and \(r_f\) of the source and detector.

We emphasize that this time delay is a very general result: it applies to GL with general asymptotic velocity v, general source/detector angular coordinate difference \(\Delta \phi _{sd}\), general SSS spacetime with a particle sphere and arbitrary n and m. Setting \(v=1\) in Eq. (36) reduces it to previously known result in Ref. [26] (Eq. (40) and (41)), which concentrated on null signals.

Although the source and detector in GL in the SFL are usually far from the BH center, one would expect however when the winding numbers of two signals n and m are both large (in this case, \(n,~m\ge 1\) are enough), the time delay between them, observed by a far away observer, should be equivalent to the circumference \(2\pi r_c\) of the particle sphere divided by local signal velocity \(v_l\) and then multiplied by the difference of loops \(\Delta l\) (not necessarily an integer) between the two paths, and finally the gravitational redshift factor \(\gamma \) from the particle sphere to the detector. That is, it is natural to expect that

$$\begin{aligned} \Delta t_{n,m}=\frac{2\pi r_c}{v_l} \cdot \Delta l\cdot \gamma . \end{aligned}$$
(37)

Here we show that indeed, the above is exactly the time delay result (36), which is found from more rigorous and lengthy calculations.

For arbitrary SSS spacetime, it is always possible to choose the metric function \(C(r)=r^2\) and therefore the its expansion coefficient at \(r_c\) is \(c_0=r_c^2\). That is, the particle sphere circumference \(2\pi r_c=2\pi \sqrt{c_0}\), i.e., the numerator of the first factor in Eq. (36). For the local velocity \(v_l\), in the SFL the signal circulates around the particle sphere, and therefore we only need to consider the velocity due to angular motion. In an SSS spacetime, this is given by

$$\begin{aligned} v_l=\frac{r_c{\dot{\phi }}}{\gamma _{sr}} \end{aligned}$$
(38)

where \(\gamma _{sr}=1/\sqrt{1-v_l^2}\) is the special relativity gamma factor. Then using Eqs. (4), (5) (setting b to \(b_c\)), (29), and \(c_0=r_c^2\) sequentially, it is just an elementary algebra to solve the local velocity as

$$\begin{aligned} v_l=\sqrt{1-a_0(1-v^2)}, \end{aligned}$$
(39)

which is exactly the denominator of the first factor in Eq. (36). Thirdly, the difference in the number of loops \(\Delta l\), after properly taking into account the opposite direction case, is simply the last factor of Eq. (36). Lastly, in an asymptotically flat SSS spacetime described by metric (1), the gravitational redshift factor from \(r_c\) to the detector which is located far away is simply \(1/\sqrt{A(r_c)}=1/\sqrt{a_0}\), the second factor of Eq. (36). Grouping these factors together, therefore it is verified that for general SSS spacetime and timelike or null signals, the time delay to the leading order in the SFL, Eq. (36), has a very simple and intuitive understanding, Eq. (37).

4 The Hayward BH spacetime case

In this section, we apply our result to some particular spacetimes to check its validity, and examine the effect of v, \(\Delta \phi _{sd}\), number of loops n and m, and more importantly the spacetime parameters. The spacetime we study is the Hayward BH spacetime whose metric functions are [40]

$$\begin{aligned} A(r)=1-\frac{2Mr^2}{r^3+2l^2M},\quad B(r)=\frac{1}{A(r)},\quad C(r)=r^2, \nonumber \\ \end{aligned}$$
(40)

where M is the spacetime mass and l is the charge parameter. \(|l|<4M/(3\sqrt{3}) \equiv l_c\) in order for the spacetime to be a BH one. We choose this spacetime because its gravitational lensing (not including the time delay) in the SFL was studied previously in Ref. [38] and we can directly quote the expansion coefficients near \(r_c\) of its metrics from there. Moreover, this spacetime also has a Schwarzschild limit \(l\rightarrow 0\) whose time delay in the SFL was studied for light rays [26]. Therefore, we can compare our result against it and study the effect of a nonzero charge parameter l in the Hayward spacetime.

Using Eqs. (5) and (9), the equation determining the particle sphere radius \(r_c\) of this spacetime becomes

$$\begin{aligned}&4 l^4 M^2 v^2-8 l^2 M^2 (v^2-1)r_c^2 + 4 l^2 M v^2 r_c^3\nonumber \\&\quad + 4 M^2 (v^2-1)r_c^4+M (1-4 v^2)r_c^5+ v^2r_c^6 =0. \end{aligned}$$
(41)

This is a six order polynomial of \(r_c\) whose solution does not have a closed algebraic form. However, after formally or numerically solving it, then substituting \(r_c\) into the metrics (40) and further into Eq. (10), the critical impact parameter \(b_c\) is found as

$$\begin{aligned} b_c=\sqrt{\frac{2 l^2 M v^2r_c^2 -2 M \left( v^2-1\right) r_c^4 + v^2r_c^5}{v^2 \left( 2 l^2 M-2 Mr_c^2+r_c^3 \right) } }. \end{aligned}$$
(42)

To solve the \(y_{n,m}\) that are needed in the total travel time (23) and the time delay (36), then we should expand the metric functions at \(r=r_c\) according to Eq. (27). The first few of these expansion coefficients are [38]

$$\begin{aligned} a_0=&\left( 1-\frac{2 M r_c^2}{2 l^2 M+r_c^3} \right) ,\quad a_1 = -\frac{2 M \left( 4 l^2 M r_c-r_c^4\right) }{\left( 2 l^2 M+r_c^3\right) ^2}, \nonumber \\ a_2=&-\frac{2 M \left( 4 l^4 M^2-14 l^2 M r_c^3+r_c^6\right) }{\left( 2 l^2 M+r_c^3\right) ^3}, \end{aligned}$$
(43a)
$$\begin{aligned} b_0\,=\,&\frac{2 l^2 M+r_c^3}{2 l^2 M-2 M r_c^2+r_c^3}, \end{aligned}$$
(43b)
$$\begin{aligned} c_0\, =\,&r_c^2,~c_1=2 r_c,~c_2=1. \end{aligned}$$
(43c)

Substituting them into Eqs. (30) and (31), we can obtain the coefficients \(y_{n,0}\) for the Hayward spacetime. The first two of them, denoted as \(y_{-1,0,{\mathrm {H}}}\) and \(y_{0,0,{\mathrm {H}}}\), are

$$\begin{aligned} y_{-1,0,{\mathrm {H}}}&=\frac{r_c}{v \sqrt{2 T_2} } \left[ \frac{ 2 l^2 M+r_c^3}{2 l^2 M+r_c^2 (r_c-2 M)} \right] ^{3/2}, \end{aligned}$$
(44a)
$$\begin{aligned} y_{0,0,{\mathrm {H}}}&=\frac{b_c\sqrt{2 l^2 M+r_c^3} }{v T_2^2 \left[ 2 l^2 M+r_c^2 (r_c-2 M)\right] ^{5/2} }\nonumber \\&\quad \times \left\{ 4 l^4 M^2 (T_2-r_c T_3)+4 l^2 M r_c^2 \left[ M (r_c T_3+2 T_2) \right. \right. \nonumber \\&\left. \quad +r_c (T_2-r_c T_3)\right] \nonumber \\&\left. \quad +r_c^5 \left[ M (2 r_c T_3-5 T_2)+r_c (T_2-r_c T_3)\right] \right\} , \end{aligned}$$
(44b)

where

$$\begin{aligned} T_2&=r_c^2 + \frac{2 M r_c^4}{v^2 \left[ 2 l^2 M-2 Mr_c^2+r_c^3\right] }, \end{aligned}$$
(45a)
$$\begin{aligned} T_3&=\frac{1}{v^2 \left( 2 l^2 M-2 Mr_c^2+r_c^3 \right) ^2} \nonumber \\&\quad \times \left[ 8 v^2 l^4 M^2 r_c + 16 \left( 1-v^2\right) l^2 M^2 r_c^3 + 8 v^2 l^2 M r_c^4 \right. \nonumber \\&\left. \quad - 8 \left( 1 - v^2\right) M^2 r_c^5 + 2 M \left( 1-4 v^2\right) r_c^6 +2 v^2 r_c^7 \right] . \end{aligned}$$
(45b)

High order \(y_{n,0,{\mathrm {H}}} ~(n>0)\) can also be obtained by similar calculation but are too long to be shown here. The total travel time in the SFL in the Hayward spacetime can then be obtained from Eq. (23)

$$\begin{aligned} t(r_s,r_d,b)= & {} \sum _{i=s,d} \left\{ - \frac{\sqrt{2}}{2} y_{-1,0,{\mathrm {H}}} \ln a + \frac{\sqrt{2}}{2} y_{-1,0,{\mathrm {H}}} \ln \left( 4 \eta _{i} \right) \right. \nonumber \\&\left. + \sum _{n=0}^{\infty } \frac{y_{n,0,{\mathrm {H}}}}{2^{\left[ \frac{n+1}{2}\right] +\frac{1}{2}}} \cdot \frac{2 \eta _{i}^{\frac{n+1}{2}}}{n+1}\right\} . \end{aligned}$$
(46)

Substituting metric expansion coefficients (43) into Eq. (36), the time delay in the Hayward spacetime is simplified to

$$\begin{aligned} \Delta t_{n,m,{\mathrm {H}}}=&\frac{2\pi r_c \left( 2 l^2 M+r_c^3\right) }{2 l^2 M+r_c^2 (r_c-2 M)} \left[ \frac{2 M r_c^2}{2 l^2 M+r_c^2 (r_c-2 M)}+v^2 \right] ^{-\frac{1}{2}} \nonumber \\&\times \left\{ \left( |n|- |m|\right) +\frac{ \left[ \mathrm {sign}(n)-\mathrm {sign}(m)\right] (\pi - \Delta \phi _{sd})}{2\pi } \right\} . \end{aligned}$$
(47)

This time delay depends on a few kinds of parameters: the spacetime parameters including its mass M and charge l, the signal property – its speed v, the winding numbers n and m, and the source/detector angular coordinate difference \(\Delta \phi _{sd}\) when n and m are not the same direction. Among these, the mass M provides an overall scale for the time delay. As pointed out in Sect. 3, the first line of Eq. (47) actually is the time interval cost for the signal to loop one cycle around the particle/photon sphere. In Schwarzschild spacetime, this time interval for light would be \(2\pi r_{c,{\mathrm {S}}}/ \sqrt{1-2M/r_{c,{\mathrm {S}}}}=6\sqrt{3}M\) where \(r_{c,{\mathrm {S}}}=3M\) for photon sphere in this spacetime. The charge l is the main parameter characterizing this spacetime and v is the parameter different from usual GL by light signal. As l deviates from zero or v from 1, then this time interval also changes from the above value in a way dictated by the first line of Eq. (47).

Fig. 2
figure 2

Total travel time in Hayward spacetime as a function of b using truncated series (48) (dashed or dotted lines) and the exact result using numerical integration of Eq. (6) (the solid line). Inset: the ratio between the result truncated at order 10 and the numerical integral

Full size image

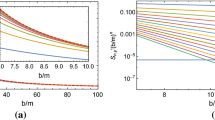
To verify whether the time delay Eq. (46) is accurate, we can first truncate the sum in its second term to order m and define

$$\begin{aligned} t_m(r_s,r_d,b)= & {} \sum _{i=s,d} \left\{ - \frac{\sqrt{2}}{2} y_{-1,0,{\mathrm {H}}} \ln a + \frac{\sqrt{2}}{2} y_{-1,0,{\mathrm {H}}} \ln \left( 4 \eta _{i} \right) \right. \nonumber \\&\left. + \sum _{n=0}^{m} \frac{y_{n,0,{\mathrm {H}}}}{2^{\left[ \frac{n+1}{2}\right] +\frac{1}{2}}} \cdot \frac{2 \eta _{i}^{\frac{n+1}{2}}}{n+1}\right\} , \end{aligned}$$
(48)

and then compare \(t_m(r_s,r_d,b)\) with the total time \(t_{{\mathrm {num}}}(r_s,r_d,b)\) obtained directly from numerical integration of Eq. (6). As long as the numerical integration is done to high enough precision, \(t_{\mathrm {num}}\) can be thought as the true value of the total travel time. In Fig. 2, we plot \(t_1,~t_5,~t_{10},~t_{20},~t_{30}\) as well as \(t_{\mathrm {num}}\) for b around \(b_c\), which is about 5.19M when we set \(l=0.1M\) and \(r_s=r_d=20M,~v=1\). It is seen that as the truncation order increases, the total time approaches its true value for all b considered, and \(t_{30}\) is non-distinguishable from \(t_{\mathrm {num}}\) in the plot. Moreover, in the inset we see that for any fixed truncation order (we took \(t_{10}\) as an example), the smaller the \(b-b_c\), the better it approximates the true value of the travel time. We also point out here that one of the advantage of the series form of the total time and time delay such as Eqs. (46) and (47) over the numerical integration method, is that the former can produce a result to high accuracy very easily because the allowed order can be very high and the involved computations are only algebraic. While the accuracy of the numerical integration method is often hindered by the singularity of the integral near \(b\rightarrow b_c\) and the smallness or largeness of the astronomical quantities used, such as the angular position of the signal source, the mass and distance of the galaxy etc.

Although the truncated \(t_m(r_s, r_d, b)\) in Eq. (48) approximates the true value pretty well in Fig. 2 in the SFL, the location of the source and especially the detector used there is much smaller than their practical values. When \(r_d/M\) (and \(r_s/M\)) is as large as in any practical GL, a numerical study shows that to achieve the same accuracy in the total travel time as in Fig. 2, the truncation order of \(t_m(r_s, r_d, b)\) would be formidably high, even in the SFL. Fortunately, this will not affect the accuracy of the time delay (36) because in the SFL, the time delay between different trajectories mainly happens when the signal is very close to the particle sphere, for which part the total time (48) is a very good approximation. In other words, for any two trajectories, the travel times corresponding to the parts from large \(r_d\) or \(r_s\) to some small radius – below which the time delay happens – cancel out. This indeed leaves the time delay formula (36) very accurate even we truncated at a relatively low order, as can be seen from Fig. 3.

Fig. 3
figure 3

a The radius of the particle sphere as a function of spacetimes parameter l and signal velocity v. Time delay between signals from same side but with different winding numbers as a function of: b l while holding \(v=1\) and; c v while holding \(l/M=0.1\). In d, the time delay as a function of \(\Delta \phi _{sd}\) for signals from opposite sides but with the same absolute wind number, with parameter \(l/M=0.1,~v=1\) and \(r_s=r_d=r_{\mathrm {Sgr~A*}}\) and \(n>0\)

Full size image

The effects of the spacetime charge l and signal velocity v, as well as \(\Delta \phi _{sd}\) when \(\mathrm {sign}(n)\ne \mathrm {sign}(m)\) are shown in Fig. 3b–d by assuming that the Sgr A* supermassive BH is a Hayward BH. To help understanding these effects, we first plot the particle sphere radius \(r_c\) as a function of l/M and v in Fig. 3a. It is seen that for any particular signal velocity, as the charge l increases from 0 to \(l_c=4/(3\sqrt{3}M)\), \(r_c\) decreases monotonically from its Schwarzschild value to a minimal value. In particular, for light signal, this is from 3M to about 2.65M. For fixed l and decreasing v on the other hand, \(r_c\) increases from its light signal value to a larger but still finite radius. Comparing to the Reissner–Nordström spacetime, we see that the effects of l and v on \(r_c\) are qualitatively similar to those of the electrostatic charge and particle velocity in that spacetime [41].

Then for the time delay \(\Delta t_{n,m,{\mathrm {H}}}\) in Eq. (47), it is clear that as l increases to \(l_c\), \(r_c\) decreases and changes of terms in both the denominator and numerator of the first factor cancel to a large extent. Therefore this factor has a very minimal variation. Similar trend happens for the second term and therefore the time delay depends relatively weakly on l, as can be seen from Fig. 3b. In the entire range of l from 0 to \(l_c\), the time delay \(\Delta t_{n,m,{\mathrm {H}}}\) for light signals from the same side of the lens changes from \(0.183|n-m|\) [h] to \(0.163|n-m|\) [h], a difference of \(7.20\times 10^1\) [s] per loop. For the signal velocity, it is seen that as v/c decreases from 1 to 0.5, the time delay increases from \(0.183|n-m|\) [h] to \(0.227|n-m|\) [h], a difference of \(2.64\times 10^2\) [s] per loop. From the time measurement perspective, fortunately both these two changes per loop are well resolvable, as long as the characteristic time scale of the source event is not larger than these values. Events satisfying this certainly include typical supernova explosion and binary BH/neutron star merger, whose characteristic time scale are maximally \(\sim 10\) s [42] and \(0.1\sim 1\) s respectively. Therefore their observation might be used to constrain the value of parameter l to good accuracy.

While to constrain signal velocity, for typical supernova neutrinos with energy at the \({\mathcal {O}}(10)\) [MeV] level, their velocity can only deviate from light speed by \(1.25\times 10^{-17}c\) at most [43] and speed of GW has already been constrained to be within \(3\times 10^{-15}c\) from light speed [20]. For these velocities, using plot Fig. 3c one can estimate the maximal difference between the time delays of these timelike signals and that of the light signal. For the former, this difference is only about \(6.60\times 10^{-15}\) [s] and for the latter \(1.58\times 10^{-12}\) [s]. These are not only much shorter than characteristic time scale of supernova and binary merger, but also smaller by several orders than the corresponding detector resolution (\({\mathcal {O}}(1)\) [ns] for neutrino observatories and \({\mathcal {O}}(1)\) [ms] for GW detectors [20]). Therefore using time delay caused by Sgr A* in the SFL to constrain speed of such ultra-relativistic signals seems not likely.

Finally, for the case of signals from opposite sides of the lens, i.e., \(\mathrm {sign}(n)\ne \mathrm {sign}(m)\), the dependence of the time delay on \(\Delta \phi _{sd}\) is shown in Fig. 3d. When \(n=-m\) and \(\Delta \phi _{sd}=\pi \), i.e., the source is perfectly aligned along the observer-lens axis and the trajectories from two sides have a mirror symmetry, then clearly we should have \(\Delta t_{-m,m,{\mathrm {H}}}(\Delta \phi _{sd}=\pi )=0\), as shown in Fig. 3d. Unlike GL in the weak field limit, angle \(\Delta \phi _{sd}\) does not need to be very close to \(\pi \) if GL in the SFL can really be observed in the future. As \(\Delta \phi _{sd}\) deviates from \(\pi \), the time delay \(\Delta t_{-1,1,{\mathrm {H}}}\) becomes linear to \((\Delta \phi _{sd}-\pi )\). The arrival time of the each series of images from one side of the lens will form an arithmetic sequence which is equivalent to \(\Delta t_{n,1,{\mathrm {H}}}~(n=2,3,\ldots )\) or \(\Delta t_{n,-1,{\mathrm {H}}}~(n=-2,-3,\ldots )\). The two sequences from two sides will have a relative shift \(\Delta t_{-n,n,{\mathrm {H}}}\) that is linear to \((\Delta \phi _{sd}-\pi )\) too, as shown in Fig. 3d. Because of this relation, it is seen that for a given characteristic time scale of the source event or observatory time resolution (whichever is larger), there exist a minimal \(\Delta \phi _{sd}-\pi \) that allows the two sequences to be temporally separated. Taking 2 [ms] for the time resolution of GW signal as an example, then it is seen that for the two sequence to be separated by this interval, \(|\Delta \phi _{sd}-\pi | \) has to be larger than 2 [\(''\)]. On the other hand, if GL of an event is to be both observed in the weak field limit and temporally resolved in the SFL, then since GL in the weak field limit are usually observed for \(\beta \lesssim 10\) [\(''\)] [47] or roughly \(\Delta \phi _{sd}\lesssim 20\) [\(''\)], Fig. 3d implies that both the characteristic time scale of the event and the observatory time resolution have to be smaller than 20 [ms]. Therefore temporally resolving the two sequences from two sides certainly imposes stringent requirement on the time measurement uncertainty of observatories, e.g., the GRB measurement uncertainty which is current about 50 [ms] [44].

5 Conclusion and discussion

In this work we proposed a perturbative method to compute the total travel time t and time delay \(\Delta t\) in the SFL in SSS spacetimes for signal with arbitrary asymptotic velocity. The total travel time takes a simple quasi-power series form

$$\begin{aligned} t=\sum _{k=0}^\infty \left[ C_k\ln a +D_k\right] a^k, \end{aligned}$$
(49)

where \(a=\left( 1-\frac{b_c}{b}\right) \) and coefficients \(C_k\) and \(D_k\) can be expressed as rational functions of the metric expansion coefficients at the particle sphere radius. In the SFL, the leading contribution to t is given by the \(\ln a\) term. Using impact parameter corresponding to each relativistic image, we were able to show that \(\Delta t\) is given by Eq. (36). This result allows an intuitive and yet quantitatively precise understanding: to the leading order of a, the time delay is given by the circumference of the particle sphere divided by the local velocity of the signal and then multiplied by the winding number difference and the redshift factor from the particle sphere to the far away detector.

We applied the results of t and \(\Delta t\) to the Hayward BH spacetime. The correctness of the total travel time is verified by truncating the series to different orders. The time delay in this case is found in Eq. (46). To understand it, we first studied the dependence of the particle sphere radius \(r_c\) on the spacetime charge l and signal velocity v. It is found that as l increases or v decreases, \(r_c\) decreases or increases respectively. Assuming the Sgr A* central BH is a Hayward BH, we were able to compute \(\Delta t\) between images on the same side and opposite sides. It is found that as l increases from 0 to its critical value, the time delay per loop can vary by \(7.2\times 10^1\) [s], which is well within the time resolution of typical light, neutrino or GW observatories. Therefore measuring \(\Delta t\) caused by the Sgr A* BH will constrain its charge l very well. On the other hand, for the supernova neutrinos or GW whose velocities deviate from that of the light by \(10^{-15}\) or less, measuring difference between \(\Delta t\)’s of different signals would not further constrain their velocities, because of the time measurement accuracy/characteristic time of the corresponding events are larger by a few orders.

Regarding directions to extend the current work, the first and most straightforward one is to extend the perturbative method to the case of the equatorial plane in the stationary and axisymmetric spacetime. Based on the weak field limit experience [46], we expect that the spin parameter would play a non-trivial role in affecting the time delay between relativistic images with different winding directions. A more interesting extension is to apply the method to the time delay of asymptotically non-flat spacetimes. From the quasi-power series (22) for the total time, we saw that the coefficients \(C_k\) and \(D_k\) are completely determined by the behavior of the metric functions around the particle sphere. Although GL in the weak field limit in these spacetimes is often problematic to study due to the difficulty to take the infinite radius limit, the metric functions behave normally at small radius and therefore the SFL can still be taken. We are pursuing along these directions.