1 Introduction

The study of higher curvature corrections to the Einstein–Hilbert action is motivated by the fact that they arise in the quantization of fields in curved spacetime [1]. Thus, in recent years we have witnessed an increased interest in higher order gravity, which involves higher derivative curvature terms, and amongst the most accepted theories is the so-called Lovelock gravity. Lovelock theories are an intriguing subset of higher curvature gravity theories which were originally introduced by Lanczos [2] and rediscovered by Lovelock [3, 4] in the 1970s. The most intriguing feature of Lovelock gravity is the field equations contain only up to second-order derivatives of the metric. Besides, the theory shares a number of additional nice properties including Bianchi identities which ensure energy conservation i.e., \(\nabla ^{i}\, T_{ij}=0\) and the quantization of the linearized theory are free of ghosts [5, 6]. Thus, Lovelock gravity appears as a natural generalization of Einstein gravity provides a natural testbed for exploring the effects of higher curvature terms on gravitational physics.

However, it turns out that apart from the first two terms corresponding to the Lovelock Lagrangian the third term is a combination of the second-order curvature term, namely Gauss–Bonnet (GB) [2]. This form generates a well-known theory of Einstein–Gauss–Bonnet (EGB) gravity in which the Einstein–Hilbert action is supplemented with the quadratic curvature GB term. This type of action is derived in the low energy effective action of heterotic string theory [7, 8]. However, to get a non-trivial contribution in 4D, one can generally associate the GB term with the inclusion of a scalar field [9]. In this context many results were reported including the spherically symmetric static black hole solution [10]. Other aspects of black hole solutions have been recently considered in [11,12,13,14,15]. In Refs. [16, 17] authors have been studying black hole solutions with a source as a cloud of strings. Since then, a number of interesting solutions have been found such as geodesic motion of a Boulware–Deser black hole spacetime [18], radius of photon spheres [19], gravitational collapse of an incoherent spherical dust cloud [20,21,22,23], regular black hole solutions [24] and wormhole solution with or without a cosmological constant [25]. In addition, compact star solutions in the context of EGB gravity have been investigated in Refs. [26,27,28].

It is speculated that stars with initial mass above \(\sim \) \(8 M_{\odot }\) end their lives as compact objects: white dwarf, neutron star or black hole. Among them neutron stars (NSs), supported by neutron-degeneracy pressure, are very compact remnants of stellar evolution that ended their lives in supernova explosions [29, 30]. Thus, the physical properties and their internal structure are one of the most fascinating and far-reaching implications of our current understanding of the compact objects. But still a comprehensive picture of core-collapse supernovae of evolved massive stars is a long-standing problem in computational astrophysics.

In most of the cases it is believed that self-gravitating objects are made of an isotropic fluid source. This means that the radial and tangential pressures are equal, in general. However, recent theoretical advances predict the existence of anisotropic spherically symmetric static configuration. Such an assumption was introduced in [31] for a relativistic anisotropic sphere and showed that one can relax the upper limits imposed on the maximum value of the surface gravitational potential. This, in turn, was extended by Bowers and Liang [32], where authors developed a model for pressure anisotropy on neutron stars. Besides mathematical plausibility, this interest has partly been stimulated by the work of Ruderman [33] in the year 1972. According to him nuclear matter tends to become anisotropic at very high densities of order \(10^{15}\) g/cm\(^3\), where the nuclear interactions must be treated relativistically. Herrera and Santos [34] conjectured that anisotropic stars could exist in a strong gravity region.

In spite of this reasoning many efforts have been done to address challenges concerning anisotropic matter such as boson stars [35], gravastars [36], neutron stars [37] and so on. In relativistic context, two-fluid dark matter models have been studied for anisotropic stars [38]. Considering anisotropy within the framework of general relativity polytropic stars have been presented in [39,40,41] and references therein. Interestingly, authors have studied all static spherically symmetric anisotropic solutions in [42]. Later, an important development in the application of anisotropy in superdense matter which may lead to significant changes in the characteristics of relativistic stars, as demonstrated, in Refs. [43,44,45,46,47,48]. Within the framework of extended modified gravity theories, anisotropic stars have also been considered in [49,50,51].

In an attempt to generate exact solutions, the Minimal Geometric Deformation (MGD) was initially proposed in [52, 53] to study the exterior geometry around spherically symmetric spacetime with a perfect fluid source in the framework of Randall–Sundrum brane-world gravity. Subsequently this method was utilized by many researchers to generate and analyze physically viable models of astrophysical objects  [54,55,56,57,58]. It was shown in [59, 60] that MGD-decoupling constitutes a novel approach to extend the deformed solutions of the Einstein equations associated with the simplest gravitational source. Indeed, by using this approach, several solutions (exact and physically acceptable) have been found for interior stellar distributions, which is a difficult task due to the existence of nonlinear terms in the matter fields, see Refs. [61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83]. Moreover, the inverse problem was addressed in [84] and the extended case, i.e., a completely deformed spacetime, was developed in [85]. Besides, the MGD approach was discussed to study extensions of GR in a cosmological context [86]. Furthermore, some interesting works have been published in the context of black hole solutions in \(2+1\) and \(3+1\) dimensions [87,88,89,90,91,92], what is more, recently new hairy black hole solutions have been found in [93] and also an algorithm has been developed to convert any non-rotating black hole spacetime into a rotating one [94, 95]. Motivated by the preceding discussion, our goal in this article is to apply the MGD approach to solve the EGB field equations for a gravitational source, and then find a physically acceptable solution that represents the behavior of compact objects.

The article is organized as follows: The EGB gravity theory is briefly presented in Sect. 2. Here, we also review the main aspects related to the MGD-decoupling method. In Sect. 3 we assume the well-behaved interior spacetime geometry to guarantee a well defined horizon free spacetime. The main aim is to find the decoupling function f(r). Subsequently, we discuss two different avenues in order to close the system of equations that coming from the source term. In Sect. 4 we match of the interior solution governed by the anisotropic fluid to an exterior Boulware–Deser vacuum solution at a junction interface. In Sect. 5 we study the physical properties of compact stars that obtained from the MGD approach to gravitational decoupling in order to build an exact anisotropic solution. We discuss the difference of the EGB gravity from EGB solution through the MGD approach. In Sect. 6 we discuss the properties of the energy conditions imposed on the energy–momentum tensor, and in Sect. 7 we carry out the detailed analysis of the self-gravitating anisotropic matter configurations and its relation with the sound speeds. Finally, we conclude our findings in Sect. 8. Some relevant computations have been presented in Appendix. Here, we adopt the signature \((-, +, +, +)\), and set \(G= c = 1\).

2 Basic equations of EGB gravity

We start from the action of the 5-dimensional EGB gravity with matter field reads:

$$\begin{aligned} \mathscr {I}_{G}&=\frac{1}{16 \pi }\int d^{5}x\sqrt{-g}\left[ R-2\Lambda +\alpha \mathscr {L}_{\text {GB}} \right] + \mathscr {S}_{\text {matter}}\nonumber \\&\quad +\beta \,\int \mathscr {S}_{\theta }\sqrt{-g}~d^{5}x, \end{aligned}$$
(1)

where R and \(\Lambda \) are 5-dimensional Ricci scalar and the cosmological constant, respectively. Since, \(\mathscr {S}_{\text {matter}}\) is the Lagrangian of the matter field with \(\mathscr {S}_{\theta }\) is the Lagrangian for extra field. The coupling constant \(\alpha \) associates with the inverse string tension and is supposed to be a positive value in string theory [10] with dimension of [\(\text {length}\)]\(^2\), while \(\beta \) has no dimension. But for generality may authors have considered both cases of \(\alpha >0\) and \(\alpha < 0\) (for a few other problems with positive and negative \(\alpha \), see the subsequent discussions in [96, 97]). In this work we restrict ourselves to the case of positive \(\alpha \), see Refs. [26, 98] for the recent progress and references therein. The Gauss–Bonnet Lagrangian \(\mathscr {L}_{\text {GB}}\) is the specific combination of Ricci scalar, Ricci tensor, and Riemann curvatures, and it is given by

$$\begin{aligned} \mathscr {L}_{\text {GB}}=R^{ijkl} R_{ijkl}- 4 R^{ij}R_{ij}+ R^2. \end{aligned}$$
(2)

The equation of motion can be directly achieved from the variation of the action (1) with respect to \(g_{ij}\),

$$\begin{aligned} G_{ij}+\alpha H_{ij} = 8 \pi T_{ij},\quad \text {where}\ T_{ij}= \hat{T}_{ij}+\beta \,\theta _{ij}, \end{aligned}$$
(3)

with

$$\begin{aligned} \hat{T}_{ij}{=}-\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}\mathscr {S}_m\right) }{\delta g^{ij}},\quad \text {and}\quad \theta _{ij}{=}\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}\mathscr {S}_\theta \right) }{\delta g^{ij}}, \end{aligned}$$
(4)

where \(G_{ij}\) is the Einstein tensor and \(H_{ij}\) is the contribution of the GB term with the following expression

$$\begin{aligned} G_{ij}&= R_{ij}-\frac{1}{2}R~ g_{ij},\nonumber \\ H_{ij}&= 2\Big ( R R_{ij}-2R_{ik} {R}^k_j -2 R_{ijkl}{R}^{kl} - R_{ikl\delta }{R}^{kl\delta }_j\Big )\nonumber \\&\quad - \frac{1}{2}~g_{ij}~\mathscr {L}_{\text {GB}}, \end{aligned}$$
(5)

where \(R_{ijkl}\) is the Riemann tensor, \(R_{ij}\) is the Ricci tensor, and R is the Ricci scalar, respectively. It is to be noted that the GB term has no effect on the gravitational dynamics in 4D spacetime.

Here, we will investigate the compact stars by adopting the static and spherically symmetric metric solution in 5-dimensional spacetime

$$\begin{aligned} ds^2_{5}= - e^{2\nu (r)} dt^2 + e^{2\lambda (r)}dr^2 + r^{2} d \Sigma ^2_3 , \end{aligned}$$
(6)

where the metric potentials \(\nu (r)\) and \(\lambda (r)\) are functions of radial coordinate r. In the above metric the term \( d \Sigma ^2_3\) is the line element of a three-dimensional hypersurface with constant scalar curvature 6k. Without loss of generality, k can be set to \(k = 1, 0, -1\) and correspond to a sphere, plane and a hyperboloid, respectively. The spherically symmetric static black hole solution for the EGB theory was first found by Boulware and Deser [10] with \(k = 1.\) Later, generalizing the black hole solutions with nontrivial horizon topology were studied in [99] with cosmological constant. In particular, those black holes are asymptotically anti-de Sitter and their event horizon can be a positive, zero or negative constant curvature hypersurface. Similar solution has been found without any need for a cosmological constant term, see [100]. In this paper, we shall restrict to k = 1 that corresponds to the spherically symmetric solution.

Here, we assume that the compact star is filled with anisotropic fluid which is characterized by the stress–energy tensor \(\hat{T}_{ij}\), as

$$\begin{aligned} \hat{T}_{ij} = \left( \hat{\rho }+\hat{p}_t\right) u_{i}u_{j}+\hat{p}_t g_{ij}+(\hat{p}_r-\hat{p}_t)\chi _{i}\,\chi _{j}, \end{aligned}$$
(7)

where \(\hat{p}_r(r)\) and \(\hat{p}_t(r)\) are the radial and tangential pressures, and \(\hat{\rho }(r)\) is the energy density of matter, respectively. Moreover, \(u^{j}\) is the contravariant 5-velocity while \(\chi ^i=\sqrt{1/g_{rr}}\,\delta ^i_1\) is the unit space-like vector in the radial direction, satisfying \(\chi ^i\chi _i=-u^{j}u_{j}=1\). Then we define the effective stress–energy tensor \(T_{ij}\),

$$\begin{aligned} T_{ij} = (\varepsilon + P_{\perp })\,u_{j} u_{j}+ P_{\perp }\, g_{ij}+(P-P_{\perp })\chi _{i}\,\chi _{j}, \end{aligned}$$
(8)

where \(P=\hat{p}_r-\beta \,\theta ^1_1\) and \(P_{\perp }=\hat{p}_t-\beta \,\theta ^2_2\) describe the radial and tangential pressures with \(\varepsilon =\hat{\rho }+\beta \,\theta ^0_0\) is the energy density for the effective stress-energy tensor. The presence of the \(\theta \)-term adds anisotropic effects on \(\hat{T}_{ij}\). From the fact that the Einstein tensor \(G_{ij}\) as well as the Gauss–Bonnet tensor \(H_{ij}\) are divergence-free (see e.g. Refs. [3, 4]), the effective energy–momentum tensor in Eq. (3) tells us that \(T_{ij}\) is also divergence-free, which yield

$$\begin{aligned} \nabla ^i\,T_{ij}=0. \end{aligned}$$
(9)

which yields an equation,

$$\begin{aligned} {\nu ^\prime }(\varepsilon +P)+P^{\prime }+\frac{3}{r}(P- P_{\perp })=0, \end{aligned}$$
(10)

The above equation is known as a general hydrostatic equation for 5D Einstein–Gauss–Bonnet gravity under the spacetime (6). Now, using the Eqs. (6), (8) with (3) one could obtain the non-vanishing components of the gravitational field equations:

$$\begin{aligned}&8 \pi \varepsilon {=} 8 \pi (\hat{\rho }{+}\beta \,\theta ^0_0) {=}\frac{-3}{e^{4 \lambda } r^{3}} \big ( 4 \alpha \lambda ^{\prime } {+} r e^{2 \lambda } {-} r e^{4 \lambda } {-} r^{2} e^{2 \lambda } \lambda ^{\prime } \nonumber \\&\quad - 4 \alpha e^{2 \lambda } \lambda ^{\prime } \big ), \end{aligned}$$
(11)
$$\begin{aligned}&8 \pi P {=} 8 \pi (\hat{p}_r{-}\beta \,\theta ^1_1){=} \frac{3}{e^{4 \lambda } r^{3}} \big (- r e^{4 \lambda } {+} \left( r^{2} \nu ^{\prime } {+} r {+} 4 \alpha \nu ^{\prime } \right) e^{2 \lambda } \nonumber \\&\quad - 4 \alpha \nu ^{\prime } \big ), \end{aligned}$$
(12)
$$\begin{aligned}&8 \pi P_{\perp } = 8 \pi (\hat{p}_t-\beta \,\theta ^2_2) = \frac{1}{e^{4 \lambda } r^{2}} \big ( -e^{4 \lambda } {-} 4 \alpha \nu ^{\prime \prime } {+} 12 \alpha \nu ^{\prime } \lambda ^{\prime } \nonumber \\&\quad - 4 \alpha \nu ^{\prime 2} \big ) + \frac{1}{e^{2 \lambda } r^{2}} \big ( 1 - r^{2} \nu ^{\prime } \lambda ^{\prime } + 2 r \nu ^{\prime } - 2 r \lambda ^{\prime } + r^2\,\nu ^{\prime \,2} \big ) \nonumber \\&\quad + \frac{1}{e^{2 \lambda } r^{2}} \left( r^{2} \nu ^{\prime \prime } - 4 \alpha \nu ^{\prime } \lambda ^{\prime } + 4 \alpha \, \nu ^{\prime 2} + 4 \alpha \nu ^{\prime \prime } \right) . \end{aligned}$$
(13)

where prime denotes the differentiation with respect to r, only. The hydrostatic equilibrium condition can be obtained from the Eq. (9) for an anisotropic fluid as,

$$\begin{aligned}&{\nu ^\prime }(\varepsilon {+}P){+}P^{\prime }{+}\frac{3}{r}(P{-} P_{\perp })=0~\Longrightarrow ~{\nu ^\prime }(\hat{\rho }{+}\hat{p}_r){+}\hat{p}^\prime _r\nonumber \\&\quad +\frac{3}{r}(\hat{p}_r-\hat{p}_t) + \beta \,\Big [{\nu ^\prime }(\theta ^0_0-\theta ^1_1)-(\theta ^1_1)^\prime -\frac{3}{r}(\theta ^1_1-\theta ^2_2)\Big ]=0. \end{aligned}$$
(14)

The addition of the source \(\theta _{ij}\) can be encoded in the geometric deformation in the metric functions given by

$$\begin{aligned}&\nu (r) \longrightarrow \xi (r)+\beta \, h(r), \end{aligned}$$
(15)
$$\begin{aligned}&e^{-2\lambda (r)}\longrightarrow \mu (r)+\beta \, f(r), \end{aligned}$$
(16)

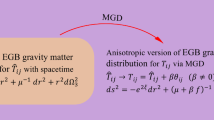
where \({h~\text {and}~ f }\) are the geometric deformations undergone by the radial and temporal metric components and \(\beta \) is a free parameter that controls the deformation. A schematic diagram has been shown in Fig. 1, where the EGB solution is forced to be a solution in the new gravitational sector by the MGD approach. Note that for the case of \(\beta =0\), one may automatically recover the domain of EGB.

Here, we deform the components of the metric minimally. Then we need to set \( h(r) = 0\) with \(f(r)\ne 0\), or \(h(r)\ne 0\) with \(f(r) = 0\). Since the first case keeps the deformation in the radial component only, which implies that the temporal deformation is unchanged. In this situation, the anisotropy in the system is introduced by the radial deformation (16) through the anisotropic tensor \(\theta _{ij}\).

Under the transformation of (16), the field equations (11)–(13) are separated in two sets. First we consider the standard EGB field equations that correspond to the anisotropic case when \(\beta = 0\), and depending on the gravitational potentials \(\mu \) and \(\nu \) the system reduces to

$$\begin{aligned}&8 \pi \hat{\rho }=\frac{1}{2r^3} \big [12\alpha \mu ^\prime (\mu -1)-3 r (\mu ^\prime r+2 \mu -2)\big ], \end{aligned}$$
(17)
$$\begin{aligned}&8 \pi \hat{p}_r=\frac{1}{r^3} \big [12 \alpha \nu ^\prime \mu (1- \mu )+3\,r (\nu ^\prime \mu r+\mu -1)\big ], \end{aligned}$$
(18)
$$\begin{aligned}&8 \pi \hat{p}_t=\frac{1}{2r^2}\big [-8\alpha \mu (\mu -1) (\nu ^{\prime \prime }+\nu ^{\prime 2})+4\alpha \mu ^\prime \nu ^\prime (1-3 \mu )\nonumber \\&\quad +2 \mu (\nu ^{\prime \prime } r^2+\nu ^{\prime 2} r^2+2 \nu ^\prime r+1)+\mu ^\prime \nu ^\prime r^2+2 \mu ^\prime r-2 \big ], \end{aligned}$$
(19)

with the following assumption the conservation quantity (14) reduce to

$$\begin{aligned} {\nu ^\prime }\,(\hat{\rho }+\hat{p}_r)+\hat{p}^\prime _r+\frac{3}{r}(\hat{p}_r-\hat{p}_t)=0. \end{aligned}$$
(20)

Thus, the interior spacetime is given by

$$\begin{aligned} ds^2_{5}&= -\, e^{2\nu (r)} dt^2 + \frac{dr^2}{\mu (r)} + r^{2}\big (d \theta ^2+\sin ^2 \theta d\phi ^2\nonumber \\&\quad +\sin ^2 \theta \sin ^2 \phi ~d\psi ^2 \big ). \end{aligned}$$
(21)

In next, we consider the second set of solution that contains the source \(\theta _{ij}\), and depending on three unknown functions \(\mu \),  \(\nu \) and f the field equations read

$$\begin{aligned}&8 \pi \theta _0^0 = \frac{1}{2r^3} \big [ 12\alpha (f^\prime (f \beta {+}\mu {-}1){+}\mu ^\prime f)-3\,r (f^\prime r+2 f)\big ], ~~~~~~~ \end{aligned}$$
(22)
$$\begin{aligned}&8 \pi \theta _1^1 = -\frac{3f}{r^3} \big [\nu ^\prime \, (-4\,\alpha \, f \beta -8\,\alpha \, \mu +4\,\alpha +r^2)+r\big ], \end{aligned}$$
(23)
$$\begin{aligned}&8 \pi \theta _2^2 = -\frac{1}{2r^2}\,\big [-4\alpha \,\{2 \nu ^{\prime \prime }\, f\, (f \beta +2 \mu -1)+f^\prime \nu ^\prime (3 f\beta \nonumber \\&\quad +3 \mu -1)+\nu ^\prime f (3 \mu ^\prime +2 \nu ^\prime (f \beta +2 \mu -1))\}+2 f^\prime \, r\nonumber \\&\quad +f^\prime \nu ^\prime \, r^2+2 f \, (\nu ^{\prime \prime } r^2+\nu ^{\prime 2} r^2+2 \nu ^\prime r+1)\big ]. \end{aligned}$$
(24)

The conservation equation \(\nabla ^i\,\theta _{ij}=0\) explicitly read

$$\begin{aligned} -{\nu ^\prime }(\theta ^0_0-\theta ^1_1)+(\theta ^1_1)^\prime +\frac{3}{r}(\theta ^1_1-\theta ^2_2)=0. \end{aligned}$$
(25)

We therefore conclude that the two sources \(T_{ij}\) and \(\theta _{ij}\) can be successfully decoupled by means of the MGD. Under these circumstances, one can see that a decoupling without exchange of energy between the sources (see Ref. [60] for more).

3 Minimally deformed solution in 5D Einstein–Gauss–Bonnet gravity

Since we have two system of equations (17)–(19) and (22)–(24), which are highly non-linear differential equations in \(\nu \) and \(\mu \). It is also noted that solution of the second system is dependent on the first system. Here, we will see that it is possible to build an exact and physically acceptable solution by using the minimal geometric deformation (MGD) approach [60] in 5D Einstein–Gauss–Bonnet gravity. Since there is no such known solution, the first obvious question is to ask what restrictions we should impose in order to close the seed Eqs. (17)–(19). To set the stage, we should retain as much of standard physics as possible for stellar structure. In the spirit of following discussion by Lake [101], the gravitational potential \(\nu (r)\) is set by the requirement that \(\nu (0)\) is a finite constant, and it follows that \(\nu ^{\prime }(0) = 0\) and \(\nu ^{\prime \prime }(0) > 0\) guarantees the regularity at the stellar interior. The energy density and the pressure gradients are everywhere positive and finite inside the star. Moreover, the pressure components are maximum at the center and decreasing monotonically towards the boundary. These features are the most important features characterizing a stellar model.

As discussed by Delgaty and Lake [102] more than 130 solutions, only few solutions could be classified as physically relevant satisfying the physical conditions. Among them some well known models are Tolman IV [103], Durgapal [104] and Finch–Skea [105] which were utilized by many authors to generate and analyze physically viable models of compact astrophysical objects. In order to accomplish the above, let us start by considering a newly proposed exact interior solution which is from now onwards known as Tolman–Finch–Skea (TFS) metric ansatz,

$$\begin{aligned} \nu (r) = 2\ln [B(1+A\,r^2)]~~~ \text {and}~~ \mu (r) = 1/(1+C\,r^2), \end{aligned}$$
(26)

where A and C are positive constants with dimension of \([\text {Length}]^{-2}\) and B is a constant without dimension. The above form of metric potentials are chosen in a systematic manner that fit for our purpose and decoupling function f(r) should be trackable. Subsequently, based on metric potentials, the solution of Eqs. (17)–(19) become

$$\begin{aligned}& 8\pi \,\hat{\rho }=\frac{3 C (2 + 4 \alpha C + 3 C r^2 + C^2 r^4)}{(1 + C r^2)^3}, \end{aligned}$$
(27)
$$\begin{aligned}&8\pi \,\hat{p}_r = \frac{3\big [C (1 + C r^2) + A (4 + 16 \alpha C + 3 C r^2 - C^2 r^4)\big ]}{(1 + A r^2) (1 + Cr^2)^2}, \end{aligned}$$
(28)
$$\begin{aligned}& 8\pi \,\hat{p}_t =\frac{G(r) + A^2 r^2 [H(r) + 16 \alpha C (5 + 2 C r^2)]}{(1 + A r^2)^2 (1 + C r^2)^3}, \end{aligned}$$
(29)

where \(G(r) = -C (3 + 4 C r^2 + C^2 r^4)+ 2 A (6 + 24 \alpha C + 7 C r^2 - C^3 r^6)\) and \(H(r)=20 + 33 C r^2 + 12 C^2 r^4 - C^3 r^6\). Here we consider two different procedures, namely, mimic approaches for solving the second system of Eqs. (22)–(24). The aim is to find the decoupling function f(r).

Fig. 1
figure 1

Schematic picture of a Minimal Geometric Deformation (MGD) approach

Full size image

3.1 Solution A: mimicking of the pressure constraint i.e. \(\hat{p}_r=\theta ^1_1\)

By mimicking of seed radial pressure \(\hat{p}_r\) from Eq. (18) with its \(\theta \)-component from Eq. (23), we get the quadratic equation in decoupling function f(r) as,

$$\begin{aligned}&-12\, \alpha \,\beta \, \nu ^\prime \, f^2 + [12 \, \alpha \, \nu ^\prime - 24\, \alpha \, \nu ^\prime \,\mu + 3 r + 3 \nu ^\prime \, r^2]\,f \nonumber \\&\quad + [12 \, \alpha \, \nu ^\prime \, \mu - 12 \, \alpha \, \nu ^\prime \, \mu ^2 - 3 r + 3 \mu r + 3 \nu ^\prime \, \mu r^2]=0. \end{aligned}$$
(30)

After solving the above quadratic equation, we get the decoupling function f in terms of gravitational potential function \(\nu \) and \(\mu \),

$$\begin{aligned} f&= \frac{-1}{{8\, \alpha \, \nu ^\prime \, \beta }}\Big [\sqrt{[\alpha \, \nu ^\prime (4 - 8 \mu ) + r (1 + \nu ^\prime r)]^2 - f_1}\nonumber \\&\quad - (4 \, \alpha \, \nu ^\prime - 8 \, \alpha \, \nu ^\prime \,\mu + r + \nu ^\prime r^2) \Big ], \end{aligned}$$
(31)

where, \(f_1=16\, \alpha \nu ^\prime \beta \,[4 \alpha \, \nu ^\prime (\mu -1)\, \mu - r ( \mu + \nu ^\prime \, \mu \,r-1)]\). Now by plugging the gravitational potentials form Eq. (26) into Eq. (31), we get f(r) as

$$\begin{aligned} f(r)&= \frac{1}{32\, \alpha \,\beta \, A \,(1 + C r^2)^2}\big (1 {-} 16 \alpha A {+} 5 A r^2 {+} 2 C r^2 \nonumber \\&\quad + 10 A C r^4 + C^2 r^4 {+} 16 \alpha A C^2 r^4 {+} 5 A C^2 r^6 {-}\sqrt{\psi }\,\big ), \end{aligned}$$
(32)

where,

$$\begin{aligned} \psi= & {} (1 + C r^2)^2\Big ( [16 \alpha A (C r^2-1) + (1 + 5 A r^2) (1 + C r^2)]^2 \\&- 64\,\alpha \,\beta \,A r^2\, [C (1 {+} C r^2) {+} A (C^2 r^4{-} 3 C r^2{-} 16 \alpha C-4)]\Big ). \end{aligned}$$

Now we have the expression for all known functions \(\nu \), \(\mu \) and f, then the expressions for \(\theta \) components are determined from Eqs. (22)–(24) as,

$$\begin{aligned} 8\pi \theta ^0_0&= \frac{-3}{256\, \alpha \,\beta \, A\, \psi \, r^2\, (1 + C r^2)^3}\bigg [8192 \alpha ^3 C (\beta -1) (C r^2-1)\nonumber \\&\quad \times (A + A C r^2)^2 - (1 + C r^2) [3 \psi ^2 - 2 \psi (-1 + 15 A r^2) \nonumber \\&\quad \times (1 + C r^2)^2 + 5 (1 + C r^2)^4 ( 15 A^2 r^4-1 - 2 A r^2)] + 256 \nonumber \\&\quad \times \alpha ^2 A [2 C \{2 (\beta -1) (1 + C r^2)^2 + \psi (1 - \beta + C r^2 \nonumber \\&\quad + C \beta r^2)\} + A (1 + C r^2)^2 \{5 + C r^2 - 21 C^2 r^4 - 5 C^3 r^6 \nonumber \\&\quad + 2 \beta (-4 - 5 C r^2 + 6 C^2 r^4 + C^3 r^6)\}] + 32 \alpha (1 + C r^2) \nonumber \\&\quad \times \big [C (-1 + \beta ) (\psi - (1 + C r^2)^2) - A^2 (r + C r^3)^2 \{3 \beta (4 \nonumber \\&\quad - 2 C r^2 - C^2 r^4) + 5 (1 + 8 C r^2 + 4 C^2 r^4)\} - A \big \{(1 + C r^2)^2 \nonumber \\&\quad \times (5 + 3 C r^2 + \beta (-4 - C r^2 + C^2 r^4)) - \psi (1 + 8 C r^2 \nonumber \\&\quad + 4 C^2 r^4 + \beta (-4 + 2 C r^2 + C^2 r^4))\big \}\big ]\bigg ] , \end{aligned}$$
(33)
$$\begin{aligned} 8\pi \theta ^1_1&=\frac{3\big [C (1 + C r^2) + A (4 + 16 \alpha C + 3 C r^2 - C^2 r^4)\big ]}{(1 + A r^2) (1 + Cr^2)^2}, \end{aligned}$$
(34)
$$\begin{aligned} 8\pi \theta ^2_2&= - \frac{1}{64 \alpha \,\beta \,\psi \, A\,r^2\, (1 + C r^2)^4 (1 + A r^2)^2}\bigg [-\psi ^3 (1 + 3 A r^2) \nonumber \\&\quad + 3 A \psi ^2 (1 + A r^2) (r + C r^3)^2 + A r^2 (1 + A r^2) (16 \alpha A -1 \nonumber \\&\quad + 3 A r^2) (1 + C r^2)^3 [-512 \alpha ^2 A C (-1 + \beta ) (-1 + C r^2) \nonumber \\&\quad + 5 (1 + 5 A r^2) (1 + C r^2)^3 - 16 \alpha (1 + C r^2) \{2 C (\beta -1) \nonumber \\&\quad + A (2 \beta (2 C r^2 + C^2 r^4-4) - 5 (2 C r^2 + C^2 r^4-1))\}] \nonumber \\&\quad + \psi (1 + C r^2) \big [(1 + C r^2)^3 (1 + 15 A r^2 + 27 A^2 r^4 + 45 \nonumber \\&\quad \times A^3 r^6) + 256 \alpha ^2 A^2 (1 - 3 C (1 + 2 \beta ) r^2 + 3 C^2 (2 \beta -1) \nonumber \\&\quad \times r^4 + C^3 r^6 + A r^2 (3 - C (5 + 6 \beta ) r^2 + C^2 (-5 + 6 \beta ) r^4 \nonumber \\&\quad + 3 C^3 r^6)) + 32 \alpha A (1 + C r^2) \big \{ C (1 + 3 \beta ) r^2 -1 + C^2 r^4 \nonumber \\&\quad + A^2 r^4 (11 C^2 r^4- 8 C r^2 -16 + 3 \beta (2 C r^2 + C^2 r^4-4)) \nonumber \\&\quad + A r^2 (4 C^2 r^4 - 7 C r^2 -9 + 3 \beta (3 C r^2 + C^2 r^4-4))\big \}\big ]\bigg ]. \end{aligned}$$
(35)

Now we move on second approach to find the decoupling function f(r) as follows:

3.2 Solution B: mimicking of the density constraint i.e. \(\hat{\rho }=\theta ^0_0\)

In this approach, we mimic the energy density \(\hat{\rho }\) for seed solution with its \(\theta \) component \(\theta ^0_0\) from Eqs. (18) and (23), then we get a nonlinear differential equation in decoupling function f(r) of the form,

$$\begin{aligned}&(12 \alpha \mu - 12 \alpha + 12 \alpha \,\beta \, f - 3 r^2)\,f^\prime + (12 \alpha \,\mu ^\prime - 6\,r)\, f \nonumber \\&\quad + (12 \alpha \,\mu ^\prime - 12 \alpha \,\mu ^\prime \, \mu - 6\,r + 6 \mu r + 3 \,\mu ^\prime \, r^2)=0. \end{aligned}$$
(36)

After inserting the \(\nu \) and \(\mu \) and integrating, we get

$$\begin{aligned} f(r)=\frac{1}{4 \alpha \beta \, (1+ C r^2)}\bigg [r^2 + 4\alpha C r^2 + C r^4- \sqrt{\frac{\Psi (r)}{C}}\bigg ], \end{aligned}$$
(37)

where,

$$\begin{aligned} \Psi (r)= & {} C r^4 (1 + C r^2)^2 + 8 \alpha (1 + C r^2)\,(\beta + \beta \,C r^2 + C^2 r^4 \\&+\beta C^2 r^4) + 16 \alpha ^2 C [C^2 r^4 - \beta \, (1 + 2 C r^2) + F\,\beta ^2\, \\&\times (1 + C r^2)^2]. \end{aligned}$$

and F is an arbitrary constant of integration which will be determined by following way: as we know that for any realistic model, \(e^{-2\lambda (r)}\) should be 1 at the centre. Since the deformed gravitational potential \(e^{-2\lambda }\) can be given as,

$$\begin{aligned} e^{-2\lambda (r)}=\mu (r)+\alpha \,f(r)=\frac{1}{1+Cr^2}+\alpha \,f(r). \end{aligned}$$
(38)

Then Eq. (38) ensures that the decoupling function must vanish at the centre i.e. \(f(0)=0\) in order to have \(e^{-2\lambda (0)}=1\). Now from Eq. (37), we get

$$\begin{aligned} f(0)&= -\frac{1}{\sqrt{2}\,\alpha \,\beta }\sqrt{\frac{\alpha \,\beta \, [1 + 2 \alpha \, C\, (F \beta -1)]}{C}}=0\nonumber \\&\Longrightarrow ~~~F =\frac{2\,\alpha \,C-1}{2\,\alpha \,\beta \,C}. \end{aligned}$$
(39)

Then the final form of the decoupling function can be written as,

$$\begin{aligned}&f(r)= \frac{1}{4\,\alpha \, \beta \, (1 + C r^2)} \big [r^2\,[(1 + 4\,\alpha \, C) + C\, r^2 \nonumber \\&\quad - \sqrt{16 \,\alpha ^2 C^2 (1 + \beta ) + 8 \,\alpha \, C (1 + \beta )(1 + C r^2) + (1 + C r^2)^2}\big ], \end{aligned}$$
(40)

and then the expressions for \(\theta \)-components under this decoupling function (40) are determined from Eqs. (22)–(24) as,

$$\begin{aligned} 8\pi \theta ^0_0&= \frac{3 C (2 + 4 \alpha C + 3 C r^2 + C^2 r^4)}{(1 + C r^2)^3}, \end{aligned}$$
(41)
$$\begin{aligned} 8\pi \theta ^1_1&= \frac{-1}{4\,\alpha \, \beta \, (1 + A r^2) (1 + C r^2)^2} \big [3 (1 + 4\, \alpha \, C + C r^2- \Psi _1)\nonumber \\&\quad \times (1 - 16 \, \alpha \, A + A r^2 + C r^2 + A C r^4 + 4 A r^2\,\Psi _1)\big ] \end{aligned}$$
(42)
$$\begin{aligned} 8\pi \theta ^2_2&= \frac{-1}{4 \alpha \,\beta \,\Psi _1\, (1 + C r^2)^3\,(1 + A r^2)^2} \bigg [512 \alpha ^3 A C^2 (1 + \, \beta \,) \nonumber \\&\quad \times (1 + A r^2) (1 + C r^2) - (-1 + \Psi _ 1 - C r^2) (1 + C r^2) \nonumber \\&\quad \times [4\, A\, \Psi ^2_ 1\, r^2 (1 + 3 A r^2) - \Psi _ 1 (1 + C r^2) (-1 + 2\, A\, r^2 \nonumber \\&\quad + 3\, A^2 \,r^4) + 2 (1 + C r^2)^2 (-1 + 2\, A\, r^2 + 3 \,A^2\, r^4)] \nonumber \\&\quad + 4 \alpha (1 + C r^2) \big [C \{\Psi _ 1 (3 + C r^2) - 2 (1 + \, \beta \,) (2 + 3 C r^2 \nonumber \\&\quad + C^2 r^4)\} + 2 A (2 (\Psi _ 1)^2 (1 + C r^2) - \Psi _ 1 (2 + C r^2) (3 \nonumber \\&\quad + C (5 + 6 \, \beta \,)\, r^2) + 2 (1 + C r^2) (2 + 2\, C\, (3 + \, \beta \,)\, r^2 \nonumber \\&\quad + C^2\, (3 + \, \beta \,)\, r^4)) + A^2\, r^2\, (12\, (\Psi _ 1)^2 (1 + C\, r^2) + 2\, \nonumber \\&\quad \times (1 + C r^2) (4 + 2 \, C\, (7 + 3 \, \beta \,)\, r^2 + C^2\, (7 + 3 \, \beta \,)\, r^4)\nonumber \\&\quad -\Psi _ 1\, (20 + C (37 + 24 \, \beta \,)\, r^2 + C^2\, (11 + 12 \, \beta \,)\, r^4))\big ] \nonumber \\&\quad +32 \alpha ^2 C \big [-C (1 + \, \beta \,) (1 + C r^2) + 2 A \{-3 \Psi _ 1 (1 \nonumber \\&\quad + C (1 + \, \beta \,) r^2) + (1 + \, \beta \,) (4 + 11 C r^2 + 9 C^2 r^4 \nonumber \\&\quad + 2 C^3 r^6)\} + A^2 r^2 \big \{-2 \Psi _ 1 (5 + C (5 + 3 \, \beta \,) r^2) \nonumber \\&\quad + (1 + \, \beta \,) (8 + 23 C r^2 + 19 C^2 r^4 + 4 C^3 r^6)\big \}\big ]\bigg ], \end{aligned}$$
(43)

where, \(\Psi _1{=}\sqrt{16 \alpha ^2 C^2 (1 {+} \beta ) {+} 8 \alpha \, C (1 {+} \beta ) (1 {+} C r^2) {+} (1 {+} C r^2)^2}\)

4 Exterior space-time and Junctions conditions

The final step to set up the system is defining the boundary conditions for the sought solutions. In the present case, we match the internal manifold \(\mathscr {M}^{-}\) described by Eq. (26) to the exterior Boulware–Deser space-time [10], with metric given by

$$\begin{aligned} ds^2_{5}&= -F(r) dt^2 + \frac{dr^2}{F(r)} + r^{2}\big (d \theta ^2+\sin ^2 \theta d\phi ^2\nonumber \\&\quad +\sin ^2 \theta \sin ^2 \phi ~d\psi ^2 \big ), \end{aligned}$$
(44)

where M is associated with the total gravitational mass with

$$\begin{aligned} F(r) =1+\frac{r^2}{4 \alpha } \left( 1-\sqrt{1+\frac{16\alpha M}{r^4}}\right) . \end{aligned}$$
(45)

It is easy to check that in the limit \(\alpha \rightarrow 0\) the above expression reduces to the 5D Schwarzschild solution. By matching the line elements (26) and (51) across the boundary, one can suitably fix the model parameters. The resulting manifolds have boundaries given by the time-like hyper-surfaces

$$\begin{aligned} ds^{2}_{\Sigma } = - d\tau ^2+R^{2}\big (d \theta ^2+\sin ^2 \theta d\phi ^2+\sin ^2 \theta \sin ^2 \phi ~d\psi ^2 \big ), \end{aligned}$$
(46)

with the intrinsic coordinates of \(\Sigma \) being \(\xi ^i\) = \((\tau , \theta , \phi , \psi )\) in \(\Sigma \), and \(\tau \) is the proper time on the boundary. Now, consider the field equations projected on the shell \(\Sigma \) (generalized Darmois–Israel formalism for Einstein–Gauss–Bonnet theory) are (see Refs. [106, 107] for more)

$$\begin{aligned} 2\langle K_{ij}-K h_{ij}\rangle + 4\alpha \langle 3J_{ij}-Jh_{ij}+2P_{iklj}K^{kl}\rangle =-\kappa ^{2}S_{ij}, \end{aligned}$$
(47)

where the \(\langle \cdot \rangle \) is the jump of a given quantity across the hyper-surface \(\Sigma \). Here \(h_{ij} = g_{ij} - n_{i}n_{i}\) is the induced metric on \(\Sigma \) with the divergence free part of the Riemann tensor is defined by

$$\begin{aligned} P_{ijkl}&= R_{ijkl}+(R_{jk}h_{li}- R_{jl}h_{ki})-(R_{ik}h_{lj}- R_{il}h_{kj}) \nonumber \\&\quad +\frac{1}{2}R(h_{ik}h_{lj}-h_{il}h_{kj}), \end{aligned}$$
(48)

and J is the trace of

$$\begin{aligned} J_{ij}=\frac{1}{3}\left[ 2KK_{ik}K^{k}_{j}+K_{kl}K^{kl}K_{ij}-2K_{ik}K^{kl}K_{lj}-K^{2}K_{ij}\right] . \end{aligned}$$
(49)

Therefore, in the present case the extrinsic curvature has the form

$$\begin{aligned} {K}^{\pm }_{ij}=-n^{\pm }_{\mu }\left( \frac{\partial ^{2}X^{\mu }}{\partial \xi ^{i}\partial \xi ^{j}}+\Gamma ^{\mu }_{\alpha \beta }\frac{\partial X^{\alpha }}{\partial \xi ^{i}}\frac{\partial X^{\beta }}{\partial \xi ^{j}}\right) _{r = R}, \end{aligned}$$
(50)

where \(\xi ^i\) are the intrinsic coordinates of the surface and the sign ± depends on the signature of the junction hyper-surface.

Furthermore, the interior stellar geometry under gravitational decoupling via minimal geometric deformation approach can be given by the following line element in the present study as,

$$\begin{aligned} ds^2_{5}&= -\,e^{2\nu (r)} dt^2 + \frac{dr^2}{\mu (r)+f(r)} + r^{2}\big (d \theta ^2+\sin ^2 \theta d\phi ^2\nonumber \\&\quad +\sin ^2 \theta \sin ^2 \phi ~d\psi ^2 \big ), \end{aligned}$$
(51)

where \(\mu (r)\) and \(\nu (r)\) are the solution for the seed spacetime given by Eq. (26), while the deformation functions f(r) for the Solution A and Solution B corresponding to \(\theta \)-sector is given by Eqs. (37) and (40), respectively. Now we analyze the junction at the outer and inner surfaces. The continuity of the first fundamental form at the boundary implies that \(g_{tt}^{-} = g_{tt}^{+}\) and \(g_{rr}^{-} = g_{rr}^{+}\), (where the symbols \(^-\) and \(^+\) denote the inner and outer spacetime) which yield

$$\begin{aligned} e^{2\lambda ^{-}}|_{r=R}=e^{2\lambda ^{+}}|_{r=R} \quad \text {and} \quad e^{2\nu ^{-}}|_{r=R}=e^{2\nu ^{+}}|_{r=R}, \end{aligned}$$
(52)

which gives

$$\begin{aligned}&e^{-2\lambda (R)} = \mu (R)+\beta f(R) =\bigg [1 + \frac{R^2}{4 \alpha }\bigg (1 - \sqrt{1 + \frac{16\, \alpha M}{R^4}}\bigg )\bigg ],\nonumber \\&\quad \text {and}\quad e^{2\nu (R)}=\bigg [1 + \frac{R^2}{4\,\alpha }\bigg (1 - \sqrt{1 + \frac{16\, \alpha M}{R^4}}\bigg )\bigg ], \end{aligned}$$
(53)

where \(\mu (R) = \big [1 + \frac{R^2}{4\,\alpha }\big (1 - \sqrt{1 + \frac{16\, \alpha \, M_{EGB}}{R^4}}\big )\big ]\) with \(M_{EGB} = m_{EGB}(R)\) is the total mass of the compact object for the metric (21) i.e., for the non-deformed space-time. Then, using (53), we have

$$\begin{aligned} M=M_{EGB}+ \frac{1}{2}\beta f(R) \left[ 2\alpha \beta f(R)-\sqrt{R^4 +16 \alpha M_{EGB}}\right] . \end{aligned}$$
(54)

On the other hand, it is necessary that the extrinsic curvature or second fundamental be continuous, leading to the condition

$$\begin{aligned} \big [(G_{ij}+\alpha \,H_{ij})\,r^j\big ]_{\Sigma }=0 , \end{aligned}$$
(55)

where \(r^{j}\) is a unit radial vector. Now, depending on the above criterion one may quantify the Eq. (3) as

$$\begin{aligned} \big [T_{ij}\,r^j\big ]_{\Sigma }=0\, \end{aligned}$$
(56)

which gives,

$$\begin{aligned} \big [P\big ]_{\Sigma }=0~~\Longrightarrow ~~\,\big [\hat{p}_r-\beta \,\theta ^1_1\big ]_{\Sigma }=0, \end{aligned}$$
(57)

where the surface \(\Sigma \) defined by \(r=R\). This condition determines the object size. This is so because, the pressure decreases as we approach to the surface and the pressure at the exterior of the star must be null, then this will correspond to the star boundary. In other words, second fundamental form says that the matter distribution is confined in a finite space-time region, in consequence the star does not expand indefinitely beyond \(\Sigma \). Thus, this matching condition takes the final form

$$\begin{aligned} \hat{p}_r(R)-\beta \,(\theta ^1_1)^{-}(R)=-\beta \,(\theta ^1_1)^{+}(R), \end{aligned}$$
(58)

where \((\theta ^1_1)^{-}(R)\) and \((\theta ^1_1)^{+}(R)\) are the \(\theta \)-components for interior and exterior space-times, respectively. The condition in Eq. (58) is the general expression for the second fundamental form associated with the equation of motion for EGB gravity given in Eq. (3).

Now, using the expression for \(\theta ^1_1\) form (23) and plugged into the Eq. (58), we obtain the second fundamental form as

$$\begin{aligned}&\hat{p}_r(R)-\beta \,(\theta ^1_1)^{-}(R)=-\beta \,(\theta ^1_1)^{+}(R), \end{aligned}$$
(59)
$$\begin{aligned}&\hat{p}_r(R)+\frac{3\,\beta \,f_R\,\big (\nu ^\prime _R (-4\,\alpha \,\beta \, f_R -8\,\alpha \,\mu _R+4\alpha +R^2)+R\big )}{8\,\pi \,R^3}\nonumber \\&\quad =-\beta \,(\theta ^1_1)^{+}(R), \end{aligned}$$
(60)

where the notations are \(f_R = f(R)\), \(\mu _{R}=\mu (R)\), and \(\nu ^\prime _R={\partial _r\nu }\big |_{r=R}\), respectively. Furthermore, using the Eq. (23) for the outer geometry in Eq. (60), which yield

$$\begin{aligned}&\hat{p}_r(R)+\frac{3\,\beta \,f_R\,\big (\nu ^\prime _R (-4\,\alpha \,\beta \, f_R -8\,\alpha \,\mu _R+4\alpha +R^2)+R\big )}{8\,\pi \,R^3} \nonumber \\&\quad =\frac{3\,\beta \,f^{*}_R}{8\,\pi \,R^3} \left[ \frac{R\, \bigg (\sqrt{1 + \frac{16\, \alpha \, \mathscr {M}}{R^4}}-1\bigg )}{\sqrt{1 + \frac{16 \,\alpha \, \mathscr {M}}{R^4}} \bigg [4 \,\alpha +R^2\, \bigg (1 - \sqrt{1 + \frac{16\,\alpha \, \mathscr {M}}{R^4}}\bigg ) \bigg ]}\right. \nonumber \\&\qquad \times \left\{ -4\,\alpha \,\beta \, f^{*}_R -8\,\alpha \,\bigg [1 + \frac{R^2}{4\,\alpha }\bigg (1 - \sqrt{1 + \frac{16\, \alpha \, \mathscr {M}}{R^4}}\bigg )\bigg ]\right. \nonumber \\&\qquad \left. \left. +4\,\alpha +R^2\right\} +R\right] , \end{aligned}$$
(61)

where \(f^{*}_R\) is the decoupling function for the outer space-time at \(r=R\) \((i.e.~f^{*}_R=f^{*}(R))\) due to the source \(\theta _{ij}\), which is given by the Boulware–Deser exterior solution for 5D space-time [10], as

$$\begin{aligned} ds^2_{5}&= - \bigg [1 + \frac{r^2}{4\,\alpha }\bigg (1 - \sqrt{1 + \frac{16\, \alpha \, \mathscr {M}}{r^4}}\bigg )\bigg ] dt^2 + \bigg [1 + \frac{r^2}{4\,\alpha }\nonumber \\&\quad \times \bigg (1 - \sqrt{1 + \frac{16\, \alpha \, \mathscr {M}}{r^4}}\bigg )+\beta \,f^{*}(r)\bigg ]^{-1} dr^2 \nonumber \\&\quad + r^{2}\left( d \theta ^2+\sin ^2 \theta d\phi ^2+\sin ^2 \theta \sin ^2 \phi ~d\psi ^2 \right) . \end{aligned}$$
(62)

All the conditions mention above are the necessary and sufficient conditions for matching the interior MGD metric (6) to the exterior “vacuum” static and spherically symmetric space-times given in (62). The matching condition (62) has an important outcome: if the exterior geometry is given by the exact Boulware–Deser metric, one must have \(f^{*}_R=0\) in Eq. (62). Then, one finds the condition

$$\begin{aligned}&P(R) = \hat{p}_r(R)+\frac{1}{8\,\pi \,R^3}\big [3\,\beta \,f_R\,\big (\nu ^\prime _R (-4\,\alpha \,\beta \, f_R -8\,\alpha \,\mu _R\nonumber \\&\quad +4\alpha +R^2)+R\big )\big ] =0, \end{aligned}$$
(63)
$$\begin{aligned}&P(R)=\hat{p}_r(R)-\beta \,\theta ^1_1(R) = 0. \end{aligned}$$
(64)

Therefore, the star will be in equilibrium in a true (Boulware–Deser) vacuum only if the total (in general anisotropic radial) pressure vanishes at the surface of the star. Using the boundary conditions (53) and (64) we find the constants A, B and total mass M. For clarity we provide a detail discussion about the bounds of the constant parameters in the Appendix.

5 Analysis of the solution

In the following sections we will analyze the physical properties of compact stars obtained from the MGD approach to gravitational decoupling in order to build an exact anisotropic solution. For this purpose we plot Fig. 2 for both the EGB theory and the minimally deformed one EGB+MGD theory. In order to have a better insight regarding the properties of these compact stars, we shall discuss first the EGB theory and then the EGB+MGD theory, consecutively by taking the values of Gauss–Bonnet constant \(\alpha =5\) and 10 to see the clear impact of MGD on the EGB stellar structure.

EGB: The total radial P and transverse \(P_{\perp }\) pressures are depicted in the upper row of Fig. 2 (left and right panel), where the green and red curves correspond to the EGB gravity i.e., \(\beta = 0\). The results reported in Fig. 2 are obtained for two different values of \(\alpha = 5\) and 10, respectively. In this setting we see that pressure in radial direction is decreasing towards the boundary with increasing the radius and vanishes at the surface of the star (see top of the left panel). Whereas the tangential pressure is behaving odd, i.e., monotonically increasing with increasing radius. This situation is not expected for a well-behaved stellar interior. However, it is found that, the total density \(\varepsilon \) (left lower panel in Fig. 2) and anisotropy factor (see Fig. 3 – left panel) are behaving as expected for a stellar configuration. This seems to indicate that without gravitational decoupling is not a very good starting point to study static and spherically symmetric anisotropic fluid solutions in EGB gravity.

5.1 Analysis for solution A: mimicking of the pressure constraint i.e. \(\hat{p}_r=\theta ^1_1\)

EGB+MGD: This situation is more reliable when the governing equations include gravitational decoupling realized via the MGD approach. Following the space-time (26), we now build an interesting solution and highlight the following pointsFootnote 1:

  1. 1.

    By setting \(h(r)=0\) in the Eq. (15), the temporal metric potential remains unaltered whilst the full modification relies on the radial metric potential through the so-called deformation or decoupler function f(r). Therefore, not only the main thermodynamic quantities are affected, that is, the density, the radial and tangential pressures, but also the mass of the object. This is because, as usual the radial metric potential is related with the mass of the object. In concerning the thermodynamic observables, when the seed solution is minimally deformed, the problem reported above for the increasing tangential pressure is overcome. Indeed, by choosing the EGB coupling constant to be \(\alpha =5\) the limit value for the coupling constant \(\beta \) is \(-0.5\) to have a decreasing transverse pressure (see right panel in Fig. 2). As can be observed, by keeping the same value of \(\alpha \) and decreasing \(\beta \), the central value of both P and \(P_{\perp }\) increases. On the other hand, by fixing \(\beta \) and varying \(\alpha \) the mentioned quantities again increase their central values. Then one can conclude that by increasing both \(\alpha \) and \(\beta \) in magnitude, the radial and tangential pressures take greater values at the core of the compact object. It is worth mentioning that the signature of \(\beta \) is quite involved in maximum value taken by the mentioned quantities at the center of the structure, especially in considering the radial pressure. This is so because, when the seed radial pressure \(\hat{p}_{r}\) is mimicking its simile in the \(\theta \)-sector ı.e., the component \(\theta ^{1}_{1}\), the total pressure in the radial direction becomes \(P=\left( 1-\beta \right) \hat{p}_{r}\). Thus, it is clear that when \(\beta <0\), the total pressure is increasing with respect to the seed pressure, what is more as the spherical symmetry entails \(P=P_{\perp }\) at \(r=0\), the transverse pressure also takes greater value than the seed transverse pressure.

  2. 2.

    As mentioned above, the density is also altered by the additional gravitational source of the \(\theta \)-sector. In general the total density acquires the following form: \(\varepsilon =\hat{\rho }+\beta \theta ^{0}_{0}\), thus a denser stellar structure with respect to the seed solution strongly depends on both the value and signature of the constant \(\beta \), and the behavior of the \(\theta ^{0}_{0}\) component. However, the behavior of \(\theta ^{0}_{0}\) is completely determined by the trend of the decoupling function f(r), the metric potential \(\mu (r)\) and their first derivative (see Eq. (22)). However, in the present situation (\(\hat{p}_{r}=\theta ^{1}_{1}\)) the deformation function f(r) has an interesting behavior. This can be seen from the right panel of Fig. 3, when the seed radial pressure is proportional to the radial component of the \(\theta \)-sector, the function f(r) vanishes at the center \(r=0\) and the surface \(r=R\) of the star. Hence, in contrast with the pressures, the density behaves in a different way. As any well behaved compact star, the density \(\rho \) attains its maximum value at the core, however a higher value is reached if both \(\alpha \) and \(\beta \) decrease in magnitude. For instance, when the pair \(\{\alpha ;\beta \}\) is equal to \(\{5;-0.5\}\) (black curve in the lower left panel of Fig. 2), but by keeping the same value of \(\alpha \) and moving \(\beta \) the central density decreases. Finally, in moving both parameters to greater values (in magnitude) the model gets less value and so on. Nevertheless, in doing that, towards the boundary of the star the surface density increases. Thus one can conclude that there is a mass displacement from the center to the surface when the coupling parameters \(\alpha \) and \(\beta \) increase in magnitude.

  3. 3.

    As the deformation is done over the radial metric potential only, being this information can be obtained by a direct integration of the field equation involving the density of the structure. For the EGB theory the general expression is obtained from the Eq. (17) leading to

    $$\begin{aligned}&\frac{8\,\pi }{3} \int ^{R}_{0} r^{3}\hat{\rho }(r)dr \equiv M_{EGB}(R)= \frac{1}{2}\,\Big ( R^2\, [1-\mu (R)]\nonumber \\&\quad +2\,\alpha \,[1-\mu (R)]^2\Big ). \end{aligned}$$
    (65)

    The first term in the brace correspond to the usual expression for the 5D Einstein gravity theory while the term proportional to \(\alpha \) is the Gauss–Bonnet contribution. Now, the incorporation of the term \(\beta f(r)\) in the radial metric potential, modifies the mass of the object, its contribution can be obtained from the Eq. (22) where

    $$\begin{aligned}&\frac{8\,\pi }{3} \int ^{R}_{0} r^{3}\,\theta ^{1}_{1}(r)dr \equiv M_{MGD}(R)= \frac{1}{2}\Big ( 2\,\alpha \,[\beta \,f^2(R)\nonumber \\&\quad +2\,f(R)\,(\mu (R)-1)]-R^2\,f(R)\Big ). \end{aligned}$$
    (66)

    Now, as \(f(0)=f(R)=0\) (see right panel in Fig. 2) in the right hand side of (66) the first term does not contribute to the total mass, what is more as \(f(r)<0\) for all \(r\in [0,R]\) the second term in the right hand side of (66) contributes in a positive way, that is, “by increasing” the mass of the object. This is because the total mass M of the object is the sum of (65) and (66). Interestingly, the fact \(f(R)=0\) is an inherent feature of the mimic constraint \(\hat{p}_{r}=\theta ^{1}_{1}\) while \(f(0)=0\) is for the consistency of the radial metric potential behavior. Indeed, as the radial metric potential already meets \(\mu (0)=1\) then it is necessary to assure \(f(0)=0\) (see left panel of Fig. 2). To prove that \(f(R)=0\) is a general statementFootnote 2 by evaluating the field equation (18) at \(r=R\), one gets

    $$\begin{aligned} \nu ^{\prime }(R)=\frac{3R\left[ 1-\mu (R)\right] }{12\alpha \mu (R)\left[ 1-\mu (R)\right] +3R^{2}\mu (R)}, \end{aligned}$$
    (67)

    where the fact \(\hat{p}_{r}(R)=0\) has been used. Next, evaluating the expression (31) at the boundary and plugging (67) into it, after some algebraic calculation it is straightforward to show that \(f(R)=0\). In summary, as the decoupling function f(r) is null at the core and the surface of the object, actually the mass of the object is not changing only is redistributed inside the structure. This fact is shown by the behavior of the density profile where the object becomes denser towards the surface as said before.

  4. 4.

    We now proceed to study the anisotropy factor \(\Delta \equiv P_{\perp }-P\), see Fig. 3. It is notable that the anisotropy factor is much higher for the seed solution compared to the deformed solution. This is because the tangential pressure is increasing in nature for the seed spacetime, which was pointed out earlier but this is not of physical interest. Thus, concentrating only on the minimally deformed inner solution, the local anisotropy induced by the \(\theta \)-sector, we obtain \(\Delta > 0\) within the stellar interior, see Fig. 3 (see left panel). It is clear that \(\Delta \) increases in magnitude towards the surface of the star when \(\alpha \) and \(\beta \) take less value, otherwise it decreases when increasing the magnitude value of them. As the seed solution is purely anisotropic, the effect coming from the \(\theta \)-sector just produces a moderate version of anisotropies in the stellar interior. This is because an increasing transverse pressure (like in this case) could potentially generate instabilities or a hydrostatic imbalance. In this concern, as it is well-known, having anisotropies in the matter distribution helps to form more compact, stable and balanced structures. Furthermore the anisotropic gradient, induced by the local anisotropies inside the matter distribution, helps to counteract the gravitational gradient avoiding the gravitational collapse.

Fig. 2
figure 2

Top panels: the left panel shows the total radial pressure (\(p^{\text {tot}}_r\)) and the right panel shows the total tangential pressure (\(p^{\text {tot}}_t\)) with respect to the radial coordinate r/R. Bottom panels: The left panel represents the total energy density (\(\rho ^{\text {tot}}\)) and the right panel shows the total radial and tangential pressures with respect to r/R. We set the numerical values \(C= 0.000341~\text {km}^{-2}\) and \(\frac{M_{EGB}}{R}=0.2516\) for plotting when \(\alpha =5\)

Full size image
Fig. 3
figure 3

The variation of total anisotropy \([\Delta ^{\text {tot}}=8\pi (P_{\perp }-P)]\) and deformation function f(r) with respect to the radial coordinate r/R. Here, we use the same set of parameters as of Fig. 2

Full size image

5.2 Analysis for solution B: mimicking of the density constraint i.e. \(\hat{\rho }=\theta ^0_0\)

Here, we will focus our discussion for the mimic constraint \(\hat{\rho }=\theta ^{0}_{0}\) model. Figures 4, 5 and 6 have been plotted for total pressures, energy density, anisotropy factor and mass–radius curves of the compact star model corresponding to different values of \(\alpha \) and \(\beta \), respectively. It is instructive to see some implications of our results as followsFootnote 3:

EGB+MGD:

  1. 1.

    Observing the Fig. 4 (upper panels and lower left panel) we see that the \(\theta \)-sector is more involved compared to the previous solution when the radial pressure constraint is employed (see Fig. 2). For instance, in comparing the central radial P and tangential \(P_{\perp }\) pressures for the solution A and solution B, In the former solution A these quantities take lesser values in comparison with the solution B when the density constraint is employed (see Figs. 2 and 4). This is so because, the \(\theta ^{1}_{1}\) component is not playing any role in the solution A, since the total radial pressure is \(P=(1-\beta )\hat{p}_{r}\). Thus the central value depends on the \(\beta \) magnitude and its signature. Furthermore, as \(P>0\) everywhere then \(\beta \) is bounded from above ı.e., \(\beta <1\). However, for the present solution B the situation is not same since the radial and tangential pressures are given by \(P=\hat{p}_{r}-\beta \theta ^{1}_{1}\) and \(P_{\perp }=\hat{p}_{t}-\beta \theta ^{2}_{2}\), respectively but total density is of the form \(\varepsilon =(1+\beta )\hat{\rho }\). Then the coupling \(\beta \) acquires the following lower bound \(-1<\beta \) due to \(\varepsilon >0\). The modifications introduced by the component \(\theta ^{1}_{1}\) of the extra source in the present case come from the junction condition process, in which the constant parameter that characterizes the model takes different values in contrast with the first solution (since the values of the constant parameters obtained in the solution A are exactly the same of the non-deformed solution). Interestingly by increasing both \(\alpha \) and \(\beta \) in magnitude the central pressure increases (see upper panel in Fig. 4). Besides, the object has a denser core (see left lower in Fig. 4).

  2. 2.

    In contrast with the first solution, here the total mass inside the fluid sphere does not remain unaltered. Of course, when the seed density \(\hat{\rho }\) is mimicking the temporal component of the \(\theta \)-sector ı.e., \(\theta ^{0}_{0}\), then the total gravitational mass is given by

    $$\begin{aligned} M(R)=\frac{8\,\pi }{3} \left( 1+\beta \right) \int ^{R}_{0}\hat{\rho }(r)\, r^{3}dr, \end{aligned}$$
    (68)

    which leads to

    $$\begin{aligned} M(R)=\frac{\big (1+\beta \big )}{2}\Big ( R^2\, [1-\mu (R)] +2\,\alpha \,[1-\mu (R)]^2\Big ).~~ \end{aligned}$$
    (69)

    Essentially, the Eq. (69) tells us that the mass of the object is proportional to the original one \(M_{EGB}(R)\), where the proportionality factor \((1+\beta )\) is carrying out the MGD information. Therefore, the object becomes denser when the deformation parameter \(\beta \) is positive, then the previous lower bound imposed the density mimic constraint, instead of being \(-1<\beta \) should be \(\beta >0\). In such a framework, the deformation function f(r) is non-vanishing at the boundary of the structure (see right panel in Fig. 5). As expected by increasing the values of \(\alpha \) and \(\beta \) lead to a higher value of mass–radius relation as shown in Fig. 6 (left panel). The consequence of this is the existence of a more compact object as demonstrated in the right panel of Fig. 6.

  3. 3.

    From the above discussion, it is clear that the mimic constraint for the density, the \(\theta \)-sector plays an important role in the physical behavior of the compact object. The anisotropic factor, \(\Delta ^{\text {tot}}=8\pi (P_{\perp }-P)\), is shown in the left panel of Fig. 5. We have seen that this value is much higher compare to our previous solution ı.e., solution A (see left panel in Fig. 3).

Fig. 4
figure 4

Top panels: the left panel shows the total radial pressure (\(p^{\text {tot}}_r\)) and the right panel shows the total tangential pressure (\(p^{\text {tot}}_t\)) with respect to the radial coordinate r/R. Bottom panels: The left panel represents the total energy density (\(\rho ^{\text {tot}}\)) and the right panel shows the total radial and tangential pressures with respect to r/R. Here, we use the same set of parameters as of Fig. 2

Full size image
Fig. 5
figure 5

The variation of total anisotropy \([\Delta ^{\text {tot}}=8\pi (P_{\perp }-P)]\) and deformation function (f(r)) versus radial coordinate r/R. Here, we use the same set of parameters as of Fig. 2

Full size image
Fig. 6
figure 6

The variation of mass function m(r) and mass-radius ratio (m/r) versus radial coordinate r/R

Full size image

It is now relevant to discuss some other astrophysical consequences, given by the mimic constraint as discussed in solutions A and B, which are required to be satisfied at every point of a star. Here we start by talking about the so-called redshift function \(z_{s}\). We know that this quantity depends on the mass–radius ratio of the compact configuration.

For the solution A, the mass of the object is not changing, then it is not possible to distinguish the surface redshift \(z_{s}\) between the seed solution (non-deformed solution) and the minimally deformed solution. This is because the mass–radius ratio M/R is the same for both scenarios, and consequently the redshift function also (i.e. non-deformed and deformed solution when we consider pressure mimic constraint). Considering the other solution B ı.e., \(\hat{\rho }=\theta ^{0}_{0}\), the surface redshift is not necessarily similar for non-deformed and deformed structure of compact objects. To clarify these situations in both solutions, we resort to the total gravitational mass obtained from the junction condition process (54). Note that the mass obtained from the matching between the inner and exterior spacetime should be the same that the mass obtained by a direct integration of the energy density (see Eqs. (65)–(66) for solution A and Eq. (69) for solution B). So, after enforcing the mentioned condition, we shall analyze the astrophysical effects introduced by MGD on the compact object employing the total gravitational mass (54). More specifically, the expression (54) is treated as a sum of two terms, one coming from the EGB sector and the other term is the product of \(\beta f(R)\) introduced by the MGD scheme. So, by imposing the condition \(\hat{p}_{r}=\theta ^{1}_{1}\), the deformation function f(r) is vanishing at \(r=R\) (see right panel of Fig. 3), then the second part at the right hand side of (54) is determined only by the EGB contribution. Then the compactness factor u remains unaltered. Indeed

$$\begin{aligned} u=\frac{M}{R^2}=\frac{M_{EGB}}{R^2}. \end{aligned}$$
(70)

Thus \(z_{s}\) remains unchanged too. Moreover, the corresponding Buchdahl limit [108]

$$\begin{aligned} u_{EGB}\equiv \frac{2M_{EGB}}{R^{2}}\le \frac{3}{4}+\frac{9}{8R^{2}}\alpha \quad \forall \ \alpha >-\frac{R^{2}}{3}, \end{aligned}$$
(71)

is not suffering from any modification. But in the solution B i.e. by imposing \(\hat{\rho }=\theta ^0_0\), it is clear from Fig. 5 (right panel) that the deformation function f(r) is non-vanishing at the surface of the structure, and the function is negative in all its domain (except at \(r=0\)). Thus the possibility of having a more compact object necessarily implies the positiveness of the second term in the right side of Eq. (54).

On the other hand, the case \(0<\beta \) should be investigated carefully. Since for \(0<\beta \), the product \(\beta f(R)\) is always negative, and hence one needs to assure the square bracket in Eq. (54) is also negative in order to produce more compact objects. However, one can find another lower bound for the coupling constant \(\beta \), which is given by

$$\begin{aligned} - \frac{\sqrt{R^{4}+16\alpha M_{EGB}}}{2\alpha |f(R)|}<\beta . \end{aligned}$$
(72)

These results show that \(\beta < 0\) is not special among the family of compact stellar solutions if we want a more compact and dense structure. In this case \(\beta > 0\) is more acceptable to study the stellar structure. Besides that it is not difficult to see the term in the square bracket in Eq. (54) is negative. In view of the above discussion for \(\beta >0 \) and \(f(r) < 0\) for all \(r\in [0,R]\), the total mass will increase and modify the surface redshift, compactness factor and the Buchdahl limit as well. From this perspective, the MGD approach for solution B is more effective than the solution A in the strong field regime.

Next, we will discuss an important source of information is the measurement of surface redshift (z) of the compact star. In the context of EGB gravity, Zhou et al. [109] have pointed out that GB terms will modify the upper bound of redshift of spectral lines from the surface of stars of uniform density. Interestingly, this upper bound is dependent on the value of density rather than a constant in GR counterpart, and thus it is not possible to found an upper bound for the redshift [108, 109]. The surface redshift is given by

$$\begin{aligned} z=\sqrt{e^{-2\nu (r)}}-1. \end{aligned}$$
(73)

From here we get some information about the central \(z_{c}\) and surface \(z_{s}\) redshift. Following the discussion in [109], the central redshift is given by

$$\begin{aligned} z_{c}=B^{-2}-1, \end{aligned}$$
(74)

and the surface redshift reads

$$\begin{aligned} z_{s}= \big [B\,(1+AR^2)\big ]^{-2}-1. \end{aligned}$$
(75)

As we can see from Tables 1 and 2, the central redshift \(z_{c}\) dominates the surface redshift \(z_{s}\) as expected. It is noted that the obtained values for \(z_{s}\) are consistent with the bound proposed in the GR scenario [110].

Table 1 Physical parameters of the MGD solution for \(0.000341\, \text {km}^{-2}\), with different coupling parameters \(\alpha \) and \(\beta \) corresponding solution A
Full size table
Table 2 Physical parameters of the MGD solution for \(0.000341~\text {km}^{-2}\), with different coupling parameters \(\alpha \) and \(\beta \) corresponding solution B
Full size table
Fig. 7
figure 7

The variation of dominant energy conditions versus radial coordinate r/R for solution A

Full size image
Fig. 8
figure 8

The variation of dominant energy conditions versus radial coordinate r/R for solution B

Full size image

6 Energy conditions

We begin this section with a discussion about energy conditions that play an important role in standard GR and are a basis of singularity theorems [111] and entropy bounds [112]. These conditions reflect the microscopic properties of the medium sourcing the energy momentum tensor. Since, the Raychaudhuri equation holds for any geometrical theory of gravitation [113], here we extend our analysis in 5D EGB gravity to check the viability of our proposed model. Thus in this context the energy conditions are just simple constraints on various linear combinations of the energy density and pressure. Now, using the modified gravitational field equations, we discuss four energy conditions which are

$$\begin{aligned} \text {NEC}&: \rho ^{\text {tot}}+ p^{\text {tot}}_{r,t}\ge 0, \end{aligned}$$
(76)
$$\begin{aligned} \text {WEC}&: \rho ^{\text {tot}}\ge 0, \quad \text {and}\quad \rho ^{\text {tot}}+ p^{\text {tot}}_{r,t}\ge 0, \end{aligned}$$
(77)
$$\begin{aligned} \text {SEC}&: \rho ^{\text {tot}}+ p^{\text {tot}}_{r}+2 p^{\text {tot}}_{t}\ge 0, \end{aligned}$$
(78)
$$\begin{aligned} \text {DEC}&: \rho ^{\text {tot}}- p^{\text {tot}}_{r}\ge 0,\quad \text {and}\quad \rho ^{\text {tot}}- p^{\text {tot}}_{t}\ge 0. \end{aligned}$$
(79)

All the above considerations are related to standard matter, and here we will focus only on dominant energy conditions (DEC) only. Because, one can easily verify that the null energy condition (NEC), weak energy condition (WEC) and strong energy condition (SEC) are always satisfied for the model as \(\rho ^{\text {tot}}\ge 0\), \(\rho ^{\text {tot}}+ p^{\text {tot}}_{r,t}\ge 0\) and \(\rho ^{\text {tot}}+ p^{\text {tot}}_{r}+2p^{\text {tot}}_{t}\ge 0\), which is evident from Figs. 2 and 4, respectively. Now, for DEC, we consider graphical discussion rather than exhaustively analytical calculations. Considering Figs. 7 and 8 and the above conditions, we observe DEC is satisfied. So, our model is suitable for consideration.

Fig. 9
figure 9

The variation of sound speed versus radial coordinate r/R for solution A

Full size image

7 Sound speeds and Herrera’s cracking condition

In order for the causality to be preserved, it is natural to require that the sound speed does not exceed the speed of light, i.e. in our units

$$\begin{aligned} \text {V}^2_r = \frac{dp_r^{\text {tot}}}{d\rho ^{\text {tot}}}< 1 \quad \text {and}\quad \text {V}^2_t = \frac{dp_t^{\text {tot}}}{d\rho ^{\text {tot}}} < 1. \end{aligned}$$
(80)

We now proceed to compute \(V^2_{r,t}\) for the stellar solution we have considered so far. Next, by using the Eqs. (11)–(13) we are able to fix the diagrams in Figs. 9 and 10 for both solutions. In both examples shown in Figs. 9 and 10 we see that the causality condition is violated for EGB gravity i.e., when \(\alpha =5, 10\) and \(\beta =0\). This means that the surface pressure decreases as the surface energy density increases, which indicates instability of the configuration for EGB gravity. Whereas in the same figures we see that the causality condition is satisfied for inclusion of \(\beta \), which means compact stars obtained from the MGD approach to gravitational decoupling satisfying the physically acceptable conditions. As we can see from Figs. 9 and 10, one can observe that the radial speed of sound (\(V^2_r\)) is greater than the tangential speed of sound (\(V^2_t\)) throughout the star, and then the quantity \(V^2_r-V^2_t\) will not show any change in sign within the compact objects i.e. no cracking will appear inside the model. Then the our gravitational decoupling model is stable [114, 115].

8 Concluding remarks

Besides their astrophysical interest, compact stars are very promising laboratories to test the viability of alternative theories of gravity. Our main goal in this paper was to develop a formalism for a comprehensive study of stellar structure in Einstein–Gauss–Bonnet (EGB) gravity which is known to be free of ghosts while expanding about the flat space. The key issue of such a model is the minimal geometric deformation (MGD) approach to gravitational decoupling in order to build an exact anisotropic solution of the Tolman–Finch–Skea interior space-time. Applying the MGD-decoupling approach, we successfully decoupled the gravitational source into two sectors, namely: the anisotropic sector corresponding to an anisotropic fluid \(T_{ij}\) and the additional source \(\theta _{ij}\) that proportional to the constant \(\beta \). These two sectors must interact only gravitationally without exchange of energy between them.

The next ingredient in our discussion was the junction conditions at the stellar surface. The surface of the star is defined by the vanishing of the pressure radial i.e., \(P (R) = 0\). In particular, the junction conditions are employed to join two different spherically symmetric spaces, where an interior compact object is matched to an exterior Boulware–Deser vacuum space-time. In particular, the continuity of the second fundamental form in Eq. (64) at the boundary implies that the total radial pressure P(R) must be zero at boundary. The total radial pressure \(P = \hat{p}_r-\beta \,\theta ^1_1\) contains both the non-deformed matter source ı.e., pressure anisotropic and the inner geometric deformation f(r) induced by the energy–momentum \(\theta _{ij}\).

Fig. 10
figure 10

The variation of sound speed versus radial coordinate r/R for solution B

Full size image

Interestingly, the mimic constraint strategy adopted here to close the \(\theta \)-sector after gravitational decoupling, entails some intriguing astrophysical consequences. As extensively discussed above, when the seed radial pressure \(\hat{p}_{r}\) is mimicking (solution A) its simile in the decoupler sector ı.e., \(\theta ^{1}_{1}\), the mass of the fluid sphere remains the same. This is so because the deformation function f(r) is vanishing at the boundary of the structure (see right panel in Fig. 3). Then the effective mass of the fluid sphere is just the original one given by the pure EGB theory. Furthermore, as P should be positive everywhere inside the compact object, the coupling constant \(\beta \) acquires an upper bound, namely \(\beta <1\). This implies that the radial pressure will be greater in magnitude than the seed radial pressure. Consequently, the anisotropic factor will increase in magnitude too. On the other hand, when the seed density \(\hat{\rho }\) is equal to \(\theta ^{0}_{0}\) (solution B) the situation becomes more interesting. In this case, as the total density is proportional to the seed one by a factor of \((1+\beta )\), the system becomes denser and more compact when \(\beta > -1\). However, the situation of physical interest is when \(\beta >0\). Moreover, in this case the radial and transverse pressures increase in magnitude, thus the local anisotropies within the compact object exert a stronger anisotropy gradient helping to counteract the gravitational attraction. From the astrophysical point of view, it is evident that the solution B entails a more exciting situation. As the mass is changing the redshift and compactness parameters also do (see Fig. 6). Then one differentiates (hypothetically speaking) between a non-minimally deformed and minimally deformed spacetimes. Notwithstanding, in the solution A as the total mass remains exactly the same (the stage before of introducing the MGD), it is not possible to distinguish between the seed and deformed solution.

As can be seen, the gravitational decoupling by means of MGD approach, seems to be a good technique to introduce new ingredients and understand easily some effects incorporated by an anisotropic stellar matter distribution. Besides, the methodology is capable of “convert” non-well behaved seed solutions into a well-behaved one after applying the deformation process. Although it cannot be guaranteed that this will happen in all cases, other models of stellar interiors in high dimensions have already been reported [69] where the seed spacetime is not well behaved and after applying MGD the structure satisfies all the necessary requirements that any astrophysical system should meet. Then gravitational decoupling by minimal geometric deformation could be seen as a regulator process in making the transition from undeformed non-well behaved stellar interior to a minimally deformed well-behaved one. Of course, the warrant of the above argument deserves a more in-depth and detailed investigation. So, in summary one can conclude that the MGD after gravitational decoupling, constitutes a simple and powerful tool to deal with a complicated set of equations, leading to an anisotropic compact object, respecting all the physical and mathematical requirements in order to represent realistic celestial bodies (at least from a theoretical point of view).