1 Introduction

Various modifications of Einstein’s general relativity have been emerged to address several shortcomings coming out in the study of the evolution of Universe. In particular, instead of introducing unknown fluids, the gravity action may be modified by adding higher curvature corrections to the Einstein action. Nonetheless, as found by Lovelock in the 1970s [1] (see [2] for reviews on this topic) the most general second order gravity theories in higher dimensional spacetimes. From an epistemological point of view, Lovelock gravity obeys generalized Bianchi identities which ensure energy conservation i.e., \(\Delta ^{\mu } T_{ij}=0\), and it is known to be free of ghosts [3, 4]. Such theory is physically motivated and capable of addressing phenomenology at galactic, extragalactic, and cosmological scales [5]. In five dimensions, the Lovelock Lagrangian consists of cosmological constant and the Einstein–Hilbert action, respectively, while the second order term is the Gauss–Bonnet (GB) Lagrangian. This leading to second order equations for the metric, so-called Einstein–Gauss–Bonnet (EGB) theory or Lovelock theory up to second order.

The EGB gravity theory has attracted serious attention over a wide span of years, because it can be obtained in the low energy effective action of heterotic string theory [6, 7]. In fact, the existence of spherically symmetric static black hole solutions in such theories has been known for a long time [8]. Followed by this, many other aspects like thermodynamic properties associated with black hole horizon and cosmological horizon have been studied for the GB solution in de Sitter and anti-de Sitter (AdS) space [9, 10]. Furthermore, there are also numerous solutions corresponding to black hole have also been intensively investigated by some authors, see e.g. Refs. [11,12,13,14,15]. A broad avenue followed by many astrophysical solution such as the gravitational collapse of an incoherent spherical dust cloud [16,17,18,19], geodesic motion of a test particle [20], the phase transition of RN-AdS black holes [21], Hawking evaporation of AdS black holes [22], radius of photon spheres [23], regular black hole solutions [24] and wormhole solutions satisfying the energy conditions was proposed in [25, 26]. There is considerable effort [27,28,29,30] to study the mass–radius relation of compact stars in EGB theories of gravity.

Investigation of EGB gravity could also be interesting for the possibility of addressing some problems in strong field regimes. In this direction the study of the stellar structure can also provide important constraints on modified theories of gravity under consideration. Presently, a large number of mass–radius relations are available form electromagnetic, and more recently gravitational-wave (GW), observations of extreme phenomena, such as short gamma-ray bursts (SGRBs). Moreover, the observational evidence for neutron stars (NSs) with masses around 2 \(M_{\odot }\) [31, 32] provide a strong constraint on the theoretical construction of the NS equation-of-state (EoS). But, the constitution and internal structure of relativistic compact objects is not known in detail.

Under the assumption of static and spherical symmetry, a large number of solutions of Einstein’s gravitational field equations describing the interior structure of relativistic compact objects have been obtained. But it is always a difficult task to derive physically acceptable exact solutions in GR due to the complexity of the Einstein field equations. This situation becomes more complicated when we deal with modified theories of gravity. It is for this reason that researchers use a variety of mathematical techniques to attain exact solutions. Several such ideas have been explored including an algorithm based on the choice of a single monotone function which generates all regular static spherically symmetric perfect-fluid solutions of Einstein’s equations [33] and its extension to locally anisotropic fluids in [34]. On the other hand, there is freedom in choosing the specific interior solution for the compact star. The first exact solution of Einstein’s field equations was obtained by Schwarzschild in 1916 [35], which allowed us to make many physical predictions with increased precision. The simplest model for describing stellar interior was initially proposed by Tolman [36] using spherically symmetric perfect fluid solutions of the Einstein equations.

In recent times there is another approach to decoupling gravitational sources in GR, which was developed from the so-called Minimal Geometric Deformation (MGD) approach. The MGD approach was initially proposed in [37, 38] to study the exterior geometry around spherically symmetric spacetime with a perfect fluid source in the context of Randall–Sundrum brane-world gravity. Before discussing literature review for the MGD works, we highlight the origin of the gravitational decoupling (GD) which is to adopt a simple matter distribution \({T}_{i j}\) and then extended to a more complex source without violating the spherically symmetry condition by adding a new source through a dimensionless coupling constant \(\beta \) as

$$\begin{aligned} T_{ij}\mapsto & {} {\tilde{T}}^{(1)}_{ij}=T_{ij}+\beta ^{(1)}\,{\hat{T}}^{(1)}_{ij}. \end{aligned}$$
(1)

Similarly we can extend the new energy momentum tensor \({\tilde{T}}^{(1)}_{ij}\) as,

$$\begin{aligned} {\tilde{T}}^{(1)}_{ij}\mapsto & {} {\tilde{T}}^{(2)}_{ij}={\tilde{T}}^{(1)}_{ij}+\beta ^{(2)}\,{\hat{T}}^{(2)}_{ij} \end{aligned}$$
(2)

and repeat the similar procedure up to n times. Using this procedure, the simple initial solution of Einstein–Gauss–Bonnet (EGB) field equation linked with the source \(T_{ij}\) can be extended into more generalised form associated with the source \(T_{ij}={\tilde{T}}^{(n)}_{ij}\), step by step and systematically. This is a new procedure to anisotropise the initial or seed solutions obtained from perfect fluid matter distributions. It is necessary to highlight that each distinct component for the source \({T}^{n}_{ij}\) is independently conserved, i.e.

$$\begin{aligned} \nabla ^i {\tilde{T}}_{ij}=\nabla ^i {T}^{(1)}_{ij} = \nabla ^i {T}^{(2)}_{ij}= \cdots = \nabla ^i {T}^{(n)}_{ij}=0. \end{aligned}$$
(3)

Furthermore, this MGD technique can be also applied in reverse order as well to find solution for the self-gravitating compact objects. For applying this reverse procedure, initially we need to separate more complex energy–momentum tensor (EMT) \(T^{*}_{ij}\) into many distinct and simpler EMT components such as \({T}^{1}_{ij},~{T}^{2}_{ij},\ldots ,{T}^{n}_{ij}\) (\(n-components\)). After these separations, the field equations corresponding to each distinct EMT components is solved individually and obtain several solutions associated with the above distinct source \({T}^{n}_{ij}\). At last, the complete solution of the field equations for the original EMT \({T^{*}}_{ij}\) can be achieved by combining of above each distinct solution for \(T^{n}_{ij}\) source through decoupling constant \(\beta \). Particular, this procedure can be understand through a specific example, which is given as: suppose the \(g_{ij}\) metric associated with total energy–momentum tensor (EMT) \(T_{ij}\) which is connected to field equations

$$\begin{aligned} G_{ij}+\alpha H_{ij} = 8\pi T_{ij}, ~~~\text {where}~~~~ T_{ij} ={\hat{T}}_{ij} + \beta \, \theta _{ij},~~~~ \end{aligned}$$
(4)

where \({\hat{T}}_{ij}\) is source EMT and \(\theta _{ij}\) is additional gravitational anisotropic source of EMT connected to metric \({\hat{g}}_{ij}\) and \(g^{\theta }_{ij}\), respectively whose field equations are,

$$\begin{aligned}&{\hat{G}}_{ij}+\alpha {\hat{H}}_{ij} = 8\pi {\hat{T}}_{ij},~~~~ \text {to find~} \{{\hat{g}}_{ij}, {\hat{T}}_{ij}\} \end{aligned}$$
(5)
$$\begin{aligned}&G^{\theta }_{ij}+\alpha H^{\theta }_{ij} = 8\pi T^{\theta }_{ij}, ~~~~\text {to find~ } \{g^{\theta }_{ij}, {\theta }_{ij}\} \end{aligned}$$
(6)

After solving both systems, we can find the gravitational potential \(g_{ij}\) by combining of \({\hat{g}}_{ij}\) and \(g^{\theta }_{ij}\). This procedure can be continued many times based on specified number of gravitational sources. In each iterations, we have to deduce EMT, and ‘merge’ together the connected gravitational potentials of the total EMT. Indeed, by using this approach, an exact and physically acceptable solution have been found, see Refs. [39,40,41,42,43]. Extending the isotropic version an anisotropic solutions for self-gravitating systems from perfect fluid solutions were studied in [44, 45]. MGD-decoupling methods represent a realistic algorithm that generate physically acceptable interior solutions for stellar systems (for reviews see [46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68]). Further, the MGD approach has been applied to study extensions of the theory of GR in a cosmological context [69]. This method is successfully applied in black hole scenarios [70,71,72,73,74,75,76] and one can extended to convert any non-rotating black hole spacetime into a rotating one [77, 78]. According to the literature mentioned above, investigations of the structure of compact stars are carried out under the supposition that their matter is described by an anisotropic fluid [79, 80]. In the present paper our goal will be to examine the possibility of existing charged compact spheres in 5D EGB gravity made of a charged fluid in the background of EGB gravity via the MGD approach, which allows us to prove that the fluid must be anisotropic. An interesting result of this analysis is that the introduction of MGD in the self-gravitating system enhances the mass and stability of the model.

The present paper is organized as follows: After a brief introduction in Sect. 1, we review the fundamentals of the MGD-decoupling applied to a static and spherically symmetric configuration made of a charged perfect fluid within the framework of EGB gravity in Sect. 2. Section 3 is devoted to study stellar interior solution generated by using the well known Krori–Barua spacetime through the MGD approach, which contains two subsections namely, Sect. 3.1: mimicking of the density constraint (\(\rho +\frac{E^2}{8\pi }=\theta ^0_0\)), and Sect. 3.2: mimicking of the pressure constraint (\(\theta ^1_1={\hat{p}}_r\)). In Sect. 4 we match of the interior solution governed by the anisotropic fluid to an exterior Boulware–Deser vacuum solution at a junction interface. Section 5 is devoted to study the physical properties of compact stars that obtained from the MGD approach to gravitational decoupling. Under this constraint, we emphasize all the possible situation where EGB gravity lead to significant deviations from GR and EGB+MGD separately.We draw final conclusions from our results in Sect. 6

2 Basic equations of EGB gravity under gravitational decoupling

The gravitationally decoupled action for the 5D EGB gravity with matter field reads:

$$\begin{aligned} {\mathcal {I}}_{G}= & {} \frac{1}{16 \pi }\int d^{5}x\sqrt{-g}\left[ R-2\Lambda +\alpha {\mathcal {L}}_{\text {GB}} \right] + {\mathcal {S}}_{\text {m}}\nonumber \\&+\int \left( {\mathcal {S}}_{E}+\beta {\mathcal {S}}_{\theta } \right) \sqrt{-g}~d^{5}x, \end{aligned}$$
(7)

where R and \(\Lambda \) are the 5D Ricci scalar and the cosmological constant, respectively. The term \({\mathcal {S}}_{\text {m}}\) is the matter action, while \({\mathcal {S}}_{E}\) and \({\mathcal {S}}_{\theta }\) represent the Lagrangian for electromagnetic field tensor and the Lagrangian density of the new source not described by standard EGB gravity. This new sector always can be seen as corrections to 5D EGB and be consolidated as part of an effective energy–momentum tensor \(\theta _{ij}\). The main purpose of introducing this extra source in original action (7) is to generalize perfect fluid charge matter distribution to anisotropic domain using gravitational decoupling approach. The Gauss–Bonnet (GB) constant \(\alpha \) is related with the inverse string tension with dimension of [\(\text {length}\)]\(^2\), while \(\beta \) is dimensionless. Within string theory, in five dimensions \(\alpha \) can be considered as an arbitrary real number with the appropriate dimensions, but here we consider the positive value of \(\alpha \), see Ref. [81, 82] for more. The Gauss–Bonnet Lagrangian \({\mathcal {L}}_{\text {GB}}\) is defined in terms of Ricci scalar, Ricci tensor, and Riemann curvatures,

$$\begin{aligned} {\mathcal {L}}_{\text {GB}}=R^{ijkl} R_{ijkl}- 4 R^{ij}R_{ij}+ R^2. \end{aligned}$$
(8)

Varying the action (7) with respect to the metric, one obtains the following gravitational field equations

$$\begin{aligned} G_{ij}+\alpha H_{ij} = 8 \pi (T_{ij}+E_{ij}) ~,~~\text{ where }~~~T_{ij}= {\hat{T}}_{ij}+\beta \,\theta _{ij},\nonumber \\ \end{aligned}$$
(9)

with

$$\begin{aligned}&{\hat{T}}_{ij}=-\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}{\mathcal {S}}_m\right) }{\delta g^{ij}}, \end{aligned}$$
(10)
$$\begin{aligned}&\theta _{ij}=\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}{\mathcal {S}}_\theta \right) }{\delta g^{ij}}, \end{aligned}$$
(11)
$$\begin{aligned}&{E}_{ij}=\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}{\mathcal {S}}_E\right) }{\delta g^{ij}}. \end{aligned}$$
(12)

where \(G_{ij}\) is the Einstein tensor and \(H_{ij}\) is the contribution of the GB term with the following expression

$$\begin{aligned} G_{ij}= & {} R_{ij}-\frac{1}{2}R~ g_{ij}, \nonumber \\ H_{ij}= & {} 2\Big ( R R_{ij}-2R_{ik} {R}^k_j -2 R_{ijkl}{R}^{kl} - R_{ikl\delta }{R}^{kl\delta }_j\Big )\nonumber \\&- \frac{1}{2}~g_{ij}~{\mathcal {L}}_{\text {GB}}, \end{aligned}$$
(13)

and \({\hat{T}}_{\mu \nu }\) is usually associated with some known solution of EGB gravity with \(\theta _{\mu \nu }\) may contain new fields or a new gravitational sector. Interestingly, this source may contain new fields, like scalar, vector and tensor fields, and it will generally produce anisotropies in self-gravitating systems. Moreover, it is noted that the GB term has no effect on the gravitational dynamics in 4D spacetime i.e., \(H_{ij} \equiv 0\), since it becomes a total derivative.

Consider the following line element in curvature coordinates for a static and spherically symmetric metric in 5D spacetime

$$\begin{aligned} ds^2_{5}= - e^{2\nu (r)} dt^2 + e^{2\lambda (r)}dr^2 + r^{2} d \Omega ^2_3, \end{aligned}$$
(14)

where the metric potentials \(\nu (r)\) and \(\lambda (r)\) are radial dependent functions and denoted the mass and the redshift functions, respectively. In the above expression \( d \Omega ^2_3\) is the metric of a 3-sphere. To achieve our goal for charged compact star, we first consider the perfect fluid form of the energy–momentum tensor, \({\hat{T}}_{ij}\), given by

$$\begin{aligned} {\hat{T}}_{ij} = \left( {\hat{\rho }}+{\hat{p}}\right) u_{i}u_{j}+{\hat{p}} g_{ij}, \end{aligned}$$
(15)

where \({\hat{\rho }}(r)\) is the energy density, \({\hat{p}}(r)\) is the pressure of the fluid which are measured by local observer, respectively, and \(u^{j}\) is the five-velocity satisfying the conditions \(u^{j}u_{j}=-1\).

The electromagnetic energy–momentum tensor of Eq. (9) is is given in terms of the Faraday–Maxwell tensor \(F_{ij}\) by the relation

$$\begin{aligned} E_{ij}=\frac{1}{4\pi }\left( F_{i}^{\gamma }F_{j\gamma }- \frac{1}{4}g_{ij} F_{\gamma \beta }F^{\gamma \beta }\right) . \end{aligned}$$
(16)

Since, \(F_{ij}\) satisfies the covariant Maxwell equations

$$\begin{aligned}{}[(-g)^{1/2} F^{j i}]_{, i} = 2\pi ^2 J^{j} (-g)^{1/2}, \end{aligned}$$
(17)

where \(J^i\) is the five-current density. Since the present choice for static stellar configurations, the only non-vanishing component of Maxwell’s tensor is \(F^{01}\) and the last equation is satisfied if \(F^{01}= -F^{10}\). From Eq. (16) one obtains the following expression for the electric field,

$$\begin{aligned} E(r) = F^{01}(r)= \frac{1}{r^2} e^{-(\nu + \lambda )} 2\pi ^2 \int _{0}^{r} r'^3 \rho _{ch} e^{ \lambda } dr', \end{aligned}$$
(18)

where \(\rho _{ch} = e^{\nu }j^{0}(r)\) is the electric charge distribution inside the star, and the charge of the system is defined as

$$\begin{aligned} q(r) = 2\pi ^2 \int _{0}^{r} r'^3 \rho _{ch} e^{\lambda } dr', \end{aligned}$$
(19)

which does not depend on the timelike coordinate t, or equivalently

$$\begin{aligned} q'(r) = 2 \pi ^2 r^3 \rho _{ch} e^{\lambda }, \end{aligned}$$
(20)

where the electric charge is connected to the electric field through the relation \(E(r)=q(r)/r^2\).

It is noted that if the new gravitational sector \(\theta _{ij}\) follows the relation \(\theta ^1_1-\theta ^2_2\ne 0\), then the matter distribution inside the fluid sphere will no longer remain in perfect fluid form. This leads to the system as an anisotropy fluid sphere. Assuming this we define the effective stress-energy tensor \(T_{ij}\),

$$\begin{aligned} T_{ij} = (\epsilon + P_{\perp })\,u_{j} u_{j}+ P_{\perp }\, g_{ij}+(P-P_{\perp })\chi _{i}\,\chi _{j}, \end{aligned}$$
(21)

where \(\chi ^i=\sqrt{1/g_{rr}}\,\delta ^i_1\) is the unit space-like vector in the radial direction, satisfying \(\chi ^i\chi _i=1\). Here, the radial and tangential pressures are given by \(P_r={\hat{p}}-\beta \,\theta ^1_1\) and \(P_{\perp }={\hat{p}}-\beta \,\theta ^2_2\), and the energy density for the effective stress-energy tensor is given by \(\epsilon ={\hat{\rho }}+\beta \,\theta ^0_0\), respectively. Moreover, the anisotropy of the decoupled system is,

$$\begin{aligned} \Pi =P_\perp -P_r=\beta \,\Pi _{\theta },~~~\text {where}~\Pi _{\theta }= \theta ^1_1-\theta ^2_2. \end{aligned}$$
(22)

It is obvious that EGB gravity satisfies the Bianchi Identity which give conservation equation of the energy–momentum tensor, \(\nabla ^i\,T_{ij}=0\), which yield

$$\begin{aligned} -{\nu ^\prime }(\epsilon +P_r)-P^{\prime }_r+\frac{3 \Pi }{r}+\frac{E\,E^{\prime }}{4\pi }+\frac{3E^2}{4\pi r}=0. \end{aligned}$$
(23)

The Eq. (23) is the hydrostatic equation for 5D EGB gravity. Now, inserting Eqs. (12) and (21) into the equation of motion (9), the components of the field equations become

$$\begin{aligned} 8 \pi \epsilon +E^2= & {} \frac{-3}{e^{4 \lambda } r^{3}} \big [ 4 \alpha \lambda ^{\prime } - r e^{4 \lambda } - e^{2 \lambda } ( r^{2} \lambda ^{\prime }\nonumber \\&+ 4 \alpha \,\lambda ^{\prime }-r) \big ], \end{aligned}$$
(24)
$$\begin{aligned} 8 \pi P_r-E^2= & {} \frac{3}{e^{4 \lambda } r^{3}} \big ( \left( r^{2} \nu ^{\prime } + r + 4 \alpha \nu ^{\prime } \right) e^{2 \lambda } - r e^{4 \lambda }\nonumber \\&- 4 \alpha \nu ^{\prime } \big ), \!\!\!\!\!\!\!\!\! \end{aligned}$$
(25)
$$\begin{aligned} 8 \pi P_{\perp }+E^2= & {} \frac{1}{e^{4 \lambda } r^{2}} \big ( -e^{4 \lambda } - 4 \alpha \nu ^{\prime \prime } + 12 \alpha \nu ^{\prime } \lambda ^{\prime } - 4 \alpha \nu ^{\prime 2} \big ) \nonumber \\&+ \frac{1}{e^{2 \lambda } r^{2}} \big ( 1 - r^{2} \nu ^{\prime } \lambda ^{\prime } + 2 r \nu ^{\prime } - 2 r \lambda ^{\prime } + r^2\,\nu ^{\prime \,2} \big ) \nonumber \\&+ \frac{1}{e^{2 \lambda } r^{2}} \left( r^{2} \nu ^{\prime \prime } - 4 \alpha \nu ^{\prime } \lambda ^{\prime } + 4 \alpha \, \nu ^{\prime 2} + 4 \alpha \nu ^{\prime \prime } \right) .\nonumber \\ \end{aligned}$$
(26)

where prime denotes the differentiation with respect to redial coordinate. The continuity equation (23) follows

$$\begin{aligned}&-{\nu ^\prime }(\epsilon +P_r)-P^{\prime }_r+\frac{3 \Pi }{r}+\frac{E\,E^{\prime }}{4\pi }+\frac{3E^2}{4\pi r}=0~\nonumber \\&\quad \Longrightarrow ~{\nu ^\prime }({\hat{\rho }}+{\hat{p}})+{\hat{p}}^\prime -\frac{q\,q^{\prime }}{4\pi \,r^4}-\frac{q^2}{4\pi r^5} + \beta \,\Big [{\nu ^\prime }(\theta ^0_0-\theta ^1_1)\nonumber \\&\qquad -(\theta ^1_1)^\prime +\frac{3\Pi _{\theta }}{r}\Big ]=0.~~ \end{aligned}$$
(27)

We have also focused our attention on the parameter \(\beta \) to consider the effects of the additional source term \(\theta _{ij}\) on the perfect fluid sphere. These effects can be encoded in the geometric deformation approach [83] where the metric functions are deformed as

$$\begin{aligned} \nu (r)\longrightarrow & {} \xi (r)+\beta \, h(r), \end{aligned}$$
(28)
$$\begin{aligned} e^{-2\lambda (r)}\longrightarrow & {} \mu (r)+\beta \, f(r), \end{aligned}$$
(29)

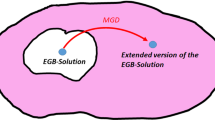
where \({h~\text {and}~ f }\) are the geometric deformations undergone by the radial and temporal metric components and \(\beta \) is a free parameter that controls the deformation. It is worthwhile to mention here that if \(\beta =0\) one may recover the domain of EGB gravity. The Fig. 1 shows that how the pure EGB solutions can be extended via MGD to anisotropic domains. Since we use the deformation along only one metric function, specifically called a minimal geometric deformation (MGD) approach, therefore we shall restrict our-self in the particular case of \( h(r) = 0\) with \(f(r)\ne 0\) which implies that the temporal deformation is unchanged. Thus, the metric in Eq. (12) is minimally deformed by \(\theta _{ij}\) source.

Fig. 1
figure 1

The above diagram describes that how pure EGB solutions can be extended via MGD to anisotropic domains

Full size image

The next task is to separate the gravitational field equations (16)–(18) into two sets: the first set of equations for EGB gravity under charge matter distributions, and the second set of equations corresponds to the \(\theta \)-sector. In arriving at the first set of equations we have used linear decomposition (21) corresponding to \(\beta = 0\), and depending on the gravitational potentials \(\mu \) and \(\nu \) the system reduces to

$$\begin{aligned} 8 \pi {\hat{\rho }}+E^2= & {} \frac{1}{2r^3} \big [12\alpha \mu ^\prime (\mu -1)-3 r (\mu ^\prime r+2 \mu -2)\big ],~~~~~\nonumber \\ \end{aligned}$$
(30)
$$\begin{aligned} 8 \pi {\hat{p}}-E^2= & {} \frac{1}{r^3} \big [12 \alpha \nu ^\prime \mu (1- \mu )+3\,r (\nu ^\prime \mu r+\mu -1)\big ],~~~~~\nonumber \\ \end{aligned}$$
(31)
$$\begin{aligned} 8 \pi {\hat{p}}+E^2= & {} \frac{1}{2r^2}\big [-8\alpha \mu (\mu -1) (\nu ^{\prime \prime }+\nu ^{\prime 2})+4\alpha \mu ^\prime \nu ^\prime \nonumber \\&\times (1-3 \mu )+2 \mu (\nu ^{\prime \prime } r^2 +\nu ^{\prime 2} r^2+2 \nu ^\prime r+1)\nonumber \\&+\mu ^\prime \nu ^\prime r^2+2 \mu ^\prime r-2 \big ].~~~~ \end{aligned}$$
(32)

With this separation the Eq. (19) reduce to

$$\begin{aligned} {\nu ^\prime }({\hat{\rho }}+{\hat{p}})+{\hat{p}}^\prime -\frac{q\,q^{\prime }}{4\pi \,r^4}+\frac{q^2}{4\pi r^5}=0, \end{aligned}$$
(33)

and the interior spacetime turns out to be

$$\begin{aligned} ds^2_{5}= - e^{2\nu (r)} dt^2 + \frac{dr^2}{\mu (r)} + r^{2} d \Omega ^2_3. \end{aligned}$$
(34)

The second set contains the source \(\theta _{ij}\) and reads

$$\begin{aligned} 8 \pi \theta _0^0= & {} \frac{3}{2r^3} \big [ 4\alpha (f^\prime (f \beta +\mu -1)+\mu ^\prime f)\nonumber \\&-r (f^\prime r+2 f)\big ], \end{aligned}$$
(35)
$$\begin{aligned} 8 \pi \theta _1^1= & {} -\frac{3f}{r^3} \big [\nu ^\prime \, (-4\,\alpha \, f \beta -8\,\alpha \, \mu +4\,\alpha +r^2)+r\big ], \end{aligned}$$
(36)
$$\begin{aligned} 8 \pi \theta _2^2= & {} -\frac{1}{2r^2}\,\big [-4\alpha \,\{2 \nu ^{\prime \prime }\, f\, (f \beta +2 \mu -1)+f^\prime \nu ^\prime (3 f\beta \nonumber \\&+3 \mu -1)+\nu ^\prime f (3 \mu ^\prime +2 \nu ^\prime (f \beta +2 \mu -1))\}\nonumber \\&+2 f^\prime \, r +f^\prime \nu ^\prime \, r^2+2 f \, (\nu ^{\prime \prime } r^2+\nu ^{\prime 2} r^2+2 \nu ^\prime r+1)\big ].\nonumber \\ \end{aligned}$$
(37)

As for the matter energy–momentum tensor, the conservation equation (23) yields \(\nabla ^i\,\theta _{ij}=0\), which leads to the expression

$$\begin{aligned} {\nu ^\prime }(\theta ^0_0-\theta ^1_1) -(\theta ^1_1)^\prime -\frac{3\Pi _{\theta }}{r}=0. \end{aligned}$$
(38)

Separation of two sets of equations implies that we have successfully decoupled the two sources \(T_{ij}\) and \(\theta _{ij}\) by means of the MGD. In [84] it was shown that there is no exchange of energy–momentum between \(T_{ij}\) and \(\theta _{ij}\), so that their interaction is purely gravitational.

3 Minimally deformed charged stellar model

As a consequence of deformations in radial and temporal metric functions, we have now two sets of equations (22–24) and (26–28), which are highly non-linear differential equations in \(\nu \), \(\mu \) and f, respectively. Since, the second set of equations are dependent on the first set of equations and thus the system of equations is underdetermined. Here, our main findings is to build an exact and physically acceptable solution by using the MGD approach [84] in 5D EGB gravity.

The first step is to turn off \(\beta \) and find a solution for charged perfect fluid EGB Eqs. (22–24). We called it a seed solution. Since the electrically charged fluid with isotropic pressure constitutes the next level of physical complexity, thus we decide to choose a simple and known solution with physical relevance, namely, the Krori–Barua (KB) metric ansatz. The Krori–Barua spacetime has widely been used for studying static and spherically static compact objects in GR [85,86,87] as well as in modified theories of gravity [88,89,90,91]. The KB spacetime is specified by the following metric functions

$$\begin{aligned} \nu (r)=(Ar^2+B)~~~~\text {and}~~~~\mu (r)=e^{-Cr^2}, \end{aligned}$$
(39)

where A and C are positive constants with dimension of \([\text {Length}]^{-2}\) and B is a constant without dimension. In our view, the above form of metric potentials will serve our purpose, and decoupling function f(r) should be tractable. Subsequently, based on metric potentials, the solution of Eqs. (22)–(24) become

$$\begin{aligned} 8\pi \,{\hat{\rho }}= & {} \!\! \frac{e^{-2 C r^2}}{r^2}\Big [ e^{C r^2} \left( A C r^4\!\!-2 A^2 r^4+4 C r^2\!\!+2 e^{C r^2}\!\!-2\right) \nonumber \\&-4 \alpha \Big \{2 A^2 r^2 \left( e^{C r^2}-1\right) +A \big (3 C r^2\nonumber \\&-e^{C r^2} \left( C r^2+2\right) +2\big )-3 C (e^{C r^2}-1)\Big \} \Big ], \end{aligned}$$
(40)
$$\begin{aligned} 8\pi \,{\hat{p}}= & {} \frac{e^{-2 C r^2}}{r^2} \Big [4 \alpha A \Big (e^{C r^2} \left( 2 A r^2-C r^2+4\right) -2 A r^2 \nonumber \\&+3 C r^2-4\Big )-e^{C r^2} \big (-2 A^2 r^4+A C r^4-6 A r^2\nonumber \\&+C r^2+2 e^{C r^2}-2\big )\Big ], \end{aligned}$$
(41)
$$\begin{aligned} E^2= & {} \frac{e^{-2 C r^2}}{r^2} \Big [ 4 \alpha A \Big (e^{C r^2} \left( 2 A r^2-C r^2-2\right) -2 A r^2 \nonumber \\&+3 C r^2 +2\Big )+e^{C r^2} \big (2 A^2 r^4-C \left( A r^4+r^2\right) \nonumber \\&+e^{C r^2}-1\big )\Big ]. \end{aligned}$$
(42)

With the same metric functions, the \(\theta \)-sector components (26–28) are given by

$$\begin{aligned} 8\pi \,\theta ^0_0= & {} \frac{1}{2 r^3}\Big [3 \Big (4 \alpha e^{-C r^2} \Big \{\zeta (r) e^{C r^2} (f(r) \beta -1)-2 C f(r) r\nonumber \\&+\zeta (r)\Big \}-r [\zeta (r) r+2 f(r)]\Big )\Big ], \end{aligned}$$
(43)
$$\begin{aligned} 8\pi \,\theta ^1_1= & {} -\frac{3 f(r) \Big (8 \alpha A \left( 1-2 e^{-C r^2}-f(r) \beta \right) +2 A r^2+1\Big )}{r^2},\nonumber \\~~~~ \end{aligned}$$
(44)
$$\begin{aligned} 8\pi \,\theta ^2_2= & {} - \frac{1}{r^2} \Big [f(r) \Big (\frac{4 \alpha A}{e^{C r^2}} \big (e^{C r^2} \left( 4 A r^2-3 \zeta (r) \beta r+2\right) -8 A r^2 \nonumber \\&+\, 6 C r^2-4\big )+4 A^2 r^4+6 A r^2+1\Big )+\zeta (r) r \big [4 \alpha A (1 \nonumber \\&-3 e^{-C r^2})+A r^2+1\big ]-8 \alpha A f^2(r) \beta (2 A r^2 +1)\Big ], ~~~\nonumber \\ \end{aligned}$$
(45)

where \(\zeta (r) =df/dr\). Now, we need to define the deformation function f(r) to get the complete spacetime geometry for gravitationally decoupled system. In the following, we adopt the well-known mimic approach [84], which have two avenues (i) mimicking of \(\theta ^0_0\) with the \({\hat{\rho }}+\frac{E^2}{8\pi }\), and (ii) \(\theta ^1_1\) mimicking with only radial pressure (\({\hat{p}}_r)\). We now discuss step by step

3.1 Mimicking of \(\theta ^0_0\) with \((\rho +\frac{E^2}{8\pi })\): \(\rho +\frac{E^2}{8\pi }=\theta ^0_0\)

Using Eqs. (24) and (29), we find the differential equation of the form,

$$\begin{aligned}&3 [4 \alpha (f^{\prime } (f k+\mu -1)+\mu ^{\prime } (f-\mu +1))+r (-f^{\prime } r+\mu ^{\prime } r\nonumber \\&\quad -2 f+2 \mu -2)]=0,~~~ \end{aligned}$$
(46)

After plugging the spacetime geometry (33), the solution of differential equation yield the deformation function f as,

$$\begin{aligned} f(r)= & {} -4 \alpha e^{-C r^2}+4 \alpha + r^2-e^{-C r^2} \nonumber \\&\quad \times \sqrt{16 \alpha ^2 \left[ \frac{(1+F \beta ^2)}{e^{-2 C r^2}}-\frac{2 (\beta +1)}{e^{-C r^2}} +\beta +1\right] +\Psi _1(r)}, \nonumber \\~~~ \end{aligned}$$
(47)

where

$$\begin{aligned} \Psi _1(r)=8 \alpha (\beta +1) r^2 e^{C r^2} \left( e^{C r^2}-1\right) +r^4 e^{2 C r^2}. \end{aligned}$$

and F is constant of integration which is be determined by setting the necessary condition \(f(0)=0\) that yields \(F=\frac{1}{\beta }\). After substituting F in (47), we get

$$\begin{aligned} f(r)= & {} \frac{1}{4 \alpha \beta }\Bigg [-e^{-C r^2} \sqrt{16 \alpha ^2 (\beta +1) \left( e^{C r^2}-1\right) ^2+\Psi _1(r)}\nonumber \\&-4 \alpha e^{-C r^2}+4 \alpha +r^2\Bigg ]. ~~~ \end{aligned}$$
(48)

3.2 Mimicking of \(\theta ^1_1\) with \({\hat{p}}_r\): \(\theta ^1_1={\hat{p}}_r\)

Using Eqs. (31) and (36), we find the differential equation of the form,

$$\begin{aligned}&4 \alpha \bigg [2 \nu ^{\prime \prime } (\mu -1) \mu r+2 \nu ^{\prime 2} (\mu -1) \mu r+\nu ^{\prime } \big (12 f^2 \beta -6 \mu \mu ^2\nonumber \\&\quad +6+12 f (2 \mu -1)-\mu ^{\prime } r+3 \mu ^{\prime } \mu r\big )\bigg ]-r \bigg [2 \mu ^{\prime } r-8\nonumber \\&\quad +\mu ^{\prime } \nu ^{\prime } r^2 +12 f (1+\nu ^{\prime } r)\nonumber \\&\quad +2 \mu \left( 4+5 \nu ^{\prime } r+\nu ^{\prime \prime } r^2+\nu ^{\prime 2} r^2\right) \bigg ]=0,~~ \end{aligned}$$
(49)

Again plugging the metric functions \(\mu \) and \(\nu \) from Eqs.(39) into Eq.(49) and integrate for f, we find deformation function f(r) as,

$$\begin{aligned} f(r)= & {} \frac{1}{48 \alpha A \beta } e^{-2 C r^2}\Big [- \sqrt{3 \Psi _2(r)}-48 \alpha A e^{C r^2}+24 \alpha A \nonumber \\&\times e^{2 C r^2}+6 A r^2 e^{2 C r^2}+3 e^{2 C r^2}\Big ].~~ \end{aligned}$$
(50)

with

$$\begin{aligned} \Psi _2(r)= & {} e^{2 C r^2} \Bigg [3 \left( 8 \alpha A \left( e^{C r^2}-2\right) +\left( 2 A r^2+1\right) e^{C r^2}\right) ^2\\&-32 \alpha A \beta \Big (e^{C r^2} \big (-2 A^2 r^4+A C r^4-6 A r^2+C r^2\\&+2 e^{C r^2}-2\big )-4 \alpha A \big (e^{C r^2} \left( 2 A r^2-C r^2+4\right) \\&-2 A r^2+3 C r^2-4\big )\Big )\Bigg ]. \end{aligned}$$

Since we have generated deformation function f(r) by using the mimic approaches which determines the components of \(\theta \)-sector. Then the deformed charged solution for the system of field Eqs. (24)–(26) in EGB gravity can be given by the following spacetime,

$$\begin{aligned} ds^2_{5}= - e^{2(Ar^2+B)} dt^2 + \frac{e^{Cr^2}}{1+\beta \,f(r)\,e^{Cr^2}} dr^2 + r^{2} d \Omega ^2_3,\nonumber \\ \end{aligned}$$
(51)

where, f(r) is given in Eqs. (48) and (50). Now, we will move to the boundary conditions in order to find the constant parameters involve in the solutions.

4 Matching conditions

We now specialize the exterior geometry to charged Boulware–Desser solution [8] (see [92] for more). Here, we match the internal solution described by Eq. (12) to the exterior vacuum solution, and the metric takes the simple form

$$\begin{aligned} ds^2_{5} = -{\mathcal {F}}(r) dt^2 + \frac{dr^2}{{\mathcal {F}}(r)} + r^{2}d \Omega ^2_3, \end{aligned}$$
(52)

where

$$\begin{aligned} {\mathcal {F}}(r) =K+\frac{r^2}{4 \alpha } \left( 1-\sqrt{1+\frac{16\alpha M}{r^4}-\frac{16\alpha Q^2}{3r^6}}\right) . \end{aligned}$$
(53)

where \(\alpha \) is a coupling constant and K is an arbitrary constant. Note that M and Q represent the gravitational mass and charge of the fluid as measured by an observer at spatial infinity. It is easy to check that in the limit \(\alpha \rightarrow 0\) the five-dimensional Einstein–Maxwell solution is recovered. On the hypersurface itself, \(r = R\), the metric is that of a 3-sphere with an additional time dimension, such that the line element is

By matching the line elements (12) and (52) across the boundary, one can suitably fix the model parameters. The resulting manifolds have boundaries given by the time–like hyper–surfaces

$$\begin{aligned} ds^{2}_{\Sigma } = - d\tau ^2+R^{2}(\tau ) \Omega ^2_3, \end{aligned}$$
(54)

with the intrinsic coordinates of \(\Sigma \) being \(\xi ^i\) = \((\tau , \theta , \phi , \psi )\) in \(\Sigma \), and \(\tau \) is the proper time on the boundary. Following [93, 94], the field equations projected on the shell \(\Sigma \) (generalized Darmois–Israel formalism for Einstein–Gauss–Bonnet theory) are

$$\begin{aligned} 2\langle K_{ij}-K h_{ij}\rangle + 4\alpha \langle 3J_{ij}-Jh_{ij}+2P_{iklj}K^{kl}\rangle =-\kappa ^{2}S_{ij},\nonumber \\ \end{aligned}$$
(55)

where the \(\langle \cdot \rangle \) is the jump of a given quantity across the hyper–surface \(\Sigma \). Since, \(h_{ij} = g_{ij} - n_{i}n_{i}\) is the induced metric on \(\Sigma \) with the divergence free part of the Riemann tensor is defined by

$$\begin{aligned} P_{ijkl}= & {} R_{ijkl}+(R_{jk}h_{li}- R_{jl}h_{ki})-(R_{ik}h_{lj}- R_{il}h_{kj}) \nonumber \\&+\frac{1}{2}R(h_{ik}h_{lj}-h_{il}h_{kj}),~~ \end{aligned}$$
(56)

and J is the trace of

$$\begin{aligned} J_{ij}\!=\frac{1}{3}\left[ 2KK_{ik}K^{k}_{j}+K_{kl}K^{kl}K_{ij}-2K_{ik}K^{kl}K_{lj}-K^{2}K_{ij}\right] .\nonumber \\ \end{aligned}$$
(57)

where \(K^{k}_{j}\) is the extrinsic curvature tensor defined by

$$\begin{aligned} {K}^{\pm }_{ij}=-n^{\pm }_{\mu }\left( \frac{\partial ^{2}X^{\mu }}{\partial \xi ^{i}\partial \xi ^{j}}+\Gamma ^{\mu }_{\alpha \beta }\frac{\partial X^{\alpha }}{\partial \xi ^{i}}\frac{\partial X^{\beta }}{\partial \xi ^{j}}\right) _{r = R}, \end{aligned}$$
(58)

with \(\xi ^i\) are the intrinsic coordinates of the surface and the sign ± depends on the signature of the junction hyper–surface.

Here, the interior solution under gravitational decoupling via MGD approach can be written through the following line element

$$\begin{aligned} ds^2_{5} = -e^{2\nu (r)} dt^2 + \frac{dr^2}{\mu (r)+f(r)} + r^{2} d \Omega ^2_3, \end{aligned}$$
(59)

where \(\mu (r)\) and \(\nu (r)\) are related with seed spacetime given by Eq. (39), and f(r) i.e., the deformation functions for the Solution A and Solution B corresponding to \(\theta \)-sector is given by Eqs. (48) and (50), respectively. Now, applying the first fundamental form associated with the two sides of the junction implies that \(g_{tt}^{-} = g_{tt}^{+}\) and \(g_{rr}^{-} = g_{rr}^{+}\), which yield

$$\begin{aligned} e^{2\lambda ^{-}}|_{r=R}=e^{2\lambda ^{+}}|_{r=R} \quad \text{ and } \quad e^{2\nu ^{-}}|_{r=R}=e^{2\nu ^{+}}|_{r=R},~~ \end{aligned}$$
(60)

where the symbols \(^-\) and \(^+\) denote the inner and outer spacetime and gives

$$\begin{aligned} e^{-2\lambda (R)}= & {} \mu (R)+\beta f(R) =\bigg [K + \frac{R^2}{4 \alpha }\nonumber \\&\times \bigg (1 -\sqrt{1 + \frac{16\, \alpha M}{R^4}-\frac{16\, \alpha \, Q^2}{3R^6}}\bigg )\bigg ], \end{aligned}$$
(61)
$$\begin{aligned} e^{2\nu (R)}= & {} \bigg [K + \frac{R^2}{4\,\alpha }\bigg (1 - \sqrt{1 + \frac{16\, \alpha M}{R^4}-\frac{16\, \alpha \, Q^2}{3R^6}}\bigg )\bigg ],\nonumber \\ \end{aligned}$$
(62)

where \(\mu (R) = \big [1 + \frac{R^2}{4\,\alpha }\big (1 - \sqrt{1 + \frac{16\, \alpha \, M_{EGB}}{R^4}-\frac{16\, \alpha \, Q^2}{3R^6}}\big )\big ]\) with \(M_{EGB} = m_{EGB}(R)\) is the total mass of the compact object for the metric (34). With the aid of the Eq. (61), we get

$$\begin{aligned} M= & {} M_{EGB}+\frac{1}{2} \beta f(R) \Big [ 2\alpha \,\beta f(R)- \frac{1}{\sqrt{3}\,R}\nonumber \\&\times \sqrt{3 R^6-16 \alpha \left( Q^2-3R^2 M_{EGB} \right) }.~~ \end{aligned}$$
(63)

Let us define the extrinsic curvature or second fundamental, which leads to the condition

$$\begin{aligned} \big [(G_{ij}+\alpha \,H_{ij})\,r^j\big ]_{\Sigma }=0, \end{aligned}$$
(64)

where \(r_{j}\) is a unit radial vector. Now, depending on the above criterion one may quantify the Eq. (9) as

$$\begin{aligned} \big [T_{ij}\,r^j\big ]_{\Sigma }=0\, \end{aligned}$$
(65)

which gives,

$$\begin{aligned} \big [P_r\big ]_{\Sigma }=0~~\Longrightarrow ~~\,\big [{\hat{p}}_r-\beta \,\theta ^1_1\big ]_{\Sigma }=0, \end{aligned}$$
(66)

where the surface \(\Sigma \) defined by \(r=R\). This condition determines the radius of the star, where the pressure vanishes at the surface of the star. Thus, the matching condition (66) takes the final form

$$\begin{aligned} {\hat{p}}_r(R)-\beta \,(\theta ^1_1)^{-}(R)=-\beta \,(\theta ^1_1)^{+}(R), \end{aligned}$$
(67)

where \((\theta ^1_1)^{-}(R)\) and \((\theta ^1_1)^{+}(R)\) are the \(\theta \)–components for interior and exterior space–times, respectively. The above condition is the general expression for the second fundamental form associated with the equation of motion for EGB gravity given in Eq. (9).

Now, plugging the expression for \(\theta ^1_1\) form (67) into the Eq. (27), we obtain the second fundamental form as

$$\begin{aligned}&\!\!\!\! {\hat{p}}_r(R)-\beta \,(\theta ^1_1)^{-}(R)=-\beta \,(\theta ^1_1)^{+}(R), \end{aligned}$$
(68)
$$\begin{aligned}&\!\!\!\!{\hat{p}}_r(R)+\frac{3\,\beta \,f_R\,\big (\nu ^\prime _R (-4\,\alpha \,\beta \, f_R -8\,\alpha \,\mu _R+4\alpha +R^2)+R\big )}{8\,\pi \,R^3}\nonumber \\&\quad =-\beta \,(\theta ^1_1)^{+}(R), \end{aligned}$$
(69)

where the notations are \(f_R = f(R)\), \(\mu _{R}=\mu (R)\), and \(\nu ^\prime _R={\partial _r\nu }\big |_{r=R}\), respectively. Moreover, using the Eq. (27) in the outer solution in Eq. (69), which gives

$$\begin{aligned}&\!\!\!{\hat{p}}_r(R)+\frac{3\,\beta \,f_R\,\big (\nu ^\prime _R (-4\,\alpha \,\beta \, f_R -8\,\alpha \,\mu _R+4\alpha +R^2)+R\big )}{8\,\pi \,R^3} \nonumber \\&~ =\frac{3\,\beta \,f^{*}_R}{8\,\pi \,R^3}\nonumber \\&\quad ~ \Bigg [ \frac{3 r^3 \sqrt{3 r^6-16 \alpha \left( Q^2-3 {\mathcal {M}} r^2\right) }-8 \sqrt{3} \alpha Q^2-3 \sqrt{3} r^6}{6 \,\alpha \, r^2\, \sqrt{3 r^6-16 \alpha \left( Q^2-3 {\mathcal {M}} r^2\right) }}\nonumber \\&\qquad \times \bigg \{-4\,\alpha \,\beta \, f^{*}_R -8\,\alpha \,\nonumber \\&\qquad ~\bigg [K + \frac{R^2}{4\,\alpha }\bigg (1 - \sqrt{1 + \frac{16\, \alpha \, {\mathcal {M}}}{R^4}-\frac{16\, \alpha \, Q}{3R^6}}\bigg )\bigg ]\nonumber \\&\qquad +4\,\alpha +R^2\bigg \}+R\Bigg ], \end{aligned}$$
(70)

where \(f^{*}_R\) is the decoupling function for the outer space–time at \(r=R\) \((i.e.~f^{*}_R=f^{*}(R))\) due to the source \(\theta _{ij}\), which represents exterior charged Boulware–Deser solution [92]

$$\begin{aligned} ds^2_{5}= & {} - \bigg [K + \frac{r^2}{4\,\alpha }\bigg (1 - \sqrt{1 + \frac{16\, \alpha \, {\mathcal {M}}}{r^4}-\frac{16\, \alpha \, Q}{3r^6}}\bigg )\bigg ] dt^2 \nonumber \\&+ \bigg [K+ \frac{r^2}{4\,\alpha } \bigg (1 - \sqrt{1 + \frac{16\, \alpha \, {\mathcal {M}}}{r^4}-\frac{16\, \alpha \, Q}{3r^6}}\bigg ) \nonumber \\&+\beta \,f^{*}(r)\bigg ]^{-1} dr^2 + r^{2} d \Omega ^2_3. \end{aligned}$$
(71)

One sees that the above conditions are necessary and sufficient conditions for matching the interior MGD metric (12) to the exterior vacuum solution given in (71). The condition (71) implies that if the exterior geometry represents exact charged Boulware–Deser metric then we get \(f^{*}_R=0\) in Eq. (71), which implies the following relations

$$\begin{aligned} P_r(R)= & {} {\hat{p}}_r(R)+\frac{1}{8\,\pi \,R^3}\big [3\,\beta \,f_R\,\big (\nu ^\prime _R (-4\,\alpha \,\beta \, f_R -8\,\alpha \,\mu _R\nonumber \\&+4\alpha +R^2)+R\big )\big ] =0,~ \end{aligned}$$
(72)
$$\begin{aligned} P_r(R)= & {} {\hat{p}}_r(R)-\beta \,\theta ^1_1(R) = 0.~~ \end{aligned}$$
(73)

Further, using the boundary conditions (51) and (73), we determine the constants A, B and total mass M for both cases as follows:

i. Constants for the solution A

$$\begin{aligned} A= & {} \frac{1}{4 R^2\big (4 \alpha \left( e^{C R^2}-1\right) +R^2 e^{C R^2}\big )}\Big [24 \alpha f^2(R) \beta ^2 e^{2 C R^2}\nonumber \\&+48 \alpha f(R) \beta e^{C R^2}-24 \alpha f(R) \beta e^{2 C R^2}\nonumber \\&+\sqrt{\Psi _1(R)-\Psi _2(R)}+4 \alpha C R^2 e^{C R^2}-12 \alpha C R^2 \nonumber \\&-16 \alpha e^{C R^2}+16 \alpha -6 f(R) \beta R^2 \times e^{2 C R^2}-6 R^2 e^{C R^2}\nonumber \\&+C R^4 e^{C R^2}\Big ], \end{aligned}$$
(74)
$$\begin{aligned} M= & {} \alpha \, e^{-2 CR^2} \left[ e^{CR^2} (\beta \,f(R) -K)+1\right] ^2+\frac{1}{2} R^2 \Big (K\nonumber \\&- e^{-CR^2}-\beta f(R) \Big )+\frac{Q^2}{3 R^2}, \end{aligned}$$
(75)
$$\begin{aligned} B= & {} \ln [e^{-CR^2}+\beta \,f(R)]-AR^2. \end{aligned}$$
(76)

ii. Constants for the solution B

$$\begin{aligned} A= & {} \frac{1}{{4 R^2 \left( 4 \alpha \left( e^{C R^2}-1\right) +R^2 e^{C R^2}\right) }}\Big [4 \alpha C R^2 e^{C R^2}-12 \alpha \nonumber \\&\times C R^2 -16 \alpha e^{C R^2}+\sqrt{8 R^2 e^{C R^2} \Psi _3(R)+\Psi _4(R)}\nonumber \\&+16 \alpha -6 R^2 e^{C R^2}+C R^4 e^{C R^2}\Big ], \end{aligned}$$
(77)
$$\begin{aligned} M= & {} \alpha \, e^{-2 CR^2} \left[ e^{CR^2} (\beta \,f(R) -K)+1\right] ^2+\frac{1}{2} R^2 \Big (K\nonumber \\&-e^{-CR^2}-\beta f(R) \Big )+\frac{Q^2}{3 R^2}, \end{aligned}$$
(78)
$$\begin{aligned} B= & {} \ln [e^{-CR^2}+\beta \,f(R)]-AR^2. \end{aligned}$$
(79)

where,

$$\begin{aligned} \Psi _1(R)= & {} \Big [R^2 e^{C R^2} \left( 6 f(R) \beta e^{C R^2}\right. \\&\left. -C R^2+6\right) -4 \alpha \big (6 f(R)\times \beta e^{2 C R^2} (f(R) \beta -1)\\&+e^{C R^2} \left( C R^2+12 f(R) \beta -4\right) -3 C R^2+4\big )\Big ]^2,\\ \Psi _2(R)= & {} 8 R^2 e^{C R^2} \left[ 4 \alpha \left( e^{C R^2}-1\right) \right. \\&\left. +R^2 e^{C R^2}\right] \Big [e^{C R^2} (3 f(R) s \beta -2) - C R^2+2\Big ],\\ \Psi _3(R)= & {} \left( C R^2+2 e^{C R^2}-2\right) \left( 4 \alpha \left( e^{C R^2}-1\right) +R^2 e^{C R^2}\right) ,\\ \Psi _4(R)= & {} \Big [4 \alpha \left( -3 C R^2+e^{C R^2} \left( C R^2-4\right) +4\right) +R^2 e^{C R^2} \\&\times \left( C R^2-6\right) \Big ]^2. \end{aligned}$$

5 Physical analysis of the solution

In the following sections, we will study the physical properties of gravitationally decoupled solutions obtained via the MGD approach for constructing the compact star model. For this purpose, we plot the Figs. 2, 3, 4, 5 and 6 that contain the curves for the GR, EGB and EGB+MGD solutions. To better understand the properties of solutions within the compact star, we will discuss all situations GR, EGB and EGB+MGD separately.

Fig. 2
figure 2

The behavior of radial pressure \(P_r(r)\) - top left, tangential pressure \(P_\perp \)-top right, energy density \(\rho (r)\) -bottom left, anisotropy factor \(\Delta (r)\)-bottom right versus radial coordinate r for the solution Sect. 3.1

Full size image
Fig. 3
figure 3

The behavior of deformation function f(r) - left panel and mass function m(r) - right panel versus r for solution Sect. 3.1

Full size image

GR and EGB i.e., \(\beta =0\): The effective radial \(P_r\) and tangential \(P_{\perp }\) pressures are described in the upper panels of Fig. 2, where the orange and blue curves are corresponding to the pure GR and EGB gravity in 5D, respectively. In order to see the effect of Gauss–Bonnet constant, we chose \(\alpha =5 \) for plotting the Fig. 2 and we see that that pressure is decreasing towards the boundary and become zero at the surface of the star, but the central pressure is increasing when \(\alpha \) increases (see blue and orange curves). The effective energy density \(\rho (r)\) is behaving well as expected for a viable compact configuration and magnitude of central and surface density is increasing when \(\alpha \) increases, which shows that the more dense object is obtained in EGB gravity as compare to pure GR. However, the anisotropy is zero throughout the stellar object because of \(\beta =0\). Now we will discuss the physical features of the solutions A and B under the MGD scenario in the next sections:

Fig. 4
figure 4

The behavior of radial pressure \(P_r(r)\) - top left, tangential pressure \(P_\perp \)-top right, energy density \(\rho (r)\) -bottom left, anisotropy factor \(\Delta (r)\)-bottom right versus radial coordinate r for the solution Sect. 3.2

Full size image

5.1 Analysis for solution Sect. 3.1: mimicking of the density constraints i.e. \({\hat{\rho }}+\frac{E^2}{8\pi }=\theta ^0_0\)

GR+MGD and EGB+MGD When we use the MGD, the situation of the pressure and density behavior remains same but magnitude of central pressure and central density decreases when \(\beta \) move from 0 to \(-0.08\). Now we will mention some other physical features of the solution under the MGD introduction: Since the MGD approach which allows us to set \(h(r)=0\) in the Eq. (28), which means that metric potential temporal components of the spacetime remains same and then the full alteration of the solution depends on the radial metric potential via decoupler function f(r). Hence, this deformation function f(r) is not only affect to main physical quantities such as the density, pressures, but also change the mass of the object. This happens as usual since the mass function is directly related to radial metric potential. As can be observed from Fig. 2, when we fix the \(\alpha =0\) and \(\beta \) decrease from 0 to − 0.04, the magnitude of effective pressures and effective density decrease but if we increase the \(\alpha \) by fixing \(\beta \), the values of pressures and density increases. This implies that Gauss–Bonnet constant \(\alpha \) introduce more pressure inside the compact configuration and leads a more denser object, however decoupling constant \(\beta \) plays an opposite impact on the pressure and density as compared to that Gauss–Bonnet constant \(\alpha \). On the other hand, the anisotropy behavior shows in Bottom right panel of Fig. 2. It is clearly observed that the anisotropy is increasing for all values of \(\beta =-0.04, -0.08\) but we get a negative anisotropy at some points within the stellar model in GR+MGD scenario which generates an attractive force but when we introduce the Gauss–Bonnet constant \(\alpha \) i.e. EGB+MGD case, we overcome from this situation. This means that the study of anisotropic solution in 5D under gravitational decoupling is more compatible in EGB gravity than pure GR gravity. Furthermore, it is already argued that when \(\beta \) and radial deformation function both are negative in the framework of the density mimicking approach the magnitude of the mass function will be less in EGB+MGD as compare to pure GR or EGB gravity, see Fig. 3, which means that the present minimally deformed solution will provide the less massive object.

5.2 Analysis for solution Sect. 3.2: mimicking of the pressure constraint i.e. \({\hat{p}}_r=\theta ^1_1\)

In this solution B, the situation will be same for GR and pure EGB gravity as discussed before in Sect. A. Now only enough to describe the GR+MGD and EGB+MGD cases, which are as follows:

5.3 Figures for the solutions Sects. 3.1 and 3.2 obtained in Sect. 3

Fig. 5
figure 5

The behavior of deformation function f(r) - left panel and mass function m(r) - right panel versus r for solution Sect. 3.2

Full size image
Fig. 6
figure 6

The behavior of electric field (E) versus r for solution Sect. 3.1 (left panel) and solution Sect. 3.2 (right panel)

Full size image

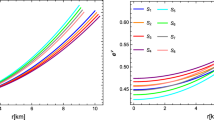
GR+MGD and EGB+MGD Since in this solution B, we use the pressure mimic constraint procedure \({\hat{p}}_r=\theta ^1_1\) to analyze the effect of MGD on the physical parameters. As, we present the behavior of energy density, radial pressure and tangential pressure along with the anisotropy inside the object by the Fig. 4. It can be seen that when the magnitude of \(\beta \) and \(\alpha \) is increasing, then central density increases but central value of the pressure decreases. On the other hand, if we increase the decoupling constant \(\beta \) the surface value of the density decreases (see the yellow and red curves for \(\beta =0\) and 0.3 corresponding \(\alpha =0\)). Since as any well–behaved compact star model, the pressure and density should be maximum at surface and decreasing monotonically for attaining their minimum value at surface. All these features are satisfied by our obtained model but when we increase the value of \(\beta \) beyond 0.7 approx., the tangential pressure start showing its increasing behavior. This implies that the gravitationally decoupled charged solution is viable for higher values of decoupling constant \(\beta \). Moreover, the anisotropy is increasing under the MGD and acting a stronger force in the outward direction for higher value of \(\beta \) which helps in avoiding the gravitational collapse. On the other hand, for the present condition (\({\hat{p}}_{r}=\theta ^{1}_{1}\)), the deformation function f(r) has an exciting behavior that can be observed from the left panel of Fig. 5. The figure shows that the deformation function f(r) vanishes at the center \(r=0\) as well as at the surface \(r=R\) of the object when the seed pressure for electrically charged matter distribution is proportional to the radial component of the \(\theta \)–sector. The same feature of f(r) is observed in other gravity theories under the condition \({\hat{p}}_{r}=\theta ^{1}_{1}\), which shows that this features of f(r) is independent of the theory. However, the vanishing deformation function on the boundary shows that there is no change in the total mass of the object in the context of MGD i.e. remains the same for all values of \(\beta \) (see Fig. 5-right panel). This implies that the mass due to MGD is distributed inside the compact object. In this connection, the compactness factor \(u_{EGB}\) for 5D EGB gravity can be written by the formula,

$$\begin{aligned} u_{EGB}=\frac{2 M_{EGB}}{R^2}, \end{aligned}$$
(80)

and corresponding Buchdahl limit [95]

$$\begin{aligned} u_{EGB}\equiv \frac{2M_{EGB}}{R^{2}}\le \frac{3}{4}+\frac{9}{8R^{2}}\alpha , \quad \forall \quad \alpha >-\frac{R^{2}}{3}. \end{aligned}$$
(81)

As mentioned in Sect. 3.1 that by imposing \({\hat{\rho }}+\frac{E^2}{8\pi }=\theta ^0_0\), the total mass of the deformed object is less than the total mass of the object in pure EGB gravity, then \(u<u_{EGB}\), where \(u_{EGB}=\frac{2 M}{R^2}\). In this situation, the mass–radius ratio for the deformed object will automatically satisfy the Buchdahl limit in 5D EGB gravity. On the other hand, there is no changes in the total mass for solution Sect. 3.2 corresponding to the case \({\hat{p}}=\theta ^1_1\), i.e. \(u =u_{EGB}\), and hence the compactness u will be less than the Buchdahl limit \((u_{BL})\), where \(u_{BL}=\frac{3}{4}+\frac{9}{8R^{2}}\alpha \). The \(M-R\) bounds are shown in Tables 1 and 2, respectively.

Table 1 The compactness and surface redshift values along with the Buchdahl limit (\(u_{BL}\)) in EGB gravity for \(R = 9\,km\) and \(C= 0.001 km^{-2}\) with different GB constant \(\alpha \) and coupling parameter \(\beta \) corresponding to the MGD solution Sect. 3.1:
Full size table
Table 2 The compactness and surface redshift values along with the Buchdahl limit (\(u_{BL}\)) in EGB gravity for \(R = 9\,km\) and \(C= 0.001 km^{-2}\) with different GB constant \(\alpha \) and coupling parameter \(\beta \) corresponding to the MGD solution Sect. 3.2:
Full size table

Further more, the electric field intensity has been also discussed for both charged anisotropic solutions. The variation of the electric field inside the charged stellar model is given in Fig. 6. As it can be observed that the electric field is increasing away from the centre which prevents the star from gravitational collapse. On the other hand, it is also pointed out that the value of electric charge is decreasing for the solution Sect. 3.1 when the magnitude of Gauss–Bonnet and decoupling constants increases, while no impact of MGD on the electric charge in solution Sect. 3.2.

In the framework of EGB gravity, Zhou et al [96] have discussed that GB terms will alter the redshift’s upper bound of the spectral lines from the boundary of stars of constant density. Remarkably, this upper bound is reliant on the value of density rather than a constant in GR complement, and thus it is not possible to found an upper bound for the redshift [95, 96]. The surface redshift is given by

$$\begin{aligned} z=\sqrt{e^{-2\nu (r)}}-1. \end{aligned}$$
(82)

Moreover, we can find some information about the surface \(z_{s}\) redshift as [96],

$$\begin{aligned} z_{s}= \big [B\,(1+AR^2)\big ]^{-2}-1. \end{aligned}$$
(83)

As we can see from Table 1, for solution Sect. 3.1 the surface redshift \(z_{s}\) is decreasing when magnitude of \(\beta \) increases while there is no impact of \(\beta \) on \(z_s\) for solution Sect. 3.2 (see Table 2). It is noted that the obtained values for \(z_{s}\) are consistent with the bound proposed in the GR scenario [97].

6 Concluding remark

In the present paper, we have investigated the physical properties of charged compact objects in the context of Einstein–Gauss–Bonnet (EGB) gravity, which is known to be free of ghosts while expanding about the flat space. An important feature of this discussion is the possibility of applying minimal geometric deformation (MGD) decoupling formulation, which we have used to study the interior of stellar type objects. Using the MGD approach, one can extend the charged isotropic model of compact object to charged anisotropic domains. The decoupling of these gravitational sources corresponding to matter distribution \(T_{ij}\) yields two systems, namely, the charged isotropic sector corresponding to an perfect fluid \({\hat{T}}_{ij}\) and the additional source \(\theta _{ij}\) that is coupled with \({\hat{T}}_{ij}\) through the constant \(\beta \). These two sectors must interact only gravitationally without exchange of energy between them.

After specifying the field equations for \(T_{ij}\) and \(\theta _{ij}\), we first solved the field equations for \(T_{ij}\) by known potentials corresponding to Krori–Barua solution for charged matter distribution while \(\theta \)-sector has been solved by two different Mimic approaches such as (i) \({\hat{\rho }}+\frac{E^2}{8\pi }=\theta ^0_0\), and (ii) \({\hat{p}}_r=\theta ^1_1\). We next identify the surface of the star where the radial pressure vanishes i.e., \(P (R) = 0\). In particular, we apply the generalized Darmois–Israel formalism for EGB theory, where the interior solution is being matched to an exterior Boulware–Deser vacuum spacetime which determines the constants involved in the solutions. For our MGD approach the effective radial pressure \(P = {\hat{p}}_r-\beta \,\theta ^1_1\), contains both the non-deformed matter source ı.e., anisotropic pressure and the deformation function f(r) induced by the additional source term \(\theta _{ij}\).

It is interesting to note that the first mimic approach provides a non-vanishing deformation function f(r) at boundary while it vanishes at the boundary for the second case. This implies that the total mass of the object remains the same under MGD for the second case. Moreover, the first solution is physically valid when \(\beta \) is negative as well as the deformation function is also negative throughout the star for \(r>0\), which shows that the total mass will decrease due to MGD and will get less massive objects.

Finally, we found that the total mass of the deformed object is less than the total mass of the object in pure EGB gravity for solution Sect. 3.1. This, of course means that the Buchdahl’s limit is automatically satisfied for 5D EGB+MGD model. Interestingly, there is no changes in the total mass for solution Sect. 3.2, where the compactness is less than the Buchdahl limit (see Tables 1 and 2). Furthermore, the calculated surface redshift for both solutions have been presented in the Tables 1 and 2. It is found that the surface redshift for deformed object is always less than or equal to the objects in GR gravity. We would like to mention here that the MGD is not only generalize the previous known solutions but it also controls the mass–radius ratio and surface redshift of the compact objects.