1 Introduction

The prominent black hole (BH) no-hair theorems [1, 2] imply vacuum astrophysical black hole can be described by a special case of Kerr-Newman metric, which could be characterized by its mass, spin and charge only [3,4,5]. Although astrophysical BHs are usually considered as electrically neutral due to charge neutralization by astrophysical plasma, quantum discharge effects, and electron-positron pair production [6,7,8], an accurate upper limit on the amount of the charges of BHs is still absent. Therefore, it is important and meaningful to give a quantitative measurement on the amount of charges of BHs. Besides, many novel charging mechanisms has been discussed theoretically, such as primordial black hole [9], and BHs formed by millicharge dark matter [10]. In the later case, the discharge process is much slower than for ordinary plasma so the charged BHs are viable. So it is meaningful to study the effect on gravitational wave if electric charges are presented in these special theories.

At present, using the shadow of supermassive BH to estimate its charge has been developed and widely practiced [11], for example Sgr A* and M87* measured by VLBI [12,13,14,15]. These proposals are either far from being accurate or model-dependent. Therefore, developing new technique to model-dependently test the charged property is needed, and gravitational wave has always been expected, which encodes the BH’s information [16]. Fortunately, after decades of hard work, LIGO-Virgo announced the first detection of the gravitational wave (GW) signal GW150914 in 2015, generated by the merger of a binary BH [17]. To characterize GW, we often use inspiral, merger and ringdown to describe the whole coalescence of a binary BH, where the inspiral stage is generally described by post-Newtonian theory [18], merger stage is generally approximated by the numerical simulation [19], and ringdown stage is described by the BH perturbation theory [20, 21]. Some waveform models, such as IMRPhenomPv2 (IMR) waveform model, have incorporated these three stages [22].

The GW waveform will be affected if the two BHs are electrically charged. For simplicity, consider the electric dipole radiation during their orbital motions, which will be reflected in the phase of inspiral stage, and thus provides us a new trick to detect charged binary BH. Depending on the amount of the charge, there are two different treatments. When the charge of the black hole is small, the dipole radiation can be taken as a perturbation or correction to the phase of the inspiral stage of the GW waveform, which can be incorporated into the parameterized post-Einsteinian (ppE) framework [16]. In this case, the correction due to the electric dipole radiation is completely described by the coefficient of the \(-1\) post-Newtonian (PN) order in the waveform, the rest part of the waveform is the same as that of the accurate waveform model describing the coalescence of two neutral black holes, such as the well-known phenomenological waveform model [22]. This is similar to the dipole radiation caused by the scalar charges carried by black holes in the scalar-tensor theory [23]. However, if the charge of the black hole is large, the ppE framework may not be applicable anymore, as the latter requires the expansion in PN is always linear, which may not be assured as a prior.

We also consider only the leading order gravitational quadrupole radiation and the electric dipole radiation, based on which we call such waveform the leading order charged (LOC) one. It is apparent that the LOC waveform has a bad accuracy when applied to the analysis of GW data unless the inspiral duration is long enough and the orbit of the two black holes decays very slow. Despite this shortcoming, the LOC waveform provides us a toy model such that the effect of the charge can be demonstrated explicitly without the assumption that the charge of the black hole is small. The detailed calculation of the LOC waveform is shown in Sect. 5.

In this work, based on IMR waveform model in LIGO-Virgo Algorithm Library [24], we use the Bayesian method to test the dipole radiation of GW signals [25, 26] with the ppE framework. As the main conclusion, we find no visible charge taking by astrophysical BH.

The rest of this paper is organized as follows. In Sect. 2, we introduce the ppE framework. In Sect. 3, we briefly introduce the Bayesian method for the GW data processing and the results are presented in Sect.4. In order to verify the consistency of the results obtained from ppE method, in Sect. 5, we introduce the toy model, the LOC waveform, to study the effect of the amount of the charge on the waveform. In Sect. 6, we summarize the calculation results and present the conclusion, and discuss the deficiencies of this work as well as what can be done further. We assume \(c = 1\) throughout the paper unless otherwise specified.

2 Effects on gravitational wave signals

In this section, we introduce the waveform models adopted in this work. We treat the charge effect as a small perturbation, which can be well described by the parameterized post-Einsteinian framework. In this case, the phase of the inspiral part of the charged binary BHs can be incorporated into the ppE formalism, which describes the gravitational waveforms of theories alternative to general relativity (GR) in a model-independent way [16, 25]. Formally, the effect of the electric dipole radiation can be captured by the ppE parameter entering at \(-1\) post-Newtonian order, similar to the dipole radiation from the scalar–tensor theory [23].

Assuming the early-inspiral stage of the IMR waveform model is reduced to the form of \(h_{\mathrm {e-ins}}(f)=A_{\mathrm {e-ins}}(f)e^{i{\Psi }_{\mathrm {e-ins}}}\), then the waveform model due to modifications from different modified gravity effects can be written as

$$\begin{aligned} h_{\mathrm {e-ins}}(f)=A_{\mathrm {e-ins}}(f)e^{i{\Psi }_{\mathrm {e-ins}}+i\Delta \Psi } \end{aligned}$$
(1)

In ppE framework [25, 26],

$$\begin{aligned} \Delta \Psi _{\mathrm{ppE}}=\beta (\pi G{\mathcal {M}}f)^{b/3}, \end{aligned}$$
(2)

where \(\beta \) is the amplitude coefficient and b is the exponent coefficient. Note that the modification enters at \((b+5)/2\) PN order for a related modified gravity. \({\mathcal {M}}=(m_1m_2)^{3/5}/(m_1+m_2)^{1/5}\) is the chirp mass with component masses \(m_1\) and \(m_2\), and f is the frequency of the GW.

The study in Tahura et al. [27] shows that at least in theories where the leading corrections enter at negative PN orders, the phase-only analyzes can produce sufficiently accurate constraints. In this analysis, we only consider the correction on the phase and neglect the correction to the amplitude. The frequency at the end of this stage is given by \(f_c=0.018/[G(m_1+m_2)]\) [26], above which this model is calibrated with numerical-relativity data and can not be applied to ppE formalism.

The effect of the charge on the waveform can be taken as a perturbation term in the phase [10, 28],

$$\begin{aligned} \Delta \Psi _q=-\frac{5}{3584}\eta ^{2/5}\zeta ^2\kappa ^2\left( \pi \kappa G{\mathcal {M}}f\right) ^{-7/3} \end{aligned}$$
(3)

where \(\eta =m_1m_2/(m_1+m_2)^2\) is symmetric mass ratio, \(\zeta \) represents the difference between the charges of the binary BH and is defined by \(\zeta =|\lambda _1-\lambda _2|/\sqrt{1-\lambda _1\lambda _2}\), where \(\lambda _i=q_i/(\sqrt{G}m_i)\) is the charge-to-mass ratio and \(q_i\) is the electric charge of a BH. Here \(\kappa =1-\lambda _1\lambda _2\approx 1\) since we consider the effects of \(\lambda _1\) and \(\lambda _2\) as small perturbations. In this case, \(\beta =-\frac{5}{3584}\eta ^{2/5}\zeta ^2\) and \(b=-7\), corresponding to Eq. (2).

In TAble I of Yunes et al. [25], obtained constraint \(|\beta |\lesssim 1.6\times 10^{-4}\) at \(-1\) PN order for GW150914. The relationship between \(\beta \) and \(\zeta \) is: \(\beta =-5/3584\eta ^{2/5}\zeta ^2\). Thus, one can derive the corresponding constraint \(\zeta \lesssim 0.45\). There are two ways to enhance the constraint on the charge. Firstly, one may expect the increase of the sensitivities of GW detectors, and a more stringent constraint on the charge should appear. Secondly, a full gravitational waveform model of charged binary BH is excepted to give a more stringent constraint on the charge. This full GW waveform should apply to the coalescence of two black holes carried with arbitrary amount of charge. It is a challenging job and in this work we move forward by developing the leading order charged (LOC) waveform model, which is introduced in Sect. 5.

3 Bayesian inference methods

To infer the uncertainty of the source parameters \(\mathbf {\mathcal {\theta }}\), which are quantified by the posterior probability distribution \(p(\mathbf {\mathcal {\theta }}|d, M)\), we perform Bayesian analysis with the prior \(p(\mathbf {\mathcal {\theta }}|M)\) and the likelihood with Gaussian noise assumption for the GW data,

$$\begin{aligned} \begin{aligned} p(d|\mathbf {\mathcal {\theta }},M)\propto \mathrm {exp}\left[ -\frac{1}{2}\sum ^{N}_{i=1}\langle d_i-h_i|d_i-h_i\rangle \right] , \end{aligned} \end{aligned}$$
(4)

where \(d_i\) is the data of the ith instrument, M is the model assumption, N is the number of detectors in the network of Advanced LIGO and Advanced Virgo, and \(h_i\) is the waveform model calculated with \(\mathbf {\mathcal {\theta }}\) for the ith detector. The noise weighted inner product \(\langle a(f)|b(f)\rangle \) is defined by

$$\begin{aligned} \langle a(f)|b(f)\rangle = 4{\mathcal {R}}\int ^{f_{high}}_{f_{low}}\frac{a(f)b(f)}{S_n(f)} \mathrm {d}f, \end{aligned}$$
(5)

where \(f_{low}\) and \(f_{figh}\) are the high and low pass cut-off frequencies respectively, \(S_n(f)\) is the power spectral density of the detector noise. The Bayesian theorem is described by

$$\begin{aligned} p(\mathbf {\mathcal {\theta }}|d,M) = \frac{p(d|\mathbf {\mathcal {\theta }},M)p(\mathbf {\mathcal {\theta }}|M)}{p(d|M)}, \end{aligned}$$
(6)

where \(p(d|M)=\int p(d|\mathbf {\mathcal {\theta }},M)p(\mathbf {\mathcal {\theta }}|M)\mathrm {d}\mathbf {\mathcal {\theta }}\) is the evidence of a specific model assumption.

There are fifteen parameters in the IMR waveform model, including the redshifted chirp mass (\({\mathcal {M}}_z\)), mass ratio (q), luminosity distance (\(d_L\)), inclination angle (\(\theta _{jn}\)), the reference orbital phase (\(\phi _c\)), the geocentric time (\(t_c\)), the polarization angle (\(\psi \)), the two dimensional sky location, and six spin parameters. And the early-inspiral stage of the IMR waveform model for ppE framework (hereafter e-insp-ppE waveform model) has an additional ppE parameter \(\zeta \). We marginalize over the reference phase \(\phi _c\) and the geocentric time \(t_c\), thus we have 14 free parameters for e-insp-ppE waveform model. The GW data and power spectral density for each event are downloaded from LIGO-Virgo GW Open Science Center [29]. To estimate parameters with data from the first two observation runs (O1 and O2), we carry out Bayesian inference with Bilby [30], using Pymultinest [31] as our sampler.

The prior on the redshifted chirp mass is chosen to be uniform in the range of \(5\,\mathrm{M}_\odot \le {\mathcal {M}}_z\le 20\,\mathrm{M}_\odot \) for GW151226 and GW170608 while \(5\,\mathrm{M}_\odot \le {\mathcal {M}}_z\le 50\,\mathrm{M}_\odot \) for the other events, the prior on the mass ratio is chosen to be uniform in the range of \(0.25\le \mathrm {q}\le 1\). We apply comoving uniform prior on the luminosity distance \(50\mathrm {Mpc}\le d_L\le 4000\mathrm {Mpc}\), while the prior on the inclination angle is chosen to be uniform in the range of \(-1\le \cos \iota \le 1\). The prior on the polarization angle is chosen to be uniform in the range of \(0\le \psi \le \pi \), and the prior of the sky location is chosen to be uniform in spherical coordinates. The prior on \(|\zeta |\) is chosen to be uniform in the range of \(0\le |\zeta |<\sqrt{2}\). For other parameters in the e-insp-ppE waveform model, we use the same priors presented in Abbott et al. [32].

4 Results of Bayesian inferences

In this section, on the promise that the BH has a small amount of charge, we set up constraints on the dipole radiation with the ppE framework. We analyze with e-insp-ppE waveform model to constrain the dipole radiation, with a high frequency cut-off at \(f_c=0.018/[G(m_1+m_2)]\). Specifically, this analysis is applied to GW150914, GW151226, GW170104, GW170608, and GW170814. We neglect other events since the early-inspiral signal-to-noise ratios (SNRs) of them are all less than 6.

Table 1 The constraints on dipole radiation of five selected binary BH events, \(90\%\) confidence intervals are shown
Full size table

As shown in Table 1, for GW170608, the GW data can constrain \(|\zeta |\) to be less than about 0.21 at \(90\%\) credible level, while the loosest case is given by GW170104, \(|\zeta |\le 0.70\) (at \(90\%\) credible level) due to its lowest SNR of the inspiral signal among all these five events. In Yunes et al. [25], the authors got constraints on scalar dipole radiation through a Fisher parameter estimation study, using a fitted spectral noise sensitivity curve. As a result, the constraint on GW150914 is \(|\zeta |\lesssim 0.45\), and the constraint on GW151226 is \(|\zeta |\lesssim 0.24\). Their results agree well with ours shown in Table 1. One can also get constraints on \(|\zeta |\) by reweighting the posteriors of parameters \(\delta \phi _{-2}\) from results in Abbott et al. [26], where \(\delta \phi _{-2}=-5/84\zeta ^2\) is the parameterized violation of GR at \(-1\) PN. Recently, a similar analysis was performed in Wang et al. [33] with both reweighting method and Bayesian inference method, and they find that the Bayesian analysis is more reliable than the reweighting analysis.

Fig. 1
figure 1

The marginalized posterior probability distributions of chirp-mass of GW150914, with different high frequency cut-off \(f_{high}=50,100,200,400,600,800\), and 1024 Hz. The uncertainty of the distribution becomes larger as \(f_{high}\) is less than 400 Hz

Full size image

To further discuss the reliability of our results, we apply Bayesian inference on GW data of GW150914 with a set of low-pass cut-off frequencies \(f_{high}\). And we show the chirp mass distribution in Fig. 1, in which the distribution becomes wider as \(f_{high}\) less than 400 Hz. Nevertheless, the result is not biased even the cut-off frequency is as low as 50 Hz, although the uncertainty is a bit larger.

Actually, the charge will significantly affect the space-time metric of the binary system if the charge is as large as the maximum allowable value. This effect will be fully reflected in waveform model when higher PN order terms are taken into account. However, an analytic solution will not be available in the forthcoming future and one can only get it numerically, i.e. Bozzola and Paschalidis [34]. In Bozzola and Paschalidis [34], the binary charged black holes were studied via numerical general relativity method, where the higher PN order effects of the charge are included and the amount of charge is set free. One of the main conclusions from this paper is that the greatest difference between charged and uncharged black holes arises in the earlier inspiral. This provides a convincing evidence to support the reasonability of our work.

For future space-based GW detectors such as Laser Interferometer Space Antenna (LISA) [35] and TianQin [36], the duration of GW strain from BH binaries are much longer [37, 38]. Since the dipole gravitational radiation dominates at \(-1\) PN order, it is more suitable for detecting by LISA and TianQin. Barausse et al. [39] shows that joint observations of GW150914-like systems by LIGO-Virgo and LISA will improve bounds on dipole emission from BH binaries by several orders of magnitude relative to current constraints. We expect that with multi-band GW the constraint on the electric charge of BH can be improved as well.

5 The leading order charged waveform

In this section, we try to learn more about the effect of the charge by developing a LOC waveform model. For this waveform model, we do not consider the spin of binary black holes since the spin evolution of the binary BH only occurs at high orders of the PN expansion [40, 41]. Therefore, we only need to analyze the orbit (circular) evolution in the inspiral phase due to the energy loss. For two point particles with mass \(m_1\) and \(m_2\) and charge \(q_1\) and \(q_2\) respectively, we define \(\lambda _i=q_i/(\sqrt{G}m_i)\). They orbit each other with orbital radius R, and the orbit decays with time t. The dissipation of total energy can be divided into two parts, one is the emission of GW, the other is electromagnetic dipole radiation, which can be written as [10]

$$\begin{aligned} \frac{d E}{d t}= & {} -\frac{d E_{\mathrm {GW}}}{d t}-\frac{d E_{\mathrm {dip}}}{d t} \nonumber \\= & {} -\frac{32}{5 } \eta ^{2} \frac{GG_{\mathrm {eff}}^{3} M^{5}}{R^{5}}-\frac{2}{3} \zeta ^{2} \frac{G_{\mathrm {eff}}^{3} m_{1}^{2} m_{2}^{2}}{R^{4}}, \end{aligned}$$
(7)

where \(M=m_1+m_2\) is total mass of the binary, \(G_{\mathrm {eff}}=G(1-\lambda _1\lambda _2)\) is the effective Newton constant, \(\zeta =|\lambda _1-\lambda _2|/\sqrt{1-\lambda _1\lambda _2}\) is used to characterize the difference between the charges of two BHs, and \(\eta =m_1m_2/(m_1+m_2)^2\) is symmetric mass ratio. The evolution equation of the orbital radius arising from Eq. (7) is

$$\begin{aligned} -\frac{d R(t)}{d t}=\frac{A}{R(t)^{3}}+\frac{B}{R(t)^{2}}, \end{aligned}$$
(8)

where \(A=64GG_{\mathrm {eff}}^{2} M m_{1} m_{2}/5\) and \(B=4 \zeta ^{2} G_{\mathrm {eff}}^{2} m_{1} m_{2}/3\). When B is not equal to zero, the relation between R and t can be parameterized as

$$\begin{aligned} \tau&=\frac{1}{3B}R^3-\frac{A}{2B}R^2+\frac{A^2}{B^3}R -\frac{A^3}{B^4}\ln \left( \frac{B}{A}R+1\right) \nonumber \\&\simeq \frac{R^4}{A}\left( \frac{1}{4}-\frac{B}{5A}R +\frac{B^2}{6A^2}R^2-\frac{B^3}{7A^3}R^3+\frac{B^4}{8A^4}R^4\right) \nonumber \\&\qquad +{\mathcal {O}}\left( \frac{BR}{A}\right) ^9 \end{aligned}$$
(9)

where \(\tau =t_c-t\) and \(t_c\) is the coalescence time. It is clear that an analytical solution of R(t) is not possible in Eq. (9), so we have to solve it numerically. Due to the last part of Eq. (9), the numerical solution is not accurate enough when \(BR/A\sim 0\), thus we expand Eq. (9) as a series of BR/A .

According to the Kepler’s law, the orbital frequency is \(\sqrt{G_{\mathrm {eff}}M/R^3}\) and the gravitational frequency is twice as much as the orbital frequency, so we have \(\omega _{gw}=2\pi f_{\mathrm {gw}}=2\sqrt{G_{\mathrm {eff}}M/R^3}\). The waveform in time domain contains two parts [41, 42]

$$\begin{aligned} \begin{aligned} h_{+}(t)&=\frac{4}{d_L}\left( \frac{G_{\mathrm {eff}} {\mathcal {M}}}{c^{2}}\right) ^{5 / 3}\left( \frac{\pi f_{\mathrm {gw}}\left( t\right) }{c}\right) ^{2 / 3} \frac{1+\cos ^{2} \iota }{2} \cos \left( \Phi \left( t\right) \right) ,\\ h_{\times }(t)&=\frac{4}{d_L}\left( \frac{G_{\mathrm {eff}} {\mathcal {M}}}{c^{2}}\right) ^{5 / 3}\left( \frac{\pi f_{\mathrm {gw}}\left( t\right) }{c}\right) ^{2 / 3} \cos \iota \sin \left( \Phi \left( t\right) \right) , \end{aligned}\nonumber \\ \end{aligned}$$
(10)

where \(\iota \) is inclination angle, \(d_L\) is luminosity distance and the phase of waveform is

$$\begin{aligned} \Phi (t+t_{\mathrm {ISCO}})=\int _{t_{\mathrm {ISCO}}}^{t} d t^{\prime } \omega _{\mathrm {gw}}\left( t^{\prime }\right) +\phi _c, \end{aligned}$$
(11)

where \(t_{\mathrm {ISCO}}\) is the time when the BH reaches the innermost stable circular orbit (ISCO). We cut the phase before \(t_{\mathrm {ISCO}}\) for three reasons: first, the phase before \(t_{\mathrm {ISCO}}\) can be included in \(\phi _c\) and the effect is equal to a time shift, which means this does not affect the results of parameter estimation; second, \(\omega _{\mathrm {gw}}\) is infinity when \(\tau =0\), and this can not be integrated; last but not least, the LOC waveform model cannot truly describe the motion of the binary BH when the orbital distance is too small.

According to Eqs. (8) and (9), \(t_{\mathrm {ISCO}}\) is fixed for a given \(R_{\mathrm {ISCO}}\). In reality, it is difficult to know the exact values of M and \(\lambda \) for the final BH. Because with a given \(\lambda _1\lambda _2\) and \(|\zeta |\), we still cannot uniquely determine the respective charge of the two BHs. For example if \(\lambda _1=a\), \(\lambda _2=b\) is the solution then \(\lambda _1=b\), \(\lambda _2=a\) could still be the solution. Approximately we take \(M=m_1+m_2, \lambda =\min \{|\frac{m_1\lambda _1+m_2\lambda _2}{m_1+m_2}|,|\frac{m_1\lambda _2+m_2\lambda _1}{m_1+m_2}|\}\). then in the similar way to Pugliese et al. [43] we obtain

$$\begin{aligned} R_{\mathrm {ISCO}}=\frac{4GM\lambda ^2}{3+1/C+C}, \end{aligned}$$
(12)

where \(C = -(9-8\lambda ^2-4\sqrt{4\lambda ^4-9\lambda ^2+5})^{1/3}\). The ISCO of a charged BH decreases with the charge, and we have \(R_{\mathrm {ISCO}}=4GM\) for \(|\lambda |=1\) and \(R_{\mathrm {ISCO}}=6GM\) for the non-rotating uncharged BH, respectively.

Fig. 2
figure 2

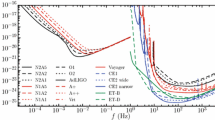
The tapered LOC gravitational waveforms for BH binaries with different charges. The rest parameters of these waveforms are the same, i.e., the detector-frame masses are \(m_1=m_2=30\,\mathrm{M}_\odot \), the luminosity distance is \(d_L=540\) Mpc, the inclination angle is \(\theta _{jn}=0\). The low cut-off frequency is \(f_{low}=20\) Hz. The green solid line represents the case of zero charge, and the red (blue) dash dotted (dashed) line in the left panel represents the waveform with parameter \(\lambda _1\lambda _2=-0.05\ (0.05)\), the red (blue) dash dotted (dashed) line in the right panel represents the waveform with parameter \(\lambda _1\lambda _2=0.15\ (0.25)\)

Full size image

Based on the discussion above, we obtain the LOC waveform model. Obviously, it reduces to the 0PN when both BHs are uncharged. As we have already pointed out, under the ppE framework, LIGO-Virgo has very weak restrictions on the charges of GW150914, with \(|\zeta |\lesssim 0.45\). Here we show that such large amount of charge could have non-negligible effect on the waveform. We choose parameters similar to GW150914, where \(m_1=m_2=30\,\mathrm{M}_\odot ,d_L=540\mathrm {Mpc},\iota =0,\phi _c=0\), and we set low cut-off frequency to be \(f_{low}=20\) Hz. For the charge of GW150914, if \(|\zeta |=0.45\), then possible allowed range of \(\lambda _1\lambda _2\) is \((-0.053, 0.80)\). For proper comparison, we have chosen four special values with \(\lambda _1\lambda _2=\{-0.05,0.05,0.15,0.25\}\) to study the effect of charge. As shown in Fig. 2, both the amplitude and phase of the GW signal will be affected significantly if GW150914 is endowed with a large amount of charges. The effect of charge on the early inspiral of the gravitational waveform is more significant, which is consistent with previous works [10, 16, 25]. It is also worth noting that \(G_{\mathrm {eff}}\) and \({\mathcal {M}}\) have similar effects on shaping the GW signals, the smaller \(G_{\mathrm {eff}}\), the lower GW amplitude, as described in Eq. (10). We also find that the larger value of \(\lambda _1\lambda _2\), the slower frequency evolution of GW signals.

6 Summary

In this work, we study the charge effect on the inspiral stage of the GW waveform. By considering the charge effect as an perturbation in the inspiral stage, we perform Bayesian inference on five events of the first Gravitational-Wave Transient Catalog (GWTC-1), GW150914, GW151226, GW170104, GW170608, and GW170814, whose SNRs are larger than 6 after applying a low-frequency cut off \(f_c\). Based on the ppE formalism, the most stringent limit from FIM up to now is \(|\zeta |\sim 0.24\) [10, 25], while our Bayesian based result is \(|\zeta |\sim 0.21\) at the \(90\%\) credible level, which is given by GW170608. The analysis on GW151226 and GW170814 give similar constraints, i.e., \(\zeta <0.26\) and \(\zeta <0.27\) at \(90\%\) credible level respectively. For GW150914, the constraint is \(\zeta <0.42\) at \(90\%\) credible level, which is similar to the analysis before [25].

To explicitly show the effect of the charge on the waveform, we developed the LOC waveform model in Sect. 5. Although due to the lack of accuracy, this waveform cannot be used to analyze the realistic GW data, this toy model has the advantage of being adjustable and intuitive. The LOC waveform is obtained by taking into account the dissipation effect caused by the electric dipole radiation and the quadrupole gravitational radiation on the circular orbit of the charged binary BHs. Like the 0PN waveform model, the spin of BH is not considered for the LOC waveform model as which emerges in the waveform only at higher orders. Besides, the analytical LOC waveform is achievable only if the charge is treated as a correction, so the general charge case is gotten numerically. We find that both the amplitude and phase of the GW signal will be strongly affected if the BHs are endowed with a large amount of charge.

The work in this paper can be improved in several aspects. For example, in the employment of the ppE framework, we only consider the electric dipole radiation, so when the two black holes have the same charge-to-mass ratio, the charge effect disappears in the phase of the ppE waveform. To overcome this problem, one can consider the electric quadrupole radiation. Moreover, as we have shown above, the constraints on the electric charges of the black holes are still not very stringent, one of the possible ways to improve this is to add higher order corrections to the waveform. However, this may not be helpful, because the parameterized constraints on the PN coefficients obtained by LIGO-Virgo show that the -1 PN gets the most stringent constraint than other higher PN orders [26], which we expect also applies to the study of the charged black holes. The contributions from the higher orders corrections of some other specific theories has been studied in Yunes et al. [25].

Above all, we give the constraints on the dipole radiations of GW events from GWTC-1. These constraints can be also converted to the constraints on radiation effects in other forms, such as the radiation caused by the magnetic or other U(1) dark charges carried by black holes. In the future, similar analysis can be applied to GW data that published in GWTC-2 [44].