Prospecting black hole thermodynamics with fractional quantum mechanics

Abstract

This paper investigates whether the framework of fractional quantum mechanics can broaden our perspective of black hole thermodynamics. Concretely, we employ a space-fractional derivative (Riesz in Acta Math 81:1, 1949) as our main tool. Moreover, we restrict our analysis to the case of a Schwarzschild configuration. From a subsequently modified Wheeler–DeWitt equation, we retrieve the corresponding expressions for specific observables. Namely, the black hole mass spectrum, M, its temperature T, and entropy, S. We find that these bear consequential alterations conveyed through a fractional parameter, $\alpha$. In particular, the standard results are recovered in the specific limit $\alpha =2$. Furthermore, we elaborate how generalizations of the entropy-area relation suggested by Tsallis and Cirto (Eur Phys J C 73:2487, 2013) and Barrow (Phys Lett B 808:135643, 2020) acquire a complementary interpretation in terms of a fractional point of view. A thorough discussion of our results is presented.

1 Introduction

Black hole (BH) physics constitutes an enthusiastic research domain for this century. On the one hand, gravitational waves resonating from colliding BHs have been measured [4] and are now a regular astronomical probing tool. Outstandingly, astrophysicists have also captured the first-ever image of a BH at the center of galaxy M87 [5, 6]. Furthermore, there is a collection of additional observational data [7] hinting at the presence of an event horizon for BHs. In general, BH candidates may be stellar-mass objects in a X-ray binary system or supermassive at the center of typical galaxies [8,9,10,11]. All these achievements have been recently conveyed and recognized within the 2020 Nobel prize in Physics [12].

On the other hand, innovative work on BH physics in the past forty years or so have also brought us to the forefront of unanticipated research directions. In the early 70’s of the last century, Bekenstein proposed that a BH entropy is proportional to its horizon area [13, 14]. Then, the evaporation of BHs (through the seminal use of quantum fields in curved spaces) was formulated by Hawking [15]. Testing this property observationally has been recently appraised, bearing promising results [16]. Thereafter, physicists realized an intimate connection between geometrical horizons, thermodynamic temperature and quantum mechanics [17,18,19]. Moreover, it was advanced [20] that the BH horizon area may be quantized, and the corresponding eigenvalues would be given by

$$\begin{aligned} A_n=\gamma L_\text {P}^2n,~~~~n=1,2,3,...~, \end{aligned}$$

(1)

where $\gamma$ is a dimensionless constant of order one and $L_\text {P}=\sqrt{G}$ is the Planck length. The literature has since then been enriched with contributions strengthening in favor of the area spectrum (1), including information-theoretic considerations [21, 22], ranging from string theory arguments [23] to the periodicity of time [24,25,26,27], plus e.g., a Hamiltonian quantization of a dust collapse [28, 29].

Within the viewpoint outlined in the previous paragraph, we suggest a complementary direction of exploration. Let us be more specific. Recently, a set of pertinent arguments and results have been put forward to apply fractional calculus [30,31,32,33,34,35] in quantum physics. Such framework is known as Fractional Quantum Mechanics (FQM), see e.g. [36]. Fractional calculus has been embraced mainly within the last century. In essence, it follows from extending the meaning of derivatives to the case where the order is any number, i.e., irrational, fractional or complex. Its peculiar interest notwithstanding, the obstacles have been fruitfully addressed. In particular, it is currently known that non-integer order systems can describe the dynamical behavior of specific classes of materials and processes over different time and frequency scales. Fractional calculus has assisted in scattering theory, diffusion, probability, potential theory and elasticity. Therefore, it was only sensible to embrace and explore it within quantum physics.

FQM was built upon Feynman and Hibbs [37] assertion about quantum mechanics and path integrals. Moreover, Nelson [38, 39] clarified about classical Brownian motion and quantum mechanical features, whereas Abbott and Wise [40] determined that in 1-dimensional settings, the fractal (or Hausdorff) dimension of those paths is 2. The essential motivation for FQM emerges in that if we restrict the path integral (Feynman) description of quantum mechanics to Brownian paths only, it will be challenging to explain a few other pertinent quantum phenomena [41]. Such difficulties have led to consider a generalization of the Feynman path integral, specifically by replacing the Gaussian probability distribution by Lévy’s [42]; the Hausdorff dimension of the Lévy path is then equal to the fractional parameter $\alpha$.

Extended versions of the Schrödinger equation (SE) are then retrieved, namely from such broader path integral. More concretely, by including non-Brownian trajectories in the path integral formalism of quantum physics, either the space-fractional [43, 44], time-fractional [45], and space-time-fractional [46] versions of the standard SE can be elaborated. Let us be precise and clarify that it is in space-fractional quantum mechanics, where the Feynman path integral method is modified such that the Gaussian probability distribution is replaced by Lévy’s [42], that we obtain the following and broadly used modified SE. More particularly, starting from the Hamiltonian

$$\begin{aligned} H=\frac{{{\mathbf {p}}}^2}{2m}+V({{\mathbf {r}}},t), \end{aligned}$$

(2)

a generalization [36, 41, 43, 44] is produced by means of

$$\begin{aligned} H_\alpha ({\mathbf {p}}, {\mathbf {r}}) : = D_\alpha |{\mathbf {p}}|^\alpha + V ({\mathbf {r}}), \qquad 1 < \alpha \le 2, \end{aligned}$$

(3)

in which $D_\alpha$ is a coefficient carrying dimension $[D_\alpha ]=\mathrm{erg}^{1-\alpha }\mathrm{cm}^\alpha \mathrm{sec}^{-\alpha }$. The parameter $\alpha$ is known as Lévy’s fractional parameter and is associated to the concept of Lévy path and its induced fractal dimension. In the Feynman path integral, the measure is generated by the process of the Brownian motion, and the path’s corresponding (fractal) dimension is $d^{\text {(Feynman)}}_\text {fractal}=2$, as we have remarked. The Lévy path integral leading to a SE would lead to a fractal dimension as $d_\text {fractal}^{(\mathrm{L\acute{e}vy})}=\alpha$. For more details, please browse through, e.g., [1, 30,31,32,33, 36, 41, 43, 44] and other references therein.

Therefore, choosing a space representation with ${\hat{{\mathbf {p}}}}\rightarrow -i\hbar \nabla$ and ${\hat{{\mathbf {r}}}}\rightarrow {{\mathbf {r}}}$, we obtain the space-fractional SE

$$\begin{aligned} i\hbar \frac{\partial \psi ({\mathbf {r}},t)}{\partial t}= D_\alpha (-\hbar ^2 {\varDelta })^{\alpha /2} \psi ({\mathbf {r}},t) + V({\mathbf {r}},t) \psi ({\mathbf {r}},t).\nonumber \\ \end{aligned}$$

(4)

In the above fractional SE, the fractional Riesz derivative [1, 36, 47], $(-\hbar ^2 {\varDelta })^{\alpha /2}$, is defined in terms of the Fourier transformation ${{\mathcal {F}}}$

$$\begin{aligned}&(-\hbar ^2 {\varDelta })^{\alpha /2} \psi ({\mathbf {r}},t) ={{\mathcal {F}}}^{-1}|{\mathbf {p}}|^\alpha {{\mathcal {F}}}\psi ({\mathbf {r}},t) \nonumber \\&\quad =\displaystyle \frac{1}{(2\pi \hbar )^3} \int d^3 p e^{i\frac{{\mathbf {p}}\cdot {\mathbf {r}}}{\hbar }} |{\mathbf {p}}|^\alpha \int e^{-i\frac{{\mathbf {p}}\cdot {\mathbf {r}}'}{\hbar }}\psi ({\mathbf {r}}',t)d^3r'. \end{aligned}$$

(5)

The infinite-well example was one of the first solutions of space-fractional SE, which Laskin solved [41]. Despite its simplicity, this problem is critical since it is the prototype of a quantum detector with internal degrees of freedom.

In what concerns the time-fractional SE, the time evolution is given by the Caputo fractional derivative [48]. In this case, the associated Hamiltonian is non-Hermitian and not local in time. The space-time fractional SE has been introduced by Wang and Xu [46], where they employed a combination of space and time-fractional models to establish their equation. The space-time fractional SE is a generalized version of the equation (4):

$$\begin{aligned} \hbar _\beta i^\beta \partial _t^\beta \psi ({\mathbf {r}},t) = \left[ D_{\alpha ,\beta }(-\hbar _\beta ^2 {\varDelta })^{\alpha /2}+V({\mathbf {r}},t)\right] \psi ({\mathbf {r}},t), \end{aligned}$$

(6)

where $1<\alpha \le 2, ~0<\beta \le 1$, $\hbar _\beta$ and $D_{\alpha ,\beta }$ are two scale coefficients with physical dimensions $[\hbar _\beta ]=\mathrm{erg}.\mathrm{sec}^\beta$ and $[D_{\alpha ,\beta }]=\mathrm{erg}^{1-\alpha }.\mathrm{cm}^\alpha .\mathrm{sec}^{-\alpha \beta }$. In addition, $\partial _t^\beta$ denotes the left Caputo fractional derivative [49] of order $\beta$:

$$\begin{aligned} \partial _t^\beta f(t)=\frac{1}{{\varGamma }(1-\beta )}\int _{0}^{t}d\tau \frac{\dot{f}(\tau )}{(t-\tau )^\beta }, \end{aligned}$$

(7)

where $\dot{f}(\tau )= \frac{df(\tau )}{d\tau }$.

Proceeding towards a broader context, we recall that Wheeler [50] seminally suggested a foam structure for spacetime on the Planck scale. Hence, allowing that a fractal quality could therein be natural. Thus, contemplating a fractional WDW equation could unveil interesting aspects regarding the gravitational domain [51, 52]. In fact, in the last few years, FQM has indeed been proposed and employed as a tool to explore features within quantum cosmology and quantum gravity [53,54,55,56,57,58,59,60,61,62]. It has pointed to exciting opportunities and sidelong connections between unexpected mathematics and physics domains. See [51, 52], for a recent survey about engaging FQM within a canonical route towards quantum gravity and cosmology. Additionally, a few more other references can be found in [63,64,65,66,67,68,69,70].

Thus, in our paper we propose to apply space-FQM to investigate thermodynamic properties of the Schwarzschild BH. The Bekenstein–Hawking entropy expression for a Schwarzchild BH with mass M is given by

$$\begin{aligned} S_\text {B--H}=4\pi GM^2=\frac{A}{4G}, \end{aligned}$$

(8)

where $A=16\pi G^2M^2$ is the BH horizon area. A suitably extended fractional version of the Wheeler–DeWitt (WDW) equation for the Schwarzschild BH will enable us to retrieve altered expressions for the entropy and other specific BH observables.

Moreover, Tsallis and Cirto recently proposed a new formulation for the Schwarzschild BH’s horizon entropy and the entropy-area relation [2]. They asserted that since the Bekenstein–Hawking entropy is proportional to the horizon area (instead of its volume), it would hint that Boltzmann-Gibbs entropy would be unsuitable to describe BHs. These authors have proposed a modified form upon the BH entropy given by Eq. (8), such that an extended expression, using a generalized non-additive entropy, would be

$$\begin{aligned} S_\delta =\gamma A^\delta , \end{aligned}$$

(9)

where $\gamma$ is an unspecified constant and $\delta$ denotes the non-additivity parameter. The above equation suggests that the entropy is a power-law function of its area.

In addition, by introducing a fractal structure for the horizon surface of the BH, Barrow [3] conceived a 3-dimensional spherical analog of a Koch Snowflake – a sphereflake – using a hierarchy of touching spheres around the event horizon. This fractal structure of the BH surface changes its actual area, which in turn leads us to a new entropy relation, namely,

$$\begin{aligned} S=\left( \frac{A}{A_P}\right) ^{1+\frac{\triangle }{2}}, \end{aligned}$$

(10)

where $A_P$ is the Planck area and $\triangle$ would suggestively denote an induced deformation of the horizon, with $\triangle =0$ reproducing the conventional Bekenstein–Hawking entropy (simplest horizon structure) and with $\triangle =1$ corresponding to the most intricate structure. Note that the Barrow modified entropy resembles Tsallis and Cirto’s non-additive entropy (9); nevertheless, the involved foundations and physical principles are entirely different. As an additional application of BH prospecting by means of FQM, we will retrieve these two extended entropy expressions but without using generalized non-additive features.

In essence, we propose and employ herewith a space-fractional formulation of the WDW equation for the Schwarzschild BH. Hence, let us then mention that the remaining of this paper is organized as follows. In Sect. 3, we summarize the canonical quantization of the Schwarzschild BH, having briefly reviewed the corresponding Hamiltonian setting in Sect. 2. In Sect. 4, we hypothesize a fractional calculus setting for the corresponding WDW equation as applied to the Schwarzschild BH. Specifically, we consider the observables reviewed in Sect. 3 and present them (e.g., the Schwarzschild BH entropy) from within the framework of FQM. Section 5 contains our conclusions and a thorough discussion. Throughout this paper we shall work in natural units, $\hbar =c = k_B = 1$.

2 Canonical quantization of a Schwarzchild black hole

We recall in this section results concerning the canonical quantization of the Schwarzschild BH that will be of relevance for our analysis in subsequent sections. The spherical symmetric ADM line element is

$$\begin{aligned} ds^2= & {} -N(r,t)^2dt^2 \nonumber \\&+ {\varLambda }(r,t)^2\Big (dr+N^r(r,t)dt\Big )^2+R(r,t)^2d{\varOmega }^2, \end{aligned}$$

(11)

where $d{\varOmega }^2$ is the line element for the unit two sphere $S^2$. We follow Kuchař’s fall-off conditions [71]. Firstly, it confirms that the coordinates r and t are extended to the Kruskal manifold, $-\infty<r,t<\infty$, and secondly, that the spacetime is asymptotically flat as well. Likewise, the fall-off conditions guarantee that the 4-momentum at the infinities, $r\rightarrow \pm \infty$, has no spatial component, which indicates that the BH is at rest concerning the left and right asymptotic Minkowski spacetimes. By fixing the asymptotic values of the lapse function, N, at infinities, $r\rightarrow \pm \infty$ to be t-dependent quantities (denoted by $N_\pm (t)$, respectively), the Hamiltonian form of the Einstein–Hilbert action functional, with appropriate boundary terms, reads then

$$\begin{aligned} {{\mathcal {S}}}= & {} \displaystyle \int dt\int _{-\infty }^{\infty }\Big \{ {\varPi }_{\varLambda } {\dot{{\varLambda }}} +{\varPi }_R\dot{R}-NH-N^rH_r\Big \}dr \nonumber \\&-\displaystyle \int \Big \{N_+M_++N_-M_-\Big \}dt, \end{aligned}$$

(12)

in which the conjugate momenta of ${\varLambda }$ and R are

$$\begin{aligned} \begin{aligned} {\varPi }_{\varLambda }&=-\frac{M^2_P}{N}R\Big (\dot{R}-R'N^r\Big ),\\ {\varPi }_R&=-\frac{M_P^2}{N}\Big [{\varLambda }\left( \dot{R}-R'N^r\right) +R\left( {\dot{{\varLambda }}}-({\varLambda } N^r)'\right) \Big ], \end{aligned}\nonumber \\ \end{aligned}$$

(13)

$M_P=1/\sqrt{G}$ is the Planck mass, $\dot{f}=\partial _t f$, $f'=\partial _rf$ and the quantities $M_{\pm }(t)$ are defined by the asymptotic fall-off of the configuration variables. Note that on a classical solution, $M_\pm$ are equal to the Schwarzschild mass of the BH. Furthermore, H and $H_r$ are the super-Hamiltonian and the radial super-momentum constraints, respectively, given by

$$\begin{aligned} \begin{aligned} H&=-\frac{1}{RM_P^2}{\varPi }_R{\varPi }_{\varLambda }+\frac{1}{2R^2M_P^2}{\varPi }_{\varLambda }^2+\frac{RR''}{{\varLambda }}\\&\quad -\frac{RR'{\varLambda }'}{{\varLambda }^2}+\frac{R'^2}{2{\varLambda }}-\frac{{\varLambda }}{2},\\ H_r&=\frac{1}{M_P^2}({\varPi }_RR'-{\varLambda }{\varPi }'_{\varLambda }). \end{aligned}\nonumber \\ \end{aligned}$$

(14)

Following Kuchař [71] introducing the following two $(M,{\varPi }_M)$ and $({{\mathcal {R}}},{\varPi }_{{{\mathcal {R}}}})$ pairs of canonical transformations

$$\begin{aligned} \begin{aligned} M&=\frac{{\varPi }_{\varLambda }^2}{2M_P^4R}-\frac{RR'^2}{2{\varLambda }^2}+\frac{R}{2}, \\ {\varPi }_M&=\frac{{\varLambda }{\varPi }_{\varLambda }}{M_P^2}\left[ \left( \frac{R'}{{\varLambda }}\right) ^2-\frac{1}{M_P^4}\left( \frac{{\varPi }_{\varLambda }}{R}\right) ^2 \right] ^{-1},\\ {{\mathcal {R}}}&=R,\\ {\varPi }_{{{\mathcal {R}}}}&=\left( \frac{{\varPi }_{\varLambda } H}{M^2_PR}+\frac{R'H_r}{{\varLambda }^2} \right) \left[ \left( \frac{R'}{{\varLambda }}\right) ^2-\frac{1}{M_P^4}\left( \frac{{\varPi }_{\varLambda }}{R}\right) ^2 \right] ^{-1}, \end{aligned}\nonumber \\ \end{aligned}$$

(15)

the action (12) becomes

$$\begin{aligned} {{\mathcal {S}}}= & {} \displaystyle \int dt\int _{-\infty }^\infty \left\{ \dot{M}{\varPi }_M+\dot{{{\mathcal {R}}}}{\varPi }_{{{\mathcal {R}}}}-N^rH_r-NH\right\} dr\nonumber \\&-\displaystyle \int \left\{ M_+N_+-M_-N_-\right\} dt, \end{aligned}$$

(16)

where the new super-Hamiltonian, H, and the super- momentum, $H_r$, are

$$\begin{aligned} H= & {} -\frac{\left( 1-\frac{2M}{M_P^2R}\right) ^{-1}M'{{{\mathcal {R}}}}'+M_P^{-4}\left( 1-\frac{2M}{M_P^2R}\right) {\varPi }_M{\varPi }_{{{\mathcal {R}}}}}{\left[ \left( 1-\frac{2M}{M_P^2R}\right) ^{-1}{{{\mathcal {R}}}}'^2-M_P^{-4}\left( 1-\frac{2M}{M_P^2R}\right) {\varPi }_M^2 \right] ^\frac{1}{2}}, \nonumber \\ H_r= & {} \frac{1}{M_P^2}\left( {\varPi }_MM'+{\varPi }_{{{\mathcal {R}}}}{{{\mathcal {R}}}}'\right) . \end{aligned}$$

(17)

The variation of ADM action (17) with respect to the lapse function N and $N^r$ imposes the Hamiltonian and momentum constraints

$$\begin{aligned} H\approx 0,~~~~H_r\approx 0, \end{aligned}$$

(18)

or equivalently

$$\begin{aligned} M'\approx 0,~~~~{\varPi }_{{{\mathcal {R}}}}\approx 0. \end{aligned}$$

(19)

The constraint $M'= 0$ means that M is homogeneous $M=M(t)$. Now, by substituting ${\varPi }_{{{\mathcal {R}}}}\approx 0$ and $M=M(t)$ back into the action (17) and in addition the new conjugate momenta of M defined by

$$\begin{aligned} P= & {} \displaystyle \int _{-\infty }^\infty {\varPi }_Mdr \nonumber \\= & {} -\displaystyle \int _{-\infty }^\infty \frac{\sqrt{\left( \frac{dR}{dr}\right) ^2-{\varLambda }\left( 1-\frac{2M}{M^2_PR}\right) }}{1-\frac{2M}{M^2_PR}}dr,~~~ -\infty<P<\infty ,\nonumber \\ \end{aligned}$$

(20)

we obtain

$$\begin{aligned} {{\mathcal {S}}}=\int \Big \{P\dot{M}-(N_++N_-)M\Big \}dt. \end{aligned}$$

(21)

Note that the new conjugate variables (M, P) obey the Poisson bracket $\{M, P\}=1$. Following Louko and Mäkelä [72], if we picked the right-hand side asymptotic Minkowski time as the observer time parameter, we should restrict $N_+=1$ and $N_-=0$. Next, the reduced action (21) reduces to the following simple form

$$\begin{aligned} {{\mathcal {S}}}=\int \left\{ P\dot{M}-H(M)\right\} dt, \end{aligned}$$

(22)

where $H(M)=M$ is the reduced Hamiltonian of the BH. One can easily show that the field equations’ solution is $M=const.$ and $P=-t$, as expected. The BH’s mass constancy follows Birkhoff’s theorem, which declares that the mass is the only time-independent and coordinate invariant solution. Moreover, the conjugate momenta, P, describes the asymptotic time coordinate at the spacelike slice. Once again, by using the canonical transformations $(M,P) \rightarrow (x,p)$, introduced by Louko and Mäkelä [72]

$$\begin{aligned} \begin{aligned} |P|&=\displaystyle \int _x^{2MG}\frac{dy}{\sqrt{\frac{2MG}{y}-1}},\\ M&=\frac{1}{2G}\left( \frac{G^2p^2}{x}+x\right) , \end{aligned} \end{aligned}$$

(23)

the reduced action (22) takes the form

$$\begin{aligned} {{\mathcal {S}}}=\int \left\{ p\dot{x}-H\right\} dt, \end{aligned}$$

(24)

where $H=M$ is the Hamiltonian and is given (utilizing the second transformation of (23)), as

$$\begin{aligned} H=\frac{M_P^2}{2}\Big (\frac{p^2}{M_P^4x}+x\Big ). \end{aligned}$$

(25)

It is of interest to acknowledge the following at this point. Transformations (23) map the BH solution into a wormhole solution, in which x represents the wormhole throat [72]. The time evolution of this corresponding wormhole throat is given by Hamilton’s equations

$$\begin{aligned} \dot{x}=\frac{p}{M_P^2x},~~~~ \dot{p}=\frac{p^2}{2M_P^2x^2}-\frac{1}{2}M_P^2 \end{aligned}$$

(26)

with a solution for the wormhole throat as

$$\begin{aligned} \begin{aligned} x&=\frac{M}{M_P^2}\Big (1+\cos (M_P\eta )\Big ),\quad x\ge 0\\ t&=\frac{M}{M_P}\Big (\eta +\frac{1}{M_P}\sin (M_P\eta )\Big ), \quad -\frac{M\pi }{M_P^2}\le t\le \frac{M\pi }{M_P^2}. \end{aligned}\nonumber \\ \end{aligned}$$

(27)

As we can see from the above solutions, it is necessary to define transformations (23) so that the time parameter t (or equivalently the conjugate momentum P) is restricted into the finite interval

$$\begin{aligned} -\frac{1}{8T_H}\le t\le \frac{1}{8T_H}, \quad T_H=\frac{M^2_P}{8\pi M}, \end{aligned}$$

(28)

where $T_H$ is, remarkably, the Hawking temperature of the BH.

3 Thermodynamic implications from the quantum Schwarzschild black hole

In the coordinate representation ${{\hat{p}}} \rightarrow -id/dx$, ${{\hat{x}}} \rightarrow x$, the canonical quantization procedure upon the previous section gives us a suitable time-independent WDW equation, for the simple one-dimensional minisuperspace of the Schwarzschild BH

$$\begin{aligned} H\left( -i\frac{d}{dx},x\right) \psi (x)=M\psi (x). \end{aligned}$$

(29)

As usual, there is an operator-ordering problem in addressing the above WDW equation, but as we are interested in BH states whose mass $M \gg M_P$, its particular resolution will not surpass our semiclassical considerations. Hence, we adopt the following wide enough factor-ordering [73]

$$\begin{aligned} \frac{p^2}{x}=\frac{1}{3}\left( x^ipx^jpx^k+x^kpx^ipx^j+x^jpx^kpx^i\right) , \end{aligned}$$

(30)

where $i+j+k=-1$. Note that because in the left hand side of (30) we have $p^2/x$, so, in its right side the power of x is also $-1$. We thus write the WDW equation (29)

$$\begin{aligned}&-\frac{1}{2M_P^2x}\frac{d^2}{d^2}\psi (x)+\frac{1}{2M_P^2x^2}\frac{d}{dx}\psi (x) \nonumber \\&+\left( \frac{1}{2}M_P^2x+\frac{q}{2M_P^2x^3}\right) \psi (x)=M\psi (x), \end{aligned}$$

(31)

where $q=(ij+ik+jk-2)/3$. If we redefine the wave function $\psi (x)\rightarrow \sqrt{x}\psi (x)$, and choose ordering in which $q=-3/4$, then Eq. (31) will reduce to

$$\begin{aligned}&-\frac{1}{2M_P}\frac{d^2}{dx^2}\psi (x)+\frac{1}{2}M_P\omega _P^2\left( x-\frac{M}{M_P^2}\right) ^2\psi (x)\nonumber \\&\quad =\frac{M^2}{2M_P}\psi (x), \end{aligned}$$

(32)

which is a SE for the harmonic oscillator of the Planck’s mass $M_P$, the Planck’s angular frequency $\omega _P=1/t_P$ defined in terms of Planck’s time $t_P=1/M_P$. The domain of definition for x is $x\ge 0$, and consequently, the Hamiltonian operator of the harmonic oscillator in (32) is defined on a dense domain $C^\infty (0,+\infty )$. Hence, H is not an essentially self-adjoint operator. It may constitute an Hermitian operator if

$$\begin{aligned} \langle \psi _1|H\psi _2\rangle =\langle H\psi _1|\psi _2\rangle ,\psi _1,\psi _2\in {{{\mathcal {D}}}}(H). \end{aligned}$$

(33)

A necessary and sufficient condition for the validity of this condition is

$$\begin{aligned} \left. \frac{\psi (x)}{\psi '(x)}\right| _{x=0}=\gamma ,\,\,\,\,\gamma \in {\mathbb {R}}, \end{aligned}$$

(34)

where a prime symbol, $\prime$, denotes the derivative of $\psi ( x )$ with respect to x. As pointed out by Tipler [74,75,76,77], the constant $\gamma$ (with dimension of length) would be a new fundamental constant of theory. To avoid such, we set it to be zero. Hence, we assume

$$\begin{aligned} \psi (x)\Big |_{x=0}=0, \end{aligned}$$

(35)

which constitutes the DeWitt boundary condition [78]. In addition, we are interested in square-integrable wave functions in the interval $0\le x<+\infty$, which implies the second boundary condition $\psi (x\rightarrow +\infty )=0$. The general solution of the WDW equation (32) is

$$\begin{aligned}&\psi (z)=e^{-\frac{z^2}{4}}\Big \{A\, _1F_1\left( -\frac{\nu }{2};\frac{1}{2};\frac{z^2}{2}\right) \nonumber \\&\quad +Bz\, _1F_1\left( \frac{1-\nu }{2};\frac{3}{2};\frac{z^2}{2}\right) \Big \}, \end{aligned}$$

(36)

where $z=\sqrt{2M_P\omega _P}(x-M/M_P^2)$ is the new dimensionless coordinate in the minisuperspace, $_1F_1(a;b;\zeta )$ is confluent hypergeometric function, $\nu =\frac{1}{2}\left( \frac{M^2}{M_P^2} - 1 \right)$, A and B are two integration constants. Moreover, from the asymptotic behavior of the confluent hypergeometric functions

$$\begin{aligned} _1F_1(a;b;\zeta \rightarrow \infty )\simeq {\varGamma }(b)e^\zeta \zeta ^{a-b}/{\varGamma }(a), \end{aligned}$$

(37)

we find that the bracket $\{ ... \}$ in Eq. (36) brings the factor $e^{z^2/2}$, which would dominate over the Gaussian exponential factor explicit in (36). In other words, the wave function is square-integrable if the remaining factor provided from the bracket$\{ ... \}$ in Eq. (36), vanishes. This fixes the relative values of A and B, leading to

$$\begin{aligned} \psi (z)= & {} N 2^{\frac{\nu }{2}}e^{-\frac{z^2}{4}}\Big \{ \frac{_1F_1\left( -\frac{\nu }{2};\frac{1}{2};\frac{z^2}{2}\right) }{{\varGamma }\bigg (\frac{1-\nu }{2}\bigg )}\nonumber \\&-z\frac{\sqrt{2}\,_1F_1\left( \frac{1-\nu }{2};\frac{3}{2};\frac{z^2}{2}\right) }{{\varGamma }\bigg (-\frac{\nu }{2}\bigg )} \Big \}, \end{aligned}$$

(38)

where N is a normalization constant. Applying the boundary condition (34) on the obtained wave function (38) gives us

$$\begin{aligned} \frac{_1F_1\left( -\frac{\nu }{2};\frac{1}{2};\left( \frac{M}{M_P}\right) ^2\right) }{{\varGamma }\left( \frac{1-\nu }{2}\right) }+\frac{2M\,_1F_1\left( \frac{1-\nu }{2};\frac{3}{2};\left( \frac{M}{M_P}\right) ^2\right) }{M_P{\varGamma }\left( -\frac{\nu }{2}\right) }=0. \end{aligned}$$

(39)

The solution of the above equation for M, gives us the mass spectrum of the BH.

We can see that the spectrum of $M^2$ is not equally spaced for small values of $\nu$. On the other hand, for large values of $\nu$ (which is defined by $\nu =\frac{1}{2}\left( \frac{M^2}{M_P^2} - 1 \right)$) if we use the asymptotic relation (37) in (39) we find

$$\begin{aligned} \frac{e^{2\nu +1}}{(2\nu +1)^{\frac{\nu +1}{2}}2^{\nu }{\varGamma }(-\nu )}=0\Rightarrow {\varGamma }(-\nu )=\pm \infty \Rightarrow \nu =n,\nonumber \\ \end{aligned}$$

(40)

which provides us the mass spectrum

$$\begin{aligned} M=M_P\sqrt{2n+1}, \end{aligned}$$

(41)

where n is an integer and $n\gg 1$. Note that the above result assumes that $M \gg M_P$, i.e., $\nu \gg 1$ and is therefore essentially semiclassical. To see this, let us apply the Bohr–Sommerfeld quantization rule to the Hamiltonian (25). The classical turning points of (25) are $x=0$ and $x=2M/M_P^2$. Hence, the conventional treatment of the Bohr–Sommerfeld quantization rule yields

$$\begin{aligned} 2\pi \left( n+\frac{1}{2}\right)= & {} 2\displaystyle \int _0^{\frac{2M}{M_P^2}}pdx \nonumber \\&=2\displaystyle \int _0^{\frac{2M}{M_P^2}}\sqrt{M^2-M_P^4\left( x-\frac{M}{M_P^2}\right) ^2}dx,\nonumber \\ \end{aligned}$$

(42)

which allows to extract the mass spectrum (41). Bekenstein [20] firstly found a similar mass spectrum. Generally, the proportionality constant for the square root of n in (41) is model dependent. Since then, several authors [20, 79] have used different arguments for a quantum BH spectrum of the type (41). Before proceeding, let us keep in mind equation (41), as this and others in this section will bear alterations that will be brought from the intrinsic features of FQM, as applied to the Schwarzshild BH (see next section).

Hawking [15, 80] showed in 1974 that due to quantum fluctuations, BHs emit black-body radiation, consistently with the corresponding entropy being one fourth of the event horizon area, namely $A=16\pi G^2M^2$. Following Refs. [81, 82], let us assume that the Hawking radiation of a massive BH where $M \gg M_P$ and $n\gg 1$, is emitted when the BH system spontaneously jumps from the state $n+1$ towards the closest lower state level, i.e., n, as described by (41). Let us now denote the frequency of the emitted thermal radiation as $\omega _0$. Then

$$\begin{aligned} \omega _0= & {} M(n+1)-M(n)\simeq \frac{M_P}{\sqrt{2n}} \nonumber \\\simeq & {} \frac{M_P^2}{M}\left[ 1+\frac{1}{2}\left( \frac{M_P}{M}\right) ^2\right] , \end{aligned}$$

(43)

which agrees with the classical BH oscillation frequencies which scales as 1/M. We thus find a BH to radiate with a characteristic temperature $T\propto M_P^2/M$, matching the Hawking temperature.

The characteristic BH time (the lifetime of the BH at the state $M(n+1)$ before decaying into the lower state M(n)) can be defined [82] as

$$\begin{aligned} \tau _n^{-1}=\frac{\dot{M}}{\omega _0}\simeq \frac{M\dot{M}}{M_P^2}\left[ 1-\frac{1}{2}\left( \frac{M_P}{M}\right) ^2\right] , \end{aligned}$$

(44)

where $\dot{M}=dM/dt$ is the mass loss of the BH because of its evaporation; in the second equality we used the definition of $\omega _0$ expressed in (43). As discussed in [81, 83], because of the interaction of the BH with the vacuum of the quantum fields, the width of the states, $W_n$, is not zero. The width of state n can be estimated [81, 83] as

$$\begin{aligned} W_n=\beta [M(n+1)-M(n)]=\beta \omega _0, \end{aligned}$$

(45)

where $\beta \ll 1$ is a numerical dimensionless factor. Then, by inserting (43) into the uncertainty relation $W_n\tau _n\simeq 1$ and eliminating $\tau _n$ in resulting equation, with the assistance of (44) we can find

$$\begin{aligned} \dot{M}=\frac{\beta M_P^4}{M^2}\left[ 1+\left( \frac{M_P}{M}\right) ^2\right] . \end{aligned}$$

(46)

If we further assume, on the one hand, that the origin of the Hawking radiation emerges from the highly blueshifted modes just outside the horizon, and, on the other hand, take the BH as a black-body, then the radiated power is given by the Stefan–Boltzmann law [84, 85]

$$\begin{aligned} \dot{M}=\sigma _SAT^4, \end{aligned}$$

(47)

where $\sigma _S=\pi ^2/60$ is the Stefan–Boltzmann constant and $A=16\pi M^2/M_P^4$ is the horizon area. Eliminating the mass loss of the BH, using Eqs. (46) and (47), gives us the effective temperature

$$\begin{aligned} T=\left( \frac{\beta }{16\pi \sigma _S}\right) ^\frac{1}{4}\frac{M_p^2}{M}\left[ 1+\frac{1}{4}\left( \frac{M_P}{M}\right) ^2\right] . \end{aligned}$$

(48)

The BH entropy can then be expressed as

$$\begin{aligned} S=\int \frac{dM}{T}. \end{aligned}$$

(49)

By choosing $\beta =1/15360\pi$ [86,87,88,89,90,91,92,93,94,95,96,97], Eqs. (48) and (49) yields

$$\begin{aligned} S=S_\text {B--H}-2\pi \ln {\left( S_\text {B--H}\right) }+const., \end{aligned}$$

(50)

where $S_\text {B--H}=4\pi GM^2$ is the Bekenstein–Hawking entropy. The logarithmic correction to the Bekenstein–Hawking entropy is obtained using other methods [86,87,88,89,90,91,92,93,94,95,96,97] except that the overall factor $2\pi$ is model dependent.

4 Fractional quantum mechanics and Schwarzschild black hole thermodynamics

In this section, we will establish and then investigate the alterations brought from employing FQM features towards a Schwarzschild BH. This will provide broader expressions for some thermodynamic observables, specifically in terms explicitly dependent on the fractional parameter, $1<\alpha \le 2$, since the limit $\alpha =2$ will conveys us to the standard case (summarized in Sects. 2 and 3).

Concretely, a fractional WDW equation for a BH will be employed, in a corresponding minisuperspace. Our approach stems from Laskin’s seminal papers [41, 98], leading to an Hamiltonian, which includes a fractional kinetic term in terms of the quantum Riesz fractional operator; this method has been extended to the WDW equation in Refs. [51, 52].

The fractional extension of the WDW equation (32) is given by

$$\begin{aligned}&\frac{1}{2}M_P^{1-\alpha }(-{\varDelta })^\frac{\alpha }{2}\psi (z)+\frac{1}{2}M_P^{\alpha -1}\omega _P^2z^\alpha \psi (z)\nonumber \\&\quad =\frac{M^2}{2M_P}\psi (z), \end{aligned}$$

(51)

where $z=x-M/M_P^2$ is the new coordinate in the 1-dimensional minisuperspace, ${\varDelta }=d^2/dz^2$, $(-{\varDelta })^\frac{\alpha }{2}$ is the Riesz fractional derivative [1, 30,31,32,33, 99] and $1<\alpha \le 2$. Unfortunately, there is no known general solution, explicitly bearing a dependence on $\alpha$ for the above fractional WDW equation. Therefore, we may resort to employ the Bohr–Sommerfeld quantization rule. By replacing $|p|=(-\nabla )^\frac{1}{2}$, the fractional WDW equation leads to the following relation

$$\begin{aligned} \frac{M_P^{1-\alpha }}{2}|p|^\alpha +\frac{M_P^{\alpha -1}}{2}\omega _P^2z^\alpha =\frac{M^2}{2M_P}, \end{aligned}$$

(52)

which is, in fact, the fractional version of (25). Hence, the classical turning points (where $|p|=0$) are $z=\pm (M^2/M_P^{2-\alpha })^\frac{1}{\alpha }$. Moreover,

$$\begin{aligned} 2\pi \left( n+\frac{1}{2}\right)= & {} \displaystyle \oint pdz=2\left( \frac{M}{M_P}\right) ^\frac{4}{\alpha }\displaystyle \int _0^1\left( 1-y^\alpha \right) ^\frac{1}{\alpha }dy \nonumber \\&=\frac{2M^\frac{4}{\alpha }}{\alpha M_P^\frac{4}{\alpha }}B\left( \frac{1}{\alpha },1+\frac{1}{\alpha }\right) , \end{aligned}$$

(53)

where $y=(M_P^{\alpha +2}/M^2)^\frac{1}{\alpha }z$ and B(a, b) is the beta function. Thus, the application of the standard Bohr–Sommerfeld quantization rule in this setting gives us the following semi-classical mass spectrum

$$\begin{aligned} M=\left( \frac{\alpha \pi {\varGamma }(\frac{2}{\alpha })}{{\varGamma }(\frac{1}{\alpha })^2} \right) ^\frac{\alpha }{4}M_P\left( n+\frac{1}{2}\right) ^\frac{\alpha }{4}. \end{aligned}$$

(54)

For $\alpha =2$ we recover spectrum (41) as written in the previous section. Figure 1 shows the BH mass spectrum for three values of $\alpha$. As we show in this figure, the mass of the BH increases with n but at a faster rate for $\alpha =2$, namely the standard case.

Fig. 1

Plot of the mass spectrum for a Schwarzschild black hole as a function of quantum number n for three values of $\alpha =1$ (circles), $\alpha =1.5$ (asterisks) and $\alpha =2$ (solid-diamonds)

Similarly to the previous Sect. 3, if we write the frequency of the radiation emitted by the BH, $\omega _0$ , we now obtain

$$\begin{aligned} \omega _0(\alpha )= & {} M(n+1,\alpha )-M(n,\alpha )\simeq \frac{\alpha BM_P}{4}n^{\frac{\alpha }{4}-1} \nonumber \\\simeq & {} \frac{\alpha B^\frac{4}{\alpha }M_P^\frac{4}{\alpha }}{4M^{\frac{4}{\alpha }-1}}\left[ 1+\frac{1}{2}\left( 1-\frac{\alpha }{4}\right) \left( \frac{BM_P}{M}\right) ^\frac{4}{\alpha }\right] , \end{aligned}$$

(55)

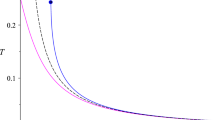
where $B=\frac{\left( \alpha \pi {\varGamma }(\frac{2}{\alpha })\right) ^\frac{\alpha }{4}}{{{\varGamma }(\frac{1}{\alpha })^\frac{\alpha }{2}}}$. Note that the energy of the emitted radiation is a function of the fractional-order $\alpha$. We then find that for a massive BH, where $M\gg M_P$, the energy of emitted radiation is minimal for $\alpha \rightarrow 1$, and it will increases up to a maximum at $\alpha =2$. Additional elements are conveyed within Fig. 2.

Interestingly, the mass spectrum (54) (which includes the standard case (41)) may induce observable signatures that gravitational waves [100,101,102] may inform about. Equation (43) shows that the frequency of the emitted Hawking radiation scales as 1/M. Hence, if we put $M\simeq 10M_\odot -50 M_\odot$ as typical of the BHs registered by LIGO-Virgo, then we obtain from Eq. (43) that $f=\frac{\omega _0}{2\pi }={{\mathcal {O}}}(10^2-10^4)$ Hz. On the other hand, the fractional frequency of radiation $f(\alpha )=\frac{\omega _0(\alpha )}{2\pi }$, whereas defined instead with (55), gives us a much wider possibility for the frequencies. For example, with $M=10M_\odot$ the range $1<\alpha \le 2$ yields ${{\mathcal {O}}}(10^{-74})\text {Hz}<f(\alpha )\le {{\mathcal {O}}}(10^4)\text {Hz}$. Figure 2 shows how $\omega _0(\alpha )$ depends on $\alpha$.

To be more clear, let us contemplate the mass spectrum as in (54) and further discuss it within a wider analysis as follows. Take the interaction of a gravitational wave with a BH. Suppose the BH is initially at state $n_1$. Regarding the mass spectrum in (54), we can also consider process whereby the BH could alternatively absorb a gravitational wave whose frequency, $f_\text {GW}$ satisfies

$$\begin{aligned} f_\text {GW}=\frac{{\varDelta } M}{2\pi }=\frac{\alpha \pi {\varGamma }(\frac{2}{\alpha }){\varDelta } n}{8{\varGamma }(\frac{1}{\alpha })^2M^{\frac{4}{\alpha }-1}}, \end{aligned}$$

(56)

where ${\varDelta } n=n_1-n_2$ and $n_2$ denotes the final state of the BH after absorption of the gravitational wave. As known in classical GR, the effective potential that describes the motion of a test particle has a maximum at the 3/2 Schwarzschild radius, called photon sphere. Essentially, this (potential barrier) screens the near-horizon region from external observers [103, 104]. The gravitational radiation proceeding towards the horizon will be scattered at the horizon if its frequency does not match, e.g., (56). Otherwise, radiation with the frequencies such as (56) in our example, would be absorbed. The previous assertions notwithstanding, if then we consider back-reaction quantum effects, BHs are not perfect absorbers of gravitational radiation and part of the radiation will be reflected from the horizon area. The reflected part of the radiation then interacts with the potential barrier at the photon sphere. Then, it will partially be transmitted, and the other portion will be reflected again back towards the horizon. This outcome generates a series of so-called gravitational-wave echoes [105]. This feature could eventually be detected either in the inspiral stage of BH binaries or during the last stages of BH relaxation following a merger. For further details and detection methods please see [106]. Therefore, BHs may act as “magnifying lenses” in the sense that they could bring new features of the BH horizon-area within the realm of gravitational waves observations.

Fig. 2

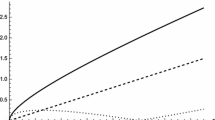
Logarithmic plot of the fractional entropy (dash), $S(\alpha )$, the temperature (dash-dot), $T(\alpha )$, the frequency of the emitted thermal radiation (line), $\omega _0(\alpha )$, and the mass loss (dot), $\dot{M}(\alpha )$ of the Schwarzschild black hole given by Eqs. (60), (58), (55) and (57) respectively, with mass $M=10M_\odot$ as a function of $\alpha$

Furthermore, using the formula of the characteristic time of an evaporating BH, $\tau ^{-1}=\dot{M}/\omega _0$, the uncertainty relation for width of states, $W_n\tau _n\simeq 1$ and the relation $W_n=\beta \omega _0$, we compute

$$\begin{aligned} \dot{M}=\frac{\alpha ^2\beta B^\frac{8}{\alpha }M_P^\frac{8}{\alpha }}{16M^{\frac{8}{\alpha }-2}}\left[ 1+\left( 1-\frac{\alpha }{4}\right) \left( \frac{BM_P}{M}\right) ^\frac{4}{\alpha }\right] , \end{aligned}$$

(57)

which will increase as mass is lost. Inserting the above relation into the Stefan–Boltzmann law (47), it gives the corresponding temperature of the BH¹

$$\begin{aligned} T= & {} \left( \frac{\beta \alpha ^2B^\frac{8}{\alpha }}{16^2\pi \sigma _S}\right) ^\frac{1}{4}\frac{M_P^{\frac{2}{\alpha }+1}}{M^\frac{2}{\alpha }}\left[ 1+\frac{1}{4}\left( 1-\frac{\alpha }{4}\right) \left( \frac{BM_P}{M}\right) ^\frac{4}{\alpha }\right] ,\nonumber \\ \end{aligned}$$

(58)

$$\begin{aligned} \beta= & {} \frac{{\varGamma }\left( \frac{1}{\alpha }\right) ^4}{15(\alpha +2)^44^{\frac{4}{\alpha }-1}{\varGamma }\left( \frac{2}{\alpha }\right) ^2\pi ^{\frac{4}{\alpha }+1}}. \end{aligned}$$

(59)

Note that for $\alpha =2$ we will recover equations of the previous section. Moreover, using (49), we find the fractional entropy of the BH to be

$$\begin{aligned} S= S_\text {B--H}^\frac{2+\alpha }{2\alpha }+\frac{\alpha (4-\alpha )(2+\alpha )4^\frac{\alpha +2}{2\alpha }\pi ^\frac{3\alpha +2}{2\alpha }{\varGamma }\left( \frac{2}{\alpha }\right) }{(2-\alpha ){\varGamma }\left( \frac{1}{\alpha }\right) ^2}\frac{1}{S_\text {B--H}^\frac{2-\alpha }{2\alpha }},\,\,\,\,\alpha \ne 2.\nonumber \\ \end{aligned}$$

(60)

To further contrast a BH with FQM features with a standard Schwarzschild BH, let us examine Eqs. (55), (57), (58) and (60) and for a stellar BH with mass approximately $10 M_\odot$. For the limiting $\alpha =2$ and $\alpha \rightarrow 1$ values of the Lévy index, the values of $S(\alpha )$, $T(\alpha )$, $\omega _0(\alpha )$ and $\dot{M}(\alpha )$ are given in Table 1.

Table 1 The fractional entropy, $S(\alpha )$, the temperature, $T(\alpha )$, the mass loss, $\dot{M}(\alpha )$ and the frequency of the emitted thermal radiation, $\omega _0(\alpha )$ of the Schwarzschild black hole given by Eqs. (55), (57), (58) and (60) respectively, with mass $M=10M_\odot$

Its first row, together with Fig. 2, shows that the entropy of fractional BH can be much larger than in the standard Schwarzschild case. The second row shows that a stellar BH temperature (with mass $10M_\odot$) in fractional formalism is always less than $10^{-9} K$. On the other hand, in the extreme case $\alpha \rightarrow 1$, the temperature of a fractional BH is approximately zero: $T(\alpha \rightarrow 1) \simeq 10^{-48}$ K. Moreover, the manner the mass decay ${{\dot{M}}}(\alpha )$ proceeds is indicated by by the third row, in agreement with the temperature range: it is quite negligible for the extreme case, $\alpha \rightarrow 1$. Since the average temperature of the Universe at the present epoch is about 2.7 K, all stellar BHs with $M=10M_\odot$ and $1<\alpha \le 2$ are absorbing more matter and radiation than they emit Hawking radiation and will not begin to evaporate until the Universe has expanded and cooled below their corresponding temperature. Therefore, in our setting, the BHs with fractional features could be almost eternal within $\alpha \rightarrow 1$.

Let us now remark the following. Tsallis and Cirto [2] investigated the entropy of a Schwarzschild BH, using appropriate non-additive generalizations for d-dimensional systems and suggested a generalized entropy. In their study [2], a non-additive entropy is defined by

$$\begin{aligned} S_\delta =\sum _i^Np_i\left( \ln \left( \frac{1}{p_i}\right) \right) ^\delta , \end{aligned}$$

(61)

for a set of N discrete states, where $\delta >0$ denotes the non-additivity parameter and $p_i$ is a probability distribution [108]. For $\delta =1$ we recover the standard Boltzmann–Gibbs entropy. Then, as Tsallis and Cirto demonstrated [2], the generalized BH entropy can be written as

$$\begin{aligned} S_\text {Tsallis}\propto S_\text {B--H}^\delta . \end{aligned}$$

(62)

If we identify the non-additivity parameter of Tsallis and Cirto as $\delta =\frac{2+\alpha }{2\alpha }$, the entropy (60) retrieved from fractional quantum mechanical methods can be rewritten as

$$\begin{aligned} S=S_\text {B--H}^\delta +\frac{\kappa }{S_\text {B--H}^{\delta -1}}, \quad 1<\delta <\frac{3}{2}, \end{aligned}$$

(63)

where

$$\begin{aligned} \kappa =\frac{\delta (2\delta -3)4^{\delta +1}\pi ^{\delta +\frac{2}{2\delta -1}}{\varGamma }(2\delta -1)}{(\delta -1)(2\delta -1)^2{\varGamma }\left( \delta -\frac{1}{2}\right) ^2}. \end{aligned}$$

(64)

This shows that the leading term of the FQM computed BH entropy can be expressed in terms of the Tsallis and Cirto result for a BH. Noteworthy, for $1<\alpha \le 2$ the fractional entropy of a BH varies in the corresponding interval as

$$\begin{aligned} S_\text {B--H}^\frac{3}{2}+\frac{36\pi ^\frac{5}{2}}{S^\frac{1}{2}_\text {B--H}}<S\le S_\text {B--H}-2\pi \ln {\left( S_\text {B--H}\right) }. \end{aligned}$$

(65)

A natural question that arises is the meaning of the entropy relation, ranging from Eqs. (60) to (65). To assist in addressing this question, let us first remind the fractal nature of the Lévy path [42] in FQM. As we know, in the Feynman path integral representation of quantum mechanics, the measure is generated by the process of the Brownian motion, and the fractal dimension of the Feynman’s path is $d^{\text {(Feynman)}}_\text {fractal}=2$. In addition,, FQM is based on the fractional path integral [41, 42]. The Lévy path integral corresponding to the SE (51) is

$$\begin{aligned} K_L(z_f,t_f|z_i,t_i)=\displaystyle \int _{z_i}^{z_f}{\mathcal {D}}ze^{-i\int _{z_i}^{z_f}V(z(t))dt}, \end{aligned}$$

(66)

where V(z(t)) is the potential as a functional of the Lévy path and $z_i$ ($z_f$) denotes the initial (final) point. In this case, the fractional path integral measure is

$$\begin{aligned} {\mathcal {D}}z(t)= & {} \displaystyle \lim _{N\rightarrow \infty }dz_1...dz_{N-1}\nonumber \\&\times \displaystyle (iD_\alpha \varepsilon )^{-\frac{N}{\alpha }}\prod _{j=1}^{N}L_\alpha \left\{ \left( \frac{1}{iD_\alpha \varepsilon }\right) ^\frac{1}{\alpha }|z_j-z_{j-1}|\right\} ,\nonumber \\ \end{aligned}$$

(67)

where $D_\alpha =M_P^{1-\alpha }$, $\varepsilon =(t_f-t_i)/N$, $z_0=z_i$, $z_N=z_f$ and the Lévy distribution function, $L_\alpha$, is indicated in terms of Fox’s H function

$$\begin{aligned}&\left( D_\alpha t\right) ^{-\frac{1}{\alpha }}L_\alpha \left\{ \left( \frac{1}{D_\alpha t}\right) ^\frac{1}{\alpha }|z| \right\} \nonumber \\&\quad =\frac{1}{\alpha |z|}H_{2,2}^{1,1}\left[ \left( \frac{1}{D_\alpha t}\right) ^\frac{1}{\alpha }|z|\Big |^{(1,\frac{1}{\alpha }),(1,\frac{1}{2})}_{(1,1),(1,\frac{1}{2})}\right] . \end{aligned}$$

(68)

The measure (67) indicates that a length increment, ${\varDelta } z=z_j-z_{j-1}$, and a time increment, ${\varDelta } t$, satisfy the fractional scaling relation

$$\begin{aligned} {\varDelta } z\propto D_\alpha ^\frac{1}{\alpha }({\varDelta } t)^\frac{1}{\alpha }. \end{aligned}$$

(69)

The above scaling relation implies that the fractal dimension of the Lévy path is $d_\text {fractal}^{(\mathrm{L\acute{e}vy})}=\alpha$. Thus, fractional features within FQM could be interpreted as being generated by a Lévy stochastic process [42] and suggesting a fractal structure.² Hence, it may be possible to theorize within the FQM framework herewith proposed, that the horizon of the BH may unveil a fractal structure whose relevance will be $\alpha$-dependent. In this context, let us rewrite the first term on the right-hand side of (60) as follows

$$\begin{aligned} S_\text {B--H}^\frac{2+\alpha }{2\alpha }=\left( \frac{A}{4G}\right) ^\frac{2+\alpha }{2\alpha }=\frac{A_\text {fractal}}{4G}, \end{aligned}$$

(70)

by means of which we hence define $A_\text {fractal}$. Being more concrete, the entropy is proportional to a surface area, but one explicitly given by

$$\begin{aligned} A_\text {fractal}=4L_p^2\left( \frac{A}{4G}\right) ^\frac{2+\alpha }{2\alpha }. \end{aligned}$$

(71)

Furthermore, the above expression additionally suggests a fractal dimension [109, 110] of the BHs surface, namely

$$\begin{aligned} D_\text {fractal}=\frac{2+\alpha }{\alpha }, \quad 2\le D_\text {fractal}<3. \end{aligned}$$

(72)

Moreover, Eq. (60) will take the following form

$$\begin{aligned} S=\frac{A_\text {fractal}}{4G}+\kappa \left( \frac{A_\text {fractal}}{4G}\right) ^{1-\frac{1}{2}D_\text {fractal}},\quad 2< D_\text {fractal}<3.\nonumber \\ \end{aligned}$$

(73)

Let us add further to the question set a few paragraphs above, namely on the meaning of entropy within Eqs. (60)–(65). By means of a very interesting paper, Barrow recently conjectured that BHs might exist with such extremely wrinkled surfaces (referred to as a rough horizon), so that the event horizon would be a fractal surface [3]. He proposed that the fractal area of the BH, $A_\text {fractal}$ is related to the ordinary area, $A=16\pi G^2M^2$, via

$$\begin{aligned} A_\text {fractal}\propto A^{1+\frac{\triangle }{2}}, \quad 0\le \triangle \le 1, \end{aligned}$$

(74)

where $\triangle =0$ is corresponding to the ordinary non-fractal horizon, and $\triangle =1$ to the most complex structure. Inserting the above area definition into entropy (60) we find

$$\begin{aligned} S_\text {B--H}=\left( \frac{A}{4G}\right) ^{1+\frac{\triangle }{2}}+\frac{\kappa }{\left( \frac{A}{4G}\right) ^{\frac{\triangle }{2}}}, \quad 0<\triangle <1, \end{aligned}$$

(75)

where we defined $\triangle =2/\alpha -1$. Note that the extreme case of Barrow $\triangle =1$, ($\alpha \ne 1$), does not exist in our model. Therefore, the above equation clarifies that the Barrow entropy can be obtained from within FQM.

We can elaborate more on the physical consequences of the above entropy (or equivalently from (60)) formula. If we assume that the number of degrees of freedom, N, in the horizon is [111]

$$\begin{aligned} N=4S, \end{aligned}$$

(76)

then, combining Eqs. (58), (75) and (76) plus some algebra, we retrieve a modified equipartition theorem

$$\begin{aligned} M=\frac{1}{2}\left( 1+\frac{\triangle }{2}\right) NT\Big \{1- \kappa _\triangle \left( \frac{T_P}{NT}\right) ^{2(\triangle +1)}\Big \}, \end{aligned}$$

(77)

where

$$\begin{aligned} \kappa _\triangle =\frac{\pi (\triangle +\frac{1}{2}){\varGamma }(\triangle +1)}{2^{2(\triangle +3)}\left( 1+\frac{\triangle }{2}\right) ^{2(\triangle +1)}{\varGamma }(\frac{\triangle +1}{2})^2}, \end{aligned}$$

(78)

and $T_P$ is the Planck temperature. The heat capacity, C of a fractional BH can be computed from the expression

$$\begin{aligned} C =-\frac{(S')^2}{S''}, \end{aligned}$$

(79)

where a prime means a derivative relative to the BH mass, M. Substituting (75) into the above definition gives

$$\begin{aligned} C=-\frac{\triangle +2}{\triangle +1}\left( \frac{M}{M_P}\right) ^{\triangle +2}\left[ 1-\frac{3\kappa _\triangle }{\triangle +2}\left( \frac{M_P}{M}\right) ^{2\triangle +2} \right] ,\nonumber \\ \end{aligned}$$

(80)

which shows that for any value of $0<\triangle <1$, the heat capacity in our semiclassical model, $M\gg M_P$, is negative and consequently the BH is unstable.

Thus, from the geometrical BH surface, we may admit that there is more to unveil. In particular, we may speculate that a behavior, suggesting a broader dimensional dynamics at the horizon, can be explored in the limit when Lévy’s parameter approaches $\alpha \rightarrow 1$, supporting the conjecture proposed in [3]. We may, therefore, be allowed to speculate about the possibility that at some scale, a broader surface area of a BH can be considered, encompassing the standard value $16\pi G^2M^2$, because of the fractal structure of the horizon. In this context, let us recall Eq. (73) regarding how the entropy varies and how the Bekenstein–Hawking expressions fits in. It brings an interesting perspective such that the entropy of a BH (according to FQM) could be proportional to a power of its fractal surface, depending on the choice of $\alpha$.

5 Discussion and outlook

The purpose in this paper was to employ FQM to discuss specific BH features. It is now well demonstrated that BHs can form [12] and a set of properties has been widely described. Moreover, BHs encompass scenarios where strong gravity and quantum mechanics can meet. New insights need therefore to be proposed. Thus, this paper was set up to explore whether thermodynamic observables might be altered if an additional ingredient is present (say, imported from a quantum mechanical framework) and if it could reveal itself in special BH situations.

Hence, we started by briefly summarizing how concrete thermodynamic properties can be retrieved from a simple quantum mechanical BH (Schwarschild). This was done in Sects. 2 and 3. We then proceeded to an analysis employing a space-fractional derivative in a corresponding WDW equation. A broader perspective about BH thermodynamics within FQM was therefore presented in Sect. 4, specifically in terms explicitly dependent on the fractional parameter, $1<\alpha \le 2$. We retrieved altered expressions for physical quantities that were then contrasted with those of the standard case ($\alpha =2$) and summarized in Sects. 2 and 3.

Then in Sect. 4 we started by elaborating on the mass spectrum of a BH and how it varies according to $\alpha$. Whereas the frequency of gravitational waves generated by a standard BH is proportional to the inverse mass, in a fractional scenario the frequency would instead allow a dependence as $1/M^{\frac{4}{\alpha }-1}$. As pointed out in [106], the horizon behaves as a filter of gravitational waves with a set of absorption lines. Admitting the possibility of the fractal structure of the horizon, the horizon radius is different from the Schwarzschild radius [3], and the effective radius is wider, $r=2MG(1+\epsilon )$, in which $\epsilon \ll 1$ depends on how the surface is correspondingly altered. Any subsequent gravitational waves may bear a delay due to the time it takes the signal to transit from the horizon (with such possible fractal structure) to the photon sphere. This delay time scales logarithmically with $\epsilon$ [106] or, as we suggested herein, the fractality of the horizon.

In addition, we have shown how the entropy, the temperature, and the mass loss of the BH are highly sensitive to the value of $\alpha$. The Bekenstein–Hawking entropy of supermassive black holes [112] is of the order of $10^{104}$ and the corresponding fractional entropy of the supermassive BHs with $\alpha \sim 1$ will be $10^{156}$. If we extend a FQM perspective to the cosmic event horizon (CEH), then we can compute that $S_\text {CEH}\propto (GH^2)^\frac{-(\alpha +1)}{2\alpha }\simeq 10^{183}$. This assumption has been interestingly employed to discuss the late-time acceleration of the Universe [121,122,123,124,125,126]. Furthermore, we retrieved a formula for the Schwarzschild BH in which the entropy is a polynomial function of its area. We then explained that the surface area of such BH can exceed the standard value $16\pi G^2M^2$ of a BH, as suggested by a possible fractal structure. In this context, Tsallis and Cirto’s formalism [2] must be mentioned, constituting an extension of Boltzmann–Gibbs statistical theory, representing a non-extensive, i.e., a non-additive entropy.³ We have indicated herewith that from a FQM perspective we can alternatively, obtain Tsallis and Cirto’s results without committing to the extended entropy features. In addition, we proposed that the inherent fractal nature of Lévy paths leads to the extension of Barrow entropy formula [3]. Barrow’s modified entropy formally coincides with Tsallis and Cirto’s definition; notwithstanding, the involved foundations and interpretation of physical results are different. This is not a surprising result because, over the last several years, it has been shown that a fractal structure in properties of physical systems could be a possible origin for non-additive statistics [127,128,129,130].

Having summarized and discussed our results, it is also pertinent to suggest an outlook of subsequent directions to prospect. A particular line in our sight is to explore BH entropy and information loss within FQM. We plan to extend the context of paper [131] with the assistance of space-fractional derivative operators in the corresponding equations therein. The results in [131] indicated that for the final stage of a BH evaporation, which included back reaction from Hawking radiation, we get a strong entangled state (between a mimicked BH and the radiation). So, given how the entropy may vary with $\alpha$, what would FQM add within a suitable set up about information and BHs?

It would also be of interest to investigate BHs within FQM and in a Brans–Dicke or even a scalar–tensor theory, where more parameters are allowed to juggle with. Or employ other dynamical configurations instead, beyond the Schwarzschild case. It is possible using other fractional derivatives as well, besides space-fractional. Most likely, the use of numerical methods would be mandatory.