Detection of gravitational waves by light perturbation

Abstract

Light undergoes perturbation as gravitational waves pass by. This is shown by solving Maxwell’s equations in a spacetime with gravitational waves; a solution exhibits a perturbation due to gravitational waves. We determine the perturbation for a general case of both light and gravitational waves propagating in arbitrary directions. It is also shown that a perturbation of light due to gravitational waves leads to a delay of the photon transit time, which implies an equivalence between the perturbation analysis of Maxwell’s equations and the null geodesic analysis for photon propagation. We present an example of application of this principle with regard to the detection of gravitational waves via a pulsar timing array, wherein our perturbation analysis for the general case is employed to show how the detector response varies with the incident angle of a light pulse with respect to the detector.

1 Introduction

Light is the most common and important tool in astronomy, due to its property of carrying energy and information about its sources: it can reach an observer even at quite a distance, providing clues about astronomical sources responsible for its creation. Artificially created light is also in use in astronomy; e.g., laser light being commonly used for interferometry. Laser interferometers exploit another prominent and interesting property of light to detect gravitational waves (GWs): its interaction with other waves – GWs. However, from a perspective based on general relativity, this interaction can be viewed as a perturbation of light due to GWs; that is, light is perturbed as GWs pass through space in which it travels.

There is considerable significance in studying the aforesaid property of light in regard to the detection of GWs; e.g., by means of laser interferometers – LIGO, VIRGO, GEO600, KAGRA, LIGO-India, eLISA, etc. [1,2,3,4,5] or pulsar timing arrays (PTAs) – EPTA, PPTA, IPTA, SKA, etc. [6,7,8,9]. In principle, in all these detection schemes, we utilize the delay of the photon transit time due to GWs; that is, the effect resulting from a photon that undergoes deviation from its straight path while propagating in a spacetime with GWs. But this effect can be shown to be equivalent to the perturbation of an electromagnetic field due to GWs, as a direct consequence of a solution of Maxwell’s equations in the spacetime perturbed by GWs.

There were numerous studies about electrodynamics in a GW background based on Maxwell’s equations. Among others, Calura and Montanari [10] solved Maxwell’s equations only in the framework of the linearized general relativity and provided the exact solution to the problem, expressed like the Fourier-integral, by considering a general case for the GW frequency, rather than using the geometrical-optics approximation. Hacyan [11, 12] analyzed the interaction of electromagnetic waves with a plane-fronted GW and derived the corresponding formulas for Stokes parameters and the rotation angle of polarization. Cabral and Lobo [13] obtained electromagnetic field oscillations induced by GWs and found that these lead to the presence of longitudinal modes and dynamical polarization patterns of electromagnetic radiation.

In this paper, we address the issue how light is perturbed in the presence of GWs from a general relativistic perspective. In the context of the geometrical-optics approach, we solve Maxwell’s equations for a general configuration, wherein both light and GWs are assumed to propagate in arbitrary directions. Unlike the aforementioned related works in the literature, in which rather simple configurations with regard to the propagation directions of light and GWs are assumed, our investigation aims to achieve full generality in this regard, thereby providing practical results that can be readily used for analyzing various detection schemes for GWs, wherein such generality might be required; e.g., in a PTA, light pulses from different pulsars may arrive at one detector with various incident angles with respect to the stationary reference frame (or detector frame), while GWs may come from arbitrary directions to cross them. Largely, the paper proceeds in three steps through Sects. 2.1–2.3 as follows. In Sect. 2.1, we solve Maxwell’s equations in a spacetime perturbed by GWs for the general configuration between light and GWs, presenting a solution to first order in the strain amplitude h. In Sect. 2.2, we establish the equivalence between a perturbation of light due to GWs and a delay of the photon transit time, with the former implied from the solution of the Maxwell’s equations obtained in Sect. 2.1 and the latter implied from the null geodesic of photon propagation. In Sect. 2.3, application of our analysis from Sect. 2.2 to the detection of GWs via a PTA is discussed. Using the equivalence in the context of the general configuration between light and GWs, we determine the detector response function for light pulses incident on a detector at various angles.

2 Analysis and results

2.1 Solving Maxwell’s equations for light perturbed by GWs

What happens to light when GWs pass through space in which it propagates? This can be answered by solving Maxwell’s equations defined in a spacetime perturbed by GWs. For example, an electromagnetic field as a solution to the Maxwell’s equations can describe a light ray from a star or a laser beam in an interferometer being perturbed by GWs. For simplicity, we consider a case of a monochromatic electromagnetic wave (EMW) perturbed by monochromatic GWs. However, for the sake of generality of the configuration, we assume that both light and GWs propagate in arbitrary directions. Our analysis follows.

Suppose that GWs propagate along the $z^{\prime }$-axis while being polarized in the $x^{\prime }y^{\prime }$-plane in a quadrupole manner:

$$\begin{aligned} h_{ij}^{+}= & {} h_{+}\left( e_{i}^{x^{\prime }}\otimes e_{j}^{x^{\prime }}-e_{i}^{y^{\prime }}\otimes e_{j}^{y^{\prime }}\right) e^{\mathrm {i}\left( kz^{\prime }-\omega _{\mathrm {g}}t\right) }, \end{aligned}$$

(1)

$$\begin{aligned} h_{ij}^{\times }= & {} h_{\times }\left( e_{i}^{x^{\prime }}\otimes e_{j}^{y^{\prime }}+e_{i}^{y^{\prime }}\otimes e_{j}^{x^{\prime }}\right) e^{ \mathrm {i}\left( kz^{\prime }-\omega _{\mathrm {g}}t-\pi /2\right) }, \end{aligned}$$

(2)

where i, j refer to the coordinates $\left( x^{\prime },y^{\prime },z^{\prime }\right)$, and $h_{+}$ and $h_{\times }$ represent the strain amplitude for $+$ and $\times$ polarization states, respectively, and $\omega _{\mathrm {g}}$ denotes the GW frequency; $\omega _{\mathrm {g}}=ck$ with c being the speed of light and k being the wavenumber for GW. Then the spacetime geometry reads in the coordinates $\left( t,x^{\prime },y^{\prime },z^{\prime }\right)$:

$$\begin{aligned} ds^{2}= & {} -c^{2}dt^{2}+\left[ 1+\mathfrak {R}\left( h_{+}e^{\mathrm {i}\left( kz^{\prime }-\omega _{\mathrm {g}}t\right) }\right) \right] dx^{\prime 2} \nonumber \\&+2\mathfrak {R}\left( h_{\times }e^{\mathrm {i}\left( kz^{\prime }-\omega _{\mathrm {g }}t-\pi /2\right) }\right) dx^{\prime }dy^{\prime } \nonumber \\&+\left[ 1-\mathfrak {R}\left( h_{+}e^{\mathrm {i}\left( kz^{\prime }-\omega _{ \mathrm {g}}t\right) }\right) \right] dy^{\prime 2}+dz^{\prime 2}. \end{aligned}$$

(3)

However, one can consider the coordinates ${\mathbf {x}}^{\prime }\equiv \left( x^{\prime },y^{\prime },z^{\prime }\right)$ as rotated from the coordinates ${\mathbf {x}}\equiv \left( x,y,z\right)$ through Euler angles $\left\{ \phi ,\theta ,\psi \right\}$ [14, 15]:

$$\begin{aligned} {\mathbf {x}}^{\prime }={\mathbf {R}}\left( \phi ,\theta ,\psi \right) \mathbf {x,} \end{aligned}$$

(4)

where we let ${\mathbf {x}}^{\prime }$ and ${\mathbf {x}}$ refer to the coordinates in the GW frame and the detector frame, respectively (see Fig. 1 for illustration), and

$$\begin{aligned} {\mathbf {R}}\left( \phi ,\theta ,\psi \right) ={\mathbf {R}}_{3}\left( \psi \right) {\mathbf {R}}_{2}\left( \theta \right) {\mathbf {R}}_{1}\left( \phi \right) , \end{aligned}$$

(5)

with

$$\begin{aligned}&{\mathbf {R}}_{1}\equiv \left[ \begin{array}{ccc} \cos \phi &{} \sin \phi &{} 0 \\ -\sin \phi &{} \cos \phi &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] ,\quad {\mathbf {R}}_{2}\equiv \left[ \begin{array}{ccc} \cos \theta &{} 0 &{} -\sin \theta \\ 0 &{} 1 &{} 0 \\ \sin \theta &{} 0 &{} \cos \theta \end{array} \right] , \nonumber \\&{\mathbf {R}}_{3}\equiv \left[ \begin{array}{ccc} \cos \psi &{} \sin \psi &{} 0 \\ -\sin \psi &{} \cos \psi &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] , \end{aligned}$$

(6)

and $\left\{ \phi ,\theta \right\}$ denote the direction angles in spherical coordinates, defined with respect to the coordinates $\left( x,y,z\right)$, and $\psi$ denotes the polarization-ellipse angle [16] . Resulting from these rotations, the spacetime geometry in the coordinates $\left( t,x^{\prime },y^{\prime },z^{\prime }\right)$ given by (3) is now rewritten in the coordinates $\left( t,x,y,z\right)$:

$$\begin{aligned} ds^{2}&=-c^{2}dt^{2} +\sum _{i,j=1,2,3}\left[ \delta _{ij}+\alpha _{ij}\left( \phi ,\theta ,\psi \right) H_{+}\right. \nonumber \\&\quad \left. +\beta _{ij}\left( \phi ,\theta ,\psi \right) H_{\times }\right] dx_{i}dx_{j}, \end{aligned}$$

(7)

where

$$\begin{aligned} \alpha _{11}\left( \phi ,\theta ,\psi \right)= & {} \cos \left( 2\psi \right) \left( \cos ^{2}\theta \cos ^{2}\phi -\sin ^{2}\phi \right) \nonumber \\&-2\sin \left( 2\psi \right) \cos \theta \cos \phi \sin \phi , \nonumber \\ \alpha _{12}\left( \phi ,\theta ,\psi \right)= & {} \cos \left( 2\psi \right) \left( 1+\cos ^{2}\theta \right) \cos \phi \sin \phi \nonumber \\&+\sin \left( 2\psi \right) \cos \theta \left( 2\cos ^{2}\phi -1\right) , \nonumber \\ \alpha _{13}\left( \phi ,\theta ,\psi \right)= & {} -\cos \left( 2\psi \right) \cos \theta \sin \theta \cos \phi \nonumber \\&+\sin \left( 2\psi \right) \sin \theta \sin \phi , \nonumber \\ \alpha _{21}\left( \phi ,\theta ,\psi \right)= & {} \alpha _{12}\left( \phi ,\theta ,\psi \right) , \nonumber \\ \alpha _{22}\left( \phi ,\theta ,\psi \right)= & {} \cos \left( 2\psi \right) \left( \cos ^{2}\theta \sin ^{2}\phi -\cos ^{2}\phi \right) \nonumber \\&+2\sin \left( 2\psi \right) \cos \theta \cos \phi \sin \phi , \nonumber \\ \alpha _{23}\left( \phi ,\theta ,\psi \right)= & {} -\cos \left( 2\psi \right) \cos \theta \sin \theta \sin \phi \nonumber \\&-\sin \left( 2\psi \right) \sin \theta \cos \phi , \nonumber \\ \alpha _{31}\left( \phi ,\theta ,\psi \right)= & {} \alpha _{13}\left( \phi ,\theta ,\psi \right) , \nonumber \\ \alpha _{32}\left( \phi ,\theta ,\psi \right)= & {} \alpha _{23}\left( \phi ,\theta ,\psi \right) , \nonumber \\ \alpha _{33}\left( \phi ,\theta ,\psi \right)= & {} \cos \left( 2\psi \right) \sin ^{2}\theta , \end{aligned}$$

(8)

and

$$\begin{aligned} \beta _{ij}\left( \phi ,\theta ,\psi \right) =\alpha _{ij}\left( \phi ,\theta ,\psi +\pi /4\right) , \end{aligned}$$

(9)

and

$$\begin{aligned} H_{+}\equiv & {} \mathfrak {R}\left( h_{+}\exp \left[ \mathrm {i}\left( \mathbf {k\cdot x} -\omega _{\mathrm {g}}t\right) \right] \right) , \end{aligned}$$

(10)

$$\begin{aligned} H_{\times }\equiv & {} \mathfrak {R}\left( h_{+}\exp \left[ \mathrm {i}\left( \mathbf { k\cdot x}-\omega _{\mathrm {g}}t-\pi /2\right) \right] \right) , \end{aligned}$$

(11)

with

$$\begin{aligned} {\mathbf {k}}= & {} \left( k_{x},k_{y},k_{z}\right) \nonumber \\\equiv & {} \left( k\sin \theta \cos \phi ,k\sin \theta \sin \phi ,k\cos \theta \right) . \end{aligned}$$

(12)

Here one should note the following important property: the dependence on the polarization angle $\psi$ in (8) and (9) exhibits the spin-2 tensor modes of the $+$ and $\times$ polarizations.

Our light perturbed by GWs can be described by Maxwell’s equations defined in curved (perturbed) spacetime as given by Eq. (7): in the Lorenz gauge [17],

$$\begin{aligned} \square A^{\mu }-R^{\mu }{}_{\nu }A^{\nu }=0, \end{aligned}$$

(13)

where $\square A^{\mu }\equiv g^{\nu \rho }\nabla _{\nu }\nabla _{\rho }A^{\mu }$ means the d’Alembertian on a vector potential, and $R{}_{\mu \nu }$ denotes the Ricci tensor. However, by direct computation using Eqs. (7)–(11), it turns out that

$$\begin{aligned} R_{\mu \nu }=\mathcal {O}\left( {h^{2}}\right) . \end{aligned}$$

(14)

Therefore, the spatial part of Eq. (13) can now be reduced:¹

$$\begin{aligned} \square A^{i}=\mathcal {O}\left( {h^{2}}\right) , \end{aligned}$$

(15)

where i refers to the coordinates $\left( x,y,z\right)$. This can be regarded as a homogeneous vector wave equation to first order in h.

Now, we aim to obtain a decomposition solution for Eq. (15) via perturbation in h:

$$\begin{aligned} A^{i}=A_{\mathrm {o}}^{i}+\delta A_{[{h}]}^{i}+\mathcal {O}\left( {h^{2}} \right) , \end{aligned}$$

(16)

where $A_{\mathrm {o}}^{i}$ denotes the zeroth-order, unperturbed solution and $\delta A_{[{h}]}^{i}$ denotes the first-order perturbation solution. Then one may recast the left-hand side of Eq. (15) as

$$\begin{aligned} \square A^{i}=\square _{\mathrm {o}}A_{\mathrm {o}}^{i}+\square _{\mathrm {o} }\delta A_{[{h}]}^{i}+\square _{[{h}]}A_{\mathrm {o}}^{i}+\mathcal {O} \left( {h^{2}}\right) , \end{aligned}$$

(17)

where $\square _{\mathrm {o}}\equiv -c^{-2}\partial ^{2}/\partial t^{2}+\partial ^{2}/\partial x^{2}+\partial ^{2}/\partial y^{2}+\partial ^{2}/\partial z^{2}$ denotes the flat d’Alembertian and $\square _{[{h }]}A_{\mathrm {o}}^{i}$ means the $\mathcal {O}\left( {h}\right)$ piece remaining from $\square A_{\mathrm {o}}^{i}-\square _{\mathrm {o}}A_{\mathrm {o} }^{i}$. Rearranging the terms in Eq. (17) for order-by-order perturbation, we obtain

$$\begin{aligned} \square _{\mathrm {o}}A_{\mathrm {o}}^{i}= & {} 0~\text {(unperturbed)}, \end{aligned}$$

(18)

$$\begin{aligned} \square _{\mathrm {o}}\delta A_{[{h}]}^{i}= & {} -\square _{[{h}]}A_{ \mathrm {o}}^{i}~\text {(first order in }h\text {)}, \end{aligned}$$

(19)

where the first equation implies that $A_{\mathrm {o}}^{i}$ is a solution for the unperturbed homogeneous wave equation defined in flat spacetime, and the second equation implies that $\delta A_{[{h}]}^{i}$ is a solution for the first-order perturbed inhomogeneous wave equation defined in flat spacetime with a source term $-\square _{[{h}]}A_{ \mathrm {o}}^{i}$, which is also first-order perturbed. It should be noted here that $\delta A_{[{h}]}^{i}$ can be obtained only after $A_{\mathrm {o} }^{i}$ is known: the source term for the first-order perturbed equation requires knowledge of $A_{\mathrm {o}}^{i}$.

To first order in h, the total solution as given from (16) is

$$\begin{aligned} A_{\mathrm {total}}^{i}\left( t,{\mathbf {x}}\right) =A_{\mathrm {o}}^{i}\left( t, {\mathbf {x}}\right) +\delta A_{[{h}]}^{i}\left( t,{\mathbf {x}}\right) . \end{aligned}$$

(20)

Suppose that the initial unperturbed light is linearly polarized and propagates along the direction of the wave vector ${\mathbf {K}}=\left( K_{x},K_{y},K_{z}\right)$. Then one can write down a solution to satisfy Eq. (18):

$$\begin{aligned} A_{\mathrm {o}}^{i}\left( t,{\mathbf {x}}\right)&=\left( -\frac{K_{y}}{\sqrt{ K_{x}^{2}+K_{y}^{2}}}\delta _{x}^{i}+\frac{K_{x}}{\sqrt{K_{x}^{2}+K_{y}^{2}}} \delta _{y}^{i}\right) \nonumber \\&\quad \times \mathcal {A}\exp \left[ \mathrm {i}\left( \mathbf {K\cdot x}-\omega _{ \mathrm {e}}t\right) \right] , \end{aligned}$$

(21)

where $\mathcal {A}$ represents the amplitude of EMW, and $\omega _{\mathrm {e} }$ denotes the EMW frequency; $\omega _{\mathrm {e}}=cK$ with c being the speed of light and $K=\sqrt{K_{x}^{2}+K_{y}^{2}+K_{z}^{2}}$ being the wavenumber for EMW.² Note here that the direction of polarization is set perpendicular to ${\mathbf {K}}$. Now, using Eq. (21 ) for Eq. (19), and by straightforward but tedious computation, we obtain a perturbation solution $\delta A_{[{h}]}^{i}\left( t,{\mathbf {x}} \right)$.³ To the full, it turns out that $\delta A_{[{h}]}^{i}\sim \mathcal {O}\left( {h}\right) +\left( \omega _{\mathrm {e} }/\omega _{\mathrm {g}}\right) \mathcal {O}\left( {h}\right)$. However, practically, $\omega _{\mathrm {e}}\gg \omega _{\mathrm {g}}$ (e.g., $\omega _{ \mathrm {e}}/\omega _{\mathrm {g}}\sim 10^{9}$ to $10^{14}$ for LIGO, $10^{12}$ to $10^{19}$ for LISA, $10^{14}$ to $10^{17}$ for PTA etc.), and therefore the part $\left( \omega _{\mathrm {e}}/\omega _{\mathrm {g}}\right) \mathcal {O} \left( {h}\right)$ would be the only meaningful piece to take for our analysis; that is, this piece remains in the geometrical-optics approximation. This finally enables us to express the solution:

$$\begin{aligned} \delta A_{[{h}]}^{i}\left( t,{\mathbf {x}}\right) =2\left( \omega _{\mathrm {e} }/\omega _{\mathrm {g}}\right) A_{\mathrm {o}}^{i}\left( t,{\mathbf {x}}\right) \mathcal {H}\left( t,{\mathbf {x}};{\mathbf {K}},{\mathbf {k}}\right) , \end{aligned}$$

(22)

where

$$\begin{aligned} \mathcal {H}\left( t,{\mathbf {x}};{\mathbf {K}},{\mathbf {k}}\right)\equiv & {} h_{+} \mathcal {F}_{+}\left( \phi ,\theta ,\psi ;{\mathbf {K}}\right) \cos \left( \mathbf {k\cdot x}-\omega _{\mathrm {g}}t\right) \nonumber \\&-h_{\times }\mathcal {F}_{\times }\left( \phi ,\theta ,\psi ;{\mathbf {K}} \right) \sin \left( \mathbf {k\cdot x}-\omega _{\mathrm {g}}t\right) , \end{aligned}$$

(23)

where

$$\begin{aligned}&\mathcal {F}_{+}\left( \phi ,\theta ,\psi ;{\mathbf {K}}\right) \nonumber \\&\quad \equiv \frac{1}{2\mathcal {D}}\left( 1+\frac{K_{x}\sin \theta \cos \phi +K_{y}\sin \theta \sin \phi +K_{z}\cos \theta }{K}\right) \nonumber \\&\qquad \times \left\{ \left[ K_{x}^{2}\left( -\cos ^{2}\theta \cos ^{2}\phi +\sin ^{2}\phi \right) \right. \right. \nonumber \\&\qquad \left. \left. -K_{x}K_{y}\left( 1+\cos ^{2}\theta \right) \sin \left( 2\phi \right) \right. \right. \nonumber \\&\qquad \left. \left. +K_{x}K_{z}\sin \left( 2\theta \right) \cos \phi +K_{y}^{2}\left( -\cos ^{2}\theta \sin ^{2}\phi +\cos ^{2}\phi \right) \right. \right. \nonumber \\&\qquad \left. \left. +K_{y}K_{z}\sin \left( 2\theta \right) \sin \phi -K_{z}^{2}\sin ^{2}\theta \right] \cos \left( 2\psi \right) \right. \nonumber \\&\qquad \left. +\left[ K_{x}^{2}\cos \theta \sin \left( 2\phi \right) -2K_{x}K_{y}\cos \theta \cos \left( 2\phi \right) \right. \right. \nonumber \\&\qquad \left. \left. -2K_{x}K_{z}\sin \theta \sin \phi -K_{y}^{2}\cos \theta \sin \left( 2\phi \right) \right. \right. \nonumber \\&\qquad \left. \left. +2K_{y}K_{z}\sin \theta \cos \phi _{_{{}}}^{^{{}}}\right] \sin \left( 2\psi \right) \right\} , \end{aligned}$$

(24)

with

$$\begin{aligned} \mathcal {D}&\equiv K_{x}^{2}\left( 1-\sin ^{2}\theta \cos ^{2}\phi \right) -K_{x}K_{y}\sin ^{2}\theta \sin \left( 2\phi \right) \nonumber \\&\quad -K_{x}K_{z}\sin \left( 2\theta \right) \cos \phi +K_{y}^{2}\left( 1-\sin ^{2}\theta \sin ^{2}\phi \right) \nonumber \\&\quad -K_{y}K_{z}\sin \left( 2\theta \right) \sin \phi +K_{z}^{2}\sin ^{2}\theta , \end{aligned}$$

(25)

and

$$\begin{aligned} \mathcal {F}_{\times }\left( \phi ,\theta ,\psi ;{\mathbf {K}}\right) =\mathcal {F }_{+}\left( \phi ,\theta ,\psi -\pi /4;{\mathbf {K}}\right) . \end{aligned}$$

(26)

Further, the expression in (24) can be reduced to a compact form:

$$\begin{aligned}&\mathcal {F}_{+}\left( \phi ,\theta ,\psi ;\phi _{\star },\theta _{\star }\right) \nonumber \\&\quad =\frac{\cos ^{2}\gamma _{2}\cos \left( 2\psi \right) -2\cos \gamma _{2}\sin \theta _{\star }\sin \left( \phi -\phi _{\star }\right) \sin \left( 2\psi \right) }{2\left( 1-\cos \gamma _{1}\right) }, \end{aligned}$$

(27)

where⁴

$$\begin{aligned} \cos \gamma _{1}\equiv & {} \cos \theta \cos \theta _{\star }+\sin \theta \sin \theta _{\star }\cos \left( \phi -\phi _{\star }\right) , \end{aligned}$$

(28)

$$\begin{aligned} \cos \gamma _{2}\equiv & {} \sin \theta \cos \theta _{\star }-\cos \theta \sin \theta _{\star }\cos \left( \phi -\phi _{\star }\right) , \end{aligned}$$

(29)

and $\left( \phi _{\star },\theta _{\star }\right)$ have been defined from $\left( K_{x},K_{y},K_{z}\right)$ by means of

$$\begin{aligned} \sin \theta _{\star }\cos \phi _{\star }=\frac{K_{x}}{K},\sin \theta _{\star }\sin \phi _{\star }=\frac{K_{y}}{K},\cos \theta _{\star }=\frac{K_{z}}{K}. \end{aligned}$$

(30)

Also,

$$\begin{aligned} \mathcal {F}_{\times }\left( \phi ,\theta ,\psi ;\phi _{\star },\theta _{\star }\right) =\mathcal {F}_{+}\left( \phi ,\theta ,\psi -\pi /4;\phi _{\star },\theta _{\star }\right) . \end{aligned}$$

(31)

It should be noted again here that the perturbation solution exhibits the spin-2 tensor modes of the $+$ and $\times$ polarizations through the dependence on $\psi$ in (24) and (26) (or (27) and (31 )).⁵

Equations (22)–(31) present the major result of our analysis; it expresses a perturbation of light due to GWs for a general configuration, wherein both light and GWs propagate in arbitrary directions. The perturbation of light will be shown to be equivalent to a delay of the photon transit time in Sect. 2.2. The equivalence will then be employed to compute the response function for the detection of GWs in Sect. 2.3. In Appendix A we show how one can obtain the solution given by (20)–(26) in a computationally tractable manner by means of coordinate transformations.

2.2 Perturbed light and delay of photon transit time

Above we have described how light is perturbed when it propagates in a spacetime with GWs, by solving Maxwell’s equations in that spacetime via a perturbation method. Suppose that light propagates along the direction of ${\mathbf {K}}=\left( K_{x},K_{y},K_{z}\right) =\left( 0,0,-K\right)$, as in the example of a PTA to be discussed in Sect. 2.3. As $K_{z}=-K<0$, our light propagates along $-z$ direction; i.e., from the sky towards the earth. Then it can be expressed by the electric field $E_{\mathrm {total} }^{i}\left( t,0,0,z\right) =-c^{-1}\left( \partial /\partial t\right) A_{ \mathrm {total}}^{i}\left( t,0,0,z\right)$, obtained from Eqs. (20)–( 22). Starting at $\left( t,z\right) =\left( t_{0},L\right)$, the propagation path can be written as $z=L-c\left( t-t_{0}\right)$ for $t_{0}\le t\le t_{0}+T$, with $L=cT$. Then we find

$$\begin{aligned}&\left. \frac{\delta E_{\left[ h\right] }^{i}}{E_{\mathrm {o}}^{i}} \right| _{z=0}-\left. \frac{\delta E_{\left[ h\right] }^{i}}{E_{\mathrm {o }}^{i}}\right| _{z=L} \nonumber \\&\quad =\frac{\omega _{\mathrm {e}}\left( h_{+}F_{+}+\mathrm {i}h_{\times }F_{\times }\right) \left\{ 1-\exp \left[ \mathrm {i}kL\left( 1+\cos \theta \right) \right] \right\} }{\omega _{\mathrm {g}}} \nonumber \\&\qquad \times \exp \left[ -\mathrm {i}\left( kL+\omega _{\mathrm {g}}t_{0}\right) \right] , \end{aligned}$$

(32)

where $E_{\mathrm {o}}^{i}=-c^{-1}\left( \partial /\partial t\right) A_{ \mathrm {o}}^{i}$, $\delta E_{\left[ h\right] }^{i}=-c^{-1}\left( \partial /\partial t\right) \delta A_{[{h}]}^{i}$, and the right-hand side is expressed in the complex representation for analytical convenience, and

$$\begin{aligned} F_{+}\equiv & {} \sin ^{2}\left( \theta /2\right) \cos \left( 2\psi \right) , \end{aligned}$$

(33)

$$\begin{aligned} F_{\times }\equiv & {} \sin ^{2}\left( \theta /2\right) \sin \left( 2\psi \right) , \end{aligned}$$

(34)

are antenna patterns for $+$ and $\times$ polarization states, respectively.⁶

On the other hand, when a photon propagates in a spacetime with GWs, its trajectory will be perturbed, resulting in a delay of its transit time. The propagation takes place along the null geodesic, i.e., $ds^{2}=0$ in Eq. ( 7), and hence one can express a delay for a photon propagating by a distance $L=cT$ along $-z$ direction, starting at $\left( t,z\right) =\left( t_{0},L\right)$; that is, along the path $z=L-c\left( t-t_{0}\right)$ for $t_{0}\le t\le t_{0}+T$ [15]:

$$\begin{aligned}&\frac{\delta T_{\left[ h\right] }}{T}=\frac{1}{2cT}\int _{L}^{0}h_{zz} \left( t_{0},0,0,z\right) dz+\mathcal {O}\left( h^{2}\right) \nonumber \\&\quad =-\mathrm {i}\frac{\left( h_{+}F_{+}+\mathrm {i}h_{\times }F_{\times }\right) \left\{ 1-\exp \left[ \mathrm {i}kL\left( 1+\cos \theta \right) \right] \right\} }{kL} \nonumber \\&\qquad \times \exp \left[ -\mathrm {i}\left( kL+\omega _{\mathrm {g}}t_{0}\right) \right] +\mathcal {O}\left( h^{2}\right) , \end{aligned}$$

(35)

where $\delta T_{\left[ h\right] }$ means the deviation of the transit time from T, and $h_{zz}$ is read off from Eq. (7) and expressed in the complex representation for analytical convenience.

Comparing Eqs. (32) and (35), we establish a relation between the delay of the photon transit time and the perturbation of light due to GWs:

$$\begin{aligned} {{\frac{\delta T_{\left[ {h}\right] }}{T}\simeq }\,\mathcal {N}}\left( \left. \frac{\delta E_{\left[ h\right] }^{i}}{E_{\mathrm {o}}^{i}}\right| _{z=0}-\left. \frac{\delta E_{\left[ h\right] }^{i}}{E_{\mathrm {o}}^{i}} \right| _{z=L}\right) , \end{aligned}$$

(36)

where $\mathcal {N}=\left( \mathrm {i}\omega _{\mathrm {e}}T\right) ^{-1}=\left( \mathrm {i}KL\right) ^{-1}$. Here one can give a physical interpretation of this relation: light perturbed by GWs, being described by Maxwell’s equations (13), leads to a delay of the photon transit time, being described by the null geodesic equation, $ds^{2}=0$ in (7).

The relation given by Eq. (36) must be true for a general configuration in which both light and GWs are assumed to propagate in arbitrary directions. That is, a delay of the photon transit time along an arbitrary path can equivalently be computed, using the solutions of Maxwell’s equations for the general case as given by Eqs. (20)–(22). Then the relation (36) is now extended to

$$\begin{aligned} {{\frac{\delta T_{\left[ {h}\right] }}{T}\simeq }\,\mathcal {N}}\left( \left. \frac{\delta E_{\left[ h\right] }^{i}}{E_{\mathrm {o}}^{i}}\right| _{ \text {earth}}-\left. \frac{\delta E_{\left[ h\right] }^{i}}{E_{\mathrm {o} }^{i}}\right| _{\text {sky}}\right) , \end{aligned}$$

(37)

where one can set the ‘earth’ location to be $\left( x,y,z\right) =\left( 0,0,0\right)$ and the ‘sky’ location to be $\left( x,y,z\right) =\left( -L\sin \theta _{\star }\cos \phi _{\star },-L\sin \theta _{\star }\sin \phi _{\star },-L\cos \theta _{\star }\right)$, with $\pi \le \theta _{\star }\le 3\pi /2$, for computational convenience. From this and with the electric field $E_{\mathrm {total}}^{i}\left( t,x,y,z\right) =-c^{-1}\left( \partial /\partial t\right) A_{\mathrm {total}}^{i}\left( t,x,y,z\right)$ for a general ${\mathbf {K}}=\left( K_{x},K_{y},K_{z}\right) =\left( K\sin \theta _{\star }\cos \phi _{\star },K\sin \theta _{\star }\sin \phi _{\star },K\cos \theta _{\star }\right)$, obtained from Eqs. (20)–(22), the delay of the photon transit time is finally written as

$$\begin{aligned} \frac{\delta T_{\left[ h\right] }}{T}&=-\mathrm {i}\frac{\left( h_{+}\mathcal {F}_{+}+\mathrm {i}h_{\times } \mathcal {F}_{\times }\right) \left\{ 1-\exp \left[ \mathrm {i}kL\left( 1-\cos \gamma _{1}\right) \right] \right\} }{kL} \nonumber \\&\quad \times \exp \left[ -\mathrm {i}\left( kL+\omega _{\mathrm {g}}t_{0}\right) \right] +\mathcal {O}\left( h^{2}\right) , \end{aligned}$$

(38)

where $\mathcal {F}_{+}$, $\mathcal {F}_{\times }$ and $\cos \gamma _{1}$ refer to (27), (31) and (28), respectively.

2.3 Application: pulsar timing array (PTA)

The property of the perturbed light as given by Eq. (37) (or (36)) can be applied to the detection of GWs, and for its simplest application, we consider a PTA. One can arrange a detector (e.g., a radio telescope) to receive photons emitted from a pulsar to measure pulse arrival time as illustrated in Fig. 1. A pulsar can serve as an astronomical clock of excellent precision, with the constancy of the measured pulse frequency $\nu _{\mathrm {o}}$. However, with GWs passing through our space, the measured frequency $\nu \left( t\right)$ will vary slightly. Then the effects of GWs can be determined from the variation of the frequency (or from the variation of the pulse period) $\left[ \nu _{\mathrm {o}}-\nu \left( t\right) \right] /\nu _{ \mathrm {o}}\simeq \left[ \tau \left( t\right) -\tau _{\mathrm {o}}\right] /\tau _{\mathrm {o}}$, where $\tau \left( t\right) =\nu ^{-1}\left( t\right)$ is the measured pulse period and $\tau _{\mathrm {o}}=\nu _{\mathrm {o}}^{-1}$ is the constancy of the measured pulse period [20, 21].

Fig. 1

An illustration of a pulsar timing array (PTA) together with the detector frame and the GW frame

For the cumulative variation, we define a “residual” [21], which can be expressed using Eq. (38) with $T=\tau _{\mathrm {o}}=L/c$ as

$$\begin{aligned} {\mathfrak {r}}\left( t\right)\equiv & {} \int _{0}^{t}\frac{\nu _{\mathrm {o}}-\nu \left( t^{\prime }\right) }{\nu _{\mathrm {o}}}dt^{\prime }\;\simeq \int _{0}^{t}\frac{\tau \left( t^{\prime }\right) -\tau _{\mathrm {o}}}{\tau _{ \mathrm {o}}}dt^{\prime } \nonumber \\\sim & {} \frac{h_{+}\mathcal {G}_{+}+\mathrm {i}h_{\times }\mathcal {G}_{\times } }{f}\exp \left( -2\mathrm {i}\pi ft\right) ,\; \end{aligned}$$

(39)

where $t^{\prime }\leftarrow t_{0}$ from Eq. (38), and $f=\omega _{ \mathrm {g}}/\left( 2\pi \right)$, and

$$\begin{aligned} \mathcal {G}_{+}\equiv & {} \frac{\mathcal {F}_{+}\exp \left( -\mathrm {i} kL\right) \left\{ 1-\exp \left[ 2\mathrm {i}\pi f\tau _{\mathrm {o}}\left( 1-\cos \gamma _{1}\right) \right] \right\} }{4\pi ^{2}f\tau _{\mathrm {o}}}, \end{aligned}$$

(40)

$$\begin{aligned} \mathcal {G}_{\times }\equiv & {} \frac{\mathcal {F}_{\times }\exp \left( - \mathrm {i}kL\right) \left\{ 1-\exp \left[ 2\mathrm {i}\pi f\tau _{\mathrm {o} }\left( 1-\cos \gamma _{1}\right) \right] \right\} }{4\pi ^{2}f\tau _{ \mathrm {o}}}, \end{aligned}$$

(41)

with $\mathcal {F}_{+}$, $\mathcal {F}_{\times }$ and $\cos \gamma _{1}$ given by (27), (31) and (28), respectively. Here $\mathcal {G} _{+}$ and $\mathcal {G}_{\times }$ are termed exact detector responses, and for ${\mathbf {K}}=\left( K_{x},K_{y},K_{z}\right) =\left( 0,0,-K\right)$ in particular, they reduce to

$$\begin{aligned} G_{+}&\equiv \frac{F_{+}\exp \left( -\mathrm {i}kL\right) \Big \{ 1-\exp \left[ 2\mathrm {i}\pi f\tau _{\mathrm {o}}\left( 1+\cos \theta \right) \right] \Big \} }{4\pi ^{2}f\tau _{\mathrm {o}}}, \end{aligned}$$

(42)

$$\begin{aligned} G_{\times }&\equiv \frac{F_{\times }\exp \left( -\mathrm {i}kL\right) \Big \{ 1-\exp \left[ 2\mathrm {i}\pi f\tau _{\mathrm {o}}\left( 1+\cos \theta \right) \right] \Big \} }{4\pi ^{2}f\tau _{\mathrm {o}}}, \end{aligned}$$

(43)

respectively, with $F_{+}$ and $F_{\times }$ given by (33) and (34).

Fig. 2

Antenna patterns of the detector responses: (A) $\left| G_{+,\times }\right|$ at $f\ll 1\,\mathrm {Hz}$, (B) $\left| G_{+,\times }\right|$ at $f=1000\,\mathrm {Hz}$ for a light ray with $\left( K_{x},K_{y},K_{z}\right) =\left( 0,0,-K\right)$ from a millisecond pulsar with $\tau _{\mathrm {o}}\sim 10^{-3}\,\mathrm {s}$; (C) $\left| \mathcal {G}_{+,\times }\right|$ at $\theta _{\star }= \pi +\cos ^{-1}\left( \sqrt{15/23}\right)$, (D) $\left| \mathcal {G}_{+,\times }\right|$ at $\theta _{\star }=3\pi /2$ for light rays with $\left( K_{x},K_{y},K_{z}\right) =\left( K\sin \theta _{\star }\cos \phi _{\star },K\sin \theta _{\star }\sin \phi _{\star },K\cos \theta _{\star }\right)$ from millisecond pulsars with $\tau _{\mathrm {o}}\sim 10^{-3}\, \mathrm {s}$, both being considered in the low-frequency regime, $f\ll 1\, \mathrm {Hz}$. Here the 3D plots are drawn in (A) and (B) from $\left| G_{+,\times }\left( \theta ,\psi \right) \right|$, and in (C) and (D) from $\left| \mathcal {G}_{+,\times }\left( \theta ,\psi \right) \right| \equiv \left| \int _{0}^{2\pi } \mathcal {G}_{+,\times }\left( \phi ,\theta ,\psi \right) d\phi /2\pi \right|$, in a Cartesian coordinate frame via $\left( X,Y,Z\right) =\left( \sin \theta \cos \psi ,\sin \theta \sin \psi ,\cos \theta \right)$. Note that the patterns for $\left| \mathcal {G} _{+}\right|$ and $\left| \mathcal {G}_{\times }\right|$ (also $\left| G_{+}\right|$ and $\left| G_{\times }\right|$) are identical except for the rotational phase difference $\pi /4$, due to $\mathcal {G}_{+}\left( \theta ,\psi \right) =\mathcal {G} _{\times }\left( \theta ,\psi +\pi /4\right)$ (also $G_{+}\left( \theta ,\psi \right) =G_{\times }\left( \theta ,\psi +\pi /4\right)$) from Eqs. (40 ) and (41) (also Eqs. (42) and (43))

Out of Eq. (39), one can express

$$\begin{aligned} \left\langle {\mathfrak {r}}^{2}\left( t\right) \right\rangle _{\mathrm {time} }&\sim f^{2}\tilde{{\mathfrak {r}}}\left( f\right) \tilde{{\mathfrak {r}}} ^{*}\left( f\right) \nonumber \\&\simeq \left| \mathcal {G}_{+}\left( f\right) \right| ^{2}\left| {\tilde{h}}_{+}\left( f\right) \right| ^{2}+\left| \mathcal {G}_{\times }\left( f\right) \right| ^{2}\left| {\tilde{h}} _{\times }\left( f\right) \right| ^{2}, \end{aligned}$$

(44)

where $\tilde{{\mathfrak {r}}}\left( f\right)$, ${\tilde{h}}_{+}\left( f\right)$ and ${\tilde{h}}_{\times }\left( f\right)$ denote the Fourier transforms of ${\mathfrak {r}}\left( t\right)$, $h_{+}\left( t\right) \equiv h_{+}\exp \left( -2\mathrm {i}\pi ft\right)$ and $h_{\times }\left( t\right) \equiv h_{\times }\exp \left( -2\mathrm {i}\pi ft\right)$, respectively, and $*$ denotes the complex conjugate.

The detector response function can be computed by taking a sky average of $\mathcal {G}_{+}\mathcal {G}_{+}^{*}+\mathcal {G}_{\times } \mathcal {G}_{\times }^{*}$ over $\left( \phi ,\theta ,\psi \right)$, with $\mathcal {G}_{+}$ and $\mathcal {G}_{\times }$ given by (40) and (41), respectively:

$$\begin{aligned} \mathcal {R}\left( f\right) \;\equiv & {} \;\frac{1}{4\pi ^{2}}\int _{0}^{\pi }d\psi \int _{0}^{2\pi }d\phi \int _{0}^{\pi }d\theta \,\sin \theta \nonumber \\&\times \left[ \mathcal {G}_{+}\left( f\right) \mathcal {G}_{+}^{*}\left( f\right) +\mathcal {G}_{\times }\left( f\right) \mathcal {G}_{\times }^{*}\left( f\right) \right] . \end{aligned}$$

(45)

For the special case with ${\mathbf {K}}=\left( K_{x},K_{y},K_{z}\right) =\left( 0,0,-K\right)$, the detector responses reduce, that is, $\mathcal {G} _{+}\rightarrow G_{+}$ and $\mathcal {G}_{\times }\rightarrow G_{\times }$, and we obtain

$$\begin{aligned} \mathcal {R}\left( f\right) =\frac{32\pi ^{3}f^{3}\tau _{\mathrm {o} }^{3}-12\pi f\tau _{\mathrm {o}}+3\sin \left( 4\pi f\tau _{\mathrm {o}}\right) }{768\pi ^{7}f^{5}\tau _{\mathrm {o}}^{5}}, \end{aligned}$$

(46)

which is a complete closed-form expression. In the limit $f\tau _{\mathrm {o} }\ll 1$, which is appropriate for ultra-low-frequency GW signals carried via millisecond pulsars, this can be approximated as

$$\begin{aligned} \mathcal {R}\approx \frac{1}{30\pi ^{2}}+\mathcal {O}\left( f^{2}\tau _{ \mathrm {o}}^{2}\right) . \end{aligned}$$

(47)

However, for a general case with ${\mathbf {K}}=\left( K_{x},K_{y},K_{z}\right) =\left( K\sin \theta _{\star }\cos \phi _{\star },K\sin \theta _{\star }\sin \phi _{\star },K\cos \theta _{\star }\right)$, the computation of the response function is rather involved, and it cannot be computed fully symbolically unlike (46) for the special case; but its approximation can be obtained in the limit $f\tau _{\mathrm {o}}\ll 1$ instead:

$$\begin{aligned} \mathcal {R}\approx \frac{29+150\cos ^{2}\theta _{\star }-115\cos ^{4}\theta _{\star }}{1920\pi ^{2}}+\mathcal {O}\left( f^{2}\tau _{\mathrm {o} }^{2}\right) . \end{aligned}$$

(48)

This manifests how the detector response function varies with $\theta _{\star }$, the incident angle of a light pulse with respect to the detector.

For a light ray with $\left( K_{x},K_{y},K_{z}\right) =\left( 0,0,-K\right)$ from a millisecond pulsar with $\tau _{\mathrm {o}}\sim 10^{-3}\,\mathrm {s}$ , the antenna patterns $\left| G_{+,\times }\right|$ of the detector responses (42) and (43) are illustrated at different frequencies, (A) $f\ll 1\,\mathrm {Hz}$ and (B) $f=1000\,\mathrm {Hz}$, in the upper panel of Fig. 2. Note the decrease in the volume of the plot for the higher frequency. On the other hand, in the lower panel of Fig. 2, we illustrate the antenna patterns $\left| \mathcal {G} _{+,\times }\right|$ of the detector responses (40) and (41) for light rays with $\left( K_{x},K_{y},K_{z}\right) =\left( K\sin \theta _{\star }\cos \phi _{\star },K\sin \theta _{\star }\sin \phi _{\star },K\cos \theta _{\star }\right)$ from millisecond pulsars with $\tau _{ \mathrm {o}}\sim 10^{-3}\,\mathrm {s}$, incident on a detector at different polar angles, (C) $\theta _{\star }=\pi +\cos ^{-1}\left( \sqrt{15/23} \right)$ and (B) $\theta _{\star }=3\pi /2$, which correspond to the maximum and the minimum detector responses, respectively as determined from (48), both being considered in the low-frequency regime, $f\ll 1\, \mathrm {Hz}$ (see Fig. 3). Note the difference in the volume between the two plots.

In Fig. 3 is plotted $\mathcal {R}_{0}$, the leading-order approximation of $\mathcal {R}$ in the limit $f\tau _{\mathrm {o}}\ll 1$ in (48), as a function of the incident angle $\theta _{\star }$ of a light ray. It should be noted here that $\mathcal {R}_{0}$ becomes maximum at $\theta _{\star }=\pi +\cos ^{-1}\left( \sqrt{15/23}\right)$ and minimum at $\theta _{\star }=3\pi /2$; that is, no extrema at $\theta _{\star }=\pi$, i.e., for the special case with $\left( K_{x},K_{y},K_{z}\right) =\left( 0,0,-K\right)$. In Fig. 4 is shown a plot of $\mathcal {R}\left( f\right)$ for the special case with $\left( K_{x},K_{y},K_{z}\right) =\left( 0,0,-K\right)$ for a millisecond pulsar with $\tau _{\mathrm {o} }\sim 10^{-3}\,\mathrm {s}$.

Fig. 3

A plot of $\mathcal {R}_{0}\left( \theta _{\star }\right) =\left( 29+150\cos ^{2}\theta _{\star }-115\cos ^{4}\theta _{\star }\right) /\left( 1920\pi ^{2}\right)$, the leading order term in (48). Note that $\mathcal {R}_{0}$ becomes maximum and minimum at $\theta _{\star }=\pi +\cos ^{-1}\left( \sqrt{15/23}\right)$ and $3\pi /2$, respectively

Fig. 4

A plot of $\mathcal {R}\left( f\right)$ for the special case with $\left( K_{x},K_{y},K_{z}\right) =\left( 0,0,-K\right)$ for a millisecond pulsar with $\tau _{\mathrm {o}}\sim 10^{-3}\,\mathrm {s}$

In view of Eqs. (44) and (45), one can determine the detector “sensitivity”:

$$\begin{aligned} h\left( f\right) \;\equiv \;f{\tilde{h}}\left( f\right) \;\;\sim \;\sqrt{\frac{ f^{2}\left\langle {\mathfrak {r}}^{2}\left( t\right) \right\rangle _{\mathrm { time}}}{\mathcal {R}\left( f\right) }}. \end{aligned}$$

(49)

Now, following Ref. [21], for a periodic GW source, we consider two supermassive black holes of mass M in a circular orbit of radius $R_{ \mathrm {o}}$, with the distance r from us. Then one can estimate

$$\begin{aligned} \sqrt{\left\langle {\mathfrak {r}}^{2}\left( t\right) \right\rangle }\sim \omega _{\mathrm {g}}^{-1}h_{\mathrm {max}}, \end{aligned}$$

(50)

with the maximum strain amplitude and the GW frequency being estimated respectively as

$$\begin{aligned} h_{\mathrm {max}}\sim & {} 5\times 10^{-14}\left( \frac{200M}{R_{\mathrm {o}}} \right) \left( \frac{M}{10^{10}M_{\odot }}\right) \left( \frac{10^{10} \mathrm {\mathrm {ly}}}{r}\right) , \end{aligned}$$

(51)

$$\begin{aligned} \omega _{\mathrm {g}}\sim & {} 2\times 10^{-8}\mathrm {s}^{-1}\left( \frac{200M }{R_{\mathrm {o}}}\right) ^{3/2}\left( \frac{10^{10}M_{\odot }}{M}\right) . \end{aligned}$$

(52)

With consideration of multiple pulsars as carriers of the GW signals, one can use the detector response function averaged over $\pi \le \theta _{\star }\le 3\pi /2$ from (48), to evaluate $h\left( f\right)$ via (49):

$$\begin{aligned} \mathcal {{\bar{R}}}\approx \frac{487}{15360\pi ^{2}}+\mathcal {O}\left( f^{2}\tau _{\mathrm {o}}^{2}\right) , \end{aligned}$$

(53)

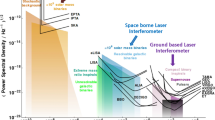
where the term $\mathcal {O}\left( f^{2}\tau _{\mathrm {o}}^{2}\right)$ can be disregarded for low-frequency GWs with $f\sim 10^{-8}\,\mathrm {Hz}$ to be detected via millisecond pulsars with $\tau _{\mathrm {o}}\sim 10^{-3}\, \mathrm {s}$. Then, for example, for GWs from a source with $M\sim 10^{9}M_{\odot }$, $R_{\mathrm {o}}\sim 2\times 10^{11}M_{\odot }$ and r $\sim 10^{10}\mathrm {\mathrm {ly}}$, we obtain a curve for $h\left( f\right)$ using Eqs. (49)–(53), as given by Fig. 5; it compares well with the actual sensitivity curves for EPTA, IPTA and SKA in the literature [22].

Fig. 5

A plot of $h\left( f\right)$ (red solid line) for GWs from a source with $M\sim 10^{9}M_{\odot }$, $R_{\mathrm {o}}\sim 2\times 10^{11}M_{\odot }$ and r $\sim 10^{10}\mathrm {\mathrm {ly}}$, detected by means of a millisecond pulsar with $\tau _{\mathrm {o}}\sim 10^{-3}\, \mathrm {s}$. It is compared with the sensitivity curves for EPTA (black dotted line), IPTA (black dashed line) and SKA (black dash-dotted line) (taken from Ref. [22])

3 Summary and discussion

From a general relativistic perspective, the interaction of light with GWs can be viewed as equivalent to a perturbation of light due to GWs. We have solved Maxwell’s equations in a spacetime perturbed by GWs and obtained a solution for a general case as given by Eqs. (20)–(22), wherein both light and GWs are assumed to propagate in arbitrary directions. Based on this solution, it has been shown that a perturbation of light due to GWs leads to a delay of the photon transit time, as given by Eq. (37). Applying this principle to a PTA, we have worked out the detector response function $\mathcal {R}$ as given by Eq. (48) and Fig. , which manifests how the detector response varies with the incident angle of a light pulse with respect to the detector. Then using this, we have obtained the curve for $h\left( f\right)$ as given by Fig. 5. Our result shows good agreement with the literature; the $h\left( f\right)$ curve compares well with the actual sensitivity curves for EPTA, IPTA and SKA, taken from Ref. [22]. However, our purpose in this analysis is rather to check how properly our detector response function $\mathcal {R}$ serves to provide the $h\left( f\right)$ curve for a given GW signal in the desired order of magnitude. A practical analysis of the detection sensitivity for the actual PTAs would be based on the accurate measurements of the timing residuals from multiple pulsars, with the consideration of systematics in the residuals such as solar system ephemeris errors mimicking a GW signal, the solar system metric contributing with an extra time delay in the modeled signal, etc.

As a means of improving our analysis in relation to a PTA, it is worth considering the cross-correlation of the residuals of two pulsars nearby in the sky [21]: the statistically-significant quadrupolar interpulsar correlation of GW background-induced timing delays as addressed in Ref. [23]. This will be discussed further in follow-up studies.

Our analysis can be extended to more complex arrays for GW detection than a PTA. For interferometers such as LIGO and LISA, we require a description of light rays in more complicated configurations, based on Eqs. (20)–( 22). We leave further discussion of this to follow-up studies.

Appendix A: Solutions to Maxwell’s equations via coordinate transformations

The total decomposition solution (20) can be obtained in the easiest manner for a particular case, in which $A_{\mathrm {o}}^{i}$ takes the simplest (but not trivial) form and so does $\delta A_{[{h}]}^{i}$ as obtained from Eq. (19). In a particular frame of the coordinates ${\mathbf {x}}^{\prime \prime }\equiv \left( x^{\prime \prime },y^{\prime \prime },z^{\prime \prime }\right)$, one can prescribe the simplest solution to satisfy Eq. (18):

$$\begin{aligned} A_{\mathrm {o}}^{i}\left( t,{\mathbf {x}}^{\prime \prime }\right) =\delta _{y^{\prime \prime }}^{i}\mathcal {A}\exp \left[ \mathrm {i}\left( Kz^{\prime \prime }-\omega _{\mathrm {e}}t\right) \right] , \end{aligned}$$

(A1)

where we let ${\mathbf {x}}^{\prime \prime }$ refer to the coordinates in the EMW frame. Then using this for Eq. (19), by straightforward computation, we obtain the simplest perturbation solution:

$$\begin{aligned}&\delta A_{[{h}]}^{i}\left( t,{\mathbf {x}}^{\prime \prime }\right) =2\left( \omega _{\mathrm {e}}/\omega _{\mathrm {g}}\right) A_{\mathrm {o}}^{i}\left( t, {\mathbf {x}}^{\prime \prime }\right) \nonumber \\&\quad \times \left[ h_{+}\cos ^{2}\left( \theta ^{\prime \prime }/2\right) \cos \left( 2\psi ^{\prime \prime }\right) \cos \left( {\mathbf {k}}^{\prime \prime } \mathbf {\cdot x}^{\prime \prime }-\omega _{\mathrm {g}}t\right) \right. \nonumber \\&\quad \left. -h_{\times }\cos ^{2}\left( \theta ^{\prime \prime }/2\right) \sin \left( 2\psi ^{\prime \prime }\right) \sin \left( {\mathbf {k}}^{\prime \prime } \mathbf {\cdot x}^{\prime \prime }-\omega _{\mathrm {g}}t\right) \right] , \end{aligned}$$

(A2)

where

$$\begin{aligned} {\mathbf {k}}^{\prime \prime }\equiv \left( k\sin \theta ^{\prime \prime }\cos \phi ^{\prime \prime },k\sin \theta ^{\prime \prime }\sin \phi ^{\prime \prime },k\cos \theta ^{\prime \prime }\right) , \end{aligned}$$

(A3)

and the angles $\left\{ \phi ^{\prime \prime },\theta ^{\prime \prime },\psi ^{\prime \prime }\right\}$ refer to the Euler rotations between ${\mathbf {x}} ^{\prime }$ in the GW frame and ${\mathbf {x}}^{\prime \prime }$ in the EMW frame,

$$\begin{aligned} {\mathbf {x}}^{\prime }={\mathbf {R}}\left( \phi ^{\prime \prime },\theta ^{\prime \prime },\psi ^{\prime \prime }\right) {\mathbf {x}}^{\prime \prime }\mathbf {.} \end{aligned}$$

(A4)

The above results can be extended to obtain the solutions for a general case, in which light propagates along an arbitrary direction; rather than along a single axis, e.g., the $z^{\prime \prime }$-axis. For this purpose, one can consider ${\mathbf {x}}^{\prime \prime }=\left( x^{\prime \prime },y^{\prime \prime },z^{\prime \prime }\right)$ in the EMW frame as rotated from ${\mathbf {x}}=\left( x,y,z\right)$ in the detector frame, in which light is seen to propagate along an arbitrary direction, as resulted from the rotations of the $z^{\prime \prime }$-axis. The relation between the two frames can be expressed by Euler angle rotations [14, 15]; but only with the direction angles $\left\{ \phi _{\star } ,\theta _{\star } \right\}$ in spherical coordinates, without the polarization-ellipse angle:

$$\begin{aligned} {\mathbf {x}}^{\prime \prime }={\mathbf {R}}\left( \phi _{\star } ,\theta _{\star } \right) \mathbf {x,} \end{aligned}$$

(A5)

where

$$\begin{aligned} {\mathbf {R}}\left( \phi _{\star } ,\theta _{\star } \right) ={\mathbf {R}}_{\mathrm {II}}\left( \theta _{\star } \right) {\mathbf {R}}_{\mathrm {I}}\left( \phi _{\star } \right) , \end{aligned}$$

(A6)

with

$$\begin{aligned} {\mathbf {R}}_{\mathrm {I}}\equiv \left[ \begin{array}{ccc} \cos \phi _{\star } &{} \sin \phi _{\star } &{} 0 \\ -\sin \phi _{\star } &{} \cos \phi _{\star } &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] ,\quad {\mathbf {R}}_{\mathrm {II}}\equiv \left[ \begin{array}{ccc} \cos \theta _{\star } &{} 0 &{} -\sin \theta _{\star } \\ 0 &{} 1 &{} 0 \\ \sin \theta _{\star } &{} 0 &{} \cos \theta _{\star } \end{array} \right] . \nonumber \\ \end{aligned}$$

(A7)

Now, by means of Eq. (A5) and the invariance relation

$$\begin{aligned} {\mathbf {K}}^{\prime \prime }\mathbf {\cdot x}^{\prime \prime }=\mathbf {K\cdot x }\Leftrightarrow Kz^{\prime \prime }=K_{x}x+K_{y}y+K_{z}z, \end{aligned}$$

(A8)

where ${\mathbf {K}}^{\prime \prime }=\left( 0,0,K\right)$ and ${\mathbf {K}} =\left( K_{x},K_{y},K_{z}\right)$ with $K=\sqrt{ K_{x}^{2}+K_{y}^{2}+K_{z}^{2}}=\omega _{\mathrm {e}}/c$, one can express $\phi _{\star }$, $\theta _{\star }$ in terms of $K_{x}$, $K_{y}$, $K_{z}$:

$$\begin{aligned} \sin \theta _{\star } \cos \phi _{\star } =\frac{K_{x}}{K},\sin \theta _{\star } \sin \phi _{\star } =\frac{K_{y}}{K} ,\cos \theta _{\star } =\frac{K_{z}}{K}. \nonumber \\ \end{aligned}$$

(A9)

Based on these, one can convert ${\mathbf {R}}\left( \phi _{\star } ,\theta _{\star } \right) \rightarrow {\mathbf {T}}\left( K_{x},K_{y},K_{z}\right)$ and rewrite Eq. (A5) as

$$\begin{aligned} {\mathbf {x}}^{\prime \prime }={\mathbf {T}}\left( K_{x},K_{y},K_{z}\right) \mathbf {x,} \end{aligned}$$

(A10)

where

$$\begin{aligned} {\mathbf {T}}=\left[ \begin{array}{ccc} \frac{K_{x}K_{z}}{K\sqrt{K_{x}^{2}+K_{y}^{2}}} &{} \frac{K_{y}K_{z}}{K\sqrt{ K_{x}^{2}+K_{y}^{2}}} &{} -\frac{\sqrt{K_{x}^{2}+K_{y}^{2}}}{K} \\ -\frac{K_{y}}{\sqrt{K_{x}^{2}+K_{y}^{2}}} &{} \frac{K_{x}}{\sqrt{ K_{x}^{2}+K_{y}^{2}}} &{} 0 \\ \frac{K_{x}}{K} &{} \frac{K_{y}}{K} &{} \frac{K_{z}}{K} \end{array} \right] . \end{aligned}$$

(A11)

The inverse transformation of (A10) is expressed by

$$\begin{aligned} {\mathbf {x}}={\mathbf {T}}^{-1}\left( K_{x},K_{y},K_{z}\right) \mathbf {{\mathbf {x}} ^{\prime \prime },} \end{aligned}$$

(A12)

where ${\mathbf {T}}^{-1}$ is given by ${\mathbf {T}}^{\mathrm {T}}$, the transpose of ${\mathbf {T}}$.

As seen in Sect. 2.1, one can consider ${\mathbf {x}}^{\prime }$ in the GW frame as rotated from ${\mathbf {x}}$ in the detector frame through the Euler angles $\left\{ \phi ,\theta ,\psi \right\}$. Thus, combining Eq. (4) with Eq. (A12), and then comparing this with Eq. (A4), we find the relation:

$$\begin{aligned} {\mathbf {R}}\left( \phi ^{\prime \prime },\theta ^{\prime \prime },\psi ^{\prime \prime }\right) ={\mathbf {R}}\left( \phi ,\theta ,\psi \right) {\mathbf {T}}^{-1}\left( K_{x},K_{y},K_{z}\right) . \end{aligned}$$

(A13)

That is, using Eqs. (5), (6) and (A11) for this, one can express $\phi ^{\prime \prime }$, $\theta ^{\prime \prime }$, $\psi ^{\prime \prime }$ in terms of $\phi$, $\theta$, $\psi$ and $K_{x}$, $K_{y}$, $K_{z}$.

By means of Eqs. (A10), (A12) and (A13), one can transform the solutions $A_{\mathrm {o}}^{i}\left( t,{\mathbf {x}}^{\prime \prime }\right)$ and $\delta A_{[{h}]}^{i}\left( t,{\mathbf {x}}^{\prime \prime }\right)$ in the EMW frame, in which light propagates along the $z^{\prime \prime }$ -axis, as given by Eqs. (A1) and (A2) respectively, to the solutions for a general case, $A_{\mathrm {o}}^{i}\left( t,{\mathbf {x}}\right)$ and $\delta A_{[{h}]}^{i}\left( t,{\mathbf {x}}\right)$ in the detector frame, in which light propagates along an arbitrary direction of ${\mathbf {K}}=\left( K_{x},K_{y},K_{z}\right)$, as given by Eqs. (21) and (22) respectively.