1 Introduction

General relativity (GR) has upgraded our understanding of the Universe. However, when managing with portraying the physical wonders at high energy phase or exceptionally short distances, the issues and defections of this theory will perhaps become the most important factor, particularly in the request for the Planck scales where gravitational effects as well as quantum effects are significant.

Due to the nowadays acknowledged existence of accelerating expansion of the Universe portrayed by dark energy (DE) through the strong negative pressure (for a review see [1,2,3,4,5,6,7,8,9,10,11,12,13,14] and references therein), the investigation of spherically symmetric solutions of the EFEs [15, 16] in presence of DE is of great importance. This investigation has previously been addressed for example in [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32].

One of the most straightforward systems for DE is the Chaplygin fluid [33,34,35,36,37,38,39]. The system depends on an ideal fluid fulfilling the EoS \(p=-A/\rho \) where \(p\) is the pressure, \(\rho \) is the energy density and \(A\) is a positive constant. In this way, other proposed models which are also plausible for dynamical investigations, for instance, phantom [40], quintessence [41], K-essence [42], quintom [43,44,45,46,47], holographic dark energy [48, 49].

The Chaplygin fluid model is well-consistent with various classes of observational tests such as supernovae data [50], gravitational lensing [51, 52], gamma ray bursts [53] and cosmic microwave background radiation [54]. As with other competing candidates to explain the overwhelming energy density of the present Universe, Chaplygin fluid model is naturally constrained through cosmological observables. So the motivation to choose Chaplygin fluid EoS depends on the observational data according to which the EoS parameter for DE can be less than \(-1\). In this respect, to obtain predictable results with observational data, the Chaplygin fluid EoS was replaced by a modified Chaplygin fluid EoS [55], or generalized Chaplygin fluid EoS [56,57,58,59,60,61]. On the other hand, the generalized Chaplygin fluid cosmology is also well-useful from holographic point of view [62, 63]. There are still other expansions such as the modified cosmic Chaplygin fluid [64] and the generalized cosmic Chaplygin fluid [65].

Recently researchers are using Chaplygin EoS with great interest since it describes the accelerating phase of the present Universe. The Chaplygin EoS is a special form of polytropic EoS, which is used to model the compact stellar systems. On the other hand, there are several construct stellar models have done for compact celestial bodies with Chaplygin EoS. In this connection, Bertolami and Páramos [66] have studied general features of a spherically symmetric object described through the generalized Chaplygin fluid EoS. Using the associated Lane–Emden equation, they highlighted that generalized Chaplygin dark star should exist in a framework unifying dark energy and dark matter. Furthermore, they have also argued that a Chaplygin dark star may arise from a density fluctuation in the context of the generalized Chaplygin fluid model of unification of dark energy and dark matter. Mubasher et al. [67] constructed a stationary, spherically symmetric and spatially inhomogeneous wormhole space-time supported by a modified Chaplygin fluid. Whereas Rahaman and co-workers [68] have described anisotropic charged fluids with a nonlinear Chaplygin EoS and were able to find solutions using an algebraic method without solving any differential equations. Similar types of solutions have also been studied to generate and analyze physically viable models of compact astrophysical objects extended in different analogy in presence of the Chaplygin fluid [21,22,23,24,25].

The study of the relativistic astrophysical configuration started with the disclosure in 1916 by Karl Schwarzschild of a universal vacuum outside EFEs solution [69]. He additionally gave the main internal astrophysical solution [15], which should be matched to the external solution. In this regard, the gravitational collapse of spherical objects produces cosmic compact objects with very high inside densities like black holes, and neutron stars which are the almost well-known finished result in the evolution of spherical objects.

One of the most fundamental assignments, when all is said in GR, is the physical modeling of a compact stellar spherical object collapsing under its own gravity. Subsequently, the revelation of pulsars and clarification of their features by supposing neutron stars rotates, the theoretical investigation of high dense stars has been achieved using both analytical and numerical approaches and the parameters of compact cosmic systems have been turned out by general relativistic processing.

The eventual fate of the compact stellar systems (the result of several stellar procedures, including the merger of binaries and supernova explosions) is chosen by the inward mass distribution of the spherical object. The features of compact spherical objects are emphatically influenced by the expected depiction of matter in their insides.

For this purpose, Alcock and co-workers [70] and Haensel and his collaborators [71] examined the comportment and the physical highlights of diverse compact spherical systems and introduced a general frame for compact stellar structures which are not made out of neutron matter, yet where, specified the states of exceptionally great density in their insides, there could instead be stage progress from nuclear to quark matter. The extraordinary states winning in the inside of compact stellar spherical objects appear to be anyway behind the extent of the straightforwardly arranged earthbound research facilities. So that the theoretical depiction of compact spherical objects matter is right now one of the exceedingly testing problems of particle physics and nuclear.

Notwithstanding considerable study, the matter nature at the extraordinary densities in the center of compact stellar spherical object stays unsure. Several scenarios ranging from hadronic and nuclear matter to exotic states implying Bose-Einstein condensation of kaons or pions, to bulk quark matter and quark matter in beads, have been suggested.

Ongoing tests in the most recent decades on relativistic nuclear impacts at the Brookhaven RHIC, and LHC in CERN, test hot intense matter revealing insight into the wonders of hot plasma shaped by intense gluons and quarks [72, 73]. Over the possibilities outcomes of obtaining high-density nuclear matter in earthbound research centers, FAIR in Germany, FRIB in USA, J-Parc in Japan and RAON in Korea sooner rather than later, the possible discoveries of gravitational waves from binary neutron star black holes (or binary neutron stars) are accepted to guarantee tests of the ultra-high density inside of compact spherical objects.

This shall unlock another window for studying compact stellar spherical systems, and allow us to better understand the uncertainties associated features of ultra-high-densities nuclear matter. Uncertainties on ultra-high-density features result in uncertainties about the most extreme conceivable mass of a compact spherical object. Now, a few of the notable features of astrophysical systems are their radii and masses. The infinitesimal distribution of matter in the spherical body is an fundamental element in determining the connection between radius and mass.

We presently make a few remarks identifying with the physical highlights of local anisotropy. The local anisotropy has been considered by several theorists especially in the work by Herrera and Santos [74] and references therein. Some recent works of the phenomenon of anisotropy are included in the study of Kileba Matondo and co-workres [75] who have recovered observational parameters of astronomical objects, for instance, SAX J1808.4-3658 and PSR J1614-2230.

At the last phase of astrophysical evolution, the ordinary baryonic matter is profoundly squeezed by gravity in the center of heavy spherical objects throughout supernova occurrences. In like kind of compact spherical objects, the inside pressure keep is anisotropic in the ultra-high-density matter in light of the fact that the radial pressure keeps not be matched by the transverse pressure. The source of this anisotropic pressure keep emerge due to the presence of type-IIIA superfluid [76, 77] or by the existence of a strong astrophysical core, electromagnetic field [78,79,80], rotation, phase transitions, pion condensation [81], etc.

As a result of these effects, the EoS of the astrophysical matter turns out to be basically anisotropic in an ultra-high-density circumstance. The main endeavors to contemplate pressure anisotropy in self-gravitating systems have been made by Jeans [82]. Additionally, considerable work has been done on anisotropic relativistic structures beginning from the successful thought of Lemaitre [83]. Bowers and Liang [84] studied anisotropic compact stellar bodies in Einsteinian gravity. Subsequently, Herrera and Santos [85] gave a detailed discussion of local anisotropy in self-gravitating systems. Heintzmann and Hillebrandt [86] introduced a basic study on the characteristic of a relativistic anisotropic neutron sphere system at high densities by methods for a few straightforward suppositions and have indicated that for a self-assertive huge anisotropy there is no constraining mass for neutron spheres, anyway the most extreme mass of a neutron sphere still lies past \(3 - 4~ M_\odot \).

The idea of cracking was presented in [74] which is straight-identified with the presence of anisotropy. Cracking is basic to describe the stability of the matter distribution near to equilibrium. In addition, a significant observational factor, the anisotropy is examined in detail by Mak and Harko [87] and they have demonstrated that for a dust-loaded Universe the cosmological development consistently finishes inside an anisotropic stage, however for the high-density matter–loaded Universes, anisotropy can occur in normal compact spheres as well as in hypothetical items like boson spheres and DE sphere [88, 89]. Notwithstanding that, several authors have additionally acquired solutions of the EFEs in various methodologies [90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120].

In this paper, we supply a framework for modeling compact spherical objects in which the interior matter distribution obeys a new version of Chaplygin fluid EoS of the form \(p_r=H\rho ^{\alpha }-K\rho ^{-\beta }\). The matter distribution is anisotropic. It is already conceivable to solve the EFEs. An exhaustive and detailed investigation manifest that the system is regular, well-defined and fulfills the criteria for physical feasibility and provide closed-form solutions which satisfactorily describe compact strange astrophysical object candidates like Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327.

The remainder of this paper is organized as follows: In Sect. 2, we have presented the spherical symmetric metric and EFEs for anisotropic matter distribution. The new solution for the anisotropic strange compact spherical systems by taking the ansatz of the gravitational potential \(Z(x)\) and radial pressure has been presented in Sect. 3. In Sect. 4, we have determined arbitrary constants by using specific conditions for the anisotropic solution. We present all the physical conditions viz., positivity of the energy density and radial pressure at the center, monotonic decrease of the energy density and the radial pressure in term of the radial coordinate r, the continuity of the extrinsic curvature through the corresponding hyper-surface, the nature of anisotropic force, the positivity of the trace of the energy tensor, \(\rho -p_r-2p_t\), energy conditions, stability of anisotropic compact sphere via adiabatic index, cracking method and Tolman–Oppenheimer–Volkoff equation, for well-behaved anisotropic astrophysical models in Sect. 5. Some other physical characteristics of the anisotropic system such as gravitational mass, compactness parameter and gravitational red-shift are examined in Sect. 6. Concluding remarks close this paper.

2 Spherically symmetric space-time

We will examine a model describing an anisotropic fluid configuration with static spherical symmetry obeying a new version of modified Chaplygin EoS. The interior of a spherical symmetric static space-time in Schwarzschild coordinates \( x^{a}= \left( t, r, \vartheta , \varphi \right) \) is represented by the following line element:

$$\begin{aligned}&ds^{2}=-e^{2 \nu \left( r \right) }dt^{2}+e^{2 \lambda \left( r \right) }dr^{2}+r^{2} \left( d \vartheta ^{2}+\sin ^{2} \vartheta d \varphi ^{2} \right) ,\nonumber \\ \end{aligned}$$
(1)

where \(\nu \) and \(\lambda \) are the gravitational potentials which are the functions of the radial coordinate, \(r\) only. The Einstein field equation is,

$$\begin{aligned}&8 \pi T_{ij}=G_{ij}. \end{aligned}$$
(2)

Here \(G_{ij}\) is the Einstein’s tensor with the accompanying functions,

$$\begin{aligned}&R_{ij}-\frac{1}{2}Rg_{ij}=G_{ij} , \end{aligned}$$
(3)

where \( R_{ij} \) is the Ricci tensor, \( R \) is the Ricci scalar and \( g_{ij} \) is the metric tensor. \( T_{ij} \) is the energy-stress tensor of the underlying fluid distribution.

Let’s suppose that the matter involved in the distribution is anisotropic in kind. By employing the overall function, so we obtain the function for energy-stress tensor in the following form:

$$\begin{aligned}&T_{i}^{j}= \rho \eta ^{j} \eta _{i}+p_{r} \chi _{i} \chi ^{j}+p_{t} \left( \eta ^{j} \eta _{i}- \chi _{i} \chi ^{j}-g_{i}^{j} \right) , \end{aligned}$$
(4)

with \( \eta ^{j} \eta _{i}= \chi _{i} \chi ^{j}=1 \) , \( \chi _{i} \) is the unit space-like vector and \( \eta ^{j} \) is the fluid four-velocity of the relaxation body and consequently \( \eta ^{j} \chi _{i}=0 \) . The expression (4) provides the components of the energy-stress tensor of an anisotropic fluid at any point in terms of the density \( \rho \) , the radial pressure \( p_{r} \) and the transverse pressure \( p_{t} \) . With the simple shape of line element, the energy-stress tensor \( T_{i}^{j} \) takes the form:

$$\begin{aligned}&T_{i}^{j}=diag \left( \rho , -p_{r},~-p_{t},-p_{t} \right) , \end{aligned}$$
(5)

and

$$\begin{aligned}&T_{i}^{j}=0 \ \ if\ i \ne j . \end{aligned}$$
(6)

Taking \( G=c=1 \) , where \( G \) is the gravitational constant and \( c \) is the speed of light. Using (5), the system of EFEs for the line element can be written as

$$\begin{aligned} \rho= & {} \frac{1}{~8 \pi } \left\{ \frac{1-e^{- \lambda }}{r^{2}}+\frac{e^{- \lambda }}{r}\frac{d \lambda }{dr} \right\} , \end{aligned}$$
(7)
$$\begin{aligned} p_{r}= & {} \frac{1}{~8 \pi } \left\{ \frac{e^{- \lambda }-1}{r^{2}}+\frac{e^{- \lambda }}{r}\frac{d \nu }{dr}\right\} , \end{aligned}$$
(8)
$$\begin{aligned} p_{t}= & {} \frac{e^{- \lambda }}{~8 \pi } \left\{ \frac{1}{2}\frac{d^{2} \nu }{dr^{2}}+\frac{1}{4} \left( \frac{d \nu }{dr} \right) ^{2}\right\} \nonumber \\&-\frac{e^{- \lambda }}{~8 \pi } \left\{ \frac{1}{4}\frac{d \nu }{dr}\frac{d \lambda }{dr}+\frac{1}{2r} \left( \frac{d \nu }{dr}-\frac{d \lambda }{dr} \right) \right\} .~~ \end{aligned}$$
(9)

Now the gravitational mass contained in the spherical object of radius \( r \) is given by,

$$\begin{aligned}&m \left( r \right) =4 \pi \int _{0}^{r} \rho \left( \epsilon \right) \epsilon ^{2}d \epsilon , \end{aligned}$$
(10)

where \( \epsilon \) is an integration variable. We now introduce the transformation was used for the first time by Durgapal and Bannerji [122]

$$\begin{aligned}&x=r^{2},\ \ Z \left( x \right) =e^{-2 \lambda \left( r \right) },\ \ y^{2} \left( x \right) =e^{2 \nu \left( r \right) } . \end{aligned}$$
(11)

In terms of these new variables expressed in (11), the line element (1) can be written in the following form

$$\begin{aligned}&ds^{2}=-y \left( x \right) dt^{2}+\frac{1}{4xZ \left( x \right) }dx^{2}+x \left( d \vartheta ^{2}+\sin ^{2} \vartheta d \varphi ^{2} \right) .\nonumber \\ \end{aligned}$$
(12)

The system of EFEs (7)–(8) can be written as

$$\begin{aligned} \rho= & {} \frac{1}{~8 \pi } \left\{ \frac{1-Z}{x}-2\frac{dZ}{dx} \right\} , \end{aligned}$$
(13)
$$\begin{aligned} p_{r}= & {} \frac{1}{~8 \pi } \left\{ 4Z \left( \frac{1}{y}\frac{dy}{dx} \right) +\frac{Z-1}{x} \right\} , \end{aligned}$$
(14)
$$\begin{aligned} p_{t}= & {} \frac{1}{~8 \pi } \left\{ 4xZ\frac{d^{2}y}{dx^{2}}+ \left( 4Z+2x\frac{dZ}{dx} \right) \left( \frac{1}{y}\frac{dy}{dx} \right) +\frac{dZ}{dx} \right\} .\nonumber \\ \end{aligned}$$
(15)

The gravitational mass expression (10) becomes

$$\begin{aligned}&m \left( x \right) =2 \pi \int _{0}^{x}\root \of { \epsilon } \rho \left( \epsilon \right) d \epsilon , \end{aligned}$$
(16)

in terms of the new variable \( x \) expressed in (11).

In order to close the system of EFEs (13)–(14), we assume that the interior matter distribution obeys a new version of Chaplygin fluid EoS as follow,

$$\begin{aligned}&p_{r}=H \rho ^{ \alpha }-K \rho ^{- \beta }~~~~~ with~~~~~ 0 \le \beta \le 1~~~~ \end{aligned}$$
(17)

which reduces to modified Chaplygin fluid EoS for \( \alpha =1 \). This modified Chaplygin fluid EoS was used by Mubasher et al. [67], Rahaman et al [68], Benaoum [121] to model compact stellar structures within the context of general relativity. The new version of modified Chaplygin fluid EoS expressed in (17) looks less economical than pure Chaplygin, due to this huge number of free parameters, it is more flexible from the point of view of the comparison with observational data. Then it is possible to write the EFEs (13)–(14) within the simplest form

$$\begin{aligned} \rho= & {} \frac{1}{~8 \pi } \left\{ \frac{1-Z}{x}-2\frac{dZ}{dx} \right\} , \end{aligned}$$
(18)
$$\begin{aligned} p_{r}= & {} \frac{1}{~8 \pi } \left\{ 4Z \left( \frac{1}{y}\frac{dy}{dx} \right) +\frac{Z-1}{x} \right\} , \end{aligned}$$
(19)
$$\begin{aligned} p_{t}= & {} p_{r}+ \Delta , \end{aligned}$$
(20)
$$\begin{aligned} \Delta= & {} \frac{1}{~8 \pi } \left\{ 4xZ\frac{d^{2}y}{dx^{2}}+\frac{dZ}{dx} \left( 1+2x \left( \frac{1}{y}\frac{dy}{dx} \right) \right) +\frac{1-Z}{x} \right\} \nonumber \\ \end{aligned}$$
(21)

Using Eqs. (17), (18) and (18) we get

$$\begin{aligned} \frac{1}{y}\frac{dy}{dx}= & {} \frac{1}{~4Z} \left\{ H \left( \frac{1}{~8 \pi } \right) ^{ \alpha -1} \left( \frac{1-Z}{x}-2\frac{dZ}{dx} \right) ^{ \alpha }\right\} \nonumber \\&-\frac{1}{~4Z} \Bigg \{K \left( \frac{1}{~8 \pi } \right) ^{- \beta }\left( \frac{1-Z}{x}-2\frac{dZ}{dx} \right) ^{- \beta }-\frac{1-Z}{x} \Bigg \}\nonumber \\ \end{aligned}$$
(22)

where the quantity \( \Delta =p_{t}-p_{r} \) is the measure of anisotropy in our model. To examine the physical characteristics, the solution should be given explicitly. Several choices can be made for the gravitational potential \( Z \left( x \right) \), but the choices need to be physically conceivable to model a achievable compact spherical object. In the next section, we will consider an easy and physically reasonable form for the gravitational potential \( Z \left( x \right) \), provides us with a simple to solve the EFEs in order to obtain the model of compact spherical object.

3 New solution for anisotropic strange compact spherical object

As we can see that the Einstein’s system of equations (18)–(19) depends on the gravitational potential \( Z \left( x \right) \). For this purpose, we assume ansatz of the gravitational potential \( Z \left( x \right) \) of the form

$$\begin{aligned}&Z \left( x \right) =\frac{1}{ \left( 1+ax \right) }, \end{aligned}$$
(23)

where \( a \) is a real constant. Here \( Z \left( x \right) =1 \) at \( x \rightarrow 0 \), which shows that the gravitational potential we chose in expression (23) is regular, positive and finite at center and well-behaved in the stellar interior. This gravitational potential expressed in (23) satisfies all the above requirements which leads to the main physical availability of solution.

Now, in order to integrate the Eq. (22), we use the function of the gravitational potential (23). In this way, from Eqs. (18)–(22) we get

$$\begin{aligned} \frac{1}{y}\frac{dy}{dx}= & {} \frac{1}{4}H \left( \frac{1}{~8 \pi } \right) ^{ \alpha -1} \left\{ a^{ \alpha } \left( 3+ax \right) ^{ \alpha } \left( 1+ax \right) ^{1-2 \alpha } \right\} \nonumber \\&-\frac{1}{4}K \left( 8 \pi \right) ^{ \beta } \left\{ a^{- \beta } \left( 3+ax \right) ^{- \beta } \left( 1+ax \right) ^{3 \beta } \right\} \nonumber \\&+\frac{1}{4}a.~~~~~~~ \end{aligned}$$
(24)

Integrating this equation we obtain

$$\begin{aligned} \ln \left( y\right)= & {} 1/4 (a x +2^{2 - 3 \alpha } a^{(1 + \alpha )} H \pi ^{(1-\alpha )} x^2 (1 + a x/3)^{- \alpha } \nonumber \\&\times (3 + a x)^{ \alpha } F_{1}\left( 2, 2 \alpha , -\alpha ; 3; -a x, -a x/3\right) \nonumber \\&+ (a^{(\alpha -1)} H (8 \pi )^{(1 - \alpha )} (1 + a x)^{(-2 \alpha )} (3 + a x)^{(1 + \alpha )} \nonumber \\&\times (1 + 1/2 (-3 - a x))^{(2 \alpha )} \nonumber \\&\times {{_2}F_1}\left( 2 \alpha , 1 + \alpha , 2 + \alpha ; 1/2 (3 + a x)\right) )/(1 + \alpha ) \nonumber \\&- (a^{(-1 - \beta )} k \pi ^\beta (1 + a x) (2 + 2 a x)^{(3 \beta )} \nonumber \\&\times (1 + 1/4 (2 + 2 a x))^{\beta } (2 + 1/2 (2 + 2 a x))^{-\beta } \nonumber \\&\times _2F_1 \left( \beta , 1 + 3\beta , 2 + 3\beta ; 1/4 (-2 -2 a x)\right) )\nonumber \\&/(1 + 3 \beta )) +C_{1} \end{aligned}$$
(25)

where \(F_{1}\left( a, b_1, b_2; c; x, y\right) \), and \(_{2}F_{1}\left( a, b, c; z\right) \) are both hyper-geometric functions and \(C_{1}\) is the integration constant, which will be determined from the boundary condition. Subsequently, the Einstein’s system of equations composed of matter density, radial pressure and transverse pressure is obtained as follows

$$\begin{aligned} \rho ~= & {} \frac{1}{~8 \pi } \left( 3a+a^{2}x \right) \left( 1+ax \right) ^{-2}, \end{aligned}$$
(26)
$$\begin{aligned} p_{r}= & {} H \rho ^{ \alpha }-K \rho ^{- \beta }, \end{aligned}$$
(27)
$$\begin{aligned} p_{t}= & {} \Delta +H \rho ^{ \alpha }-K \rho ^{- \beta }, \end{aligned}$$
(28)

and using Eqs. (20) and (23) we get the anisotropic parameter

$$\begin{aligned} \Delta= & {} \frac{1}{~8 \pi } \left\{ \frac{4x}{ \left( 1+ax \right) }\frac{d^{2}y}{dx^{2}}-\frac{a}{ \left( 1+ax \right) ^{2}} \left( 1+2x \left( \frac{1}{y}\frac{dy}{dx} \right) \right) \right\} \nonumber \\&+\frac{1}{~8 \pi } \left\{ \frac{a}{1+ax} \right\} \end{aligned}$$
(29)

where \( y \) is given by the expression (25) mentioned above. The anisotropic parameter is attractive in nature if \( \Delta <0 \) and repulsive if \( \Delta >0 \) .

Table 1 Constant parameters calculated for radii and mass for some strange star candidates
Full size table

4 Matching conditions for anisotropic solution

In this section, we match our inner space-time to the Schwarz-schild outer solution at the boundary \( r=r_{a} \), where \( r_{a} \) is the radius of the spherical object and it is evident that \( r_{a}>2M \) , \( M \) is the total gravitational mass of the spherical object. The outer space-time is provided by the line element

$$\begin{aligned} ds^{2}= & {} - \left( 1-\frac{2M}{r} \right) dt^{2}+ \left( 1-\frac{2M}{r} \right) ^{-1}dr^{2}\nonumber \\&+r^{2} \left( d \vartheta ^{2}+\sin ^{2} \vartheta d \varphi ^{2} \right) . \end{aligned}$$
(30)

The correspondence between the internal line element (1) and the external line element (30) at the boundary \( r=r_{a} \) imposes the prerequisites

$$\begin{aligned} e^{2 \nu \left( r_{a} \right) }= & {} \left( 1-\frac{2M}{r_{a}} \right) , \end{aligned}$$
(31)
$$\begin{aligned} e^{2 \lambda \left( r_{a} \right) }= & {} \left( 1-\frac{2M}{r_{a}} \right) ^{-1}= \left( 1+ar_{a}^{2} \right) ^{-1}. \end{aligned}$$
(32)

The condition (31) imposes the following limitation on the integration constant \( C_{1} \) as

$$\begin{aligned} C_{1}= & {} \frac{1}{2} \ln \left( 1-\frac{2M}{r_{a}} \right) -1/4 (a x +2^{2 - 3 \alpha } a^{(1 + \alpha )} H \pi ^{(1-\alpha )} x^2 \nonumber \\&\times (1 + a x/3)^{- \alpha } (3 + a x)^{ \alpha } F_{1}\left( 2, 2 \alpha , -\alpha ; 3; -a x, -a x/3\right) \nonumber \\&+ (a^{(\alpha -1)} H (8 \pi )^{(1 - \alpha )} (1 + a x)^{(-2 \alpha )} (3 + a x)^{(1 + \alpha )} \nonumber \\&\times (1 + 1/2 (-3 - a x))^{(2 \alpha )} \nonumber \\&\times {{_2}F_1}\left( 2 \alpha , 1 + \alpha , 2 + \alpha ; 1/2 (3 + a x)\right) )/(1 + \alpha ) \nonumber \\&- (a^{(-1 - \beta )} k \pi ^\beta (1 + a x) (2 + 2 a x)^{(3 \beta )} \nonumber \\&\times (1 + 1/4 (2 + 2 a x))^{\beta } (2 + 1/2 (2 + 2 a x))^{-\beta } \nonumber \\&\times _2F_1 \left( \beta , 1 + 3\beta , 2 + 3\beta ; 1/4 (-2 -2 a x)\right) )/(1 + 3 \beta )),\nonumber \\ \end{aligned}$$
(33)

which imposes a restriction on the parameters \( H \), \( K \), \( a \), \( \alpha \) and \( \beta \), which can be solved in the case that we specify the radius of the compact stellar spherical body. By choosing some reasonable values to these parameters, we obtain the central density of the compact stars between \(1.7199\times 10^{15}\) \(\mathrm{g}/\mathrm{cm}^3\) and \(1.8160 \times 10^{15}\) \(\mathrm{g}/\mathrm{cm}^3\) as shown in Table 2. From these results, the pressure anisotropy is chosen motivated by the fact that the central density is beyond the nuclear density (\(\sim 10^{15}\) \(\mathrm{g}/\mathrm{cm}^3\)). Whereas, relaxing the stringent condition \(p_r=p_t\) to allow local anisotropies \(\Delta = p_r-p_t\) in the stellar medium constitutes a more realistic situation from the astrophysical point of view. In this respect Ruderman [123], Canuto [124,125,126], and Canuto et al.   [127,128,129,130] investigations revealed that, if the density of matter overcomes the nuclear density, this problem is anisotropic in nature and should be treated in a relativistic way. In this direction, Bowers and Liang [84] presented one of the first studies based on anisotropic matter distributions. Furthermore, the existence of anisotropy in the matter distribution allows adding important benefits in the description of the system, highlighting three important point: Firstly, the presence of an extra gradient, repulsive in nature when \(\Delta >0\) (otherwise is attractive). This fact is relevant since the presence of a repulsive anisotropy gradient offset the gravitational attraction avoiding a gravitational collapse. Secondly, the possibility to obtain more compact objects, and thirdly, the stability of the system is enhanced.

To determine the radial dependence of the physical quantities of our stellar system, which includes energy density, transverse pressure, radial pressure and the some other physical features of the anisotropic stellar model. We have employed the data values can be seen from Table (1), which could be very near the observational data of five compact strange astrophysical objects: two X-ray binaries, namely Cyg X-2 and Vela X-1 performed by Rawls et al. [131], two low-mass-X-ray binaries, namely, 4U 1608-52 and 4U 1636-536 performed by G\(\ddot{u}\)ver et al. [132]; Kaaret et al. [133] and one binary millisecond pulsars, namely PSR J1903+327 performed by Freire et al. [134], by showing the anisotropic effects presented by taking into account a spherically symmetric inside space-time metric in the Einstein’s general relativity framework.

5 Physical analysis

We are now in a position to examine the physical strengths of the anisotropic stellar system presented in the previous sections. In order to represent a achievable compact spherical object, our anisotropic stellar system must meet the following physical prerequisites:

  1. 1.

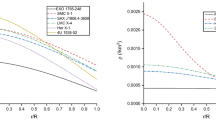
    Positivity of the energy density and radial pressure at the center   In the specific model, since \( \rho \left( 0 \right) =\frac{3a}{~8 \pi } \), the matter density \( \rho \) is regular and positive at the center. We also have \( p_{r} \left( 0 \right) =H \left( \frac{3a}{~8 \pi } \right) ^{ \alpha }-K \left( \frac{3a}{~8 \pi } \right) ^{- \beta } \). To ensure that the positiveness of radial pressure \( p_{r} \) at the origin we must have \( \frac{K}{H}< \left( \frac{3a}{~8 \pi } \right) ^{ \alpha + \beta } \) . The behavior of energy density and radial pressure are depicted in Figs. 1 and 2, respectively. From these figures, it is evident that our specific system of a strange compact spherical object satisfies this condition.

  2. 2.

    Monotonic decrease of the energy density and the radial and pressure against the radial coordinate   \( r \)

    Since the gradient of energy density and radial pressure are strictly negative for all \( r \in ] \text {0, R} [ \) , the energy density \( \rho \) and radial pressure \( p_{r} \) are monotonous decreasing functions from the origin to surface of the compact spherical object. The profiles of the gradient of energy density \( \left( \frac{d \rho }{dr} \right) \) and radial pressure \( \left( \frac{dp_{r}}{dr} \right) \) are outlined in Figs. 3 and 4, for specific choice of parameters.

  3. 3.

    The continuity of the extrinsic curvature through the corresponding hyper-surface, \( K_{ij}^{-}=K_{ij}^{+} \)   Continuity of the extrinsic curvature through the matching hyper-surface, at the boundary of the compact stellar spherical system \( r=R \) yields the condition

    $$\begin{aligned}&\left( p_{r} \right) _{r=R}=0 , \end{aligned}$$
    (34)

    which gives

    $$\begin{aligned} R= & {} \frac{1}{4\root \of { \pi } \left( \frac{K}{~H} \right) ^{\frac{1}{2 \left( \alpha + \beta \right) }}}\left\{ a^{2}-16 \pi a \left( \frac{K}{~H} \right) ^{\frac{1}{ \alpha + \beta }}\right. \nonumber \\&\times \left\{ \left( 16 \pi a \left( \frac{K}{~H} \right) ^{\frac{1}{ \alpha + \beta }}-a^{2} \right) ^{2}+32 \pi \left( \frac{K}{~H} \right) ^{\frac{1}{ \alpha + \beta }}\right. \nonumber \\&\times \left. \left. \left( 3a+8 \pi \left( \frac{K}{~H} \right) ^{\frac{1}{ \alpha + \beta }} \right) \right\} ^{1/2}\right\} ^{1/2}, \end{aligned}$$
    (35)

    which is finite for suitable choice of variables \( H \), \( K \), \( a \), \( \alpha \) and \( \beta \).

  4. 4.

    The nature of anisotropic force  The behavior of the anisotropic parameter \( \Delta =p_{t}-p_{r} \) against the radial coordinate, r is exhibit in Fig. 5. Indeed, this result shows that the anisotropic force is repulsive in type and at the origin of the compact strange spherical object the anisotropic parameter vanishes, which is expected.

  5. 5.

    The positivity of the trace of the energy tensor, \( \rho -p_{r}-2p_{t} \)  For a compact stellar spherical structure of anisotropic fluid, the trace of the energy tensor ought be positive, as the condition suggested by Bondi [135]. To verify this condition for our specific system, we plot the trace of the energy tensor \( \rho -p_{r}-2p_{t} \) as a function of radial coordinate \( r \) which is shown graphically in Fig. 6. So from this figure, it is evident that our stellar model satisfies the condition suggested by Bondi [135].

  6. 6.

    Stability of anisotropic compact sphere via adiabatic index  As specified by Heintzmann and Hillebrandt [86], an anisotropic compact strange star model is stable if the adiabatic index \( \Gamma \), is strictly greater than \( 4/3 \) everywhere within the compact strange star where the relativistic adiabatic index \( \Gamma \) is given by

    $$\begin{aligned} \Gamma= & {} \left\{ \Bigg ( H \left( 3a+a^{2}r^{2} \right) ^{ \beta + \alpha }+ \left( 8 \pi \left( 1+ar^{2} \right) ^{2} \right) ^{ \alpha -1} \right. \nonumber \\&\times \left( 3a+a^{2}r^{2} \right) ^{ \beta +1}-K \left( 8 \pi \left( 1+ar^{2} \right) ^{2} \right) ^{ \alpha + \beta }\Bigg )\nonumber \\&\left. \times \Bigg (H \left( 3a+a^{2}r^{2} \right) ^{ \alpha + \beta }-K \left( 8 \pi \left( 1+ar^{2} \right) ^{2} \right) ^{ \alpha + \beta }\Bigg )^{-1} \right\} \nonumber \\&\times \left\{ \alpha H \left( \frac{3a+a^{2}r^{2}}{8 \pi \left( 1+ar^{2} \right) ^{2}} \right) ^{2 \beta + \alpha -1}\right. \nonumber \\&\left. + \beta K \left( \frac{3a+a^{2}r^{2}}{8 \pi \left( 1+ar^{2} \right) ^{2}} \right) ^{ \beta -1} \right\} .~~~~~ \end{aligned}$$
    (36)

    We plot the variation of the relativistic adiabatic index, \( \Gamma \), in Fig. 7. From this figure, we can see that the relativistic adiabatic index, \( \Gamma \), is strictly greater than \( 4/3 \) everywhere inside the anisotropic strange star, which implies according to Heintzmann and Hillebrandt [86] that our specific anisotropic compact strange star model is well-stable.

  7. 7.

    Stability of anisotropic compact sphere via the cracking method  Our proposed specific model of an anisotropic compact strange spherical object will be physically available if the square of radial ( \( v_{sr}^{2}=\frac{dp_{r}}{d \rho } \) ) and transverse ( \( v_{st}^{2}=\frac{dp_{t}}{d \rho } \) ) speeds of sound must fulfill the inequalities \( 0 \le v_{sr}^{2} \le 1 \) and \( 0 \le v_{st}^{2} \le 1 \) all over inside the anisotropic compact strange spherical object [136, 137], which is known as a causality condition.

    Due to the complexity of the function of transverse pressure \( p_{t} \), we illustrate the above causality condition using a graphical representation. From Fig. 8 we can obviously see that the tangential and radial velocities of the sound are always less than 1 and thus fulfill the causality condition : the velocity of sound is less than the velocity of light everywhere inside the specific compact stellar object. Moreover, according to the inequality, \( v_{sr}^{2}-v_{st}^{2}<1 \), proposed by Andréasson [138], which involves that the difference between radial and tangential velocity must be less than \( 1 \). For this purpose, Fig. 8 shows that our specific model is satisfied with this condition everywhere within the stellar configuration.

  8. 8.

    Energy conditions  We will check if our particular model of the anisotropic strange compact sphere meets all the requirements of the energy conditions. It is well-defined that for a physically agreeable system, the following energy conditions must be respected everywhere within the compact anisotropic fluid spherical object:

    $$\begin{aligned}&(\textit{i})~~~Null~~Energy~~Condition~~~~(NEC) : \nonumber \\&\quad \rho \ge 0,~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
    (37)
    $$\begin{aligned}&(\textit{ii})~~~Weak~~Energy~~Condition~~~~(WEC) :\nonumber \\&\quad \rho +p_{r} \ge 0, \rho +p_{t} \ge 0,~~~~~~~~~~~ \end{aligned}$$
    (38)
    $$\begin{aligned}&(\textit{iii})~~~Strong~~Energy~~Condition~~~~(SEC) : \nonumber \\&\quad \rho +p_{r}+2p_{t} \ge 0. \end{aligned}$$
    (39)

    Figure 10 shows that our specific anisotropic compact strange spherical object developed here validated the availability of the energy conditions characterized by the inequalities (37)–(39) which are fulfilled everywhere within the anisotropic compact strange spherical object.

  9. 9.

    Stable equilibrium condition via Tolman–Oppenheimer–Volkoff equation  The Tolman–Oppenheimer–Volkoff (TOV) equation represents the inner configuration of the anisotropic compact sphere which is a link between two physical quantities, the energy density and the pressure radial. We use the TOV equation, we want to determine if our current system is in a state of stable equilibrium under under the three different forces, namely the anisotropic \( F_{a} \), hydrostatic \( F_{h} \) and gravitational \( F_{g} \) forces. The generalized TOV equation with the help of the Tolman–Whittaker formula can be composed as follows [15, 16]:

    $$\begin{aligned}&-\frac{M_{G}}{r^{2}} \left( \rho +p_{r} \right) \exp \left( \frac{ \lambda - \nu }{2} \right) _{~}-\frac{dp_{r}}{dr}+\frac{2}{r} \left( p_{t}-p_{r} \right) =0,\nonumber \\ \end{aligned}$$
    (40)

    where \( M_{G}=\frac{1}{2}r^{2}\exp \left( \frac{ \nu - \lambda }{2} \right) \frac{d \nu }{dr} \) is the effective gravitational mass inside an anisotropic fluid sphere of radius \( r \). Therefore, this last Eq. (40) involves that the sum of the three various forces mentioned above is zero :

    $$\begin{aligned}&F_{a}+F_{h}+F_{g}=0, \end{aligned}$$
    (41)

    where the explicit expressions of these three different forces are written as

    $$\begin{aligned} F_{a}= & {} \frac{2}{~r} \left( p_{t}-p_{r} \right) , \end{aligned}$$
    (42)
    $$\begin{aligned} F_{h}= & {} -\frac{dp_{r}}{dr}, \end{aligned}$$
    (43)
    $$\begin{aligned} F_{g}= & {} -\frac{1}{~2} \left( \rho +p_{r} \right) \frac{d \nu }{~dr}. \end{aligned}$$
    (44)

    To simplify these Eqs. (42)–(43) mentioned above, we have traced the profiles of \( F_{a} \), \( F_{h} \) and \( F_{g} \) which are shown in Fig. 11. This figure displays that our suggested stellar system is in static equilibrium, which is feasible under the three mentioned forces.

Fig. 1
figure 1

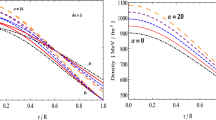
Behaviour of the matter density \( \rho \) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 2
figure 2

Behaviour of the radial pressure \( p_{r} \) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 3
figure 3

Behaviour of the gradient of energy density \( \left( \frac{d \rho }{dr} \right) \) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 4
figure 4

Behaviour of the gradient of radial pressure \( \left( \frac{dp_{r}}{dr} \right) \) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given Table 1

Full size image
Fig. 5
figure 5

Behaviour of the anisotropic parameter \( \left( \Delta =p_{t}-p_{r} \right) \) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 6
figure 6

Behaviour of the trace of the energy tensor \( \left( \rho -p_{r}-2p_{t} \right) \) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 7
figure 7

Behaviour of the index adiabatic \( \left( \Gamma \right) \) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 8
figure 8

Behaviour of the square of radial and transverse speeds of sound against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 9
figure 9

Behaviour of the difference between the square of radial and transverse speeds of sound against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 10
figure 10

Behaviour of the energy conditions (\(\rho \)), (\(\rho +p_{r}\)), (\(\rho +p_{t}\)), (\(\rho +p_{r}+2p_{t}\)) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 11
figure 11

Behaviour of the three different forces ( \( F_{a} \) , \( F_{h} \) and \( F_{g} \) ) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 12
figure 12

Behaviour of the gravitational mass against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 13
figure 13

Behaviour of the compactness parameter ( \( u \left( r \right) \) ) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image
Fig. 14
figure 14

Behaviour of the gravitational red-shift ( \( z_{s} \) ) against the radial coordinate \( r \) of our stellar model for strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327 for the parameters given in Table 1

Full size image

6 Gravitational mass, compactness parameter and gravitational red-shift

The gravitational mass of the strange star can be examined by the following formula:

$$\begin{aligned}&m \left( r \right) =4 \pi \int _{0}^{r} \rho \left( \epsilon \right) \epsilon ^{2}d \epsilon =\frac{a}{2} \left( \frac{r^{3}}{1+ar^{2}} \right) . \end{aligned}$$
(45)

We plot the behavior of the mass function \( m \left( r \right) \) in Fig. 12. From this figure, it is evident that the gravitational mass is monotonically increasing with the radial coordinate \( r \) and positive within the stellar system, as well as the regularity at the center of the spherical object, is verified.

It is well known that the mass-to-radius ratio recognized as the compactness parameter, for any physically strange star model must be satisfied to the maximum allowed as predicted by Buchdahl [139], which has shown that for a (3+1)-dimensional fluid spherical object \( \frac{M}{R}<\frac{4}{9} \approx 0.4444 \) . For the above gravitational mass formula, the compactness parameter of the strange spherical object for the proposed stellar model can be written as

$$\begin{aligned}&u \left( r \right) =\frac{m \left( r \right) }{r}=\frac{a}{2} \left( \frac{r^{2}}{1+ar^{2}} \right) . \end{aligned}$$
(46)

Consequently, the gravitational red-shift of the surface corresponding to the mentioned compactness parameter \( u \left( r \right) \) can be obtained as

$$\begin{aligned}&z_{s}=\frac{1-\root \of {1-2u \left( r \right) }}{\root \of {1-2u \left( r \right) }}=\root \of {1+ar^{2}}-1. \end{aligned}$$
(47)
Table 2 Some physical parameters calculated for radii and mass for some strange star candidates
Full size table

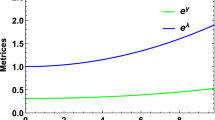
The behavior of the compactness parameter and the gravitational red-shift are illustrated in Figs. 13 and 14. From these two figures, we can see that the \( u \left( r \right) \) and \( z_{s} \) are monotonic increasing functions respectively with respect to the radial coordinate \( r \) . To see the maximum acceptable compactness parameter, we have obtained the value of \( \frac{M}{R}=0.2886 \) from our stellar model, which fulfills the Buchdahl condition. This involves that the mass-to-radius ratio of any spherical object cannot be arbitrarily massive. Moreover, the surface red-shift attains the maximum at the boundary for our stellar model with corresponding value \( z_{s}=0.5380 \) .

According to observational tests, the fluid pressure of the highly compact celestial bodies like low and high mass x-ray binaries: Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52, X-ray buster: 4U 1820-30, millisecond pulsars: PSR J1903+327, SAXJ1804.4-3658, etc. becomes anisotropy in nature which means the pressure can be rotten into two components such that one is radial pressure (\(p_r\)) and the other is transverse pressure (\(p_t\)). Now, \(\Delta \) is known as the anisotropic parameter. The anisotropy may arise for the different cases such as the existence of solid core, in presence of type P superfluid, phase transition, rotation, magnetic field, mixture of two fluids, and existence of external field. Generally, strange quark matter contains u, d, and s quarks. There are two ways to classify the formation of strange matter [141]. One way is the transformation of the quark hadron phase in the early universe and the other way is the reformation of neutron stars to strange matter at ultrahigh densities. A strange star is composed of the strange matter. Again the strange star can be classified into two types: Type I strange star with \(M/R> 0.3\) and Type II strange star with \(0.2< M/R < 0.3\). Depending on mass, radius, and energy density, the strange star is distinguished from the neutron star . From our stellar model, we have shown that the numerical values of the mass-to-radius ratio have been obtained for the compact strange stars as \(0.2819< M/R < 0.2886\) (see Table 2). In this regard, it is worth mentioning from the mass-to-radius ratio that our stellar model is compatible with the Type II strange star (\(0.2< M/R < 0.3\)). Hence it can be concluded that our obtained Chaplygin star behaves as a strange star.

7 Concluding remarks

In this paper, we provide a general system for modeling anisotropic relativistic compact stellar objects in which the interior matter distribution obeys a new version of Chaplygin fluid EoS of the form \(p_r=H\rho ^{\alpha }-K\rho ^{-\beta }\).

The field equations are solved by using an easy and physically conceivable form for the gravitational potential \(Z(x)\), and under reasonable limit condition the interior line element (1) has been incorporated easily at the boundary of spherical objects (\(r = R\)), to an outside Schwarzschild line element whose mass is equivalent to \(m ( r = R ) = M\) [140]. As a result, the obtained set of solutions is related to the physical properties of some compact stellar spherical bodies, which incorporate strange spherical objects. It is seen that the model is suitable in conjunction with several physical highlights, which are very interesting and worthwhile as suggested by other researchers [90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120] during the system of general theory of relativity. We have found a set of physically viable and free from singularity solutions of the new generalized class representing various attributes of the anisotropic relativistic model. Moreover, we have considered the physical behavior of five compact strange astrophysical objects: two X-ray binaries, namely Cyg X-2 and Vela X-1 studied by Rawls et al. [131], two low mass-X-ray binaries, namely, 4U 1608-52 and 4U 1636-536 performed by G\(\ddot{u}\)ver et al. [132]; Kaaret et al. [133] and one binary millisecond pulsars, namely PSR J1903 327 performed by Freire et al. [134], by showing the anisotropic effects presented by taking into account a spherically symmetric inside space-time metric in the arena of general theory of relativity.

As an exhaustive discussion we might want to advance here is that various confirmation schemes of the model have been made and we would want to highlight some of the eminent characteristics of the current systems which are described below.

It has been seen that the behavior of physical amounts of the present astrophysical system, viz, the energy density \( \rho \), the radial \( p_r \) and tangential \( p_t \) pressures respectively, against the radial coordinate \( r \) for the strange astrophysical stars Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327, are totally limited and positive amounts inside the astrophysical structure, which is described in Figs. 1 and 2. So from these figures, we confirm that our astrophysical model is totally free from any physical and geometrical singularity. In addition, the behaviors of the gradient of energy density \( \left( \frac{d\rho }{dr} \right) \) and radial pressure \( \left( \frac{dp_{r}}{dr} \right) \) are presented in Figs. 3 and 4, for specific choice of parameters. It shows that the energy density \( \left( \rho \right) \) and radial pressure \( \left( p_{r}\right) \) are monotonous decreasing functions from the core to surface of the compact stellar object. Figure 5 featured the behavior of anisotropy against the radial coordinate \( r \). From this figure, we observe that the anisotropy of the stellar model increases as the radius increases which is taking a minimum value at the core and maximum at the boundary (surface). Consequentely, we have checked the positivity of the trace of the energy tensor, \( \left( \rho -p_{r}-2p_{t}\right) \) of our specific model versus the radial coordinate \(r\) showing graphically in Fig. 6, which confirm that our model, fulfills the condition suggested by Bondi [135].

To examine the stability of the framework we have analyzed both the Herrera cracking condition and the causality condition. Figure 7 exhibits that for our stellar model the relativistic adiabatic index \(\Gamma \) is greater than the critical limit \(4/3\) and are also increasing monotonically outward, which affirms that our stellar model is totally steady according to the suggestion of Heintzmann and Hillebrandt [86]. Once more, Figs. 8 and 9 displays that for all the cases the inequalities \( 0 \le v_{sr}^{2} \le 1 \), \( 0 \le v_{st}^{2} \le 1 \) and \( v_{sr}^{2}-v_{st}^{2}<1 \), proposed by Herrera [136], Abreu et al. [137] and Andréasson [138] are validate at the same time and hence affirms stability of the astrophysical model in terms of the velocity of sound of the stellar system. The energy conditions viz., The NEC, WEC, and SEC are represented in Fig. 10 which includes that as our stellar model is compatible with all the inequalities at the same time, it affirms that the accomplished solution is physically reasonable. We note from Fig. 11 that the gravitational force \( \left( F_{g}\right) \) in the structure corresponds to the joint effect of hydrostatic \( \left( F_{h}\right) \) and anisotropic \( \left( F_{a}\right) \) force and hence the solution fulfills the generalized TOV equation (40) which is in static equilibrium under the three mentioned forces. We have highlighted in Figs. 12, 13 and 14, respectively, the profiles of gravitational mass, compactness parameter and gravitational red-shift versus the radial coordinate \(r\). From our astrophysical system, we find that \(M/R < 4/9\) for the five specific strange spherical object candidates chosen i.e. Cyg X-2, 4U 1636-536, Vela X-1, 4U 1608-52 and PSR J1903+327. In this regard, Buchdahl’s condition [139] holds useful for our astrophysical model. Moreover, since the radius \(r\) tends to zero, we find the gravitational mass \(m(r)\) also tends to zero, which shows that the gravitational mass is regular in the core of the compact stellar spherical configuration for all the values of the parameter chosen in Table 1. The effect over the gravitational red-shift \(Z_s\) for different strange spherical object candidates due to the existence of anisotropies in the framework is exhibited their values in Table 2. The acquired values got here are in agreement with the normal values for compact stellar spherical structures including uncharged anisotropic matter distribution. Furthermore, Fig. 13 displays the pattern of the gravitational red-shift interior the spherical object. As should be obvious it can not be subjective huge due to the value of mass-to-radius ratio (\(M/R\)) of the spherical systems. At long last, in Table 1 we have showed the possible estimates of the constant parameters \(a\), \(\alpha \), \(\beta \), \(H\) and \(K\) determined for radii and mass for some strange spherical structure candidates. Whereas, Table 2 shows some physical parameters such as the central energy density, surface energy density, and central pressure radial determined for radii and mass for some strange spherical structure candidates are within the range of the data and in total concurrence, as predicted by several authors [87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120, 122].

As a final comment, it very well may be inferred that an analytic solution to the EFEs has been acquired, which meets all the necessities to be a physically and mathematically permissible solution describing to a static, spherically symmetric space-time represented by an anisotropic stress-energy tensor.