1 Introduction

The series of observations for more than last two decades strongly confirm that our universe is currently going through a phase of accelerated expansion [1] preceding a smooth transition from decelerated era in recent past. There is a difference in opinion about the cause of this transition among the cosmologists. One group has preferred modification of the gravity theory while others are in favour of Einstein gravity with introduction of some exotic matter having large −ve pressure (known as dark energy (DE)). Observational evidences show that the cosmic fluid consists of 69% DE, 26% dark matter (DM) and rest is in the form of baryonic matter and radiation [2]. Although, the cosmological constant is the simplest choice for the DE candidate and is observationally most favourable one, still cosmologists search for dynamical DE models due to two severe drawbacks namely cosmological constant problem and cosmic coincidence problem of cosmological constant [3]. Initially, Cosmologists have chosen the dynamic DE in the form of perfect fluid with variable equation of state parameter of various forms (viz; quintessence, tachyon, phantom [4] and chameleon [5, 6] etc). Subsequently, some complicated fields namely spinors [7], vectors [8], and even higher order spin fields are chosen as DE candidate. A three-form field has been shown in Ref. [9, 10] as a possible DE candidate and the dynamical system analysis of the corresponding cosmological model has been studied in Ref. [11]. It has been shown that the dual of the three form fields is a scalar field and for non-quadratic potential, the kinetic term of the scalar field is non-canonical to have an equivalence with K-inflation model [12]. Further, a non-quadratic dependence on the three-form Faraday term is responsible for self-coupling nature of the scalar field [9]. For non-minimal coupling of the three form, the dual scalar field character of the three-form will no longer hold. There are no observational/experimental evidences for the fundamental scalar particles. In fact, some higher form field are very much likely to be a candidate for DE and from cosmological point of view these field do not violet the cosmological principle. The higher form fields are very common in String theory. Hence, attempts have been made to use a vector field, a one-form field the DE candidate [13,14,15,16]. However, most of the vector field models (also two-form fields) are not stable in nature [17]. However, it is found that three-form field models are very much stable [18, 19]. Hence, it is interesting to consider a three-form field as a candidate for DE. In recent past, it has been shown [19] that a three-form field as a DE candidate provides accelerating universe. The present work deals with dynamical system analysis of the evolution equations of the Cosmological model with three form scalar field as the choice of DE while interacting DM in the form of dust. Although the choice of interaction is purely phenomenological but still the interaction term may resolve the coincidence problem as energy densities of DE and DM are comparable at stable fixed points.

Our present work has lots of differences with earlier works in [11, 20, 21]. In Ref. [11] the autonomous system [19,20,21] is identical to our autonomous system (22–24), but they have determined few critical points and have analyzed only one critical point by center manifold theory. On the other hand, we have determined all possible critical points both for interacting and non-interacting cases. For non-hyperbolic critical points center manifold theory has been used and global stability has been discussed with reference to bifurcation analysis using Poincaré index. In another work [20] the authors have similar autonomous system confined to a finite region. They have also analyzed few critical points from cosmological point of view. Some of our cosmic epochs are identical to them but we have procured other significant cosmic eras. They have not analyzed the critical points using center manifold theory and have not discussed global stability (as we have extensively done in our work), rather they have performed cosmological perturbations. In Ref. [21] the authors have 5D phase space as they have considered baryon and radiation as matter field in addition to interacting DE (three-form field) and DM. They have chosen various form of the interaction term and have analyzed some of the critical points in cosmological context. They have not employed center manifold theory nor have discussed global stability for any critical point. Therefore, present work is rich in dynamical system analysis and have studied various cosmic scenarios with reference to cosmic phase transition using bifurcation analysis [22,23,24].

The paper is organized as follows: Basic equations for interacting 3-form field with DM in the form of dust has been formulated in Sect. 2. In Sect. 3 the above evolution equations are converted into an autonomous system by suitable choice of the dimensionless variables and critical points are determined. Also stability of the non-hyperbolic equilibrium points are discussed by formulating center manifold at the equilibrium points. Finally cosmological implications and conclusions are presented in Sect. 4.

2 Basic equations for three-form field cosmological model

The action of a three-form field \(A_{\mu \nu \rho }\), minimally coupled to gravity is given by [11]

$$\begin{aligned} S_A= & {} -\int d^4x \sqrt{-g}\left[ \frac{1}{2{\kappa }^2}R-\frac{F^2}{48}-V\left( A^2\right) \right] , \end{aligned}$$
(1)

where R is the Ricci scalar and \(V(A^2)\) is the potential of the three-form field \(A_{\mu \nu \rho }\) having field strength tensor

$$\begin{aligned} F_{\mu \nu \rho \sigma }= & {} 4\bigtriangledown _{_[\mu }A_{\nu \rho \sigma ]} \end{aligned}$$
(2)

By notation, the square bracket indicates anti-symmetrization of the indices involved and \(A^2=A^{\mu \nu \rho }A_{\mu \nu \rho }\). Now, variation of the above action with respect to the metric tensor gives the usual Einstein field equations: \(G_{\mu \nu }=\kappa ^2T{\mu \nu }\) with

$$\begin{aligned} T_{\mu \nu }= & {} \frac{1}{6}F_{\mu \alpha \beta \gamma }F^{\alpha \beta \gamma }_{\nu }+6V'(A^2)A_{\mu \alpha \beta }A^{\alpha \beta }_{\nu }-g_{\mu \nu }\nonumber \\&\times \left( \frac{1}{48}F_{\alpha \beta \gamma \rho }F^{\alpha \beta \gamma \rho }+V\left( A^2\right) \right) \end{aligned}$$
(3)

while the equation of motion of the three form field is obtained by varying the action (1) with respect to \(A^{\mu \gamma \rho }\) as

$$\begin{aligned} \bigtriangledown ^{\alpha }F_{\alpha \mu \gamma \rho }= & {} 12 V'(A^2)A_{\mu \gamma \rho } \end{aligned}$$
(4)

with \(V'(A^2)=\frac{dV}{dA^2}\). As in the present work, we are considering homogeneous and isotropic FLRW space-time geometry, so the three-form field depends only on time. Hence, the evolution equation (4) gives \(A_{0\mu \nu }=0\) i.e; a zero component of the three-form field is non-dynamical and spatial components are given by

$$\begin{aligned} A_{ijk}= & {} a^3(t)\epsilon _{ijk}X(t). \end{aligned}$$
(5)

The co-moving field X is related to the three field as \(A^2=6X^2\) and the evolution equation (4) simplifies to

$$\begin{aligned} {\ddot{X}}= & {} -3H{\dot{X}}-3{\dot{H}}X-V,_{X} \end{aligned}$$
(6)

where an over dot indicates differentiation with respect to the cosmic time ’t’ and a comma in the suffix denotes differentiation with respect to the corresponding variable. Further, the energy–density and thermodynamic pressure of the effective perfect fluid corresponding to the energy–momentum tensor (3) of the three-form field are given by

$$\begin{aligned}&\rho _{A}=-T^{0}_{0}=\frac{1}{2}\left( {\dot{X}}+3HX\right) ^2+V(X), \end{aligned}$$
(7)
$$\begin{aligned}&p_A=T^i_i=-\frac{1}{2}\left( {\dot{X}}+3HX\right) ^2-V(X)+XV,_X \end{aligned}$$
(8)

with equation of state

$$\begin{aligned} \omega _A=\frac{p_A}{\rho _A}=-1+\frac{XV,_X}{\rho _A}. \end{aligned}$$
(9)

Now, in the context of series of recent observations the above three-form field (chosen as dark energy), interacting with dark matter (in the form of dust) is chosen as the matter context in the universe. So, the explicit form of the Einstein field equations in the background of homogeneous and isotropic space-time model are

$$\begin{aligned} 3H^2= & {} \kappa ^2(\rho _A+\rho _{DM}), \end{aligned}$$
(10)
$$\begin{aligned} 2{\dot{H}}= & {} -\kappa ^2\left[ (\rho _A+p_A)+\rho _{DM}\right] \end{aligned}$$
(11)

with energy conservation equations

$$\begin{aligned} {\dot{\rho }}_{DM}+3H\rho _{DM}= & {} Q, \end{aligned}$$
(12)
$$\begin{aligned} \dot{\rho _A}+3H(\rho _A+p_A)= & {} -Q. \end{aligned}$$
(13)

Here the two matter components are assumed to be interacting and Q represents arbitrary coupling. As a result of this coupling between the matter fields the evolution equation (6) modifies to

$$\begin{aligned} {\ddot{X}}+3H{\dot{X}}+3{\dot{H}}X+\frac{dV}{dX}= & {} -\frac{Q}{{\dot{X}}+3HX}. \end{aligned}$$
(14)

3 Autonomous system, critical points and stability analysis

In the present work we shall consider interacting three-form field with exponential potential as

$$\begin{aligned} V(X)=V_0 e^{-\mu X}, \end{aligned}$$
(15)

where \( \mu \) is a dimensionless parameter and \( V_0 > 0 \). This type of potential is termed as runaway potential, i.e., \(\underset{X \rightarrow \infty }{\lim } V(X) = 0\) and \( \frac{dV}{dX}<0~\forall ~X\). The runaway potential will correspond to well-behaved evolution of the background [21].

Using the dimensionless variables (u, v, w, s) as defined in [11], viz;

$$\begin{aligned} u:= & {} \frac{1}{\sqrt{6}H}({\dot{X}}+3HX), \end{aligned}$$
(16)
$$\begin{aligned} v:= & {} \frac{\sqrt{V}}{\sqrt{3}H}, \end{aligned}$$
(17)
$$\begin{aligned} w:= & {} \frac{2}{\pi }\tan ^{-1}\frac{3X}{\sqrt{6}}, \end{aligned}$$
(18)
$$\begin{aligned} s:= & {} \frac{\sqrt{\rho _{DM}}}{\sqrt{3}H}. \end{aligned}$$
(19)

The expression of equation of state parameter \(\omega _X=p_X/\rho _X\) and the total equations of state parameters \(\omega _{tot}\) can be written as [11],

$$\begin{aligned} \omega _{X}= & {} -1+\frac{XV,_X}{\rho _X}=-1-\frac{1}{u^2+v^2}\sqrt{\frac{2}{3}}v^2\mu ~ \tan \left[ \frac{\pi w}{2}\right] ,\nonumber \\ \end{aligned}$$
(20)
$$\begin{aligned} \omega _{tot}= & {} \frac{p_{tot}}{\rho _{tot}}=\frac{p_X}{\rho _X+\rho _{DM}}=-u^2-\frac{1}{3}v^2\nonumber \\&\left( 3+\sqrt{6}\mu ~ \tan \left[ \frac{\pi w}{2}\right] \right) . \end{aligned}$$
(21)

Thus the evolution equations in Sect. 2 can be converted to an autonomous system as follows [11]

$$\begin{aligned} u'= & {} \frac{3}{2}u(1-u^2-v^2)+\sqrt{\frac{3}{2}}{v^2} \mu \left( 1-u\tan \left[ \frac{\pi w}{2}\right] \right) \nonumber \\&-\alpha \frac{\left( 1-u^2-v^2\right) }{2u} \end{aligned}$$
(22)
$$\begin{aligned} v'= & {} \frac{3}{2}v(1-u^2-v^2)-\sqrt{\frac{3}{2}} v \mu \left( u+(-1+v^2)\tan \left[ \frac{\pi w}{2}\right] \right) \end{aligned}$$
(23)
$$\begin{aligned} w'= & {} \frac{6}{\pi }\cos ^2\left[ \frac{\pi w}{2}\right] \left( u-\tan \left[ \frac{\pi w}{2}\right] \right) \end{aligned}$$
(24)

where the interaction Q is chosen as \(Q=\alpha \rho _{DM} H\) [21] and dash over a variable denotes differentiation with respect to \( N=\ln ~a \). Hence, the first Friedmann equation gives constraint on the variables as

$$\begin{aligned} u^2+v^2+s^2=1 \end{aligned}$$
(25)

(as s is not independent so the dynamical system is of 3D nature). The phase space is confined in a half cylinder of height 2 where \(-1\leqslant u\leqslant 1\), \(0\leqslant v\leqslant 1\), \(-1\leqslant s\leqslant 1\) and \(-1\leqslant w\leqslant 1\). Some non-hyperbolic critical points are already analyzed in [11]. In the present work, on non-hyperbolic critical points are studied with a view to analyze bifurcation and Poincaré index. Cosmological evolutions are also examined near these critical points.

3.1 Non interacting model: \(\alpha =0\)

Due to \(\alpha =0\) the above autonomous system (22–24) simplifies to

$$\begin{aligned} u'= & {} \frac{3}{2}u(1-u^2-v^2)+\sqrt{\frac{3}{2}} v^2 \mu \left( 1-u \tan \left[ \frac{\pi w}{2}\right] \right) ,\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned} v'= & {} \frac{3}{2}v(1-u^2-v^2)-\sqrt{\frac{3}{2}}v\mu \nonumber \\&\left( u+(-1+v^2)\tan \left[ \frac{\pi w}{2}\right] \right) , \end{aligned}$$
(27)
$$\begin{aligned} w'= & {} \frac{6}{\pi }\cos ^2\left[ \frac{\pi w}{2}\right] \left( u-\tan \left[ \frac{\pi w}{2}\right] \right) . \end{aligned}$$
(28)

As the critical points of the above system are enclosed by a half cylinder, so the only critical points are

$$\begin{aligned} P_1\left( 1,0,\frac{1}{2}\right) , P_2\left( -1,0,-\frac{1}{2}\right) ~\text {and}~ P_3(0,0,0) \end{aligned}$$

and these critical points are same as in Ref. [11]. But the authors have analyzed only one critical point by using center manifold theory. But in this context we analyze the stability of all critical points by center manifold theory (for non-hyperbolic case) and Hartman–Grobman theorem (for hyperbolic case) and also discuss global stability with reference to bifurcation analysis using Poincaré index. The cosmological parameters, eigenvalues and the nature of critical points are presented in Table 1.

Table 1 The cosmological parameters, eigenvalues (\( \lambda _1 \), \( \lambda _2 \), \( \lambda _3 \)) and the nature of critical points for this non-interacting model
Full size table

All the three critical points of the above autonomous system for non-interacting case has \(v=0\) which corresponds to vanishing of the potential (as well as vanishing of the potential slope for the present choice of V(X) ). Thus the three-form field behaves as a cosmological constant. Also for the first two critical points, i.e., \( P_1 \) and \( P_2 \) there is no DM so the cosmological scenario purely corresponds to de Sitter phase [20, 21]. For the third critical point \( P_3 \), the evolution corresponds to non-interacting three form field (behaves as cosmological constant) with dark matter (DM) in the form of dust. Here DM dominates (three-form field DE is sub-dominant) the evolution and the resulting cosmic scenario represents the matter dominated era of evolution. This type of critical point is also obtained in [21] (see critical point (a) in Table 1 of Ref. [21]).

Stability analysis

We now investigate the stability of above non-hyperbolic critical points corresponding to this non interacting model. Most of the cases stability of non-hyperbolic critical points can be determined by center manifold (CM) theory. For this we first perform coordinate transformations so that the critical points moves to the origin.

3.1.1 Critical point \(P_1\)

First we shift the critical point \(P_1\) to the origin by using the coordinate transformation \(u\rightarrow U+1\), \(v\rightarrow V\), \(w\rightarrow W+\frac{1}{2}\), then the system of equations (26–28) changes to

$$\begin{aligned} U'= & {} -3U-\frac{9}{2}U^2-\frac{3}{2}U^3-\frac{3}{2} V^2-\frac{3}{2}UV^2-\sqrt{\frac{3}{2}}\mu UV^2\nonumber \\&-\sqrt{\frac{3}{2}}\pi \mu V^2 W + \text {higher~~order~~ terms}, \end{aligned}$$
(29)
$$\begin{aligned} V'= & {} -\left( 3+\sqrt{\frac{3}{2}}\mu \right) UV-\frac{3}{2}U^2V-\left( \frac{3}{2}+\sqrt{\frac{3}{2}}\mu \right) V^3\nonumber \\&+\sqrt{\frac{3}{2}}\pi \mu VW\nonumber \\&+\frac{\sqrt{3}}{2\sqrt{2}}\pi ^2 \mu V W^2 + \text {higher~order~terms}, \end{aligned}$$
(30)
$$\begin{aligned} W'= & {} -3W+\frac{3}{\pi } U-3UW +\left( 3-\frac{3\pi }{2}\right) W^2+\frac{\pi ^2}{2} W^3\nonumber \\&+ \text {higher~order~terms}. \end{aligned}$$
(31)

The Jacobian matrix at the origin for this autonomous system can be written as

$$\begin{aligned} J(P_1)=\begin{bmatrix} -3 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ \frac{3}{\pi } &{} 0 &{} -3\\ \end{bmatrix} \end{aligned}$$
(32)

So, the eigenvalues of the above matrix are \(0, -3, -3\) and \([0,1,0]^T\) and \([0,0,1]^T\) are the eigenvectors corresponding to the eigenvalue 0 and \(-3\) respectively. As Hartman–Grobman Theorem can not be used to analyze the non-hyperbolic critical point, we shall use center manifold theory (CMT).

So, by center manifold theory there exist a continuously differentiable function h:\({\mathbb {R}}\) \(\rightarrow \) \({\mathbb {R}}^2\) such that

$$\begin{aligned} h(V)=\begin{bmatrix} U \\ W \end{bmatrix} =\begin{bmatrix} a_1V^2+a_2V^3 + {\mathcal {O}}\left( V^4\right) \\ b_1V^2+b_2V^3 + {\mathcal {O}}\left( V^4\right) \end{bmatrix} \end{aligned}$$
(33)

Differentiating both side with respect to N yields

$$\begin{aligned} U'= & {} (2a_1V+3a_2V^2)V'+\text {higher~order~terms}, \end{aligned}$$
(34)
$$\begin{aligned} W'= & {} (2b_1V+3b_2V^2)V'+\text {higher~order~terms} \end{aligned}$$
(35)

Comparing coefficients corresponding to power of V we get, \(a_1=-\frac{1}{2}\) and \(a_2=0\); \(b_1=-\frac{1}{2\pi }\) and \(b_2=0\), i.e, the expression of center manifold can be written as

$$\begin{aligned} U= & {} -\frac{1}{2} V^2 + {\mathcal {O}}\left( V^4\right) , \end{aligned}$$
(36)
$$\begin{aligned} W= & {} -\frac{1}{2\pi } V^2 + {\mathcal {O}}\left( V^4\right) . \end{aligned}$$
(37)

The flow on the CM near the origin is determined by :

$$\begin{aligned} \frac{dV}{dN}= & {} -\sqrt{\frac{3}{2}}\mu V^3 + {\mathcal {O}}\left( V^4\right) . \end{aligned}$$
(38)

Here the stability of the vector field depends on the sign of \(\mu \). If \(\mu >0 \) then \(V' <0\) for \(V > 0\) and \(V' >0\) for \(V < 0\). So, for \(\mu >0\) the origin is a stable node. The vector field in UV-plane is shown in Fig. 1 and the vector field near the origin in WV-plane is also same as. If \(\mu < 0\) then \(V' >0\) for \(V > 0\) and \(V' <0\) for \(V < 0\). So, for \(\mu <0\) the origin is a saddle node, i.e; unstable in nature. The vector field in UV-plane near the origin is shown as in Fig. 2 and the vector-+-+-+-+- field near the origin in WV-plane is also same as Fig. 2.

Fig. 1
figure 1

Vector field near the origin for the critical point \(P_1\) in UV-plane (\(\mu >0\))

Full size image
Fig. 2
figure 2

Vector field near the origin for the critical point \(P_1\) in UV-plane (\(\mu <0\))

Full size image

If \(\mu =0\), the expression of center manifold is same as of Eqs. (36) and (37) and the flow on the center manifold is determined by

$$\begin{aligned} \frac{dV}{dN}= & {} -\frac{3}{8}V^5 +{\mathcal {O}}\left( V^6\right) . \end{aligned}$$
(39)

So the origin is a stable node and the flow near the origin is same as for \(\mu >0\) case (Fig. 1).

3.1.2 Critical point \(P_2\)

First we shift the critical point \(P_2\) to the origin by using the coordinate transformation \(u\rightarrow U-1\),\(v\rightarrow V\),\(w\rightarrow W-\frac{1}{2}\). The calculation change the system of equations (26–28) due to this coordinate transformation is shown in Appendix A.

The Jacobian matrix for this autonomous system is same as \(J(P_1)\). So the set of eigenvalues and the eigenvectors corresponding to each eigenvalue of the Jacobian matrix are also same. So, by center manifold theory there exist a continuously differentiable function \(h:{\mathbb {R}}\) \(\rightarrow \) \({\mathbb {R}}^2\) such that

$$\begin{aligned} h(V)=\begin{bmatrix} U \\ W \\ \end{bmatrix} =\begin{bmatrix} a_1V^2+a_2V^3 + {\mathcal {O}}\left( V^4\right) \\ b_1V^2+b_2V^3 +{\mathcal {O}}\left( V^4\right) \\ \end{bmatrix} \end{aligned}$$
(40)

Differentiating both side with respect to N yields

$$\begin{aligned} U'= & {} (2a_1V+3a_2V^2)V'+\text {higher~order~terms}, \end{aligned}$$
(41)
$$\begin{aligned} W'= & {} (2b_1V+3b_2V^2)V'+\text {higher~order~terms}. \end{aligned}$$
(42)

Comparing coefficients corresponding to different power of V, we have \(a_1=\frac{1}{2}\) and \(a_2=0\), \(b_1=\frac{1}{2\pi }\) and \(b_2=0\). Then the center manifold is given by

$$\begin{aligned} U= & {} \frac{1}{2} V^2 + {\mathcal {O}}\left( V^3\right) , \end{aligned}$$
(43)
$$\begin{aligned} W= & {} \frac{1}{2\pi } V^2 + {\mathcal {O}}\left( V^3\right) . \end{aligned}$$
(44)

The flow on the CM near the origin is determined by :

$$\begin{aligned} V'= & {} \sqrt{\frac{3}{2}}\mu V^3 + {\mathcal {O}}\left( V^4\right) . \end{aligned}$$
(45)
Fig. 3
figure 3

Vector field near the origin in UV-plane for the critical point \(P_2\). L.H.S. figure is for (\(\mu >0\)) and R.H.S. figure is for (\(\mu <0\))

Full size image

Here the stability of the vector field depends on the sign of \(\mu \). If \(\mu >0\) then the origin is a saddle node,i.e., unstable in nature and the vector field near the origin is shown as (Fig. 3a) and the flow on the center manifold in the WV-plane is also same as in (Fig. 3a). If \(\mu <0\) then the origin is a stable node and the vector field near the origin is shown as in (Fig. 3b) and the flow on the CM in WV-plane is also same as (Fig. 3b). If \(\mu =0\) then the center manifold is same as of Eqs. (43) and (44) and the flow on the center manifold is same as of Eq. (39), that is., the plot of the vector field near the origin is same as for \(\mu <0\) case (Fig. 3b).

3.1.3 Critical point \(P_3\)

The Jacobian matrix at \(P_3\) for the autonomous system (26–28) can be put as

$$\begin{aligned} J(P_3)=\begin{bmatrix} \frac{3}{2} &{} 0 &{} 0\\ 0 &{} \frac{3}{2} &{} 0\\ \frac{6}{\pi } &{} 0 &{} -3\\ \end{bmatrix} \end{aligned}$$
(46)

The eigenvalues of the above Jacobian matrix are \(\frac{3}{2}\), \(\frac{3}{2}\) and \(-3\). \([\frac{3\pi }{4}, 0, 1]^T\) and \([0, 1, 0]^T\) are the eigenvectors corresponding to the eigenvalue \(\frac{3}{2}\) and \([0, 0, 1]^T\) be the eigenvector corresponding to the eigenvalue \(-3\). Since the critical point \( P_3 \) is hyperbolic in nature, so we can analyze the stability of this critical point by Hartman–Grobman theorem. Since two eigenvalues are positive and one is negative, so the origin is a saddle node and the phase portrait near the origin is unstable in nature (Fig. 4).

Fig. 4
figure 4

3 dimensional phase plot for the critical point \(P_3\)

Full size image

Poincaré index and bifurcation analysis

The index of an isolated critical point of a vector field is defined by the winding number of a small counter-clockwise oriented circle with center at that point. If we restrict ourselves on VW-plane, \(P_1\) is stable node in nature for \(\mu \geqslant 0\) and the index of \(P_1|_{VW}\) is 1. On the other hand, \(P_1\) is saddle for \(\mu <0\) and index of \(P_1|_{VW}\) is \(-1\). We get identical nature of \(P_1\) restricted on the UV-plane. On UW-plane, \(P_1\) is stable node for all \(\mu \) and the index is 1. Thus at \(\mu =0\) the system is structurally unstable in nature and bifurcation occurs.

If we restrict ourselves on VW-plane, \(P_2\) is saddle in nature for \(\mu > 0\) and the index of \(P_2|_{VW}\) is \(-1\). On the other hand, \(P_2\) is stable node for \(\mu \leqslant 0\) and index of \(P_2|_{VW}\) is \(-1\). We get identical nature of \(P_2\) restricted on the UV-plane. On UW-plane, \(P_2\) is stable node for all \(\mu \) and the index is 1. Thus at \(\mu =0\) the system is structurally unstable in nature and bifurcation occurs.

The index of \(P_3\) restricted on any plane is independent of \(\mu \). So in this case there is no bifurcation value.

Thus \(P_1\) is stable for \(\mu \geqslant 0\) and the universe undergoes an exponential de-sitter expansion near \(P_1\). For \(\mu <0\), the universe goes away from \(P_1\) as time evolves. On the other hand, \(P_2\) is unstable in nature for \(\mu >0\) and sable for \(\mu \leqslant 0\). So there may be a de-Sitter generic evolution of the universe from the neighborhood of \(P_2\) towards \(P_1\) for \(\mu >0\) and reverses the trajectory for \(\mu <0\). At \(\mu =0\), there may be a non-generic evolution from early time decelerating phase to late time accelerating phase. So a non-generic evolution of the universe may occur when \(\mu \) passes through the bifurcation value.

3.2 Interaction model: \(\alpha \ne 0\)

Now we shall study the stability analysis for interacting model with \(\alpha \) as arbitrary parameter. For this case we consider the primary autonomous system (22–24). The critical points for this autonomous system are:

$$\begin{aligned}&P_4\left( 1,0,\frac{1}{2}\right) ,P_5\left( -1,0,-\frac{1}{2}\right) ,~~\\&\quad P_6\left( \sqrt{\frac{\alpha }{3}},0,\frac{2}{\pi }\cos ^{-1}\left[ \sqrt{\frac{3}{\alpha +3}}\right] \right) ~~\\&\quad \text {and}~ P_{7}\left( -\sqrt{\frac{\alpha }{3}},0,-\frac{2}{\pi }\cos ^{-1}\left[ \sqrt{\frac{3}{\alpha +3}}\right] \right) \end{aligned}$$

There is also a line of critical point: \(P_{l_c}=\left( u_c, \sqrt{\frac{3(1-u_c^2)}{3+\sqrt{6}u_c\mu }},\frac{2}{\pi }\tan ^{-1} u_c\right) \), where \(u_c\in [-1,0) \cup (0,1]\) and which exists only for \(\alpha =3\). The cosmological parameters corresponding to \(P_{l_c}\) are given by \(\omega _X=-\left( \frac{\sqrt{3}+\sqrt{2}\mu u_c}{\sqrt{3}+\sqrt{2}\mu u_c^3}\right) \), \(\omega _{tot}=-1\) and \(q=-1\). Note that except line of critical points \(P_{l_c}\) all critical points are same as in Ref. [11]. But the authors have analyzed only one critical point by using center manifold theory. But in this context we analyze the stability of all critical points by center manifold theory (for non-hyperbolic case) and Hartman–Grobman theorem (for hyperbolic case) for all possible values of the parameters \(\alpha \) and \(\mu \) and also discuss global stability with reference to bifurcation analysis using Poincaré index. The cosmological parameters, eigenvalues and the nature of critical points for this interacting model are presented in Table 2.

Table 2 Table shows the value of cosmological parameters, eigenvalues(\( \lambda _1 \), \(\lambda _2\), \(\lambda _3\)) corresponding to the critical points and the nature of the critical points for this interaction model
Full size table

In the present interacting DE (in the form of three-form field) and DM (in the form of dust) cosmological model, the above autonomous system has four critical points of which top two (i.e., \( P_4 \) and \( P_5 \))are identical in nature to the critical points \( P_1 \) and \( P_2 \) for the non-interacting case. The other two critical points namely \( P_6 \) and \( P_7 \) are quite interesting as they may stand for various cosmological scenarios [20, 21] with different choices of the interaction coupling parameter ’\(\alpha \)’. Note that \(\alpha \) should positive to have these critical points to be real and as a consequence there is a flow of matter from DM to DE (as speculated by recent observations for DE dominance). If \(\alpha \) is very small (i.e., close to zero) then the present model has DM dominance and the cosmic scenario corresponds to matter dominated era while DE (i.e., 3-form field as cosmological constant) will dominate the evolution for \(\alpha >1\) and may be termed as LCDM model. In fact by adjusting \(\alpha \) (\(\alpha \approx 3\)), it is possible to match recent Plank observation \( \omega =-1.028\pm 0.031 \) [25]. Further there is a line of critical points given by \(P_{l_c}\)=\(\left( u_c, \sqrt{\frac{3(1-u_c^2)}{3+\sqrt{6}u_c\mu }},\frac{2}{\pi }\tan ^{-1} u_c\right) \), with \(u_c\in [-1,0)\cup (0,1]\) and it exists only for \( \alpha =3 \). For this line of critical points the three form field behaves as a perfect fluid with equation of state parameter \(\omega _X=-\left( \frac{\sqrt{3}+\sqrt{2}\mu u_c}{\sqrt{3}+\sqrt{2}\mu u_c^3}\right) <-1\), i.e., a phantom fluid. However, interacting with DM, the resulting single fluid behaves as a cosmological constant. So effectively this line of critical points correspond to de Sitter era of evolution.

Stability analysis

We shall discuss the stability analysis of the critical point (\( P_4-P_7 \)) both for \( \alpha =3 \) and \( \alpha \ne 3 \). The stability analysis for the line of critical point \(P_{l_c}\) is very complicated and laborious, so here we will not present the stability of this critical point.

3.2.1 Critical point \(P_4\)

\({\underline{\mathbf{Case }}}\) 1: \(\alpha \)=3

At first we put \( \alpha =3 \) in (22) and then shift the critical point \(P_4\) to the origin by using the coordinate transformation \(u\rightarrow U+1\), \(v\rightarrow V\), \(w\rightarrow W+\frac{1}{2}\). Then the system of equations (22–24) modifies to

$$\begin{aligned} U'= & {} -6U^2-\left( 3+\sqrt{\frac{3}{2}}\mu \right) UV^2-\sqrt{\frac{3}{2}}\pi \mu V^2 W \nonumber \\&+ \text {higher order terms}, \end{aligned}$$
(47)
$$\begin{aligned} V'= & {} -\left( 3+\sqrt{\frac{3}{2}}\mu \right) UV-\frac{3}{2}U^2V-\left( \frac{3}{2}+\sqrt{\frac{3}{2}}\mu \right) V^3\nonumber \\&+\sqrt{\frac{3}{2}}\pi VW\mu \nonumber \\&+\frac{\sqrt{3}}{2\sqrt{2}}\pi ^2 \mu V W^2 + \text {higher order terms}, \end{aligned}$$
(48)
$$\begin{aligned} W'= & {} -3W+\frac{3}{\pi } U - 3UW +\left( -\frac{3\pi }{2}+3\right) W^2+\frac{\pi ^2}{2} W^3\nonumber \\&+ \text {higher order terms}. \end{aligned}$$
(49)

The Jacobian matrix at the origin corresponding to the above autonomous system can be written as

$$\begin{aligned} J(P_4)|_{\alpha =3}=\begin{bmatrix} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ \frac{3}{\pi } &{} 0 &{} -3\\ \end{bmatrix} \end{aligned}$$
(50)

So, the eigenvalues of the above matrix are 0, 0, \(-3\) and \([1,0,\frac{1}{\pi }]^T\) and \([0,1,0]^T\) are the eigenvectors corresponding to the eigenvalue 0 and \([0,0,1]^T\) be the eigenvector corresponding to the eigenvalue \(-3\). By computing the matrix of eigenvectors of the stability matrix of the system in U, V, W we introduce another set of new coordinates

$$\begin{aligned} \begin{bmatrix} U_T\\ V_T \\ W_T \\ \end{bmatrix} =\begin{bmatrix} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ -\frac{1}{\pi } &{} 0 &{}1\\ \end{bmatrix} \begin{bmatrix} U\\ V\\ W\\ \end{bmatrix} \end{aligned}$$
(51)

In these coordinates the system of equations is now in the correct form

$$\begin{aligned} \begin{bmatrix} U_T'\\ V_T'\\ W_T'\\ \end{bmatrix} =\begin{bmatrix} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{}-3\\ \end{bmatrix} \begin{bmatrix} U_T\\ V_T\\ W_T\\ \end{bmatrix} + \begin{bmatrix} \text {non}\\ \text {linear}\\ \text {terms}\\ \end{bmatrix} \end{aligned}$$
(52)

So, by center manifold theory there exist a continuously differentiable function \(h:{\mathbb {R}}^2\) \(\rightarrow \) \({\mathbb {R}}\) such that \(W_T=h(U_T,V_T)=aU_T^2+bU_TV_T+cV_T^2+\text {higher~~order~~ terms},\text {where}~ a,~b,~c~ \in ~{\mathbb {R}}\). We only concern about the non-zero coefficients of the lowest power terms in CMT as we analyze arbitrary small neighborhood of the origin.

Now differentiating both side with respect to N yields

$$\begin{aligned} \frac{dW_T}{dN}=\begin{bmatrix} 2aU_T+bV_T&bU_T+2cV_T \end{bmatrix}\begin{bmatrix} \frac{dU_T}{dN}\\ ~\\ \frac{dV_T}{dN}\\ \end{bmatrix} \end{aligned}$$
(53)

Comparing L.H.S. and R.H.S. of (53) we get, \(a=\frac{3}{2\pi }\), \(b=0\) and \(c=0\) i.e; the expression of center manifold can be written as

$$\begin{aligned} W_T= & {} \frac{3}{2\pi } U_T^2. \end{aligned}$$
(54)

The flow on the CM near the origin is determined by:

$$\begin{aligned} \frac{dU_T}{dN}= & {} -6U_T^2-(3+\sqrt{6}\mu )U_TV_T^2+\text {higher order terms}, \end{aligned}$$
(55)
$$\begin{aligned} \frac{dV_T}{dN}= & {} -3U_TV_T+\left( \sqrt{6}\mu -\frac{3}{2}\right) U_T^2V_T\nonumber \\&+\left( \frac{3}{2}+\sqrt{\frac{3}{2}}\mu \right) V_T^3+\text {higher order terms}. \end{aligned}$$
(56)

Now for analyzing the stability of this critical point, Dividing both sides of (55) by 6 and dividing both sides of (56) by 3. Since we divided both sides of these equation by positive terms, so the direction of the vector field is unchanged. We take \(r^2=U_T^2+V_T^2\), then differentiating both sides with respect to N and using (55) and (56) yields \(r'=-U_Tr\). So \(r'\) depends on the sign of \(U_T\). If \(U_T>0\) then \(r'<0\) and if \(U_T<0\) then \(r'>0\). So, the origin is a saddle node and hence the vector field near the origin is unstable in nature (Fig. 5). Now we try to see the vector field near the origin for \(\mu =-\sqrt{\frac{3}{2}}\) because for \(\mu =-\sqrt{\frac{3}{2}}\) the coefficient of \(V^3\) in Eq. (48) vanishes. The vector field in VW-plane near the origin for \(\mu =-\sqrt{\frac{3}{2}}\) is shown as in Fig. 6.

Fig. 5
figure 5

Projection of the vector field on (\(U_T\) \(W_T\))-plane near the origin for the critical point \(P_4\) (\(\alpha =3\))

Full size image
Fig. 6
figure 6

Vector field near the origin in VW plane for the critical point \(P_4\) \((\alpha =3,\mu =-\sqrt{\frac{3}{2}})\)

Full size image

\({\underline{\mathbf{Case 2: }}}\) \(\alpha \ne \)3

After shifting the critical point \(P_4\) to the origin and by using same transformation as above the autonomous system (22–24) changes to

$$\begin{aligned} U'= & {} \left( -3+\alpha \right) U-\left( \frac{9+\alpha }{2}\right) U^2+\left( \frac{-3+\alpha }{2}\right) U^3\nonumber \\&+\left( \frac{-3+\alpha }{2}\right) V^2+\left( \frac{-3+\alpha }{2}\right) UV^2-\sqrt{\frac{3}{2}}\mu UV^2\nonumber \\&-\frac{\sqrt{3}}{\sqrt{2}}\pi \mu V^2 W + \text {higher order terms}, \end{aligned}$$
(57)
$$\begin{aligned} V'= & {} -\left( 3+\sqrt{\frac{3}{2}}\mu \right) UV-\frac{3}{2}U^2V-\left( \frac{3}{2}+\sqrt{\frac{3}{2}}\mu \right) V^3\nonumber \\&+\sqrt{\frac{3}{2}}\pi VW\mu \!+\!\frac{\sqrt{3}}{2\sqrt{2}}\pi ^2 \mu V W^2 \!+\! \text {higher order terms},\nonumber \\ \end{aligned}$$
(58)
$$\begin{aligned} W'= & {} -3W+\frac{3}{\pi } U - 3UW +\left( -\frac{3\pi }{2}+3\right) W^2+\frac{\pi ^2}{2} W^3\nonumber \\&+ \text {higher order terms}. \end{aligned}$$
(59)

The Jacobian matrix at the origin corresponding to the above autonomous system can be written as

$$\begin{aligned} J(P_4)|_{\alpha \ne 3}=\begin{bmatrix} -3+\alpha &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ \frac{3}{\pi } &{} 0 &{} -3\\ \end{bmatrix} \end{aligned}$$
(60)

So, the eigenvalues of the above matrix are \(-3+\alpha , 0, -3\) and \([\frac{\pi \alpha }{3},0,1]^T\), \([0, 1, 0]^T\), \([0, 0, 1]^T\) are the corresponding eigenvectors respectively. Then by using similar arguments which we have done for the critical point \( P_1 \), the center manifold can be expressed as

$$\begin{aligned} U= & {} -\frac{1}{2} V^2 + {\mathcal {O}}\left( V^4\right) , \end{aligned}$$
(61)
$$\begin{aligned} W= & {} -\frac{1}{2\pi } V^2 + {\mathcal {O}}\left( V^4\right) . \end{aligned}$$
(62)
Fig. 7
figure 7

Vector field near the origin in UV-plane for the critical point \(P_4\). L.H.S. figure is for (\(\alpha <3,\mu >0\)) and R.H.S. figure is for (\(\alpha>3,\mu >0\))

Full size image

The flow on the center manifold near the origin is determined by

$$\begin{aligned} \frac{dV}{dN}= & {} -\sqrt{\frac{3}{2}}\mu V^3 + {\mathcal {O}}\left( V^4\right) . \end{aligned}$$
(63)

For \(\alpha \ne 3\) we get four different phase diagram near the origin depending on the values of \(\alpha \) and \(\mu \). For \(\mu>\) 0 there arises two cases \(\alpha >3\) and \(\alpha <3\) and for \(\mu <0\) there also arises two cases \(\alpha >3\) and \(\alpha <3\).

Case (i)::

\(\mu>\) 0 For \(\alpha<\) 3 the origin is a stable node, i.e., the vector field near the origin is stable in nature (Fig. 7a). For \( \alpha >3 \) the origin is a saddle node, i.e., the vector field near the origin is unstable in nature (Fig. 7b).

Case (ii)::

\(\mu<\) 0 In this case the origin is a saddle node for \(\alpha<\) 3 (Fig. 8a) and an unstable node for \(\alpha>\) 3 (Fig. 8b), i.e., for both of the cases the vector field near the origin is unstable in nature .

Case (iii)::

\(\mu =\) 0 If we calculate the center manifold for \(\mu =0\) then the center manifold is same as of Eqs. (61) and (62) and the flow on the center manifold is determined by

$$\begin{aligned} \frac{dV}{dN}= & {} -\frac{3}{8}V^5 + {\mathcal {O}}\left( V^6\right) . \end{aligned}$$
(64)

For \(\alpha >3\) the origin is a saddle node, i.e., unstable in nature and for \(\alpha <3\) the origin is a stable node, i.e., stable in nature and the vector field near the origin is same as for \(\mu >0\) case (Fig. 7).

Fig. 8
figure 8

Vector field near the origin in UV-plane for the critical point \(P_4\). L.H.S. figure is for (\(\alpha<3,\mu <0\)) and R.H.S. figure is for (\(\alpha >3,\mu <0\))

Full size image

3.2.2 Critical point \(P_5\)

\({\underline{\mathbf{Case 1: }}}\) \(\alpha =3\)

Similarly as above after putting \( \alpha =3 \) in (22), we shift the critical point \(P_5\) to the origin by using the coordinate transformation \(u\rightarrow U-1\), \(v\rightarrow V\), \(w\rightarrow W-\frac{1}{2}\). The calculation change the system of equations (22–24) due to this coordinate transformation is shown in Appendix B. The Jacobian matrix at the origin for this autonomous system can be written as

$$\begin{aligned} J(P_5)|_{\alpha =3}=\begin{bmatrix} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ \frac{3}{\pi } &{} 0 &{} -3\\ \end{bmatrix} \end{aligned}$$
(65)

So the eigenvalues of the above matrix are 0, 0, \(-3\) and \([1,0,\frac{1}{\pi }]^T\) and \([0,1,0]^T\) are the eigenvectors corresponding to the eigenvalue 0 and \([0,0,1]^T\) be the eigenvector corresponding to the eigenvalue \(-3\). By computing the matrix of eigenvectors of the Jacobian matrix of the system in U, V, W; we introduce another set of new coordinates \((U_T,V_T,W_T)\) in terms of (U, V, W) as follows

$$\begin{aligned} \begin{bmatrix} U_T\\ V_T \\ W_T \\ \end{bmatrix} =\begin{bmatrix} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ -\frac{1}{\pi } &{} 0 &{}1\\ \end{bmatrix} \begin{bmatrix} U\\ V\\ W\\ \end{bmatrix} \end{aligned}$$
(66)

In these coordinates the system of equations is now in the correct form

$$\begin{aligned} \begin{bmatrix} U_T'\\ V_T'\\ W_T'\\ \end{bmatrix} =\begin{bmatrix} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{}-3\\ \end{bmatrix} \begin{bmatrix} U_T\\ V_T\\ W_T\\ \end{bmatrix} + \begin{bmatrix} \text {non}\\ \text {linear}\\ \text {terms}\\ \end{bmatrix} \end{aligned}$$
(67)

Thus by center manifold theory there exist a continuously differentiable function \(h:{\mathbb {R}}^2\) \(\rightarrow \) \({\mathbb {R}}\) such that \(W_T=h(U_T,V_T)=aU_T^2+bU_TV_T+cV_T^2+\text {higher~order~terms,~where}~ a,~b,~c~ \in ~{\mathbb {R}}\). We only concern about the nonzero coefficients of the lowest power terms in CMT as we analyze arbitrary small neighborhood of the origin.

Now differentiating both side with respect to N, we get

$$\begin{aligned} \frac{dW_T}{dN}=\begin{bmatrix} 2aU_T+bV_T&bU_T+2cV_T \end{bmatrix}\begin{bmatrix} \frac{dU_T}{dN}\\ ~\\ \frac{dV_T}{dN}\\ \end{bmatrix} \end{aligned}$$
(68)

Comparing L.H.S. and R.H.S. of (68) we get, \(a=-\frac{3}{2\pi }\), \(b=0\) and \(c=0\), i.e., the center manifold can be written as

$$\begin{aligned} W_T= & {} -\frac{3}{2\pi } U_T^2. \end{aligned}$$
(69)

The flow on the center manifold near the origin is determined by

$$\begin{aligned} \frac{dU_T}{dN}= & {} 6U_T^2+(-3+\sqrt{6}\mu )U_TV_T^2+\text {higher~order~terms}, \end{aligned}$$
(70)
$$\begin{aligned} \frac{dV_T}{dN}= & {} 3U_TV_T-{\left( \sqrt{6}\mu +\frac{3}{2}\right) U_T^2V_T-\left( \frac{3}{2}-\sqrt{\frac{3}{2}}\mu \right) V_T^3}\nonumber \\&+\text {higher~order~terms}. \end{aligned}$$
(71)
Fig. 9
figure 9

Projection of vector field on the (\(U_T\) \(W_T\))-plane near the origin for the critical point \(P_5\) (\(\alpha \)=3)

Full size image

Similarly for analyzing the stability of this critical point, first we divide both sides of (70) by 6 and divide both sides of (71) by 3. Since we divided both sides of these equations by positive terms, so the direction of vector field is unchanged. We take \(r^2=U_T^2+V_T^2\), then differentiating both sides with respect to N and using (70) and (71) yields \(r'=U_Tr\). So \(r'\) depends on the sign of \(U_T\). If \(U_T>0\) then \(r'>0\) and if \(U_T<0\) then \(r'<0\). So, the origin is a saddle node and hence the vector field near the origin is unstable in nature (Fig. 9). Now we try to see the vector field near the origin for \(\mu =\sqrt{\frac{3}{2}}\) because for \(\mu =\sqrt{\frac{3}{2}}\) the coefficient of \(V^3\) in R.H.S. of the second equation of Appendix B vanishes. The vector field in VW plane near the origin for \(\mu =\sqrt{\frac{3}{2}}\) is shown as in Fig. 10.

Fig. 10
figure 10

Vector field near the origin in VW plane for the critical point \(P_5\) \((\alpha =3,\mu =\sqrt{\frac{3}{2}})\)

Full size image
Fig. 11
figure 11

Vector field near the origin in UV plane for the critical point \(P_5\). L.H.S. figure is for (\(\alpha <3,\mu >0\)) and R.H.S. figure is for (\(\alpha>3,\mu >0\))

Full size image

\({\underline{\mathbf{Case 2: }}}\) \(\alpha \ne \)3

After shifting the critical point \(P_5\) to the origin, the calculation change the system of equations (22–24) due to this coordinate transformation is shown as in Appendix C.

By similar calculation we can easily see that the Jacobian matrix for the above autonomous system is same as (60). Hence, we have the same eigenvalues and corresponding eigenvectors which already obtained for (60) and the center manifold near the origin can be written as

$$\begin{aligned} U= & {} \frac{1}{2} V^2 + {\mathcal {O}}\left( V^4\right) , \end{aligned}$$
(72)
$$\begin{aligned} W= & {} \frac{1}{2\pi } V^2 + {\mathcal {O}}\left( V^4\right) . \end{aligned}$$
(73)

The flow on the center manifold near the origin is determined by

$$\begin{aligned} \frac{dV}{dN}= & {} \sqrt{\frac{3}{2}}\mu V^3 +{\mathcal {O}}\left( V^4\right) . \end{aligned}$$
(74)

For \(\alpha \ne 3\) we get four different phase diagram near the origin depending on the values of \(\alpha \) and \(\mu \). For \(\mu >0\) there arises two cases \(\alpha >3\) and \(\alpha <3\) and for \(\mu <0\) there also arises two cases \(\alpha >3\) and \(\alpha <3\).

Case (i): \(\mu >0\) The origin is a saddle node if \(\alpha<\)3 (Fig. 11a) and an unstable node if \(\alpha>\)3 (Fig. 11b), i.e., the vector field near the origin is unstable in nature for both of the cases.

Fig. 12
figure 12

Vector field near the origin in UV plane for the critical point \(P_5\). L.H.S. figure is for (\(\alpha<3,\mu <0\)) and R.H.S. figure is for (\(\alpha >3,\mu <0\))

Full size image

Case (ii): \(\mu <0\) For \(\alpha<\) 3 the origin is a stable node, i.e., the vector field near the origin is stable in nature (Fig. 12a). The origin is a saddle node if \(\alpha>\)3, i.e., the vector field near the origin is unstable in nature (Fig. 12b).

Fig. 13
figure 13

Phase potrait near the origin for the critical point \( P_6 \). L.H.S. is for \( \alpha >3 \) (taking \( \alpha =4 \)) and R.H.S. is for \( \alpha <3 \) (taking \( \alpha =2 \))

Full size image

Case (iii): \(\mu =0\) If we calculate the center manifold for \(\mu =0\) then the expression of center manifold is same as of Eqs. (72) and (73) and the flow on the center manifold is determined by

$$\begin{aligned} \frac{dV}{dN}= & {} -\frac{3}{8}V^5 + {\mathcal {O}}\left( V^6\right) . \end{aligned}$$
(75)

For \(\alpha>\)3 the origin is a saddle node, i.e., unstable in nature and for \(\alpha <3\) the origin is a stable node,i.e., stable in nature and the flow near the origin is same as the flow near the origin for \(\mu <0\) case (Fig. 12).

3.2.3 Critical point \(P_6\)

First we shift the critical point \( P_6 \) to the origin by using the coordinate transformation \(u\rightarrow U+\frac{\alpha }{3}\), \(v\rightarrow \)V and \(w\rightarrow W+\frac{2}{\pi }\cos ^{-1}\left[ \sqrt{\frac{3}{\alpha +3}}\right] \). Now the Jacobian matrix at the origin for the transformed autonomous system can be written as

$$\begin{aligned} J(P_6)=\begin{bmatrix} 3-\alpha &{} 0 &{} 0\\ 0 &{} \frac{3-\alpha }{2} &{} 0\\ \frac{18}{\pi (\alpha +3)} &{} 0 &{} -3\\ \end{bmatrix} \end{aligned}$$
(76)

The eigenvalues of the above Jacobian matrix are \((3-\alpha )\), \(\frac{(3-\alpha )}{2}\) and \(-3\). \([1,0,\frac{18}{\pi (3+\alpha )(6-\alpha )}]^T\), \([0, 1, 0]^T\) and \([0, 0, 1]^T\) are the eigenvectors corresponding to the eigenvalues \((3-\alpha )\), \(\frac{(3-\alpha )}{2}\) and \(-3\) respectively. Since the Jacobian matrix have nonzero real eigenvalues for \(\alpha \ne 3\), so the critical point is hyperbolic and so we can analyze the stability of the critical point by Hartman–Grobman theorem [26]. For \(\alpha >3\) all eigenvalues are negative and hence the origin is a stable node and the phase portrait near the origin is stable in nature (Fig. 13a). For \(\alpha <3\) two eigenvalues are positive and one is negative and hence the origin is a saddle node and the phase portrait near the origin is unstable in nature (Fig. 13b).

3.2.4 Critical point \(P_{7}\)

If we determine the Jacobian matrix corresponding to the autonomous system (22–24) at the critical point \(P_7\), then we will get the same Jacobian matrix as (76) and hence we have the same eigenvalues and corresponding eigenvectors. Since, the eigenvalues are nonzero, so we analyze the stability of this critical point by Hartman–Grobman theorem. The phase portrait near the origin is Fig. 13.

For \(\alpha =3\) the critical points \(P_6\) and \(P_7\) are non-hyperbolic. For this case the stability analysis of those critical points are same as Case 1 of the critical points \(P_4\) and \(P_5\) respectively.

Poincaré index and bifurcation analysis

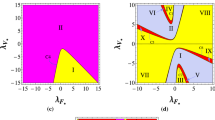
For \(\alpha <3\) four critical points (\(P_4\)-\(P_7\)) appear to exist but at \(\alpha =3\) two critical points (\(P_6\) and \(P_7\)) disappear. Again they appear for \(\alpha >3\). If we restrict ourselves on UW-plane, \(P_4\) and \(P_5\) are stable node in nature for \(\alpha <3\) and index of each \(P_4, P_5|_{UW}\) is 1. On the UV-plane, for \(\mu >0\), \(P_4\) is stable node for \(\alpha <3\) with index 1 and saddle for \(\alpha >3\) with index \(-1\). For \(\mu =0\), the index of \(P_4|_{UV}\) is 0 as the neighborhood has two hyperbolic sectors. On the VW-plane, for \(\alpha \ne 3\), the index of \(P_4|_{VW}\) is 1 for \(\mu >0\) and \(-1\) for \(\mu \leqslant 0\). For \(\alpha =3\), index of \(P_4|_{VW}\) is \(-1\) for \(\mu \geqslant -\sqrt{\frac{3}{2}}\) and 1 for \(\mu <-\sqrt{\frac{3}{2}}\).

Similarly on the UV-plane, for \(\mu >0\), \(P_5\) is saddle for \(\alpha <3\) with index \(-1\) and stable node for \(\alpha >3\) with index 1. For \(\mu =0\), the index of \(P_5|_{UV}\) is 0 as the neighborhood has two hyperbolic sectors. For \(\mu <0\), \(P_5\) is stable node for \(\alpha <3\) with index 1 and saddle for \(\alpha >3\) with index \(-1\). For \(\mu =0\), the index of \(P_5|_{UV}\) is 0 as the neighborhood has two hyperbolic sectors.On the VW-plane, for \(\alpha \ne 3\), the index of \(P_5|_{VW}\) is \(-1\) for \(\mu \geqslant 0\) and 1 for \(\mu < 0\). For \(\alpha =3\), index of \(P_4|_{VW}\) is 1 for \(\mu >\sqrt{\frac{3}{2}}\) and \(-1\) for \(\mu \leqslant \sqrt{\frac{3}{2}}\). Again \(P_6\) and \(P_7\) are saddle for \(\alpha <3\) and stable node for \(\alpha >3\). So at \(\alpha =3\) and \(\mu = 0, \pm \sqrt{\frac{3}{2}}\) the system is structurally unstable.

For \(\alpha <3\) and \(\mu >0\), \(P_4\) is a stable node and \(P_5\) is a saddle in nature. So generic de-Sitter evolution can be found from \(P_5\) of index \(-1\) plane to \(P_4\) of index 1 plane. For \(\mu <0\), the generic evolution reverses its direction. At \(\alpha <3\) and \(\mu =0\) there may occur a non-generic evolution from \(P_6\) or \(P_7\) to \(P_4\) or \(P_5\) and the universe changes its phase from decelerating matter dominated era to phantom barrier. A similar non-generic evolution also can be found for \(\alpha >3\). At \(\alpha =3\) a de-Sitter generic evolution can be found from the plane of index \(-1\) of \(P_5\) to the plane of index 1 of \(P_4\) for \(\mu <-\sqrt{\frac{3}{2}}\) and the direction reverses for \(\mu >\sqrt{\frac{3}{2}}\).

3.3 Interaction model: \(Q=2u\rho _{DM} H\)

For this interaction the autonomous system (26–28) modifies to

$$\begin{aligned} {\dot{u}}= & {} \left( \frac{3}{2}u-1\right) (1-u^2-v^2)+\sqrt{\frac{3}{2}} v^2 \mu \left( 1-u \tan \left[ \frac{\pi w}{2}\right] \right) \end{aligned}$$
(77)
$$\begin{aligned} {\dot{v}}= & {} \frac{3}{2}v(1-u^2-v^2)-\sqrt{\frac{3}{2}}v\mu \left( u+(-1+v^2)\tan \left[ \frac{\pi w}{2}\right] \right) \end{aligned}$$
(78)
$$\begin{aligned} {\dot{w}}= & {} \frac{6}{\pi }\cos ^2\left[ \frac{\pi w}{2}\right] \left( u-\tan \left[ \frac{\pi w}{2}\right] \right) \end{aligned}$$
(79)

The above autonomous system has the following three critical points:

$$\begin{aligned} P_{8}\left( 1,0,\frac{1}{2}\right) , P_{9}\left( -1,0,-\frac{1}{2}\right) ~\text {and}~ P_{10}\left( \frac{2}{3},0,\frac{2}{\pi }~\tan ^{-1}\left[ \frac{2}{3}\right] \right) \end{aligned}$$

Note that in Ref. [11] the authors have not analyzed this model. So all critical points are new and here we analyze each critical points by center manifold theory (for non-hyperbolic case) and Hartman–Grobman theorem (for hyperbolic case) and also discuss global stability with reference to bifurcation analysis using Poincaré index. The cosmological parameters, eigenvalues and the nature of critical points are presented in Table 3.

Table 3 Table shows the value of cosmological parameters, eigenvalues ( \( \lambda _1 \), \(\lambda _2\), \(\lambda _3\)) and the nature of the critical points for this interaction model
Full size table

The three critical points \( P_8-P_{10} \) for the second choice of the interaction are very similar to the previous ones. The critical points \( P_8 \) and \( P_9 \) are exactly identical to \( P_1 \) and \( P_2 \) (or \( P_4 \) and \( P_5 \)). The critical point \( P_{10} \) represent a DE dominated era of evolution. Due to interaction of the three form field (i.e., cosmological constant in the present context) with DM (in the form of dust) the resulting single fluid is in the quintessence era not closed to phantom divide line. This critical point may be termed as LCDM model.

Stability analysis

3.3.1 Critical point \(P_{8}\)

First we shift the critical point \(P_8\) to the origin by using the coordinate transformation \(u\rightarrow U+1\),\(v\rightarrow V\),\(w\rightarrow W+\frac{1}{2}\). The calculation change the system of equations (77–79) due to this coordinate transformation is shown in Appendix D.

If we determine the Jacobian matrix at the origin for the autonomous system Appendix D, we have the eigenvalues \(-1\), 0 and \(-3\) and \([1, 0, \frac{3}{2\pi }]^T\), \([0, 1, 0]^T\) and \([0, 0, 1]^T\) are the corresponding eigenvectors respectively. Since, the critical point is non hyperbolic so we use center Manifold theory for analyzing the stability of the critical point. Proceeding in similar way for determining the center manifold, the center manifold can be expressed as

$$\begin{aligned} U= & {} -\frac{1}{2} V^2 + {\mathcal {O}}\left( V^3\right) \end{aligned}$$
(80)
$$\begin{aligned} W= & {} -\frac{1}{2\pi } V^2 +{\mathcal {O}}\left( V^3\right) \end{aligned}$$
(81)

The flow on the CM near the origin is determined by

$$\begin{aligned} V'= & {} -\sqrt{\frac{3}{2}}\mu V^3 +{\mathcal {O}}\left( V^4\right) . \end{aligned}$$
(82)

Here the stability of the center manifold depends on the sign of \(\mu \). If \(\mu>\) 0 then the origin is a stable node and if \(\mu<\) 0 then the origin is a saddle node, i.e., unstable in nature.

3.3.2 Critical point \(P_{9}\)

We shift the critical point \(P_9\) to the origin by the coordinate transformation \(u\rightarrow U-1\),\(v\rightarrow V\),\(w\rightarrow W-\frac{1}{2}\). The calculation change the system of equations (77–79) due to this coordinate transformation is shown in Appendix E. If we determine the Jacobian matrix at the origin for this autonomous system we have the eigenvalues \(-5\), 0 and \(-3\) and \([1, 0, -\frac{3}{2\pi }]^T\), \([0, 1, 0]^T\) and \([0, 0, 1]^T\) are the corresponding eigenvectors respectively. Since, the critical point is non-hyperbolic so we shall use center Manifold theory for analyzing the stability of the critical point. Proceeding in similar way for determining center manifold, the expression of center manifold can be written as

$$\begin{aligned} U= & {} \frac{1}{2} V^2 + {\mathcal {O}}\left( V^3\right) , \end{aligned}$$
(83)
$$\begin{aligned} W= & {} \frac{1}{2\pi } V^2 + {\mathcal {O}}\left( V^3\right) . \end{aligned}$$
(84)

The flow on the center manifold near the origin is determined by:

$$\begin{aligned} V'= & {} \sqrt{\frac{3}{2}}\mu V^3 +{\mathcal {O}}\left( V^4\right) . \end{aligned}$$
(85)

The stability of the manifold depends on the sign of \(\mu \). If \(\mu>\) 0 then the origin is a saddle node, i.e., unstable in nature and if \(\mu<\) 0 then the origin is a stable node, i.e., stable in nature.

3.3.3 Critical point \(P_{10}\)

We shift the critical point \(P_9\) to the origin by using the coordinate transformation \(u\rightarrow U+\frac{2}{3}\), \(v\rightarrow V\), \(w\rightarrow W+\frac{2}{\pi }\tan ^{-1}\left[ \frac{2}{3}\right] \). Now the Jacobian matrix at the origin for the transformed autonomous system can be written as

$$\begin{aligned} J(P_{10})=\begin{bmatrix} \frac{5}{6} &{} 0 &{} 0\\ 0 &{} \frac{5}{6} &{} 0\\ \frac{54}{13\pi } &{} 0 &{} -\frac{33}{13} \end{bmatrix} \end{aligned}$$
(86)

The eigenvalues of the above Jacobian matrix are \(\frac{5}{6}\), \(\frac{5}{6}\), \( -\frac{33}{13} \) and \([1, 0, \frac{324}{263}]^T\) and \([0, 1, 0]^T\) are the eigenvectors corresponding to the eigenvalue \(\frac{5}{6}\) and \([0, 0, 1]^T\) is the eigenvector corresponding to the eigenvalue \( -\frac{33}{13} \). Since, the critical point is hyperbolic in nature, so by Hartman–Grobman theorem we can analyze the stability of this critical point. Since two eigenvalues are positive and one is negative, so the origin is a saddle node and the phase portrait near the origin is unstable in nature (Fig. 14).

Fig. 14
figure 14

3 Dimensional phase plot for the critical point \(P_{10}\)

Full size image

Poincaré index and bifurcation analysis

Critical points \(P_8\) and \(P_9\) are sink (sum of index is 2) in nature when restricted on UW-plane. On the other hand, \(P_8\) and \(P_9\) swap their stability and indices (1 to \(-1\) or \(-1\) to 1) when the parameter \(\mu \) passes through zero. Similar phenomenon can be found on the VW-plane. Despite each of \(P_8\) and \(P_9\) changes its stability at \(\mu =0\), they together produce topological equivalent phase space for all \(\mu \). Since the phase space in confined in a finite region of space, there is a trajectory of non-generic evolution between \(P_8\) and \(P_9\) on UV or VW-plane. As there is no \(\mu \) in the eigenvalues of (86), so qualitative behavior near \(P_{10}\) does not depend on \(\mu \). The Poincaré index of \(P_{10}\) restricted on uv-eigenplane is 1 and each on the two other plans is \(-1\) and is independent of the sign of \(\mu \) . But in cosmological point of view, near the critical point \(P_{10}\), for \(\mu >0\), the comoving field behaves as a phantom field with runaway potential, whereas the field behaves as non-phantom with non-runaway potential when crosses the phantom barrier at \(\mu =0\) from positive to negative.

Table 4 Table shows the set of critical points corresponding to the autonomous system (87–89) and the value of cosmological parameters corresponding to each critical pointss
Full size table

Now we consider a power-law potential as

$$\begin{aligned} V(X)=V_1X^{-\lambda } \end{aligned}$$

where \(\lambda \) is a dimensionless parameter and \(V_1>0\). Then by using similar dimensionless variables (16–19) we have the following autonomus system

$$\begin{aligned} u'&=\frac{3}{2}u(1-u^2-v^2)+\frac{3}{2}\lambda v^2\left( \cot \left[ \frac{\pi w}{2}\right] -u\right) \nonumber \\&-\frac{\alpha }{2u}(1-u^2-v^2), \end{aligned}$$
(87)
$$\begin{aligned} v'&=\frac{3}{2}v(1-u^2-v^2)-\frac{3}{2}\lambda v\left( u\cot \left[ \frac{\pi w}{2}\right] +v^2-1\right) , \end{aligned}$$
(88)
$$\begin{aligned} w'&=\frac{6}{\pi }\cos ^2\left[ \frac{\pi w}{2}\right] \left( u-\tan \left[ \frac{\pi w}{2}\right] \right) \end{aligned}$$
(89)

We have two non-hyperbolic critical points \(R_1\) and \(R_2\) similar as \(P_1\) and \(P_2\) respectively corresponding to the non-interacting case, four non-hyperbolic critical points \(R_3\), \(R_4\), \(R_5\) and \(R_6\) similar as \(P_4\), \(P_5\), \(P_6\) and \(P_7\) respectively corresponding to the interacting case when \(\alpha \ne 0\). Note that \(R_5\) and \(R_6\) are hyperbolic for \(\alpha \ne 3\). Lastly, for \(\alpha =2u\) we have two non-hyperbolic critical points \(R_7\) and \(R_8\) similar as \(P_8\) and \(P_9\) respectively and one hyperbolic critical points \(R_{10}\) similar as \(P_{10}\) \(\omega _X=p_X/\rho _X\) and the total equations of state parameters \(\omega _{tot}\) corresponding to this model can be expressed as

$$\begin{aligned} \omega _{X}= & {} -1-\frac{\lambda v^2}{u^2+v^2}, \end{aligned}$$
(90)
$$\begin{aligned} \omega _{tot}= & {} -u^2-(\lambda +1)v^2. \end{aligned}$$
(91)

To avoid similar calculations we only state the stability of every critical points, value of Poincaré index and bifurcation value on the \(\alpha -\lambda \) plane corresponding to each critical points in tabular form (Table 5) and the value of cosmological parameters corresponding to each critical points are shown as in Table 4.

Table 5 Table shows stability of every critical points corresponding to the autonomous system (87–89), value of Poincaré index and bifurcation value on the \(\alpha -\lambda \) plane corresponding to each critical points
Full size table

4 Cosmological implications and conclusions

The present work deals with a cosmological model where the matter field in the context of recent observations is chosen as DE and DM interacting/non-interacting in nature. The three-form field acts as DE, interacting with CDM (Table 5). Due to very complicated form of the evolution equations the present cosmological model has been studied by dynamical system analysis, forming the autonomous system from the evolution equations by transformation with suitable dimensionless variables. There are two hyperbolic critical points (namely \( P_3 \) and \( P_{10} \)) and remaining eight critical points in \( P_1-P_{10} \) are non-hyperbolic in nature. Also there is a line of critical points \( P_{l_c} \) for the first choice of the interacting term and only for these critical points the three-form field behaves as perfect fluid with variable equation of state in phantom era. In the present work, non-hyperbolic critical points are mainly studied using center manifold theory and global stability has been examined through bifurcation scenarios using Poincaré index.

For the critical points \( (P_1,P_2) \), \( (P_4,P_5) \) and \( (P_8,P_9) \), DM is absent and the cosmic matter is only the three-form field behaving as cosmological constant. So they represent the early inflationary era or the de Sitter phase. For critical point \( P_3 \) the three form field (i.e., DE) is insignificant and cosmic evolution represents dust era due to dominance of DM. Similarly, for the critical point \( P_{10} \), the three form field (i.e., DE) has an edge over DM and there is accelerated expansion in the quintessence era and this can be termed as LCDM model. The remaining two critical points \( P_6 \) and \( P_7 \) have the same features-both of them represents the scaling cosmological solution with ’\(\alpha \)’ as the scaling parameter-for very small \(\alpha \) (i.e., \(\alpha \) is positive but very close to zero) the present model corresponds to matter dominated era while late time accelerated era is represented for \(\alpha >1\). For the power-law potential \(V(X)=V_1X^{-\lambda }\), the autonomous system (87–89) has nine equilibrium points \(R_i~(i=1,2,\ldots ,n)\), of which three are hyperbolic (\(R_5\), \(R_6\) and \(R_9\)) in nature while the remaining six are non-hypernbolic type. These equilibrium points are similar to the critical points \(P_i\) for the exponential potential form discussed earlier. The equilibrium points \(R_1\), \(R_2\), \(R_3\), \(R_4\), \(R_7\) and \(R_8\) correspond to de Sitter era of cosmic evolution. Here the universe is fully dominated by DE which behaves as cosmological constant. The remaining three equilibrium points (\(R_5\), \(R_6\) and \(R_9\)) represent cosmological scaling solution. \(R_9\) still has DE dominance and the universe is in accelerating phase. The critical points \(R_5\) and \(R_6\) correspond to matter dominated era of evolution for \(\alpha <1\), while they will also correspond to accelerated model of the universe for \(\alpha >1\).

As the phase space for the present model is confined to a finite region (given in Eq. 25), so there should not be an critical point at infinity. Thus the critical points correspond to different cosmic scenarios (namely, inflationary era, matter dominated epoch and present accelerated phase) and stability analysis (using center manifold theory for non-hyperbolic equilibrium points) has been presented with existence of possible bifurcation at cosmic transition.