Abstract
We study collective features of the scattering of gravitational waves on relic wormholes and normal matter objects. We derive and solve the GW energy transport equation and show that the scattered signal lies in the same frequency spectrum bands as the basic signal. The scattering forms long living tails which always accompany the basic signal and have a universal form. The scattering on normal matter objects forms tails which have always the retarded character, while wormholes lead to advanced tails as well. In addition, wormholes may produce considerably stronger effect when the total energy in tails detected on the Earth exceeds that in the incident direct wave. In both cases the retarding tails have a long living character when the mean amplitude behaves with time as \(h\sim 1/\sqrt{t+R/c}\). For a single GW event the echo tails give only a tiny contribution to the mean amplitude. However such tails accumulate with events and form a stochastic GW background which may be observed by the contribution to the noise.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The gravitational-wave (GW) event GW150914 [1] has opened a new window in the Universe that gave rise to the birth of the gravitational wave astronomy. Further observations [2] and new GW projects launched (e.g., see [3]) promise new and more detailed information about the structure and different processes in our Universe. In particular, several different groups have recently claimed tentative evidence for repeating echoes in the LIGO/Virgo observations of binary black hole mergers [4,5,6,7]. The last group claims the significance to reach \(4.2\sigma \) at \(f\simeq 72\) Hz. We leave aside numerous possible mechanisms of origin of such echoes discussed in literature (e.g., see, [8,9,10] and references in the above papers) and, in the present paper, explore properties of echoes which are generated by the scattering of the basic GW signals on a distribution of relic wormholes and normal matter objects. Namely, we consider collective effects of such a scattering which do not depend on the exact specific structure of wormholes or other compact objects.
To avoid misunderstanding we point out that the echoes generated by the scattering of GWs have much bigger timescales as compared to the near-horizon or other strong field effects discussed in [8,9,10]. Indeed the typical timescale for echoes in the case of near-horizon effects has the order \(\delta t\sim M\epsilon \), where M is the mass of a compact object and \(\epsilon \) some small parameter which determines the closeness of the object to a black hole, e.g., see details in [10]. In the case of scattering the typical value has the order \(\delta t \sim sR/c\), where R is the distance to the source, c is the speed of light, and, in general situation, a parameter s is not even small. In this sense the detected echoes have no the direct relation to effects discussed in our paper.
The simplest natural echo events may appear simply by lensing effects (e.g. see [11]). Indeed, in considering the scattering of GWs on normal astrophysical objects the most rough estimate gives for the cross-section the value of the order \( \sigma _g\propto r_{g}^{2}\), where \(r_{g}=2GM\) is the gravitational radius of an object. This will cause the deflection angle \(\theta \sim 2r_{g}/r\) (r is the distance from the ray to the object) and the time delay for additional images of the source \(\delta t/\varDelta t\sim \theta ^{2}\) (\(\varDelta t\) is the time passed from the emission to the detection). In general, for compact objects all such values are extremely small. A considerable effects may appear in two cases, when the distance from the ray to the object is sufficiently small, or when the mass is sufficiently big. On cosmological distances the time delay accumulates and becomes random. The accumulated random delays affect also the primary ray, which sets additional difficulties in observations of such effects. This means that in the first place the GW astronomy allows to probe only very large astrophysical objects (lensing on galaxies, clusters etc.).
Despite to the fact that the creation of relic wormholes in the very early Universe from quantum spacetime foam seems to be a rather natural process (e.g., see [12, 13]), wormholes are still assumed to be exotic astrophysical objects. This happens, in the first place, due to the absence of a direct observational evidence for wormholes. Unlike normal objects wormholes possess the cross-section of the order \( \sigma _w\propto b^{2}\), where b is the throat radius, which can take very big values \(b\gg r_{g}\). In addition to lensing, it is possible to observe a more detailed diffraction picture which appears due to the scattering on a single wormhole [14, 15]. In this case the necessary condition is to have a wormhole on the line of sight between the source of GW radiation and the observer. That seems to be an extremely rare situation. However, if we consider a distribution of relic wormholes, then the scattering of GWs on wormholes should give a noticeable contribution to the scattered signal. Indeed, in the models in which dark matter phenomenon appears due to a distribution of relic wormholes [16, 17] the total energy in the scattered signal may exceed the energy of the direct GW signal on the factor \(4\pi \tau e^{\tau }\times 2.4674\), e.g., see Eq. (40), where \(\tau \) is the mean optical depth for GWs.
We recall that for the scattering of GWs on normal astrophysical objects (e.g., stars) the optical depth is negligible \(\tau _s \sim \sigma _s n_s \ell \ll 1\), where \(\sigma _s\sim \left<r_g^2\right>\) is the mean cross-section for a typical star, \(n_s\) is the mean density of stars, and \(\ell \) is the traversed path along the ray, and the Universe is completely transparent (e.g., for \(\ell =50\,\mathrm{Mpc}\), \(\sigma _ s = \sigma _{\odot } \), and \( n_s =\rho _b /M_{\odot }\) we get \(\tau \sim 10^{-27 }\)). In the presence of wormholes however the Universe may be completely transparent only for some particular directions/rays. Indeed, according to lattice quantum gravity models [12, 13] we should expect fractal properties of space and of the relic wormhole distribution. We present the exact simple model of a fractal Universe elsewhere, while here we only point out that such a Universe possesses one important feature. Two any points of space can be connected by a direct ray so that the direct signals can be always seen (they are not screened by an obstacle). However in general, such rays do not give the shortest distance and the mean value of \(\tau _w\) is determined by rays emitted from the source which go in all possible directions. Therefore, it can reach sufficiently big values. In models where dark matter appears due to the presence of wormholes only [16, 17] the mean value of \(\tau _w\) can be estimated by the dark to luminous matter ratio. For the mean value it gives \(e^{\tau _w}\sim 6\), while due to local inhomogeneities it may reach even stronger values (e.g., in low surface brightness galaxies the mass to luminosity ratio M/L may reach \(10^{3}\) already at the edge of the optical disk which gives \(e^{\tau _w}\sim 10^3\) in such galaxies).
We also point out that it is not difficult to suggest parameters of a single wormhole that produce the scattered signal exceeding or having the same order as the direct GW signal. The only problem here is that the arrival times will be considerably separated (up to millions of years).
The estimate \(\sigma _w\propto b^{2}\) follows from the geometrical optics which assumes wavelengths \(\lambda \ll b\). Therefore, for wavelengths obeying the above inequality such an estimate is valid for all types of radiation scattered by wormholes (CMB, GWs, Cosmic Rays, radiation emitted by galaxies, etc.) and results presented in the present paper maybe equally applied to any type of radiation. Effects of scattering of radiation (different from GWs) on wormholes mix with analogous effects produced by normal matter [15]. It is very difficult to separate them. In this sense GWs give a unique tool to probe the existence of wormholes in space, since they are weakly scattered by ordinary matter and ordinary astrophysical objects. See however [18] where possible effects of magnetic wormholes were discussed. In the present paper we demonstrate that the scattering of the basic GW signal from a binary merger forms a specific halo of secondary sources and at the Earth every GW impulse will have heavy long- living tails. In the case of wormholes there are both - advancedFootnote 1 and retarded tails, while the total energy flux emitted by the halo and the energy contained in the tails may exceed that in the basic signal. However this energy is widely distributed in time.
The two basic features of such a scattering are that the scattered signal gets into the same frequency window as the basic signal and that the mean GW amplitude h (\(h\sim \sqrt{I_{\omega } }\), where \( I_{\omega }\sim \) \(\left\langle {\dot{h}}^2\right\rangle =\frac{1}{T}\int _T ({\dot{h}}^2_\times +{\dot{h}}^2_+)dt\), \(T=2\pi /\omega \), and \({\dot{h}}=\partial h/\partial t\)) in the tail decays with time very slowly \(\delta I_{\omega }\sim 1/(t+R/c)\), where R is the distance to the GW source and, therefore, \(h(t)\sim 1/\sqrt{t+R/c}\). The amplitude ratio \(\delta I/I^0\) has the order \(\tau e^{\tau }c\delta t/R\ll 1\), where \(\tau \) is the optical depth and \(\delta t\) is the duration of the basic signal and, therefore, the direct detection of such tails is not possible. However, when taking into account all different binary merger events, tails accumulate which gives an additional multiplier \(N\sim a\nu R/c\gg 1\), see Eq. (49), where \(\nu \) is the rate of events and the coefficient a characterizes how long such tails live. Therefore, we should predict essentially enhanced level of the stochastic GW background in the given frequency band (roughly by the factor \(\rho _{DM}/\rho _{b}\) as compared with the measured/predicted rate of mergers, where \(\rho _{DM}\) and \(\rho _{b} \) are the dark matter and baryon densities).
The paper is organized as follows. In Sect. 2 we describe the topological structure of space in the presence of a distribution of relic wormholes. We also illustrate the origin of echoes for the exact model, i.e., a torus-like wormhole in the open Friedman model, and construct the map of geodesics for a spherical thin-shell wormhole which contains both entrances in the same space. In Sect. 3 we derive the energy transport equation (ETE) for gravitational waves. The range of applicability of ETE is restricted by geometric optics (slow variation of the background metric as compared to the wavelengths) and it assumes random phases of GWs. In Sect. 4 we present solutions for ETE for a point-like GW source and in the approximation when the expansion of the Universe may be neglected. That corresponds to the local Universe with redshifts \(z< 0.1\) We show that the scattering leads to the damping of the intensity along rays and forms a distributed halo of secondary sources which emit omnidirectional secondary flux. We also show how solutions generalize to the case of the expanding background (to an arbitrary redshifts). The secondary sources form tails for the direct basic signal. The structure of such tails is described in Sect. 5. In Sect. 6 we discuss possible astronomical implications and further perspectives.
2 Topological structure of space with a distribution/gas of relic wormholes
In general relativity topological structure of space is determined by onset, as additional initial conditions [19] (see also recent discussion in [20]). The most natural initial conditions correspond to a fractal topological structure of space, i.e., to a fractal distribution of wormholes. Indeed, lattice quantum gravity models predict fractal properties of space at sub-planckian scales (e.g., see [12, 13]), while the inflationary phase in the past should enormously stretch all scales and temper such a structure as initial conditions.
We point out that the space which contains a distribution of wormholes cannot be covered by a single coordinate map. In astrophysical applications however it is convenient to describe wormholes in terms of the single coordinate map which is commonly used to describe points in the homogeneous and isotropic Universe (e.g., the red shift and two angles on the Sky, or any other coordinates of the flat Friedman model). This is achieved by making cuts along the minimal sections of wormhole throats. As the result we get the space manifold with a set of couples of boundaries at which we should specify specific boundary conditions. Boundary conditions follow simply from the fact that all physical fields are continuous at throats. On sky such boundaries will be seen as couples of specific/exotic astrophysical objects which in general have a rather complex form (couples of two-dimensional surfaces \(S_{A}\), where the index \(A=1,\ldots N\) numerates wormhole throats). Those surfaces/objects may move, rotate, possess equal masses and magnetic poles. The boundary conditions are induced by the cutting procedure. For example, if we consider a couple of such surfaces \( S_{\pm }\) which correspond to the same wormhole, then the internal region of space restricted by \(S_{+}\) (or, in general, some part of it) admits a one-to-one map on a portion of the outer region for the conjugated surface \( S_{-}\). This defines the boundary conditions in a unique way.
In general case throat sections (their space-like part) have the form of a sphere with n handles \(S_{n}^{2}\). As it was discussed in [21] the simplest wormhole has the section which has the form of a torus. We recall that such wormholes do not require the presence of exotic forms of matter and they do evolve. In open Friedman models their rate of evolution exactly coincides with the common cosmological expansion and they are stable. In the case of the flat space the rate of their evolution is still not investigated properly. Some encouraging results were obtained in the limit when one radius of a torus-like throat tends to infinity and the geometry acquires cylindrical configuration. In particular, in a series of papers [22,23,24,25] static and stationary cylindrical wormhole solutions were found and it was demonstrated that asymptotically flat wormhole configurations do not require exotic matter violating the weak energy condition. We point out that if such a torus-like wormhole rotates in space, this surely should prevent it from very fast collapse. The thorough investigation of such objects represents too complex problem which still waits for its investigation.
In the present paper we, for the sake of simplicity, assume spherical throats of wormholes. Some words to approve the use of such an approximation worth adding. Indeed, spherical wormholes collapse very quickly and, therefore, they cannot be distinguished from ordinary black holes. Stable traversable spherical wormholes may exist only in the presence of exotic forms of matter and in modified theories, where the role of the exotic matter is played by an appropriate modification [26,27,28]. So far, there is no any rigorous experimental evidence for the existence of exotic forms of matter, or for the presence of any modification of general relativity (we leave aside possible quantum corrections which work only in the quasi-classical region, e.g., at Planck scales). This means that the approximation of spherical throats should be very rough. Nevertheless, in considering collective effects of GW scattering on a distribution of wormholes, such an approximation works rather well. Owing to the fact that more general wormhole throats have random orientations in space and assuming that they have an isotropic distribution, the final result always contains the averaging over orientations. When we perform such an averaging, then every throat restores the spherical symmetry. The spherical wormhole, in turn, is much more simple object to work with and it admits a much more simple consideration.
In conclusion of this section we consider the exact illustrative model of the scattering on a single torus-like wormhole in the open model (see the exact description of the appropriate metric in [20, 21]) and construct the map of geodesic lines at boundaries for a spherical wormhole.
2.1 Echoes from a single wormhole
Consider first the open Freedman model. Then the space-like part represents the standard Lobachevsky space. The simplest wormhole which connects two Lobachevsky spaces is obtained by a factorization over a discrete subgroup of the group of motions. The discrete subgroup G is determined by a couple of generators \(T_{a}(l_{1})\) and \(T_{b}(l_{2})\) which describe two shifts of the space in orthogonal directions (\(l_{1}\) and \(l_{2}\) denote two orthogonal geodesics) on distances \(r_{1}=a\) and \(r_{2}=b\). Any element \( g_{A}\in G\) may be constructed merely as \(g_{A}=T_{a}^{m}T_{b}^{n}\) with \(m,n=0,\pm 1,\pm 2,...\). We point out that the shifts \(T_{a}(l_{1})\) and \(T_{b}(l_{2})\) do not commute and elements \(g\in G\) are classified by a more complicated way. This however is not important for subsequent consideration.
The minimal section of the throat has the form of a torus with two radii \(r_{1}\) and \(r_{2}\). As it was demonstrated in [20] it is possible to introduce such coordinates on the Lobachevsky space \(\left( \chi _{1},\chi _{2},\chi _{3}\right) \) that the shift is merely \(g_{A}\left( \chi _{1},\chi _{2},\chi _{3}\right) =\left( \chi _{1}+2\pi m,\chi _{2}+2\pi n,\chi _{3}\right) \), while perturbations of the metric \(\delta g_{\alpha \beta }(x)\) obey the ”periodic” property
Consider now the retarded Green function \(G_{F}\) for the open Friedman model which describes the propagation of a single GW impulse. The above periodicity means that in the presence of the wormhole any source in the Friedman space also obeys the periodic conditions and, therefore, in terms of the unrestricted Friedman space it induces multiple additional images
where \(\gamma \) comes from the metric on the Lobachevsky space. Then in the presence of the wormhole the true Green function has the obvious structure
Any signal emitted by binary mergers acquires the same structure. Here the first term corresponds to the direct GW signal, while the sum corresponds to echoes. The amplitudes of echoes depend on the position of the source (with respect to the wormhole center) and the parameters of the wormhole (radii a and b). We point out that the general structure of echoes (3) appears also for spherically symmetric wormholes in the asymptotically flat space [8], e.g., see also [29, 30]. Therefore, it is not a specific feature of the model discussed. When we have a distribution of such wormholes the general structure remains the same, while the GW signal becomes much more complicated. Moreover, part of echoes overrun the basic signal.
In general amplitudes of echoes are extremely small and phases become random. This happens in the first place due to a random distribution of relic wormholes. We point out that this does not mean that a particular wormhole cannot produce a rather strong effect. Some particular terms in (3) may reach sufficiently big values which depends on a specific position of a particular wormhole, e.g., see examples in [8,9,10]. However from the statistical standpoint such situations are too rare and when we make the averaging over possible positions of a wormhole all terms become small.
It was shown in [16, 17] that additional images of an actual source (2) may play the role of dark matter. In this case the distribution of DM in the Universe is determined by the distribution of wormholes, while the observed in galaxies rigid relation between visible and dark matter components acquires the most natural explanation. This means also that the multiple echoes have the same origin and the intensity of echoes relates somehow to the distribution of dark matter. This feature will be used for estimates of the intensity of the stochastic GW background.
2.2 Geodesic map for spherical wormholes
As it was pointed out the space with wormholes cannot be covered by a single coordinate atlas. For practical aims it is convenient to have a single atlas (e.g., a part of the Friedman space). In this case we cut the wormhole throat by the minimal section of the throat. Then the wormhole represents a couple of surfaces \(\varSigma _{\pm }=S_{\pm }\times R\) (which are the direct product of a sphere and the time axis) whose internal regions are removed, while surfaces of the spheres are glued. From the topological standpoint this corresponds to the standard Minkowski space with boundaries. In general case for a remote observer such boundaries move in space and are glued by the Poincare motion \( x_{+}^{\alpha }-X_{+}^{\alpha }=\varLambda _{\beta }^{\alpha }\left( x_{-}^{\beta }-X_{-}^{\beta }\right) \). The gluing means that when the ray \( x(\ell )\) reaches one such a boundary \(\varSigma _{-}\) at some finite value \( \ell _{0}\), i.e., \(x_{-}^{\alpha }(\ell _{0})\in \varSigma _{-}\) and particular values of \(k_{\mu }^{-}(\ell _{0})\), it’s continuation comes from the other boundary \(\varSigma _{+}\) with new initial data \(x_{+}^{\alpha }(\ell _{0})\in \varSigma _{+}\) and \(k_{\mu }^{+}(\ell _{0})\) related by the Poincare map \(x_{+}^{\alpha }-X_{+}^{\alpha }=\varLambda _{\beta }^{\alpha }\left( x_{-}^{\beta }-X_{-}^{\beta }\right) \) and \(k_{+}^{\alpha }=\varLambda _{\beta }^{\alpha }k_{-}^{\beta }\). In general, there is some back reaction (some change in parameters \(X_{+}^{\alpha }\), \(X_{-}^{\beta }\), and \(\varLambda _{\beta }^{\alpha }\)) as described in [17]. In the present paper we neglect the back reaction. In the reference frames in which the throat entrances are at rest the map corresponds simply to the inversion of the spheres. This can be easily seen for the simplest Ellis-Bronnikov metric (EB-wormhole) \(ds^2 =dt^2-f^2(r)dl^2\), where \(f(r)=1+b^2/r^2\) and \(dl^2=dr^2+r^2(\sin ^2\theta d\phi ^2+d\theta ^2)\) is the standard line element of the flat space. The inversion map \(r'=b^2/r\) simply interchanges the inner and outer regions of the sphere \(r=b\) which is the minimal throat section of the EB-wormhole. Close to the minimal section \(r=b\) almost any spherical metric with a smooth source can be reduced to this case.
First, for the sake of simplicity we assume that the space is flat (this is not an approximation since in the neighborhood of any point of the surfaces \( \varSigma _{\pm }\) the metric can be taken as a flat Minkowski metric, the only exclusion case is the so-called thin-shell wormholes). Second, we assume \( X_{\pm }^{\alpha }=(t,{\mathbf {R}}_{\pm })\) (the shift of time is absent), and velocities \(\frac{d}{dt}{\mathbf {R}}_{\pm }={\mathbf {V}}_{\pm }\) \(\ll c\) (velocities of centers of spheres \(S_{\pm }\)). Then \(\varLambda _{\beta }^{\alpha }\) is a composition of a space rotation \(U_{\beta }^{\alpha }\) and Lorentz boost.
Consider the incident wave \((\omega _{in},{\mathbf {k}}_{in})\). Let it falls on the throat \(S_{-}\) at the point \({\mathbf {x}}_{-}^{\prime }=b {\mathbf {n}}_{-}^{\prime }+{\mathbf {R}}_{-}\) (where \(b{\mathbf {n}}_{-}^{\prime }= \mathbf {\xi }_{-}^{\prime }={\mathbf {x}}_{-}^{\prime }-{\mathbf {R}}_{-}\)). Since the throat \(S_{-}\) moves in space with the velocity \({\mathbf {V}}_{-}\) the frequency and the wave number in the coordinate system in which the throat \( S_{-}\) is at rest are (we assume \( V_{\pm }/c\ll 1\))
This wave (ray) is absorbed by the throat \(S_{-}\) and re-radiates from \( S_{+} \) at the point \({\mathbf {x}}_{+}^{\prime }=b{\mathbf {n}}_{+}^{\prime }+ {\mathbf {R}}_{+}\) which relates to \({\mathbf {x}}_{-}^{\prime }\) by the relation (rotation)
In the reference system in which \(S_{+}\) is at rest the frequency and the wave number of the outgoing (re-radiated) wave are
Thus in the initial coordinate system we find the re-radiated values \( (\omega _{out},{\mathbf {k}}_{out})\)
3 Energy transport equation
The incoherent nature of the scattered signal shows that the exact form of the wavefront is not important for observations. It may be important only for observing the scattering on a particular single wormhole. If we are so happy to make all the necessary conditions meet, then we will need the detailed structure of the scattered signal. However the situation is such that in the nearest future we may hope to detect only collective effects of their scattering. To this end the most convenient way to use the equations for the transport of energy. Such an equation comes out from the standard kinetic equation for the number of gravitons N(k, r) in the phase space \( \Gamma =(k,r)\). Indeed, in the case when phases of GWs are random the energy of the GWs can be written as follows
In the above expression the index j stands for polarizations. In what follows we will omit the index j. In Eq. (6) \(W_{k}\) is the spectral energy density (energy in a unit volume of space and a unit volume of wave numbers). In the isotropic case (more generally, when the number of gravitons depends only on the frequency \(N_{\omega }\)) the spectral energy is described by \(W_{k}d^{3}k\) \(=W_{k}k^{2}dkd\varOmega \) \(=W_{k}k^{2}\left| \frac{ dk}{d\omega }\right| d\omega d\varOmega \) \(=W_{\omega }d\omega d\varOmega \). When considering radiation it is commonly used the spectral intensity of GW radiation (Poynting vector or the energy flux)
where \(\frac{d\omega }{d{\mathbf {k}}}={\mathbf {V}}_{g}\) is the group velocity. In general relativity \(\left| {\mathbf {V}}_{g}\right| =c\), while in different modified theories its value may change. We see that intensity of waves relates to \(W_{k}\), \(W_{\omega }\) simply as \(I_{k}=cW_{k}\).
Consider the number of gravitons/photons (\(W_{k}=\hbar \omega (k,r)N_{k}\))
The equation for \(N_{k}\) may be obtained from the geometric optics for simplest case of a set of gravitons. One may consider gravitons as massless (spin-2) particles with the momenta \(p_{\mu }=\hbar k_{\mu }\) and the dispersion relation \(k_{\mu }k_{\nu }g^{\mu \nu }=0\) which defines the energy \(\omega (k,r,t)\). Here \(\gamma _{ij}\) is the space metric, \(\left( {\mathbf {r}}(t),{\mathbf {k}}(t)\right) =\) \(\Gamma _{k}(t)\) corresponds to a particular isotropic geodesic line and \(\omega (k,r,t)\) obeys to
Then the kinetic equation has the form (e.g., see [17])
where we use the definition
\({\widetilde{\alpha }}_{k}\) is the emission of particles/gravitons in the unit time and unit volume, \(\varSigma \) is the scattering matrix
In the above expression \(\sigma \left( \Gamma ,\Gamma _{w},\Gamma ^{\prime },\Gamma _{w}^{\prime }\right) \) is the cross-section of the scattering on a wormhole \(\Gamma ,\Gamma _{w}\rightarrow \Gamma ^{\prime },\Gamma ^{\prime }{}_{w}\), (here \(\Gamma \) and \(\Gamma _{w}\) are parameters before the scattering (incident) and \(\Gamma ^{\prime }\) and \(\Gamma _{w}^{\prime }\) are parameters after the scattering) which are determined by (4) and (5), \(N_{w}\left( \Gamma _{w}\right) \) is the number of wormholes in the configuration space \(\Gamma _{w}\), and \(\Gamma _{w}=\left( R_{\pm },V_{\pm },b,U,...\right) \) are all the parameters of the wormholes. In what follows we will assume the case when wormhole are infinitely heavy objects (neglect the back reaction), then we get
In the general case it is given by \(\sigma =\sigma _- +\sigma _+\) (e.g., see [17, 31])
where \(\Gamma ^{\prime }=\Gamma _{in}=(x_{in},{\mathbf {k}}_{in})\) and \(\Gamma =\Gamma _{out}=(x_{out},{\mathbf {k}}_{out})=(r,{\mathbf {k}})\). The sign \(\sigma _{-}\) means here that GW ray falls on \(S_{-}\). The second term in (13) corresponds to the absorption on \(S_{-}\) and the first term corresponds to the re-radiating of the absorbed signal from \(S_{+}\). Analogous term \(\sigma _{+}\) corresponds to the wave which falls on \(S_{+}\) and re-radiates from \( S_{-}\). In the final expression (29) it gives only the factor 2 (due to the symmetry between entrances).
The equation for the energy transport is found to be
where
\(\varSigma \) is defined by (12), and the energy density \(W_{k}\) for a set of gravitons is
In Eq. (14) the term \(\alpha _{k}=\hbar \omega \widetilde{\alpha }_{k}\) describes spontaneous radiation and \(\mu \) describes adsorption/re-radiation (induced radiation) of the GW radiation in a unit volume of the medium.
We point out that Eq. (14) works also in the case when the medium consists of normal matter objects (stars or black holes, gas, etc.). In such a case however the scattering matrix \(\varSigma \) should be determined separately and in (15) \(N_w\rightarrow N_s\). There exist however a phenomenological way to get estimates for the GW scattering on stars or black holes. It corresponds to the limit when the separation of wormhole entrances vanishes \(R_+=R_-\) and the throat radius becomes the gravitational radius of the object \(b=r_g\). Then the scattering laws (4) - (5) correspond simply to the reflection of rays from the gravitational radius of the object. This case does not require a separate consideration, since it can be modeled by a specific form of the wormhole distribution \(N_w(\Gamma _{w})={\tilde{N}}_s(\Gamma _-)\delta ({\mathbf {R}}_+ -{\mathbf {R}}_-)\), where \(\Gamma _-\) corresponds to the set of parameters of a single wormhole entrance.
The second term in l.h.s. of (14) describes the change of the energy flux due to the non-stationarity of the background. In particular, in an expanding Universe the frequency changes according to the cosmological shift only \(\frac{1}{\omega }\frac{d\omega }{dt}=-H\) (here the dependence on time goes through \(\lambda (t)\sim r=a(t)x\)) and the change of the volume element is \(\frac{1}{\sqrt{\gamma }}\frac{d\sqrt{\gamma }}{dt}=3H\), where H is the Hubble constant (\(\sqrt{\gamma }=a^{3}(t)\)). If we neglect the effects of the expansion (the red shift of the frequency), then (14) reduces merely to
where we used the relation \(\frac{d\ell }{dt}=V_{g}=\left| \frac{d\omega }{d{\mathbf {k}}}\right| \), \(\ell \) is the natural parameter along the ray (the length), and \(\frac{d}{d\ell }=\frac{d{\mathbf {r}}}{d\ell }\frac{\partial }{\partial {\mathbf {r}}}+\frac{d{\mathbf {k}}}{d\ell }\frac{\partial }{\partial {\mathbf {k}}}\).
The aim of this section was to derive the energy transport equation which is given by (14). It is important that the structure of the scattering term (15) which is determined by the scattering matrix (13) provides the rigorous conservation law for the number of absorbed and emitted gravitons. The energy of gravitons however depends on the redshift and the total energy does not conserve. It conserves only when we apply those equation to the local Universe with redshifts \(z< 0.1\) (distances up to a billion of light years). In this case we can neglect the expansion and use the more simple Eq. (16).
4 Scattering of gravitational waves
4.1 Direct signal
Let the spacetime be flat \(\omega =ck\) and let us take the source in the form
Then at the moment \(t^{\prime \prime }\) we have radiation with the spectrum \(w_{0}(k) =L \delta \left( \omega -\omega _{0}\right) \) from the point \(x^{\prime \prime }\). We point out that binary mergers form the source in the form
where the amplitude \(L(t)=Q(t)^{2}\) and \(\omega _{0}(t)\) correspond to the chirp signal [32]. The real signal can be simply taken as the sum of type ( 17) signals.
In the leading order, without taking into account the scattering on wormholes, we find the solution of (16) in the form (see Appendix D)
where \(R=\left| {\mathbf {r}}-{\mathbf {r}}^{\prime \prime }\right| \) and \(\theta ^{\prime }\), \(\phi ^{\prime }\) relate to the direction of the velocity \({\mathbf {V}}_{g}\). The chirp signal (18) forms the energy density as follows
where we denote \(\left[ f(t)\right] _{ret}=f\left( t-\frac{\left| {\mathbf {r}}-{\mathbf {r}}^{\prime \prime }\right| }{c}\right) \).
4.2 Damping and echoes: the halo of secondary sources
The additional signal comes from the additional sources (the so-called a distributed hallo)
If the distribution of wormholes in terms of the matrix U is isotropic, then re-radiation will come out in an isotropic way (omnidirectional flux). Then we should follow only the frequency shift which is given by (4), (5)
We point out that in and out states are symmetric. Here the unit vector \( {\mathbf {m}}_{in}=\left( {\mathbf {R}}_{-}-{\mathbf {x}}^{\prime \prime }\right) /\left| {\mathbf {R}}_{-}-{\mathbf {x}}^{\prime \prime }\right| \) and \( {\mathbf {m}}_{out}=\left( {\mathbf {x}}-{\mathbf {R}}_{+}\right) /\left| \mathbf {x-R}_{+}\right| \) points to the observer.
Let us evaluate the term which corresponds to the absorption of radiation. We point out that the absorption term in (13) defines simply damping of the intensity and has the structure in (16)
where
Above n(r, b) is the number density of wormholes at the point r and with the throat radius b, \(\sigma \left( b,\omega \right) \) is the total cross-section of such wormholes (in the most general case it depends on \(\omega \)), and the multiplier 2 comes from taking into account absorption on both throats \(S_{+}\) and \(S_{-}\) (both give equal contribution due to the symmetry \(+\leftrightarrow -\)). The term (23) simply defines damping along the ray \(W_{k}\sim e^{-\tau }W^0_{k}\), where \(\tau =\frac{1}{c}\int \mu d\ell \) is the optical depth. It is important that in the case of the GW propagation through the normal matter the damping is determined by the same term (23) with \(\mu (\omega )=c\sigma _s n_s(r)\), where \(\sigma _s \) and \(n_s\) are the cross-section and the number density of respective objects (stars, black holes, gas, or any other objects).
The additional radiation capability (secondary sources) is more complex term which is
Now, if we use the approximation (due to \(\left| R_{-}-x^{\prime \prime }\right| \gg \xi _{+}\))
which means that in the first approximation throat is a point source at the position \({\mathbf {R}}_{+}\), and using the assumption that throat re-radiates in isotropic way (due to averaging over the rotation matrix U), then we find
Using different distributions for wormholes \(N_{w}\left( \Gamma _{w}^{\prime }\right) \) we may get different answers. The simplest distribution seems to be (recall that due to the property \({\mathbf {V}}_{+}=U{\mathbf {V}}_{-}\) only \( {\mathbf {V}}_{+}\) is independent and \(V_{+}^{2}=V_{-}^{2}\))
where \( f({\mathbf {V}}_{-} ) =( 2\pi \sigma ^2_V) ^{-3/2}\exp ( - \frac{V_{-} ^{2}}{2\sigma _V ^{2}})\). The normalization condition gives \(\int N_{w}( \Gamma _{w}) dbd^{3}R_{+}d^{3}R_{-}d^3V_{-}^{3}=n_{w}V\) (V is the volume of space and \(n_w\) is the wormhole number density). Such a distribution corresponds to the case when wormholes are homogeneously distributed in space and all wormholes have the same throat radius \(b=b_{0}\) and the same distance between entrances \(\left| R_{+}-R_{-}\right| =\varLambda \).
The fact that density \(\alpha _{k}\) and, therefore, \(W_{k}^{0}\) depend only on \(\omega \) simplifies essentially the re-radiation terms. Let \(\sigma _V ^{2}\rightarrow 0\) (i.e., \( V_{+}^{2}=V_{-}^{2}=0\) and throats are static), then \(\omega _{in}=\omega _{out}\) and we find
Then for the additional energy density we find
where we denote \({\mathbf {n}}_{+}=\left( {\mathbf {x}}- {\mathbf {R}}_{+}\right) /\left| {\mathbf {x}}-{\mathbf {R}}_{+}\right| \), \({\mathbf {n}}_{+}^{\prime }={\mathbf {k}}/k\), and \(dR_{\pm }=d^3R_{+}d^3R_{-}\). The function \([w( \omega ,t)]_{ret}= w\left( \omega ,t-\frac{\left| R_{+}-x\right| }{c}-\frac{\left| R_{-}-x^{\prime \prime }\right| }{c}\right) \) shows that the retarding sums. Integrating this over directions \({\mathbf {k}}/k={\mathbf {n}} _{+}^{\prime }\) gives the spectral energy by the relations \(\delta W_{k}d^{3}k=k^{2}\delta W_{k}dkd\varOmega ^{\prime }=\frac{\omega ^{2}}{c^{3}} \delta W_{\omega }d\omega d\varOmega ^{\prime }\) and, therefore, we define the spectral energy flux \(\delta {\widetilde{I}}_{\omega }= \frac{\omega ^{2}}{c^{2}} \int \delta W_{\omega }d\varOmega ^{\prime }\) as
In agreement to (3) for a discrete set of wormholes the energy flux can be written as the sum
where the sum is taken over wormhole entrances numbered by j and s (\(s=\pm \)). Here all cross terms which may arise from (3) disappear due to loss of coherence. Comparing this to the basic energy flux (20) of the direct signal
we see that every echo signal, i.e., every particular term in (31), has the same spectral composition and the same form. The difference appears only in the arrival times, directions to the source, and amplitudes.
4.3 Corrections
The above expressions assume that the space is flat and the red shift is absent. The redshift can be straightforwardly accounted for, it gives in (31) and (32) the additional multiplier \((1+z)^{-3}\), the shift of frequencies, i.e., the replacement \(\omega \rightarrow (1+z)\omega \) in the function \(w( \omega )\) (e.g., in the case when \(w=w_0\delta (\omega -\omega _0)\) we should replace it with \(\frac{w_0}{(1+z)}\delta (\omega -\frac{\omega _0}{1+z})\)) and the replacement \(t\rightarrow a(t)\int dt/a\). Moreover, they assume also that wormholes have negligible length of throats, while the substitution (26) produces an error in the time delay of the order \(\eta \sim 2b/c\). In a long throat however the actual flux (it’s amplitude) does not decrease but remains almost constant. From the other side the spherical symmetry assumes that wormhole metric remains conformally flat (for the space-like part of the metric). Therefore, formally the behavior of the energy density scattered by a single wormhole remains the same \(\delta {\widetilde{W}}_{\omega A}\sim 1/R_{A}^{2}\). All what is actually changed is the retarding time. This means that the main effect is the adding an additional retarding time \(\eta _{A}\) to every particular wormhole. From the rigorous standpoint \(\eta _{A}\) can be found by considering geodesics with the exact metric of a wormhole and it explicitly depends on all wormhole parameters and the positions of the source \(x''\) and the observer x, i.e., \(\eta _{A}=\tau (x,x',\Gamma _{w})\). Phenomenologically, however, such a quantity can be added as an additional parameter to \(\Gamma _{w}\), while (31) transforms to
Every particular term in the above expression describes a particular echo signal. In principle, some terms may produce a considerable and even detectable signal. This depends essentially on the specific positions in space of wormholes and the primary source. Such terms may be considered separately and they describe effects of GW scattering on a single wormhole. In the present paper first of all we are interested in collective effects. Moreover, most of terms give only a tiny contribution to the sum. When we consider a random statistical distribution of wormholes, all such signals merge and form a long-living tails for the basic signal. The structure and the dependence on time of the tail we consider in the next section.
5 Tails: time structure of the scattered signal
Since durations of actual GW signals from binary mergers are very short (as compared to the travel time R/c), in the leading order every such a signal can be approximated by delta-like impulse. Consider the source in the form \(w\left( \omega ,t\right) =w_{0}\left( \omega \right) \delta \left( t-t^{\prime \prime }\right) \). Then the spectral energy flux \(I_{\omega }^{0}( x,t) \) in the direct signal is
where \(R^{2}=\left| x-x^{\prime \prime }\right| ^{2}\), which determines the values
where \(4\pi F=4\pi \int \frac{\omega ^{2}}{c^{3}}w_{0}\left( \omega \right) d\omega \) has the sense of the total energy emitted by the source. We point out that the expression (34) does not account for the damping due to the absorption of radiation on wormholes. According to (23) the actual signal detected by an observer contains the additional multiplier \(e^{-\tau }\) which gives \(I_{\omega }^{vis}=e^{-\tau }I_{\omega }^{0}\).
The distribution of wormholes we take in the simplest form (28) but for static wormholes, i.e., \(\sigma _V\rightarrow 0\) and \(N_{w}=\frac{n_{w} }{4\pi \varLambda ^{2}}\delta \left( \varLambda -\left| {\mathbf {R}}_{+}-\mathbf { R}_{-}\right| \right) \delta \left( b-b_{0}\right) \). For simplicity we assume that the delay parameter \(\eta _{\pm }=const\). Such a distribution corresponds to the case when all wormholes have the same throat radius \(b=b_{0}\) and the same distance between entrances \(\left| \mathbf { R}_{+}-{\mathbf {R}}_{-}\right| =\varLambda \). The more general case one obtains by averaging results with an additional distribution \(p\left( \varLambda ,b_{0}\right) \) (which has sense of the probability density for wormholes \(\int p\left( \varLambda ,b_{0}\right) d\varLambda db_{0}=1\)).
Let us define the multiplier
Then the additional energy flux \(\delta I_{\omega }=c\delta {\widetilde{W}} _{\omega }\ \)(spectral energy which falls on a unit square per unit time) can be cast to the form
First, we determine the total energy in the tails.
5.1 Total energy in tails
The total energy in the tail which falls on a unit square is
Now using the substitutions \({\mathbf {R}}_{+}={\mathbf {X}}+{\mathbf {R}} _{-}\) and the set of variables \({\mathbf {X}}=X{\mathbf {n}}\), \({\mathbf {R}}_{-}=r{\mathbf {l}}+{\mathbf {x}}^{\prime \prime }\), \({\mathbf {l}}^{2}={\mathbf {n}}^2=1\), we get
where we have defined variables \(R=\left| \mathbf {x-x}^{\prime \prime }\right| \), \(\chi =\frac{\varLambda }{R}\), and the function \(C( \chi )\) is determined by the integral
In the above integral we rescale the integration variable \(y=\frac{r}{R}\), and \({\mathbf {m}}=({\mathbf {x}}-{\mathbf {x}}^{\prime \prime })/R\). This function is determined in Appendix A and has the form
where the numerical constant is \(C(0)=2.\,4674\). This determines the total energy flux in the tail as
where \(\tau =2\pi b_{0}^{2}n_{w}R\) and \(\Phi _{\omega }^{vis}=e^{-\tau }\Phi _{\omega }^{0}\) is the energy flux detected by an observer. We see that the ratio of amplitudes depends on \(\tau =\tau _w=2\pi \left\langle b^{2}\right\rangle Rn_{w}\), which has sense of the optical depth, i.e. the mean number of wormholes contained in the volume \( 2\pi b_{0}^{2}R\). In the case of stars \(\tau =\tau _s=\pi \left\langle r_g^{2}\right\rangle Rn_{s}\) and we get \(\tau _s\ll 1\) (the multiplier 2 appears in \(\tau _w\) since every wormhole has two entrances). The mean optical depth determines damping of the basic signal (23) when propagating in all possible directions and it reaches values \(\tau _w> 1\).
5.2 Estimates for the optical depth
It is necessary to stress that the definition \(\tau =2\pi \left\langle b^{2}\right\rangle Rn_{w}\) does not mean that the basic signal from a sufficiently remote source does not reach the observer, since in general case wormholes are distributed rather irregularly by a fractal law and wormhole parameters \(\left\langle b^{2}\right\rangle \) and \(n_{w} \) also depend on the scale R. In particular, in a fractal medium there may always be directions in which the Universe is transparent (there will be no wormholes on the line of sight). Moreover, for a fractal distribution of wormholes the optical depth may reach a finite limiting value \(\tau (R)\rightarrow \tau _0\) as \(R\rightarrow \infty \).
If we accept that wormholes are responsible for dark matter phenomenon, then the estimate for the optical depth can be obtained as follows [33]. Consider a ball with the radius R around any galaxy. We assume that space around the galaxy possesses the isotropy. The fractal topological structure means that the volume contains wormholes and that the physical volume of such a ball behaves with the increase of the radius as \(V_{ph}(R)\sim R^D\) with the Hausdorff dimension \(D<3\) (dark matter halos of galaxies favor for the value \(D\simeq 2\)). Then the area of the surface which restricts such a ball behaves as \(S_{ph}(R)=dV_{ph}(R)/dR\). We point out that this area accounts only the external surface, while every wormhole also introduces a couple of closed surfaces which lay completely inside the ball. We also recall that in the standard flat space we expect the coordinate volume is \(V_{coor}=4/3 \pi R^3\) and \(S_{coor}=4\pi R^2\). The difference between the actual value \(S_{ph}(R)\) and \(S_{coor}(R)\) we see as the presence of some extra amount of matter or of dark matter, while in the case of radiation it determines some extra radiation which comes as a diffuse halo. Indeed, the total mass and the total luminosity reduce to the surface integrals, and, therefore, we can use the Gauss theorem to estimate the partition on the direct visible and dark/diffuse values. Consider the total luminosity emitted by the galaxy which is given by
where \(I_n\) is the normal component of the Pointing’s vector. This defines the behavior of the mean intensity of radiation with scales as
Here the first term corresponds to the direct signal and the second term corresponds to the scattered diffuse radiation which determines the partition of the total flux as \(I_{tot}=I_{dir}+I_{diff}\). The total energy emitted splits \(L=I_{tot}S_{ph}=e^{-\tau }L+(1-e^{-\tau })L\), where the ratio \(S_{ph}/S_{coor}=I_{dir}/I_{tot}=e^{-\tau }\) determines the mean value of the optical depth \(\tau \).
Analogous relation holds true for the mass within the ball
where G is the gravitational constant and \(F_n\) is the normal component of the Newton’s force. We point out that the expression of the total mass via the surface integral is the general feature of general relativity and it is not specific for Newton’s limit only. Therefore, our consideration here has the most general character.
The total mass and the force also split onto two parts which correspond to the visible matter and dark matter \(F=F_{vis}+F_{dm}\). This allows to relate
Thus the optical depth as well as the mass of dark halo depends on the distance from the galaxy R. If we neglect local inhomogeneities in the distribution of dark matter we find the constant mean value which already does not depend on the distance R and it is expressed via the cosmological parameters as \(e^{\tau }=1+\rho _{DM}/\rho _{vis}\sim 6\).
In the above picture the inhomogeneity of dark matter distribution reflects the inhomogeneity of local topological structure. This causes the analogous inhomogeneity of the optical depth. For example, in Low Surface Brightness galaxies the ratio of dark to luminous matter may reach the order \(M_{DM}/M _{b}\sim e^{\tau }\sim 10^3\). Such a value much exceeds the mean cosmological value \(e^{\tau }\sim 6\) and we may expect that it does not increase with distances. This however means that the actual luminosity of such galaxies is three orders higher, while almost all radiation comes from a diffuse halo around such a galaxy.
In High Surface Brightness galaxies the amount of dark matter is more modest which gives \(e^{\tau }\sim 2\div 3\). Apparently this parameter still depends on the distance from such a galaxy until it reaches the limiting cosmological value \(e^{\tau }\sim 6\).
5.3 The dependence on time
In the variables \({\mathbf {R}}_{+}={\mathbf {X}}+{\mathbf {R}}_{-}\) and \({\mathbf {R}} _{-}={\mathbf {R}}\) the energy flux (37) reads
Using coordinates \(\mathbf {X=}x{\mathbf {n}}\), \({\mathbf {n}}^{2}=1\) and integrating over x we get
where we use the set of variables as \({\mathbf {R}}=\mathbf {Y+x}^{\prime \prime }\), \({\mathbf {x}}-\mathbf { x}^{\prime \prime }=R{\mathbf {m}}\), and \(R=\left| \mathbf {x-x}^{\prime \prime }\right| \). This can be re-written as
where we have denoted \(\xi =\frac{\left( t-t^{\prime \prime }-\eta \right) c}{R}\) , \(\chi =\frac{\varLambda }{R}\), and (we use the variable \(\mathbf {y }=\mathbf {Y/}R\) in the integral)
The exact form of \(J(\xi ,\chi )\) is determined in Appendix B and Appendix C.
First, we consider the tail for the scattering by normal matter \(\chi =0\). This case can be considered as the limit when the distance between entrances into the same wormhole tends to zero \(\varLambda =|R_+-R_-|\rightarrow 0\) which means that scattered radiation comes from the same point where it was adsorbed.
In the approximation \(\chi \ll 1\) and for the region \(\xi >1+\chi \) Eq. (42) gives
The plot of \(J(\xi ,0)\) is given on Fig. 1. In the limit \(\chi \rightarrow 0\) the distance between throats vanishes and the advanced signal is merely absent (e.g., in the region \(0<\xi <1\) we get \(J(\xi ,0)=0\)). All the scattered signal comes with a retarding. The infinite value of J at \(\xi =1\) does not mean that the echo is very strong, since it should be compared with the delta impulse (34). In considering the incident signal of a finite duration \(\delta t\), the tail smoothes and takes a finite value. Indeed, for very small times \(\xi -1\ll 1\) we have an approximation \(\xi =1+\varDelta \xi \) and therefore \(J(\xi ,0)=16\pi ^2\left( \ln 2-\ln \varDelta \xi +\frac{\varDelta \xi }{2}\ln \frac{ e\varDelta \xi ^{2}}{4}+\cdots \right) \). Integrating this over \(t''\) (\(dt''=\varDelta t d\xi \), where \(\varDelta t=R/c\)) gives already the finite value
Qualitatively, the smoothed function \(\left<J(\xi ,0)\right>\) behaves as \(J(\xi ,\chi )\) for \(\chi \ll 1\) which we describe below. The case \(\chi =0\) corresponds to the scattering on normal matter when re-radiation has an isotropic character. In this case however the optical depth \(\tau _s \ll 1\) and \(\delta I_{\omega }/ I_{\omega }^{0}\rightarrow 0\). We point out that the value \(\tau _s \) has here the statistical character. In the case when there is an object, on the way of the ray, the echo signal may be considerable. This case is described by lensing or scattering on a single object.
Consider now the case of wormholes. For non-vanishing values \(\chi \) the advanced signal does exist in the region \(\xi >1-\chi \) and increases till the maximal value \(J_{\max }\) which is reached at the point \(\xi =1+\chi \). This gives
The plot of \(J_{max}\) is presented on Fig. 2.
From (41) we see that \(J_{max}\) determines the maximal possible amplitude in the echo. Different forms of tails \(J(\xi ,\chi )\) for different values of \(\chi \) are presented on Fig. 3. Dashed line corresponds to the case \(\chi \rightarrow 0\). The advanced signal corresponds to the region \(0<\xi <1\) and it does exist only for values \(0<\chi <2\). In the region \(\chi >2\) the tail is completely retarded. Indeed, the values \(\chi >2\) correspond to the case when the mean distance between throat entrances \(\varLambda \) exceeds (at least on the factor two) the distance to the source R and, therefore, the time required for the signal to go through a wormhole exceeds the time required for the direct signal.
In the approximation \(\chi \gg 1\) we find
Here the advanced signal is also absent (since the travel time to wormhole entrances exceeds the value \(\varDelta t=c/R\)). As we see from Fig. 3 for sufficiently big \(\xi \) the decrease of tails with time as \(\sim 1/\xi \sim 1/t\) is the common feature of tails for all values of \(\chi \).
5.4 Structure of general GW signals with tails
In the case of a delta-like impulse the total signal is described by
where \(\Phi _{\omega }^{0}\) is determined by (35). An arbitrary GW emission we obtain, if we replace \(w_0(\omega )\) with a function \(w_0( \omega ,t^{\prime \prime })\) and integrate the above equation over \(t^{\prime \prime }\). This defines the spectral energy flux as
The typical duration of emission is very short, while the function \(J(\xi ,\chi )\) is very slow function (recall that \(\xi =\frac{\left( t-t^{\prime \prime }-\eta \right) c}{R}\) almost does not change with a small change of \(t^{\prime \prime }\), i.e., \(\varDelta \xi =c\varDelta t^{\prime \prime }/R\ll 1\)). This means that the multiplier \(\frac{\tau }{4\pi }\frac{c}{R}J(\xi ,\chi )\) can be taken at the moment of the start of emission \(t^{\prime \prime }=t_0\) and can be removed from the integration. As it was pointed out above in the case \(\chi =0\) one should replace J with \(\left<J\right>\) from (44) and for simplicity we set \(\eta =0\). Then integrating this over frequencies \(I=\int I_{\omega }d\omega \) we find
We see that tails have indeed a universal structure. For a short impulse \(\int I^0 dt\sim I^{0}\delta t\sim 2\pi I^{0}/\omega _{0}\), where \(\delta t\) is the duration of the basic signal. The value \(R/c=\varDelta t\) is the propagation time, and therefore we find
The typical ratio \(\frac{\delta t}{\varDelta t}\) is extremely small \(\frac{\delta t}{\varDelta t}\sim 10^{-15}\) and, therefore, the direct detection of the tail signal is hardly possible. Indeed, the energy flux relates to the amplitude h as follows
where \(h_{\times }\) and \(h_{+}\) correspond to the two independent polarizations. Assuming the periodic signal \(\sim e^{-i\omega _0 t}\) we find
This explicitly shows that the tail contribution is \(\delta h \ll h\). However, while the duration of the direct signal h is very short, the tail part \(\delta h ^2\) decays with time very slowly \(J(\xi _0,\chi )\sim \varDelta t/(\varDelta t+t)\sim 1\) and the total energy in the tail, according to (40), may exceed the energy in the basic signal (i.e., \(\int \delta h ^2 dt\gg \int h^2 dt\)). This means that the presence of such a heavy tail may be nevertheless observed by the increase of the noise level. The tails live for an extremely long period of time, at least \(J(\xi _0,\chi )\ge 1\) for \(t\sim \varDelta t\), and during this time all such tails from different binary mergers accumulate. This roughly gives the additional multiplier \(N\simeq \nu \varDelta t\), where \(\nu \) is the mean rate of events and this gives already the factor
instead of (48), where for estimates we used \(\nu \delta t \sim 10^{-5} \), \(\chi =0.24\), and \(\tau e^{\tau } \sim 10\). Therefore the total noise level can be considerable and the reported in [4,5,6,7] echoes may simply detect the stochastic background of GW radiation.
In conclusion we point out that we have assumed the specific model of the wormholes distribution when the distance between wormhole entrances has the same value \(\varLambda =\left| R_{+}-R_{-}\right| \) and all wormholes have the same throat value \(b=b_0\). To obtain the more general case we have to carry out an additional averaging with some probability density \(p(\varLambda ,b)\) which surely changes the structure of tails. This can be done directly in (47), (48), and (49) which simply corresponds to the replacement \(J\rightarrow \left<J\right>=\int Jp(\varLambda , b)d\varLambda db\).
6 Conclusions
In this manner we have demonstrated that the scattering of gravitational waves on wormholes may have a rather considerable effect, it produces the GW noise (49) which belongs to the same frequency range as the original ingoing signal. In the present paper we discuss gravitational waves and use the approximation of the geometric optics. From one side this puts some restrictions on parameters of wormholes and frequencies of radiation. From the other side our consideration equally works for all kinds of radiation and it is not specific for gravitational waves only. The basic effect is the formation of a stochastic GW background due to the scattering on wormholes of signals from all possible discrete sources. The intensity of such a background depends on the number density of such sources (49) and essentially on the specific distribution of wormholes \(p(\varLambda , b)\).
We have assumed that the distribution of relic wormholes possesses fractal properties which is predicted by lattice quantum gravity models [12]. In a series of papers we have already demonstrated that such wormholes may produce effects which are indistinguishable from effects of dark matter [16, 17, 33]. The origin of dark matter of such a kind shows a deep analogy with the origin of the background radiation due to scattering on wormholes, e.g. see Sect. 5.2. Moreover, if the dark matter phenomenon appears indeed due to wormholes, this should have a rather important consequences for observations. First of all this should mean that intensities of discrete sources are somewhat underestimated. Sufficiently remote sources have the additional optical depth \(e^{\tau }\sim 6\) which appears due to scattering on wormholes, while for some particular sources surrounded by a more dense dark matter halos it may give much bigger values (e.g., for LSB galaxies it may reach the value \(e^{\tau }\sim 10^3\)). This should somewhat change predictions derived from observations of discrete sources (e.g., the values of masses of black holes in binary mergers [34], the Hubble constant [35], etc.).
However, before presenting any specific astrophysical predictions our approach should be developed further. First of all, this concerns effects related to the cosmological evolution and the dependence on the redshift. For the local Universe (\(z<0.1\)) the shift due to the expansion is rather small and in the leading order can be neglected. However for deeper sources the dependence on the redshift is essential, e.g., the most distant source GW190521 gives considerable shift of frequencies \(\varDelta \omega /\omega \sim 1\). Moreover, the most distant galaxy GN-z11 is observed at \(z=11.09\) [36] and we may expect that signals from binary mergers may come even from more remote regions with \(z>11\). In particular, the explicit form of tails \(J(\xi ,\chi )\) corresponds to the local Universe when the redshift is neglected and for a particular distribution of wormholes having the same distance between entrances into every wormhole \(\chi \). In a more general case we have to make some averaging over possible values of \(\chi \) and account for the dependence on z. In other words, together with the noise from the local Universe there should come a shifted noise from extremely remote regions. The way how the dependence on the redshift can be incorporated we discussed in Sect. 4.3, however this problem requires the further investigation.
In conclusion we point out that the behavior of long-living tails \(h^2\sim 1/t\) can be naively associated with a small effective mass for the graviton. Such an interpretation indeed may take place. In particular, a homogeneous distribution of wormholes was shown to give rise to the origin of additional massive gravitons [15]. However in the case of wormholes the effective mass term was incorrect sign. The scattering of gravitons on normal matter has always the retarded character which should produce an analogous effective mass with correct sing. In general there will be a competition between such two effects. This problem however requires a more deep investigation.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment:This is theoretical work in which no experimental data are generated and/or analyzed.]
Notes
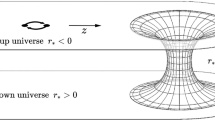
In the present paper the advanced signal means that it comes to an observer before the basic signal. Such signals go merely through some wormhole throats which give shortcuts and therefore they travel shorter distances.
References
B.P. Abbott et al., Phys. Rev. Lett. 116, 061102 (2016)
B.P. Abbott et al., Astrophys. J., 851, L35, (2017)
Kagra Collaboration et al., Nat. Astron. 3, 35 (2019)
J. Abedi, H. Dykaar, N. Afshordi, Phys. Rev. D 96, 082004 (2017)
R.S. Conklin, B. Holdom, J. Ren, Phys. Rev. D 98, 044021 (2018)
J. Westerweck et al., Phys. Rev. D 97, 124037 (2018)
J. Abedi, N. Afshordi, JCAP 11, 010 (2019)
V. Cardoso, E. Franzin, P. Pani, Phys. Rev. Lett. 116, 171101 (2016)
V. Cardoso et al., Phys. Rev. D 94, 084031 (2016)
V. Cardoso, P. Pani, Living Rev. Rel. 22, 4 (2019)
L. Dai et al., Phys. Rev. D 98, 104029 (2018)
J. Ambjorn, J. Jurkiewicz, R. Loll, Phys. Rev. Lett. 95, 171301 (2005)
J. Laiho, D. Coumbe, Phys. Rev. Lett. 107, 161301 (2011)
G. Clement, Int. J. Theor. Phys. 23, 335 (1984)
A.A. Kirillov, E.P. Savelova, Universe 4, 35 (2018)
A.A. Kirillov, E.P. Savelova, Phys. Lett. B 660, 93 (2008)
A.A. Kirillov, E.P. Savelova, Mon. Not. RAS 412, 1710 (2011)
A.A. Kirillov, E.P. Savelova, Eur. Phys. J. C 80, 810 (2020)
R.P. Geroch, J. Math. Phys. 8, 782 (1967)
A.A. Kirillov, E.P. Savelova, Eur. Phys. J. C 80, 45 (2020)
A.A. Kirillov, E.P. Savelova, Int. J. Mod. Phys. D 25, 1650075 (2016)
K.A. Bronnikov, V.G. Krechet, J.P.S. Lemos, Phys. Rev. D 87, 084060 (2013)
K.A. Bronnikov, J.P.S. Lemos, Phys. Rev. D 79, 104019 (2009)
A.K. Bronnikov, V.G. Krechet, Phys. Rev. D 99, 084051 (2019)
K.A. Bronnikov, S.V. Bolokhov, M.V. Skvortsova, Int. J. Mod. Phys. D 28, 1941008 (2019)
D. Hochberg, A. Popov, S.V. Sushkov, Phys. Rev. Lett. 78, 2050 (1997)
T. Harko, F.S.N. Lobo, M.K. Mak, S.V. Sushkov, Phys. Rev. D 87, 067504 (2013)
R. Myrzakulov, L. Sebastiani, S. Vagnozzi, S. Zerbini, Class. Quantum Gravit. 33, 125005 (2016)
J. Ghersi, T. Galvez, A.V. Frolov, D.A. Dobre, Class. Quantum Gravit. 36, 135006 (2019)
P. Bueno et al., Phys. Rev. D 97, 024040 (2018)
A.A. Kirillov, E.P. Savelova, P.S. Zolotarev, Phys. Lett. B 663, 372 (2008)
C. Culter, E.E. Flanagan, Phys. Rev. D 49, 2658 (1997)
A.A. Kirillov, E.P. Savelova, Gravit. Cosmol. 14, 256–261 (2008)
LIGO Scientific Collaboration, Phys. Rev. X 9, 031040 (2019)
A.G. Riess et al., Astrophys. J. 876, 85 (2019)
P.A. Oesch et al., Astrophys. J. 819, 129 (2016)
A.A. Kirillov, E.P. Savelova, Gravit. Cosmol. 24, 337–343 (2018)
Acknowledgements
We acknowledge valuable comments and the advice of the referee which helped us to clarify some important points and essentially improve the presentation of this work.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Function \(C( \chi )\)
The function \(C( \chi )\) is determined by the integral
where \(d^{2}\varOmega \) is the solid angle. Assuming \(\chi =\frac{\varLambda }{R}\ll 1\) we get \(C( \chi ) \approx C( 0) \)
The opposite case \(\chi \gg 1\) reduces to the analogous expression
In the general case we define \({\mathbf {m}}-\chi {\mathbf {n}}=\gamma {\mathbf {k}}\), where \({\mathbf {k}}^{2}=1\), \( \gamma =\sqrt{\chi ^{2}-2\chi \cos \alpha +1}\), and \(\cos \alpha =(\mathbf {mn})\), then we get
where \(r=\frac{y}{\gamma }\). This transforms the integral into
which gives
Finally we find the expression
Appendix B: Function \(J(\xi ,0)\)
In the approximation \(\chi \rightarrow 0\) Eq. (42) reduces to
Let us use \(x=\cos \theta \), then the above integral gives
Let us use new variable \(u=\sqrt{y^{2}+2yx+1}>0\), \(dx=\frac{u}{y}du\) whose range is \(\left| y-1\right|<u<y+1\). Then we get
This integral splits in two parts which should be considered separately \(J(\xi ,0)=8\pi ^{2}(J_1+J_2)\)
Consider the first part \(J_{1}\). In the regions \(\xi <1\) and \( \xi >3\) the delta function has no roots and we find simply \(J_{1}=0\). In the rest region \(1<\xi <3\) the delta function possesses roots only for \(y>\frac{1}{2}\left( \xi -1\right) \) and therefore
which defines
Now let us consider the second part \(J_2\). Again in the region \(\xi <1\) the delta function has no roots and \(J_{2}=0\). In the region \(1<\xi <3\) roots exist for \(y<\frac{1 }{2}\left( \xi +1\right) \) and we find
In the region \(\xi >3\) we find the upper and lower limits for y as \(y=\frac{1}{2} \left( \xi \pm 1\right) \) which gives
Now collecting all we find
where \(\theta ( \xi -1) \) is the step function. We also point out that \(\int J(\xi ,0)d\xi = (4\pi )^2 C(0)=8\pi ^2\times 4.\,9348\).
Appendix C: Function \(J(\xi ,\chi )\)
Consider the function \(J(\xi ,\chi )\) which is determined by the integral (42).
If we define new variables as \({\mathbf {m}}-\chi {\mathbf {n}}=\gamma {\mathbf {k}}\) with \(\gamma =\sqrt{\chi ^{2}-2\chi \cos \alpha +1}\), \(\cos \alpha =(\mathbf {mn})\), and \(r=y/\gamma \), then the integral reduces to the function \(J(\xi ,0)\) as
Now by means of introducing \(\gamma \) as a new integration variable instead of \(\cos \alpha \) we find
Substituting here (B.10) we get
where \(\theta \left( 1 -x \right) \) is the step function. This integral has different forms for different regions.
First region is \(\xi <\left| \chi -1\right| \). It gives \(x>1 \) and, therefore,
The second region is \(\left| \chi -1\right|<\xi <\chi +1\). The step function defines the upper limit \(x=1\) and we get
The last region is \(\xi >\chi +1\). Then \(\theta \left( 1 -x \right) =1\) and we find
Appendix D: Free motion
For a point-like source \(\alpha _{k}=w_{0}\left( \omega \right) \delta \left( x-x^{\prime \prime }\right) \delta \left( t-t^{\prime \prime }\right) \) and in the absence of the scattering on wormholes (i.e., in the case of free motion) Eq. (14) can be solved by the characteristics method. Indeed the geodesic motion of particles is described by rays
Then, if we take \((k_{0},r_{0})\) as new coordinates, the energy density becomes \(W\left( k_{0},r_{0},t\right) =W\left[ k\left( k_{0},r_{0},t\right) ,r\left( k_{0},r_{0},t\right) \right] \) and (14) reads
which has the obvious solution in the form
where \(\theta \left( t-t^{\prime \prime }\right) \) is the step function ( \( \theta \left( x\right) =1\) as \(x>0\)). Now to return to the initial coordinates \(\left( k,r\right) \) we should simply replace back
which gives (we assume \(t>t^{\prime \prime }\))
In terms of the spherical coordinates \({\mathbf {V}}_{g}=(c,\theta ^{\prime },\phi ^{\prime })\) and \({\mathbf {r}}-{\mathbf {r}}^{\prime \prime }=\left( \left| {\mathbf {r}}-{\mathbf {r}}^{\prime \prime }\right| ,\theta ,\phi \right) \) the above expression transforms to
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Kirillov, A.A., Savelova, E.P. & Lecian, O.M. On generation of a stochastic GW background by the scattering on relic wormholes. Eur. Phys. J. C 81, 263 (2021). https://doi.org/10.1140/epjc/s10052-021-09061-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-021-09061-4