1 Introduction

Up to date, mainly non-relativistic quantum systems were in the scope of the quantum resource theory [1,2,3,4,5,6,7,8,9,10]. However, its concepts such as coherence and mixedness are universal and firmly can be extended to the relativistic quantum systems and neutrinos in particular [11]. Neutrinos host dichotomic left-right helicity and different lepton flavour (electron, muon, and tau) and, when propagating, they can change their type, or oscillate. Neutrino oscillations is an inherently quantum mechanical phenomenon [12,13,14,15,16,17,18] that exhibits such essentially quantum features as entanglement [19,20,21,22,23,24,25] and can be interpreted in terms of quantum resource theory. An interesting case of this phenomenon is expected when neutrinos propagate in the presence of a magnetic field: neutrinos can change both their flavour and helicity (see, for instance, Refs. [26, 27] and references therein). The indicated oscillations can serve as a manifestation of new physics, namely neutrino electromagnetic interactions [28, 29], and can be especially relevant for cosmic neutrinos that propagate in various astrophysical environments, where nonzero magnetic fields are known to exist. Typical examples of this kind are the solar and supernova neutrino problems. Here, however, we are interested in the interstellar neutrino problem [26], where matter effects play a negligible role compared to the stellar cases.

Before proceeding further, we shortly outline the relation of the neutrino oscillation problem to the concept of quantum correlations. The neutrino state can be constructed either on the flavour or mass basis:

$$\begin{aligned}&\vert \nu (t)\rangle =\sum \limits _{\alpha =e,\mu ,\tau }\nu _\alpha (t)\vert \nu _\alpha \rangle = \sum \limits _{j=1,2,3}\nu _j(t)\vert \nu _j\rangle . \end{aligned}$$
(1)

Vectors of two different bases are connected through the unitary transformation. Therefore the wave function propagated in time on one basis can be converted into the second basis and vice versa. Note that the massive neutrino states propagate freely in vacuum, but in stellar environments their propagation is affected by the interaction with matter. Depending on the matter density profile, this interaction can be accounted for by means of well established approaches (see, for instance, Refs. [30,31,32]). Using the occupation number representation for flavour and massive modes (see [15]), the neutrino state can be presented in the form

$$\begin{aligned}&\vert \nu (t)\rangle =a(t)\vert 100\rangle +b(t)\vert 010\rangle +c(t)\vert 001\rangle . \end{aligned}$$
(2)

This wave function is the essence of the entangled superposition of the flavour modes. The entanglement of the system can be quantified through the flavour entropy [15], which is the entanglement measure appropriate for the pure but not for the mixed states (see below).

Magnetic fields generated by the cosmic objects extend beyond the objects’ size to the regions where the matter density is very low. Therefore, neutrinos in the interstellar space can be mainly affected by the neutrino magnetic moment interaction with a magnetic field that has both deterministic and stochastic components [33, 34]. With regard to the latter aspect, we admit the pioneering works of Nikolaidis [35] and of Loreti and Balantekin [36] dedicated to the neutrino oscillations in noisy magnetic fields and media. In particular, Loreti and Balantekin derived the Redfield equation for the neutrino density matrix in a noisy environment. They then solved the Redfield equation in the Lindblad limit, assuming that the correlation time of the environment is short. Results obtained by Loreti and Balantekin correspond to the simplest case of a two-level problem. This two-level approach was utilized in studies of neutrino conversions in random solar and supernova magnetic fields [36,37,38,39,40], and the approximation treatments of the four-level case can be found in Refs. [41,42,43,44].

In the present work, we propose a mathematically rigorous formulation of neutrino spin and spin-flavour oscillations in a noisy magnetic field based on the Lindblad master equation. The Lindbladian evolution of the open quantum system is related to the formation of mixed states. Hence, pure state measures considered in [15] are irrelevant for quantifying spin-flavour entanglement of mixed states in our case. We use entanglement measures of mixed states [45] developed in the quantum resource theory. Specifically, we explore coherence and mixedness, two cornerstone measures adopted in the quantum resource theory. We also analyze the tradeoff relation between coherence and mixedness. The formal mathematical language of quantum resource theory is based on the free (given) states and operations (local operations and classical communications) done on these states. In realistic physical systems, operations are not free, and they consume a quantum state’s coherence as a resource. In our case, in particular, the given state is the quantum state of the cosmic neutrino, for example, emitted after the supernova explosion or produced in the interactions of high energy protons and nuclei with cosmic radiation and dust. The operation done on the state is the neutrino propagation in the interstellar space and the process is described through the Lindblad channel. Coherence is the measure of inherently quantum correlations (correlations that vanish in the classical limit). There are several coherence measures, and one of the most reliable and mathematically robust measures we will use is the relative entropy, the metric distance between two density matrices. One of these density matrices is the neutrino density matrix and the second matrix is its diagonal part. Another proper coherence measure we will use is the \(l_1\) norm of coherence, which is given by the sum of absolute values of nondiagonal elements of the neutrino density matrix. Mixedness characterizes how close is the state of the system to the maximally mixed state (the state with maximally possible entropy). We note that coherence (specifically, the \(l_1\) norm) and mixedness are related to each other through the nontrivial tradeoff relation that imposes only an upper limit on both quantifiers. Therefore knowing coherence is not enough for knowing mixedness, so that both quantities we calculate independently. We also note that our present approach recovers in the limit of zero noise the unitary neutrino evolution [26]. We tackle the problem in the limit of weak noise when the nonunitary term in the Lindblad equation is smaller than the unitary one. Under such conditions, the method secures high accuracy of the solution.

The paper is organized as follows. In Sect. 2, we formulate the Lindblad master equation [46] for neutrino evolution that accounts for the dissipative effect due to a stochastic magnetic-field component, which can be present in different neutrino propagation environments, for example, in such as the interstellar space (see Refs. [34, 47]). Then, in Sect. 3, we outline basic properties of the analytical solution of the Lindblad master equation for the neutrino density matrix. The numerical results based on the obtained solution, which quantify the coherence effects in neutrino oscillations of various types, are presented and discussed in Sect. 4. The conclusions are drawn in Sect. 5. Throughout we use the units in which \(\hbar =c=1\), unless otherwise specified.

2 The neutrino evolution equation

We limit ourselves to two neutrino generations and start with Dirac neutrino helicity basis states \(\vert \nu _{1,s=\pm 1}\rangle \) and \(\vert \nu _{2,s=\pm 1}\rangle \) with masses \(m_1\) and \(m_2\) (\(m_2>m_1\)). The neutrino left- and right-handed flavour states are then given by

$$\begin{aligned} \vert \nu _{e}^{R,L}\rangle= & {} \cos \theta \vert \nu _{1,s=\pm 1}\rangle +\sin \theta \vert \nu _{2,s=\pm 1}\rangle ,\nonumber \\ \vert \nu _{\mu }^{R,L}\rangle= & {} \sin \theta \vert \nu _{1,s=\pm 1}\rangle +\cos \theta \vert \nu _{2,s=\pm 1}\rangle , \end{aligned}$$
(3)

where \(\theta \) is the mixing angle and the subscripts e and \(\mu \) designate the electron and muon flavours respectively. The nonzero mixing angle (\(\sin ^2\theta \approx 0.3\) [48]) is responsible for the customary, neutrino flavour oscillations \(\nu _{e(\mu )}^{L}\leftrightarrow \nu _{\mu (e)}^{L}\). In the presence of a magnetic field, the interaction of neutrino magnetic moments of diagonal (\(\mu _{11}\) and \(\mu _{22}\)) and transition (\(\mu _{12}\)) types with a magnetic field induces the neutrino spin \(\nu _{e(\mu )}^{L}\leftrightarrow \nu _{e(\mu )}^{R}\) and spin-flavour \(\nu _{e(\mu )}^{L}\leftrightarrow \nu _{\mu (e)}^{R}\) oscillations. The exact solution of the problem in the case of a constant magnetic field \(\mathbf {B}\) can be found in our earlier work [26]. Here, we wish to take into account the presence of magnetic-field fluctuations and to develop a general approach based on the quantum resource theory for the treatment of neutrino flavour, spin and spin-flavour oscillations.

The effective Hamiltonian of the problem is [26]

$$\begin{aligned}&{\hat{H}}_{eff}={\hat{H}}_{vac} +{\hat{H}}_{B}, \end{aligned}$$
(4)

where \({\hat{H}}_{vac}\) is the vacuum part and the term \({\hat{H}}_{B}\) describes the neutrino interaction with a magnetic field. The vacuum Hamiltonian in the flavour basis (3) has the form

$$\begin{aligned} {{{\hat{H}}}}_{vac}=\omega _\nu \begin{pmatrix} -\cos 2 \theta &{} 0 &{} \sin 2 \theta &{} 0 \\ 0 &{} -\cos 2 \theta &{} 0 &{} \sin 2 \theta \\ \sin 2 \theta &{} 0 &{} \cos 2\theta &{} 0 \\ 0 &{} \sin 2 \theta &{} 0 &{} \cos 2\theta \end{pmatrix}, \end{aligned}$$
(5)

with

$$\begin{aligned} \omega _\nu = \frac{\varDelta m^2}{4 E_\nu }, \qquad \varDelta m^2 =m_2^2 - m_1^2, \end{aligned}$$
(6)

and \(E_\nu \) being the neutrino energy.

The Hamiltonian of the neutrino interaction with a magnetic field in the flavor representation can be presented as [49]

$$\begin{aligned} {\hat{H}}_{B}= \begin{pmatrix} \displaystyle -{\tilde{\mu }}_{ee} {B_\parallel } &{}&{} \mu _{ee}B_{\perp } &{}&{} \displaystyle -{\tilde{\mu }}_{ e\mu }{B_\parallel } &{}&{} \mu _{e\mu }B_\perp \\ \mu _{ee}B_\perp &{}&{} \displaystyle {\tilde{\mu }}_{ee}{B_\parallel } &{}&{} \mu _{e\mu } B_\perp &{}&{} \displaystyle {\tilde{\mu }}_{e\mu }{B_\parallel } \\ \displaystyle -{\tilde{\mu }}_{e\mu }{B_\parallel } &{}&{} \mu _{e\mu }B_{\perp } &{}&{} \displaystyle -{\tilde{\mu }}_{\mu \mu }{B_\parallel } &{}&{} \mu _{\mu \mu } B_\perp \\ \mu _{e\mu }B_{\perp } &{}&{} \displaystyle {\tilde{\mu }}_{e\mu }{B_\parallel } &{}&{} \mu _{\mu \mu }B_\perp &{}&{} \displaystyle {\tilde{\mu }}_{\mu \mu }{B_\parallel } \end{pmatrix}, \end{aligned}$$
(7)

where \(B_\parallel \) and \(B_\perp \) are the parallel and transverse magnetic-field components with respect to the neutrino velocity, and the neutrino magnetic moments \({\mu }_{\ell \ell '}\) and \({\tilde{\mu }}_{\ell \ell '}\) (\(\ell ,\ell '=e,\mu \)) are related to those in the mass representation \(\mu _{jk}\) (\(j,k=1,2\)) as follows:

$$\begin{aligned} \mu _{ee}&=\mu _{11} \cos ^2 \theta +\mu _{22} \sin ^2 \theta +\mu _{12} \sin 2\theta , \nonumber \\ \mu _{e\mu }&=\mu _{12}\cos 2\theta + \frac{1}{2} \left( \mu _{22} - \mu _{11}\right) \sin 2\theta , \nonumber \\ \mu _{\mu \mu }&=\mu _{11} \sin ^2 \theta +\mu _{22} \cos ^2 \theta -\mu _{12} \sin 2\theta , \end{aligned}$$
(8)

and

$$\begin{aligned} {\tilde{\mu }}_{ee}&= \frac{\mu _{11}}{\gamma _{1}}\,\cos ^2 \theta + \frac{\mu _{22}}{\gamma _{2}}\,\sin ^2 \theta + \frac{\mu _{12}}{\gamma _{12}}\,\sin 2\theta , \nonumber \\ {\tilde{\mu }}_{e\mu }&= \frac{\mu _{12}}{\gamma _{12}}\,\cos 2\theta +\frac{1}{2}\left( \frac{\mu _{22}}{\gamma _{2}}-\frac{\mu _{11}}{\gamma _{1}} \right) \sin 2\theta ,\nonumber \\ {\tilde{\mu }}_{\mu \mu }&= \frac{\mu _{11}}{\gamma _{1}}\,\sin ^2 \theta +\frac{\mu _{22}}{\gamma _{2}}\,\cos ^2 \theta -\frac{\mu _{12}}{\gamma _{12}}\,\sin 2\theta . \end{aligned}$$
(9)

Here \(\gamma _1\) and \(\gamma _2\) are the Lorenz factors of the massive neutrinos, and

$$\begin{aligned} \frac{1}{\gamma _{12}}=\frac{1}{2}\left( \frac{1}{\gamma _1}+\frac{1}{\gamma _2}\right) . \end{aligned}$$
(10)

In what follows, we consider the effect of the interstellar random magnetic field. Following Ref. [26], we neglect the neutrino interaction with the interstellar matter. This is motivated by the fact that even for the current most stringent upper limits on neutrino magnetic moments (\(\lesssim 10^{-12}\mu _B\) [48]) the strength of this interaction \(\lesssim 10^{-31}\) eV appears to be by many orders of magnitude weaker than the neutrino interaction with both the deterministic and stochastic components of an interstellar magnetic field. Due to the equivalence between time and distance travelled by the neutrino, the analysis on equal footing applies to the time and spatial autocorrelation functions of the random magnetic field. In addition to the usual deterministic part \(\mathbf {B}\) that enters Eq. (7), the interstellar magnetic field has a stochastic component \(\mathbf {h}\) related to the cosmic dust. The stochastic field is characterized by the mean value \(\langle \mathbf {h}(t)\rangle =0\) and the correlation function of the form [36, 37, 42]

$$ \langle h_\alpha (t)h_\beta (0)\rangle =\delta _{\alpha \beta }\eta B^2 f(t), $$

where \(\eta =\langle h^2\rangle /B^2\), and the correlator function f(t) takes the \(\delta \)-correlator form \(f(t)=L_0\delta (t)\) if the correlation length \(L_0\) is much less than the neutrino oscillation length \(L_{osc}\) [42]. Therefore we can present the correlation function \(\langle h_\alpha (t)h_\beta (0)\rangle \) as

$$\begin{aligned} \langle h_\alpha (t)h_\beta (0)\rangle =\frac{\delta _{\alpha \beta }w^2}{2\mu _\nu ^2}\,\delta (t), \end{aligned}$$
(11)

where \(\mu _\nu \) is a putative value of the neutrino magnetic moment and \(w^2=2\eta (\mu _\nu B)^2L_0\) is the dissipation parameter (see below). For the interstellar case, one has \(B\simeq 3\) \(\mu \)G [50], \(\eta \sim 1\) and \(L_0\sim 50\) pc [33]. Let us note that one can introduce the effective temperature [51] \(w^2=k_BT\), which characterizes the swiftness of equilibration (“thermalization”) of the density matrix of the neutrino propagating in the noisy interstellar magnetic field. In particular, in the center of M51, the ratio between stochastic and regular components is on the order of 10\(\%\) [33]. This indicates that the stochastic field is strong enough to cause the “thermalization” process.

To describe the neutrino motion in a fluctuating magnetic field, we employ the Lindblad master equation, which is widely used in studies of neutrino quantum decoherence in different environments and under various experimental conditions (see Ref. [52] and references therein). The density matrix of the system thus obeys the following equation:

$$\begin{aligned} \frac{d{\hat{\varrho }}}{dt}= & {} -{i}\left[ {{\hat{H}}}, {{\hat{\rho }}}\right] -\frac{w^{2}}{2}\,\left( {\hat{\varrho }}\hat{V^2}+\hat{V^2}{\hat{\varrho }}-2{\hat{V}}{\hat{\varrho }}{\hat{V}}\right) . \end{aligned}$$
(12)

We analytically solve it in the eigenbasis \(\vert \psi _{i=1,2,3,4}\rangle \) of the Hamiltonian \({\hat{H}}_{eff}\) (see Ref. [26] for details). The equation for the density matrix takes the form

$$\begin{aligned} \frac{d\varrho _{nm}}{dt}&= -i (E_n - E_m)\varrho _{mn} - \frac{w^2}{2} \sum _q \left( \varrho _{nq} V^2_{qm} + V^2_{nq} \varrho _{qn}\right) \nonumber \\&\quad + w^2 \sum _{q,s} V_{nq} \rho _{qs} V_{sm}, \end{aligned}$$
(13)

where \(E_{i=1,2,3,4}\) are the eigenenergies of the Hamiltonian \({\hat{H}}_{eff}\). The matrix V has the following general form:

$$\begin{aligned} V_{ik} = \left\langle \psi _i \right| {\hat{I}}_1 \otimes {\hat{v}}_2 + {\hat{I}}_2 \otimes {\hat{v}}_1 \left| \psi _k \right\rangle , \end{aligned}$$
(14)

where \({\hat{v}}\) is a \(2 \times 2\) matrix, and the subscripts 1, 2 denote the action of a matrix on the space of the first and second massive neutrinos, respectively. The matrix \({\hat{v}}\) can be expanded into the basis of \(2\times 2\) unit matrix and three Pauli matrices:

$$\begin{aligned} {\hat{v}} = v_0 {\hat{I}} + {\mathbf {v}} \cdot \hat{{\varvec{\sigma }}}. \end{aligned}$$
(15)

Let us present the density matrix as

$$\begin{aligned} {{\hat{\varrho }}} = \begin{pmatrix} {{\hat{\varrho }}}^{(11)} &{} {{\hat{\varrho }}}^{(12)} \\ {{\hat{\varrho }}}^{(21)} &{} {{\hat{\varrho }}}^{(22)} \end{pmatrix}. \end{aligned}$$
(16)

The quadrants \({{\hat{\varrho }}}^{(\alpha )}\) are \(2\times 2\) minors of the full density matrix and can be expanded in terms of the unit and Pauli matrices:

$$\begin{aligned} {{\hat{\varrho }}}^{(\alpha )} = r_0^{(\alpha )}{\hat{I}} + {\mathbf {r}}^{(\alpha )}\cdot \hat{{\varvec{\sigma }}}, \end{aligned}$$
(17)

where the expansion coefficients are defined by

$$\begin{aligned} r_{i=1,2,3}^{(\alpha )} = \frac{1}{2} \,\text{ tr }\{ {{\hat{\varrho }}}^{(\alpha )}{{\hat{\sigma }}}_{i=1,2,3} \}, \qquad r_0^{(\alpha )} = \frac{1}{2}\, \text{ tr }{{\hat{\varrho }}}^{(\alpha )}. \end{aligned}$$
(18)

In Eq. (13), the dissipative term contains the following two matrix terms arising from the combinations of \({\hat{v}}\) and \({{\hat{\varrho }}}^{(\alpha )}\):

$$\begin{aligned} {\hat{L}}^{(\alpha )}_1 = {\hat{v}}^2 {{\hat{\varrho }}}^{(\alpha )} + {{\hat{\varrho }}}^{(\alpha )}{\hat{v}}^2 \end{aligned}$$
(19)

and

$$\begin{aligned} {\hat{L}}^{(\alpha )}_2= {\hat{v}} {{\hat{\varrho }}}^{(\alpha )}{\hat{v}} \end{aligned}$$
(20)

for the first and second sums, respectively.

We now transform Eqs. (19) and (20) using Eqs. (15) and (17):

$$\begin{aligned} {\hat{L}}^{(\alpha )}_1&= 2 \left[ \left( v_0^2 + v^2 \right) r^{(\alpha )}_0 + 2 v_0 {\mathbf {v}} \cdot {\mathbf {r}}^{(\alpha )} \right] {\hat{I}}\nonumber \\&\quad + 4 v_0 r^{(\alpha )}_0 {\mathbf {v}} \cdot {\hat{\varvec{\sigma }}} + 2 \left( v_0^2 + v^2 \right) {\mathbf {r}}^{(\alpha )} \cdot \hat{{\varvec{\sigma }}}, \end{aligned}$$
(21)

and

$$\begin{aligned} {\hat{L}}^{(\alpha )}_2= & {} \left[ \left( v_0^2 + v^2 \right) r^{(\alpha )}_0 + 2 v_0 {\mathbf {v}} \cdot {\mathbf {r}}^{(\alpha )} \right] {\hat{I}}\nonumber \\&+2 \left[ v_0 r^{(\alpha )}_0 + {\mathbf {v}} \cdot {\mathbf {r}}^{(\alpha )}\right] {\mathbf {v}} \cdot \hat{{\varvec{\sigma }}}\nonumber \\&+ \left( v_0^2 - v^2 \right) {\mathbf {r}}^{(\alpha )}\cdot \hat{{\varvec{\sigma }}}. \end{aligned}$$
(22)

Summing up Eqs. (21) and (22) with the same weights as in Eq. (13), one gets the full dissipative term:

$$\begin{aligned} {\hat{L}}^{(\alpha )}&= - \frac{w^2}{2} {\hat{L}}^{(\alpha )}_1 + w^2 {\hat{L}}^{(\alpha )}_2\nonumber \\&= 2 w^2 \left[ ({\mathbf {v}} \cdot {\mathbf {r}}^{(\alpha )}) {\mathbf {v}} \cdot \hat{{\varvec{\sigma }}} - v^2 {\mathbf {r}}^{(\alpha )} \cdot \hat{{\varvec{\sigma }}}\right] . \end{aligned}$$
(23)

We also decompose Eq. (23) in the basis of \(2 \times 2\) matrices:

$$\begin{aligned} {\hat{L}}^{(\alpha )} = \varLambda ^{(\alpha )}_0 {\hat{I}} + {\varvec{\Lambda }}^{(\alpha )} \cdot \hat{{\varvec{\sigma }}}, \end{aligned}$$
(24)

where

$$\begin{aligned} \varLambda ^{(\alpha )}_0&= 0, \end{aligned}$$
(25)
$$\begin{aligned} \varLambda ^{(\alpha )}_i&= 2 w^2 \left[ ({\mathbf {v}} \cdot {\mathbf {r}}^{(\alpha )}) v_i - v^2 r_i^{(\alpha )} \right] . \end{aligned}$$
(26)

Using Eqs. (17), (21), (22), (23), and (13), one gets the system of equations for the elements of the minor \({{\hat{\varrho }}}^{(11)}\):

$$\begin{aligned} \frac{d}{dt}\varrho _{11} (t)&= \frac{d}{dt} [r^{(11)}_0(t) + r^{(11)}_3(t)] = \varLambda ^{(11)}_3(t), \end{aligned}$$
(27)
$$\begin{aligned} \frac{d}{dt} \varrho _{22}(t)&= \frac{d}{dt} [r^{(11)}_0(t) - r^{(11)}_3(t)]= -\varLambda ^{(11)}_3(t), \end{aligned}$$
(28)
$$\begin{aligned} \frac{d}{dt} \varrho _{12}(t)&= \frac{d}{dt} r^{(11)}_-(t) = - i\omega _{12} r^{(11)}_-(t) + \varLambda ^{(11)}_-(t), \end{aligned}$$
(29)
$$\begin{aligned} \frac{d}{dt} \varrho _{21}(t)&= \frac{d}{dt} r^{(11)}_+ (t)= - i \omega _{21} r^{(11)}_+(t) + \varLambda ^{(11)}_+(t), \end{aligned}$$
(30)

where \(r_\pm = r_1 \pm i r_2\), \(\varLambda _\pm = \varLambda _1 \pm \varLambda _2\) and \(\omega _{12} = E_1 - E_2 = -\omega _{21}\). Note that the sum of the diagonal matrix elements \(\varrho _{11}(t) +\varrho _{22}(t) = 2 r^{(11)}_0(t)\) is time-independent.

The set of equations for another “diagonal” minor, \({{\hat{\varrho }}}^{(22)}\), is obtained from Eqs. (27)–(30) by changing \(r^{(11)}_{i=0,1,2,3}\) to the corresponding \(r^{(22)}_{i=0,1,2,3}\), and \(\omega _{12}\) to \(\omega _{34}\). Similarly, \(\varrho _{33}(t) + \varrho _{44}(t) = 2 r^{(22)}_0(t)\) is time-independent, as well as the complete trace of the density matrix \(\text{ tr }{\hat{\varrho }}(t)=2 [r^{(11)}_0(t)+r^{(22)}_0(t)]=1\).

The system of equations for the minor \({{\hat{\varrho }}}^{(12)}\) is

$$\begin{aligned} \frac{d}{dt}\varrho _{13}(t)&= \frac{d}{dt} [r^{(12)}_0(t) + r^{(12)}_3(t)]\nonumber \\&=- i \omega _{13}[r^{(12)}_0(t) + r^{(12)}_3(t)] + \varLambda ^{(12)}_3(t), \end{aligned}$$
(31)
$$\begin{aligned} \frac{d}{dt} \varrho _{24}(t)&= \frac{d}{dt} [r^{(12)}_0(t) - r^{(12)}_3(t)] \nonumber \\&=- i \omega _{24}[r^{(12)}_0(t) - r^{(12)}_3(t)] - \varLambda ^{(12)}_3(t), \end{aligned}$$
(32)
$$\begin{aligned} \frac{d}{dt} \varrho _{14}(t)&= \frac{d}{dt} r^{(12)}_-(t) = - i \omega _{14} r^{(12)}_-(t) + \varLambda ^{(12)}_-(t), \end{aligned}$$
(33)
$$\begin{aligned} \frac{d}{dt} \varrho _{23}(t)&= \frac{d}{dt} r^{(12)}_+(t) = - i\omega _{23} r^{(12)}_+ (t) + \varLambda ^{(2)}_+(t). \end{aligned}$$
(34)

Finally, the equations for the matrix elements of \({{\hat{\varrho }}}^{(21)}\) are obtained from Eqs. (31)–(34) by means of Hermitian conjugation.

3 Solution of the master equation

For illustrative purposes we assume that

$$\begin{aligned} \mu _{11}=\mu _{22}=\mu _{12} = \mu _\nu . \end{aligned}$$
(35)

Since neutrinos are ultrarelativistic particles, the terms involving Lorentz factors in Eq. (7) (i.e., the \(\pm {\tilde{\mu }}_{\ell \ell '}B_\parallel \) terms) can be safely neglected. In what follows, we set \(B_\perp =B\). The resulting effective Hamiltonian (4) has the following characteristic equation:

$$\begin{aligned} E^4 - 2(\omega _\nu ^2 +2 \mu _\nu ^2 B^2) E^2 + \omega _\nu ^4 =0. \end{aligned}$$
(36)

Its roots are given by

$$\begin{aligned} E_{1,2,3,4} = \mp \left( \sqrt{\omega _\nu ^2 + {\mu _\nu ^2 B^2 }} \pm {\mu _\nu B}\right) , \end{aligned}$$
(37)

where the eigenenergies \(E_{1,2}\) (\(E_{3,4}\)) correspond to the minus (plus) sign in front of the brackets. Let us define the energy splitting \(\omega _B\) due to the presence of a magnetic field:

$$\begin{aligned} \omega _{B} = E_1 - E_2 = E_3-E_4 = 2\mu _\nu B. \end{aligned}$$
(38)

This energy value determines the characteristic frequency scale of neutrino spin oscillations, while that for flavor oscillations is represented by the modified frequency

$$\begin{aligned} \omega _{N} = \frac{\omega _{31} + \omega _{42}}{2} = \sqrt{\omega _\nu ^2 + \mu _\nu ^2 B^2 }. \end{aligned}$$
(39)

Consider now the system of equations for the minor \({{\hat{\varrho }}}^{(11)}\). One can rewrite Eqs. (27)–(30) as

$$\begin{aligned} \frac{d}{d\tau } r_0^{(11)}(\tau )&= 0, \end{aligned}$$
(40)
$$\begin{aligned} \frac{d}{d\tau } r_+^{(11)} (\tau )&= \left( \frac{v_+ v_-}{2} - v_3^2 - i {\bar{\omega }}\right) r_+^{(11)}(\tau ) + \frac{v_+^2}{2} r_-^{(11)}(\tau ) \nonumber \\&\quad +v_+ v_3 r_3^{(11)}(\tau ), \end{aligned}$$
(41)
$$\begin{aligned} \frac{d}{d\tau } r_-^{(11)}(\tau )&= \frac{v_-^2}{2} r_+^{(11)}(\tau ) + \left( - \frac{v_+ v_-}{2} - v_3^2 + i {\bar{\omega }}\right) r_-^{(11)}(\tau )\nonumber \\&\quad +v_- v_3 r_3^{(11)}(\tau ), \end{aligned}$$
(42)
$$\begin{aligned} \frac{d}{d\tau } r_3 (\tau )&= \frac{v_-v_3}{2} {r_+^{(11)}(\tau )} + \frac{v_+v_3}{2} {r_-^{(11)}(\tau )}\nonumber \\&\quad - v_+ v_- r_3^{(11)}(\tau ), \end{aligned}$$
(43)

where \(v_\pm =v_1\pm iv_2\) and we introduced the reduced time variable \(\tau = 2 w^2 t\) and the reduced frequency \({\bar{\omega }}= \omega _{12}/2w^2=\mu _\nu B/w^2={\bar{\omega }}_B\).

The relevant components of the matrix \({\hat{v}}\) are expressed by a three-dimensional vector \({\mathbf {v}}\) [as can be seen above, the component \(v_0\) is no longer relevant because it does not appear in the final expression for the dissipative term in Eq. (23)], which can be parametrized as

$$\begin{aligned} {\mathbf {v}} = ( v\cos \varphi \sin \beta , v\sin \varphi \cos \varphi , v\cos \beta ), \end{aligned}$$
(44)

where \(\varphi \) and \(\beta \) are some angle parameters. Since the norm v appears in the combination with \(w^2\), it can be included in the definition of the latter parameter and set to \(v=1\). We also assume the matrix \({{\hat{v}}}\) to be real, setting \(\varphi =0\), and hence

$$\begin{aligned} {\mathbf {v}} = (\sin \beta , 0 , \cos \beta ). \end{aligned}$$
(45)

Using \(r_{1,2}^{(11)}\) instead of \(r_\pm ^{(11)}\) in Eqs. (40)–(43), we get

$$\begin{aligned} \frac{d}{d\tau } r^{(11)}_0&= 0, \end{aligned}$$
(46)
$$\begin{aligned} \frac{d}{d\tau } r^{(11)}_1&= -r^{(11)}_1\cos ^2 \beta + r^{(11)}_2 {\bar{\omega }}_{B} + r^{(11)}_3 \sin \beta \cos \beta , \end{aligned}$$
(47)
$$\begin{aligned} \frac{d}{d\tau } r^{(11)}_2&= - r^{(11)}_1 {\bar{\omega }}_{B} - r^{(11)}_2 \cos ^2 \beta , \end{aligned}$$
(48)
$$\begin{aligned} \frac{d}{d\tau } r^{(11)}_3&= r^{(11)}_1 \sin \beta \cos \beta - r^{(11)}_3 \sin ^2 \beta . \end{aligned}$$
(49)

The system of equations for the variables \(r^{(22)}_{i=0,1,2,3}(t)\) is obtained in a similar manner.

In the case of the minor \({{\hat{\varrho }}}^{(12)}\) we deduce from Eqs. (31)–(34):

$$\begin{aligned} \frac{d}{d\tau } r^{(12)}_ 0&= - i {\bar{\omega }}_+ r^{(12)}_ 0 - i {\bar{\omega }}_- r^{(12)}_3, \end{aligned}$$
(50)
$$\begin{aligned} \frac{d}{d\tau } r^{(12)}_1&= ( - \cos ^2 \beta - i {\bar{\omega }}_+) r^{(12)}_1 + {\bar{\omega }}_0 r^{(12)}_2 \nonumber \\&\quad + r^{(12)}_3 \sin \beta \cos \beta , \end{aligned}$$
(51)
$$\begin{aligned} \frac{d}{d\tau } r^{(12)}_2&= - {\bar{\omega }}_0 r^{(12)}_1 + ( -\cos ^2 \beta - i {\bar{\omega }}_+)r^{(12)}_2, \end{aligned}$$
(52)
$$\begin{aligned} \frac{d}{d\tau } r^{(12)}_3&= -i {\bar{\omega }}_- r^{(12)}_0 + r^{(12)}_1 \sin \beta \cos \beta \nonumber \\&\quad - ( i{\bar{\omega }}_+ + \sin ^2 \beta )r^{(12)}_3. \end{aligned}$$
(53)

The reduced frequencies are given by

$$\begin{aligned} {\bar{\omega }}_0&= \frac{{\bar{\omega }}_{12} + {\bar{\omega }}_{34} }{2} = {\bar{\omega }}_{B}, \end{aligned}$$
(54)
$$\begin{aligned} {\bar{\omega }}_\pm&= \frac{{\bar{\omega }}_{31} \pm {\bar{\omega }}_{42} }{2} = \frac{{\bar{\omega }}_{N} \pm {\bar{\omega }}_{N}}{2}, \end{aligned}$$
(55)

where \({\bar{\omega }}_{ij}=\omega _{ij}/2w^2\) and \({\bar{\omega }}_{N}=\omega _{N}/2w^2\). Utilizing the substitution

$$\begin{aligned} r^{(12)}_i (\tau ) = e^{-i{\bar{\omega }}_{N} \tau } R^{(12)}_i (\tau ) \end{aligned}$$
(56)

in Eqs. (50)–(53) and taking into account Eqs. (54) and (55), we find that functions \(R^{(12)}_i(\tau )\) obey exactly the same system of equations as that given by Eqs. (46)–(49).

In Eqs. (46)–(49) the first equation is trivial and therefore the solution of the system requires diagonalization of the \(3\times 3\) matrix

$$\begin{aligned} {\mathcal {M}}^{(1)}_3 = \begin{pmatrix} - \cos ^2\beta &{}&{} {\bar{\omega }}_B &{}&{} \sin \beta \cos \beta \\ -{\bar{\omega }}_B &{}&{} - \cos ^2\beta &{}&{} 0 \\ \sin \beta \cos \beta &{}&{} 0 &{}&{} -\sin ^2\beta \end{pmatrix}. \end{aligned}$$
(57)

The general solution to the system is a sum of exponents:

$$\begin{aligned} r^{(11)}_i (\tau ) = \sum _{k=1}^{3} C_{ik} e^{\zeta _k \tau }, \end{aligned}$$
(58)

where \(\zeta _i\) are the eigenvalues of the matrix (57). The integration constants are given by the following expressions:

$$\begin{aligned} C_{i1}&= \frac{B_{0i} \zeta _2 \zeta _3 - B_{1i} (\zeta _2 + \zeta _3) + B_{2i}}{(\zeta _1 - \zeta _2)(\zeta _1 - \zeta _3)}, \end{aligned}$$
(59)
$$\begin{aligned} C_{i2}&= \frac{B_{0i} \zeta _1 \zeta _3 - B_{1i} (\zeta _1 +\zeta _3) +B_{2i}}{(\zeta _2 - \zeta _1)(\zeta _2 - \zeta _3)}, \end{aligned}$$
(60)
$$\begin{aligned} C_{i3}&= \frac{B_{0i} \zeta _1 \zeta _2 - B_{1i} (\zeta _1 + \zeta _2) +B_{2i}}{(\zeta _3 - \zeta _1)(\zeta _3 -\zeta _2)}, \end{aligned}$$
(61)

where

$$\begin{aligned} B_{0i}&= r^{(11)}_i(0), \end{aligned}$$
(62)
$$\begin{aligned} B_{1i}&= \sum _k {\mathcal {M}}^{(1)}_{3\,ik}r^{(11)}_{k}(0), \end{aligned}$$
(63)
$$\begin{aligned} B_{2i}&= \sum _{kl} {\mathcal {M}}^{(1)}_{3\,ik} {\mathcal {M}}^{(1)}_{3\,kl}r^{(11)}_{l}(0). \end{aligned}$$
(64)

The characteristic equation for the system of Eqs. (46)–(49) is

$$\begin{aligned} \zeta ^3 + (2-\sin ^2 \beta )\zeta ^2 +({\bar{\omega }}_B^2 + \cos ^2 \beta ) \zeta +{\bar{\omega }}_B^2 \sin ^2 \beta =0.\nonumber \\ \end{aligned}$$
(65)

It has three roots: the one (\(\zeta _3\)) is always real and the other two are complex conjugate to each other (\(\zeta _1=\zeta _2^*\)).

Let us briefly outline properties of the solution in the two limiting cases \(\beta =0\) and \(\pi /2\). In the \(\beta =0\) case, the matrix \({\hat{v}}\) has a diagonal form, \({\hat{v}}={\hat{\sigma }}_z\). The roots of the characteristic equation (65) are given by \(\zeta _{1,2} = -1\pm i {\bar{\omega }}_B\) and \(\zeta _3=0\). From Eqs. (46)–(49) it follows that the “longitudinal” component \(r^{(11)}_3\) is time-independent and the “transverse” components \(r^{(11)}_1\) and \(r^{(11)}_2\) decay as \(\propto e^{-\tau }\), oscillating with frequency \({\bar{\omega }}_B\). If one sets them zero in the initial moment of time \(\tau =0\) the density matrix remains constant and diagonal for all times \(\tau > 0\). In the \(\beta =\pi /2\) case, the real root of the characteristic equation (65) is \(\zeta _3 = -1\), and the other two are purely imaginary: \(\zeta _{1,2} = \pm i{\bar{\omega }}_B\). The “longitudinal” component decays, \(r^{(11)}_3(\tau )\propto e^{-\tau }\), and the “transverse” components \(r^{(11)}_1\) and \(r^{(11)}_2\) oscillate with frequency \({\bar{\omega }}_B\).

When \(0< \beta < \pi /2\), the solution is more involved. Figure 1 shows the dependence of the real root \(\zeta _3\) on the angle \(\beta \). One can see that \(\zeta _3\) monotonically decreases from 0 to \({}-1\) with increasing \(\beta \) from 0 to \(\pi /2\), and the indicated decrease is faster for larger \({\bar{\omega }}_B\) values. This means that the dissipation effect associated with the \(\zeta _3\) term in Eq. (58) is stronger for larger values of \(\beta \) and \({\bar{\omega }}_B\). From Fig. 2 it can be seen that at a fixed value of \(\beta \) the real root \(\zeta _3\) drops from 0 to some asymptotic value with increasing \({\bar{\omega }}_B\). In agreement with Fig. 1, the modulus of the asymptotic value is larger for larger \(\beta \). This observation is opposite to the behavior of the real part of two complex roots \(\zeta _{1, 2}\) shown in Fig. 3. As follows from the results presented in Fig. 3, the dissipation effect associated with the \(\zeta _{1,2}\) terms in Eq. (58) appears to be weaker for larger values of \(\beta \) and \({\bar{\omega }}_B\), in contrast to the \(\zeta _3\) case.

Fig. 1
figure 1

The real root of the cubic equation (65) as a function of angular parameter \(\beta \) for different values of the reduced frequency \({\bar{\omega }}_B=\omega _B/2w^2\)

Full size image
Fig. 2
figure 2

The real root of the cubic equation (65) as a function of the reduced frequency \({\bar{\omega }}_B\) for particular values of the angle \(\beta \). Each \(\beta \) is characterized by the asymptotic value of \(\zeta _3\)

Full size image
Fig. 3
figure 3

The real part of the two complex roots of the cubic equation (65) as a function of the reduced frequency \({\bar{\omega }}_B\) for particular values of the angle \(\beta \)

Full size image

The behavior of the imaginary parts of the complex roots \(\zeta _{1,2}\) as functions of \({\bar{\omega }}_B\) is shown in Fig. 4. It can be seen that the modulus of the imaginary parts grows with increasing \({\bar{\omega }}_B\) and the curves corresponding to distinct \(\beta \) values merge to nearly a linear function at large values of \({\bar{\omega }}_B\). The proportionality coefficient asymptotically approaches unity. Note that, as discussed above, the dependence is exactly linear for \(\beta =0,\pi /2\).

Fig. 4
figure 4

The modulus of the imaginary parts of two complex roots of the cubic equation (65) as a function of the reduced frequency \({\bar{\omega }}_{B}\) for selected \(\beta \) values. The curves corresponding to different values of the angle \(\beta \) merge when \({\bar{\omega }}_B\) is large

Full size image

The Lindblad equation parameter \(w^2\) characterizes the strength of the dissipation effects and is usually equal to some fraction of the energy of particle interaction with a magnetic field. In our case, this fraction is determined by \(w^2/\mu _\nu B =1/ {\bar{\omega }}_B\). Figure 5 shows the time evolution of the density-matrix component \(r^{(11)}_3\) for an intermediate value of \(\beta \), namely \(\beta =\pi /4\). The result of the calculation demonstrates that the functions \(r^{(11)}_3(\tau )\) for two different frequencies, \({\bar{\omega }}_B=5\) and 10, decay at the same rate. This feature agrees with the results presented in Figs. 2 and 3. The behaviors of time evolution of \(r^{(11)}_3\) at a fixed \({\bar{\omega }}_B\) value for different values of \(\beta \) is shown in Fig. 6. It is clearly seen that the dissipation effect is \(\beta \)-dependent and is stronger for larger \(\beta \). This observation is in line with results in Fig. 2, but not with those in Fig. 3. It points out that the decay of the \(r^{(11)}_3(\tau )\) function is dominated by the \(\zeta _3\) term rather than the \(\zeta _{1,2}\) terms in Eq. (58).

Fig. 5
figure 5

The function \(r^{(11)}_3(\tau )\) for two different values of the reduced frequency \({\bar{\omega }}\) and a fixed value \(\beta =\pi /4\). The initial conditions are \(r^{(11)}_0(0)=1/2\), \(r^{(11)}_\pm (0) = 0\), \(r^{(11)}_3(0)= 1/2\), meaning that \(\varrho ^{(11)}_{11}(0) =1\) and \(\rho _{12}^{(11)}=\rho _{21}^{(11)}=\rho _{22}^{(11)}=0\). The results are in line with the asymptotic behaviors of \(\zeta _3\) and \(\mathrm{Re}(\zeta _{1,2})\) in Figs. 2 and 3 respectively

Full size image
Fig. 6
figure 6

Time dependence of the density-matrix component \(r^{(11)}_3\) for the reduced frequency \({\bar{\omega }}=\mu _\nu B/2w^2 =10\) and three different values of the angular parameter \(\beta \). The initial conditions are the same as in Fig. 5

Full size image

4 Neutrino oscillations’ probability, coherence and mixedness

Coherence is a hardwired feature of quantum systems, a key ingredient in versatile applications. The resource theory of quantum coherence exploits ideas of optimal consumption of resources and proper management of costs. The free states and free operations require per se zero costs. However, free resources are not enough for quantum information protocols. Rather briefly, we recall the underlying formalism of resource theory.

Let \(\mathcal {{\hat{A}}}\) be the set of free states (i.e., the initial neutrino density matrix \(\mathcal {{\hat{A}}}\equiv \varrho (0)\) and \(\mathcal {{\hat{Q}}}\) the set of free quantum operations (i.e., Lindbladian propagation \(\mathcal {{\hat{L}}}\equiv \mathcal {{\hat{Q}}}\) and \(\varrho (t)=\mathcal {{\hat{L}}}(\varrho (0))\)). In the resource theory one always implies that the following criteria hold: \(\mathcal {{\hat{Q}}}_n\left( \mathcal {{\hat{A}}}_n\right) \in \mathcal {{\hat{A}}}\) for \(\forall \mathcal {{\hat{A}}}_n\in \mathcal {{\hat{A}}}\) and \(\forall \mathcal {{\hat{Q}}}_n\in \mathcal {{\hat{Q}}}\). In the entanglement theory, typically \(\mathcal {{\hat{A}}}\) is the set of separable states and \(\mathcal {{\hat{Q}}}\) are local operations and classical communications. In the realistic physical systems operations, \(\mathcal {{\hat{Q}}}\) can be provided at a low cost but not for free. Nevertheless, for the open quantum systems, we do not count resources supplied from the environment. Below, we propose the basis-dependent rigorous formulation of resource theory of coherence for neutrino flavour, spin and spin-flavour oscillations. We exploit the incoherent states \(\mathcal {{\hat{I}}}_n\) as a free state, and a magnetic field we exploit as a source of operations for generating the coherence \(\mathcal {{\hat{Q}}}_n\left( \mathcal {{\hat{I}}}_n\right) \notin \mathcal {{\hat{I}}}\).

Coherence is a resource because it enables performing operations not allowed in an incoherent system. Coherence is related to the non-diagonal matrix elements of the density matrix. One can define coherence as an antithesis of the incoherent states. The state is termed as incoherent if it is diagonal in a preferred basis \(\vert i\rangle \) (i. e., in the energy eigenbasis):

$$\begin{aligned} {{\hat{\varrho }}}=\sum \limits p_i \vert i\rangle \langle i\vert , \end{aligned}$$
(66)

where \(p_i\) are probabilities. Any state which cannot be written in the form of Eq. (66) we term coherent state. One can quantify coherence through the following expression [2, 53, 54]

$$\begin{aligned} {\mathcal {C}}=\frac{2N}{N-2}\sum \limits _{i,j>i}\vert \varrho _{ij}\vert ^2, \end{aligned}$$
(67)

where N is the dimension of the Hilbert space. In the most general form, incoherent dissipative evolution of the system can be described via trace-preserving map:

$$\begin{aligned} {\mathcal {P}}\left[ {{\hat{\varrho }}}\right] =\sum \limits _n{{\hat{K}}}_n{{\hat{\varrho }}}{{\hat{K}}}_n^\dagger , \end{aligned}$$
(68)

where \({{\hat{K}}}_n,~{{\hat{K}}}_n^\dagger \) are Kraus operators. Incoherent operation cannot generate coherence, meaning that \({\mathcal {C}}\left( {\mathcal {P}}\left[ {{\hat{\varrho }}}\right] \right) \leqslant {\mathcal {C}}\left( {{\hat{\varrho }}}\right) \). However, we note that we consider a specific type of Lindbladian evolution. In our case, a magnetic field influences not only the spin of the neutrino but also its flavor (due to a nonzero neutrino transition magnetic moment \(\mu _{e\mu }\)). Therefore, spin-flavor transitions in our evolution scheme may lead to the generation of coherence in the system.

Suppose that at the initial moment of time \(t=0\) the neutrino is in the active, left-handed electron-flavor state \(\left| \nu _e^L \right\rangle \). The neutrino oscillations are typically characterized by the probabilities of the corresponding transitions \(P_{\nu _e^L\rightarrow \nu _\mu ^L}(t)\) (flavor), \(P_{\nu _e^L\rightarrow \nu _e^R}(t)\) (spin), and \(P_{\nu _e^L\rightarrow \nu _\mu ^R}(t)\) (spin-flavor), and by the survival probability \(P_{\nu _e^L\rightarrow \nu _e^L}(t)\). These probabilities can be expressed in terms of the neutrino density matrix \({{\hat{\varrho }}}(t)\) as follows:

$$\begin{aligned} P_{\nu _e^L\rightarrow \nu _e^L}(t)&=\text{ tr }\left\{ {{\hat{\varrho }}}(t)\left| \nu _e^L \right\rangle \left\langle \nu _e^L \right| \right\} =\rho _{d22}(t), \end{aligned}$$
(69)
$$\begin{aligned} P_{\nu _e^L\rightarrow \nu _\mu ^L}(t)&=\text{ tr }\left\{ {{\hat{\varrho }}}(t)\left| \nu _\mu ^L \right\rangle \left\langle \nu _\mu ^L \right| \right\} =\rho _{d44}(t), \end{aligned}$$
(70)
$$\begin{aligned} P_{\nu _e^L\rightarrow \nu _e^R}(t)&=\text{ tr }\left\{ {{\hat{\varrho }}}(t)\left| \nu _e^R \right\rangle \left\langle \nu _e^R \right| \right\} =\rho _{d11}(t), \end{aligned}$$
(71)
$$\begin{aligned} P_{\nu _e^L\rightarrow \nu _\mu ^R}(t)&=\text{ tr }\left\{ {{\hat{\varrho }}}(t)\left| \nu _\mu ^R \right\rangle \left\langle \nu _\mu ^R \right| \right\} =\rho _{d33}(t), \end{aligned}$$
(72)

where \(\rho _{dnn}\) are diagonal elements of the neutrino density matrix \({{\hat{\varrho }}}(t)\) in the flavor basis (3). The initial density matrix \({{\hat{\varrho }}}(0)\) contains only the left-handed electron neutrino, meaning that \({{\hat{\varrho }}}(0)=\rho _{d22}(0)\vert \nu _{e}^{L}\rangle \langle \nu _{e}^{L}\vert \), with \(\rho _{d22}(0)=1\).

The neutrino transition probabilities (69)–(72) in an interstellar magnetic field are shown in Figs. 7 and 8 for the case of an ultra-high energy neutrino (\(E_\nu \sim 10\) ZeV) with a magnetic moment \(\mu _\nu \sim 10^{-12}\mu _B\). As we can see, the spin-up and spin-down states of both flavors “thermalize”, leading to an unpolarized steady state. On the other hand, we see a clear dominance of the electron neutrino in the final steady state: \(\rho _{d11}(t)+\rho _{d22}(t)>\rho _{d33}(t)+\rho _{d44}(t)\). This dominance reflects the memory of the system about the initial neutrino flavor. In the case of the initial muon neutrino state (not shown), i.e., \({{\hat{\varrho }}}(0)=\rho _{44}(0)\vert \nu _{\mu }^{L}\rangle \langle \nu _{\mu }^{L}\vert \), with \(\rho _{44}(0)=1\), we find the same memory effect of the initial neutrino flavor.

Fig. 7
figure 7

The time dependence of \(\rho _{d22}\) and \(\rho _{d11}\) when \(\beta =\pi /6\), \({\bar{\omega }}_B=10\) and \(\mu _\nu B /\omega _\nu =5\). In the initial moment of time \(\rho _{d22}(0)=1\) and all other elements of the density matrix \({{\hat{\varrho }}}(0)\) in the flavor representation are zero

Full size image
Fig. 8
figure 8

The same as in Fig. 7, but for \(\rho _{d44}\) and \(\rho _{d33}\)

Full size image

We now wish to quantify coherence of neutrino oscillations. For this purpose we employ two different proper measures of coherence [2]. Namely we use (i) the relative entropy as an entropic measure of coherence and (ii) the \(l_1\) norm of coherence [55, 56]:

$$\begin{aligned} {\mathcal {C}}\left( {\hat{\varrho }}(t)\vert {\hat{\varrho }}_d(t)\right)= & {} \text{ tr }\left\{ {\hat{\varrho }}(t) \ln {\hat{\varrho }}(t)-{\hat{\varrho }}(t)\ln {\hat{\varrho }}_d(t)\right\} ,\nonumber \\ C_{l_1}({{\hat{\varrho }}})= & {} \sum \limits _{i\ne j}\vert {{\hat{\varrho }}}_{ij}\vert . \end{aligned}$$
(73)

Here \({\hat{\varrho }}_d(t)\) is the diagonal part of \({\hat{\varrho }}(t)\) in the flavor basis (3), i.e., \({\hat{\varrho }}_d=\mathop {\mathrm{diag}}(\rho _{d11},\rho _{d22},\rho _{d33},\rho _{d44})\). Further, we use mixedness [57, 58]

$$\begin{aligned} M({\hat{\varrho }}(t))=\frac{d}{d-1}\left( 1-\text{ tr }{\hat{\varrho }}^2\right) , \end{aligned}$$
(74)

where in our case \(d=4\), and study the tradeoff relation between the \(l_1\) norm of coherence and mixedness [58]:

$$\begin{aligned} \frac{C^2_{l_1}({{\hat{\varrho }}})}{(d-1)^{2}}+M({\hat{\varrho }}(t))\leqslant 1. \end{aligned}$$
(75)

For computing the coherence, mixedness and tradeoff relation, we exploit the spectral expansion \({\hat{\varrho }}(t)=\sum \limits _n\rho _{nn}\vert n\rangle \langle n\vert \), where \(\vert n\rangle \) and \(\rho _{nn}\) are eigenvectors and eigenvalues of the time-evolved density matrix and

$$ \ln {\hat{\varrho }}(t)=\sum \limits _n\ln (\rho _{nn})\vert n\rangle \langle n\vert . $$

Figure 9 shows the time evolution of the eigenvalues of the density matrix sorted in decreasing order of magnitude. As can be seen, in its eigenbasis, the density matrix has the form of an effective two-level system.

Fig. 9
figure 9

The time dependence of eigenvalues \(\rho _{nn}\) of the density matrix \({{\hat{\varrho }}}\) when \(\beta = \pi /6\), \({\bar{\omega }}_B=\mu _\nu B/w^2=10\) and \(\mu _\nu B/\omega _\nu =5\)

Full size image
Fig. 10
figure 10

The time dependence of coherence, mixedness and their tradeoff when \(\beta = \pi /6\), \({\bar{\omega }}_B=\mu _\nu B/w^2=10\) and \(\mu _\nu B/\omega _\nu =5\)

Full size image

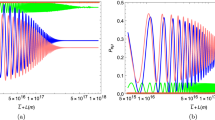
The numerical results for the coherence (73), mixedness (74) and their trade off relation (75) are shown in Fig. 10. The coherence, quantified in terms of the relative entropy, exhibits an interesting behavior with time. Starting from a zero initial value it reaches a maximal value and, after decaying, it goes into a persistent steady-state oscillation regime. We see that the tradeoff relation holds and that the \(l_1\) norm of coherence also exhibits steady-state oscillations.

Thus, we found that after dissipative evolution, the initial spin-polarized state entirely “thermalizes”, and in the final steady state, the spin-up/down states have the same populations. On the other hand, the flavor states also “thermalize”. However, the populations of two flavor states do not equate to each other. The initial flavor still dominates in the steady state, and coherence expressed in terms of an entropy measure exhibits persistent oscillations from zero to some constant value which is less than unity.

5 Conclusions

Traditionally optical photons and electromagnetic interaction were the primary sources for astronomers to study the distant universe. However, after technological progress achieved during the last few decades, using messengers of other fundamental interactions in the multimessenger astronomy became experimentally feasible [59]. Exploiting neutrino beams for these purposes is one of the most promising developments. Owing to the weak interaction with matter, neutrino beams have the advantage to penetrate the areas where electromagnetic waves are damped. Their propagation is characterized by the flavor, spin, and spin-flavor oscillations, which are essentially due to the superposition of neutrino states with different masses and helicities. Therefore the phenomenon of quantum coherence plays an essential role in the multimessenger astronomy. When the cosmic neutrino beam traverses dissipative interstellar space, the superposition of the different flavor and spin states converts to the mixed state described by the neutrino density matrix. In the present work, we studied the coupling of the neutrino spin with a random interstellar magnetic field and developed a framework for treating and quantifying the dissipation and coherence effects in neutrino propagation and oscillations. The stochastic field “thermalizes” the spin state and, due to the spin-flavor channel, impacts the flavor states as well. We observed that the system never “thermalizes” to the absolutely mixed state. Tradeoff theorem holds, and coherence is preserved in the final steady state. We expect that our results might be useful in the multimessenger astrophysics, in particular, in the case of ultrahigh energy neutrinos as messengers. Finally, we note that persistent spin-flavor coherence may be important for neutrino quantum information protocols, for example, such as neutrino-based interstellar communication [60], in the foreseeable future.